ЛЕКЦИЯ №4
Общие положения
остойчивости. Остойчивость при малых
наклонениях. Метацентр, метацентрический
радиус, метацентрическая высота.
Метацентрические формулы остойчивости.
Определение параметров посадки и
остойчивости при перемещении грузов
на судне. Влияние на остойчивость
незакрепленных и жидких грузов.
Опыт кренования.
Остойчивостью
называется способность судна, выведенного
из положения нормального равновесия
какими-либо внешними силами, возвращаться
в свое первоначальное положение после
прекращения действия этих сил. К внешним
силам, способным вывести судно из
положения нормального равновесия,
относятся: ветер, волны, перемещение
грузов и людей, а также центробежные
силы и моменты, возникающие при поворотах
судна. Судоводитель обязан знать
особенности своего судна и правильно
оценивать факторы, влияющие на его
остойчивость.
Различают поперечную
и продольную остойчивость. Поперечная
остойчивость судна характеризуется
взаимным расположением центра тяжести
G
и центра величины С.
Рассмотрим поперечную остойчивость.
Если судно накренить
на один борт на малый угол (5—10°) (рис.1),
ЦВ переместится из точки С в точку
![]() .
.
Соответственно сила поддержания,
действующая перпендикулярно к поверхности,
пересечет диаметральную плоскость (ДП)
в точке М.
Точка пересечения
ДП судна с продолжением направления
силы поддержания при крене называется
начальным
метацентром М.
Расстояние от точки приложения силы
поддержания С
до начального метацентра называется
метацентрическим
радиусом.
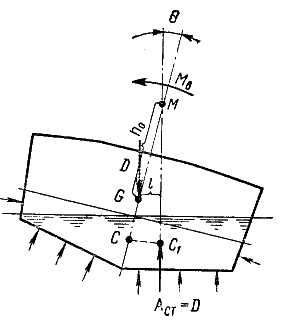
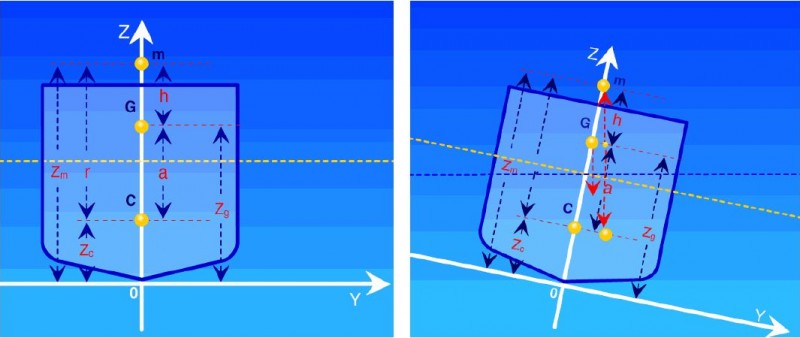
Рис.1
– Статические
силы, действующие на судно при малых
накренениях
Расстояние от
начального метацентра М
до центра тяжести G
называется начальной
метацентрической высотой
![]() .
.
Начальная
метацентрическая высота характеризует
остойчивость при малых наклонениях
судна, измеряется в метрах и является
критерием начальной остойчивости судна.
Как правило, начальная метацентрическая
высота мотолодок и катеров считается
хорошей, если она больше 0,5 м,
для некоторых
судов она допустима меньше, но не менее
0,35 м.
Рекомендуется
практически начальную метацентрическую
высоту (для килеватых судов) определять
следующим приближенным способом.
Резким наклонением
вызывается поперечная качка судна и
секундомером замеряется период свободной
качки, т. е время полного размаха от
одного крайнего положения до другого
и обратно. Поперечную метацентрическую
высоту судна определяют по формуле:
![]() ,
,
м
где В
— ширина
судна, м; Т
— период
качки, сек.
Для оценки полученных
результатов служит кривая на рис. 2,
построенная по данным у дачно
дачно
спроектированных катеров.
Ри.2
– Зависимость
начальной метацентрической высоты от
длины судна
Если начальная
метацентрическая высота
![]() ,
,
определенная по вышеприведенной формуле,
окажется ниже заштрихованной полосы,
то означает, что судно будет иметь
плавную качку, но недостаточную начальную
остойчивость, и плавание на нем может
быть опасным. Если метацентр расположен
выше заштрихованной полосы, судно будет
отличаться стремительной (резкой)
качкой, но повышенной остойчивостью, и
следовательно, такое судно более
мореходно, но обитаемость на нем
неудовлетворительна. Оптимальными
будут значения, попадающие в зону
заштрихованной полосы.
Крен судна на один
из бортов измеряется углом
![]()
между новым наклоненным положением
диаметральной плоскости с вертикальной
линией.
Накрененный борт
будет вытеснять воды больше, чем
противоположный, и ЦВ сместится в сторону
крена. Тогда равнодействующие силы
поддержания и веса будут неуравновешенными,
образующими пару сил с плечом, равным
![]() .
.
Повторное действие
сил веса и поддержания измеряется
восстанавливающим моментом:
![]() .
.
где D
— сила плавучести, равная силе веса
судна; l
— плечо остойчивости.
Эта формула
называется метацентрической формулой
остойчивости и справедлива только для
малых углов крена, при которых метацентр
можно считать постоянным. При больших
углах крена метацентр не является
постоянным, вследствие чего нарушается
линейная зависимость между восстанавливающим
моментом и углами крена.
Малый
(![]() )
)
и большой (![]() )
)
метацентрические радиусы можно вычислить
по формулам профессора А.П.Фан-дер-Флита:
![]() ;
;
![]() .
.
Взаимным расположением
груза на судне судоводитель всегда
может найти наиболее выгодное значение
метацентрической высоты, при которой
судно будет достаточно остойчивым и
меньше подвергаться качке.
Кренящим моментом
называется произведение веса груза,
перемещаемого поперек судна, на плечо,
равное расстоянию перемещения. Если
человек весом 75 кг,
сидящий на
банке, переместится поперек судна на
0,5 м, то
кренящий момент будет равен 75*0,5 = 37,5
кг/м.
Для изменения
момента, накреняющего судно па 10°, надо
загрузить судно до полного водоизмещения
совершенно симметрично относительно
диаметральной плоскости. Загрузку судна
следует проверить по осадкам, измеряемым
с обоих бортов. Креномер устанавливается
строго перпендикулярно ДП таким образом,
чтобы он показал 0°.
После этого надо
перемещать грузы (например, людей) на
заранее размеченные расстояния до тех
пор, пока креномер не покажет 10°. Опыт
для проверки следует произвести так:
накренить судно на один, а затем на
другой борт. Зная крепящие моменты
накреняющего судно на различные (до
наибольшего возможного) углы, можно
построить диаграмму статической
остойчивости (рис. 3), что позволит оценить
остойчивость судна.
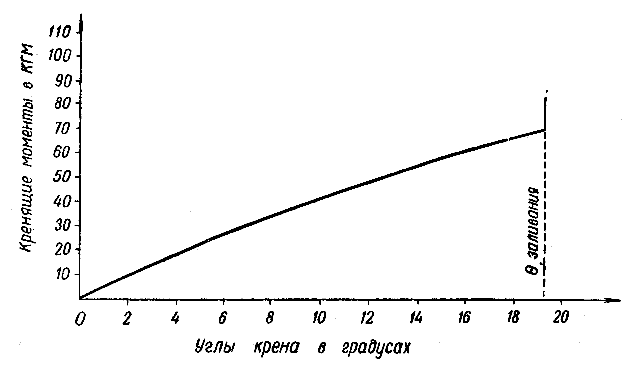
Рис.3 – Диаграмма
статической остойчивости
Остойчивость можно
увеличивать за счет увеличения ширины
судна, понижения ЦТ, устройства кормовых
булей.
Если ЦТ судна
расположен ниже ЦВ, то судно считается
весьма остойчивым, так как сила поддержания
при крене не изменяется по величине и
направлению, но точка ее приложения
смещается в сторону наклона судна (рис.
4, а). Поэтому при крене образуется пара
сил с положительным восстанавливающим
моментом, стремящимся вернуть судно в
нормальное вертикальное положение па
прямой киль. Легко убедиться, что h>0,
при этом метацентрическая высота равна
0. Это типично для яхт с тяжелым килем и
нетипично для более крупных судов с
обычным устройством корпуса.
Если ЦТ расположен
выше ЦВ, то возможны три случая
остойчивости, которые судоводитель
должен хорошо знать.
1-й случай
остойчивости
Метацентрическая
высота h>0.
Если центр тяжести расположен выше
центра величины, то при наклонном
положении судна линия действия силы
поддержания пересекает диаметральную
плоскость выше центра тяжести (рис. 4,
б).
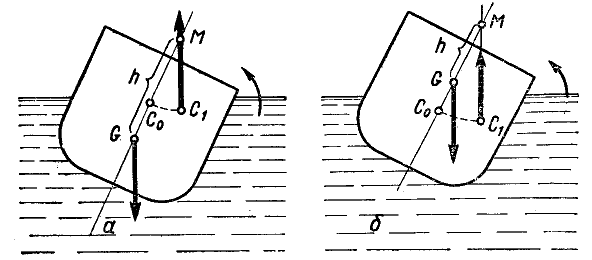
Рис.4 – Случай
остойчивого судна
В этом случае также
образуется пара сил с положительным
восстанавливающим моментом. Это типично
для большинства судов обычной формы.
Остойчивость в этом случае зависит от
корпуса и положения центра тяжести по
высоте. При крене кренящийся борт входит
в воду и создает дополнительную
плавучесть, стремящуюся выровнять
судно. Однако при крене судна с жидкими
и сыпучими грузами, способными перемещаться
в сторону крена, центр тяжести также
сместится в сторону крена. Если центр
тяжести при крене переместится за
отвесную линию, соединяющую центр
величины с метацентром, то судно
опрокинется.
2-ой случай
неостойчивого судка при безразличном
равновесии
Метацентрическая
высота h
= 0. Если ЦТ лежит выше ЦВ, то при крене
линия действия силы поддержания проходит
через ЦТ MG=0 (рис. 5).
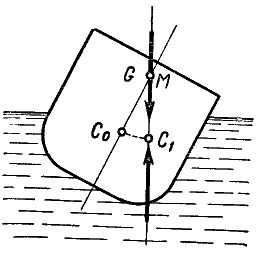
Рис.5 – Случай
неостойчивого судна при безразличном
равновесии
В данном случае
ЦВ всегда располагается на одной
вертикали с ЦТ, поэтому восстанавливающаяся
пара сил отсутствует. Без воздействия
внешних сил судно не может вернуться в
прямое положение. В данном случае особо
опасно и совершенно недопустимо
перевозить на судне жидкие и сыпучие
грузы: при самой незначительной качке
судно перевернется. Это свойственно
шлюпкам с круглым шпангоутом.
3-й случай
неостойчивого судна при неустойчивом
равновесии
Метацентрическая
высота h<0.
ЦТ расположен выше ЦВ, а в наклонном
положении судна линия действия силы
поддержания пересекает след диаметральной
плоскости ниже ЦТ (рис. 6). Сила тяжести
и сила поддержания при малейшем крене
образуют пару сил с отрицательным
восстанавливающим моментом и судно
опрокидывается.
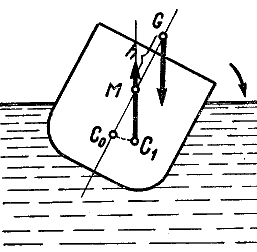
Рис.6
– Случай
неостойчивого судна при неустойчивом
равновесии
Разобранные случаи
показывают, что судно остойчиво, если
метацентр расположен выше ЦТ судна. Чем
ниже опускается ЦТ, тем судно более
остойчиво. Практически это достигается
расположением грузов не на палубе, а в
нижних помещениях и трюмах.
Вследствие
воздействия на судно внешних сил, а
также в результате недостаточно прочного
закрепления груза, возможно его
перемещение на судне. Рассмотрим влияние
данного фактора на изменение параметров
посадки судна и его остойчивость.
Вертикальное
перемещение груза.
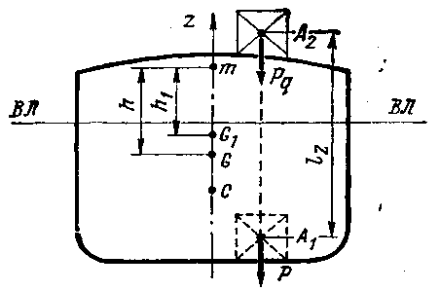
Рис.1 – Влияние
вертикального перемещения груза на
изменение метацентрической высоты
Определим изменение
посадки и остойчивости судна, вызванное
перемещением малого груза
![]()
в вертикальном направлении (рис.1) из
точки
![]()
в точку![]() .
.
Поскольку масса груза не меняется, то
и водоизмещение судна остается неизменным.
Следовательно, соблюдается первое
условие равновесия:
![]() .
.
Из теоретической механики известно,
что при перемещении одного из тел ЦТ
всей системы перемещается в том же
направлении. Следовательно, ЦТ судна
![]()
переместится в точку
![]() ,
,
а сама вертикаль пройдет, как и прежде,
через центр величины
![]() .
.
Будет соблюдено
второе условие равновесия:
![]() .
.
Так как в нашем
случае оба условия равновесия соблюдены,
то можно сделать вывод: при
вертикальном перемещении груза судно
не изменяет своего положения равновесия.
Рассмотрим изменение
начальной поперечной остойчивости. Так
как формы погруженного в воду объема
корпуса судна и площади ватерлинии не
изменились, то положение центра величины
![]()
и поперечного метацентра при перемещении
груза по вертикали остается неизменным.
Перемещается только ЦТ судна, что
повлечет уменьшение метацентрической
высоты
![]() ,
,
а также
![]() ,
,
откуда
![]() ,
,
где
![]()
– вес перемещаемого груза, кН;
![]()
– расстояние, на которое переместился
ЦТ груза в вертикальном направлении,
м.
Таким образом,
новое значение
![]() ,
,
где знак (+) применяется при перемещении
груза вверх, а знак (-) вниз.
Из формулы видно,
что вертикальное перемещение груза
вверх вызывает уменьшение поперечной
остойчивости судна, а при перемещении
вниз поперечная остойчивость увеличивается.
Изменение
остойчивости равно произведению
![]() .
.
Изменение поперечной остойчивости
будет относительно меньше у судна с
большим водоизмещением, чем у судна с
малым, поэтому на судах с большим
водоизмещением перемещение грузов
безопаснее, чем на малых судах.
Поперечное
горизонтальное перемещение груза.
Перемещение груза
![]()
из точки
![]()
в точку
![]()
(рис.2) на расстояние
![]()
вызовет крен судна на угол
![]()
и смещение его ЦТ в направлении,
параллельном линии перемещения груза.

Рис.2 – Возникновение
кренящего момента при поперечном
перемещении груза
Накренившись на
угол
![]() ,
,
судно приходит в новое положение
равновесия, сила тяжести судна
![]() ,
,
приложенная теперь в точке
![]()
и сила поддержания
![]() ,
,
приложенная в точке
![]() ,
,
действуют по одной вертикали,
перпендикулярной новой ватерлинии
![]() .
.
Перемещение груза
приводит к образованию кренящего
момента:
![]() ,
,
где
![]()
– плечо перемещения груза, м.
Восстанавливающий
момент по метацентрической формуле
остойчивости
![]() .
.
Так как судно
находится в равновесии, то
![]()
и
![]() ,
,
откуда угол крена при поперечном
перемещении груза
![]() .
.
Так как угол крена мал, то
![]() .
.
Если судно уже
имеет начальный угол крена, то после
горизонтального перемещения груза угол
крена будет
![]() .
.
12
Соседние файлы в папке Cудовое конструирование
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Intact Stability Regulations II
Adrian Biran, Rubén López-Pulido, in Ship Hydrostatics and Stability (Second Edition), 2014
10.3 Summary
In the preceding chapter we have shown that longitudinal and quartering waves affect stability by changing the instantaneous moment of inertia that enters into the calculation of the metacentric radius. This effect is taken into account in the stability regulations of the German Navy and it has been proposed to consider it also for merchant ships (Helas, 1982). As shown in Chapter 9, German researchers were the first to investigate parametric resonance in ship stability. They also took into consideration this effect when they elaborated stability regulations for the German Navy. These regulations require that the righting arm be calculated both in still water and in waves. The latter righting arm is the mean of the cross-curves in wave trough and on wave crest.
In the German regulations, the criterion of stability under wind regard the difference between the righting arm and the wind heeling arm. This difference, hRES=GZ¯-kw, is called residual arm. If the angle of static equilibrium is ϕST, stability shall be checked at a reference angle, ϕREF, defined by
ϕREF=35°ifϕST≤15°5°+2·ϕSTotherwise
At this reference angle, the residual arm shall be not smaller than the value given by
hRES=0.1ifϕST≤15°0.01·ϕST-0.05otherwise
Finally, let us return to the influence of ship forms. Traditionally ship forms have been chosen as a compromise between contradictory requirements of reduced hydrodynamic resistance, good seakeeping qualities, convenient space arrangements, and stability in still water. The study of the Mathieu effect has added another criterion: small variation of righting arms in waves. A formulation of this subject can be found in Burcher (1979). Pérez and Sanguinetti (1994) experimented with models of two small fishing vessels of similar size but different forms. They show that the model with round stern and round bilge displayed less metacentric height variation in wave than the model with transom stern. The influence of new ship forms, such as used in container, RoRo, and RoPax ships was discussed in the preceding chapter.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780080982878000104
Geometric Properties of Areas and Volumes
Adrian Biran, in Geometry for Naval Architects, 2019
3.5.9 Examples in Naval Architecture
The second moments of the waterplane are used in the calculation of metacentric heights (see Biran and López-Pulido, 2014, Chapter 2). The transverse metacentric radius is given by
(3.63)BM‾=Ixx∇
where ∇ is the volume of the submerged hull. The longitudinal metacentric radius is
(3.64)BML‾=IL∇
where IL is the moment of inertia of the waterplane with respect to the principal axis that passes through the centre of floatation, F, and is parallel to the axis y. For an axis of inclination Fxα that makes an angle α with the axis x the initial metacentric radius is
Ixα=Ixxcos2α−Ixysin2α+ILsin2α∇
As Ixx and IL are principal moments, Ixy is zero and we remain with
(3.65)BMα‾=BM‾Tcos2α+BM‾Lsin2α
Another application that requires the calculation of moments of inertia of areas is in the calculation of the sectional modulus; it is discussed in Example 3.12.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780081003282000122
Basic Ship Hydrostatics
Adrian Biran, Rubén López-Pulido, in Ship Hydrostatics and Stability (Second Edition), 2014
2.11 Metacentres for Various Axes of Inclination
In Eq. (2.32) the moment of inertia, I, is calculated about the axis of inclination. This axis passes through the centroid, F, of the waterplane and so does any other axis of inclination. It can be shown that there is a pair of orthogonal axes such that the moment of inertia about one of them is minimum and about the other maximum. Then, the metacentric radius corresponding to the former axis is minimum, and the moment about the latter axis is maximum (see, for example, Hahn, 1992; Meriam and Kraige, 2008; or Rumpl and Sondershausen, 1994). Correspondingly, one of the metacentric radii is minimum and the other maximum. In some European countries the smallest radius is denoted by r and is called small metacentric radius, while the largest radius is denoted by R and is called large metacentric radius.
The fact that the minimum and the maximum metacentric radii are measured in planes that are perpendicular one to the other is a consequence of an important theorem in the differential geometry of curves and surfaces. This theorem, due to Euler, is mentioned in some detail in Chapter 13. The theory of principal curvatures it treated, for example, in Struik, 1961, Sections 2–6; Davies and Samuels, 1996, Section 4.3; Banchoff and Lovett, 2010, Section 6.4; or Marsh, 2000, Theorem 10.10. In fact, the minimum and the maximum metacentric radii are the inverses of the principal curvatures, that is they are the principal radii of curvature of the surface of the centre of buoyancy.
In the theory of moments of inertia the two axes for which we obtain the extreme values of moments of inertia are called principal axes and the corresponding moments, principal moments of inertia. When the waterplane area has an axis of symmetry, this axis is one of the principal axes; the other one is perpendicular to the first. The waterplane area of ships in upright condition has an axis of symmetry: the intersection of the waterplane and the centreline plane. The moment of inertia about this axis is the smallest one; it is used to calculate the transverse metacentric radius. The moment of inertia about the axis perpendicular in F to the centreline is the largest; it enters in the calculation of the longitudinal metacentric radius.
To give an idea of the relative orders of magnitude of the transverse and longitudinal metacentric radii, let us consider a parallelepipedic barge whose length is L, breadth, B, and draught, T. The volume of displacement equals ∇=LBT. The transverse metacentric radius results from
BM¯=LB3/12LBT=B212T
The longitudinal metacentric radius is given by
BML¯=BL3/12LBT=L212T
The ratio of the two metacentric radii is
BML¯BM¯=LB2
The length-breadth ratio ranges from 3.1, for some motor boats, to 10.5, for fast cruisers. Correspondingly, the ratio of the longitudinal to the transverse metacentric radius varies roughly between 10 and 110. As a rule of thumb, the longitudinal metacentric radius is of the same order of magnitude as the ship length.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780080982878000025
Curvature
Adrian Biran, in Geometry for Naval Architects, 2019
5.7 Differential Metacentric Radius
In Fig. 4.9 the waterlines for various heel angles are tangent to the curve C. As we are going to learn in Section 5.11, the curve C is the envelope of the waterlines. The radius of curvature of C is given by
ρC=dId∇
and is called differential metacentric radius. Here, the moment of inertia of the waterplane with respect to the axis of inclination, I, and the volume of displacement, ∇, are considered functions of the draught, T. We remind this notion only as an example of radius of curvature in Naval Architecture. The reader interested in proofs of the formula can find them in Semyonov-Tyan-Shansky (2004), pp. 99–102, or Hervieu (1985), pp. 120–124. As the centre of floatation, F, lies on the cylinder with trace C, the curve is often noted by F.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780081003282000158
Stability in Waves
Adrian Biran, Rubén López-Pulido, in Ship Hydrostatics and Stability (Second Edition), 2014
9.2 The Influence of Waves on Ship Stability
In this section we explain why the metacentric height varies when a wave travels along the ship. We illustrate the discussion with data calculated for a 29 m fast patrol boat (further denoted as FPB) whose offsets are described by Talib and Poddar (1980). For hulls like the one chosen here the influence of waves is particularly visible. Figure 9.1 shows an outline of the boat and the location of three stations numbered 36, 9, and 18. This is the original numbering in the cited reference. The shapes of those sections are shown in Figure 9.2. We calculated the hydrostatic data of the vessel for the draught 2.5 m, by means of the same ARCHIMEDES programme that Talib and Podder used. The waterline corresponding to the above draught appears as a solid line in Figures 9.1 and 9.2. Let us see what happens in waves. Calculations and experiments show that the maximum influence of longitudinal waves on ship stability occurs when the wavelength is approximately equal to that of the ship waterline. Consequently, we choose a wavelength

Figure 9.1. Wave profiles on a fast patrol boat outline—S = still water, T = wave trough, C = wave crest

Figure 9.2. Wave profiles on FPB transverse sections—S = still water, T = wave trough, C = wave crest
λ=Lpp=27.3m
The wave height prescribed by the German Navy is
H=λ10+0.05λ=27.310+0.05×27.3=2.402m
The dot-dot lines in Figures 9.1 and 9.2 represent the waterline corresponding to the situation in which the wave crest is in the midship section plane. We say that the ship is on wave crest. In Figure 9.2 we see that in the midship section the waterline lies above the still-water line. The breadth of the waterline almost does not change in that section. In sections 36 and 18 the waterline descends below the still-water position. In section 18 the breadth decreases. This effect occurs in a large part of the forebody. In the calculation of the metacentric radius, BM¯, breadths enter at the third power (at constant displacement!). Therefore, the overall result is a decrease of the metacentric radius.
The dash-dash lines in Figures 9.1 and 9.2 represent the situation in which the position of the wave relative to the ship changed by half a wavelength. The trough of the wave reached now the midship section and we say that the ship is in a wave trough. In Figure 9.2 we see that the breadth of the waterline increased significantly in the plane of station 18, decreased insignificantly in the midship section, and increased slightly in the plane of station 36. The overall effect is an increase of the metacentric radius.
A quantitative illustration of the effect of waves on stability appears in Figure 9.3. For some time the common belief was that the minimum metacentric radius occurs when the ship is on a wave crest. It appeared, however, that for forms like those of the FPB the minimum occurs when the wave crest is approximately 0.3Lpp astern of the midship section. Calculations carried by us for various ship forms showed that the relationships can change. Figure 9.3 shows, indeed, that for draughts under 1.6 m KM¯ is larger on wave crest than in wave trough. Similar conclusions can be reached for the righting-arm curves in waves. For example, the righting arm in wave trough can be the largest in a certain heeling-angle range, and ceases to be so outside that range. The reader is invited to use the data in Exercise 9.1 and check the effect of waves on the righting arm of another vessel, named Ship No. 83074 by Poulsen (1980).

Figure 9.3. The influence of waves on KM
More explanations of the effect of waves on righting arms can be found in Wendel (1958), Arndt (1962), and Abicht (1971). Detailed stability calculations in waves, for a training ship, are described by Arndt et al. (1960), and results for a cargo vessel with CB=0.63, are presented by Arndt (1964). A few results of calculations and model tests for RoRo ships can be found in Sjöholm and Kjellberg (1985).
To develop a simple model of the influence of waves we assume that the wave is a periodic function of time with period T. Then, also GM¯ is a periodic function with period T. We write
GM(t)¯=GM0¯+δGM(t)¯
where
δGM(t)¯=δGM(t+T)¯
for any t. In Section 6.7 we developed a simple model of the free rolling motion. To include the variation of the metacentric height in waves we can rewrite the roll equation as
ϕ¨+gi2(GM0¯+δGM¯)ϕ=0
Going one step further we assume that the wave is harmonic (regular wave) and the GM¯ variation also harmonic, so that the free rolling motion can be modelled by
(9.1)ϕ¨+gi2(GM0¯+δGM¯cosωet)ϕ=0
This is a Mathieu equation; those of its properties that interest us are described in Section 9.4.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780080982878000098
Flooding and Damage Condition
Adrian Biran, Rubén López-Pulido, in Ship Hydrostatics and Stability (Second Edition), 2014
11.3 Two Methods for Finding the Ship Condition After Flooding
There are two ways of calculating the effect of flooding. One way is known as the method of lost buoyancy, the other as the method of added weight.
The method of lost buoyancy assumes that a flooded compartment does not supply buoyancy. This is what happens in reality. If we refer to Figures 2.4 and 2.5Figure 2.4Figure 2.5, we can imagine that if there is open communication between a compartment and the surrounding water, the water inside the compartment exercises pressures equal to and opposed to those of the external water. Then, the buoyancy force predicted by the Archimedes’ principle is cancelled by the pressure of the flooding water.
In the method of lost buoyancy the volume of the flooded compartment does not belong anymore to the vessel, while the weight of its structures is still part of the displacement. The ‘remaining’ vessel must change position until force and moment equilibria are reestablished. During the process not only the displacement, but also the position of the centre of gravity remains constant. The method is also known as method of constant displacement. As the flooding water does not belong to the ship, it causes no free-surface effect.
In the method of added weight the water entering a damaged compartment is considered as belonging to the ship; its mass must be added to the ship displacement. Hence the term ‘added weight.’ Following modern practice we actually work with masses; however, we keep the traditional name of the method, that is we use the word ‘weight.’ Another reason may be the need to avoid confusion with the term added mass mentioned in Section 6.13 and detailed in Chapter 12. The latter term does not belong to the theory of flooding and damage stability.
In the method of added weight the displacement of the flooded vessel is calculated as the sum of the intact displacement and the mass of the flooding water. The position of the centre of gravity of the damaged vessel is obtained from the sums of the moments of the intact vessel and of the flooding water. Becoming part of the vessel, the flooding water produces a free-surface effect that must be calculated and considered in all equations.
For very small trim and negligible heel changes we can write
(11.2)ΔF=ΔI+ρvLCGF·ΔF=LCGI·ΔI+lcg·ρ·vTCGF·ΔF=tcg·ρ·v
where the subscript F distinguishes the properties of the flooded vessel, and the subscript I those of the intact ship. By lcg we mean the longitudinal centre of gravity of the flooding water volume, v, and by tcg its transverse centre of gravity. We assume TCGI=0. The vertical centre of gravity, KG¯, must be recalculated. When the trim and the heel are not negligible, we must consider the vertical coordinates of the centres of gravity of the intact ship and of the flooding water volume. Example 11.1 shows how to do this for non-zero trim and zero heel.
To exemplify the above principles we follow an idea presented in Handbuch der Werften and later used by Watson (1998). While the latter solves algebraically the general problem, we prefer to solve it numerically and allow thus the reader to visualize the differences between methods and those between the intact and the damaged vessel. We choose the very simple example of the pontoon shown in Figure 11.2. Two transverse bulkheads subdivide the hull into three watertight compartments. In the following two subsections we assume that Compartment 2 is damaged and calculate the consequences of its flooding. We choose deliberately a compartment symmetric about the midship transverse plane of symmetry of the pontoon. Thus, the flooding of Compartment 2 produces no trim. Also, the compartment extends for the full ship breadth and its flooding produces no heel. The only change of position is parallel sinking. Thus, the complex calculations necessary for conventional ship forms, for large trim, or for unsymmetrical flooding, do not obscure the principles and it is possible to obtain immediately a good insight of the processes involved. For the same reasons we assume that the volume and surface permeabilities are equal to 1. We leave to an exercise the informal proof that taking permeability into account does not change the qualitative results. Although based on different physical models, calculations by the two methods yield the same final draught, as it should be expected. Moreover, the stability properties calculated by the two methods are identical, if we compare the initial righting moments. Here, the term “initial” has the meaning defined in Chapter 2 where we consider ‘initial stability’ as a property governing the behaviour of the floating body in a small heel range around the upright position. In that range the righting moment equals

Figure 11.2. A simple pontoon—intact condition
MR=ΔGM¯sinϕ
As we are going to see, we obtain by the two methods the same MR value. In the method of lost buoyancy the displacement remains equal to that of the intact vessel. In the method of added weight the displacement increases by the mass of the flooding water. To keep the product MR constant, the other factor, GM¯, must be smaller. At a first glance it may be surprising that the two methods yield different metacentric heights. The explanation given above shows that it should be so because the considered displacements are different. What should be kept in mind, after reading the examples, is that displacement and metacentric height have different significances in the two methods. Therefore, damage stability data should include the mention of the method by which they were obtained. Computer programmes use the method of lost buoyancy for final-stage calculations.
The length of the assumed pontoon is L=20m, the beam, B=5m, and the draught in intact condition, TI=1.5m. Let the vertical centre of gravity be KGI¯=1.5m. The following calculations were carried on in MATLAB, using the full precision of the software. The results are rounded off to a reasonable number of decimal digits. We first find the data of the intact pontoon. The displacement volume is
∇I=LBTI=20×5×1.5=150m3
The mass displacement equals
ΔI=ρ∇I=1.025×150=153.75t
The moment of inertia of the waterplane area about the centreline equals
II=B3L12=53×2012=208.3333m4
and the resulting metacentric radius is
BM¯I=II∇I=208.3333150=1.389m
For such a simple form we could have found directly the metacentric radius as
BM¯I=B3L/12LBTI=B212TI=5212×1.5=1.389m
The height of the centre of buoyancy is
KB¯I=TI2=0.75m
and the metacentric height
GM¯I=KB¯I+BM¯I-KG¯I=0.75+1.389-1.50=0.639m
For small heel angles the righting moment in intact condition is calculated as
MRI=ΔIGM¯Isinϕ=153.75×0.639×sinϕ=98.229sinϕtm
11.3.1 Lost Buoyancy
Four translations of the term ‘method of lost buoyancy’ are
| Fr | La méthode des carènes perdues |
| G | Methode des wegfallender Verdrängung |
| I | Il metodo per perdita di galleggiabilità |
| S | Método de la pérdida de empuje |
In the method of lost buoyancy the flooded compartment does not supply buoyancy. As shown in Figure 11.3, the buoyant hull is composed only of Compartments 1 and 3. After loosing the central compartment, the waterplane area is equal to

Figure 11.3. A simple pontoon—damage calculation by the method of lost buoyancy
AL=(L-l)B=(20-4)×5=80m2
To compensate for the loss of buoyancy of the central compartment the draught increases to
TL=∇IAL=15080=1.875m
The height of the centre of buoyancy increases to
KB¯L=TL2=1.8752=0.938m
We calculate the moment of inertia of the waterplane as
IL=B3(L-l)12=53(20-4)12=166.6667m4
and the metacentric radius as
BM¯L=IL∇I=166.6667150=1.111m
Finally, the metacentric height is
GM¯L=KB¯L+BM¯L-KG¯I=0.938+1.111-1.5=0.549m
and the righting moment for small heel angles, in the lost-buoyancy method
MRL=ΔIGM¯Lsinϕ=153.75×0.549sinϕ=84.349sinϕtm
11.3.2 Added Weight
The translations of the term “added-weight method” in four other languages are
| Fr | La méthode par addition de poids |
| G | Methode des hinzukommenden Gewichts |
| I | Il metodo del peso imbarcato |
| S | Método del peso añadido |
For this subsection see Figure 11.4. Because of the added weight of the flooding water the draught of the pontoon must increase by a quantity δT. The volume of flooding water equals

Figure 11.4. A simple pontoon—damage calculation by the method of added weight
(11.3)v=lB(TI+δT)
The additional buoyant volume of the vessel, due to parallel sinking, is
(11.4)δ∇=LBδT
To obtain the draught increment, δT, we equate the two volumes, that is we write v=δ∇. Algebraic manipulation and numerical calculation yield
δT=lTIL-l=4×1.520-4=0.375m
The draught after flooding is
TA=TI+δT=1.500+0.375=1.875m
The volume of flooding water is calculated as
v=lBTA=4×5×1.875=37.5m3
and the height of its centre of gravity
kb¯=TA2=1.8752=0.938m
The displacement volume of the flooded pontoon is
∇A=LBTA=20×5×1.875=187.5m3
We consider the flooding water as an added weight; therefore, we must calculate a new centre of gravity. The calculations are shown in Table 11.1.
Table 11.1. KG¯ by the method of added weight
| Volume | Centre of Gravity | Moment | |
|---|---|---|---|
| Initial | 150.0 | 1.5 | 225.000 |
| Added | 37.5 | 0.938 | 35.156 |
| Total | 187.5 | 1.388 | 260.156 |
The moment of inertia of the damage waterplane is the same as in the initial condition, that is IA=208.333m4. Then, the metacentric radius equals
BM¯A=IA∇A=208.333187.5=1.111m
In this method the flooding water is considered as belonging to the displacement. Therefore, if there is a free surface its effect must be calculated. The moment of inertia of the free surface in the flooded compartment equals
i=B3l12=53×412=41.667m4
and the lever arm of the free surface effect is
ℓF=ρiρ∇A=41.667187.5=0.222m
The height of the centre of buoyancy is yielded by
KB¯A=TA2=1.8752=0.938m
The corresponding metacentric height is calculated as
GMA¯=KB¯A+BM¯A-KG¯A-ℓF=0.938+1.111-1.388-0.222=0.439m
With the mass displacement
ΔA=ρ∇A=1.025×187.5=192.188t
we obtain the righting moment for small angles of heel, in the added-weight method
MRA=ΔAGM¯Asinϕ=192.188×0.439sinϕ=84.349sinϕtm
11.3.3 The Comparison
Table 11.2 summarizes the results of the preceding two subsections. As expected, both the method of lost buoyancy and that of added weight yield the same draught 1.875 m, and the same initial righting moment, 84.349sinϕtm. The displacements and the metacentric heights are different, but their products, ΔGM¯, are the same. As happens in most cases, the righting moment in damage condition is less than in intact condition.
Table 11.2. Flooding calculations—a comparison of methods
| Intact Condition | Damaged, Lost Buoyancy | Damaged, by Added Weight | |
|---|---|---|---|
| Draught, m | 1.500 | 1.875 | 1.875 |
| ∇,m3 | 150.000 | 150.000 | 187.500 |
| Δ,t | 153.750 | 153.750 | 192.188 |
| KB¯,m | 0.750 | 0.938 | 0.938 |
| BM¯,m | 1.389 | 1.111 | 1.111 |
| KG¯,m | 1.500 | 1.500 | 1.388 |
| GM¯,m | 0.639 | 0.549 | 0.439 |
| ΔGM¯,tm | 98.229 | 84.349 | 84.349 |
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780080982878000116
Effects of mooring configurations on the hydrodynamic performance of a floating offshore oscillating water column wave energy converter
Eric Gubesch, … Christopher Chin, in Renewable and Sustainable Energy Reviews, 2022
2.1.2 Dynamics of floating structures
For a given maritime structure to float freely in the static condition, the structure must displace a mass of water that is equivalent to the mass of the structure (Equation (11)). In the static case, the dominate forces that are acting on the structure include gravity and the restoring force from buoyancy.
(11)Δ=∇ρw
where Δ is the total mass of the structure; and ∇ is the volumetric displacement of the structure.
Satisfying Equation (11) will ensure a structure will float; however, it will not ensure the structure has sufficient hydrostatic stability. Hydrostatic stability (Equation (12) and (13)) is governed by the geometric locations of the vessels centre of gravity, centre of buoyancy, the arrangement of the vessels waterplane area, and the volumetric displacement of the structure. A floating vessel displays positive stability if it returns to a stable condition after an external force or moment has been removed from the structure. For this to occur, the longitudinal and transverse metacentric height (GML, GMT) must remain positive for the range of expected conditions. A GM greater than 5 m is usually desired in the static condition.
(12)GML/T=KB+BM−KG
(13)BM=ICL∇
Here, GM is the metacentric height, L/T is the longitudinal or transverse direction, KB is the distance from the keel to the centre of buoyancy, BM is the metacentric radius, KG is the distance from the keel to the centre of gravity, and ICL is the moment of inertia of the vessel’s total waterplane area about its centre line.
A floating structure will respond dynamically when external forces from environmental loading (i.e., waves, wind and current) unbalances static equilibrium. Forces generated from ocean waves include inertial (Froude-Krylov, diffraction and radiation) and drag (viscous and friction) forces [32]. A detailed discussion regarding the fluid-structure interactions, dynamic responses, and equations of motions for WECs can be found in Gullaksen [33], and Det Norske Veritas [34].
When ocean waves interact with a free-floating structure, the amplitude and distribution of the water surrounding the hull fluctuates which changes the structures volumetric displacement, however, the structural mass remains unchanged. This imbalance generates a dynamic response from the structure as it seeks to return to equilibrium. As such, the dynamic response of a free-floating structure when excited by ocean waves is dependent on the spatial distribution of the hulls wetted surface area.
The dynamics of structures that include an internal moonpool like drill ships, Spars, or OWC WECs are complicated due to coupling between the structure’s motions and the heaving motions of the water inside the moonpool. The water inside the moonpool may be heaving vertically (piston mode) at a different rate or phase to the heave motions of the structure, which may damp or excite the structure’s motions. The size and mass of the structure and geometry of the moonpool are important factors when considering the effects from moonpool coupling.
Moorings influence the dynamic behaviour of floating structures as they provide a restoring force that oppose the forces from environmental loading. The effects of the mooring system on the structure’s dynamic behaviour are dependent on the specific configuration. Spread mooring systems like a catenary utilise the weight of the chain to regulate the structure’s motions, specifically horizontal offset (i.e., surge). Whereas the dynamic response for structures with taut mooring systems is largely governed by the elasticity of the tendons. Additionally, the location of the fairleads can have a significant effect on the roll and pitch motions as a couple can be generated between the vertical location of the fairlead and the geometric centre of the environmental loading.
Floating structures respond in six degrees of freedom (DoF) including translational and rotational modes. Translational modes include surge, sway, and heave, which are denoted with subscripts (j) 1, 2 and 3. The rotational modes include roll, pitch, and yaw, and are denoted with subscripts (j) 4, 5 and 6. Fig. 4 defines the coordinate systems and respective DoF used in this paper.

Fig. 3. Moored floater with a single catenary mooring line adapted from Faltinsen [35].

Fig. 4. (Plan perspective and top-side dimensions of the WEC, (b) isometric view of the WEC and data acquisition componentry, (c) forward perspective and dimensions of the WEC, (d) side perspective and dimensions of the WEC.
A response amplitude operator (RAO) is a transfer function that equates the translation or rotation amplitude of an individual DoF to the amplitude of the incident wave for a given wave frequency. RAO’s for the WEC’s translations and rotations were calculated with Equation (14).
(14)RAOj=φja
where φj is the amplitude of the relevant DoF parameter of interest (i.e., surge, sway, heave, roll, pitch, or yaw); and a is the amplitude of the incident waves at the OWC.
Read full article
URL:
https://www.sciencedirect.com/science/article/pii/S1364032122005366

Кренящий (дифферентующий) и восстанавливающий моменты действуют в противоположных направлениях и при равновесном положении судна равны.
Различают поперечную остойчивость, соответствующую наклонению судна в поперечной плоскости (крен судна), и продольную остойчивость (дифферент судна).
Продольная остойчивость морских судов заведомо обеспечена и ее нарушение практически невозможно, в то время как размещение и перемещение грузов приводит к изменениям поперечной остойчивости.
При наклонении судна его центр величины (ЦВ) будет перемещаться по некоторой кривой, называемой траекторией ЦВ. При малом наклонении судна (не более 12°) допускают, что траектория ЦВ совпадает с плоской кривой, которую можно считать дугой радиуса r с центром в точке m.
Радиус r называют поперечным метацентрическим радиусом судна, а его центр m – начальным метацентром судна.
Метацентр – центр кривизны траектории, по которой перемещается центр величины С в процессе наклонения судна. Если наклонение происходит в поперечной плоскости (крен), метацентр называют поперечным, или малым, при наклонении в продольной плоскости (дифферент) – продольным, или большим.
Соответственно различают поперечный (малый) r и продольный (большой) R метацентрические радиусы, представляющие радиусы кривизны траектории С при крене и дифференте.
Расстояние между начальным метацентром т и центром тяжести судна G называют начальной метацентрической высотой (или просто метацентрической высотой) и обозначают буквой h. Начальная метацентрическая высота является измерителем остойчивости судна.
h = zc + r – zg; h = zm ~ zc; h = r – a,
где а – возвышение центра тяжести (ЦТ) над ЦВ.
Метацентрическая высота (м.в.) – расстояние между метацентром и центром тяжести судна. М.в. является мерой начальной остойчивости судна, определяющей восстанавливающие моменты при малых углах крена или дифферента.
При возрастании м.в. остойчивость судна повышается. Для положительной остойчивости суд- на необходимо, чтобы метацентр находился выше ЦТ судна. Если м.в. отрицательна, т.е. метацентр располагается ниже ЦТ судна, силы, действующие на судно, образуют не восстанавливающий, а кренящий момент, и судно плавает с начальным креном (отрицательная остойчивость), что не допускается.
Элементы начальной поперечной остойчивости:
OG – возвышение центра тяжести над килем; OM – возвышение метацентра над килем;
GM – метацентрическая высота; CM – метацентрический радиус;
m – метацентр; G – центр тяжести; С – центр величины
Возможны три случая расположения метацентра m относительно центра тяжести судна G:
метацентр m расположен выше ЦТ судна G (h > 0). При малом наклонении силы тяжести и силы плавучести создают пару сил, момент которой стремится вернуть судно в первоначальное равновесное положение;
ЦТ судна G расположен выше метацентра m (h < 0). В этом случае момент пары сил веса и плавучести будет стремиться увеличить крен судна, что ведет к его опрокидыванию;
ЦТ судна G и метацентр m совпадают (h = 0). Судно будет вести себя неустойчиво, так как отсутствует плечо пары сил.
Физический смысл метацентра заключается в том, что эта точка служит пределом, до которого можно поднимать центр тяжести судна, не лишая судно положительной начальной остойчивости.
Остойчивость судна
-
SEATRACKER
-
Форум
-
Палуба и мостик
-
Судоводители
![]()
![]()
317
28-Сен-2012 01:28
![]()
![]()
258
— спустя 23 дня
21-Окт-2012 12:09
Немного теории решил выложить ![]()
Теория судна – специальная прикладная инженерная дисциплина, изучающая теоретические основы мореходных качеств судна. Теория судна разделяется на: Статика ( Плавучесть , Остойчивость , Непотопляемость ) и Динамика ( Ходкость , Управляемость ,Качка судна )
Базовые плоскости судна – 1. диаметральная плоскость (ДП) , 2.плоскость мидель-шпангоута
3.основная плоскость.
Чтобы найти положение (координаты) какой-либо точки на судне, необходимо знать расстояние этой точки до некоторых воображаемых плоскостей, рассекающих судно в различных направлениях – эти плоскости и есть базовые!!!!!
1. Диаметральная плоскость – Это вертикальная плоскость, условно рассекающая корпус вдоль на две
симметричные половинки. Все поперечные размеры на корпусе откладываются на правый или левый борт только от ДП
2. Плоскость мидель-шпангоута – Это поперечно- вертикальная плоскость , перпендикулярная ДП, которая делит
длину судна пополам. В Российском флоте принято все размеры вдоль судна откладывать только от миделя. Размеры в
нос от миделя обозначаются со знаком плюс (плюс обычно не пишется), в корму – со знаком минус. Такая система отсчета имеет
определенное неудобство – при расчетах посадки судна необходимо очень внимательно следить за знаками. На судах
иностранной постройки отсчет обычно ведется от кормового перпендикуляра, т.е. от оси баллера руля, когда большинство
продольных размеров будут положительными.
3. Основная плоскость – это горизонтальная плоскость, перпендикулярная ДП и миделю, на которую, упрощенно
говоря, можно поставить судно, если снять пояс обшивки в районе киля и все, что ниже ее. Все вертикальные размеры откладываются
вверх от ОП.
Осадка, отложенная от действующей ватерлинии до наиболее заглубленной точки на днище является фактической осадкой – она нанесена на марках углубления.
Следы взаимного пересечения базовых плоскостей образуют жестко связанную с судном систему прямоугольных координат
Ось x – след пересечения ДП с ОП: она направлена вдоль судна в нос с началом отсчета на миделе.
Ось y – след пересечения миделя с ОП: она направлена поперек судна с началом отсчета на ДП.
Ось z – след пересечения ДП с миделем с началом отсчета на ОП.
Обозначение, положение и направление осей координат следует зрительно четко и ясно себе представлять !!!
Термины:
Плавучесть – это способность судна плавать, т.е. находиться в неподвижном состоянии на поверхности раздела двух сред (воды и воздуха) в
заданном положении и выполнять поставленные задачи. Практическая значимость для судоводителей этого раздела статики
судна велика. Она состоит в том, что дает возможность не только понять почему и при каких условиях судно плавает, но и
решить ряд практических задач: например, какова должна быть предельная загрузка судна, какова посадка судна, как влияет
место расположения грузов на посадку судна и пр.
СИЛЫ ПОДДЕРЖАНИЯ СУДНА:
Закон Архимеда – «на погруженное в жидкость тело действует выталкивающая сила (т.е. сила поддержания), величина которой равна весу жидкости в вытесненном объеме».
точка (С) называется центром величины (ЦВ). Ее физический смысл состоит в том, что она является геометрическим центром подводного объема судна, и поэтому ее положение зависит от формы подводного объема, иначе говоря, от формы корпуса судна. Проектант уже вычислил координаты ЦВ еще в процессе проектирования судна и привел их в главе «Справочные материалы» «Информации об остойчивости».
Положение ЦВ определяется координатами xс и zс . Центр величины при отсутствии крена всегда лежит в плоскости симметрии судна (ДП), так как он является геометрическим центром симметричного подводного объема. Поэтому третью координату yс = 0 можно не рассматривать.
Вычисленные координаты точки С проектант приводит в судовой документации (в «Информации об остойчивости»), откуда их можно получить для дальнейших расчетов.
Весовое водоизмещение – это равнодействующая (сумма) сил тяжести всех элементов, из которых состоит судно. Она всегда направлена вертикально вниз и приложена в точке G, называемой центром тяжести (ЦТ) судна (см. рис. 3.2.1.1.). Для выполнения судоводительских расчетов очень важно знать положение ЦТ на судне. В отличие от ЦВ, положение ЦТ никак не зависит от формы корпуса, а зависит лишь от весовой нагрузки судна, т.е. от веса (постоянных и переменных грузов) и мест расположения всех элементов, из которых состоит судно.
Постоянные грузы – грузы, входящие в водоизмещение судна порожнем (вес корпуса, механизмов, судовых систем, приборов, мебели,
отделки и прочих элементов, из которых построено судно). – все вычисления, связанные с постоянными грузами
выполняет проектант
Переменные грузы – грузы, входящие в дедвейт, которые могут менять свою величину в процессе эксплуатации судна (все виды
перевозимых грузов, жидких запасов, снабжения, провизия, экипаж с багажом, запчасти, рыба в обработке и пр.)
Количество и расположение переменных грузов могут знать только члены экипажа, при которых загружалось
судно. Главным ответственным лицом за учет переменных грузов и все расчеты, связанные с ними, является
(грузовой) помощник капитана.
весовое водоизмещение D можно разделить на два слагаемых: D = Do + Σpi,
Do – водоизмещение порожнем – сумма постоянных грузов
Σpi – сумма переменных грузов (жидкие грузы, груз в трюмах или на палубе, снабжение, экипаж с багажом и пр.).
Определить расстояние zg ЦТ объекта от горизонтальной (базовой) плоскости. Расчет ведется в следующей последовательности:
1. Объект расчленяется (мысленно) на отдельные элементы.
2. Определяется вес каждого элемента (Р1, Р2, Р3, Р4, Р5).
3. Определяется положение ЦТ элемента и расстояние (плечо) ЦТ от базовой плоскости: (Z1, Z2, Z3, Z4, Z5).
4. Определяются статические моменты каждого элемента относительно выбранной базовой плоскости:
(Р1*Z1, Р2*Z2, Р3*Z3, Р4*Z4, Р5*Z5).
5. Суммируются вычисленные статические моменты:
(Р1*Z1 + Р2*Z2 + Р3*Z3 + Р4*Z4 + Р5*Z5) = Σ(Pi*Zi) (краткая запись суммы).
6. Суммируется вес всех элементов: (Р1+Р2+Р3+Р4+Р5) = ΣPi (краткая запись суммы).
7. Искомая координата Zg находится делением сумм статических моментов на сумму веса всех элементов:
Аналогичным путем определяются координаты ЦТ судна. Судно разбивается на отдельные элементы, относящиеся к постоянным грузам, входящим в водоизмещение порожнем Dо, и к переменным грузам, входящим в дедвейт Σpi. Соответственно этому, вычисляется статический момент по порожнего судна (его вычисляет проектант и вводит в «Информацию об остойчивости» в статью нагрузки «Судно порожнем») и статический момент дедвейта – вычисляет судоводитель.
На основании изложенного, координаты ЦТ судна вычисляются по формулам:
xg – отстояние ЦТ от миделя – по формуле:
zg – отстояние ЦТ от основной плоскости – по формуле:
Метацентр– условная точка, вокруг которой смещается центр величины: геометрически эта точка является
точкой пересечения линий действия сил поддержания до крена и после крена.
Метацентрическая высота – расстояние между метацентром и центром тяжести судна – количественный
измеритель начальной остойчивости.
Метацентрический радиус – расстояние от центра величины до метацентра (геометрический смысл); физический
его смысл – отношение момента инерции площади ватерлинии относительно
продольной оси x) к подводному объему судна.
![]()
— спустя 3 месяца 11 дней
02-Фев-2013 02:15
Есть вопрос, касается дипломной и тоже по остойчивости. Подскажите, оси Х, Y, Z, к каким англ. аббревиатурам относятся (есть в таблице Capacity plan следующие сокращения: L.C.G; V.C.G; T.C.G ). последние буквы C.G. наверное Center of Gravity
![]()
![]()
2
— спустя 21 день
23-Фев-2013 20:39
![]()
![]()
1
— спустя 10 месяцев 22 дня
17-Янв-2014 23:44
Просьба знающих помочь с задачей:
Определить метацентрическую высоту судна в грузу и балласте по периоду качки и допустима ли данная скорость судна при входе на малую глубину или в “Мёртвую воду”.
Исходные значения: H-8.20 m, L-160 m, Vср.-15 уз, B-21 m, T-13 сек.
![]()
![]()
4
— спустя 1 год
15-Фев-2015 12:34
Люди, есть у кого UC коды для карт дальневосточного бассейна на картографию MaxSeaTimeZero.1.9.6???????????
![]()
![]()
1
— спустя 1 год 2 месяца
22-Апр-2016 22:15
Всем доброго времени суток. Уважаемые коллеги не сталкивался кто с прогой по расчёту остойчивости и т.п. TSB Supercargo ( контейнеровозы). Буду весьма признателен за рабочий образец под любую вместимость ящиков или хотя б “буквари” по самой проги в ознакомительных целях. Заранее спасибо.
![]()
— спустя 10 месяцев 18 дней
11-Мар-2017 14:49
Здравствуйте. Не подскажете, а то туплю, метацентрическая высота когда будет больше: при балласте или в грузу?
![]()
![]()
2316
— спустя 6 часов
11-Мар-2017 21:11
![]()
11-Мар-2017 21:11
![]()
![]()
566
— спустя 6 месяцев 2 дня
14-Сен-2017 00:13
Делаю программу расчета остойчивости для своего контейнеровозика. Все готово, кроме расчета Bending Moment и Shear Forces
Нужна помощь в этой теме.
Buoyancy Forces и диаграмму на нашел и построй через масштаб Бонжана
Кривую нагрузки для Light Ship тоже сделал
Осталось найти Load Curve для текущей погрузки и высчитать SF и BM
Принцип как и что я понимаю, но расчеты не сходятся с данными из грузовой программы
![]()
![]()
566
— спустя 9 минут
14-Сен-2017 00:22
![]()
![]()
1
— спустя 5 лет 4 месяца
21-Янв-2023 22:32
Коллеги, доброго времени суток. Подскажите, кто может сделать расчет остойчивости в эксель программе? Конечно за вознаграждение)
Похожие темы
| # | Тема | Форум | Автор |
|---|---|---|---|
|
?? |
Ответы “Дельта-Вахтенный матрос” 2014 |
Тестирование | zxc |
|
RU |
Ответы на вопросы ГКК Севастополь, для командного состава [2011, PDF] |
Ответы на тесты | Astart |
|
RU |
ОНМА вопросы и ответы СУДОВОЖДЕНИЕ уровень Бакалавр [DOC] |
Учебные материалы | roman3007 |
|
?? |
Группа VK которая поможет сдать экзамен на моториста 2 кл |
Мотористы | jebjikovich |
|
?? |
Cдача экзамена | Вопросы и ответы ГКК Одесса для механиков |
Машинная команда | dumon1979 |
|
RU |
Ответы “Дельта-Вахтенный механик” (v.2) [2013, PDF] |
Ответы на тесты | zxc |
|
?? |
Тест Вахтенный моторист Река-Море |
Тестирование | Vampiro |
|
RU |
Ответы на вопросы для устного экзамена на Старпома для ММК в Питере [2014, DOC] |
Ответы на тесты | zxc |
|
?? |
Дельта вопросы и ответы для реф.механика (реф.машиниста) |
Тестирование | 62nikolay |
|
?? |
Доброе время суток товарищи |
Ищу книгу… | MechanikDVS |
-
SEATRACKER
-
Форум
-
Палуба и мостик
-
Судоводители
- Ответить
Move & Copy & Delete
13. Метацентр и метацентрический радиус
Способность тела восстанавливать свое первоначальное равновесное состояние после прекращения внешнего воздействия называют остойчивостью.
По характеру действия различают статистическую и динамическую остойчивость.
Поскольку мы находимся в рамках гидростатики, то и разберемся со статистической остойчивостью.
Если образовавшийся после внешнего воздействия крен необратим, то остойчивость неустойчива.
В случае сохранения после прекращения внешнего воздействия, равновесие восстанавливается, то остойчивость устойчива.
Условием статистической остойчивости является плавание.
Если плавание подводное, то центр тяжести должен быть расположен ниже центра водоизмещения на оси плавания. Тогда тело будет плавать. Если надводное, то остойчивость зависит от того, на какой угол ? повернулось тело вокруг продольной оси.
При ? < 15o, после прекращения внешнего воздействия равновесие тела восстанавливается; если ? ? 15o, то крен необратим.
Точку пересечения архимедовой силы с осью плавания называют метацентром: при этом проходит также через центр давления.
Метацентрическим радиусом называют радиус окружности, частью которой является дуга, по которой центр давления перемещается в метацентр.
Приняты обозначения: метацентр – M, метацентрический радиус – ?м.
При ? < 15о

где I0 – центральный момент плоскости относительно продольной оси, заключенной в ватерлинии.
После введения понятия «метацентр» условия остойчивости несколько изменяются: выше говорили, что для устойчивой остойчивости центр тяжести должен находиться выше центра давления на оси плавания. Теперь предоложим, что центр тяжести не должен находиться выше метацентра. В противном случае силы и будут увеличивать крен.
Как очевидно, при крене расстояние ? между центром тяжести и центром давления меняется в пределах ?< ?м.

При этом расстояние между центром тяжести и метацентром называют метацентрической высотой, которая при условии (2) положительна. Чем больше метацентрическая высота, тем меньше вероятность крена плавающего тела. Наличие остойчивости относительно продольной оси плоскости, содержащей в себе ватерлинию, является необходимым и достаточным условием остойчивости относительно поперечной оси той же плоскости.
Данный текст является ознакомительным фрагментом.