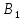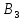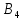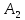Как найти метод северо западного угла

Метод северо-западного угла.

При
нахождении опорного плана транспортной
задачи методом северо-западного угла
на каждом шаге рассматривает первый из
оставшихся пунктов отправления и первый
из оставшихся пунктов назначения.
Заполнения клеток таблицы условий
начинается с левой верхней клетки для
неизвестного
(«северо-западный угол») и заканчивается
клеткой для неизвестногот.е. идет как бы по диагонали таблицы.

Рассмотрим
пример(2):

На
три базы
,,поступил однородный груз в количествах,
соответственно равных 140,180 и 160 единиц.
Этот груз требуется перевезти в пять
пунктов назначения,,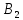,соответственно в количествах 60,70,120,130
и 100 единиц. Тарифы перевозок единицы
груза с каждого из пунктов назначения
указаны в следующей таблицы:

Таблица
2

Пункты отправления	Пункты назначения	Запасы
	2	3	4	2	4	140
	8	4	1	4	1	180
	9	7	3	7	2	160
Потребности	60	70	120	130	100	480

Найти
план перевозок данной транспортной
задачи методом северо-западного угла.

Решение.

Здесь
число пунктов отправления
,
а число пунктов назначения.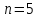
Следовательно, опорный план задачи
определяется числами, стоящими взаполненных клетках.

Заполнение
таблицы начнем с клетки для неизвестного
,
т.е. попытаемся удовлетворить первого
пункта назначения за счет запасов
первого пункта отправления. Так как
запасы пунктабольше, чем потребности пункта,
то полагаем,
записываем это значение в соответствующей
клетке таблицы 2 и временно исключаем
из рассмотрения столбец,считая
при этом запасы пунктаравными
80.

Рассмотрим
первые из оставшихся пунктов отправления
и
назначения.
Запасы пунктабольше потребностей пункта.
Положим,запишем
это значение в соответствующей клетке
таблицы 3 и временно исключим из
рассмотрения столбец.
В пункте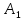запасы считаем равным 10 единиц. Снова
рассмотрим первые из оставшихся пунктов
отправления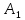и назначения.
Потребности пункта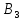больше
оставшихся запасов пункта.Положим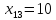и исключим из рассмотрения строку.
Значение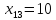запишем в соответствующую клетку таблицы
3 и считаем потребности пунктаравными 110 единиц.

Теперь
перейдем к заполнению клетки для
неизвестного
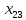и так далее. Через шесть шагов остается
один пункт отправления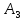с запасом груза 100 единиц и один пункт
назначенияс потребностью 100 единиц. Соответственно
имеется одна свободная клетка, которую
заполняем, пологая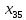=100
(таблица 3). В результате получаем опорный
план:

Таблица
3

Пункты отправления	Пункты назначения	Запасы
	2 60	3 70	4 10	2	4	140
	8	4	1 110	4 70	1	180
	9	7	3	7 60	2 100	160
Потребности	60	70	120	130	100	480

Согласно
данному плану перевозок, общая стоимость
перевозок всего груза составляет

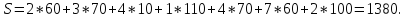
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #

  07.02.201556.11 Кб442.doc

• #

  07.02.2015141.32 Кб412.docx

• #
• #

  07.02.2015130.02 Кб842.docx
• #
• #
• #
• #
• #

Общее представление о транспортной задаче

Ведение логистической деятельности (прежде всего, при выполнении функции транспортировки) зачастую связано с решением, так называемой, транспортной задачи. Она представляет собой математическую задачу, которая связана с нахождением оптимального варианта распределения поставок однородной продукции. В данном случае речь идет про определение оптимальной доставки груза из пункта отправления в пункт назначения в условиях заданных и численно выраженных затрат на подготовку и осуществление перевозки.

Общее решение транспортной задачи изначально было найдено в результате применения методов линейной алгебры, т. е. к транспортной задаче относились как к задаче линейного программирования специального вида. Письменное представление транспортной задачи, как правило, имеет вид прямоугольной таблицы.

Строки таблицы закрепляются за поставщиками с определенными товарно-материальными запасами. Столбцы таблицы закрепляются за потребителями с определенными потребностями. В ячейках таблицы на пересечении соответствующего потребителя и поставщика записывается цена перевозки, которая может быть выражена, например, в рублях за 1 килограмм груза).

Искомая (т. е. неизвестная) величина в транспортной задаче – это объем перевозки от поставщиков к потребителям, при котором общие затраты на транспортировку минимизируются. Данная величина может быть определена путем применения различных методов. Так, чаще всего обращаются к таким методам, как:

• метод северо-западного угла;
• метод минимальных тарифов;
• метод Фогеля;
• метод потенциалов;
• симплекс-метод.

«Решение транспортной задачи методом северо-западного угла» 👇

Помимо этого, решение транспортной задачи можно быть также найдено в программном продукте Microsoft Office Excel.

Общее представление о методе северо-западного угла

Метод северо-западного угла представляет собой метод (правило) получения допустимого начального решения транспортной задачи. Данный метод впервые был предложен американским математиком Джорджем Бернардом Данцигом в 1951 году. Название этому методу было присвоено другими американскими экономистами – Абрахамом Чэрнсом и Уильямом Вейджером Купером.

Метод северо-западного угла предполагает проведение последовательного перебора строк и столбцов транспортной таблицы. Начинается эта работа с левого столбца и верхней строки (именно поэтому метод был назван правилом северо-западного угла: вверх таблицы рассматривался как север, а ее левая сторона – как запад).

Согласно данному методу, в соответствующие ячейки таблицы выписываются максимально возможные отгрузки. При этом необходимо следить за тем, чтобы заявленные в задаче возможности поставщика или потребности потребителя не были превышены. Кроме того, в этом методе не обращают внимания на цены доставки, так как предполагается дальнейшая оптимизация отгрузок (например, методом потенциалов).

Пример использования метода северо-западного угла

Для того чтобы прояснить суть метода северо-западного угла, распишем пример решения одной транспортной задачи. В качестве начальных вводных условий мы будем предполагать существование поставщиков определенной продукции (поставщик А1 с запасом в 30 кг; поставщик А2 с запасом в 40 кг; поставщик А3 с запасом в 20 кг) и потребителей этой продукции (потребитель В1 с потребностью в 20 кг, потребитель В2 с потребностью в 30 кг, потребитель В3 с потребностью в 30 кг, потребитель В4 с потребностью в 10 кг).

Распределение поставок продукции начинается с первой, «северо-западной» ячейки транспортной таблицы, где пересекаются поставщик А1 и потребитель В1. В ячейку вписывается максимальный объем, который позволяет и запас поставщика, и спрос потребителя. Этот объем соответствует минимуму между заявленными запасами поставщика А1 (30 кг) и потребностями потребителя В1 (20 кг).

Следовательно, в ячейку записывается значение 20 кг. Спрос потребителя В1 полностью удовлетворен, поэтому ячейки соответствующего (первого) столбца заполняться больше не будут.

Переходим в следующую северо-западную ячейку, которая соответствует пересечению поставщика А1 и потребителя В2. В данном случае минимум выбираем между 10 кг запасов поставщика А1 и 30 кг потребностей потребителя В2.

В ячейку записывается значение 10 кг. Запасы поставщика А1 полностью исчерпаны, поэтому ячейки соответствующей (первой) строки заполняться больше не будут.

Следующая «северо-западная» ячейка – это пересечение поставщика А2 и потребителя В2. Здесь в ячейку будет записано значение в 20 кг. После этого спрос потребителя В2 окажется полностью удовлетворенным, в связи с чем в дальнейшем ячейки второго столбца заполняться не будут.

При переходе к следующей «северо-западной» ячейке будут сопоставляться запасы поставщика А2 (20 кг) и спрос потребителя В3 (30 кг). В ячейку запишут значение 20 кг. Это будет свидетельствовать об исчерпании всех запасов у поставщика А2, поэтому вторая строка больше заполняться не будет.

Дальше предметом изучения станет сопоставление данных по поставщику А3 (запасы – 20 кг) и потребителю В3 (спрос – 10 кг). Для заполнения ячейки запишем в нем значение в 10 кг.

И наконец остается последняя ячейка, которая соответствует «столкновению» запасов поставщика А3 и потребностей потребителя В4. Согласно условиям нашего примера, они равны друг другу – по 10 кг. Следовательно, весь груз от поставщиков (продукция) должен быть распределен по потребителям. Если же на данном этапе был зафиксирован недостаток или избыток груза, то это означает, что была допущена арифметическая ошибка, или задача не была приведена к закрытому виду.

Транспортная задача линейного программирования

Прочие статьи цикла

Транспортная задача линейного программирования относится к перечню классических задач, решаемых в практике деятельности людей. Эта задача методами классической математики не решается. В задаче необходимо отыскивать экстремум целевой функции. В задаче целевая функция – линейная. Ограничения на переменные (их может быть очень много) описываются также линейными зависимостями. Казалось бы чего проще. Но как раз ограничения и порождают трудности, связанные не просто с поиском max и min при отсутствии ограничений, а с необходимостью учета таких ограничений. Искать требуется не просто экстремум, а условный экстремум. Методы решения задачи позволяют учитывать особенности структуры задачи и даже отказаться от симплексного метода решения в чистом виде.

I. Основные параметры, термины и обозначения

Для ощущения масштаба задачи приведу парочку изображений того, что рассматривается в транспортной задаче линейного программирования.

Зеленый цвет – пассажирские суда, желтые – грузовые, розовый – частные яхты, оранжевый – танкеры и др. Аналогичная картина наблюдается и для авиационных перевозок, перевозок по железной дороге или автотранспортом. Изображения получены в начальном периоде Пандемии короновируса, что привело к огромным пробкам в узостях мирового Океана (Панамский, Суэцкий и др. каналы). Танкеры отправили отстаиваться на рейде, экипажам судов на берег сойти не разрешалось. Это форс-мажорные обстоятельства, которые в теории должны рассматриваться и учитываться специальным образом, что пока к сожалению перевозчиков не сделано.

В теории в тексте задачи Хичкока ничего не говорится о равенстве имеющегося общего запаса судов в портах отправления и общей потребности в судах в портах прибытия (назначения). Если такого равенства нет, то система ограничений несовместна. В случае равенства

транспортная задача называется «сбалансированной». Задачи, в которых условие баланса не задано, должны быть приведены к «сбалансированному» виду. Это можно выполнить использованием «фиктивных» перевозок. Рассматриваем два случая:

Метод содержит три последовательных этапа:

1. Формирование опорного плана;

2. Проверка опорного плана на оптимальность;

3. Переход к новому опорному плану, если предыдущий не оптимален.

II. Формирование опорного плана перевозок

Затем, если a₁ > b₁, то определяется остаток (a₁ – b₁) продукта на первом пункте отправления и его запас реализуется на 2-м пункте назначения. Остаток потребностей 2-го пункта назначения удовлетворяется за счет 2-го пункта отправления, остатки которого направляются в 3-й пункт назначения и т.д. Ниже метод будет иллюстрирован числовым примером.

Пример 1. Построение опорного плана методом Северо-Западного угла

Заданы значения: m = 3, n = 4; a₁ = 60, a₂ = 80, a₃ =100, b₁ = 40,b₂ = 60, b₃ = 80, b₄ = 60. Слева в таблице приведены d_ij удельные стоимости перевозок; справа – В_ij стоимости совместно с предложениями a_i и потребностями b_{j .}

Требуется найти план Х [m,n] перевозок, удовлетворяющий условиям на целевую функцию Q и переменные х_ij задачи Q.

РЕШЕНИЕ Построить исходный опорный план способом северо-западного угла. Строим симплексную таблицу:                                        Таблица 3.   Опорный план задачи

Q = d₁₁∙x₁₁ + d₁₂∙x₁₂ + d₂₂∙x₂₂ + d₂₃ ∙x₂₃+ d₃₃ ∙x₃₃+ d₃₄ ∙x₃₄ = = 5∙40 + 2∙20 + 10∙40 + 2∙40 + 8∙40 + 5∙60 = 200+40+400 + 80 + 320+ 300 = 1340 ед

Коэффициенты d_ij называются фиктивными или косвенными стоимостями; их выражают через косвенные величины α и β, d’_ij = α_i +β_j . Здесь параметры α_i и ( – β_j ), по аналогии с механикой называют потенциалами i-го пункта отправления и j-го пункта прибытия. Значения потенциалов определяется из системы линейных уравнений: α_i + β_j = d_ij Каждому из таких уравнений соответствует какая-либо базисная переменная х_ij Система уравнений с потенциалами содержит m+n неизвестных потенциалов, число же уравнений равняется числу базисных ячеек таблицы, т.е. (m + n – 1). Следовательно, один из потенциалов можно задать произвольно, положив его равным, например, нулю.

Решая далее систему уравнений для потенциалов, находим значения потенциалов строк и столбцов, все фиктивные стоимости d_ij и коэффициенты γ_ij. Если для всех свободных клеток γ_rs ≤ 0, то перевод в базис любой свободной переменной не уменьшит значения целевой функции и, следовательно, выбранный опорный план не является оптимальным. Если же некоторые γ_rs >0, то данный план можно улучшить путем перевода в базис свободной переменной, соответствующей max γ_rs, а также путем исключения из базиса, принадлежащей ему переменной, первой обращающейся в нуль. Переход к новому опорному плану и поиск оптимального плана рассмотрим на примере. Другой способ формирования опорного плана предложен Фогелем. Этот способ при первом чтении можно пропустить, так как дальше он в тексте не используется.

Пример 2. Способ аппроксимации Фогеля

В большинстве случаев этот способ дает опорный план наиболее близкий к оптимальному. Удобен для матриц большой размерности. Используется концепция штрафов, взимаемых за выбор не самого оптимального с точки зрения транспортных издержек маршрута. Штраф по каждой строке и каждому столбцу определяется из анализа маршрутов с различными показателями издержек (как разность двух различных уровней транспортных издержек). Первой заполняется клетка матрицы (таблицы), в которой фиксируется самый крупный штраф. После заполнения клетки штрафы пересчитываются и так до тех пор, пока все ресурсы не будут распределены. Исходные данные для этого примера заполняют таблицу слева вверху.

Этапы алгоритма: 1.     Вычисление разностей в каждой строке и в каждом столбце между наименьшей стоимостью и ближайшей к ней по величине. Разности по строкам записываются справа в столбце разностей, разности по столбцам – внизу в строке разностей. Например, для строк А₁ разность равна А₁В₂ – А₁В₃ = 38 – 24 = 14 и т. д.

ТАБЛИЦА 2 – Метод Фогеля для получения опорного плана транспортной задачи

2.     Поиск из всех разностей, как по строкам, так и по столбцам максимальный. В нашем примере максимальная разность равна 38 и находится в строке А₂. Обведем максимальную разность рамкой.

3.     Размещение в клетку, где находится наименьшая стоимость (А₂В₂ = 18) (строка с наибольшей разностью), максимально возможного количества ресурсов. Оно равно 20, т.е. всему ресурсу отправителя А₂. Поскольку все ресурсы отправителя А₂ исчерпаны, строку А₂ исключаем из дальнейших расчетов, для чего отметим все клетки этой строки точками.

4.     Вычисление разностей столбцам и строкам, не принимая во внимание стоимость в клетках, имеющих ресурсы и клетках с точкой (исключенную строку или столбец) и определение максимальной разности в строке или столбце (В₃ = 76).

5.     Поиск минимального элемента в строке или в столбце с максимальной разностью (А₁В₃ = 24) и размещения в данную клетку максимально возможного количества ресурса, возвращение к этапу №4 и т.д. Окончательно

ЦФ Q=23∙19 + 7∙3 + 20∙18 + 2∙10 + 14∙24 + 1∙100 +3∙48 = = 437 + 21 + 360 + 20 +3 36 + 100 + 272 =1546 ед. Это значение соответствует опорному плану Фогеля.

III. Транспортная задача линейного программирования

Как основной метод решения транспортной задачи – используется метод потенциалов. Ни симплексный метод, ни распределительный метод здесь не рассматриваются. У них имеются свои плюсы и минусы, но объем изложения достаточно велик. Возможно этому позднее я уделю внимание и время, но пока отвечаю на пожелание читателя Хабра.

Пример 3 – Транспортная задача. Метод потенциалов

Исходные данные задачи удобно представить двумя матрицами.

ТАБЛИЦА – Исходные данные

Базисные n + m – 1 = 3 + 4 – 1 = 6 переменные:  
x₁₁ =70, x₁₂ = 20, x₂₂ = 10, x₂₃ = 20, x₂₄ = 0, x₃₄ = 40.
Остальные переменные nm – n + m – 1 = 12 – 6 = 6 свободные:
x₁₃ = x₁₄ = x₂₁ = x₂₄ = x₃₁= x₃₂ = 0 .
Суммарная стоимость перевозок для опорного плана получает представление:
Q = d₁₁ ∙x₁₁ + d₁₂∙x₁₂ + d₂₂∙x₂₂ + d₂₃∙x₂₃+ d₂₄∙x₂₄+ d₃₄∙x₃₄ =
=2∙70 + 3∙20 + 3∙10 + 1∙20 + 2∙0 + 2∙40 = 140 + 60 + 30 + 20 + 0 +80  = 330 ед.

2. Проверка опорного плана на оптимальность

Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].

Выделяем в Г [m, n] свободные ячейки, содержащие γ_rs. Проверяем наличие положительных переменных γ_i,j > 0. Так как в матрице (в свободных ячейках) имеем γ₃₂ = 2 > 0, то исходный опорный план может быть улучшен, он не является оптимальным.

3. Переход к новому (улучшенному) опорному плану

Переменную x₃₂ =x следует ввести в базис.  Обозначим ее предварительно через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся начальным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок

Обозначим ее предварительно через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся начальным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок   Очевидно, что наибольшее x определяется теми x_ij в базисных клетках, из которых этот х вычитается. Следовательно, x₁₁ = min{х₂₂, х₃₄} = {10, 40} = 10. При x >10 перевозка х₂₂ становится отрицательной. Переменную х₂₂ исключаем из базиса и переводим ее в разряд свободных переменных. Далее повторяются рекурсивно три пункта алгоритма.

1. Получаем из модифицированного плана новый опорный план

   В нем объемы перевозок распределены иначе чем в начальном опорном плане.

Суммарная стоимость перевозок для этого опорного плана получает представление:
Q = d₁₁ ∙x₁₁ + d₁₂∙x₁₂ + d₂₃∙x₂₃ + d₃₂∙x₃₂ + d₂₄∙x₂₄+ d₃₄∙x₃₄ =
=2∙70 + 3∙20 + 2∙10 + 1∙20 + 1∙10 + 2∙30 = 140 + 60 + 20 + 20 + 10 + 60  = 310 ед. Затраты на перевозки при этом плане уменьшились на 330 – 310 = 20 ед.

Является ли найденный опорный план оптимальным? Ответ может быть получен после составления и решения системы уравнений для потенциалов.

2. Проверка опорного плана на оптимальность

Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].

Свободные ячейки матрицы Г [m, n] содержат γ_i,j > 0 (γ₁₄ = 1>0). План не оптимален.

3. Переход к новому (улучшенному) опорному плану

Из свободных переменных с x_ij > 0, выбираем одну x₁₄  для введения ее в базис. Обозначим ее как и ранее через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся очередным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок  

Очевидно, что наибольшее x определяется теми x_ij в базисных клетках, из которых этот х вычитается. Следовательно, x₁₁ = min{х₁₂, х₃₄} = {20, 30} = 20. При х₁₂ >20 перевозка х₁₂ становится отрицательной. Переменную х₁₂ исключаем из базиса и переводим ее в разряд свободных переменных. Переходим к новой итерации

1. Получаем из модифицированного плана новый опорный план.

В нем объемы перевозок распределены иначе чем в предшествующем опорном плане.

Суммарная стоимость перевозок для этого опорного плана получает представление:
Q = d₁₁ ∙x₁₁ + d₁₄∙x₁₄ + d₂₃∙x₂₃ + d₃₂∙x₃₂ + d₂₄∙x₂₄+ d₃₄∙x₃₄ =
=2∙70 + 3∙20 + 1∙20 + 2∙10 + 1∙30 + 2∙10 = 140 + 60 + 20 + 20 + 30 + 20  = 290 ед. Затраты на перевозки при этом плане уменьшились на 310 – 290 = 20 ед. Является ли найденный опорный план оптимальным? Ответ может быть получен после составления и решения системы уравнений для потенциалов.

2. Проверка опорного плана на оптимальность

Определим систему уравнений для потенциалов и вычислим их значения:
α₁ + β₁ = d₁₁ = 2;
α₁ + β₄ = d₁₄ = 3;
α₂ + β₃ = d₂₃ = 1;
α₂ + β₄ = d₂₄ = 2;
α₃ + β₂ = d₃₂ = 1;
α₃ + β₄ = d₃₄ = 2. Каждое из этих значений соответствует одной базисной ячейке. Одну из неизвестных в системе можно задавать произвольно. Пусть β₁ = 0. Тогда после решения системы получены значения потенциалов: α₁= 2, α₂= 2, α₃= 2, β₁ =0, β₂=1, β₃ =–1, β₄ =0.

Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].

При переходе к новому опорному плану проверяем наличие положительных свободных переменных γ_i,j >0. Но таких переменных не оказалось. Отсюда следует вывод, что полученный последним модифицированный план является оптимальным и ему соответствует значение линейной формы
Q’= 2∙70 + 3∙20 + 1∙20 + 2∙10 + 1∙30 + 2∙10 = 290.

Заключение

Вся теория исследования операций с позиций математики решает неклассические задачи оптимизации целевых функций. Отличие от классики в том, что те ограничения на переменные, которые исследователи вынуждены накладывать в рамках моделей, созданы и вызваны реальностью. Отыскивать требуется экстремумы функций при многих ограничениях, так называемые условные экстремумы. Классика не позволяет этого делать. Взятие производных и приравнивание их нулю “не видит” ограничений. Лучшее, что там имеется это функция Лагранжа, но ее использование также весьма ограничено. Транспортные задачи – частный, но важный случай в исследовании операций. Надеюсь, что читатель разобравшись в приведенных примерах, лучше стал понимать логику задачи и сумеет самостоятельно постигать интересующие его вопросы по другим публикациям в учебниках и журнальных статьях.

Литература

Методов формирования опорного плана в транспортной задаче придумано немало, но, пожалуй, самый простой из них — метод «Северо-Западного угла» (диагональный метод). Алгоритм заполнения клеток транспортной таблицы в его случае сводится к следующему: сначала заполняется клетка в верхнем левом («северо-западном») углу, затем следующая клетка справа и т. д., пока не заполнится вся строка. Затем мы переходим ко второй строке и снова заполняем ее слева направо. И так далее.

Метод «Северо-Западного угла», в самом деле, прост и понятен, но его недостаток — низкая эффективность. Сформированный с его помощью план в большинстве случаев не является оптимальным.

Формирование опорного плана методом Северо-Западного угла

Итак, у нас имеется транспортная таблица с исходными данными.

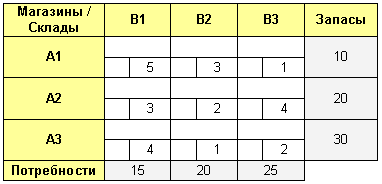
Формирование опорного плана начинаем с внесения в верхнюю левую клетку максимально возможного объема перевозки.

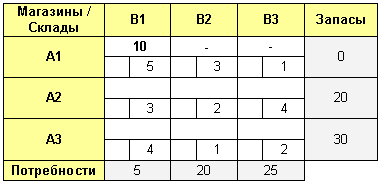
Запасы на складе A₁ закончились, поэтому в оставшиеся ячейки данной строки ставим прочерки. Затем переходим к следующей строке и заполняем ее ячейки слева направо.

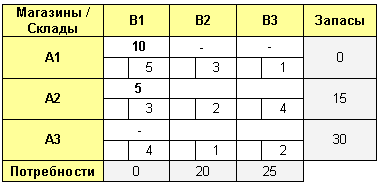
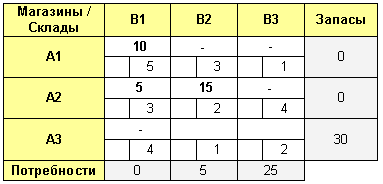
Переходим к третьей строке и тоже заполняем ее слева направо.

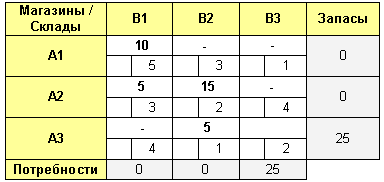
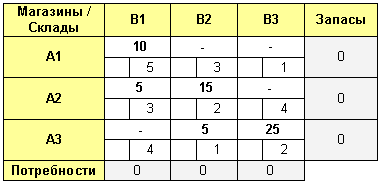
Все, нами получен опорный план. Еще раз отмечу, что при методе «Северо-Западного угла» транспортная таблица просто заполняется в направлении сверху вниз и слева-направо (образно говоря, по диагонали).

© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.

Нашли опечатку? Помогите сделать статью лучше! Выделите орфографическую ошибку мышью и нажмите Ctrl + Enter.

Библиографическая запись для цитирования статьи по ГОСТ Р 7.0.5-2008:
Галяутдинов Р.Р. Транспортная задача: метод Северо-Западного угла // Сайт преподавателя экономики. [2013]. URL: https://galyautdinov.ru/post/metod-severo-zapadnogo-ugla (дата обращения: 20.05.2023).

Методы северо-западного угла, минимального элемента, Фогеля и двойного предпочтения

• Метод северо-западного угла
• Метод минимального элемента
• Метод Фогеля
• Метод двойного предпочтения

Метод северо-западного угла

---

Рассмотрим метод северо-западного угла. Сущность его состоит в
следующем.  Будем распределять груз в
таблице, начиная с загрузки левой верхней, условно называемой
«северо-западной», клетки (1,1), двигаясь затем от нее по строке вправо или по
столбцу вниз. В клетку (1,1) занесем меньшее из чисел

,
то есть

.
Если

,
то

 и первый потребитель

 будет полностью удовлетворен. В дальнейшем 1-й
столбец таблицы в расчет не принимается: в нем переменные

 для

.

Двигаясь вправо по первой строке таблицы, заносим в соседнюю клетку
(1,2) меньшее из чисел

 и

,
то есть

.
Если

,
то запасы первого поставщика исчерпаны и первая строка
таблицы в дальнейшем в расчет не принимается. Переходим к аналогичному
распределению запаса груза второго поставщика.

Если

,
то

.
При этом запас первого поставщика будет исчерпан, а потому

 для

.
Первая строка из дальнейшего рассмотрения исключается. Переходим к распределению
запасов второго поставщика. В клетку (2,1) заносим наименьшее из чисел

.

Заполнив таким образом клетку (1,2) или
(2,1), переходим к загрузке следующей клетки по второй строке либо по второму
столбцу. Процесс распределения по второй, третьей и последующим строкам
(столбцам) производится аналогично распределению по первой строке или по
первому столбцу до тех пор, пока не исчерпаются ресурсы. Последней
заполняется клетка

.

---

Задача 1

Однородный продукт, сосредоточенный на трех  складах фирмы в количествах

единиц,
необходимо распределить между четырьмя магазинами, которым необходимо
соответственно

единиц
продукта. Стоимость перевозки единицы продукта из  i-го пункта отправления    
 (i = 1, 2, 3) в  j-й пункт назначения (j = 1, 2, 3, 4) равна 

   и известна для всех маршрутов.

Вектор запасов продукта на складах 

вектор запросов продукта магазинами 

и матрица транспортных тарифов 

Построить начальный опорный план транспортной задачи методом
северо-западного угла.

Решение

Стандартная транспортная задача разрешима только в том случае,
когда выполняется условие баланса:

В нашем случае:

Модель транспортной задачи закрытая.

Построим начальный опорный план по правилу северо-западного угла.

Начинаем заполнение с левого верхнего угла и далее двигаемся по
диагонали к правому нижнему углу.

Число занятых клеток должно быть

.

В нашем случае число занятых клеток равно 6 – опорный план является
невырожденным.

Найдем стоимость перевозок опорного плана:

Дальнейшее решение транспортной задачи, заключающееся в нахождении
оптимального плана перевозок, производится
методом потенциалов
.

Метод минимального элемента

---

Рассмотрим правило
минимального элемента. Сущность его состоит в следующем. Просматриваются
тарифы таблицы и в первую очередь заполняется клетка с минимальным
значением тарифа. При этом в клетку записывается максимально возможное значение
поставки. Затем из рассмотрения исключают строку, соответствующую поставщику,
запасы которого полностью израсходованы, или столбец, соответствующий
потребителю, спрос которого полностью удовлетворен. После этого из оставшихся
клеток таблицы снова выбирают клетку с наименьшим тарифом. Процесс
распределения заканчивается, когда все запасы поставщиков исчерпаны, а спрос
потребителей полностью удовлетворен. В результате получаем опорный план,
который должен содержать

 загруженных
клеток.

В процессе заполнения
таблицы могут быть одновременно исключены строка и столбец. Так бывает, когда
полностью исчерпывается запас груза и полностью удовлетворяется спрос
(вырожденная задача). В этом случае в свободные клетки надо записать число 0 –
«нуль загрузка», условно считая эту клетку занятой. Однако число 0 записывается
в те свободные клетки, которые не образуют циклов с ранее занятыми клетками.

---

Задача 2

На предприятиях

 производится однородная продукция в количестве

 единиц. Себестоимость производства одной
единицы продукции на i-м предприятии равна соответственно

 ден.ед. Готовая продукция поставляется
потребителям

, потребности которых составляют

 единиц. Для полного удовлетворения
потребностей необходимо увеличить выпуск продукции. Для этого освоить выпуск
данной продукции на предприятии

 с
себестоимостью производства продукции

 ден.ед. 
Стоимости перевозки одной единицы продукции от каждого предприятия
каждому потребителю задаются матрицей

.

Требуется построить начальный опорный план транспортной задачи методом
минимального элемента.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Условие баланса:

В нашем случае:

Вводим дополнительного
поставщика

, у которого имеется  2600-1800=800 единиц груза.

Составим матрицу затрат на производство и транспортировку
продукции.

Построим начальный опорный план по
правилу минимального элемента.

Просматривая таблицу замечаем, что
наименьшие затраты соответствуют маршруту (2,4), поэтому в клетку помещаем

.
В этом случае 2-я строка в расчет не принимается. Просматриваем оставшиеся
таблицы клетки. Наименьший тариф имеет клетка (4,3).

Далее, действуя по аналогичной
схеме, получаем:

Число занятых клеток должно быть

.

В нашем случае число занятых
клеток равно 7 – опорный план является невырожденным.

Найдем стоимость перевозок опорного плана:

Дальнейшее решение транспортной задачи, заключающееся в нахождении
оптимального плана перевозок, производится
методом потенциалов
.

Метод Фогеля

---

Сущность его состоит в
следующем. В таблице по строкам и столбцам определяется разность между двумя
наименьшими тарифами. Отмечается наибольшая разность рамкой. Далее в строке
(столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом.
Строки (столбцы) с нулевым остатком груза в дальнейшем в расчет не принимаются.
На каждом этапе загружается только одна клетка. Распределение груза
производится, как и по выше рассмотренным правилам.

---

Задача 3

Ниже приведены числовые
данные транспортной задачи. Стоимость перевозки единицы продукции записана в клетках
таблицы. Запасы указаны справа от таблиц, а потребности – снизу.

Требуется построить
начальный план методом Фогеля.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Стандартная транспортная задача разрешима только в том случае,
когда выполняется условие баланса:

В нашем случае:

Модель транспортной задачи закрытая.

Воспользуемся способом Фогеля для нахождения начального опорного
плана транспортной задачи. В каждом ряду и столбце матрицы

 найдем минимальный и ближайший к нему элементы
и их разность по абсолютной величине записываем в конце соответствующего ряда
справа и снизу. Находим максимальную из этих разностей (число
29 заключено в рамку). В ряду (или столбце), соответствующем максимальной
разности, находим минимальный элемент

.
В клетку (3,5) вписываем число

С оставшейся матрицей поступаем аналогично предыдущему. Все
вычисления сведены в таблицу.

Получили начальный опорный
план транспортной задачи методом Фогеля.

Найдем стоимость перевозок опорного плана:

Дальнейшее решение транспортной задачи, заключающееся в нахождении
оптимального плана перевозок, производится
методом потенциалов
.

Метод двойного предпочтения

---

Суть метода двойного
предпочтения отражена в его названии. В таблице найдем наименьшие элементы в
каждой строке и в каждом столбце. Поставим в соответствующую клетку знак *.
Если встречаются такие клетки, отмеченные двумя знаками, то их заполняем в
первую очередь. Распределение груза производится, как и по выше рассмотренным
правилам.

---

Задача 4

Составить план перевозки
зерна из районов

 на
пять элеваторов

 (запасы
районов и мощности элеваторов приведены) с минимальными издержками за перевозку.
Затраты на перевозку 1 ц заданы.

Начальный план перевозок
составить по правилу двойного предпочтения.

Решение

Стандартная транспортная
задача разрешима только в том случае, когда выполняется условие баланса:

В
нашем случае:

Модель транспортной задачи
закрытая.

Заполняем таблицу по
правилу двойного предпочтения.

Сначала в каждой строке находим клетку с минимальным тарифом. Если таких
клеток несколько (одинаковые значения) то выбираем их все. В выбранных ячейках
ставим отметку *.

Затем выполняем те же самые действия, только на тот раз по столбцам. То
есть в каждом столбце тоже находим клетку (клетки) с минимальным тарифом и
ставим в ней отметку – *.

Начинаем заполнять
транспортную таблицу. В первую очередь заполняем ячейки с двумя звездочками (если
их несколько, выбираем ту в которой меньший тариф). Далее заполняем клетки с
одной звездочкой. Если остались нераспределенные запасы и неудовлетворенные
потребности – заполняем оставшиеся клетки без звездочек.

Найдем стоимость перевозок опорного плана:

Дальнейшее решение транспортной задачи, заключающееся в нахождении
оптимального плана перевозок, производится
методом потенциалов
.