Как найти межплоскостные расстояния

Рис.
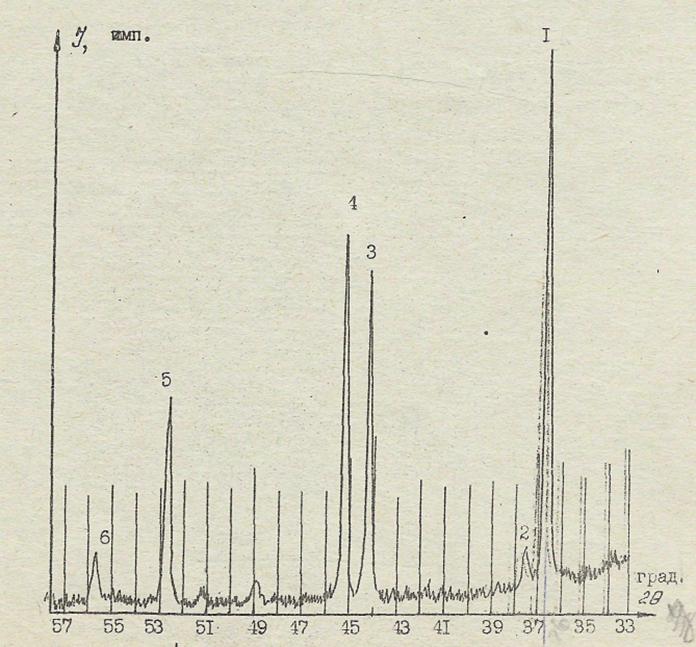
13. Фрагмент рентгенограммы сплава свинца
и олова

  На
рис. 13 представлен фрагмент рентгенограммы
сплава свинца и олова. Такой сплав, как
и любое поликристаллическое вещество,
обладает своей кристаллической решеткой.
Семейства атомных плоскостей, образующих
эту решетку, обладают своим характерным
только для данной решетки набором
значений межплоскостных расстояний
d_HKL.
Знания межплоскостных расстояний
исследуемого вещества позволяют во
многих случаях установить вещество или
фазу. Данные о межплоскостных расстояниях
для различных фаз можно найти в специальных
таблицах и справочной литературе [3,5].
Как уже указывалось, значения d_HKL
можно рассматривать как межплоскостные
расстояния для семейств условных
плоскостей {HKL}. Из формулы Вульфа-Брэгга
2d sin
= n
следует, что:

Рентгенограмма
получена с использованием рентгеновской
трубки с медным анодом, для которого
длина волны известна и составляет
_ср=1,541 Å.
Таким образом, задача нахождения d_HKL
сводится к определению угла дифракции
,
который рассчитывается непосредственно
по рентгенограмме. На рентгенограмме
представлено шесть дифракционных
максимумов, по оси y отражена интенсивность
линий, ось x представляет собой брэгговские
углы дифракции 2,
которые определяют по максимуму пика.
Значения d_HKL
рассчитываются по формуле Вульфа-Брэгга.
Результаты расчета помещены в таблицу
1.

Таблица
1 – Пример расчета dHKL по рентгенограмме.

4 Практическая часть

Для
расчета межплоскостных расстояний с
последующим установлением вещества по
данным о межплоскостных расстояниях
необходимо:

1)
Снять рентгенограмму поликристаллического
вещества.

2)
Пронумеровать дифракционные линии на
рентгенограмме. Нумерацию линий проводить
в порядке возрастания углов 
от малых углов к большим.

3)
Для каждой линии рентгенограммы
рассчитать брэгговский угол дифракции
по максимуму дифракционного пика. Отсчет
угла следует вести от меньшего угла к
большему.

4)
Для каждой линии рентгенограммы
рассчитать межплоскостные расстояния
по формуле Вульфа-Брэгга.

5)
Произвести оценку интенсивности линий
по предлагаемой схеме

6)Результаты
замеров и расчетов занести в таблицу:

7)Сопоставить
экспериментальные данные с данными
справочных таблиц [3,5] и установить, от
какого вещества была снята рентгенограмма.

РАССЧЕТ

,
=
0,70930
Å.

1. d_HKL1=
   =2,84934
   Å;

2. d_HKL2=
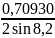
   =2,48652
   Å;

3. d_HKL3=
   =1,74888
   Å;

4. d_HKL4=
   =1,49209
   Å;

5. d_HKL5=
   =1,42607
   Å;

6. d_HKL6=
   =1,23776
   Å;

7. d_HKL6=
   =1,13850
   Å;

8. d_HKL6=
   =1,10616
   Å;

9. d_HKL7=
   =1,01033Å;

10. d_HKL8=
    =0,95084
    Å;

11. d_HKL9=
    =0,87537
    Å;

12. d_HKL10=
    =0,83761
    Å;

13. d_HKL11=
    =0,82379
    Å;

14. d_HKL12=
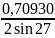
    =0,78118
    Å.

Вывод:
в
ходе данной лабораторной работы
ознакомились с методом рентгеноструктурного
анализа (РСА), а также с элементами
структурной кристаллографии и свойствами
рентгеновских лучей, так же были получены
практические навыки в определении
межплоскостного расстояния кристаллической
решетки. И определенно исследуемое что
исследуемое вещество являлось Pb
(свинец) .

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Teachs.ru

Условие Брэгга — Вульфа (также условие Вульфа — Брэггов) определяет направление максимумов дифракции упруго рассеянного на кристалле рентгеновского излучения. Выведено в 1913 независимо У. Л. Брэггом^[1] и Г. В. Вульфом^[2]. Имеет вид:

где d — межплоскостное расстояние, θ — угол скольжения (брэгговский угол), n — порядок дифракционного максимума, λ — длина волны.

Брэгговская дифракция может наблюдаться не только для электромагнитных волн, но и для волн материи (волновых функций). В частности, экспериментально это было впервые продемонстрировано для нейтронов в 1936 году^[3], а позднее также для отдельных атомов^[4], конденсата Бозе — Эйнштейна^[5], электронов^[6], двухатомных^[7] и многоатомных^[8] молекул.

Вывод[править | править код]

Пусть плоская монохроматическая волна любого типа падает на решётку с периодом d, под углом θ, как показано на рисунке.
Как видно, есть разница в путях между лучом, отражённым вдоль AC’ и лучом, прошедшим ко второй плоскости атомов по пути AB и только после этого отражённым вдоль BC. Разница в путях запишется как

Если эта разница равна целому числу волн n, то две волны придут в точку наблюдения с одинаковыми фазами, испытав интерференцию. Математически можно записать:

где λ — длина волны излучения. Используя теорему Пифагора можно показать, что

, ,

как и следующие соотношения:

Собрав всё вместе получим известное выражение:

После упрощения получим закон Брэгга

Применение[править | править код]

Условие Брэгга — Вульфа позволяет определить межплоскостные расстояния d в кристалле, так как λ обычно известна, а углы θ измеряются экспериментально. Условие (1) получено без учёта эффекта преломления для безграничного кристалла, имеющего идеально-периодическое строение. В действительности дифрагированное излучение распространяется в конечном угловом интервале θ±Δθ, причём ширина этого интервала определяется в кинематическом приближении числом отражающих атомных плоскостей (то есть пропорциональна линейным размерам кристалла), аналогично числу штрихов дифракционной решётки. При динамической дифракции величина Δθ зависит также от величины взаимодействия рентгеновского излучения с атомами кристалла. Искажения решётки кристалла в зависимости от их характера ведут к изменению угла θ, или возрастанию Δθ, или к тому и другому одновременно.

Условие Брэгга — Вульфа является исходным пунктом исследований в рентгеновском структурном анализе, рентгенографии материалов, рентгеновской топографии.

Условие Брэгга — Вульфа остаётся справедливым при дифракции γ-излучения, электронов и нейтронов в кристаллах, при дифракции в слоистых и периодических структурах излучения радио- и оптического диапазонов, а также звука.

В нелинейной оптике и квантовой электронике при описании параметрических и неупругих процессов применяются различные условия пространственного синхронизма волн, близкие по смыслу условию Брэгга — Вульфа.

Примечания[править | править код]

См. также[править | править код]

• Дифракция

Литература[править | править код]

• Bragg W. L., «The Diffraction of Short Electromagnetic Waves by a Crystal», Proceedings of the Cambridge Philosophical Society, 17, 43 (1914).
• Физическая энциклопедия / Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др. — М.: Сов. энциклопедия. Т. 1: Аронова — Бома эффект — Длинные линии. — М.: БСЭ, 1988. — 704 с., ил.

When atoms form themselves into lattice structures, as they do in metals, ionic solids and crystals, you can think of them as making geometrical shapes, such as cubes and tetrahedrons. The actual structure a particular lattice assumes depends on the sizes, valencies and other characteristics of the atoms forming it. Interplanar spacing, which is the separation between sets of parallel planes formed by the individual cells in a lattice structure, depends on the radii of the atoms forming the structure as well as on the shape of the structure. There are seven possible crystal systems, and within each system are a number of subsystems, making for a total of 14 different lattice structures. Each structure has its own formula for calculating interplanar spacing.

Miller Indices

It makes sense to talk about spacing between planes only if they are parallel to each other. Crystallographers identify a family of parallel planes by their Miller indices. To find them, you choose a plane from the family and note the intercepts of the plane on the x, y and z axes. The Miller intercepts are the reciprocals of the intercepts. When one or more of the intercepts is a fractional number, the convention is to multiply all three indices by a factor that eliminates the fraction. Miller indices are generally denoted by the letters h, k and l. Crystallographers identify a particular plane by enclosing the indices in round brackets (hkl) and show a family of planes by enclosing them in parentheses {hkl}.

Lattice Constants

The lattice constant of a particular crystal structure is a measure of how closely packed the atoms in the structure are. This is a function of the radius (r) of each of the atoms in the structure as well as the geometric configuration of the lattice. The lattice constant (a) for a simple cubic structure, for example, is a = 2r. A cubic structure that includes an atom in the center of each cube is a body-centered cubic (BCC) structure, and its lattice constant is a = 4R/√3. A cubic structure that includes an atom in the center of each face is a face-centered cubic, and its lattice constant is a = 4r/√2. Lattice constants for more complex shapes are accordingly more complex.

Interplanar Spacing for Cubic System and Tetragonal Systems

The spacing between planes in a family with the Miller indices h, k and l is denoted by d_hkl. A formula relating this distance to the Miller indices and the lattice constant (a) exists for each crystal system. The equation for a cubic system is:

Big(frac{1}{d_{hkl}}Big)^2=frac{h^2+k^2+l^2}{a^2}

For other systems, the relationship is more complicated because you need to define for parameters to isolate a particular plane. For example, the equation for a tetragonal system is:

Big(frac{1}{d_{hkl}}Big)^2=frac{h^2+k^2}{a^2}+frac{l^2}{c^2}

where c is the intercept on the z-axis.