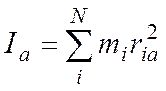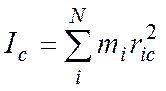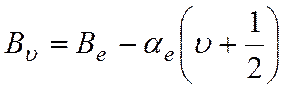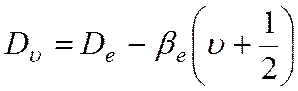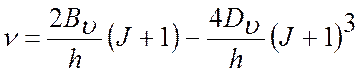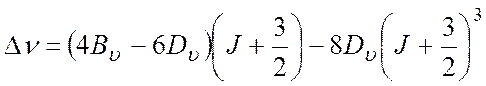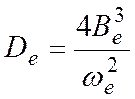Определение межъядерных расстояний молекулы по вращательным спектрам
Страницы работы
Содержание работы
ОПРЕДЕЛЕНИЕ МЕЖЪЯДЕРНЫХ
РАССТОЯНИЙ МОЛЕКУЛЫ ПО ВРАЩАТЕЛЬНЫМ СПЕКТРАМ
Цель работы:Изучить
закономерности вращательных спектров молекул, рассчитать межъядерное расстояние
двухатомной молекулы на основе ее экспериментального вращательного спектра
Задание
1.
Изучить принципиальную схему
регистрации вращательных спектров поглощения.
2.
Изучить следующие теоретические
вопросы:
·
Вращательная энергия и спектр
двухатомной молекулы в приближении жесткого ротатора.
·
Влияние нежесткости химической
связи молекулы на ее вращательные постоянные и спектр.
· Расчет равновесного и
эффективного межъядерных расстояний двухатомной
молекулы.
3.
Решить задачу.
Теоретическое введение
Вращательная энергия – это
энергия периодического вращения молекулы как целого вокруг ее центра масс.
Наиболее удобной и естественной системой координат, в которой рассматривается
вращение, является система главных осей инерции а, b,
с.
В
модели жесткого ротатора имеем:
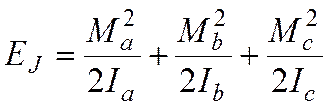
(1)
где
Ма, Мb, Мc – проекции вращательного момента молекулы
на главные оси инерции (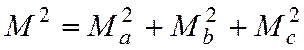
моменты инерции относительно главных осей инерции.
Для N – атомной молекулы имеем:
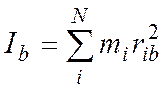
(2)
здесь
ria, rib, ric – расстояние i-того атома
от осей а, b, c. В этой системе справедливо:
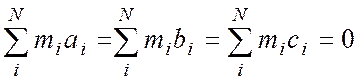
Рассмотрим двухатомную молекулу ХУ, связав с ней
систему главных осей инерции (смотри рисунок).
Точка 0 помещена в центр инерции молекулы.
Тогда в соответствии с (2), видим:
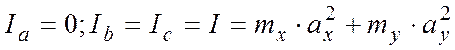
С учетом (3), а также с учетом 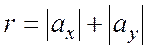
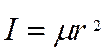
(4)
где
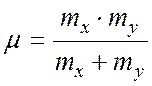
 |
Используя выражение (1), для двухатомной молекулы
получим:
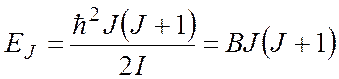
(5)
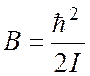
постоянная
(6)
В микроволновом (МВ) спектре поглощения реализуется
следующее правило обора:
,
следовательно,
в МВ спектре возможны переходы с частотой
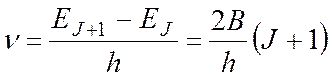
Во вращательном спектре комбинационного рассеяния (КР)
реализуются следующие правила отбора:
.
Тогда смещение линии в КР спектре определится:
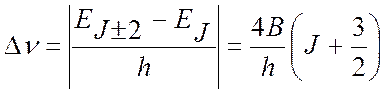
(8)
Более точной моделью для описания вращательных
спектров является модель нежесткого ротатора, в которой учитывается деформация
молекулы (изменение длины связей и валентных углов) в результате ее колебаний и
центробежного растяжения.
Влияние колебаний на вращательную энергию молекулы
может быть внесено в виде поправки во вращательную постоянную. Для двухатомной
молекулы вращательная постоянная Вυ для данного υ-го колебательного состояния имеет вид
где
Ве – эффективное значение вращательной постоянной,
постоянное для всех υ данной молекулы; αе – постоянная колебательно-вращательного
взаимодействия; υ – колебательное квантовое число.
Таким образом, с учетом колебаний в формулах (5), (7),
(8) необходимо использовать .
Влияние центробежного растяжения, усиливающегося с
ростом j, учитывается следующим образом:
,
(10)
где
– вращательная постоянная, учитывающая
центробежное растяжение молекулы.
Тогда выражение для частот спектральных линий в
спектре ИК-поглощения (7) и в спектре комбинационного рассеяния (8) примут
вид:
Проанализировав ИК либо КР спектры и определив ν либо
Δν, находим Вυ и Dυ. Воспользовавшись формулами (4), (6) и полученными
значениями Вυ, рассчитаем .
Формула (9) позволяет на основе измеренных значений Вυ
получить значения Ве и αе, что, в свою очередь, дает возможность с помощью формул (4), (6) найти
значение re.
ЗАДАЧА 1
В микроволновом спектре поглощения паров фторида лития
(6LiF)
измерены следующие линии поглощения, отнесенные к колебательным состояниям υ =
0, 1, 2 и 3.
|
υ |
переход |
ν, МГц |
|
0 |
1 – 0 |
89740,46 |
|
0 |
3 – 2 |
269179,18 |
|
0 |
4 – 3 |
358859,19 |
|
0 |
5 – 4 |
448491,07 |
|
0 |
6 – 5 |
538072,65 |
|
1 |
1 – 0 |
88319,18 |
|
1 |
2 – 1 |
176627,91 |
|
1 |
3 – 2 |
264915,79 |
|
1 |
4 – 3 |
353172,23 |
|
1 |
5 – 4 |
441386,83 |
|
2 |
1 – 0 |
86921,20 |
|
2 |
2 – 1 |
173832,06 |
|
2 |
3 – 2 |
260722,24 |
|
2 |
4 – 3 |
347581,39 |
|
3 |
2 – 1 |
171082,27 |
|
3 |
3 – 2 |
256597,84 |
|
3 |
4 – 3 |
340822,66 |
Определите вращательные постоянные Вυ
и Dυ (в см-1), связанные с волновыми числами
линий через выражение
(для
упрощения расчетов можно поделить левую и правую части на (J
+ 1)). Определите Ве, Dе, αе и re и
оцените колебательную частоту ωе
через Ве и Dе.
ЗАДАЧА 2.
Во вращательном КР-спектре изотопной модификации хлора
35Cl2 измерены следующие средние значения положения линий в
стоксовой и антистоксовой областях
|
J |
Δνср, см-1 |
J |
Δνср, см-1 |
J |
Δνср, см-1 |
|
15 |
16,0452 |
20 |
20,8945 |
25 |
25,7446 |
|
16 |
17,0143 |
21 |
21,8703 |
26 |
26,7125 |
|
17 |
17,9858 |
22 |
22,8367 |
27 |
27,6965 |
|
18 |
18,9571 |
23 |
23,8116 |
28 |
28,6559 |
|
19 |
19,9253 |
24 |
24,7843 |
29 |
29,6245 |
Определите вращательные постоянные Во
и Dо (в см-1),
связанные с волновыми числами линий через выражение
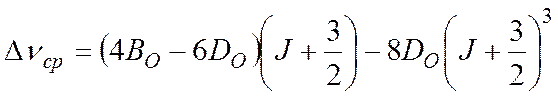
Определите межъядерное расстояние ro и примерное значение J
для наиболее интенсивной линии при
температуре 300 К.
Литература
1.
А.А. Мальцев. Молекулярная
спектроскопия. – М., 1980.
2.
К. Бенуэлл. Основы молекулярной
спектроскопии. – М., 1985.
3.
Н.Г. Бахшиев. Введение в
молекулярную спектроскопию. – Л., 1987.
Похожие материалы
- Определение симметрии молекул из анализа их колебательных спектров
- Построение характеристической кривой фотопластинки
- Проверка закона Бугера-Ламберта-Бера
Информация о работе
Тип:
Методические указания и пособия
УЧЕБНАЯ КНИГА ПО ХИМИИ
ДЛЯ УЧИТЕЛЕЙ СРЕДНИХ ШКОЛ,
СТУДЕНТОВ ПЕДАГОГИЧЕСКИХ ВУЗОВ И ШКОЛЬНИКОВ 9–10
КЛАССОВ,
РЕШИВШИХ ПОСВЯТИТЬ СЕБЯ ХИМИИ И ЕСТЕСТВОЗНАНИЮ
УЧЕБНИКЗАДАЧНИК
ЛАБОРАТОРНЫЙ ПРАКТИКУМ
НАУЧНЫЕ РАССКАЗЫ ДЛЯ ЧТЕНИЯ
Продолжение. См. № 4–14, 16–28, 30–34, 37–44, 47,
48/2002;
1, 2, 3,
4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22/2003
§ 5.3 Вещество
в кристаллическом состоянии
(продолжение)
ЛАБОРАТОРНЫЕ ИССЛЕДОВАНИЯ
1. Определение межъядерного расстояния в
кристаллическом железе.
В этой экспериментальной работе вы
познакомитесь с определением плотности металла
– очень важной характеристикой, благодаря
которой можно судить, например, о составе и
времени изготовления металлического изделия.
Когда и от кого пошло восклицание «Эврика!»?
Древнегреческий ученый Архимед родился в
Сиракузах (остров Сицилия) около 287 г. до н. э. и был
убит римским солдатом при взятии города во время
2-й Пунической войны. Последние слова Архимеда:
«Не трогай мои чертежи». Архимеду приписывают
фразу: «Дай мне, где стать, и я сдвину Землю».
Архимед нашел решение задачи об определении
количества золота и серебра в жертвенной короне
сиракузского правителя Гиерона, когда принимал
ванну. Он побежал нагим домой с криком «Эврика!»,
что значит «Нашел!». Попытайтесь в самом общем
виде рассказать, как Архимед доказал, что в
короне было больше серебра, чем требовалось.
Вам предстоит настоящее научное
исследование!
Работу выполняют небольшой группой – 2–4
человека. Внимательно прочитайте описание
работы, составьте подробный план эксперимента
(имея в наличии образец металла и мерную посуду) и
предварительно распределите обязанности (кто
что будет делать).
Эксперимент заключается в определении плотности
металла, позволяющей, воспользовавшись числом
Авогадро, рассчитать межъядерное расстояние, т.
е. расстояние между ядрами атомов в кристалле или
молекуле. Это расстояние и является одной из
постоянных характеристик данного вещества.
Размеры атомов и молекул выражают разными
единицами: сантиметрами (см), нанометрами
(1 нм = 1•10–9 м) и пикометрами (1 пм = 1•10–12
м). Раньше широко использовали внесистемную
единицу длины – ангстрем
Возьмите кусок металла (железа, меди, алюминия,
свинца), например, железный шарик от большого
подшипника. Можно воспользоваться толстым
железным гвоздем, предварительно отпилив его
шляпку и острие, чтобы получился цилиндр.
Определите взвешиванием массу взятого металла.
Определите объем измеренной массы того же
металла. Если имеющийся металл имеет форму
правильной геометрической фигуры – куба, шара,
цилиндра или другой, измерьте ее размеры
линейкой или штангенциркулем. Воспользовавшись
математическими познаниями, рассчитайте объем
заготовки.
Вы можете взять большую автомобильную гайку
или винт, кусок свинцовой оплетки от кабеля.
Необязательно брать металл в виде одного куска,
можно взять горсть гвоздей, мелких шариков, дроби
и т. п. Если вы имеете кусок металла неправильной
формы или мелкие куски (шарики, винтики, гайки,
гвозди, скрепки и т.п., изготовленные из одного
металла, а не сплава), вам следует самим
предложить способ определения объема металла
известной массы (вы уже успели взвесить горсть
или кучку кусочков металла, ничего не потеряв?).
Можно поступить так. Заполните измерительный
цилиндр примерно наполовину водой и запишите ее
объем (точнее!). Поместите кусочки металла в
цилиндр с водой, чтобы вода покрывала металл, и
запишите полученный объем воды и металла. Чему
равен объем металла? Может случиться, что воды
окажется меньше и она не покроет весь металл. Как
поступить тогда? Подумайте.
В другой измерительный цилиндр налейте точно
известный объем воды и вылейте в цилиндр с
металлом столько воды, чтобы она покрывала
металл. Запишите положения уровней воды в обоих
цилиндрах. Теперь вы можете рассчитать объем
воды в цилиндре с металлом и объем, занимаемый
водой и металлом. Найдите объем металла и, зная
его массу, определите его плотность.
Далее рассчитайте объем, который приходился бы
на число Авогадро атомов металла. Определите
объем, приходящийся на один атом, и вычислите
межъядерное расстояние, приравняв его к длине
ребра куба, заключающего внутри себя атом.
Имейте в виду, что этот метод определения
межъядерных расстояний приближенный. Тем не
менее вычисленные этим методом межъядерные
расстояния в кристаллах металлов хорошо
совпадают с полученными другими методами.
Вместо железа можно взять другие металлы – медь,
свинец, даже золото и серебро.
Как определить размеры одного атома, например,
железа? Вам известно, что 1 моль Fe имеет массу
55,845 г.; плотность железа была определена ранее
экспериментально. (По справочным данным
кристаллическое железо имеет плотность= 7,87 г/см3). Вычислим
объем 1 моль железа:55,845 (г)/7,87 (г/см3) = 7,1 см3.
Определим объем, приходящийся на долю одного
атома в кристаллической структуре железа. Для
этого разделим объем 1 моль атомов (мольный объем)
на число Авогадро атомов:7,1 (см3)/6,02•1023 = 1,18•10–23 см3.
Будем считать, что атом представляет собой шар,
вписанный в куб. Приравняем длину ребра куба, т. е.
диаметр атома, к корню кубическому из
полученного объема:
Таким образом, диаметр атома железа в кристалле
приближенно равен 0,000000023 см. Это и есть
межъядерное расстояние. Полученное число – не
диаметр изолированного атома, т. к. электронные
оболочки атомов представляют собой нечто
похожее на облака с сильно размытыми краями. В
строгой научной литературе по химии и физике не
пользуются выражениями «диаметр атома» или
«радиус атома», а применяют термин «межъядерное
расстояние» и обозначение l («эль»). Почему
диаметр атома железа D и его межъядерное
расстояние l равны, вам станет ясно из рис. 5.6.
По справочным данным радиус атома железа равен
124,1 пм = 1,24•10–8 см, поэтому межъядерное
расстояние равно 2,48•10–8 см.
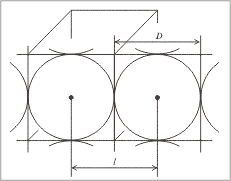 |
Рис. 5.6.
|
Выразите межъядерное расстояние в
кристаллическом железе в различных единицах
измерения.
2. Изучение межъядерных расстояний других
элементов
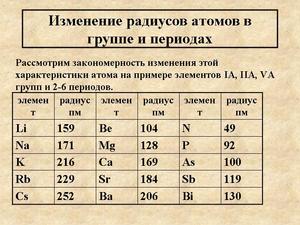
Проследим изменение межъядерных расстояний на
примере элементов 4-го периода, находящихся в
кристаллическом состоянии (при обычной
температуре):
| Элемент | Радиус, см | Межъядерное расстояние, см |
|
|---|---|---|---|
| Калий | К | 2,27•10–8 | 4,54•10–8 |
| Кальций | Са | 1,97•10–8 | 3,94•10–8 |
| Скандий | Sc | 1,61•10–8 | 3,22•10–8 |
| Титан | Ti | 1,44•10–8 | 2,88•10–8 |
| Ванадий | V | 1,32•10–8 | 2,64•10–8 |
| Хром | Cr | 1,24•10–8 | 2,48•10–8 |
| Марганец | Mn | 1,24•10–8 | 2,48•10–8 |
| Железо | Fe | 1,24•10–8 | 2,48•10–8 |
| Кобальт | Co | 1,25•10–8 | 2,50•10–8 |
| Никель | Ni | 1,24•10–8 | 2,48•10–8 |
| Медь | Cu | 1,28•10–8 | 2,56•10–8 |
| Цинк | Zn | 1,33•10–8 | 2,66•10–8 |
| Галлий | Ga | 1,22•10–8 | 2,44•10–8 |
| Германий | Ge | 1,23•10–8 | 2,46•10–8 |
| Мышьяк | As | 1,25•10–8 | 2,50•10–8 |
| Селен | Se | 2,15•10–8 | 4,30•10–8 |
Нарисуйте график изменения
межъядерных расстояний при переходе от калия к
селену. Если вам удастся объяснить ход изменения
межъядерных расстояний, то вы поймете некоторые
особенности построения периодической таблицы
элементов Д.И.Менделеева.
Если вам в будущем придется приготовлять сплавы
различных металлов, то сведения по радиусам
атомов помогут вам предсказать свойства сплавов.
Сплавы металлов – твердые системы, образованные
из двух и более металлов (а также металлов и
неметаллов). Сплавы обладают лучшими свойствами
по сравнению с составляющими их металлами. Одна
из классификаций сплавов основана на числе фаз,
составляющих сплав. Если в сплаве только одна
фаза, то это однофазная система, или твердый
раствор одного металла в другом.
Несколько слов скажем о твердых растворах.
Полная взаимная растворимость металлов в любых
соотношениях наблюдается редко. Такое может быть
у компонентов, близких по свойствам. Например,
золото и серебро могут растворяться друг в друге
в любых соотношениях, т. к. они находятся в одной
подгруппе и размеры их атомов близки (1,442•10–8
и 1,444•10–8 см соответственно).
Твердый раствор – фаза
переменного состава, в которой атомы различных
элементов размещены в общей кристаллической
решетке. Различают твердые растворы замещения
и внедрения.
Твердый раствор замещения образуется при
расположении атомов растворяемого металла в
заселяемых местах (узлах) решетки растворяющего
металла. Радиусы атомов в таких растворах
отличаются друг от друга не более чем на 15% (для
сплавов железа – не более чем на 8%). Предскажите,
какие твердые растворы могут быть образованы
приведенными выше металлами. Другое важное
требование для образования твердых растворов
замещения – металлы должны быть
электрохимически подобны, т. е. находиться не
слишком далеко друг от друга в ряду напряжений
(точнее, в ряду электродных потенциалов).
Твердый раствор внедрения образуется в
результате того, что атомы растворяемого металла
размещаются в пустотах между заселяемыми
местами (узлами) кристаллической решетки. Размер
атомов растворяемого металла не должен быть
больше чем на 63% размера атома растворяющего
металла.
О.С.ЗАЙЦЕВ
Информацию о строении вещества можно
получить, исследуя его физические и
химические свойства. С помощью физических
методов определяют основные параметры
молекул: межъядерные расстояния (т.е.
расстояния между центрами атомов) и
углы между связями (валентные углы).
Межъядерное расстояние между химически
связаннами атомами называется длиной
связи.Например, в молекуле воды длина
связи О-Н (расстояние между ядрами
водорода и кислорода) равна 0,96
,
а угол между связями О-Н, направленными
от атома кислорода, равен 104,5о.
Важнейшей характеристикой химической
связи является энергия связи Е,
определяющая ее прочность. Мерой
прочности связи может служить количество
энергии, затрачиваемое на ее разрыв.
Например, средняя энергия связи О-Н в
молекуле Н2О составляет 498 кДж/моль.
Длина и энергия связи, валентные углы,
а также экспериментально определяемые
магнитные, оптические, электрические
и другие свойства веществ непосредственно
зависят от характера распределения
электронной плотности в молекулах.
Окончательное заключение о строении
вещества делают после сопоставления
информации, полученной разными методами.
2.9. Метод молекулярных орбиталей
Рассмотренный
метод ВС обладает многими достоинствами.
Он относительно прост и нагляден и
позволяет предсказать свойства многих
молекул, таких как пространственная
конфигурация, полярность, энергия и
длина связи и др. Однако свойства
некоторых молекул и ионов метод ВС
объяснить не в состоянии.
Более
общим является метод молекулярных
орбиталей (МО), который позволяет
объяснить ряд явлений, не понятных с
точки зрения метода ВС (парамагнетизм
молекул кислорода; бóльшую прочность
связей в молекулярных ионах F2+
и O2+,
чем соответственно в молекулах F2
и O2
и др.).
В
основе метода молекулярных орбиталей
лежит представление об общих молекулярных
орбиталях. Электроны в атоме принадлежат
не каждому атому в отдельности, а всей
молекуле в целом, образуя молекулярные
орбитали. Если в методе ВС атомы молекул
сохраняют определенную индивидуальность,
то в методе МО молекула рассматривается
как единая система.
Перекрывание
атомных орбиталей соответствует
математической операции сложения
электронных плотностей, при которой
возникает молекулярная орбиталь.
Операция сложения осуществляется только
с атомными орбиталями, имеющими
антипараллельные спины.
Если
спины атомных орбиталей параллельны,
то эти электроны отталкиваются, что
соответствует операции вычитания
электронных плотностей. Так как в
молекулах имеются орбитали как с
антипараллельными спинами, так и с
параллельными, то необходимо при описании
электронного состояния учитывать и
взаимодействие орбиталей, отвечающее
операции вычитания.
Указанный
метод расчета химической связи называется
методом
линейной комбинации атомных орбиталей
(ЛКАО).
Две
молекулярные орбитали, которые всегда
образуются при комбинировании двух
атомных орбиталей, различаются по
энергии.
При
операции суммирования, когда электронная
плотность в области между ядрами
возрастает и образуется связь, энергия
системы понижается. Молекулярная
орбиталь, которая возникает при
суммировании атомных орбиталей и которая
энергетически более выгодна, называется
связывающей.
По
аналогии со связывающими орбиталями
вводится представление о разрыхляющих
орбиталях, получаемых операцией
вычитания.
Связывающей
МО отвечает повышенная электронная
плотность в области
связывания
(между атомными ядрами), а разрыхляющей
МО– повышенная электронная плотность
в области
разрыхления
(по обе стороны за атомными ядрами).
Образование
связывающих МО снижает энергию молекулы
и укрепляет химическую связь, а электроны
на разрыхляющих МО ослабляют химическую
связь. Вероятность пребывания электронов
в связывающих МО высокая, а в разрыхляющих
– низкая, поэтому электроны при
образовании молекулы вначале занимают
связывающие МО, а затем – разрыхляющие
МО.
Так
как каждые две атомные орбитали дают
одну связывающую и одну разрыхляющую
орбитали, то общее число молекулярных
орбиталей равно общему числу атомных.
Число электронов на молекулярных
орбиталях равно сумме электронов на
атомных орбиталях.
По
аналогии с атомными s
-,
p-,
d
-, f
–орбиталями молекулярные орбитали
обозначаются греческими буквами
,
,
,
.
Молекулярные
орбитали, полученные при комбинации s
–
АО, называются
s
– МО (рис.27); при комбинации рх
–
АО –
–
МО
(где х – координата по линии, соединяющей
ядра атомов); при комбинации рy
–
АО и pz
–
АО – –
и –
МО (рис.28).
Рис.
27. Образование связывающей и разрыхляющей
молекулярных орбиталей из атомных s
–орбиталей
Рис.
28. Образование связывающей и разрыхляющей
молекулярных орбиталей из атомных рХ
–орбиталей
Заполнение
молекулярных орбиталей электронами
подчиняется правилам заполнения атомных
орбиталей.
-
Молекулярные орбитали заполняются
в порядке увеличения их энергии. -
Заполнение молекулярных уровней
начинается с орбитали самого низкого
энергетического уровня:
Энергетическое
состояние молекулы зависит от числа
комбинаций операций суммирования и
вычитания, проводимых с атомными
орбиталями при формировании молекулярных
орбиталей.
В
соответствии с принципом Паули в молекуле
не может быть двух электронов со всеми
одинаковыми квантовыми числами (и
одновременно
находящихся на одной молекулярной
орбитали).
Заполнение
молекулярных орбиталей одного
энергетического уровня подчиняется
правилу Гунда. Сначала
энергетически равноценные молекулярные
орбитали заполняются одиночными
электронами, а затем происходит их
заполнение вторыми электронами.
Схему
формирования молекулярных орбиталей
(рис. 29)
Рис.
29. Энергетическая схема образования
МО из атомных s-орбиталей
принято
изображать в виде энергетической
диаграммы молекулярных орбиталей, где
по вертикали откладывают значение
энергии, причем уровни атомных орбиталей
(АО) располагают по обе стороны от уровней
молекулярных орбиталей (МО) получающейся
молекулы.
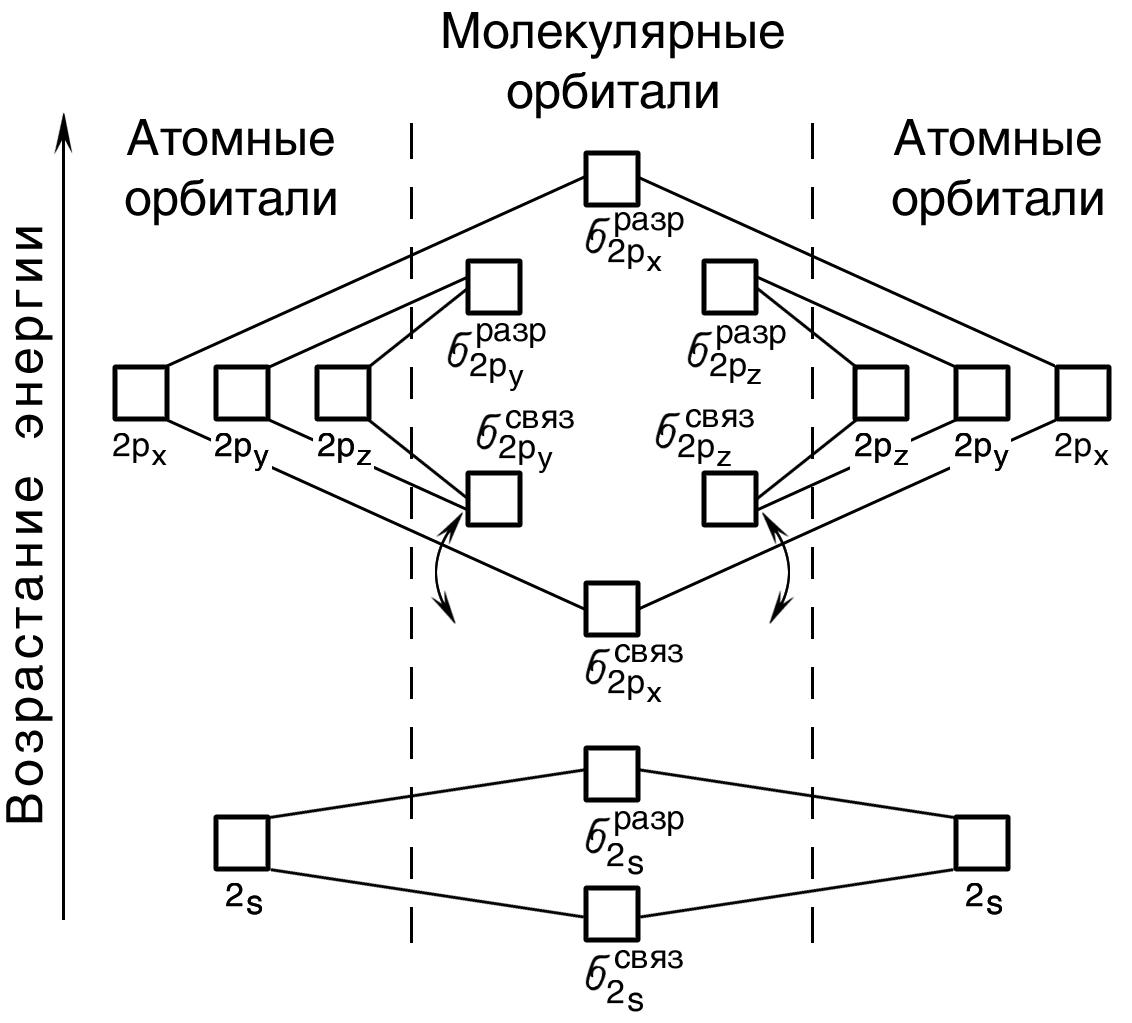
На
рис. 30 изображена энергетическая схема
образования молекулярных орбиталей из
атомных для двухатомных гомоядерных
(одного и того же элемента) молекул
элементов второго периода.
Рис.
30. Энергетическая схема образования
молекулярных орбиталей из атомных для
гомоядерных молекул второго периода
Следует
отметить, что при образовании молекул
B2,
C2
и N2
энергия
связывающей
–
орбитали больше энергии связывающих– и
– орбиталей, тогда как в молекулах О2
и F2
наоборот: энергия связывающих
–
и– орбиталей больше энергии связывающей
–
орбитали. Это нужно учитывать при
изображении энергетических схем
соответствующих молекул.
Образование
химической связи в молекуле кислорода
можно представить электронными
конфигурациями:
2
О […2s22p4
]
→ O2
O2
[()2(
)2(
)2(
)2(
)2
()1(
)1.
Две
атомные 2s
– орбитали дают две молекулярные
орбитали:
и
,
на которых может быть размещено четыре
электрона. Из трех атомных
-,
–
и
-орбиталей каждого атома кислорода
образуются три связывающие и три
разрыхляющие молекулярные орбитали
(рис. 31).
Рис.
31. Диаграмма энергетических уровней
молекулы O2
Перекрывыние
атомных рХ
– орбиталей приведет к образованию
двух молекулярных
-орбиталей
– (связывающей и разрыхляющей) – в
соответствии с операциями сложения и
вычитания, причем энергетический уровень
ниже
уровня
.
Две
другии орбитали 2рY
и
2pZ
перекрываются боковыми поверхностями
с образованием
–
связей. Операции сложения и вычитания
дают две молекулярные орбитали
и
,
причем энергия первой ниже, и две
орбитали
и
.
Из
восьми 2р
–
электронов двух атомов О размещенными
оказываются только шесть, которые
занимают три связывающие МО (2рх,
2рy
,
2
pz).
По принципу минимума энергии оставшиеся
два 2р-электрона
размещаются на двух разрыхляющих МО
(2рy,
2pz),
которые ниже по энергии, чем
.
Наличие
двух неспаренных электронов с параллельными
спинами на разрыхляющих (несвязывающих)
разрy,
разрz
–
орбиталях хорошо объясняет парамагнетизм
молекулы кислорода; молекулы О2
втягиваются в магнитное поле в отличие
от диамагнитных
молекул (не имеющих неспаренных
электронов) N2
и F2.
Порядок
связи n
в молекуле определяется разностью между
числом связывающих и разрыхляющих
электронов, деленной на два. Порядок
связи может быть равен нулю (молекула
не существует), целому или дробному
положительному числу.
Порядок
связи в
молекуле кислорода равен
(6
-2) / 2 = 2.
Рассмотренные
методы валентных связей и молекулярных
орбиталей не исключают, а взаимно
дополняют друг друга. Метод ВС позволяет
объяснить химические связи и свойства
многих соединений. Метод МО обеспечивает
общий подход ко всем типам химических
соединений и позволяет рассчитать с
помощью ЭВМ параметры связей и соединений.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
-
Укажите, у каких из приведенных молекул
химические связи имеют полярный
характер: F2,CO,N2,HBr,Br2. -
Объясните донорно-акцепторный механизм
образования ковалентной связи на
примере иона NH4+. -
Укажите тип гибридизации и валентный
угол в молекулах С2Н2, С2Н4,
С2Н6.
Л И Т Е Р А Т
У Р А
1.
Глинка, Н.Л. Общая химия: учеб. / Н.Л.
Глинка. – М.: Интеграл – Пресс, 2002. Гл. 4.
2.
Глинка, Н.Л. Задачи и упражнения по общей
химии. / Н.Л.Глинка. – М.: Интеграл – Пресс,
2001. Гл. IV.
3.
Коровин, Н.В. Общая химия: учеб. / Н.В.
Коровин. – М.: Высшая школа, 2002. Гл. 2 (§1
– 3).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Чтобы разобраться в вопросе, что в современной науке называется радиусом атома, вспомним, что из себя представляет сам атом. По классическим представлениям в центре атома находится ядро, состоящее из протонов и нейтронов, а вокруг ядра каждый на своей орбите вращаются электроны.
Содержание:
- Радиус атома в физике
- Атомный радиус в химии и кристаллографии
- Какие бывают виды
- Как зависит от типа химической связи
- Видео
Радиус атома в физике
Поскольку в данной модели строения атома электроны являются пространственно ограниченными частицами, т. е. корпускулами, логично считать атомным радиусом (а. р.) расстояние от его ядра до самой дальней, или внешней, орбиты, по которой вращаются так называемые валентные электроны.
Однако по современным, квантовомеханическим представлениям, определить данный параметр нельзя так однозначно, как это делается в классической модели. Здесь электроны уже не представляются в виде частиц-корпускул, а получают свойства волн, т. е. пространственно-неограниченных объектов. В такой модели точно определить положение электрона просто невозможно. Здесь эта частица уже представляется в виде электронной орбитали, плотность которой меняется, в зависимости от расстояния до ядра атома.
Итак, в современной модели строения атома его радиус нельзя определить однозначно. Поэтому в квантовой физике, общей химии, физике твердого тела и других смежных науках эту величину сегодня определяют как радиус сферы, в центре которой находится ядро, внутри которой сосредоточено 90-98% плотности электронного облака. Фактически это расстояние и определяет границы атома.
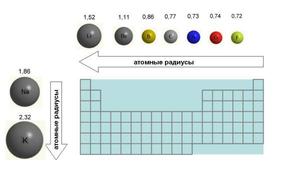
Если рассмотреть Периодическую таблицу химических элементов (таблицу Менделеева), в которой приведены атомные радиусы, можно увидеть определенные закономерности, которые выражаются в том, что в пределах периода эти числа уменьшаются слева направо, а в пределах группы они увеличиваются сверху вниз. Такие закономерности объясняются тем, что внутри периода при движении слева направо заряд атома возрастает, что увеличивает силу притяжения им электронов, а при движении внутри группы сверху вниз все больше заполняется электронных оболочек.
Атомный радиус в химии и кристаллографии
Какие бывают виды
Данная характеристика сильно варьируется, в зависимости от того, в какой химической связи состоит атом. Поскольку все вещества в природе в подавляющем своем большинстве состоят из молекул, понятие а. р. используют для определения межатомных расстояний в молекуле. А данная характеристика зависит от свойств входящих в молекулу атомов, т. е. их положения в Периодической системе химических элементов. Обладая разными физическими и химическими свойствами, молекулы образуют все огромное разнообразие веществ.
По сути, эта величина очерчивает сферу действия силы электрического притяжения ядра атома и его внешних электронных оболочек. За пределами этой сферы в действие вступает сила электрического притяжения соседнего атома. Существует несколько типов химической связи атомов в молекуле:
- ковалентная;
- ионная;
- металлическая;
- ван-дер-ваальсова.
Соответственно этим связям таким же будет и атомный радиус.
Как зависит от типа химической связи
При ковалентной связи АР определяется как половина расстояния между соседними атомами в одинарной химической связи Х—Х, причем Х — это неметалл, ибо данная связь свойственна неметаллам. Например, для галогенов ковалентный радиус будет равен половине межъядерного расстояния Х—Х в молекуле Х2, для молекул селена Se и серы S — половине расстояния Х—Х в молекуле Х8, для углерода С он будет равен половине кратчайшего расстояния С—С в кристалле алмаза.
Данная химическая связь обладает свойством аддитивности, т. е. суммирования, что позволяет определять межъядерные расстояния в многоатомных молекулах. Если связь в молекуле двойная или тройная, то ковалентный АР уменьшается, т. к. длины кратных связей меньше одинарных.
При ионной связи, образующейся в ионных кристаллах, используют значения ионного АР для определения расстояния между ближайшими анионом и катионом, находящимися в узлах кристаллической решетки. Такое расстояние определяется как сумма радиусов этих ионов.
Существует несколько способов определения ионных радиусов, при которых отличаются значения у индивидуальных ионов. Но в результате эти способы дают примерно одинаковые значения межъядерных расстояний. Эти способы или системы были названы в честь ученых, проводивших в этой области соответствующие исследования:
- Гольдшмидта;
- Полинга;
- Белова и Бокия;
- других ученых.
При металлической связи, возникающей в кристаллах металлов, АР принимаются равными половине кратчайшего расстояния между ними. Металлический радиус зависит от координационного числа К. При К=12 его значение условно принимается за единицу. Для координационных чисел 4, 6 и 8 металлические радиусы одного и того же элемента соответственно будут равны 0.88, 0.96 и 0.98.
Если взять два разных металла и сравнить металлические радиусы их элементов, то близость этих значений друг к другу будет означать необходимое, но недостаточное условие взаимной растворимости этих металлов по типу замещения. Например, жидкие калий К и литий Li в обычных условиях не смешиваются и образуют два жидких слоя, потому что их металлические радиусы сильно различаются (0.236 нм и 0.155 нм соответственно), а калий К с цезием Cs образуют твердый раствор благодаря близости их радиусов (0.236 нм и 0.268 нм).
Ван-дер-ваальсовы АР используют для определения эффективных размеров атомов благородных газов, а также расстояний между ближайшими одноименными атомами, принадлежащими разным молекулам и не связанными химической связью (пример — молекулярные кристаллы). Если такие атомы сблизятся на расстояние, меньшее суммы их ван-дер-ваальсовых радиусов, между ними возникнет сильное межатомное отталкивание. Эти радиусы определяют минимально допустимые границы контакта двух атомов, принадлежащих соседним молекулам.
Кроме того, данные АР используют для определения формы молекул, их конформаций и упаковки в молекулярных кристаллах. Известен принцип “плотной упаковки”, когда молекулы, образующие кристалл, входят друг в друга своими “выступами” и “впадинами”. На основе этого принципа интерпретируются данные кристаллографии и предсказываются структуры молекулярных кристаллов.
Видео
Это полезное видео поможет вам понять, что такое радиус атома.
Еслн расчет методом конфигурационного взаимодействия проводится при различных значениях R и если он сопровождается вариационным определением эффективного заряда ядра, то для Нг получается равновесное межъядерное расстояние 1,45 ат. ед. Полная энергия при таком межъядерном расстоянии равна [c.218]
Поэтому возникновение этого спектра малых смещений связано с вращательной характеристикой молекул. Таким образом, наблюдение малых смещений является методом определения постоянной В, а следовательно, момента инерции и межъядерного расстояния молекулы. [c.255]
Первоначально сложилось представление об эффективных радиусах атомов, проявляющихся в их действиях, т.е. в химических соединениях. Эффективные радиусы определяли из экспериментальных данных по межъядерным расстояниям в молекулах и кристаллах. При этом предполагалось, что атомы представляют собой несжимаемые шары, которые соприкасаются своими поверхностями в соединениях. При определении значения эффективного радиуса из межъядерных расстояний в ковалентных молекулах подразумевали ковалентные радиусы, при вычислении их из данных для металлических кристаллов — металлические радиусы. Наконец, эффективные радиусы, рассчитанные для кристаллов с преимущественно ионной связью, назывались ионными радиусам[и. Для этого определяли радиус какого-нибудь иона, а затем вычисляли ионные радиусы других элементов из экспериментальных данных по межъядерным расстояниям в кристаллических решетках. Так, с помощью оптических методов, а затем расчетом был определен радиус аниона фтора, равный 0,11.3 нм. А расстояние между атомами Na и Г в решетке МаГ было установлено равным 0,231 нм. Отсюда радиус иона Ма равен 0,231 — 0,113 = 0,118 нм. Металлические радиусы получены делением пополам расстояния между центрами двух смежных атомов в кристаллических решетках металлов. Ковалентные радиусы неметаллов также вычислены как половина межъядерного расстояния в молекулах или кристаллах соответствующих простых веществ. Для одного и того же элемента эффективные радиусы (ковалентный, ионный, металлический) не совпадают между собой. Это свидетельствует о зависимости эффективных радиусов не только от природы атомов, но и от характера химической связи, координационного числа и других факторов (см. табл. 4). Изменение эффективных радиусов атомов носит периодический характер (рис. 22). В периодах по мере роста заряда ядра эффективные радиусы атомов уменьшаются, так как происходит стягивание электронных слоев к ядру (при постоянстве их числа для данного периода). Наибольшее уменьшение характерно для 5- и р-элементов. В больших периодах для и /-элементов наблюдается более плавное уменьшение эффективных радиусов, называемое соответственно г- и /сжатием. Эффективные радиусы атомов благородных газов, которыми заканчиваются периоды системы, значительно больше эффективных радиусов предшествующих им р-элементов. Значения эффективных радиусов благородных газов (см. табл. 4) получены из межъядерных расстояний в кристаллах этих веществ, существующих при низких температурах. А в кристаллах благородных газов действуют слабые силы Ван-дер-Ваальса в отличие, например, от молекул галогенов, в которых имеются прочные ковалентные связи. [c.52]
В таблице приведены межъядерные расстояния, определенные рентгенографическим методом. [c.342]
К основным характеристикам молекул относят длину связей (межъядерные расстояния), валентные углы, определяемые как углы между связями, пространственное строение или конфигурацию, энергии связей, электрические и магнитные свойства. Определение всех этих характеристик стало возможным благодаря развитию физических и физико-химических методов исследования. [c.199]
Прямое связьшание двух магнитных моментов г и в пространстве, Dij, зависит от где — межъядерное расстояние. Вследствие молекулярного беспорядка среднее прямое взаимодействие в растворе равно нулю. Несмотря на то что современные методы ЯМР позволяют наблюдать прямое спин-спиновое взаимодействие в монокристаллах и аморфных твердых веществах, выделение полезной информации из полученных данных затруднено вследствие того, что присутствуют как меж-, так и внутримолекулярные взаимодействия. Использование жидких кристаллов как ориентирующих растворителей позволяет избежать этого недостатка твердых тел за счет усреднения межмоле-кулярного прямого взаимодействия, при этом значение внутримолекулярного взаимодействия остается ненулевым. Спектроскопия ЯМР ориентированных молекул в жидких кристаллах в настоящее время является эффективным методом определения структуры малых молекул, имеющих до десяти магнитных ядер. [c.391]
В табл. 13 приведены некоторые межъядерные расстояния и валентные углы, определенные, с одной стороны, с помош ью инфракрасной спектроскопии, а с другой — методом дифракции электронов молекулами в газовой фазе, [c.465]
Средний радиус вращения [188], определяемый главными моментами инерции I и массой М молекулы, может быть строго рассчитан из картезианских координат и масс атомов. Исходные для вычисления межъядерные расстояния и углы между связями для различных веществ приведены в [185, 1891. Для линейных молекул а для нелинейных R = 1а в сУ / Удовлетворительный альтернативный метод определения R дает его корреляция с парахором Р [1901 [c.188]
Первоначально сложилось представление об эффективных радиусах атомов, проявляющихся в их действиях, т. е. в химических соединениях. Эффективные радиусы определяли из экспериментальных данных по межъядерным расстояниям в молекулах и кристаллах. При этом предполагалось, что атомы представляют собой несжимаемые шары, которые соприкасаются своимн поверхностями в соединениях. При определении значения эффективного радиуса из межъядерных расстояний в ковалентных молекулах подразумевали ковалентные радиусы, при вычислении их из данных для металлических кристаллов — металлические радиусы. Наконец, эффективные радиусы, рассчитанные для кристаллов с преимущественно ионной связью назывались ионными радиусами. Для этого определяли радиус какого-нибудь иона, а затем вычисляли ионные радиусы других элементов из экспериментальных данных по межъядерным расстояниям в кристаллических решетках. Так, с помощью оптических методов, а затем расчетом был определен радиус аниона фтора, равный 0,113 нм. А расстояние между ядрами N3 и Р в решетке ЫаР было установлено равным 0,231 нм. Отсюда радиус иона Ыа+ 0,231—0,113 = 0,098 нм. Металлические радиусы получены делением пополам расстояния между центрами двух смежных атомов в кристаллических решетках металлов. Ковалентные радиусы неметаллов также вычислены как половина межъя-дерного расстояния в молекулах или кристаллах соответствующих [c.67]
Электронограмма газов и кристаллов приведены на рис. 105, а, 6. Электронограмма состоит из центрального пятна и окружающих его колец различной интенсивности. Центральное пятно обусловлено нерассеянным пучком электронов, а кольца возникают за счет электронов, рассеянных под соответствующими углами к первоначальному направлению пучка. Характер колец и их интенсивность зависят от строения исследуемых молекул. Соответствующие методы расшифровки дают возможность установить форму молекулы, взаимное расположение в ней атомов, валентные углы и межъядерные расстояния. Результаты электронографического определения структуры некоторых молекул приведены в табл. 17. [c.172]
Для демонстрации метода определения межъядерных расстояний [c.409]
Результаты расчета методом валентных связей тоже можно улучшить, проводя вариационное определение эффективного заряда ядра при каждом межъядерном расстоянии. Таким способом находят, что минимум энергии соответствует значению R = 1,44 ат. ед., а полная энергия прн этом оказывается равной — 1,1389 ат. ед. (энергия диссоциации 0,1389 ат. ед.). Зна- [c.215]
Если провести вычисления методом валентных связей с учетом конфигурационного взаимодействия в зависимости от межъядерного расстояния R, включив в них вариационное определение эффективного заряда ядра I, то результаты оказываются идентичными с полученными методом молекулярных орбиталей при учете конфигурационного взаимодействия. Численное опре-дел ие коэффициентов приводит к одинаковым волновым функциям. Этот результат имеет общий характер если исходить из заданного базисного набора, то молекулярно-орбитальный подход с полным учетом конфигурационного взаимодействия приводит к таким же результатам, как и метод валентных связей с полным учетом конфигурационного взаимодействия. [c.219]
Задача 3-5. Для определения структуры молекул в газовой фазе широко используют спектроскопический метод, который позволяет найти межъядерные расстояния по спектрам молекул. По спектроскопическим данным были рассчитаны межъядерные расстояния в молекуле Big”, г(В — I) = 0,210 нм, г(1—I) = 0,364 нм. Определите, какую геометрическую фигуру образуют ядра атомов в этой молекуле. Какой тип гибридизации центрального атома позволяет описать строение данной молекулы [c.35]
Величины валентных углов вычисляют по межъядерным расстояниям и моментам инерции, определяемым по спектрам комбинационного рассеяния света или другими методами. На основании этих определений считают, что тетрагональный углеродный атом имеет тетраэдрическую структуру, характеризующуюся углами около 110° (I). Для тригонального атома углерода этиленовых соединений свойственна плоскостная структура с величиной углов около 120° (П). Дигональный углерод ацетиленовых соединений имеет противоположно направленные валентности с углом 180°(И1). [c.409]
МЕЖАТОМНЫЕ РАССТОЯНИЯ (межъядерные расстояния), экспериментально определяемые расстояния между ядрами атомов в молекулах н кристаллах. Точность определения в значит, мере зависит от сложности объекта и метода определения. [c.317]
Указанные методы дают представление об эффективной протяженности электронной оболочки. Точное определение межъядерных расстояний возможно, например, при помощи дифракции рентгеновских и электронных лучей в газах. [c.416]
В первую группу включена дифракция рентгеновых лучей, электронов и нейтронов. Наиболее прямым методом определения межъядерных расстояний в индивидуальных молекулах является метод, который использует дифракцию излучения, имеющего длину волны, сравнимую с размерами молекул. Например, длина волны рентгеновых лучей и нейтронов находится в области от 0,7 до 2,5 А, область длин волн электронов — от 0,05 до 0,07 А. Дифракция рентгеновых лучей использовалась для определения [c.193]
Другие важные методы определения пространственной структуры молекулы и межъядерных расстояний рентгеноструктурный анализ молекулярных кристаллов (см. ФХ 4.1.3,1), молекулярные спектры (см. ФХ 2.2.5). [c.417]
В тех немногих случаях, когда авторы справочника признавали необходимым оценить межъядерное расстояние определенной молекулы, это выполнялось несколькими методами, и при близком совпадении результатов выбирали наиболее надежное значение. [c.13]
В тех случаях, когда не удается получить количество изотопических разновидностей, достаточное для однозначного”определения структуры молекул с помощью спектроскопии, можно привлечь данные, полученные другим методом, например, электронографическим, если с его помощью измерены некоторые из межъядерных расстояний в молекуле. [c.30]
Говоря здесь о спектроскопическом определении межъядерных расстояний, мы и.меем в виду, в основном, метод радиоспектроскопии, так как благодаря высоким значениям моментов инерции многоатомных молекул линии вращательных переходов, как следует из (15), попадают в область сверхвысоких частот радиодиапазона (сантиметровые волны). Только для наиболее легких молекул (типа ПВО, Н08. и т. п.) спектр лежит в области микроволнового диапазона (миллиметровые волны). Хотя интенсивность спектра в этих областях мала, очень высокая чувствительность радиоспектроскопии позволяет определить межъядерные расстояния в многоатомных молекулах с точностью от 0,02 до 0,001 А, а в некоторых случаях и до 0,0005 А. [c.30]
Возможны и другие пути применения периодического закона для определения неизвестных физико-химических констант. Целесообразна остановиться на использовании периодического закона в методах сравнительного расчета, разработанных М. X. Карапетьянцем. В этих методах, как и в методе Д. И. Менделеева, физико-химические константы на.чо-дят сопоставлением известных величин. Рассмотрим использование периодического закона в методе, который называется пер-вы.и методом сравнительного расчета (всего таких методов шесть) на примере определения межъядерного расстояния N — 1 в неизученной молекуле МЬ. [c.38]
Потенциал появления молекулярных ионов, определенный методом электронного удара, совпадает с адиабатическим в том случае, если равновесные межъядерные расстояния в молекуле и молекулярном ионе равны. В большинстве случаев в молекулярных ионах равновесное расстояние больше, и поэтому соответствующие вертикальные потенциалы ионизации больше адиабатических. [c.28]
Возможны и другие пути применения Периодического закона для определения неизвестных физико-химических постоянных. В частности, предложено использовать Периодический закон в методах сравнительного расчета (М. X. Карапетьянц). В этих методах физико-химические постоянные находят сопоставлением известных величин. Рассмотрим применение одного из методов сравнительного расчета (всего таких методов шесть) на примере определения межъядерного расстояния N-I в молекуле трииодида азота N b- [c.42]
J ня на первый возбужденный уровень вра– щения У = 1. Расстояние между последующими линиями поглощения также составляет 2 Всм . На рис. VI.27, а стрелками показаны переходы между вращательными уровнями при поглощении радиации, а в нижней части рис. VI.27, б схематически изображен соответствующий спектр поглощения жесткого ротатора. Практически -S наблюдается картина поглощения типа изображенной на рис. VI.26. Как уже говорилось, минимумы пропускания света веществом соответствуют на этом рисунке линиям поглощения. Определяя расстояние между минимумами, находим 2В. Но так как В = Н./8лЧс, то, зная В, можно найти /, т. е. по спектру в далекой инфракрасной области определяется важная характеристика молекулы — ее момент инерции. По значению /, а также известным массам атомов по формуле (VI. 180) вычисляется межъядерное расстояние л Так, для хлористого водорода (см. рис. VI. 26) 2В = = /о = 20,68 см” , т. е. В = 10,34 см . Отсюда момент инерции молекулы НО / = 2,71 10 г-см . Если же считать приведенную массу ц = 1,63-10″ г, можно найти межъядерное расстояние г = == 1,29-10 . Это значение г находится в удовлетворительном совпадении со значениями, определенными другими методами. [c.250]
Важное значение для химика-неорганика имеют радиусы ионов ионные радиусы). Если кристалл состоит из ионов, например Ка С1, (Га Р5, то межионное (межъядерное) расстояние можно рассматривать как сумму ионных радиусов л. Предложены различные способы разделения межионных расстояний на слагаемые, отвечающие отдельным ионам. Соответственно известен ряд шкал ионных радиусов (Гольдшмидта, Полинга и др). Наиболее распространена в настоящее время шкала так называемых физических радиусов ионов, предложенная физиками Шенноном и Прюиттом в 1969 г. В этой системе радиусов границей между ионами считается точка минимума электронной плотности иа линии, соединяющей центры ионов. Такую систему радиусов удалось разработать благодаря появлению метода точного определения электронной плотности в кристаллах по рассеянию кристаллами рентгеновского излучения. Ионные радиусы по шкале Шеннона и Прюитта представлены в табл. 1.5 (указаны значения радиуса иона в кристаллической решетке при окружении его шестью ближайшими соседями). [c.51]
Равновесная конфигурация молекулы. При определении вариационным методом энергии молекулы Е для минимума потенциальной кривой (потенциальной повер> ности) одновременно определяются и ее равновесные геометрические ггараметры. Для двухатомной молекулы, например СО, существует один такой параметр—это равновесное межъядерное расстояние. Для молекул с небольшим числом электронов расчеты аЬ initio дают довольно близкое совпадение с опытом (табл. 13). Это позволяет использовать методы неэмпирического расчета для предсказания равновесных расстояний в двухатомных молекулах, когда экспериментальные данные отсутствуют. [c.151]
В этом разделе рассмотрены методы, основанные на дифракции рентгеновских лучей, электронов и нейтронов. При выборе метода исследования нужно помнить, что наиболее точным методом определения межъядерных расстояний в индивидуальных молекулах будет тот, который использует дифракцию излучения с длиной волны, сравнимой с размерами молекул. Длина волны рентгеновских лучей и нейтронов находится в области от -0,7 до 2,5 A, а область длин волн электронов —от 0,05 до 0,07 A. По-видимому, наиболее приемлемым методом определения структуры является метод, основанный на дифракции рентгеновских лучей. Начало его применению положила работа Брэгга, который в 1912 г. определил строение Na l, K l и ZnS, направляя пучок монохроматических рентгеновских лучей на кристаллы этих соединений. [c.290]
Данные о стабильной конфигурации ядер молекулы получают обычно с помощью спектроскопических, электроиографических и нейтронографических методов исследования или квантово-механических расчетов, которые дают возможность приближенно оценивать взаимные расположения ядер атомов молекул. Наиболее полная и надежная информация может быть получена с помощью методов реитгеноструктурного анализа, электронографии и нейтронографии, которые позволяют оценить относительные положения ядер в молекуле и расстояния между ядрами любой пары атомов элементов 81 и Эг, входящих в состав. молекулы. В простейшем случае равновесная конфигурация молекулы может быть задана в виде набора точек (точечного множества аЯ = т. ), расположенных в пространстве с указанием типа ядер и их декартовых или кристаллографических координат, пли же может быть описана в терминах внутренних координат — набора межатомных расстояний, углов между отрезками, соединяющих ядра, а также двухгранных углов. Положения ядер атомов, как правило, не являются эквивалентными. В достаточно сложных молекулах расстояния между некоторыми ядрами значительно превосходят другие межъядерные расстояния. Это дает возможность провести более наглядное описание равновесной конфигурации молекулы, используя для этого различные критерии разбиения элементов множества ЗЯ на пары. Один из таких критериев основан па выделении для каждой пары атомов элементов Э, и Э характерного интервала /(Э,-, Э ) межатомных расстояний г(Э Э ), который может быть определен па основании экспериментальных данных. Обычно границы таких интервалов незначительно отличаются от равновесных расстояний в соответствующих двухатомных системах, усредненных по конфигурациям нескольких нижних возбужденных состояний. Для атомов углерода, например, в качестве такого интервала может быть выбран интервал (1,19 1,55), а для атомов С и Н — (0,8 1,15), [c.11]
Электронография основана на явлении дифракции электронов на ядрах атомов. Метод применяется для изучения структуры различных веществ в газообразном состоянии. Дифракционная картина взаимодействия быстрых электронов с неществом фиксируется на фотопластинке в виде электронограммы. Она состоит из центрального пятна, образованного неотклонивщимися электронами, и колец различной интенсивности, являющихся результатом действия рассеянных электронов. Характер колец и их интенсивность обусловлены строением исследуемого соединения. Расшифровка электронограмм путем использования определенных математических соотношений дает возможность установить геометрическую форму, расположение атомов, межъядерные расстояния и валентные углы несложных молекул. В случае сложных соединений применение электронографии затруднено. > [c.512]
Рассмотрим методы нахождения величин, входящих в уравнения (1.3) и (1.4). Для этого необходимо определить вид спектра поглощенной при ионизации молекулы АВ энергии. При переходе к определенному электронному состоянию АВ+ вид этого спектра зависит только от возмоншых изменений в колебательной и вращательной энергиях. Вариации колебательной энергии можно получить из простого положения Франка, согласно которому межъядерное расстояние исходной молекулы не успевает заметно измениться за время электронных перестроек. Следовательно, ионизацию на диаграмме энергия — межъядерное расстояние (рис. 1.1Х можно характеризовать вертикальной линией. Расстояние по этой линии между кривыми 1 и 2 соответствует поглощенной энергии, а вероятность соответствующего перехода равна вероятности нахождения исходной молекулы в состоянии с данным мгновенным межъядерным расстоянием. Поскольку вероятность зависит от колебательного состояния молекулы АВ, то указанное правило определяет в конечном счете вероятность различных колебательных переходов. Оправданность такого подхода была подтверждена приближенными квантово-механическими расчетами Кондона [39, с. 147]. [c.12]
Длины связей, т. е. межъядерные расстояния в молекулах, можно измерить многими способами, и в настоящее время есть значительное число таких данных. Если рассмотреть гомоядерные двухатомные молекулы с простой связью, такие, как Еа или С1а, атомам Е и С1 можно приписать ковалентные радиусы простых связей, равные половине межъядерного расстояния в соответствующих молекулах. Следует отметить, что очень часто сумма ковалентных радиусов равна межъядерному расстоянию в межгалогенидах, таких, как С1—Вг (вычислено 2,13 найдено 2,14). Для элементов, которые не могут образовать двухатомные молекулы с простыми связями, используют другие методы определения радиусов. Так, поскольку расстояние С—С в алмазе и множестве органических молекул найдено равным 1,54+0,01 А, то ковалентный радиус атома углерода принимают равным 0,77. Чтобы получить ковалентный радиус атома азота, вычитают 0,77 из расстояния С—N в молекуле НзС—ЫНа, при этом получают 0,70. Этим способом можно составить таблицу ковалентных радиусов простых связей (табл. 4.4). [c.127]
Давно известно, что молекула НгО имеет угловое строение с ао=Ю7° (25]. Метильные группы в диметило-вом эфире (СНз)гО лишь немного увеличивают этот угол (до 11Г 126, 27]). Необычное увеличение валентного угла кислорода найдено в дисилоксане (51Нз)20, ао = = 144° [28]. В самое последнее время обнаружены еще большие изменения этого угла. Так, молекулы 20, КОН, СзОН [29—31] линейны, т. е. ао = 180°. Высокотемпературные электронографические исследования [32, 33] показали, что эффективный валентный угол атома О в субокисях Оа, 1п и Т1 (общей формулы МегО) значительно больше, чем величина этого угла в молекулах воды и диметилового эфира, и составляет величину – 150°. Трудность определения равновесного значения валентного угла атома О в этих молекулах электронографическим методом была обусловлена тем, что частота деформационного колебания этих молекул мала и точно не определена. Последнее приводит к тому, что функция распределения межъядерных расстояний металл — металл имеет несимметричную форму. Для определения равновесной геометрической конфигурации этих молекул необходимо совместное использование спектроскопических и электронографических данных. К сожалению, надежные спектроскопические данные в настоящее время отсутствуют. [c.381]
Для молекулы СЦБ и ДХОБ указанные в тексте разложения пиков на кривые радиального расшределения (КРР) были проведены в 11970 г., вследствие отсутствия необходимых программ в (1966 г. Случайные ошибки в определении межъядерных расстояний оценивались по известным формулам работы 23] ошибки в валентных углах получались из метода проб и ошибок. Расчеты проводились с использованием ЗВ М Сетунь . [c.434]