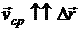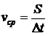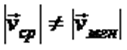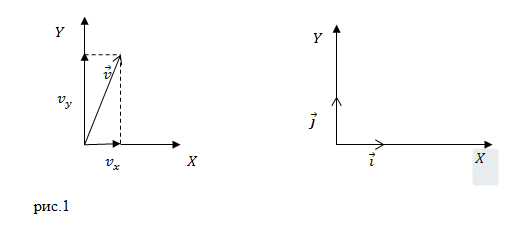Загрузить PDF
Загрузить PDF
Скорость — это быстрота перемещения объекта в заданном направлении. [1]
В общих целях нахождение скорости объекта (v) — простая задача: нужно разделить перемещение (s) в течение определенного времени (s) на это время (t), то есть воспользоваться формулой v = s/t. Однако таким способом получают среднюю скорость тела. Используя некоторые вычисления, можно найти скорость тела в любой точке пути. Такая скорость называется мгновенной скоростью и вычисляется по формуле v = (ds)/(dt), то есть представляет собой производную от формулы для вычисления средней скорости тела.[2]
-
1
Начните с уравнения. Для вычисления мгновенной скорости необходимо знать уравнение, описывающее перемещение тела (его позицию в определенный момент времени),[3]
то есть такое уравнение, на одной стороне которого находится s (перемещение тела), а на другой стороне — члены с переменной t (время).[4]
Например:s = -1.5t2 + 10t + 4
- В этом уравнении:
-
- Перемещение = s. Перемещение — пройденный объектом путь. Например, если тело переместилось на 10 м вперед и на 7 м назад, то общее перемещение тела равно 10 – 7 = 3 м (а на 10 + 7 = 17 м).
- Время = t. Обычно измеряется в секундах.
-
- В этом уравнении:
-
2
Вычислите производную уравнения. Чтобы найти мгновенную скорость тела, чьи перемещения описываются приведенным выше уравнением, нужно вычислить производную этого уравнения. Производная — это уравнение, позволяющее вычислить наклон графика в любой точке (в любой момент времени). Чтобы найти производную, продифференцируйте функцию следующим образом: если y = a*xn, то производная = a*n*xn-1. Это правило применяется к каждому члену многочлена.
- Другими словами, производная каждого члена с переменной t равна произведению множителя (стоящему перед переменной) и степени переменной, умноженному на переменную в степени, равную исходной степени минус 1. Свободный член (член без переменной, то есть число) исчезает, потому что умножается на 0. В нашем примере:
s = -1.5t2 + 10t + 4
(2)-1.5t(2-1) + (1)10t1 – 1 + (0)4t0
-3t1 + 10t0
-3t + 10
- Другими словами, производная каждого члена с переменной t равна произведению множителя (стоящему перед переменной) и степени переменной, умноженному на переменную в степени, равную исходной степени минус 1. Свободный член (член без переменной, то есть число) исчезает, потому что умножается на 0. В нашем примере:
-
3
Замените “s” на “ds/dt”, чтобы показать, что новое уравнение — это производная от исходного уравнения (то есть производная s от t). Производная — это наклон графика в определенной точке (в определенный момент времени). Например, чтобы найти наклон линии, описываемой функцией s = -1.5t2 + 10t + 4 при t = 5, просто подставьте 5 в уравнение производной.
- В нашем примере уравнение производной должно выглядеть следующим образом:
ds/dt = -3t + 10
- В нашем примере уравнение производной должно выглядеть следующим образом:
-
4
В уравнение производной подставьте соответствующее значение t, чтобы найти мгновенную скорость в определенный момент времени.[5]
Например, если вы хотите найти мгновенную скорость при t = 5, просто подставьте 5 (вместо t) в уравнение производной ds/dt = -3 + 10. Затем решите уравнение:ds/dt = -3t + 10
ds/dt = -3(5) + 10
ds/dt = -15 + 10 = -5 м/с- Обратите внимание на единицу измерения мгновенной скорости: м/с. Так как нам дано значение перемещения в метрах, а время — в секундах, и скорость равна отношению перемещения ко времени, то единица измерения м/с — правильная.
Реклама
-
1
Постройте график перемещения тела. В предыдущей главе вы вычисляли мгновенную скорость по формуле (уравнению производной, позволяющему найти наклон графика в определенной точке).[6]
Построив график перемещения тела, вы можете найти его наклон в любой точке, а следовательно определить мгновенную скорость в определенный момент времени.- По оси Y откладывайте перемещение, а по оси X — время. Координаты точек (x,у) получите через подстановку различных значений t в исходное уравнение перемещение и вычисления соответствующих значений s.
- График может опускаться ниже оси X. Если график перемещения тела опускается ниже оси X, то это значит, что тело движется в обратном направлении от точки начала движения. Как правило, график не распространяется за ось Y (отрицательные значения x) — мы не измеряем скорости объектов, движущихся назад во времени!
-
2
Выберите на графике (кривой) точку P и близкую к ней точку Q. Чтобы найти наклон графика в точке P, используем понятие предела. Предел — состояние, при котором величина секущей, проведенной через 2 точки P и Q, лежащих на кривой, стремится к нулю.
- Например, рассмотрим точки P(1,3) и Q(4,7) и вычислим мгновенную скорость в точке P.
-
3
Найдите наклон отрезка PQ. Наклон отрезка PQ равен отношению разницы значений координат «у» точек P и Q к разнице значений координат «х» точек P и Q. Другими словами, H = (yQ – yP)/(xQ – xP), где H — наклон отрезка PQ. В нашем примере наклон отрезка PQ равен:
H = (yQ – yP)/(xQ – xP)
H = (7 – 3)/(4 – 1)
H = (4)/(3) = 1.33 -
4
Повторите процесс несколько раз, приближая точку Q к точке P. Чем меньше расстояние между двумя точками, тем ближе значение наклона полученных отрезков к наклону графика в точке P. В нашем примере проделаем вычисления для точки Q с координатами (2,4.8), (1.5,3.95) и (1.25,3.49) (координаты точки P остаются прежними):
Q = (2,4.8): H = (4.8 – 3)/(2 – 1)
H = (1.8)/(1) = 1.8Q = (1.5,3.95): H = (3.95 – 3)/(1.5 – 1)
H = (.95)/(.5) = 1.9Q = (1.25,3.49): H = (3.49 – 3)/(1.25 – 1)
H = (.49)/(.25) = 1.96 -
5
Чем меньше расстояние между точками P и Q, тем ближе значение H к наклону графика в точке P При предельно малом расстоянии между точками P и Q, значение H будет равно наклону графика в точке P Так как мы не можем измерить или вычислить предельно малое расстояние между двумя точками, графический способ дает оценочное значение наклона графика в точке Р.
- В нашем примере при приближении Q к P мы получили следующие значения H: 1.8; 1.9 и 1.96. Так как эти числа стремятся к 2, то можно сказать, что наклон графика в точке P равен 2.
- Помните, что наклон графика в данной точке равен производной функции (по которой построен этот график) в этой точке. График отображает перемещение тела с течением времени и, как отмечалось в предыдущем разделе, мгновенная скорость тела равна производной от уравнения перемещения этого тела. Таким образом, можно заявить, что при t = 2 мгновенная скорость равна 2 м/с (это оценочное значение).
Реклама
-
1
Вычислите мгновенную скорость при t = 4, если перемещение тела описывается уравнением s = 5t3 – 3t2 + 2t + 9. Этот пример похож на задачу из первого раздела с той лишь разницей, что здесь дано уравнение третьего порядка (а не второго).
- Сначала вычислим производную этого уравнения:
s = 5t3 – 3t2 + 2t + 9
s = (3)5t(3 – 1) – (2)3t(2 – 1) + (1)2t(1 – 1) + (0)9t0 – 1
15t(2) – 6t(1) + 2t(0)
15t(2) – 6t + 2 - Теперь подставим в уравнение производной значение t = 4:
s = 15t(2) – 6t + 2
15(4)(2) – 6(4) + 2
15(16) – 6(4) + 2
240 – 24 + 2 = 22 м/с
- Сначала вычислим производную этого уравнения:
-
2
Оценим значение мгновенной скорости в точке с координатами (1,3) на графике функции s = 4t2 – t. В этом случае точка P имеет координаты (1,3) и необходимо найти несколько координат точки Q, лежащий близко к точке P. Затем вычислим H и найдем оценочные значения мгновенной скорости.
- Сначала найдем координаты Q при t = 2, 1.5, 1.1 и 1.01.
s = 4t2 – t
t = 2: s = 4(2)2 – (2)
4(4) – 2 = 16 – 2 = 14, so Q = (2,14)t = 1.5: s = 4(1.5)2 – (1.5)
4(2.25) – 1.5 = 9 – 1.5 = 7.5, so Q = (1.5,7.5)t = 1.1: s = 4(1.1)2 – (1.1)
4(1.21) – 1.1 = 4.84 – 1.1 = 3.74, so Q = (1.1,3.74)t = 1.01: s = 4(1.01)2 – (1.01)
4(1.0201) – 1.01 = 4.0804 – 1.01 = 3.0704, so Q = (1.01,3.0704) - Теперь вычислим H:
Q = (2,14): H = (14 – 3)/(2 – 1)
H = (11)/(1) = 11Q = (1.5,7.5): H = (7.5 – 3)/(1.5 – 1)
H = (4.5)/(.5) = 9Q = (1.1,3.74): H = (3.74 – 3)/(1.1 – 1)
H = (.74)/(.1) = 7.3Q = (1.01,3.0704): H = (3.0704 – 3)/(1.01 – 1)
H = (.0704)/(.01) = 7.04 - Так как полученные значения H стремятся к 7, то можно сказать, что мгновенная скорость тела в точке (1,3) равна 7 м/с (оценочное значение).
Реклама
- Сначала найдем координаты Q при t = 2, 1.5, 1.1 и 1.01.
Советы
- Чтобы найти ускорение (изменение скорости с течением времени), используйте метод из первой части, чтобы получить производную функции перемещения. Затем возьмите еще раз производную от полученной производной. Это даст вам уравнение для нахождения ускорения в данный момент времени — все, что вам нужно сделать, это подставить значение для времени.
- Уравнение, описывающее зависимость у (перемещение) от x (время), может быть очень простым, например: у = 6x + 3. В этом случае наклон является постоянным и не надо брать производную, чтобы его найти. Согласно теории линейных графиков, их наклон равен коэффициенту при переменной x, то есть в нашем примере =6.
- Перемещение подобно расстоянию, но оно имеет определенное направление, что делает его векторной величиной. Перемещение может быть отрицательным, в то время как расстояние будет только положительным.
Реклама
Об этой статье
Эту страницу просматривали 83 377 раз.
Была ли эта статья полезной?
Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.
Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.
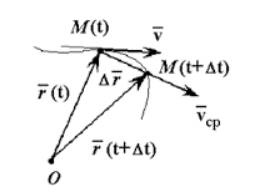
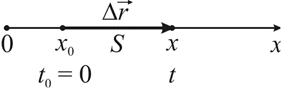
Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения υ=∆r∆t; υ↑↑∆r.
Рисунок 1. Средняя скорость сонаправлена перемещению
Модуль средней скорости по пути равняется υ=S∆t.
Мгновенная скорость точки. Формулы
Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.
Мгновенной скоростью называют предел, к которому стремится средняя скорость υ при стремлении промежутка времени ∆t к 0:
υ=lim∆t∆r∆t=drdt=r˙.
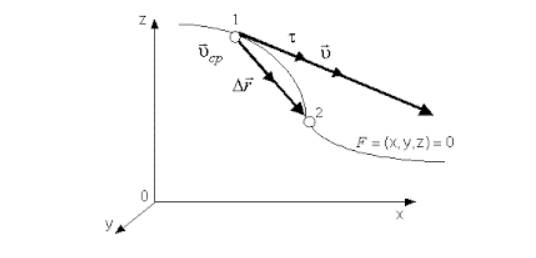
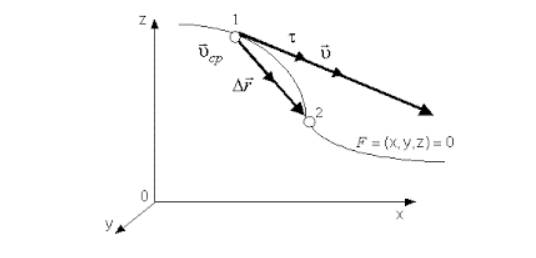
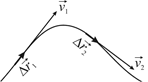
Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение dr совпадает с бесконечно малым элементом траектории ds.
Рисунок 2. Вектор мгновенной скорости υ
Имеющееся выражение υ=lim∆t∆r∆t=drdt=r˙ в декартовых координатах идентично ниже предложенным уравнениям:
υx=dxdt=x˙υy=dydt=y˙υz=dzdt=z˙.
Перемещение и мгновенная скорость
Запись модуля вектора υ примет вид:
υ=υ=υx2+υy2+υz2=x2+y2+z2.
Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r=rq1, q2, q3, тогда значение скорости запишется как:
υ=drdt=∑i=13∂r∂qi∂qi∂r=∑i=13∂r∂qiq˙i.
Рисунок 3. Перемещение и мгновенная скорость в системах криволинейных координат
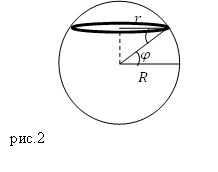
При сферических координатах предположим, что q1=r; q2=φ; q3=θ, то получим υ, представленную в такой форме:
υ=υrer+υφeφ+υθφθ, где υr=r˙; υφ=rφ˙sin θ; υθ=rθ˙; r˙=drdt; φ˙=dφdt; θ˙=dθdt; υ=r1+φ2sin2θ+θ2.
Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением dr=υ(t)dt
Дан закон прямолинейного движения точки x(t)=0,15t2-2t+8. Определить ее мгновенную скорость через 10 секунд после начала движения.
Решение
Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:
υ(t)=x˙(t)=0.3t-2; υ(10)=0.3×10-2=1 м/с.
Ответ: 1 м/с.
Движение материальной точки задается уравнением x=4t-0,05t2. Вычислить момент времени tост, когда точка прекратит движение, и ее среднюю путевую скорость υ.
Решение
Вычислим уравнение мгновенной скорости, подставим числовые выражения:
υ(t)=x˙(t)=4-0,1t.
4-0,1t=0;tост=40 с;υ0=υ(0)=4;υ=∆υ∆t=0-440-0=0,1 м/с.
Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0,1 м/с.
Содержание материала
- Советы
- Видео
- Что такое мгновенная скорость на реальных примерах
- Как найти мгновенную скорость из средней скорости
- Мгновенная скорость при криволинейном движении
- Ускорение. Касательное ускорение. Центростремительное ускорение
- Об особенностях понятия мгновенной скорости
- Что мы узнали?
Советы
- Чтобы найти ускорение (изменение скорости с течением времени), используйте метод из первой части, чтобы получить производную функции перемещения. Затем возьмите еще раз производную от полученной производной. Это даст вам уравнение для нахождения ускорения в данный момент времени — все, что вам нужно сделать, это подставить значение для времени.
- Уравнение, описывающее зависимость у (перемещение) от x (время), может быть очень простым, например: у = 6x + 3. В этом случае наклон является постоянным и не надо брать производную, чтобы его найти. Согласно теории линейных графиков, их наклон равен коэффициенту при переменной x, то есть в нашем примере =6.
- Перемещение подобно расстоянию, но оно имеет определенное направление, что делает его векторной величиной. Перемещение может быть отрицательным, в то время как расстояние будет только положительным.
Видео
Что такое мгновенная скорость на реальных примерах
Реальные примеры мгновенной скорости
Если мы рассмотрим пример мяча для сквоша, мяч возвращается в исходную точку; в это время полное смещение и средняя скорость будут равны нулю. В таких случаях движение рассчитывается по формуле мгновенная скорость.
Как найти мгновенную скорость из средней скорости
Для того, чтобы найти мгновенная скорость в точке, мы должны сначала найти среднюю скорость в этой точке.
Вы можете найти мгновенную скорость при t = a с помощью вычисление средней скорости графика зависимости положения от времени путем взятия меньшего и большего приращения точки, в которой вы хотите определить Vinst.
Мгновенная скорость при криволинейном движении
Положение материальной точки на траектории зададим радиус-вектором $overline{r}(t)$, который проведем в точку наблюдения из какой-либо неподвижной точки, которую примем за начало координат. Тогда мгновенной скоростью материальной точки будет векторная величина, равная:
скорость — это вектор, направленный по касательной к траектории движения материальной точки в месте нахождения частицы.
Ускорение. Касательное ускорение. Центростремительное ускорение
Продолжая речь о телах, движущихся неравномерно, необходимо сказать о такой физической величине, как ускорение.
Единицы измерения ускорения:

Если скорость тела меняется не равномерно на выбранном участке пути, нужно поступить так же, как и в случае с поиском мгновенной скорости: разделить на маленькие отрезки времени и рассматривать ускорение на каждом из них.
Поскольку ускорение получается из разности векторов скорости (конечной и начальной), в общем случае оно будет направлено под некоторым углом к мгновенной скорости (а, следовательно, и к вектору перемещения, и к касательной к траектории).

Об особенностях понятия мгновенной скорости
Для того чтобы вычислить мгновенную скорость на практике, следует понимать, что она представляет собой функцию времени. Следует определить на какое расстояние переместился объект в течение крайне малого промежутка времени, который называют моментом времени. Насколько же мал этот допустимый интервал? Если рассматривать совершенные приборы, например радиолокационные станции, то даже самые точные из них позволяют отслеживать скорость за время, которое примерно составляет около 10-6 с. Согласитесь, что несмотря на ничтожную малость этого значения, оно ни в коей мере не является моментом времени, а представляет собой временной промежуток. По этой причине отношение физиков к понятию скорости в определенный момент времени неоднозначное, и оно считается не наделенным конкретным физическим смыслом. Хотя на практике термин «мгновенная скорость» широко используется при управлении навигацией в авиации и космонавтике.
Подобным образом можно рассуждать и о мгновенном ускорении, которое представляет собой зависимость, а точнее производную от скорости и имеет с ней одно направление.
Что касается мгновенной скорости физического тела, находящегося в состоянии покоя относительно выбранной системы отсчета, то она будет равняться нулю.
Что мы узнали?
Мгновенная скорость – это скорость прохождения данного малого участка пути за малый промежуток времени. В идеале мгновенная скорость определяется на текущем бесконечно малом промежутке времени, за который совершается бесконечно малое перемещение.
Теги
Определение
Скорость — это термин, который характеризует изменение заданной координаты в движении.
В ситуации, когда координаты изменяют свое положение относительно оси, следовательно, их материальная точка будет находится в процессе движения.
Средняя скорость — это величина векторного типа, которая имеет определенное числовое равенство относительно перемещения совершаемого в конкретную единицу времени, и направлена совместно я с векторным перемещением.
Средняя скорость – довольно простое понятие в разделе кинематика.
Определение
Следовательно, средняя скорость – это конкретная величина, которая равна отношению пройденного пути, к величине времени, за которое данный путь пройден телом.
[v_{mathrm{cp}}=frac{S}{t}]
Основные моменты, на которые следует уделить внимание при определении средней скорости:
- Необходимое время, которое учитывается, когда тело в процессе движения может делать кратковременные остановки;
- Определение правильной величины средней скорость тела, которое начинает движение в пункте А и оканчивает его в пункте В. Но в процессе движения, может повернуть несколько раз обратно, а затем снова продолжает движение в заданном направлении, двигаясь в пункт В.
Модуль для определения средней скорости движения вычисляется по следующей формуле: V=s/t.
Определение
Мгновенная скорость — это некий числовой предел, к которому стремится показатель средней скорости.
Мгновенная скорость, как правило, характеризует заданное движение точки в конкретный и определенный момент времени.
Для любой категории характерно бесконечное количество точек. Потому что каждый временной интервал включает в себя бесконечное количество мгновений.
Когда сам временной интервал стремится к нулевому значению, то он автоматически преобразуется в мгновение.
Формула
Мгновение скорости можно определить по следующей формуле: v=s/Δt
где:
v – скорость мгновения, м/с
s – движение, перемещение тела, м ( если Δt→0 )
Δt – временной интервал, который стремится к нулевому значению, с.
Стоит отметить, что мгновенная скорость – это величина, которая изображена как вектор. Она равняется отношению движения к временному интервалу. А именно: промежуток времени, за который данное перемещение происходит, при условии, что временной интервал стремится к нулевому значению.
Временной интервал движения тела – это всегда скляр с положительным значением. Поэтому мгновенная скорость и ее векторное значение, всегда сонаправлено с перемещением, которое имеет значение стремящееся к нулю.
Нет времени решать самому?
Наши эксперты помогут!
Направление и перемещение действия средней и мгновенной скорости относительно координатной оси
Средняя скорость всегда направлена вместе с перемещением:
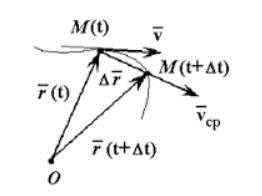
Для мгновенной скорости характерно движение в конкретный момент времени.
Направление векторной скорости, которая обозначается как: υ расположено по касательной, относительно криволинейной траектории.
Так как непрерывное малое перемещение однозначно совпадает с бесконечно малым элементом траектории.
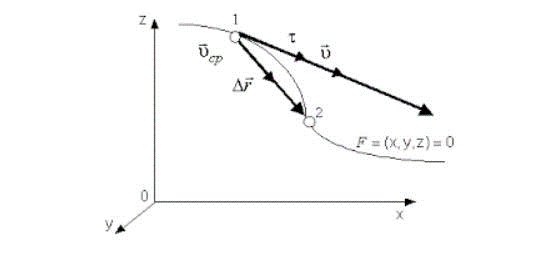
Примеры решения задач по определению мгновенной и средней скорости
Пример №1:
Имеет ли способность мгновенная скорость, изменять свое значение только относительно направления, при этом не меняя модульную величину.
Используя основные термины и формулы, решим данную задачу. При решении необходимо рассмотреть пример:
- Движение тела происходит по криволинейной траектории. На ней необходимо обозначить начальный и конечный пункты, а именно: точки А и В.
- Далее нужно обозначить основное направление мгновенной скорости в заданных ранее точках.
- Следует помнить, что мгновенная скорость имеет направление относительно касательной по траектории.
- Расстояние и скорость имеют одинаковые значения по модулю и, следовательно, равны 5 м/с.
[left|vec{V}_{A}right|=left|vec{V}_{B}right|=5 frac{м}{c}]
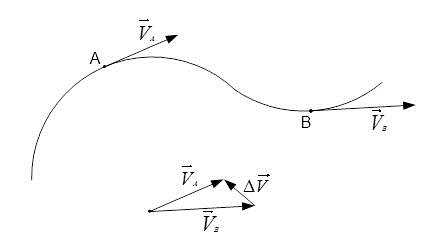
Следующее равенство вида: [vec{V}_{A}=vec{V}_{B}] будет неверным. Так как скорость – является векторной величиной. Поэтому очень важно задать не только числовое значение, но направление по которому будет осуществляться движение.
В случае, когда [vec{V}_{A}=vec{V}_{B}] можно составить равенство следующего вида:[vec{V}_{A}-vec{V}_{B}=0] однако определив вектор разности значений [Delta vec{V}], можно сделать вывод, что его значение не равно нулевому.
Следовательно, [vec{V}_{A} neq vec{V}_{B}], другими словами мгновенная скорость может быть равна нулевому значению и быть равной по модулю. Однако, при этом различаться по основному направлению движения.
Пример №2:
Возможно ли изменение по модульному значению мгновенной скорости, но при этом направление остается неизменным.
Алгоритм решения:
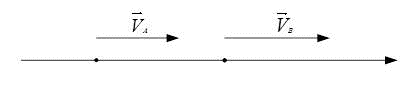
Рассмотрев рисунок, который приведен выше, можно сделать вывод, что:
- в точке А и в точке В направление движения мгновенной скорости одинаково;
- рассматриваемое тело, которое осуществляет движение, делает это с равным ускорением, следовательно:
[vec{V}_{A}=vec{V}_{B}]
Мгновенная и средняя скорость
Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.
Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.
Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения ” open=” υ = ∆ r ∆ t ; ” open=” υ ↑ ↑ ∆ r .
Рисунок 1 . Средняя скорость сонаправлена перемещению
Модуль средней скорости по пути равняется ” open=” υ = S ∆ t .
Мгновенная скорость точки. Формулы
Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.
Мгновенной скоростью называют предел, к которому стремится средняя скорость ” open=” υ при стремлении промежутка времени ∆ t к 0 :
υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ .
Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение d r совпадает с бесконечно малым элементом траектории d s .
Рисунок 2 . Вектор мгновенной скорости υ
Имеющееся выражение υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ в декартовых координатах идентично ниже предложенным уравнениям:
υ x = d x d t = x ˙ υ y = d y d t = y ˙ υ z = d z d t = z ˙ .
Перемещение и мгновенная скорость
Запись модуля вектора υ примет вид:
υ = υ = υ x 2 + υ y 2 + υ z 2 = x 2 + y 2 + z 2 .
Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r = r q 1 , q 2 , q 3 , тогда значение скорости запишется как:
υ = d r d t = ∑ i = 1 3 ∂ r ∂ q i ∂ q i ∂ r = ∑ i = 1 3 ∂ r ∂ q i q ˙ i .
Рисунок 3 . Перемещение и мгновенная скорость в системах криволинейных координат
При сферических координатах предположим, что q 1 = r ; q 2 = φ ; q 3 = θ , то получим υ , представленную в такой форме:
υ = υ r e r + υ φ e φ + υ θ φ θ , где υ r = r ˙ ; υ φ = r φ ˙ sin θ ; υ θ = r θ ˙ ; r ˙ = d r d t ; φ ˙ = d φ d t ; θ ˙ = d θ d t ; υ = r 1 + φ 2 sin 2 θ + θ 2 .
Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением d r = υ ( t ) d t
Дан закон прямолинейного движения точки x ( t ) = 0 , 15 t 2 – 2 t + 8 . Определить ее мгновенную скорость через 10 секунд после начала движения.
Решение
Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:
υ ( t ) = x ˙ ( t ) = 0 . 3 t – 2 ; υ ( 10 ) = 0 . 3 × 10 – 2 = 1 м / с .
Ответ: 1 м / с .
Движение материальной точки задается уравнением x = 4 t – 0 , 05 t 2 . Вычислить момент времени t о с т , когда точка прекратит движение, и ее среднюю путевую скорость ” open=” υ .
Решение
Вычислим уравнение мгновенной скорости, подставим числовые выражения:
υ ( t ) = x ˙ ( t ) = 4 – 0 , 1 t .
4 – 0 , 1 t = 0 ; t о с т = 40 с ; υ 0 = υ ( 0 ) = 4 ; ” open=” υ = ∆ υ ∆ t = 0 – 4 40 – 0 = 0 , 1 м / с .
Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0 , 1 м / с .
Средняя и мгновенная скорость
Физическая величина, которая характеризует быстроту изменения координаты – скорость ( 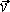
Средняя скорость движения – это физическая величина, равная отношению вектора перемещения точки к интервалу времени, за который это перемещение произошло.
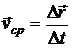
Средняя скорость – это величина, численно равная перемещению в единицу времени..
Направление вектора средней скорость всегда совпадает с направлением вектора перемещения:
Если точка движется прямолинейно в одном направлении , то S = | 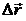
Следовательно, модуль средней скорости по пути равен:
В международной системе единиц (СИ) скорость измеряется в метрах в секунду:
В системе единиц СГС (название по первым буквам трех основных единиц: сантиметр, грамм, секунда) скорость измеряется в сантиметрах в секунду:
Мгновенной скоростью 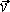
Мгновенная скорость определяется как предел отношения вектора перемещения к интервалу времени, за который это перемещение происходит, при стремлении интервала времени к нулю:
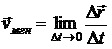
С точки зрения математики формула представляет собой определение первой производной по времени от радиус-вектора:
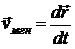
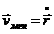
Вектор скорости, как и любой вектор, можно задавать тремя компонентами по осям координат:
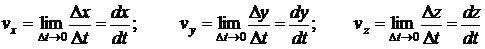
т.е. компоненты вектора скорости выражаются производными по времени от соответствующих координат точки.
Примечание. Если известен вид функций, выражающих зависимость координат от времени, то компоненты скорости получим, дифференцируя эти функции по времени. Наоборот, если известно, как компоненты скорости точки зависят от времени, то при помощи обратной операции – интегрирования – мы найдем вид функций, выражающих зависимость координат от времени (см. примечание в § 7).
Вектор мгновенной скорости направлен по касательной к траектории (рис. 12). Исходя этого, можно дать следующее определение траектории:
Траектория – это линия, касательная к каждой точке которой совпадает с направлением вектора скорости в этих точках.
По характеру изменения скорости механические движения классифицируются на равномерные и неравномерные.
При равномерном движении модуль скорости в любой момент времени – величина постоянная:
| 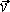
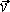
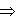
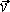
При неравномерном (переменном) движении модуль скорости изменя-ется:
– Переменное движение, при котором модуль скорости увеличивается, (v > v0) – это ускоренное движение.
– Переменное движение, при котором модуль скорости уменьшается (v
Дата добавления: 2015-01-15 ; просмотров: 10 ; Нарушение авторских прав
Формула линейной скорости
Скорость движения тела ($overline$) называют линейной, если хотят подчеркнуть ее отличие от угловой скорости ($omega $). Чаще величину $overline$, являющуюся векторной величиной, основной характеристикой движения тела, называют просто скоростью.
Формула мгновенной скорости
Мгновенная скорость (обычно просто скорость) – это векторная величина, равная первой производной от радиус-вектора ($overline$), определяющего положение движущейся материальной точки, по времени ($t$):
Представим вектор $overline$ в декартовой системе координат в виде:
где $overline$; $overline$; $overline$ – единичные орты соответствующих осей координат, постоянные во времени, при этом формулой скорости можно считать выражение:
Проекциями вектора скорости на оси координат X, Y,Z являются:
Величину (модуль) скорости найдем в соответствии с формулой:
Если движение задается при помощи параметров траектории, что означает: известны траектория и функция пути от времени ($s(t)$); путь отсчитывают от точки траектории, которую считают начальной; каждая точка траектории характеризуется своей величиной $s$; радиус – вектор является функцией от $s,$ и траекторию можно задать при помощи уравнения:
в таком случае в формуле (1) $overlineleft(tright)$ будем рассматривать как сложную функцию: $overlineleft[sleft(tright)right]$, формулой скорости станет:
Величина $Delta s$ – это расстояние между двумя точками по траектории движения тела. Модуль $left|Delta overlineright|$ – расстояние между этими точками по кратчайшему направлению – прямой. При сближении рассматриваемых двух точек разница между $Delta s$ и $left|Delta overlineright|$ уменьшается. Имеем:
где $overline<tau >$ – единичный вектор, касательный к траектории движения материальной точки. Кроме этого:
модуль скорости движения точки по траектории. Уравнение (6) представим как:
Формула (9) показывает, что мгновенная скорость направлена по касательной к траектории движения тела (материальной точки).
Формулы средней скорости
Вектор средней скорости ($leftlangle overlinerightrangle $) при движении между двумя точками определяют как:
где в скобках у вектора средней скорости указан промежуток времени, для которого найдена средняя скорость; $Delta overline$ – вектор перемещения точки; $Delta t$- время движения.
При неравномерном движении средняя скорость для разных промежутков времени не одинакова. Устремляя $Delta t$ к нулю, мы получим, что средняя скорость стремится к величине мгновенной скорости.
Иногда при вычислении средней скорости (ее называют средне путевой) применяют другую формулу:
[leftlangle vrightrangle =fracleft(11right),]
где $s$- весь путь пройденный точкой; $t$ – все время ее движения. В этом случае средняя скорость – это скаляр.
Формулы линейной скорости при движении разных видов
Если тело движется равномерно, скорость постоянная величина. Ее формулой считают:
где $s$ – путь; $t$ – время движения. При равномерном прямолинейном движении у скорости постоянным является не только величина, но и направление, при этом записывают:
Если тело перемещается с постоянным ускорением (при $overline=const$) скорость равна:
Угловая и линейная скорости
При движении по кривой вместе со скоростью движения по траектории ($v$- линейная скорость) вводят угловую скорость ($omega $), которая характеризует быстроту изменения угла поворота $varphi $:
Связь между линейной и угловой скоростями определена формулой:
где $R$ – радиус кривизны траектории, по которой движется точка.
Примеры задач с решением
Задание. Положение материальной точки, задано радиус-вектором $overlineleft(tright),$ который является функцией времени: $overlineleft(tright)=<2t>^4overline+t^2overline,$ где $overline$ и $overline$ – единичные векторы осей X и Y (рис.1). Чему равен модуль скорости точки в момент времени $t=1$c?
Решение. В качестве основы для решения задачи воспользуемся формулой скорости:
Подставим в выражение (1.1) $overlineleft(tright)=t^4overline+3t^2overline,$ получим:
Из уравнения (1.2) имеем:
Используя теорему Пифагора, величину скорости вычислим как:
Ответ. $v=sqrt<68>frac<м><с>$
Задание. С какой скоростью должен лететь самолет с востока на запад на широте $varphi $, чтобы за окном иллюминатора всегда было светло? Радиус Земли считать равным R.
Решение. Сделаем рисунок.
Самолет летит по окружности (рис.2), радиус которой найдем как:
Для того чтобы не наступала ночь, тело должно двигаться с угловой скоростью, которая равна скорости вращения Земли вокруг своей оси ($omega $). Для вычисления скорости движения самолета воспользуемся формулой:
Угловую скорость вращения Земли найдем, зная, что период вращения Земли составляет 24 ч ($T=24 ч$), следовательно, величину угловой скорости вращения Земли можно считать известной и равной:
Окончательно получим, скорость движения самолёта равна:
[spoiler title=”источники:”]
http://lektsii.com/1-72688.html
http://www.webmath.ru/poleznoe/fizika/fizika_133_formula_linejnoj_skorosti.php
[/spoiler]
- A.Линейную скорость тела
- I. средняя скорость; II. мгновенная скорость; III. вектор скорости, выраженный через проекции на оси; IV. величина (модуль) скорости.
- А) Скорость вывода на печать и качество печати высокая
- Автомобиль двигался первую половину пути со скоростью , а вторую половину пути со скоростью . Найти среднюю скорость автомобиля на всем пути
- Билет №14. Средняя гармоническая: простая и взвешенная; особенности применения
- Вектор скорости. Средняя и мгновенная скорость.
- Глава 2. Скорость движения
- Движение точки по окружности. Угол поворота, угловая скорость, частота и период обращения. Связь между линейной и угловой скоростью.
- Движение частицы в центральном поле. Сохранение момента импульса в центральном поле сил. Секториальная скорость.
- Динамика семейных конфликтов характеризуется классическими этапами, но вместе с тем они отличаются повышенной эмоциональностью и скоростью протекания каждого из этапов.