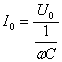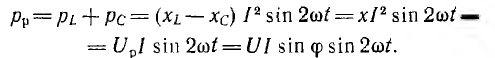|
Емкостное сопротивление в цепи переменного тока |
|
|
При включении конденсатора в цепь постоянного напряжения сила тока I=0, а при включении конденсатора в цепь переменного напряжения сила тока I ? 0. Следовательно, конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока. |
|
|
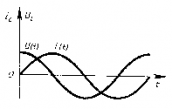
Мгновенное значение напряжения равно Мгновенное значение силы тока равно: Таким образом, колебания напряжения отстают от колебаний тока по фазе на π/2. |
|
|
Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению, то для максимальных значений тока и напряжения получим: |
|
|
Емкостное сопротивление не является характеристикой проводника, т.к. зависит от параметров цепи (частоты). |
|
|
Чем больше частота переменного тока, тем лучше пропускает конденсатор ток (тем меньше сопротивление конденсатора переменному току). |
|
|
Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и емкостной нагрузкой. Такая нагрузка наз. реактивной. |
|
|
Индуктивное сопротивление в цепи переменного тока |
|
|
В катушке, включенной в цепь переменного напряжения, сила тока меньше силы тока в цепи постоянного напряжения для этой же катушки. Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения. |
|
|
Мгновенное значение силы тока: |
|
|
Мгновенное значение напряжения можно установить, учитывая, что u = – εi, где u – мгновенное значение напряжения, а εi – мгновенное значение эдс самоиндукции, т. е. при изменении тока в цепи возникает ЭДС самоиндукции, которая в соответствии с законом электромагнитной индукции и правилом Ленца равна по величине и противоположна по фазе приложенному напряжению. |
|
|
Следовательно Напряжение опережает ток по фазе на π/2. |
|
|
Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональная сопротивлению, то приняв величину ωL за сопротивление катушки переменному току, получим: – закон Ома для цепи с чисто индуктивной нагрузкой. |
|
|
Величина |
|
|
Т.о. в любое мгновение времени изменению силы тока противодействует ЭДС самоиндукции. ЭДС самоиндукции — причина индуктивного сопротивления. |
|
|
В отличие от активного сопротивления, индуктивное не является характеристикой проводника, т.к. зависит от параметров цепи (частоты): чем больше частота переменного тока, тем больше сопротивление, которое ему оказывает катушка. |
|
|
Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и индуктивной нагрузкой. Такая нагрузка наз. реактивной. |
Содержание:
Цепи переменного тока:
Основное применение в электротехнике и радиотехнике имеют переменные напряжения и токи, являющиеся периодическими функциями времени. Мгновенные значения периодических напряжений u и токов i повторяются через промежуток времени Т, называемый периодом:
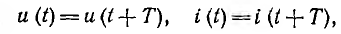
где t — время; число периодов в единицу времени 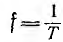
Электротехника сильных токов использует в основном низкие частоты. Промышленной частотой в СССР и Европе является 50 гц, в Америке 60 гц, в некоторых областях техники применяют частоты в сотни герц и выше. Техника проводной и радиосвязи использует широкий диапазон частот от долей герц до 1012 гц. Постоянные э.д. с. и токи можно рассматривать как частный случай переменных, частота которых равна нулю (f — 0).
Простейшими и широко применяемыми в электротехнических и радиотехнических устройствах являются периодические напряжения и токи, изменяющиеся по закону синуса. Для случая синусоидального закона изменения функций разработаны простые методы расчета цепей, подобные методам расчета цепей постоянного тока. Если закон изменения периодического напряжения u (t) или i (t) отличен от синусоиды, эти функции могут быть разложены в ряд Фурье, т. е. представлены в виде суммы синусоид, что позволит при расчетах линейных цепей применить метод наложения и свести расчеты к синусоидальным функциям.
Что такое цепь постоянного тока
Цепью постоянного тока называется такая цепь, в которой ЭДС, токи и напряжения остаются постоянными по величине и не зависят от времени.
Цепи делятся на два больших класса:
- линейные;
- нелинейные.
Электрические цепи, содержащие только элементы с линейными вольтамперными характеристиками, называются линейными цепями.
Генератор синусоидального напряжения
Для получения синусоидальных переменных токов в линейных цепях э. д. с. также должны изменяться по синусоиде. Простейшим генератором синусоидальной э. д. с. может служить прямоугольная катушка, вращающаяся с постоянной угловой скоростью в однородном магнитном поле вокруг оси, перпендикулярной к направлению линий магнитной индукции (рис. 6.1). При этом пронизывающий катушку магнитный поток изменяется, и в ней по закону электромагнитной индукции индуктируется э. д. с. Цепь нагрузки подключается к генератору с помощью щеток, наложенных на два кольца, соединенных с катушкой.
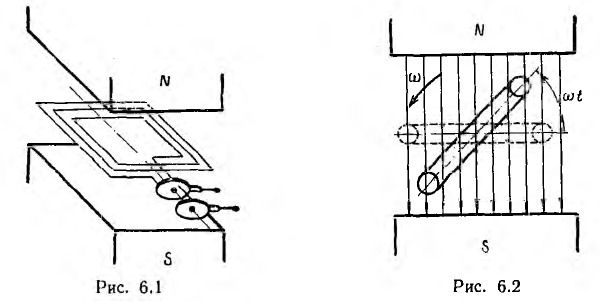
Пусть в начальный момент времени t=О плоскость катушки будет перпендикулярна магнитным линиям (пунктир на рис. 6.2). Тогда магнитный поток, пронизывающий катушку, будет иметь максимальное (амплитудное) значение Фm. Если угловая скорость вращения катушки с числом витков w равна ω, то в момент времени t катушка окажется повернутой на угол ωt, и мгновенные значения ее потока и потокосцепления будут равны
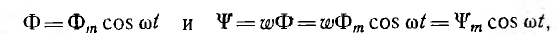
где 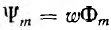 — максимальное значение потокосцепления.
— максимальное значение потокосцепления.
Тогда мгновенное значение э. д. с. катушки
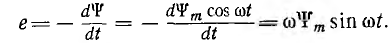
Величина 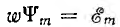 представляет собой максимальное значение
представляет собой максимальное значение
э. д. с., которое она получает, когда sinωt становится равным единице.
Следовательно, 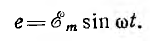
Временные диаграммы
Временная диаграмма магнитного потока и электродвижущей силы катушки показана на рис. 6.3, а. Максимальная э. д. с. индуктируется в моменты, когда поток, пронизывающий катушку, равен нулю, так как тогда скорость изменения потока достигает наибольшего значения. Э д. с. равна нулю в моменты, когда поток получает максимальное значение, так как при этом поток не меняет своей величины.
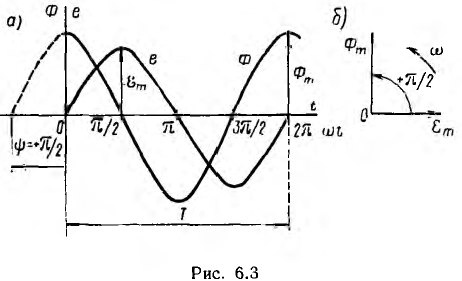
Как видно из рис. 6.3, а,
откуда 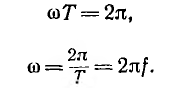
Величина ω, пропорциональная частоте f и равная в данном случае угловой скорости вращения катушки, называется угловой частотой.
Общее выражение для синусоидальной функции времени имеет вид:
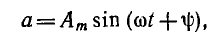
где а — мгновенное значение функции; Аm — ее максимальное значение (амплитуда); ω— угловая частота; угол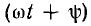 — фаза, а угол ψ — начальная фаза. Начальная фаза определяет значение функции для начального момента времени:
— фаза, а угол ψ — начальная фаза. Начальная фаза определяет значение функции для начального момента времени:
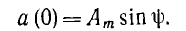
Так, для рассмотренного источника синусоидальной э. д. с.
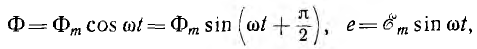
начальная фаза потока равна + π/2 , э. д. с. — нулю, т. е. магнитный поток и э. д. с. сдвинуты по фазе на π/2.
На временной диаграмме, как видно из рис. 6.3, а, положительная начальная фаза откладывается от начала координат влево, т. е. в сторону отрицательных значений ωt, а отрицательную начальную фазу следует откладывать в сторону положительных значений ωt.
Векторные диаграммы
Расчеты в цепях с синусоидальными напряжениями и токами весьма упрощаются, если вместо синусоид оперировать с их изображениями — вращающимися векторами.
Пусть NOM является прямоугольной системой осей координат и пусть положительные углы откладываются против направления вращения стрелки часов (рис. 6.4). Если нужно найти, например, мгновенные значения синусоиды э. д. с. 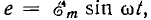 то для этого можно взять вектор ОА, длина которого равна в выбранном масштабе максимальному значению э. д. с.
то для этого можно взять вектор ОА, длина которого равна в выбранном масштабе максимальному значению э. д. с. 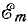 считать начальным положением вектора ОА0 такое, при котором он образует с осью ON угол, равный начальной фазе, т. е. в данном случае совпадает с 0N: вращать этот вектор в положительном направлении с постоянной угловой скоростью, равной угловой частоте ω. Тогда угол, который вектор образует с осью ON в момент времени е, будет равен ωt и мгновенное значение э. д. с. е
считать начальным положением вектора ОА0 такое, при котором он образует с осью ON угол, равный начальной фазе, т. е. в данном случае совпадает с 0N: вращать этот вектор в положительном направлении с постоянной угловой скоростью, равной угловой частоте ω. Тогда угол, который вектор образует с осью ON в момент времени е, будет равен ωt и мгновенное значение э. д. с. е
для этого момента времени будет равно проекции Оа вектора ОА на ось ОМ:
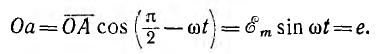
Проекция вектора ОА на ось ОМ для начального момента времени 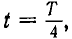
будет равна нулю, для момента времени, когда вектор повернется на угол π/2, проекция будет равна 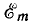 полный цикл изменений э. д. с. получится за один полный оборот вектора ОА.
полный цикл изменений э. д. с. получится за один полный оборот вектора ОА.
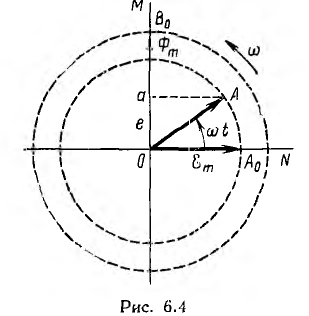
Таким же образом можно находить мгновенные значения потока 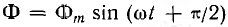 , с той разницей, что для начального момента
, с той разницей, что для начального момента
времени вектор ОВ0, изображающий в выбранном масштабе максимальное значение потока Фm, необходимо направить по оси ОМ, так как он должен образовать с осью ON угол + π/2, равный начальной фазе потока.
Таким образом, можно условиться изображать синусоидальную функцию вектором, длина которого определяется максимальным ее значением, а направление — ее начальной фазой, при этом положительная начальная фаза откладывается от горизонтальной оси в сторону вращения векторов. В результате получается векторная диаграмма, показанная для рассмотренного примера потока и э. д. с. на рис. 6.3, б.
Векторы, изображающие синусоидальные функции времени, имеют совсем другой смысл, чем векторы, изображающие, например, силы в механике. Вектор силы дает ее величину и направление в пространстве, вектор, изображающий синусоиду, является вращающимся вектором, дающим своей проекцией на неподвижную ось мгновенное значение синусоиды. Такой вектор чертится в начальном своем положении, которое дает начальную фазу синусоиды, но, конечно, не направление изображаемой величины впространстве. Подобным вектором можно изображать любую синусоидально изменяющуюся величину, в том числе скалярную — э. д. с., тон, поток и т. п.
Векторные диаграммы особенно удобны при сложении или вычитании синусоид одинаковой частоты. Как известно, результатом будет также синусоида той же частоты. При сложении нескольких синусоид нужно складывать их мгновенные значения, т. е. проекции векторов, изображающих эти синусоиды, но так как сумма проекций векторов на какую-либо ось равна проекции геометрической суммы этих векторов на ту же ось, то эга геометрическая сумма и будет вектором, изображающим результирующую синусоиду. Длина вектора даст амплитуду результирующей синусоиды, угол с горизонтальной осью — ее начальную фазу.
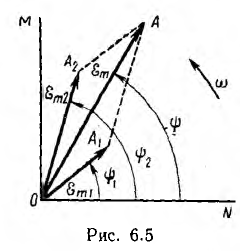
Так, например, для двух синусоид (рис. 6.5)
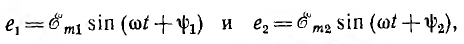
изображаемых векторами 0А1 и 0А2, вектор ОА, изображающий суммарную синусоиду
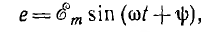
будет геометрической суммой векторов OA1 и ОА2. Он имеет величину 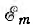 и составляет с осью ON угол ψ. Так как синусоиды е1 и е2 имеют одну и ту же частоту, изображающие их векторы вращаются с одинаковой угловой скоростью, углы между ними не изменяются, и результирующий вектор сохраняет постоянную длину, вращаясь с той же угловой скоростью.
и составляет с осью ON угол ψ. Так как синусоиды е1 и е2 имеют одну и ту же частоту, изображающие их векторы вращаются с одинаковой угловой скоростью, углы между ними не изменяются, и результирующий вектор сохраняет постоянную длину, вращаясь с той же угловой скоростью.
Аналогично, путем геометрического вычитания, может быть найден вектор, изображающий результирующую синусоиду разности двух синусоид. Следовательно, алгебраическому суммированию синусоид, т.е. суммированию их мгновенных значений, соответствуют геометрические действия над изображающими их векторами.
Особенности цепей переменного тока
Для цепей переменного тока справедливы законы Ома, Кирхгофа и Джоуля — Ленца применительно к мгновенным значениям напряжений, токов и мощностей для одного и того же момента времени. Однако в отличие от пассивной цепи постоянного тока, в которой ток определяется приложенным к ней напряжением и ее сопротивлением, в пассивной цепи переменного тока возникают внутренние переменные э. д. с. самоиндукции и э. д. с. емкости, которые должны, быть учтены, кроме приложенного напряжения, при составлении уравнений по основным законам.
Так же, как и в цепях постоянного тока, при составлении уравнений по этим законам для цепей переменного тока необходимо задаться условным положительным направлением напряжений и токов, хотя действительные их направления периодически меняются. По аналогии с цепями постоянного тока удобно принять, что положительные направления напряжения и тока всей цепи и каждого из ее элементов — резистора, катушки индуктивности и конденсатора — совпадают. Тогда мгновенная мощность р = ui всей цепи и каждого из ее элементов будет положительной, когда действительные направления их напряжения и тока совпадают, т. е. когда цепь или ее элементы являются потребителями энергии, что принято характеризовать положительной мощностью.
Выбранные положительные направления для мгновенных значений напряжений и токов сохраняются при переходе к векторам— сумме (разности) мгновенных значений соответствует геометрическая сумма (разность) изображающих их векторов.
Физические и энергетические процессы на участках цепи с сопротивлением, с индуктивностью, с емкостью весьма различны, поэтому предварительно они рассматриваются раздельно до изучения цепей с их сочетанием.
Цепь с сопротивлением
Постоянный ток распределяется по всему сечению проводника равномерно, т. е. во всех точках его сечения плотность тока одинакова.
Плотность переменного тока возрастает от оси проводника к его поверхности. Это явление называется поверхностным эффектом, рассматриваемым в ч. IV. Приближенно можно считать, что переменный ток в проводнике использует только часть s’ его сечения s. Следовательно, сопротивление R постоянному току, называемое обычно омическим, будет меньше сопротивления r переменному току:
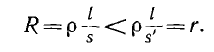
Сопротивление г получило название активного сопротивления проводника.
Поверхностный эффект проявляется тем сильней, чем больше частота, сечение, удельная проводимость и магнитная проницаемость проводника. При промышленной частоте (50 гц) и тонких медных или алюминиевых проводах поверхностным эффектом можно пренебречь и считать активное сопротивление равным омическому.
Пусть к активному сопротивлению (рис. 6.6, а) приложено синусоидальное напряжение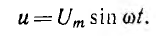
По закону Ома ток
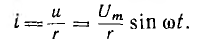
Ток получает максимальное значение 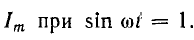 . Тогда
. Тогда
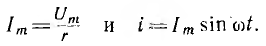
Следовательно, в цепи с сопротивлением r напряжение и ток совпадают по фазе (рис. 6.6, 6.) На векторной диаграмме вектор напряжении совпадает по направлению с вектором тока (рис. 6.6, в). Максимальные значения напряжения и тока также подчинены закону Ома.
Мгновенная мощность р равна произведению мгновенных значений напряжения и тока:
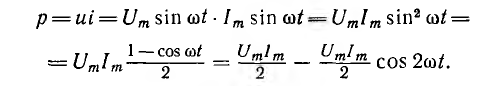
Как видно из этого выражения, мгновенная мощность имеет постоянную составляющую 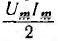 и переменную составляющую, изменяющуюся по косинусоиде двойной частоты
и переменную составляющую, изменяющуюся по косинусоиде двойной частоты 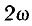 с амплитудой
с амплитудой 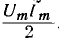
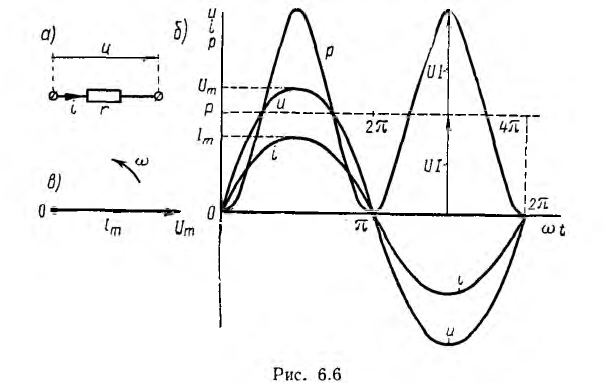
Кривая мощности также изображена на рис. 6.6, б. Мощность равна нулю при u = 0 и i = 0, всегда положительна и получает максимальное значение в те моменты, когда напряжение и ток также максимальны.
Среднее значение мощности за период — средняя мощность
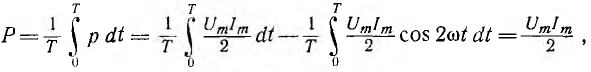
т. e. равна постоянной составляющей мгновенной мощности.
Пользуясь зависимостью между максимальными значениями напряжения и тока, выражение для средней мощности можно переписать следующим образом:
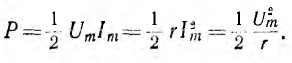
Обычно величина переменного тока характеризуется действующим значением. Так называется значение постоянного тока I, которое дает ту же мощность Р в том же сопротивлении r:
следовательно, 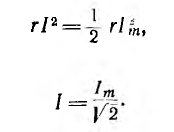
Аналогично, действующее значение напряжения
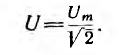
Следовательно, мгновенная мощность
средняя мощность 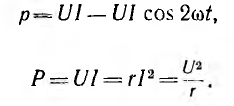
Энергия, поглощаемая активным сопротивлением,
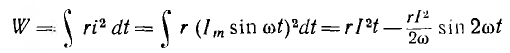
непрерывно растет. Эта энергия поставляется источником, питающим цепь.
Цепь с индуктивностью и цепь с емкостью
Цепь с индуктивностью и цепь с емкостью являются накопителями энергии соответственно электрического и магнитного поля. Чтобы подчеркнуть эту аналогию, цепь с индуктивностью и цепь с емкостью
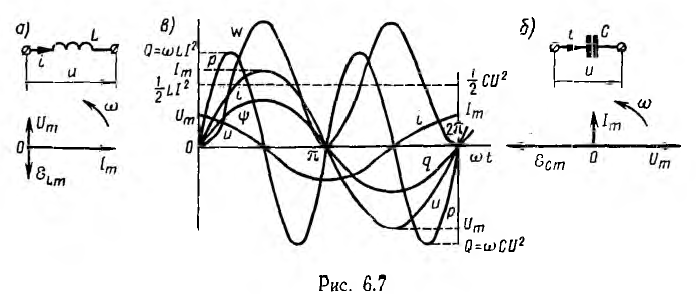
рассматриваются одновременно. Величины, определяющие процессы в них, — ток в цепи с индуктивностью и напряжение на цепи с емкостью — задаются с одинаковой фазой.
Пусть ток цепи с индуктивностью L (рис. 6.7, а)
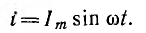
Тогда потокосцепление
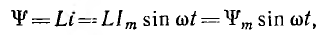
т. e. совпадает по фазе с током.
Пусть напряжение цепи с емкостью С (рис. 6.7, б)
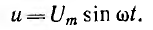
Тогда заряд
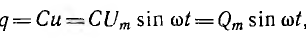
т. e. совпадает по фазе с напряжением.
Временная диаграмма этих и далее вычисляемых величин изображена на рис. 6.7, в, причем обозначения кривых показаны соответственно слева и справа.
Энергия, запасаемая в электрическом поле,
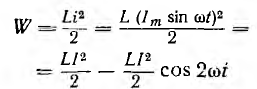
пульсирует с двойной частотой 2ω около среднего значения 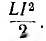 Увеличиваясь с ростом тока за счет энергии источника, энергия поля при уменьшении тока возвращается источнику.
Увеличиваясь с ростом тока за счет энергии источника, энергия поля при уменьшении тока возвращается источнику.
Энергия, запасаемая в магнитном поле,
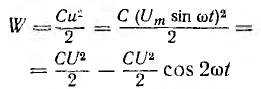
пульсирует с двойной частотой 2ω около среднего значенияя 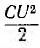 . Увеличиваясь с ростом напряжения за счет энергии источника, энергия поля при уменьшении напряжения возвращается источнику.
. Увеличиваясь с ростом напряжения за счет энергии источника, энергия поля при уменьшении напряжения возвращается источнику.
Мгновенная мощность, равная производной энергии по времени,

также изменяется с двойной частотой, будучи положительной, когда энергия поступает в приемник, и отрицательной, когда приемник возвращает энергию источнику.
Средняя мощность
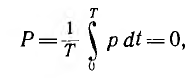
т. е. процесс колебаний энергии между источником и приемником не сопровождается потерями. Максимальное значение мощности
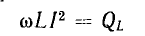 называется индуктивнои мощностью.
называется индуктивнои мощностью.
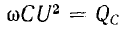 называется емкостной мощностью.
называется емкостной мощностью.
В системе СИ эти мощности измеряются в реактивных вольтамперах (вар).
Мгновенное значение напряжения
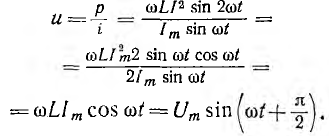
Векторная диаграмма цепи с L показана на рис. 6.7, а. Следовательно, в цепи с L ток отстает от напряжения пофазе на угол 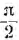 . Так как направление отсчета этого угла от вектора тока к вектору напряжения совпадает с направлением вращения векторов, этот угол считается положительным, т. е.
. Так как направление отсчета этого угла от вектора тока к вектору напряжения совпадает с направлением вращения векторов, этот угол считается положительным, т. е. 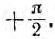
Максимальное значение напряжения
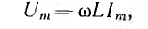 отсюда частные
отсюда частные 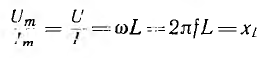
Мгновенное значение тока
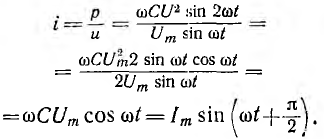
Векторная диаграмма цепи с С показана на рис. 6.7, б. Следовательно, в цепи с С ток опережает напряжение по фазе на угол 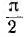 . Так как направление отсчета этого угла от вектора тока к вектору напряжения противоположно направлению вращения векторов, этот угол считается отрицательным, т. е. —
. Так как направление отсчета этого угла от вектора тока к вектору напряжения противоположно направлению вращения векторов, этот угол считается отрицательным, т. е. —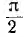 .
.
Максимальное значение тока
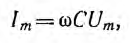 отсюда частные
отсюда частные 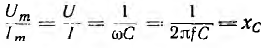
играют роль сопротивления применительно к максимальным и действующим значениям напряжения и тока. Они называются индуктивным сопротивлением емкостным сопротивлением и в системе единиц СИ измеряются в омах.
Емкостное сопротивление обратно пропорционально емкости и частоте; при постоянном напряжении оно равно бесконечности.
В цепи с емкостью величина
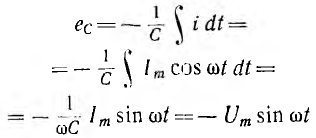
может быть названа э. д. с. емкости. Она равна и противоположна по фазе напряжению цепи.
Индуктивное сопротивление прямо пропорционально индуктивности и частоте; при постоянном токе оно равно нулю.
В цепи с индуктивностью возникает э. д. с. самоиндукции
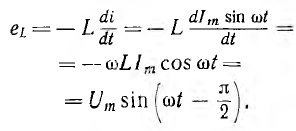
Она равна и противоположна по фазе напряжению цепи.
Отсюда видно, что применять индуктивное или емкостное сопротивления в соотношениях между мгновенными напряжениями и токами нельзя, так как

Соотношения u = —е, полученные в предположении их одинакового положительного направления, аналогичны соотношениям для напряжения U и э. д. с. 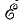 источника энергии без внутреннего сопротивления при выборе для них одинакового направления
источника энергии без внутреннего сопротивления при выборе для них одинакового направления 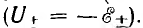
Итак, соотношения в цепи с индуктивностью и в цепи с емкостью аналогичны. От зависимостей в одной цепи к зависимостям в другой можно перейти, заменяя соответствующие величины по табл. 6.1.
Таблица 6.1
| Цепь с индуктивностью | L | ψ | u | i | ω | t | W | p |
| Цепь с емкостью | C | q | i | u | ω | t | W | p |
Измерения в цепях переменного тока
Для измерения переменного тока и напряжения могут быть применены амперметры и вольтметры электромагнитной и электродинамической систем, рассмотренные. При включении такого aмперметра в цепь переменного тока его мгновенный момент вращения mвр будет пропорционален квадрату мгновенного значения тока i, подвижная же часть прибора, очевидно, даст отклонение, пропорциональное среднему значению этого момента:
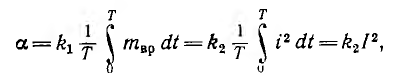
т. е. прибор измерит действующее значение тока. Аналогично, вольтметры этих двух систем измеряют действующее значение напряжения.
Для измерения мгновенных значений переменных токов и напряжений применяется осциллограф, основным элементом которого является вибратор — прибор магнитоэлектрической системы, подвижной частью которой является легкая петелька; ее момент вращения и угол отклонения пропорциональны измеряемой величине. Вместо стрелки на подвижной части укреплено зеркальце, отражающее луч света на движущуюся фотопленку, на которой записывается временная диаграмма тока или напряжения.
Для измерения средней мощности в цепях переменного тока применим ваттметр электродинамической системы. Как следует из , его мгновенный момент вращения mвр будет пропорционален мгновенной мощности р = ui. Тогда отклонение подвижней части пропорционально ее среднему значению:
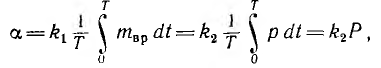
т. е. средней мощности.
Для получения положительного отклонения ваттметр следует включать по схеме рис. 2.9. В цепях только с индуктивностью и с емкостью ваттметр, очевидно, должен дать нулевое показание.
Анализ и расчет простых цепей переменного тока
Основной особенностью цепей переменного тока (по сравнению с цепями постоянного тока) является наличие в них реактивных элементов – емкостей и индуктивностей . Реактивные элементы, не рассеивая мощность электромагнитных колебаний, изменяют разность фаз между колебаниями электрического тока и напряжения на участке цепи. Вследствие этого амплитудные значения напряжения и силы тока достигаются не одновременно. При расчете электрической цепи переменного тока необходимо учитывать эту особенность, т.е. учитывать фазовые отношения между колебаниями токов и напряжений.
Цепь с последовательным соединением участков с сопротивлением, с индуктивностью и с емкостью
По закону Ома мгновенное значение тока в цепи с последовательно
включенными активным сопротивлением r, индуктивностью L и емкостью С (рис. 7.1, а) зависит не только от приложенного напряжения и, но и от возникающих в цепи э. д. с. индуктивности eL и э. д.с. емкости ес–
отсюда 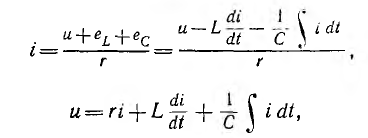
т. е. приложенное напряжение распадается на три напряжения, из которых первое Ua=ri преодолевает активное сопротивление цепи, второе 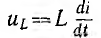
уравновешивает противоположную ему по знаку э. д. с. индуктивности eL и третье 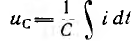 уравновешивает противоположную ему по знаку э. д.с емкости ес.
уравновешивает противоположную ему по знаку э. д.с емкости ес.
Задавшись током цепи
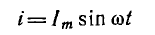
и подставив это выражение тока в уравнение напряжений:
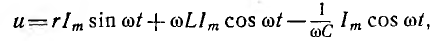
можно видеть, что отдельные составляющие напряжения представляют собой синусоиды и, следовательно, суммарное напряжение также будет синусоидой, вектор которой равен геометрической сумме векторов составляющих синусоид.
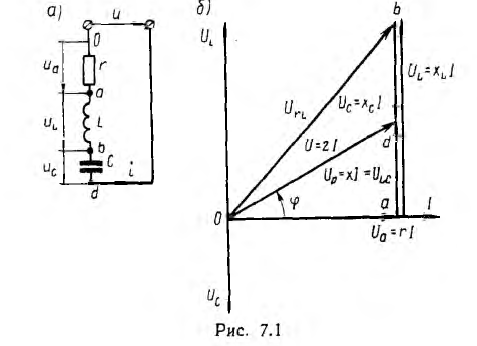
Это построение сделано на рис. 7.1, б для векторов, равных по величине действующим значениям. Вектор активного напряжения UB=rl совпадает по фазе с вектором тока I. Индуктивное напряжение
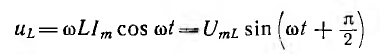
опережает ток на 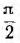 и, следовательно, вектор индуктивного напряжения
и, следовательно, вектор индуктивного напряжения
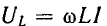 сдвинут относительно вектора тока по вращению векторов на тот же угол. Емкостное напряжение
сдвинут относительно вектора тока по вращению векторов на тот же угол. Емкостное напряжение
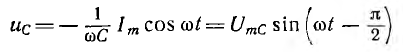
и его вектор 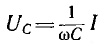 противоположен по фазе вектору UL. На рис. 7.1, б он отложен из конца вектора UL в противоположную сторону. Замыкающий вектор и есть вектор полного напряжения U. Необходимо отметить интересную особенность векторной диаграммы рис. 7.1, б.
противоположен по фазе вектору UL. На рис. 7.1, б он отложен из конца вектора UL в противоположную сторону. Замыкающий вектор и есть вектор полного напряжения U. Необходимо отметить интересную особенность векторной диаграммы рис. 7.1, б.
При ее построении векторы напряжений на участках цепи откладывались в той же последовательности, в какой эти участки включены в цепь рис. 7.1, а. Поэтому отдельным точкам векторной диаграммы (0, a, b, d) соответствуют одноименные точки цепи. Такая диаграмма может быть названа топографической. Она позволяет сразу найти векторы напряжений между любыми точками цепи, соединив их прямой линией. На рис. 7.1, б показаны векторы напряжений UrL и ULC на участках rL и LC.
В результате сложения векторов получается прямоугольный треугольник напряжений с гипотенузой, равной полному напряжению U, катетом, равным активному напряжению UB и катетом Up = UL — Uc; напряжение Up называется реактивным. На диаграмме рис. 7.1, б преобладает индуктивное напряжение (UL > Uс) и поэтому реактивное напряжение совпадает по фазе с индуктивным.
Из треугольника напряжений видно, что
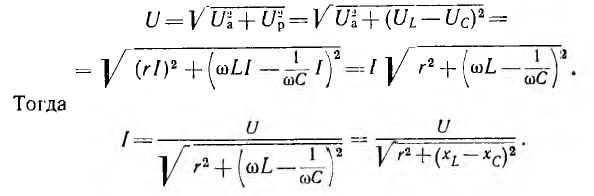
Сопротивление  называется реактивным и обозначается буквой х. Знаменатель выражения для тока
называется реактивным и обозначается буквой х. Знаменатель выражения для тока
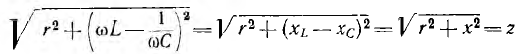
играет роль сопротивления и называется полным сопротивлением.
В системе единиц СИ z также измеряется в омах.
Следовательно,
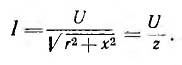
Полученные выражения могут рассматриваться как аналог закона Ома для переменного тока. Необходимо подчеркнуть, что закон Ома в таком виде справедлив только для максимальных и действующих значений переменного тока и напряжения. Для мгновенных значений но в таком виде неприменим; написать 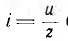 было бы грубой ошибкой, так как мгновенные значения тока и напряжения не находятся в линейной зависимости.
было бы грубой ошибкой, так как мгновенные значения тока и напряжения не находятся в линейной зависимости.
Здесь полезно сопоставить различные выражения закона Ома для этой цепи. Для мгновенных значений

для векторов, очевидно, можно было бы написать:

где 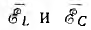 — векторы э. д. с. индуктивности и емкости, а для действующих значений аналог закона Ома:
— векторы э. д. с. индуктивности и емкости, а для действующих значений аналог закона Ома:

Отсюда видно, что физически существующие э. д. с. индуктивности и емкости, входящие в выражения (7.1) и (7.2), в выражении (7.3) формально учитываются через реактивные сопротивления xL и хс.
Вектор тока сдвинут по фазе относительно вектора напряжения на острый угол 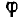 ; на диаграмме рис. 7.1, б вектор тока отстает от век тора напряжения. Угол
; на диаграмме рис. 7.1, б вектор тока отстает от век тора напряжения. Угол 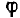 может быть определен из треугольника напряжений:
может быть определен из треугольника напряжений:
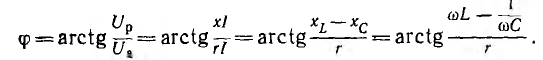
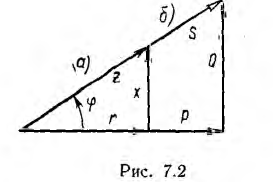
Если разделить все стороны треугольника напряжений на общий множитель I, получится подобный ему треугольник сопротивлений с гипотенузой z и
катетами r и х (рис. 7.2, а), откуда
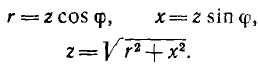
Мгновенная мощность цепи равна произведению мгновенных значений напряжения и тока:
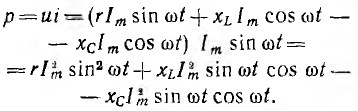
После подстановки значений 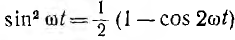 и
и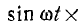
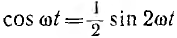
выражение для мгновенной мощности получает вид
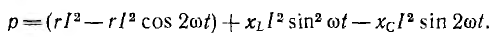
Первый член правой части есть мгновенная мощность активного сопротивления
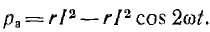
После подстановки соотношений из треугольника напряжений
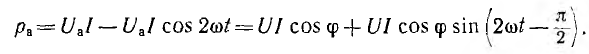
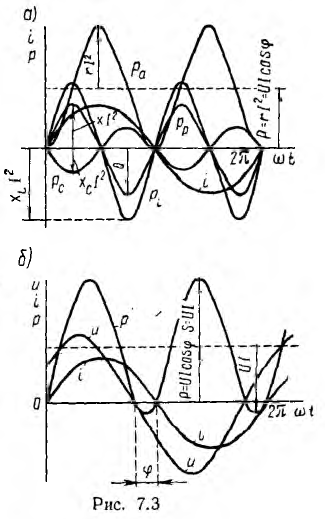
Эта мощность (рис. 7.3, a) имеет постоянную составляющую
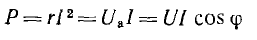
переменную — синусоиду двойной частоты с такой же амплитудой.
Величина Р является, очевидно, средней мощностью за период. Она называется активной мощностью. В системе СИ мгновенная и активная мощности измеряются в ваттах (вт).
Второй и третий член дают мгновенную мощность индуктивности и емкости (см. рис. 7.3, а):
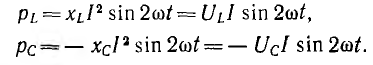
Эти мощности изменяются по синусоидам двойной частоты противоположным по фазе, т. е. когда индуктивность отдает энергию, емкость ее получает, и наоборот. Среднее значение pL и рс равно нулю. В сумме они дают мгновенную мощность реактивных участков цепи:
Амплитуда синусоиды этой мощности
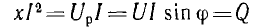
называется реактивной мощностью. В системе СИ реактивная мощность измеряется в реактивных вольт-амперах (вар).
Теперь выражение для мгновенной мощности всей цепи может быть
преобразовано:
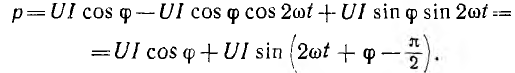
Таким образом, мгновенная мощность р всей цепи имеет постоянную составляющую UI cos ф и переменную составляющую — синусоиду с амплитудой UI (рис. 7.3, б); р равно нулю когда u = 0 или i = 0.
Так как амплитуда переменной части UI больше постоянной составля
ющей UI cosϕ, мощность в определенные промежутки времени становится отрицательной. Когда мощность положительна, цепь получает энергию от источника; когда мощность отрицательна, цепь отдает энергию источнику. Очевидно, возврат энергии источнику получается за счет энергии поля того из реактивных участков цепи, мощность которого больше (для рис. 7.3, б за счет индуктивности). Отдавая запасенную в своем поле энергию, индуктивность снабжает энергией емкость, отдает часть своей энергии безвозвратно активному сопротивлению, а остаток возвращает источнику. Промежутки времени, в течение которых мощность положительна, больше, чем те, при которых мощность отрицательна.
Амплитуда переменной части мгновенной мощности всей цепи
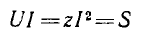
называется полной мощностью и измеряется в системе СИ в вольт-амперах (ва).
Если умножить все стороны треугольника сопротивлений на общий множитель I2, получается подобный ему прямоугольный треугольник мощностей (см. рис. 7.2, б) с углом у вершины, равным ϕ, гипотенузой, равной полной мощности 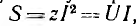 катетом равным активной мощности
катетом равным активной мощности 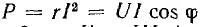 и другим катетом равным реактивной мощности
и другим катетом равным реактивной мощности 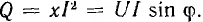 Из треугольник; мощностей видно, что
Из треугольник; мощностей видно, что
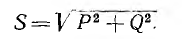
Полная мощность S является характерной величиной для всякой электрической установки, любой электрической машины, аппарата, линии передачи и т. п. Сечение их проводов рассчитывается на ток I таким образом, чтобы провода не перегревались от выделяемого в них тепла. Изоляция рассчитывается на напряжение U; сердечник и н. с. обмотки электромагнитных механизмов рассчитываются на магнитный поток, который также пропорционален напряжению (см., например, формулу для 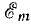 ). Другими словами, любая электрическая установка рассчитывается на напряжение и на ток, т. е. на полную мощность UI, средняя же мощность
). Другими словами, любая электрическая установка рассчитывается на напряжение и на ток, т. е. на полную мощность UI, средняя же мощность
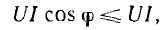
так как 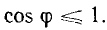 . Следовательно, полная мощность есть та максимальная активная мощность, которая может быть получена при данных действующих значениях напряжения и тока. Из-за сдвига фаз расчетная (полная) мощность установки используется неполностью. Отсюда ясна важность высокого cosϕ, называемого коэффициентом мощности.
. Следовательно, полная мощность есть та максимальная активная мощность, которая может быть получена при данных действующих значениях напряжения и тока. Из-за сдвига фаз расчетная (полная) мощность установки используется неполностью. Отсюда ясна важность высокого cosϕ, называемого коэффициентом мощности.
В общем случае напряжение и и ток i цепи записываются так:
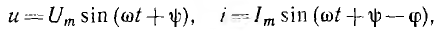
где ψ — начальная фаза напряжения;
ϕ — разность фаз напряжения и тока.
Если в рассмотренной цепи 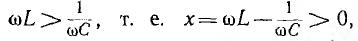 то
то 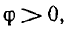 и ток отстает по фазе от напряжения. Если
и ток отстает по фазе от напряжения. Если 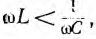 т.е.
т.е. 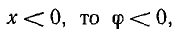 и ток опережает напряжение.
и ток опережает напряжение.
Для цепи с последовательным соединением сопротивления r и индуктивности L аналог закона Ома и сдвиг по фазе могут быть получены 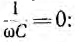
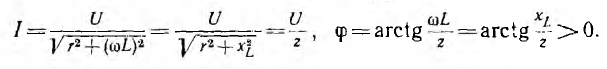
Аналогично, для цепи с последовательным соединением сопротивления r и емкости С, положив 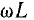 = 0:
= 0:
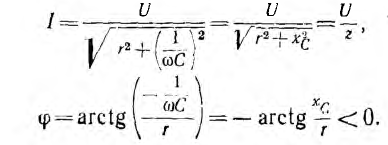
Резонанс напряжений
В электрических цепях, содержащих индуктивности и емкости, возможно явление резонанса, при котором напряжение и ток цепи совпадают по фазе. В цепи с последовательным соединением сопротивления, индуктивности и емкости (см. рис. 7.1, а) будет резонанс напряжений, когда
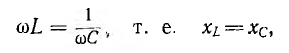
так как в этом случае ток и разность фаз напряжения и тока
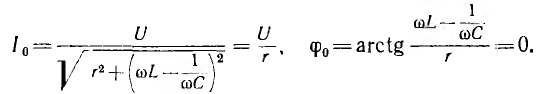
Напряжения на участках цепи при резонансе
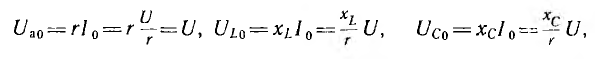
т. е. активное напряжение равно полному, а индуктивное напряжение — емкостному напряжению, так как индуктивное сопротивление xL равно емкостному хс. Если
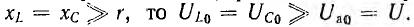
При резонансе, ограниченный лишь активным сопротивлением, при малом r также может получить большое значение.
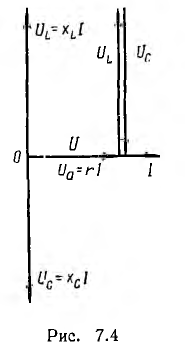
На рис. 7.4 показана векторная диаграмма для случая резонанса. Как видно из этой диаграммы и приведенных соотношений, при резонансе цепь, несмотря на наличие в ней индуктивности и емкости, ведет себя как активное сопротивление. Ток совпадает по фазе с напряжением и получает наибольшее значение. Реактивное напряжение
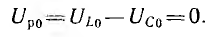
Так как условием резонанса является равенство 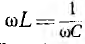 то для данных двух величин из трех (L, С, ω) резонанс может быть получен подбором третьей. Итак, резонанс будет при
то для данных двух величин из трех (L, С, ω) резонанс может быть получен подбором третьей. Итак, резонанс будет при
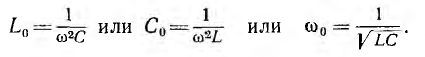
Индуктивное и емкостное сопротивления при резонансе
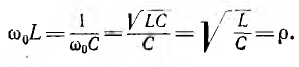
Величина р называется характеристическим сопротивлением цепи, а ее отношение к активному сопротивлению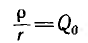 называется добротностью цепи (контура). Добротность равна также отношению индуктивного или емкостного напряжения при резонансе к напряжению всей цепи. Обратная величина
называется добротностью цепи (контура). Добротность равна также отношению индуктивного или емкостного напряжения при резонансе к напряжению всей цепи. Обратная величина
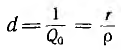
называется затуханием цепи. Чем меньше r, а следовательно, и d, тем при резонансе больше активная (средняя) мощность
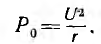
Мгновенные мощности индуктивности и емкости при резонансе равны по величине и обратны по знаку (рис. 7.5):
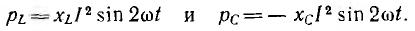
Индуктивная QL = xLP2 и емкостная Qc = ХсР2 мощности также равны друг другу. Следовательно, при резонансе мгновенная мощность рр и реактивная мощность Q всей цепи будут
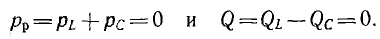
Этого следовало ожидать, так как при резонансе, как показано, цепь ведет себя как активное сопротивление.
Максимальное значение энергии индуктивности
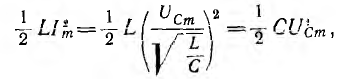
т. е. равно максимальному значению энергии емкости. Тогда, если
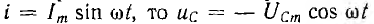 и мгновенное значение суммарной энергии индуктивности и емкости равно:
и мгновенное значение суммарной энергии индуктивности и емкости равно:
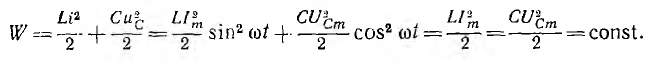
Отсюда видно, что при резонансе суммарная энергия, запасенная реактивными элементами цепи, постоянна и равна максимальной энергии индуктивности, равной, в свою очередь, максимальной энергии емкости. Колебания энергии индуктивности и емкости противоположны по фазе и в цепи происходит полный обмен энергиями между ними.
Источник не участвует в этом обмене и доставляет лишь энергию активному сопротивлению цепи.
Таким образом, при резонансе происходит взаимная компенсация индуктивных и емкостных сопротивлений, напряжений и мощностей.
Далее рассмотрен режим, когда напряжение на зажимах цепи постоянно, а частота изменяется от 0 до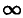 .
.
Ток I = 0 при ω = 0 и ω = 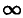 и максимален при резонансе, когда ω = ω0.
и максимален при резонансе, когда ω = ω0.
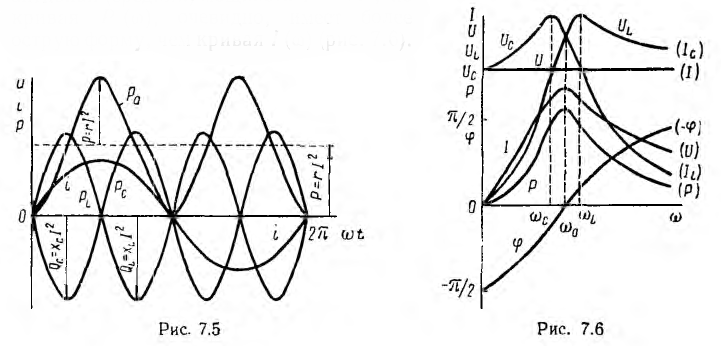
Аналогично изменяется активное напряжение Uа = rl и активная (средняя) мощность Р = rI2, но кривая Р (ω), очевидно, имеет более острую форму, чем кривая I(ω) (рис. 7.6). Индуктивное напряжение UL = 0 при ω = 0. При ω =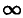 UL = U, при резонансе
UL = U, при резонансе 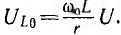 . Для определения частоты
. Для определения частоты 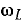 , при которой UL максимально, вместо исследования на максимум величины
, при которой UL максимально, вместо исследования на максимум величины
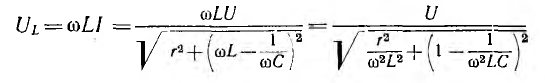
проще исследовать подрадикальное выражение на минимум, взяв его
производную по ω и приравняв нулю:
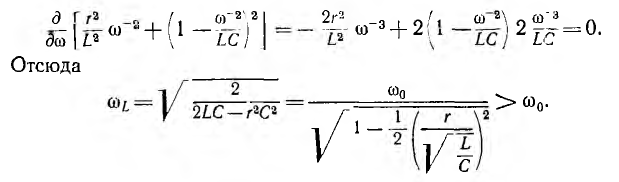
Значение ULmax получится после подстановки значения 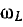 в общее выражение для UL:
в общее выражение для UL:
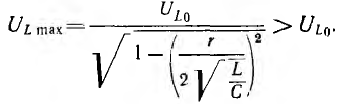
Емкостное напряжение Uc = U при ω=0, U=0 при ω= 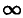 при резонансе
при резонансе 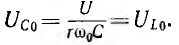
Определение частоты 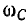 , при которой Uc проходит через максимум, и значение Ucmax можно провести аналогично предыдущему:
, при которой Uc проходит через максимум, и значение Ucmax можно провести аналогично предыдущему:
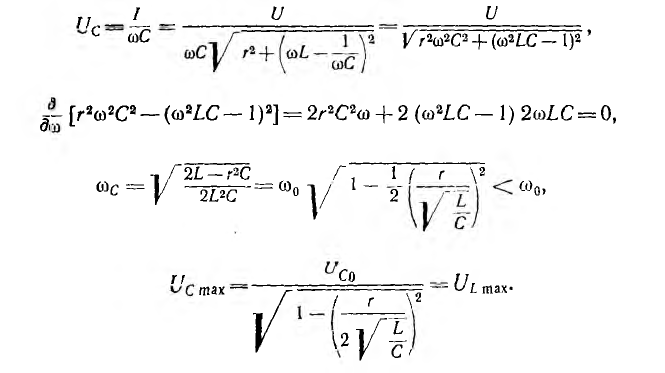
Таким образом, наибольшие значения напряжений на индуктивности и емкости равны между собой.
Графики зависимостей 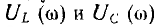 показаны также на рис. 7.6.
показаны также на рис. 7.6.
При увеличении активного сопротивления r цепи 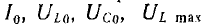
и Ucmax уменьшаются, а частоты ωL и ωс удаляются от резонансной частоты
ω0; при 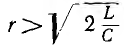 максимумов нет.
максимумов нет.
Кривые на рис. 7.6 называются резонансными кривыми или частотными характеристиками цепи.
Явление резонанса имеет широкое применение в радиотехнике.
Например, в ряде устройств используется зависимость режима работы
цепи с последовательным соединением L и С от частоты и повышение тока этой цепи при резонансе.
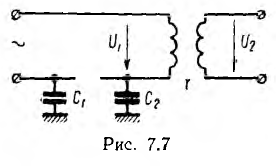
В электротехнике резонанс напряжений часто является аварийным режимом; так при обрыве линии передачи, питающей отключенный со вторичной стороны трансформатор Т (рис. 7.7), может наступить резонанс между емкостью
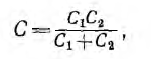
(С1 и С2 — емкости на землю двух участков линии передачи) и индуктивностью L первичной обмотки трансформатора, что вызовет недопустимое для изоляции и безопасности установки повышение напряжения U1 в первичной и, следовательно, U2 во вторичной обмотках трансформатора.
Цепь с параллельным соединением участков с сопротивлением, с индуктивностью и с емкостью. Резонанс токов
Основные соотношения:
При параллельном соединении сопротивления r, индуктивности L и емкости С (рис. 7.8, а) мгновенное значение тока i всей цепи, согласно первому закону Кирхгофа, равно алгебраической сумме мгновенных значений токов отдельных приемников:
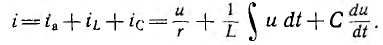
После подстановки в это выражение напряжения 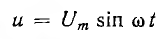 ток всей цепи представляется суммой ‘синусоид:
ток всей цепи представляется суммой ‘синусоид:
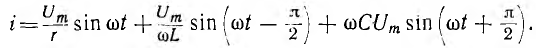
Следовательно, ток всей цепи также будет синусоидой, вектор которой может быть найден как геометрическая сумма векторов слагающих синусоид. Векторная диаграмма для действующих значений дана на рис. 7.8, б.
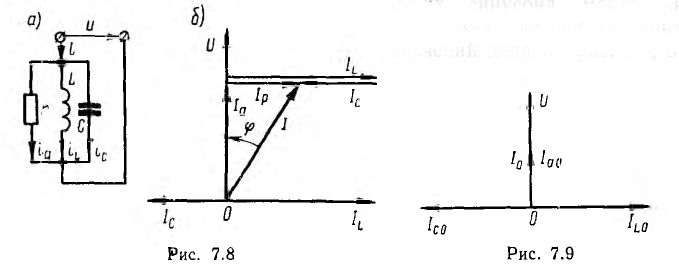
Активный ток 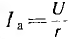 совпадает по фазе с напряжением U, индуктивный ток
совпадает по фазе с напряжением U, индуктивный ток 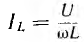 отстает отнапряжения на
отстает отнапряжения на 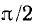 емкостный ток Iс = ωCU опережает напряжение на
емкостный ток Iс = ωCU опережает напряжение на 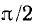 , реактивный ток
, реактивный ток 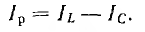
Тогда действующее значение тока всей цепи а разность фаз напряжения и тока
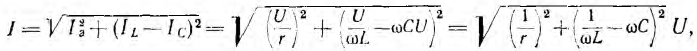
а разность фаз напряжения и тока
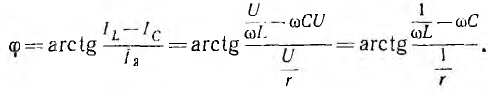
Резонанс токов наступит при
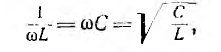
т. е. при условии, аналогичном условию резонанса напряжений.
Тогда
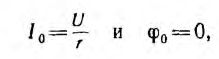
т. е. цепь будет вести себя как активное сопротивление.
Токи ветвей цепи при резонансе:
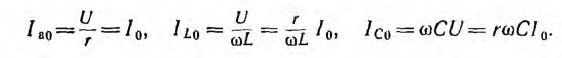
Векторная диаграмма для случая резонанса изображена на рис. 7.9.
Так как векторы 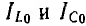 равны между собой и направлены противоположно, сумма их — реактивный ток — равна нулю. Ток цепи I0 равен активному току Iа0 и совпадает по фазе с напряжением.
равны между собой и направлены противоположно, сумма их — реактивный ток — равна нулю. Ток цепи I0 равен активному току Iа0 и совпадает по фазе с напряжением.
При 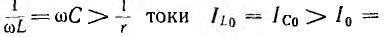 Ia0 т. е. токи в индуктивности и в
Ia0 т. е. токи в индуктивности и в
емкости будут больше тока всей цепи, равного току в активном сопротивлении.
Энергетическая сторона процесса здесь такая же, как и при резонансе напряжений: суммарная энергия, запасенная в полях цепи, постоянна и равна максимальной энергии емкости, равной в свою очередь максимальной индуктивности. Колебания энергии емкости и индуктивности противоположны по фазе, и в цепи происходит полный обмен энергиями между ними. Источник не участвует в этом обмене, он доставляет лишь энергию активному сопротивлению.
Если в рассматриваемой цепи поддерживать неизменным напряжение U и увеличивать частоту ω, активный ток 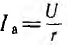 и активная мощность
и активная мощность 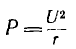 останутся неизменными, индуктивныи ток
останутся неизменными, индуктивныи ток 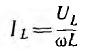 будет убывать, а емкостный ток
будет убывать, а емкостный ток 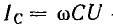 — возрастать; при резонансе
— возрастать; при резонансе 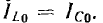 Частотные характеристики цепи показаны на рис 7.10.
Частотные характеристики цепи показаны на рис 7.10.
Ток всей цепи
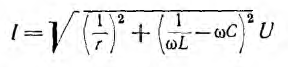
получает при резонансе, когда 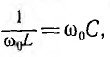 , минимальное значение
, минимальное значение 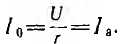 Фазный сдвиг
Фазный сдвиг  положителен при ω< ω0, равен нулю при ω = ω0 и отрицателен при ω > ω0.
положителен при ω< ω0, равен нулю при ω = ω0 и отрицателен при ω > ω0.
В высокочастотных генераторах, усилителях и других радиотехнических устройствах используется зависимость режимов работы от частоты в цепи с параллельным соединением L и С и повышение напряжения этой цепи при резонансе токов.
Дуальные цепи
При сравнении уравнения, написанного для цепи с параллельным соединением r, L и С (см. рис. 7.8, а) на основе первого закона Кирхгофа,
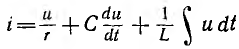
с уравнением для цепи с последовательным соединением r, L и С (см. рис. 7.1, а), написанного на основе второго закона Кирхгофа,
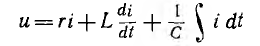
видно, что оба уравнения имеют в качестве независимой переменной время t и совершенно аналогичны, причем одно получается из другого при взаимной замене схемы и величин по табл. 7.1.
Таблица 7.1
| Парaллельное соединение | i | u | 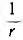 |
L | C |
| Последовательное соединение | u | i | r | C | L |
Две цепи, в которых напряжения первой цепи ведут себя, как токи второй и, наоборот, токи первой ведут себя, как напряжения второй, называются дуальными. Цепь с L и цепь с С, как видно, дуальны. Дуальными являются также цепи с последовательным и параллельным соединениями r, L и С, и все выводы, сделанные для последовательной схемы, можно перенести на параллельную, если заменить величины так, как указано в приведенной таблице. Взаимная замена напряжения и тока должна, очевидно, производиться
и для их действующих значений U и I, а частота ш для обеих схем должна быть одинакова.
Так, например, результаты исследования последовательной схемы при U = const и ω = var, изображенные на рис. 7.6, могут быть целиком перенесены на параллельную схему, работающую при I = const и ω= var, причем кривая, изображающая изменение тока I цепи, будет изображать кривую изменения напряжения U, кривая UL — кривую Iс и кривая Uc — кривую IL. Зависимость активной (средней) мощности 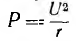 от частоты будет такой же, зависимость
от частоты будет такой же, зависимость  будет отличаться только знаком (рис. 7.6, обозначения кривых даны
будет отличаться только знаком (рис. 7.6, обозначения кривых даны
справа в скобках). Дуальными будут и векторные диаграммы, что можно видеть, например, из сравнения рис. 7.1, б и 7.3, б.
Общему выражению для емкостного напряжения последовательной схемы будет соответствовать общее выражение для индуктивного тока параллельной схемы:
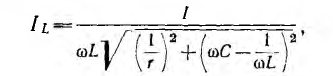
выражению для максимумов напряжений UL и Uc будет соответствовать выражение для максимумов токов Iс и IL:
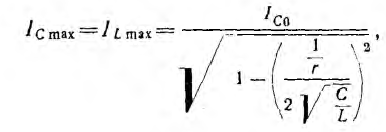
выражению для частоты 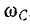 , при которой Uc проходит через максимум, будет соответствовать выражение
, при которой Uc проходит через максимум, будет соответствовать выражение 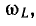 , при которой IL проходит через максимум:
, при которой IL проходит через максимум:
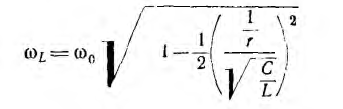
Совершенно аналогичны между собой и режимы работы параллельной цепи при ω = var и U = const (см. рис. 7.10) и последовательной — при ω = var и 1=const, если произвести указанную замену величин (обозначения кривых даны справа в скобках). Интересно отметить,что при неизменном токе напряжение U последовательной цепи при резонансе, когда 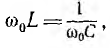 получает минимальное значение.
получает минимальное значение.
Повышение коэффициента мощности
Схема, в которой возможен резонанс токов, используется в электротехнике для повышения коэффициента мощности. Обычно приемники электрической энергии имеют активно-индуктивный характер, т. е. работают со сдвигом фаз 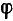 >0 между напряжением и током. Так, электрический двигатель переменного тока может быть представлен в виде схемы с параллельным соединением r и XL (рис. 7.11, а), где активная мощность Р, расходуемая в сопротивлении г, равна сумме полезной мощности двигателя и всех потерь в нем, а реактивная мощность Q индуктивного сопротивления XL равна индуктивной мощности двигателя, связанной с его магнитным полем.
>0 между напряжением и током. Так, электрический двигатель переменного тока может быть представлен в виде схемы с параллельным соединением r и XL (рис. 7.11, а), где активная мощность Р, расходуемая в сопротивлении г, равна сумме полезной мощности двигателя и всех потерь в нем, а реактивная мощность Q индуктивного сопротивления XL равна индуктивной мощности двигателя, связанной с его магнитным полем.
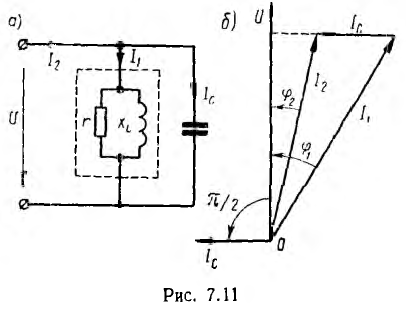
Источник энергии, питающий такой приемник, а также линия передачи должны быть рассчитаны на полную мощность S = UI, превышающую среднюю мощность приемника Р = UI cosϕ. Для меньшения полной мощности источника и линии передачи путем повышения коэффициента мощности часто применяется параллельное пюдключение к приемнику батареи конденсаторов, т. е. схема, в которой возможен резонанс токов.
На рис. 7.11, б показана векторная диаграмма этой цепи. Здесь r1 — ток нагрузки, ϕ1 — фазный сдвиг, / с — ток батареи конденсаторов, который при пренебрежении потерями в них опережает напряжение U по фазе на угол 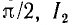 — ток источника, ϕ2 — новый фазный сдвиг. На основании этой диаграммы можно вычислить емкость С батареи конденсаторов, необходимой для уменьшения фазного сдвига ϕ1 до величины ϕ2:
— ток источника, ϕ2 — новый фазный сдвиг. На основании этой диаграммы можно вычислить емкость С батареи конденсаторов, необходимой для уменьшения фазного сдвига ϕ1 до величины ϕ2:
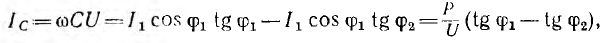
где Р — средняя мощность приемника.
Отсюда
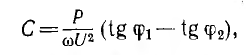
при ϕ2 = 0 емкость
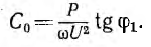
Элементарные методы расчета простых цепей переменного тока
Эквивалентные схемы:
При расчете цепи любой приемник может быть заменен эквивалентной схемой с сосредоточенными параметрами, имеющей равные ток и фазный сдвиг при том же напряжении и той же частоте. Если приемник (рис. 7.12, а) при напряжении U и частоте f потребляет ток I с фазным сдвигом 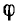 (рис. 7.12, б), то полное сопротивление r и полная мощность S этого приемника и его эквивалентной схемы будут:
(рис. 7.12, б), то полное сопротивление r и полная мощность S этого приемника и его эквивалентной схемы будут:
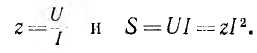
Первой простейшей эквивалентной схемой является последовательное соединение активного г и реактивного х сопротивлени, (рис. 7.12, в для случая преобладания индуктивного сопротивления)
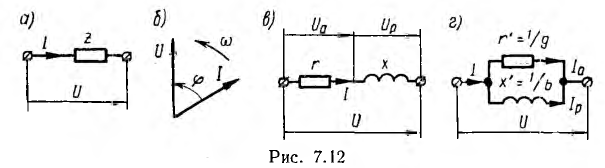
Тогда активные и реактивные сопротивления, напряжения и мощности этой эквивалентной схемы соответственно равны:
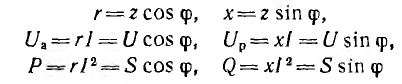
и могут быть представлены катетами подобных прямоугольных треугольников, гипотенузы которых равны полным величинам:
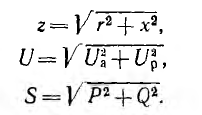
Треугольники сопротивлений, напряжений и мощностей изображены на рис. 7.13, а.
Второй простейшей эквивалентной схемой того же приемника является параллельное соединение активного r’ и реактивного x’ сопротивлений (рис. 7.12, г), не равных r и х эквивалентной ей последовательной схемы. Параллельную схему удобней характеризовать проводимостями: активной 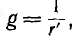 реактивной
реактивной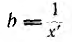 и полной у. Полная проводимость и полная мощность приемника и его параллельной эквивалентной схемы соответственно равны:
и полной у. Полная проводимость и полная мощность приемника и его параллельной эквивалентной схемы соответственно равны:
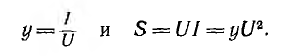
Токи ветвей параллельной эквивалентной схемы, называемые активным и реактивным:
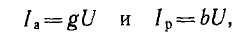
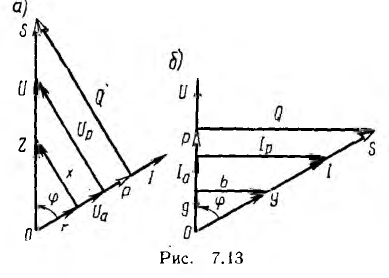
изображены на векторной диаграмме рис. 7.13, б. Так как они сдвинуты между собой по фазе на угол π/2, полный ток
откуда 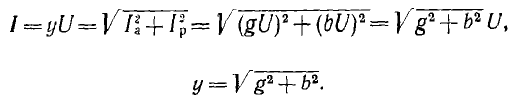
На рис. 7.13, б прямоугольный треугольник токов совмещен стреугольником проводимостей, а также с треугольником мощностей, гипотенуза которого равна полной мощности S, а катеты —активной и реактивной мощностям:

Все эти треугольники имеют у вершины угол 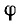 и подобны.
и подобны.
Сопротивления и проводимости часто называют параметрами приемников. Это определение полностью справедливо для и у, величины же r, х и g, b правильней называть параметрам и эквивалентных схем.
Так как последовательная и параллельная схемы эквивалентны между собой, активные, реактивные и полные мощности их должны быть также между собой равны:
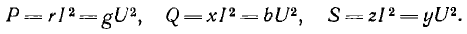
Отсюда могут быть получены переходные формулы зт сопротивлений последовательной схемы к проводимостям параллельной схемы:
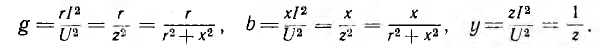
Аналогичным образом могут быть получены переходные формулы от проводимостей параллельной схемы к сопротивлениям последовательной:
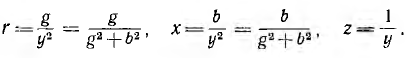
Таким образом, обратными друг другу являются только полные сопротивление г и проводимость у, активные и реактивные сопротивления и проводимости находятся в более сложной зависимости.
При анализе поведения какого-либо приемника при переменной частоте необходимо заменять его эквивалентной схемой, близкой физической сущности этого приемника, т. е. схемой, в которой сопротивления, индуктивности и емкости ее элементов могут быть приняты пастояинными. Так, в некотором диапазоне частот можно пренебречь поверхностным эффектом, и, например, для кольцевого соленоида считать сопротивление r и индуктивность L независящими от частоты, определяя их по формулам:
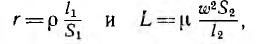
где l1 и l2 — соответственно длины провода обмотки и сердечника, S1, и S2 — их сечения. Пренебрегая током через межвитковые емкости соленоида, что допустимо только при низких частотах, следует представить соленоид в виде последовательной эквивалентной схемы постоянными параметрами r и L (см. рис. 7.12, в). Тогда при постоянном токе (ω = 0) соленоид и его эквивалентная схема будут иметь сопротивление r, а с ростом частоты ω его сопротивление z = 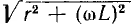 будет возрастать, что соответствует действительности, cопротивление параллельной схемы с постоянными параметрами r’ и L’ (см. рис. 7.12, г) при ω = 0 было бы равно нулю, при ω=
будет возрастать, что соответствует действительности, cопротивление параллельной схемы с постоянными параметрами r’ и L’ (см. рис. 7.12, г) при ω = 0 было бы равно нулю, при ω= 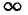 стало бы равным активному сопротивлению, что не соответствует действительности. Поэтому параметры г’ и L’ параллельной эквивалентно схемы должны изменяться с частотой.
стало бы равным активному сопротивлению, что не соответствует действительности. Поэтому параметры г’ и L’ параллельной эквивалентно схемы должны изменяться с частотой.
Цепи с последовательным и параллельным соединением приемников
При последовательном соединении нескольких приемников каждый из них удобно заменить эквивалентной схемой, состоящей из последовательного соединения активного г и реактивного х сопротивлений.
Ток всех приемников такой цепи одинаков, а мгновенное значение напряжения, согласие второму закону Кирхгофа, равно алгебраической сумме мгновенных значений напряжений отдельных приемников. При переходе к векторам алгебраическая сумма заменяется геометрической.
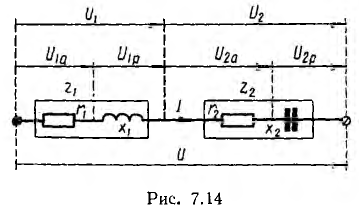
В качестве примера на рис. 7.15, а показана векторная диаграмма для цепи рис. 7.14, состоящей из последовательного соединения двух приемников —одного с индуктивным характером нагрузки и другого с емкостным. Векторы напряжения приемников и всей цени разлагаются на составляющие: активные Uа — по вектору тока и реактивные Uр — перпендикулярно вектору тока. Если разделить все напряжения (стороны треугольников напряжений: 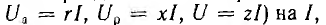 получится подобный рис. 7.15, а многоугольник сопротивлений (рис. 7.15, б). При умножении напряжений на I получится подобный рис. 7.15, а многоугольник мощностей со сторонами
получится подобный рис. 7.15, а многоугольник сопротивлений (рис. 7.15, б). При умножении напряжений на I получится подобный рис. 7.15, а многоугольник мощностей со сторонами 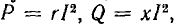
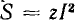 (рис. 7.15, в).
(рис. 7.15, в).
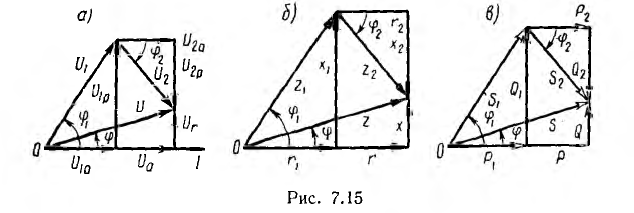
При параллельном соединении нескольких приемников каждый из них удобно заменить эквивалентной схемой, состоящей из параллельного соединения активной g и реактивной b проводимостей. Напряжение всех приемников такой цепи одинаково, а мгновенное значение тока цепи, согласно первому закону Кирхгофа, равно алгебраической сумме мгновенных значений токов отдельных приемников. При пере ходе к векторам алгебраическая сумма заменяется геометрической.
В качестве примера на рис. 7.17 дана векторная диаграмма для цепи, состоящей из параллельного соединения приемника с индуктивным характером нагрузки и приемника с емкостной нагрузкой (рис. 7.16). Векторы тока приемников и всей цепи разлагаются на составляющие:
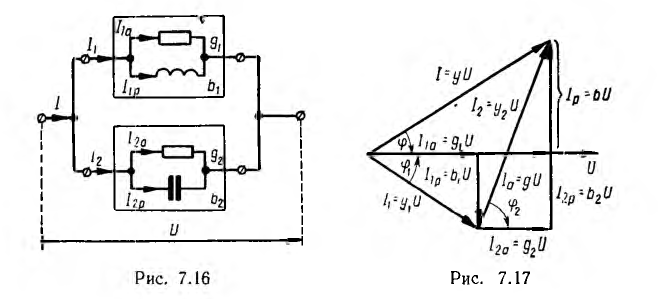
активные Iа по вектору напряжения U и реактивные Iр — перпендикулярно вектору напряжения. Если разделить все токи (стороны треугольников токов: 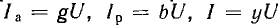 ) на U, получится подобный рис. 7.17 многоугольник проводимостей (g, b, у), а при умножении токов на U — подобный многоугольник мощностей (Р = gU2 , Q = bU2, , S = yU2).
) на U, получится подобный рис. 7.17 многоугольник проводимостей (g, b, у), а при умножении токов на U — подобный многоугольник мощностей (Р = gU2 , Q = bU2, , S = yU2).
Из многоугольников рис. 7.15 и 7.17 видно, что при последовательном соединении складываются сопротивления, напряжения и мощности, а при параллельном — проводимости, токи и тоже мощности. Активные величины складываются арифметически, реактивные — алгебраически, а полные — геометрически.
Расчет цепей со смешанным соединением приемников методами преобразования и пропорционального пересчета
При смешанном (параллельно-последовательном) соединении приемников с заданными параметрами, питаемых одним источником энергии, токи, напряжения и мощности ветвей цепи могут быть определены аналитически методом преобразования, заключающимся в постепенной замене сложной цепи более простой, ей эквивалентной. Ход решения подобной задачи показан на рис. 7.18.
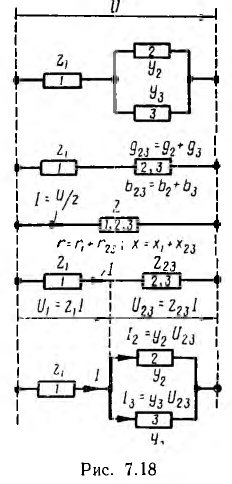
Группа приемников, соединенных параллельно, заменяется одним, активная проводимость которого равна арифметической сумме активных проводимостей приемников, а реактивная—алгебраической сумме реактивных. Группа приемников, соединенных последовательно, заменяется одним, активное сопротивление которого равно арифметической сумме активных сопротивлений отдельных приемников, а реактивное — алгебраической сумме. После замены всей цени одним приемником определяется ток при заданном напряжении или напряжение при заданном токе и сдвиг фаз между ними. Затем схема разворачивается в первоначальную цепь с постепенным определением напряжений, токов и фазных сдвигов в отдельных приемниках.
В процессе решения этой задачи несколько раз приходится при менять переходные формулы от сопротивлений к проводимостях и от проводимостей к сопротивлениям.
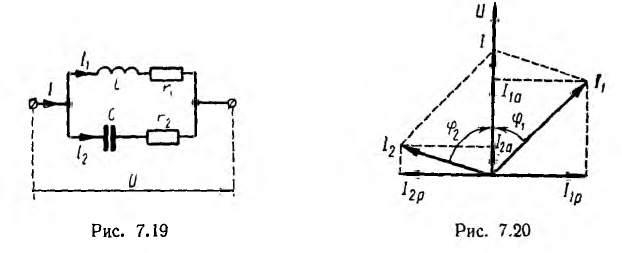
В качестве примера далее решается важная для электротехники задача определения частоты ω, при которой в схеме рис. 7.19 наступит резонанс токов, т. е. напряжение и ток всей цепи будут совпадать по фазе. Для этого, очевидно, реактивная проводимость всей цепи должна быть равна нулю:
откуда 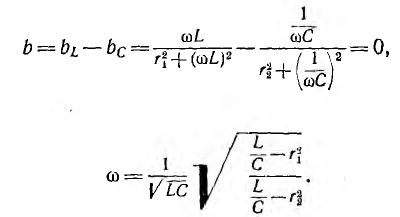
Таким образом, в общем случае, когда 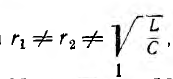 частота ω резонанса в этой цепи отличается от частоты
частота ω резонанса в этой цепи отличается от частоты 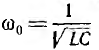 резонанс; при последовательном или параллельном соединении L и С. Векторная диаграмма для резонанса в цепи рис. 7.19 изображена на рис. 7.2G Реактивные составляющие токов ветвей в сумме дают нуль, и ток все цепи равен сумме активных составляющих.
резонанс; при последовательном или параллельном соединении L и С. Векторная диаграмма для резонанса в цепи рис. 7.19 изображена на рис. 7.2G Реактивные составляющие токов ветвей в сумме дают нуль, и ток все цепи равен сумме активных составляющих.
Так как в общем случае токи ветвей сдвинуты по фазе не на π/2, их мгновенные мощности, изменяющиеся с двойной частотой, будут сдвинуты по фазе на угол, отличный от π, т. е. они не находятся в противофазе. Это значит, что в общем случае резонанса полного обмена энергиями между индуктивной и емкостной ветвями не происходит.
Интересно отметить частные случаи:
1) при 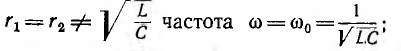
2) при 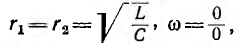 т. е. резонанс будет при любой частоте;
т. е. резонанс будет при любой частоте;
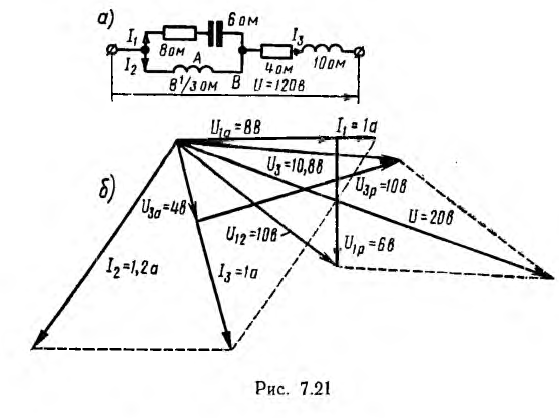
3) при  резонансная частота будет мнимым числом, а это значит, что резонанс в этой цепи невозможен.
резонансная частота будет мнимым числом, а это значит, что резонанс в этой цепи невозможен.
Расчет подобных цепей может быть произведен также графоаналитически — методом пропорционального пересчета. Он основан на том, что в линейной цепи токи пропорциональны напряжениям, следовательно, векторная диаграмма напряжений и токов, рассчитанная или построенная для одного значения питающего цепь напряжения, сохранит свой вид при изменении этого напряжения, и лишь масштабы для напряжения и тока изменятся во столько же раз.
Например, для цепи рис. 7.21, а, решая задачу графоаналитически, целесообразно строить векторную диаграмму, задавшись током первой ветви l1, = 1а. Затем последовательно вычисляются и в выбранном масштабе наносятся на диаграмму векторы в соответствии со своей фазой, после чего они складываются графически (рис. 7.21, б):
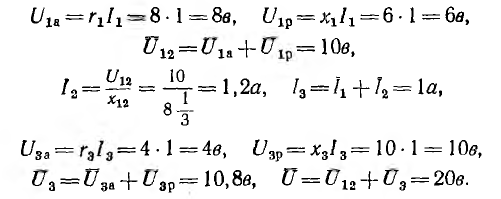
Таким образом, напряжение всей цепи оказалось равным 20 б вместо заданных 120 в. Следовательно, векторная диаграмма рис. 7.21, б остается действительной и для заданного напряжения, если увеличить масштабы для напряжений и токов в 120/20 = 6 раз.
Элементы и параметры электрических цепей переменного тока
Все реальные электротехнические устройства обладают электрическим сопротивлением R, индуктивностью L и емкостью С, которые являются параметрами электрической цепи переменного тока. Однако влияние каждого из параметров на ток в цепи различно, поэтому в некоторых случаях из расчетной схемы исключаются те, влияние которых незначительно.
Таким образом схема электрической цепи переменного тока характеризуется одним из указанных параметров R, L, C или комбинацией их при различных способах соединения элементов.
Цепь с активным сопротивлением
Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R.
Для схемы, изображенной на рис. 13.1, а, заданы сопротивление R и напряжение, изменяющееся по закону
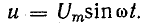
Требуется определить ток и мощность цепи.
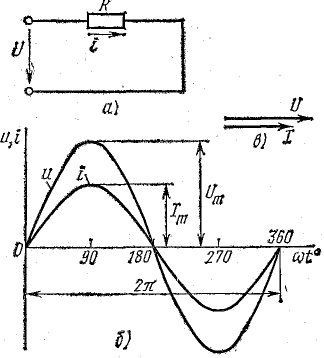
Рис. 13.1. К вопросу о цепи с активным сопротивлением
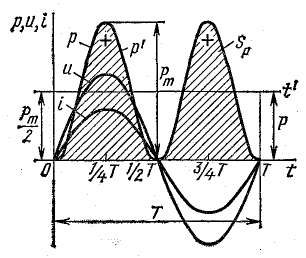
Рис. 13.2. График мгновенной мощности в цепи с активным сопротивлением
Ток в цепи
Выражение для мгновенного тока найдем по закону Ома:
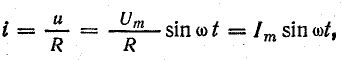
где 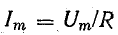 — амплитуда тока.
— амплитуда тока.
Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, т. е. напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 13.1, б, в).
Действующий ток найдем, разделив амплитуду на 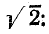
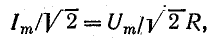
отсюда
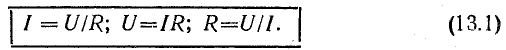
Формулы (13.1) выражают закон Ома для цепи переменного тока с сопротивлением R. Внешне они ничем не отличаются от формулы (2.6) для цепи постоянного тока, если переменные напряжение и ток выражены действующими величинами.
Мгновенная мощность
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока:
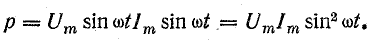
Из тригонометрии найдем
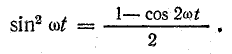
Учитывая это, запишем
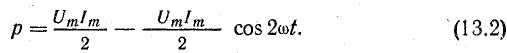
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2).
Если ось времени t поднять по чертежу на величину р = Рm/2 = UmIm/2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
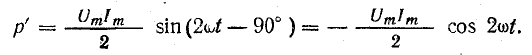
Таким образом, в первоначальной системе координат мгновенная мощность равна сумме постоянной величины 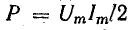 и переменной р’:
и переменной р’: 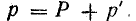
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Активная мощность
Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.
Активная мощность — среднее арифметическое мгновенной мощности за период.
Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2.
Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).
Равенство площадей РТ = Sр выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности Рm.
В этом случае часть площади Sр, находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:
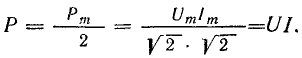
Активная мощность цепи с сопротивлением равна произведению действующих величин напряжения и тока:
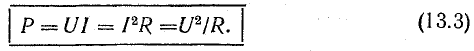
С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности р(t) [см. выражение (13.2)].
Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:
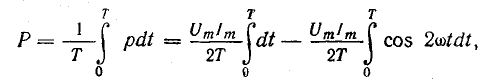
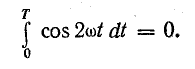
Поэтому
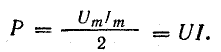
Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.
Цепь с индуктивностью
Исследуемая далее цепь, содержащая только индуктивность, является искусственной, так как катушки, линии электропередачи и другие устройства кроме индуктивности L имеют и активное сопротивление.
Однако рассмотрение идеальной катушки (при R = 0) необходимо для уяснения физических процессов в реальных цепях.
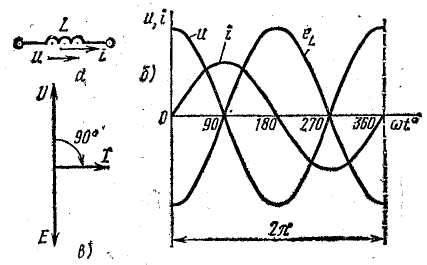
Рис. 13.4. К вопросу о цепи с индуктивностью
Это тем более важно, что в отдельных случаях активным сопротивлением и емкостью можно пренебречь из-за их малости. Например, ненагруженный трансформатор в схеме замещения в ряде случаев может быть представлен только своей индуктивностью.
Допустим, что для цепи (рис. 13.4, а) известны индуктивность L и ток, изменяющийся по закону

Требуется определить напряжение и мощность цепи.
Индуктивное напряжение
Переменный ток в катушке вызывает э. д. с. самоиндукции. При отсутствии активного сопротивления приложенное к катушке напряжение уравновешивается только э. д. с. самоиндукции, поэтому в соответствии со вторым законом Кирхгофа в любой момент времени 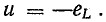
Э. д. с. самоиндукции пропорциональна скорости изменения тока [см. формулу (10.10)]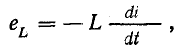
а напряжение
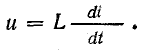
Уравнение приложенного напряжения можно найти, рассматривая векторную диаграмму на рис. 13.5, где ток изображен вектором Im, который предполагается вращающимся с угловой скоростью, равной угловой частоте ω. В начальном положении (при t = 0) вектор Im направлен по горизонтальной оси вправо. Это соответствует уравнению тока (13.4), если мгновенные величины i определять проекцией вращающегося вектора Im на вертикальную ось.
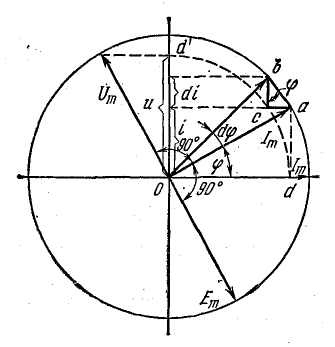
Рис. 13.5. Векторная диаграмма цепи с индуктивностью
Рассмотрим промежуточные положения вектора Im, отстоящие от начального на угол 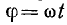 и
и 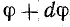 , где dφ — элементарный угол, на который вектор Im поворачивается за малый промежуток времени dt. За время dt ток изменился на di. Приращение тока выражается катетом прямоугольного треугольника abc, гипотенуза которого ab при весьма малом угле dφ может быть приравнена дуге окружности между точками а и b, а угол при вершине b равен φ. Поэтому отрезок ab в масштабе тока имеет значение
, где dφ — элементарный угол, на который вектор Im поворачивается за малый промежуток времени dt. За время dt ток изменился на di. Приращение тока выражается катетом прямоугольного треугольника abc, гипотенуза которого ab при весьма малом угле dφ может быть приравнена дуге окружности между точками а и b, а угол при вершине b равен φ. Поэтому отрезок ab в масштабе тока имеет значение 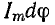 и
и 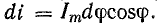
Уравнение напряжения
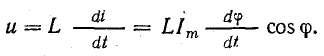
Но
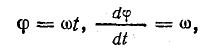
поэтому
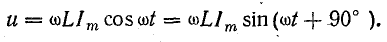
Это уравнение можно получить, дифференцируя уравнение тока:
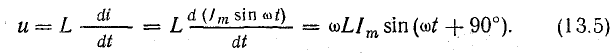
Индуктивное сопротивление
Действующая величина напряжения определяется из уравнения (13.5), где 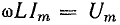 — амплитуда напряжения.
— амплитуда напряжения.
Разделив это выражение на 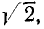 получим
получим
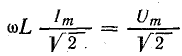
Отсюда
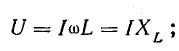

Коэффициент пропорциональности между действующими величинами напряжения и тока, равный произведению индуктивности и угловой частоты ωL, обозначают XL и называют реактивным сопротивлением индуктивности или индуктивным сопротивление е м.
Индуктивное сопротивление выражается в омах:
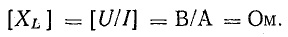
Действующая величина тока в цепи с индуктивностью равна отношению действующей величины напряжения к индуктивному сопротивлению.
Формула (13.6) похожа на формулу Ома. Это позволяет ток в цепи с индуктивностью определять так же, как ток в цепи с активным сопротивлением. Но нужно помнить, что индуктивное сопротивление с физической точки зрения ничего общего с обычным сопротивлением не имеет. Понятие об индуктивном сопротивлении, введенное для облегчения расчета, заменяет в расчете фактическое влияние э. д. с. самоиндукции на ток в цени, т. е. отражает инерционные свойства электрической цепи.
Векторная диаграмма цепи
Сопоставление уравнений тока (13.4) и напряжения (13.5) показывает, что в цепи с индуктивностью ток отстает от напряжения по фазе на четверть периода, или в угловой мере на π/2. Это видно также на рис. 13.5. Мгновенное напряжение выражается отрезком о-d в масштабе, отличающемся от масштаба тока в ωL раз. Перенесем этот отрезок на вертикальную ось (отрезок о-d’), где откладываются мгновенные величины тока. Этому мгновенному напряжению и соответствует вектор Um, опережающий вектор Im по ходу вращения на угол 90°. Э.д.с. самоиндукции, направленная против приложенного напряжения, имеет уравнение
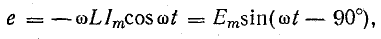
а на рис. 13.5 изображена вектором Еm, отстающим от вектора тока Im на 90°. На рис. 13.4 это показано отдельно на графике и векторной диаграмме (на векторной диаграмме отложены действующие величины).
Мгновенная и реактивная мощности
Мгновенная мощность 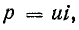 или
или
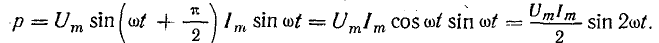
График изменения мощности (рис. 13.6) представляет собой синусоиду двойной частоты с амплитудой
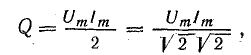
или

Наибольшая величина мощности в цепи с индуктивностью равна произведению действующих напряжения и тока.
Для выяснения физического смысла энергетических процессов обратим еще раз внимание на график мощности. Из него видно, что мгновенная мощность в течение периода четыре раза меняет знак (в моменты времени Т/4; Т/2; 3/4Т; Т). Изменение знака мощности означает, что направление потока энергии меняется.
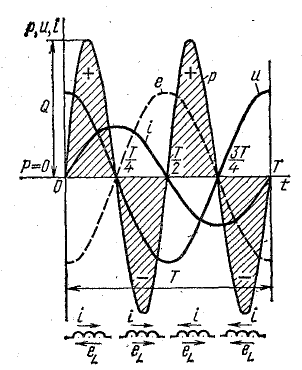
Рис. 13.6. График мгновенной мощности в цепи с индуктивностью
В первую четверть периода, когда ток в цепи увеличивается, энергия накапливается в магнитном поле катушки за счет энергии источника. Катушка в это время является приемником энергии, ток направлен против э. д. с. самоиндукции. Во вторую четверть периода, когда ток уменьшается, энергия возвращается в сеть (источнику).
Направления э. д. с. самоиндукции и тока в катушке совпадают — катушка является источником энергии. В следующую половину периода процесс повторяется. Нетрудно заметить, что количество энергии, накапливаемой в катушке за одну четверть периода (заштрихованная площадь «+»), точно равно количеству энергии, возвращаемой обратно в следующую четверть периода (заштрихованная площадь «—»).
Средняя (активная) мощность за период в цепи с индуктивностью равна нулю (Р = 0), так как в цепи с индуктивностью преобразования электрической энергии в другие виды энергии (тепловую, механическую) не происходит.
Скорость накопления и убыли энергии магнитного поля меняется по гармоническому закону. Амплитуда кривой мгновенной мощности Q является характеристикой этого процесса и называется реактивной мощностью.
Единицу мощности в этом случае называют вар — вольт-ампер реактивный — в отличие от единицы активной мощности — ватта.
Задача 13.4.
Катушка имеет индуктивность L = 15,9 мГн, активное сопротивление R = 0. Начертить график зависимости индуктивного сопротивления и тока в катушке от частоты приложенного напряжения, если действующее напряжение U = 100 В остается неизменным.
Решение. Нужно задаться несколькими величинами частоты, определить соответствующие индуктивные сопротивления, а затем величины тока.
Для частоты f = 50 Гц
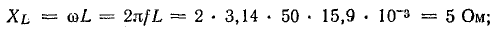
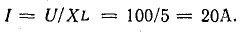
По результатам расчета для других частот (f = 0,25, 100, 500, 1000, 10 000 Гц) постройте в прямоугольной системе координат графики согласно условию задачи.
Цепь с емкостью
В конденсаторе с идеальным диэлектриком предполагается полное отсутствие тока проводимости и потерь энергии. Изменение напряжения между обкладками конденсатора сопровождается электрическим током смешения, величина которого зависит от емкости С. При напряжении на конденсаторе (рис. 13.7, а) 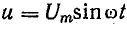 определим ток и мощность.
определим ток и мощность.
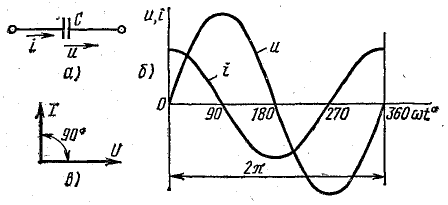
Рис. 13.7, К вопросу о цепи с емкостью
Электрический ток смещения
Внешнее электрическое поле вызывает поляризацию диэлектрика.
При всяком изменении электрического поля изменяется поляризованность диэлектрика, причем связанные заряженные частицы, входящие в состав атомов и молекул вещества, перемещаются, образуя электрический ток.
Явление движения связанных заряженных частиц в диэлектрике при изменении поляризации диэлектрика называют электрическим током поляризации.
Ток поляризации, согласно формуле (2.2),
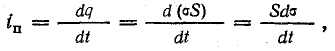
где σ —плотность электрического смещения заряда; отсюда
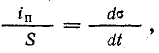
где 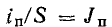 — плотность тока поляризации.
— плотность тока поляризации.
Учитывая формулу (7.20), найдем, что плотность тока поляризации равна скорости изменения поляризованности:
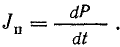
При изменении электрического поля меняется не только вектор поляризации Р, но и вектор электрического смещения в вакууме D0.Из выражений (7.22) и (7.24) следует
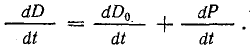
Второе слагаемое в правой части этого уравнения есть плотность тока поляризации, связанного с движением заряженных частиц диэлектрика. Первое слагаемое также имеет размерность плотности тока, но характеризует физический процесс в самом электрическом поле при его изменении во времени.
Величину 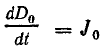 называют плотностью электрического смещения в вакууме. Плотность полного электрического тока смещения
называют плотностью электрического смещения в вакууме. Плотность полного электрического тока смещения
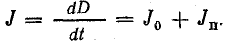
Введение понятия о токе смещения позволяет рассматривать электрическую цепь с конденсатором непрерывной: на участках из проводников имеется ток проводимости, а в диэлектрике — равный ему ток смещения.
Ток в цепи с емкостью
Заряд конденсатора пропорционален напряжению между его обкладками [см. формулу (7.28)], поэтому изменение напряжения сопровождается изменением заряда:
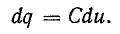
Скорость изменения заряда пропорциональна скорости изменения напряжения:
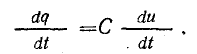
Но скорость изменения заряда равна электрическому току [см. формулу (2.2)]:

При этом во внешнем по отношению к конденсатору участке цепи происходит движение электронов (ток проводимости) через источник. Одновременно при увеличении напряжения совершается поляризация диэлектрика в конденсаторе и возникает ток смещения. При уменьшении напряжения диэлектрик деполяризуется.
Таким образом, ток в цепи с конденсатором пропорционален скорости изменения напряжения на его обкладках.
Уравнение (13.8) по форме подобно уравнению (13.5). Поэтому характер изменения тока при синусоидальном напряжении можно проследить на векторной диаграмме аналогично тому, как это сделано при рассмотрении цепи с индуктивностью (см. рис. 13.5), отнеся рассуждения к скорости изменения напряжения.
На диаграмме векторы тока и напряжения следует поменять местами . В связи с этим уравнение тока для цепи с емкостью можно записать аналогично уравнению для напряжения в цепи с индуктивностью:
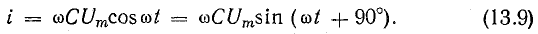
Уравнение тока можно получить, дифференцируя уравнение напряжения:
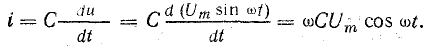
Емкостное сопротивление
Величина 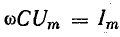 есть амплитуда тока. Разделив это выражение на
есть амплитуда тока. Разделив это выражение на 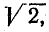 получим
получим

Величину 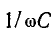 обозначают ХС и называют реактивным сопротивлением емкости или емкостным сопротивлением. Емкостное сопротивление — величина, обратная произведению емкости и угловой частоты.
обозначают ХС и называют реактивным сопротивлением емкости или емкостным сопротивлением. Емкостное сопротивление — величина, обратная произведению емкости и угловой частоты.
Действующий ток в цепи с емкостью равен отношению действующего напряжения к емкостному сопротивлению.
Формула (13.10) по форме совпадает с формулой Ома. Однако емкостное сопротивление физически ничего общего с обычным сопротивлением R не имеет.
Понятие о емкостном сопротивлении, введенное для облегчения расчетов, отражает в расчете противодействие заряженного конденсатора току в цепи.
Сопоставление уравнений напряжения и тока показывает, что в цепи с емкостью напряжение отстает от тока по фазе на четверть периода, или в угловой мере на π/2. На рис. 13.7, б, в это показано на графике и векторной диаграмме.
Мощность в цепи
Построение графика мгновенной мощности (рис. 13.8) выполняется точно так же, как и для цепи с индуктивностью, если иметь в виду, что мгновенная мощность выражается таким же произведением:
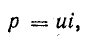
или
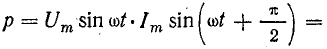
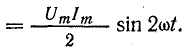
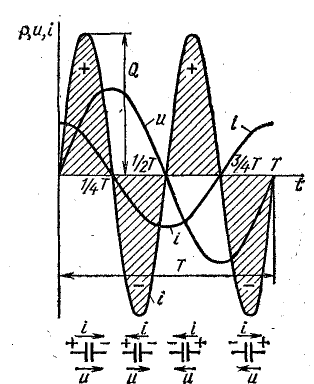
Рис. 13.8. График мгновенной мощности в цепи с емкостью
Из графика видно, что мгновенная мощность, как и в цепи с индуктивностью, четыре раза в течение периода меняет знак. В первую четверть периода, когда напряжение на конденсаторе увеличивается, энергия накапливается в электрическом поле конденсатора за счет работы источника. Конденсатор в это время заряжается, т. е. является приемником энергии: направления тока и приложенного напряжения совпадают. Во вторую четверть периода, когда напряжение уменьшается, энергия в том же количестве возвращается в сеть (к источнику), ток в цепи направлен против напряжения сети, т. е. конденсатор является источником энергии (разряжается).
Проведя рассуждения, аналогичные тем, какие были вделаны для цепи с индуктивностью, найдем, что активная мощность в цепи с емкостью равна нулю (Р = 0), а реактивная мощность равна произведению действующих величин напряжения и тока:

Таким образом, в цепи с емкостью, так же как и в цепи с индуктивностью, преобразования электрической энергии в другие виды энергии (тепловую, механическую) не происходит.
Задача 13.7. Конденсатор имеет емкость С = 637 мкФ. Начертить график зависимости емкостного сопротивления и тока в конденсаторе от частоты приложенного напряжения, действующее значение которого U = 100 В остается неизменным.
Решение. Для решения задачи нужно задаться несколькими значениями частоты. Определить соответствующие величины емкостного сопротивления, а затем тока.
Для частоты 50 Гц

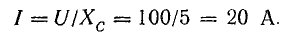
По результатам расчета для других частот (f = 0,25, 100, 500, 1000, 10 000 Гц) постройте и прямоугольной системе координат графики согласно условию задачи.
Цепь с реальной катушкой индуктивности
Реальная катушка отличается от идеальной тем, что переменный ток в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля.
Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р , а изменение энергии в магнитном поле — реактивной мощностью Q .
В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому в схеме замещения реальная катушка должна быть представлена активным и реактивным элементами.
Деление реальной катушки на два элемента искусственно, так как конструктивно оба элемента неразделимы. Однако такой же схемой замещения можно представить реальную цепь из двух конструктивно не совмещенных элементов, один из которых характеризуется только активной мощностью Р(Q = 0), а другой — реактивной (индуктивной) мощностью Q (Р = 0).
Схема замещения катушки с последовательным соединением элементов
В схеме с последовательным соединением элементов реальная катушка характеризуется активным сопротивлением R и индуктивностью L.
Активное сопротивление определяется величиной мощности потерь
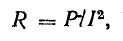
а индуктивность — конструкцией катушки. Предположим, что ток в катушке (рис. 13.9, а) выражается уравнением 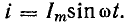 Требуется определить напряжение в цепи и мощность.
Требуется определить напряжение в цепи и мощность.
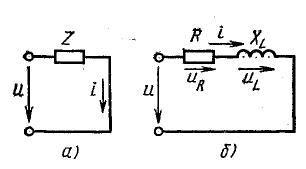
Рис. 13.9. Схема замещения реальной катушки индуктивности (цепь R, L)
При переменном токе в катушке возникает э. д. с. самоиндукции еL, поэтому ток зависит от действия приложенного напряжения и э. д. с. еL. Уравнение электрического равновесия цепи, составленное по второму закону Кирхгофа, имеет вид
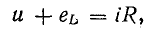
или
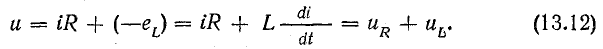
Приложенное к катушке напряжение состоит из двух слагаемых, одно из которых uR равно падению напряжения в активном сопротивлении, а другое 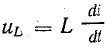 уравновешивает э. д. с. самоиндукции.
уравновешивает э. д. с. самоиндукции.
В соответствии с этим катушку в схеме замещения можно представить активным и индуктивным сопротивлениями, соединенными последовательно (рис. 13.9, б).
Дополнительно заметим, что оба слагаемых в правой части равенства (13.12) являются синусоидальными функциями времени. Согласно выводам, полученным, uR совпадает по фазе с током, а uL опережает ток на 90°.
Поэтому
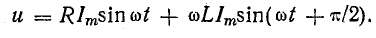
Векторная диаграмма напряжений. Полное сопротивление катушки
Несовпадение по фазе слагаемых в выражении (13.12) затрудняет определение амплитуды и действующей величины приложенного к цепи напряжения U. Поэтому воспользуемся векторным способом сложения синусоидальных величин. Амплитуды составляющих общего напряжения
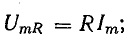
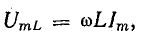
а действующие величины
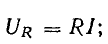
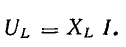
Вектор общего напряжения
Для того чтобы найти величину вектора U, построим векторную диаграмму (рис. 13.10, а), предварительно выбрав масштабы тока Мi и напряжения Мu.
За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза заданного тока ψi = 0). Как и ранее, эту ось удобно (но не обязательно) направить по горизонтали.
Вектор UR по направлению совпадает с вектором тока I, а вектор UL направлен перпендикулярно вектору I с положительным углом.
Из диаграммы видно, что вектор тока I общего напряжения U отражает вектор тока I на угол φ > 0, но <90°, а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения в активном и индуктивном сопротивлениях UR и UL:

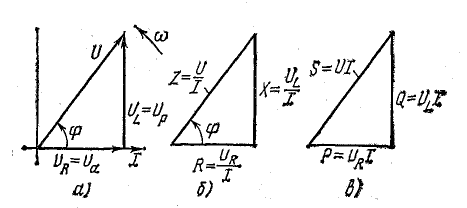
Рис. 13.10. Векторная диаграмма цепи, треугольники сопротивлений и мощностей
Проекция вектора напряжения U на направление вектора тока называется активной составляющей вектора напряжения и обозначается Ua. Для катушки по схеме рис. 13.9 при Uа = UR

Проекция вектора напряжения U на направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения и обозначается Uр. Для катушки Up = UL

При токе 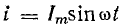 уравнение напряжения можно записать на основании векторной диаграммы в виде
уравнение напряжения можно записать на основании векторной диаграммы в виде
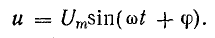
Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений (рис. 13.10, б), катетами которого являются активное 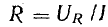 и индуктивное
и индуктивное 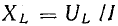 сопротивления, а гипотенузой — величина
сопротивления, а гипотенузой — величина 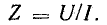
Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи. Стороны треугольника сопротивлений нельзя считать векторами, так как сопротивления не являются функциями времени.
Из треугольника сопротивлений следует

Понятие о полном сопротивлении цепи Z позволяет выразить связь между действующими величинами напряжения и тока формулой, подобной формуле Ома (2.6):
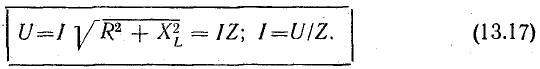
Из треугольников напряжений и сопротивлений определяются
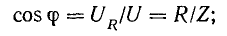
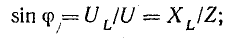
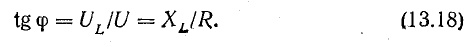
Мощность катушки
Мгновенная мощность катушки
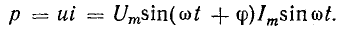
Из графика мгновенной мощности (рис. 13.11) видно, что в течение периода мощность четыре раза меняет знак; следовательно, направление потока энергии и в данном случае в течение периода меняется. Относительно некоторой оси t’, сдвинутой параллельно оси t на величину Р, график мгновенной мощности является синусоидальной функцией двойной частоты.
При положительном значении мощности энергия переходит от источника в приемник, а при отрицательном — наоборот. Нетрудно заметить, что количество энергии, поступившей в приемник (положительная площадь), больше возвращенной обратно (отрицательная площадь).
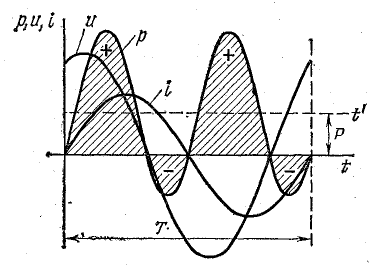
Рис. 13.11. График мгновенной мощности цепи
Следовательно, в цепи с активным сопротивлением и индуктивностью часть энергии, поступающей от генератора, необратимо превращается в другой вид энергии, но некоторая часть возвращается обратно. Этот процесс повторяется в каждый период тока, поэтому в цепи наряду с непрерывным превращением электрической энергии в другой вид энергии (активная энергия) часть ее совершает колебания между источником и приемником (реактивная энергия).
Скорость необратимого процесса преобразования энергии оценивается средней мощностью за период, или активной мощностью Р, скорость обменного процесса характеризуется реактивной мощностью Q.
На основании выводов, в активном сопротивлении 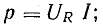
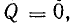 а в индуктивном
а в индуктивном 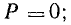
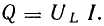
Активная мощность всей цепи равна активной мощности в сопротивлении R, а реактивная — реактивной мощности в индуктивном сопротивлении ХL . Подставляя значения 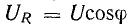 и
и 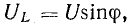 определяемые из треугольника напряжений по формулам (13.18), получим:
определяемые из треугольника напряжений по формулам (13.18), получим:


Кроме активной и реактивной мощностей пользуются понятием полной мощности S, которая определяется произведением действующих величин напряжения и тока цепи:

Величину полной мощности можно получить из выражения (13.22), которое легко доказать на основании формул (13.19) и (13.20):
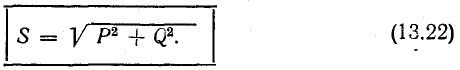
Мощности S, Р, Q графически можно выразить сторонами прямоугольного треугольника (см. рис. 13.10, в). Треугольник мощностей получается из треугольника напряжений, если стороны последнего, выраженные в единицах напряжения, умножить на ток.
Из треугольника мощностей можно определить
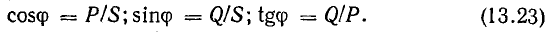
Полная мощность имеет ту же размерность, что Р и Q, но для различия единицу полной мощности называют вольт-ампер (В • А).
Активная мощность Р меньше или равна полной мощности цепи. Отношение активной мощности цепи к ее полной мощности 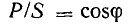 называют коэффициентом мощности.
называют коэффициентом мощности.
Назначение приемников электрической энергии — преобразование ее в другие виды энергии. Поэтому колебания энергии в цепи не только бесполезны, но и вредны, так как при этом в приемнике не совершается полного преобразования электрической энергии в работу или тепло, а в соединительных проводах она теряется.
Схема замещения катушки с параллельным соединением элементов
Для реальной катушки можно составить и другую расчетную схему — с параллельным соединением двух ветвей: с активной G и индуктивной ВL проводимостями. На рис. 13.12, б эта схема показана в сравнении со схемой последовательного соединения активного и индуктивного сопротивлений (рис. 13.12, а), рассмотренной ранее.
Покажем, что схемы рис. 13.12, а, б эквивалентны в том смысле, что при одинаковом напряжении сохраняются неизменными ток в неразветвленной части цепи, активная и реактивная мощности.
Вектор тока I можно разложить на две взаимно перпендикулярные составляющие и в соответствии со схемой и векторной диаграммой на рис. 13.12, б выразить векторным равенством

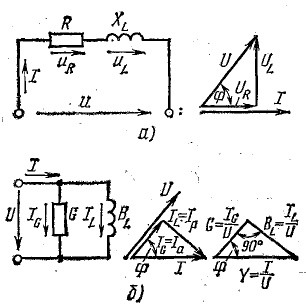
Рис. 13.12. Варианты схемы замещения катушки индуктивности
Для схемы параллельного соединения активного и индуктивного элементов общим является приложенное напряжение, а токи разные: IG — ток в ветви с активной проводимостью, по фазе совпадает с напряжением; IL — ток в ветви с индуктивной проводимостью, по фазе отстает от напряжения на угол 90°.
Вектор тока I и его составляющие IG и ILобразуют прямоугольный треугольник, поэтому

Составляющая тока в активном элементе

Проекция вектора тока I на направление напряжения называется активной составляющей вектора тока и обозначается Iа. Для катушки по схеме на рис. 13.12, 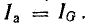
Составляющая тока в реактивном элементе

Проекция вектора тока I на направление, перпендикулярное вектору напряжения, называется реактивной составляющей вектора тока и обозначается Iр. Для катушки Iр = IL .
Стороны треугольника токов, выраженные в единицах тока, можно разделить на напряжение U и получить подобный треугольник проводимостей, катетами которого являются активная 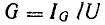 и индуктивная
и индуктивная 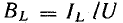 проводимости, а гипотенузой — величина
проводимости, а гипотенузой — величина 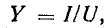 называемая полной проводимостью цепи.
называемая полной проводимостью цепи.
Из треугольника проводимостей и с учетом ранее полученных выражений из треугольника сопротивлений получим
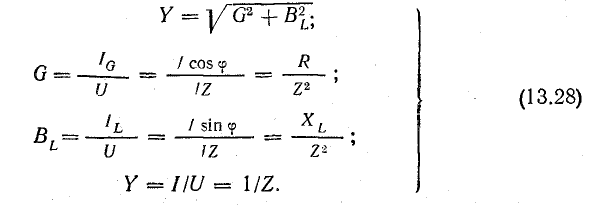
Кроме того,
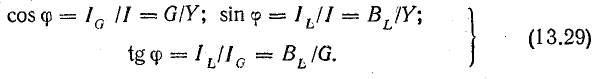
Задача 13.10.
Для определения параметров катушки R и L ее включили сначала в цепь постоянного тока, а затем в цепь переменного тока с частотой f = 50 Гц по схемам рис. 13.13, а, б.
При постоянном токе I1 = 4 А вольтметр показал U1 = 12 В, а при переменном I2 = 5А — U2 = 25 В. Определить активное сопротивление и индуктивность катушки и при переменном токе активную, реактивную и полную мощности. Построить векторную диаграмму и треугольник сопротивлений.
Решение. При постоянном токе э. д. с. самоиндукции в катушке не возникает. Поэтому индуктивное сопротивление ХL = 0. Ток определяется приложенным напряжением и активным сопротивлением.
По формуле Ома,
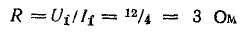
При переменном токе отношение напряжения к току даст величину полного сопротивления
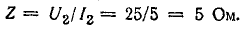
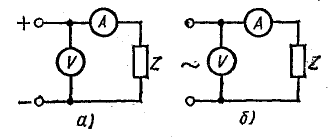
Рис. 13.13. к задаче 13.10
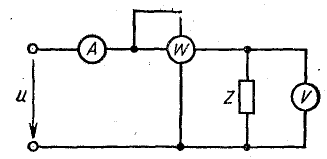
Рис. 13.14. К задачам 13.12, 13.13
Индуктивное сопротивление
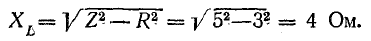
Индуктивность
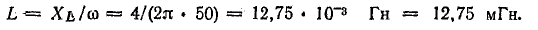
При разборе решения данной задачи на отдельном листе миллиметровой бумаги рекомендуется построить векторную диаграмму цепи и треугольники сопротивлений и мощностей, предварительно определив необходимые величины.
Задача 13.12.
В цепи переменного тока с активным сопротивлением и индуктивностью (рис. 13.14) при частоте f = 100 Гц измерительные приборы показывают: амперметр — 10 А, вольтметр — 200 В, ваттметр — 1600 Вт. Определить параметры схем замещения цепи с последовательным (R, XL) и параллельным (G, ВL) соединением элементов; реактивную и полную мощности цепи. Построить векторные диаграммы применительно к обеим схемам замещения.
Решение (для схемы замещения с последовательным соединением элементов).
Сопротивления:
активное
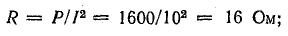
полное
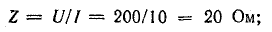
индуктивное
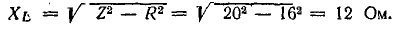
Мощности цепи:
реактивная
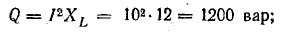
полная
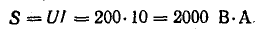
Для построения векторной диаграммы дополнительно определим активную и реактивную составляющие напряжения:
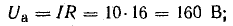
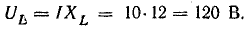
Векторная диаграмма показана на рис. 13.10, а.
Цепь с реальным конденсатором
При переменном напряжении на реальном конденсаторе кроме тока смещения имеются небольшие токи проводимости через толщу диэлектрика (объемный ток) и по поверхности (поверхностный ток). Токи проводимости и поляризацию диэлектрика сопровождают потери энергии.
Таким образом, в реальном конденсаторе наряду с изменением энергии электрического поля (это характеризует реактивная мощность Q) из-за несовершенства диэлектрика идет необратимый процесс преобразования электрической энергии в тепло, скорость которого выражается активной мощностью Р. Поэтому в схеме замещения реальный конденсатор должен быть представлен активным и реактивным элементами.
Деление реального конденсатора на два элемента — это расчетный прием, так как конструктивно их выделить нельзя. Однако такую же схему замещения имеет реальная цепь из двух элементов, один из которых характеризуется только активной мощностью Р (Q = 0), другой — реактивной (емкостной) мощностью Q(Р = 0).
Схема замещения конденсатора с параллельным соединением элементов
Реальный конденсатор (с потерями) можно представить эквивалентной схемой параллельного соединения активной G и емкостной Вс проводимостей (рис. 13.15), причем активная проводимость определяется мощностью потерь в конденсаторе 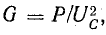 а емкость — конструкцией конденсатора .
а емкость — конструкцией конденсатора .
Предположим, что проводимости G и Вс для такой цепи известны, а напряжение имеет уравнение 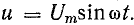
Требуется определить токи в цепи и мощность.
Исследование цепи с активным сопротивлением и цепи с емкостью показало, что при синусоидальном напряжении токи в них также синусоидальны.
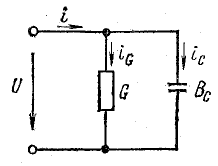
Рис. 13.15. Схема замещения реального конденсатора
При параллельном соединении ветвей G и Вс , согласно первому закону Кирхгофа, общий ток i равен сумме токов в ветвях с активной и емкостной проводимостями:

Учитывая, что ток iG совпадает по фазе с напряжением, а ток ic опережает напряжение на четверть периода, уравнение общего тока можно записать в следующем виде:
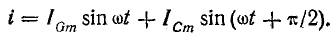
Так как
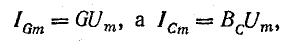
то
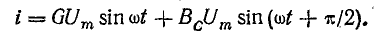
Векторная диаграмма токов
Для определения действующей величины общего тока I методом векторного сложения построим векторную диаграмму согласно уравнению
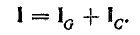
Действующие величины составляющих тока:


Первым на векторной диаграмме изображается вектор напряжения U (рис. 13.16, а), его направление совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза напряжения 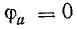 ).
).
Вектор IG совпадает по направлению с вектором U, а вектор Iс направлен перпендикулярно вектору U с положительным углом.
Из векторной диаграммы видно, что вектор общего напряжения отстает от вектора общего тока на угол φ, величина которого больше нуля, но меньше 90′.
Вектор I является гипотенузой прямоугольного треугольника, катеты которого — составляющие его векторы IG и IC:
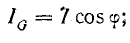
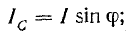
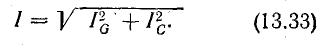
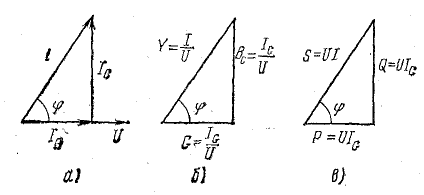
Рис. 13.16. Треугольники токов, проводимостей, мощностей
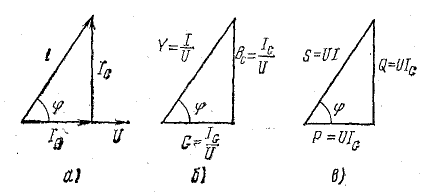
Рис. 13.17. График мгновенной мощности цепи
При напряжении 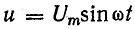 в соответствии с векторной диаграммой уравнение тока
в соответствии с векторной диаграммой уравнение тока
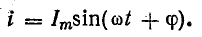
Треугольник проводимостей
Стороны треугольников токов, выраженные в единицах тока, разделим на напряжение U. Получим подобный треугольник проводимостей (рис. 13.16, б), катетами которого являются активная 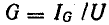 и емкостная
и емкостная 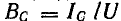 проводимости, а гипотенузой — полная проводимость цепи
проводимости, а гипотенузой — полная проводимость цепи 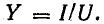
Из треугольника проводимостей

Связь между действующими величинами напряжения и тока выражается формулами
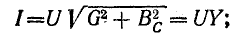
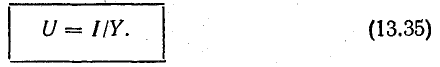
Из треугольников токов и проводимостей определяют величины
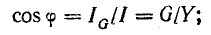
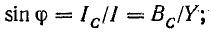
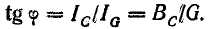
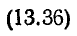
Мощность
Выражение мгновенной мощности реального конденсатора
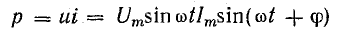
совпадает с выражением мгновенной мощности катушки.
Рассуждения, аналогичные тем, которые сделаны при рассмотрении графика мгновенной мощности катушки (см. рис.13. 11), можно провести и для реального конденсатора на основе графика рис. 13.17.
Величины активной, реактивной и полной мощностей выражаются теми же формулами, какие были получены для катушки [см. (13.19)— (13.22)].
Это нетрудно показать, если стороны треугольника токов, выраженные в единицах тока, умножить на напряжение U.
В результате умножения получится подобный треугольник мощностей (рис. 13.16, в), катетами которого являются мощности:
активная
реактивная
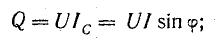
полная
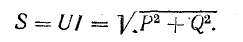
Схема замещения конденсатора с последовательным соединением элементов
Реальный конденсатор, так же как и катушка, на расчетной схеме может быть представлен последовательным соединением двух участков: с активным R и емкостным Хс сопротивлениями.
На рис. 13.18, а такая схема показана в сравнении со схемой параллельного соединения активной и емкостной проводимостей (рис.13.18, б). Все выводы и формулы, полученные для катушки, остаются в силе и для конденсатора при условии замены индуктивного сопротивления емкостным.
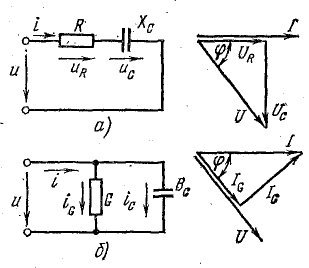
Рис. 13.18. Варианты схемы замещения реального конденсатора
Конденсаторы, применяемые на практике, имеют относительно малые потери энергии. Поэтому в схемах замещения они представлены чаще всего только реактивной частью, т. е. емкостью 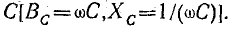
Участки цепи, где последовательно соединены отдельные элементы — резистор R и конденсатор С, имеют такую схему замещения, как показано на рис. 13.18, а.
Задача 13.13.
В цепи переменного тока с активным сопротивлением и емкостью (см. рис. 13.14) при частоте f = 100 Гц измерительные приборы показывают. амперметр — 6 А, вольтметр — 180 В, ваттметр — 360 Вт. Определите параметры схем замещения цепи с параллельным (G, ВL) и последовательным (R, ХC) соединением элементов: реактивную и полную мощности цепи. Постройте векторные диаграммы применительно к обеим схемам замещения.
Решение (для схемы замещения с параллельным соединением элементов). Проводимости:
активная
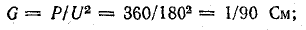
полная
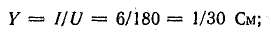
емкостная
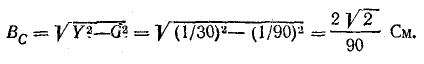
Мощности цепи
реактивная
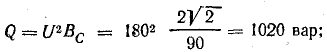
полная
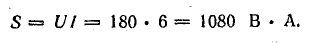
Для построения векторной диаграммы дополнительно определим активную и реактивную составляющие тока:
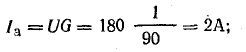
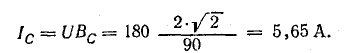
Векторная диаграмма показана на рис. 13.16, а.
Решить задачу для схемы с последовательным соединением элементов.
Расчет электрических цепей переменного тока с помощью векторных диаграмм
В данной главе будут рассмотрены электрические цепи переменного тока, содержащие три параметра R, L, С при последовательном, параллельном соединении резисторов, катушек и конденсаторов.
Расчет таких цепей можно вести на основе векторных диаграмм, из которых получаются расчетные формулы.
Последовательное соединение катушки и конденсатора
При последовательном соединении катушки и конденсатора на расчетной схеме каждый из этих элементов электрической цепи может быть представлен активным и реактивным сопротивлениями или активной и реактивной проводимостями.
Для расчета более простой является схема рис. 14.1, а, где элементы соединены последовательно, а в схеме рис. 14.1, б они соединены смешанно.
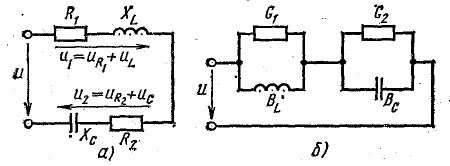
Рис. 14.1. Схемы замещения катушки и конденсатора при последовательном соединении
Предположим известными параметры катушки R1, L и конденсатора R2С; ток в цепи 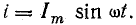
Требуется определить напряжение на участках цепи и мощность.
Векторная диаграмма и полное сопротивление цепи
Мгновенную величину общего напряжения можно представить суммой мгновенных напряжений на отдельных элементах схемы:
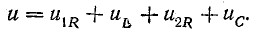
Имея в виду несовпадение по фазе активных и реактивных напряжений, общее напряжение получим векторным сложением:
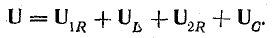
Для построения векторной диаграммы находим:
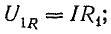
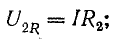
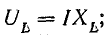
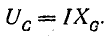
В зависимости от соотношения величин реактивных сопротивлений индуктивности и емкости можно отметить три случая.
1.  . Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U1 и U2 на этих элементах.
. Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U1 и U2 на этих элементах.
Векторная сумма напряжений 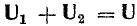 дает общее напряжение в цепи. Вместе с тем вектор UI является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения, цепи (Uа и Uр). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются:
дает общее напряжение в цепи. Вместе с тем вектор UI является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения, цепи (Uа и Uр). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются: 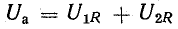 .
.
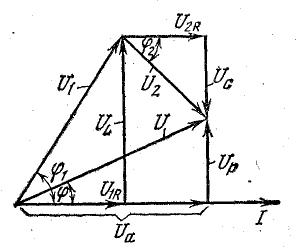
Рис. 14.2. Векторная диаграмма при ХL > ХC
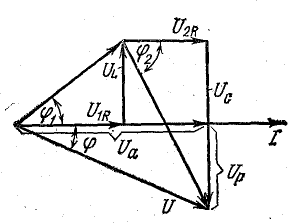
Рис. 14.3. Векторная диаграмма при ХL < X
Векторы реактивных составляющих напряжения направлены по одной прямой в противоположные стороны, поэтому им придают разные знаки: реактивное напряжение индуктивности считают положительным, а напряжение емкости — отрицательным: 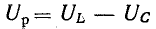
При одинаковом токе во всех элементах цепи 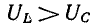 . Ток отстает от общего напряжения по фазе на угол φ. Из треугольника напряжений следует
. Ток отстает от общего напряжения по фазе на угол φ. Из треугольника напряжений следует
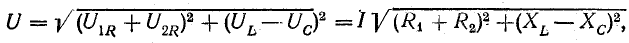
или
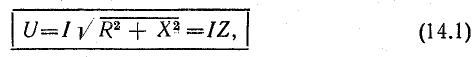
где 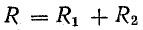 и
и 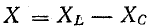 — общее активное и реактивное сопротивления цепи;
— общее активное и реактивное сопротивления цепи; 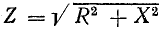 — полное сопротивление цепи.
— полное сопротивление цепи.
Эти сопротивления графически можно изобразить сторонами прямоугольного треугольника сопротивлений, который получают уже известным способом из треугольника напряжений.
Полное сопротивление цепи Z является коэффициентом пропорциональности между действующими величинами тока и общего напряжения цепи:
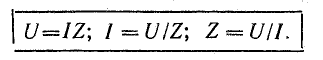
Из треугольников напряжения и сопротивлений определяют следующие величины:
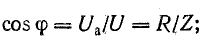
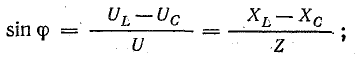
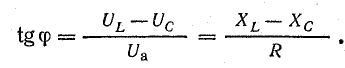
Угол сдвига по фазе между напряжением и током в цепи положительный (φ > 0) (фазовые углы отсчитываются от вектора тока).
2.  . Векторная диаграмма изображена на рис. 14.3, где UL < UC, поэтому общее напряжение отстает от тока на угол φ < 0.
. Векторная диаграмма изображена на рис. 14.3, где UL < UC, поэтому общее напряжение отстает от тока на угол φ < 0.
Реактивное сопротивление цепи носит емкостный характер. Расчетные формулы для первого случая остаются без изменения и для второго случая.
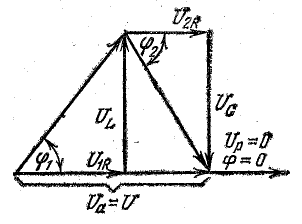
Рис. 14.4. Векторная диаграмма при XL = XC
3. 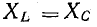 . В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы:
. В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы: 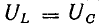 (рис. 14.4). Поэтому реактивная составляющая общего напряжения и общее реактивное сопротивление равны нулю, а полное сопротивление цепи Z = R. Общее напряжение совпадает по фазе с током и равно по величине активной составляющей напряжения.
(рис. 14.4). Поэтому реактивная составляющая общего напряжения и общее реактивное сопротивление равны нулю, а полное сопротивление цепи Z = R. Общее напряжение совпадает по фазе с током и равно по величине активной составляющей напряжения.
Угол φ сдвига фаз между током и общим напряжением равен нулю.
Ток в цепи и общее напряжение связаны формулой
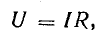 или
или 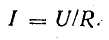
В случае ХL = ХC в цепи имеет место явление резонанса напряжений.
Энергетический процесс в цепи
Из треугольника напряжений легко получить треугольник мощностей, из которого следуют уже известные формулы:
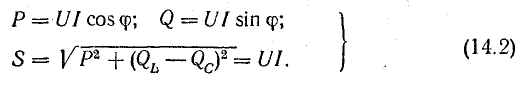
Реактивные мощности входят в расчеты также с разными знаками: индуктивная мощность положительна, а емкостная — отрицательна.
В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует и из формул (14.2).
При φ > 0 Q > 0; при φ < 0 Q < 0.
Активная мощность положительна при любом угле, так как 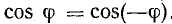
Полная мощность также всегда положительна.
На основании формул (14.2) можно сделать вывод, что в рассматриваемой цепи совершается преобразование электрической энергии 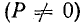 и обменный процесс между генератором и приемником
и обменный процесс между генератором и приемником 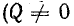 при
при 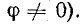
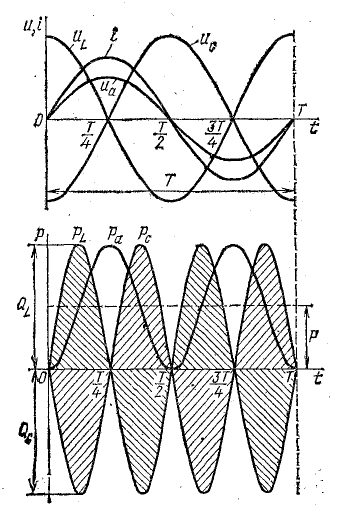
14.5. Графики u, i, p при XL = XC
Энергетические процессы в данном случае сложнее, чем в ранее рассмотренных простых цепях. Усложнение объясняется тем, что наряду с обменом энергией между генератором и приемником совершается обмен энергией внутри приемника, между катушкой и конденсатором.
Особенности энергетического процесса в цепи с последовательным соединением катушки и конденсаторов отражены на рис. 14.5, где показаны графики мгновенной мощности отдельных элементов и цепи в целом при 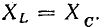
Катушка и конденсатор в течение полупериода накапливают равные количества энергии. Однако в первую четверть периода, когда ток увеличивается, а напряжение на конденсаторе уменьшается, энергия накапливается в магнитном поле катушки и уменьшается в электрическом поле конденсатора, причем скорость изменения энергии (мощность) в любой момент времени одинакова. Это дает основание считать, что обмен энергией происходит только в приемнике между катушками и конденсатором.
Для преобразования электрической энергии в другой вид приемник получает ее от генератора со средней скоростью (мощностью) Р.
Задача 14.1.
Конденсатор емкостью С = 3,4 мкФ и катушка с активным сопротивлением R = 50 Ом и индуктивностью L = 29,8 мГн подключены последовательно к генератору с напряжением U = 200 В (рис. 14.6). Определить ток, активную, реактивную и полную мощности катушки, конденсатора и всей цепи при неизменном напряжении генератора и трех значениях частоты: 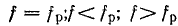 где fр — резонансная частота.
где fр — резонансная частота.
Решение. Для примера далее приведен расчет при частоте f = 250 Гц.
Реактивное сопротивление индуктивности
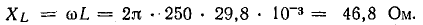
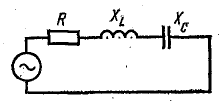
Рис. 14.6. К задаче 14.1
Реактивное сопротивление емкости
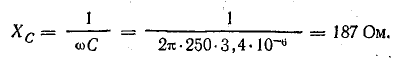
Полное сопротивление
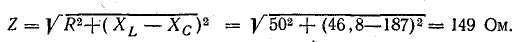
Ток в цепи
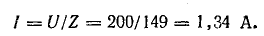
Угол сдвига фаз между током и напряжением
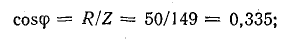

Активная мощность
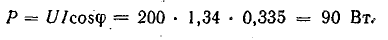
Реактивная мощность индуктивности
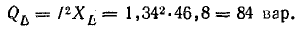
Реактивная мощность емкости
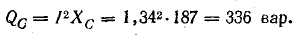
Реактивная мощность цепи
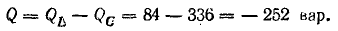
Сделать аналогичный подсчет для частот: f = fр; f < fр; f > fр.
Расчет неразветвленных цепей переменного тока
Порядок расчета, установленный для цепи при последовательном соединении катушки и конденсатора, можно применить и для цепи, содержащей произвольное число катушек и конденсаторов, соединенных последовательно.
На рис. 14.7, а для примера дана схема неразветвленной цепи, состоящей из пяти участков: конденсатора (R1, Х1) и катушки (R2, Х2), представленных активными и реактивными сопротивлениями; резистора R3; идеальных конденсатора Х4 и катушки Х5.
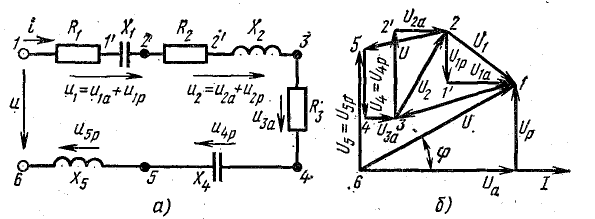
Рис. 14.7. Расчетная схема неразветвленной цепи и ее векторная диаграмма
Предположим, что кроме сопротивлений известен ток в цепи i = Imsinωt.
Требуется найти напряжения на участках, общее напряжение в цепи и мощность.
Векторная диаграмма
Выберем условно-положительное направление тока i, как указано на схеме. Для мгновенных величин в соответствии со вторым законом Кирхгофа уравнение напряжений
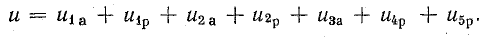
Переходя к действующим величинам напряжений, нужно написать векторную сумму:
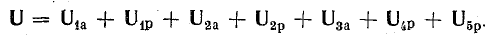
Численно векторы напряжений определяются произведением тока и сопротивления соответствующего участка.
На рис. 14.7, б построена векторная диаграмма, соответствующая этому уравнению. За исходный, как обычно при расчете неразветвленных цепей, принят вектор тока, а затем проведены векторы падения напряжения на каждом участке схемы, причем направления их относительно вектора тока выбраны в соответствии с характером сопротивления участков.
При построении диаграммы напряжений начальной точкой выбрана точка 6, совпадающая с началом вектора тока I. Из этой точки проведен вектор U5р реактивного напряжения индуктивности (по фазе опережает ток на 90°) между точками 5 и 6 цепи. Из конца его проведен вектор U4р реактивного напряжения емкости (по фазе отстает от тока на 90°) между точками 4 и 5 цепи. Затем отложен вектор U3a активного напряжения на резисторе (совпадает по фазе с током) между точками 3 и 4 цепи и т. д., если следовать по цепи против направления тока. Точки векторной диаграммы, где сходятся начало следующего вектора с концом предыдущего, обозначены теми же номерами, какими на схеме обозначены точки, отделяющие один элемент от другого.
При таком, построении напряжение между любыми двумя точками цепи можно найти по величине и фазе, проведя вектор на диаграмме между точками с теми же номерами. Например, напряжение U5.2 между точками 5 и 2 выражается вектором, проведенным из точки 2 в точку 5 (вектор U5.2 направлен в обратную сторону); напряжение U3.1 между точками 3 и 1 выражается вектором, проведенным из точки 1 в точку 3.
Векторная диаграмма, построенная в соответствии с чередованием элементов цепи, называется топографической, так как точки, отделяющие векторы друг от друга, соответствуют точкам, разделяющим элементы схемы.
Расчетные формулы
Из векторной диаграммы видно, что все активные составляющие векторов напряжений направлены одинаково — параллельно вектору тока, поэтому векторное сложение их можно заменить арифметическим и найти активную составляющую напряжения цепи: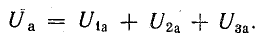
Реактивные составляющие векторов напряжений перпендикулярны вектору тока, причем индуктивные напряжения направлены в одну сторону, а емкостные — в другую. Поэтому реактивная составляющая напряжения цепи Uр определяется их алгебраической суммой, в которой индуктивные напряжения считаются положительными, а емкостные — отрицательными: 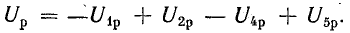
Векторы активного, реактивного и полного напряжений цепи образуют прямоугольный треугольник, из которого следует

Подставив падения напряжения, выраженные через ток и соответствующие сопротивления, получим:
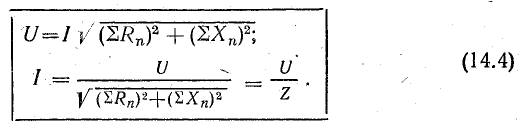
Таким образом снова получена знакомая уже формула, связывающая ток, напряжение и полное сопротивление цепи [ср. (14.4) и (14.1)].
В этой формуле 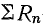 — общее активное сопротивление, равно арифметической сумме всех активных сопротивлений, входящих в неразветвленную цепь;
— общее активное сопротивление, равно арифметической сумме всех активных сопротивлений, входящих в неразветвленную цепь; 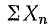 — общее реактивное сопротивление, равное алгебраической сумме всех реактивных сопротивлений, входящих в неразветвленную цепь. В этой сумме индуктивные сопротивления считаются положительными, а емкостные —отрицательными. Полное сопротивление неразветвленной цепи
— общее реактивное сопротивление, равное алгебраической сумме всех реактивных сопротивлений, входящих в неразветвленную цепь. В этой сумме индуктивные сопротивления считаются положительными, а емкостные —отрицательными. Полное сопротивление неразветвленной цепи
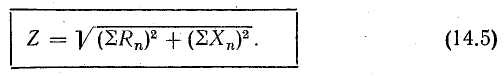
В общем случае полное сопротивление цепи определяется как гипотенуза прямоугольного треугольника, катетами которого являются выраженные в определенном масштабе активное и реактивное сопротивления всей цепи. Из треугольника сопротивлений следует:
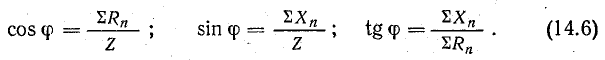
От треугольника напряжений можно перейти также к треугольнику мощностей и получить уже известные формулы для определения мощностей в цепи:
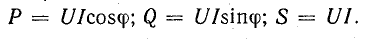
Вместе с тем активную мощность цепи можно представить как арифметическую сумму активных мощностей в элементах с активным сопротивлением. Реактивная мощность цепи равна алгебраической сумме мощностей реактивных элементов.
В этой сумме мощность индуктивных элементов считается положительной, а емкостных — отрицательной:
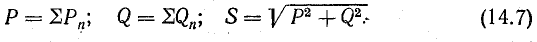
Формулы (14.2)—(14.7) являются общими; из них можно получить конкретное выражение для любой неразветвленной цепи.
Задача 14.3.
Определить ток и составить баланс мощностей для цепи, схема которой изображена на рис. 14.8. Построить топографическую диаграмму и по ней определить напряжение U8.5 между точками 8 и 5 и U6.1 между точками 6 и 1.
Дано:
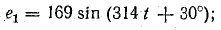
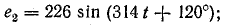
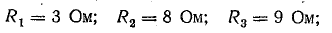
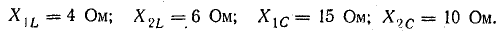
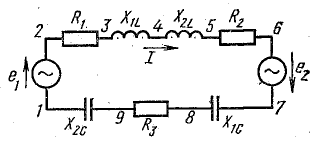
Рис. 14.8. К задаче 14.3
Решение. Согласно второму закону Кирхгофа, составим уравнение напряжений в векторной форме, предварительно выбрав условно-положительные направления э. д. с. и тока в схеме (их целесообразно выбрать одинаковыми независимо от того, в каком режиме работает источник э. д. с., так как фазовый угол сдвига, полученный в результате расчета, укажет истинный режим его работы):
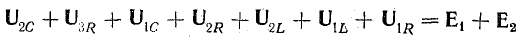
или
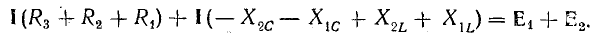
Общее активное сопротивление
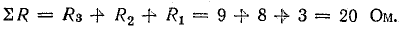
Общее реактивное сопротивление
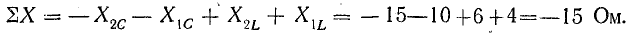
Как видно, общее реактивное сопротивление имеет емкостный характер. Полное сопротивление цепи
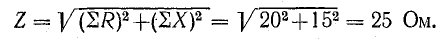
Действующие величины э. д. с.:
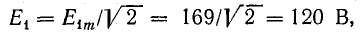
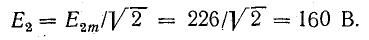
Для определения действующей величины суммы двух э. д. с. ( Е1 + Е2) построим векторную диаграмму (рис. 14.9, а) (рекомендуется построить на отдельном листе миллиметровой бумаги в масштабе Ми = 40 В/см).
Измерение вектора Е показывает, что величина суммарной э. д. с. Е = 200 В. Э. д. с. можно найти, учитывая, что ее составляющие взаимно перпендикулярны. В этом случае
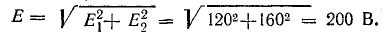
Ток
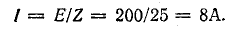
Напряжения на отдельных участках схемы:
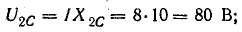
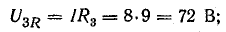
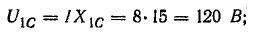
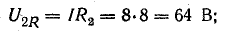
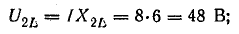
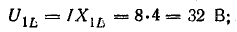
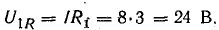
Для построения векторной топографической диаграммы (рис. 14.9, б) выберите масштабы Мi = 2 А/см; Ми = 40 В/см (рекомендуется построить на отдельном листе миллиметровой бумаги).
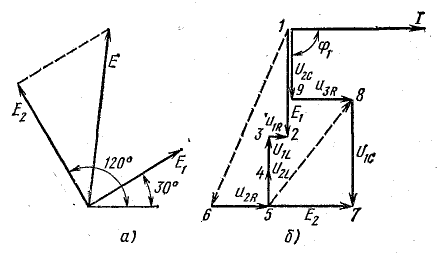
Рис. 14.9. К задаче 14.3
По векторной диаграмме найдены углы сдвига фаз между током и э. д. с. Е1 и Е2: φ1 = –90°, φ2 = 0.
Мощности участков приемника:
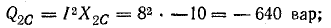
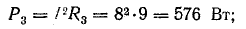
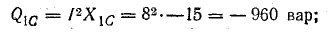
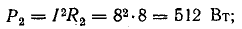
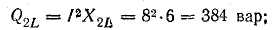
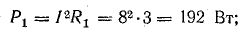
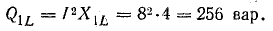
Мощности источников:
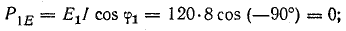
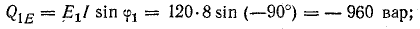
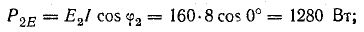
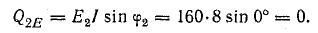
Баланс мощностей:
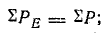
1280 = 192 + 576 + 512 = 1280;
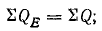
— 960 = — 640— 960 + 384 + 256 = — 960.
Реактивные мощности емкостного характера Q2С, Q1С и Q1E и отрицательны, так как между векторами напряжений и токов, определяющими их, углы отрицательны.
Для определения напряжений U8.5 и U6.1, проведем векторы между соответствующими точками топографической диаграммы. Вектор направляется к точке, стоящей первой в обозначении напряжения. Например, вектор U8.5 направлен в точку 8 из точки 5. Измерение векторов U8.5 и U6.1 дает:
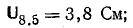
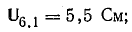
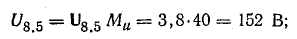
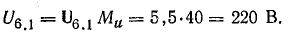
Параллельное соединение катушки и конденсатора
Для рассмотрения параллельного соединения катушки и конденсатора представим их на схеме активными и реактивными проводимостями (рис. 14.11, а).
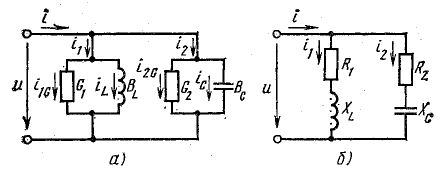
Рис. 14.11. Схемы замещения катушки и конденсатора при параллельном соединении
На схеме рис. 14.11, б те же катушки и конденсатор представлены активными и реактивными сопротивлениями. Первая схема имеет некоторое преимущество, так как в ней все элементы соединены параллельно, а в другой они соединены смешанно.
Считая известными параметры катушки G1, ВL и конденсатора G2, Вс, а также напряжение 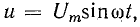 , определим токи в цепи и ее мощность.
, определим токи в цепи и ее мощность.
Векторная диаграмма цепи. Полная проводимость цепи
Согласно первому закону Кирхгофа, мгновенная величина общего тока равна сумме мгновенных токов отдельных ветвей:
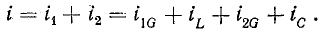
Имея в виду несовпадение по фазе активных и реактивных токов, величину общего тока найдем векторным сложением:
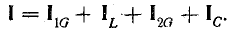
Для построения векторной диаграммы находим:
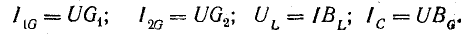
В зависимости от соотношения величин реактивных проводимостей ветвей с индуктивностью и емкостью можно отметить три случая.
Рис. 14.12. Векторные диаграммы:
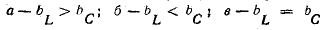
1. 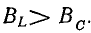 Для этого случая векторная диаграмма представлена на рис. 14.12, а. На диаграмме построены треугольники токов для катушки и конденсатора и найдены векторы токов I1 и I2 в этих элементах:
Для этого случая векторная диаграмма представлена на рис. 14.12, а. На диаграмме построены треугольники токов для катушки и конденсатора и найдены векторы токов I1 и I2 в этих элементах:
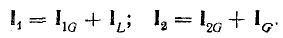
Векторная сумма токов 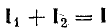 дает общий ток в цепи. Вместе с тем вектор I является гипотенузой прямоугольного треугольника токов, катеты которого — составляющие вектора тока по двум взаимно перпендикулярным осям:
дает общий ток в цепи. Вместе с тем вектор I является гипотенузой прямоугольного треугольника токов, катеты которого — составляющие вектора тока по двум взаимно перпендикулярным осям:
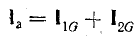 — активная составляющая;
— активная составляющая;
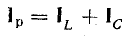 — реактивная составляющая.
— реактивная составляющая.
Векторы активных составляющих токов направлены в одну сторону, поэтому их численные значения складываются. Векторы реактивных составляющих токов направлены перпендикулярно вектору напряжения в противоположные стороны, поэтому им даются разные знаки: индуктивные токи считаются положительными, а емкостные — отрицательными. При одинаковом напряжении на всех элементах цепи  Общий ток отстает от общего напряжения по фазе на угол φ. Из треугольника токов следует
Общий ток отстает от общего напряжения по фазе на угол φ. Из треугольника токов следует
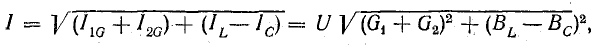
или
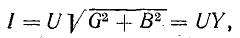
где 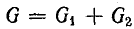 и
и 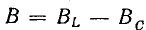 — общие активная и реактивная проводимости цепи;
— общие активная и реактивная проводимости цепи; 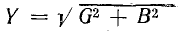 — полная проводимость цепи.
— полная проводимость цепи.
Эти три проводимости графически можно изобразить сторонами прямоугольного треугольника проводимостей, который получается уже известным способом из треугольника токов.
Полная проводимость цепи У является коэффициентом пропорциональности между действующими величинами общего тока и напряжения цепи:
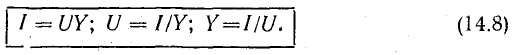
Из треугольников токов и проводимостей определяются величины:
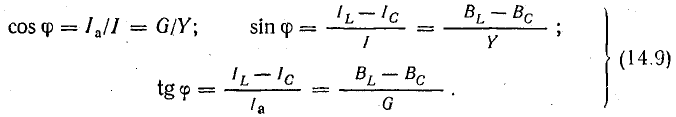
Угол сдвига по фазе между напряжением и общим током в цепи положительный (φ > 0) (фазовые углы отсчитываются от вектора тока).
2. 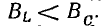 Векторная диаграмма изображена на рис. 14.12, б. Так как
Векторная диаграмма изображена на рис. 14.12, б. Так как 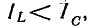 то напряжение отстает от общего тока на угол φ < 0.
то напряжение отстает от общего тока на угол φ < 0.
Реактивная проводимость цепи имеет емкостный характер. Расчетные формулы, полученные для случая 1, действительны и для этого случая.
3. 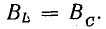 В этом случае реактивные составляющие токов катушки и конденсатора равны по величине:
В этом случае реактивные составляющие токов катушки и конденсатора равны по величине:  Реактивная составляющая общего тока и общая реактивная проводимость равны нулю. Общий ток совпадает по фазе с напряжением и равен по величине активной составляющей тока. Угол φ сдвига фаз между общим током и напряжением равен нулю.
Реактивная составляющая общего тока и общая реактивная проводимость равны нулю. Общий ток совпадает по фазе с напряжением и равен по величине активной составляющей тока. Угол φ сдвига фаз между общим током и напряжением равен нулю.
Общий ток в цепи и напряжение связаны формулой
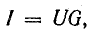 , или
, или 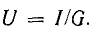
В случае 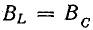 в цепи имеет место резонанс токов.
в цепи имеет место резонанс токов.
Энергетический процесс в цепи
Из векторной диаграммы токов легко получить треугольник мощностей, из которого следуют те же формулы (14.2), которые были получены для последовательного соединения катушки и конденсатора.
Реактивные мощности индуктивности и емкости входят в расчет с разными знаками: реактивная мощность индуктивности положительна, а реактивная мощность емкости отрицательна. В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует из формул (14.2).
Если φ > 0, то Q > 0; при φ < 0 Q < 0.
Активная мощность положительна при любом значении угла. Полная мощность тоже всегда положительна.
В рассматриваемой цепи активная мощность имеет определенную величину 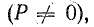 следовательно, имеет место преобразование электрической энергии в другой вид. Кроме того, часть энергии, полученной от генератора, возвращается обратно в генератор
следовательно, имеет место преобразование электрической энергии в другой вид. Кроме того, часть энергии, полученной от генератора, возвращается обратно в генератор 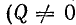 при
при 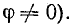 Обмен энергией совершается также между катушкой и конденсатором.
Обмен энергией совершается также между катушкой и конденсатором.
Задача 14.5.
В цепи, схема которой изображена на рис. 14.13, определить ток, активную, реактивную и полную мощность катушки, конденсатора и всей цепи при неизменном напряжении U = 200 В и частоте источника f = 100 Гц. Параметры цепи: R1 = 10 Ом, L = 55,2 мГн, С = 138 мкФ, R2 = 0.
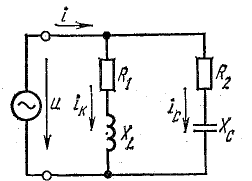
Рис. 14.13. К задаче 14.5
Решение. При частоте f = 100 Гц индуктивное сопротивление первой ветви
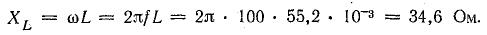
Проводимости:
активная
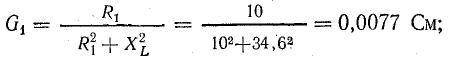
реактивная
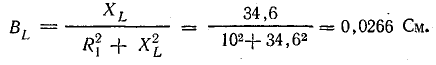
Полная проводимость катушки
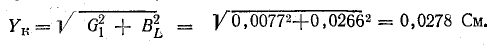
Проводимости второй ветви:
активная

реактивная
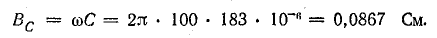
Полная проводимость цепи
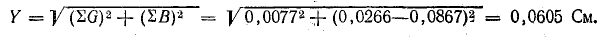
Токи:
в неразветвленной части цепи
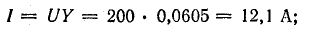
в конденсаторе
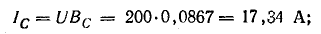
в катушке
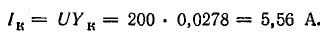
Коэффициент мощности цепи
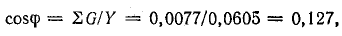
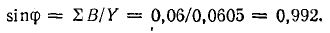
Реактивные мощности:
катушки
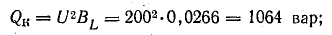
конденсатора
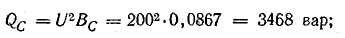
цепи
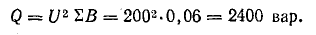
Активная мощность цепи
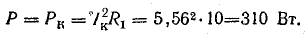
Полные мощности:
катушки
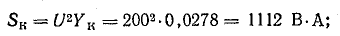
конденсатора
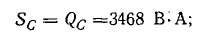
цепи
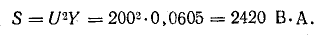
Задача 14.6.
Для схемы рис. 14.13 по данным условия задачи 14.5 найти резонансную частоту fр. Выполнить расчет цепи в порядке, изложенном при решении задачи 14.4, для двух значений частоты источника: 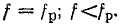
Решение. При резонансе 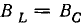 , т. е.
, т. е.
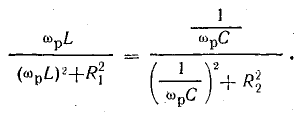
Решая относительно резонансной частоты, можно получить формулу
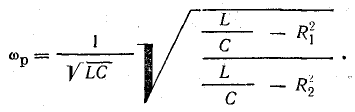
Учитывая, что R2 = 0, и подставляя другие данные, получим:
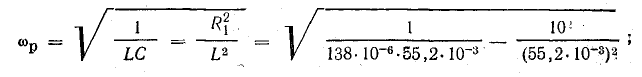
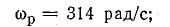
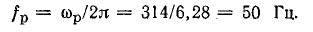
Далее расчет цепи по условию задачи выполните самостоятельно.
Расчет цепей с параллельным соединением ветвей
Расчет электрической цепи, рассмотренный в предыдущем параграфе, можно распространить на цепи, содержащие произвольное число приемников, соединенных параллельно.
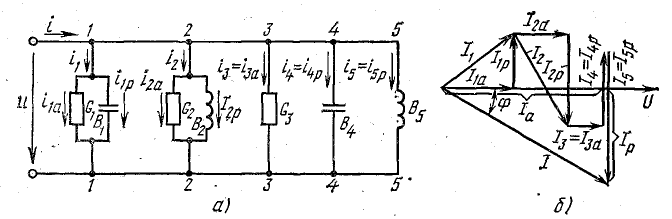
Рис. 14.14. Расчетная схема разветвленной цепи с двумя узлами и ее векторная диаграмма
На рис. 14.14, а параллельно соединены те же элементы цепи, были рассмотрены при последовательном соединении (см. рис. 14.7, а). Предположим, что для этой цепи известны напряжение 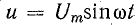 и параметры элементов цепи R, L, C. Требуется найти токи в цепи и мощность.
и параметры элементов цепи R, L, C. Требуется найти токи в цепи и мощность.
Векторная диаграмма
Для мгновенных величин в соответствии с первым законом Кирхгофа уравнение токов
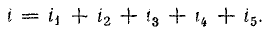
Представляя ток в каждой ветви суммой активной и реактивной составляющих, получим
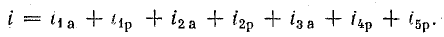
Для действующих токов нужно написать векторное уравнение
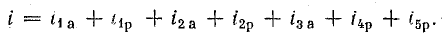
Численные значения векторов токов определяются произведением напряжения и проводимости соответствующей ветви.
На рис. 14.14, б построена векторная диаграмма, соответствующая этому уравнению. За исходный вектор принят, как обычно при расчете цепей с параллельным соединением ветвей, вектор напряжения U, а затем нанесены векторы тока в каждой ветви, причем направления их относительно вектора напряжения выбраны в соответствии с характером проводимости ветвей. Начальной точкой при построении диаграммы токов выбрана точка, совпадающая с началом вектора напряжения . Из этой точки проведен вектор I1а активного тока ветви I-I (по фазе совпадает с напряжением), а из конца его проведен вектор I1p реактивного тока той же ветви (опережает напряжение на 90°). Эти два вектора являются составляющими вектора I1 тока первой ветви. Далее в том же порядке отложены векторы токов других ветвей. Следует обратить внимание на то, что проводимость ветви 3-3 активная, поэтому реактивная составляющая тока в этой ветви равна нулю. В ветвях 4-4 и 5-5 проводимости реактивные, поэтому в составе этих токов нет активных составляющих.
Расчетные формулы
Из векторной диаграммы видно, что все активные составляющие векторов тока направлены одинаково — параллельно вектору напряжения, поэтому векторное сложение их можно заменить арифметическими найти активную составляющую общего тока: 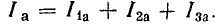
Реактивные составляющие векторов токов перпендикулярны вектору напряжения, причем индуктивные токи направлены в одну сторону, а емкостные — в другую. Поэтому реактивная составляющая общего тока в цепи определяется их алгебраической суммой, в которой индуктивные токи считаются положительными, а емкостные — отрицательными: 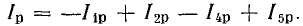
Векторы активного, реактивного и полного тока всей цепи образуют прямоугольный треугольник, из которого следует

Подставив величины токов в ветвях, выраженные через напряжение и соответствующие проводимости, получим
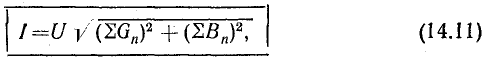
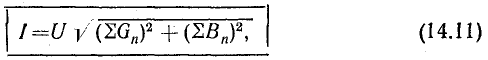
где 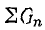 — общая активная проводимость, равная арифметической сумме активных проводимостей всех ветвей;
— общая активная проводимость, равная арифметической сумме активных проводимостей всех ветвей; 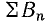 — общая реактивная проводимость, равная алгебраической сумме реактивных проводимостей всех ветвей (в этой сумме индуктивные проводимости считаются положительными, а емкостные — отрицательными); Y — полная проводимость цепи;
— общая реактивная проводимость, равная алгебраической сумме реактивных проводимостей всех ветвей (в этой сумме индуктивные проводимости считаются положительными, а емкостные — отрицательными); Y — полная проводимость цепи;
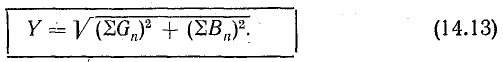
Таким образом получена знакомая уже формула (14.12), связывающая напряжение, ток и проводимость цепи [ср. (14.12) и (14.8)].
Следует обратить внимание на возможные ошибки при определении полной проводимости цепи по известным проводимостям отдельных ветвей: нельзя складывать арифметически проводимости ветвей, если токи в них не совпадают по фазе.
Полную проводимость цепи в общем случае определяют как гипотенузу прямоугольного треугольника, катетами которого являются выраженные в определенном масштабе активная и реактивная проводимости всей цепи:
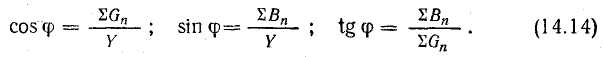
От треугольника токов можно перейти также к треугольнику мощностей и для определения мощности получить известные уже формулы
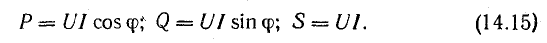
Активную мощность цепи можно представить как арифметическую сумму активных мощностей ветвей.
Реактивная мощность цепи равна алгебраической сумме мощностей ветвей. В этом случае индуктивная мощность берется положительной, а емкостная — отрицательной:
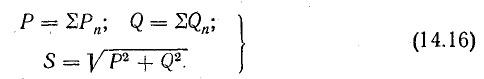
Расчет цепи без определения проводимостей ветвей
Расчет электрической цепи при параллельном соединении ветвей можно выполнить без предварительного определения активных и реактивных проводимостей, т. е. представляя элементы цепи в схеме замещения их активными и реактивными сопротивлениями (рис. 14.15, а).
Определяют токи в ветвях по формуле (14.4):
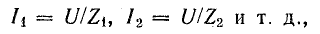
где Z1, Z2 и т. д. — полные сопротивления ветвей.
Полное сопротивление ветви, в которую входят несколько элементов, соединенных последовательно, определяют по формуле (14.5).
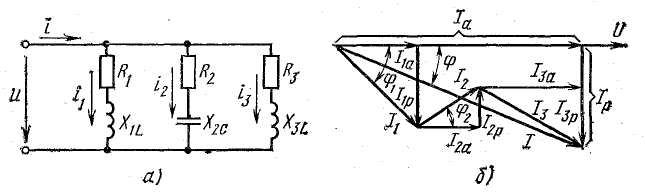
Рис. 14.15. Схема электрической цепи и ее векторная диаграмма
Для построения векторной диаграммы токов (рис. 14.15, б) можно определить активную и реактивную составляющие тока каждой ветви по формулам
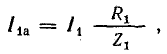
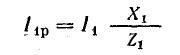
и т. д. для всех ветрей.
В этом случае отпадает необходимость определения углов φ1, φ2 и построения их на чертеже.
Ток в неразветвленной части цепи
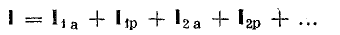
Общий ток и мощность цепи определяются далее в том же порядке, какой был показан ранее [см. формулы (14.10), (14.15), (14.16)].
Задача 14.7.
Определить ток в неразветвленной части цепи (рис. 14.16, а), активную, реактивную и полную мощности всей цепи. Построить векторную диаграмму токов и напряжений. Дано: R1 = 6 Ом, L1 = 25,5 мГн, R2 = 20 Ом, R2 = 15 Ом; L3 = 47,9 мГн, С3 = 159 мкФ, и 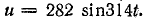
Решение. Реактивные сопротивления ветвей:
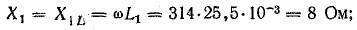
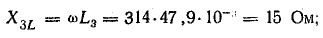
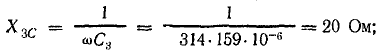
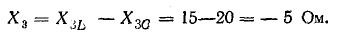
Полные сопротивления ветвей:
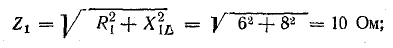
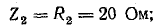
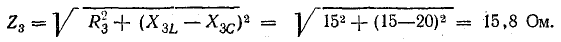
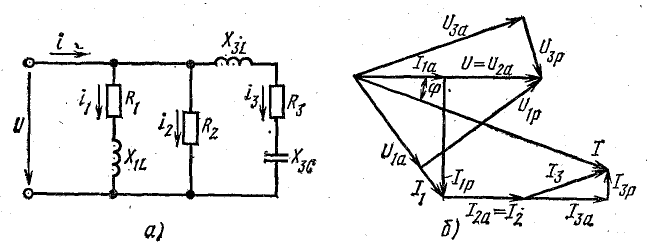
Рис. 14.16. к задаче 14.7
Действующее, напряжение
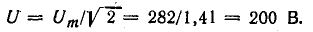
Токи в ветвях:
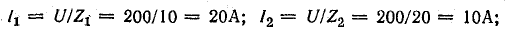
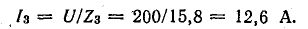
Составляющие токов ветвей:
активные
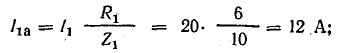
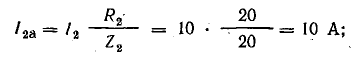
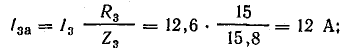
реактивные
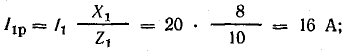
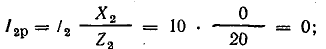
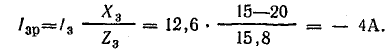
Общий ток:
активный
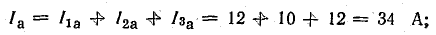
реактивный
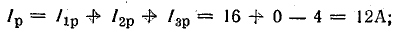
в неразветвленной части цепи
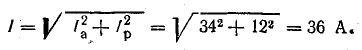
Активные мощности:
ветвей
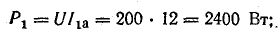
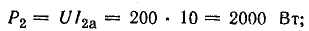
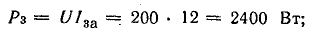
всей цепи
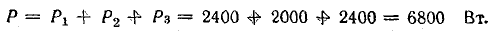
Реактивные мощности:
ветвей
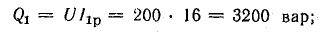
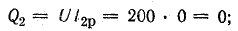
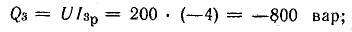
всей цепи
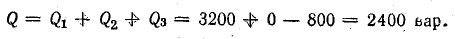
Полная мощность цепи
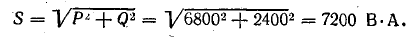
Проверка правильности подсчета мощности:
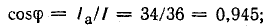
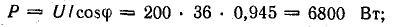
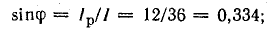
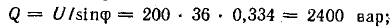
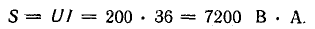
Для построения векторной диаграммы дополнительно определим активные и реактивные напряжения ветвей:
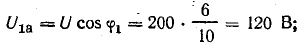
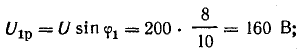
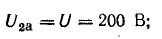
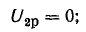
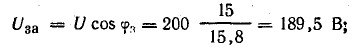
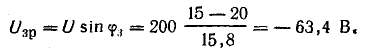
Векторная диаграмма показана на рис. 14.16, б.
- Символический метод расчета цепей
- Четырехполюсники
- Линейные диаграммы
- Круговые диаграммы
- Энергия в электрических цепях
- Линейные электрические цепи
- Нелинейные электрические цепи
- Магнитные цепи и их расчёт
Активное сопротивление в цепи переменного тока

Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R.
Для схемы, изображенной на рис. 13.1, а, заданы сопротивление R и напряжение, изменяющееся по закону
u = Umsinωt
Найдём ток и мощность в цепи.


Ток в цепи переменного тока с активным сопротивлением.
По закону Ома найдем выражение для мгновенного тока:
где Im = Um/R — амплитуда тока
Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, т. е. напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 13.1, б, б).
Действующий ток найдем, разделив амплитуду на √ 2:
Формулы (13.1) выражают закон Ома для цепи переменного тока с сопротивлением R. Внешне они ничем не отличаются от формулы для цепи постоянного тока, если переменные напряжение и ток выражены действующими величинами.
Мгновенная мощность в цепи переменного тока с активным сопротивлением.
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = Umsinωt * Imsinωt = UmImsin 2 ωt
Из тригонометрии найдём 
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р = UmIm√2 и перемен- ной р’:
р = Р + р’
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Активная мощность для цепи переменного тока с активным сопротивлением
Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.
Активная мощность — среднее арифметическое мгновенной мощности за период.
Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).
Равенство площадей РТ = Sp выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности Pm.
В этом случае часть площади Sp , находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:
P = UI
Активная мощность для данной цепи равна произведению действующих величин тока и напряжения:
P = UI = I 2 R
С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности p(t) [см. выражение (13.2)].
Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода: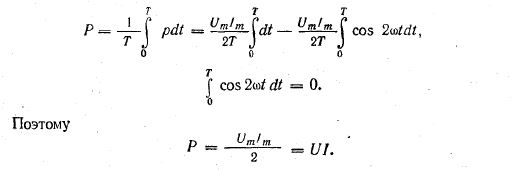
Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.
Электрические цепи синусоидального тока
Содержание:
Электрические цепи синусоидального тока:
В общем случае цепь переменного тока характеризуется тремя параметрами: активным сопротивлением R, индуктивностью L и емкостью С. В технике часто применяются цепи переменного тока, в которых преобладает один или два из этих параметров.
При анализе работы и расчетах цепей исходят из того, что для мгновенных значений переменного тока можно использовать все правила и законы постоянного тока.
Цепь с активным сопротивлением
Активным сопротивлением R обладают элементы, которые нагреваются при прохождении через них тока (проводники, лампы накаливания, нагревательные приборы и т.д.).
Если к активному сопротивлению R (рис. 11.1) приложено синусоидальное напряжение 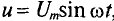
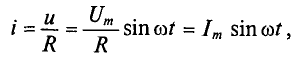
где 
Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны ( 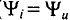 = 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.
= 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.
Математическое выражение закона Ома для цепи переменного тока с активным сопротивлением имеет вид:

Это вытекает из выражения (11.1), если левую и правую части уравнения разделить на 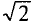 =1,41.
=1,41.
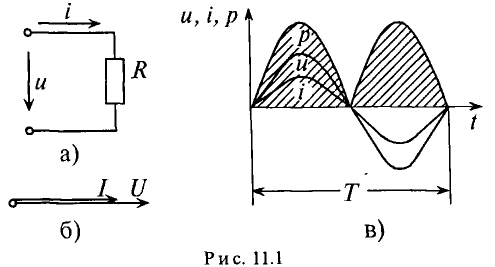
Таким образом, действующее значение синусоидального тока I пропорционально действующему значению синусоидального напряжения U и обратно пропорционально сопротивлению R участка цепи, к которому приложено напряжение U. Такая интерпретация закона Ома справедлива как для мгновенных, так и для действующих и амплитудных значений синусоидального тока.
Активная мощность
Мгновенная мощность в цепи с активным сопротивлением определяется произведением мгновенных значений напряжения ка, т. е. р = ui. Это действие производится над кривыми тока и ряжения в определенном масштабе (рис. 11.1в). В результате учена временная диаграмма мгновенной мощности р. Как видно из временной диаграммы, мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению (рис. 11.1в). Эта мощность (энергия) необратима. От источника она поступает на потребитель и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется активной.
Поэтому и сопротивление R, на котором происходит подобное образование, называется активным сопротивлением, цепи с активным сопротивлением мгновенная мощность характеризует скорость преобразования электрической энергии в другие виды энергии.
Количественно мощность в цепи с активным сопротивлением определяется следующим образом:
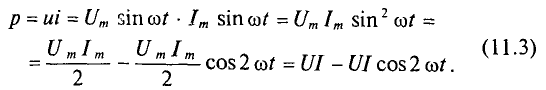
Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин -постоянной мощности UI и переменной 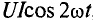 , изменяющейся с двойной частотой.
, изменяющейся с двойной частотой.
Средняя за период мощность, равная постоянной составляющей мгновенной мощности UI, является активной мощностью Р. Среднее за период значение переменной составляющей, как и всякой синусоидальной величины, равно нулю, то есть
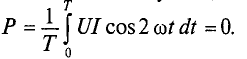
Таким образом, величина активной мощности в цепи синусоидального тока с активным сопротивлением с учетом закона Ома определяется выражением:
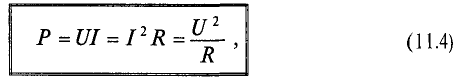
где U- действующее значение напряжения; I— действующее значение тока.
Единицей активной мощности является ватт:
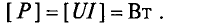
Поверхностный эффект и эффект близости
Сопротивление проводника постоянному току 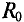 называют омическим сопротивлением и определяют выражением (2.8)
называют омическим сопротивлением и определяют выражением (2.8) 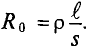 Сопротивление проводника переменному току R называют активным.
Сопротивление проводника переменному току R называют активным.
Оказывается, что сопротивление проводника переменному току больше его омического сопротивления за счет так называемого поверхностного эффекта и эффекта близости, т. е. 
Увеличение активного сопротивления вызвано неодинаковой плотностью тока в различных сечениях проводника (рис. 11.2а).
На рис. 11.2а изображено магнитное поле проводника цилиндрического сечения. Если по проводнику проходит переменный ток, то он создает переменный магнитный поток внутри и вне проводника. Этот поток в различных сечениях проводника индуктирует ЭДС самоиндукции, которая, согласно правилу Ленца. противодействует изменению тока как причине создания ЭДС Очевидно, центр проводника охвачен большим количеством магнитных линий (большее потокосцепление), чем слои, близкие к поверхности. Следовательно, в центре проводника ЭДС (сопротивление) больше, чем на поверхности проводника. Плотность на поверхности больше, чем в центре. Поэтому это явление и называется поверхностным эффектом.
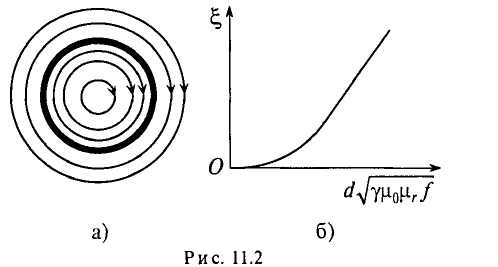
Таким образом, поверхностный эффект уменьшает сечение проводника для переменного тока, а следовательно, увеличивает активное сопротивление R.
Отношение активного сопротивления проводника к его сопротивлению определяет коэффициент поверхностного эффекта 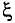 (кси)
(кси)
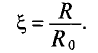
График зависимости коэффициента поверхностного эффекта от параметра проводника d, его удельной проводимости  , магнитной проницаемости материала проводника
, магнитной проницаемости материала проводника  и частоты переменного тока
и частоты переменного тока  , проходящего по проводнику, показан на рис. 11.26.
, проходящего по проводнику, показан на рис. 11.26.
При токах большой частоты  (радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.
(радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.
На величину активного сопротивления проводника R оказывает влияние и эффект близости.
Если токи в двух параллельных проводах, расположенных близко друг к другу, направлены в одну сторону, то элементы сечения водников, удаленных на большее расстояние друг от друга, цепляются с меньшим магнитным потоком и имеют большую плотность тока (заштриховано на рис. 11.3а), чем элементы сечения проводников, расположенные близко друг к другу.
Если же токи в близко расположенных параллельных проводах направлены в различные стороны, то большая плотность тока на-дается в элементах сечения проводников, расположенных ближе друг к другу (заштриховано на рис. 11.36).
Таким образом, эффект близости в проводниках также влияет активное сопротивление проводников за счет наведения в различных элементах сечений проводников различных ЭДС взаимоиндукции, направление которых определяется правилом Ленца.
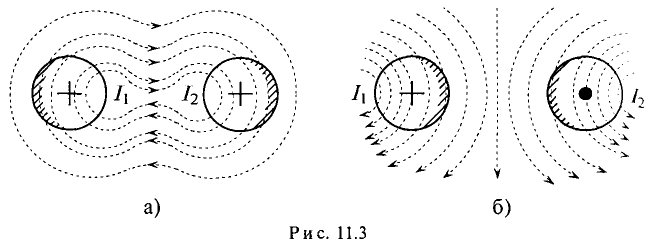
Цепь с идеальной индуктивностью
Идеальной называют индуктивность L такой катушки, активным сопротивлением R и емкостью С которой можно пренебречь, т.е. R= О и С=0.
Если в цепи идеальной катушки индуктивностью L (рис. 11.4а) проходит синусоидальный ток 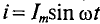 , то этот ток создает в катушке синусоидальный магнитный поток
, то этот ток создает в катушке синусоидальный магнитный поток 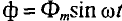 , который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)
, который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)
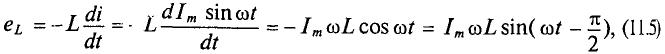
так как 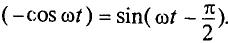
Очевидно, эта ЭДС достигает своего амплитудного значения 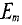 тогда, когда
тогда, когда 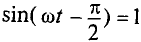 :
:
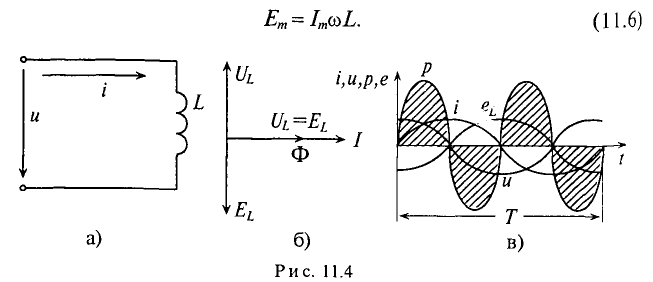
Тогда 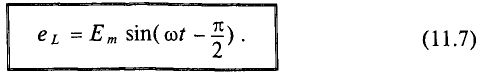
Таким образом, ЭДС самоиндукции в цепи с идеальной индуктивностью L, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90° = 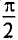 (рис. 11.46, в).
(рис. 11.46, в).
По второму закону Кирхгофа для мгновенных значений можно записать

Откуда 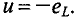
Тогда напряжение, приложенное к цепи с идеальной индуктивностью (см. (11.5)):
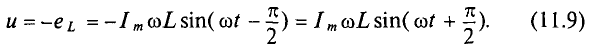
Очевидно, напряжение достигает своего амплитудного значения Um тогда, когда 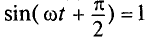 :
:

Следовательно, 
Таким образом, напряжение, приложенное к цепи с идеальной ин-ивностью, как и ток в этой цепи, изменяется по синусоидально-жону, но опережает ток по фазе на угол 90°= 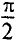 (рис. 11.46, в).
(рис. 11.46, в).
Резюмируя все вышесказанное, можно сделать вывод: для существования тока в цепи с идеальной индуктивностью необходимо ожить к цепи напряжение, которое в любой момент времени но по величине, но находится в противофазе с ЭДС, вызванной таким током (рис. 11.46, в).
Временная диаграмма (рис. 11.4в) еще раз иллюстрирует правило Ленца: ЭДС 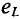 противодействует изменению тока.
противодействует изменению тока.
Если уравнение (11.10) разделить на 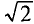 =1,41, то получается
=1,41, то получается 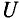 =
=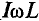 , откуда
, откуда

Это уравнение (11.12а) и есть математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью. Очевидно, знаменатель этого уравнения есть не что иное, как сопротивление, которое называют индуктивным сопротивлением XL.

Закон Ома для этой цепи можно записать иначе:

Индуктивное сопротивление XL — это противодействие, которое ЭДС самоиндукции eL оказывает изменению тока.
Реактивная мощность в цепи с индуктивностью
Мгновенная мощность для цепи синусоидального тока с идеальной катушкой равна произведению мгновенных значений напряжения и тока
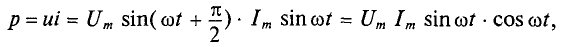
где 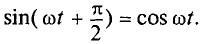
Следовательно, 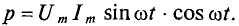
Полученное уравнение умножают и делят на 2:
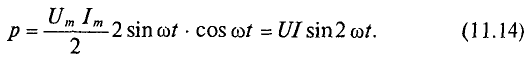
Таким образом, мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой.
Следовательно, среднее значение этой мощности за период Яс, как и любой синусоидальной величины, т. е. активная потребляемая мощность, в этой цепи равна нулю, Р= 0.
Временная диаграмма (рис. 11,4в) подтверждает этот вывод. На диаграмме видно, что мгновенная мощность (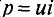 ) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.
) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.
То есть в 1-ю и 3-ю четверти периода мощность (энергия) источника накапливается в магнитном поле индуктивности. Максимальное значение накапливаемой в магнитном поле идеальной катушки энергии по (9.12) равно
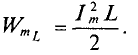
Во 2-ю и 4-ю четверти периода эта мощность (энергия) из магнитного поля идеальной катушки возвращается к источнику.
Таким образом, в цепи переменного тока с идеальной катушки мощность не потребляется (Р= 0), а колеблется между источником и магнитным полем индуктивности, загружая источник и провода.
Такая колеблющаяся мощность (энергия), в отличие от активной, потребляемой, называется реактивной.
Обозначается реактивная мощность буквой Q и измеряется в варах, т.е. [Q]=вар (вольт-ампер реактивный).
Величина реактивной мощности в рассматриваемой цепи определяется выражением
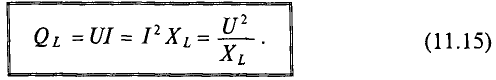
Так как реактивная мощность QL имеет место в цепи с индуктивным сопротивлением, то индуктивное сопротивление считается реактивным сопротивлением X индуктивного характера, т. е. XL.
Цепь с емкостью
Если конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора ходит в цепи очень короткое время, пока напряжение на конденсаторе Uc не станет равным напряжению источника U.
Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I=0).
Если же конденсатор подключить к источнику с синусоидальным напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжена конденсаторе Uc отстает по фазе от напряжения источника и зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 – конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.
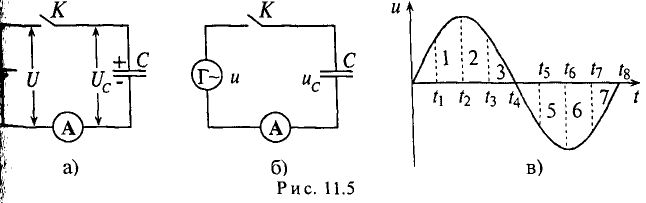
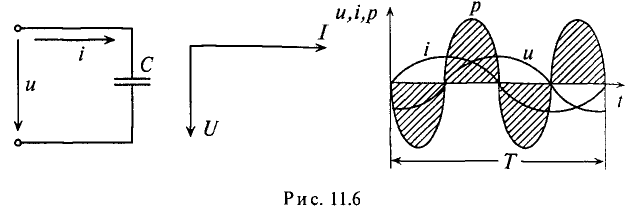
Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение 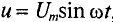 , то в цепи конденсатора проходит ток i (рис. 11.6а):
, то в цепи конденсатора проходит ток i (рис. 11.6а):
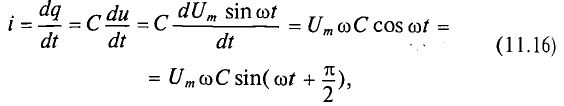
где q= Си согласно (6.3).
Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда 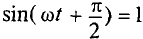 :
:

Тогда 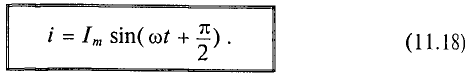
Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90°=
Следовательно, напряжение отстает по фазе от тока на 90° =  (рис. 11.66).
(рис. 11.66).
Если уравнение (11.17) разделить на 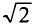 = 1,41, то получится равенство
= 1,41, то получится равенство 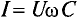 или
или

Это равенство (11.19а) и является математическим выражением закона Ома для цепи переменного тока с емкостью.
Очевидно, знаменатель этого равенства является сопротивлением конденсатора Хс, которое называется емкостным сопротивлением:

Когда закон Ома для цепи с конденсатором можно записать:

Емкостное сопротивление – это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11,5а).
Реактивная мощность в цепи с конденсатором
Если в цепи конденсатора емкостью 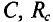 = 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:
= 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:
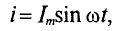
Напряжение и, приложенное к этому конденсатору (рис. 11.6), будет равно
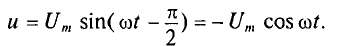
Мгновенная мощность в цепи с конденсатором
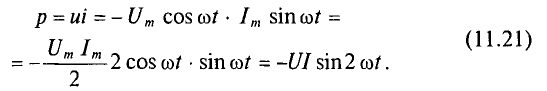
Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой (рис. 11.6в).
Следовательно, активная мощность Р в рассматриваемой цепи 1С. 11.6а), равная среднему значению мгновенной мощности за период, имеет нулевое значение, Р= 0.
Это следует и из временной диаграммы (рис. 11.6в). На временной диаграмме видно, что изменение мгновенной мощности р по синусоидальному закону происходит с двойной частотой: 2-ю и 4-ю четверти периода мощность (энергия) источника накапливается в электрическом поле конденсатора.
Максимальное значение энергии, накапливаемой в электрическом поле конденсатора, равно
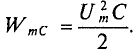
В 1-ю и 3-ю четверти периода эта мощность (энергия) из электрического поля конденсатора возвращается к источнику.
Таким образом, в цепи переменного тока с конденсатором происходит колебание мощности (энергии) между источником и электрическим полем конденсатора. Такая колеблющаяся, но не потребляемая мощность называется реактивной мощностью.
Величина реактивной мощности в цепи конденсатора определяется выражением
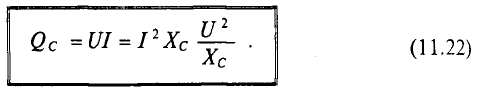
Из временных диаграмм (рис. 11.4в, 11.6в) видно, что реактивная мощность в цепи конденсатора изменяется в противофазе с реактивной мощностью в цепи с идеальной катушкой. Отсюда и знак «минус» в уравнении (11.21) – аналитическом выражении мгновенной мощности в цепи с конденсатором.
Так как реактивная мощность Qc имеет место в цепи с емкостным сопротивлением, то это емкостное сопротивление считается реактивным сопротивлением Х емкостного характера (Хс).
Расчет линейных электрических цепей синусоидального тока
Расчет электрических цепей синусоидального тока производится преимущественно с помощью векторных диаграмм. В нашей главе рассматривается расчет неразветвленных цепей синусоидального тока, содержащих активное сопротивление R, активность L и емкость С в различных сочетаниях.
Цепь с активным сопротивлением и индуктивностью
Если по цепи с реальной катушкой, обладающей активным сопротивлением R и индуктивностью L, проходит синусоидальный ток 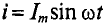 (рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки
(рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки 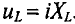
Следовательно, по второму закону Кирхгофа, для мгновенных значений, приложенное к реальной катушке напряжение можно записать

Это равенство справедливо для неразветвленной цепи синусоидального тока с последовательно включенными активным сопротивлением R и индуктивным сопротивлением XL (рис. 12.16).
Активное напряжение (рис. 11.16) совпадет по фазе с током и может быть записано 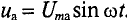 . Индуктивное напряжение
. Индуктивное напряжение 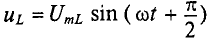 опережает ток на угол 90° =
опережает ток на угол 90° = 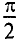 .
.
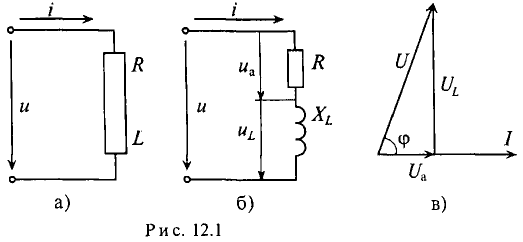
Мгновенное значение напряжения, приложенного к цепи, определяется алгебраической суммой мгновенных значений напряжений 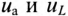 согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений
согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений
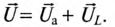
Это равенство лежит в основе построения векторной диаграммы (рис. 12.1 в).
Из векторной диаграммы (рис. 12.1 в) видно, что напряжение U, приложенное к реальной катушке, опережает по фазе ток 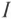 на угол ф. Мгновенное значение этого напряжения может быть записано:
на угол ф. Мгновенное значение этого напряжения может быть записано:
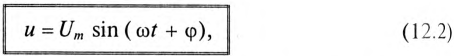
где ф — это международное обозначение угла сдвига фаз между током и напряжением для любой цепи переменного тока.
Воспользовавшись теоремой Пифагора для определения гипотенузы прямоугольного треугольника, по векторной диаграмме (рис. 12.1 в) определяется напряжение
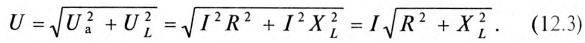

Равенство (12.4) является математическим выражением закона Ома для цепи синусоидального тока с активным R и индуктивным XL сопротивлениями в неразветвленной цепи.
Знаменатель этого равенства является сопротивлением этой цепи, которое называется полным, или кажущимся, сопротивлением цепи синусоидального тока. Обозначается кажущееся (полное) сопротивление любой цепи переменного тока буквой Z:

где Zk — полное, или кажущееся, сопротивление реальной катушки.
Тогда закон Ома для любой цепи переменного тока в общем виде можно записать

где Z — кажущееся сопротивление этой цепи.
Треугольники напряжений, сопротивлений, мощностей
Треугольник, все стороны которого изображены векторами напряжений, называется треугольником напряжений. Пользуясь векторной диаграммой для неразветвленной цепи с активным и индуктивным сопротивлениями (рис. 12.1в), выделяем треугольник напряжений (рис. 12.2а).
Связь между напряжениями в данной цепи можно рассматривать как соотношение между сторонами и углами прямоугольного треугольника:
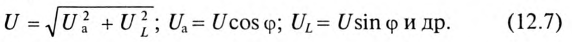
Если все стороны треугольника напряжений разделить на ве-1ину тока в цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают сопротивления цепи, т. е. получится треугольник составлений (рис. 12.16). Сопротивления не являются векторными величинами. Из треугольника сопротивлений можно определить:
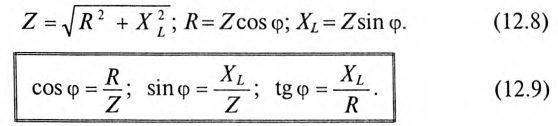
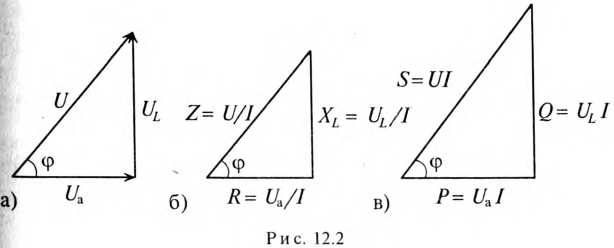
Обычно тригометрические функции угла ф определяются из треугольника сопротивлений отношением (12.9).
Если все стороны треугольника напряжений умножить на величину тока цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают мощности цепи, т.е. получится треугольник мощностей (рис. 12.2в).
Произведение напряжения и тока цепи характеризует полную мощность цепи

которая измеряется в вольт-амперах, т.е. 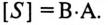
Однако потребляется в цепи только часть полной мощности – активная мощность
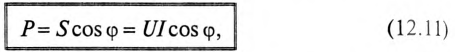
где cos ф показывает, какая часть полной мощности 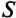 потребляется в цепи, поэтому cos ф называют коэффициентом мощности:
потребляется в цепи, поэтому cos ф называют коэффициентом мощности:

Полная мощность цепи S называется кажущейся. Из того же треугольника мощностей (рис. 12.2в) записать:
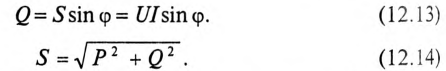
Построив треугольники напряжений, сопротивлений и мощностей для любой цепи синусоидального тока, по выражениям (12.7)—(12.14) можно рассчитать параметры этой цепи.
Цепь с активным сопротивлением и емкостью
Если в цепи с последовательно включенными активным сопротивлением R и емкостью С протекает синусоидальный ток 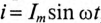 , то он создает падение напряжения на активном сопротивлении
, то он создает падение напряжения на активном сопротивлении 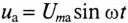 и на емкостном сопротивлении
и на емкостном сопротивлении 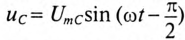 . Векторная диаграмма для этой цепи изображена на рис. 12.36.
. Векторная диаграмма для этой цепи изображена на рис. 12.36.
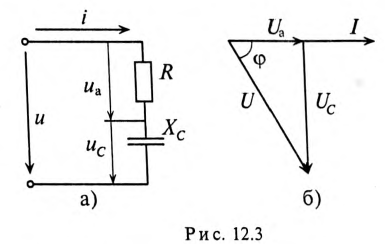
Напряжение цепи изменяется, как и ток, по синусоидальному закону и отстает по фазе от тока на угол ф
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Цепь с активным сопротивлением
Напряжение и ток
 Цепь, изображенная на рис. 5 -17, обладает активным сопротивлением г и индуктивностью L. Примером такой цепи может служить катушка любого электромагнитного прибора или аппарата.
Цепь, изображенная на рис. 5 -17, обладает активным сопротивлением г и индуктивностью L. Примером такой цепи может служить катушка любого электромагнитного прибора или аппарата.
При прохождении переменного тока i в цепи будет индуктироваться э. д. с. самоиндукции eL .
Согласно второму правилу Кирхгофа u + eL = i r
откуда напряжение на зажимах цепи
Первая слагающая uа = i r называется активным напряжением, мгновенное значение которого пропорционально току, а вторая uL = — eL = L( d i /dt) реактивным напряжение м, мгновенное значение которого пропорционально скорости изменения тока.
Если ток изменяется по закону синуса
Рис. 5-17, Цепь с активным сопротивлением и индуктивностью.
Оно изменяется также синусоидально, совпадая по фазе с током.

Амплитудное значение активного напряжения
а действующее значение
Оно изменяется синусоидально, опережая по фазе ток на 90°.
Амплитудное значение реактивного напряжения
 а действующее значение
а действующее значение
Напряжение на зажимах цепи
Напряжение на зажимах изменяется синусоидально, опережая ток по фазе на угол φ.
На рис. 5-18 показаны графики; i , иa, uL и и, а на рис. 5-19 — векторная диаграмма цепи. На диаграмме векторы напряжений U, U a и U L образуют прямоугольный треугольник напряжений, из которого непосредственно следует со отношение, связывающее эти величины:
Аналогичная зависимость имеет место и для амплитудных значений
Угол сдвига фаз между напряжением на зажимах
Рис 5-18. Графики тока и напряжения в цепи с активным сопротивлением и индуктивностью.
Рис 5 -19. Вектор ная диаграмма це пи с активным сопротивлением и индуктивностью.
цепи и током в ней находится из треугольника напряжений по одной из формул
 Чем больше реактивное напряжение по сравнению с ак тивным, тем на больший угол ток отстает по фазе от напря жения на зажимах цепи.
Чем больше реактивное напряжение по сравнению с ак тивным, тем на больший угол ток отстает по фазе от напря жения на зажимах цепи.
Сопротивления цепи
Уравнение (5-30) можно переписать в следующем виде
откуда ток в цепи
называется полным сопротивлением цепи.
Сопротивления r, xL и z графически можно изобразить сторонами прямоугольного треугольника — треугольника сопротивлении (рис. 5-20), который можно получить из треугольника напряжений, уменьшив каждую из его сторон в I раз.
Так как треугольники сопротивлений и напряжений подобны, то угол сдвига φ между напряжением и током, равный углу между сторонами треугольника z и r, можно определить через
Рис 5-20. Треугольник сопротивлений цепи с активным сопротивлением и индуктивностью
Мощности
Мгновенное значение мощности р = u i = Uм sin (ωt + φ) I м sin ωt = Uм I м sin (ωt + φ) sin ωt Учитывая, что
sin (со/ + φ) sin ωt = 1/2 cos φ — 1/2 cos (2 ωt + φ)
а также (5-28), можно написать другое выражение ной мощности
Р = U I cos φ — U I cos (2ωt + φ)
Написанное выражение состоит из двух членов: постоянного, независимого от времени UI cos φ и переменного си-
нусоидального U I cos (2ωt + φ). Среднее значение мощности за период, которым обычно пользуются при расчете цепей переменного тока, будет равно постоянному члену UI cos φ , так как среднее значение за период синусоидальной функции равно нулю.
Таким образом, среднее значение мощности цепи равно произведению действующих значений напряжения и тока, умноженному на cos φ , т.е.
Следовательно, средняя мощность цепи равна среднему значению мощности в активном сопротивлении. Поэтому среднюю мощность любой цепи называют; еще и активной мощностью.

Реактивная мощность цепи :
т.е. реактивная мощность цепи равна произведению действующих значений напряжения и тока, умножен ному на sin φ .
Рис.5- 21. Т ре угольник мощностей
Полной мощностью цепи называется произведение действующих значений напряжения и тока, т. е.
Учитывая, что sin 2 φ + cos 2 φ = 1 можно написать: (U I cos φ ) 2 + (U I sin φ ) 2 = ( U I ) 2
Мощности Р, Q и S графически можно изобразить сторонами прямоугольного треугольника — тре у го ль ника мощностей (рис 5-21), который можно получить из треугольника напряжений, умножая на I все его стороны.
т.е отношение активной мощности к полной называется коэффициентом мощности.
Единица полной мощности с называется вольт-ампер (в •а).
Необходимость применения понятия полной мощности обусловлена тем, что конструкция, габариты, вес и стоимость машины или аппарата определяются их номинальной полной мощностью Sн = Uн Iн а полная мощность S при том или ином режиме работы их определяет степень их использования.
Статья на тему Цепь с активным сопротивлением
Похожие страницы:
Понравилась статья поделись ей
Leave a Comment
Для отправки комментария вам необходимо авторизоваться.
Уравнения мгновенных значений тока и напряжения в цепи с активным сопротивлением
«Физика – 11 класс»
Активное сопротивление
Сила тока в цепи с резистором
Есть цепь, состоящая из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R.
Сопротивление R называется активным сопротивлением, т.к. при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора.
Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.
Напряжение на зажимах цепи меняется по гармоническому закону:
u = Um cos ωt
Мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения.
По закону Ома мгновенное значение силы тока:
В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения, а амплитуда силы тока определяется равенством
Мощность в цепи с резистором
В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение меняются.
При прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет меняться во времени.
Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой
Р = I 2 R
Мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой
Р = i 2 R
Cреднее значение мощности за период (используем формулу для мгновенного значения силы тока и выражение ):
График зависимости мгновенной мощности от времени (рис.а):
Согласно графику (рис.б) среднее за период значение cos 2ωt равно нулю, а значит равно нулю второе слагаемое в формуле для среднего значения мощности за период.
Тогда средняя мощность равна:
Действующие значения силы тока и напряжения.
Среднее за период значение квадрата силы тока:
Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока.
Действующее значение силы переменного тока обозначается через I:
Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.
Действующее значение переменного напряжения определяется аналогично:
Закон Ома для участка цепи переменного тока с резистором в действующих значениях:
В случае электрических колебаний важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность.
Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.
Действующие значения непосредственно определяют среднее значение мощности Р переменного тока:
р = I 2 R = UI.
Итак:
Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.
Источник: «Физика – 11 класс», учебник Мякишев, Буховцев, Чаругин
Электромагнитные колебания. Физика, учебник для 11 класса – Класс!ная физика
[spoiler title=”источники:”]
http://www.evkova.org/elektricheskie-tsepi-sinusoidalnogo-toka
http://znaesh-kak.com/e/e/%D1%86%D0%B5%D0%BF%D1%8C-%D1%81-%D0%B0%D0%BA%D1%82%D0%B8%D0%B2%D0%BD%D1%8B%D0%BC-%D1%81%D0%BE%D0%BF%D1%80%D0%BE%D1%82%D0%B8%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5%D0%BC
http://class-fizika.ru/11_27.html
[/spoiler]
Для расчетов напряжений и токов через элементы электрической цепи нужно знать их общее сопротивление. Источники энергии делятся на два типа:
- постоянного тока (батарейки, выпрямители, аккумуляторы), электродвижущая сила (ЭДС) которых не изменяется во времени;
- переменного тока (бытовые и промышленные сети), ЭДС которых изменяется по синусоидальному закону с определенной частотой.
Активные и реактивные сопротивления
Сопротивление нагрузки бывает активным и реактивным. Активное сопротивление (R) не зависит от частоты сети. Это означает, что ток в нем изменяется синхронно с напряжением. Это то сопротивление, которое мы измеряем мультиметром или тестером.
 Обозначение активного сопротивления
Обозначение активного сопротивления
Реактивное сопротивление делится на два вида:
— индуктивное (трансформаторы, дроссели);
 Обозначение индуктивного сопротивления
Обозначение индуктивного сопротивления
— емкостное ( конденсаторы).
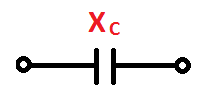 Обозначение емкостного сопротивления
Обозначение емкостного сопротивления
Отличительная черта реактивной нагрузки – наличие опережения или отставания тока от напряжения. В емкостной нагрузке ток опережает напряжение, а в индуктивной – отстает от него.
Физически это выглядит так: если разряженный конденсатор подключить к источнику постоянного тока, то в момент включения ток через него максимальный, а напряжение – минимальное. Со временем ток уменьшается, а напряжение — возрастает, пока конденсатор не зарядится.
Если подключить конденсатор к источнику переменного тока, то он будет постоянно перезаряжаться с частотой сети, а ток — увеличиваться раньше, чем напряжение.
Физические величины в формулах
| Обозначение | Единица измерения | Наименование |
| С | Фарада (Ф) | емкость |
| ѡ | 1/с | угловая частота |
| f | Герц (Гц) | частота |
| L | Генри (Гн) | индуктивность |
Полное сопротивление электрической цепи переменного тока
В сети переменного тока нет нагрузки только активной или только реактивной. Нагревательный элемент помимо активного содержит индуктивное сопротивление, в электродвигателе индуктивное сопротивление преобладает над активным.
Величину полного сопротивления, учитывающего все активные и реактивные составляющие электрической цепи, подсчитывают по формуле:
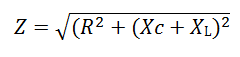
Расчет эквивалентного сопротивления элементов цепи
К одному источнику питания может быть подключено несколько сопротивлений. Для вычисления тока нагрузки источника подсчитывают эквивалентное сопротивление нагрузки. В зависимости от соединения элементов между собой, используются два способа.
Последовательное соединение сопротивлений.
В этом случае их величины складываются:
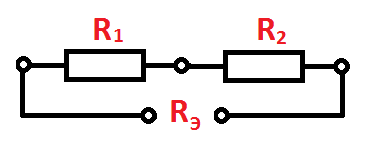 Последовательное соединение двух сопротивлений
Последовательное соединение двух сопротивлений
![]()
Чем больше сопротивлений соединено последовательно, тем больше эквивалентное сопротивление этой цепи. Бытовой пример: если контакт в штепсельной вилке ухудшится, это равносильно подключению последовательно с нагрузкой дополнительного сопротивления. Эквивалентное сопротивление нагрузки вырастет, а ток через нее – уменьшится.
- Параллельное соединение сопротивлений.
- Формула расчета выглядит намного сложнее:
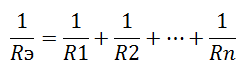
- Случай применения этой формулы для двух параллельно соединенных сопротивлений:
- Случай для соединения n одинаковых сопротивлений R:
Чем больше сопротивлений соединить параллельно, тем итоговое сопротивление цепи меньше. Это мы наблюдаем и в повседневной жизни: чем больше к сети подключить потребителей, тем меньше эквивалентное сопротивление и больше ток нагрузки.
Таким образом, расчет полного сопротивления электрической цепи происходит поэтапно:
- Рисуется схема замещения цепи, содержащая активные и реактивные сопротивления.
- Рассчитываются эквивалентные сопротивления отдельно для активной, индуктивной и емкостной составляющих нагрузки.
- Рассчитывается полное сопротивление электрической цепи
- Рассчитываются токи и напряжения в цепи источника питания.
Источник: http://electric-tolk.ru/polnoe-soprotivlenie-elektricheskoj-cepi/
Соединение элементов в цепи переменного напряжения и тока
Всем доброго времени суток! В прошлой статье я рассказал о воздействии переменного напряжения на элементы цепи (сопротивление, индуктивность и ёмкость) и воздействие этих элементов на напряжение, ток и мощность. В данной статье я расскажу о последовательном и параллельном соединении элементов цепи и воздействии на такие цепи переменного напряжения и тока.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Последовательное соединение элементов цепи при переменном напряжении
Начнём с последовательного соединения сопротивления R, индуктивности L и ёмкости C и рассмотрим воздействие на неё переменного напряжения с частотой ω.
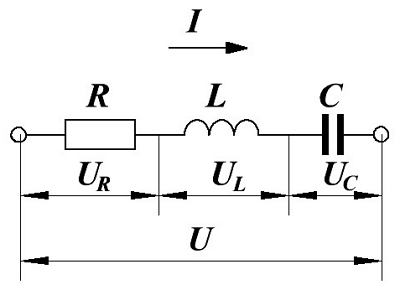
В данной цепи входное переменное напряжение U в соответствии со вторым законом Кирхгофа будет равно алгебраической сумме переменных напряжений на отдельных элементах
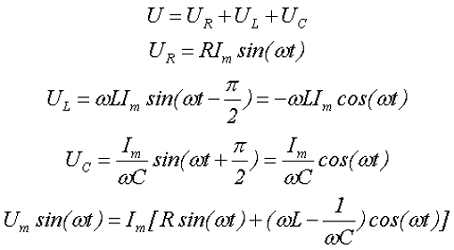
- где UR, UL, UC – напряжение на элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,
- Im – амплитудное значение переменного тока.
- Графическое изображение напряжений и токов на последовательно соединённых элементах цепи представлено ниже
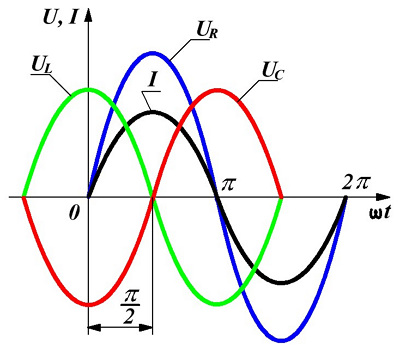
Итоговое выражение является тригонометрической формой записи второго закона Кирхгофа для мгновенных напряжений и его можно переписать в виде
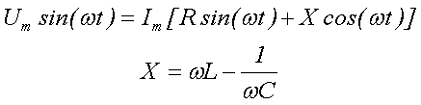
- где R – активное сопротивление,
- Х – реактивное сопротивление.
- Значение активного сопротивления R всегда только положительно, а реактивное сопротивление Х может принимать, как положительное значение Х > 0, тогда оно имеет индуктивный характер, так и отрицательное значение X < 0, в этом случае реактивное сопротивление имеет ёмкостный характер.
- В случае же нулевого значения реактивного сопротивления, имеет место резонанс напряжений
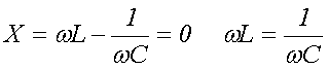
В этом случае сопротивление цепи представлено только активной нагрузкой R, а следовательно сдвиг фаз между напряжением и током будет нулевым.
При расчётах нас интересует не столько ток и напряжение на отдельных элементах, сколько ток и напряжение всей цепи. Для этого продолжим преобразовывать напряжение
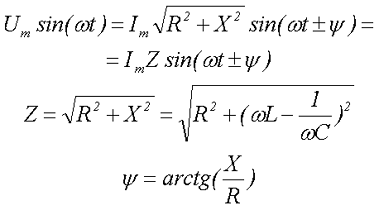
- где Z – полное сопротивление цепи,
- ψ – разность фаз между напряжением и током.
- Таким образом, амплитудное значение напряжения Um и амплитудное значение тока Im связаны между собой следующим соотношением
![]()
- где Um – амплитудное значение переменного напряжения,
- Im – амплитудное значение переменного тока,
- Z – полное сопротивление цепи.
Параллельное соединение элементов цепи при переменном напряжении
Теперь рассмотрим параллельное соединение элементов цепи (сопротивления, индуктивности и ёмкости) и прохождение по ним переменного тока.
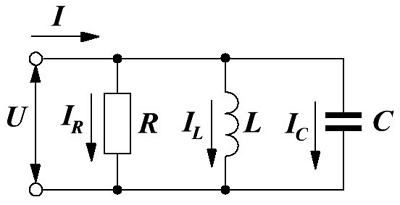
Подадим на вход такой цепи переменное напряжение U, тогда электрический ток в цепи I, в соответствии с первым законом Кирхгофа, будет равняться алгебраической суммы токов проходящей через элементы цепи
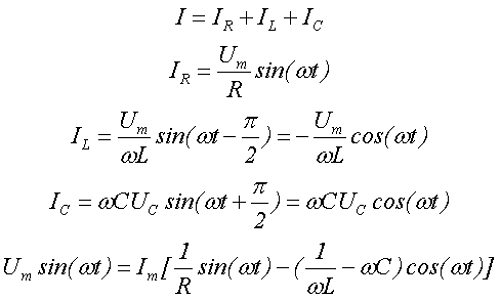
- IR, IL, IC – токи в элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,
- Um – амплитудное значение переменного тока.
- Графическое изображение напряжений и токов в параллельно соединённых элементах цепи представлено ниже
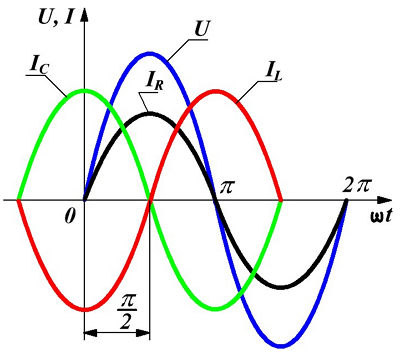
- Аналогично второму закону Кирхгофа, для первого закона также существует тригонометрическая форма записи, которая соответствует получившемуся выражению. Выполним ещё одно преобразование данного выражения
- где g – активная проводимость, b – реактивная проводимость.
Как видно из формулы, реактивная проводимость может быть положительной b > 0, тогда она имеет индуктивный характер, а может быть отрицательной b < 0, тогда реактивная проводимость имеет ёмкостный характер. А активная проводимость может быть только положительной.
- Отдельный случай представляет собой реактивная проводимость равная нулю, то есть в этом случае проводимость индуктивности и ёмкости одинаковы
- Такой случай называется резонансом токов, в этом случае общая проводимость будет определяться только активной проводимостью, а сдвиг фаз между напряжением и током в цепи будет нулевым.
- Определим зависимость между напряжением и силой тока в параллельной цепи
- где y – полная проводимость,
- ψ – разность фаз между напряжением и током в цепи.
- Тогда зависимость между напряжением и током в цепи с параллельно соединёнными элементами будет иметь вид
- где Um – амплитудное значение переменного напряжения,
- Im – амплитудное значение переменного тока,
- y – полная проводимость цепи.
Чему равна мощность в цепи при синусоидальном напряжении?
- Мощность является основной энергетической характеристикой, поэтому рассмотрим мощность в цепи переменного напряжения.
Мгновенная мощность в цепи будет равна
- Как видно из получившегося выражения, мгновенная мощность состоит из постоянной составляющей UIcos(φ) и переменной составляющей UIcos(2ωt – φ), изменяющейся с удвоенной частотой по сравнению с частотой напряжения (тока).
- Теперь определим среднее значение мощности за период или активную мощность, которая будет равна
- где U – действующее значение переменного напряжения,
- I – действующее значение переменного тока,
- cos(φ) – коэффициент мощности.
- Таким образом, активная мощность в цепи переменного напряжения (тока), равна произведению действующих значений напряжения и тока на коэффициент мощности.
При разработке и проектировании цепей переменного напряжения стараются сделать коэффициент мощности как можно больше, в идеале должен быть равен единице cos(φ) = 1. При небольших значениях данного коэффициента для создания в цепи необходимой мощности Р необходимо повышать величину напряжения U (тока I).
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Источник: https://www.electronicsblog.ru/silovaya-elektronika/soedinenie-elementov-v-cepi-peremennogo-napryazheniya-i-toka.html
Полное сопротивление: общие сведения, зависимость от других величин и формулы расчета

Все вещества по проводимости электрического тока (ЭТ) делятся на проводники, полупроводники и диэлектрики. Проводниками являются элементы, хорошо проводящие ЭТ. Это обусловлено наличием свободных электронов (СЭ). Полупроводники — особая группа веществ, проводимость которых зависит от внешних факторов, например, от температуры, освещенности и т. д. Диэлектриками являются все вещества, которые не проводят ЭТ из-за отсутствия или недостаточного количества СЭ. Для протекания тока по веществу требуется наличие СЭ, количество которых зависит от электронной конфигурации.
Электронная конфигурация какого-либо элемента берется из таблицы Менделеева. Ток оказывает на проводник тепловое действие, так как происходит взаимодействие СЭ с кристаллической решеткой (КР).Они замедляются, но с течением времени под действием электромагнитного поля снова ускоряются, после чего процесс взаимодействия повторяется много раз.
Процесс взаимодействия свободных заряженных частиц с КР вещества называется электрическим сопротивлением проводника. Обозначается сопротивление или электропроводимость буквой R, единицей измерения этой величины является Ом.
Зависимость электропроводимости
R зависит от внешних факторов окружающей среды, электрических величин, а также характерных особенностей проводника. Эти зависимости используются при расчетах схем и изготовлении радиодеталей. Существует несколько способов нахождения R, а иногда они комбинируются для получения эффективности и точности вычислений.
Электрические величины
 К электрическим величинам, от которых зависит величина R, относятся I, U, электродвижущая сила (ЕДС обозначается е) и тип тока. R в электрических цепях рассчитывается по закону Ома для определенного участка цепи: I, протекающая в заданном участке электрической цепи, прямо пропорциональна U на этом участке и обратно пропорциональна R выбранного участка цепи. В виде формулы его можно записать следующим образом: I = U / R.
К электрическим величинам, от которых зависит величина R, относятся I, U, электродвижущая сила (ЕДС обозначается е) и тип тока. R в электрических цепях рассчитывается по закону Ома для определенного участка цепи: I, протекающая в заданном участке электрической цепи, прямо пропорциональна U на этом участке и обратно пропорциональна R выбранного участка цепи. В виде формулы его можно записать следующим образом: I = U / R.
Исходя из следствия этого закона, можно получить сопротивление участка цепи: R = U / I.
Если требуется произвести расчет R на всем участке цепи, то нужно воспользоваться формулой (следствием из закона Ома для полной цепи) с учетом внутреннего R источника питания: R = (e / I) — R внутреннее.
Величина электрической проводимости рассчитывается не только при помощи законов Ома, но и с использованием геометрических параметров проводника и температуры. Кроме того, необходимо учитывать и тип тока (постоянный или переменный).
Геометрические параметры и тип вещества
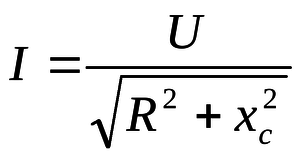
Зависимость от материала выражается коэффициентом, обозначающимся p. Он характеризует показатель удельного R проводника. Его значение берется из таблицы (при температуре +20 °C). Величина, обратная p, называется удельной проводимостью и обозначается σ. Взаимосвязь σ и p можно выразить формулой p = 1 / σ.
Кроме того, от площади поперечного сечения (S) также зависит R проводника.
Эта зависимость обусловлена тем, что при маленьком сечении плотность потока Э протекает через проводник и взаимодействие с КР становится более частым. Площадь поперечного сечения достаточно просто вычислить.
Для этого необходимо воспользоваться некоторым алгоритмом, если проводник (П) представляет собой провод цилиндрической формы:
- Измерение диаметра проводника при помощи штангенциркуля (ШЦ).
- Нахождение S при помощи формулы S = 3,1416 * sqr (d) / 4.
П может из себя представлять многожильный провод, поэтому для точного расчета необходимо найти S одной жилы, воспользовавшись алгоритмом нахождения для цилиндрической формы П, а затем результат умножить на количество жил.
Кроме того, бывают провода в форме квадрата и прямоугольника, но они встречаются редко. Для этого нужно выполнить следующие вычисления:
- Для квадратной формы нужно замерить ШЦ одну из сторон и возвести ее в квадрат: S = sqr(a).
- Для прямоугольной формы следует измерить две противолежащие стороны при помощи ШЦ, а затем произвести расчет по формуле S = a * b.
Из этих алгоритмов нахождения S можно сделать универсальный (абстрактный алгоритм). Он подходит для нахождения или расчетов величин, независимо от формы П при его разрезе, выполненном строго перпендикулярно относительно П. Алгоритм имеет следующий вид:
- Визуально определить геометрическую фигуру при разрезе П.
- Найти в справочнике формулу S.
- Произвести измерения при помощи ШЦ необходимых величин.
- Подставить в формулу и вычислить S.
Еще одной величиной является длина П, при увеличении которой R увеличивается. На основании этих величин можно вывести следующую формулу зависимости от типа вещества, длины (L) и S проводника: R = p * L / S.
Однако это значение R можно определить при температуре +20 °C. Для получения более точных расчетов нужно рассмотреть зависимость от температуры.
Температура проводника
Научно подтвержденным является факт, что p зависит от температуры. Это утверждение можно доказать практическим путем. Для проведения опыта необходимы следующие элементы, изображенные на схеме: спираль из нихрома (используется в нагревательных элементах), соединительные медные провода, источник питания, амперметр (для измерения I), вольтметр (измеряет U) и реостат.
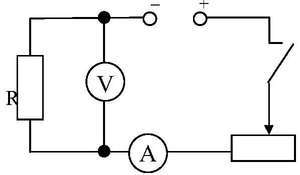
На схеме нагревательный элемент изображен в виде резистора. При его включении следует внимательно наблюдать за показаниями амперметра. Спираль начинает нагреваться, и показания амперметра уменьшаются по мере нагревания.
Согласно закону Ома для участка цепи необходимо сделать вывод, что при росте R ток уменьшается (обратно пропорциональная зависимость). Следовательно, значение R зависит от температуры.
При нагревании происходит увеличение ионов в КР нихромовой спирали и Э начинают чаще сталкиваться с ними.
В формуле R = p * L / S можно методом исключения найти показатель, зависящий от температуры. Последняя не оказывает влияния на длину П.
По формуле вычисления S зависимость также не прослеживается, поскольку геометрия П не зависит от температуры. Остается p, который зависит от температуры.
В физике существует формула зависимости p = p0 * [1 + a * (t — 20)]. Буква а является температурным коэффициентом:
- для металлов а > 0;
- для электролитов a < 0.
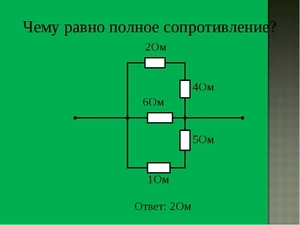
В этом случае происходит увеличение p. Процесс является обратимым, поэтому часть дефектов уменьшается (рекристаллический отжиг). Если на металл действуют силы растяжения или сжатия, то эта деформация является упругой.
Величина p уменьшается под действием силы сжатия, при которой происходит резкое уменьшение тепловых колебаний (ТК), а Э легче двигаются.
Но под действием силы растяжения происходит прямо пропорциональное увеличение p, при котором амплитуда ТК увеличивается.
Конечную формулу можно записать в виде R = p0 * [1 + a * (t — 20)] * L / S. Однако этот вариант нахождения R был рассмотрен в цепях с постоянным I, а под действием переменного I появляются новые величины, влияющие на расчеты.
Цепь переменного тока
Закон Ома применяется только для цепей постоянного тока. Для переменного U он изменен и, следовательно, существуют другие формулы нахождения R. Сопротивление в цепях с переменным I (ПТ) бывает:
- активным;
- индуктивным;
- емкостным;
- полным.

Активное сопротивление свидетельствует о том, что в цепи присутствует резистор или любая другая неемкостная или неиндуктивная нагрузка. Для его расчета необходимо произвести измерение значений амплитуд Um и Im.
При помощи приборов можно получить только действующие значения этих величин. Амплитудные значения рассчитываются по формулам Um = Ud * sqrt(2) и Im = Id * sqrt(2). Для определения активного сопротивления (обозначается R) нужно воспользоваться формулой Iм = Uм / R.
Из неё можно получить R = Ud * sqrt(2) / Im = Id * sqrt(2).
Если в цепи переменного I (ЦПТ) присутствуют катушка индуктивности, дроссель, контур и т. д., то появляется индуктивное R, которое обозначается Xl. Для расчета необходимо воспользоваться формулой Xl = w * L, предварительно измеряв частоту ПТ и рассчитав индуктивность.
Величина циклической частоты находится по формуле, для которой нужно измерять частоту ПТ (f): w = 2 * 3,1416 * f. Последняя измеряется при помощи осциллографа или частотомера. Для расчета индуктивности катушки необходимо воспользоваться справочником по физике или онлайн-калькулятором.
При наличии в ЦПТ емкости (конденсатора) возникает емкостное R, которое обозначается Xc. При протекании постоянного U конденсатор не пропускает I, а в ЦПТ он пропускает I и обладает емкостью (C) и Xc. Рассчитывается это значение по формуле Xc = 1 / (w * C), где:
- w — циклическая частота, которая рассчитывается аналогично вычислению Xl;
- C — емкость конденсатора, указанная на корпусе или измеренная соответствующим прибором.
Полное сопротивление цепи обозначается Z и представляет собой сумму всей нагрузки ЦПТ (активного, индуктивного и емкостного сопротивления). Для расчета нужно воспользоваться формулой полного сопротивления: Z = sqrt [sqr(R) + sqr (Xc — Xl)]. В ЦПТ величина Z зависит от:
- геометрии П;
- типа вещества, из которого сделан П;
- температуры;
- деформации различного вида;
- электрических показателей I, U, f, L, C и R.
Закон Ома для участка цепи принимает следующий вид: I = U / Z. Необязательно рассчитывать электропроводимость П, так как для этих целей существуют омметры. Расчет Xl и Xс следует производить самостоятельно.
Измерение сопротивления

Для измерения R необходимо обесточить участок или радиокомпонент и проследить за разрядкой цепей, где присутствуют конденсаторы. Перед проведением измерений нужно выставить необходимый режим на приборе и закоротить щупы для проверки прибора на исправность. Некоторые модели снабжены функцией звукового сигнала. После теста прибора следует приступить к измерениям.

Для нахождения точной величины Z проводника необходимо учитывать все величины, от которых оно зависит.
Вычисление Z позволяет точно рассчитать электрическую схему какого-либо устройства для избегания трудоемких измерений.
Измерить омметром можно только величину активного сопротивления, а Xl и Xc следует рассчитывать самостоятельно. Однако при помощи онлайн-калькуляторов сделать это не составит особого труда.
Источник: https://220v.guru/fizicheskie-ponyatiya-i-pribory/moschnost/soprotivlenie/raschet-polnogo-soprotivleniya-cepi-pod-deystviem-peremennogo-toka.html
Электрический импеданс
Импеданс (impedance) – комплексное, полное сопротивление переменному току электрической цепи с активным и реактивным сопротивлением.
Импеданс и общий сдвиг фаз для синусоидального тока можно рассчитать исходя из последовательного или параллельного соединения элементов цепи.
Последовательное соединение
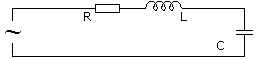
При последовательном соединении, согласно Закону Ома для переменного тока, во всех элементах цепи ток будет общим I = U/Z, а значения напряжений на каждом элементе определятся пропорционально его сопротивлению:
на выводах резистора UR = IR; на выводах конденсатора UC = IXC; на выводах катушки UL = IXL.
Векторы индуктивной и ёмкостной составляющих напряжения направлены в противоположные стороны.
С учётом отрицательного ёмкостного сдвига, общее напряжение на реактивных элементах UX = UL — UC . Пропорционально напряжению, получим общее реактивное сопротивление X = XL — XC . Векторы напряжений на активной и реактивной составляющей импеданса имеют угол сдвига фаз 90 градусов.
U , UR и UX представим в виде прямоугольного треугольника напряжений с углом сдвига фаз φ.
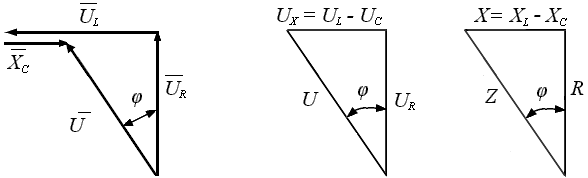
Тогда получим соотношение, согласно Теореме Пифагора, U ² = UR² + UX² .
Следовательно, с учётом пропорциональности элементов R, L, C значениям напряжений на их выводах, определим импеданс, который будет равен квадратному корню из суммы квадратов активного и реактивного сопротивлений цепи.
![]()
XL = ωL = 2πfL — реактивное сопротивление индуктивности. XC = 1/(ωC) = 1/(2πfC) — реактивное сопротивление ёмкости.
Угол сдвига фаз φ и его дополнение до 90° δ
определятся тригонометрическими функциями из треугольника сопротивлений с катетами R, X и гипотенузой Z, как показано на рисунке:
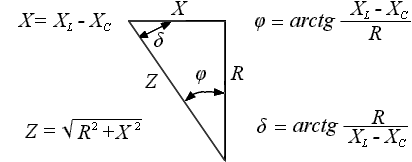
-
Обычно, для облегчения расчётов, импеданс представляют в виде комплексного числа,
где действительной его частью является активное сопротивление, а мнимой — реактивное.
Для последовательного соединения импеданс можно записать в комплексном виде следующим образом: - Z = R + jX
-
Тогда в тригонометрической интерпретации модулем этого числа будет импеданс, а аргументом — угол φ.
В соответствии с формулой Эйлера, запишем показательную форму комплексного импеданса: - Z = |Z|ejargZ = Zejφ
- Отсюда активная составляющая импеданса R = Zcosφ
Реактивная составляющая X = Zsinφ.
Параллельное соединение
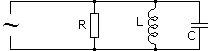
- Для вычисления импеданса при параллельном соединении активных и реактивных сопротивлений будем исходить из суммы обратных им величин — проводимостей y = 1/Z, G = 1/R, b = 1/X.
- y = 1/Z = √(G2 + b2)
- Сдвиг фаз в этом случае будет определён треугольником сопротивлений следующим образом:
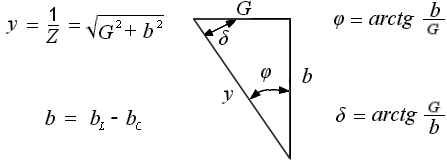
- Комплексную проводимость, как величину, обратную комплексному импедансу, запишем в алгебраической форме:
- Y = G — jb
- Либо в показательной форме:
- Y = |Y|e -jφ = ye -jφ
Здесь: Y — комплексная проводимость.
G — активная проводимость.
b — реактивная проводимость.
y — общая проводимость цепи, равная модулю комплексной проводимости.
e — константа, основание натурального логарифма.
j — мнимая единица. φ — угол сдвига фаз.
Онлайн-калькулятор расчёта импеданса и угла сдвига фаз
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
| Последовательное соединениеZ = √(R²+(XL-Xc)²) | Параллельное соединениеZ = 1/√(1/R²+(1/XL-1/Xc)²) |
Похожие страницы с расчётами:
Реактивное сопротивление. Расчёт.
Частота резонанса колебательного контура LC. Расчёт.
Реактивная мощность и компенсация. Расчёт.
Замечания и предложения принимаются и приветствуются!
Источник: https://tel-spb.ru/impedance/
Расчет импеданса в параллельном соединении элементов цепи
Любая электрическая цепь включает в себя ряд элементов, среди которых встречаются активные и реактивные составляющие. При параллельном соединении активного, емкостного и индуктивного элемента схема выглядит таким образом:
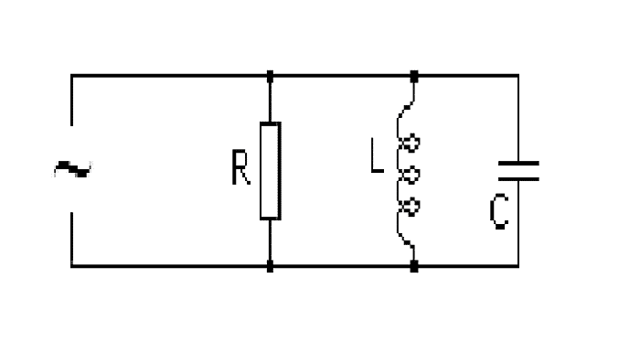 Рис. 1. Параллельное соединение элементов электрической цепи
Рис. 1. Параллельное соединение элементов электрической цепи
В зависимости от конкретной ситуации тот или иной элемент может исключаться из цепи, меняя тем самым характер нагрузки. Для геометрического определения суммарного значения всех сопротивлений производится сложение векторов. В зависимости от типа реактивной нагрузки результирующий вектор импеданса будет смещаться в положительный или отрицательный квадрант.
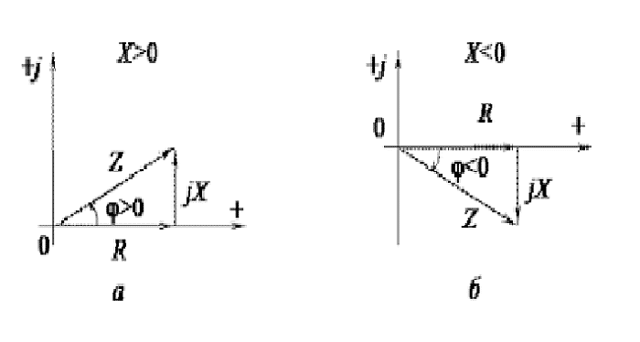 Рис. 2. Векторное сложение сопротивления
Рис. 2. Векторное сложение сопротивления
Для вычисления полного сопротивления Z составляется уравнение согласно теоремы пифагора. Только сложению подлежит не сопротивление, а проводимость цепи. Из-за чего уравнение для определения сопротивления можно будет выразить по следующей формуле:
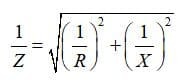
Где Z – комплексное сопротивление участка, R – активное сопротивление участка, X – реактивное сопротивление участка.
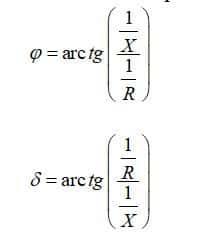
В связи с большим количеством расчетов, применяемых формул и необходимостью использования тригонометрических функций определение импеданса в параллельной цепи является достаточно сложной задачей, особенно, если делать это вручную. Но, при использовании онлайн калькулятора для расчета комплексного сопротивления достаточно ввести частоту, емкость конденсатора, индуктивность катушки и омическое сопротивление резистора. А все расчеты система произведет самостоятельно.
Источник: https://www.asutpp.ru/kalkulyator-rascheta-impedansa-v-parallelnom-soedinenii-elementov-tsepi.html
Полное сопротивление
Главная > Теория > Полное сопротивление
К любому базовому элементу схемы можно применить математическое описание, используя ток, напряжение и сопротивление. И если для постоянного тока эти зависимости просты, то математические выражения для систем переменного тока должны учитывать синусоидальный характер параметров цепи.
Разные элементы схемы переменного тока
Что такое импеданс
Полное сопротивление цепи переменного тока, или импеданс, обозначаемый Z, является отражением меняющегося во времени значения тока. Импеданс представляет собой векторную (двумерную) величину, состоящую из двух независимых скалярных одномерных значений: активного и реактивного сопротивления.
Активное сопротивление
Активная часть импеданса, обозначенная R, является мерой степени, с которой материал противостоит движению электронов между его атомами. Чем легче атомы высвобождают или принимают электроны, чем ниже сопротивление, которое выражается в положительном действительном числе ом.
Важно! Активное сопротивление неизменно при переменном и постоянном токе.
Примеры материалов с низким сопротивлением: медь, серебро, золото. Высокоомные вещества называются изоляторами, или диэлектриками, и включают в свой перечень слюду, стекло, полиэтилен и др. Материалы с промежуточным уровнем сопротивления – полупроводники, к примеру, арсенид галлия, кремний, германий.
При активной нагрузке ток и напряжение являются синфазными, то есть одновременно достигают пиковых значений и падают до нуля. Они меняются по закону:
- I(t) = Im x sin (ωt + θ);
- U(t) = R x Um x sin (ωt + θ), где:
- Im и Um – максимальные амплитуды тока и напряжения,
- ω – угловая частота,
- θ – угол сдвига фаз между ними, который будет равен 0.
На векторной диаграмме синфазный эффект представляется как наложение друг на друга векторов I и U вдоль одной оси.
Активная нагрузка на переменном токе
- При использовании резисторов в цепях синусоидального тока слово «импеданс» и символ Z используются для обозначения его сопротивления:
- R = Z.
- Импеданс может быть представлен также комплексным числом, так как он зависит от частоты схемы. Но в случае чисто резистивной нагрузки реактивная часть всегда будет равна 0:
- Z = R + j0 = R.
- Практические расчеты можно также выполнять по формуле:
- Z = Um/Im.
Реактивное сопротивление
Реактивная часть, обозначенная Х, – выражение степени, с которой электронный компонент схемы хранит или высвобождает энергию, когда ток и напряжение колеблются при каждом цикле. Х выражается в мнимом числе Ом.
Энергия может храниться и выделяться в двух видах:
- Магнитного поля. Тогда реактивное сопротивление является индуктивным (+jXL);
- Электрического поля. При этом реактивное сопротивление будет емкостным (-jXC).
Индуктивная нагрузка
Противодействие переменному току в цепи с катушкой зависит не только от ее индуктивности, но и от частоты токового сигнала. С ростом частоты увеличивается индуктивное сопротивление.
Чистой индуктивности в природе нет. Все электрические катушки, реле и трансформаторы имеют определенное активное сопротивление, обусловленное удельным сопротивлением медного провода. Тогда можно рассматривать индуктивную катушку как последовательное сопротивление R и XL.
Индуктивная нагрузка на переменном токе
- Когда две и более индуктивных катушки соединены последовательно, или одиночная катушка также соединяется с резисторными элементами, то общее сопротивление резисторов:
- R = R1+ R2 + R3 + …,
- а общее значение:
- XL = XL1 + XL2 + XL3 + …
- Комплексное сопротивление цепи с катушкой принимает вид:
- Z = R + jXL.
Мнимый показатель j показывает, что сигналы тока и напряжения сдвинуты по фазе на 90 градусов. Знак «+» указывает на отставание тока на этот угол.
Фактические расчеты ведутся по формуле:
XL = 2π x f x L, где:
- f – токовая частота (Гц),
- L – значение индуктивности.
- Так как угловая частота ω = 2π x f, то XL = ω x L.
- Результирующая векторная диаграмма – прямоугольный треугольник, в котором катетами являются R и XL, а гипотенуза и будет полным сопротивлением Z.
- Исходя из соотношения сторон треугольника:
- Z² = R² + XL² и Z = √ (R² + XL²).
Емкостная нагрузка
Конденсаторы хранят энергию на проводящих пластинах в виде электрозаряда. На постоянном токе они могут удерживать этот заряд неограниченное количество времени (для чистого конденсатора). Чистых конденсаторных элементов не существует, они всегда имеют определенное внутреннее сопротивление, и появляется ток утечки.
При переменном синусоидальном сигнале конденсатор сначала заряжается в одном направлении, а в другой полупериод меняет полярность на противоположную. Таким образом, во времени заряд меняется, а энергия выделяется в цепь.
Емкостная нагрузка на переменном токе
- Выражение для комплексного емкостного сопротивления:
- Z = R – jXC,
- где j со знаком «минус» указывает на опережение током напряжения на 90 градусов.
- XC вычисляют по формуле:
- XC = 1/(2π x f x C) = 1/ω x С.
Важно! Каждый конденсаторный элемент можно представлять в виде активного сопротивления R, соединенного последовательно с чистой емкостью С.
Формулой полного сопротивления электроцепи с емкостью будет:
Z = √ (R² + XС²).
Важно! Когда резисторы и конденсаторы последовательно соединены в одной и той же схеме, общий импеданс на векторной диаграмме имеет фазовый угол между 0 и 90 градусами, в зависимости от значения используемых компонентов.
- При наличии в одной схеме конденсатора и индуктивной катушки реактивная часть импедансов рассчитывается как:
- Z = XL – XC.
- Соответственно, выражение для полного импеданса:
- Z = √ (R² + (XL – XС)²).
Параллельные схемы RLC более сложны для анализа. Для вычисления импеданса значения активной и реактивной части сопротивления преобразуются в обратную величину – проводимость.
- Комплексная проводимость равна Y = 1/Z = g – jb, где:
- g = R/(R² + X²),
- b = X/(R² + X²).
- Численное значение импеданса в параллельной цепи:
Z = 1/√(1/R² + (1/XL² – 1/XС²).
Для практических расчетов можно воспользоваться калькуляторами в онлайн режиме, где просто вводятся параметры элементов схемы, в зависимости от вида их соединения.
Видео
Сопротивление тока: формула
Источник: https://jelectro.ru/teoriya/polnoe-soprotivlenie.html
2.5. Сопротивления в цепи переменного тока
В цепях
переменного тока выделяют следующие
виды сопротивлений.
Активное.
Активным называют сопротивление
резистора. Условное обозначение
Единицей
измерения сопротивления является Ом.
Сопротивление резистора не зависит от
частоты.
Реактивное.
В разделе реактивные выделяют три вида
сопротивлений: индуктивное xL и емкостное
хс и собственно реактивное. Для
индуктивного сопротивления выше была
получена формула XL = ωL.
Единицей измерения индуктивного
сопротивления также является Ом. Величина
xL линейно зависит от частоты.
Для
емкостного сопротивления выше была
получена формула XC = 1 / ωC.
Единицей измерения емкостного
сопротивления является Ом. Величина хс
зависит от частоты по обратно-пропорциональному
закону. Просто реактивным сопротивлением
цепи называют величину X = XL — XC.
Полное
сопротивление.
Полным сопротивлением цепи называют
величину
(2.28)
-
Из этого
соотношения следует, что сопротивления
Z, R и X образуют треугольник: Z – гипотенуза,
R и X – катеты. Для удобства в этом
треугольнике рассматривают угол φ,
который определяют уравнением - (2.29)
-
φ
= arctg((XL — XC)
/ R), -
и называют
углом сдвига фаз. С учетом него можно
дать дополнительные связи - (2.30)
-
R
= Z cos φ, - (2.31)
-
X
= Z sin φ.
2.6. Мощности в цепях переменного тока
По аналогии
с мощностью в цепях постоянного тока
P = U I, в цепях переменного тока
рассматривают мгновенную мощность
p = u i. Для упрощения рассмотрим
мгновенную мощность в каждом из элементов
R, L и С отдельно.
Элемент r (резистор)
-
Зададим
напряжение и ток в виде соотношений -
u(t)
= Um
sin(ωt
+ ψu), -
i(t)
= Im
sin(ωt
+ ψi). -
Известно,
что для резистора ψu
= ψi,
тогда для р получим -
(2.
32)
-
p(t)
= u(t) i(t) = Um
Im
sin2(ωt
+ ψi).
Из
уравнения (2.32) видно, что мгновенная
мощность всегда больше нуля и изменяется
во времени.
В таких случаях принять
рассматривать среднюю за период Т
мощность
(2.33)
-
Если
записать Um
и Im
через действующие значения U и I: ,,
то получим - (2.34)
- P = U I.
По форме
уравнение (2.34) совпадает с мощностью на
постоянном токе. Величину Р равную
произведению действующих значений тока
и напряжения называют активной мощностью.
Единицей ее измерения является Ватт
(Вт).
Элемент l (индуктивность)
Известно,
что в индуктивности соотношение фаз
ψu = ψi + 90°.
Для мгновенной мощности имеет
(2.35)
Усредняя
уравнение (2.35) по времени за период Т
получим
-
Для
количественной оценки мощности в
индуктивности используют величину QL
равную максимальному значению рL - (2.36)
-
QL
= (Um
Im)
/ 2
и называют
ее реактивной (индуктивной) мощностью.
Единицей ее измерения выбрали ВАр
(вольт-ампер реактивный). Уравнение
(2.36) можно записать через действующие
значения U и I и используя формулу
UL = I XL получим
(2.37)
QL = I2 XL.
Элемент с (ёмкость)
Известно,
что в емкости соотношение фаз ψu = ψi — 90°.
Для мгновенной мощности получаем
pC(t)
= u(t) I(t) = (Um
Im)
/ 2 · sin(2ωt).
Среднее
значение за период здесь также равно
нулю. По аналогии с уравнением (2.36) вводят
величину QC = I2 XC,
которую называют реактивной (емкостной)
мощностью. Единицей ее измерения также
является ВАр.
-
Если в
цепи присутствуют элементы R, L и С, то
активная и реактивная мощности
определяются уравнениями - (2.37)
-
P
= U I cos φ, - (2.38)
- Q = QL — QC,
- (2.39)
-
Q
= U I sin φ, -
где
φ
– угол
сдвига
фаз. -
Вводят
понятие полной мощности цепи - (2.40)
С учетом
уравнений (2.37) и (2.39), (2.40) можно записать
в виде
- (2.41)
- S = U I.
-
Единицей
измерения полной мощности является ВА
– вольт-ампер.
Источник: https://studfile.net/preview/6219684/page:4/
Активное сопротивление в цепи переменного тока
На векторных диаграммах можно показать, что ток и напряжение совпадают по фазе (рис. 52,а) или э. д.с. сдвинуты по фазе на некоторый угол (рис. 52,6). Условно принято считать, что векторы перемещаются в направлении против движения часовой стрелки.
Если векторы имеют различную длину, следовательно, их действующие значения разные (см. рис. 52, б).
- § 52. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную работу или в тепловую энергию, называется активным сопротивлением.
- К активным сопротивлениям при промышленной частоте (50 гц) относятся, например, электрические лампы накаливания и электронагревательные устройства.
Рассмотрим цепь переменного тока (рис. 53), в которую включено активное сопротивление. В такой цепи под действием переменного напряжения протекает переменный ток. Изменение тока в Цепи, согласно закону Ома, зависит только от изменения напряжения, подключенного к ее зажимам.
Когда напряжение равно нулю, ток в цепи также равен нулю. По мере увеличения напряжения ток в Цепи возрастает и при максимальном значении напряжения ток становится наибольшим. При уменьшении напряжения ток убывает.
Когда напряжение изменяет свое направление, ток также изменяет свое направление и т. д.
Из сказанного следует, что в цепи переменного тока с активным сопротивлением по мере изменения по величине и направлению напряжения одновременно пропорционально меняются величина и Направление тока. Это значит, что ток и напряжение совпадают по фазе.
Построим векторную диаграмму действующих величин тока и напряжения для цепи с активным сопротивлением. Для этого отлов жим в выбранном масштабе по горизонтали вектор напряжения Чтобы на векторной диаграмме показать, что напряжение и ток в цепи совпадают по фазе (=0), откладываем вектор тока I по направлению вектора напряжения.
- Сила тока в такой цепи определяется по закону Ома:
- В этой цепи среднее значение мощности, потребляемой активным сопротивлением, выражается произведением действующих значения тока и напряжения.
Пример. К цепи переменного тока с активным сопротивлением r=55 ом подключен генератор, максимальное значение напряжения которого Um=310,2 в.
Определить:
показание вольтметра, подключенного к зажимам генератора; показание амперметра, включенного в цепь; среднее значение мощности, потребляемой сопротивлением.
Решение. Известно, что электроизмерительные приборы, включенные в цепь переменного тока, измеряют действующие значения. Поэтому показание вольтметра, измеряющего напряжение,
Показание амперметра, измеряющего действующее значение тока,
Среднее значение активной мощности, потребляемой сопротивлением, Р=220х4 = 880 вт или Р=I2r=42×55=16×55=880 вт.
§ 53. ИНДУКТИВНОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Прохождение электрического тока по проводнику или катушки сопровождается появлением магнитного поля. Рассмотрим электрическую цепь переменного тока (рис. 54,а), в которую включена катушка индуктивности, имеющая небольшое количество витком проволоки сравнительно большого сечения, активное сопротивления которой можно считать практически равным нулю.
Под действием э. д. с. генератора в цепи протекает переменный ток, возбуждающий переменный магнитный поток. Этот поток пересекает «собственные» витки катушки и в ней возникает электродвижущая сила самоиндукции
- (55)
- где L — индуктивность катушки,
- — скорость изменения тока в ней.
Электродвижущая сила самоиндукции, согласно правилу Ленца, всегда противодействует причине, вызывающей ее. Так как э. д. с. самоиндукции всегда противодействует изменениям переменного тока, вызываемым э. д.с. генератора, то она препятствует прохождению переменного тока. При расчетах это учитывается по индуктивному сопротивлению, которое обозначается ХL и измеряется
в омах. Таким образом, индуктивное сопротивление катушки ХL зависит от величины э. д. с. самоиндукции, а следовательно, оно, как и э. д. с. самоиндукции, зависит от скорости изменения тока в катушке (от частоты ) и от индуктивности катушки L:
- где XL, — индуктивное сопротивление, ом,
- ώ — угловая частота переменного тока, рад/сек,
- L — индуктивность катушки, гн.
- Так как угловая частота переменного тока , то индуктивное сопротивление
где, f—-частота переменного тока, гц.
Пример. Катушка, обладающая индуктивностью L=0,5 гн, присоединена к источнику переменного тока, частота которого f=50 гц. Определить:
- 1) индуктивное сопротивление катушки при частоте f=50 гц;
- 2) индуктивное сопротивление этой катушки переменному току, частота которого f=800 гц.
- Решение. Индуктивное сопротивление переменному току при f=50 гц
При частоте тока f=800 гц
Приведенный пример показывает, что индуктивное сопротивление катушки повышается с увеличением частоты переменного тока, протекающего по ней. По мере уменьшения частоты тока индуктивное сопротивление убывает.
Для постоянного тока, когда ток в катушке не изменяется и магнитный поток не пересекает ее витки, э. д. с. самоиндукции не возникает, индуктивное сопротивлений катушки ХL равно нулю.
Катушка индуктивности для постоянного тока представляет собой лишь сопротивление
Выясним, как изменяется э. д. с. самоиндукции, когда по катушке индуктивности протекает переменный ток.
Известно, что при неизменной индуктивности катушки э. д. с. самоиндукции зависит от скорости изменения силы тока и она всегда направлена навстречу причине, вызвавшей ее.
На графике (рис. 54, в) переменный ток показан в виде синусоиды (сплошная линия). В первую четверть периода сила тока возрастает от нулевого до максимального значения. Электродвижущая сила самоиндукции ес, согласно правилу Ленца, препятствует увеличению тока в цепи.
Поэтому на графике (пунктирной линией) показано, что ес в это время имеет отрицательное значение. Во вторую четверть периода сила тока в катушке убывает до нуля. В это время э. д.с. самоиндукции изменяет свое направление и увеличивается препятствуя убыванию силы тока.
В третью четверть периода том изменяет свое направление и постепенно увеличивается до максимального значения; э. д. с. самоиндукции имеет положительное значение и далее, когда сила тока убывает, э. д. с.
самоиндукции опять меняет свое направление и вновь препятствует уменьшению силы тока в цепи.
Источник: http://fiziku5.ru/uchebnye-materialy-po-fizike/aktivnoe-soprotivlenie-v-cepi-peremennogo-toka
Для школьников.
Рассмотренные в предыдущих трёх статьях электрические цепи переменного тока. содержащие только активное, только емкостное и только индуктивное сопротивления были взяты для того, чтобы полнее раскрыть свойства перечисленных сопротивлений.
В реальных электрических цепях присутствуют все перечисленные сопротивления: активное, индуктивное, емкостное.
Сейчас будем говорить о цепях, содержащих последовательно соединённые активное сопротивление, катушку индуктивности и конденсатор.
Нам предстоит найти полное сопротивление показанной на рисунке цепи и разность фаз между действующими значениями тока и напряжения в ней.
Мгновенное значение приложенного к цепи напряжения (на зажимах цепи) складывается из мгновенных значений напряжений на каждом сопротивлении, то есть будет равно сумме мгновенных напряжений на активном, индуктивном и емкостном сопротивлениях:
Но действующее значение напряжения на зажимах цепи U не будет равно алгебраической сумме напряжений на каждом участке цепи из-за разности фаз между током и напряжением U на каждом сопротивлении (активном, индуктивном, емкостном).
Для нахождения связи между перечисленными напряжениями удобно пользоваться векторной диаграммой.
Векторная диаграмма – это графическое изображение значений периодически изменяющихся величин и соотношений между ними при помощи направленных отрезков – векторов.
Например, мы знаем, что напряжение на зажимах цепи переменного тока меняется по синусоидальному закону, то есть колебания напряжения сети изображается синусоидой.
Мгновенные значения напряжения внешнего источника можно рассматривать ещё как проекции вектора напряжения U (вектора ОВ) на вертикальную ось при равномерном вращении этого вектора против часовой стрелки.
Точно также векторами можно изобразить переменный ток в цепи, переменные напряжения на активном сопротивлении, на емкостном и индуктивном сопротивлениях.
Колебания перечисленных величин имеют одну частоту, но сдвинуты по фазе относительно друг друга.
Их взаимное расположение со временем не меняется. Тогда все перечисленные вектора можно показать на одной диаграмме.
Действующее значение вектора напряжения внешнего источника U будет равно геометрической сумме векторов напряжений на каждом сопротивлении цепи.
Такое сложение векторов значительно проще сложения синусоид, поэтому векторные диаграммы применяют очень часто.
Ниже рассказано как построена диаграмма, изображённая на рис. 15, которая решает задачу нахождения полного сопротивления рассматриваемой электрической цепи и нахождения сдвига фаз между током и напряжением.
Как видим из формулы закона Ома, полное сопротивление цепи не равно простой сумме активного R и реактивного сопротивлений.
Индуктивное и емкостное напряжения имеют разные знаки – они направлены навстречу друг другу.
Итак, полное сопротивление цепи переменного тока:
Индуктивное сопротивление:
Емкостное сопротивление:
На рис 15 прямоугольный треугольник векторной диаграммы составлен следующими векторами: вектором активного напряжения,
вектором индуктивного напряжения
вектором емкостного напряжения:
и вектором действующего напряжения U стороннего источника.
Из диаграммы, применив закон Пифагора, получим выражение для действующего напряжения:
Если каждое из этих напряжений (рис. 15) разделить на ток, то получим такой же треугольник, составленный сопротивлениями.
Прилежащий к углу катет даёт активное сопротивление цепи R, противолежащий катет – общее реактивное сопротивление цепи X, а гипотенуза треугольника даёт полное сопротивление цепи Z, состоящей из последовательно соединённых активного, индуктивного и ёмкостного сопротивлений..
Из представленного треугольника сопротивлений получаем соотношение:
то есть сдвиг фаз (угол фи) между током и напряжением в цепи определяется отношением реактивного сопротивления цепи к её активному сопротивлению.
Возможны следующие случаи:
Когда индуктивное сопротивление больше емкостного, то есть когда в цепи преобладает индуктивность, то ток отстаёт от напряжения на угол “фи”.
Когда индуктивное сопротивление меньше емкостного, то есть когда в цепи преобладает емкостное сопротивление, то ток опережает напряжения на угол “фи”.
Из треугольника сопротивлений получаем ещё такое выражение:
то есть
определяется отношением активного сопротивления цепи к её полному сопротивлению. Его называют коэффициентом мощности.
Значение коэффициента мощности определяет активную (полезную) мощность цепи.
Посмотрим, как получают выражение для мощность цепи переменного тока.
Мгновенное значение мощности равно произведению мгновенных значений напряжения и силы тока, которые выражаются формулами:
Взяв произведение мгновенных значений тока и напряжения и проанализировав полученное выражение, придём к выводу, что мощность может быть как положительной (когда энергия от источника поступает в цепь), так и отрицательной (когда уходит из цепи в источник).
Практически важно знать среднюю за период мощность, так как только средняя мощность характеризует энергию, потребляемую цепью за единицу времени.
После математических преобразований получается следующее выражение для средней мощности, которую можно называть просто мощностью цепи:
то есть мощность электрической цепи переменного тока равна произведению действующих значений напряжения и силы тока на косинус угла между током и напряжением,
Косинус сдвига фаз между током и напряжением назвали коэффициентом мощности.
Видим, что коэффициент мощности оказывает очень большое влияние на мощность электрической цепи.
Коэффициент мощности достигает максимального значения, равного единице, при угле “фи” (сдвиге фаз) равном нулю или когда индуктивное сопротивление равно емкостному сопротивлению:
При этом условии цепь переменного тока имеет минимальное сопротивление, равное активному сопротивлению цепи.
Ток же в цепи в этом случае достигает максимального значения (явление резонанса).
Приложенное к цепи напряжение U равно активному напряжению (напряжению на активном сопротивлении R).
Но при этом есть и индуктивное напряжение и равное ему по модулю, но противоположное по направлению (сдвинутое по фазе на половину периода) емкостное напряжение.
Причём они могут достигать достаточно больших значений, гораздо больших, чем напряжение сети U. Реактивные напряжения (индуктивное, емкостное) будут превышать напряжение сети U во столько раз, во сколько раз реактивные сопротивления (индуктивное, емкостное) будут больше активного сопротивления R.
Поэтому рассмотренное явление резонанса называется резонансом напряжений.
При резонансе мгновенные мощности в реактивных участках цепи (в катушке индуктивности и конденсаторе) равны и противоположны по знаку. Это значит, что увеличение энергии магнитного поля в катушке индуктивности происходит в результате уменьшения электрической энергии запасённой в конденсаторе, и наоборот, а энергия генератора расходуется только на активном сопротивлении.
Для электрической цепи промышленного тока резонанс вреден, так как может привести к пробою изоляции катушки и конденсатора.
По этой причине коэффициент мощности на предприятиях поднимают до 0,9 – 0,95, чтобы получить большую мощность, но чтобы не получить явление резонанса.
Какие меры применяются для повышения коэффициента мощности на промышленных предприятиях будет сказано позднее.
Пример.
В цепь переменного тока (120В, 50 Гц) последовательно включены катушка с активным сопротивлением 3 Ом и индуктивным сопротивлением 4 Ом и конденсатор. При какой ёмкости конденсатора наступит резонанс напряжений? Какими будут при этом ток в цепи, активное, индуктивное и емкостное напряжения?
При резонансе емкостное сопротивление равно индуктивному:
Емкостное сопротивление равно 4 Ом:
Отсюда найдём ёмкость конденсатора, при которой наступит резонанс в цепи. Эта ёмкость равна 0,0008 Ф.
Ток в цепи:
равен 40 А.
Анодное напряжение:
равно 120 В.
Емкостное напряжение
(и равное ему по модулю, но противоположное по направлению) индуктивное напряжение, будут иметь значения по 160 В, то есть больше напряжения сети, равного 120 В.
Таким образом, при последовательном соединении активного сопротивления, индуктивности и ёмкости (при равенстве индуктивного и емкостного сопротивлений) наступает резонанс напряжений, когда индуктивное и емкостное напряжения больше напряжения на источнике, в чём убедились, рассмотрев пример.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись : Катушка индуктивности в цепи переменного тока. Индуктивное сопротивление.
Следующая запись : Расчёт цепей переменного тока, содержащих активное сопротивление, индуктивность и ёмкость,
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58 .
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70. .
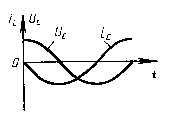
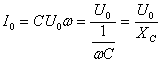 , где
, где