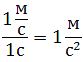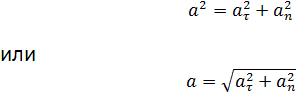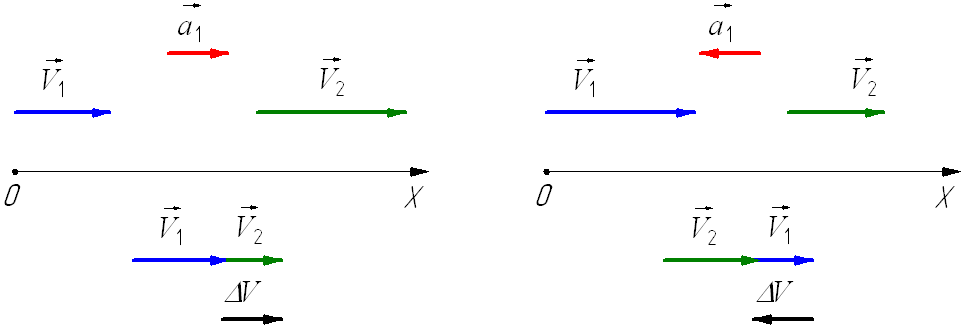Как найти мгновенное ускорение точки

Как найти мгновенное ускорение точки

Автор статьи

Сергей Сергеевич Соев

Эксперт по предмету «Физика»

Задать вопрос автору статьи

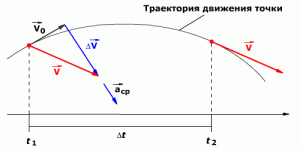
Пусть за время $Delta $t движущаяся точка перешла из положения А в положение В (рис. 1.).

Мгновенное ускорение и его составляющие

Рисунок 1. Мгновенное ускорение и его составляющие

Вектор $overrightarrow{v}$ задает скорость точки в положении А. В положении В точка приобрела скорость, отличную от $overrightarrow{v}$ как по величине, так и по направлению и стала равной $overrightarrow{v_1}=overrightarrow{v}+triangle overrightarrow{v}$ . Перенесем вектор $overrightarrow{v_1}$ в точку А и найдем $Delta $$overrightarrow{v}$.

Определение

Мгновенным ускорением, или просто ускорением материальной точки в момент времени t, называется предел среднего ускорения $leftlangle overrightarrow{a}rightrangle =$ $frac{triangle overrightarrow{v}}{triangle t}$ при бесконечно малом приращении времени: $overrightarrow{a}left(t+triangle tright)={mathop{lim}_{triangle tto 0} frac{triangle overrightarrow{v}}{triangle t}=dot{v}left(tright) }$.

Логотип baranka

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Таким образом, ускорение есть векторная величина, равная первой производной скорости по времени.

Разложим вектор $Delta $$overrightarrow{v}$ на две составляющие. Для этого из точки А по направлению скорости $overrightarrow{v}$ отложим вектор AD, по модулю равный ${overrightarrow{v}}_1$. Тогда вектор CD, равный $Delta $${overrightarrow{v}}_{tau }$, определяет изменение скорости по модулю (величине) за время $Delta $t, т.е. $Delta $${overrightarrow{v}}_{tau }={overrightarrow{v}}_1-overrightarrow{v}$. Вторая же составляющая вектора $triangle overrightarrow{v}$ характеризует изменение скорости на время $Delta $t по направлению – $Delta $${overrightarrow{v}}_n$. Составляющая ускорения, определяющая изменение скорости по величине, называется тангенциальным ускорением ${overrightarrow{a}}_{tau }$. Численно она равна первой производной по времени от модуля скорости: $a_{tau }=frac{dv}{dt}$.

Найдем вторую составляющую ускорения, называемую нормальным ускорением ${overrightarrow{a}}_n$. Допустим, что точка В достаточно близка к точке А, поэтому путь $Delta $s можно считать дугой окружности некоторого радиуса r, мало отличающегося от хорды АВ. Из подобия треугольников АОВ и ЕАD следует, что $frac{{triangle v}_n}{AB}=frac{v_1}{r}$, или, учитывая, что $ABapprox triangle s=vtriangle t$, получим: $frac{{triangle v}_n}{vtriangle t}=frac{v_1}{r}$, откуда $frac{{triangle v}_n}{triangle t}=frac{vv_1}{r}$. Учитывая, что при бесконечно малом приращении времени $v_1to v$, и переходя к пределу, получим: $a_n={mathop{lim}_{triangle tto 0} frac{{triangle v}_n}{triangle t} }=frac{v^2}{r}$.

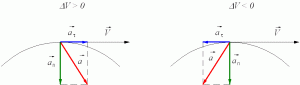
Нормальное ускорение характеризует быстроту изменения скорости по направлению и направлено к центру кривизны траектории по нормали. Его называют также центростремительным ускорением. Полное мгновенное ускорение есть геометрическая сумма тангенциальной и нормальной составляющих: $overrightarrow{a}={overrightarrow{a}}_{{mathbf tau }}+{overrightarrow{a}}_n$

Полное ускорение

Рисунок 2. Полное ускорение

Модуль полного мгновенного ускорения $a=sqrt{a^2_{tau }+a^2_n}$.

Направление полного ускорения определяется углом $varphi $ между векторами ${overrightarrow{a}}_{{mathbf tau }}$ и $overrightarrow{a}$. Как видно из рис. 2, $varphi =arctgfrac{a_n}{a_{tau }}$.

Движение материальной точки может быть следующих видов:

  1. ${overrightarrow{a}}_{{mathbf tau }} = 0$, ${overrightarrow{a}}_n = 0$ — прямолинейное равномерное движение (s=vt);
  2. ${overrightarrow{a}}_{{mathbf tau }} = const neq 0$, ${overrightarrow{a}}_n= 0$ — прямолинейное равнопеременное движение.
  3. ${overrightarrow{a}}_{{mathbf tau }} = f(t)$, ${overrightarrow{a}}_n$ $= 0$ — прямолинейное движение с переменным ускорением;
  4. ${overrightarrow{a}}_{{mathbf tau }} = 0$, ${overrightarrow{a}}_n = const$ — равномерное движение по окружности;
  5. ${overrightarrow{a}}_{{mathbf tau }} = 0$, ${overrightarrow{a}}_n neq 0$ — равномерное криволинейное движение;
  6. ${overrightarrow{a}}_{{mathbf tau }} = const$, ${overrightarrow{a}}_n neq 0$ — криволинейное равнопеременное движение;
  7. ${overrightarrow{a}}_{{mathbf tau }}$ = $f(t)$, ${overrightarrow{a}}_n neq 0$ — криволинейное движение с переменным ускорением.

«Мгновенное ускорение» 👇

Задача 1

Тело движется равноускоренно с начальной скоростью $v_0 = 5 м/с$. Определить мгновенное ускорение тела момент времени $t=7 с$, если его скорость в этот момент составила $26 м/с$.

Решение

[a=leftlangle arightrangle =frac{triangle v}{triangle t}=frac{26-5}{7}=21 м/c^2]

Задача 2

Материальная точка движется по кривой с постоянным радиусом кривизны $R = 3 м$. Линейная скорость точки описывается уравнением $v=2t+t^2$. Найти мгновенное ускорение точки в момент $t = 3 c$. Определить тип движения точки.

Решение

Модуль полного мгновенного ускорения $a=sqrt{a^2_{tau }+a^2_n}$

Тангенциальное ускорение $a_{tau }left(3right)=frac{dv}{dt}=2+2t=2+6=8 м/с^2$

Скорость $vleft(5right)=2times 3+3^2=15 м/c$

Нормальное ускорение $a_nleft(3right)=frac{v^2}{r}=frac{{15}^2}{3}=75$

Полное мгновенное ускорение $aleft(3right)=sqrt{8^2+{75}^2}=75.43 м/с^2$

Точка равномерно движется по окружности радиусом 3 м

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Мгновенная скорость в физике

Определение

Мгновенной скоростью называется скорость объекта в данный момент времени в конкретной точке. Это векторная физическая величина, которая обозначается символом vec v и определяется по формуле:

(vec v=frac{Deltavec S}{Delta t})

Где (Deltavec S) — перемещение, а (Delta t ) — промежуток времени.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Величина измеряется в м/с.

Мгновенное ускорение в физике

Определение

Мгновенное ускорение — это векторная физическая величина, численно равная изменению скорости в единицу времени. 

Обозначается (vec a).

Единицами измерения мгновенного ускорения являются м/с2.

Мгновенное ускорение

 

Как направлены мгновенная скорость и ускорение

Вектор мгновенной скорости всегда направлен по касательной к траектории движения объекта в любой момент времени. Графически это выглядит так:

Как направлены мгновенная скорость и ускорение

 

У вектора vec a две составляющие: (vec a_tg) (касательное или тангенциальное (vec a)) и (vec a_n) (нормальное (vec a)). Каждая из них имеет свое направление вектора.

Тангенциальное и нормальное ускарение

 

Как найти мгновенное ускорение, формула

Ускорение определяется по формуле:

(vec a=lim_{trightarrow0}frac{Deltavec V}{Delta t})

Где (Deltavec V) — изменение скорости, (Delta t) — промежуток времени, когда происходило изменение скорости.

Составляющими данной векторной величины являются:

  • касательное или тангенциальное ускорение;
  • нормальное ускорение.

Касательное — указывает, насколько быстро изменяется скорость объекта по модулю. Оно вычисляется по формуле:

(a_т=frac{dV}{dt})

Вектор тангенциального ускорения направлен по касательной к траектории движения тела.

Нормальное — характеризует быстроту изменения скорости по направлению и всегда направлено к центру кривизны траектории. Определяется по формуле:

(a_н=frac{v^2}r )

Задача на определение мгновенного ускорения

Для усвоения теоретического материала важно закрепить знания на практике. Решим задачу на определение мгновенного ускорения.

Задача

С каким ускорением движется гоночный болид, если его скорость изменилась со 144 км/ч до 216 км/ч за 6 секунд?

Решение:

Записываем все известные вводные:

(V_0)=144 км/ч, (V)=216 км/ч, t=6 с, a=?

Переводим км/ч в м/с, получаем:

(V_0)=40 м/с, (V)=60 м/с.

Формула:

(vec a=frac{Deltavec V}{Delta t})

Где (Deltavec V=V-V_0)

Получаем значение ускорения, равное 3,33 м/с2.

Источник

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).

Среднее ускорение

Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:

uskor-01

Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:

uskor-02

При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть

v2 > v1

а направление вектора ускорения совпадает с вектором скорости uskor-03

Если скорость тела по модулю уменьшается, то есть

v2 < v1

то направление вектора ускорения противоположно направлению вектора скорости uskor-03 Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а < 0). На рис. 1.9 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.

Рис. 1.9. Мгновенное ускорение.

При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).

Тангенциальное ускорение

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Рис. 1.10. Тангенциальное ускорение.

Направление вектора тангенциального ускорения uskor-05 (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой uskor-06Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

(согласно теореме Пифагора для прямоугольно прямоугольника).

Направление полного ускорения также определяется правилом сложения векторов:

uskor-04

Источник

В прошлой статье мы немножко разобрались с тем, что такое механика  и зачем она нужна. Мы уже знаем, что такое система отсчета,  относительность движения и материальная точка. Что ж, пора двигаться дальше!  Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики  и приведем практический пример решения задачи.

Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.

Траектория, радиус-вектор, закон движения тела

Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад  в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.

Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.

Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.

Радиус-вектор – вектор, задающий положение точки в пространстве.

Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат  (или радиус-вектора точки) от времени.

Перемещение и путь

Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.

Перемещение и путь

 

В системе СИ перемещение и длина пути измеряются в метрах.

Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.

Скорость и ускорение

Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

Скорость и ускорение

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.

Мгновенная скорость – векторная физическая величина, равная производной  от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

Мгновенная скорость формула

В системе СИ скорость измеряется в метрах в секунду

Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.

Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Мгновенное ускорение формула

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.

Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Тангенциальное ускорение формула

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Нормальное ускорение как найти

Здесь R – радиус окружности, по которой движется тело.

Векторы нормального, тангенциального и полного ускорения

 

Закон равноускоренного движения

Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Закон равноускоренного движения

Здесь  – x нулевое- начальная координата. v нулевое – начальная скорость. Продифференцируем по времени, и получим скорость

Закон равноускоренного движения

Производная по скорости от времени даст значение ускорения a, которое является константой.

Пример решения задачи

Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы. 

Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.

Кинематика пример решения задачи

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.

Источник

Коллоквиум.

1. Механическое движение. Относительность
механического движения.

Механическое движение – это изменение
положения тела в пространстве относительно
других тел.

Относительность механического движения

Все тела во Вселенной движутся, поэтому
не существует тел, которые находятся в
абсолютном покое. По той же причине
определить движется тело или нет, можно
только относительно какого-либо другого
тела.

Например, автомобиль движется по дороге.
Дорога находится на планете Земля.
Дорога неподвижна. Поэтому можно измерить
скорость автомобиля относительно
неподвижной дороги. Но дорога неподвижна
относительно Земли. Однако сама Земля
вращается вокруг Солнца. Следовательно,
дорога вместе с автомобилем также
вращается вокруг Солнца. Следовательно,
автомобиль совершает не только
поступательное движение, но и вращательное
(относительно Солнца). А вот относительно
Земли автомобиль совершает только
поступательное движение. В этом
проявляется относительность механического
движения.

Относительность механического движения
– это зависимость траектории движения
тела, пройденного пути, перемещения и
скорости от выбора системы отсчёта.

2. Перемещение и скорость.

Перемещение
– это вектор, соединяющий начальное и
конечное положение точки. Направление
и величина перемещения определяются
отрезком прямой между начальной и
конечной точками движения.

Скорость.
Механическое
движение характеризуется еще и тем,
насколько быстро движется точка (тело).
Эта характеристика называется скорость
движения.
Скорость – величина векторная. Для того,
чтобы полностью задать ее, надо задать
собственно величину скорости и
направление, вдоль которого она измерена.
Обычно рассматривается скорость тела
вдоль траектории его движения. Тогда
величина скорости определяется как
путь, пройденный в единицу времени.
Иначе говоря, для того, чтобы найти
скорость вдоль траектории движения
надо путь разделить на время, за которое
он был пройден.

Формулы
для решения:

Пусть
v
–
скорость, s
–
путь, t
– время. Скорость
измеряется вдоль траектории движения.
Тогда:


Перемещение
определяется как геометрическая сумма
отрезков пути. Для простейшего случая,
когда один участок пути направлен
перпендикулярно другому решается
прямоугольный треугольник:

3. Виды движения. Ускорение.

В современной механике движение тела
подразделяется на виды, и существует
следующая классификация видов движения
тела:

1. Поступательное движение,
при котором любая прямая линия, связанная
с телом, остается при движении параллельной
самой себе.
2. Вращательное движение
или вращение тела вокруг своей оси,
считающейся неподвижной.
3. Сложное
движение тела, состоящее из
поступательного и вращательного
движений.

Ускорение – это величина,
которая характеризует быстроту изменения
скорости.

Среднее ускорение

Среднее
ускорение> – это отношение
изменения скорости к промежутку времени,
за который это изменении произошло.
Определить среднее ускорение можно
формулой:

где

–
вектор ускорения.

Направление
вектора ускорения совпадает с направлением
изменения скорости Δ
=
–

0
(здесь
0
– это начальная скорость, то есть
скорость, с которой тело начало
ускоряться).

В
момент времени t1 (см. рис 1.8) тело имеет
скорость
0.
В момент времени t2 тело имеет скорость

.
Согласно правилу вычитания векторов
найдём вектор изменения скорости Δ
=
–

0.
Тогда определить ускорение можно так:

Рис.
1.8. Среднее ускорение.

В
СИ единица ускорения – это 1
метр в секунду за секунду (или метр на
секунду в квадрате), то есть

Метр
на секунду в квадрате равен ускорению
прямолинейно движущейся точки, при
котором за одну секунду скорость этой
точки увеличивается на 1 м/с. Иными
словами, ускорение определяет, насколько
изменяется скорость тела за одну секунду.
Например, если ускорение равно 5 м/с2,
то это означает, что скорость тела каждую
секунду увеличивается на 5 м/с.

Мгновенное ускорение

Мгновенное
ускорение тела (материальной точки)
в данный момент времени – это физическая
величина, равная пределу, к которому
стремится среднее ускорение при
стремлении промежутка времени к нулю.
Иными словами – это ускорение, которое
развивает тело за очень короткий отрезок
времени:

Направление
ускорения также совпадает с направлением
изменения скорости Δ
при очень малых значениях промежутка
времени, за который происходит изменение
скорости. Вектор ускорения может быть
задан проекциями на соответствующие
оси координат в данной системе отсчёта
(проекциями аХ, aY, aZ).

При
ускоренном прямолинейном движении
скорость тела возрастает по модулю, то
есть

v2
> v1

а направление вектора ускорения совпадает
с вектором скорости
2.

Если
скорость тела по модулю уменьшается,
то есть

v2
< v1

то направление вектора ускорения
противоположно направлению вектора
скорости
2.
Иначе говоря, в данном случае происходит
замедление движения, при этом
ускорение будет отрицательным (а < 0).
На рис. 1.9 показано направление векторов
ускорения при прямолинейном движении
тела для случая ускорения и замедления.

Рис.
1.9. Мгновенное ускорение.

При
движении по криволинейной траектории
изменяется не только модуль скорости,
но и её направление. В этом случае вектор
ускорение представляют в виде двух
составляющих (см. следующий раздел).

Тангенциальное ускорение

Тангенциальное
(касательное) ускорение – это
составляющая вектора ускорения,
направленная вдоль касательной к
траектории в данной точке траектории
движения. Тангенциальное ускорение
характеризует изменение скорости по
модулю при криволинейном движении.

Рис.
1.10. Тангенциальное ускорение.

Направление
вектора тангенциального ускорения
τ
(см. рис. 1.10) совпадает с направлением
линейной скорости или противоположно
ему. То есть вектор тангенциального
ускорения лежит на одной оси с касательной
окружности, которая является траекторией
движения тела.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Добавить комментарий