|
Помогите решить задачу по физике, прошу, не словами, а цифрами или хотябы формулами, рисунок тоже приветствуется: В однородном магнитном поле с индукцией 0.2Тл равномерно с частотой 10 с(в минус первой степени) вращается рамка, площадь которой 100 см(в квадрате). Определить мгновенное значение эдс соответствующее углу 45(градусов) между плоскостью рамки и силовыми линиями магнитного поля.
Частота 10 Гц легко переводится в угловую частоту (напомню, что ω = 2пи*f). Эдс во вращающейся рамке, опять же напомню, изменяется по закону e = ωBScosωt. 45 градусов – это как раз ωt и есть. Коммент: в физике ориентация плоскости определяется направлением нормали к плоскости, а в этой задачке – направлением самой плоскости. Поэтому в формуле косинус, а не синус (как было бы в книжках). автор вопроса выбрал этот ответ лучшим 273440637250 7 лет назад Ответ к задаче: В=0,2Тл V=10c(в -1 степени)=10Гц ωt=45(градусов) S=100см(в квадрате)=0.01м(в квадрате) ω=2*3,14*10=62,8рад/с е=62,8*0,2*0,01*1/(кв.корень из 2) = 0,089В Знаете ответ? |
1.
Закон электромагнитной индукции (закон
Фарадея):
мгновенное значение
ЭДС индукции
![]()
;
среднее значение
ЭДС индукции
![]()
.
2.
Разность потенциалов на концах прямого
проводника, движущегося со скоростью
в однородном магнитном поле
![]()
где
l
– длина проводника;
– угол между векторами
и
.
3.
Индуктивность контура
![]()
Мгновенное значение
ЭДС самоиндукции
![]()
;
среднее значение
ЭДС самоиндукции
![]()
Индуктивность
соленоида
L
= 0n2V,
где
n = N/l
– число витков N,
приходящееся на единицу длины l
соленоида; V
– объем соленоида.
6.
Энергия магнитного поля контура с током
![]()
.
7.
Объемная плотность энергии магнитного
поля
![]()
Для однородного
поля
![]()
Примеры решения задач
Задача
1
В
центре плоской круговой рамки, состоящей
из 50 витков радиусом 20 см, находится
маленькая рамка, состоящая из 100 витков
площадью 1 см2.
Маленькая рамка вращается вокруг одного
из диаметров большой рамки с постоянной
угловой скоростью 300 рад/с. Найти
максимальное значение ЭДС индукции,
если в обмотке рамки течет ток силой 10
А.
|
Дано: |
Решение: |
|
N1 N2 R S = I |
При и нормалью к плоскости рамки и, (1) |
|
imax |
где
= N2Ф
– потокосцепление.
Так
как размеры маленькой рамки малы по
сравнению с размерами большой рамки,
то поле в пределах маленькой рамки можно
считать однородным. Магнитную индукцию
В этого поля можно выразить через
индукцию поля в центре рамки
![]()
.
(2)
Для
однородного поля магнитный поток,
пронизывающий маленькую рамку, равен
Ф = ВScos.
С учетом того, что при вращении рамки с
постоянной угловой скоростью мгновенное
значение угла
= t,
получим:
Ф
= ВS
cos
= BS cost.
Подставив
в формулу (1) выражение для Ф
и продифференцировав по времени, найдем
мгновенное значение ЭДС индукции
i
= N2BSsint.
Максимальное значение эдс индукции равно
imax
= N2BS.
Учитывая формулу (2), получим:
![]()
.
Произведя
вычисления, получим:
![]()
Задача
2
Контур в виде
квадрата со стороной 10 см находится в
однородном магнитном поле с индукцией
0,5 мТл, причем его плоскость составляет
угол 60о c силовыми линиями
поля. Какой заряд протечет по контуру
при выключении магнитного поля?
Сопротивление контура 1 мОм.
|
Дано: |
Решение: |
|
а В 10-4 = R |
Рис. |
|
q |
При
выключении магнитного поля магнитный
поток Ф,
пронизывающий контур, меняется. В контуре
возникает ЭДС индукции, мгновенное
значение которой по закону Фарадея
равно
![]()
.
Мгновенное
значение силы индукционного тока
определяется по закону Ома
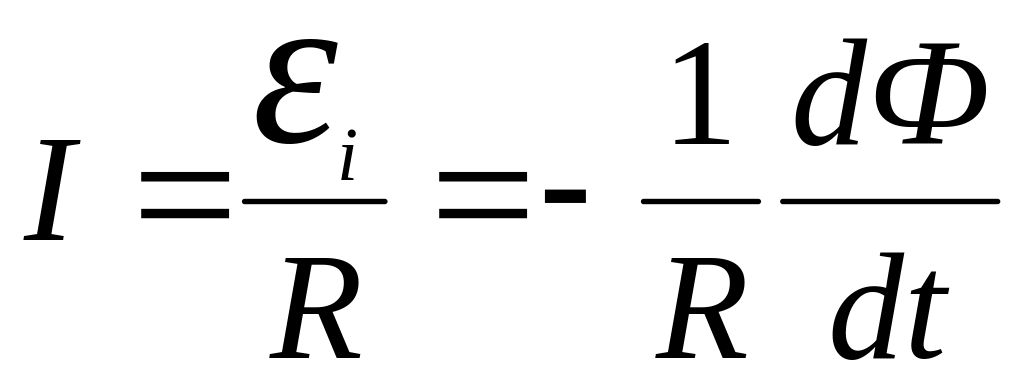
.
За
время dt
по контуру протечет заряд
![]()
.
Проинтегрировав
это выражение, найдем полный заряд:

.
Для однородного
магнитного поля начальный магнитный
поток равен
Ф1
= BS
cos,
где
– угол между вектором
и нормалью к плоскости контура (рис. 8);
S = а2
– площадь контура.
Из
рис. 8 видно, что
= 90о
–
.
Следовательно, cos
= sin.
Конечный
магнитный поток Ф2
= 0.
Таким образом,
![]()
.
Произведя
вычисления, получим:
![]()
Кл
.
Проверим,
дает ли расчетная формула единицу
заряда. Для этого в правую часть формулы
вместо символов величин подставим их
единицы измерений:
![]()
Но
из закона Ампера
![]()
,
а из закона Ома
![]()
.
Таким образом,

.
Из
определения потенциала
![]()
.
Задача
3
Соленоид
с сердечником из немагнитного материала
содержит 1200 витков провода, плотно
прилегающих друг к другу. При силе тока
4 А магнитный поток равен 4 мкВб. Определить
индуктивность соленоида и энергию его
магнитного поля.
|
Дано: |
Решение: |
|
N I Ф 10-6 |
Индуктивность
= |
|
L |
В
свою очередь, потокосцепление можно
найти через поток Ф
и число витков N
(когда витки плотно прилегают друг к
другу):
=
NФ .
( 2 )
Из
формул (1) и (2) находим индуктивность
соленоида
![]()
.
( 3 )
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Написать уравнение для мгновенных значений ЭДС индукции, возникающих при равномерном вращении витка в однородном магнитном поле,
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,299
- гуманитарные 33,622
- юридические 17,900
- школьный раздел 607,247
- разное 16,834
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Уравнение мгновенного значения для эдс
Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
Переменным током (напряжением, ЭДС и т.д.) называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, – периодом Т. Для периодического тока имеем
 , , |
(1) |
Величина, обратная периоду, есть частота, измеряемая в герцах (Гц):
 , , |
(2) |
Диапазон частот, применяемых в технике: от сверхнизких частот (0.01 ¸ 10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .
Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:
i – мгновенное значение тока  ;
;
u – мгновенное значение напряжения  ;
;
е – мгновенное значение ЭДС  ;
;
р – мгновенное значение мощности  .
.
Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ) .
 – амплитуда тока;
– амплитуда тока;
 – амплитуда напряжения;
– амплитуда напряжения;
 – амплитуда ЭДС.
– амплитуда ЭДС.
Действующее значение переменного тока
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:
 , , |
(3) |
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Изображение синусоидальных ЭДС, напряжений
и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е1 и е2 соответствуют уравнения:

 .
.

Значения аргументов синусоидальных функций  и
и  называются фазами синусоид, а значение фазы в начальный момент времени ( t =0):
называются фазами синусоид, а значение фазы в начальный момент времени ( t =0):  и
и  – начальной фазой (
– начальной фазой ( 
 ).
).
Величину  , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на
, характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на  рад., то угловая частота есть
рад., то угловая частота есть  , где f– частота.
, где f– частота.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.
Для синусоидальных ЭДС е1 и е2 угол сдвига фаз:
 .
.
Векторное изображение синусоидально
изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е1 и е2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени ( t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток  равен сумме токов
равен сумме токов  и
и  двух ветвей:
двух ветвей:

 .
.
Каждый из этих токов синусоидален и может быть представлен уравнением
 и
и  .
.
Результирующий ток также будет синусоидален:
 .
.
Определение амплитуды  и начальной фазы
и начальной фазы  этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы.
этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы.

На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным  .
.
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
 .
.
Построение векторной диаграммы в масштабе позволяет определить значения  и
и  из диаграммы, после чего может быть записано решение для мгновенного значения
из диаграммы, после чего может быть записано решение для мгновенного значения  путем формального учета угловой частоты:
путем формального учета угловой частоты:  .
.
Представление синусоидальных ЭДС, напряжений
и токов комплексными числами
Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.

Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :
показательной 
тригонометрической  или
или
алгебраической  – формах.
– формах.
Например, ЭДС  , изображенной на рис. 7 вращающимся вектором, соответствует комплексное число
, изображенной на рис. 7 вращающимся вектором, соответствует комплексное число
 .
.
Фазовый угол  определяется по проекциям вектора на оси “+1” и “+j” системы координат, как
определяется по проекциям вектора на оси “+1” и “+j” системы координат, как
 .
.
В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:
 , , |
(4) |
Комплексное число  удобно представить в виде произведения двух комплексных чисел:
удобно представить в виде произведения двух комплексных чисел:
 , , |
(5) |
Параметр  , соответствующий положению вектора для t =0 (или на вращающейся со скоростью w комплексной плоскости), называют комплексной амплитудой:
, соответствующий положению вектора для t =0 (или на вращающейся со скоростью w комплексной плоскости), называют комплексной амплитудой:  , а параметр
, а параметр  – комплексом мгновенного значения.
– комплексом мгновенного значения.
Параметр  является оператором поворота вектора на угол w t относительно начального положения вектора.
является оператором поворота вектора на угол w t относительно начального положения вектора.
Вообще говоря, умножение вектора на оператор поворота  есть его поворот относительно первоначального положения на угол ± a .
есть его поворот относительно первоначального положения на угол ± a .
Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “j” произведения комплекса амплитуды  и оператора поворота
и оператора поворота  :
:
 .
.
Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:
 , , |
(6) |
Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:
 ,
,
– то для записи ее в показательной форме, необходимо найти начальную фазу  , т.е. угол, который образует вектор
, т.е. угол, который образует вектор  с положительной полуосью +1:
с положительной полуосью +1:
 .
.
Тогда мгновенное значение напряжения:
 ,
,
где  .
.
При записи выражения для определенности было принято, что  , т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если
, т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если  , то при
, то при  (второй квадрант)
(второй квадрант)
 , , |
(7) |
а при  (третий квадрант)
(третий квадрант)
 |
(8) |
 |
(9) |
Если задано мгновенное значение тока в виде  , то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:
, то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:
 .
.
Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.
Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока  по рис. 5 получим:
по рис. 5 получим:

где  ;
;
 .
.
Действующее значение синусоидальных ЭДС, напряжений и токов
В соответствии с выражением (3) для действующего значения синусоидального тока запишем:
 .
.
Аналогичный результат можно получить для синусоидальных ЭДС и напряжений. Таким образом, действующие значения синусоидальных тока, ЭДС и напряжения меньше своих амплитудных значений в  раз:
раз:
 . . |
(10) |
Поскольку, как будет показано далее, энергетический расчет цепей переменного тока обычно проводится с использованием действующих значений величин, по аналогии с предыдущим введем понятие комплекса действующего значения
 .
.
1. Основы теории цепей: Учеб. для вузов /Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
1. Какой практический смысл имеет изображение синусоидальных величин с помощью векторов?
2. Какой практический смысл имеет представление синусоидальных величин с использованием комплексных чисел?
3. В чем заключаются преимущества изображения синусоидальных величин с помощью комплексов по сравнению с их векторным представлением?
4. Для заданных синусоидальных функций ЭДС и тока  записать соответствующие им комплексы амплитуд и действующих значений, а также комплексы мгновенных значений.
записать соответствующие им комплексы амплитуд и действующих значений, а также комплексы мгновенных значений.
5. На рис. 5  , а
, а  . Определить
. Определить  .
.
Ответ:  .
.
Что такое электродвижущая сила (ЭДС) и как ее рассчитать
Электродвижущая сила или сокращено ЭДС – это способность источника тока ил по-другому питающий элемент, создавать в электрической цепи разность потенциалов. Элементами питания являются аккумуляторы или батареи. Это скалярная физическая величина, равная работе сторонних сил для перемещения одного заряда с положительной величиной. В данной статье будут рассмотрены теоритические вопросы ЭДС, как она образуется, а также для чего она может быть использована на практике и где используются, а главное как рассчитать ее.
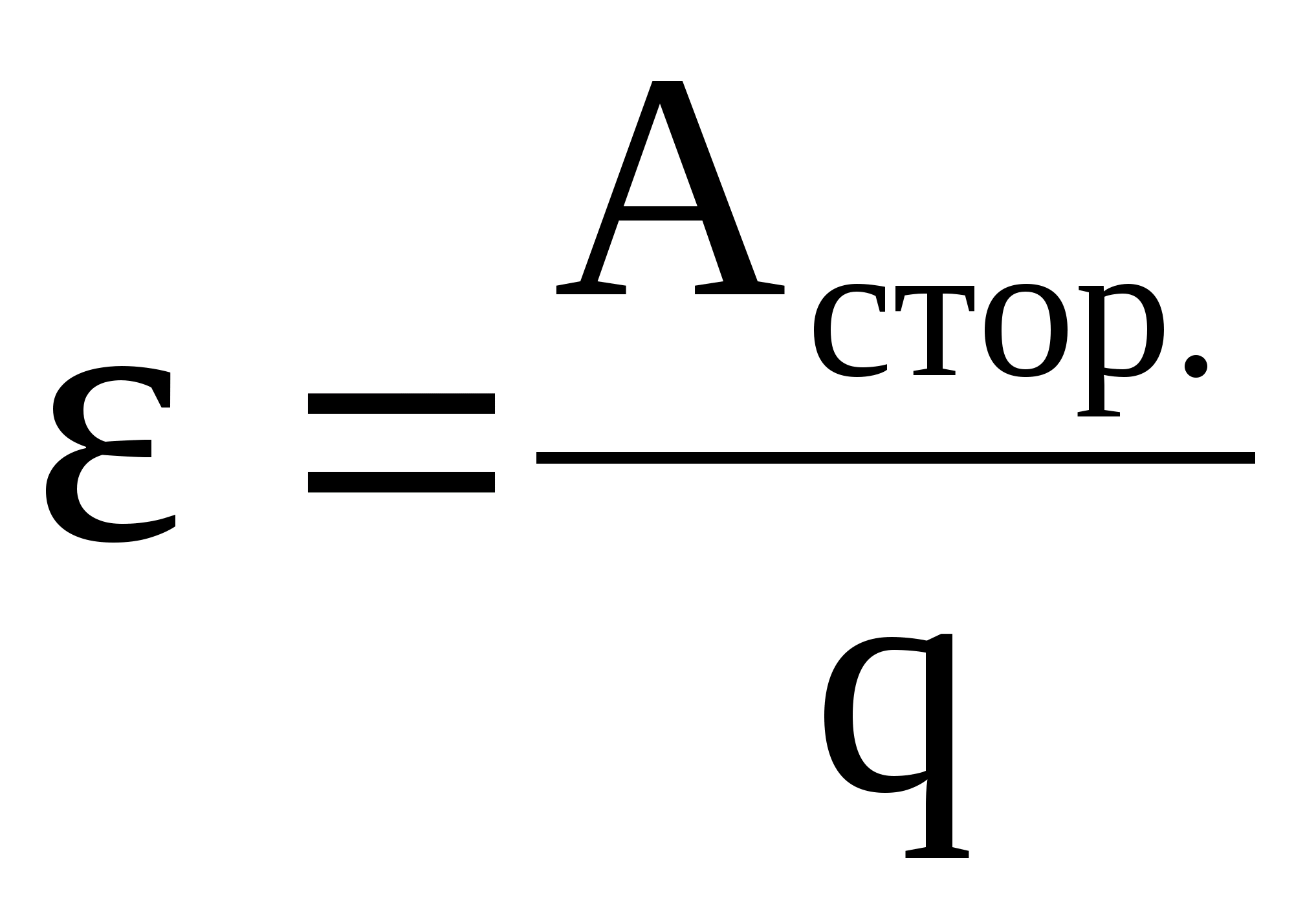
Что такое ЭДС: объяснение простыми словами
Под ЭДС понимается удельная работа сторонних сил по перемещению единичного заряда в контуре электрической цепи . Это понятие в электричестве предполагает множество физических толкований, относящихся к различным областям технических знаний. В электротехнике — это удельная работа сторонних сил, появляющаяся в индуктивных обмотках при наведении в них переменного поля. В химии она означает разность потенциалов, возникающее при электролизе, а также при реакциях, сопровождающихся разделением электрических зарядов.
В физике она соответствует электродвижущей силе, создаваемой на концах электрической термопары, например. Чтобы объяснить суть ЭДС простыми словами – потребуется рассмотреть каждый из вариантов ее трактовки. Прежде чем перейти к основной части статьи отметим, что ЭДС и напряжение очень близкие по смыслу понятия, но всё же несколько отличаются. Если сказать кратко, то ЭДС — на источнике питания без нагрузки, а когда к нему подключают нагрузку — это уже напряжение. Потому что количество вольт на ИП под нагрузкой почти всегда несколько меньше, чем без неё. Это связано с наличием внутреннего сопротивления таких источников питания, как трансформаторы и гальванические элементы.
Электродвижущая сила (эдс), физическая величина, характеризующая действие сторонних (непотенциальных) сил в источниках постоянного или переменного тока; в замкнутом проводящем контуре равна работе этих сил по перемещению единичного положительного заряда вдоль контура. Если через Eстр обозначить напряжённость поля сторонних сил, то эдс в замкнутом контуре (L) равна , где dl — элемент длины контура. Потенциальные силы электростатического (или стационарного) поля не могут поддерживать постоянный ток в цепи, т. к. работа этих сил на замкнутом пути равна нулю. Прохождение же тока по проводникам сопровождается выделением энергии — нагреванием проводников.
Сторонние силы приводят в движение заряженные частицы внутри источников тока: генераторов, гальванических элементов, аккумуляторов и т. д. Происхождение сторонних сил может быть различным. В генераторах сторонние силы — это силы со стороны вихревого электрического поля, возникающего при изменении магнитного поля со временем, или Лоренца сила, действующая со стороны магнитного поля на электроны в движущемся проводнике; в гальванических элементах и аккумуляторах — это химические силы и т. д. Эдс определяет силу тока в цепи при заданном её сопротивлении (см. Ома закон). Измеряется эдс, как и напряжение, в вольтах.

Природа ЭДС
Причина возникновения ЭДС в разных источниках тока разная. По природе возникновения различают следующие типы:
- Химическая ЭДС. Возникает в батарейках и аккумуляторах вследствие химических реакций.
- Термо ЭДС. Возникает, когда находящиеся при разных температурах контакты разнородных проводников соединены.
- ЭДС индукции. Возникает в генераторе при помещении вращающегося проводника в магнитное поле. ЭДС будет наводиться в проводнике, когда проводник пересекает силовые линии постоянного магнитного поля или когда магнитное поле изменяется по величине.
- Фотоэлектрическая ЭДС. Возникновению этой ЭДС способствует явление внешнего или внутреннего фотоэффекта.
- Пьезоэлектрическая ЭДС. ЭДС возникает при растяжении или сдавливании веществ.
Электромагнитная индукция (самоиндукция)
Начнем с электромагнитной индукции. Это явление описывает закон электромагнитной индукции Фарадея. Физический смысл этого явления состоит в способности электромагнитного поля наводить ЭДС в находящемся рядом проводнике. При этом или поле должно изменяться, например, по величине и направлению векторов, или перемещаться относительно проводника, или должен двигаться проводник относительно этого поля. На концах проводника в этом случае возникает разность потенциалов.
Опыт демонстрирует появление ЭДС в катушке при воздействии изменяющегося магнитного поля постоянного магнита. Есть и другое похожее по смыслу явление — взаимоиндукция. Оно заключается в том, что изменение направления и силы тока одной катушки индуцирует ЭДС на выводах расположенной рядом катушки, широко применяется в различных областях техники, включая электрику и электронику. Оно лежит в основе работы трансформаторов, где магнитный поток одной обмотки наводит ток и напряжение во второй.
В электрике физический эффект под названием ЭДС используется при изготовлении специальных преобразователей переменного тока, обеспечивающих получение нужных значений действующих величин (тока и напряжения). Благодаря явлениям индукции и самоиндукции инженерам удалось разработать множество электротехнических устройств: от обычной катушки индуктивности (дросселя) и вплоть до трансформатора. Понятие взаимоиндукции касается только переменного тока, при протекании которого в контуре или проводнике меняется магнитный поток.
ЭДС в быту и единицы измерения
Другие примеры встречаются в практической жизни любого рядового человека. Под эту категорию попадают такие привычные вещи, как малогабаритные батарейки, а также другие миниатюрные элементы питания. В этом случае рабочая ЭДС формируется за счет химических процессов, протекающих внутри источников постоянного напряжения. Когда оно возникает на клеммах (полюсах) батареи вследствие внутренних изменений – элемент полностью готов к работе. Со временем величина ЭДС несколько снижается, а внутреннее сопротивление заметно возрастает.
В результате если вы измеряете напряжение на не подключенной ни к чему пальчиковой батарейке вы видите нормальные для неё 1.5В (или около того), но когда к батарейке подключается нагрузка, допустим, вы установили её в какой-то прибор — он не работает. Почему? Потому что если предположить, что у вольтметра внутреннее сопротивление во много раз выше, чем внутреннее сопротивлении батарейки — то вы измеряли её ЭДС. Когда батарейка начала отдавать ток в нагрузке на её выводах стало не 1.5В, а, допустим, 1.2В — прибору недостаточно ни напряжения, ни тока для нормальной работы.
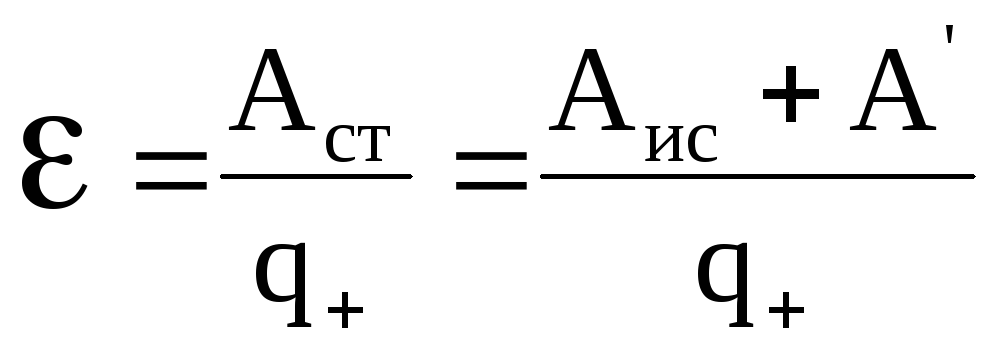
Как раз вот эти 0.3 В и упали на внутреннем сопротивлении гальванического элемента. Если батарейка совсем старая и её электроды разрушены, то на клеммах батареи может не быть вообще никакой электродвижущей силы или напряжения — т.е. ноль. Совсем небольшая по величине электродвижущая сила наводится и в рамках антенны приемника, которая усиливается затем специальными каскадами, и мы получаем наш телевизионный, радио и даже Wi-Fi сигнал.
Как образуется ЭДС
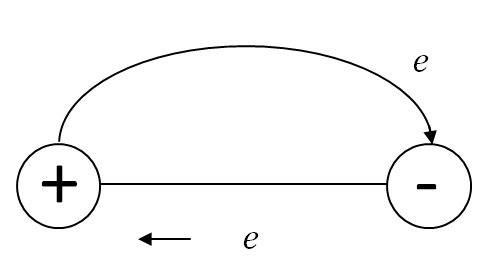
Идеальный источник ЭДС – генератор, внутреннее сопротивление которого равно нулю, а напряжение на его зажимах не зависит от нагрузки. Мощность идеального источника ЭДС бесконечна. Реальный источник ЭДС, в отличие от идеального, содержит внутреннее сопротивление Ri и его напряжение зависит от нагрузки (рис. 1., б), а мощность источника конечна. Электрическая схема реального генератора ЭДС представляет собой последовательное соединение идеального генератора ЭДС Е и его внутреннего сопротивления Ri.
На практике для того чтобы приблизить режим работы реального генератора ЭДС к режиму работы идеального, внутреннее сопротивление реального генератора Ri стараются делать как можно меньше, а сопротивление нагрузки Rн необходимо подключать величиной не менее чем в 10 раз большей величины внутреннего сопротивления генератора, т.е. необходимо выполнять условие: Rн >> Ri
Для того чтобы выходное напряжение реального генератора ЭДС не зависело от нагрузки, его стабилизируют применением специальных электронных схем стабилизации напряжения. Поскольку внутреннее сопротивление реального генератора ЭДС не может быть выполнено бесконечно малым, его минимизируют и выполняют стандартным для возможности согласованного подключения к нему потребителей энергии. В радиотехнике величины стандартного выходного сопротивления генераторов ЭДС составляют 50 Ом (промышленный стандарт) и 75 Ом (бытовой стандарт).
Например, все телевизионные приемники имеют входное сопротивление 75 Ом и подключены к антеннам коаксиальным кабелем именно такого волнового сопротивления. Для приближения к идеальным генераторам ЭДС источники питающего напряжения, используемые во всей промышленной и бытовой радиоэлектронной аппаратуре, выполняют с применением специальных электронных схем стабилизации выходного напряжения, которые позволяют выдерживать практически неизменное выходное напряжение источника питания в заданном диапазоне токов, потребляемых от источника ЭДС (иногда его называют источником напряжения).
На электрических схемах источники ЭДС изображаются так: Е — источник постоянной ЭДС, е(t) – источник гармонической (переменной) ЭДС в форме функции времени. Электродвижущая сила Е батареи последовательно соединенных одинаковых элементов равна электродвижущей силе одного элемента Е, умноженной на число элементов n батареи: Е = nЕ.
Электродвижущая сила (ЭДС) источника энергии
Для поддержания электрического тока в проводнике требуется внешний источник энергии, создающий все время разность потенциалов между концами этого проводника. Такие источники энергии получили название источников электрической энергии (или источников тока). Источники электрической энергии обладают определенной электродвижущей силой (сокращенно ЭДС), которая создает и длительное время поддерживает разность потенциалов между концами проводника.
[spoiler title=”источники:”]
http://toehelp.ru/theory/toe/lecture03/lecture03.html
[/spoiler]
Условие задачи:
Мгновенное значение ЭДС синусоидального тока 120 В для фазы 45°. Каково действующее значение ЭДС?
Задача №9.10.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(rm E=120) В, (varphi=45^circ), (rm E_д-?)
Решение задачи:
Уравнение колебаний ЭДС в цепи переменного тока в общем виде выглядит так:
[{rm E} = {{rm E}_m}sin left( {omega t} right);;;;(1)]
Здесь (rm E_m) – максимальное (амплитудное) значение ЭДС, (omega) – циклическая частота колебаний.
Аргумент синуса (left( {omega t} right)) называется фазой колебаний (varphi), поэтому уравнение (1) также можно записать в виде:
[{rm E} = {{rm E}_m}sin varphi ;;;;(2)]
Выразим из уравнения (2) максимальное значение ЭДС (rm E_m):
[{{rm E}_m} = frac{{rm E}}{{sin varphi }};;;;(3)]
Действующее значение ЭДС (rm E_д) связано с максимальным значением ЭДС (rm E_m) по формуле:
[{{rm E}_д} = frac{{{{rm E}_m}}}{{sqrt 2 }};;;;(4)]
Подставим выражение (3) в формулу (4), так мы получим решение задачи в общем виде:
[{{rm E}_д} = frac{{rm E}}{{sqrt 2 sin varphi }}]
Численный ответ равен:
[{{rm E}_д} = frac{{120}}{{sqrt 2 cdot sin 45^circ }} = 120;В]
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
9.10.2 Катушка индуктивностью 20 мГн включена в сеть промышленного переменного тока
9.10.4 Напряжение на концах участка цепи, по которой течет переменный ток, изменяется
9.10.5 В цепь переменного тока включены последовательно конденсатор емкостью 1 мкФ
Сергей Сергеевич Соев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение электромагнитной индукции
Возникновение электрического тока в проводнике, движущемся в магнитном поле, называют явлением индукцией в движущихся проводниках. В случае движения проводника в магнитном поле, его свободные электроны приходят в движение относительно проводника под воздействием силы Лоренца. Явление электромагнитной индукции обнаружил Фарадей в 1831 г. в проводящем контуре. Он заметил, что в замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, которую ограничивает контур, появляется электрический ток. Это также явление электромагнитной индукции, возникающий ток в контуре, называют индукционным.
Итак, явление электромагнитной индукции состоит в возникновении электрического тока в замкнутом проводнике при изменении потока магнитной индукции, охватываемого контуром. При этом контур может быть неподвижным.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
ЭДС индукции
Существование явления электромагнитной индукции говорит о том, что при изменении магнитного потока в контуре появляется электродвижущая сила индукции (ЭДС, ${{mathcal E}}_i$). Величина ${{mathcal E}}_i$ не зависит от способа изменения магнитного потока $(Ф)$, и связана со скоростью его изменения ($frac{dФ}{dt}$). С изменением знака скорости изменения потока направление ЭДС индукции тоже изменяется:
Знак потока $Ф$ и знак ${{mathcal E}}_i$ связывают с выбором направления нормали к плоскости контура. ${{mathcal E}}_i$ считают положительной если ее направление образует с направлением нормали к контуру правый винт. Для рис 1. и заданном направлении нормали «от нас», перпендикулярно плоскости рисунка ($overrightarrow{n}$) $frac{dФ}{dt} >0, {{mathcal E}}_i
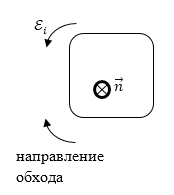
Рисунок 1.
«Электромагнитная индукция» 👇
Основной единицей измерения индукционной ЭДС служит вольт $(В)$. Если скорость изменения магнитного потока равна $1frac{Вб}{с}$ в контуре индуцируется ЭДС, равная $1 В$.
В гауссовой системе формула (1) принимает вид:
где $с$ – скорость света в вакууме. Основной единицей измерения магнитного потока в СГСЭ является максвелл $(Мкс)$, тогда ${{mathcal E}}_i$ измеряется в СГСЭ – единицах потенциала. Для того, чтобы перевести ЭДС из системы гаусса в вольты необходимо умножить имеющееся значение на $300$. Следовательно, формулой связи системы СИ и СГСЭ можно записать выражение:
Среднее значение ЭДС индукции может быть определено как:
Поток сцепления
Если контур, в котором индуцируется ЭДС, состоит из $N$ витков (соленоид), витки соединены последовательно, ${{mathcal E}}_i$ равна сумме ЭДС, которые индуцируются каждым витком в отдельности. Следовательно, используя формулу (1), можно записать:
Величину $Psi$, равную:
называют потоком сцепления, или полным магнитным потоком. В том случае, если поток, который пронизывает каждый из витков, одинаковый, то можно записать, что:
В сложном контуре ${{mathcal E}}_i$ вычисляют как:
Уравнение (8) называют основным законом электромагнитной индукции (уравнением Фарадея – Максвелла).
Частные случаи применения закона электромагнитной индукции
- Если проводник длины $l $движется в однородном магнитном поле (с индукцией $В$) с постоянной скоростью $v$, то на его концах возникает разность потенциалов $U$:
где $alpha $ – угол между направлением скорости и вектором магнитной индукции.
- ЭДС индукции возникает в рамке, которая содержит $N$ витков, имеет площадь $S$ и вращается с постоянной угловой скоростью $omega$ в однородном магнитном поле с индукцией $В$ и она равна:
где $omega t$ – мгновенное значение угла между вектором магнитной индукции ($overrightarrow{B}$) и вектором нормали к плоскости рамки ($overrightarrow{n}$).
Пример 1
Задание: Найдите мгновенное значение ЭДС индукции рамки, которое соответствует углу поворота рамки $alpha ,$ площадь рамки, равна $S$, она содержит $N$ витков. Рамка вращается в постоянном магнитном поле с индукцией $B$. Частота вращения рамки равна $n$.
Решение:
За основу решения задачи примем уравнение Фарадея – Максвелла:
[{{mathcal E}}_i=-frac{d Psi}{dt} left(1.1right),]
где потокосцепление можно определить как:
[Psi=NФ left(1.2right),]
где $N$ – количество витков, которые пронизывает магнитный поток $Ф$. Соответственно (1.1) примет вид:
[{{mathcal E}}_i=-Nfrac{dФ}{dt} left(1.3right).]
Если рамку вращать, то магнитный поток изменяется в соответствии с законом:
[Ф=BScosomega tleft(1.4right),]
где $omega $ — угловая частота вращения. Подставим выражение (1.4) в (1.3), получим:
[{{mathcal E}}_i=NBSomega sinomega tleft(1.5right).]
Связь угловой частоты и часты вращения, определим как:
[omega =2pi n left(1.6right),] [omega t=alpha left(1.7right).]
Подставим выражения (1.6), (1.7) в формулу (1.5) получим:
[{{mathcal E}}_i=2pi nNBSsinalpha .]
Ответ: ${{mathcal E}}_i=2pi nNBSsinalpha .$
Пример 2
Задание: Определите среднее ЭДС индукции ($leftlangle {{mathcal E}}_irightrangle )$, если магнитный поток, который пронизывает контур, изменяется от $Ф_1=40Вб$ до $Ф_2=0Вб$ в течении промежутка времени равного $2 с$.
Решение:
За основу решения примем формулу, определяющую среднюю ЭДС индукции:
[leftlangle {{mathcal E}}_irightrangle =-frac{Delta Ф}{Delta t}left(2.1right).]
Проведем вычисления:
[leftlangle {{mathcal E}}_irightrangle =-frac{0-40}{2}=20 left(Вright).]
Ответ: $leftlangle {{mathcal E}}_irightrangle =20 В$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме



