Мгновенная
угловая скорость равна первой производной
углового перемещения по времени:
(6)
При
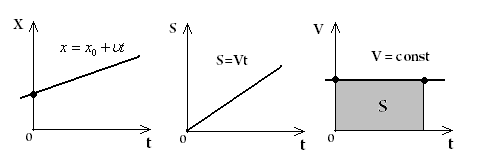
равномерном вращении
,
тогда
(7)
6. Связь линейной и угловой скоростей.
Если продолжить
(3), то получим:
или
(8)
(9)
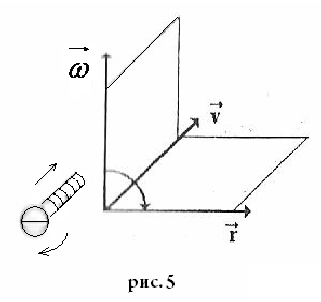
Вектор линейной
скоростисовпадает по направлению
с векторным произведением.
Векторное произведение всегда связано
справилом правого
винта: вращая головку винта по
направлению вектора,
стоящего на первом месте в (9), к вектору,
стоящему на втором месте, определяем
по поступательному движению винта
направление третьего вектора,
см. рис. 5.
Модуль
векторного произведения:
(10)
7. Модуль и направление углового ускорения.
При
вращении за время
угловая скорость получит приращение
,
тогда (8) примет вид:
(11)
Разделим
обе части на
,
получим:
,
(12)
где
отношение
– есть среднее угловое ускорение.
т.е.
(13)
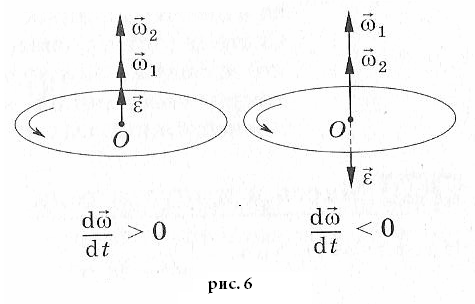
Вектор
углового ускорения
сонаправлен с вектором угловой скости
прии противоположен ему при
,
см. рис 6.
8. Связь тангенциального и углового ускорения.
При
вращении за время
угловая скорость получит приращение
,
тогда (8) примет вид:
(14)
Разделим
обе части на
,
получим:
(15)
или
(16)
Векторное
произведение:
(17)
Вектор тангенциального
ускорениясовпадает по направлению
с векторным произведением.
Векторное произведение всегда связано
справилом правого
винта: вращая головку винта по
направлению вектора,
стоящего на первом месте в (13), к вектору,
стоящему на втором месте, определяем
по поступательному движению винта
направление третьего вектора.
9. Мгновенное угловое ускорение.
При
получим мгновенное угловое ускорение:
,
(18)
т.е.
мгновенное угловое ускорение численно
равно первой производной угловой
скорости по времени или – второй
производной углового перемещения по
времени.
Приложение 1.
|
тип |
рисунок, |
формулы |
|
|
Равномерное |
|
|
|
|
Равноускоренное движение |
|
|
|
|
|
|
||
|
Движение |
|
При |
|
|
При |
|||
|
Движение |
|
|
|
|
При |
|||
|
Движение |
|
|
|
|
Движение |
|
|
|
|
Движение |
Т
При движении по Тангенциальное Направление
Нормальное
Модуль полного
Направление
|
|
|
Движение
с постоянным ускорением при действии
постоянной силы
Первый
этап — определение типа движения.
Второй
этап — физическая формулировка задачи:
выбор системы отсчета, определение
действующих сил и начальных условий.
Третий
этап — математическая формулировка
задачи: запись уравнений,
Если
md2х/dt2
=F=mа
не
равно 0, то
движение ускоренное
t
= 0, v
= v0;
x=
x0
Четвертый
этап — математическое решение задачи.
a
= d2х/dt2;
или
a
= dv/dt;
Откуда
dv
= adt;
Интегрируя
обе части
∫ dv
=∫ adt;
Взятие
интеграла дает
v
= at
+ C
постоянные
интегрирования определяюся из начальных
условий
Например,
при
t
= 0, v
= v0;
тогда
v
= v0
+ at
или
используя выражение для скорости
dx/dt
= v0
+ at;
разделяя
переменные
dx
=(v0
+ at)dt;
перемножая
почленно
dx
= atdt
+ v0dt;
Применяя
операцию почленного интегрирования(свойство
интеграла суммы)
∫dx
= ∫ atdt
+ ∫
v0dt
Получаем
интеграл
x
= at2/2
+ x0
+ v0t.
Постоянные
интегрирования определяются из начальных
условий для координаты частицы и скорости
Следует
особо!!!!!! Отметить, что задаются
одновременно координата и скорость
частицы
Это
позволяет делать только классическая
механика
Пятый
этап — проверка полученного решения.
Прием
первый — проверка ответа по размерности.
Прием
второй — проверка ответа по заранее
очевидным результатам.
Редко
используемое и неточное выражение для
средней скорости
vср.
=(t)
t1
t2
∫
vdt
Движение
материальной точки под действием
постоянной силы –размерная задача
Прежде
всего, к такому типу движения относится
при определенных условиях движение под
действием силы тяжести. Сила тяжести,
как и любая сила, является векторной
величиной. Примем упрощающее предположение,
что
ее модуль постоянен. Но так как эта сила
направлена к центру Земли, то ее
направление в разных точках земной
поверхности различно. Однако при
исследовании движений тел, перемещающихся
на расстояния, которые намного меньше
радиуса Земли (R ~ 6000 км), можно
пренебречь
кривизной земной поверхности и с хорошей
точностью считать, что сила тяжести не
меняет своего направления, оставаясь
перпендикулярной этой поверхности. В
этих условиях сила тяжести может
рассматриваться постоянной как по
модулю, так и по направлению. Помимо
силы тяжести, с постоянными силами
приходится часто сталкиваться при
рассмотрении работы различных технических
устройств, когда их различные детали
испытывают действие постоянных сил со
стороны других деталей.
Какой
вид имеет траектория камня? От чего
зависит дальность полета? Аристотель
утверждал, например, что на начальном
участке траектория брошенного под углом
к вертикали тела является прямой линией,
и это, вроде бы, подтверждается
непосредственными наблюдениями.
Потребовалось почти два тысячелетия,
чтобы понять, что траектория на самом
деле является криволинейной на всех
участках полета.
Изучение
движения брошенного тела включает в
себя несколько этапов, характерных для
решения большинства задач механики.
Первый
этап — определение типа движения.
Второй
этап — физическая формулировка задачи:
выбор системы отсчета, определение
действующих сил и начальных условий.
любая
точка поверхности движется с ускорением,
обусловленным вращением Земли вокруг
своей оси и вокруг Солнца. Но для многих
практических задач этот эффект
«неинерциальности» является несущественным,
и мы будем полагать, что и в нашей задаче
этим эффектом можно пренебречь и считать
выбранную систему отсчета инерциальной.
В инерциальной системе отсчета справедлив
второй закон Ньютона , где теперь под F
подразумевается постоянная сила тяжести.
Мы изобразили эту силу на рис. 4.2 а для
некоторого произвольного момента
времени после начала движения, поместив
тело известной массы в некоторой
произвольной точке над поверхностью.
Истинное положение тела в различные
моменты времени, то есть траекторию его
движения, мы сможем определить только
после окончательного решения задачи.
рис 4.2
Третий
этап — математическая формулировка
задачи: запись уравнений,
соответствующих физической формулировке.
Уравнение D.3) содержит в качестве
неизвестных векторные величиныr(t)
и v(t). Поэтому оно фактически представляет
собой совокупность трех уравнений для
трех проекций вышеупомянутых величин.
Для
проекций радиуса-вектора тела введем
обозначения: rх= х,rу= у, rz = z.
Взяв проекции на оси координат от левой
и правой частей уравнения движения, мы
получаем три уравнения:
Справа
от каждого из уравнений записаны
начальные условия, являющиеся
неотъемлемыми
элементами физической и математической
формулировки задачи. Знак «минус» перед
mgв последнем уравнении
отражает тот факт, что сила тяжести
направлена в отрицательном направлении
осиOz.
Четвертый
этап — математическое решение задачи.Составляющая скоростиvzимеет вид:
Константу
определяем из условия
Интегрируем
еще раз:
Новую
константу определяем из условия z(0)
= 0.
окончательно
решение:
Найденные
выражения определяют зависимость от
времени всех трех проекций радиуса-вектора
тела, движущегося под действием силы
тяжести.
Тем
самым задача о нахождении траектории
движения решена.
достаточно
выразить tчерез х в первом
из равенств и подставить результат в
выражение дляz(t).
Это даетуравнение траекториив плоскостиzOx:
Из
геометрии известно, что это соотношение
представляет собой уравнение
параболической
кривой, и следовательно, ни на одном
из участков полета тела его траектория
не является прямой линией.
дальность
полетатела. При падении на поверхностьz= 0, и из этого условия
находим
Пятый
этап — проверка полученного решения.
Прием
первый — проверка ответа по размерности.
Прием
второй — проверка ответа по заранее
очевидным результатам.
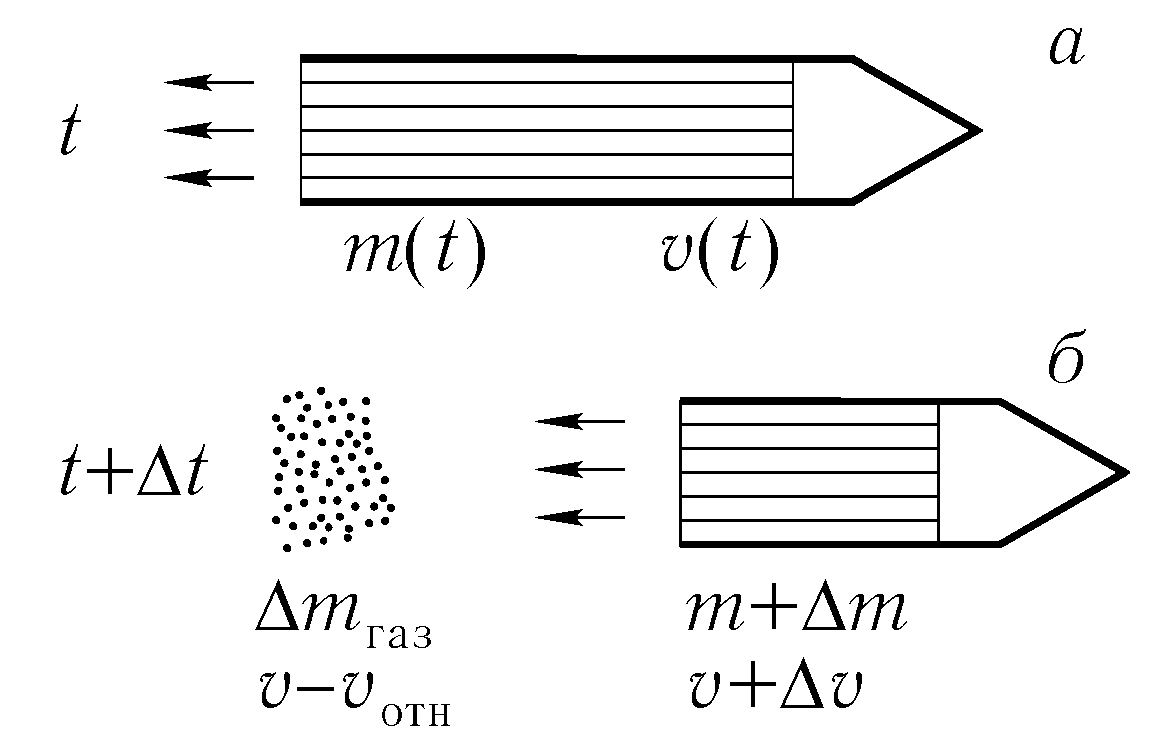
Движение
ракеты
Первый
этап — определение типа движения.
Второй
этап — физическая формулировка задачи:
выбор системы отсчета, определение
действующих сил и начальных условий.
Скорость
выброса газов относительно корпуса
ракеты-известна(конструкция сопла, тип
топлива, параметры горения)-это
относительная скорость.
Задача-найти
скорость ракеты, массу и т.д.
Третий
этап — математическая формулировка
задачи: запись уравнений,
Четвертый
этап — математическое решение задачи.
Формула
Циолковского
Пятый
этап — проверка полученного решения.
Прием
первый — проверка ответа по размерности.
Прием
второй — проверка ответа по заранее
очевидным результатам.
При
переменной во времени скорости истечения
Для
описания движения ракеты в поле Земли
следует добавить силу
Уравнение
Мещерского
Силы
Сила
– степень взаимодействия между объектами
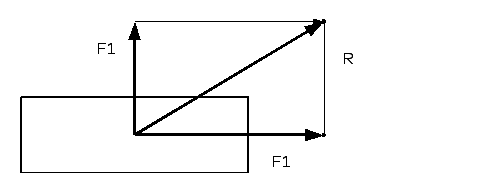
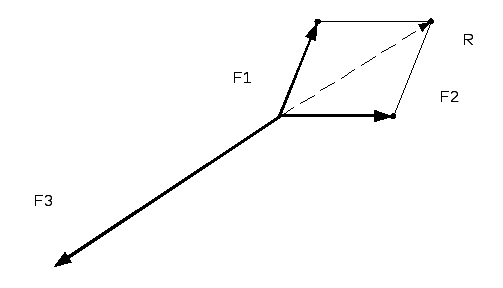
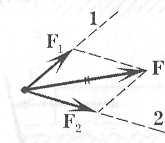
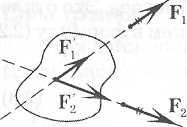
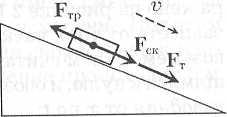
Разложение
сил
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
| Угловая скорость | |
|---|---|
 |
|
| Размерность | T −1 |
| Единицы измерения | |
| СИ | рад/с |
| СГС | рад/с |
| Другие единицы |
градус/с об/с об/мин |
Углова́я ско́рость — векторная величина, характеризующая быстроту и направление вращения материальной точки или абсолютно твёрдого тела относительно оси вращения. Модуль угловой скорости для вращательного движения совпадает с мгновенной угловой частотой вращения, а направление перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта. Строго говоря, угловая скорость представляется псевдовектором (аксиальным вектором), и может быть также представлена в виде кососимметрического тензора[1].
Угловая скорость в двухмерном пространстве[править | править код]
|
|
Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 августа 2016) |
Векторное представление в трёхмерном пространстве[править | править код]
В трёхмерном пространстве вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения за единицу времени:
а направлен по оси вращения согласно правилу буравчика, то есть в ту сторону, в которую ввинчивался бы буравчик или винт с правой резьбой, если бы вращался в эту сторону. Другой мнемонический подход для запоминания взаимной связи между направлением вращения и направлением вектора угловой скорости состоит в том, что для условного наблюдателя, находящегося на конце вектора угловой скорости, выходящего из центра вращения, само вращение выглядит происходящим против часовой стрелки.
Угловая скорость является аксиальным вектором (псевдовектором). При отражении осей системы координат компоненты обычного вектора (например, радиус-вектора точки) меняют знак. В то же время компоненты псевдовектора (в частности, угловой скорости) при таком преобразовании координат остаются прежними.
Тензорное представление[править | править код]
|
|
Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 августа 2016) |
Единицы измерения[править | править код]
Единица измерения угловой скорости, принятая в Международной системе единиц (СИ) и в системах СГС и МКГСС, — радиан в секунду (русское обозначение: рад/с, международное: rad/s)[2][Комм 1]. В технике также используются обороты в секунду, намного реже — градусы, минуты, секунды дуги в секунду, грады в секунду. Часто в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто на глаз, подсчитывая число оборотов за единицу времени.
Свойства[править | править код]
Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке
Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки (вектор угловой скорости направлен навстречу направлению взгляда наблюдателя)
Вектор мгновенной скорости любой точки абсолютно твёрдого тела, вращающегося с угловой скоростью 
где 


- В случае плоского вращения, то есть когда все векторы скоростей точек тела всегда лежат в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось вращения, то есть на прямую, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается. Однако в общем случае угловая скорость может менять со временем направление в трёхмерном пространстве, и такая упрощенная картина не работает.
- Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю). Равномерное вращение является частным случаем плоского вращения.
- Производная угловой скорости по времени есть угловое ускорение.
- Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчёта, отличающихся положением начала отсчёта и скоростью его движения, но двигающихся равномерно прямолинейно и поступательно друг относительно друга. Однако в этих инерциальных системах отсчёта может различаться положение оси или центра вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
- В случае движения точки в трёхмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:
где
— радиус-вектор точки (из начала координат),
— скорость этой точки,
— векторное произведение,
— скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы
подходящие по определению, по-другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как даёт разные
для каждой точки, а при вращении абсолютно твёрдого тела вектора угловой скорости вращения всех его точек совпадают). Однако в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.
- В случае равномерного вращательного движения (то есть движения с постоянным вектором угловой скорости) абсолютно твёрдого тела декартовы координаты точек вращающегося так тела совершают гармонические колебания с угловой (циклической) частотой, равной модулю вектора угловой скорости.
Связь с конечным поворотом в пространстве[править | править код]
Примечания[править | править код]
Комментарии[править | править код]
- ↑ Плоский угол, определяемый как отношение длины дуги окружности, заключённой между двумя радиусами, к длине радиуса, безразмерен, поэтому единицей измерения плоских углов является число «один», а единицей измерения угловой скорости в системе СИ — с−1. Однако, в случае плоских углов единице «один» присвоено специальное наименование «радиан» для того, чтобы в каждом конкретном случае облегчить понимание того, какая именно физическая величина имеется в виду[3].
Источники[править | править код]
- ↑ Ишлинский А. Ю. Классическая механика и силы инерции / Отв. ред. Б. В. Раушенбах. — М.: «Наука», 1987. — С. 239.
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 98. — 240 с. — ISBN 5-7050-0118-5.
- ↑ Units for dimensionless quantities, also called quantities of dimension one (англ.). SI Brochure: The International System of Units (SI). Международное бюро мер и весов (2006; обновлено в 2014). Дата обращения: 2016-1-29.
См. также[править | править код]
- Угловая частота
- Угловое ускорение
- Момент импульса
Литература[править | править код]
- Лурье А. И. Аналитическая механика. — М.: ГИФМЛ, 1961. — С. 100-136. — 824 с.
Что такое угловая скорость
Угловая скорость (обозначается как (omega)) — векторная величина, характеризующая скорость и направление изменения угла поворота со временем.
Модуль угловой скорости для вращательного движения совпадает с мгновенной угловой частотой вращения, а направление перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта.
Единица измерения
В Международной системе единиц (СИ) принятой единицей измерения угловой скорости является радиан в секунду (рад/с)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Формула угловой скорости
Вектор угловой скорости определяется отношением угла поворота ((varphi)) к интервалу времени ((mathcal t)), за которое произошел поворот:
(omega=frac{trianglevarphi}{trianglemathcal t})
Зависимость угловой скорости от времени
Зависимость (varphi ) от (mathcal t) наглядно показана на графике:
Угол, на который повернулось тело, характеризуется площадью под кривой.
Угловая скорость вращения, формула
Через частоту
(omega=2pimathcal n)
(mathcal n) — частота вращения ((1/с))
(pi) — число Пи ((approx 3,14))
(mathcal n=frac1T)
(T )— период вращения (время, за которое тело совершает один оборот)
Через радиус
(omega=frac vR)
(v) — линейная скорость(м/с)
(R) — радиус окружности (м)
Как определить направление угловой скорости
Направление скорости в физике можно определять двумя способами:
- Правило буравчика. Буравчик имеет правую резьбу (вращательное движение вправо при закручивании). Если вращать буравчик в направлении вращения тела, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.
- Правило правой руки. Представим, что взяли тело в правую руку. Следует направлять и вращать его туда, куда указывают четыре пальца. Отведенный в сторону большой палец покажет направление угловой скорости при этом вращении.
Связь линейной и угловой скорости
Линейная скорость ((v)) тела, расположенного на расстоянии (R) от оси вращения, прямо пропорциональна угловой скорости.
(v=Romega)
(R) — радиус окружности (м)
Чему равна мгновенная угловая скорость
Мгновенную угловую скорость нужно находить как предел, к которому стремится средняя угловая скорость при (trianglemathcal trightarrow0) :
(omega=lim_{trianglerightarrow0}frac{trianglevarphi}{trianglemathcal t})
Измеряется в рад/с
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
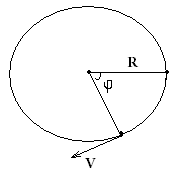
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
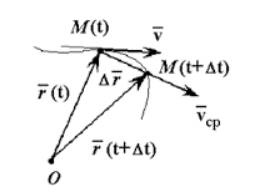
Мгновенная и средняя скорость
Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.
Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.
Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения ” open=” υ = ∆ r ∆ t ; ” open=” υ ↑ ↑ ∆ r .
Рисунок 1 . Средняя скорость сонаправлена перемещению
Модуль средней скорости по пути равняется ” open=” υ = S ∆ t .
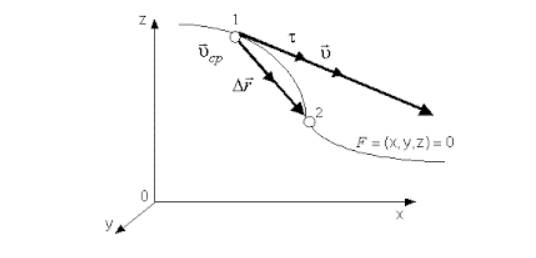
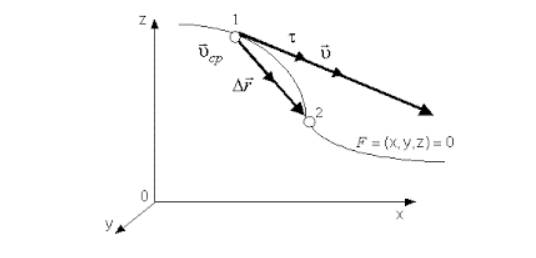
Мгновенная скорость точки. Формулы
Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.
Мгновенной скоростью называют предел, к которому стремится средняя скорость ” open=” υ при стремлении промежутка времени ∆ t к 0 :
υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ .
Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение d r совпадает с бесконечно малым элементом траектории d s .
Рисунок 2 . Вектор мгновенной скорости υ
Имеющееся выражение υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ в декартовых координатах идентично ниже предложенным уравнениям:
υ x = d x d t = x ˙ υ y = d y d t = y ˙ υ z = d z d t = z ˙ .
Перемещение и мгновенная скорость
Запись модуля вектора υ примет вид:
υ = υ = υ x 2 + υ y 2 + υ z 2 = x 2 + y 2 + z 2 .
Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r = r q 1 , q 2 , q 3 , тогда значение скорости запишется как:
υ = d r d t = ∑ i = 1 3 ∂ r ∂ q i ∂ q i ∂ r = ∑ i = 1 3 ∂ r ∂ q i q ˙ i .
Рисунок 3 . Перемещение и мгновенная скорость в системах криволинейных координат
При сферических координатах предположим, что q 1 = r ; q 2 = φ ; q 3 = θ , то получим υ , представленную в такой форме:
υ = υ r e r + υ φ e φ + υ θ φ θ , где υ r = r ˙ ; υ φ = r φ ˙ sin θ ; υ θ = r θ ˙ ; r ˙ = d r d t ; φ ˙ = d φ d t ; θ ˙ = d θ d t ; υ = r 1 + φ 2 sin 2 θ + θ 2 .
Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением d r = υ ( t ) d t
Дан закон прямолинейного движения точки x ( t ) = 0 , 15 t 2 – 2 t + 8 . Определить ее мгновенную скорость через 10 секунд после начала движения.
Решение
Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:
υ ( t ) = x ˙ ( t ) = 0 . 3 t – 2 ; υ ( 10 ) = 0 . 3 × 10 – 2 = 1 м / с .
Ответ: 1 м / с .
Движение материальной точки задается уравнением x = 4 t – 0 , 05 t 2 . Вычислить момент времени t о с т , когда точка прекратит движение, и ее среднюю путевую скорость ” open=” υ .
Решение
Вычислим уравнение мгновенной скорости, подставим числовые выражения:
υ ( t ) = x ˙ ( t ) = 4 – 0 , 1 t .
4 – 0 , 1 t = 0 ; t о с т = 40 с ; υ 0 = υ ( 0 ) = 4 ; ” open=” υ = ∆ υ ∆ t = 0 – 4 40 – 0 = 0 , 1 м / с .
Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0 , 1 м / с .
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/fizika/kinematika/mgnovennaja-i-srednjaja-skorost/
[/spoiler]
Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.
Обозначение угловой скорости: ω (омега).
Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.
С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.
Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:
Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.
Быстрота изменения угла φ (перемещения плоскости П из положения П1 в положение П2) – это и есть угловая скорость:
Приняв вектор k как единичный орт положительного направления оси, получим:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
- если известно количество оборотов n за единицу времени t:
- если задан угол поворота φ за единицу времени:
- если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
Размерности угловой скорости:
- Количество оборотов за единицу времени [об/мин], [c-1].
- Угол поворота за единицу времени [рад/с].
Определение угловой скорости
Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.
Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.
Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.
Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.
Другие примеры решения задач >
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:
Обозначение: ε (Эпсилон)
Единицы измерения углового ускорения: [рад/с2], [с-2]
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
Расчет углового ускорения
Пример: По заданному значению касательной составляющей полного ускорения aτ точки B, расположенной на расстоянии r от центра вращения колеса.
Требуется определить величину и направление углового ускорения колеса ε, если aτ = 10 м/с2, r = 50 см.
Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.
Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:
Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
ω = 1,5 с-1 = 9,42 рад/с.
Смотрите также:
- Примеры расчета угловой скорости и ускорения
- Скорости и ускорения точек вращающегося тела

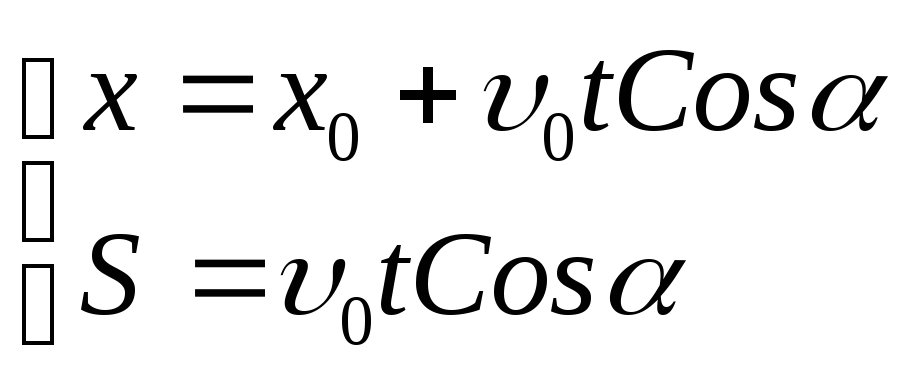
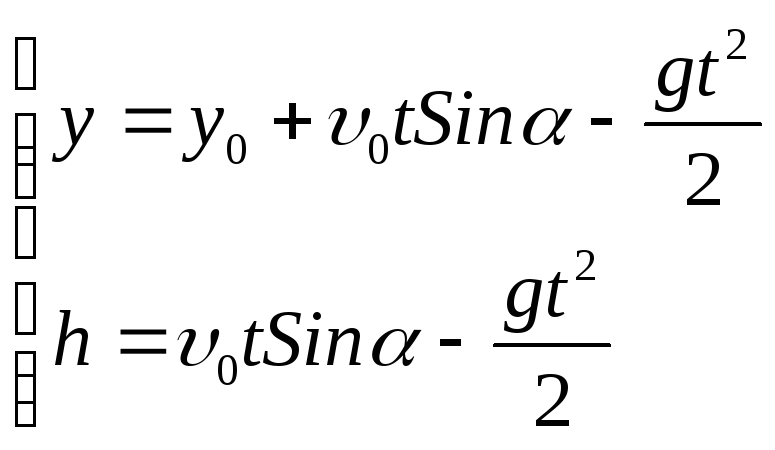
 ангенциальное
ангенциальное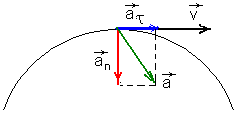

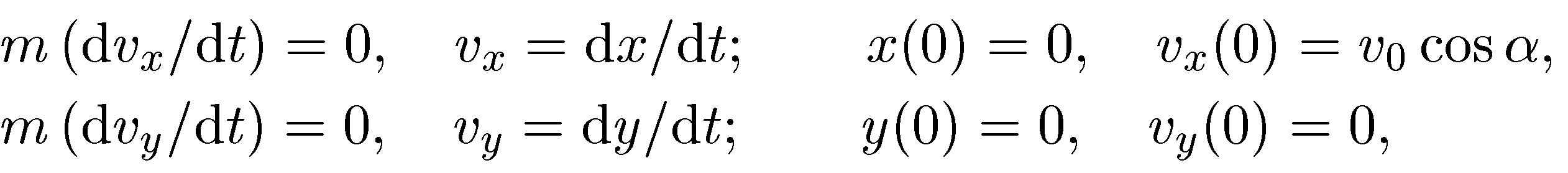
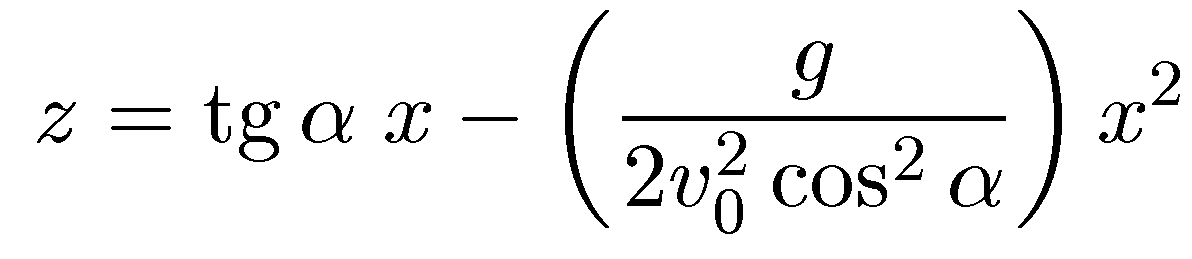
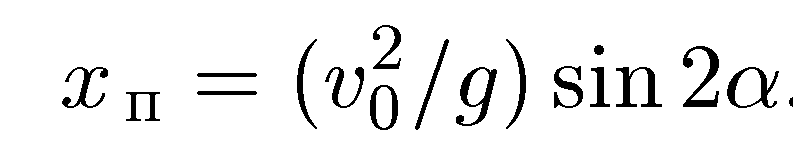
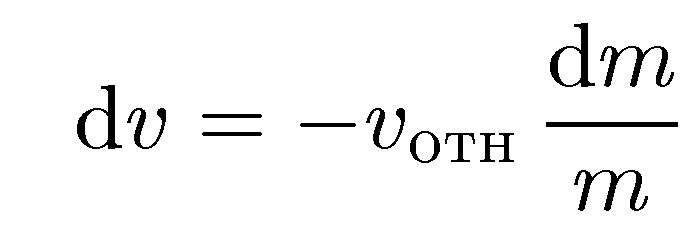
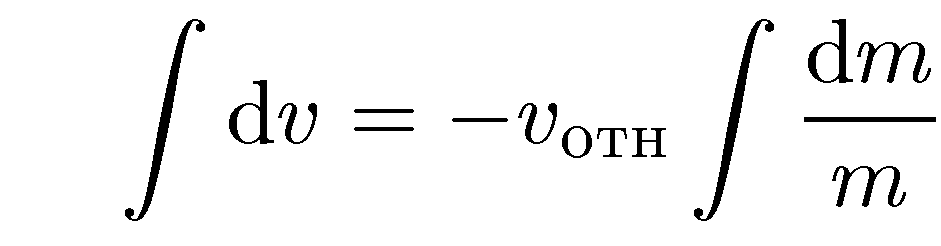






![{vec v}=[ {vec omega },{vec r} ],](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf77d103c0490cb68964169060fade3d70aeecab)