Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.
Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.
Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения υ=∆r∆t; υ↑↑∆r.
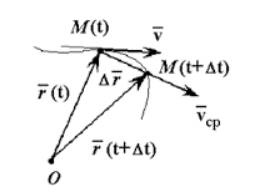
Рисунок 1. Средняя скорость сонаправлена перемещению
Модуль средней скорости по пути равняется υ=S∆t.
Мгновенная скорость точки. Формулы
Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.
Мгновенной скоростью называют предел, к которому стремится средняя скорость υ при стремлении промежутка времени ∆t к 0:
υ=lim∆t∆r∆t=drdt=r˙.
Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение dr совпадает с бесконечно малым элементом траектории ds.
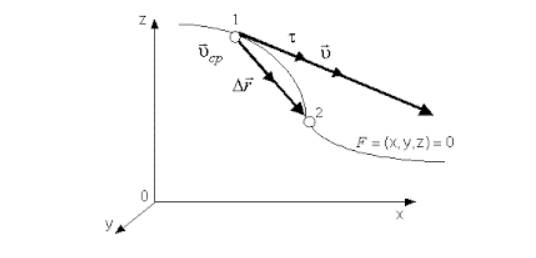
Рисунок 2. Вектор мгновенной скорости υ
Имеющееся выражение υ=lim∆t∆r∆t=drdt=r˙ в декартовых координатах идентично ниже предложенным уравнениям:
υx=dxdt=x˙υy=dydt=y˙υz=dzdt=z˙.
Перемещение и мгновенная скорость
Запись модуля вектора υ примет вид:
υ=υ=υx2+υy2+υz2=x2+y2+z2.
Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r=rq1, q2, q3, тогда значение скорости запишется как:
υ=drdt=∑i=13∂r∂qi∂qi∂r=∑i=13∂r∂qiq˙i.
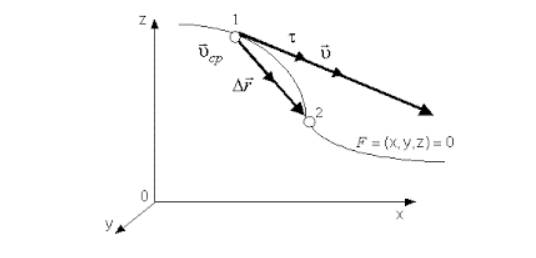
Рисунок 3. Перемещение и мгновенная скорость в системах криволинейных координат
При сферических координатах предположим, что q1=r; q2=φ; q3=θ, то получим υ, представленную в такой форме:
υ=υrer+υφeφ+υθφθ, где υr=r˙; υφ=rφ˙sin θ; υθ=rθ˙; r˙=drdt; φ˙=dφdt; θ˙=dθdt; υ=r1+φ2sin2θ+θ2.
Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением dr=υ(t)dt
Дан закон прямолинейного движения точки x(t)=0,15t2-2t+8. Определить ее мгновенную скорость через 10 секунд после начала движения.
Решение
Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:
υ(t)=x˙(t)=0.3t-2; υ(10)=0.3×10-2=1 м/с.
Ответ: 1 м/с.
Движение материальной точки задается уравнением x=4t-0,05t2. Вычислить момент времени tост, когда точка прекратит движение, и ее среднюю путевую скорость υ.
Решение
Вычислим уравнение мгновенной скорости, подставим числовые выражения:
υ(t)=x˙(t)=4-0,1t.
4-0,1t=0;tост=40 с;υ0=υ(0)=4;υ=∆υ∆t=0-440-0=0,1 м/с.
Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0,1 м/с.
В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.
Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.
Траектория, радиус-вектор, закон движения тела
Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.
Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.
Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.
Радиус-вектор – вектор, задающий положение точки в пространстве.
Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.
Перемещение и путь
Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.

В системе СИ перемещение и длина пути измеряются в метрах.
Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.
Скорость и ускорение
Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.
Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

В системе СИ скорость измеряется в метрах в секунду
Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.
Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.
Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Здесь R – радиус окружности, по которой движется тело.

Закон равноускоренного движения
Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Здесь – x нулевое- начальная координата. v нулевое – начальная скорость. Продифференцируем по времени, и получим скорость

Производная по скорости от времени даст значение ускорения a, которое является константой.
Пример решения задачи
Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.
Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.
Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.
Д

Рис. 2.7
вижения различных тел различаются
тем, что тела за одинаковые промежутки
(равные) времени проходят различные по
величине пути. Для характеристики такого
движения вводят понятие скорости.
1) Введем понятие
средней скорости (![]()
)
– это величина, равная отношению
перемещения
к тому промежутку времени, в течение
которого это перемещение произошло
![]()
.
2) За малый промежуток
времени t
точка проходит путь S,
совершая перемещение
(рис. 2.6). При t0
отношения
![]()
и
![]()
практически перестают изменяться как
по величине, так и по направлению и
стремятся к определенному пределу
![]()
и
![]()
который будет выражать
вектор мгновенной скорости,
т.е. скорости в данный момент времени.
В
математике данный предел называется
производной, следовательно, скорость
можно определить как производную
радиус-вектора движущейся точки по
времени:
![]()
или по модулю
![]()
.
При бесконечном
уменьшении t
различие между S
и
будет уменьшаться и в пределе они
совпадут, тогда можно записать, что
модуль скорости
![]()
, (2.1)
т.е. мгновенная скорость
при неравномерном движении численно
равна первой производной пути по времени.
Итак,
вектор мгновенной скорости в любой
точке траектории направлен по касательной
к траектории (и совпадает с направлением
вектора перемещения) и численно равен
первой производной пути по времени.
Единица
измерения v: [v]=м/с.
Если
рассматривать движение в пространстве,
то величину и направление вектора
скорости можно представить через
проекции этого вектора на направления
осей x, y, z
(рис. 2.7).
![]()
;
где
![]()
,
![]()
– единичные вектора по осям x,
y, z.
Тогда

Следовательно,
![]()
![]()
2.4. Путь при неравномерном движении.
З
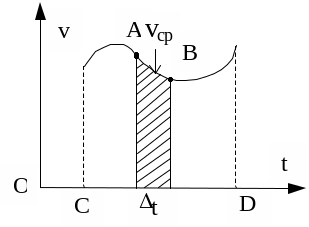
Рис. 2.8
а малый промежуток времени t
перемещение графически изображается
в виде прямоугольника, высота которого
равна некоторому значению средней
скорости v (рис.2.8). Тогда
для любого промежутка времени от 0 до t
суммируют все эти элементарные площадки
S,
т.е. графически эта сумма представляет
собой площадь фигуры ABCD
(vср.t).
Чаще всего площадь фигуры дает нам также
путь, пройденный при неравномерном
движении (математически это записывается
как предел).
![]()

.
Если v(t)
= const, то движение равномерное,
v(t)
const
– то движение неравномерное.
2.5.
Ускорение. Ускорение при равнопеременном
и неравнопеременном прямолинейном
движении.
При
неравномерном движении необходимо
знать закономерность, по которой скорость
изменяется со временем. Для этого
вводится величина, характеризующая
быстроту изменения скорости со временем
и называемая ускорением «![]()
».
П
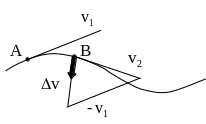
Рис.
2.9
усть материальная точка переместилась
за малый промежуток времени t
из точки А, где она имела скорость
![]()
в точку В, где скорость
![]()
(рис.2.9). Приращение скорости точки есть
вектор
![]()
,
равный разности конечной и начальной
скоростей:
![]()
.
О
Справка 1.

тношение изменения скорости к
промежутку времени, за который это
изменение произошло, называется
средним
ускорением
![]()
![]()
.
Это понятие
вводится для неравнопеременного
движения.
Среднее
ускорение направлено также как приращение
скорости, т.е. под углом к траектории в
сторону ее вогнутости.
В общем
случае величина среднего ускорения
может быть различной на различных
участках траектории и зависеть от
величины промежутка времени t,
по которому проводится усреднение. В
пределе при t
0
точка В будет стремиться к точке А и
среднее ускорение по пути АВ превратится
в мгновенное или истинное ускорение
в
точке А.
Поэтому
![]()
. (2.2)
Итак,
мгновенное ускорение движения в любой
точке траектории есть вектор, направленный
под углом к траектории в сторону ее
вогнутости, а по величине равный пределу
среднего ускорения при стремлении
промежутка времени к нулю.
Из выше
приведенных формул следует, что ускорение
измеряется в м/с2; [а] = м/с2.
По
модулю величина ускорения равна

.
Т.е. величина ускорения определяется
первой производной скорости v
по времени или второй производной пути
по времени.
Если
рассматривать движение тела в пространстве,
то вектор ускорения
можно представить через его проекции
на оси X, Y,
Z, аналогично как это
делали для вектора
![]()
.
![]()
;
![]()
Замечание:
Следует помнить, что ускорение
характеризует не только изменение
модуля скорости, но и изменение направления
вектора скорости. Например, равномерное
движение по окружности является
ускоренным из-за изменения направления
вектора скорости с течением времени,
хотя модуль скорости остается неизменным.
Рассмотрим
частный случай ускоренного движения.
Прямолинейное
движение с постоянным ускорением
называется равноускоренным (a
= const). В этом случае
мгновенное ускорение будет равно
среднему ускорению за любой промежуток
времени. И тогда

;
(2.3)

Рис. 2.10
В зависимости от поведения скорости
со временем различают равноускоренное
и «равнозамедленное» движения. Кавычки
поставлены, чтобы подчеркнуть, что в
любом случае движение происходит с
постоянным ускорением.
1. Если
а > 0, то движение равноускоренное.
Из (2.3) следует, что v=v0+a(t
– t0) и при t0
= 0
v=v0+at
при a
> 0 скорость v возрастает.
Направления
и
совпадают.
2. Если
a < 0, то движение
равнозамедленное и скорость v
уменьшается.
Зная
зависимость v от t
можно подсчитать путь, пройденный телом
при равнопеременном движении (рис.
2.10).
Имеем v=v0
+ at, домножим на dt.
dS = v·dt = v0·dt +
a·t·dt.
Интегрируем слева от
0 до S, справа от 0 до t.
Получаем, что

.
Тогда
![]()
. (2.4)
Данная формула верна,
если за время движения знаки начальной
скорости и ускорения совпадают. Наклон
прямой v0+at
на рисунке 2.10 зависит от величины «а»,
чем «а» больше, тем больше угол наклона.
«S» численно рано площади
заштрихованной фигуры.
|
ЛЕКЦИЯ 2 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Мгновенная и средняя скорость
Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.
Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.
Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения ” open=” υ = ∆ r ∆ t ; ” open=” υ ↑ ↑ ∆ r .

Рисунок 1 . Средняя скорость сонаправлена перемещению
Модуль средней скорости по пути равняется ” open=” υ = S ∆ t .
Мгновенная скорость точки. Формулы
Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.
Мгновенной скоростью называют предел, к которому стремится средняя скорость ” open=” υ при стремлении промежутка времени ∆ t к 0 :
υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ .
Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение d r совпадает с бесконечно малым элементом траектории d s .

Рисунок 2 . Вектор мгновенной скорости υ
Имеющееся выражение υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ в декартовых координатах идентично ниже предложенным уравнениям:
υ x = d x d t = x ˙ υ y = d y d t = y ˙ υ z = d z d t = z ˙ .
Перемещение и мгновенная скорость
Запись модуля вектора υ примет вид:
υ = υ = υ x 2 + υ y 2 + υ z 2 = x 2 + y 2 + z 2 .
Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r = r q 1 , q 2 , q 3 , тогда значение скорости запишется как:
υ = d r d t = ∑ i = 1 3 ∂ r ∂ q i ∂ q i ∂ r = ∑ i = 1 3 ∂ r ∂ q i q ˙ i .

Рисунок 3 . Перемещение и мгновенная скорость в системах криволинейных координат
При сферических координатах предположим, что q 1 = r ; q 2 = φ ; q 3 = θ , то получим υ , представленную в такой форме:
υ = υ r e r + υ φ e φ + υ θ φ θ , где υ r = r ˙ ; υ φ = r φ ˙ sin θ ; υ θ = r θ ˙ ; r ˙ = d r d t ; φ ˙ = d φ d t ; θ ˙ = d θ d t ; υ = r 1 + φ 2 sin 2 θ + θ 2 .
Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением d r = υ ( t ) d t
Дан закон прямолинейного движения точки x ( t ) = 0 , 15 t 2 – 2 t + 8 . Определить ее мгновенную скорость через 10 секунд после начала движения.
Решение
Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:
υ ( t ) = x ˙ ( t ) = 0 . 3 t – 2 ; υ ( 10 ) = 0 . 3 × 10 – 2 = 1 м / с .
Ответ: 1 м / с .
Движение материальной точки задается уравнением x = 4 t – 0 , 05 t 2 . Вычислить момент времени t о с т , когда точка прекратит движение, и ее среднюю путевую скорость ” open=” υ .
Решение
Вычислим уравнение мгновенной скорости, подставим числовые выражения:
υ ( t ) = x ˙ ( t ) = 4 – 0 , 1 t .
4 – 0 , 1 t = 0 ; t о с т = 40 с ; υ 0 = υ ( 0 ) = 4 ; ” open=” υ = ∆ υ ∆ t = 0 – 4 40 – 0 = 0 , 1 м / с .
Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0 , 1 м / с .
Формула средней скорости
Определение и формула средней скорости
Средней путевой скоростью материальной точки на отрезке времени $Delta t$называется скалярная физическая величина, равная отношению длины пути, пройденного точкой к промежутку времени, в течение которого данный путь пройден. Среднюю скорость обозначают:
$$langle vrangle, bar, v_$$
Математически определение средней скорости можно записать в следующем виде:
где $Delta s=s(t+Delta t)-s(t)$ – длина пути, которую прошла точка за время $Delta t$.
Если перейти к пределу при $Delta t rightarrow 0$ , получим:
средняя путевая скорость в пределе совпадает с величиной (модулем) мгновенной скорости точки в момент времени t.
При равномерном движении:
Вектор средней скорости
Вектором средней скорости $langlevecrangle$ материальной точки на отрезке времени $Delta t$называют величину, равную приращению радиус-вектора, который определяет положение данной точки к промежутку времени $Delta t$:
где $Delta bar$ – приращение радиус-вектора материальной точки.
Вектор средней скорости в пределе при $Delta t rightarrow 0$ совпадает с вектором скорости в момент времени t:
где $bar(t)$ – вектор мгновенной скорости токи.
Если точка совершает равномерное и прямолинейное движение, то выполняется равенство:
Средняя путевая скорость и модуль вектора средней скорости равны $(langle vrangle=|langlebarrangle|)$ только при прямолинейном движении. При всех остальных видах движения выполняется неравенство:
Единицы измерения
Основной единицей измерения средней скорости в системе СИ является: м/с
Примеры решения задач
Задание. Какова средняя скорость материальной точки за время ее движения, если точка прошла первую половину пути имея скорость v1, остальную часть пути данная точка 1/2 времени двигалась со скоростью v2, последний участок пути точка двигалась со скоростью v3.
Решение. В качестве основы для решения задачи формулу:
где время потраченное на путь ($Delta t$) делится на три части:
При этом имеют место следующие соотношения между отрезками пути, скоростью их преодоления и временем:
Ответ. $langle vrangle=frac<2 v_<1>left(v_<2>+v_<3>right)>+v_<3>+2 v_<1>>$

Задание. Какова средняя скорость частицы, движущейся по оси Xза время в течение которого, она пройдет первые s метров пути, если функция скорости задана уравнением: $v=A sqrt$, где A=const>0. Считать, что x=0 при t=0.
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для средней путевой скорости, так как движение прямолинейное, то средняя путевая скорость равна модулю вектора средней скорости. По условию задачи точка движется по оси X, тогда:
По условиям x(t=0)=0, среднюю скорость ищем, когда тело находится в точкеx=sследовательно, выражение (2.1) преобразуем к виду:
Найдем зависимость скорости от времени, исходя из определения мгновенной скоростидля движения точки по оси X:
Выразим из (2.2) x:
Так как движение происходит по оси X, то $x=s=frac t^<2>><4>$ . Выразим время, которое точка затратила на путьs :
Подставим время из (2.4) в формулу (2.2):
Ответ. $langle vrangle=frac <2>sqrt$
Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.
В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
[spoiler title=”источники:”]
http://www.webmath.ru/poleznoe/formules_21_34_srednjaja_skorost.php
[/spoiler]
Наталья Николаевна Пушкина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Средняя скорость
Если тело перемещается неравномерно, то описывая его движение в качестве одного из параметров можно воспользоваться средней скоростью движения на отдельных отрезках пути. Но такое описание дает очень приближенную, грубую характеристику перемещения. Поскольку находя средние скорости, мы проводим замену неравномерного движения на движение с постоянной скоростью на избранных отрезках пути, думая, что скорость изменяется скачкообразно при переходе от одного отрезка времени к другому. Графиком пути, отражающем перемещение тела, с постоянной скоростью, отличающейся на разных временных отрезках, станет ломаная линия, имеющая звенья с различным наклоном.
Допустим, что материальная точка перемещается вдоль прямой линии, которая не совпадает с осями координат. При этом ее положение определяет радиус- вектор $vec r_1$, соответствующий моменту времени $t_1$. В момент времени $t_2$ положение материальной точки в пространстве определяет вектор $vec r_2$.
Вектор перемещения нашей материальной точки определим как:
$Delta vec r=vec r_2-vec r_1(1).$
Определение 1
Средняя скорость материальной точки будет определена выражением:
$ vec v_{sr}=frac{Delta vec r}{Delta t}=frac{vec r_2-vec r_1}{t_2-t_1}(2).$
Из формулы (2) видно, что в ней происходит деление вектора на скаляр, в результате мы имеем вектор, направление которого совпадает с направлением вектора перемещения.
Векторы скорости и перемещения обладают одинаковыми направлениями.
Переход от средней скорости к мгновенной скорости
В выражении (2) средняя скорость найдена для отрезка времени, равного $Delta t$. Разделим данный временной отрезок на более мелкие. Если материальная точка перемещается неравномерно, то вновь найденные средние скорости будут отличаться, от средней скорости для всего отрезка $Delta t$. Уменьшим временной отрезок $Delta t$, станут меньше и отрезки времени внутри него. Средние скорости в уменьшенных промежутках времени будут отличаться от средней скорости на всем отрезке времени, но величина различия станет меньше.
«Мгновенная скорость» 👇
Устремим рассматриваемый промежуток времени к нулю (∆t→0), средняя скорость при этом устремится к предельному значению, которое называют мгновенной скоростью.
Определение 2
Мгновенной скоростью или скоростью в данный момент времени называют векторную величину, равную:
$vec v(t)= frac {dvec r}{dt}(3).$
Если тело перемещается равномерно, то мгновенная скорость его движения в каждый момент времени совпадает со скоростью этого движения. Говорят, что мгновенная скорость равномерного движения является постоянной.
Мгновенная скорость неравномерного перемещения – это переменный параметр, который принимает разные значения для разных моментов времени. При этом мгновенную скорость можно считать изменяющейся непрерывно на всем отрезке времени, на котором рассматривается движение.
Мгновенную скорость в каждый момент времени можно определить как тангенс угла наклона касательной к кривой – траектории движения в рассматриваемой точке.
Компоненты вектора мгновенной скорости в декартовой системе координат
В декартовой системе координат радиус-вектор запишем как:
$vec r(t)=x(t)vec i+y(t)vec j+z(t)vec k (4)$,
принимая во внимание, что единичные орты ($vec i ; vec j; vec k$) не изменяются во времени, и используя определение мгновенной скорости (3), получаем:
$vec v(t)=frac{dx}{dt}vec i+frac{dy}{dt}vec j+frac{dz}{dt}vec k (5).$
Из формулы (5) мы видим, что составляющие вектора скорости в декартовой системе координат задаются выражениями:
$ v_x=frac{dx}{dt} (6),$
$ v_y=frac{dy}{dt} (7),$
$ v_z=frac{dz}{dt} (8).$
При этом величину мгновенной скорости можно найти как:
$ v^2=v_x^2+v_y^2+v_z^2 (9).$
Направление мгновенной скорости
Будем описывать движение материальной точки через параметры траектории. При этом нам известны траектория движения точки и связь пути ($s$) и времени $t$. Путь отмеряется по траектории, от точки траектории, которую мы принимаем за начальную. При этом любая точка траектории характеризуется собственной величиной $s$. Из сказанного выше следует, что радиус-вектор – это функция от $s$, траекторию зададим уравнением:
$vec r = vec r(s)(10)$.
Получаем, что в определении мгновенной скорости (3) мы можем считать радиус – вектор как сложную функцию ($vec r(s(t))$). При этом ее производную найдем, применяя правило дифференцирования сложной функции:
$vec v=frac{dvec r}{dt}=frac{dvec r}{ds}frac{ds}{dt}(11)$,
где по определению мгновенной скорости ее величина равна: $v=frac{ds}{dt}$.
Обозначим $Delta s$ – расстояние между парой точек по траектории; $|Delta vec r|$– расстояние между рассматриваемыми точками по кратчайшему расстоянию (прямой). При сближении наших точек разница между $Delta s$ и $|Delta vec r|$ уменьшается, запишем:
$frac{dvec r}{ds}=lim_{Delta sto 0} (frac {Delta vec r}{Delta s})=lim_{Delta sto 0}(frac{Delta vec r}{|Delta r|}frac {|Delta r|}{Delta s})=vec tau (12).$
где $vec tau$ – единичный вектор, являющийся касательным к траектории движения точки.
Принимая во внимание сказанное выше выражение (12) для мгновенной скорости можно записать как:
$vec v=vvec tau$(13).
Из формулы (13) становится очевидно, что мгновенная скорость направлена по касательной к траектории движения материальной точки.
Рассматривая направления мгновенной скорости движения материальной точки подчеркнем, что:
- Мгновенная скорость материальной точки перемещающейся по прямой – это вектор, который направлен по траектории ее движения.
- При перемещении материальной точки по криволинейной траектории вектор мгновенной скорости имеет направление по касательной к траектории движения точки.
Скорость при равнопеременном движении
Самым простым способом неравномерного движения является равнопеременное перемещение тела, движение с постоянным ускорением. Это движение бывает:
- равноускоренным, если скорость и ускорение имеют одинаковые направления, при этом величина скорости увеличивается;
- равнозамедленное, при противоположном направлении скорости и ускорения, в этом случае скорость по модулю уменьшается.
При равнопеременном движении скорость в любой момент времени можно вычислить, если использовать выражение:
$vec v(t)=vec v_0+vec a bullet t (14),$
где $vec v_0$ – начальная скорость движения точки; $vec a$ – постоянное ускорения точки.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
