Как найти минимальное кодовое расстояние кода

Как найти минимальное кодовое расстояние кода

Корректирующие коды «на пальцах»

Время на прочтение
11 мин

Количество просмотров 62K

Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.

Давайте же разберёмся, что это такое.

Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.

Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.

Каналы с ошибкой

Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.

Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем $k$ ошибок. Это будет характеристикой канала связи.

Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами ($A$, $B$, $C$, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.

Кодирование и декодирование будем обозначать прямой стрелкой ($rightarrow$), а передачу по каналу связи — волнистой стрелкой ($rightsquigarrow$). Ошибки при передаче будем подчёркивать.

Например, пусть мы хотим передавать только сообщения $A=0$ и $B=1$. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):

$ begin{aligned} A &to 0,\ B &to 1. end{aligned} $

Передача по каналу, в котором возникла ошибка будет записана так:

$ A to 0 rightsquigarrow underline{1} to B. $

Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это $0$ и $1$.

Код с утроением

Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:

$ begin{aligned} A &to 00,\ B &to 11. end{aligned} $

Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:

$ A to 00 rightsquigarrow 0underline{1} to ?. $

Какие выводы мы можем сделать, когда получили $01$? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква $B$. А может, во втором, и была передана $A$.

То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.

$ begin{aligned} A &to 000,\ B &to 111. end{aligned} $

Проверим в деле:

$ A to 000 rightsquigarrow 0underline{1}0 to A?. $

Получили $010$. Тут у нас есть две возможности: либо это $B$ и было две ошибки (в крайних цифрах), либо это $A$ и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква $A$. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.

Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква $A$.

Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.

Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.

Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.

Расстояния между кодами

Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.

И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.

Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.

Пусть мы передавали $000$, а получили $001$. Видно, что эта цепочка больше похожа на исходные $000$, чем на $111$. А так как других кодовых слов у нас нет, то и выбор очевиден.

Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.

Можно ввести некоторую величину $d(alpha, beta)$, равную количеству различающихся цифр в соответствующих разрядах цепочек $alpha$ и $beta$. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.

Например, $d(010, 010) = 0$, так как все цифры в соответствующих позициях равны, а вот $d(010101, 011011) = 3$.

Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:

  1. Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
  2. Расстояние в обе стороны одинаково.
  3. Путь через третью точку не короче, чем прямой путь.

Достаточно разумные требования.

Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):

  1. $d(x, y) geqslant 0,quad d(x, y) = 0 Leftrightarrow x = y;$
  2. $d(x, y) = d(y, x);$
  3. $d(x, z) + d(z, y) geqslant d(x, y)$.

Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.

Окрестности

Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.

Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.

Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.

Так, скажем, окрестность кодового слова $000$ радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:

$ {000, 100, 010, 001}. $

Да, вот так странно выглядят шары в пространстве кодов.

А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим $000$! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.

Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение $x$, мы получим один из кодов, который принадлежит окрестности $x$ радиусом 2.

Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.

Сколько ошибок может исправить код?

Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.

В коде с удвоением между кодовыми словами $00$ и $11$ расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.

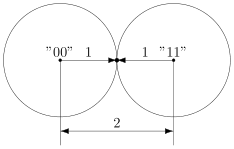
Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.

Что интересно, точек касания в нашем странном пространстве у шаров две — это коды $01$ и $10$. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.

В случае кода с утроением, между шарами будет зазор.

Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).

В общем случае получаем следующее.

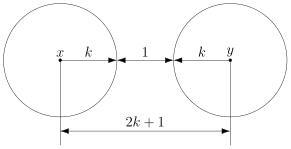
Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием $d_{min}$ будет успешно работать в канале с $k$ ошибками, если выполняется соотношение

$ d_{min} geqslant 2k+1. $

Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает $k$ ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса $k$ других кодовых слов. Математически это записывается так:

$d_{min}geqslant k + 1.$

Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.

$ begin{aligned} A to 10100,\ B to 01000,\ C to 00111,\ D to 11011.\ end{aligned} $

Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.

A B C D
A — 3 3 4
B 3 — 4 3
C 3 4 — 3
D 4 3 3 —

Минимальное расстояние $d_{min}=3$, а значит $3geqslant2k+1$, откуда получаем, что такой код может исправить до $k=1$ ошибок. Обнаруживает же он две ошибки.

Рассмотрим пример:

$ A to 10100 rightsquigarrow 101underline{1}0. $

Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.

$ begin{aligned} A:, d(10110, 10100) &= 1,\ B:, d(10110, 01000) &= 4,\ C:, d(10110, 00111) &= 2,\ D:, d(10110, 11011) &= 3. end{aligned} $

Минимальное расстояние получилось для символа $A$, значит вероятнее всего передавался именно он:

$ A to 10100 rightsquigarrow 101underline{1}0 to A?. $

Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.

Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.

Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы $2^5 = 32$ варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.

Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.

Интерлюдия: поле GF(2)

Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.

Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):

$ begin{aligned} 0 + 0 &= 0,\ 0 + 1 &= 1,\ 1 + 0 &= 1,\ 1 + 1 &= 0. end{aligned} $

Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.

Множество из двух элементов ${0, 1}$ с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.

У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.

$ x + x = 0. $

Это свойство прямо следует из определения.

$ x + y = x - y. $

А в этом можно убедиться, прибавив $y$ к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.

Проверяем корректность

Вернёмся к коду с утроением.

$ begin{aligned} A &to 000,\ B &to 111. end{aligned} $

Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.

Пусть мы приняли вектор-строку $x$ из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)

$dots rightsquigarrow x = (x_1, x_2, x_3). $

Математически равенство всех трёх цифр можно записать как систему:

$ left{ begin{aligned} x_1 &= x_2,\ x_2 &= x_3. end{aligned} right. $

Или, если воспользоваться свойствами сложения в GF(2), получаем

$ left{ begin{aligned} x_1 + x_2 &= 0,\ x_2 + x_3 &= 0. end{aligned} right. $

Или

$ left{ begin{aligned} 1cdot x_1 + 1cdot x_2 + 0cdot x_3 &= 0,\ 0cdot x_1 + 1cdot x_2 + 1cdot x_3 &= 0. end{aligned} right. $

В матричном виде эта система будет иметь вид

$ Hx^T = 0, $

где

$ H = begin{pmatrix} 1 & 1 & 0\ 0 & 1 & 1 end{pmatrix}. $

Транспонирование здесь нужно потому, что $x$ — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.

Будем называть матрицу $H$ проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.

Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.

Кодирование

Итак, у нас есть система для проверки

$ left{ begin{aligned} x_1 + x_2 &= 0,\ x_2 + x_3 &= 0. end{aligned} right. $

Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице $H$) найдём кодовые слова.

Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:

$ H = begin{pmatrix} 1 & 0 & 1 & 0 & 0 \ 0 & 1 & 1 & 0 & 1\ 0 & 0 & 0 & 1 & 1 end{pmatrix}. $

Соответствующая система имеет вид:

$ left{ begin{aligned} x_1 + x_3 &= 0,\ x_2 + x_3 + x_5 &= 0,\ x_4 + x_5 &= 0. end{aligned} right. $

Чтобы найти кодовые слова соответствующего кода нужно её решить.

В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если $a$ и $b$ — решения системы, то для их суммы верно

$H(a+b)^T=Ha^T+Hb^T=0+0=0,$

что означает, что она тоже — решение.

Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.

Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить $x_1, x_2, x_4$.

Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.

Итак, получаем:

$ left{ begin{aligned} x_1 &= x_3,\ x_2 &= x_3 + x_5,\ x_4 &= x_5. end{aligned} right. $

Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.

$ begin{aligned} x_3=1, x_5=0:quad x_1=1, x_2=1, x_4=0 Rightarrow x^{(1)} = (1, 1, 1, 0, 0),\ x_3=0, x_5=1:quad x_1=0, x_2=1, x_4=1 Rightarrow x^{(2)} = (0, 1, 0, 1, 1). end{aligned} $

Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:

$ a_1 x^{(1)}+a_2 x^{(2)}, $

где $a_1, a_2$ равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно $2^2=4$ сочетания.

Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.

$ (a_1, a_2)cdot begin{pmatrix} 1 & 1 & 1 & 0 & 0 \ 0 & 1 & 0 & 1 & 1 end{pmatrix} = aG. $

Строчки здесь — линейно независимые решения, которые мы получили. Матрица $G$ называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:

$ a to aG. $

Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)

$ begin{aligned} 00 &to 00000,\ 01 &to 01011,\ 10 &to 11100,\ 11 &to 10111. end{aligned} $

Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?

$ a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to Hx^T = (110)^T neq 0. $

А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!

Для кода с утроением, кстати, порождающая матрица выглядит очень просто:

$G=begin{pmatrix}1&1&1end{pmatrix}.$

Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.

Ошибка по синдрому

Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!

Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение $x$, а было отправлено кодовое слово $v$. Тогда вектор ошибки по определению

$ e = x - v. $

Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:

$ begin{aligned} v &= x + e,\ x &= v + e. end{aligned} $

В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.

Как мы уже говорили раньше, если мы получили сообщение $x$ с ошибкой, то $Hx^Tneq 0$. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?

Назовём результат умножения на проверочную матрицу синдромом:

$ s(x)=Hx^T.$

И заметим следующее

$ s(x) = Hx^T = H(v+e)^T = He^T = s(e). $

Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.

Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?

А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.

Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.

$s(x)$ $x$
$000$ $underline{00000}, 11100, 01011, 10111$
$001$ $underline{00010}, 11110, 01001, 10101$
$010$ $underline{01000}, 10100, 00011, 11111$
$011$ $01010, 10110, underline{00001}, 11101$
$100$ $underline{10000}, 01100, 11011, 00111$
$101$ $underline{10010}, 01110, 11001, underline{00101}$
$110$ $11000, underline{00100}, 10011, 01111$
$111$ $11010, underline{00110}, underline{10001}, 01101$

В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.

Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.

Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.

$ a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to s(x)=Hx^T = (110)^T to e=(00100). $

Вектор ошибки равен $(00100)$, а значит ошибка в третьем разряде. Как мы и загадали.

Ура, всё работает!

Что же дальше?

Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.

Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.

Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.

Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.

Источник

Понятие о минимальном кодовом расстоянии

Одним из основных понятий, на котором базируется любая теория помехоустойчивого
кодирования, является понятие о кодовом расстоянии вообще и о минимальном
кодовом расстоянии в частности.

Пример. Допустим, m = 8, и сообщения
закодированы простым неизбыточным двоичным кодом. Тогда из выражения M
= 2n = 2m следует m

= n = 3. Список рабочих комбинаций имеет следующий вид:

Изобразим так называемую геометрическую модель кода, вводя систему координат
из трех осей, каждая из которых отображает один из разрядов. Модель кода
– куб (рис.25). Каждая кодовая комбинация отображается одной из вершин
куба. Будем называть ребро кубы, определяющее две соседние кодовые комбинации,
одним кодовым переходом и рассматривать как единичное расстояние
между двумя соседними кодовыми комбинациями. Кодовым расстоянием
между парой любых кодовых комбинаций будем называть минимальное число ребер
(кодовых переходов), разделяющих эти комбинации:

кодовых переходов .

Например,

Рис. 25 Геометрическая модель двоичного трехразрядного кода

Понятие минимального кодового расстояния характеризует код в целом.
Минимальным кодовым расстоянием dmin
является минимум среди всех кодовых расстояний данного кода, то есть определяется
по всем возможным парам кодовых комбинаций данного кода

Для рассматриваемого кода dmin= 1. Учитывая, что рассматриваемый код по построению является неизбыточным,
можно утверждать, что любой неизбыточный код имеет dmin= 1 и наоборот, если dmin= 1, код является неизбыточным.

Из геометрической модели кода видно, что любая, даже одиночная, ошибка
не может быть обнаружена кодом с dmin= 1, так как любая кодовая комбинация, в которой произошла ошибка,
переместившись на один кодовый переход, совпадет с соседней кодовой комбинацией
и будет разрешенной.

Для построения простейшего избыточного кода, который может обнаруживать
одну ошибку (r = 1) нужно отобрать рабочие
комбинации на расстоянии

В рассматриваемом коде можно выбрать следующие комбинации:

где MРАБ
– число рабочих комбинаций.

Избыточность полученного кода

.

Если требуется обнаруживать две ошибки (r =
2), то рабочих комбинаций будет только две (например, 000 и 111), минимальное
кодовое расстояние в этом случае dmin
= 3, избыточность

.

Если r = 3, dmin≥ 4, что невозможно обеспечить в рассматриваемом
коде, так как кодовое расстояние

.

Если бы сообщения кодировались неизбыточным кодом, то для получения
четырех кодовых комбинаций потребовалось бы m =
2 информационных элементов.

В двоичных кодах кодовое расстояние между любыми двумя комбинациями
можно определить как число отличающихся разрядов.

В общем случае в кодах, используемых в режиме обнаружения ошибок кратности
r должно обеспечиваться минимальное кодовое
расстояние

dmin ≥ r + 1. (4)

Определим минимальное кодовое расстояние в кодах, работающих в режиме
исправления s ошибок.

Для исправления s ошибок нужно, очевидно,
искаженную кодовую комбинацию bi
отождествить с комбинацией ai, которая
является рабочей и из которой bi

получилась в результате s искажений. Такое
отождествление производится на базе критерия правдоподобия, под которым
понимается

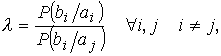
где P(bi / ai) – вероятность образования bi из

ai;

P(ai / bi) – вероятность образования ai из

bi.

λ сравнивается с некоторым
пороговым значением, чаще всего с единицей. Если λ > 1,
то выносится решение о том, что bi
получилось из ai. Если λ < 1,
то выносится решение о том, что bi

нельзя отождествлять с ai.

Значения условных вероятностей, необходимых для вычисления λ,
нельзя установить непосредственно, но можно воспользоваться связью между
ними и соответствующими кодовыми расстояниями. Из факта уменьшения вероятности
появления ошибки при увеличении ее кратности следует:

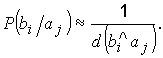
Кодовое расстояние между bi и

ai равно

.

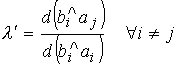Если , то bi
получилось из aj, так как ai

ближе к bi, чем ai.
Если , то bi
получилось из ai.

Геометрически этот результат можно интерпретировать следующим образом:

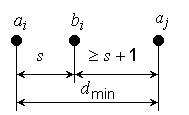
Минимальное расстояние кода, работающего в режиме исправления s
ошибок,

dmin ≥ 2s + 1. (5)

По аналогии можно утверждать, что код, способный обнаруживать r
ошибок и исправлять s из них, должен иметь
минимальное кодовое расстояние

dmin ≥ r + s + 1 (r ≥

s). (6)

Выражения (5) и (6) не противоречат друг другу, так как прежде чем исправлять
ошибку, ее надо сначала обнаружить

Можно показать, что для исправления e ошибок
стирания нужно обеспечить минимальное кодовое расстояние

dmin ≥ e + 1. (7)

В общем случае для обнаружения r ошибок
трансформации, исправления s из них и для исправления
e ошибок стирания нужно обеспечить минимальное
кодовое расстояние

dmin ≥ r + s + e + 1 (r ≥

s). (8)

Выражения (4) – (7) вытекают из (8).

Источник

При взаимно
независимых ошибках наиболее вероятен
переход в кодовую комбинацию, отличающуюся
от данной в наименьшем числе символов.

Степень
отличия любых двух кодовых комбинаций
характеризуется расстоянием между ними
в смысле Хэмминга
или просто
кодовым
расстоянием.

Кодовое
расстояние выражается числом символов,
в которых комбинации отличаются одна
от другой, и обозначается через d.

Чтобы
получить кодовое расстояние между двумя
комбинациями двоичного кода, достаточно
подсчитать число единиц в сумме этих
комбинаций по модулю 2.
Например

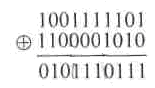
Минимальное
расстояние, взятое по всем парам кодовых
разрешенных комбинаций кода, называют
минимальным
кодовым расстоянием.

Более
полное представление о свойствах кода
дает матрица
расстояний
D,
элементы которой dij
(i,j
= 1,2,…,n)
равны расстояниям между каждой парой
из всех m
разрешенных комбинаций.

Пример:
Представить симметричной матрицей
расстояний код X1
= 000; Х2 = 001; Х3 = 010;X4=111

Решение.
. Минимальное кодовое расстояние для
кода d=1.

Это вытекает из
рассмотрения симметричная матрицы
всех возможных кодовых расстояний между
словами кода.

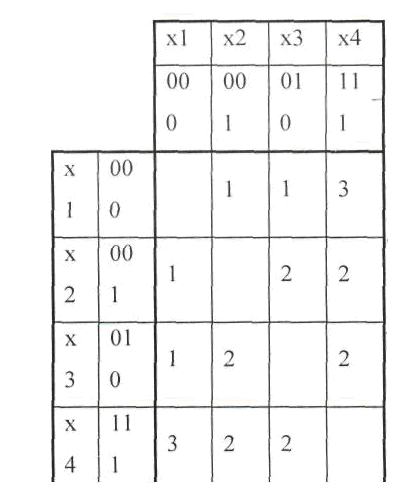
Таблица
5.1

Декодирование
после приема производится таким образом,
что принятая кодовая комбинация
отождествляется с той разрешенной,
которая находится от нее на наименьшем
кодовом расстоянии.

Такое
декодирование называется декодированием
по методу
максимального правдоподобия.

Лекция 6.

6.1 Корректирующие свойства кодов с избыточностью.

Рассмотрим сущность
помехоустойчивого кодирования на уже
рассмотренном на предыдущей лекции
рисунке

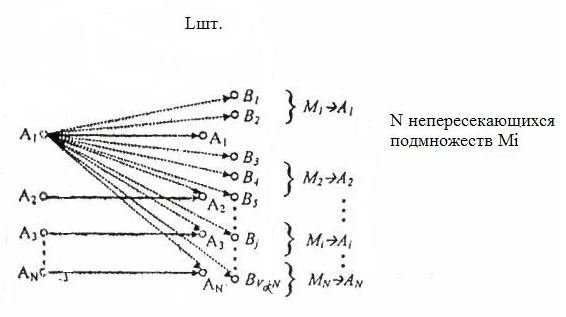
На
этом рисунке через Ai
(N
шт.)обозначенные
разрешеные кодовые слова, Bj
(L–N)шт.запрещенные
слова, а Mi
(Nшт.)
некоторые подмножества, элементами
которых являются те или
другие запрещенные кодовые слова.

Из
рисунка видно, что при передаче кодовой
комбинации Ai
она может под воздействием помех
перейти в одну из комбинаций Bj,
то есть ошибка может быть выявлена (L–N)
случаях из общего количества
L
кодовых
слов. Так происходит каждый раз, когда
передается любая из N
разрешенных
кодовых комбинаций. Общее количество
ошибочных комбинаций, которые
обнаруживаются ,
равняется N(L–1)
а
общее количество возможных комбинаций
L*N
поэтому часть
ошибочных комбинаций, которые
обнаруживаются , равняется

µ=1-(N/L);

Аналогичный
прием используется и для исправления
ошибок. Для использования кода как
корректирующего
надо разбить множества Bj
всего
(L–N)шт.запрещенных
кодовых
комбинаций –на
N
непересекающихся
подмножеств
Mi.
Каждое из подмножеств Mi
приписывается одному из кодовых слов
Ai
. Способ корректировки или исправления
ошибок заключается в том, что когда
принятая комбинация Bj
принадлежит
Мi,
тогда считается, что передана комбинация
Аi.
При таком способе декодирования
существует возможность исправления
ошибок.

Из
рисунка видно, что при любом способе
разбития ошибка может быть исправлена
в L–N
(для Bj)
случаях
и обнаружена
в
N(L–N)
случаях.
Отношение количества ошибочных
комбинаций, которые
исправляются, к количеству ошибочных
комбинаций равно 1/N.

Наконец,
определим, что количество -ошибок,
которые не исправляются равняется
N*(N-1)
,при
этом часть некорректируемых ошибок по
отношению к общему количеству последствий
равняется (N-1)/L.
Отмеченные результаты имеют общий
характер и верны для всех корректирующих
кодов.

Мы говорили о
корректирующих свойствах кодов с
избыточностью.

Рассмотрим
теперь простые примеры, которые связывают
кодовое расстояние d
с корректируюшими свойствами кода.

Очевидно,
что при кодовом расстоянии d=1
все кодовые комбинации являются
разрешенными.

Например,
при n=3
разрешенные комбинации образуют
следующее множество:

000,001,010,011,
100,
101, 110, 111
с кодовым расстоянием d=1.

Любая
одиночная ошибка трансформирует данную
комбинацию в другую разрешенную
комбинацию. Это случай безызбыточного
кода, не обладающего корректирующей
способностью.

Если
d
= 2,
то ни одна из разрешенных кодовых
комбинаций при одиночной ошибке не
переходит в другую разрешенную комбинацию.
Например, подмножество разрешенных
кодовых комбинаций может быть образовано
по принципу четности в нем числа
единиц. Например, для n=3,
d=2:

011,
101,
110-разрешенные
комбинации;

010,
100,
111
– запрещенные комбинации.

При
любой одиночной ошибке разрещенная
комбинация преращается в запрещенную.
Код
обнаруживает одиночные ошибки, а также
другие ошибки нечетной кратности .

В
общем случае при необходимости
обнаруживать ошибки кратности до г
включительно
минимальное хэммингово расстояние
между разрешенными кодовыми комбинациями
должно быть по крайней мере на единицу
больше r,
т.е d
>r+1.

Действительно,
в этом случае ошибка, кратность которой
не превышает r,
не в состоянии перевести одну разрешенную
кодовую комбинацию в другую.

Для
исправления
одиночной
ошибки кодовой комбинации необходимо
сопоставить подмножество запрещенных
кодовых комбинаций множеству исходных
кодовыхкомбинаций.

Чтобы
эти подмножества не пересекались,
хэммингово расстояние между разрешенными
кодовыми комбинациями должно быть не
менее трех. При n=3
за разрешенные кодовые комбинации
можно, например, принять 000
и 111
с d=3.
Тогда разрешенной комбинации 000
необходимо приписать подмножество
запрещенных кодовых комбинаций 001,
010,
100,
образующихся в результате двоичной
ошибки в комбинации 000.

Подобным
же образом разрешенной комбинации 111
необходимо приписать подмножество
запрещенных кодовых комбинаций: 110,
011,
101,
образующихся в результате возникновения
единичной ошибки в комбинации 111:

Разрешенной
комбинации 000
соответствуют запрещенные комбинации
001
010
100.

Если
принято любое кодовое слово из этого
набора, то по принципу максимального
правдоподобия можно предположить, что
передавалось кодовое слово 000.

Разрешенной
комбинации 111
соответствуют запрещенные комбинации
011
101
110.

Если
принято любое кодовое слово из этого
набора, то по принципу максимального
правдоподобия передавалось кодовое
слово 111.

Таким
образом для кода 000
и 111
с d=3
может быть исправлена одна ошибка.

В
общем случае для обеспечения возможности
исправления всех ошибок кратности до
s
включительно каждая из ошибок должна
приводить к запрещенной комбинации,
относящейся
к подмножеству исходной разрешенной
кодовой комбинации.

Ошибка
будет не только обнаружена, но и
исправлена, если искаженная комбинация
остается ближе к первоначальной, чем к
любой другой разрешенной комбинации,
то есть должно быть:

d>=2S+1;

Рассмотрим
геометрическую интерпретацию кодового
расстояния d
и его связь с числом обнаруживаемых и
исправляемых ошибок.

Для
выявления произвольных ошибок, которые
изменяют в кодовых словах, , не больше
r символов,
необходимо и достаточно, чтобы никакие
r-кратные
ошибки не переводили одно кодовое слово
кода в другое, смотри рисунок.

Это
условие будет выполнено, если кодовые
комбинации выбраны так, что среди
них нет таких, которые находятся на
расстоянии, меньше чем r+1.
Если такой
код использован для кодировки сообщения,
тогда принятое кодовое слово Y,
которого нет в списке разрешенных слов,
является признаком обнаружением ошибки.
Рассмотренные
ранее 4
комбинации –000,
011,
101,
110,-
представляют код с обнаружением
одиночной ошибки, потому что для них
кодовое расстояние d
= 2.
Для
того, чтобы код исправлял все ошибки,
кратность которых не превосходит
s,.векторы
каждой пары Xi,
Xj
должны находиться один от другого на
расстоянии, не
меньшем чем 2s+1.

В
общем случае для выявления ошибок
кратности r,
одновременного
исправления ошибок кратности s
необходимо
и достаточно выполнение условия

d>=r+s+1.

Кодовое
расстояние лишь частично характеризует
качество кода, потому что кроме ошибок,
которые полностью исправляются или
обнаруживаются, часто обнаруживаются
или исправляются ошибки большей
кратности.

Рассмотрим
понятие качества корректирующего кода
более подробно.

Одной из основных
характеристик корректирующего кода
является избыточность кода, указывающая
степень удлинения кодовой комбинации
для достижения определенной корректирующей
способности.

Если
на каждые n
символов выходной последовательности
кодера канала приходится k
информационных и r
проверочных, то относительная избыточность
кода может быть выражена как:

ρ
=(n–k)/n=r/n=0…1;

Коды, обеспечивающие
заданную корректирующую способность
при минимально возможной избыточности,
называют оптимальными.

В
связи с нахождением оптимальных кодов
оценим, например, возможное наибольшее
число Q
разрешенных или информационных комбинаций
n-значного
двоичного кода, обладающего способностью
исправлять взаимно независимые ошибки
кратности до
s включительно.
Это равносильно отысканию числа
комбинаций, кодовое расстояние между
которыми не менее d=2s+l.

Общее
число различных
исправляемых ошибок
для каждой разрешенной комбинации
составляет

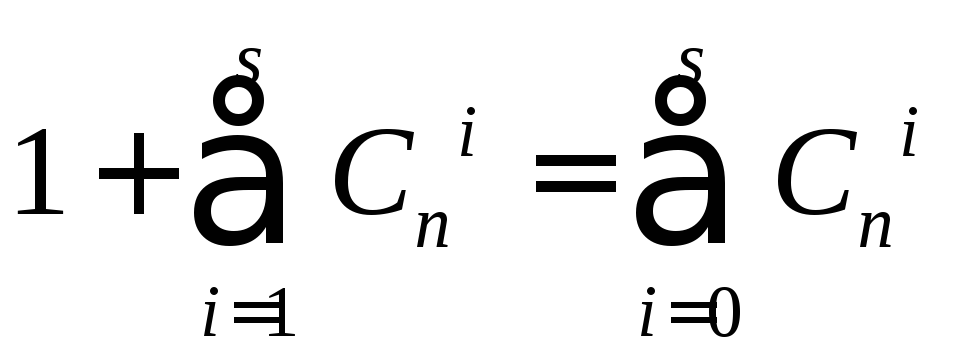
где
Сni–
число ошибок кратности i<s.

Каждая
из таких ошибок должна приводить к
запрещенной комбинации, входящей в
подмножество Mi
для данной разрешенной комбинации.
Совместно с этой разрешенной комбинацией
подмножество включает всего вот столько
комбинаций.

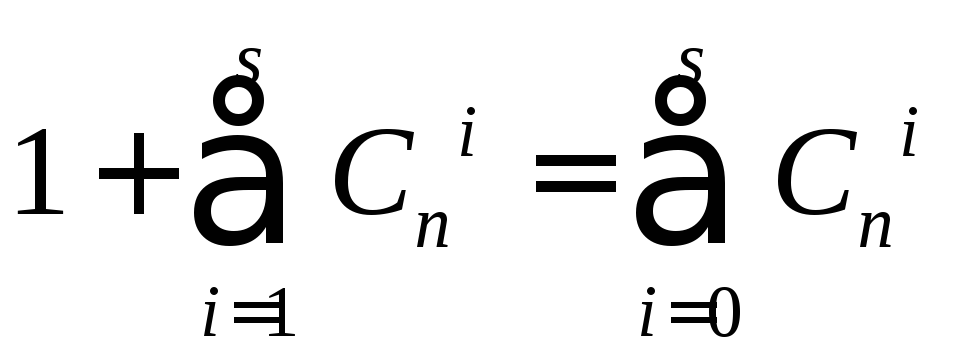
Однозначное
декодирование возможно только в том
случае, когда указанные
подмножества
не пересекаются. Так как общее число
различных комбинаций n–
значного
двоичного кода составляет 2n,
то число
разрешенных комбинаций не может превышать

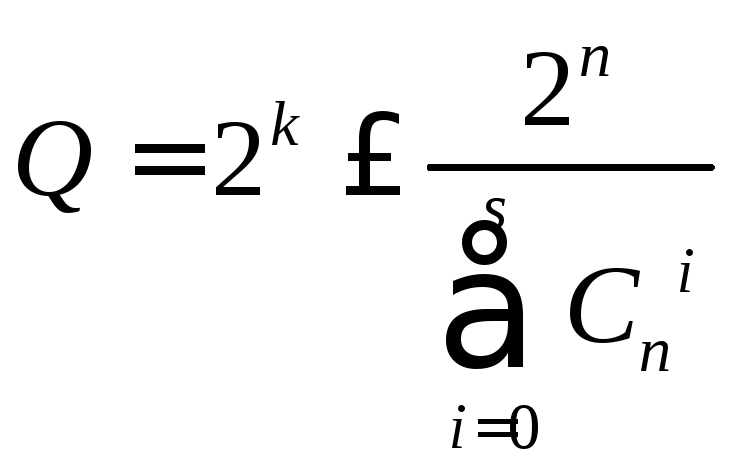
Эта
верхняя оценка найдена Хэммингом. Для
некоторых конкретных значений кодового
расстояния d,
соответствующие Q
укажем в таблице:

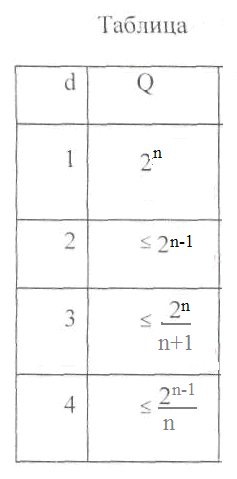
Коды,
для которых в приведенном соотношении
достигается равенство, называют также
плотно
упакованными.

Однако
не всегда целесообразно стремиться к
использованию кодов, близких к оптимальным.
Необходимо учитывать другой, не менее
важный показатель качества корректирующего
кода – сложность технической реализации
процессов кодирования и декодирования.
Здесь должен искаться компромисс между
корректирующими свойствами кода и
сложностью технической реализации.

Если
информация должна передаваться но
медленно действующей и дорогостоящей
линии связи, а кодирующее и декодирующее
устройства предполагается
выполнить на высоконадежных и
быстродействующих элементах, то сложность
этих устройств не играет существенной
роли. Решающим фактором в этом случае
является повышение эффективности
пользования линией связи, поэтому
желательно применение корректирующих
кодов с минимальной избыточностью.

Если же корректирующий
код должен быть применен в системе,
выполненной на элементах, надежность
и быстродействие которых равны или
близки надежности и быстродействию
элементов кодирующей и декодирующей
аппаратуры. Это возможно, например, для
повышения достоверности воспроизведения
информации с запоминающего устройства
ЭВМ. Тогда критерием качества
корректирующего кода является надежность
системы в целом, то есть с учетом возможных
искажений и отказов в устройствах
кодирования и декодирования. В этом
случае часто более целесообразны коды
с большей избыточностью, но простые в
технической реализации.

Источник
Определение:
Линейный код (англ. Linear code) — код фиксированной длины (блоковый код), исправляющий ошибки, для которого любая линейная комбинация кодовых слов также является кодовым словом.

Линейные коды обычно делят на блоковые коды и свёрточные коды. Также можно рассматривать турбо-коды, как гибрид двух предыдущих.[1]

По сравнению с другими кодами, линейные коды позволяют реализовывать более эффективные алгоритмы кодирования и декодирования информации (см. синдромы ошибок).

Содержание

  • 1 Формальное определение
  • 2 Порождающая матрица
  • 3 Проверочная матрица
  • 4 Кодирование и декодирование, примеры
    • 4.1 Пример
  • 5 Минимальное расстояние и корректирующая способность
  • 6 Синдромы и метод обнаружения ошибок в линейном коде
  • 7 Преимущества и недостатки линейных кодов
  • 8 Примечания
  • 9 Источники информации

Формальное определение

Определение:
Линейный код длины и ранга является линейным подпространством размерности векторного пространства , где — конечное поле (поле Галуа) из элементов. Такой код с параметром называется -арным кодом (напр. если  — то это 5-арный код). Если или , то код представляет собой двоичный код, или тернарный соответственно.

Векторы в называют кодовыми словами. Размер кода — это количество кодовых слов, т.е. .

Весом кодового слова называют число его ненулевых элементов. Расстояние между двумя кодовыми словами определяется как расстояние Хэмминга. Расстояние линейного кода — это минимальный вес его ненулевых кодовых слов или равным образом минимальное расстояние между всеми парами различных кодовых слов.

Линейный код длины , ранга и с расстоянием называют -кодом (англ. [n,k,d] code). Параметр d в обозначении кода часто опускается, потому что через него не задается структура кода. В таком случае пишут просто -код. В литературе встречается обозначение как в квадратных, так и в круглых скобках.[2][3]

Порождающая матрица

Определение:
Порождающая матрица — это матрица, столбцы которой задают базис линейного кода.

Так как линейный код является линейным подпространством , целиком код (может быть очень большим) может быть представлен как линейная оболочка набора из кодовых слов (т.е. базис). Этот базис часто объединяют в столбцы матрицы и называют такую матрицу порождающей матрицей кода .

В случае, если , где — это единичная матрица размера , а — это матрица размера говорят, что матрица находится в каноническом виде.

Имея матрицу можно получить из некоторого входного вектора кодовое слово линейного кода

,

где и — векторы-строки. Порождающая матрица линейного -кода имеет вид . Число избыточных бит тогда определяется как .

Проверочная матрица

Определение:
Проверочная матрица линейного кода — это порождающая матрица ортогонального дополнения . Другими словами, это матрица, которая описывает правила, которым должны удовлетворять части кодового слова.

Используется, чтобы определить, является ли некий вектор кодовым словом, а также в алгоритмах декодирования (напр. syndrome decoding).

Кодовое слово принадлежит коду тогда и только тогда, когда или, что то же самое, .

Проверочную матрицу можно получить из порождающей и наоборот: пусть дана порождающая матрица в каноническом виде , тогда проверочную матрицу можно получить по формуле

,

так как .

Кодирование и декодирование, примеры

Предположим, что имеется линия связи, по которой мы можем пересылать и принимать биты. В среднем какой-то известный процент переданных битов будет поврежден, ошибочен. Такая модель называется двоичным симметричным каналом.

Блок из символов сообщения будет кодироваться в кодовое слово , где ; эти кодовые слова образуют код.

Первая часть кодового слова состоит из информационных битов сообщения:

,

за которым следуют проверочных битов . Проверочные биты выбраны так, чтобы кодовые слова удовлетворяли уравнению

,

где — проверочная матрица.

Пример

Проверочная матрица

определяет код с и . Для этого кода

.

Сообщение кодируется в кодовое слово , которое начинается с самого сообщения:

,

а последующих три проверочных символа выбираются так, чтобы выполнялось уравнение .

Если сообщение , то , и проверочные биты легко определяются: , так что кодовое слово .

Минимальное расстояние и корректирующая способность

Линейность гарантирует, что расстояние Хэмминга между кодовым словом и любым другим кодовым словом не зависит от . Так как — тоже кодовое слово, а , то

Иными словами, чтобы найти минимальное расстояние между кодовыми словами линейного кода, необходимо рассмотреть ненулевые кодовые слова. Тогда ненулевое кодовое слово с минимальным весом будет иметь минимальное расстояние до нулевого кодового слова, таким образом показывая минимальное расстояние линейного кода.

Минимальное расстояние кода однозначно определяет количество ошибок, которое способен обнаружить () и исправить () данный код.

Синдромы и метод обнаружения ошибок в линейном коде

Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова соответствует наиболее вероятное переданное слово . Однако, данный метод требует применения огромных таблиц уже для кодовых слов сравнительно небольшой длины.

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора вычисляется синдром . Поскольку , где  — кодовое слово, а  — вектор ошибки, то . Затем с помощью таблицы по синдрому определяется вектор ошибки, с помощью которого определяется переданное кодовое слово. При этом таблица получается гораздо меньше, чем при использовании предыдущего метода.

Преимущества и недостатки линейных кодов

+ Благодаря линейности для запоминания или перечисления всех кодовых слов достаточно хранить в памяти кодера или декодера существенно меньшую их часть, а именно только те слова, которые образуют базис соответствующего линейного пространства. Это существенно упрощает реализацию устройств кодирования и декодирования и делает линейные коды весьма привлекательными с точки зрения практических приложений.

– Хотя линейные коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока.

Примечания

  1. ↑ William E. Ryan and Shu Lin (2009). Channel Codes: Classical and Modern. Cambridge University Press. p. 4. ISBN 978-0-521-84868-8.
  2. ↑ В. А. Липницкий, Н. В. Чесалин — Линейные коды и кодовые последовательности: учеб.-метод. пособие для студентов мех.-мат. фак. БГУ. Минск: БГУ, 2008. — 41 с., стр. 6
  3. ↑ Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки: Пер. с англ. — М: Связь, 1979. — 744 с., стр. 17

Источники информации

  • wikipedia.org — Линейный код
  • wikipedia.org — Linear code
  • Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки: Пер. с англ. — М: Связь, 1979. — 744 с., стр. 12-33
  • Ф.И. Соловьева — Введение в теорию кодирования
  • В. А. Липницкий, Н. В. Чесалин — Линейные коды и кодовые последовательности: учеб.-метод. пособие для студентов мех.-мат. фак. БГУ. Минск: БГУ, 2008. — 41 с.
Источник
  • Авторы
  • Резюме
  • Файлы
  • Ключевые слова
  • Литература


Могилевская Н.С.

1

1 ФГБОУ ВПО «Донской государственный технический университет»

В работе исследована возможность использования генетических алгоритмов для решения задачи вычисления минимального кодового расстояния линейных блочных кодов. Предполагается, что исследуемые коды не случайные, а получены с использованием различных методов модификации из известных кодов, обладающих хорошими корректирующими свойствами. В работе рассмотрены два известных генетических алгоритма поиска минимального кодового расстояния, а также построен новый алгоритм, который в экспериментальном исследовании показал наилучшие результаты. Сделаны выводы о чувствительности результатов работы исследованных генетических алгоритмов к их настройкам. Показано, что при поиске значения минимального кодового расстояния в случае кодов, заданных не случайным образом, использование нижней алгебраической оценки минимального кодового расстояния предпочтительнее, чем использование для этой цели генетических алгоритмов.

минимальное кодовое расстояние

генетический алгоритм

базовые оценки кодов

линейные блочные коды

1. Могилевская Н.С., Сухоставская К.С. Об экспериментальном исследовании характеристик модифицированных помехоустойчивых блочных двоичных кодов // Вестник Донского гос. техн. ун-та. – 2007. – Т.7. – №3. – С. 276-282.

2. Могилевская Н.С., Шпыгарь С.М. Свидетельство о государственной регистрации программы для ЭВМ №2009615850 Российская Федерация. Программа модификации блочных линейных кодов «New Code». Зарегистр. 12.07.2009. – 24 с.

3. Морелос-Саргоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. – М.: Техносфера, 2005. – 320 с.

4. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы. – М.: Горячая линия – Телеком. – 2006. – С. 124-170.

5. Сидельников В.М. Теория кодирования. – М.: ФИЗМАТЛИТ. – 2008. – 324 с.

6. Askali M., Azouaoui A., Nouh S., Belkasmi M. On the Computing of the Minimum Distance of Linear Block Codes by Heuristic Methods // International Journal of Communications, Network and System Sciences. – 2012. – № 5. – P. 774-784.

7. Grassl M. Bounds on the minimum distance of linear codes and quantum codes // URL: http://www.codetables.de. (accessed on 26.11.2014).

8. Vardy A. The intractability of computing the minimum distance of a code // IEEE Trans. Inf. Theory, vol. 43, no. 6, pp. 1757–1766, 1997.

Линейным блочным (n,k)q-кодом называют подмножество линейно-векторного пространства размерности k (k<n), где – поле Галуа мощностью q [3, 5]. Одним из важных параметров линейных кодов является минимальное кодовое расстояние (МКР), определяемое расстоянием между кодовыми словами в метрике Хемминга, и определяющее способность кода по исправлению и обнаружению ошибок. Значение МКР произвольного блочного (n,k)q-кода можно вычислить по формуле [3, 5]:

,

где – кодовое слово кода , функция возвращает вес Хемминга слова , т.е. число ненулевых позиций в этом векторе. Один из способов задания кода состоит в использовании порождающей матрицы кода , в этом случае оператор кодирования

(1)

определен формулой , где – информационное слово, а – кодовое слово.

Нахождение минимального кодового расстояния для произвольных кодов является NP-полной задачей [8], а поиск эффективных алгоритмов вычисления – открытая проблема в теории кодирования. МКР является важным параметром, не только для приложений, использующих помехоустойчивое кодирование для обеспечения достоверности передаваемых данных, но и в ряде криптографических приложений. Отметим, что чем больше значение , тем лучшими корректирующими способностями обладает помехоустойчивый код. Для небольшого числа кодов, в основе которых лежит некоторая комбинаторная или алгебраическая структура найдены аналитические формулы для вычисления МКР, примерами таких кодов являются коды Хемминга, Рида-Маллера, Рида-Соломона. У большинства кодов в порождающей матрице отсутствует какая-либо структура, такие коды называют кодами общего положения [5]. Задать такой код можно, например, с помощью порождающей матрицы, выбранной случайным образом среди всех матриц определенных размерностей.

В работе [6] предложено использовать эвристические алгоритмы для поиска значения МКР линейного кода, заданного порождающей матрицей .

Цель настоящей работы состоит в проведении исследования по оценке эффективности использования генетических алгоритмов (ГА) для нахождения МКР не случайного двоичного линейного помехоустойчивого кода и получении вывода о целесообразности использования генетических алгоритмов для решения задачи поиска .

Общая идея использования генетических алгоритмов в задаче поиска МКР

Генетические алгоритмы относятся к стохастическим, эвристическим методам поиска решений задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, аналогичных естественному отбору в природе, см., например [4]. Уточним основные понятия, используемые в теории ГА, применительно к решаемой задаче поиска МКР линейного блочного (n,k)2-кода . В качестве особи, входящей в популяцию, будем рассматривать информационные слова кода , которые представляют собой векторы , заданные над полем . Геном назовем символ особи . Пусть , где функция веса Хемминга, – оператор кодирования (1), тогда функцию приспособленности (фитнес-функцию) определим следующим образом:

. (2)

Оператор мутации с вероятностью инвертирует значения различных генов особи . Оператор скрещивания cross(s1, s2, pc, z) с вероятностью pc репродуцирует особей-родителей s1 и s2 и порождает двух особей-потомков ch1 и ch2. Если согласно вероятности скрещивание должно произойти, то случайным образом определяется z различных точек скрещивания lz, где lzÎ[1..k-1]. В данной работе рассматривается одно- и двухточечное скрещивание. При одноточечном скрещивании, у одного из потомков на позициях от 1 до lz которого стоят гены первого родителя, а на позициях от lz+1 до k стоят гены второго родителя, у второго потомка, на позициях от 1 до lz которого стоят гены второго родителя, а на позициях от lz+1 до k стоят гены первого родителя. В случае двухточечного скрещивания потомки наследуют фрагменты наборов родительских генов, определяемые двумя случайно выбранными точками скрещивания.

Генетические алгоритмы нахождения минимального кодового расстояния

Ниже в работе рассмотрены два генетических алгоритма, обозначенные в данной работе как алгоритм А и алгоритм Б, предложенные в работе [6], а также новый генетический алгоритм поиска минимального кодового расстояния линейного блочного кода, обозначенный далее, как алгоритм B.

На вход всех алгоритмов поступают параметры (n,k)q-кода , определенного порождающей матрицей , параметры операторов мутации и скрещивания, M – число особей в популяции, Nmax – число популяций, которое необходимо сгенерировать. На выходе алгоритмов формируется значение, которое предположительно является минимальным кодовым расстоянием кода . В алгоритме Б в список входных параметров дополнительно подается число элитных особей Ne. Результатом работы алгоритмов является наименьшее значение фитнес-функции особей из поколения с номером Nmax.

Рассмотрим алгоритм А [6]. Начальная популяция формируется случайным образом из M особей вида , для каждой особи вычисляется функция приспособленности (2). Затем генерируется Nmax популяций, при этом каждая популяция Ni строится из предыдущей популяции N(i-1) по следующей схеме. Особи поколения N(i-1) сортируются в порядке возрастания значений их функций приспособленности. В поколение Ni включаются M/2 особей с наименьшим значением функции (2) из популяции N(i-1). Для генерации оставшихся M/2 особей из особей поколения N(i-1) случайным образом выбираются две особи и , к каждой из которых применяется оператор мутации, а затем одноточечный оператор скрещивания:

, , .

Потомок с наименьшим значением функции приспособленности, включается в поколение Ni.

В алгоритме Б [6] начальная популяция генерируется случайным образом из M особей вида , для каждой особи вычисляется функция (2). Следующие Nmax популяций генерируются рекурсивно. Особи популяции N(i-1) сортируются в порядке возрастания значений их функций приспособленности. В поколение Ni включаются Ne особей с наименьшим значением фитнес-функции из популяции N(i-1). Для генерации оставшихся (M-Ne) особей с помощью турнирного отбора из поколения N(i‑1) выбираются две особи s1 и s2 для репродукции, с вероятностью pc эти особи скрещиваются , к потомкам применяется функция мутации , , затем оба потомка переходят в следующее поколение.

Первая особь начальной популяции алгоритма В формируется в виде нулевого вектора из , остальные (M-1) особей генерируются случайно в виде , для каждой особи, кроме первой, вычисляется функция (2). Для построения следующего поколения особи популяции N(i-1) сортируются в порядке возрастания значений их фитнес-функций. В поколение Ni включаются нулевая особь и две особи с наименьшим значением функции (2) из N(i-1). Для получения остальных особей нового поколения выполняются следующие действия. Для каждой новой (i=2,3,4,…) особи из формируемого поколения Ni выбирается случайным образом особь для скрещивания . Потомок с максимальным значением фитнес-функции отбрасывается, к потомку с минимальным значением функции приспособленности применяется оператор мутации: Из особей поколения Ni случайным образом выбирается еще одна особь . Для особей и вычисляется значение функций приспособленности, затем особь, с наименьшим значением функции (2) включается в формируемое поколение.

Экспериментальное исследование

Описанные алгоритмы реализованы с использованием математического пакета Matlab. В работе исследовано 38 различных кодов, длина n которых варьируется от 5 до 512. В этот набор вошли как случайные коды, так и известные коды Хемминга, Голея, БЧХ, а также модификации известных кодов методами укорочения, перфорации, расширения и др. Описание использованных методов можно найти в работах [1], [3], для выполнения различных модификаций рассматриваемых кодов использовано специализированное программное средство [2]. Реальное значение МКР получено с использованием переборного алгоритма, в ходе которого вычислялись веса всех кодовых слов.

В одной из серий экспериментов исследованы БЧХ-коды, использованные в [6] с применением указанных там же параметров алгоритмов А и Б. Среднее значение разницы между результатами, полученными в данной работе, и данными из [6] составляет 29% от значения истинного минимального кодового расстояния. Полагаем, что такое расхождение не противоречит эвристической природе использованных алгоритмов.

В табл. 1 представлены результаты поиска минимального кодового расстояния рассмотренными выше генетическими алгоритмами для некоторых кодов, случайным образом выбранных из набора исследуемых кодов. Отметим, что значения, указанные в таблице, являются лучшими результатами, полученными при различных размерах начальной популяции, а так же различных вероятностях мутации и кроссовера. Структура таблицы следующая: в первом столбце указан исследуемый код и его параметры в виде тройки (n,k,dmin), второй-четвертый столбцы содержат значения минимального кодового расстояния, полученные с использованием генетических алгоритмов А, Б из [6] и нового алгоритма В, соответственно. Содержимое последнего столбца будет рассмотрено позже.

Таблица 1

Значение МКР, найденного генетическими алгоритмами А, Б и В

Код

Минимальное кодовое расстояние

Алгоритм А

Алгоритм Б

Алгоритм В

Оценки

(7,4,3)

3

3

3

3..3

(15,6,6)

6

6

6

6..6

(23,12,7)

7

7

7

7..7

(63,51,5)

12

14

5

5..5

(63,51,2)

2

2

2

5..5

(127,64,21)

24

27

21

21..28

(127,92,10)

13

16

12

11..14

(127,113,5)

24

28

7

5..5

(255,71,59)

73

90

67

61..89

(255,71,8)

8

9

8

61..89

(255,223,9)

12

16

11

9..10

Из табл. 1 видно, что алгоритм Б показал наихудшие, а новый алгоритм B наилучшие результаты, аналогичные результаты справедливы и для других исследованных кодов.

Результаты работы генетических алгоритмов поиска минимального кодового расстояния значительно зависят от параметров алгоритмов, а именно, от размера и числа популяции, вероятностей кроссовера и мутации. Так полученные данные демонстрируют понижение точности при повышении вероятности мутации, что может объясняться повышающейся вероятностью спонтанного наделения отбираемых особей плохими свойствами. Так же можно говорить о том, что точность результата определяется размерами пространства поиска: для повышения точности следует увеличивать размер исходной популяции, что, в свою очередь повышает время выполнения алгоритма. Выявить четкую зависимость эффективности рассматриваемых алгоритмов от диапазона значений того или иного стохастического оператора не удалось в силу нестабильности полученных результатов.

Точный результат исследуемые ГА выдают всегда в случае, когда рассматриваемый код содержит небольшое число кодовых слов. Этот факт имеет простое объяснение, пусть, например, в ГА формируется 400 популяций из 1000 особей. При поиске МКР для кода (7,4,3), содержащего всего 24=16 кодовых слов, с большой долей вероятности в начальной популяции слово минимального веса будет сформировано. Более того, для этого кода поиск МКР прямым перебором окажется быстрее. Однако, если применить эти же настройки параметры для (63,51,5)-кода, содержащего 251=(23)17»1017кодовых слов, то при поиске МКР вероятность генерации в начальной популяции слова минимального веса резко падает.

Проведенное исследование выявило следующие недостатки изучаемых генетических алгоритмов: длительное время работы, возможную вырождаемость решений, невысокую точность.

На вход исследуемых генетических алгоритмов поступали коды, заданные порождающими матрицами, генерация которых производилась как случайным образом (коды (63,51,2) и (255,71,8)), так и не случайным образом (все остальные коды из табл. 1). В случае случайных кодов результаты работы ГА достаточно точные. Однако в практических приложениях коды, имеющие большую избыточность и малую корректирующую способность, не используются. При использовании помехоустойчивых кодов в реальных приложениях, как для защиты данных от помех, так и в криптографических задачах, используют коды, обладающие хорошими корректирующими способностями. При использовании таких кодов следует ожидать, что значение минимального кодового расстояния будет достаточно большим для заданных длины и размерности кода.

Алгебраическая оценка минимального кодового расстояния

В теории помехоустойчивого кодирования известен ряд оценок, связывающих параметры линейных блочных кодов. К таким оценкам относятся, например, хорошо известные границы Хемминга, Варшамова-Гилберта, Синглтона, Бассалыго-Элайеса, Грайсмера и другие [3], [5]. Используя данные оценки для (n,k)q-кода можно оценить верхнюю и нижнюю границы значения минимального кодового расстояния (n,k)q-кода. Рассмотрим, например, границы Хемминга и Гилберта. По отношению друг к другу граница Хемминга является «верхней», а граница Гилберта «нижней». Так, если произвольно выбранные параметры кода n, k и dmin не удовлетворяют границе Хемминга, то кода с такими параметрами не существует. Если параметры кода удовлетворяют границе Гилберта, то код с такими параметрами существует. Если же выбранные параметры удовлетворяют границе Хемминга, но не удовлетворяют границе Гилберта, то вопрос о существовании такого кода не решен полностью (не смотря на множество частных результатов) [5].

Электронный ресурс [7], посвященный линейным блочным кодам, позволяет для введенных значений длины n, размерности k и мощности q кода вычислить нижнюю и верхнюю оценки МКР кода с использованием целого ряда известных оценок. Для всех кодов, использованных в исследовании генетических алгоритмов, были вычислены такие оценки минимального кодового расстояния кода (см. последний столбец табл. 1). Для кода длиной 127 и размерностью 64 нижняя оценка равна 21, а верхняя – 28, следовательно, использованный в экспериментах (127,64,21)-код можно назвать «хорошим», т.к. его МКР лежит на нижней границе, т.е. значение dmin=21 является максимальным для которого, согласно базовым оценкам линейных блочных кодов, гарантировано существует код с указанными параметрами длины и размерности. Для (255,71)2-кода базовые оценки гарантируют существование кода с dmin=61, а у кода, использованного в эксперименте это значение меньше и равно 59, это говорит о том, что можно построить (255,71)2-код с большей корректирующей способностью.

Анализ реального значения минимального кодового расстояния исследуемых кодов, значений МКР, найденных с использованием генетических алгоритмов, а также значений нижней оценки МКР, позволяет сделать вывод о том, что для кодов, чьи порождающие матрицы заданы не случайно, а обладают некоторой полезной комбинаторной или алгебраической структурой, вместо использования генетических алгоритмов для поиска минимального кодового расстояния целесообразно использовать нижнюю оценку МКР. В этом случае погрешность между реальным значением МКР и его нижней оценкой не превосходит погрешность между реальным значением МКР и значением, найденным с использованием генетического алгоритма. К тому же время вычисления оценки значительно меньше времени работы генетического алгоритма.

Заключение

В работе построен новый генетический алгоритм поиска минимального кодового расстояния линейного блочного кода, заданного порождающей матрицей. Результаты экспериментов показали, что новый алгоритм работает эффективнее алгоритмов из [6], взятых за основу. Однако все рассмотренные в работе алгоритмы выдают результат с невысокой точностью. В работе показано, что в случае двоичных линейных блочных кодов, порождающие матрицы которых построены не случайно, использование нижней оценки минимального кодового расстояния предпочтительнее применения описанных генетических алгоритмов с точки зрения времени работы и точности результата.

Рецензенты:

Габриэльян Д.Д., д.т.н., профессор, заместитель начальника научно-технического комплекса «Антенные системы» по науке, Федеральный научно-производственный центр ФГУП «РНИИРС» г. Ростов-на-Дону;

Звездина М.Ю., д.ф.-м.н., доцент, зав. кафедрой «Радиоэлектроника», Минобрнауки России, ФБГОУ ВПО «Донской государственный технический университет», г. Ростов-на-Дону.

Библиографическая ссылка

Могилевская Н.С. О ВЫЧИСЛЕНИИ МИНИМАЛЬНОГО РАССТОЯНИЯ ДВОИЧНОГО ЛИНЕЙНОГО БЛОЧНОГО КОДА С ИСПОЛЬЗОВАНИЕМ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ // Современные проблемы науки и образования. – 2015. – № 1-1.
;

URL: https://science-education.ru/ru/article/view?id=17153 (дата обращения: 14.05.2023).

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

Источник

Добавить комментарий