Между кубами
различной размерности, входящими в
кубический комплекс K(f),
существует отношение включения или
покрытия. Принято говорить, что куб А
меньшей размерности покрывается кубом
B
большей размерности. Куб А
включается в куб B,
если при образовании куба B
хотя бы в
одном склеивании участвует куб А.
Отношение включения
(покрытия) между кубами принято обозначать
А
B.
В теории множеств отношение включения
связывает между собой некоторое множество
и его подмножества.
Для рассмотренного
примера отношения включения имеют место
между следующими кубами: 0010Х1;
011Х11Х1Х.
Любой 1-куб покрывает два 0-куба, 2-куб –
четыре 0-куба и четыре 1-куба, 3-куб
покрывает восемь 0-кубов, двенадцать
1-кубов и шесть 2-кубов (см. геометрическую
интерпретацию).
Определение.
Покрытием
булевой функции
f
называется такое подмножество кубов
из кубического комплекса K(f),
которое покрывает все существенные
вершины функции.
В связи с тем, что
любому кубу комплекса K(f)
можно поставить в соответствие
конъюнктивный терм, для любого покрытия
можно составить некоторую ДНФ булевой
функции.
Частным случаем
покрытия булевой функции является
кубический комплекс K0(f),
покрытие C0(f)=K0(f).
Этому покрытию соответствует КДНФ.
Для рассмотренного
выше примера покрытием является также
комплекс K1(f):

.
Этому покрытию
соответствует ДНФ вида:
![]()
Приведенная ДНФ
не является минимальной.
В качестве еще
одного варианта покрытия можно
использовать множество максимальных
кубов. Для рассмотренного выше примера
![]()
.
Действительно,
кубы, входящие в Z(f),
покрывают все существенные вершины:
0Х1(001,
011), Х1Х(010,
011, 110, 111).
Замечание.
Множество максимальных кубов булевой
функции всегда является ее покрытием.
Покрытию С2(f)
соответствует ДНФ вида:
![]()
Эта ДНФ является
минимальной.
Определение.
Покрытие булевой функции, которое
соответствует минимальной ДНФ, называется
минимальным
покрытием.
Замечание:
Минимальное покрытие должно состоять
только из максимальных кубов.
В частном случае,
множество максимальных кубов может
являться минимальным покрытием. Это
справедливо для рассмотренного выше
примера. В общем случае множество
максимальных кубов является избыточным
и для получения минимального покрытия
достаточно выделить некоторое его
подмножество.
Пример:

K2(
f
)
= .
;

;
Для данного примера
множество максимальных кубов совпадает
с комплексом K1(f):
Z(f)=K1(f).
Минимальными
покрытиями являются

;

.
О![]()
пределение.
ДНФ, соответствующая множеству
максимальных кубов, называется сокращенной
(СДНФ).
Для
рассматриваемого примера СДНФ:
Из анализа покрытия
существенных вершин максимальными
кубами из комплекса K1(f)
следует:
1. Куб 00Х должен
обязательно включаться в покрытие, так
как он и только он покрывает существенную
вершину 001, аналогично только куб 11Х
покрывает существенную вершину 111.
Определение.
Множество максимальных кубов, без
которых не может быть образовано покрытие
булевой функции, называется ядром
покрытия
и обозначается T(f):
T(f)={00Х,
11Х}.
2. Так как ядром
покрытия, кроме существенных вершин
001 и 111, покрываются также существенные
вершины 000 и 110, то не покрытой ядром
остается только существенная вершина
100. Для ее покрытия достаточно взять
любой из оставшихся максимальных кубов:
Х00 или 1Х0.
Выводы:
1. Задача получения
минимальной ДНФ сводится к задаче
получения минимального покрытия булевой
функции.
2. В общем случае:
получение минимального покрытия
осуществляется в следующем порядке:
-
находится множество
максимальных кубов; -
выделяется ядро
покрытия; -
из максимальных
кубов, не вошедших в ядро, выбирается
такое минимальное подмножество, которое
покрывает существенные вершины, не
покрытые ядром.
3. Частные случаи.

1) Cmin(f)
= K0(f) МДНФ=КДНФ;
2) Cmin(f)
= Z(f) МДНФ=СДНФ;
3)
Cmin(f)
Z(f);
а)
Cmin(f)
= T(f);
б)
T(f)
Cmin(f);
в)
T(f)
= .
Цена покрытия
Цена покрытия
используется при решении задачи
минимизации булевых функций как
количественная оценка качества покрытия
в смысле его минимальности. Эта оценка
базируется на понятии цены кубов,
составляющих покрытие.
Цена r-куба
представляет собой количество несвязанных
координат: Sr=
n
– r.
П![]()
ринято
использовать два вида цены покрытия:
где Nr
– количество
r-кубов,
входящих в покрытие, m
– максимальная размерность кубов,
входящих в покрытие. Цена Sa
представляет собой сумму цен кубов,
входящих в покрытие.
2![]()
.
г![]()
де
k
– количество кубов, входящих в покрытие.
Определение.
Минимальным
покрытием
называется покрытие, обладающее
минимальной ценой Sa
по сравнению с любым другим покрытием
этой функции.
Можно показать,
что покрытие, обладающее минимальной
ценой Sa,
обладает также и минимальной ценой Sb.
![]()
Пример:
C0(f)=K0(f);
Sa=53=15;
Sb=Sa+5=20;
C1(f)=K1(f);
Sa=42=8;
Sb=Sa+4=12;
Cmin(f)
: Sa=32=6
; Sb=9.
Цены покрытия Sa
и Sb
связаны с
ДНФ, соответствующей этому покрытию,
следующим образом:
– цена покрытия
Sa
представляет
собой количество букв, входящих в ДНФ;
– цена Sb
представляет
для ДНФ сумму количества букв и количества
термов.
Ц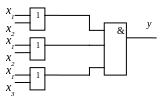
ена
покрытия хорошо согласуется с ценой
схемы по Квайну SQ,
которая строится по нормальной форме,
соответствующей этому покрытию.
Для приведенной
схемы цена по Квайну SQ=
9 =
Sb
(9 – число входов в элементы).
В принципе, между
SQ
и ценами Sa
и Sb
существует соотношение Sa
SQ
Sb.
Это неравенство имеет место при следующих
допущениях:
-
Схема строится
по нормальной форме (ДНФ или КНФ). -
Схема строится
на элементах булевого базиса (И, ИЛИ). -
На входы схемы
можно подавать как прямые, так и инверсные
значения входных переменных, представляющие
собой значения аргументов булевой
функции (схема с парафазными входами).
В соответствии с этим элементы НЕ
(инверторы) в схеме отсутствуют.
Нулевое покрытие
булевой функции и получение минимальной
КНФ
Выше было рассмотрено
покрытие булевой функции на наборах
аргументов, для которых функция равна
единице.
Такие покрытия
можно назвать единичными. Наряду с
единичными покрытиями существуют и
нулевые, для которых покрываются наборы
аргументов, на которых функция равна
нулю, то есть покрытие реализуется для
существенных вершин, но не самой функции,
а ее отрицания (инверсии).
Нулевое покрытие
строится также как и единичное, но только
для отрицания исходной функции.
![]()

![]()
Sa=9
Sb=12;
![]()
Sa=5
Sb=7.
Цена минимального
нулевого покрытия оказалась меньше
цены минимального единичного покрытия.
Так как заранее
предсказать какое из минимальных
покрытий данной функции, единичное или
нулевое, будет иметь меньшую цену
невозможно, то для построения схемы,
обладающей минимальной ценой по Квайну,
целесообразно решать задачу минимизации
в отношении обоих покрытий.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
6.1 Сокращенная и тупиковая ДНФ
6.2 Метод импликантных матриц
Цель данного раздела – изложение основных методов построения минимальных дизъюнктивно нормальных форм.
6.1 Сокращенная и тупиковая ДНФ. В разделе 3 было показано, что любая булева функция может быть представлена дизъюнктивной нормальной формой. Следует отметить, что дизъюнктивная нормальная форма часто допускает упрощение. При этом путем различных тождественных преобразований получится дизъюнктивная нормальная форма, эквивалентная исходной, но содержащая меньшее число вхождений символов.
Дизъюнктивная нормальная форма называется Минимальной, если она включает минимальное число символов по сравнению со всеми другими эквивалентами ей дизъюнктивными нормальными формами.
Заметим, что если некоторый символ в формуле, скажем ![]() , встречается, например, два раза, то при подсчете числа символов в формуле он учитывается два раза.
, встречается, например, два раза, то при подсчете числа символов в формуле он учитывается два раза.
Основной вопрос данного параграфа – это как для произвольной булевой функции построить ей минимальную дизъюнктивную нормальную форму. Эта задача называется Проблемой минимизации булевых функций.
Существует тривиальный алгоритм построения минимальной ДНФ для произвольной булевой функции ![]() . Для этого все ДНФ, составленные из символов
. Для этого все ДНФ, составленные из символов ![]() упорядочиваются по числу букв и по порядку для каждой ДНФ Д проверяется соотношение
упорядочиваются по числу букв и по порядку для каждой ДНФ Д проверяется соотношение ![]() . Первая по порядку ДНФ, для которой это соотношение выполняется, есть, очевидно, минимальная ДНФ функции
. Первая по порядку ДНФ, для которой это соотношение выполняется, есть, очевидно, минимальная ДНФ функции ![]() .
.
Число различных ДНФ, составленных из переменных ![]() , равно
, равно ![]() .
.
Прежде чем доказать данное утверждение, приведем следующее определение.
Конъюнкция ![]() называется Элементарной, если
называется Элементарной, если ![]() при
при ![]() .
.
Число R называется Рангом элементарной конъюнкции. В случае r=0 конъюнкция называется Пустой и Полагается равной 1.
Так как каждая из N переменных ![]() либо не входит в элементарную, либо входят в нее с отрицанием, либо без отрицания, то число элементарных конъюнкций, составленных из
либо не входит в элементарную, либо входят в нее с отрицанием, либо без отрицания, то число элементарных конъюнкций, составленных из ![]() равно
равно ![]() . Ясно, что число различных ДНФ, составленных из переменной
. Ясно, что число различных ДНФ, составленных из переменной ![]() , равно числу подмножеств множества, из
, равно числу подмножеств множества, из ![]() элементов, т. е.
элементов, т. е. ![]() .
.
Рассмотрим геометрическую интерпретацию задачи минимизации булевых функций.
Обозначим через ![]() множество всех точек
множество всех точек ![]() , где
, где ![]() . Ясно, что
. Ясно, что ![]() – множество всех вершин единичного n-мерного куба.
– множество всех вершин единичного n-мерного куба.
Сопоставим каждой булевой функции ![]() Подмножество
Подмножество ![]() Из
Из ![]() , определенное следующим образом:
, определенное следующим образом:
![]()
Например, функции
|
X |
Y |
Z |
|
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Соответствует подмножество ![]()
Вершин трехмерного единичного куба

Данное соответствие является взаимно однозначным и обладает следующими свойствами:
1) булевой функции ![]() Соответствует подмножество
Соответствует подмножество ![]() ;
;
2) булевой функции ![]() соответствует подмножество
соответствует подмножество ![]() ;
;
3) булевой функции ![]() соответствует подмножество
соответствует подмножество ![]() .
.
Докажем утверждение 2. Пусть ![]()
Отсюда ![]() .
.
Тогда ![]() .
.
А это значит, что ![]() .
.
Отсюда ![]() .
.
Пусть ![]() ДНФ, где
ДНФ, где ![]() – элементарные конъюнкции. Подмножество
– элементарные конъюнкции. Подмножество ![]() называется интервалом R-го ранга, если оно соответствует элементарной конъюнкции К R-го ранга. Как показано выше,
называется интервалом R-го ранга, если оно соответствует элементарной конъюнкции К R-го ранга. Как показано выше, ![]() . Итак, с каждой ДНФ функции F связано покрытие
. Итак, с каждой ДНФ функции F связано покрытие ![]() такими интервалами
такими интервалами ![]() , что
, что ![]() .
.
Пусть ![]() – ранг интервала
– ранг интервала ![]() . Тогда
. Тогда ![]() совпадает с числом букв в ДНФ
совпадает с числом букв в ДНФ ![]() функции
функции ![]() .
.
Теперь ясно, что задача построения минимальной ДНФ сводится к отысканию такого покрытия подмножества ![]() интервалами
интервалами ![]() , чтобы число
, чтобы число ![]() было наименьшим.
было наименьшим.
Интервал ![]() , содержащий
, содержащий ![]() , называется Максимальным для булевой функции, если не существует интервала
, называется Максимальным для булевой функции, если не существует интервала ![]() , такого, что
, такого, что ![]() .
.
Заметим, что соотношение ![]() выполняется тогда и только тогда, когда элементарная конъюнкция
выполняется тогда и только тогда, когда элементарная конъюнкция ![]() получается из элементарной конъюнкции К путем вычеркивания непустого числа сомножителей.
получается из элементарной конъюнкции К путем вычеркивания непустого числа сомножителей.
Очевидно, что каждый интервал ![]() из
из ![]() содержится в некотором максимальном интервале. Если
содержится в некотором максимальном интервале. Если ![]() – список всех максимальных интервалов подмножества
– список всех максимальных интервалов подмножества ![]() , то нетрудно видеть, что
, то нетрудно видеть, что ![]() .
.
ДНФ ![]() булевой функции f, соответствующая покрытию подмножества
булевой функции f, соответствующая покрытию подмножества ![]() всеми максимальными интервалами, называется Сокращенной ДНФ функции F.
всеми максимальными интервалами, называется Сокращенной ДНФ функции F.
Ясно, что сокращенная ДНФ для любой булевой функции f определяется однозначно.
Пример 1. Пусть ![]() . Обозначим
. Обозначим ![]() ,
, ![]() ,
, ![]() . Найдем соответствующие этим конъюнкциям интервалы
. Найдем соответствующие этим конъюнкциям интервалы ![]() ,
, ![]() ,
, ![]() .
.
Изобразим эти интервалы

Очевидно, что ![]() и
и ![]() – все максимальные интервалы. Интервал
– все максимальные интервалы. Интервал ![]() не является максимальным, ибо
не является максимальным, ибо ![]() . Следовательно, покрытию подмножества
. Следовательно, покрытию подмножества ![]() соответствует сокращенная ДНФ функции
соответствует сокращенная ДНФ функции ![]() , равная
, равная ![]() .
.
Данный геометрический подход дает и метод построения сокращенной ДНФ.
Теперь рассмотрим аналитический метод построения сокращенной ДНФ – метод Блейка. Этот метод основан на следующей теореме.
Теорема 1. Если в произвольной ДНФ булевой функции F произвести все возможные обобщения склеивания и устранить затем все элементарные поглощения, то в результате получиться сокращенная ДНФ функции F.
Следовательно, чтобы найти сокращенную ДНФ, надо к произвольной ДНФ данной функции применить правило обобщенного склеивания ![]() до тех пор, пока это возможно, а затем правило поглощения.
до тех пор, пока это возможно, а затем правило поглощения.
Пример 2. Найти сокращенную ДНФ для функции ![]() . Применяя правило обобщенного склеивания, получаем:
. Применяя правило обобщенного склеивания, получаем: ![]() .
.
Затем правило поглощения и находим сокращенную ДНФ: ![]() .
.
Рассмотрим еще один метод построения сокращенной ДНФ – метод Нельсона. Этот метод основан на следующей теореме.
Теорема 2. Если в произвольной КНФ булевой функции раскрыть все скобки в соответствии с дистрибутивным законом и устранить все элементарные поглощения, то в результате получится сокращенная ДНФ этой функции.
Пример 3. Найти сокращенную ДНФ для функции
![]()
После раскрытия скобок с помощью дистрибутивного закона, получаем:
![]() .
.
Так как ![]() ,
, ![]() , то имеем:
, то имеем:
![]() .
.
Далее, применяя правило поглощения, получаем сокращенную ДНФ:
![]() .
.
Рассмотрим табличный метод построения сокращенной ДНФ. Этот метод основан на составлении прямоугольной таблицы (минимизирующей карты).
Минимизирующие карты для булевых функций от трех и от четырех переменных изображены на следующих таблицах.
|
Z X y |
0 |
1 |
|
00 |
||
|
01 |
||
|
11 |
||
|
10 |
|
X4 X3 X1 X2 |
0 0 |
0 1 |
1 1 |
1 0 |
|
0 0 |
||||
|
0 1 |
||||
|
1 1 |
||||
|
1 0 |
Объединяя соседние клетки, соответствующие единичным значениям булевой функции f в максимальные интервалы, и сопоставляя им элементарные конъюнкции, получим сокращенную ДНФ. Отметим, что клетки, расположенные по краям таблицы, также считаются соседними. Покажем работу этого метода на следующем примере.
Пример 4. Найти сокращенную ДНФ для функции, заданной следующей таблицей.
|
X4 X3 X1 X2 |
0 0 |
0 1 |
1 1 |
1 0 |
|
0 0 |
1 |
1 |
0 |
1 |
|
0 1 |
0 |
1 |
1 |
0 |
|
1 1 |
1 |
1 |
1 |
0 |
|
1 0 |
0 |
1 |
0 |
0 |
В данной таблице объединены клетки в максимальные интервалы
![]()
![]()
![]()
![]()
![]() .
.
Этим интервалам соответствуют элементарные конъюнкции
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Следовательно, сокращенная ДНФ для данной функции имеет вид:
![]()
Построение сокращенной ДНФ есть только первый этап решения задачи минимизации булевой функции. В общем случае сокращенная ДНФ не является минимальной. Следующая теорема устанавливает связь между минимальной и сокращенной ДНФ.
Теорема 3. Минимальная ДНФ булевой функции получается из сокращенной ДНФ данной функции путем удаления некоторых элементарных конъюнкций.
Доказательство этого утверждения следует из того факта, что покрытие подмножества ![]() , отвечающее минимальной ДНФ, состоит только из максимальных интервалов. Действительно, если бы покрытие содержало не максимальный интервал, то его можно было бы заменить объемлющим максимальным интервалом. В результате этого сумма рангов интервалов данного покрытия уменьшилась бы, что противоречит предположению о минимальности ДНФ.
, отвечающее минимальной ДНФ, состоит только из максимальных интервалов. Действительно, если бы покрытие содержало не максимальный интервал, то его можно было бы заменить объемлющим максимальным интервалом. В результате этого сумма рангов интервалов данного покрытия уменьшилась бы, что противоречит предположению о минимальности ДНФ.
Покажем, что в классе монотонных функций понятия минимальной и сокращенной ДНФ совпадают.
Теорема 4. Сокращенная ДНФ монотонной булевой функции не содержит отрицаний переменных и является минимальной ДНФ этой функции.
Пусть К – элементарная конъюнкция, входящая в сокращенную ДНФ. Предположим, что К содержит отрицание переменных. Обозначим через ![]() произведение всех переменных, входящих в К без отрицания. Пусть
произведение всех переменных, входящих в К без отрицания. Пусть ![]() – набор переменных, в которых всем переменным, входящим в
– набор переменных, в которых всем переменным, входящим в ![]() , приписано значение 1, а всем остальным – значение 0. Ясно, что при этом наборе значение функции
, приписано значение 1, а всем остальным – значение 0. Ясно, что при этом наборе значение функции ![]() Равно 1. Элементарная конъюнкция
Равно 1. Элементарная конъюнкция ![]() обращается в 1 при всех наборах
обращается в 1 при всех наборах ![]() . Очевидно, что при этих наборах значение функции
. Очевидно, что при этих наборах значение функции ![]() также равно 1. Следовательно,
также равно 1. Следовательно, ![]() .
.
Получили противоречие с максимальностью интервала ![]() . Итак, сокращенная ДНФ булевой функции
. Итак, сокращенная ДНФ булевой функции ![]() Не содержит отрицаний переменных.
Не содержит отрицаний переменных.
Пусть ![]() – любая элементарная конъюнкция из сокращенной ДНФ. Конъюнкция К является единственной конъюнкцией сокращенной ДНФ, которая обращается в единицу в вершине с координатами
– любая элементарная конъюнкция из сокращенной ДНФ. Конъюнкция К является единственной конъюнкцией сокращенной ДНФ, которая обращается в единицу в вершине с координатами ![]() . Действительно, если бы в сокращенной ДНФ какая-нибудь другая элементарная конъюнкция
. Действительно, если бы в сокращенной ДНФ какая-нибудь другая элементарная конъюнкция ![]() обращалась в этой вершине в 1, то не содержала бы, во-первых, букв
обращалась в этой вершине в 1, то не содержала бы, во-первых, букв ![]() , и, во-вторых, букв
, и, во-вторых, букв ![]() . Поэтому в конъюнкцию
. Поэтому в конъюнкцию ![]() могли бы входить лишь буквы
могли бы входить лишь буквы ![]() , причем не все. Но тогда
, причем не все. Но тогда ![]() . Получили противоречие с максимальностью интервала
. Получили противоречие с максимальностью интервала ![]() . Следовательно, для любого максимального интервала
. Следовательно, для любого максимального интервала ![]() существует вершина куба
существует вершина куба ![]() , которая покрывается только этим интервалом. Поэтому из покрытия
, которая покрывается только этим интервалом. Поэтому из покрытия ![]() соответствующего сокращенной ДНФ, нельзя удалить ни одного из интервалов. Теперь, применяя предыдущую теорему, получаем требуемый результат.
соответствующего сокращенной ДНФ, нельзя удалить ни одного из интервалов. Теперь, применяя предыдущую теорему, получаем требуемый результат.
Следует отметить, что сокращенная ДНФ в большинстве случаев допускает дальнейшие упрощения за счет того, что некоторые элементарные конъюнкции могут поглощаться дизъюнкциями других элементарных конъюнкций. Действительно, в сокращенной ДНФ
![]()
Элементарная конъюнкция ![]() поглощается дизъюнкцией остальных элементарных конъюнкций, т. е.
поглощается дизъюнкцией остальных элементарных конъюнкций, т. е. ![]() .
.
Ввиду этого введем следующее определение.
Покрытие области истинности булевой функции максимальными интервалами называется Неприводимым, если после удаления из него любого интервала оно перестает быть покрытием. ДНФ булевой функции ![]() , соответствующая неприводимому покрытию, называется Тупиковой.
, соответствующая неприводимому покрытию, называется Тупиковой.
Теорема 5. Всякая минимальная ДНФ является тупиковой.
Доказательство этого утверждения следует из того, что покрытие, соответствующее минимальной ДНФ, является неприводимым.
Заметим, что булева функция может обладать несколькими различными минимальными ДНФ. Существуют также тупиковые ДНФ, не являющиеся минимальными ДНФ. Соответствующие примеры будут разобраны ниже.
Из того, что минимальная ДНФ является тупиковой, следует общая схема решения задачи минимизации булевых функций.
1. Выделяются все максимальные интервалы, и строится сокращенная ДНФ.
2. Строятся все тупиковые ДНФ.
3. Среди всех тупиковых ДНФ выделяются все минимальные ДНФ.
Рассмотрим алгоритм построения всех тупиковых ДНФ. Суть данного алгоритма состоит в следующем:
1) для булевой функции ![]() строим сокращенную ДНФ;
строим сокращенную ДНФ;
2) для каждой вершины ![]() из
из ![]() выделяем в сокращенной ДНФ функции F все такие элементарные конъюнкции
выделяем в сокращенной ДНФ функции F все такие элементарные конъюнкции ![]() , что
, что ![]() ;
;
3) составляем выражение вида
![]() (*)
(*)
4) применяем к выражению вида (*) законы дистрибутивности и поглощения. В результате получаем ![]() .
.
Теперь каждая ДНФ ![]() является тупиковой ДНФ функции
является тупиковой ДНФ функции ![]() .
.
Рассмотрим работу данного алгоритма на следующем примере.
Пример 5. Рассмотрим булеву функцию, заданную следующей таблицей:
|
X |
Y |
Z |
|
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
Найдем сокращенную ДНФ данной функции по методу Нельсона. Для этого составим КНФ данной функции ![]() .
.
Применяя законы дистрибутивности, получаем:
![]() .
.
Обозначим ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]()
Составляем выражение (*)
![]()
Преобразуем данное выражение к виду
![]() =
= ![]()
![]() =
=![]() .
.
Таким образом, ![]() имеет шесть тупиковых ДНФ:
имеет шесть тупиковых ДНФ:
![]()
![]()
![]()
![]()
![]()
![]()
Две из них ![]() и
и ![]() являются минимальными.
являются минимальными.
6.2 Метод импликантных матриц. Для булевой функции ![]() находим сокращенную ДНФ
находим сокращенную ДНФ ![]() . Построим для этой функции импликантную матрицу, представляющую собой таблицу, в вертикальные входы которой записываются
. Построим для этой функции импликантную матрицу, представляющую собой таблицу, в вертикальные входы которой записываются ![]() , а в горизонтальные
, а в горизонтальные ![]() .
.
|
|
|
… |
|
… |
|
|
|
|
||||||
|
|
||||||
|
… |
||||||
|
|
+ |
|||||
|
… |
||||||
|
|
Для каждой ![]() находим набор
находим набор ![]() такой, что
такой, что ![]() .
.
Клетку импликантной матрицы, образованную пересечением I-строки и J-столбца отметим крестиком.
Чтобы получить минимальную ДНФ заданной функции, достаточно найти минимальное число ![]() , которые совместно накрывают крестиками все столбцы импликантной матрицы.
, которые совместно накрывают крестиками все столбцы импликантной матрицы.
Пример 6. Найти минимальные ДНФ для функции
![]() .
.
Из предыдущего примера следует, что сокращенная ДНФ для данной функции ![]() . Очевидно, что
. Очевидно, что
![]() .
.
Строим импликантную матрицу
|
(0,0,1) |
(0,1,0) |
(0,1,1) |
(1,0,0) |
(1,0,1) |
(1,1,0) |
|
|
|
+ |
+ |
||||
|
|
+ |
+ |
||||
|
|
+ |
+ |
||||
|
|
+ |
+ |
||||
|
|
+ |
+ |
||||
|
|
+ |
+ |
Отсюда видно, что данная функция имеет два минимальные ДНФ:
![]() ;
; ![]() .
.
Вопросы для самоконтроля.
1. Дайте определение основных логических операций булевой алгебры.
2. Дайте определение булевой функции.
3. Что такое таблицы истинности булевой функции?
4. Каково число булевых функций от ![]() переменных?
переменных?
5. Какие булевы функции называются элементарными?
6. Дайте определение формулы алгебры логики.
7. Какие формулы алгебры логики называются равносильными?
8. Сформулируйте законы алгебры логики.
9. Какая формула алгебры логики называется двойственной к данной формуле алгебры логики?
10. Сформулируйте принцип двойственности.
11. Сформулируйте теорему о разложении и следствие из нее.
12. Дайте определение СДНФ.
13. Приведите алгоритмы построения СДНФ.
14. Дайте определение СКНФ.
15. Приведите алгоритмы построения СКНФ.
16. Дайте определение ДНФ.
17. Как найти ДНФ?
18. Дайте определение КНФ.
19. Как найти КНФ?
20. Какая формула алгебры логики называется тождественно истинной?
21. Какая формула алгебры логики называется тождественно ложной?
22. Какая формула алгебры логики называется выполнимой?
23. Что называется проблемой разрешимости?
24. Сформулируйте методы решения проблемы разрешения.
25. Что называется алгеброй Жегалкина?
26. Сформулируйте законы алгебры Жегалкина.
27. Что называется полиномом Жегалкина?
28. Сформулируйте алгоритмы построения полиномов Жегалкина.
29. Какая система булевых функций называется полной?
30. Что называется замыканием множества булевых функций?
31. Какой класс булевых функций называется замкнутым?
32. Дайте определение пяти важнейших замкнутых классов.
33. Сформулируйте теорему о полноте.
34. Сформулируйте алгоритм Поста.
35. Какая система булевых функций называется несократимой?
36. Каково максимальное возможное число функций в несократимой полной системе булевых функций?
37. Что такое релейно-контактная схема?
38. Почему любую булеву функцию можно изобразить в виде релейно-контактной схемы?
39. В чем состоит проблема анализа релейно-контактных схем?
40. В чем состоит проблема синтеза релейно-контактных схем?
41. Что такое логические элементы?
42. Приведите геометрическое изображение логических элементов.
43. Что такое логическая схема?
44. Что Вы понимаете под двоичным сумматором?
45. Какая ДНФ называется минимальной?
46. Чему равно число всех ДНФ от ![]() переменных?
переменных?
47. Сформулируйте тривиальный алгоритм построения МДНФ?
48. Что такое элементарная конъюнкция?
49. Что такое ранг элементарной конъюнкции?
50. Что называется интервалом элементарной конъюнкции?
51. Какой интервал называется максимальным?
52. Что называется областью истинности булевой функции?
53. Сформулируйте теорему об области истинности булевой функции.
54. Что называется покрытием области истинности булевой функции?
55. Какое число элементов содержится в интервале?
56. Какая ДНФ называется сокращенной?
57. В чем состоит геометрическая интерпретация задачи минимизации булевой функции?
58. Сформулируйте геометрический метод построения сокращенной ДНФ.
59. Сформулируйте метод Нельсона построения сокращенной ДНФ.
60. Сформулируйте метод Блейка построения сокращенной ДНФ.
61. Сформулируйте метод карт Карно построения сокращенной ДНФ.
62. Какая связь между МДНФ и сокращенной ДНФ?
63. Какое покрытие области истинности булевой функции называется неприводимым.
64. Какая ДНФ называется тупиковой?
65. Какая связь между МДНФ и тупиковой ДНФ?
66. Сформулируйте алгоритм построения всех тупиковых ДНФ.
67. Как строится импликантная матрица?
68. Сформулируйте алгоритм нахождения МДНФ методом импликантных матриц.
| < Предыдущая | Следующая > |
|---|
Калькулятор
Метод Квайна
В основе две операции:
где под p понимается некоторая элементарная конъюнкция.
Теорема.
Если в СДНФ какой-либо переключательной функции выполнить все возможные операции неполного попарного склеивания и элементарного поглощения, то в результате получится СкДНФ(сокращенная дизъюнктивная нормальная форма), эквивалентная исходной функции.
Итерационый алгоритм. Задача в нахождении по полной системе импликант (конституэнт единицы) полной системы простых импликант.
Алгоритм:
- Исходным является множество конституэнт единицы функции – импликанты нулевого ранга.
- Выполняются все возможные операции неполного попарного склеивания для элементарных конъюнкций длины n. (где n-кол-во аргументов).
Согласно соотношениям “a.” и “b.” результат – дополнительная импликанта p.
- Выполняются все возможные операции элементарного поглощения для элементарных конъюнкций длины n-1. (общая часть “p” имеет длину n-1)
- В результате получилось множество элементарных конъюнкций, разделяемых на два подмножества(по длине):
- подмножество элементарных конъюнкций длины n (оставшиеся)
- подмножество элементарных конъюнкций длины n-1
Элементарные конъюнкции длины n не участвовали в склеивания, а, следовательно, и в поглощении (т.к. поглощаются собственной частью те, которые участвовали в склеивании).
Следовательно, подмножество элементарных конъюнкций длины n входит в множество простых импликант (импликант нулевого ранга). - Если множество элементарных конъюнкций длины n-1 не пусто, то выполняются шаги со второго для конъюнкций длины n-1 и т.д.
Алгоритм завершается, когда подмножество является пустым, либо нельзя выполнить ни одной операции неполного попарного склеивания.
Таким образом, получаем систему простых импликант функции.
Нахождение тупиковых ДНФ
Стратегическая задача нахождения приведенной системы простых импликант заключается в нахождении наилучших покрытий единиц функции простыми импликантами.
Для системы простых импликант для заданной функции может быть получено несколько приведенных систем. Следует считать, что среди них есть такая, которая дает тупиковую нормальную форму минимальной длины.
Алгоритм нахождения приведенных систем простых импликант также является переборным. Задача в том, чтобы обеспечить направленный перебор. Для этого алгоритм строится в виде итерационной процедуры, которая содержит следующие шаги:
- Находятся такие единицы функции, которые покрываются только какой-то одной импликантой из системы простых импликант (для каждой единицы считаем сколько ее покрывает импликант и отмечаем их).
Этим импликанты образуют, так называемое, ядро функции. Такие импликанты будут входить в приведенную систему простых импликант. Следовательно, конъюнкции будут входить во все ТДНФ( в том числе минимальные).
- Исключаются из рассмотрения все единицы функции, покрываемые ядром.
- Осталось множество непокрытых ядром единицы функции и множество простых импликант, которые не вошли в ядро.
Повторяем шаг 1 и шаг 2 для оставшихся множеств (находится псевдоядро). Но перед повторением должен быть дополнительный шаг, который уменьшает перебор. (выкидываем из тех, которые покрывают одни и те же единицы(из оставшихся) ту импликанту, которая имеет наибольшую длину)
И так далее до тех пор, пока не будут покрыты все единицы функции.
Велика вероятность, что на каком-то шаге не найдется ни одной единицы функции, которая покрывается одной импликантой. В этом случае ищется наилучшее (наименьшей длины) покрытие оставшихся единиц функции методом перебора:
Если единица функции покрывается импликантами A,B,C,…
- Пусть A входит в ТДНФ, а B,C,… нет.
- Пусть В входит в ТДНФ, а A,C,… нет.
- Пусть C входит в ТДНФ, а A,B,… нет.
- …
Таким образом, получаем множество ТДНФ. Затем выбираем из них ДНФ наименьшей длины – получаем {МДНФ}.
Пример минимизации переключательной функции методом Квайна
Функция задана вектором: 883F. Запишем 16-ричное число 883F в двоичной виде в столбец значений функции таблицы истинности.
| Набор> | Значение исходной функции | Набор> | Значение исходной функции |
| 0000 | 1 | 1000 | 0 |
| 0001 | 0 | 1001 | 0 |
| 0010 | 0 | 1010 | 1 |
| 0011 | 0 | 1011 | 1 |
| 0100 | 1 | 1100 | 1 |
| 0101 | 0 | 1101 | 1 |
| 0110 | 0 | 1110 | 1 |
| 0111 | 0 | 1111 | 1 |
Цена ДНФ является суммой длин всех входящих в нее конъюнкций.
Минимизация функции методом Квайна.
На данном шаге все импликанты участвовали в операциях попарного неполного склеивания и были поглощены своими собственными частями. Поэтому простые импликанты на этом шаге не получены.
В результате на данном шаге получаем простые импликанты:![]()
![]()
![]() ,
, ![]()
![]()
![]()
В результате на данном шаге получаем простые импликанты:![]()
![]() ,
, ![]()
![]()
СкДНФ: ![]()
![]()
![]() v
v ![]()
![]()
![]() v
v ![]()
![]() v
v ![]()
![]()
Нахождение тупиковых форм.
Обозначения:
- Единицы ДНФ, покрываемые импликантами СкДНФ, обозначаются “+”.Импликанты, попадающие в ядро помечаются “*”.
- Единицы функции, которые покрываются только какой-то одной импликантой из системы простых импликант, помечаются “>”.
- Единицы функции, покрываемые ядром, но не покрываемые только какой-то одной импликантой из системы простых импликант, помечаются “>>”.
| > |
>> |
> |
> |
>> |
> |
>> |
>> |
|
| + | + | |||||||
| + | + | |||||||
| + | + | + | + | |||||
| + | + | + | + |
Ядро: ![]()
![]()
![]() v
v ![]()
![]() v
v ![]()
![]()
МДНФ: ![]()
![]()
![]() v
v ![]()
![]() v
v ![]()
![]() , цена=7
, цена=7
Графический метод минимизации – Карты Карно
Карты Карно – это графическое представление операций попарного неполного склеивания и элементарного поглощения.
Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции.
Карты Карно – определенная плоская развертка n-мерного булева куба.
Строится таблица истинности функции определенным образом. Каждая клетка таблицы соответствует вполне определенной вершине булева куба. Нулевые значения не записываются.
Карта Карно для функции 4-х переменных:
Карта Карно рассматривается как поверхность фигуры под названием тор (“бублик”).
p-клетки – клетки карты Карно, соответствующие единичному значению функции.
Соседние наборы – наборы, которые различаются только одним аргументом (одной орбитой).
Любой паре соседних наборов в Карте Карно соответствуют соседние клетки.
Две соседние p-клетки на карте Карно дают импликанту первого ранга. Например, клетки 1100 и 1101 отличаются только значением переменной x3, следовательно, они дают импликанту ![]() 1
1![]() 2
2![]() 4.
4.
Две соседние импликанты первого ранга образуют импликанту второго ранга.
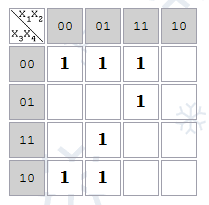
На этой карте соседние клетки образуют импликанты a,b,c,d,e. При этом импликанты a и b являются соседними, поэтому они образуют импликанту второго ранга.
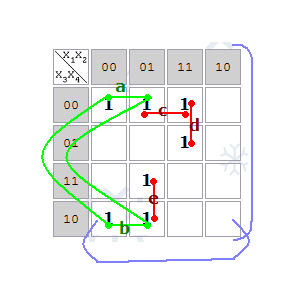
Если функция имеет 5 переменных, то рисуются 2 Карты Карно: для x5=0 и для x5=1. Если 6 переменных – 4 Карты, так чтобы в соседних картах соседние клетки имели одинаковые координаты:
Соседние p-клетки, соответствующие импликанте образуют компактную группу.
Количество p-клеток в компактной группе является степенью двойки.
Задача минимизации переключательной функции с помощью карт Карно заключается в нахождении импликант высшего ранга (соответствующих компактным группам наибольшей размерности), покрывающих p-клетки функции наилучшим образом.
Если на картах Карно выделить все компактные группы наибольшей размерности, то дизъюнкция соответствующих конъюнкций даст СкДНФ.
Пример минимизации функции 4-х переменных методом Карт Карно
Компактных групп размера 4 – 2
Компактных групп размера 2 – 2
Нахождение тупиковых форм.
Обозначения:
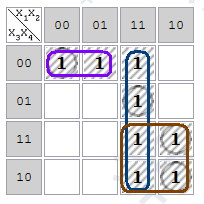
Цветом выделены компактные группы наибольшей размерности, вошедшие в ядро.
Ядро: ![]()
![]()
![]() v
v ![]()
![]() v
v ![]()
![]()
МДНФ: ![]()
![]()
![]() v
v ![]()
![]() v
v ![]()
![]() , цена=7
, цена=7
Машинно-ориентированные методы минимизации переключательных функций.
Основаны на применении соответствующих алгебр(или соответствующих алгебраический преобразований).
Вопрос 1. Интервальная форма задания функции. Постановка задачи минимизации.
Геометрический представление: (отображение функции на n-мерный булев куб)
Любому набору значений аргументов соответствует элементарная конъюнкция, содержащая все эти переменные – конституента единицы.
Те вершины n-мерного булева куба, в которых функция принимает единичное значение называются 0-кубами.
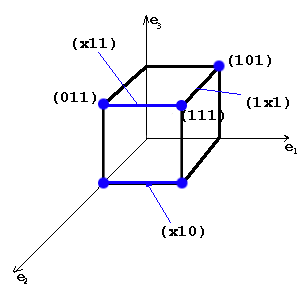
Два 0-куба образуют 1-куб, если соответствующие булевы вектора(их координаты) отличаются между собой значением только одной координаты(или одной компоненты). Эти координаты носят название свободной координаты. Обозначение x, остальные координаты 0-куба называются связанными и имеют либо 1, либо 0 значение. 0-кубы, образующие 1-куб называются его гранями. Два 1-куба образуют 2-куб, если свободная координата у них одинакова и они различаются значением только одной связанной компоненты.( 1-кубы – грани соответствующего 2-куба).
…
И так далее до n-куба( в случае тавтологии).
В общем случае, r-куб-это такой куб в булевом пространстве, у которого r свободных компонент и n-r связанных компонент.
Пример:
(1x1xx1) – 3-куб
(1x1x01),(1x1x11)- два 2-куба. Они являются гранями этого 3-куба(образуют его).
Если для какой-то функции взять все возможные кубы одинаковой размерности, то получаем множество кубов(или комплекс кубов).
Kr(f) – комплекс r-кубов функции f/
Для некоторой функции всегда есть комплекс
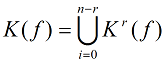
(Если Kn(f) содержит куб, то f – константа 1
оператор граней:
Cr=(a1a2…an-1an)-куб,
где a∈{0,1,x}, тогда для этого куба можно вычислить грани этого куба. Грани куба:
| ∂ip(a1a2…an-1an)= | a1a2…ai-1 p ai+1…an-1an, ai=x, p∈{0;1} | |
| ∅, ai ≠ x |
где C-получаемый куб.
При ai=x есть две грани (вместо i-ой либо 0, либо 1).
Оператор сограней
позволяет вычислить куб большей размерности, гранью которого может быть этот куб.
| δi(a1a2…an-1an)= | a1a2…ai-1 x ai+1…an-1an, ai≠x, Cr+1⊆K(f) | |
| ∅, ai=x, Cr+1⊄K(f) |
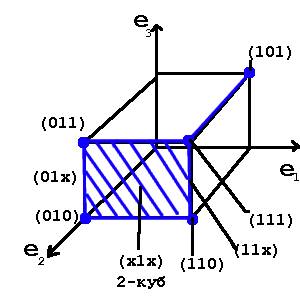
Подмножество вершин булева куба, соответствующие кубу размерности r называется интервалом булева пространства ранга r. (интервал 1 ранга – 1×1, интервал 2 ранга – x1x)
Для нашего примера:
K0(f)={101,110,111,010,011}
K1(f)={01x,11x,1×1,x11,x10}
K2(f)={x1x}
В общем случае комплекс кубов определенного ранга не является покрытием исходной функции(за исключением K0).
В нашем примере K2 не является покрытием, хотя K1 – покрытие.
K(f)=K0∪K1∪K2 – для нашей функции
Куб большей размерности покрывает кубы меньшей размерности, если они могут быть получены из него последовательным применением оператора граней.
(x1x) имеет грани (01x) и (11x), которые имеют грани : (010),(011) и (110),(111)
Если взять интервал булева пространства, то аналитически его можно описать в виде соответствующих элементарных конъюнкций.
Некоторый комплекс кубов – L, таких, что каждая вершина из комплекса K0(f) включена по крайней мер в один из кубов комплекса L, называется покрытием комплекса K функции f.
Каждое покрытие комплекса K(f) определяет некоторую ДНФ переключательной функции.
Покрытие можно рассматривать (с точки зрения реализации), как двухуровневую схему.
| Аргументы (0-ой уровень) | конъюнктивные члены(элементарные конъюнкции) (1-ый уровень) | дизъюнкция (2-ой уровень) |
Не учитывается инверсия аргументов на нулевом уровне.
Минимизация
Цена r-куба: c=n-r – число связанных переменных, количество символов в элементарной конъюнкции(совпадает с ценой в смысле Квайне)
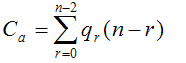
–цена покрытия, где qr-количество кубов размерности r в покрытии L.
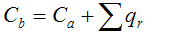 -вторая функция цены покрытия(учитывает число кубов)
-вторая функция цены покрытия(учитывает число кубов)
Задача минимизации: Найти такое покрытие L комплекса K(f), цена которого будет минимальна – минимизация в смысле Квайне.
Задача решается алгебраически, вводится свой математический аппарат. Это аппарат исчисления кубических комплексов (задает операции над кубами).
Каждая операция проходит в два этапа:
I Этап. Предварительное вычисление путем покоординатной обработки кубов по правилам, задаваемым с помощью таблиц покоординатной обработки.
II Этап. Окончательный.
Зададим операции над кубами:
a = (a1 a2 … an)
b = (b1 b2 … bn)
- Операция *: c=a*b
По содержанию * – это нахождение куба некоторой размерности r, грани которого содержаться в кубах a и b.
ci=ai*bi 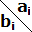
0 1 x 0 0 y 0 1 y 1 1 x 0 1 x a*b = 
∅, если ∑αici>1 c, если ∑αici≤1 где αici = 
0, ci≠y 1, ci=y c = ([a1*b1] … [an*bn]).
При чем, если результат операции – y, то y заменяется на x.
(101)*(111)
после предварительной обработки:
=(1y1)
Окончательный вариант:
=(1×1)(x11)*(101)=(1×1)
(x10) (101) (1yy) ∅ – нет общих граней - Операция пересечения кубов.
c = a ∩ b
покоординатно!
ci=ai∩bi 
0 1 x 0 0 ∅ 0 1 ∅ 1 1 x 0 1 x a ∩ b = 
∅, если ∃i (ai∩bi = ∅ c в противном случае Пересечение – нахождение общей части булева пространства, покрываемой этими кубами (т.е. куба или грани какого-то уровня)

(1×1)∩(x1x)=(111) - Операция вычитания кубов (#).
ci=ai#bi 
0 1 x 0 z y z 1 y z z x 1 0 z * и ∪ обладают свойством коммутативности, но a#b ≠ b#a !
Операция вычитания кубов удаляет из куба a общую часть кубов уменьшаемого и вычитаемого (т.е. пересечение кубов a и b).
В результате вычитания можем иметь несколько кубов.
Если куб a входит в куб b, то результат – ∅
Пример:
a#b = (1×1)#(x11) = (z0z) = (101)
c#b = (1xx)#(x11) = (z00) = {(10x),(1×0)}
Нахождение множества простых импликант
K(f)=K0∪K1∪…∪Ki∪…∪Kn-1 – комплекс K функции f
z⊆K является простой импликантой этого комплекса, если δi(z)=∅ (δi – оператор сограней), то есть не существует какого-либо другого куба, который бы включал в себя исходный куб z.
Z(f)={z} – множество импликант для функции f
Необходимо получить весь комплекс K функции f, используя операторы граней и сограней.
Берем куб z из K и проверяем, есть ли какой-то куб, гранью которого является рассматриваемый.
Операция *(“звездочка”) позволяет получить множество Z – кубов, соответствующих простым импликантам функции.
Алгоритм (*) – нахождение множества кубов, соответствующих простым импликантам функции.
Предположим есть некоторый комплекс Ĉ0, являющийся покрытием комплекса K(f), т.е.
- Ĉ0(f) – неупорядоченное покрытие
причем одна и та же единица функции может покрываться несколькими кубами - C0 = Ĉ0 – {c1 | c1 ∈ Ĉ0 ∧ c2 ∈ Ĉ0 ∧ c1 ⊆ c2}
(тоже, что и поглощение в методе Квайне) - C0*C0 попарно
- в результате 3) находится множество 0-кубов:
Z0 = { c0 | c0 * C0 не содержит никаких 1-кубов }
– это такие кубы, которые в результате операции * не дают никаких 1-кубов - вычисляется Ĉ1:
Ĉ1 = C0 ∪ (C0*C0) - C1 = Ĉ1 – { c | c ⊆ d, c,d∈Ĉ1 } – {0-кубы, получившиеся в результате операции *, и Z0}
( (1×1)*(x11)= (111) ) - C1 * C1
- Z1
- Ĉ2
- C2 (удаляем 0-кубы и 1-кубы)
и так далее (итерационный процесс)
Ĉ0(f) – исходное покрытие K(f)
C1(f) и т.д. в общем случае покрытием функции не являются
C1(f) ∪ Z0 ⊆ K – является покрытием K(f)
Алгоритм заканчивается, когда на каком-то шаге получаем множество C, содержащее один куб.
Результат – множество Z – множество простых импликант.
Z = ∪Zi
Алгоритм извлечения
ИЗ множества простых импликант извлечь те (выбрать такое подмножество кубов) простые импликанты, которые:
- Является покрытием исходного множества кубов функции;
- С минимальной ценой покрытия, если покрытий несколько.
Для решения этой задачи исходные данные фактически – исходный комплекс функции, то есть некоторый исходный комплекс K0(f) и Z(f).
Определение: возьмем некоторую вершину d∈K0. Говорят, что эта вершина является обособленной вершиной комплекса на множестве простых импликант Z, если существует такой куб z∈Z, что вершина d накрывается только этой импликантой z.
Такая импликанта будет простая. Вершина d называется различающей. А импликанта получила название экстремаль.
Любое минимальное покрытие содержит экстремали нулевого ранга.
Пример:
Различающие вершины: (0;0;1) и (0;1;0)
E0={ a, d}, осталось покрыть одну вершину – (1;1;1)
Задача минимизации: необходимо найти все обособленные вершины и выделить импликанты, накрывающие эти обособленные вершины.
Такие импликанты образуют множество экстремалей.
Задача решается, если известно K0(f), то есть все вершины.
В общем случае задачи минимизации функция задана некоторым комплексом K(f), который состоит не только из 0-кубов. Тогда можно найти все 0-кубы и решить задачу, а можно и не находить.
- Некоторая простая импликанта e∈Z является экстремалью, если e∩K ≠ e∩U'(e,Z)∩K, а e∩K ≠ ∅,
U'(e,Z) = U(e,Z) – e,
U(e,Z) = { z | z∈Z, Z∩e ≠ ∅}.
Z – множество простых импликант,
U(e,Z) – окрестность куба e, т.е. все простые импликанты из Z, которые имеют общие части с импликантой e.
U'(e,Z) – окрестность без самой импликанты.Функция может быть не полностью определена:
L – комплекс, где функция определена и равна 1,
D – комплекс, где значение функции не определено,
тогда K=L∪D.
но чаще экстремали вычисляют по одному соотношению:
- [e#(Z-e)]∩K≠∅
e#(Z-e) – те вершины булева куба, которые накрываются только e и не накрываются всех оставшейся частью Z.
+ эти вершины присутствуют в комплексе K (или L для неполностью определенной функции)Если из простой импликанты e удалить все подкубы (Z-e), и остается, по крайней мере, одна вершина булева куба, которая содержится в исходном комплексе функции, то оставшиеся вершины является выделенными, или отмеченными.
Алгоритм нахождения экстремалей также итерационный.
Нахождение множества экстремалей
- Каждая простая импликанта проверяется на наличие в ней выделенной вершины, т.е. вычисляется e#(Z-e), если результат вычитания кубов не пустой, то такая импликанта может быть экстремалью.
Как правило, вычитание e#(Z-e) сводится в таблицу.
- Каждый кандидат на экстремаль проверяется на пересечение с комплексом единичных значений функции.
Если результат пересечения не пустой, значит в L (комплексе единичных значений) имеются обособленные вершины, а e является экстремалью.
Получаем множество экстремалей нулевого ранга – E0 = {e}. В смысле Квайна оно соответствует ядру функции.
- Находим
 1 = Z0 – E0
1 = Z0 – E0
Т.е. из множества простых импликант удаляем множество экстремалей нулевого ранга.
Находим L1 = L0 # E0, т.е. находятся все вершины, не покрытые экстремалями.
 1 – оставшаяся часть множества простых импликант, неупорядоченное множество простых импликант.
1 – оставшаяся часть множества простых импликант, неупорядоченное множество простых импликант.
Операция, которая позволяет сократить в последующем перебор и исключить из
 i не максимальные кубы – упорядочивание.
i не максимальные кубы – упорядочивание.
Пусть u∈
 1, v∈
1, v∈ 1. Говорят, что u1 удовлетворяет условию u∩L1 ⊆ v∩L1.
1. Говорят, что u1 удовлетворяет условию u∩L1 ⊆ v∩L1.
( вершины из L1, покрываемые u, покрываются и кубов v )В этом случае из кубов u,v выбираем при упорядочивание куб v.
Если кубы разной размерности, а вершины покрывают одинаковые – то оставляем куб большей размерности ( цена = n – r ).
Таким образом,
 1 => Z1 (находится Z1 – упорядоченной множество оставшихся простых импликант), применением процедуры упорядочивания.
1 => Z1 (находится Z1 – упорядоченной множество оставшихся простых импликант), применением процедуры упорядочивания.
- Остались Z1 и L1
(Z1,L1) => E1 по тому же алгоритму.
Затем
 2 => Z2; L2 = L1#E1; (Z2,L2) => E2 и т.д.
2 => Z2; L2 = L1#E1; (Z2,L2) => E2 и т.д.
Два варианта окончания алгоритма:
- L = ∅ => покрытие единственное
E = ∪Ei - L ≠ ∅ Если проверка на экстремальность не дает результата, т.е. ни одна простая импликанта не содержит квазеопорных вершин, а операция упорядочивания не дает результата.
Пример:
В этом случае не остается никакого другого варианта решения, кроме волюнтаристского.
Берется любая простая импликанта, для которой выдвигается две гипотезы (Алгоритм ветвления):
- простая импликанта входит в минимальное покрытие
e∈E
находим Li+1=Li#{e}, упорядочиваем Z и вновь применяем алгоритм извлечения (возможно еще ветвление). - простая импликанта не входит в минимальное покрытие
e∉E
удаляем e из Zi (находим i+1), упорядочиваем
i+1), упорядочиваем  i+1 => Zi+1
i+1 => Zi+1
Li+1 = Li
И применяем алгоритм извлечения.
Таким образом, при ветвление получаем множество покрытий, сравниваем по цене и выбираем наименьшей.
- простая импликанта входит в минимальное покрытие
Все вычисления в ручном варианте сводятся к вычислениям над таблицами.
Минимизация функции методом кубических покрытий.
Рассмотрим комплекс кубов К(f) = L D, где L – множество единичных наборов, D – множество наборов, на которых ДНФ не определена.
Будем выполнять операцию “*” для получения множества простых импликант.
| 0000 | 0010 | 0100 | 0110 | 1010 | 1100 | 1101 | 1110 | |
| 0000 | – | 00×0 | 0x00 | Ø | Ø | Ø | Ø | Ø |
| 0010 | 00×0 | – | Ø | 0x10 | x010 | Ø | Ø | Ø |
| 0100 | 0x00 | Ø | – | 01×0 | Ø | x100 | Ø | Ø |
| 0110 | Ø | 0x10 | 01×0 | – | Ø | Ø | Ø | x110 |
| 1010 | Ø | x010 | Ø | Ø | – | Ø | Ø | 1×10 |
| 1100 | Ø | Ø | x100 | Ø | Ø | – | 110x | 11×0 |
| 1101 | Ø | Ø | Ø | Ø | Ø | 110x | – | Ø |
| 1110 | Ø | Ø | Ø | x110 | 1×10 | 11×0 | Ø | – |
Z0=Ø
Ĉ1=C0∪(C0*C0)
C1=>
| 00×0 | 0x00 | 0x10 | x010 | 01×0 | x100 | x110 | 1×10 | 110x | 11×0 | |
| 00×0 | – | 0000 | 0010 | 0010 | 0xx0 | 0x00 | 0x10 | x010 | Ø | Ø |
| 0x00 | 0000 | – | 0xx0 | 00×0 | 0100 | 0100 | 01×0 | Ø | x100 | x100 |
| 0x10 | 0010 | 0xx0 | – | 0010 | 0110 | 01×0 | 0110 | xx10 | Ø | x110 |
| x010 | 0010 | 00×0 | 0010 | – | 0x10 | Ø | xx10 | 1010 | Ø | 1×10 |
| 01×0 | 0xx0 | 0100 | 0110 | 0x10 | – | 0100 | 0110 | x110 | x100 | x1x0 |
| x100 | 0x00 | 0100 | 01×0 | Ø | 0100 | – | x1x0 | 11×0 | 1100 | 1100 |
| x110 | 0x10 | 01×0 | 0110 | xx10 | 0110 | x1x0 | – | 1110 | 11×0 | 1110 |
| 1×10 | x010 | Ø | xx10 | 1010 | x110 | 11×0 | 1110 | – | 11×0 | 1110 |
| 110x | Ø | x100 | Ø | Ø | x100 | 1100 | 11×0 | 11×0 | – | 1100 |
| 11×0 | Ø | x100 | x110 | 1×10 | x1x0 | 1100 | 1110 | 1110 | 1100 | – |
Z1=
Ĉ2=C1∪(C1*C1)
C2=>
| 0xx0 | xx10 | x1x0 | |
| 0xx0 | – | 0x10 | 01×0 |
| xx10 | 0x10 | – | x110 |
| x1x0 | 01×0 | x110 | – |
Z2=
Ĉ3=C2∪(C2*C2)
C3=>Ø
Z = Z0∪Z1∪Z2
Z=>
Нахождение тупиковых форм.
| 110x | 0xx0 | xx10 | x1x0 | ||
|
110x |
– |
110x |
110x |
1101 |
v |
|
0xx0 |
0xx0 |
– |
0x00 |
0000 |
v |
|
xx10 |
xx10 |
1×10 |
– |
1010 |
v |
|
x1x0 |
x110 |
1110 |
Ø | – |
E0:
L1=L0#E0
| 110x | 0xx0 | xx10 | |
|
0000 |
0000 |
1010 |
Ø |
L1:Ø
 1=Z0-E0
1=Z0-E0
 1 => Z1
1 => Z1
Z1:
E:
МДНФ:![]()
![]()
![]() v
v ![]()
![]() v
v ![]()
![]() , цена=7
, цена=7
Содержание
- Постановка задачи
- Решение задачи
- Анализ переключательной функции
- Метод Квайна
- Карты Карно
- Кубические покрытия
- Анализ полученных результатов
- Список литературы
1. Постановка задачи
Минимизировать переключательную функцию шести аргументов. Функция задана в виде наборов, на которых значения функции равны единице либо не определены. Наборы задаются в шестнадцатеричной системе счисления. В скобках заданы наборы, на которых значение функции не определено:
y => (2) v (3B) v (20) v (21) v (1D) v (6) v (1B) v (D) v (24) v (2C) v (23) v (B) v 36 v 1C v 3A v 7 v A v 8 v 10 v 38 v 12 v 15 v 5 v 1F v 3F v 1A v 17 v 3E v 3D v 39 v 9 v 37 v 19 v 2A v 11 v 18 v 4 v 3C v 2E v 29 v 0 v 2D v 28 v 25 v 14 v 1E
Необходимо выполнить следующие задачи:
- Доопределить функцию нулями, минимизировать полученную функцию методом Квайна;
- Доопределить функцию единицами и произвести минимизацию, используя карты Карно;
- Минимизировать исходную функцию методом кубических покрытий;
- Проанализировать полученные результаты;
2. Решение задачи
2.1 Анализ переключательной функции
Представим исходную последовательность в виде таблицы истинности.
Исходная последовательность:
(2) v (3B) v (20) v (21) v (1D) v (6) v (1B) v (D) v (24) v (2C) v (23) v (B) v 36 v 1C v 3A v 7 v A v 8 v 10 v 38 v 12 v 15 v 5 v 1F v 3F v 1A v 17 v 3E v 3D v 39 v 9 v 37 v 19 v 2A v 11 v 18 v 4 v 3C v 2E v 29 v 0 v 2D v 28 v 25 v 14 v 1E
| Набор | Значение исходной функции | Набор | Значение исходной функции |
|---|---|---|---|
| x1x2x3x4x5x6 | x1x2x3x4x5x6 | ||
| 000000 | 1 | 100000 | ? |
| 000001 | 0 | 100001 | ? |
| 000010 | ? | 100010 | 0 |
| 000011 | 0 | 100011 | ? |
| 000100 | 1 | 100100 | ? |
| 000101 | 1 | 100101 | 1 |
| 000110 | ? | 100110 | 0 |
| 000111 | 1 | 100111 | 0 |
| 001000 | 1 | 101000 | 1 |
| 001001 | 1 | 101001 | 1 |
| 001010 | 1 | 101010 | 1 |
| 001011 | ? | 101011 | 0 |
| 001100 | 0 | 101100 | ? |
| 001101 | ? | 101101 | 1 |
| 001110 | 0 | 101110 | 1 |
| 001111 | 0 | 101111 | 0 |
| 010000 | 1 | 110000 | 0 |
| 010001 | 1 | 110001 | 0 |
| 010010 | 1 | 110010 | 0 |
| 010011 | 0 | 110011 | 0 |
| 010100 | 1 | 110100 | 0 |
| 010101 | 1 | 110101 | 0 |
| 010110 | 0 | 110110 | 1 |
| 010111 | 1 | 110111 | 1 |
| 011000 | 1 | 111000 | 1 |
| 011001 | 1 | 111001 | 1 |
| 011010 | 1 | 111010 | 1 |
| 011011 | ? | 111011 | ? |
| 011100 | 1 | 111100 | 1 |
| 011101 | ? | 111101 | 1 |
| 011110 | 1 | 111110 | 1 |
| 011111 | 1 | 111111 | 1 |
‘?’ обозначено значение наборов, на которых функция не определена.
Цена ДНФ является суммой длин всех входящих в нее конъюнкций.
2.2 Минимизация функции методом Квайна.
Доопределим функцию нулями, получим конституэнты единицы, затем выполним операции попарного неполного склеивания и элементарного поглощения.
|
|
На данном шаге все импликанты участвовали в операциях попарного неполного склеивания и были поглощены своими собственными частями. Поэтому простые импликанты на этом шаге не получены.
|
|
В результате на данном шаге получаем простые импликанты:
x2x3x4x5x6 , x1x2x4x5x6
|
|
В результате на данном шаге получаем простые импликанты:
x1x3x5x6 , x1x4x5x6 , x1x3x4x5 , x1x3x4x6 , x1x2x3x5 , x1x2x4x5 , x1x2x4x6 , x1x2x5x6 , x2x4x5x6 , x2x3x4x5 , x1x3x5x6 , x1x3x5x6 , x1x2x4x5 , x1x2x3x5 , x1x2x3x4
|
В результате на данном шаге получаем простые импликанты:
x3x4x5 , x3x4x6 , x2x3x6
СкДНФ:
x2x3x4x5x6 v x1x2x4x5x6 v x1x3x5x6 v x1x4x5x6 v x1x3x4x5 v x1x3x4x6 v x1x2x3x5 v x1x2x4x5 v x1x2x4x6 v x1x2x5x6 v x2x4x5x6 v x2x3x4x5 v x1x3x5x6 v x1x3x5x6 v x1x2x4x5 v x1x2x3x5 v x1x2x3x4 v x3x4x5 v x3x4x6 v x2x3x6
Нахождение тупиковых форм.
Обозначения:
- Единицы ДНФ, покрываемые импликантами СкДНФ, обозначаются “+”.Импликанты, попадающие в ядро помечаются “*”.
- Единицы функции, которые покрываются только какой-то одной импликантой из системы простых импликант, помечаются “>”.
- Единицы функции, покрываемые ядром, но не покрываемые только какой-то одной импликантой из системы простых импликант, помечаются “>>”.
|
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
|
| x2x3x4x5x6 | + | + | ||||||||||||||||||||||||||||||||
| x1x2x4x5x6 | + | + | ||||||||||||||||||||||||||||||||
| x1x3x5x6 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x4x5x6 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x3x4x5 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x3x4x6* | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x3x5 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x4x5 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x4x6* | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x5x6 | + | + | + | + | ||||||||||||||||||||||||||||||
| x2x4x5x6 | + | + | + | + | ||||||||||||||||||||||||||||||
| x2x3x4x5 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x3x5x6 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x3x5x6* | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x4x5* | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x3x5 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x3x4 | + | + | + | + | ||||||||||||||||||||||||||||||
| x3x4x5* | + | + | + | + | + | + | + | + | ||||||||||||||||||||||||||
| x3x4x6* | + | + | + | + | + | + | + | + | ||||||||||||||||||||||||||
| x2x3x6 | + | + | + | + | + | + | + | + |
Ядро: x1x3x4x6 v x1x2x4x6 v x1x3x5x6 v x1x2x4x5 v x3x4x5 v x3x4x6
До упорядочивания:
|
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
|
| x2x3x4x5x6 | + | ||||||||||
| x1x2x4x5x6 | + | + | |||||||||
| x1x3x5x6 | + | + | + | ||||||||
| x1x4x5x6 | + | ||||||||||
| x1x3x4x5 | + | + | |||||||||
| x1x2x3x5 | + | + | |||||||||
| x1x2x4x5 | + | ||||||||||
| x1x2x5x6 | + | + | |||||||||
| x2x4x5x6 | + | ||||||||||
| x2x3x4x5 | + | + | |||||||||
| x1x3x5x6 | + | + | |||||||||
| x1x2x3x5 | + | + | |||||||||
| x1x2x3x4 | + | + | |||||||||
| x2x3x6 | + | + | + |
После упорядочивания:
|
x1x2x3x4x5x6> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
|
| x1x2x4x5x6* | + | + | |||||||||
| x1x3x5x6* | + | + | + | ||||||||
| x1x2x3x5* | + | + | |||||||||
| x1x2x5x6 | + | + | |||||||||
| x2x3x4x5* | + | + | |||||||||
| x1x3x5x6 | + | + | |||||||||
| x1x2x3x5 | + | + | |||||||||
| x2x3x6 | + | + | + |
Псевдоядро: x1x2x4x5x6 v x1x3x5x6 v x1x2x3x5 v x2x3x4x5
До упорядочивания:
| x1x2x3x4x5x6 | x1x2x3x4x5x6 | x1x2x3x4x5x6 | |
| x1x2x5x6 | + | ||
| x1x3x5x6 | + | ||
| x1x2x3x5 | + | + | |
| x2x3x6 | + | + |
После упорядочивания:
| x1x2x3x4x5x6> | x1x2x3x4x5x6>> | x1x2x3x4x5x6> | |
| x1x2x3x5* | + | + | |
| x2x3x6* | + | + |
Псевдоядро: x1x2x3x5 v x2x3x6
МДНФ: x1x3x4x6 v x1x2x4x6 v x1x3x5x6 v x1x2x4x5 v x3x4x5 v x3x4x6 v x1x2x4x5x6 v x1x3x5x6 v x1x2x3x5 v x2x3x4x5 v x1x2x3x5 v x2x3x6, цена=46
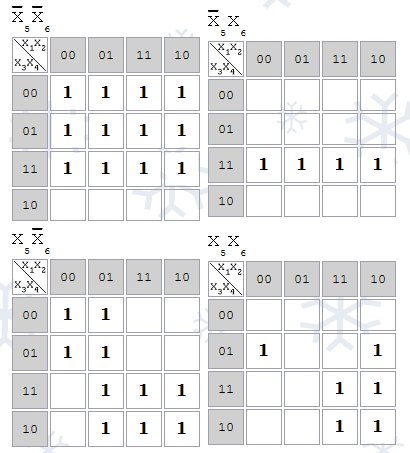
2.3 Минимизация функции методом Карт Карно.
Дополним функцию единицами и построим Карты Карно.
Компактных групп размера 16 – 1
Компактных групп размера 8 – 9
Компактных групп размера 4 – 13
Компактных групп размера 2 – 1
Нахождение тупиковых форм.
Обозначения:
Ядро: x1x2x3x4x6 v x1x2x4x5 v x1x4x6 v x1x3x4 v x1x2x5 v x1x3x6 v x2x3
Псевдоядро: x1x2x3x4 v x1x3x4x6
Псевдоядро: x1x2x5
Псевдоядро: x3x5x6
МДНФ: x1x2x3x4x6 v x1x2x4x5 v x1x4x6 v x1x3x4 v x1x2x5 v x1x3x6 v x2x3 v x1x2x3x4 v x1x3x4x6 v x1x2x5 v x3x5x6, цена=37
2.4 Минимизация функции методом кубических покрытий.
Рассмотрим комплекс кубов К(f) = L D, где L – множество единичных наборов, D – множество наборов, на которых ДНФ не определена.
Будем выполнять операцию “*” для получения множества простых импликант.
| K(f) = |
|
=> C0 => |
|
| 000000 | 000010 | 000100 | 000101 | 000110 | 000111 | 001000 | 001001 | 001010 | 001011 | 001101 | 010000 | 010001 | 010010 | 010100 | 010101 | 010111 | 011000 | 011001 | 011010 | 011011 | 011100 | 011101 | 011110 | 011111 | 100000 | 100001 | 100011 | 100100 | 100101 | 101000 | 101001 | 101010 | 101100 | 101101 | 101110 | 110110 | 110111 | 111000 | 111001 | 111010 | 111011 | 111100 | 111101 | 111110 | 111111 | |
| 000000 | – | 0000×0 | 000×00 | Ø | Ø | Ø | 00×000 | Ø | Ø | Ø | Ø | 0x0000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000010 | 0000×0 | – | Ø | Ø | 000×10 | Ø | Ø | Ø | 00×010 | Ø | Ø | Ø | Ø | 0x0010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000100 | 000×00 | Ø | – | 00010x | 0001×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000101 | Ø | Ø | 00010x | – | Ø | 0001×1 | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | Ø | 0x0101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000110 | Ø | 000×10 | 0001×0 | Ø | – | 00011x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000111 | Ø | Ø | Ø | 0001×1 | 00011x | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001000 | 00×000 | Ø | Ø | Ø | Ø | Ø | – | 00100x | 0010×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001001 | Ø | Ø | Ø | Ø | Ø | Ø | 00100x | – | Ø | 0010×1 | 001×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001010 | Ø | 00×010 | Ø | Ø | Ø | Ø | 0010×0 | Ø | – | 00101x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0010×1 | 00101x | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001101 | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | 001×01 | Ø | Ø | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010000 | 0x0000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | – | 01000x | 0100×0 | 010×00 | Ø | Ø | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01000x | – | Ø | Ø | 010×01 | Ø | Ø | 01×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010010 | Ø | 0x0010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0100×0 | Ø | – | Ø | Ø | Ø | Ø | Ø | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010100 | Ø | Ø | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010×00 | Ø | Ø | – | 01010x | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010101 | Ø | Ø | Ø | 0x0101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010×01 | Ø | 01010x | – | 0101×1 | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010111 | Ø | Ø | Ø | Ø | Ø | 0x0111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0101×1 | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 011000 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | Ø | Ø | Ø | Ø | 01×000 | Ø | Ø | Ø | Ø | Ø | – | 01100x | 0110×0 | Ø | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 011001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | Ø | 01×001 | Ø | Ø | Ø | Ø | 01100x | – | Ø | 0110×1 | Ø | 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø |
| 011010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | 01×010 | Ø | Ø | Ø | 0110×0 | Ø | – | 01101x | Ø | Ø | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø |
| 011011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0110×1 | 01101x | – | Ø | Ø | Ø | 011×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11011 | Ø | Ø | Ø | Ø |
| 011100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | 011×00 | Ø | Ø | Ø | – | 01110x | 0111×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø |
| 011101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | 011×01 | Ø | Ø | 01110x | – | Ø | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø |
| 011110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | 0111×0 | Ø | – | 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | Ø |
| 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | 011×11 | Ø | 0111×1 | 01111x | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 |
| 100000 | x00000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | – | 10000x | Ø | 100×00 | Ø | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10000x | – | 1000×1 | Ø | 100×01 | Ø | 10×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1000×1 | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100100 | Ø | Ø | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×00 | Ø | Ø | – | 10010x | Ø | Ø | Ø | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100101 | Ø | Ø | Ø | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×01 | Ø | 10010x | – | Ø | Ø | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 101000 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×000 | Ø | Ø | Ø | Ø | – | 10100x | 1010×0 | 101×00 | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 101001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×001 | Ø | Ø | Ø | 10100x | – | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø |
| 101010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1010×0 | Ø | – | Ø | Ø | 101×10 | Ø | Ø | Ø | Ø | 1×1010 | Ø | Ø | Ø | Ø | Ø |
| 101100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×100 | Ø | 101×00 | Ø | Ø | – | 10110x | 1011×0 | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø |
| 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×101 | Ø | 101×01 | Ø | 10110x | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø |
| 101110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 101×10 | 1011×0 | Ø | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | Ø |
| 110110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | – | 11011x | Ø | Ø | Ø | Ø | Ø | Ø | 11×110 | Ø |
| 110111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11011x | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11×111 |
| 111000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | – | 11100x | 1110×0 | Ø | 111×00 | Ø | Ø | Ø |
| 111001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | 11100x | – | Ø | 1110×1 | Ø | 111×01 | Ø | Ø |
| 111010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | Ø | Ø | Ø | Ø | 1110×0 | Ø | – | 11101x | Ø | Ø | 111×10 | Ø |
| 111011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1110×1 | 11101x | – | Ø | Ø | Ø | 111×11 |
| 111100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | Ø | 111×00 | Ø | Ø | Ø | – | 11110x | 1111×0 | Ø |
| 111101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | Ø | 111×01 | Ø | Ø | 11110x | – | Ø | 1111×1 |
| 111110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 11×110 | Ø | Ø | Ø | 111×10 | Ø | 1111×0 | Ø | – | 11111x |
| 111111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11×111 | Ø | Ø | Ø | 111×11 | Ø | 1111×1 | 11111x | – |
Z0=Ø
Ĉ1=C0∪(C0*C0)
C1=>
| 0000×0, 000×00, 00×000 0x0000, x00000, 000×10 00×010, 0x0010, 00010x 0001×0, 0x0100, x00100 0001×1, 00×101, 0x0101 x00101, 00011x, 0x0111 00100x, 0010×0, 0x1000 x01000, 0010×1, 001×01 0x1001, x01001, 00101x 0x1010, x01010, 0x1011 0x1101, x01101, 01000x 0100×0, 010×00, 01×000 010×01, 01×001, 01×010 01010x, 01×100, 0101×1 01×101, 01×111, x10111 01100x, 0110×0, 011×00 x11000, 0110×1, 011×01 x11001, 01101x, 011×10 x11010, 011×11, x11011 01110x, 0111×0, x11100 0111×1, x11101, 01111x x11110, x11111, 10000x 100×00, 10×000, 1000×1 100×01, 10×001, 10010x 10×100, 10×101, 10100x 1010×0, 101×00, 1×1000 101×01, 1×1001, 101×10 1×1010, 10110x, 1011×0 1×1100, 1×1101, 1×1110 11011x, 11×110, 11×111 11100x, 1110×0, 111×00 1110×1, 111×01, 11101x 111×10, 111×11, 11110x 1111×0, 1111×1, 11111x |
| 0000×0 | 000×00 | 00×000 | 0x0000 | x00000 | 000×10 | 00×010 | 0x0010 | 00010x | 0001×0 | 0x0100 | x00100 | 0001×1 | 00×101 | 0x0101 | x00101 | 00011x | 0x0111 | 00100x | 0010×0 | 0x1000 | x01000 | 0010×1 | 001×01 | 0x1001 | x01001 | 00101x | 0x1010 | x01010 | 0x1011 | 0x1101 | x01101 | 01000x | 0100×0 | 010×00 | 01×000 | 010×01 | 01×001 | 01×010 | 01010x | 01×100 | 0101×1 | 01×101 | 01×111 | x10111 | 01100x | 0110×0 | 011×00 | x11000 | 0110×1 | 011×01 | x11001 | 01101x | 011×10 | x11010 | 011×11 | x11011 | 01110x | 0111×0 | x11100 | 0111×1 | x11101 | 01111x | x11110 | x11111 | 10000x | 100×00 | 10×000 | 1000×1 | 100×01 | 10×001 | 10010x | 10×100 | 10×101 | 10100x | 1010×0 | 101×00 | 1×1000 | 101×01 | 1×1001 | 101×10 | 1×1010 | 10110x | 1011×0 | 1×1100 | 1×1101 | 1×1110 | 11011x | 11×110 | 11×111 | 11100x | 1110×0 | 111×00 | 1110×1 | 111×01 | 11101x | 111×10 | 111×11 | 11110x | 1111×0 | 1111×1 | 11111x | |
| 0000×0 | – | 000000 | 000000 | 000000 | 000000 | 000010 | 000010 | 000010 | 000×00 | 000xx0 | 000×00 | 000×00 | Ø | Ø | Ø | Ø | 000×10 | Ø | 00×000 | 00x0x0 | 00×000 | 00×000 | Ø | Ø | Ø | Ø | 00×010 | 00×010 | 00×010 | Ø | Ø | Ø | 0x0000 | 0x00x0 | 0x0000 | 0x0000 | Ø | Ø | 0x0010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x00000 | x00000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000×00 | 000000 | – | 000000 | 000000 | 000000 | 000xx0 | 0000×0 | 0000×0 | 000100 | 000100 | 000100 | 000100 | 00010x | 00010x | 00010x | 00010x | 0001×0 | Ø | 00×000 | 00×000 | 00×000 | 00×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0000 | 0x0000 | 0x0x00 | 0x0000 | Ø | Ø | Ø | 0x0100 | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x00x00 | x00000 | Ø | Ø | Ø | x00100 | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00×000 | 000000 | 000000 | – | 000000 | 000000 | 0000×0 | 00x0x0 | 0000×0 | 000×00 | 000×00 | 000×00 | 000×00 | Ø | Ø | Ø | Ø | Ø | Ø | 001000 | 001000 | 001000 | 001000 | 00100x | 00100x | 00100x | 00100x | 0010×0 | 0010×0 | 0010×0 | Ø | Ø | Ø | 0x0000 | 0x0000 | 0x0000 | 0xx000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | 0x1000 | 0x1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x00000 | x0x000 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x01000 | x01000 | x01000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0000 | 000000 | 000000 | 000000 | – | 000000 | 0000×0 | 0000×0 | 0x00x0 | 000×00 | 000×00 | 0x0x00 | 000×00 | Ø | Ø | Ø | Ø | Ø | Ø | 00×000 | 00×000 | 0xx000 | 00×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010000 | 010000 | 010000 | 010000 | 01000x | 01000x | 0100×0 | 010×00 | 010×00 | Ø | Ø | Ø | Ø | 01×000 | 01×000 | 01×000 | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x00000 | x00000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x00000 | 000000 | 000000 | 000000 | 000000 | – | 0000×0 | 0000×0 | 0000×0 | 000×00 | 000×00 | 000×00 | x00x00 | Ø | Ø | Ø | Ø | Ø | Ø | 00×000 | 00×000 | 00×000 | x0x000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0000 | 0x0000 | 0x0000 | 0x0000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100000 | 100000 | 100000 | 10000x | 10000x | 10000x | 100×00 | 100×00 | Ø | 10×000 | 10×000 | 10×000 | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000×10 | 000010 | 000xx0 | 0000×0 | 0000×0 | 0000×0 | – | 000010 | 000010 | 0001×0 | 000110 | 0001×0 | 0001×0 | 00011x | Ø | Ø | Ø | 000110 | 00011x | Ø | 00×010 | Ø | Ø | Ø | Ø | Ø | Ø | 00×010 | 00×010 | 00×010 | Ø | Ø | Ø | Ø | 0x0010 | Ø | Ø | Ø | Ø | 0x0010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00×010 | 000010 | 0000×0 | 00x0x0 | 0000×0 | 0000×0 | 000010 | – | 000010 | Ø | 000×10 | Ø | Ø | Ø | Ø | Ø | Ø | 000×10 | Ø | 0010×0 | 001010 | 0010×0 | 0010×0 | 00101x | Ø | Ø | Ø | 001010 | 001010 | 001010 | 00101x | Ø | Ø | Ø | 0x0010 | Ø | Ø | Ø | Ø | 0xx010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0x1010 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | x01010 | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0010 | 000010 | 0000×0 | 0000×0 | 0x00x0 | 0000×0 | 000010 | 000010 | – | Ø | 000×10 | Ø | Ø | Ø | Ø | Ø | Ø | 000×10 | Ø | Ø | 00×010 | Ø | Ø | Ø | Ø | Ø | Ø | 00×010 | 0xx010 | 00×010 | Ø | Ø | Ø | 0100×0 | 010010 | 0100×0 | 0100×0 | Ø | Ø | 010010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×010 | Ø | Ø | Ø | Ø | Ø | 01×010 | 01×010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00010x | 000×00 | 000100 | 000×00 | 000×00 | 000×00 | 0001×0 | Ø | Ø | – | 000100 | 000100 | 000100 | 000101 | 000101 | 000101 | 000101 | 0001xx | 0001×1 | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | 00×101 | Ø | Ø | 0x0100 | Ø | 0x0101 | Ø | Ø | 0x010x | 0x0100 | 0x0101 | 0x0101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00100 | Ø | Ø | x00101 | Ø | x0010x | x00100 | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0001×0 | 000xx0 | 000100 | 000×00 | 000×00 | 000×00 | 000110 | 000×10 | 000×10 | 000100 | – | 000100 | 000100 | 0001xx | 00010x | 00010x | 00010x | 000110 | 00011x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0100 | Ø | Ø | Ø | Ø | 0x0100 | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00100 | Ø | Ø | Ø | Ø | x00100 | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0100 | 000×00 | 000100 | 000×00 | 0x0x00 | 000×00 | 0001×0 | Ø | Ø | 000100 | 000100 | – | 000100 | 00010x | 00010x | 0x010x | 00010x | 0001×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010×00 | 010×00 | 010100 | 010×00 | 01010x | Ø | Ø | 010100 | 010100 | 01010x | 01010x | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | 01×100 | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | x00100 | Ø | Ø | Ø | Ø | x00100 | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x00100 | 000×00 | 000100 | 000×00 | 000×00 | x00x00 | 0001×0 | Ø | Ø | 000100 | 000100 | 000100 | – | 00010x | 00010x | 00010x | x0010x | 0001×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0100 | Ø | Ø | Ø | Ø | 0x0100 | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×00 | 100100 | 100×00 | Ø | 10010x | Ø | 100100 | 100100 | 10010x | Ø | Ø | 10×100 | Ø | Ø | Ø | Ø | Ø | 10×100 | 10×100 | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0001×1 | Ø | 00010x | Ø | Ø | Ø | 00011x | Ø | Ø | 000101 | 0001xx | 00010x | 00010x | – | 000101 | 000101 | 000101 | 000111 | 000111 | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | 00×101 | Ø | Ø | Ø | Ø | 0x0101 | Ø | Ø | 0x0101 | Ø | 0x01x1 | 0x0101 | 0x0111 | 0x0111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00101 | Ø | x00101 | Ø | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00×101 | Ø | 00010x | Ø | Ø | Ø | Ø | Ø | Ø | 000101 | 00010x | 00010x | 00010x | 000101 | – | 000101 | 000101 | 0001×1 | 0001×1 | 001×01 | Ø | Ø | Ø | 001×01 | 001101 | 001×01 | 001×01 | Ø | Ø | Ø | Ø | 001101 | 001101 | Ø | Ø | Ø | Ø | 0x0101 | Ø | Ø | 0x0101 | Ø | 0x0101 | 0xx101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | 0x1101 | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00101 | Ø | x00101 | Ø | x0x101 | Ø | Ø | Ø | Ø | x01101 | Ø | Ø | Ø | x01101 | Ø | Ø | x01101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0101 | Ø | 00010x | Ø | Ø | Ø | Ø | Ø | Ø | 000101 | 00010x | 0x010x | 00010x | 000101 | 000101 | – | 000101 | 0001×1 | 0x01x1 | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | Ø | Ø | Ø | 0xx101 | 00×101 | 010×01 | Ø | 01010x | Ø | 010101 | 010×01 | Ø | 010101 | 01010x | 010101 | 010101 | 0101×1 | 0101×1 | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | 01×101 | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00101 | Ø | x00101 | Ø | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x00101 | Ø | 00010x | Ø | Ø | Ø | Ø | Ø | Ø | 000101 | 00010x | 00010x | x0010x | 000101 | 000101 | 000101 | – | 0001×1 | 0001×1 | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | x0x101 | Ø | Ø | Ø | Ø | 0x0101 | Ø | Ø | 0x0101 | Ø | 0x0101 | 0x0101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×01 | 10010x | Ø | 100×01 | 100101 | 100×01 | 100101 | 10010x | 100101 | Ø | Ø | Ø | Ø | 10×101 | Ø | Ø | Ø | 10×101 | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00011x | 000×10 | 0001×0 | Ø | Ø | Ø | 000110 | 000×10 | 000×10 | 0001xx | 000110 | 0001×0 | 0001×0 | 000111 | 0001×1 | 0001×1 | 0001×1 | – | 000111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0111 | Ø | 0x0111 | 0x0111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0111 | Ø | Ø | Ø | Ø | Ø | 00011x | Ø | Ø | 0001×1 | 00011x | Ø | Ø | 000111 | 0001×1 | 0x01x1 | 0001×1 | 000111 | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0101×1 | Ø | Ø | 0101×1 | Ø | 010111 | 0101×1 | 010111 | 010111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | 01×111 | Ø | 01×111 | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00100x | 00×000 | 00×000 | 001000 | 00×000 | 00×000 | Ø | 0010×0 | Ø | Ø | Ø | Ø | Ø | Ø | 001×01 | Ø | Ø | Ø | Ø | – | 001000 | 001000 | 001000 | 001001 | 001001 | 001001 | 001001 | 0010xx | 0010×0 | 0010×0 | 0010×1 | 001×01 | 001×01 | Ø | Ø | Ø | 0x1000 | Ø | 0x1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x100x | 0x1000 | 0x1000 | 0x1000 | 0x1001 | 0x1001 | 0x1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | Ø | Ø | x01001 | Ø | Ø | Ø | x0100x | x01000 | x01000 | x01000 | x01001 | x01001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0010×0 | 00x0x0 | 00×000 | 001000 | 00×000 | 00×000 | 00×010 | 001010 | 00×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 001000 | – | 001000 | 001000 | 0010xx | 00100x | 00100x | 00100x | 001010 | 001010 | 001010 | 00101x | Ø | Ø | Ø | Ø | Ø | 0x1000 | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x10x0 | 0x1000 | 0x1000 | Ø | Ø | Ø | 0x1010 | 0x1010 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x010x0 | x01000 | x01000 | Ø | Ø | x01010 | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x1000 | 00×000 | 00×000 | 001000 | 0xx000 | 00×000 | Ø | 0010×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 001000 | 001000 | – | 001000 | 00100x | 00100x | 0x100x | 00100x | 0010×0 | 0x10x0 | 0010×0 | Ø | Ø | Ø | 01×000 | 01×000 | 01×000 | 011000 | Ø | 01100x | 0110×0 | Ø | 011×00 | Ø | Ø | Ø | Ø | 011000 | 011000 | 011000 | 011000 | 01100x | 01100x | 01100x | 0110×0 | 0110×0 | 0110×0 | Ø | Ø | 011×00 | 011×00 | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x01000 | x01000 | xx1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | x11000 | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x01000 | 00×000 | 00×000 | 001000 | 00×000 | x0x000 | Ø | 0010×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 001000 | 001000 | 001000 | – | 00100x | 00100x | 00100x | x0100x | 0010×0 | 0010×0 | x010x0 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | 0x1000 | xx1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×000 | 10×000 | 101000 | Ø | Ø | 10100x | Ø | 101×00 | Ø | 101000 | 101000 | 101000 | 101000 | 10100x | 10100x | 1010×0 | 1010×0 | 101×00 | 101×00 | 101×00 | Ø | Ø | Ø | Ø | Ø | 1×1000 | 1×1000 | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0010×1 | Ø | Ø | 00100x | Ø | Ø | Ø | 00101x | Ø | Ø | Ø | Ø | Ø | Ø | 001×01 | Ø | Ø | Ø | Ø | 001001 | 0010xx | 00100x | 00100x | – | 001001 | 001001 | 001001 | 001011 | 00101x | 00101x | 001011 | 001×01 | 001×01 | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | 0x10x1 | 0x1001 | 0x1001 | 0x1011 | Ø | Ø | 0x1011 | 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | x01001 | x01001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001×01 | Ø | Ø | 00100x | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | 00×101 | 001101 | 00×101 | 00×101 | Ø | Ø | 001001 | 00100x | 00100x | 00100x | 001001 | – | 001001 | 001001 | 0010×1 | Ø | Ø | 0010×1 | 001101 | 001101 | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | 0x1001 | Ø | Ø | Ø | 0x1001 | 0x1x01 | 0x1001 | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | 0x1101 | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | x01101 | x01001 | Ø | Ø | Ø | x01x01 | x01001 | Ø | Ø | x01101 | Ø | Ø | x01101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x1001 | Ø | Ø | 00100x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 001×01 | Ø | Ø | Ø | Ø | 001001 | 00100x | 0x100x | 00100x | 001001 | 001001 | – | 001001 | 0010×1 | Ø | Ø | 0x10x1 | 0x1x01 | 001×01 | 01×001 | Ø | Ø | 01100x | 01×001 | 011001 | Ø | Ø | Ø | Ø | 011×01 | Ø | Ø | 011001 | 01100x | 01100x | 01100x | 011001 | 011001 | 011001 | 0110×1 | Ø | Ø | 0110×1 | 0110×1 | 011×01 | Ø | Ø | 011×01 | 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | x01001 | xx1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | x11001 | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x01001 | Ø | Ø | 00100x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 001×01 | Ø | Ø | Ø | Ø | 001001 | 00100x | 00100x | x0100x | 001001 | 001001 | 001001 | – | 0010×1 | Ø | Ø | 0010×1 | 001×01 | x01x01 | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | 0x1001 | 0x1001 | xx1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×001 | Ø | 10100x | 10×001 | 10×001 | 101001 | Ø | Ø | 101×01 | 101001 | 10100x | 10100x | 10100x | 101001 | 101001 | Ø | Ø | 101×01 | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | 1×1001 | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00101x | 00×010 | Ø | 0010×0 | Ø | Ø | 00×010 | 001010 | 00×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0010xx | 001010 | 0010×0 | 0010×0 | 001011 | 0010×1 | 0010×1 | 0010×1 | – | 001010 | 001010 | 001011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | 0x1011 | Ø | Ø | 0x101x | 0x1010 | 0x1010 | 0x1011 | 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | x01010 | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x1010 | 00×010 | Ø | 0010×0 | Ø | Ø | 00×010 | 001010 | 0xx010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0010×0 | 001010 | 0x10x0 | 0010×0 | 00101x | Ø | Ø | Ø | 001010 | – | 001010 | 0x101x | Ø | Ø | Ø | 01×010 | Ø | 0110×0 | Ø | Ø | 011010 | Ø | Ø | Ø | Ø | Ø | Ø | 0110×0 | 011010 | 0110×0 | 0110×0 | 01101x | Ø | Ø | 011010 | 011010 | 011010 | 01101x | 01101x | Ø | 011×10 | Ø | Ø | Ø | 011×10 | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | x01010 | xx1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | x11010 | x11010 | Ø | Ø | Ø | Ø | Ø |
| x01010 | 00×010 | Ø | 0010×0 | Ø | Ø | 00×010 | 001010 | 00×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0010×0 | 001010 | 0010×0 | x010x0 | 00101x | Ø | Ø | Ø | 001010 | 001010 | – | 00101x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0x1010 | xx1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1010×0 | Ø | Ø | Ø | Ø | Ø | Ø | 1010×0 | 101010 | 1010×0 | 1010×0 | Ø | Ø | 101010 | 101010 | Ø | 101×10 | Ø | Ø | 101×10 | Ø | Ø | Ø | Ø | 1×1010 | Ø | Ø | Ø | 1×1010 | 1×1010 | Ø | Ø | Ø | Ø | Ø |
| 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | 00101x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0010×1 | 00101x | Ø | Ø | 001011 | 0010×1 | 0x10x1 | 0010×1 | 001011 | 0x101x | 00101x | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0110×1 | 01101x | Ø | Ø | Ø | Ø | 011×11 | Ø | 0110×1 | 01101x | Ø | Ø | 011011 | 0110×1 | 0110×1 | 011011 | 01101x | 01101x | 011011 | 011011 | Ø | Ø | Ø | 011×11 | Ø | 011×11 | Ø | 011×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11011 | Ø | x11011 | Ø | x11011 | Ø | Ø | Ø | Ø |
| 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | 00×101 | 001101 | 0xx101 | 00×101 | Ø | Ø | 001×01 | Ø | Ø | Ø | 001×01 | 001101 | 0x1x01 | 001×01 | Ø | Ø | Ø | Ø | – | 001101 | Ø | Ø | Ø | Ø | 01×101 | 011×01 | Ø | 01×101 | 01110x | 01×101 | 011101 | 0111×1 | Ø | 011×01 | Ø | 01110x | Ø | 011×01 | 011101 | 011×01 | Ø | Ø | Ø | 0111×1 | Ø | 011101 | 01110x | 01110x | 011101 | 011101 | 0111×1 | Ø | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | Ø | Ø | Ø | x01101 | Ø | Ø | Ø | x01101 | Ø | Ø | xx1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | x11101 | Ø | x11101 | Ø |
| x01101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | 00×101 | 001101 | 00×101 | x0x101 | Ø | Ø | 001×01 | Ø | Ø | Ø | 001×01 | 001101 | 001×01 | x01x01 | Ø | Ø | Ø | Ø | 001101 | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | 0x1101 | xx1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×101 | 101×01 | 10×101 | 10110x | 101101 | 101×01 | Ø | 10110x | Ø | 101101 | 101×01 | Ø | Ø | 101101 | 10110x | 10110x | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | 1×1101 | Ø | 1×1101 | Ø |
| 01000x | 0x0000 | 0x0000 | 0x0000 | 010000 | 0x0000 | Ø | Ø | 0100×0 | Ø | Ø | 010×00 | Ø | Ø | Ø | 010×01 | Ø | Ø | Ø | Ø | Ø | 01×000 | Ø | Ø | Ø | 01×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | – | 010000 | 010000 | 010000 | 010001 | 010001 | 0100×0 | 010x0x | 010×00 | 010×01 | 010×01 | Ø | Ø | 01x00x | 01×000 | 01×000 | 01×000 | 01×001 | 01×001 | 01×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0100×0 | 0x00x0 | 0x0000 | 0x0000 | 010000 | 0x0000 | 0x0010 | 0x0010 | 010010 | Ø | Ø | 010×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | 01×010 | Ø | Ø | Ø | Ø | 010000 | – | 010000 | 010000 | 01000x | 01000x | 010010 | 010×00 | 010×00 | Ø | Ø | Ø | Ø | 01×000 | 01x0x0 | 01×000 | 01×000 | Ø | Ø | Ø | 01×010 | 01×010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010×00 | 0x0000 | 0x0x00 | 0x0000 | 010000 | 0x0000 | Ø | Ø | 0100×0 | 0x0100 | 0x0100 | 010100 | 0x0100 | Ø | Ø | 01010x | Ø | Ø | Ø | Ø | Ø | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010000 | 010000 | – | 010000 | 010x0x | 01000x | 0100×0 | 010100 | 010100 | 01010x | 01010x | Ø | Ø | 01×000 | 01×000 | 01xx00 | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | 01×100 | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01×000 | 0x0000 | 0x0000 | 0xx000 | 010000 | 0x0000 | Ø | Ø | 0100×0 | Ø | Ø | 010×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | 011000 | 0x1000 | Ø | Ø | 01100x | Ø | Ø | 0110×0 | Ø | Ø | Ø | Ø | 010000 | 010000 | 010000 | – | 01000x | 01x00x | 01x0x0 | 010×00 | 01xx00 | Ø | Ø | Ø | Ø | 011000 | 011000 | 011000 | 011000 | 01100x | 01100x | 01100x | 0110×0 | 0110×0 | 0110×0 | Ø | Ø | 011×00 | 011×00 | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | x11000 | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010×01 | Ø | Ø | Ø | 01000x | Ø | Ø | Ø | Ø | 0x0101 | Ø | 01010x | Ø | 0x0101 | 0x0101 | 010101 | 0x0101 | Ø | 0101×1 | Ø | Ø | Ø | Ø | Ø | Ø | 01×001 | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | 010001 | 01000x | 010x0x | 01000x | – | 010001 | Ø | 010101 | 01010x | 010101 | 010101 | 0101×1 | 0101×1 | 01×001 | Ø | Ø | Ø | 01×001 | 01xx01 | 01×001 | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | 01×101 | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01×001 | Ø | Ø | Ø | 01000x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010×01 | Ø | Ø | Ø | 0x1001 | Ø | 01100x | Ø | 0x1001 | 0x1001 | 011001 | 0x1001 | Ø | Ø | Ø | 0110×1 | 011×01 | Ø | 010001 | 01000x | 01000x | 01x00x | 010001 | – | Ø | 010×01 | Ø | 010×01 | 01xx01 | Ø | Ø | 011001 | 01100x | 01100x | 01100x | 011001 | 011001 | 011001 | 0110×1 | Ø | Ø | 0110×1 | 0110×1 | 011×01 | Ø | Ø | 011×01 | 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | x11001 | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01×010 | 0x0010 | Ø | Ø | 0100×0 | Ø | 0x0010 | 0xx010 | 010010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0110×0 | Ø | Ø | Ø | Ø | Ø | 0x1010 | 011010 | 0x1010 | 01101x | Ø | Ø | 0100×0 | 010010 | 0100×0 | 01x0x0 | Ø | Ø | – | Ø | Ø | Ø | Ø | Ø | Ø | 0110×0 | 011010 | 0110×0 | 0110×0 | 01101x | Ø | Ø | 011010 | 011010 | 011010 | 01101x | 01101x | Ø | 011×10 | Ø | Ø | Ø | 011×10 | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | x11010 | x11010 | Ø | Ø | Ø | Ø | Ø |
| 01010x | Ø | 0x0100 | Ø | 010×00 | Ø | Ø | Ø | Ø | 0x010x | 0x0100 | 010100 | 0x0100 | 0x0101 | 0x0101 | 010101 | 0x0101 | Ø | 0101×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | 010x0x | 010×00 | 010100 | 010×00 | 010101 | 010×01 | Ø | – | 010100 | 010101 | 010101 | 0101×1 | 0101×1 | Ø | Ø | 01×100 | Ø | Ø | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | 01x10x | 01×100 | 01×100 | 01×101 | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01×100 | Ø | 0x0100 | Ø | 010×00 | Ø | Ø | Ø | Ø | 0x0100 | 0x0100 | 010100 | 0x0100 | Ø | Ø | 01010x | Ø | Ø | Ø | Ø | Ø | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01110x | Ø | 010×00 | 010×00 | 010100 | 01xx00 | 01010x | Ø | Ø | 010100 | – | 01010x | 01x10x | Ø | Ø | 011×00 | 011×00 | 011100 | 011×00 | Ø | 01110x | Ø | Ø | 0111×0 | Ø | Ø | Ø | 011100 | 011100 | 011100 | 01110x | 01110x | 0111×0 | 0111×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | x11100 | x11100 | Ø | Ø |
| 0101×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0101 | Ø | 01010x | Ø | 0x01x1 | 0x0101 | 010101 | 0x0101 | 0x0111 | 010111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | 010×01 | Ø | 01010x | Ø | 010101 | 010×01 | Ø | 010101 | 01010x | – | 010101 | 010111 | 010111 | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | Ø | Ø | 01×111 | Ø | 01×101 | Ø | Ø | 01x1x1 | 01×101 | 01×111 | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0101 | Ø | 01010x | Ø | 0x0101 | 0xx101 | 010101 | 0x0101 | Ø | 0101×1 | Ø | Ø | Ø | Ø | Ø | 0x1101 | 011×01 | Ø | Ø | Ø | Ø | Ø | 011101 | 0x1101 | 010×01 | Ø | 01010x | Ø | 010101 | 01xx01 | Ø | 010101 | 01x10x | 010101 | – | 01x1x1 | 0101×1 | 011×01 | Ø | 01110x | Ø | 011×01 | 011101 | 011×01 | Ø | Ø | Ø | 0111×1 | Ø | 011101 | 01110x | 01110x | 011101 | 011101 | 0111×1 | Ø | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | x11101 | Ø | x11101 | Ø |
| 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0111 | Ø | 0101×1 | Ø | 0x0111 | 010111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×11 | 0111×1 | Ø | Ø | Ø | Ø | Ø | 0101×1 | Ø | Ø | 0101×1 | Ø | 010111 | 01x1x1 | – | 010111 | Ø | Ø | Ø | Ø | 011×11 | 0111×1 | Ø | 011×11 | 01111x | Ø | 011111 | 011×11 | 0111×1 | 01111x | Ø | 011111 | 0111×1 | 011111 | 01111x | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | x1x111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | Ø | Ø | x11111 | x11111 |
| x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0111 | Ø | 0101×1 | Ø | 0x0111 | 010111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0101×1 | Ø | Ø | 0101×1 | Ø | 010111 | 0101×1 | 010111 | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | 01×111 | Ø | 01×111 | Ø | x1x111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 110111 | 11011x | 110111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11×111 | Ø | Ø | 11×111 | 11×111 |
| 01100x | Ø | Ø | 0x1000 | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x100x | 0x1000 | 011000 | 0x1000 | 0x1001 | 0x1001 | 011001 | 0x1001 | Ø | 0110×0 | Ø | 0110×1 | 011×01 | Ø | 01x00x | 01×000 | 01×000 | 011000 | 01×001 | 011001 | 0110×0 | Ø | 011×00 | Ø | 011×01 | Ø | Ø | – | 011000 | 011000 | 011000 | 011001 | 011001 | 011001 | 0110xx | 0110×0 | 0110×0 | 0110×1 | 0110×1 | 011x0x | 011×00 | 011×00 | 011×01 | 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | x11000 | x11000 | x11001 | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0110×0 | Ø | Ø | 0x1000 | 01×000 | Ø | Ø | 0x1010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x10x0 | 011000 | 0x1000 | Ø | Ø | 01100x | Ø | 0x1010 | 011010 | 0x1010 | 01101x | Ø | Ø | 01×000 | 01x0x0 | 01×000 | 011000 | Ø | 01100x | 011010 | Ø | 011×00 | Ø | Ø | Ø | Ø | 011000 | – | 011000 | 011000 | 0110xx | 01100x | 01100x | 011010 | 011010 | 011010 | 01101x | 01101x | 011×00 | 011xx0 | 011×00 | Ø | Ø | 011×10 | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | x110x0 | x11000 | Ø | Ø | x11010 | x11010 | Ø | Ø | Ø | Ø | Ø |
| 011×00 | Ø | Ø | 0x1000 | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | 011000 | 0x1000 | Ø | Ø | 01100x | Ø | Ø | 0110×0 | Ø | Ø | 01110x | Ø | 01×000 | 01×000 | 01xx00 | 011000 | Ø | 01100x | 0110×0 | 01×100 | 011100 | Ø | 01110x | Ø | Ø | 011000 | 011000 | – | 011000 | 01100x | 011x0x | 01100x | 0110×0 | 011xx0 | 0110×0 | Ø | Ø | 011100 | 011100 | 011100 | 01110x | 01110x | 0111×0 | 0111×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | x11000 | x11000 | x11x00 | Ø | Ø | Ø | Ø | Ø | x11100 | x11100 | Ø | Ø |
| x11000 | Ø | Ø | 0x1000 | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | 011000 | xx1000 | Ø | Ø | 01100x | Ø | Ø | 0110×0 | Ø | Ø | Ø | Ø | 01×000 | 01×000 | 01×000 | 011000 | Ø | 01100x | 0110×0 | Ø | 011×00 | Ø | Ø | Ø | Ø | 011000 | 011000 | 011000 | – | 01100x | 01100x | x1100x | 0110×0 | 0110×0 | x110x0 | Ø | Ø | 011×00 | 011×00 | x11x00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | 1×1000 | 1×1000 | 111000 | Ø | 11100x | Ø | 1110×0 | Ø | Ø | 111×00 | Ø | Ø | Ø | Ø | Ø | 111000 | 111000 | 111000 | 11100x | 11100x | 1110×0 | 1110×0 | Ø | 111×00 | 111×00 | Ø | Ø |
| 0110×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | 01100x | Ø | 0x10x1 | 0x1001 | 011001 | 0x1001 | 0x1011 | 01101x | Ø | 011011 | 011×01 | Ø | 01×001 | Ø | Ø | 01100x | 01×001 | 011001 | 01101x | Ø | Ø | Ø | 011×01 | 011×11 | Ø | 011001 | 0110xx | 01100x | 01100x | – | 011001 | 011001 | 011011 | 01101x | 01101x | 011011 | 011011 | 011×01 | Ø | Ø | 011xx1 | 011×01 | 011×11 | Ø | 011×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | x110x1 | x11001 | x11011 | Ø | x11011 | Ø | Ø | Ø | Ø |
| 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | 01×101 | Ø | Ø | Ø | 0x1001 | Ø | 01100x | Ø | 0x1001 | 0x1x01 | 011001 | 0x1001 | Ø | Ø | Ø | 0110×1 | 011101 | 0x1101 | 01×001 | Ø | Ø | 01100x | 01xx01 | 011001 | Ø | 01×101 | 01110x | 01×101 | 011101 | 0111×1 | Ø | 011001 | 01100x | 011x0x | 01100x | 011001 | – | 011001 | 0110×1 | Ø | Ø | 011xx1 | 0110×1 | 011101 | 01110x | 01110x | 011101 | 011101 | 0111×1 | Ø | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | x11001 | x11x01 | Ø | Ø | Ø | x11101 | Ø | x11101 | Ø |
| x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | 01100x | Ø | 0x1001 | 0x1001 | 011001 | xx1001 | Ø | Ø | Ø | 0110×1 | 011×01 | Ø | 01×001 | Ø | Ø | 01100x | 01×001 | 011001 | Ø | Ø | Ø | Ø | 011×01 | Ø | Ø | 011001 | 01100x | 01100x | x1100x | 011001 | 011001 | – | 0110×1 | Ø | Ø | 0110×1 | x110x1 | 011×01 | Ø | Ø | 011×01 | x11x01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | 1×1001 | Ø | Ø | 11100x | 1×1001 | 111001 | Ø | Ø | Ø | Ø | Ø | 111×01 | Ø | Ø | Ø | Ø | 111001 | 11100x | 11100x | 111001 | 111001 | 1110×1 | Ø | 1110×1 | 111×01 | Ø | 111×01 | Ø |
| 01101x | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0110×0 | Ø | 0x1011 | Ø | 0110×1 | Ø | 0x101x | 011010 | 0x1010 | 011011 | Ø | Ø | Ø | 01×010 | Ø | 0110×0 | Ø | 0110×1 | 011010 | Ø | Ø | Ø | Ø | 011×11 | Ø | 0110xx | 011010 | 0110×0 | 0110×0 | 011011 | 0110×1 | 0110×1 | – | 011010 | 011010 | 011011 | 011011 | Ø | 011×10 | Ø | 011×11 | Ø | 011x1x | 011×10 | 011×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | x11011 | Ø | x1101x | x11010 | x11011 | Ø | Ø | Ø | Ø |
| 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0110×0 | Ø | Ø | Ø | Ø | Ø | 0x1010 | 011010 | 0x1010 | 01101x | Ø | Ø | Ø | 01×010 | Ø | 0110×0 | Ø | Ø | 011010 | Ø | 0111×0 | Ø | Ø | 01111x | Ø | 0110×0 | 011010 | 011xx0 | 0110×0 | 01101x | Ø | Ø | 011010 | – | 011010 | 011x1x | 01101x | 0111×0 | 011110 | 0111×0 | 01111x | Ø | 011110 | 011110 | 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | x11110 | Ø | x11110 | Ø | Ø | x11010 | Ø | Ø | Ø | x11010 | x11x10 | Ø | Ø | x11110 | Ø | x11110 |
| x11010 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0110×0 | Ø | Ø | Ø | Ø | Ø | 0x1010 | 011010 | xx1010 | 01101x | Ø | Ø | Ø | 01×010 | Ø | 0110×0 | Ø | Ø | 011010 | Ø | Ø | Ø | Ø | Ø | Ø | 0110×0 | 011010 | 0110×0 | x110x0 | 01101x | Ø | Ø | 011010 | 011010 | – | 01101x | x1101x | Ø | 011×10 | Ø | Ø | Ø | 011×10 | x11x10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | 1110×0 | Ø | Ø | 1×1010 | 111010 | Ø | Ø | Ø | Ø | 111×10 | Ø | 111×10 | Ø | 1110×0 | 111010 | 1110×0 | 11101x | Ø | 111010 | 111010 | 11101x | Ø | 111×10 | Ø | 111×10 |
| 011×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | 0x1011 | Ø | 0110×1 | Ø | 0x1011 | 01101x | Ø | 011011 | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | 0110×1 | 01101x | Ø | Ø | 01×111 | 0111×1 | 011111 | 01×111 | 0110×1 | 01101x | Ø | Ø | 011011 | 011xx1 | 0110×1 | 011011 | 011x1x | 01101x | – | 011011 | 0111×1 | 01111x | Ø | 011111 | 0111×1 | 011111 | 01111x | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | Ø | Ø | Ø | x11011 | Ø | x11011 | Ø | x11x11 | Ø | Ø | x11111 | x11111 |
| x11011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1011 | Ø | 0110×1 | Ø | 0x1011 | 01101x | Ø | 011011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0110×1 | 01101x | Ø | Ø | Ø | Ø | 011×11 | Ø | 0110×1 | 01101x | Ø | Ø | 011011 | 0110×1 | x110x1 | 011011 | 01101x | x1101x | 011011 | – | Ø | Ø | Ø | 011×11 | Ø | 011×11 | Ø | x11x11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1110×1 | Ø | 11101x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 111×11 | 1110×1 | 11101x | Ø | 111011 | 1110×1 | 111011 | 11101x | 111011 | Ø | Ø | 111×11 | 111×11 |
| 01110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | 0x1101 | 01×101 | Ø | Ø | Ø | Ø | Ø | 011×00 | Ø | Ø | 0x1101 | 011×01 | Ø | Ø | Ø | Ø | Ø | 011101 | 0x1101 | Ø | Ø | 01×100 | 011×00 | 01×101 | 011×01 | Ø | 01x10x | 011100 | 01×101 | 011101 | 0111×1 | Ø | 011x0x | 011×00 | 011100 | 011×00 | 011×01 | 011101 | 011×01 | Ø | 0111×0 | Ø | 0111×1 | Ø | – | 011100 | 011100 | 011101 | 011101 | 0111xx | 0111×0 | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | x11101 | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | x11101 | Ø | Ø | Ø | x1110x | x11100 | x11101 | Ø |
| 0111×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | Ø | 01110x | Ø | Ø | Ø | 01×100 | 011×00 | Ø | Ø | 011×10 | 01×100 | 011100 | Ø | 01110x | 01111x | Ø | 011×00 | 011xx0 | 011100 | 011×00 | Ø | 01110x | Ø | 011×10 | 011110 | 011×10 | 01111x | Ø | 011100 | – | 011100 | 0111xx | 01110x | 011110 | 011110 | 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | x11110 | Ø | x11110 | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | x11110 | Ø | x11100 | x111x0 | Ø | x11110 |
| x11100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01110x | Ø | Ø | Ø | 01×100 | 011×00 | Ø | Ø | Ø | 01×100 | 011100 | Ø | 01110x | Ø | Ø | 011×00 | 011×00 | 011100 | x11x00 | Ø | 01110x | Ø | Ø | 0111×0 | Ø | Ø | Ø | 011100 | 011100 | – | 01110x | x1110x | 0111×0 | x111x0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | 1×1100 | 111×00 | Ø | Ø | Ø | Ø | 1×1100 | 1×1100 | 111100 | 11110x | 1111×0 | Ø | 1111×0 | Ø | 111×00 | 111×00 | 111100 | Ø | 11110x | Ø | 1111×0 | Ø | 111100 | 111100 | 11110x | 1111×0 |
| 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | 01×101 | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | 0x1101 | 011×01 | Ø | Ø | Ø | Ø | 011×11 | 011101 | 0x1101 | Ø | Ø | Ø | Ø | 01×101 | 011×01 | Ø | 01×101 | 01110x | 01x1x1 | 011101 | 011111 | 01×111 | 011×01 | Ø | 01110x | Ø | 011xx1 | 011101 | 011×01 | 011×11 | 01111x | Ø | 011111 | 011×11 | 011101 | 0111xx | 01110x | – | 011101 | 011111 | 01111x | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | x11111 | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | x11111 | x11101 | Ø | x111x1 | x11111 |
| x11101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | 011×01 | Ø | Ø | Ø | Ø | Ø | 011101 | xx1101 | Ø | Ø | Ø | Ø | 01×101 | 011×01 | Ø | 01×101 | 01110x | 01×101 | 011101 | 0111×1 | Ø | 011×01 | Ø | 01110x | Ø | 011×01 | 011101 | x11x01 | Ø | Ø | Ø | 0111×1 | Ø | 011101 | 01110x | x1110x | 011101 | – | 0111×1 | Ø | x111x1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | Ø | 1×1101 | 111×01 | Ø | Ø | 1×1101 | Ø | 11110x | 111101 | Ø | Ø | Ø | 1111×1 | 111×01 | Ø | 11110x | 111×01 | 111101 | Ø | Ø | 1111×1 | 111101 | 11110x | 111101 | 1111×1 |
| 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | 011×11 | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | 0111×0 | 01×111 | 0111×1 | 011111 | 01×111 | Ø | 011×10 | 0111×0 | Ø | 011×11 | 0111×1 | Ø | 011x1x | 011110 | 011×10 | 011111 | 011×11 | 0111xx | 011110 | 0111×0 | 011111 | 0111×1 | – | 011110 | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | Ø | x11110 | x11111 | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | x11111 | Ø | x11110 | x11111 | x1111x |
| x11110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | 0111×0 | Ø | Ø | 01111x | Ø | Ø | 011×10 | 0111×0 | Ø | Ø | Ø | Ø | 011×10 | 011110 | x11x10 | 01111x | Ø | 0111×0 | 011110 | x111x0 | 01111x | Ø | 011110 | – | x1111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 111×10 | Ø | 1×1110 | 1111×0 | Ø | 111110 | 11×110 | 111110 | 11111x | Ø | 111×10 | 1111×0 | Ø | Ø | 111×10 | 111110 | 11111x | 1111×0 | 111110 | 11111x | 111110 |
| x11111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×11 | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | 0111×1 | 011111 | x1x111 | Ø | Ø | Ø | Ø | 011×11 | 0111×1 | Ø | 011×11 | 01111x | Ø | 011111 | x11x11 | 0111×1 | 01111x | Ø | 011111 | x111x1 | 011111 | x1111x | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1111×1 | 11111x | 11×111 | 11111x | 111111 | Ø | Ø | Ø | 111×11 | 1111×1 | 111×11 | 11111x | 111111 | 1111×1 | 11111x | 111111 | 111111 |
| 10000x | x00000 | x00000 | x00000 | x00000 | 100000 | Ø | Ø | Ø | Ø | Ø | Ø | 100×00 | Ø | Ø | Ø | 100×01 | Ø | Ø | Ø | Ø | Ø | 10×000 | Ø | Ø | Ø | 10×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | – | 100000 | 100000 | 100001 | 100001 | 100001 | 100x0x | 100×00 | 100×01 | 10x00x | 10×000 | 10×000 | 10×000 | 10×001 | 10×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100×00 | x00000 | x00x00 | x00000 | x00000 | 100000 | Ø | Ø | Ø | x00100 | x00100 | x00100 | 100100 | Ø | Ø | Ø | 10010x | Ø | Ø | Ø | Ø | Ø | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100000 | – | 100000 | 10000x | 100x0x | 10000x | 100100 | 100100 | 10010x | 10×000 | 10×000 | 10xx00 | 10×000 | Ø | Ø | Ø | Ø | 10×100 | 10×100 | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 10×000 | x00000 | x00000 | x0x000 | x00000 | 100000 | Ø | Ø | Ø | Ø | Ø | Ø | 100×00 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x01000 | x01000 | 101000 | Ø | Ø | Ø | 10100x | Ø | Ø | 1010×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100000 | 100000 | – | 10000x | 10000x | 10x00x | 100×00 | 10xx00 | Ø | 101000 | 101000 | 101000 | 101000 | 10100x | 10100x | 1010×0 | 1010×0 | 101×00 | 101×00 | 101×00 | Ø | Ø | Ø | Ø | Ø | 1×1000 | 1×1000 | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 1000×1 | Ø | Ø | Ø | Ø | 10000x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100001 | 10000x | 10000x | – | 100001 | 100001 | 100×01 | Ø | 100×01 | 10×001 | Ø | Ø | Ø | 10×001 | 10×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100×01 | Ø | Ø | Ø | Ø | 10000x | Ø | Ø | Ø | x00101 | Ø | Ø | 10010x | x00101 | x00101 | x00101 | 100101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×001 | Ø | Ø | Ø | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100001 | 100x0x | 10000x | 100001 | – | 100001 | 100101 | 10010x | 100101 | 10×001 | Ø | Ø | Ø | 10xx01 | 10×001 | Ø | Ø | 10×101 | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 10×001 | Ø | Ø | Ø | Ø | 10000x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×01 | Ø | Ø | x01001 | Ø | Ø | 10100x | x01001 | x01001 | x01001 | 101001 | Ø | Ø | Ø | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100001 | 10000x | 10x00x | 100001 | 100001 | – | 100×01 | Ø | 10xx01 | 101001 | 10100x | 10100x | 10100x | 101001 | 101001 | Ø | Ø | 101×01 | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | 1×1001 | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 10010x | Ø | x00100 | Ø | Ø | 100×00 | Ø | Ø | Ø | x0010x | x00100 | x00100 | 100100 | x00101 | x00101 | x00101 | 100101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100x0x | 100100 | 100×00 | 100×01 | 100101 | 100×01 | – | 100100 | 100101 | Ø | Ø | 10×100 | Ø | 10×101 | Ø | Ø | Ø | 10x10x | 10×100 | 10×100 | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 10×100 | Ø | x00100 | Ø | Ø | 100×00 | Ø | Ø | Ø | x00100 | x00100 | x00100 | 100100 | Ø | Ø | Ø | 10010x | Ø | Ø | Ø | Ø | Ø | 101×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | Ø | Ø | 100×00 | 100100 | 10xx00 | Ø | 10010x | Ø | 100100 | – | 10x10x | 101×00 | 101×00 | 101100 | 101×00 | 10110x | Ø | 1011×0 | Ø | 101100 | 101100 | 101100 | 10110x | 1011×0 | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | Ø | Ø | 1×1100 | 1×1100 | Ø | Ø |
| 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00101 | Ø | Ø | 10010x | x00101 | x0x101 | x00101 | 100101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | 101×01 | Ø | Ø | Ø | Ø | x01101 | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | 100×01 | 10010x | Ø | 100×01 | 100101 | 10xx01 | 100101 | 10x10x | – | 101×01 | Ø | 10110x | Ø | 101101 | 101×01 | Ø | Ø | 101101 | 10110x | 10110x | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | 1×1101 | Ø | 1×1101 | Ø |
| 10100x | Ø | Ø | x01000 | Ø | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x0100x | x01000 | x01000 | 101000 | x01001 | x01001 | x01001 | 101001 | Ø | Ø | 1010×0 | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10x00x | 10×000 | 101000 | 10×001 | 10×001 | 101001 | Ø | 101×00 | 101×01 | – | 101000 | 101000 | 101000 | 101001 | 101001 | 1010×0 | 1010×0 | 101x0x | 101×00 | 101×00 | 101×01 | Ø | Ø | Ø | Ø | 1x100x | 1×1000 | 1×1000 | 1×1001 | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 1010×0 | Ø | Ø | x01000 | Ø | 10×000 | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x010x0 | x01000 | 101000 | Ø | Ø | Ø | 10100x | x01010 | x01010 | 101010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×000 | 10×000 | 101000 | Ø | Ø | 10100x | Ø | 101×00 | Ø | 101000 | – | 101000 | 101000 | 10100x | 10100x | 101010 | 101010 | 101×00 | 101xx0 | 101×00 | Ø | 101×10 | Ø | Ø | Ø | 1×1000 | 1x10x0 | 1×1000 | Ø | Ø | 1×1010 | 1×1010 | Ø | Ø | Ø | Ø | Ø |
| 101×00 | Ø | Ø | x01000 | Ø | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x01000 | x01000 | 101000 | Ø | Ø | Ø | 10100x | Ø | Ø | 1010×0 | Ø | Ø | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | Ø | Ø | 10×000 | 10xx00 | 101000 | Ø | Ø | 10100x | 10×100 | 101100 | 10110x | 101000 | 101000 | – | 101000 | 101x0x | 10100x | 101xx0 | 1010×0 | 101100 | 101100 | 101100 | 10110x | 1011×0 | Ø | Ø | Ø | 1×1000 | 1×1000 | 1x1x00 | Ø | Ø | Ø | Ø | Ø | 1×1100 | 1×1100 | Ø | Ø |
| 1×1000 | Ø | Ø | x01000 | Ø | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x01000 | xx1000 | 101000 | Ø | Ø | Ø | 10100x | Ø | Ø | 1010×0 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | x11000 | x11000 | 111000 | Ø | Ø | 11100x | Ø | Ø | 1110×0 | Ø | Ø | Ø | Ø | 111×00 | Ø | Ø | Ø | Ø | Ø | 10×000 | 10×000 | 101000 | Ø | Ø | 10100x | Ø | 101×00 | Ø | 101000 | 101000 | 101000 | – | 10100x | 1x100x | 1010×0 | 1x10x0 | 101×00 | 101×00 | 1x1x00 | Ø | Ø | Ø | Ø | Ø | 111000 | 111000 | 111000 | 11100x | 11100x | 1110×0 | 1110×0 | Ø | 111×00 | 111×00 | Ø | Ø |
| 101×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | 10×101 | Ø | Ø | x01001 | Ø | Ø | 10100x | x01001 | x01x01 | x01001 | 101001 | Ø | Ø | Ø | Ø | x01101 | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | 10×001 | Ø | 10100x | 10×001 | 10xx01 | 101001 | 10×101 | 10110x | 101101 | 101001 | 10100x | 101x0x | 10100x | – | 101001 | Ø | Ø | 101101 | 10110x | 10110x | 101101 | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | 1×1001 | 1x1x01 | Ø | Ø | Ø | 1×1101 | Ø | 1×1101 | Ø |
| 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | 10100x | x01001 | x01001 | xx1001 | 101001 | Ø | Ø | Ø | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | 11100x | x11001 | x11001 | 111001 | Ø | Ø | Ø | Ø | 1110×1 | Ø | Ø | Ø | Ø | 111×01 | Ø | Ø | Ø | 10×001 | Ø | 10100x | 10×001 | 10×001 | 101001 | Ø | Ø | 101×01 | 101001 | 10100x | 10100x | 1x100x | 101001 | – | Ø | Ø | 101×01 | Ø | Ø | 1x1x01 | Ø | Ø | Ø | Ø | 111001 | 11100x | 11100x | 111001 | 111001 | 1110×1 | Ø | 1110×1 | 111×01 | Ø | 111×01 | Ø |
| 101×10 | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | 1010×0 | Ø | Ø | Ø | Ø | x01010 | x01010 | 101010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | Ø | Ø | Ø | 1010×0 | Ø | Ø | Ø | Ø | 1011×0 | Ø | 1010×0 | 101010 | 101xx0 | 1010×0 | Ø | Ø | – | 101010 | 1011×0 | 101110 | 1011×0 | Ø | 101110 | Ø | 1×1110 | Ø | Ø | 1×1010 | Ø | Ø | Ø | 1×1010 | 1x1x10 | Ø | Ø | 1×1110 | Ø | 1×1110 |
| 1×1010 | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | 1010×0 | Ø | Ø | Ø | Ø | x01010 | xx1010 | 101010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | 1110×0 | Ø | Ø | Ø | x11010 | x11010 | 111010 | Ø | 11101x | Ø | Ø | Ø | Ø | Ø | Ø | 111×10 | Ø | Ø | Ø | 1010×0 | Ø | Ø | Ø | Ø | Ø | Ø | 1010×0 | 101010 | 1010×0 | 1x10x0 | Ø | Ø | 101010 | – | Ø | 101×10 | Ø | Ø | 1x1x10 | Ø | 111×10 | Ø | 1110×0 | 111010 | 1110×0 | 11101x | Ø | 111010 | 111010 | 11101x | Ø | 111×10 | Ø | 111×10 |
| 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×100 | Ø | x01101 | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | 101×00 | Ø | x01101 | Ø | 101×01 | Ø | Ø | Ø | Ø | x01101 | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | 1×1101 | Ø | Ø | Ø | Ø | 10×100 | 101×00 | Ø | 10×101 | 101×01 | 10x10x | 101100 | 101101 | 101x0x | 101×00 | 101100 | 101×00 | 101101 | 101×01 | 1011×0 | Ø | – | 101100 | 101100 | 101101 | 1011×0 | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | 1×1101 | Ø | Ø | Ø | 1x110x | 1×1100 | 1×1101 | Ø |
| 1011×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 101×00 | Ø | Ø | Ø | Ø | Ø | Ø | 101×10 | Ø | Ø | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | 1×1110 | Ø | Ø | 10×100 | 101×00 | Ø | Ø | Ø | 10×100 | 101100 | 10110x | 101×00 | 101xx0 | 101100 | 101×00 | 10110x | Ø | 101110 | 101×10 | 101100 | – | 101100 | 10110x | 101110 | Ø | 1×1110 | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | 1×1110 | Ø | 1×1100 | 1x11x0 | Ø | 1×1110 |
| 1×1100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 101×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | 111×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | x11100 | 111100 | Ø | 11110x | Ø | 1111×0 | Ø | Ø | 10×100 | 101×00 | Ø | Ø | Ø | 10×100 | 101100 | 10110x | 101×00 | 101×00 | 101100 | 1x1x00 | 10110x | Ø | 1011×0 | Ø | 101100 | 101100 | – | 1x110x | 1x11x0 | Ø | 1111×0 | Ø | 111×00 | 111×00 | 111100 | Ø | 11110x | Ø | 1111×0 | Ø | 111100 | 111100 | 11110x | 1111×0 |
| 1×1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | 101×01 | Ø | Ø | Ø | Ø | xx1101 | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | 111×01 | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | 11110x | x11101 | 111101 | Ø | Ø | 1111×1 | Ø | Ø | Ø | Ø | 10×101 | 101×01 | 10×101 | 10110x | 101101 | 101×01 | Ø | 10110x | Ø | 101101 | 1x1x01 | Ø | Ø | 101101 | 10110x | 1x110x | – | Ø | Ø | Ø | 1111×1 | 111×01 | Ø | 11110x | 111×01 | 111101 | Ø | Ø | 1111×1 | 111101 | 11110x | 111101 | 1111×1 |
| 1×1110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 101×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | 111×10 | Ø | Ø | Ø | x11110 | 1111×0 | Ø | Ø | x11110 | 111110 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1011×0 | Ø | Ø | 101×10 | 1011×0 | Ø | Ø | Ø | 101110 | 1x1x10 | 1011×0 | 101110 | 1x11x0 | Ø | – | 11×110 | 111110 | 11111x | Ø | 111×10 | 1111×0 | Ø | Ø | 111×10 | 111110 | 11111x | 1111×0 | 111110 | 11111x | 111110 |
| 11011x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | x10111 | 110111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11×110 | 11×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11×110 | – | 110110 | 110111 | Ø | Ø | Ø | Ø | Ø | Ø | 11×110 | 11×111 | Ø | 11×110 | 11×111 | 11x11x |
| 11×110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11011x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | 111×10 | Ø | Ø | Ø | x11110 | 1111×0 | Ø | Ø | x11110 | 111110 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 111×10 | Ø | 1×1110 | 1111×0 | Ø | 111110 | 110110 | – | 11x11x | Ø | 111×10 | 1111×0 | Ø | Ø | 111×10 | 111110 | 11111x | 1111×0 | 111110 | 11111x | 111110 |
| 11×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | x1x111 | 110111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | 111×11 | Ø | Ø | Ø | x11111 | 1111×1 | x11111 | 11111x | 111111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1111×1 | 11111x | 110111 | 11x11x | – | Ø | Ø | Ø | 111×11 | 1111×1 | 111×11 | 11111x | 111111 | 1111×1 | 11111x | 111111 | 111111 |
| 11100x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | Ø | Ø | x11001 | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | x11000 | x11000 | 111000 | x11001 | x11001 | 111001 | Ø | Ø | 1110×0 | Ø | 1110×1 | Ø | Ø | 111×00 | Ø | 111×01 | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | 1×1001 | Ø | Ø | Ø | 1x100x | 1×1000 | 1×1000 | 111000 | 1×1001 | 111001 | Ø | 1110×0 | Ø | Ø | 111×00 | 111×01 | Ø | Ø | Ø | Ø | – | 111000 | 111000 | 111001 | 111001 | 1110xx | 1110×0 | 1110×1 | 111x0x | 111×00 | 111×01 | Ø |
| 1110×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | Ø | Ø | Ø | Ø | Ø | x11010 | 1×1010 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | x110x0 | x11000 | 111000 | Ø | Ø | 11100x | x11010 | x11010 | 111010 | Ø | 11101x | Ø | Ø | 111×00 | Ø | Ø | Ø | 111×10 | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | 1x10x0 | 1×1000 | 111000 | Ø | 11100x | 1×1010 | 111010 | Ø | Ø | 111×00 | Ø | 111×10 | Ø | 111×10 | Ø | 111000 | – | 111000 | 1110xx | 11100x | 111010 | 111010 | 11101x | 111×00 | 111xx0 | Ø | 111×10 |
| 111×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | x11000 | x11000 | x11x00 | 111000 | Ø | Ø | 11100x | Ø | Ø | 1110×0 | Ø | Ø | x11100 | x11100 | 111100 | Ø | 11110x | Ø | 1111×0 | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | 1×1100 | Ø | 1×1000 | 1×1000 | 1x1x00 | 111000 | Ø | 11100x | Ø | 1110×0 | 1×1100 | 1×1100 | 111100 | 11110x | 1111×0 | Ø | 1111×0 | Ø | 111000 | 111000 | – | 11100x | 111x0x | 1110×0 | 111xx0 | Ø | 111100 | 111100 | 11110x | 1111×0 |
| 1110×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | 1×1001 | Ø | Ø | Ø | x11011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | 11100x | x110x1 | x11001 | 111001 | x11011 | Ø | 11101x | x11011 | 111011 | Ø | Ø | Ø | Ø | 111×01 | Ø | Ø | 111×11 | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | 1×1001 | Ø | Ø | 11100x | 1×1001 | 111001 | Ø | 11101x | Ø | Ø | Ø | 111×01 | Ø | Ø | Ø | 111×11 | 111001 | 1110xx | 11100x | – | 111001 | 111011 | 11101x | 111011 | 111×01 | Ø | 111xx1 | 111×11 |
| 111×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | 1×1001 | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | x11001 | Ø | Ø | 11100x | x11001 | x11x01 | 111001 | Ø | Ø | Ø | Ø | 1110×1 | x11101 | Ø | 11110x | x11101 | 111101 | Ø | Ø | 1111×1 | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | 1×1101 | 1×1001 | Ø | Ø | 11100x | 1x1x01 | 111001 | Ø | Ø | 1×1101 | Ø | 11110x | 111101 | Ø | Ø | Ø | 1111×1 | 111001 | 11100x | 111x0x | 111001 | – | 1110×1 | Ø | 111xx1 | 111101 | 11110x | 111101 | 1111×1 |
| 11101x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | 1×1010 | x11011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | 1110×0 | x11011 | Ø | 1110×1 | x1101x | x11010 | 111010 | x11011 | 111011 | Ø | Ø | Ø | Ø | Ø | Ø | 111×10 | 111×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | 1110×0 | Ø | 1110×1 | 1×1010 | 111010 | Ø | Ø | Ø | Ø | 111×10 | Ø | 111×10 | 111×11 | 1110xx | 111010 | 1110×0 | 111011 | 1110×1 | – | 111010 | 111011 | Ø | 111×10 | 111×11 | 111x1x |
| 111×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | 1×1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | 1110×0 | Ø | Ø | Ø | x11010 | x11x10 | 111010 | Ø | 11101x | Ø | x11110 | 1111×0 | Ø | Ø | x11110 | 111110 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | 1110×0 | Ø | Ø | 1x1x10 | 111010 | Ø | 1×1110 | 1111×0 | Ø | 111110 | 11×110 | 111110 | 11111x | 1110×0 | 111010 | 111xx0 | 11101x | Ø | 111010 | – | 111x1x | 1111×0 | 111110 | 11111x | 111110 |
| 111×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | 11×111 | Ø | Ø | Ø | Ø | x11011 | Ø | 1110×1 | x11011 | Ø | 11101x | x11x11 | 111011 | Ø | Ø | Ø | x11111 | 1111×1 | x11111 | 11111x | 111111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1110×1 | Ø | 11101x | Ø | Ø | Ø | 1111×1 | 11111x | 11×111 | 11111x | 111111 | 1110×1 | 11101x | Ø | 111011 | 111xx1 | 111011 | 111x1x | – | 1111×1 | 11111x | 111111 | 111111 |
| 11110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | x11101 | Ø | Ø | Ø | Ø | x11100 | 111×00 | Ø | x11101 | 111×01 | Ø | Ø | Ø | Ø | Ø | x1110x | x11100 | 111100 | x11101 | 111101 | Ø | 1111×0 | 1111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | 1×1101 | Ø | Ø | 1×1100 | 111×00 | 1×1101 | 111×01 | Ø | Ø | 1x110x | 1×1100 | 111100 | 111101 | 1111×0 | Ø | 1111×0 | 1111×1 | 111x0x | 111×00 | 111100 | 111×01 | 111101 | Ø | 1111×0 | 1111×1 | – | 111100 | 111101 | 1111xx |
| 1111×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | 111×00 | Ø | Ø | Ø | Ø | x11110 | 111×10 | Ø | Ø | x11100 | x111x0 | 111100 | Ø | 11110x | x11110 | 111110 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | 1×1100 | 111×00 | Ø | Ø | 1×1110 | 111×10 | 1×1100 | 1x11x0 | 111100 | 11110x | 111110 | 11×110 | 111110 | 11111x | 111×00 | 111xx0 | 111100 | Ø | 11110x | 111×10 | 111110 | 11111x | 111100 | – | 1111xx | 111110 |
| 1111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | x11111 | 11×111 | Ø | Ø | Ø | Ø | Ø | x11101 | 111×01 | Ø | Ø | Ø | x11111 | 111×11 | x11101 | Ø | 11110x | x111x1 | 111101 | x11111 | 11111x | 111111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | Ø | 1×1101 | 111×01 | Ø | Ø | 1×1101 | Ø | 11110x | 111101 | 11111x | 11×111 | 11111x | 111111 | 111×01 | Ø | 11110x | 111xx1 | 111101 | 111×11 | 11111x | 111111 | 111101 | 1111xx | – | 111111 |
| 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | 11×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | 111×10 | x11111 | 111×11 | Ø | x11110 | 1111×0 | x11111 | 1111×1 | x1111x | 111110 | 111111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 111×10 | Ø | 1×1110 | 1111×0 | 1111×1 | 111110 | 11x11x | 111110 | 111111 | Ø | 111×10 | 1111×0 | 111×11 | 1111×1 | 111x1x | 111110 | 111111 | 1111xx | 111110 | 111111 | – |
Z1=
Ĉ2=C1∪(C1*C1)
C2=>
| 000xx0, 00x0x0, 0x00x0 0x0x00, x00x00, 0xx000 x0x000, 0xx010, 0001xx 0x010x, x0010x, 0x01x1 0xx101, x0x101, 0010xx 0x100x, x0100x, 0x10x0 x010x0, xx1000, 0x10x1 0x1x01, x01x01, xx1001 0x101x, xx1010, xx1101 010x0x, 01x00x, 01x0x0 01xx00, 01xx01, 01x10x 01x1x1, x1x111, 0110xx 011x0x, x1100x, 011xx0 x110x0, x11x00, 011xx1 x110x1, x11x01, 011x1x x1101x, x11x10, x11x11 0111xx, x1110x, x111x0 x111x1, x1111x, 100x0x 10x00x, 10xx00, 10xx01 10x10x, 101x0x, 1x100x 101xx0, 1x10x0, 1x1x00 1x1x01, 1x1x10, 1x110x 1x11x0, 11x11x, 1110xx 111x0x, 111xx0, 111xx1 111x1x, 1111xx |
| 000xx0 | 00x0x0 | 0x00x0 | 0x0x00 | x00x00 | 0xx000 | x0x000 | 0xx010 | 0001xx | 0x010x | x0010x | 0x01x1 | 0xx101 | x0x101 | 0010xx | 0x100x | x0100x | 0x10x0 | x010x0 | xx1000 | 0x10x1 | 0x1x01 | x01x01 | xx1001 | 0x101x | xx1010 | xx1101 | 010x0x | 01x00x | 01x0x0 | 01xx00 | 01xx01 | 01x10x | 01x1x1 | x1x111 | 0110xx | 011x0x | x1100x | 011xx0 | x110x0 | x11x00 | 011xx1 | x110x1 | x11x01 | 011x1x | x1101x | x11x10 | x11x11 | 0111xx | x1110x | x111x0 | x111x1 | x1111x | 100x0x | 10x00x | 10xx00 | 10xx01 | 10x10x | 101x0x | 1x100x | 101xx0 | 1x10x0 | 1x1x00 | 1x1x01 | 1x1x10 | 1x110x | 1x11x0 | 11x11x | 1110xx | 111x0x | 111xx0 | 111xx1 | 111x1x | 1111xx | |
| 000xx0 | – | 0000×0 | 0000×0 | 000×00 | 000×00 | 000000 | 000000 | 000010 | 0001×0 | 000100 | 000100 | 0001xx | 00010x | 00010x | 00x0x0 | 00×000 | 00×000 | 00x0x0 | 00x0x0 | 00×000 | Ø | Ø | Ø | Ø | 00×010 | 00×010 | Ø | 0x0x00 | 0x0000 | 0x00x0 | 0x0x00 | Ø | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00x00 | x00000 | x00x00 | Ø | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00x0x0 | 0000×0 | – | 0000×0 | 000000 | 000000 | 00×000 | 00×000 | 00×010 | 000xx0 | 000×00 | 000×00 | Ø | Ø | Ø | 0010×0 | 001000 | 001000 | 0010×0 | 0010×0 | 001000 | 0010xx | 00100x | 00100x | 00100x | 001010 | 001010 | Ø | 0x0000 | 0xx000 | 0xx0x0 | 0xx000 | Ø | Ø | Ø | Ø | 0x10x0 | 0x1000 | 0x1000 | 0x10x0 | 0x10x0 | 0x1000 | Ø | Ø | Ø | 0x1010 | 0x1010 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x0x000 | x0x000 | Ø | Ø | x01000 | x01000 | x010x0 | x010x0 | x01000 | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x00x0 | 0000×0 | 0000×0 | – | 0x0000 | 000000 | 0x0000 | 000000 | 0x0010 | 000xx0 | 0x0x00 | 000×00 | Ø | Ø | Ø | 00x0x0 | 0xx000 | 00×000 | 0xx0x0 | 00x0x0 | 0xx000 | Ø | Ø | Ø | Ø | 0xx010 | 0xx010 | Ø | 010000 | 010000 | 0100×0 | 010000 | 01000x | 010×00 | Ø | Ø | 01x0x0 | 01×000 | 01×000 | 01x0x0 | 01x0x0 | 01×000 | Ø | Ø | Ø | 01×010 | 01×010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x00000 | x00000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0x00 | 000×00 | 000000 | 0x0000 | – | 000×00 | 0x0000 | 000000 | 0x00x0 | 000100 | 0x0100 | 000100 | 0x010x | 0x010x | 00010x | 00×000 | 0xx000 | 00×000 | 0xx000 | 00×000 | 0xx000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010×00 | 010000 | 010000 | 010×00 | 010x0x | 010100 | 01010x | Ø | 01×000 | 01xx00 | 01×000 | 01xx00 | 01×000 | 01xx00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | 01×100 | 01×100 | Ø | Ø | x00x00 | x00000 | x00x00 | Ø | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x00x00 | 000×00 | 000000 | 000000 | 000×00 | – | 000000 | x00000 | 0000×0 | 000100 | 000100 | x00100 | 00010x | 00010x | x0010x | 00×000 | 00×000 | x0x000 | 00×000 | x0x000 | x0x000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0x00 | 0x0000 | 0x0000 | 0x0x00 | Ø | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×00 | 100000 | 100×00 | 100x0x | 100100 | 10xx00 | 10×000 | 10xx00 | 10×000 | 10xx00 | Ø | Ø | 10×100 | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0xx000 | 000000 | 00×000 | 0x0000 | 0x0000 | 000000 | – | 00×000 | 0xx0x0 | 000×00 | 0x0x00 | 000×00 | Ø | Ø | Ø | 001000 | 0x1000 | 001000 | 0x1000 | 001000 | 0x1000 | 0x100x | 0x100x | 00100x | 0x100x | 0x10x0 | 0x10x0 | Ø | 010000 | 01×000 | 01×000 | 01×000 | 01x00x | 01xx00 | Ø | Ø | 011000 | 011000 | 011000 | 011000 | 011000 | 011000 | 01100x | 01100x | 01100x | 0110×0 | 0110×0 | 0110×0 | Ø | 011×00 | 011×00 | 011×00 | Ø | Ø | x00000 | x0x000 | x0x000 | Ø | Ø | x01000 | xx1000 | x01000 | xx1000 | xx1000 | Ø | Ø | Ø | Ø | Ø | x11000 | x11000 | x11000 | Ø | Ø | Ø |
| x0x000 | 000000 | 00×000 | 000000 | 000000 | x00000 | 00×000 | – | 00x0x0 | 000×00 | 000×00 | x00x00 | Ø | Ø | Ø | 001000 | 001000 | x01000 | 001000 | x01000 | x01000 | 00100x | 00100x | x0100x | x0100x | 0010×0 | x010x0 | Ø | 0x0000 | 0xx000 | 0xx000 | 0xx000 | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | xx1000 | 0x1000 | xx1000 | xx1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100000 | 10×000 | 10×000 | 10x00x | 10xx00 | 101000 | 101000 | 101000 | 101000 | 101000 | 10100x | 1010×0 | 101×00 | 101×00 | Ø | 1×1000 | 1×1000 | 1×1000 | Ø | Ø | Ø |
| 0xx010 | 000010 | 00×010 | 0x0010 | 0x00x0 | 0000×0 | 0xx0x0 | 00x0x0 | – | 000×10 | Ø | Ø | Ø | Ø | Ø | 001010 | 0x10x0 | 0010×0 | 0x1010 | 001010 | 0x10x0 | 0x101x | Ø | Ø | Ø | 0x1010 | 0x1010 | Ø | 0100×0 | 01x0x0 | 01×010 | 01x0x0 | Ø | Ø | Ø | Ø | 011010 | 0110×0 | 0110×0 | 011010 | 011010 | 0110×0 | 01101x | 01101x | Ø | 011010 | 011010 | 011010 | 01101x | 011×10 | Ø | 011×10 | Ø | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | xx1010 | Ø | Ø | xx1010 | Ø | Ø | Ø | x11010 | Ø | x11010 | Ø | x11010 | Ø |
| 0001xx | 0001×0 | 000xx0 | 000xx0 | 000100 | 000100 | 000×00 | 000×00 | 000×10 | – | 00010x | 00010x | 0001×1 | 000101 | 000101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | 00×101 | Ø | Ø | Ø | 00×101 | 0x010x | Ø | Ø | 0x0100 | 0x0101 | 0x010x | 0x01x1 | 0x0111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x0010x | Ø | x00100 | x00101 | x0010x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x010x | 000100 | 000×00 | 0x0x00 | 0x0100 | 000100 | 0x0x00 | 000×00 | Ø | 00010x | – | 00010x | 0x0101 | 0x0101 | 000101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0xx101 | 00×101 | Ø | Ø | Ø | 0xx101 | 01010x | 010x0x | 010×00 | 010100 | 010101 | 01010x | 010101 | 0101×1 | Ø | 01x10x | Ø | 01×100 | Ø | 01×100 | 01×101 | Ø | 01×101 | Ø | Ø | Ø | Ø | 01x10x | 01x10x | 01×100 | 01×101 | Ø | x0010x | Ø | x00100 | x00101 | x0010x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x0010x | 000100 | 000×00 | 000×00 | 000100 | x00100 | 000×00 | x00x00 | Ø | 00010x | 00010x | – | 000101 | 000101 | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | x0x101 | Ø | Ø | Ø | x0x101 | 0x010x | Ø | Ø | 0x0100 | 0x0101 | 0x010x | 0x0101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10010x | 100x0x | 100100 | 100101 | 10010x | 10x10x | Ø | 10×100 | Ø | 10×100 | 10×101 | Ø | 10x10x | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x01x1 | 0001xx | Ø | Ø | 0x010x | 00010x | Ø | Ø | Ø | 0001×1 | 0x0101 | 000101 | – | 0x0101 | 000101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0xx101 | 00×101 | Ø | Ø | Ø | 0xx101 | 010101 | 010×01 | Ø | 01010x | 010101 | 010101 | 0101×1 | 010111 | Ø | 01×101 | Ø | Ø | Ø | Ø | 01x1x1 | Ø | 01×101 | 01×111 | Ø | Ø | 01×111 | 01x1x1 | 01×101 | Ø | 01x1x1 | 01×111 | x00101 | Ø | Ø | x00101 | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø |
| 0xx101 | 00010x | Ø | Ø | 0x010x | 00010x | Ø | Ø | Ø | 000101 | 0x0101 | 000101 | 0x0101 | – | 00×101 | 001×01 | 0x1x01 | 001×01 | Ø | Ø | Ø | 0x1x01 | 0x1101 | 001101 | 0x1x01 | Ø | Ø | 0x1101 | 010101 | 01xx01 | Ø | 01x10x | 01×101 | 01×101 | 01×101 | 01x1x1 | 011×01 | 011101 | 011×01 | 01110x | Ø | 01110x | 011101 | 011×01 | 011101 | 0111×1 | Ø | Ø | 0111×1 | 011101 | 011101 | 01110x | 011101 | 0111×1 | x00101 | Ø | Ø | x0x101 | x0x101 | x01101 | Ø | Ø | Ø | Ø | xx1101 | Ø | xx1101 | Ø | Ø | Ø | x11101 | Ø | x11101 | Ø | x11101 |
| x0x101 | 00010x | Ø | Ø | 00010x | x0010x | Ø | Ø | Ø | 000101 | 000101 | x00101 | 000101 | 00×101 | – | 001×01 | 001×01 | x01x01 | Ø | Ø | Ø | 001×01 | 001101 | x01101 | x01x01 | Ø | Ø | x01101 | 0x0101 | Ø | Ø | Ø | 0xx101 | 0xx101 | 0xx101 | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | 0x1101 | Ø | xx1101 | Ø | Ø | Ø | Ø | 0x1101 | xx1101 | Ø | xx1101 | Ø | 100101 | 10xx01 | 10x10x | 10×101 | 10×101 | 101101 | 101×01 | 10110x | Ø | 10110x | 101101 | Ø | 101101 | 10110x | Ø | Ø | 1×1101 | Ø | 1×1101 | Ø | 1×1101 |
| 0010xx | 00x0x0 | 0010×0 | 00x0x0 | 00×000 | 00×000 | 001000 | 001000 | 001010 | Ø | Ø | Ø | Ø | 001×01 | 001×01 | – | 00100x | 00100x | 0010×0 | 0010×0 | 001000 | 0010×1 | 001001 | 001001 | 001001 | 00101x | 001010 | 001×01 | Ø | 0x100x | 0x10x0 | 0x1000 | 0x1001 | Ø | Ø | Ø | 0x10xx | 0x100x | 0x100x | 0x10x0 | 0x10x0 | 0x1000 | 0x10x1 | 0x10x1 | 0x1001 | 0x101x | 0x101x | 0x1010 | 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | x0100x | x01000 | x01001 | Ø | x0100x | x0100x | x010x0 | x010x0 | x01000 | x01001 | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x100x | 00×000 | 001000 | 0xx000 | 0xx000 | 00×000 | 0x1000 | 001000 | 0x10x0 | Ø | Ø | Ø | Ø | 0x1x01 | 001×01 | 00100x | – | 00100x | 0x1000 | 001000 | 0x1000 | 0x1001 | 0x1001 | 001001 | 0x1001 | 0x10xx | 0x10x0 | 0x1x01 | 01x00x | 01100x | 011000 | 011000 | 011001 | 011x0x | 011×01 | Ø | 01100x | 01100x | 01100x | 011000 | 011000 | 011000 | 011001 | 011001 | 011001 | 0110xx | 0110xx | 0110×0 | 0110×1 | 011x0x | 011x0x | 011×00 | 011×01 | Ø | Ø | x0100x | x01000 | x01001 | Ø | x0100x | xx100x | x01000 | xx1000 | xx1000 | xx1001 | Ø | Ø | Ø | Ø | x1100x | x1100x | x11000 | x11001 | Ø | Ø |
| x0100x | 00×000 | 001000 | 00×000 | 00×000 | x0x000 | 001000 | x01000 | 0010×0 | Ø | Ø | Ø | Ø | 001×01 | x01x01 | 00100x | 00100x | – | 001000 | x01000 | x01000 | 001001 | 001001 | x01001 | x01001 | 0010xx | x010x0 | x01x01 | Ø | 0x100x | 0x1000 | 0x1000 | 0x1001 | Ø | Ø | Ø | 0x100x | 0x100x | xx100x | 0x1000 | xx1000 | xx1000 | 0x1001 | xx1001 | xx1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10x00x | 10100x | 101000 | 101001 | 101x0x | 10100x | 10100x | 101000 | 101000 | 101000 | 101001 | 1010×0 | 101x0x | 101×00 | Ø | 1x100x | 1x100x | 1×1000 | 1×1001 | Ø | Ø |
| 0x10x0 | 00x0x0 | 0010×0 | 0xx0x0 | 0xx000 | 00×000 | 0x1000 | 001000 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | 0010×0 | 0x1000 | 001000 | – | 0010×0 | 0x1000 | 0x10xx | 0x100x | 00100x | 0x100x | 0x1010 | 0x1010 | Ø | 01×000 | 011000 | 0110×0 | 011000 | 01100x | 011×00 | Ø | Ø | 0110×0 | 011000 | 011000 | 0110×0 | 0110×0 | 011000 | 0110xx | 0110xx | 01100x | 011010 | 011010 | 011010 | 01101x | 011xx0 | 011×00 | 011xx0 | Ø | 011×10 | Ø | x01000 | x01000 | Ø | Ø | x01000 | xx1000 | x010x0 | xx10x0 | xx1000 | Ø | xx1010 | Ø | Ø | Ø | x110x0 | x11000 | x110x0 | Ø | x11010 | Ø |
| x010x0 | 00x0x0 | 0010×0 | 00x0x0 | 00×000 | x0x000 | 001000 | x01000 | 001010 | Ø | Ø | Ø | Ø | Ø | Ø | 0010×0 | 001000 | x01000 | 0010×0 | – | x01000 | 0010xx | 00100x | x0100x | x0100x | 001010 | x01010 | Ø | Ø | 0x1000 | 0x10x0 | 0x1000 | Ø | Ø | Ø | Ø | 0x10x0 | 0x1000 | xx1000 | 0x10x0 | xx10x0 | xx1000 | Ø | Ø | Ø | 0x1010 | xx1010 | xx1010 | Ø | Ø | Ø | Ø | Ø | Ø | 10×000 | 101000 | 101000 | 10100x | 101×00 | 101000 | 101000 | 1010×0 | 1010×0 | 101000 | 10100x | 101010 | 101×00 | 101xx0 | Ø | 1x10x0 | 1×1000 | 1x10x0 | Ø | 1×1010 | Ø |
| xx1000 | 00×000 | 001000 | 0xx000 | 0xx000 | x0x000 | 0x1000 | x01000 | 0x10x0 | Ø | Ø | Ø | Ø | Ø | Ø | 001000 | 0x1000 | x01000 | 0x1000 | x01000 | – | 0x100x | 0x100x | x0100x | xx100x | 0x10x0 | xx10x0 | Ø | 01×000 | 011000 | 011000 | 011000 | 01100x | 011×00 | Ø | Ø | 011000 | 011000 | x11000 | 011000 | x11000 | x11000 | 01100x | x1100x | x1100x | 0110×0 | x110x0 | x110x0 | Ø | 011×00 | x11x00 | x11x00 | Ø | Ø | 10×000 | 101000 | 101000 | 10100x | 101×00 | 101000 | 1×1000 | 101000 | 1×1000 | 1×1000 | 1x100x | 1x10x0 | 1x1x00 | 1x1x00 | Ø | 111000 | 111000 | 111000 | 11100x | 1110×0 | 111×00 |
| 0x10x1 | Ø | 0010xx | Ø | Ø | Ø | 0x100x | 00100x | 0x101x | Ø | Ø | Ø | Ø | 0x1x01 | 001×01 | 0010×1 | 0x1001 | 001001 | 0x10xx | 0010xx | 0x100x | – | 0x1001 | 001001 | 0x1001 | 0x1011 | 0x101x | 0x1x01 | 01×001 | 011001 | 0110xx | 01100x | 011001 | 011×01 | 011xx1 | 011×11 | 0110×1 | 011001 | 011001 | 0110xx | 0110xx | 01100x | 0110×1 | 0110×1 | 011001 | 011011 | 011011 | 01101x | 011011 | 011xx1 | 011×01 | Ø | 011xx1 | 011×11 | Ø | x01001 | Ø | x01001 | Ø | x01001 | xx1001 | Ø | Ø | Ø | xx1001 | Ø | Ø | Ø | Ø | x110x1 | x11001 | Ø | x110x1 | x11011 | Ø |
| 0x1x01 | Ø | 00100x | Ø | Ø | Ø | 0x100x | 00100x | Ø | 00×101 | 0xx101 | 00×101 | 0xx101 | 0x1101 | 001101 | 001001 | 0x1001 | 001001 | 0x100x | 00100x | 0x100x | 0x1001 | – | 001×01 | 0x1001 | 0x10x1 | Ø | 0x1101 | 01xx01 | 011001 | 01100x | 011x0x | 011×01 | 011101 | 011101 | 0111×1 | 011001 | 011×01 | 011001 | 011x0x | 01100x | 011x0x | 011×01 | 011001 | 011×01 | 011xx1 | 0110×1 | Ø | 011xx1 | 011101 | 011101 | 01110x | 011101 | 0111×1 | Ø | x01001 | Ø | x01x01 | x01101 | x01x01 | xx1001 | Ø | Ø | Ø | xx1x01 | Ø | xx1101 | Ø | Ø | x11001 | x11x01 | Ø | x11x01 | Ø | x11101 |
| x01x01 | Ø | 00100x | Ø | Ø | Ø | 00100x | x0100x | Ø | 00×101 | 00×101 | x0x101 | 00×101 | 001101 | x01101 | 001001 | 001001 | x01001 | 00100x | x0100x | x0100x | 001001 | 001×01 | – | x01001 | 0010×1 | Ø | x01101 | Ø | 0x1001 | Ø | Ø | 0x1x01 | 0x1101 | 0x1101 | Ø | 0x1001 | 0x1x01 | xx1001 | Ø | Ø | Ø | 0x1x01 | xx1001 | xx1x01 | Ø | Ø | Ø | Ø | 0x1101 | xx1101 | Ø | xx1101 | Ø | 10xx01 | 101001 | 101x0x | 101×01 | 101101 | 101×01 | 101001 | 101x0x | 10100x | 101x0x | 101×01 | Ø | 101101 | 10110x | Ø | 1×1001 | 1x1x01 | Ø | 1x1x01 | Ø | 1×1101 |
| xx1001 | Ø | 00100x | Ø | Ø | Ø | 0x100x | x0100x | Ø | Ø | Ø | Ø | Ø | 0x1x01 | x01x01 | 001001 | 0x1001 | x01001 | 0x100x | x0100x | xx100x | 0x1001 | 0x1001 | x01001 | – | 0x10x1 | Ø | xx1x01 | 01×001 | 011001 | 01100x | 01100x | 011001 | 011×01 | 011×01 | Ø | 011001 | 011001 | x11001 | 01100x | x1100x | x1100x | 011001 | x11001 | x11001 | 0110×1 | x110x1 | Ø | x110x1 | 011×01 | x11x01 | Ø | x11x01 | Ø | 10×001 | 101001 | 10100x | 101001 | 101×01 | 101001 | 1×1001 | 10100x | 1x100x | 1x100x | 1×1001 | Ø | 1x1x01 | Ø | Ø | 111001 | 111001 | 11100x | 111001 | 1110×1 | 111×01 |
| 0x101x | 00×010 | 001010 | 0xx010 | Ø | Ø | 0x10x0 | 0010×0 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | 00101x | 0x10xx | 0010xx | 0x1010 | 001010 | 0x10x0 | 0x1011 | 0x10x1 | 0010×1 | 0x10x1 | – | 0x1010 | Ø | Ø | 0110xx | 011010 | 0110×0 | 0110×1 | Ø | 011×11 | 011×11 | 01101x | 0110xx | 0110xx | 011010 | 011010 | 0110×0 | 011011 | 011011 | 0110×1 | 01101x | 01101x | 011010 | 011011 | 011x1x | Ø | 011×10 | 011×11 | 011x1x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | xx1010 | Ø | Ø | xx1010 | Ø | Ø | Ø | x1101x | Ø | x11010 | x11011 | x1101x | Ø |
| xx1010 | 00×010 | 001010 | 0xx010 | Ø | Ø | 0x10x0 | x010x0 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | 001010 | 0x10x0 | x010x0 | 0x1010 | x01010 | xx10x0 | 0x101x | Ø | Ø | Ø | 0x1010 | – | Ø | Ø | 0110×0 | 011010 | 0110×0 | Ø | Ø | Ø | Ø | 011010 | 0110×0 | x110x0 | 011010 | x11010 | x110x0 | 01101x | x1101x | Ø | 011010 | x11010 | x11010 | x1101x | 011×10 | Ø | x11x10 | Ø | x11x10 | Ø | 1010×0 | 1010×0 | Ø | Ø | 1010×0 | 1x10x0 | 101010 | 1×1010 | 1x10x0 | Ø | 1×1010 | Ø | 1x1x10 | 111×10 | 111010 | 1110×0 | 111010 | 11101x | 111010 | 111×10 |
| xx1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | 0xx101 | x0x101 | 0xx101 | 0x1101 | x01101 | 001×01 | 0x1x01 | x01x01 | Ø | Ø | Ø | 0x1x01 | 0x1101 | x01101 | xx1x01 | Ø | Ø | – | 01×101 | 011×01 | Ø | 01110x | 011101 | 011101 | 011101 | x111x1 | 011×01 | 011101 | x11x01 | 01110x | Ø | x1110x | 011101 | x11x01 | x11101 | 0111×1 | Ø | Ø | x111x1 | 011101 | x11101 | x1110x | x11101 | x111x1 | 10×101 | 101×01 | 10110x | 101101 | 101101 | 101101 | 1x1x01 | 10110x | Ø | 1x110x | 1×1101 | Ø | 1×1101 | 1x110x | 1111×1 | 111×01 | 111101 | 11110x | 111101 | 1111×1 | 111101 |
| 010x0x | 0x0x00 | 0x0000 | 010000 | 010×00 | 0x0x00 | 010000 | 0x0000 | 0100×0 | 0x010x | 01010x | 0x010x | 010101 | 010101 | 0x0101 | Ø | 01x00x | Ø | 01×000 | Ø | 01×000 | 01×001 | 01xx01 | Ø | 01×001 | Ø | Ø | 01×101 | – | 01000x | 010000 | 010×00 | 010×01 | 01010x | 010101 | 0101×1 | 01x00x | 01xx0x | 01x00x | 01xx00 | 01×000 | 01xx00 | 01xx01 | 01×001 | 01xx01 | Ø | Ø | Ø | Ø | 01x10x | 01x10x | 01×100 | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01x00x | 0x0000 | 0xx000 | 010000 | 010000 | 0x0000 | 01×000 | 0xx000 | 01x0x0 | Ø | 010x0x | Ø | 010×01 | 01xx01 | Ø | 0x100x | 01100x | 0x100x | 011000 | 0x1000 | 011000 | 011001 | 011001 | 0x1001 | 011001 | 0110xx | 0110×0 | 011×01 | 01000x | – | 01×000 | 01×000 | 01×001 | 01xx0x | 01xx01 | Ø | 01100x | 01100x | 01100x | 011000 | 011000 | 011000 | 011001 | 011001 | 011001 | 0110xx | 0110xx | 0110×0 | 0110×1 | 011x0x | 011x0x | 011×00 | 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | Ø | x11000 | x11000 | x11001 | Ø | Ø | Ø | Ø | x1100x | x1100x | x11000 | x11001 | Ø | Ø |
| 01x0x0 | 0x00x0 | 0xx0x0 | 0100×0 | 010000 | 0x0000 | 01×000 | 0xx000 | 01×010 | Ø | 010×00 | Ø | Ø | Ø | Ø | 0x10x0 | 011000 | 0x1000 | 0110×0 | 0x10x0 | 011000 | 0110xx | 01100x | Ø | 01100x | 011010 | 011010 | Ø | 010000 | 01×000 | – | 01×000 | 01x00x | 01xx00 | Ø | Ø | 0110×0 | 011000 | 011000 | 0110×0 | 0110×0 | 011000 | 0110xx | 0110xx | 01100x | 011010 | 011010 | 011010 | 01101x | 011xx0 | 011×00 | 011xx0 | Ø | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | x110x0 | x11000 | Ø | x11010 | Ø | Ø | Ø | x110x0 | x11000 | x110x0 | Ø | x11010 | Ø |
| 01xx00 | 0x0x00 | 0xx000 | 010000 | 010×00 | 0x0x00 | 01×000 | 0xx000 | 01x0x0 | 0x0100 | 010100 | 0x0100 | 01010x | 01x10x | Ø | 0x1000 | 011000 | 0x1000 | 011000 | 0x1000 | 011000 | 01100x | 011x0x | Ø | 01100x | 0110×0 | 0110×0 | 01110x | 010×00 | 01×000 | 01×000 | – | 01xx0x | 01×100 | 01x10x | Ø | 011000 | 011×00 | 011000 | 011×00 | 011000 | 011×00 | 011x0x | 01100x | 011x0x | 011xx0 | 0110×0 | 011xx0 | Ø | 011100 | 011100 | 011100 | 01110x | 0111×0 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | x11000 | x11x00 | Ø | Ø | x11100 | x11100 | Ø | x11000 | x11x00 | x11x00 | Ø | Ø | x11100 |
| 01xx01 | Ø | Ø | 01000x | 010x0x | Ø | 01x00x | Ø | Ø | 0x0101 | 010101 | 0x0101 | 010101 | 01×101 | 0xx101 | 0x1001 | 011001 | 0x1001 | 01100x | Ø | 01100x | 011001 | 011×01 | 0x1x01 | 011001 | 0110×1 | Ø | 011101 | 010×01 | 01×001 | 01x00x | 01xx0x | – | 01×101 | 01×101 | 01x1x1 | 011001 | 011×01 | 011001 | 011x0x | 01100x | 011x0x | 011×01 | 011001 | 011×01 | 011xx1 | 0110×1 | Ø | 011xx1 | 011101 | 011101 | 01110x | 011101 | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | x11x01 | Ø | x11101 | Ø | Ø | x11001 | x11x01 | Ø | x11x01 | Ø | x11101 |
| 01x10x | 0x0100 | Ø | 010×00 | 010100 | 0x0100 | 01xx00 | Ø | Ø | 0x010x | 01010x | 0x010x | 010101 | 01×101 | 0xx101 | Ø | 011x0x | Ø | 011×00 | Ø | 011×00 | 011×01 | 011101 | 0x1101 | 011×01 | Ø | Ø | 011101 | 01010x | 01xx0x | 01xx00 | 01×100 | 01×101 | – | 01×101 | 01x1x1 | 011x0x | 01110x | 011x0x | 011100 | 011×00 | 011100 | 011101 | 011×01 | 011101 | 0111xx | Ø | 0111×0 | 0111×1 | 01110x | 01110x | 011100 | 011101 | 0111xx | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | x11101 | Ø | x1110x | x11100 | Ø | Ø | x1110x | x11100 | x11101 | Ø | x1110x |
| 01x1x1 | Ø | Ø | Ø | 01010x | Ø | Ø | Ø | Ø | 0x01x1 | 010101 | 0x0101 | 0101×1 | 01×101 | 0xx101 | Ø | 011×01 | Ø | Ø | Ø | Ø | 011xx1 | 011101 | 0x1101 | 011×01 | 011×11 | Ø | 011101 | 010101 | 01xx01 | Ø | 01x10x | 01×101 | 01×101 | – | 01×111 | 011xx1 | 011101 | 011×01 | 0111xx | Ø | 01110x | 0111×1 | 011xx1 | 011101 | 011111 | 011×11 | 01111x | 011111 | 0111×1 | 011101 | 0111xx | 0111×1 | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | x11101 | Ø | x1x111 | Ø | x11101 | Ø | x111x1 | x11111 | x111x1 |
| x1x111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0111 | 0101×1 | Ø | 010111 | 01x1x1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×11 | 0111×1 | Ø | Ø | 011×11 | Ø | x111x1 | 0101×1 | Ø | Ø | Ø | 01x1x1 | 01x1x1 | 01×111 | – | 011×11 | 0111×1 | Ø | 01111x | Ø | Ø | 011111 | x11x11 | x111x1 | 011111 | x11x11 | x1111x | x11111 | 011111 | x111x1 | x1111x | x11111 | x11111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1111×1 | 11111x | 1111×1 | 11111x | 11×111 | 111×11 | 1111×1 | 11111x | 111111 | 111111 | 111111 |
| 0110xx | Ø | 0x10x0 | 01x0x0 | 01×000 | Ø | 011000 | 0x1000 | 011010 | Ø | Ø | Ø | Ø | 011×01 | Ø | 0x10xx | 01100x | 0x100x | 0110×0 | 0x10x0 | 011000 | 0110×1 | 011001 | 0x1001 | 011001 | 01101x | 011010 | 011×01 | 01x00x | 01100x | 0110×0 | 011000 | 011001 | 011x0x | 011xx1 | 011×11 | – | 01100x | 01100x | 0110×0 | 0110×0 | 011000 | 0110×1 | 0110×1 | 011001 | 01101x | 01101x | 011010 | 011011 | 011xxx | 011x0x | 011xx0 | 011xx1 | 011x1x | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | Ø | x110x0 | x11000 | x11001 | x11010 | Ø | Ø | Ø | x110xx | x1100x | x110x0 | x110x1 | x1101x | Ø |
| 011x0x | Ø | 0x1000 | 01×000 | 01xx00 | Ø | 011000 | 0x1000 | 0110×0 | Ø | 01x10x | Ø | 01×101 | 011101 | 0x1101 | 0x100x | 01100x | 0x100x | 011000 | 0x1000 | 011000 | 011001 | 011×01 | 0x1x01 | 011001 | 0110xx | 0110×0 | 011101 | 01xx0x | 01100x | 011000 | 011×00 | 011×01 | 01110x | 011101 | 0111×1 | 01100x | – | 01100x | 011×00 | 011000 | 011×00 | 011×01 | 011001 | 011×01 | 011xxx | 0110xx | 011xx0 | 011xx1 | 01110x | 01110x | 011100 | 011101 | 0111xx | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | Ø | x11000 | x11x00 | x11x01 | Ø | x1110x | x11100 | Ø | x1100x | x11x0x | x11x00 | x11x01 | Ø | x1110x |
| x1100x | Ø | 0x1000 | 01×000 | 01×000 | Ø | 011000 | xx1000 | 0110×0 | Ø | Ø | Ø | Ø | 011×01 | Ø | 0x100x | 01100x | xx100x | 011000 | xx1000 | x11000 | 011001 | 011001 | xx1001 | x11001 | 0110xx | x110x0 | x11x01 | 01x00x | 01100x | 011000 | 011000 | 011001 | 011x0x | 011×01 | Ø | 01100x | 01100x | – | 011000 | x11000 | x11000 | 011001 | x11001 | x11001 | 0110xx | x110xx | x110x0 | x110x1 | 011x0x | x11x0x | x11x00 | x11x01 | Ø | Ø | 1x100x | 1×1000 | 1×1001 | Ø | 1x100x | 11100x | 1×1000 | 111000 | 111000 | 111001 | 1110×0 | 111x0x | 111×00 | Ø | 11100x | 11100x | 111000 | 111001 | 1110xx | 111x0x |
| 011xx0 | Ø | 0x10x0 | 01x0x0 | 01xx00 | Ø | 011000 | 0x1000 | 011010 | Ø | 01×100 | Ø | Ø | 01110x | Ø | 0x10x0 | 011000 | 0x1000 | 0110×0 | 0x10x0 | 011000 | 0110xx | 011x0x | Ø | 01100x | 011010 | 011010 | 01110x | 01xx00 | 011000 | 0110×0 | 011×00 | 011x0x | 011100 | 0111xx | 01111x | 0110×0 | 011×00 | 011000 | – | 0110×0 | 011×00 | 011xxx | 0110xx | 011x0x | 011×10 | 011010 | 011×10 | 011x1x | 0111×0 | 011100 | 0111×0 | 0111xx | 011110 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | x110x0 | x11x00 | Ø | x11x10 | x11100 | x111x0 | x11110 | x110x0 | x11x00 | x11xx0 | Ø | x11x10 | x111x0 |
| x110x0 | Ø | 0x10x0 | 01x0x0 | 01×000 | Ø | 011000 | xx1000 | 011010 | Ø | Ø | Ø | Ø | Ø | Ø | 0x10x0 | 011000 | xx1000 | 0110×0 | xx10x0 | x11000 | 0110xx | 01100x | Ø | x1100x | 011010 | x11010 | Ø | 01×000 | 011000 | 0110×0 | 011000 | 01100x | 011×00 | Ø | Ø | 0110×0 | 011000 | x11000 | 0110×0 | – | x11000 | 0110xx | x110xx | x1100x | 011010 | x11010 | x11010 | x1101x | 011xx0 | x11x00 | x11xx0 | Ø | x11x10 | Ø | 1×1000 | 1×1000 | Ø | Ø | 1×1000 | 111000 | 1x10x0 | 1110×0 | 111000 | 11100x | 111010 | 111×00 | 111xx0 | 111×10 | 1110×0 | 111000 | 1110×0 | 1110xx | 111010 | 111xx0 |
| x11x00 | Ø | 0x1000 | 01×000 | 01xx00 | Ø | 011000 | xx1000 | 0110×0 | Ø | 01×100 | Ø | Ø | 01110x | Ø | 0x1000 | 011000 | xx1000 | 011000 | xx1000 | x11000 | 01100x | 011x0x | Ø | x1100x | 0110×0 | x110x0 | x1110x | 01xx00 | 011000 | 011000 | 011×00 | 011x0x | 011100 | 01110x | Ø | 011000 | 011×00 | x11000 | 011×00 | x11000 | – | 011x0x | x1100x | x11x0x | 011xx0 | x110x0 | x11xx0 | Ø | 011100 | x11100 | x11100 | x1110x | x111x0 | Ø | 1×1000 | 1x1x00 | Ø | 1×1100 | 1x1x00 | 111000 | 1x1x00 | 111000 | 111×00 | 111x0x | 111xx0 | 111100 | 111100 | 1111×0 | 111000 | 111×00 | 111×00 | 111x0x | 111xx0 | 111100 |
| 011xx1 | Ø | Ø | Ø | Ø | Ø | 01100x | Ø | 01101x | Ø | 01×101 | Ø | 01x1x1 | 011101 | 0x1101 | 0x10x1 | 011001 | 0x1001 | 0110xx | Ø | 01100x | 0110×1 | 011×01 | 0x1x01 | 011001 | 011011 | 01101x | 011101 | 01xx01 | 011001 | 0110xx | 011x0x | 011×01 | 011101 | 0111×1 | 011111 | 0110×1 | 011×01 | 011001 | 011xxx | 0110xx | 011x0x | – | 0110×1 | 011×01 | 011×11 | 011011 | 011x1x | 011×11 | 0111×1 | 011101 | 0111xx | 0111×1 | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | x11x01 | Ø | x11101 | Ø | x11111 | x110x1 | x11x01 | Ø | x11xx1 | x11x11 | x111x1 |
| x110x1 | Ø | Ø | Ø | Ø | Ø | 01100x | Ø | 01101x | Ø | Ø | Ø | Ø | 011×01 | Ø | 0x10x1 | 011001 | xx1001 | 0110xx | Ø | x1100x | 0110×1 | 011001 | xx1001 | x11001 | 011011 | x1101x | x11x01 | 01×001 | 011001 | 0110xx | 01100x | 011001 | 011×01 | 011xx1 | x11x11 | 0110×1 | 011001 | x11001 | 0110xx | x110xx | x1100x | 0110×1 | – | x11001 | 011011 | x11011 | x1101x | x11011 | 011xx1 | x11x01 | Ø | x11xx1 | x11x11 | Ø | 1×1001 | Ø | 1×1001 | Ø | 1×1001 | 111001 | Ø | 1110xx | 11100x | 111001 | 11101x | 111×01 | Ø | 111×11 | 1110×1 | 111001 | 1110xx | 1110×1 | 111011 | 111xx1 |
| x11x01 | Ø | Ø | Ø | Ø | Ø | 01100x | Ø | Ø | Ø | 01×101 | Ø | 01×101 | 011101 | xx1101 | 0x1001 | 011001 | xx1001 | 01100x | Ø | x1100x | 011001 | 011×01 | xx1x01 | x11001 | 0110×1 | Ø | x11101 | 01xx01 | 011001 | 01100x | 011x0x | 011×01 | 011101 | 011101 | x111x1 | 011001 | 011×01 | x11001 | 011x0x | x1100x | x11x0x | 011×01 | x11001 | – | 011xx1 | x110x1 | Ø | x11xx1 | 011101 | x11101 | x1110x | x11101 | x111x1 | Ø | 1×1001 | Ø | 1x1x01 | 1×1101 | 1x1x01 | 111001 | Ø | 11100x | 111x0x | 111×01 | Ø | 111101 | 11110x | 1111×1 | 111001 | 111×01 | 111x0x | 111×01 | 111xx1 | 111101 |
| 011x1x | Ø | 0x1010 | 01×010 | Ø | Ø | 0110×0 | Ø | 011010 | Ø | Ø | Ø | 01×111 | 0111×1 | Ø | 0x101x | 0110xx | Ø | 011010 | 0x1010 | 0110×0 | 011011 | 011xx1 | Ø | 0110×1 | 01101x | 011010 | 0111×1 | Ø | 0110xx | 011010 | 011xx0 | 011xx1 | 0111xx | 011111 | 011111 | 01101x | 011xxx | 0110xx | 011×10 | 011010 | 011xx0 | 011×11 | 011011 | 011xx1 | – | 01101x | 011×10 | 011×11 | 01111x | 0111xx | 011110 | 011111 | 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | x11x10 | Ø | x11110 | x1111x | x1101x | Ø | x11x10 | x11x11 | x11x1x | x1111x |
| x1101x | Ø | 0x1010 | 01×010 | Ø | Ø | 0110×0 | Ø | 011010 | Ø | Ø | Ø | Ø | Ø | Ø | 0x101x | 0110xx | Ø | 011010 | xx1010 | x110x0 | 011011 | 0110×1 | Ø | x110x1 | 01101x | x11010 | Ø | Ø | 0110xx | 011010 | 0110×0 | 0110×1 | Ø | 011×11 | x11x11 | 01101x | 0110xx | x110xx | 011010 | x11010 | x110x0 | 011011 | x11011 | x110x1 | 01101x | – | x11010 | x11011 | 011x1x | Ø | x11x10 | x11x11 | x11x1x | Ø | Ø | Ø | Ø | Ø | Ø | 1110xx | 1×1010 | 111010 | 1110×0 | 1110×1 | 111010 | Ø | 111×10 | 111x1x | 11101x | 1110xx | 111010 | 111011 | 11101x | 111x1x |
| x11x10 | Ø | 0x1010 | 01×010 | Ø | Ø | 0110×0 | Ø | 011010 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0110×0 | Ø | 011010 | xx1010 | x110x0 | 01101x | Ø | Ø | Ø | 011010 | x11010 | Ø | Ø | 0110×0 | 011010 | 011xx0 | Ø | 0111×0 | 01111x | x1111x | 011010 | 011xx0 | x110x0 | 011×10 | x11010 | x11xx0 | 011x1x | x1101x | Ø | 011×10 | x11010 | – | x11x1x | 011110 | x111x0 | x11110 | x1111x | x11110 | Ø | Ø | Ø | Ø | Ø | Ø | 1110×0 | 1x1x10 | 111010 | 111xx0 | Ø | 111×10 | 1111×0 | 111110 | 111110 | 111010 | 111xx0 | 111×10 | 111x1x | 111×10 | 111110 |
| x11x11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01101x | Ø | Ø | Ø | 01×111 | 0111×1 | Ø | 0x1011 | 0110×1 | Ø | 01101x | Ø | Ø | 011011 | 011xx1 | Ø | x110x1 | 011011 | x1101x | x111x1 | Ø | 0110×1 | 01101x | Ø | 011xx1 | 0111×1 | 011111 | x11111 | 011011 | 011xx1 | x110x1 | 011x1x | x1101x | Ø | 011×11 | x11011 | x11xx1 | 011×11 | x11011 | x11x1x | – | 011111 | x111x1 | x1111x | x11111 | x11111 | Ø | Ø | Ø | Ø | Ø | Ø | 1110×1 | Ø | 11101x | Ø | 111xx1 | 111x1x | 1111×1 | 11111x | 111111 | 111011 | 111xx1 | 111x1x | 111×11 | 111×11 | 111111 |
| 0111xx | Ø | Ø | Ø | 01×100 | Ø | 011×00 | Ø | 011×10 | Ø | 01x10x | Ø | 01x1x1 | 011101 | 0x1101 | Ø | 011x0x | Ø | 011xx0 | Ø | 011×00 | 011xx1 | 011101 | 0x1101 | 011×01 | 011x1x | 011×10 | 011101 | 01x10x | 011x0x | 011xx0 | 011100 | 011101 | 01110x | 0111×1 | 011111 | 011xxx | 01110x | 011x0x | 0111×0 | 011xx0 | 011100 | 0111×1 | 011xx1 | 011101 | 01111x | 011x1x | 011110 | 011111 | – | 01110x | 0111×0 | 0111×1 | 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | x11101 | x11110 | x1110x | x111x0 | x1111x | Ø | x1110x | x111x0 | x111x1 | x1111x | x111xx |
| x1110x | Ø | Ø | Ø | 01×100 | Ø | 011×00 | Ø | Ø | Ø | 01x10x | Ø | 01×101 | 011101 | xx1101 | Ø | 011x0x | Ø | 011×00 | Ø | x11x00 | 011×01 | 011101 | xx1101 | x11x01 | Ø | Ø | x11101 | 01x10x | 011x0x | 011×00 | 011100 | 011101 | 01110x | 011101 | x111x1 | 011x0x | 01110x | x11x0x | 011100 | x11x00 | x11100 | 011101 | x11x01 | x11101 | 0111xx | Ø | x111x0 | x111x1 | 01110x | – | x11100 | x11101 | x111xx | Ø | Ø | 1×1100 | 1×1101 | 1x110x | 1x110x | 111x0x | 1×1100 | 111×00 | 111100 | 111101 | 1111×0 | 11110x | 111100 | 1111xx | 111x0x | 11110x | 111100 | 111101 | 1111xx | 11110x |
| x111x0 | Ø | Ø | Ø | 01×100 | Ø | 011×00 | Ø | 011×10 | Ø | 01×100 | Ø | Ø | 01110x | Ø | Ø | 011×00 | Ø | 011xx0 | Ø | x11x00 | Ø | 01110x | Ø | Ø | 011×10 | x11x10 | x1110x | 01×100 | 011×00 | 011xx0 | 011100 | 01110x | 011100 | 0111xx | x1111x | 011xx0 | 011100 | x11x00 | 0111×0 | x11xx0 | x11100 | 0111xx | Ø | x1110x | 011110 | x11x10 | x11110 | x1111x | 0111×0 | x11100 | – | x111xx | x11110 | Ø | Ø | 1×1100 | Ø | 1×1100 | 1×1100 | 111×00 | 1x11x0 | 111xx0 | 111100 | 11110x | 111110 | 111100 | 1111×0 | 111110 | 111xx0 | 111100 | 1111×0 | 1111xx | 111110 | 1111×0 |
| x111x1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | 01x1x1 | 011101 | xx1101 | Ø | 011×01 | Ø | Ø | Ø | Ø | 011xx1 | 011101 | xx1101 | x11x01 | 011×11 | Ø | x11101 | 01×101 | 011×01 | Ø | 01110x | 011101 | 011101 | 0111×1 | x11111 | 011xx1 | 011101 | x11x01 | 0111xx | Ø | x1110x | 0111×1 | x11xx1 | x11101 | 011111 | x11x11 | x1111x | x11111 | 0111×1 | x11101 | x111xx | – | x11111 | Ø | Ø | Ø | 1×1101 | 1×1101 | 1×1101 | 111×01 | Ø | Ø | 11110x | 111101 | 11111x | 111101 | 1111xx | 111111 | 111xx1 | 111101 | 1111xx | 1111×1 | 111111 | 1111×1 |
| x1111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | Ø | Ø | 01×111 | 0111×1 | Ø | Ø | Ø | Ø | 011×10 | Ø | Ø | 011×11 | 0111×1 | Ø | Ø | 011x1x | x11x10 | x111x1 | Ø | Ø | 011×10 | 0111×0 | 0111×1 | 0111xx | 011111 | x11111 | 011x1x | 0111xx | Ø | 011110 | x11x10 | x111x0 | 011111 | x11x11 | x111x1 | 01111x | x11x1x | x11110 | x11111 | 01111x | x111xx | x11110 | x11111 | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 111×10 | 1111×0 | 1111×1 | 111110 | 1111xx | 111110 | 11111x | 111x1x | 1111xx | 111110 | 111111 | 11111x | 11111x |
| 100x0x | x00x00 | x00000 | x00000 | x00x00 | 100×00 | x00000 | 100000 | Ø | x0010x | x0010x | 10010x | x00101 | x00101 | 100101 | Ø | Ø | 10x00x | Ø | 10×000 | 10×000 | Ø | Ø | 10xx01 | 10×001 | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | – | 10000x | 100×00 | 100×01 | 10010x | 10xx0x | 10x00x | 10xx00 | 10×000 | 10xx00 | 10xx01 | Ø | 10x10x | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 10x00x | x00000 | x0x000 | x00000 | x00000 | 100000 | x0x000 | 10×000 | Ø | Ø | Ø | 100x0x | Ø | Ø | 10xx01 | x0100x | x0100x | 10100x | x01000 | 101000 | 101000 | x01001 | x01001 | 101001 | 101001 | Ø | 1010×0 | 101×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1x100x | Ø | 1×1000 | 1×1000 | Ø | 1×1001 | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10000x | – | 10×000 | 10×001 | 10xx0x | 10100x | 10100x | 101000 | 101000 | 101000 | 101001 | 1010×0 | 101x0x | 101×00 | Ø | 1x100x | 1x100x | 1×1000 | 1×1001 | Ø | Ø |
| 10xx00 | x00x00 | x0x000 | x00000 | x00x00 | 100×00 | x0x000 | 10×000 | Ø | x00100 | x00100 | 100100 | Ø | Ø | 10x10x | x01000 | x01000 | 101000 | x01000 | 101000 | 101000 | Ø | Ø | 101x0x | 10100x | Ø | 1010×0 | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | 1×1000 | 1x1x00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | 1×1100 | Ø | Ø | 100×00 | 10×000 | – | 10xx0x | 10×100 | 101×00 | 101000 | 101×00 | 101000 | 101×00 | 101x0x | 101xx0 | 101100 | 101100 | Ø | 1×1000 | 1x1x00 | 1x1x00 | Ø | Ø | 1×1100 |
| 10xx01 | Ø | Ø | Ø | Ø | 100x0x | Ø | 10x00x | Ø | x00101 | x00101 | 100101 | x00101 | x0x101 | 10×101 | x01001 | x01001 | 101001 | Ø | 10100x | 10100x | x01001 | x01x01 | 101×01 | 101001 | Ø | Ø | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | 1×1001 | 1x1x01 | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | 1×1101 | Ø | 100×01 | 10×001 | 10xx0x | – | 10×101 | 101×01 | 101001 | 101x0x | 10100x | 101x0x | 101×01 | Ø | 101101 | 10110x | Ø | 1×1001 | 1x1x01 | Ø | 1x1x01 | Ø | 1×1101 |
| 10x10x | x00100 | Ø | Ø | x00100 | 100100 | Ø | 10xx00 | Ø | x0010x | x0010x | 10010x | x00101 | x0x101 | 10×101 | Ø | Ø | 101x0x | Ø | 101×00 | 101×00 | Ø | x01101 | 101101 | 101×01 | Ø | Ø | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | 1×1101 | Ø | Ø | Ø | Ø | Ø | 1x110x | 1×1100 | 1×1101 | Ø | 10010x | 10xx0x | 10×100 | 10×101 | – | 10110x | 101x0x | 101100 | 101×00 | 101100 | 101101 | 1011×0 | 10110x | 101100 | Ø | Ø | 1x110x | 1×1100 | 1×1101 | Ø | 1x110x |
| 101x0x | Ø | x01000 | Ø | Ø | 10xx00 | x01000 | 101000 | Ø | Ø | Ø | 10x10x | Ø | x01101 | 101101 | x0100x | x0100x | 10100x | x01000 | 101000 | 101000 | x01001 | x01x01 | 101×01 | 101001 | Ø | 1010×0 | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1x100x | Ø | 1×1000 | 1x1x00 | Ø | 1×1001 | 1x1x01 | Ø | Ø | Ø | Ø | Ø | 1x110x | 1×1100 | 1×1101 | Ø | 10xx0x | 10100x | 101×00 | 101×01 | 10110x | – | 10100x | 101×00 | 101000 | 101×00 | 101×01 | 101xx0 | 10110x | 101100 | Ø | 1x100x | 1x1x0x | 1x1x00 | 1x1x01 | Ø | 1x110x |
| 1x100x | Ø | x01000 | Ø | Ø | 10×000 | xx1000 | 101000 | Ø | Ø | Ø | Ø | Ø | Ø | 101×01 | x0100x | xx100x | 10100x | xx1000 | 101000 | 1×1000 | xx1001 | xx1001 | 101001 | 1×1001 | Ø | 1x10x0 | 1x1x01 | Ø | x1100x | x11000 | x11000 | x11001 | Ø | Ø | Ø | x1100x | x1100x | 11100x | x11000 | 111000 | 111000 | x11001 | 111001 | 111001 | Ø | 1110xx | 1110×0 | 1110×1 | Ø | 111x0x | 111×00 | 111×01 | Ø | 10x00x | 10100x | 101000 | 101001 | 101x0x | 10100x | – | 101000 | 1×1000 | 1×1000 | 1×1001 | 1x10x0 | 1x1x0x | 1x1x00 | Ø | 11100x | 11100x | 111000 | 111001 | 1110xx | 111x0x |
| 101xx0 | Ø | x010x0 | Ø | Ø | 10xx00 | x01000 | 101000 | x01010 | Ø | Ø | 10×100 | Ø | Ø | 10110x | x010x0 | x01000 | 101000 | x010x0 | 1010×0 | 101000 | Ø | Ø | 101x0x | 10100x | x01010 | 101010 | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | 1x10x0 | 1x1x00 | Ø | Ø | Ø | Ø | 1×1010 | 1x1x10 | Ø | Ø | 1×1100 | 1x11x0 | Ø | 1×1110 | 10xx00 | 101000 | 101×00 | 101x0x | 101100 | 101×00 | 101000 | – | 1010×0 | 101×00 | 101x0x | 101×10 | 101100 | 1011×0 | 1×1110 | 1x10x0 | 1x1x00 | 1x1xx0 | Ø | 1x1x10 | 1x11x0 |
| 1x10x0 | Ø | x010x0 | Ø | Ø | 10×000 | xx1000 | 101000 | xx1010 | Ø | Ø | Ø | Ø | Ø | Ø | x010x0 | xx1000 | 101000 | xx10x0 | 1010×0 | 1×1000 | Ø | Ø | 10100x | 1x100x | xx1010 | 1×1010 | Ø | Ø | x11000 | x110x0 | x11000 | Ø | Ø | Ø | Ø | x110x0 | x11000 | 111000 | x110x0 | 1110×0 | 111000 | Ø | 1110xx | 11100x | x11010 | 111010 | 111010 | 11101x | Ø | 111×00 | 111xx0 | Ø | 111×10 | 10×000 | 101000 | 101000 | 10100x | 101×00 | 101000 | 1×1000 | 1010×0 | – | 1×1000 | 1x100x | 1×1010 | 1x1x00 | 1x1xx0 | 111×10 | 1110×0 | 111000 | 1110×0 | 1110xx | 111010 | 111xx0 |
| 1x1x00 | Ø | x01000 | Ø | Ø | 10xx00 | xx1000 | 101000 | Ø | Ø | Ø | 10×100 | Ø | Ø | 10110x | x01000 | xx1000 | 101000 | xx1000 | 101000 | 1×1000 | Ø | Ø | 101x0x | 1x100x | Ø | 1x10x0 | 1x110x | Ø | x11000 | x11000 | x11x00 | Ø | x11100 | Ø | Ø | x11000 | x11x00 | 111000 | x11x00 | 111000 | 111×00 | Ø | 11100x | 111x0x | Ø | 1110×0 | 111xx0 | Ø | x11100 | 111100 | 111100 | 11110x | 1111×0 | 10xx00 | 101000 | 101×00 | 101x0x | 101100 | 101×00 | 1×1000 | 101×00 | 1×1000 | – | 1x1x0x | 1x1xx0 | 1×1100 | 1×1100 | 1111×0 | 111000 | 111×00 | 111×00 | 111x0x | 111xx0 | 111100 |
| 1x1x01 | Ø | Ø | Ø | Ø | Ø | Ø | 10100x | Ø | Ø | Ø | 10×101 | Ø | xx1101 | 101101 | x01001 | xx1001 | 101001 | Ø | 10100x | 1x100x | xx1001 | xx1x01 | 101×01 | 1×1001 | Ø | Ø | 1×1101 | Ø | x11001 | Ø | Ø | x11x01 | x11101 | x11101 | 1111×1 | x11001 | x11x01 | 111001 | Ø | 11100x | 111x0x | x11x01 | 111001 | 111×01 | Ø | 1110×1 | Ø | 111xx1 | x11101 | 111101 | 11110x | 111101 | 1111×1 | 10xx01 | 101001 | 101x0x | 101×01 | 101101 | 101×01 | 1×1001 | 101x0x | 1x100x | 1x1x0x | – | Ø | 1×1101 | 1x110x | 1111×1 | 111001 | 111×01 | 111x0x | 111×01 | 111xx1 | 111101 |
| 1x1x10 | Ø | x01010 | Ø | Ø | Ø | Ø | 1010×0 | xx1010 | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | 1010×0 | xx1010 | 101010 | 1x10x0 | Ø | Ø | Ø | Ø | xx1010 | 1×1010 | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | 11111x | x11010 | Ø | 1110×0 | x11x10 | 111010 | 111xx0 | Ø | 11101x | Ø | x11x10 | 111010 | 111×10 | 111x1x | x11110 | 1111×0 | 111110 | 11111x | 111110 | Ø | 1010×0 | 101xx0 | Ø | 1011×0 | 101xx0 | 1x10x0 | 101×10 | 1×1010 | 1x1xx0 | Ø | – | 1x11x0 | 1×1110 | 111110 | 111010 | 111xx0 | 111×10 | 111x1x | 111×10 | 111110 |
| 1x110x | Ø | Ø | Ø | Ø | 10×100 | Ø | 101×00 | Ø | Ø | Ø | 10x10x | Ø | xx1101 | 101101 | Ø | Ø | 101x0x | Ø | 101×00 | 1x1x00 | Ø | xx1101 | 101101 | 1x1x01 | Ø | Ø | 1×1101 | Ø | Ø | Ø | x11100 | x11101 | x1110x | x11101 | 1111×1 | Ø | x1110x | 111x0x | x11100 | 111×00 | 111100 | x11101 | 111×01 | 111101 | Ø | Ø | 1111×0 | 1111×1 | x1110x | 11110x | 111100 | 111101 | 1111xx | 10x10x | 101x0x | 101100 | 101101 | 10110x | 10110x | 1x1x0x | 101100 | 1x1x00 | 1×1100 | 1×1101 | 1x11x0 | – | 1×1100 | 1111xx | 111x0x | 11110x | 111100 | 111101 | 1111xx | 11110x |
| 1x11x0 | Ø | Ø | Ø | Ø | 10×100 | Ø | 101×00 | Ø | Ø | Ø | 10×100 | Ø | Ø | 10110x | Ø | Ø | 101×00 | Ø | 101xx0 | 1x1x00 | Ø | Ø | 10110x | Ø | Ø | 1x1x10 | 1x110x | Ø | Ø | Ø | x11100 | Ø | x11100 | Ø | 11111x | Ø | x11100 | 111×00 | x111x0 | 111xx0 | 111100 | Ø | Ø | 11110x | x11110 | 111×10 | 111110 | 11111x | x111x0 | 111100 | 1111×0 | 1111xx | 111110 | 10×100 | 101×00 | 101100 | 10110x | 101100 | 101100 | 1x1x00 | 1011×0 | 1x1xx0 | 1×1100 | 1x110x | 1×1110 | 1×1100 | – | 111110 | 111xx0 | 111100 | 1111×0 | 1111xx | 111110 | 1111×0 |
| 11x11x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 111×10 | 1111×1 | Ø | Ø | Ø | Ø | Ø | Ø | x1x111 | 11×111 | Ø | Ø | Ø | x11110 | 111×10 | 1111×0 | x11111 | 111×11 | 1111×1 | x1111x | 111x1x | 111110 | 111111 | x1111x | 1111xx | 111110 | 111111 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 111×10 | 1111×0 | 1111×1 | 111110 | 1111xx | 111110 | – | 111x1x | 1111xx | 111110 | 111111 | 11111x | 11111x |
| 1110xx | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | 1x100x | x110x0 | 1x10x0 | 111000 | x110x1 | x11001 | 1×1001 | 111001 | x1101x | 111010 | 111×01 | Ø | x1100x | x110x0 | x11000 | x11001 | Ø | Ø | 111×11 | x110xx | x1100x | 11100x | x110x0 | 1110×0 | 111000 | x110x1 | 1110×1 | 111001 | x1101x | 11101x | 111010 | 111011 | Ø | 111x0x | 111xx0 | 111xx1 | 111x1x | Ø | 1x100x | 1×1000 | 1×1001 | Ø | 1x100x | 11100x | 1x10x0 | 1110×0 | 111000 | 111001 | 111010 | 111x0x | 111xx0 | 111x1x | – | 11100x | 1110×0 | 1110×1 | 11101x | 111xxx |
| 111x0x | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | Ø | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | x1100x | 1x100x | x11000 | 1×1000 | 111000 | x11001 | x11x01 | 1x1x01 | 111001 | Ø | 1110×0 | 111101 | Ø | x1100x | x11000 | x11x00 | x11x01 | x1110x | x11101 | 1111×1 | x1100x | x11x0x | 11100x | x11x00 | 111000 | 111×00 | x11x01 | 111001 | 111×01 | Ø | 1110xx | 111xx0 | 111xx1 | x1110x | 11110x | 111100 | 111101 | 1111xx | Ø | 1x100x | 1x1x00 | 1x1x01 | 1x110x | 1x1x0x | 11100x | 1x1x00 | 111000 | 111×00 | 111×01 | 111xx0 | 11110x | 111100 | 1111xx | 11100x | – | 111×00 | 111×01 | 111xxx | 11110x |
| 111xx0 | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | x110x0 | 1x10x0 | 111000 | Ø | Ø | Ø | 11100x | x11010 | 111010 | 11110x | Ø | x11000 | x110x0 | x11x00 | Ø | x11100 | Ø | 11111x | x110x0 | x11x00 | 111000 | x11xx0 | 1110×0 | 111×00 | Ø | 1110xx | 111x0x | x11x10 | 111010 | 111×10 | 111x1x | x111x0 | 111100 | 1111×0 | 1111xx | 111110 | Ø | 1×1000 | 1x1x00 | Ø | 1×1100 | 1x1x00 | 111000 | 1x1xx0 | 1110×0 | 111×00 | 111x0x | 111×10 | 111100 | 1111×0 | 111110 | 1110×0 | 111×00 | – | 111xxx | 111×10 | 1111×0 |
| 111xx1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | x11001 | 1×1001 | Ø | Ø | 11100x | x110x1 | x11x01 | 1x1x01 | 111001 | x11011 | 11101x | 111101 | Ø | x11001 | Ø | Ø | x11x01 | x11101 | x111x1 | 111111 | x110x1 | x11x01 | 111001 | Ø | 1110xx | 111x0x | x11xx1 | 1110×1 | 111×01 | x11x11 | 111011 | 111x1x | 111×11 | x111x1 | 111101 | 1111xx | 1111×1 | 111111 | Ø | 1×1001 | Ø | 1x1x01 | 1×1101 | 1x1x01 | 111001 | Ø | 1110xx | 111x0x | 111×01 | 111x1x | 111101 | 1111xx | 111111 | 1110×1 | 111×01 | 111xxx | – | 111×11 | 1111×1 |
| 111x1x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | 1×1010 | 1110×0 | x11011 | Ø | Ø | 1110×1 | x1101x | 111010 | 1111×1 | Ø | Ø | x11010 | Ø | Ø | Ø | x11111 | 111111 | x1101x | Ø | 1110xx | x11x10 | 111010 | 111xx0 | x11x11 | 111011 | 111xx1 | x11x1x | 11101x | 111×10 | 111×11 | x1111x | 1111xx | 111110 | 111111 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | 1110xx | 1x1x10 | 111010 | 111xx0 | 111xx1 | 111×10 | 1111xx | 111110 | 11111x | 11101x | 111xxx | 111×10 | 111×11 | – | 11111x |
| 1111xx | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | Ø | Ø | Ø | Ø | 111×00 | Ø | x11101 | 1×1101 | 111×01 | Ø | 111×10 | 111101 | Ø | Ø | Ø | x11100 | x11101 | x1110x | x111x1 | 111111 | Ø | x1110x | 111x0x | x111x0 | 111xx0 | 111100 | x111x1 | 111xx1 | 111101 | x1111x | 111x1x | 111110 | 111111 | x111xx | 11110x | 1111×0 | 1111×1 | 11111x | Ø | Ø | 1×1100 | 1×1101 | 1x110x | 1x110x | 111x0x | 1x11x0 | 111xx0 | 111100 | 111101 | 111110 | 11110x | 1111×0 | 11111x | 111xxx | 11110x | 1111×0 | 1111×1 | 11111x | – |
Z2=
Ĉ3=C2∪(C2*C2)
C3=>
| 0xx0x0, 0x10xx, xx100x xx10x0, xx1x01, 01xx0x 011xxx, x110xx, x11x0x x11xx0, x11xx1, x11x1x x111xx, 10xx0x, 1x1x0x 1x1xx0, 111xxx |
| 0xx0x0 | 0x10xx | xx100x | xx10x0 | xx1x01 | 01xx0x | 011xxx | x110xx | x11x0x | x11xx0 | x11xx1 | x11x1x | x111xx | 10xx0x | 1x1x0x | 1x1xx0 | 111xxx | |
| 0xx0x0 | – | 0x10x0 | 0x1000 | 0x10x0 | 0x100x | 01×000 | 0110×0 | 0110×0 | 011000 | 0110×0 | 0110xx | 011010 | 011xx0 | x0x000 | xx1000 | xx10x0 | x110x0 |
| 0x10xx | 0x10x0 | – | 0x100x | 0x10x0 | 0x1001 | 01100x | 0110xx | 0110xx | 01100x | 0110×0 | 0110×1 | 01101x | 011xxx | x0100x | xx100x | xx10x0 | x110xx |
| xx100x | 0x1000 | 0x100x | – | xx1000 | xx1001 | 01100x | 01100x | x1100x | x1100x | x11000 | x11001 | x110xx | x11x0x | 10100x | 1x100x | 1×1000 | 11100x |
| xx10x0 | 0x10x0 | 0x10x0 | xx1000 | – | xx100x | 011000 | 0110×0 | x110x0 | x11000 | x110x0 | x110xx | x11010 | x11xx0 | 101000 | 1×1000 | 1x10x0 | 1110×0 |
| xx1x01 | 0x100x | 0x1001 | xx1001 | xx100x | – | 011×01 | 011×01 | x11001 | x11x01 | x11x0x | x11x01 | x11xx1 | x11101 | 101×01 | 1x1x01 | 1x1x0x | 111×01 |
| 01xx0x | 01×000 | 01100x | 01100x | 011000 | 011×01 | – | 011x0x | 01100x | 011x0x | 011×00 | 011×01 | 011xxx | 01110x | Ø | x11x0x | x11x00 | x11x0x |
| 011xxx | 0110×0 | 0110xx | 01100x | 0110×0 | 011×01 | 011x0x | – | 0110xx | 011x0x | 011xx0 | 011xx1 | 011x1x | 0111xx | Ø | x11x0x | x11xx0 | x11xxx |
| x110xx | 0110×0 | 0110xx | x1100x | x110x0 | x11001 | 01100x | 0110xx | – | x1100x | x110x0 | x110x1 | x1101x | x11xxx | 1x100x | 11100x | 1110×0 | 1110xx |
| x11x0x | 011000 | 01100x | x1100x | x11000 | x11x01 | 011x0x | 011x0x | x1100x | – | x11x00 | x11x01 | x11xxx | x1110x | 1x1x0x | 111x0x | 111×00 | 111x0x |
| x11xx0 | 0110×0 | 0110×0 | x11000 | x110x0 | x11x0x | 011×00 | 011xx0 | x110x0 | x11x00 | – | x11xxx | x11x10 | x111x0 | 1x1x00 | 111×00 | 111xx0 | 111xx0 |
| x11xx1 | 0110xx | 0110×1 | x11001 | x110xx | x11x01 | 011×01 | 011xx1 | x110x1 | x11x01 | x11xxx | – | x11x11 | x111x1 | 1x1x01 | 111×01 | 111xxx | 111xx1 |
| x11x1x | 011010 | 01101x | x110xx | x11010 | x11xx1 | 011xxx | 011x1x | x1101x | x11xxx | x11x10 | x11x11 | – | x1111x | Ø | 111xxx | 111×10 | 111x1x |
| x111xx | 011xx0 | 011xxx | x11x0x | x11xx0 | x11101 | 01110x | 0111xx | x11xxx | x1110x | x111x0 | x111x1 | x1111x | – | 1x110x | 11110x | 1111×0 | 1111xx |
| 10xx0x | x0x000 | x0100x | 10100x | 101000 | 101×01 | Ø | Ø | 1x100x | 1x1x0x | 1x1x00 | 1x1x01 | Ø | 1x110x | – | 101x0x | 101×00 | 1x1x0x |
| 1x1x0x | xx1000 | xx100x | 1x100x | 1×1000 | 1x1x01 | x11x0x | x11x0x | 11100x | 111x0x | 111×00 | 111×01 | 111xxx | 11110x | 101x0x | – | 1x1x00 | 111x0x |
| 1x1xx0 | xx10x0 | xx10x0 | 1×1000 | 1x10x0 | 1x1x0x | x11x00 | x11xx0 | 1110×0 | 111×00 | 111xx0 | 111xxx | 111×10 | 1111×0 | 101×00 | 1x1x00 | – | 111xx0 |
| 111xxx | x110x0 | x110xx | 11100x | 1110×0 | 111×01 | x11x0x | x11xxx | 1110xx | 111x0x | 111xx0 | 111xx1 | 111x1x | 1111xx | 1x1x0x | 111x0x | 111xx0 | – |
Z3=
Ĉ4=C3∪(C3*C3)
C4=>
| x11xxx | |
| x11xxx | – |
Z4=
Ĉ5=C4∪(C4*C4)
C5=>Ø
Z = Z0∪Z1∪Z2∪Z3∪Z4
Z=>
| 1000×1, 000xx0, 0x0x00 x00x00, x0x000, 0001xx 0x010x, x0010x, 0x01x1 0xx101, x0x101, 01x1x1 x1x111, 11x11x, 0xx0x0 0x10xx, xx100x, xx10x0 xx1x01, 01xx0x, 10xx0x 1x1x0x, 1x1xx0, x11xxx |
Нахождение тупиковых форм.
| 1000×1 | 000xx0 | 0x0x00 | x00x00 | x0x000 | 0001xx | 0x010x | x0010x | 0x01x1 | 0xx101 | x0x101 | 01x1x1 | x1x111 | 11x11x | 0xx0x0 | 0x10xx | xx100x | xx10x0 | xx1x01 | 01xx0x | 10xx0x | 1x1x0x | 1x1xx0 | x11xxx | ||
|
1000×1 |
– |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
100011 |
100011 |
100011 |
100011 |
v |
|
000xx0 |
000xx0 |
– |
000×10 |
000×10 |
000×10 |
000010 |
000010 |
000010 |
000010 |
000010 |
000010 |
000010 |
000010 |
000010 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
0x0x00 |
0x0x00 |
010×00 |
– |
010×00 |
010×00 |
010×00 |
010000 |
010000 |
010000 |
010000 |
010000 |
010000 |
010000 |
010000 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
x00x00 |
x00x00 |
100×00 |
100×00 |
– |
100100 |
100100 |
100100 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
x0x000 |
x0x000 |
x01000 |
x01000 |
x01000 |
– |
x01000 |
x01000 |
x01000 |
x01000 |
x01000 |
x01000 |
x01000 |
x01000 |
x01000 |
101000 |
101000 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
0001xx |
0001xx |
0001×1 |
0001×1 |
0001×1 |
0001×1 |
– |
000111 |
000111 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
0x010x |
0x010x |
0x0101 |
0x0101 |
0x0101 |
0x0101 |
010101 |
– |
010101 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
x0010x |
x0010x |
x00101 |
x00101 |
x00101 |
x00101 |
100101 |
100101 |
– |
100101 |
100101 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
0x01x1 |
0x01x1 |
0x01x1 |
0x01x1 |
0x01x1 |
0x01x1 |
0101×1 |
010111 |
010111 |
– |
010111 |
010111 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
0xx101 |
0xx101 |
0xx101 |
0xx101 |
0xx101 |
0xx101 |
0x1101 |
0x1101 |
0x1101 |
0x1101 |
– |
011101 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
x0x101 |
x0x101 |
x0x101 |
x0x101 |
x0x101 |
x0x101 |
x01101 |
x01101 |
x01101 |
x01101 |
101101 |
– |
101101 |
101101 |
101101 |
101101 |
101101 |
101101 |
101101 |
Ø | Ø | Ø | Ø | Ø | Ø | |
|
01x1x1 |
01x1x1 |
01x1x1 |
01x1x1 |
01x1x1 |
01x1x1 |
01x1x1 |
01×111 |
01×111 |
011111 |
011111 |
011111 |
– | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x11111 |
x11111 |
x11111 |
111111 |
– | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11×110 |
– |
11×110 |
11×110 |
11×110 |
11×110 |
11×110 |
11×110 |
11×110 |
11×110 |
110110 |
110110 |
v |
|
0xx0x0 |
0xx0x0 |
0x10x0 |
0x10x0 |
0x10x0 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
– |
010010 |
010010 |
010010 |
010010 |
010010 |
010010 |
010010 |
010010 |
010010 |
v |
|
0x10xx |
0x10xx |
0x10xx |
0x10xx |
0x10xx |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
– |
0x1011 |
0x1011 |
0x1011 |
0x1011 |
0x1011 |
0x1011 |
0x1011 |
001011 |
v |
|
xx100x |
xx100x |
xx100x |
xx100x |
xx100x |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
1×1001 |
– |
1×1001 |
Ø | Ø | Ø | Ø | Ø | Ø | |
|
xx10x0 |
xx10x0 |
xx10x0 |
xx10x0 |
xx10x0 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
1×1010 |
1×1010 |
1×1010 |
– |
1×1010 |
1×1010 |
1×1010 |
1×1010 |
Ø | Ø | |
|
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
1×1001 |
111101 |
111101 |
– |
111101 |
111101 |
Ø | Ø | Ø | |
|
01xx0x |
01xx0x |
01xx0x |
01xx01 |
01xx01 |
01xx01 |
01xx01 |
01×001 |
01×001 |
01×001 |
01×001 |
01×001 |
01×001 |
01×001 |
01×001 |
01×001 |
010001 |
010001 |
010001 |
010001 |
– |
010001 |
010001 |
010001 |
010001 |
v |
|
10xx0x |
10xx00 |
10xx00 |
10xx00 |
101×00 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
– | Ø | Ø | Ø | |
|
1x1x0x |
1x1x0x |
1x1x0x |
1x1x0x |
1x1x0x |
1x1x01 |
1x1x01 |
1x1x01 |
1x1x01 |
1x1x01 |
1x1x01 |
1×1001 |
1×1001 |
1×1001 |
1×1001 |
1×1001 |
1×1001 |
111101 |
111101 |
1×1100 |
1×1100 |
111100 |
– | Ø | Ø | |
|
1x1xx0 |
1x1xx0 |
1x1xx0 |
1x1xx0 |
1x1xx0 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1×1010 |
1×1010 |
1×1010 |
1×1010 |
101110 |
101110 |
101110 |
101110 |
101110 |
– |
101110 |
v |
|
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xx0 |
x11xx0 |
x11xx0 |
x11xx0, x11x10, x1101x |
x11x00, x110x0, 011xx0 |
x11100, 111×00, 1110×0 |
x11100, 111×00, 1110×0 |
x11100 |
x11100 |
x11100 |
111100 |
111100 |
011110 |
011110 |
– | v |
E0:
L1=L0#E0
| 11x11x | 0xx0x0 | 01xx0x | 1x1xx0 | x11xxx | |
|
000000, 000100, 000101 |
000000, 000100, 000101 |
000100, 000101, 000111 |
000100, 000101, 000111 |
000100, 000101, 000111 |
000100 |
L1:
 1=Z0-E0
1=Z0-E0
До упорядочивания:
| 000100 | 000101 | 000111 | 001001 | 010111 | 100101 | 101001 | 101101 | |
| 1000×1 | ||||||||
| 000xx0 | + | |||||||
| 0x0x00 | + | |||||||
| x00x00 | + | |||||||
| x0x000 | ||||||||
| 0001xx | + | + | + | |||||
| 0x010x | + | + | ||||||
| x0010x | + | + | + | |||||
| 0x01x1 | + | + | + | |||||
| 0xx101 | + | |||||||
| x0x101 | + | + | + | |||||
| 01x1x1 | + | |||||||
| x1x111 | + | |||||||
| 0x10xx | + | |||||||
| xx100x | + | + | ||||||
| xx10x0 | ||||||||
| xx1x01 | + | + | + | |||||
| 10xx0x | + | + | + | |||||
| 1x1x0x | + | + |
После упорядочивания:
| 000100 | 000101 | 000111 | 001001 | 010111 | 100101 | 101001 | 101101 | |
| 0001xx | + | + | + | |||||
| x0010x | + | + | + | |||||
| 0x01x1 | + | + | + | |||||
| x0x101 | + | + | + | |||||
| xx1x01 | + | + | + | |||||
| 10xx0x | + | + | + |
 1 => Z1
1 => Z1
Z1:
| 0001xx | x0010x | 0x01x1 | x0x101 | xx1x01 | 10xx0x | ||
|
0001xx |
– |
00011x |
000110 |
000110 |
000110 |
000110 |
v |
|
x0010x |
10010x |
– |
10010x |
100100 |
100100 |
Ø | |
|
0x01x1 |
0101×1 |
0101×1 |
– |
0101×1 |
0101×1 |
0101×1 |
v |
|
x0x101 |
x01101 |
x01101 |
x01101 |
– | Ø | Ø | |
|
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1001 |
– |
x11001 |
v |
|
10xx0x |
10xx0x |
10x00x |
10x00x |
10x00x |
10×000 |
– | v |
E1:
L2=L1#E1
| 0x01x1 | xx1x01 | |
|
000100 |
000100 |
000100 |
L2:
 2=Z1-E1
2=Z1-E1
До упорядочивания:
| 000100 | 100101 | |
| 0001xx | + | |
| x0010x | + | + |
| x0x101 | + | |
| 10xx0x | + |
После упорядочивания:
| 000100 | 100101 | |
| x0010x | + | + |
| 10xx0x | + |
 2 => Z2
2 => Z2
Z2:
| x0010x | 10xx0x | ||
|
x0010x |
– |
00010x |
v |
|
10xx0x |
10x00x |
– | v |
E2:
L3=L2#E2
| x0010x | |
|
000100 |
Ø |
L3:Ø
 3=Z2-E2
3=Z2-E2
 3 => Z3
3 => Z3
Z3:
E:
МДНФ:x1x2x4x5 v x1x4x6 v x1x2x5 v x1x3x6 v x2x3 v x1x3x4x6 v x3x5x6 v x2x3x4x5, цена=26
3. Анализ полученных результатов
Все результаты:
Результат метода Квайна
f1 = x1x3x4x6 v x1x2x4x6 v x1x3x5x6 v x1x2x4x5 v x3x4x5 v x3x4x6 v x1x2x4x5x6 v x1x3x5x6 v x1x2x3x5 v x2x3x4x5 v x1x2x3x5 v x2x3x6, цена=46
Результат метода Карно
f2 = x1x2x3x4x6 v x1x2x4x5 v x1x4x6 v x1x3x4 v x1x2x5 v x1x3x6 v x2x3 v x1x2x3x4 v x1x3x4x6 v x1x2x5 v x3x5x6, цена=37
Результат метода Кубических покрытий
f3 = x1x2x4x5 v x1x4x6 v x1x2x5 v x1x3x6 v x2x3 v x1x3x4x6 v x3x5x6 v x2x3x4x5, цена=26
| Набор | Исходная | После Квайна | После Карно | После Кубических покрытий |
| x1x2x3x4x5x6 | f0 | f1 | f2 | f3 |
| 000000 | 1 | 1 | 1 | 1 |
| 000001 | 0 | 0 | 0 | 0 |
| 000010 | ? | 0 | 1 | 1 |
| 000011 | 0 | 0 | 0 | 0 |
| 000100 | 1 | 1 | 1 | 1 |
| 000101 | 1 | 1 | 1 | 1 |
| 000110 | ? | 0 | 1 | 0 |
| 000111 | 1 | 1 | 1 | 1 |
| 001000 | 1 | 1 | 1 | 1 |
| 001001 | 1 | 1 | 1 | 1 |
| 001010 | 1 | 1 | 1 | 1 |
| 001011 | ? | 0 | 1 | 0 |
| 001100 | 0 | 0 | 0 | 0 |
| 001101 | ? | 0 | 1 | 1 |
| 001110 | 0 | 0 | 0 | 0 |
| 001111 | 0 | 0 | 0 | 0 |
| 010000 | 1 | 1 | 1 | 1 |
| 010001 | 1 | 1 | 1 | 1 |
| 010010 | 1 | 1 | 1 | 1 |
| 010011 | 0 | 0 | 0 | 0 |
| 010100 | 1 | 1 | 1 | 1 |
| 010101 | 1 | 1 | 1 | 1 |
| 010110 | 0 | 0 | 0 | 0 |
| 010111 | 1 | 1 | 1 | 1 |
| 011000 | 1 | 1 | 1 | 1 |
| 011001 | 1 | 1 | 1 | 1 |
| 011010 | 1 | 1 | 1 | 1 |
| 011011 | ? | 0 | 1 | 1 |
| 011100 | 1 | 1 | 1 | 1 |
| 011101 | ? | 0 | 1 | 1 |
| 011110 | 1 | 1 | 1 | 1 |
| 011111 | 1 | 1 | 1 | 1 |
| 100000 | ? | 0 | 1 | 0 |
| 100001 | ? | 0 | 1 | 0 |
| 100010 | 0 | 0 | 0 | 0 |
| 100011 | ? | 0 | 1 | 0 |
| 100100 | ? | 0 | 1 | 1 |
| 100101 | 1 | 1 | 1 | 1 |
| 100110 | 0 | 0 | 0 | 0 |
| 100111 | 0 | 0 | 0 | 0 |
| 101000 | 1 | 1 | 1 | 1 |
| 101001 | 1 | 1 | 1 | 1 |
| 101010 | 1 | 1 | 1 | 1 |
| 101011 | 0 | 0 | 0 | 0 |
| 101100 | ? | 0 | 1 | 1 |
| 101101 | 1 | 1 | 1 | 1 |
| 101110 | 1 | 1 | 1 | 1 |
| 101111 | 0 | 0 | 0 | 0 |
| 110000 | 0 | 0 | 0 | 0 |
| 110001 | 0 | 0 | 0 | 0 |
| 110010 | 0 | 0 | 0 | 0 |
| 110011 | 0 | 0 | 0 | 0 |
| 110100 | 0 | 0 | 0 | 0 |
| 110101 | 0 | 0 | 0 | 0 |
| 110110 | 1 | 1 | 1 | 1 |
| 110111 | 1 | 1 | 1 | 1 |
| 111000 | 1 | 1 | 1 | 1 |
| 111001 | 1 | 1 | 1 | 1 |
| 111010 | 1 | 1 | 1 | 1 |
| 111011 | ? | 0 | 1 | 1 |
| 111100 | 1 | 1 | 1 | 1 |
| 111101 | 1 | 1 | 1 | 1 |
| 111110 | 1 | 1 | 1 | 1 |
| 111111 | 1 | 1 | 1 | 1 |
АНАЛИЗ
По таблице истинности видно, что минимизация функции проведена верно.
В результате минимизации получили минимальные дизъюнктивные нормальные формы:
- Доопределив функцию нулями, методом Квайна получили МДНФ цены 46
- Доопределив функцию единицами, методом карт Карно получили МДНФ цены 37
- Доопределяя функцию по ходу выполнения алгоритма, методом кубических покрытий получили МДНФ цены 26
Метод кубических покрытий приводит к наименьшей МДНФ. Это связано с тем, что минимизируется не полностью определенная функция. В результате минимальная форма принимает на наборах, на которых исходная функция не определена, такие значения, которые соответствуют наиболее оптимальному покрытию. Из всех методов наиболее трудоемким оказывается также метод кубических покрытий, но он удобен для программной реализации минимизации. Наименее трудоемким оказался метод Квайне.
4 Список литературы
- http://www.google.com/search?q=минимизация+переключательных+функций
- file:///C:/Users/Viktor/Desktop/tmp2/minsf/index.html#24
и
нформационные технологии в управлении
УДК 621.396
МЕТОД РЕШЕНИЯ ЗАДАЧИ О МИНИМАЛЬНОМ ПОКРЫТИИ КАК СРЕДСТВО ПЛАНИРОВАНИЯ В GRID
B.C. Пономаренко(1), С.В. Листровой(2)
(1) Харьковский национальный экономический университет;
(2) Украинская академия железнодорожного транспорта, г. Харьков
Предложен метод решения задач о наименьшем покрытии и наименьшем вершинном покрытии в произвольных графах, позволяющий строить эффективные алгоритмы решения задачи определения минимального числа кластеров, позволяющего решить в GRID заданное подмножество задач с требуемой эффективностью.
ВВЕДЕНИЕ
Глобальные вычислительные сети GRID [1] были предложены в качестве новой парадигмы для решения крупномасштабных вычислительных задач в науке, технике и бизнесе [2]. Они дают возможность одновременного использования многочисленных вычислительных ресурсов [3], принадлежащих различным организациям и расположенных в различных административных регионах. Системы GRID объединяют разнородные вычислительные ресурсы (персональные компьютеры, рабочие станции, кластеры, суперкомпьютеры), используя разные стратегии доступа, выполняя различные приложения (научные, инженерные и коммерческие), предъявляющие к системе различные требования. Ресурсы принадлежат различным организациям, имеющим свои правила управления, использования и определения их стоимости для различных пользователей в различное время. Доступность и загруженность ресурсов также может динамически изменяться во времени. Последние работы в области GRID позволяют приложениям использовать вычислительные ресурсы, принадлежащие различным организациям, распределенным по различным странам и континентам. Один из видов ресурсов GRID — однородные многопроцессорные системы (кластеры), которые могут состоять из сотен или даже тысяч процессоров. В процессе распределения ресурсов в GRID возникает необходимость в определении
минимального числа кластеров, на которых можно выполнить заданное подмножество задач.
Рассмотрим двухуровневую систему, в которой на первом уровне несколько независимых брокеров распределяют вычислительные задачи на кластеры, а на втором уровне каждый кластер распределяет задачи, присвоенные ему локальным планировщиком. Пусть имеется п кластеров и каждый і-й процессор в кластере в состоянии решить некоторое подмножество Ьі задач с требуемой эффективностью. Положим, что на решение поступило т задач, которые нужно решить. Требуется определить минимальное число кластеров, обеспечивающее решение всех т задач, как правило, т > п. Пусть возможности по решению задач определены графом, приведенным на рис. 1, кластеры
Кластеры 1 2 3 4
1 2 3 4 5 6
Задачи
Рис. 1. Граф, отображающий возможности решения задач
соединены ребрами с теми задачами, которые они могут выполнить с требуемой эффективностью.
Требуется найти минимальное число кластеров, обеспечивающих выполнение всех задач с требуемой эффективностью. Представим граф (см. рис. 1) булевой матрицей В, в которой строкам соответствуют задачи, а столбцам — кластеры. Элемент (i, у) матрицы будем считать равным 1, если у-й кластер способен с требуемой эффективностью обеспечить решение ^й задачи, и равным нулю — в противном случае:
B =
1 2 3 4
1 І І О І
2 І І І О
3 І О І І
4 О І О О
5 О О І І
6 О О І І
В данном случае задача сводится к определению минимального числа столбцов в матрице В, покрывающих единицами все строки в ней. Эта же задача может быть сформулирована как задача линейного булевого программирования, постановка которой в общем виде имеет вид:
L = V c.x. ^ min J J
j = і
(І)
при ограничениях
n
V в, xj 1 І, i = І, m, xj є {О, І}; c. 1 О, (2) j = і
где
ву =
1, если i-я переменная может быть покрыта переменной х^,
0 — в противном случае.
(З)
Задачи о наименьшем покрытии (ЗНП) и о наименьшем вершинном покрытии (ЗНВП) имеют широкое прикладное значение в теории построения сложных систем, в системах диагностики вычислительных систем и сетей [4], при разработке их программного и математического обеспечения, а также для планирования распределения ресурсов в GRID. Основное требование к алгоритмам решения данных задач состоит в высокой оперативности решения и обеспечении минимально возможной погрешности этих решений.
Частным случаем ЗНП является задача о наименьшем разбиении (ЗНР), которая получается из задачи (1)—(3) путем замены неравенства (2) на
равенство. Вследствие особой природы задачи часто при ее исследовании удается сделать хорошо известные заранее выводы и упрощения [4, 5]: например, если в строке матрицы В присутствует одна единица, то столбец, в котором находится эта единица, обязательно принадлежит минимальному покрытию; если в матрице В есть столбцы, частично совпадающие с другими, но покрывающие меньшее число строк, то они могут быть исключены из анализа, так как любое множество, которое покрывает столбец с большим числом единиц, покрывает и все множества, которые покрывает столбец с меньшим числом единиц. Таким образом, в этом случае столбец с большим числом единиц доминирует над столбцом с меньшим числом единиц.
Ряд методов сначала разрабатывался для решения ЗНР, а потом адаптировался к решению в работах [6, 7]. В работе [1] предложены методы решения ЗНП, в которых используется дерево поиска и линейное программирование. Подходы, базирующиеся на рассмотрении отсекающих плоскостей и подобные в принципе тем, которые применяются в общем 0-1-программировании [8], представлены в работах [4, 9]. Сравнение этих методов и исследование их вычислительных характеристик приведено в работе [4]. Наиболее полный обзор методов решения ЗНП как задачи линейного булевого программирования, дан в статье [10], где показано, что алгоритмы на основе идей рангового подхода [15, 16] отличаются от методов, основанных на идеях метода ветвей и границ, меньшими временной сложностью и погрешностью.
Задачу нахождения независимых максимальных множеств или вершинных покрытий можно, например, решить последовательным перебором независимых множеств с одновременной проверкой каждого множества на максимальность (последнее осуществляется добавлением к исследуемому множеству дополнительной вершины, не принадлежащей ему, и выяснением, сохраняется ли независимость) и запоминанием максимальных множеств.
Однако с увеличением числа вершин этот способ становится весьма громоздким. На основе усовершенствования этой процедуры построены алгоритмы Брона и Кэрбоша [4]. Как показано в работах [13, 14], задача вершинного покрытия является ЛР-полной, и эффективные алгоритмы ее решения для произвольных графов неизвестны. Для двудольных графов на основе алгоритмов Хоп-крофта и Карпа (с поиском в глубину) разработаны методы [11], позволяющие находить минимальное вершинное покрытие и максимальное независимое множество вершин в произвольном двудольном графе Н = (X, Y, Е) за время 0((т + п)4п), где п = IX и Y| и т = |Е|. Полиномиальные алгоритмы
n
вычисления числа устойчивости были получены для совершенных графов — графов, у которых для любого его порожденного подграфа хроматическое число равно кликовому числу. Алгоритм вычисления числа устойчивости графа [16] основан на методе эллипсоидов и использует процедуру отделения матриц графа. В вычислительном плане этот алгоритм обладает рядом существенных недостатков, не позволяющих использовать его на практике. Как показано в работе [16], получить правильное решение при числе вершин в графе более 10-ти практически невозможно. Применение т-алгоритмов позволило увеличить размерность решаемых задач до 50, а при использовании двойственных оценок в схеме ветвей и границ — до 100, с погрешностью, не превышающей 5 % [16].
Таким образом, поскольку размерности задач, решаемых в GRID-системах, достаточно велики, представляется актуальной разработка эффективного приближенного алгоритма, решающего с единых позиций ЗНВП и ЗНП и обладающего малой временной сложностью и погрешностью.
1. ПОСТАНОВКА И МЕТОД РЕШЕНИЯ ЗАДАЧИ
Для решения с единых позиций ЗНВП и ЗНП будем представлять как граф Є (X, Е), так и произвольную матрицу В в виде булевой функции. Рассмотрим конъюнктивное представление булевой матрицы В. Пусть задана булева матрица В с п столбцами и т строками. Столбцы будем задавать вектором X = {х1, х2, …, хп}, а строки — вектором М = {ц1, ц2,…, цт}. Покрытием 0 строк Мматрицы В назовем такое множество столбцов В, которое покрывает единицами все строки М. Для определения всех покрытий матрицы будем применять алгебраический метод получения по импликант-ной таблице приведенных систем простых импли-кант булевых функций. Если каждый столбец из совокупности X = {х1, х2, …, хп} рассматривать как «простую импликанту», покрывающую совокупность строк М = {ц1, ц2,…, цт}, каждую строку ц, как набор переменных, покрываемых простыми импликантами, то матрицу В можно представить как импликантную таблицу булевой функции. При такой интерпретации матрицы В для каждой строки ц, можно записать дизъюнкцию столбцов Ьі, покрывающих рассматриваемую строку, в следующем виде:
= (X V хк V …)
… (4)
^ = (X, V X V …).
Конъюнкция дизъюнкций (4) по всем строкам ц1, ц2, …, цт матрицы В образует конъюнктивное
О
5
Рис. 2. Граф Є
представление матрицы В, содержащее в себе все покрытия совокупности строк М:
к(М) = аЦ • ф2 •…• =
= (X V Хк V …)-…-(Хр V X V …). (5)
Раскрывая скобки в соответствии с законами дистрибутивности, получаем дизъюнктивное представление матрицы В, образующее перечень всех возможных покрытий совокупности строк М = {ц1, ц2, …, цш}. Так, в соответствии с выражением (5) конъюнктивное представление матрицы
1 2 3 4 5 6 7
1- -2 1 1 0 0 0 0 0’
1- 3 1 0 1 0 0 0 0
1- 4 1 0 0 1 0 0 0
2- -7 0 1 0 0 0 0 1
3- -6 0 0 1 0 0 1 0
4- -5 0 0 0 1 1 0 0
задающей граф Є (рис. 2), имеет вид:
F = (X V Х)(Х V XXX V XXX V X) х
х (X V Х)(Х V X). (6)
Как показано в работе [17], если f — булева функция, построенная по графу Є = (V, Е) в виде произведения дизъюнктов (V, V V ), где {V,} Є {0, 1},
і = (1, п), j = (1, п), і ф у, и при этом каждый дизъюнкт (V, V V) соответствует ребру (V,, V), то все наборы переменных {V,, ^}, на которых она принимает значение «истинно», соответствуют вершинным покрытиям в графе Є = (V, Е). И для перечисления всех вершинных покрытий графа Є = (V, Е) необходимо определить те системы зна-
чений переменных {у,, V.}, при которых высказывание
F(^1, ^, …, Г„) = 1 (7)
«истинно». Чтобы найти эти системы значений переменных {у, у.}, необходимо привести левую часть выражения (7) к минимальной дизъюнктивной нормальной форме, раскрывая скобки и пользуясь законом поглощения. Такая форма единственная, ввиду отсутствия в выражении (7) логических отрицаний.
Введем следующие понятия и определения для элементов булевой матрицы В, задающей некоторый граф G (X, Е). Если в матрице В выделить произвольный столбец у, то с ним можно связать некоторое подмножество столбцов {#}, с которыми данный столбец пересекается, поскольку столбец у соответствует вершине графа, а число единиц в столбце определяется степенью вершины А., и подмножество {#} будет всегда содержать А. таких столбцов. Будем говорить, что подмножество столбцов {#}■ образует связку столбцов относительно столбца у. Число столбцов в матрице В равно числу вершин п в графе (/(X, Е), а число возможных связок столбцов для матрицы В равно п. Отметим, что все столбцы в матрице В пересекаются друг с другом только в одной строке, поскольку в каждой строке матрицы В находится по две единицы. Поэтому, с точки зрения их пересекаемости, возможность их принадлежности минимальному покрытию равновелика. Каждая связка столбцов {#}.. покрывает определенное число строк IСвязку {#}., покрывающую максимальное число строк в матрице В, назовем максимальной. Если в графе С (X, Е) есть висячие вершины, то это означает, что в матрице В есть столбцы Р, содержащие только одну единицу, и, следовательно, связки этих столбцов содержат только по одному столбцу в каждой. Эти столбцы обладают интересным свойством, которое для произвольных графов С (X, Е) определяет следующее
Утверждение. Если граф Е) содержит
некоторое подмножество висячих вершин О е X, то подмножество вершин Р е X смежных с О может быть дополнено до одного из минимальных вершинных покрытий графа С (X, Е)>
Доказательство. Пусть граф С(X, Е) содержит висячую вершину у, которая соединена с ним ребром (/, у). Тогда граф С (X, Е) можно представить в виде объединения подграфов С”‘ и С””, при этом вершина / является точкой сочленения, т. е. принадлежит подграфам С’ и С”. Пусть подграф С’ содержит к вершин, тогда степени вершин в подграфе С” могут изменяться от 1 до к — 1. Предпо-
ложим, что в графе С^, Е) покрытие {^^ не включает в себя вершину /, но тогда оно должно включать в себя вершину у (т. е. у е {^^ш) ддя того, чтобы ребро (/, у) оказалось покрытым. Пусть степень вершины / в подграфе С” равна 1 и вершина / в подграфе С” соединена с вершиной XI. Поскольку ребро (/, XI) должно быть покрыто, а вершина / в покрытие не входит, то XI е {^^щ. Следовательно, обе вершины (/, XI) е {^^щ. Если вместо вершин (/, XI) в покрытие ввести вершину /, то мы получаем новое покрытие {X,}, которое содержит на одну вершину меньше, чем покрытие {^^т. Это противоречит первоначальному предположению о том, что покрытие {^^т, содержащее вершину у, является минимальным вершинным покрытием в графе С (X, Е). Аналогичное рассуждение можно провести, полагая степени вершины / в подграфе С” равными 2, 3, …, к — 1; следовательно, по индукции следует, что во всех возможных случаях возникает противоречие с первоначальным предположением, и вершина / принадлежит минимальному вершинному покрытию. Поскольку аналогичное рассуждение можно провести для любой висячей вершины графа С (X, Е), то по индукции утверждение можно считать доказанным. ♦
В общем случае, если в графе существует несколько минимальных вершинных покрытий, то могут существовать и минимальные вершинные покрытия без вершины, смежной с висячей вершиной графа С (X, Е), но если оно одно, то эта вершина обязательно в нем присутствует. Таким образом, если в матрице В есть столбец у, содержащий одну единицу, то связка столбцов относительно столбца у (в данном случае она состоит из одного столбца) принадлежит минимальному покрытию Xmin. В случае представления графа в виде булевой функции F(X1, 22, …, 2^) данное утверждение эквивалентно тому, что если в дизъюнктах есть переменная Хр, которая в них встречается один раз, то переменная Xи, составляющая ей пару, в дизъюнкции входит в покрытие. И, следовательно, данную дизъюнкцию можно заменить переменной 2^, при этом исключить из анализа все дизъюнкции, содержащие переменную Xи. В работе [8] при анализе графов С(X, Е), не имеющих висячих вершин, представленных в конъюнктивной нормальной форме в виде некоторой булевой функции Е, для определения наименьшего множества переменных {X,.}, которые покрывают все дизъюнкты в конъюнктивном представлении графа С (X, Е), предложено применять принцип су-
перпозиции в булевой алгебре, основанный на следующем равенстве:
ЛХ, А2,…, X,,) = f(Xl = 0, X, …, X,,) V
V Д^, ^2 = 0, …, X,) V … V f(Xl, 2^, …, X, = 0). (8)
Не нарушая принципа суперпозиции, соотношение (8) можно представить в виде
ЛХ, X, …, X,) = ХЛ(Х, х, …, X,) V
V ^2 Д^, ^2, …, X,) V … V X, Д^, ^2, …, X,). (9)
Особенность конъюнктивного представления графа Є (X, Е) в виде булевой функции состоит в том, что она содержит число дизъюнктов, равное числу ребер в графе, а число переменных в каждом дизъюнкте равно 2, и каждая переменная соответствует некоторой вершине графа Є (X, Е). Введем
понятие характеристического вектора hq = (й,-^ 1, ^2= 2, …, М”= п)Ч некоторой булевой функции
Л = ^•…Ч Л^р ^ …, ^ (10)
в которой переменные X,, X., …, X, не встречаются
у п 4
в функции Д(Х, X2, …, X,).
Вес у, в векторе h указывает, как часто переменная X встречается в дизъюнктах функции Д^, X2, …, X,), а сам вектор будем описывать суммарной весовой характеристикой
V, = I у,.
(11)
, = 1
Рассмотрим алгоритм решения данной задачи в виде следующей процедуры А преобразования булевой функции XXI, X2, …, X,), задающей некоторый граф С (X, Е).
Шаг 1. Проверяем, есть ли в дизъюнктах /(XI, X2, …, X,) переменные {X} встречающиеся по одному разу. Если да, то умножаем/(XI, X2, …, X,) на переменные {X}, стоящие совместно в дизъюнктах с переменными и образующие сомножитель X -Х, •… -X,, состоящий из г переменных, нахо-
р п Я.
дившихся в дизъюнктах совместно с Хк, при этом все дизъюнкты в/(XI, X2, …, X,), содержащие переменные X, X,,
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Р,
X,, исключаем из дальнейшего
анализа.
Шаг 2. Проверяем, встречаются ли в полученной функции / = X,•X/^•…•X^•/(X1, X2, …, X,) оставшиеся переменные по одному разу или нет; если да, то мы получили минимальное вершинное покрытие, в которое входят вершины, соответствующие переменным X • X. •… • X, и переменным,
у п Я
выбираемым по одной из каждого оставшегося дизъюнкта, и процедура заканчивается; если нет, то выполняем следующий шаг.
Шаг 3. Полученные функции / = Xр•Xn•… … • X, X2, …, X,) умножаем поочередно на пе-
ременные X,, оставшиеся в/^^ Х,…, X,), и исключаем при этом дизъюнкты, содержащие X., если их #, то мы получим q таких функций /2, …, У’,},
и для каждой функции вычисляем характеристи-
ческий вектор hq = (h^1= 1, ^2= 2,
весовую характеристику V, = I /. Среди них вы, = 1
бираем функцию Д с минимальным значением весовой характеристики и переходим к шагу 1. Если же все весовые характеристики функций окажутся одинаковыми, то выбираем любую из них. ♦
Данная процедура представляет собой «жадный» алгоритм, который строит минимальное вершинное покрытие в графе Є (X, Е) заданным в виде конъюнктивного представления матрицы В, в которой столбцам і соответствуют вершины графа {X}, а строкам 5 — ребра (X,, X) є Е графа.
, 0.3
В процессе выполнения алгоритма, когда мы полагаем X = 1, появляется произведение XуX:, …, X,, которое поглощает все дизъюнкты, содержащие эти переменные, последнее эквивалентно удалению из графа вершин (і, р, к, …, с) и ребер, им инцидентных. В результате такого преобразования исходного графа возможны два варианта: вновь полученный подграф может содержать или не содержать висячие вершины.
Если подграф содержит висячую вершину, то, включая ее в минимальное покрытие и удаляя из графа вместе с инцидентными ей ребрами, получим новый подграф. Если в процессе преобразования мы каждый раз получаем подграф с висячими вершинами, то в соответствии с утверждением мы получим в худшем случае за п шагов минимальное вершинное покрытие исходного графа. Так, если исходный граф является деревом, содержащим п ярусов и имеющим ширину, равную h (под шириной дерева подразумевается максимально возможное число вершин на ярусе дерева), то данная стратегия последовательного включения в покрытие вершин, смежных с висячими, позволит построить минимальное вершинное покрытие дерева за О^п) шагов.
В случае, когда после удаления вершин (і, р, к, …, с) и ребер, им инцидентных, получается подграф, не содержащий висячих вершин, можно выделить три варианта: два предельных случая, когда получаемый подграф является полно связанным компонентом или образует простой цикл на остав-
,
,
шемся множестве вершин, и оптимальность работы алгоритма в этих крайних случаях очевидна; промежуточный вариант — когда в подграфе нет висячих вершин и степени его вершин произвольны. Обоснование оптимальности работы алгоритма в этом случае дает следующая
Теорема. Если при Xj = 1 получается связка
столбцов {q}*, покрывающая максимальное число
строк в матрице B, то применение к ней процедуры A приводит к построению минимального покрытия матрицы B. ♦
Доказательство. Предположим, что множество столбцов, принадлежащее связке {q}* покрывает максимально возможное из всех связок столбцов число строк l, а оставшиеся (m — l) строк непокрытые. Процедура A, добавляющая число столбцов до полного покрытия строк матрицы B, на каждом шаге добавляет в покрытие каждый раз столбец, покрывающий максимальное число строк из непокрытых. Следовательно, к столбцам {q }*
добавится минимальное число столбцов {р}. Итак, мы получили покрытие, состоящее из множества
столбцов {q }* u {p}. Предположим, что оно не
минимально, но поскольку число добавленных до покрытия столбцов {р} процедурой A минимально, последнее возможно, если существует связка столбцов, а связку столбцов {q}. покрывает число строк k > l. Это противоречит первоначальному предположению о том, что {q }* является максимальной
связкой столбцов, следовательно наше предположение неверно и множество столбцов образует минимальное покрытие матрицы B графа G (X, Е)> Потеря оптимального решения при работе процедуры A происходит тогда, когда возникает ситуация, при которой весовые характеристики всех булевых функций f в процедуре A оказываются одинаковыми, и тогда мы выбираем любую из них. Однако возникновение такой ситуации возможно в основном на однородных графах, что в задачах планирования ресурсов в GRID встречается довольно редко. Ясно, что процедура A может быть применена не только для булевых матриц, которые задают некоторый граф G (X, Е), но и для произвольных булевых матриц.
Пример. Определим минимальное вершинное покрытие в графе, приведенном на рис. 3.
Строим булеву функцию графа:
f = (Xj V x2)(xt V *3)^ V x5)(x2 V x3) S s (x2 V x6)(x3 V x4)(x4 V x5)(x5 V x6).
Определяем, есть ли переменные, которые встречаются один раз. Если да, то умножаем функцию на переменную, соседнюю с ней, иначе вы-
Рис. 3. Граф G
писываем все функции, умноженные поочередно на все переменные, присутствующие в ней, и вычисляем векторы, характеризующие данные функции и их весовые характеристики:
Д = х1(х2 V х3)(х2 V х6)(х3 V х4)(х4 V х5)(х5 V Х6);
*1 = (22, 13, 24, 25, 2б); ^ = 9;
Д Х2(х1 V х3)(х1 V х5)(хз V х4)(х4 V х5)(х5 V х6);
*2 = (21, 23, 24, З5, 1б); V, = 10;
Д3 Х3(Х1 V х5)(х2 V х6)(х4 V х5)(х5 V Х6);
*3 = (21, 22, 14, 25, 26); ^3 = 9;
Д = Х4(х1 V х2)(х1 V х3)(х1 V х5)(х2 V х3)(х2 V Х3) X
X (х5 V х6); *4 = (31, 32, 23, 25, 26); V2 = 12;
Д = х5(х1 V х2)(х1 V х3)(х2 V х3)(х2 V х6)(х3 V х4);
*5 = (31, 22, 23, 14, 16); V, = 9*;
Д = Х6(х1 V х2)(х1 V х3)(х1 V х5)(х2 V х3)(х3 V Х4) X
X (х4 V х5); *6 = (31, 22, 33, 24, 25); V5 = 12.
Из полученных таким образом функций выбираем ту, в которой суммарная весовая характеристика вектора минимальна: функция /5. Поскольку в выражении для Д переменная х4 встречается только один раз, умножаем Д на переменную соседнюю с ней — это х3 — и получаем:
Д53 = х5х3(х1 V х2)(х2 V х6).
Поскольку в выражении для Д53 переменные х6 и х 1 встречается только один раз, то умножаем Д на переменную соседнюю с ней — это х2 — и получаем:
*^532 = х5х3х2.
Таким образом, минимальное вершинное покрытие образуют вершины {2, 3, 5}.
2. ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ
Исследование временной сложности разработанного алгоритма проводилось для произвольных графов с различными плотностями ребер в графе. Плотность А изменялась от 0,1 до 0,5, а число N вершин — от 4 до 100. Графики зависимости числа Q элементарных операций от числа вершин в графе приведены на рис. 4. Как видно, временная сложность алгоритма определения минимальных вершинных покрытий в графе в среднем не
превышает величины 0(0,9п ).
Все результаты получены с доверительной вероятностью 0,95, погрешность решений не превышала 2—6 %, а процент неточных решений не превышал 20 %.
ЗАКЛЮЧЕНИЕ
Предложенный метод позволяет с достаточно высокой оперативностью и точностью решать как задачи о наименьшем покрытии, так и задачи о наименьшем вершинном покрытии. Временную сложность соответствующего алгоритма можно
легко понизить до O(n ), если его реализовывать на n-процессорной вычислительной системе, поскольку функции f при реализации процедуры А можно вычислять одновременно независимо друг от друга, что очень важно для планирования распределением ресурсов в системах, работающих в реальном времени, к которым и относятся системы распределения ресурсов в GRID. Данный ме-
Qx ю5
10i——
9——–
8——–
7——–
6——–
5——–
4——–
3——–
2——–
1——–
0 ЬЮЮЮ«В
4 12 20 28 36 44 52 60 68 76 84 92 п
Рис. 4. Зависимость числа элементарных операций от размерности графа при различных значениях плотностей ребер
в графе:———— Л = 0,1; —х— — Л = 0,3;
-а- — Л = 0,5;————–Л = 0,9и3
тод даст возможность эффективно решать динамически изменяющуюся задачу определения минимального числа кластеров, позволяющих решить заданное подмножество задач с требуемой эффективностью.
ЛИТЕРАТУРА
1. Brucker P. Scheduling Algorithms. — Springer Ferlag, 1998. — P. 217—218.
2. Methods and Experiences of Parallelizing Flood Models / L. Hluchy, et al. // The 10th EuroPVM/MPI Conference. LNCS 2840. Sept. 2003, Venice. — P. 677—681.
3. Baker B.S., Brown D.J. and Katseff H.P. A 5/4 algorithm for two-dimensional packing // Jornal of Algorithms. — 1981. — Vol. 2, — P. 348—368.
4. Кристофидес Н. Теория графов. Алгоритмический подход. — М.: Мир, 1978. — 309 с.
5. Balinski M. Integer programming: methods, uses, computation // Man. Sci. — 1965. — N 12. — P. 253.
6. Garfmkel R.S., Nemhauser G.L. The set partitioning problem: set covering with equality constraints // Ops. Res. — 1969. — N 17. — P. 848.
7. Pierce J.F. Application of combinatorial programming to a class of all-zero-one integer programming problems // Man. Sci. — 1968. — N 15. — P. 191.
8. Gomory R. An algorithm for integer solutions to linear programs, Recent Advances in mathematical Programming. — N-Y.: McGraw-Hill, 1963.
9. Bellmore M., Ratliff H.D. Set covering and involuntary bases // Man. Sci. — 1971. — N 18. — P. 427.
10. Листровой С.В., Симашкевич О.Н. Об использовании гарантированных прогнозов в методах решения задач буле-вого программирования на основе рангового подхода // Электронное моделирование. — 2003. — Т. 25. — № 4. — С. 89—103.
11. Липский В. Комбинаторика для программистов. — М.: Мир, 1988. — 203 с.
12. Шор Н.З., Стеценко С.И. Квадратичные экстремальные задачи и недифференцируемая оптимизация. — Киев: Наукова думка, 1989. — 196 с.
13. Пападимитриу К., Стайглиц М. Комбинаторная оптимизация. Алгоритмы и сложность. — М.: Мир, 1985. — 512 с.
14. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. — М.: Мир, 1982. — 416 с.
15. Листровой С.В., Гуль А.Ю. Метод решения задачи о минимальном покрытии на основе рангового подхода // Электронное моделирование. — 1999. — № 1. — С. 58—70.
16. Listrovoy S.V. and Gul A.Yu. Method of Minimum Covering Problem Solution on the Basis of Rank Approach // Engineering Simulation. — 1999. — Vol. 17. — P. 73—89.
17. Листровой С.В., Яблочков С.В. Метод решения задачи определения минимальных вершинных покрытий и независимых максимальных множеств // Электронное моделирование. — 2003. — Т. 25. — № 2. — С. 31—43.
@ +38057-730-10-62, e-mail: om1@yandex.ru
Статья представлена к публикации членом редколлегии В.Д. Малюгиным. □
84
CONTROL SCIENCES № З • 2008
Введение
Данная статья имеет, в основном, историческое значение. Мне хотелось бы вспомнить и описать красивый метод булевой оптимизации, которому нас учили в ЛЭТИ в 80х годах прошлого века. В наше время, в связи с широким распространением компьютерных программ логического синтеза (например. Simplify), актуальность этого метода значительно снизилась, но, тем не менее надеюсь, что ценители красоты оценят его по достоинству.
Задача о покрытии в булевой алгебре
Данный метод предназначен для решения важнейшей практической задачи в булевой алгебре – а именно задачи о покрытии. Неформальная формулировка может звучать так: имеется булева функция от нескольких входных переменных (возможно, не полностью определенная). Требуется найти минимальное покрытие этой функции в заданном базисе. (Причем, в качестве базиса может применяться номенклатура элементов какой-либо логической серии микросхем либо просто библиотека элементов для ПЛИС либо ASIC)
Данная задача имеет прикладное практическое значение в области цифровой электроники и логического синтеза. Иногда эту задачу сводят к нахождению минимальной ДНФ или КНФ, но в практическом плане наше определение более полезно. Причем, как правило, решается она в два этапа – сначала находится минимальная ДНФ либо КНФ, а затем ищется ее оптимальное покрытие в заданном базисе. Сейчас такие задачи решаются программами компьютерного логического синтеза. Наилучшее решение, в общем случае, находится методом полного перебора, который в случае достаточно большого числа переменных требует нереальных затрат ресурсов и времени. (Известно, что количество всех возможных булевых функций зависит от числа входных переменных n как 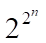 . Таким образом, от одной переменной мы имеем всего 4 различных функции, от двух – 16, от трех – уже 256 и так далее.)
. Таким образом, от одной переменной мы имеем всего 4 различных функции, от двух – 16, от трех – уже 256 и так далее.)
Поэтому на практике используют различные эвристики, и результат может сильно отличаться от оптимального.
Простой практический пример
Зададим простую булеву функцию от 2хвходных переменных и напишем для нее ДНФ и КНФ. Функцию зададим следующей таблицей:
|
Вх. X1 |
Вх. X0 |
Вых. Y |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Чтобы написать для нее ДНФ, надо написать формулы для всех строчек, где Y равна единице и соединить их через функцию “или”:
Y = !X1&X0 | X1&!X0
Чтобы получить КНФ, надо закодировать все нули через операции “или” и соединить их через операцию “и”:
Y=X1|X0 & !X1|!X0
Легко понять, что формулы эти эквивалентны:
(!X1&X0) | (X1&!X0) ó (!X1&X0)|X1 & (!X1&X0)|!X0 ó(!X1|X1) & (X0|X1) & (!X1|!X0) & (X0|!X0) ó(X0|X1) & (!X1|!X0)
Чтобы реализовать эту логическую функцию в виде электронной схемы, надо закодировать (покрыть) одну из этих формул доступными нам логическими элементами. Это могут быть либо микросхемы, реализующие функции программируемой логики, либо библиотечные функции из какой-либо библиотеки элементов. Например, использовав микросхемы К1533ЛА3, содержащие элементы 2И-НЕ, можно покрыть эту функцию так:
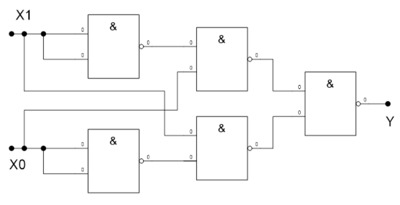
Рис. 1. Реализация функции “исключающее или” на элементах 2И-НЕ
Здесь мы использовали тождество Y = !X1&X0 | X1&!X0 ó! [!(!X1&X0) & !(X1&!X0)]
При этом мы израсходовали 5 логических вентилей и 2 корпуса, т.к. в каждом корпусе содержатся 4 лог. вентиля. Можно убедиться (самостоятельно), что использование функции 2ИЛИ-НЕ приводит к аналогичному результату.
Если нам доступен более широкий набор логических элементов, как это бывает в библиотеках функций для ПЛИС или ASIC, то можно покрыть эту логическую функцию иначе, например так:
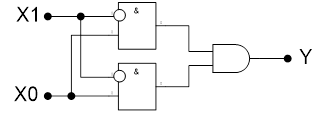
Рис. 2. Реализация той же функции на других логических вентилях.
Если же, например, у нас имеется мультиплексор, то мы можем реализовать эту функцию непосредственно на нем:
Рис. 3. Вариант реализации на мультиплексоре
Конечно, ввиду того, что сам мультиплексор реализуется с посредством нетривиальных логических функций, такой прием неэффективен при проектировании для ASIC и ПЛИС, но он широко применялся при проектировании на схемах малой степени интеграции.
Даже на таком простом примере видно, что задача покрытия – весьма нетривиальна. Добавим, что с повышением числа входных переменных, сложность ее решения растет экспоненциально и уже для нескольких сотен переменных решение “в лоб”, т.е. полным перебором становится нереализуемым на любом современном компьютере.
И, в заключение, для тех, кто еще не догадался – мы рассматривали реализацию функции “исключающее или”.
Задача поиска минимальной ДНФ (КНФ)
ДНФ и КНФ
В общем случае, логическую функцию можно задать таблицей. В ней будет 2^n строк, где n – число входных переменных. Наша задача – записать функцию, заданную этой таблицей в виде логической формулы от входных переменных. Имеется много способов решения данной задачи.
В частности, имеется математическая теорема, что любую логическую функцию от n переменных можно покрыть функциями вида 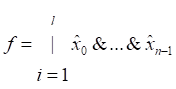 . Здесь знаком “|” обозначена операция “логическое или”, а индекс i пробегает по всем выходным единицам. Выражение вида
. Здесь знаком “|” обозначена операция “логическое или”, а индекс i пробегает по всем выходным единицам. Выражение вида 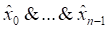 называется “логический терм”, а домик означает переменную либо ее инверсию. Такое представление называется “дизъюнктивная форма”, сокращенно ДНФ. ДНФ может быть “совершенной”, когда присутствуют все n входных переменных, либо сокращенной, когда количество переменных в терме меньше n.
называется “логический терм”, а домик означает переменную либо ее инверсию. Такое представление называется “дизъюнктивная форма”, сокращенно ДНФ. ДНФ может быть “совершенной”, когда присутствуют все n входных переменных, либо сокращенной, когда количество переменных в терме меньше n.
Соответственно, выражение вида
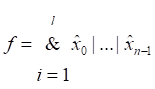
называется “конъюктивная форма”, сокращенно КНФ. Все вышесказанное сказанное про ДНФ относится и к КНФ, за исключением того, что операции “и” и “или” меняются местами, а термы выписываются для выходных значений, равных 0.
Постановка задачи
Задача – найти минимальную ДНФ (КНФ) для заданной функции. При этом, в общем случае, функция может быть не полностью определена. Это значит, что имеются входные комбинации, которые никогда не используются (либо безразличны). Для того, чтобы описать методы решения (для небольшого числа входных переменных), рассмотрим несложную учебную задачу.
Учебная задача
Задача: Разработать схему преобразования цифр от 0 до 9, заданных в двоичном коде в сигналы управления семисегментного индикатора. Выход – 1 – сегмент включен, 0 – сегмент выключен. Так же условимся, что код больше, чем 9 в двоичном представлении появиться не может.
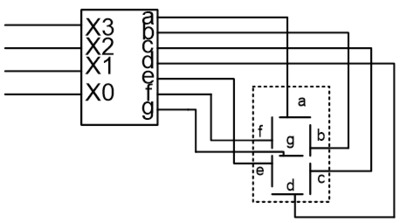
Рис. 4. Модуль управления семисегментным индикатором
Как решаются задачи такого типа?
Для начала выпишем таблицу функций для всех входных и выходных переменных:
|
Дес. цифра |
Входы X |
Выходы abcdefg |
|
0 |
0000 |
0000000 |
|
1 |
0001 |
0110000 |
|
2 |
0010 |
1101101 |
|
3 |
0011 |
1111001 |
|
4 |
0100 |
0110011 |
|
5 |
0101 |
1011011 |
|
6 |
0110 |
1011111 |
|
7 |
0111 |
1110000 |
|
8 |
1000 |
1111111 |
|
9 |
1001 |
1111011 |
|
– |
1010 |
******* |
|
– |
1011 |
******* |
|
– |
1100 |
******* |
|
– |
1101 |
******* |
|
– |
1110 |
******* |
|
– |
1111 |
******* |
Как видим, функция оказалась недоопределенной на некоторых входных значениях. Это облегчает дальнейшую оптимизацию. Кроме того, выход получился векторным, что для нас означает необходимость минимизации семи отдельных выходных функций вместо одной.
Общий принцип минимизации
Общий принцип – исключение из терма незначащих переменных. Так, для кодирования одной точки нам требуются все n входных переменных. Для кодирования отрезка – n-1. Квадрат кодируется n-2 переменными, а куб – n-2. И так далее. Таким образом, мы должны находить элементы с общими переменными и исключать эти переменные из термов. Для этого нам нужно находить в многомерном пространстве входных переменных геометрические элементы – точки отрезки, плоскости, кубы и гиперкубы.
Это объяснение кажется очень абстрактным, но после рассмотрения простого примера все станет понятно.
Карты Карно
Можно записать скалярную булеву функцию в виде двумерной таблицы. Запишем, например значение функции для выхода a:
|
X3 X2 X1X0 |
11 |
10 |
01 |
00 |
|
11 |
* |
* |
* |
* |
|
10 |
* |
* |
1 |
1 |
|
01 |
1 |
1 |
1 |
0 |
|
00 |
1 |
1 |
0 |
0 |
Такая таблица называется картой Карно и на ней, в принципе, можно отыскивать вышеописанные геометрические закономерности. Как это сделать, можно посмотреть, например, в Википедии по ссылке, где тема исчерпывающе объяснена, поэтому мы ее больше затрагивать не будем. Мы же подробно рассмотрим менее известный альтернативный метод минимизации булевых функций, а именно – минимизацию на многомерных булевых кубиках, которая, по нашему мнению, гораздо удобнее и нагляднее.
Минимизация на многомерных булевых кубиках
Что такое булевый кубик
Рассмотрим ось, соответствующую какой-либо булевой переменной, на которой имеются два входных значения – 0 и 1. Нарисуем на ней два кружочка. Значение входных переменных будем писать под кружочками, а выходной – внутри. Получаем булевый отрезок.
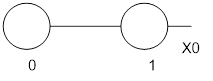
Рис. 5. Булевый отрезок
В этом случае возможны всего 4 булевы функции – константы 0 и 1, повторитель и логический инвертор. Они запишутся так:
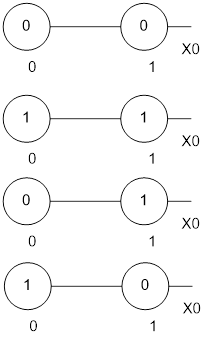
Рис. 6. Все функции от двух булевых переменных
Для двух входных переменных у нас получится булевый квадрат и количество реализуемых функций составит 16 (перечислять их не будем):
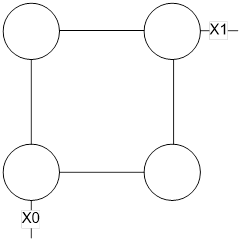
Рис. 7. Булевый квадрат
Абсолютно аналогично, получим булевый кубик:
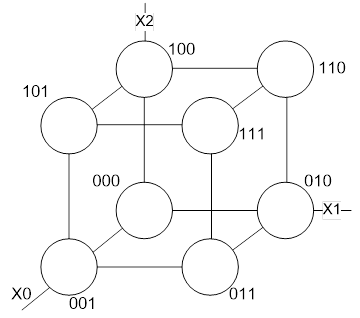
Рис. 8. Булевый куб
Здесь мы подписали под кружочками входные переменные в формате {X2,X1,X0}
И здесь начинается самое интересное! Мы можем продолжить рисование наших кубиков и для размерности больше 3. Это весьма удивительно, ведь в реальном мире размерность больше трех воспринимается как абстракция, которую нельзя изобразить! В дискретной математике, однако, все иначе, и мы можем рисовать кубики размерности большей, чем 3. Поскольку в нашей задаче производится минимизация функции от четырех входных переменных, нам нужен четырехмерный кубик, и мы его сейчас нарисуем!
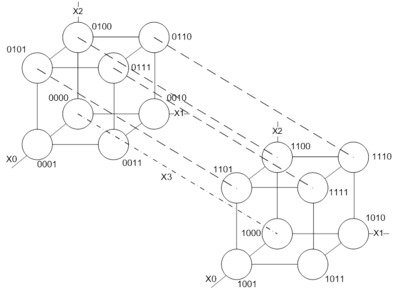
Рис.9 . Четырехмерный булевый гиперкуб
Вот он какой, наш четырехмерный кубик! Кружочки подписаны значением входных переменных, что можно и не делать. Штрих-пунктирной линией обозначена переменная X3, а пунктиром – трехмерный подкубик X2=1. (Вообще, легко показать, что один 4х-мерный гиперкуб содержит в себе 8 трехмерных разрезов).
При наличии минимальной практики, на таком кубике хорошо визуально различимы различные геометрические элементы, что позволяет легко находить минимальные формы.
Теперь рассмотрим кубики более высокой размерности, а затем вернемся к нашей задаче.
Булевы гиперкубы размерностью выше четвертой
Возникает вопрос, а существует ли предел размерности, которую можно отобразить на гиперкубе. Нет, такого предела не существует, но, к сожалению, имеется предел человеческого восприятия. Как оказалось, максимальная размерность входных переменных, при которой человек способен различать геометрические элементы является семи. Нарисуем сразу гиперкубик этой размерности, причем он содержит в себе все гиперкубики более низких размерностей:
Рис. 10. Семимерный булевый гиперкуб (развертка на плоскости)
Возможно, впрочем, правило 7 измерений относится только к развертке на плоскости, изображенной на предыдущем рисунке. На рисунке ниже изображен гиперкубик размерности 9, состоящий из 64х обычных трехмерных кубиков. Честно признаемся, мы с таким кубиком не работали, но выглядит он так, что похоже, его можно использовать на практике.
Рис. 11. Девятимерный булевый гиперкуб
Учебная задача (продолжение)
Покажем, как решается наша задача на примере работы с четырехмерным кубиком. Сначала минимизируем 7 выходных функций отдельно друг от друга.
Сегмент a
Произведем минимизацию булевой функции для сегмента “a” семисегментного индикатора. Для начала нарисуем сам кубик. Естественно, так подробно, как на Рис. 9 в практической работе его не прорисовывают. Кружочки для быстроты не рисуют, а выходы пишут рядом с кружочками. Тогда у нас получается что-то вроде:
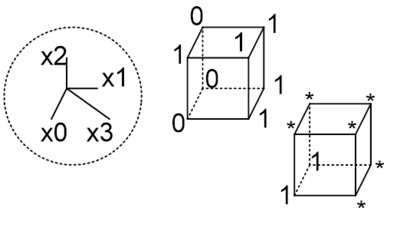
Рис. 12. Логическая функция для сегмента “a” с неопределенными состояниями
В пунктирном круге мы разместили напоминалку о направлении координат. Обычно ее не так же специально не вырисовывают, а держат в уме. Теперь мы можем приступить к минимизации. Это можно сделать разными способами. В зависимости от того, какими функциями мы будем в дальнейшем покрывать нашу форму. Возможны 4 варианта: ДНФ, КНФ, а так же ДНФ и КНФ с инверсией.
Объясним, как пишется ДНФ. Мы должны покрыть все единицы, нули нас не интересуют. При этом мы можем доопределять звездочки так, как нам удобно.
Если доопределить звездочки как 1, то сразу видим, что мы имеем два гиперкубика и одну гиперплоскость, которые частично перекрываются. Для удобства они выделены цветом:
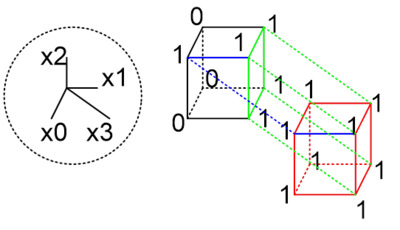
Рис. 13. Логическая функция для сегмента “a” с доопределением состояний
Таким образом, нашу функцию для сегмента a можно закодировать всего тремя неполными термами:
a= X[3] | X[1] | (X[0] & X[2])
Если в библиотеке элементов имеются функции 3ИЛИ и 2И, то для покрытия потребуются всего две логические ячейки:
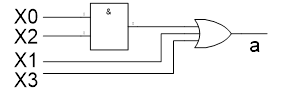
Рис. 14. Вариант покрытия функции для сегмента “a”
Теперь минимизируем остальные 6 функций:
Сегмент b
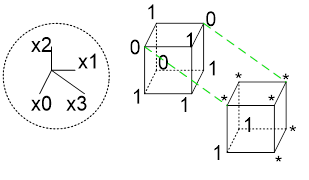
Рис. 15. Логическая функция для сегмента “b” с неопределенными состояниями
Будем кодировать КНФ. Доопредилив звездочки на зеленых отрезках как 0, получим два отрезка. И еще один ноль придется закодировать полным термом:
b= ( X[3] | X[2] | X[1] | X[0] ) & ( !X[2] | !X[1] | X[0] ) & ( !X[2] | X[1] | !X[0] )
Сегмент c
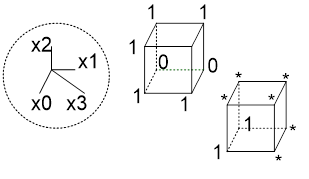
Рис. 16. Логическая функция для сегмента “c” с неопределенными состояниями
Кодируем КНФ, требуется всего один неполный терм:
c= X[3] | X[2] | X[0]
Сегмент d
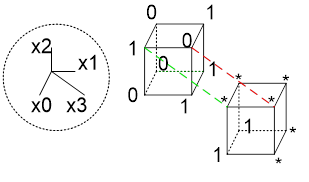
Рис. 17. Логическая функция для сегмента “d” с неопределенными состояниями
Здесь ситуация более сложная. Если кодировать ДНФ, то получаем один куб, две плоскости и один отрезок (обозначен зеленым пунктиром), всего 4 терма. Если же кодировать КНФ, то получаем 3 отрезка (два на первом кубе и один обозначен красным пукнктиром), соответственно, 3 терма. Приведем ДНФ:
d= X[3] | ( !X[0] & X[1] ) | ( !X[2] &X[1] ) | (X[2] & !X[1] & X[0])
Сегмент e
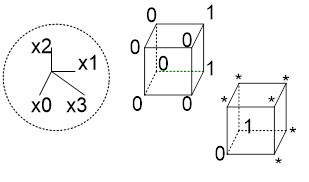
Рис. 18. Логическая функция для сегмента “e” с неопределенными состояниями
Здесь видно, что если кодировать ДНФ, то получаем две плоскости, всего два коротких терма:
e= (X1 & !X0) | ( X3 & !X0) (ДНФ)
Интересно, что от переменной X2 вообще ничего не зависит!
Сегмент f
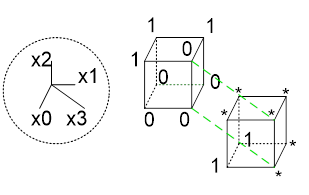
Рис. 19. Логическая функция для сегмента “f” с неопределенными состояниями
Кодируя КНФ, получаем две плоскости, и, соответственно, всего два терма:
f= (X3 | X2) & (!X0 | !X1) (КНФ)
Сегмент g
И, наконец, последний оставшийся сегмент
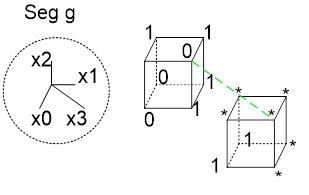
Рис. 20. Логическая функция для сегмента “g” с неопределенными состояниями
Если кодировать ДНФ, получается 4 терма – кубик и три плоскости. Если же кодировать КНФ, получаем 2 плоскости и, соответственно, два терма. Поэтому выбираем второй способ:
g= (X[3] | X[2] | X[1] ) & (!X[2] | !X[1] | !X[0]) (КНФ)
Собираем все вместе
Теперь можно написать все семь формул вместе:
a= X[3] | X[1] | (X[0] & X[2])
b= ( X[3] | X[2] | X[1] | X[0] ) & ( !X[2] | !X[1] | X[0] ) & ( !X[2] | X[1] | !X[0] )
c= X[3] | X[2] | X[0]
d= X[3] | (!X[0] & X[1] ) | ( !X[2] &X[1] ) | (X[2] & !X[1] & X[0])
e= (X1 & !X0) | ( X3 & !X0)
f= (X3 | X2) & (!X0 | !X1)
g= (X[3] | X[2] | X[1] ) & (!X[2] | !X[1] | !X[0])
Следующий этап – совместная оптимизация. Для этого нужно выделить и совместно использовать общие части формул. Мы, однако, сделаем это позже, а сейчас проверим полученные нами формулы. Ведь, если мы где-то ошиблись, оптимизация окажется бессмысленной.
Как производить такую проверку? И здесь самое время перейти к современным средствам автоматизированной верификации и языкам описания аппаратуры (HDL).
Совместная оптимизация
Один из возможных вариантов совместной оптимизации приведен в виде модуля drv7seg_OPT на языке verilog а так же схемы на Рис. 21, ниже.
Компьютерная симуляция
Чтобы провести компьютерную симуляцию, нам надо написать функциональные модули, а так же модули, необходимые только для тестирования. Симуляцию будем вести на языкае verilog, а в качестве симулятора – программу modelsim/questasim.
Описание на языке Verilog
Сначала мы написали 4 модуля на верилоге – один для полного дешифратора кодов от 0 до 14 и 3 для дешифрации кодов от 0 до 9. В модулях drv7seg_1 и drv7seg_varA мы использовали оператор case, позволяющий задать все выходы a-g, в то время как в модуле drv7seg_varB использовались индивидуальные оптимизированные формулы для каждого выхода, а в модуле drv7seg_OPT – совместно оптимизированные. Так же был написан тестбенч GTB, подающий на входы всех модулей код от 0 до15 и считывающий их выходы. Для удобства наблюдения была написана функция, переводящая выходы семисегментного индикатора обратно в целочисленное представление.
См. Код Модулей
Соответственно, по этим формулам можно составить следующую схему:
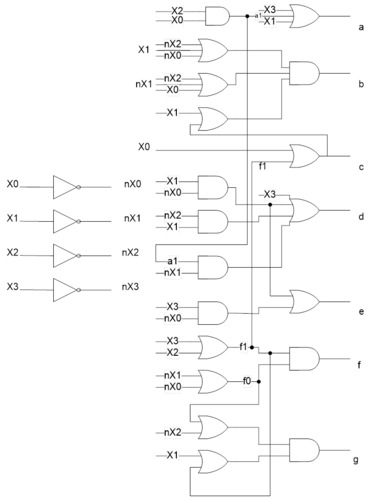
Рис. 21. Пример реализации схемы на элементах НЕ, ИЛИ, И с оптимизацией
Результаты симуляции
Результаты симуляции приведены ниже. На вход всех модулей подается icode, далее с выхода считываются коды управления семисегментным индикатором, которые преобразуются обратно в целочисленный код. Кодом -1 кодируются комбинации, не соответствующие ни одной 16-ричной цифре. Дополнительно были выведены выходы сегмента a всех 4х тестируемых модулей. Как видно, все выходные коды на отрезке 0-9 совпадают друг с другом. Что касается отрезка 10-15, то там коды различаются, что связано с процессом оптимизации. Выходные коды модулей drv7seg_varB и drv7seg_OPT совпадают, что говорит о том, что совместная оптимизация проведена корректно. У модуля drv7seg_varA результат на отрезке 10-15 не определен, что соответствует примененному оператору case.
Рис. 22. Симуляция в программе modelsim
Синтез и имплементация
Чтобы проверить, как результаты оптимизации повлияют на результат для ПЛИС, была проведена имплементация модулей drv_7seg_* на платформах Intel Cyclone-V, Xilinx Artix-7 и Lattice. Для Intel и Xilinx использовались собственные синтезаторы, а для Lattice – Synplify Pro for Lattice. (Использовались пакеты Xilinx Vivado 2017.1, Intel Quartus Prime 17.1 и Lattice Diamond 3.10)
В результате оказалось, что ручная оптимизация вообще никак не влияет на конечный результат! Этот результат, конечно, не удивителен, т.к. элементная база ПЛИС – ячейки LUT (до 6и входов включительно), которые позволяют реализовать любую функцию от 6и и менее входов табличным способом, т.е. для любой реализации нашей задачи потребуется всего 7 ячеек LUT! Единственное отличие – в имплементации семисегментного индикатора 0-9 или 0-15. Причем синтезаторы Intel и Xilinx выполнили свою работу абсолютно одинаково! Для Lattice результат еще интереснее – Synplify реализовал этот логический блок на одном модуле блочной памяти!
Рис. 23. Имплементация схемы управления семисегментным индикатором для цифр 0-F в САПР Vivado
Рис. 24. Имплементация схемы управления семисегментным индикатором для цифр 0-9 в САПР Vivado
Выводы
Какое практическое значение имеет навык минимизации булевых функций при проектировании для ПЛИС в наше время? Скорее всего – никакого! Современные программы синтеза делают эту работу лучше человека, к тому же они учитывают множество других факторов, таких как особенности архитектуры ПЛИС, а так же производят множество дополнительных оптимизаций (например, балансировку булевых функций относительно триггеров). Возможно, при проектировании для ASIC, навык минимизации мог бы пригодиться, т.к. там библиотека компонентов более похожа на классическую логику, в отличие от LUT, используемых в ПЛИС.
Все же прогресс не стоит на месте, поэтому сейчас больший эффект дает оптимальное проектирование на системном уровне, а все оптимизации на локальном уровне берет на себя компьютер. И, если программа синтеза работает неэффективно, логично улучшать программу, а не возиться с локальной оптимизацией самостоятельно.
