Задача о вершинном покрытии
Время на прочтение
3 мин
Количество просмотров 31K
Введение.
На данный момент не известно полиномиальных по времени алгоритмов точного решения NP-трудных задач. Более того, специалисты по теории сложности склоняются к варианту, что таких алгоритмов не существует. Однако, NP-трудные задачи часто встречаются в жизни. Одним из способов борьбы с NP-трудными задачами на практике является применение приближенных алгоритмов.
Рассмотрим лучший известный приближенный алгоритм решения задачи о вершинном покрытии.
Постановка задачи.
Вершинное покрытие – это такое множество S вершин графа, что у каждого ребра графа хотя бы один конец входит в S.
Задача заключается в том, чтобы выбрать в неориентированном графе минимальное (по количеству вершин) вершинное покрытие.
Цель.
Построим простой алгоритм решения этой задачи, ошибающийся не более чем в два раза. Это означает, что если есть оптимальное решение — множество вершин T, то полученное нами решение S удовлетворяет неравенству |S| <= 2|T|.
Пример.

В приведенном примере вершинным покрытием является, например, множество вершин {0, 1, 2, 4}. Все шесть вершин графа также образуют вершинное покрытие. Однако, минимальным вершинным покрытием в рассматриваемом графе будет множество, состоящее всего из двух вершин. Например, это могут быть вершины с номерами 1 и 3. Действительно, все ребра графа покрываются двумя этими вершинами.
Алгоритм.
На каждом шаге алгоритма производим следующие действия:
- Выбираем случайное ребро графа e=(u, v).
- Добавляем в решение S обе выбранные вершины u и v.
- Удаляем из графа все ребра, инцидентные вершинам u или v.
Повторяем этот шаг до тех пор, пока не удалим все ребра графа.
Пример работы алгоритма.

В приведенном примере минимальное вершинное покрытие содержит три вершины. Например, это могут быть вершины 1, 3 и 6. Рассмотрим работу нашего алгоритма на приведенном примере.
Первая итерация:
- Выбираем случайное ребро. Например, ребро (1, 3).
- Добавляем в решение S обе вершины выбранного ребра: S={1, 3}.
- Удаляем из графа все ребра, инцидентные вершинам 1 или 3.

Вторая итерация:
- Выбираем случайное ребро. Пусть это будет ребро (4, 6).
- Добавляем в решение S обе вершины выбранного ребра: S={1, 3, 4, 6}.
- Удаляем из графа все ребра, инцидентные вершинам 4 или 6.
В графе не осталось ребер. Следовательно, результатом работы нашего алгоритма будет вершинное покрытие S={1, 3, 4, 6}.
Доказательство.
Докажем, что построенное множество является вершинным покрытием. Действительно, на каждом шаге мы удаляли лишь уже покрытые ребра. Мы повторяли эту итерацию, пока в графе еще оставались ребра. Таким образом, мы покрыли все ребра графа.
Докажем, что наш алгоритм ошибается не более, чем в 2 раза.
Все рассматриваемые алгоритмом ребра e не имеют общих вершин. Следовательно, из каждого из этих рёбер в оптимальное решение T должна входить хотя бы одна вершина. Это значит, что 2|T|>=|S|.
Немного истории
В знаменитой работе Ричарда Карпа «Reducibility among combinatorial problems» под названием Node Cover рассматривается соответствующая Vertex Cover задача разрешимости и доказывается ее NP-полнота.
Рассмотренный нами алгоритм был независимо разработан Fanica Gavril и Mihalis Yannakakis в 1974 году.
Лучшая известная на сегодняшний день оценка приближенного алгоритма задачи Vertex Cover  принадлежит George Karakostas. Оценка доказана в работе A better approximation ratio for the vertex cover problem.
принадлежит George Karakostas. Оценка доказана в работе A better approximation ratio for the vertex cover problem.
Заключение.
На данный момент не известно полиномиальных приближенных алгоритмов для Vertex Cover значительно улучшающих полученную нами точность. То есть, не известно полиномиального по времени алгоритма, который бы ошибался не более, чем в 1.999 раза. Таким образом, мы получили простой полиномиальный по времени алгоритм с хорошей точностью для решения NP-трудной задачи.
Содержание
- 1 Минимальное вершинное покрытие
- 1.1 Теорема о мощности минимального вершинного покрытия и максимального паросочетания
- 1.2 Алгоритм построения минимального вершинного покрытия
- 2 См. также
- 3 Источники информации
Минимальное вершинное покрытие
| Определение: |
| Вершинным покрытием (англ. vertex covering) графа называется такое подмножество множества вершин графа , что любое ребро этого графа инцидентно хотя бы одной вершине из множества . |
| Определение: |
| Минимальным вершинным покрытием (англ. minimum vertex covering) графа называется вершинное покрытие, состоящее из наименьшего числа вершин. |
Множество вершин красного цвета — минимальное вершинное покрытие.
Теорема о мощности минимального вершинного покрытия и максимального паросочетания
| Теорема (Кёниг): |
|
В произвольном двудольном графе мощность максимального паросочетания равна мощности минимального вершинного покрытия. |
| Доказательство: |
|
Пусть в построено максимальное паросочетание. Ориентируем ребра паросочетания, чтобы они шли из правой доли в левую, ребра не из паросочетания — так, чтобы они шли из левой доли в правую. Запустим обход в глубину из всех не насыщенных паросочетанием вершин левой доли. Разобьем вершины каждой доли графа на два множества: те, которые были посещены в процессе обхода, и те, которые не были посещены в процессе обхода.
Очевидно, что ребер из в и из в быть не может. Заметим, что минимальным вершинным покрытием является либо , либо , либо . Тогда равна мощности максимального паросочетания. Множество вершин является минимальным вершинным покрытием. Значит мощность максимального паросочетания равна мощности минимального вершинного покрытия. |
Алгоритм построения минимального вершинного покрытия
Из доказательства предыдущей теоремы следует алгоритм поиска минимального вершинного покрытия графа:
- Построить максимальное паросочетание.
- Ориентировать ребра:
- Из паросочетания — из правой доли в левую.
- Не из паросочетания — из левой доли в правую.
- Запустить обход в глубину из всех свободных вершин левой доли, построить множества .
- В качестве результата взять .
См. также
- Теорема о максимальном паросочетании и дополняющих цепях
- Связь вершинного покрытия и независимого множества
Источники информации
- Википедия — Теорема Кёнига
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 мая 2020 года; проверки требуют 3 правки.
Задача о вершинном покрытии — NP-полная задача информатики в области теории графов. Часто используется в теории сложности для доказательства NP-полноты более сложных задач.
Определение[править | править код]

Вершинное покрытие для неориентированного графа 


Размером (size) вершинного покрытия называется число входящих в него вершин.
Пример: Граф, изображённый справа, имеет вершинное покрытие 


Задача о вершинном покрытии состоит в поиске вершинного покрытия наименьшего размера для заданного графа (этот размер называется числом вершинного покрытия графа).
- На входе: Граф
.
- Результат: множество
— наименьшее вершинного покрытие графа
.
Также вопрос можно ставить как эквивалентную задачу разрешения:
- На входе: Граф
и положительное целое число
.
- Вопрос: Существует ли вершинное покрытие
для графа
размера не более
?
Задача о вершинном покрытии сходна с задачей о независимом множестве. Поскольку множество вершин 

NP-полнота[править | править код]
Поскольку задача о вершинном покрытии является NP-полной, то, к сожалению, неизвестны алгоритмы для её решения за полиномиальное время. Однако существуют аппроксимационные алгоритмы, дающие «приближённое» решение этой задачи за полиномиальное время — можно найти вершинное покрытие, в котором число вершин не более чем вдвое превосходит минимально возможное.
Один из первых, приходящих в голову, подходов решения задачи – аппроксимация через жадный алгоритм: Необходимо добавлять вершины с максимальным количеством соседей в вершинное покрытие, пока задача не будет решена, однако такое решение не имеет 

Другой вариант решения – нахождение максимального паросочетания 











В общем случае задача о вершинном покрытии может быть аппроксимирована с фактором 
Задача о вершинном покрытии в двудольных графах[править | править код]
В двудольных графах задача о вершинном покрытии разрешима за полиномиальное время, поскольку сводится к задаче о наибольшем паросочетании (Теорема Кёнига).
Ссылки[править | править код]
- A compendium of NP optimization problems
- Challenging Benchmarks for Maximum Clique, Maximum Independent Set, Minimum Vertex Cover and Vertex Coloring
Литература[править | править код]
- Томас Х. Кормен и др. Глава 36. NP-полнота // Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 1-е изд. — М.: Московского центра непрерывного математического образования, 2001. — С. 866.
A vertex cover of an undirected graph is a subset of its vertices such that for every edge (u, v) of the graph, either ‘u’ or ‘v’ is in vertex cover. There may be a lot of vertex covers possible for a graph.
Problem Find the size of the minimum size vertex cover, that is, cardinality of a vertex cover with minimum cardinality, for an undirected connected graph with V vertices and m edges.
Examples:
Input: V = 6, E = 6
6
/
/
1 -----5
/|
3 |
|
2 4
Output: Minimum vertex cover size = 2
Consider subset of vertices {1, 2}, every edge
in above graph is either incident on vertex 1
or 2. Hence the minimum vertex cover = {1, 2},
the size of which is 2.
Input: V = 6, E = 7
2 ---- 4 ---- 6
/| |
1 | |
| |
3 ---- 5
Output: Minimum vertex cover size = 3
Consider subset of vertices {2, 3, 4}, every
edge in above graph is either incident on
vertex 2, 3 or 4. Hence the minimum size of
a vertex cover can be 3.
Method 1 (Naive) We can check in O(E + V) time if a given subset of vertices is a vertex cover or not, using the following algorithm.
Generate all 2V subsets of vertices in graph and do following for every subset. 1. edges_covered = 0 2. for each vertex in current subset 3. for all edges emerging out of current vertex 4. if the edge is not already marked visited 5. mark the edge visited 6. edges_covered++ 7. if edges_covered is equal to total number edges 8. return size of current subset
An upper bound on time complexity of this solution is O((E + V) * 2V)
Method 2 (Binary Search) If we generate 2V subsets first by generating VCV subsets, then VC(V-1) subsets, and so on upto VC0 subsets(2V = VCV + VC(V-1) + … + VC1 + VC0). Our objective is now to find the minimum k such that at least one subset of size ‘k’ amongst VCk subsets is a vertex cover [ We know that if minimum size vertex cover is of size k, then there will exist a vertex cover of all sizes more than k. That is, there will be a vertex cover of size k + 1, k + 2, k + 3, …, n. ] Now let’s imagine a boolean array of size n and call it isCover[]. So if the answer of the question; “Does a vertex cover of size x exist?” is yes, we put a ‘1’ at xth position, otherwise ‘0’. The array isCover[] will look like:
| 1 | 2 | 3 | . | . | . | k | . | . | . | n |
| 0 | 0 | 0 | . | . | . | 1 | . | . | . | 1 |
The array is sorted and hence binary searchable, as no index before k will have a ‘1’, and every index after k(inclusive) will have a ‘1’, so k is the answer. So we can apply Binary Search to find the minimum size vertex set that covers all edges (this problem is equivalent to finding last 1 in isCover[]). Now the problem is how to generate all subsets of a given size. The idea is to use Gosper’s hack.
What is Gosper’s Hack? Gosper’s hack is a technique to get the next number with same number of bits set. So we set the first x bits from right and generate next number with x bits set until the number is less than 2V. In this way, we can generate all VCx numbers with x bits set.
CPP
int set = (1 << k) - 1;
int limit = (1 << V);
while (set < limit)
{
doStuff(set);
int c = set & -set;
int r = set + c;
set = (((r^set) >>> 2) / c) | r;
}
Javascript
let set = (1 << k) - 1;
let limit = (1 << V);
while (set < limit) {
doStuff(set);
let c = set & -set;
let r = set + c;
set = (((r^set) >>> 2) / c) | r;
}
Java
int set = (1 << k) - 1;
int limit = (1 << V);
while (set < limit) {
doStuff(set);
int c = set & -set;
int r = set + c;
set = (((r ^ set) >>> 2) / c) | r;
}
C#
int set = (1 << k) - 1;
int limit = (1 << V);
while (set < limit) {
DoStuff(set);
int c = set & -set;
int r = set + c;
set = (((r ^ set) >>> 2) / c) | r;
}
Python
set = (1 << k) - 1
limit = (1 << V)
while set < limit:
DoStuff(set)
c = set & -set
r = set + c
set = (((r ^ set) >> 2) // c) | r
Source : StackExchange We use gosper’s hack to generate all subsets of size x(0 < x <= V), that is, to check whether we have a ‘1’ or ‘0’ at any index x in isCover[] array.
C++
#include<bits/stdc++.h>
#define maxn 25
using namespace std;
bool gr[maxn][maxn];
bool isCover(int V, int k, int E)
{
int set = (1 << k) - 1;
int limit = (1 << V);
bool vis[maxn][maxn];
while (set < limit)
{
memset(vis, 0, sizeof vis);
int cnt = 0;
for (int j = 1, v = 1 ; j < limit ; j = j << 1, v++)
{
if (set & j)
{
for (int k = 1 ; k <= V ; k++)
{
if (gr[v][k] && !vis[v][k])
{
vis[v][k] = 1;
vis[k][v] = 1;
cnt++;
}
}
}
}
if (cnt == E)
return true;
int c = set & -set;
int r = set + c;
set = (((r^set) >> 2) / c) | r;
}
return false;
}
int findMinCover(int n, int m)
{
int left = 1, right = n;
while (right > left)
{
int mid = (left + right) >> 1;
if (isCover(n, mid, m) == false)
left = mid + 1;
else
right = mid;
}
return left;
}
void insertEdge(int u, int v)
{
gr[u][v] = 1;
gr[v][u] = 1;
}
int main()
{
int V = 6, E = 6;
insertEdge(1, 2);
insertEdge(2, 3);
insertEdge(1, 3);
insertEdge(1, 4);
insertEdge(1, 5);
insertEdge(1, 6);
cout << "Minimum size of a vertex cover = "
<< findMinCover(V, E) << endl;
memset(gr, 0, sizeof gr);
V = 6, E = 7;
insertEdge(1, 2);
insertEdge(1, 3);
insertEdge(2, 3);
insertEdge(2, 4);
insertEdge(3, 5);
insertEdge(4, 5);
insertEdge(4, 6);
cout << "Minimum size of a vertex cover = "
<< findMinCover(V, E) << endl;
return 0;
}
Java
class GFG
{
static final int maxn = 25;
static boolean [][]gr = new boolean[maxn][maxn];
static boolean isCover(int V, int k, int E)
{
int set = (1 << k) - 1;
int limit = (1 << V);
boolean [][]vis = new boolean[maxn][maxn];;
while (set < limit)
{
for(int i = 0; i < maxn; i++)
{
for(int j = 0; j < maxn; j++)
{
vis[i][j] = false;
}
}
int cnt = 0;
for (int j = 1, v = 1 ; j < limit ; j = j << 1, v++)
{
if ((set & j) != 0)
{
for (int co = 1 ; co <= V ; co++)
{
if (gr[v][co] && !vis[v][co])
{
vis[v][co] = true;
vis[co][v] = true;
cnt++;
}
}
}
}
if (cnt == E)
return true;
int co = set & -set;
int ro = set + co;
set = (((ro^set) >> 2) / co) | ro;
}
return false;
}
static int findMinCover(int n, int m)
{
int left = 1, right = n;
while (right > left)
{
int mid = (left + right) >> 1;
if (isCover(n, mid, m) == false)
left = mid + 1;
else
right = mid;
}
return left;
}
static void insertEdge(int u, int v)
{
gr[u][v] = true;
gr[v][u] = true;
}
public static void main(String[] args)
{
int V = 6, E = 6;
insertEdge(1, 2);
insertEdge(2, 3);
insertEdge(1, 3);
insertEdge(1, 4);
insertEdge(1, 5);
insertEdge(1, 6);
System.out.print("Minimum size of a vertex cover = "
+ findMinCover(V, E) +"n");
for(int i = 0; i < maxn; i++)
{
for(int j = 0; j < maxn; j++)
{
gr[i][j] = false;
}
}
V = 6;
E = 7;
insertEdge(1, 2);
insertEdge(1, 3);
insertEdge(2, 3);
insertEdge(2, 4);
insertEdge(3, 5);
insertEdge(4, 5);
insertEdge(4, 6);
System.out.print("Minimum size of a vertex cover = "
+ findMinCover(V, E) +"n");
}
}
Python3
def isCover(V, k, E):
Set = (1 << k) - 1
limit = (1 << V)
vis = [[None] * maxn for i in range(maxn)]
while (Set < limit):
vis = [[0] * maxn for i in range(maxn)]
cnt = 0
j = 1
v = 1
while(j < limit):
if (Set & j):
for k in range(1, V + 1):
if (gr[v][k] and not vis[v][k]):
vis[v][k] = 1
vis[k][v] = 1
cnt += 1
j = j << 1
v += 1
if (cnt == E):
return True
c = Set & -Set
r = Set + c
Set = (((r ^ Set) >> 2) // c) | r
return False
def findMinCover(n, m):
left = 1
right = n
while (right > left):
mid = (left + right) >> 1
if (isCover(n, mid, m) == False):
left = mid + 1
else:
right = mid
return left
def insertEdge(u, v):
gr[u][v] = 1
gr[v][u] = 1
maxn = 25
gr = [[None] * maxn for i in range(maxn)]
V = 6
E = 6
insertEdge(1, 2)
insertEdge(2, 3)
insertEdge(1, 3)
insertEdge(1, 4)
insertEdge(1, 5)
insertEdge(1, 6)
print("Minimum size of a vertex cover = ",
findMinCover(V, E))
gr = [[0] * maxn for i in range(maxn)]
V = 6
E = 7
insertEdge(1, 2)
insertEdge(1, 3)
insertEdge(2, 3)
insertEdge(2, 4)
insertEdge(3, 5)
insertEdge(4, 5)
insertEdge(4, 6)
print("Minimum size of a vertex cover = ",
findMinCover(V, E))
Javascript
const maxn = 25;
const gr = Array.from({ length: maxn }, () => new Array(maxn).fill(false));
function isCover(V, k, E) {
let set = (1 << k) - 1;
const limit = 1 << V;
const vis = Array.from({ length: maxn }, () => new Array(maxn).fill(false));
while (set < limit) {
for(let i = 0; i < maxn; i++) {
for(let j = 0; j < maxn; j++) {
vis[i][j] = false;
}
}
let cnt = 0;
for (let j = 1, v = 1 ; j < limit ; j = j << 1, v++) {
if ((set & j) !== 0) {
for (let co = 1 ; co <= V ; co++) {
if (gr[v][co] && !vis[v][co]) {
vis[v][co] = true;
vis[co][v] = true;
cnt++;
}
}
}
}
if (cnt === E) {
return true;
}
const cO = set & -set;
const rO = set + cO;
set = (((rO^set) >> 2) / cO) | rO;
}
return false;
}
function findMinCover(n, m) {
let left = 1;
let right = n;
while (right > left) {
let mid = (left + right) >> 1;
if (isCover(n, mid, m) === false) {
left = mid + 1;
} else {
right = mid;
}
}
return left;
}
function insertEdge(u, v) {
gr[u][v] = true;
gr[v][u] = true;
}
let V = 6, E = 6;
insertEdge(1, 2);
insertEdge(2, 3);
insertEdge(1, 3);
insertEdge(1, 4);
insertEdge(1, 5);
insertEdge(1, 6);
console.log("Minimum size of a vertex cover = " + findMinCover(V, E) + "n");
for (let i = 0; i < maxn; i++) {
for (let j = 0; j < maxn; j++) {
gr[i][j] = false;
}
}
V = 6;
E = 7;
insertEdge(1, 2);
insertEdge(1, 3);
insertEdge(2, 3);
insertEdge(2, 4);
insertEdge(3, 5);
insertEdge(4, 5);
insertEdge(4, 6);
console.log("Minimum size of a vertex cover = " + findMinCover(V, E) + "n");
C#
using System;
class GFG
{
static readonly int maxn = 25;
static bool [,]gr = new bool[maxn, maxn];
static bool isCover(int V, int k, int E)
{
int set = (1 << k) - 1;
int limit = (1 << V);
bool [,]vis = new bool[maxn, maxn];;
while (set < limit)
{
for(int i = 0; i < maxn; i++)
{
for(int j = 0; j < maxn; j++)
{
vis[i, j] = false;
}
}
int cnt = 0;
for (int j = 1, v = 1 ; j < limit ; j = j << 1, v++)
{
if ((set & j) != 0)
{
for (int co = 1 ; co <= V ; co++)
{
if (gr[v, co] && !vis[v, co])
{
vis[v, co] = true;
vis[co, v] = true;
cnt++;
}
}
}
}
if (cnt == E)
return true;
int cO = set & -set;
int rO = set + cO;
set = (((rO^set) >> 2) / cO) | rO;
}
return false;
}
static int findMinCover(int n, int m)
{
int left = 1, right = n;
while (right > left)
{
int mid = (left + right) >> 1;
if (isCover(n, mid, m) == false)
left = mid + 1;
else
right = mid;
}
return left;
}
static void insertEdge(int u, int v)
{
gr[u, v] = true;
gr[v, u] = true;
}
public static void Main(String[] args)
{
int V = 6, E = 6;
insertEdge(1, 2);
insertEdge(2, 3);
insertEdge(1, 3);
insertEdge(1, 4);
insertEdge(1, 5);
insertEdge(1, 6);
Console.Write("Minimum size of a vertex cover = "
+ findMinCover(V, E) +"n");
for(int i = 0; i < maxn; i++)
{
for(int j = 0; j < maxn; j++)
{
gr[i,j] = false;
}
}
V = 6;
E = 7;
insertEdge(1, 2);
insertEdge(1, 3);
insertEdge(2, 3);
insertEdge(2, 4);
insertEdge(3, 5);
insertEdge(4, 5);
insertEdge(4, 6);
Console.Write("Minimum size of a vertex cover = "
+ findMinCover(V, E) +"n");
}
}
Output
Minimum size of a vertex cover = 2 Minimum size of a vertex cover = 3
Conclusion:
Time Complexity : O (E * ( VCV/2 + VCV/4 + VCV/8 +…upto VCk ) ) These terms are not more than log(V) in worst case.
Auxiliary Space Complexity : O(V^2)
Note: Gosper’s hack works for upto V = 31 only, if we take ‘long long int’ instead of ‘int’ it can work upto V = 63. This article is contributed by Saumye Malhotra .
If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Last Updated :
06 Apr, 2023
Like Article
Save Article
Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Паросочетания
Задача. Пусть есть (n) мальчиков и (m) девочек. Про каждого мальчика и про каждую девочку известно, с кем они не против танцевать. Нужно составить как можно больше пар, в которых партнёры хотят танцевать друг с другом.
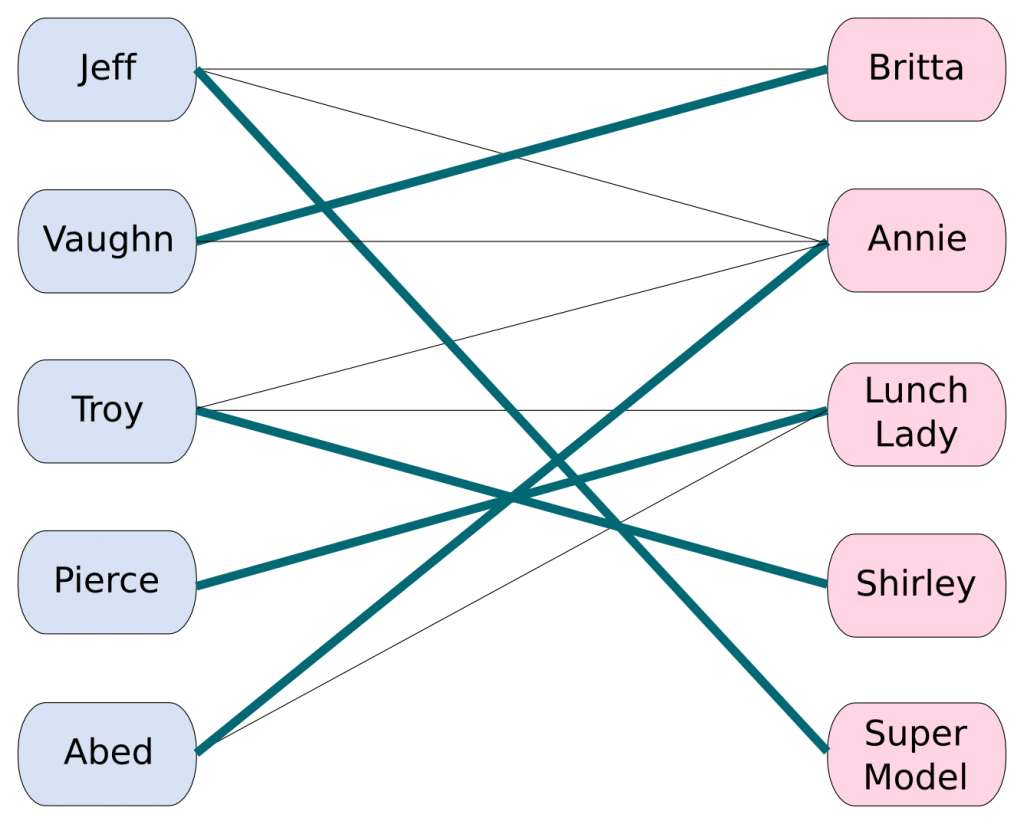
Формализуем эту задачу, представив мальчиков и девочек как вершины в двудольном графе, рёбрами которого будет отношение «могут танцевать вместе».
Паросочетанием (M) называется набор попарно несмежных рёбер графа (иными словами, любой вершине графа должно быть инцидентно не более одного ребра из (M)).
Все вершины, у которых есть смежное ребро из паросочетания (т.е. которые имеют степень ровно один в подграфе, образованном (M)), назовём насыщенными этим паросочетанием.
Мощностью паросочетания назовём количество рёбер в нём. Наибольшим (максимальным) паросочетанием назовём паросочетание, мощность которого максимальна среди всех возможных паросочетаний в данном графе, а совершенным — где все вершины левой доли им насыщенны.
Паросочетания можно искать в любых графах, однако этот алгоритм неприятно кодить, и он работает за (O(n^3)), так что сегодня мы сфокусируемся только на двудольных графах. Будем в дальнейшем обозначать левую долю графа как (L), а правую долю как (R).
Цепью длины (k) назовём некоторый простой путь (т.е. не содержащий повторяющихся вершин или рёбер), содержащий ровно (k) рёбер.
Чередующейся цепью относительно некоторого паросочетания назовём простой путь длины (k) в которой рёбра поочередно принадлежат/не принадлежат паросочетанию.
Увеличивающей цепью относительно некоторого паросочетания назовём чередующуюся цепь, у которой начальная и конечная вершины не принадлежат паросочетанию.

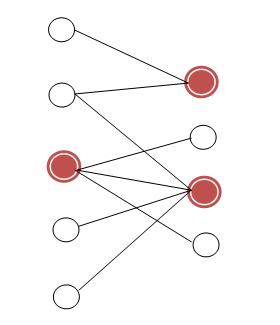
Здесь красными помечены вершины паросочетания, а в графе есть увеличивающая цепь: (1 to 8 to 4 to 6 to 3 to 7).
Зачем нужны увеличивающие цепи? Оказывается, можно с их помощью увеличивать паросочетание на единицу (отсюда и название). Можно взять такой путь и провести чередование — убрать из паросочетания все рёбра, принадлежащие цепи, и, наоборот, добавить все остальные. Всего в увеличивающей цепи нечетное число рёбер, а первое и последнее были не в паросочетании. Значит, мощность паросочетания увеличилась ровно на единицу.
В примере добавятся синие рёбра ((1, 8)), ((3, 7)) и ((4, 6)), а удалятся красные ((3, 6)) и ((4, 8)). С ребром ((2, 5)) ничего не случится — оно не в увеличивающей цепи. Таким образом, размер паросочетания увеличится на единицу.
Алгоритм Куна в этом и заключается — будем искать увеличивающую цепь, пока ищется, и проводить чередование в ней. Увеличивающие цепи удобны тем, что их легко искать: можно просто запустить поиск пути из произвольной свободной вершины из левой доли в какую-нибудь свободную вершину правой доли в том же графе, но в котором из правой доли можно идти только по рёбрам паросочетания (то есть у вершин правой доли будет либо одно ребро, либо ноль). Это можно делать как угодно (для упражнения автор рекомендует явно строить такой граф, искать путь и явно проводить чередования), однако устоялась эффективная реализация в виде dfs на 20 строчек кода, приведённая ниже.
const int maxn;
vector<int> g[maxn]; // будем хранить только рёбра из левой доли в правую
int mt[maxn]; // с какой вершиной сматчена вершина правой доли (-1, если ни с какой)
bool used[maxn]; // вспомогательный массив для поиска пути dfs-ом
// dfs возвращает, можно ли найти путь из вершины v
// в какую-нибудь вершину правой доли
// если можно, то ещё и проводит чередование
bool dfs(int v) {
if (used[v])
return false;
used[v] = true;
for (int u : g[v]) {
// если вершина свободна, то можно сразу с ней соединиться
// если она занята, то с ней можно соединиться только тогда,
// когда из её текущей пары можно найти какую-нибудь другую вершину
if (mt[u] == -1 || dfs(mt[u])) {
mt[u] = v;
return true;
}
}
return false;
}
// где-то в main:
memset(mt, -1, sizeof mt);
for (int i = 0; i < n; i++) {
memset(used, 0, sizeof mt);
if (dfs(i))
cnt++;
}Корректность
Для доказательства алгоритма нам будет достаточно ещё доказать, что если увеличивающие цепи уже не ищутся, то паросочетание в принципе нельзя увеличить.
Теорема (Бержа). Паросочетание без увеличивающих цепей является максимальным.
Доказательство проведём от противного: пусть есть два паросочетания вершин (|A| leq |B|), и для (A) нет увеличивающих путей, и покажем, как найти этот путь и увеличить (A) на единицу.
Раскрасим ребра из паросочетания, соответствующего (A) в красный цвет, (B) — в синий, а ребра из обоих паросочетаний — в пурпурный. Рассмотрим граф из только красных и синих ребер. Любая компонента связности в нём представляет собой либо путь, либо цикл, состоящий из чередующихся красных и синих ребер. В любом цикле будет равное число красных и синих рёбер, а так как всего синих рёбер больше, то должен существовать путь, начинающийся и оканчивающийся синим ребром — он и будет увеличивающей цепью для (A), а значит (A) не оптимальное, и мы получили противоречие.
Скорость работы
Такой алгоритм ровно (n) раз ищет увеличивающий путь, каждый раз просматривая не более (m) рёбер, а значит работает за (O(nm)).
Что примечательно, его можно не бояться запускать на ограничениях и побольше ((n, m approx 10^4)), потому что для него есть мощные неасимптотические оптимизации:
-
Eго можно жадно инициализировать (просто заранее пройтись по вершинам левой доли и сматчить их со свободной вершиной правой, если она есть).
-
Можно не заполнять нулями на каждой итерации массив
used, а использовать следующий трюк: хранить в нём вместо булева флага версию последнего изменения, а конкретно – номер итерации, на которой это значение сталоtrue. Если этот номер меньше текущего номера итерации, то мы можем воспринимать это значение какfalse. В каком-то смысле это позволяет эмулировать очищение массива за константу. -
Очень часто граф приходит из какой-то другой задачи, природа которой накладывает ограничения на его вид. Например, в задачах на решетках (когда есть двумерный массив, и соседние клетки связаны друг с другом) граф двудольный, но степень каждой вершины маленькая, и граф имеет очень специфичную структуру, и на нём алгоритм Куна работает быстрее, чем ожидается из формулы (n times m). Контрпримеры в таких задачах на самом деле почти всегда можно сгенерировать, но авторы редко так заморачиваются.
Вообще говоря, увлекаться ускорением алгоритма Куна не стоит — существует более асимптотически быстрый алгоритм. Задача нахождения максимального паросочетания — частный случай задачи о максимальном потоке, и если применить алгоритм Диница к двудольным графам с единичной пропускной способностью, то выясняется, что работать он будет за (O(m sqrt n)).
Покрытие путями DAG-а
Сводить задачи к поиску максимального паросочетания обычно не очень трудно, но в некоторых случаях самому додуматься сложно. Разберём одну такую известную задачу. Дан ориентированный ациклический граф (G) (англ. directed acyclic graph). Требуется покрыть его наименьшим числом путей, то есть найти наименьшее множество простых путей, где каждая вершина принадлежит ровно одному пути.
Построим соответствующие изначальному графу (G) два двудольных графа (H) и (overline{H}) следующим образом:
- В каждой доле графа (H) будет по (n) вершин. Обозначим их через (a_i) и (b_i) соответственно.
- Для каждого ребра ((i, j)) исходного графа (G) проведём соответствующее ребро ((a_i, b_j)) в графе (H).
- Теперь из графа (H) сделаем граф (overline{H}), добавив обратное ребро ((b_i, a_i)) для каждого (i).
Если мы рассмотрим любой путь (v_1, v_2, ldots, v_k) в исходном графе (G), то в графе (overline{H}) ему будет соответствовать путь (a_{v_1}, b_{v_2}, a_{v_2}, b_{v_3}, ldots, a_{v_{k-1}}, b_{v_k}). Обратное тоже верно: любой путь, начинающийся в левой доле (overline{H}) и заканчивающийся в правой будет соответствовать какому-то пути в (G).
Итак, есть взаимно однозначное соответствие между путями в (G) и путями (overline{H}), идущими из левой доли в правую. Заметим, что любой такой путь в (overline{H}) — это паросочетание в (H) (напомним, это (overline{H}) без обратных рёбер). Получается, любому пути из (G) можно поставить в соответствие паросочетание в (H), и наоборот. Более того, непересекающимся путям в (G) соответствуют непересекающиеся паросочетания в (H).
Заметим, что если есть (p) непересекающихся путей, покрывающих все (n) вершин графа, то они вместе содержат (r = n – p) рёбер. Отсюда получаем, что чтобы минимизировать число путей (p), мы должны максимизировать число рёбер (r) в них.
Мы теперь можем свести задачу к нахождению максимального паросочетания в двудольном графе (H). После нахождения этого паросочетания мы должны преобразовать его в набор путей в (G). Это делается тривиальным алгоритмом: возьмем (a_1), посмотрим, с какой (b_k) она соединена, посмотрим на (a_k) и так далее. Некоторые вершины могут остаться ненасыщенными — в таком случае в ответ надо добавить пути нулевой длины из каждой из этих вершин.
Лемма Холла
Лемма Холла (или: теорема о свадьбах) — очень удобный критерий в задачах, где нужно проверить, что паросочетание существует, но при этом не требуется строить его явно.
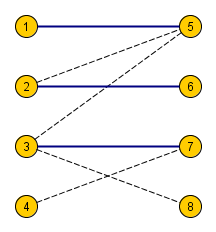
Лемма Холла. Полное паросочетание существует тогда и только тогда, когда любая группа вершин левой доли соединена с не меньшим количеством вершин правой доли.
Доказательство. В одну сторону понятно — если совершенное паросочетание есть, то для любого подмножества вершин левой доли можно взять вершины правой, соединенные с ним паросочетанием.
В другую сложнее — нужно воспользоваться индукцией. Будем доказывать, что если паросочетание не полное, то можно в таком графе найти увеличивающую цепь, и с её помощью увеличить паросочетание на единицу.
База индукции: одна вершина из (L), которая по условию соединена с хотя бы одной вершиной из (R).
Индукционный переход: пусть после (k < n) шагов построено паросочетание (M). Докажем, что в (M) можно добавить вершину (v) из (L), не насыщенную паросочетанием.
Рассмотрим множество вершин (H) — все вершины, достижимые из (x), если можно ходить из правой доли в левую только по рёбрам паросочетания, а из левой в правую — по любым (мы такой граф по сути строим, когда ищем увеличивающую цепь в алгоритме Куна)
Тогда в (H) найдется вершина (y) из (R), не насыщенная паросочетанием. Иначе, если такой вершины нет, то получается, что если рассмотреть вершины (H_L) (вершины левой доли, насыщенные паросочетанием), то для них не будет выполнено условие, что (|H_L| leq |N(H_L)|) (здесь (N(X)) — множество вершин, соединенным паросочетанием с (X)).
Тогда должен существовать путь из (x) в (y), и он будет увеличивающим для паросочетания (M), потому что из (R) в (L) мы всегда шли только по ребрам паросочетания. Проведя чередование вдоль этого пути, получим большее паросочетание, следовательно предположение индукции верно.
Минимальное вершинное покрытие
Задача. Дан граф. Назовем вершинным покрытием такое множество вершин, что каждое ребро графа инцидентно хотя бы одной вершине из множества. Необходимо найти вершинное покрытие наименьшего размера.
Следует заметить, что в общем случае это очень сложная задача, но для двудольных графов она имеет достаточно простое решение.
Теорема. (mid V_{min} mid le mid M mid), где (V_{min}) — минимальное вершинное покрытие, а (M) — максимальное паросочетание.
Доказательство. (mid V_{min} mid ge mid M mid), поскольку (M) — множество независимых ребер. Теперь приведем алгоритм, который строит вершинное покрытие размера (mid M mid). Очевидно, оно будет минимальным.
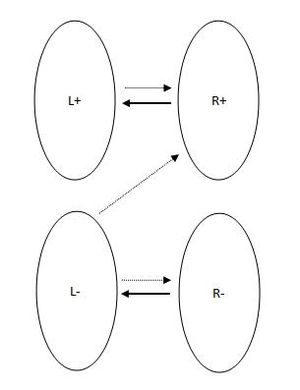
Алгоритм. Мысленно ориентируем ребра графа: ребра из (M) проведем из правой доли в левую, остальные — из левой в правую, после чего запустим обход в глубину из всех вершин левой доли, не включенных в (M).

Заметим, что граф разбился на несколько множеств: (L^+, L^-, R^+, R^-), где “плюсовые” множества — это множества посещенных в процессе обхода вершин. В графе такого вида не бывает ребер (L^+ rightarrow R^-), (L^- leftarrow R^+) по очевидным соображениям. Ребер (L^+ leftarrow R^-) не бывает, потому что в противном случае паросочетание (M) не максимальное — его можно дополнить ребрами такого типа.
[
L^- cup R^+ = V_{min}
]
Понятно, что данное множество покроет все ребра. Осталось выяснить, почему (L^- cup R^+). Это верно потому, что (L^- cup R^+) покрывает все ребра (M) ровно один раз (ведь ребра (L^- rightarrow R^+) не принадлежат (M)), а также потому, что в нем нет вершин, не принадлежащих (M) (для (L^-) это справедливо по определению, для (R^+) можно провести доказательство от противного с использованием чередующихся цепей).
Упражнение. Подумайте, как это можно применить к решению задачи о нахождении максимального независимого множества.
Для ноулайферов: матроиды
С весьма большой вероятностью матроиды вам никогда не пригодятся в школьных олимпиадах, однако, если вам совсем нечего делать, можете про них почитать.
Математика вообще занимается тем, что обобщает всякие объекты и старается формулировать все теоремы максимально абстрактно. Так, концепцию хороших подмножеств (паросочетаний) обобщает понятие матроида. Практическое применение — жадный алгоритм Радо-Эдмондса, который нужен для обоснования большого числа жадников, где нужно набрать какое-то подмножество минимального / максимального веса. Сам алгоритм максимально простой: давайте отсортируем эти объекты по весу и будем добавлять их в таком порядке в наше хорошее множество, если оно после добавления остается хорошим.
Применимо к паросочетаниям: пусть у вершин левой доли есть вес, и нам нужно набрать максимальное паросочетание минимального веса. Тогда выясняется, что можно просто отсортировать вершины левой доли по весу и пытаться в таком порядке добавлять их в паросочетание стандартным алгоритмом Куна.