Какой отрезок времени считается минимальным в физике?
Leon Polinezi
3 октября 2017 · 2,2 K
На самом деле вопрос не имеет смысла поскольку большинство физиков сейчас сходятся во мнении, что расстояние и время это не фундаментальные величины. Типа как температура есть мера кинетической энергии атомов и молекул, время и пространство появляется только на (относительно) макроскопическом уровне.
Не может существовать минимального интервала времени или расстояния поскольку их можно растянуть/сократить посредством перехода к другой системе отсчета (преобразования Лоренца).
Нарушений Лоренц-инвариантности не обнаружено, следовательно минимальных длин и времен быть не может.
718
Я понимаю,что не в тему,но хочу вставить свои 5 копеек.Температура не есть мера кинетической энергии молекулы. Она… Читать дальше
Комментировать ответ…Комментировать…
Я полагаю, что ответ на ваш вопрос – Планковское Время.
Это то время, за которое частица, без массы, пройдет планковскую длину.
Сразу скажу, что планковская длина, это некое минимальное расстояние, на котором само понятие длины перестает существовать. И это, примерно, 10^-35 метров.
Так вот, те крошечные доли крошечных долей секунды и будут – тем самым минимально… Читать далее
304
Комментировать ответ…Комментировать…
-
-
September 7 2010, 14:35
- Общество
- Cancel
Пружинный маятник
 |
Задача: Смещение груза пружинного маятника меняется с течением времени по закону x = A·sin(2π·t/T), где период T = 1 с. Через какое минимальное время, начиная с момента t = 0, потенциальная энергия маятника достигнет половины своего максимума? |
 |
Читаем: Смещение груза пружинного маятника с течением времени по закону x = A·sin(2π·t/T), где период T = 1 с. Пока, вроде всё понятно. Пружинный маятник – шарик, прикреплённый к пружинке. Колебания гармонические незатухающие. Силой тяжести, силой трения (как и многим другим) можно пренебречь. Через какое минимальное время, начиная с момента t = 0, потенциальная энергия маятника достигнет половины своего максимума? Найти аналитическое выражение для потенциальной энергии маятника. Проанализировав его, найти минимальное время, через которое потенциальная энергия достигнет половины своего максимума. |
 |
Думаем: Во-первых: почему минимальное время? Потому что имеет место колебательный процесс и потенциальная энергия изменяется тоже циклически, поэтому “половин максимума” может быть сколько угодно. Нам нужно найти первую :). Далее: Потенциальная энергия пружины описывает её “желание вернуться в исходное состояние” (т.е. не сжатое или не растянутое). Таким образом, потенциальная энергия маятника равна работе, которую должна совершить пружина для возвращение в исходное состояние: Подставив в это выражение x, мы найдём аналитическое выражение для потенциальной энергии маятника. |
 |
Решаем: Поскольку потенциальная энергия прямо пропорциональна квадрату синуса от времени (см. рассуждения выше), то она достигнет половины максимума (первый раз) тогда, когда sin(2π·t/T) = 1/√2 или когда 2π·t/T = π/4 (45°). Выразить время теперь не составит труда: t/T = 1/8, тогда t = T/8 = 1/8 сек. Ответ: минимальное время, через которое потенциальная энергия достигнет половины своего максимума – 1/8 секунды или 0.125 сек. |
 |
Примечание: Лишним не будет напоминание о том, что гармонические процессы присутствуют практически везде, а поэтому очень полезным будет знать наизусть уравнение гармонических колебаний и значение синусов и косинусов в определённых углах. Также нужно безошибочно строить графики синуса и косинуса. Будьте внимательны: в данной задаче синус был равен 1/√2, а это означало, что аргумент синуса равен π/4, а не t = π/4. Понять, в чём же дело, поможет такое упражнение: постройте на одном графике две функции: sin x и sin 2x. Затем посмотрите, чему равны оба синуса в точках x = 0, π/4 и π/2, и чему должен равняться x, чтобы синусы стали равны 1/2 и 1. Подсказка: аргумент первой функции – x, аргумент второй – 2x. |
Формула периода колебаний пружинного маятника в физике
Формула периода колебаний пружинного маятника
Определение
Период – это минимальное время, за которое совершается одно полное колебательное движение.
Обозначают период буквой $T$.
[T=frac{Delta t}{N}left(1right),]
где $Delta t$ – время колебаний; $N$ – число полных колебаний.
Уравнение колебаний пружинного маятника
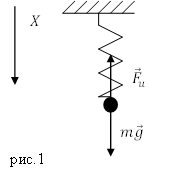
Рассмотрим простейшую колебательную систему, в которой можно реализовать механические колебания. Это груз массы $m$, подвешенный на пружине, коэффициент упругости которой равен $k $(рис.1). Рассмотри вертикальное движение груза, которое обусловлено действием силы тяжести и силы упругости пружины. В состоянии равновесия такой системы, сила упругости равна по величине силе тяжести. Колебания пружинного маятника возникают, когда систему выводят из состояния равновесия, например, слегка дополнительно растянув пружину, после этого маятник предоставляют самому себе.
Допустим, что масса пружины мала в сравнении с массой груза, при описании колебаний ее учитывать не будем. Началом отсчета будем считать точку на оси координат (X), которая совпадает с положением равновесия груза. В этом положении пружина уже имеет удлинение, которое обозначим $b$. Растяжение пружины происходит из-за действия на груз силы тяжести, следовательно:
[mg=kb left(2right).]
Если груз смещают дополнительно, но закон Гука еще выполняется, то сила упругости пружины становится равна:
[F_u=-kleft(x+bright)left(3right).]
Ускорение груза запишем, помня, что движение происходит по оси X, как:
[a=frac{d^2x}{dt^2}=ddot{x }left(4right).]
Второй закон Ньютона для груза принимает вид:
[mddot{x}=-kleft(x+bright)+mg left(5right).]
Учтем равенство (2), формулу (5) преобразуем к виду:
[mddot{x}=-kx-kb+mg=-kx-mg+mg=-kx left(6right).]
Если ввести обозначение: ${omega }^2_0=frac{k}{m}$, то уравнение колебаний запишем как:
[ddot{x}+{omega }^2_0x=0left(7right),]
где ${omega }^2_0=frac{k}{m}$ – циклическая частота колебаний пружинного маятника. Решением уравнения (7) (это проверяется непосредственной подстановкой) является функция:
[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(8right),]
где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ – амплитуда колебаний; ${(omega }_0t+varphi )$ – фаза колебаний; $varphi $ и ${varphi }_1$ – начальные фазы колебаний.
Формулы периода колебаний пружинного маятника
Мы получили, что колебания пружинного маятника описывается функцией косинус или синус. Это периодические функции, значит, смещение $x$ будет принимать равные значения через определенные одинаковые промежутки времени, которые называют периодом колебаний.
Обозначают период буквой T.
Еще одной величиной, характеризующей колебания является величина обратная периоду колебаний, ее называют частотой ($nu $):
[T=frac{1}{nu }left(9right).]
Период связан с циклической частотой колебаний как:
[T=frac{2pi }{{omega }_0}left(10right).]
Выше мы получали для пружинного маятника ${omega }_0=sqrt{frac{k}{m}}$, следовательно, период колебаний пружинного маятника равен:
[T=2pi sqrt{frac{m}{k}} left(11right).]
Формула периода колебаний пружинного маятника (11) показывает, что $T$ зависит от массы груза, прикрепленного к пружине и коэффициента упругости пружины, но не зависит от амплитуды колебаний (A). Данное свойство колебаний называют изохронностью. Изохронность выполняется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, появляется зависимость колебаний от амплитуды. Подчеркнем, что формула (11) для вычисления периода колебаний пружинного маятника справедлива при малых колебаниях.
Примеры задач на период колебаний
Пример 1
Задание. Пружинный маятник совершил 50 полных колебаний за время равное 10 с . Каков период колебаний маятника? Чему равна частота этих колебаний?
Решение. Так как период – это минимальное время необходимое маятнику для совершения одного полного колебания, то найдем его как:
[T=frac{Delta t}{N}left(1.1right).]
Вычислим период:
[T=frac{10}{50}=0,2 left(сright).]
Частота – величина обратная периоду, следовательно:
[nu =frac{1}{T}left(1.2right).]
Вычислим частоту колебаний:
[nu =frac{1}{0,2}=5 left(Гцright).]
Ответ. $1) T=0,2$ с; 2) 5Гц
Пример 2
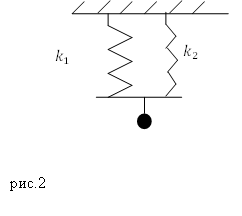
Задание.Две пружины, имеющие коэффициенты упругости $k_1$ и $k_2$ соединены параллельно (рис.2), к системе присоединен груз массы $M$. Каков период колебаний полученного пружинного маятника, если массами пружин можно пренебречь, сила упругости, действующая на груз, подчиняется закону Гука?
Решение. Воспользуемся формулой для вычисления периода колебаний пружинного маятника:
[T=2pi sqrt{frac{M}{k}} left(2.1right).]
При параллельном соединении пружин результирующая жесткость системы находится как:
[k=k_1{+k}_2left(2.2right).]
Это означают, что вместо $k$ в формулу для вычисления периода пружинного маятника подставим правую часть выражения (2.2), имеем:
[T=2pi sqrt{frac{M}{k_1{+k}_2}}.]
Ответ. $T=2pi sqrt{frac{M}{k_1{+k}_2}}$
Читать дальше: формула плеча силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Переправы.
Рассмотрите решение задач.
Задача 1. Минимальное время, которое необходимо, чтобы переплыть в лодке реку, равно $t_0$. Ширина русла реки равна $H$. Скорость течения реки постоянна в любом месте русла и в $beta$ раз больше скорости лодки ($beta > 1$), плывущей в стоячей воде.
1. Найдите скорость лодки в стоячей воде.
2. На какое расстояние снесет лодку за минимальное время переправы?
3. Определите наименьшее расстояние, на которое может снести лодку за время переправы.
4. Найдите время переправы лодки в том случае, когда ее сносит на минимальное расстояние.
Решение.
1. Минимальное расстояние между берегами – это ширина реки. Если направить лодку перпендикулярно берегу, то время ее движения будет минимальным
$t_0 = frac{H}{v_Л}$,
так как $H$ – минимально, а $v_Л$ – максимальна, тогда
$v_Л = frac{H}{t_0}$. (1)
2. Так как вектор скорости лодки направлен перпендикулярно берегу, то снос лодки зависит только от скорости течения. Скорость течения реки
$v_T = beta v_Л$
за время переправы лодку снесет на расстояние
$L = v_T cdot t_0 = beta v_Л cdot t_0 = beta H frac{t_0}{t_0} = beta H$
Снос лодки (за минимальное время движения) составит
$L = beta H$ (2)
3. Снос лодки во время переправы будет зависеть от двух факторов: скорости лодки в направлении течения и скорости лодки в направлении перпендикулярном берегу. Необходимо определиться с углом вектора скорости лодки. Относительно простым способом нахождения угла является графический метод. Скорость лодки относительно системы координат, связанной с берегом, равна векторной сумме скоростей течения и лодки (рис. 6.1). Из рисунка видно, что минимальное расстояние $L_{min}$ сноса лодки соответствует случаю, когда относительная скорость лодки направлена по касательной к окружности радиуса $v_Л$. Из подобия треугольников скоростей и расстояний, имеющих общий угол $alpha$, получим
$frac{L_{min}}{H} = frac{v}{v_Л}$,
и так как $v perp v_0$, находим
$L_{min} = Hfrac{v}{v_Л} = H frac{sqrt{v_T^2 – v_Л^2}}{v_Л} = Hfrac{sqrt{beta^2 frac{H^2}{t_0^2} − frac{H^2}{t_0^2}}}{H/t_0} = H sqrt{beta^2 − 1}$. (3)
4. Время переправы лодки, когда ее сносит на минимальное расстояние, зависит от проекции скорости лодки на ось $Oy$.
Проекция скорости лодки на $Oy$ равна
$v_y = v_Л cdot cosalpha$
С другой стороны
$cosalpha = frac{L_{min}}{sqrt{L_{min}^2 + H^2}} = frac{Hsqrt{beta^2 − 1}}{sqrt{H^2 (beta^2 − 1) + H^2}} = frac{sqrt{beta^2 − 1}}{beta}$.
Время переправы в этом случае
$t = frac{H beta}{v_Л sqrt{beta^2 − 1}} = frac{beta t_0}{sqrt{beta ^2 − 1}}$. (4)
Замечание 1. Минимальное время переправы лодки через руку будет в случае движения лодки перпендикулярной берегу.
Замечание 2. Минимальный снос лодки будет в случае, когда вектор скорости лодки будет перпендикулярен вектору относительной скорости лодки.
Замечание 3. Определение угла между вектором скорости лодки и (например) вертикалью, для минимального сноса при переправе через реку возможно следующими способами:
Через исследование функции. При переправе на другой берег
$H = v_Л cosalpha cdot t$ и $L = (v_T – v_Л sinalpha) cdot t$.
Составим уравнение траектории $L(H)$
$L = (v_T – v_Л sinalpha)frac{H}{v_Л cosalpha} = v_T frac{H}{v_Л cosalpha} – Htgalpha$.
Окончательно,
$L = v_T frac{H}{v_Л cosalpha} – H cdot tgalpha$.
Продифференцировав последнее уравнение по углу $alpha$ и, приравняв к нулю производную, найдем, при каких значениях угла $alpha$ расстояние $L$ будет минимальным.
$(frac{v_T H}{v_Л cosalpha} – Htgalpha)^/ = frac{v_T H sinalpha}{v_Л cos^2 alpha} − frac{H}{cos^2 alpha} = 0$,
$sinalpha = frac{v_Л}{v_T} = frac{1}{beta}$.
Через тригонометрическую единицу
$sin^2 alpha + cos^2 alpha = 1$,
Найдем
$cos alpha = frac{sqrt{beta^2 − 1}}{beta}$.
Методом дискриминанта.
Уравнение траектории перепишем в виде
$L = v_T frac{H}{v_Л cosalpha} – frac{Hsinalpha}{cosalpha}$
или
$Lcosalpha = beta H – Hsinalpha$.
Возведем уравнение в квадрат
$L^2 cos^2 alpha = beta^2 H^2 + H^2 sin^2 alpha – 2beta H^2 sinalpha$.
Воспользовавшись тригонометрической единицей
$sin^2alpha + cos^2alpha = 1$
Тогда
$L^2 (1 – sin^2alpha) = beta^2 H^2 + H^2 sin^2 alpha – 2beta H^2 sinalpha$
Мы получили квадратное уравнение относительно искомого угла $alpha$. Преобразуем его к «нормальному» (удобному виду).
$(L^2 + H^2) sin^2 alpha – 2beta H^2 sinalpha − (L^2 − (beta H)^2) = 0$.
Решение квадратного уравнения имеет вид:
$sinalpha_{1,2} = frac{beta H^2 pm sqrt{(beta H^2)^2) – (beta^2 H^2 – L^2)(L^2 + H^2)}}{L^2 + H^2}$.
При этом $D geq 0$:
$beta^2 H^4 – (beta^2 H^2 – L^2)(L^2 + H^2) = L^2 (L^2 − beta^2 H^2 + H^2) geq 0$.
При уменьшении $L$ уменьшается дискриминант. Минимальное значение $D = 0$. Тогда,
$L^2 = beta^2 H^2 – H^2$, и $L = H sqrt{beta^2 − 1}$,
что соответствует минимальному сносу.
Из рисунка видно, что
$cosalpha = frac{L_{min}}{sqrt{L_{min}^2 + H^2}} = frac{Hsqrt{beta^2 − 1}}{sqrt{H^2 (beta^2 − 1) + H^2}} = frac{sqrt{beta^2 − 1}}{beta}$.
Замечание 4. Если скорость течения меньше скорости лодки, то минимальный снос возможен только при движении лодки за минимальное время (см. решение 1).
Задачи для самостоятельного решения.
1. Катер, переправляясь через реку шириной $800$ м, двигался со скоростью $4$ м/с так, что время его переправы оказалось минимальным. На сколько будет снесен катер течением, если скорость течения реки равна $1,5$ м/с?
2. При переправе через реку шириной $60$ м надо попасть в точку, лежащую на $80$ м ниже по течению, чем точка старта. Лодочник управляет моторной лодкой так, что она движется точно к цели со скоростью $8$ м/с относительно берега. Какова при этом скорость лодки относительно воды, если скорость течения реки $2,8$ м/с?
3. Под каким углом к берегу должна идти моторная лодка, чтобы пересечь реку шириной $300$ м за минимальное время, если скорость лодки относительно воды $18$ км/ч, а скорость течения $2$ м/с? На сколько при этом сместится лодка вдоль берега?
4. На лодке переплывают реку, отправляясь из пункта $A$. Скорость лодки в стоячей воде $5$ м/с, скорость течения реки $3$ м/с, ширина реки $200$ м. а) В какой точке лодка пристанет к противоположному берегу, если держать курс перпендикулярно берегам? б) Какой курс следует держать, чтобы попасть в точку $B$, находящуюся на противоположном берегу напротив точки $A$? Для обоих случаев найдите время переправы.
5. Пловец хочет переплыть реку шириной $h$. Под каким углом $alpha$ к направлению течения реки он должен плыть, чтобы переправиться за наименьшее время? Какой путь он проплывет? Скорость течения реки $u$, скорость пловца относительно воды $v$. За какое время он переплывет реку по наикратчайшему пути?
6. Два катера вышли одновременно из пунктов $A$ и $B$ находящихся на разных берегах, причем пункт $B$ ниже по течению. Оба катера движутся по прямой $AB$, длина которой равна $l = 1$ км. Прямая $AB$ образует угол $alpha = 60^0$ с направлением скорости течения, которая равна $v = 2$ м/с. Катера встретились через $3$ мин после отхода от причалов. На каком расстоянии от пункта B произошла встреча?
7. Турист, сплавлявшийся на байдарке по реке, заметил, что поток несет его к середине упавшего и перегородившего ему путь дерева в тот момент, когда расстояние от носа байдарки до дерева было $S = 30$ м. Оценить, под каким углом к скорости течения он должен направить байдарку, чтобы обойти преграду. Скорость течения реки $u = 3$ км/ч, скорость байдарки относительно воды $6$ км/ч, длина дерева $l = 20$ м.
8. Скорость течения реки $5$ м/с, ее ширина $32$ м. Переправляясь через реку на лодке, скорость которой относительно воды $4$ м/с, рулевой обеспечил наименьший возможный снос лодки течением. Чему равен этот снос?
9. Из пункта $A$, расположенного на берегу реки, необходимо попасть в пункт в пункт $B$, находящийся на противоположном берегу, выше по течению на расстоянии $2$ км от перпендикуляра, проведенного из точки $A$ к противоположному берегу. Ширина реки $1$ км, максимальная скорость лодки относительно воды $5$ км/ч, а скорость течения реки $2$ км/ч. Сможет ли лодка переплыть за $30$ мин на другой берег, двигаясь по прямой $AB$.
10. Две моторные лодки, расположенные друг против друга на противоположных берегах прямолинейного участка шириной $H = 200$ м, совершают переправу так, что время переправы одной лодки и перемещение другой лодки за время ее переправы минимальны. Скорость $v = 5$ м/с каждой лодки относительно воды в $n = 2$ раза больше скорости течения. Найти минимальное расстояние между лодками и время $T$ их движения для сближения на это расстояние, если лодки начинают переправу одновременно. Скорость течения и скорость движения каждой лодки в течение переправы считать постоянными.
Если заметили неточность, ошибку, есть замечания, предложения, то пишите сюда
«Формула времени. Решение задач»
Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Виды движений: 1) равномерное (прямолинейное, криволинейное и по окружности), 2) равноускоренное (с постоянным ускорением), 3) гармоническое. Для каждого вида движения своя формула времени.
Время обозначается как t. Единица измерения времени – с (секунды).
Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.
При равноускоренном движении время равняется частному от деления разницы конечной и начальной скорости на ускорение: t = (v — v0) / a или частному от деления пути на разность конечной и начальной скорости: t = S / (v — v0).
Решение задач через формулу времени
Задача № 1.
Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?

Задача № 2.
Двигаясь с ускорением 5 м/с2 скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?
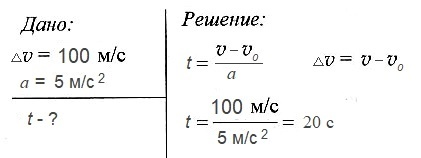
Задача № 3.
Пункты А и В находятся на берегу реки на некотором расстоянии друг от друга. Моторная лодка проходит расстояние АВ вниз по течению реки за время t1 = 3 ч, а плот то же расстояние – за время t0 =12 ч. Какое время t2 затратит моторная лодка на обратный путь?
Решение. Обозначим расстояние между пунктами А и В через L, скорость моторной лодки относительно воды через vл , а скорость течения через vт. Тогда t0 = L / vт , t1 = L / (vл + vт) , t2 = L / (vл — vт) . Исключая из записанной системы уравнений L, vл и vт
находим
Ответ: 6 ч.
Конспект урока «Формула времени. Решение задач».
Следующая тема: «».