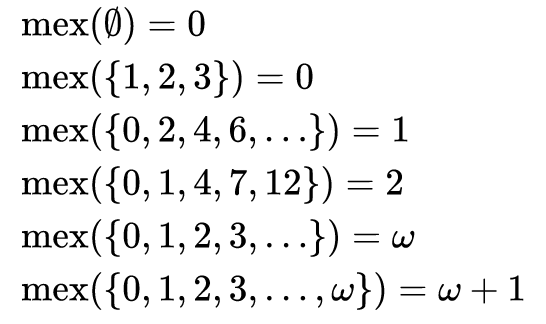/
/
/ Найти максимальное и минимальное число
Найти максимальное и минимальное число
Онлайн калькулятор поможет найти максимально большое число и минимальное число в строке, массиве. Находит минимальное и максимальное значение целых, дробных, натуральных чисел.
Минимальное и максимальное число |
|||
|
|||
|
|
|||
|
Разделитель групп разрядов Округлить до Число прописью |
Скачать калькулятор
Рейтинг: 3.8 (Голосов 9)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Среднее арифметическое взвешенное | Среднее геометрическое | Среднее гармоническое | Среднее квадратичное |
| Выборочная дисперсия | Среднее арифметическое | Медиана чисел | Расчет выборки |
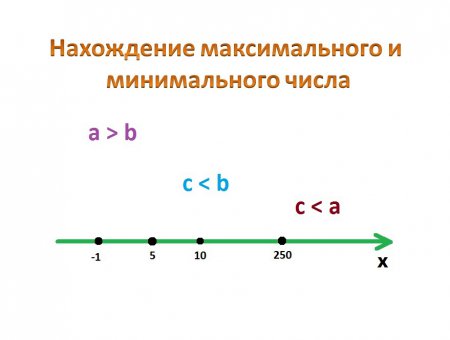
В этой статье мы рассмотрим сравнение чисел.
При сравнении чисел мы выбираем то число, которое банально больше. Ну, например, при сравнении числа 2 и 3 мы выберем максимальным числом 3, а минимальным 2. Графически 3 на числовой оси X находится правее, чем 2.
Я покажу один из самых рациональных алгоритмов выбора максимального и минимального числа, подходящего для общего случая. Это присвоение для переменных, выражающих минимальное и максимальное значение, значение одного из элементов заданных чисел/массива.
Ну теперь перейдем к практике.
Простая программка для сравнения 3 чисел(min_max_1):
Program Min_Max;
var a,b,c,min,max:integer;
begin
write(‘Введите 3 числа для сравнения (через пробел) : ‘);read(a,b,c);
min:=a;max:=a;
if b>max then max:=b;if b<min then min:=b;
if c>max then max:=c;if c<min then min:=c;
writeln(‘Максимальное число : ‘,max);
writeln(‘Минимальное число : ‘,min);
readln;
end.
Теперь подробнее.
var a,b,c,min,max:integer;
Ну смысл этой строки понятен, если хотите, можете выразить переменные через тип real, но особой разницы нету.
write(‘Введите 3 числа для сравнения (через пробел): ‘);read(a,b,c);
Мы вводим три числа через пробел, т.к. здесь оператор write.
min:=a;max:=a;
Здесь мы присваиваем переменным min и max значение одного из введенных чисел, если вы хотите разнообразия, то можете вместо переменной a написать b или c.
if b>max then max:=b; if b<min then min:=b;
if c>max then max:=c; if c<min then min:=c;
Здесь происходит сравнение оставшихся введенных переменные со значениями переменных min и max.
writeln(‘Максимальное число : ‘,max);
writeln(‘Минимальное число : ‘,min);
Ну здесь у нас происходит вывод ответа, думаю, объяснять где, какое значение выводится не надо=)
readln;
Это используется для того, чтобы мы увидели результат программы.
end.
Ну собственно логическое завершение программы=)
Дополнение:
- Кто хочет, чтобы экран самоочищался от результатов каждый раз, может добавить в начале программы
Uses crt;
и
Begin clrscr;
На чтение 3 мин Просмотров 1.3к. Опубликовано
В программировании часто возникает необходимость нахождения минимального значения в списке, кортеже или в числе. В этой статье мы рассмотрим, как найти минимальную цифру в числе в языке программирования Python. Рассмотрим несколько способов, которые позволят получить нужный результат.
Содержание
- Использование преобразования числа в строку и цикла for для нахождения минимальной цифры
- Использование функции min() для нахождения минимальной цифры
- Нахождение минимальной цифры числа с помощью арифметических операций
Использование преобразования числа в строку и цикла for для нахождения минимальной цифры
Для нахождения минимальной цифры в числе можно использовать цикл for. Алгоритм заключается в следующем:
- Преобразовать число в строку
- Пройти по всем символам строки с помощью цикла
for - Найти минимальное значение среди всех цифр
Пример реализации данного алгоритма:
num = 5823479
min_digit = 9 # Задаем начальное значение минимальной цифры
for digit in str(num):
if int(digit) < min_digit:
min_digit = int(digit)
print(min_digit) # Выведет 2Здесь мы задали начальное значение переменной min_digit как 9, так как любая возможная цифра в числе будет равна или меньше 9. Затем мы проходим по каждой цифре в числе, сравнивая ее с текущим минимальным значением min_digit. Если текущая цифра меньше min_digit, то мы обновляем значение min_digit. После прохождения цикла мы получаем минимальную цифру в числе.
Использование функции min() для нахождения минимальной цифры
Для нахождения минимальной цифры числа мы также можем использовать функцию min(), которая возвращает минимальный элемент в итерируемом объекте.
Для использования функции min() в качестве аргумента, нужно передать ей итерируемый объект, в данном случае строку, которая является представлением числа:
number = 123456
min_digit = min(str(number))
print(min_digit) # выведет 1Здесь мы используем функцию min() для нахождения наименьшего элемента в строке, которую мы получаем преобразованием числа в строку. Функция min() возвращает наименьший элемент, то есть минимальную цифру в числе.
Обратите внимание, что функция min() работает корректно только в том случае, если все символы в строке являются цифрами. Если в строке есть другие символы, они будут учитываться при вычислении минимального значения.
number = 1234a56
min_digit = min(str(number))
print(min_digit) # выведет aЗдесь в строке присутствует символ «a», который не является цифрой, поэтому функция min() возвращает его как минимальный элемент. Чтобы избежать таких ситуаций, следует предварительно проверять, что все символы в строке являются цифрами.
Нахождение минимальной цифры числа с помощью арифметических операций
Для нахождения минимальной цифры числа можно также использовать арифметические операции. Алгоритм заключается в извлечении последней цифры числа с помощью операции остатка от деления на 10 и сравнении ее с текущей минимальной цифрой. Если текущая цифра меньше минимальной, то она становится новой минимальной цифрой. После чего последняя цифра числа отсекается с помощью целочисленного деления и цикл повторяется пока после отсечения последней цифры с помощью целочисленного деления мы не получим 0.
Вот пример кода, который иллюстрирует этот подход:
number = 456128
min_digit = number % 10
while number > 0:
digit = number % 10
if digit < min_digit:
min_digit = digit
number //= 10
print("Минимальная цифра числа:", min_digit)В этом примере мы начинаем с инициализации переменной min_digit первой (т.е. последней) цифрой числа number, извлеченной с помощью операции остатка от деления на 10. Затем мы проходим по всем цифрам числа, пока число не достигнет нуля, извлекая каждую цифру таким же образом и сравнивая ее с текущей минимальной цифрой. Если текущая цифра меньше минимальной, то она становится новой минимальной цифрой.
Как найти минимальное число
Нахождение максимального и минимального значения.
В этой статье мы рассмотрим сравнение чисел.
При сравнении чисел мы выбираем то число, которое банально больше. Ну, например, при сравнении числа 2 и 3 мы выберем максимальным числом 3, а минимальным 2. Графически 3 на числовой оси X находится правее, чем 2.
Я покажу один из самых рациональных алгоритмов выбора максимального и минимального числа, подходящего для общего случая. Это присвоение для переменных, выражающих минимальное и максимальное значение, значение одного из элементов заданных чисел/массива.
Ну теперь перейдем к практике.
Простая программка для сравнения 3 чисел(min_max_1):
Program Min_Max;
var a,b,c,min,max:integer;
begin
write(‘Введите 3 числа для сравнения (через пробел) : ‘);read(a,b,c);
min:=a;max:=a;
if b>max then max:=b;if b<min then min:=b;
if c>max then max:=c;if c<min then min:=c;
writeln(‘Максимальное число : ‘,max);
writeln(‘Минимальное число : ‘,min);
readln;
end.
Теперь подробнее.
Ну смысл этой строки понятен, если хотите, можете выразить переменные через тип real, но особой разницы нету.
write(‘Введите 3 числа для сравнения (через пробел): ‘);read(a,b,c);
Мы вводим три числа через пробел, т.к. здесь оператор write.
Здесь мы присваиваем переменным min и max значение одного из введенных чисел, если вы хотите разнообразия, то можете вместо переменной a написать b или c.
if b>max then max:=b; if b<min then min:=b;
if c>max then max:=c; if c<min then min:=c;
Здесь происходит сравнение оставшихся введенных переменные со значениями переменных min и max.
Ну здесь у нас происходит вывод ответа, думаю, объяснять где, какое значение выводится не надо=)
MEX (Minimum EXcluded) Алгоритм поиска минимального отсутствующего числа
Добрый день. Сегодня хочется поговорить о том, как найти MEX (минимальное отсутствующие число во множестве).
Мы разберем три алгоритма и посмотрим на их производительность.
Добро пожаловать под cut
Предисловие
Перед тем как начать, хотелось бы рассказать — почему я вообще за этот алгоритм взялся?
Всё началось с задачки на OZON.
Как видно из задачи, в математике результатом работы функции MEX на множестве чисел является наименьшим значением из всего набора, который не принадлежит этому множеству. То есть это минимальное значение набора дополнений. Название «MEX» является сокращением для «Minimum EXcluded» значение.
И покопавшись в сети, оказалось, что нет общепринятого алгоритма нахождения MEX…
Есть решения в лоб, есть варианты с дополнительными массивами, графами, но, как-то всё это раскидано по разным углам интернета и нет единой нормальной статьи по этому поводу. Вот и родилась идея — написать эту статью. В этой статье мы разберем три алгоритма нахождения MEX и посмотрим, что у нас получиться по скорости и по памяти.
Код будет на языке C#, но в целом там не будет специфичных конструкций.
Базовый код для проверок будет таким.
И еще один момент в статье я часто упоминаю слово «массив», хотя более правильным будет «множество», то заранее хочу извиниться перед теми, кому будет резать слух данное допущение.
Примечание 1 на основе комментариев: Многие придрались к O(n), мол все алгоритмы O(n) и по фигу, что «O» везде разное и не даёт фактически сравнить количество итераций. То для душевного спокойствия поменяем O на T. Где T более-менее понятная операция: проверка или присвоение. Так, как я понимаю, всем будет проще
Примечание 2 на основе комментариев: мы рассматриваем случай когда исходное множество НЕупорядоченное. Ибо сортировка это множества — тоже требует времени.
1) Решение в лоб
Как нам найти «минимальное отсутствующие число»? Самый простой вариант – сделать счетчик и перебирать массив до тех пор, пока не найдем число равное счетчику.
Максимально базовый случай. Сложность алгоритма составляет T(n*cell(n/2))… Т.к. для случая нам нужно будет перебрать все числа т.к. совершить 15 операций. А для полностью заполного ряда из 100 числе 5050 операций… Так себе быстродейственность.
2) Просеивание
Второй по сложности вариант в реализации укладывается в T(n)… Ну или почти T(n), математики хитрят и не учитывают подготовку данных… Ибо, как минимум, — нам нужно знать максимальное число во множестве.
С точки зрения математики выглядит так.
Берется битовый массив S длинной m (где m – длина массива V) заполненный 0. И в один проход исходному множеству (V) в массиве (S) ставятся 1. После этого в один проход находим первое пустое значение. Все значения больше m можно просто игнорировать т.к. если в массиве «не хватает» значений до m, то явно будет меньше длины m.
Т.к. «математики» – хитрые люди. То они говорят, что алгоритм T(n) ведь проход по исходному массиву всего один…
Вот сидят и радуются, что такой крутой алгоритм придумали, но правда такова.
Первое — нужно пройтись по исходному массиву и отметить это значение в массиве S T1(n)
Второе — нужно пройтись по массиву S и найти там первую попавшеюся свободную ячейку T2(n)
Итого, т.к. все операции в целом не сложные можно упростить все расчеты до T(n*2)
Но это явно лучше решения в лоб… Давайте проверим на наших тестовых данных:
- Для случая : В лоб: 11 итераций, просеивание: 8 итераций
- Для случая : В лоб: 15 итераций, просеивание: 10 итераций
- Для случая : В лоб: 441 итерация, просеивание: 108 итерация
- Для случая : В лоб: 500500 итераций, просеивание: 2000 итераций
Давайте сделаем это, и оптимизируем код.
Что мы тут сделали. Во-первых, в 64 раза уменьшили количество оперативной памяти, которая необходима.
Во-вторых, оптимизировали финальную проверку: мы проверяем сразу блок на вхождение первых 64 значений: if (sieve[i] != maxInblock) и как только убедились в том, что значение блока не равно бинарным 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111, только тогда ищем уже вхождение на уровне блока: ((sieve[i] & (one << j)) == 0
В итоге алгоритм просеивание нам дает следующие результат:
- Для случая : просеивание: 8 итераций, просеивание с оптимизацией: 8 итераций
- Для случая : просеивание: 10 итераций, просеивание с оптимизацией: 11 итераций
- Для случая : просеивание: 108 итерация, просеивание с оптимизацией: 108 итерации
- Для случая : просеивание: 2000 итераций, просеивание с оптимизацией: 1056 итераций
T(n*3) мы превратили в T(n*2) + T(n / 64) в целом, чуть увеличили скорость, да еще объём оперативной памяти уменьшили аж в 64 раза. Что хорошо)
3) Сортировка
Как не сложно догадаться, самый простой способ найти отсутствующий элемент во множестве – это иметь отсортированное множество.
Самый быстрый алгоритм сортировки — это «quicksort» (быстрая сортировка), которая имеет сложность в T1(n log(n)). И итого мы получим теоретическую сложность для поиска MEX в T1(n log(n)) + T2(n)
Шикарно. Ничего лишнего.
Проверим количество итераций
- Для случая : просеивание с оптимизацией: 8, сортировка:
Вот у меня и возникла идея оптимизировать quicksort для поиска MEX. Данный вариант алгоритма я не находил в интернете, ни с точки зрения математики, и уж тем более с точки зрения программирования. То код будем писать с 0 по дороге придумывая как он будет выглядеть 😀
Но, для начала, давайте вспомним как вообще работает quicksort. Я бы ссылку дал, но нормальное пояснение quicksort на пальцах фактически нет, создается ощущение, что авторы пособий сами разбираются в алгоритме пока его рассказывают про него…
Так вот, что такое quicksort:
У нас есть неупорядоченный массив
Нам потребуется «случайное число», но лучше взять любое из массива, — это называется опорное число (T).
И два указателя: L1 – смотрит на первый элемент массива, L2 смотрит на последний элемент массива.
0, 12, 4, 7, 1
L1 = 0, L2 = 1, T = 1 (T взял тупа последние)
Первый этап итерации:
Пока работам только с указателем L1
Сдвигаем его по массиву вправо пока не найдем число больше чем наше опорное.
В нашем случае L1 равен 8
Второй этап итерации:
Теперь сдвигаем указатель L2
Сдвигаем его по массиву влево пока не найдем число меньше либо равное чем наше опорное.
В данном случае L2 равен 1. Т.к. я взял опорное число равным крайнему элементу массива, а туда же смотрел L2.
Третей этап итерации:
Меняем числа в указателях L1 и L2 местами, указатели не двигаем.
И переходим к первому этапу итерации.
Эти этапы мы повторяем до тех пор, пока указатели L1 и L2 не будет равны, не значения по ним, а именно указатели. Т.е. они должны указывать на один элемент.
После того как указатели сойдутся на каком-то элементе, обе части массива будут всё еще не отсортированы, но уже точно, с одной стороны «обединённых указателей (L1 и L2)» будут элементы, которые меньше T, а со второй больше T. Именно этот факт нам и позволяет разбить массив на две независимые группы, которые можно сортировать в разных потоках в дальнейших итерациях.
Проверим реальное количество итераций:
- Для случая : просеивание с оптимизацией: 8, сортировка: 11 итераций
- Для случая : просеивание с оптимизацией: 11 итераций, сортировка: 14 итераций
- Для случая : просеивание с оптимизацией: 108 итерации, сортировка: 1520 итераций
- Для случая : просеивание с оптимизацией: 1056 итераций, сортировка: 500499 итераций
Т.е. если мы точно знаем, что в одной из частей нет элементов больше определённого значения, то само это отсутствующие число нужно искать во второй части массива. В целом так работает алгоритм бинарного поиска.
В итоге у меня родилась мысль упростить quicksort для поиска MEX объединив его с бинарным поиском. Сразу скажу нам не нужно будет полностью отсортировывать весь массив только те части, в которых мы будем осуществлять поиск.
В итоге получаем код
Проверим количество итераций
- Для случая : просеивание с оптимизацией: 8, сортировка MEX: 8 итераций
- Для случая : просеивание с оптимизацией: 11 итераций, сортировка MEX: 4 итераций
- Для случая : просеивание с оптимизацией: 108 итерации, сортировка MEX: 1353 итераций
- Для случая : просеивание с оптимизацией: 1056 итераций, сортировка MEX: 999 итераций
Итого
Мы получили разные варианты поиска MEX. Какой из них лучше — решать вам.
В целом. Мне больше всех нравится просеивание, и вот по каким причинам:
У него очень предсказуемое время выполнения. Более того, этот алгоритм можно легко использовать в многопоточном режиме. Т.е. разделить массив на части и каждую часть пробегать в отдельном потоке:
Единственное, нужен lock при записи sieve[values[i] / size]. И еще — алгоритм идеален при выгрузке данных из базы данных. Можно грузить пачками по 1000 штук например, в каждом потоке и всё равно он будет работать.
Но если у нас строгая нехватка памяти, то сортировка MEX – явно выглядит лучше.
Pascal: Занятие № 4. Логический тип данных Boolean, поиск максимума и минимума в Паскале
Мы уже научились писать программы, основанные на линейных алгоритмах, в Паскале. И даже уже составляем нелинейные алгоритмы — с ветвлением — в которых используются логические выражения, которые принимают значения true или false .
Значения логического типа:
TRUE
FALSE
В примере ниже, на экран выводится результат логического выражения:
var A: integer; begin A := 5; write(A > 0); end.
Для записи результата логического выражения используется специальная логическая переменная, которая имеет в Паскале тип boolean и может также принимать одно из двух значений — true или false .
Посмотрим, как работает та же самая задача с логической переменной:
var A: integer; b: boolean; begin A := 5; b:=A > 0; write(b); end.
var a:boolean; begin a:=true; if a=true then writeln (‘истина’) else writeln(‘ложь’); end.
Для создания сложных условий используются специальные логические операции: and , or , not и xor .
[Название файла: task_bool1.pas ]
Рассмотрим пример с использованием логической операции XOR :
program Boolean; var x,y: integer; c :boolean; begin write(‘Введите X, Y: ‘); read(x,y); c := (Odd(x)) xor (Odd(y)); writeln(‘Только одна из переменных X и Y имеет нечетное значение — ‘, c); end.
Рассмотрим еще одно решение задачи в Паскале с использованием логической переменной:
[Название файла: task_bool2.pas ]
Рассмотрим решение более сложной задачи с переменной логического типа:
const a=348; var d_n, s_n, e_n: integer; flag:boolean; begin flag:=false; s_n:=a div 100; d_n:=((a mod 100)div 10); e_n:=a mod 10; if (s_n<>d_n) and (d_n<>e_n) and (e_n<>s_n) then flag:=true; writeln(flag); end.
Здесь каждый разряд получается путем использования операций деления нацело и взятия остатка от деления: s_n — это цифра сотого разряда, d_n — цифра десятого разряда, e_n — единицы.
[Название файла: task_bool3.pas ]
Минимальное и максимальное число в Паскале.
[Название файла: task_bool4.pas ]
При организации поиска минимального или максимального числа среди ряда чисел всегда на помощь приходит старенький «бабушкин» алгоритм:
- Представим ситуацию, что мы жарим пирожки, и уже нажарили целую большую горку; теперь надо выбрать из них самый большой, т.е. в нашем случае максимальный.
- Берем верхний пирожок, т.е. первый, и говорим, что он пока самый большой и откладываем его в сторону.
- Затем берем второй и сравниваем с самым большим, если этот второй пирожок оказывается больше — откладываем его на место «бывшего самого большого» и говорим, что теперь он самый большой.
- Берем следующий и повторяем действия. Так осуществляем данную процедуру со всеми пирожками.
Иногда в качестве первоначального максимума назначается самое малое возможное число (в зависимости от контекста задачи). А в качестве минимума — напротив, самое большое возможное число. Например, если сказано, что необходимо найти максимальное / минимальное среди положительных чисел, меньших 1000, то:
max:=integer.MinValue;; // минимальное среди типа Integer min:=integer.MaxValue;; // максимальное среди типа Integer
print(max(2,8)); // 8 print(min(2,8)); // 2
Рассмотрим теперь решение задачи на Паскале нахождения максимального числа:
var i, chislo, max:integer; begin // первое введенное число //сразу определяем как максимальное: readln(max); for i:=2 to 10 do begin readln (chislo); if chislo > max then max:= chislo end; writeln(max) end.
begin // первое введенное число //сразу определяем как максимальное: var maximum:=readInteger(); for var i:=2 to 10 do begin var chislo:=readInteger(); // используем стандартную функцию max(): maximum := max(chislo,maximum); end; writeln(maximum) end.
Аналогично осуществляется поиск минимального из чисел.
Для лучшего понимания темы поиска максимального или минимального значения предлагаем посмотреть видео урок:
[Название файла: task_max1.pas ]
[Название файла: task_max2.pas ]
[Название файла: task_max3.pas ]
Потренируйтесь в решении задач по теме, щелкнув по пиктограмме:
Допустим, у нас есть список [32, 54, 67, 21] и мы хотим найти наименьшее число в этом списке. Очевидно, что это 21. В этой статье мы разберем три способа поиска наименьшего числа при помощи Python: при помощи функции min(), метода sort() и перебора списка в цикле for.
1. Ищем наименьшее число с помощью функции min()
min() — это встроенная в Python функция, которая принимает список в качестве аргумента и возвращает наименьшее значение в нем. Пример:
# Задаем список
list1 = [-1, 65, 49, 13, -27]
print("list = ", list1)
# Находим наименьшее число
s_num = min(list1)
print("The smallest number in the given list is ", s_num)
# Результат:
# The smallest number in the given list is -27
Это один из самых простых способов найти наименьшее значение в списке. Все, что вам нужно сделать, это передать список функции min() в качестве аргумента.
2. Поиск наименьшего числа при помощи sort()
sort() – это встроенный в Python метод. Он не возвращает наименьшее значение, а сортирует список в порядке возрастания. Отсортировав список и получив доступ к его первому элементу, мы найдем наименьшее число. Давайте теперь перейдем к коду:
# Задаем список
list1 = [17, 53, 46, 8, 71]
print("list = ", list1)
# Сортируем список
list1.sort()
# Выводим в консоль наименьшее значение
print("The smallest number in the given list is ", list1[0])
# Результат:
# The smallest number in the given list is 8
3. Как найти наименьшее число при помощи цикла for
ls1 = []
total_ele = int(input(" How many elements you want to enter? "))
# Получаем элементы списка от пользователя
for i in range(total_ele):
n = int(input("Enter a number:"))
ls1.append(n)
print(ls1)
min = ls1[0]
# Находим наименьшее число
for i in range(len(ls1)):
if ls1[i] < min:
min = ls1[i]
print("The smallest element is ", min)
В приведенном выше коде мы используем два цикла for: один для получения элементов списка от пользователя, а второй — для поиска наименьшего числа из списка.
После получения элементов от пользователя мы определяем первый элемент списка (с индексом 0) как наименьшее число (min). Затем с помощью цикла for мы сравниваем каждый элемент списка с min. Если находится элемент меньше, это значение присваивается min.
Таким образом в итоге переменной min будет присвоено минимальное значение.
Результат работы вышеприведенного кода в консоли:
How many elements you want to enter? 4 Enter a number: 15 Enter a number: 47 Enter a number: 23 Enter a number: 6 [15, 47, 23, 6] The smallest number is 6
Заключение
Итак, мы рассмотрели три подхода к поиску наименьшего числа в списке. Надеемся, что вы все поняли. Если есть вопросы, не стесняйтесь, задавайте ниже.
Перевод статьи “3 Easy Methods to Find the Smallest Number in Python”.