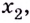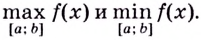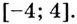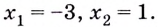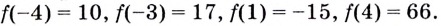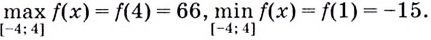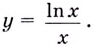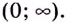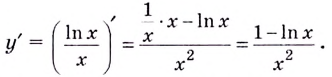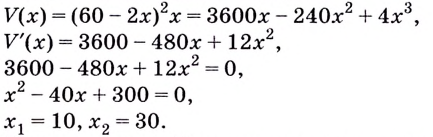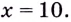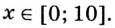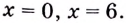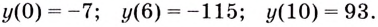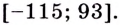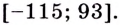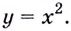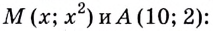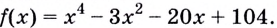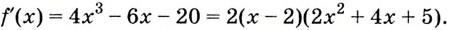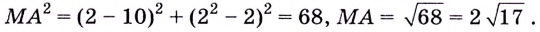На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно осуществить поиск и определить оптимальное значение какого-либо параметра или количество. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Обычно нами строится выражение этих значений в рамках некоторого интервала x, который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [a; b], так и открытый интервал (a; b), (a; b], [a; b), бесконечный интервал (a; b), (a; b], [a; b) либо бесконечный промежуток -∞; a, (-∞; a], [a; +∞), (-∞; +∞).
В этом материале мы расскажем, как найти наибольшее и наименьшее значение явно заданной функции с одной переменной y=f(x)y=f(x), чтобы вам не нужно было искать это самостоятельно онлайн.
Основные определения
Начнем, как всегда, с формулировки основных определений: какое значение называют максимальным и минимальным?.
Наибольшее значение функции y=f(x) на некотором промежутке x – это значение max y=f(x0)x∈X, которое при любом значении xx∈X, x≠x0 делает справедливым неравенство f(x)≤f(x0).
Минимальное значение функции y=f(x) на некотором промежутке x– это значение minx∈Xy=f(x0), которое при любом значении x∈X, x≠x0 делает справедливым неравенство f(Xf(x)≥f(x0).
Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее наибольшее число, которое она может принимать на известном интервале при абсциссе x0, а наименьшее – это самое маленькое принимаемое значение на том же интервале при x0.
Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0.
Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или то, что больше всего, значение на некотором промежутке именно в одной из стационарных точек.
Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.
Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы можем определить наибольшее или найти наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с интервалом, не имеющим конца. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения (мало и много). В этих случаях определить или найти наибольшее и/или наименьшее значение не представляется возможным.
Более понятными эти моменты станут после изображения на графиках:
Наибольшее и наименьшее значение функции на отрезке
Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения (max y и min y) в стационарных точках, расположенных на отрезке [-6;6].
Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [1;6] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [-3;2]. Они соответствуют наибольшему и наименьшему значению заданной функции.
Наибольшее и наименьшее значение функции на открытом интервале
Теперь посмотрим на четвертый рисунок. В нем функция принимает max y (наибольшее значение) и min y (наименьшее значение) в стационарных точках на открытом интервале (-6;6).
Если мы возьмем интервал [1;6), то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x, равном 6, если бы x=6 принадлежала интервалу. Именно этот случай нарисован на графике 5.
На графике 6 наименьшее значение данная функция приобретает в правой границе интервала (-3;2], а о наибольшем значении мы не можем сделать определенных выводов.
Наибольшее и наименьшее значение функции на бесконечности
На рисунке 7 мы видим, что функция будет иметь max y в стационарной точке, имеющей абсциссу, равную 1. Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y=3.
Если мы возьмем интервал x∈2; +∞, то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения. Если x стремится к 2, то значения функции будут стремиться к минус бесконечности, поскольку прямая x=2 – это вертикальная асимптота. Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y=3. Именно этот случай изображен на рисунке 8.
Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке
Как найти наибольшее и наименьшее значение функции на отрезке?
В этом пункте мы приведем последовательность действий, которую нужно выполнить, чтобы найти наибольшее значение функции на некотором отрезке или как найти наименьшее значение функции.
- Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.
- Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
- Далее выясним, какие стационарные точки попадут в заданный отрезок. Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
- Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x=a и x=b.
- У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.
Посмотрим, как правильно применить этот алгоритм при решении задач.
Условие: задана функция y=x3+4×2. Определите ее наибольшее и наименьшее значение на отрезках [1;4] и [-4;-1].
Решение:
Начнем с нахождения области определения данной функции. В этом случае ей будет множество всех действительных чисел, кроме 0. Иными словами, D(y): x∈(-∞; 0)∪0; +∞. оба отрезка, заданных в условии, будут находиться внутри области определения.
Теперь вычисляем производную функции согласно правилу дифференцирования дроби:
y’=x3+4×2’=x3+4’·x2-x3+4·x2’x4==3×2·x2-(x3-4)·2xx4=x3-8×3
Мы узнали, что производная функции будет существовать во всех точках отрезков [1;4] и [-4;-1].
Теперь нам надо определить стационарные точки функции. Сделаем это с помощью уравнения x3-8×3=0. У него есть только один действительный корень, равный 2. Он будет стационарной точкой функции и попадет в первый отрезок [1;4].
Вычислим значения функции на концах первого отрезка и в данной точке, т.е. для x=1, x=2 и x=4:
y(1)=13+412=5y(2)=23+422=3y(4)=43+442=414
Мы получили, что наибольшее значение функции max yx∈[1; 4]=y(2)=3 будет достигнуто при x=1, а наименьшее min yx∈[1; 4]=y(2)=3 – при x=2.
Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:
y(-1)=(-1)3+4(-1)2=3
Значит, max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.
Ответ: Для отрезка [1;4] – max yx∈[1; 4]=y(2)=3, min yx∈[1; 4]=y(2)=3, для отрезка [-4;-1] – max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.
См. на рисунке:
Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнавать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
- Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
- Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
- Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0, решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям. Их определяет вид интервала.
- Если интервал имеет вид [a;b), то нам надо вычислить значение функции в точке x=a и односторонний предел limx→b-0f(x).
- Если интервал имеет вид (a;b], то нам надо вычислить значение функции в точке x=b и односторонний предел limx→a+0f(x).
- Если интервал имеет вид (a;b), то нам надо вычислить односторонние пределы limx→b-0f(x),limx→a+0f(x).
- Если интервал имеет вид [a; +∞), то надо вычислить значение в точке x=a и предел на плюс бесконечности limx→+∞f(x).
- Если интервал выглядит как (-∞; b], вычисляем значение в точке x=b и предел на минус бесконечности limx→-∞f(x).
- Если -∞; b, то считаем односторонний предел limx→b-0f(x) и предел на минус бесконечности limx→-∞f(x)
- Если же -∞; +∞, то считаем пределы на минус и плюс бесконечности limx→+∞f(x), limx→-∞f(x).
- В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4-8 в первой части материала.
Условие: дана функция y=3e1x2+x-6-4. Вычислите ее наибольшее и наименьшее значение в интервалах -∞; -4, -∞; -3, (-3;1], (-3;2), [1;2), 2; +∞, [4; +∞).
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный (квадратичный) трехчлен, который не должен обращаться в 0:
x2+x-6=0D=12-4·1·(-6)=25×1=-1-52=-3×2=-1+52=2⇒D(y): x∈(-∞; -3)∪(-3; 2)∪(2; +∞)
Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.
Теперь выполним дифференцирование функции и получим:
y’=3e1x2+x-6-4’=3·e1x2+x-6’=3·e1x2+x-6·1×2+x-6’==3·e1x2+x-6·1’·x2+x-6-1·x2+x-6′(x2+x-6)2=-3·(2x+1)·e1x2+x-6×2+x-62
Следовательно, производные функции существуют на всей области ее определения.
Перейдем к нахождению стационарных точек. Производная функции обращается в 0 при x=-12. Это стационарная точка, которая находится в интервалах (-3;1] и (-3;2).
Вычислим значение функции при x=-4 для промежутка (-∞; -4], а также предел на минус бесконечности:
y(-4)=3e1(-4)2+(-4)-6-4=3e16-4≈-0.456limx→-∞3e1x2+x-6=3e0-4=-1
Поскольку 3e16-4>-1, значит, max yx∈(-∞; -4]=y(-4)=3e16-4. Это не дает нам возможности однозначно определяться с наименьшим значением функции. Мы можем только сделать вывод, что внизу есть ограничение -1, поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.
Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к -3 с левой стороны, мы получим только интервал значений:
limx→-3-03e1x2+x-6-4=limx→-3-03e1(x+3)(x-3)-4=3e1(-3-0+3)(-3-0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→-∞3e1x2+x-6-4=3e0-4=-1
Значит, значения функции будут расположены в интервале -1; +∞
Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке x=-12, если x=1. Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к -3 с правой стороны:
y-12=3e1-122+-12-6-4=3e425-4≈-1.444y(1)=3e112+1-6-4≈-1.644limx→-3+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1-3+0+3(-3+0-2)-4==3e1(-0)-4=3e-∞-4=3·0-4=-4
У нас получилось, что наибольшее значение функция примет в стационарной точке max yx∈(3; 1]=y-12=3e-425-4. Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до -4.
Для интервала (-3;2) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:
y-12=3e1-122+-12-6-4=3e-425-4≈-1.444limx→-3+03e1x2+x-6-4=-4limx→2-03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2-0+3)(2-0-2)-4==3e1-0-4=3e-∞-4=3·0-4=-4
Значит, max yx∈(-3; 2)=y-12=3e-425-4, а наименьшее значение определить невозможно, и значения функции ограничены снизу числом -4.
Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [1;2) наибольшее значение функция примет при x=1, а найти наименьшее невозможно.
На промежутке (2; +∞) функция не достигнет ни наибольшего, ни наименьшего значения, т.е. она будет принимать значения из промежутка -1; +∞.
limx→2+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2+0+3)(2+0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→+∞3e1x2+x-6-4=3e0-4=-1
Вычислив, чему будет равно значение функции при x=4, выясним, что max yx∈[4; +∞)=y(4)=3e114-4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y=-1.
Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.
Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
Наибольшим или наименьшим значением функции в определенной области называют наибольшее или наименьшее значение, которое достигает эта функция на указанной области.
Чтобы найти наибольшее или наименьшее значение функции в данной области, нужно решить задачу на экстремум, то есть найти производную заданной функции, приравнять её к нулю и найти точки, в которых производная функции обращается в нуль. Потом из этих точек нужно выбрать только те, которые входят в нашу заданную область. Затем нужно вычислить значение функций в этих точках. Кроме этого, нужно найти значение функции в граничных точках заданной области (если это отрезок) и сравнить их со значениями в точках экстремума. Потом можно сделать вывод о наименьшем или наибольшем значении функции в данной области.
Определить наименьшее и наибольшее значения функции y=x3−6×2+9y=x^3-6x^2+9 на отрезке [−1;2][-1;2].
Решение
Сначала вычисляем производную исходной функции:
y′=3×2−12xy’=3x^2-12x
Затем приравниваем ее к нулевому значению и решаем уравнение:
3×2−12x=03x^2-12x=0
x(3x−12)=0x(3x-12)=0
x1=0x_1=0
x2=4x_2=4
Затем — непосредственный поиск максимального и минимального значений функции на заданном отрезке. Важно отметить, что точка x=4x=4 не входит в заданный отрезок, поэтому значение функции в этой точке вычислять не требуется.
Находим значение функции в точке x1x_1:
f(0)=9f(0)=9
Кроме этого, нужно найти значение функции в граничных точках нашего отрезка, то есть в точках x=−1x=-1 и x=2x=2:
f(−1)=−1−6+9=2f(-1)=-1-6+9=2
f(2)=8−24+9=−7f(2)=8-24+9=-7
Получаем, что на заданном отрезке, наименьшее значение функции, которое равно −7-7, достигается в точке x=2x=2 , а наибольшее значение, равное 99, достигается в точке x=0x=0.
Найти наибольшее и наименьшее значение функции-параболы y=3x2y=3x^2 на всей области её определения.
Решение
Функция y=3x2y=3x^2 определена на всем интервале от минус бесконечности к плюс бесконечности. Найдем производную этой функции:
y′=6xy’=6x
Приравниваем производную к нулю:
6x=06x=0
x=0x=0
Точка x=0x=0 — единственный экстремум этой функции. В этой точке функция равна f(0)=0f(0)=0. Остается решить максимум это или минимум.
Так как график нашей функции это парабола, ветви которой направлены вверх (поскольку 3>03>0), то точка x=0x=0 — точка минимума этой функции. Следовательно, функция y=3x2y=3x^2 достигает своего минимального значения в точке x=0x=0 равного 00. Максимального значения эта функция не имеет. Оно только приближается к сколь угодно большому числу когда значение аргумента стремится к плюс или минус бесконечности.
Тест по теме “Наибольшие и наименьшие значения функции”
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).


Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:
– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
– если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
– если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
– если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью
Преподаватель который помогает студентам и школьникам в учёбе.
Наибольшее и наименьшее значения функции с примерами решения
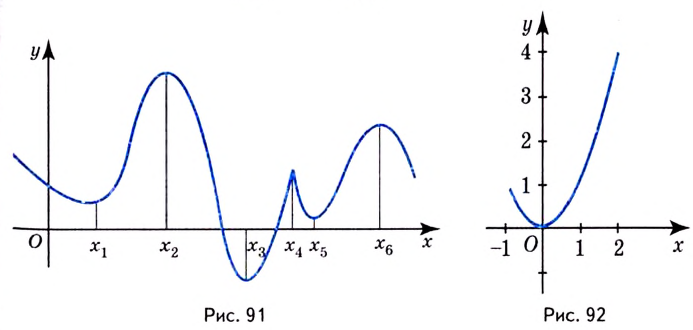
От максимумов и минимумов функции следует отличать её наибольшее и наименьшее значения на промежутке. Функция может иметь несколько максимумов (минимумов) на некотором промежутке (рис. 91), но не более одного наибольшего (наименьшего) значения. Функция может не иметь максимума (минимума) на промежутке, но иметь наибольшее (наименьшее) значение.
Например функция, график которой изображён на рисунке 91, наибольшее значение имеет в точке
Наибольшее и наименьшее значения функции тесно связаны с её областью значений. Если область значений непрерывной функции — промежуток 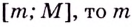
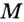
Поскольку непрерывная функция наибольшее и наименьшее значения может иметь только в точках экстремума или на концах отрезка, то для нахождения этих значений пользуются таким правилом.
Чтобы найти наибольшее и наименьшее значения непрерывной функции 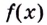
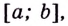
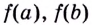
Записывают так:
Пример №1
Найдите наибольшее и наименьшее значения функции 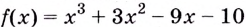
Решение:
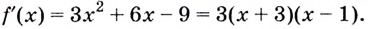
Из этих четырёх значений функции наименьшим является -15, а наибольшим — 66.
Ответ,
Пример №2
Найдите наибольшее и наименьшее значения функции
Решение:
Областью определения функции является промежуток
Если 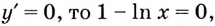
Если 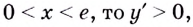
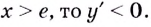

Поскольку на промежутке 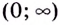
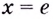
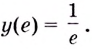
Ответ, 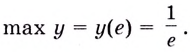
К нахождению наибольшего или наименьшего значений функции сводится решение многих прикладных задач.
Пример №3
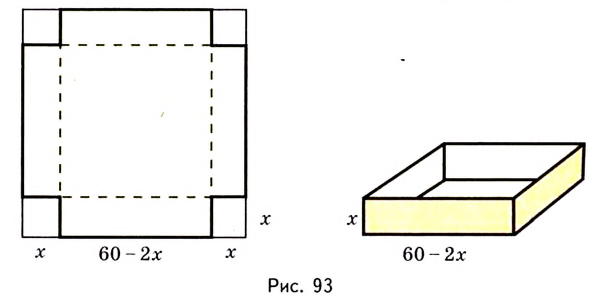
Есть квадратный лист жести со стороной 60 см. Найдите размеры квадратов, которые надо вырезать в углах данного листа, чтобы из полученной заготовки сделать коробку наибольшего объёма {рис. 93).
Решение:
Чтобы получить коробку (в форме прямоугольного параллелепипеда), надо вырезать равные квадраты в углах листа. Пусть 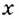
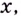
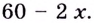
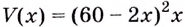
Надо исследовать математическую модель задачи: при каком значении 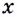
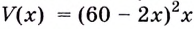
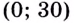
Значение 
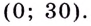
Поскольку при 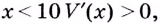
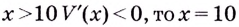
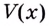
Ответ. Надо вырезать квадраты, стороны которых равны 10 см.
- Заказать решение задач по высшей математике
Пример №4
Найдите область значений функции 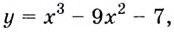
Решение:
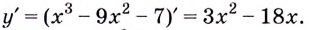
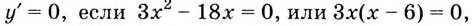
Найдём значение функции на концах промежутка 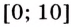
Заданная функция непрерывна, её наибольшее значение 93, а наименьшее -115, значит, область её значений — отрезок
Ответ.
Пример №5
Найдите кратчайшее расстояние от точки 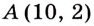
Решение:
Пусть ближайшая к 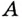
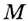
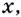
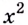
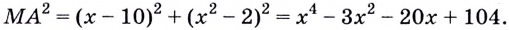
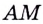
Уравнение 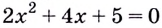
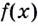
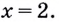
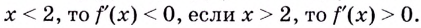
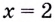
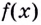
Наименьшее значение квадрата расстояния
Ответ.
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
- Прогрессии в математике – арифметическая, геометрическая
- Рациональная дробь
- Функция в математике
- Правило Лопиталя
- Вычисления в Mathematica с примерами
Математики и Data Science-специалисты должны хорошо разбираться в функциях. Предлагаем попрактиковаться в решении задач на обнаружение максимальных и минимальных значений у заданных функций.
Максимум
Задумываясь над тем, как найти максимальное значение функции, нужно четко понимать, с чем предстоит иметь дело. Для этого нужно запомнить такое определение:
Наибольшее значение функции y = f(x) на промежутке x – это max y = f(x0). Оно будет при любом значении x€ X, x≠x0 делает справедливым неравенство: f(x)≤f(x0).
Максимальное значение (максимум) – это точка на функции, в которой значение функции больше, чем в соседних «отметках».
Минимум
Наименьшее значение функции находить так же легко, как и наибольшее. Но сначала нужно понимать, что это такое.
Значение функции на отрезке будет считаться минимумом, если оно меньше, чем в соседних «отметках». Здесь действует такое определение:
Наименьшее значение функции y=f(x) на промежутке x – это miny=f(x0), которое при любом значении x€ X, x≠x0 делает справедливым неравенство f(x)≥f(x0).
Соответствующие определения являются достаточными и очевидными. Если говорить простыми словами, то максимум функции – это ее самое большое значение на заданном промежутке (участке) при абсциссе x0, а минимум – самое маленькое.
Стационарные точки
При решении вопроса о том, как найти наибольшее или наименьшее значение функции, стоит обратить внимание на так называемые «стационарные точки». Это – значения аргумента функции, при которых ее производная будет равняться нулю.
Стационарная точка – это «отметка», в которой расположен экстремум дифференцируемой функции. А именно – локальный минимум или максимум. В одной из таких «отметок» записанное выражение будет достигать своих предельных параметров.
Здесь рекомендуется запомнить следующее:
- Экстремум функции – это минимумы и максимумы.
- Если определить производную в точках экстремумов, она будет равно 0.
- Когда говорят «экстремумы», подразумевается значение функции. Если же речь идет об «отметках» экстремумов, рассматривать стоит x, в которых достигаются соответствующие пределы.
Этого достаточно для того, чтобы разобраться, как найти наибольшее на заданном отрезке у выражения. Для реализации поставленной задачи вовсе не обязательно составлять график. Поэтому сначала воспользуемся записями формул и вычислений.
План действий
Пример – дана функция f(x) на отрезке [a, b]. Наибольшее и наименьшее значение такой непрерывной функции достигаются в определенных местах. Это – критические точки. Там, где производная записанного выражения будет равно нулю.
Для того, чтобы найти наибольшие значения уравнения, потребуется придерживаться следующего алгоритма:
- Узнайте, какая перед вами функция. Для этого нужно проверить ее на непрерывность. В расчет обязательно берется заданный отрезок.
- Если запись непрерывная – ищем производную.
- После того, как найдем производную, приравниваем ее к нулю. Это поможет найти точки экстремумов. В результате получаются корни.
- Образовавшиеся корни – это критические точки. Нужно выбрать те «параметры», что относятся к промежутку [a, b].
- Вычислить значения функции на концах отрезка [a, b].
- Определить значения имеющегося выражения в критических «отметках».
Теперь понятно, как найти наибольшие функции на заданном отрезке. После произведенных подсчетов остается выбрать из результатов M (максимум) и m (минимум).
На отрезке
Разобравшись в тем, как найти наибольшие «параметры» выражения «на бумаге», стоит рассмотреть соответствующий процесс на графиках. Определять максимумы/минимумы в данном случае будет проще.
Первый график указывает на выражение, у которого точка минимума и максимума находятся в стационарных точках на промежутке [-6;6]. Соответствующие «пределы» обозначены жирным.
Второй график указывает на изменение отрезка. Теперь он будет [1;6]. Минимальное значение останется прежним. А вот максимальное – изменится. Оно образуется в правой части в точке с абсциссой. Поиск минимального «параметра» окажется в критической точке.
Задумываясь, как найти наименьшие или «самые крупные» параметры выражения на графике, можно также рассмотреть третий рисунок. Здесь функция принадлежала промежутку [-3;2]. Чтобы найти наибольшее и наименьшее в таком случае, предстоит учитывать абсциссы. В них достигаются соответствующие пределы.
Открытый интервал
Если промежуток задан конкретным числом, определить экстремумы будет не так сложно. Иначе происходит, если интервал открыт.
Здесь:
- Функция будет принимать максимум/минимум по значению в стационарных точках на открытом интервале от -6 до 6. Ответ – на 4 рисунке.
- Если взять отрезок [1;6), минимум будет достигнут в стационарной точке. А вот максимум – неизвестен. Связано это с тем, что 6 не принадлежит к заданному интервалу. Если бы «шестерка» относилась к соответствующему промежутку, ответ на вопрос относительно определения максимума оказался понятным. Максимальный параметр был бы в точке с абсциссой 6.
- На рисунке 6, задумываясь, как найти наименьшие «параметры», нужно обратить внимание на заданный интервал. Он равен (-3;2]. Минимум будет достигнут в правой границе. А вот максимум – не определен.
Найти значения на графиках обычно проще, чем «в чистых формулах». Соответствующие задания можно отыскать тут.
Бесконечность
Иногда значения функций нужно найти на бесконечном промежутке. Графически возможны такие ситуации:
На 7 рисунке функция достигает максимума в стационарной точке с абсциссой 1. Минимум окажется на границе интервала справа. На минус бесконечности значения приближаются к y=3 асимптотически.
Если взять интервал от 2-х до «плюс бесконечности», заданная функция не будет иметь ни максимумов, ни минимумов. Значения здесь стремятся к бесконечности. Связано это с тем, что x=2 является вертикальной асимптотой. Если абсцисса стремится к плюс бесконечности, значения будут асимптотически подходить к y=3. Соответствующий пример показан на рисунке 8.
Чтобы не приходилось долго разбираться с тем, как найти наименьшее у заданной функции, не путаться с тем, какие знаки производной использовать, а также легко строить графики, можно воспользоваться специальными онлайн калькуляторами. А еще – закончить тематические дистанционные онлайн курсы.