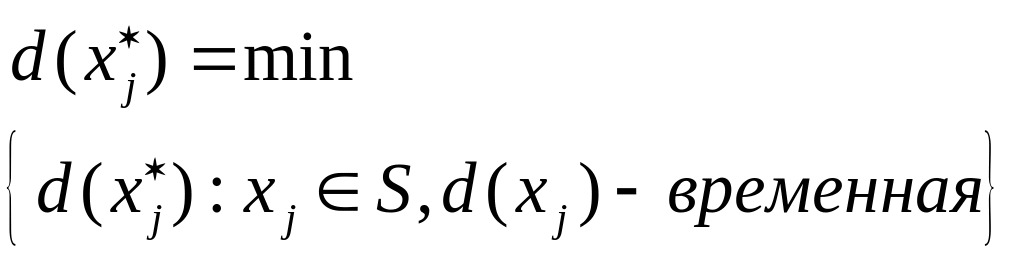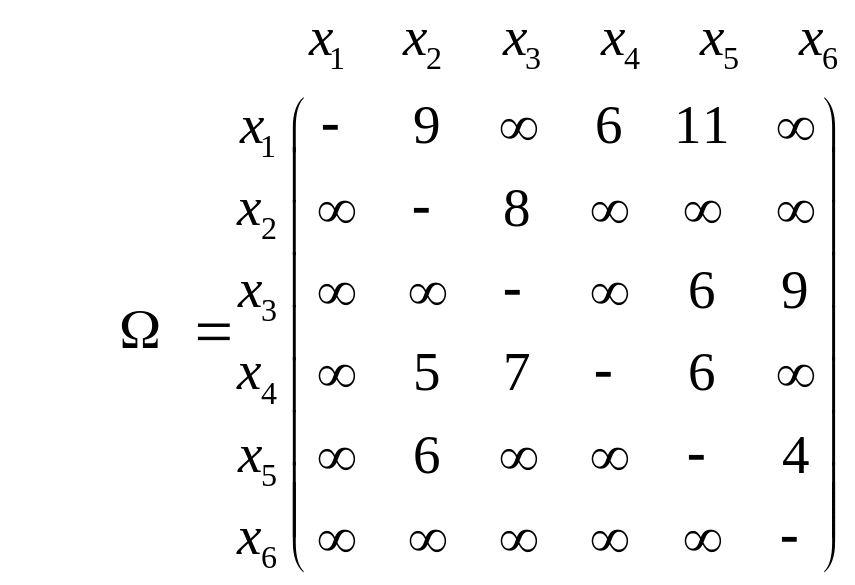Как найти минимальное значение пути

1. Нахождение кратчайших путей. Алгоритм Дейкстры

Пусть G={S,U,Ω}
– ориентированный граф со взвешенными
дугами. Обозначим s –
вершину – начало пути и t
– вершину конец пути. Веса дуг должны
быть положительными.

Этап
1.
Нахождение
длины кратчайшего пути.

Шаг 1.
Присвоение вершинам
начальных меток.

Полагаем

и считаем эту метку постоянной (постоянные
метки помечаются сверху звёздочкой).
Для остальных вершин

полагаем
d(x)
= ∞ и считаем эти метки временными. Пусть

обозначение
текущей вершины.

Шаг 2.
Изменение меток.

Для каждой вершины x_i
с временной меткой, непосредственно
следует за вершиной

,
меняет её метку в соответствии со
следующим правилом:

(1)

Шаг
3.
Превращение
метки
из
временной
в
постоянную.

Из всех вершин с временными метками
выбираем вершину

с наименьшим значением метки:

(2)

Превращаем
эту метку в постоянную и полагаем

.

Шаг 4.
Проверка на
завершение первого
этапа.

Если

–
длина кратчайшего пути от S
до t. В противном случае
происходит возвращение ко второму шагу.

Этап 2.
Построение кратчайшего
пути.

Шаг
5.
Последовательный
поиск
дуг
кратчайшего
пути.

Среди вершин, непосредственно
предшествующих вершине

с постоянными метками, находим вершину
х_i,
удовлетворяющую соотношению

.
(3)

Включаем дугу

в
искомый путь и полагаем

.

Шаг
6.
Проверка
на
завершение
второго
этапа.

Если

,
то кратчайший путь найден – его образует
последовательность дуг, полученных на
пятом шаге и выстроенных в обратном
порядке. В противном случае возвращаемся
к пятому шагу.

Пример. Задана весовая
матрица Ω сети G:

Рис.
34

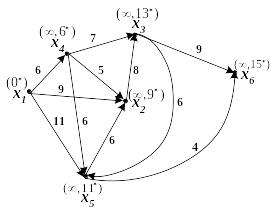
Найти
минимальный путь из вершины х₁
в вершину х₆ по алгоритму
Дейкстры.

Решение. Т.к. в данном
графе есть цикл между вершинами х₂,
х₃ и х₅, то
вершины графа нельзя упорядочить по
алгоритму Фалкерсона.

Этап 1.

Шаг 1.
Полагаем

.

Первая итерация.

Шаг 2.
Множество вершин, непосредственно
следующих за

с
временными метками

.
Пересчитываем временные метки этих
вершин.

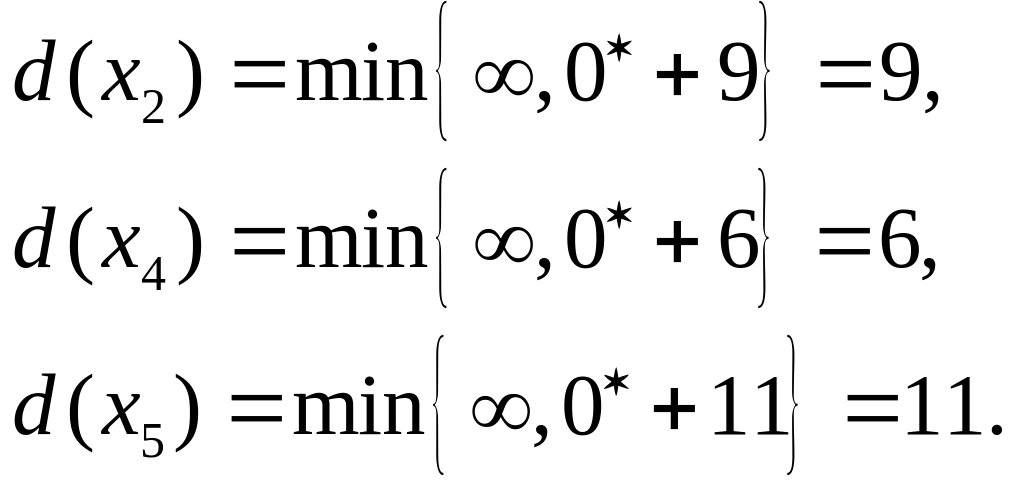
Шаг 3.
Одна из временных меток превращается
в постоянную:

Шаг 4.

происходит возвращение на второй шаг.

Вторая итерация.

Шаг 2.

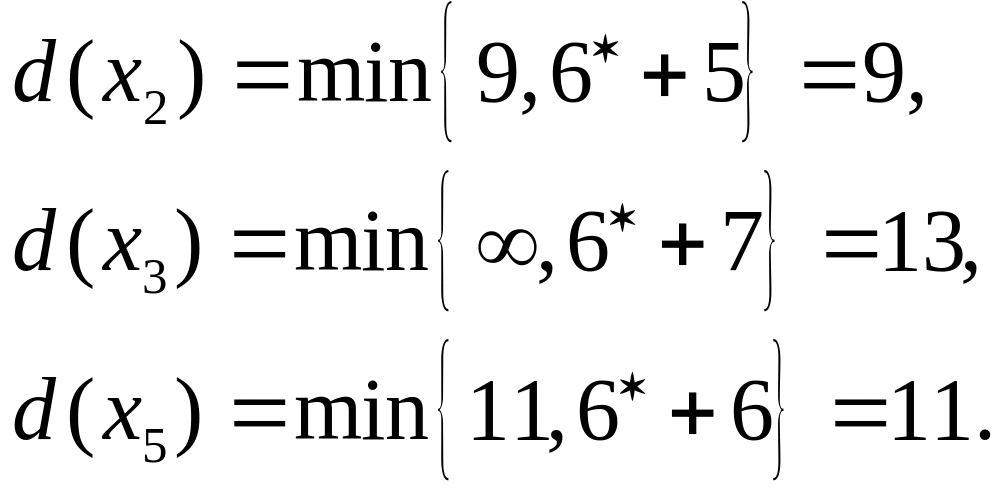
Шаг 3.

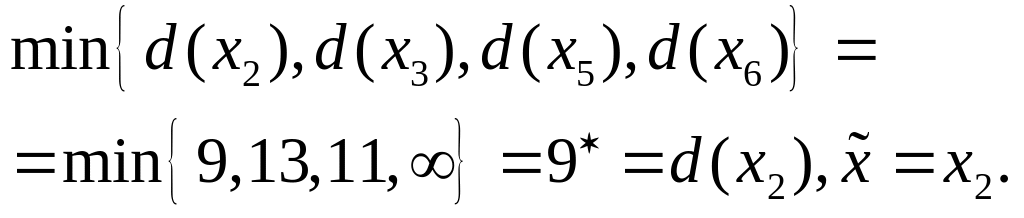
Шаг 4.

,
возвращение на 2-ой шаг.

Третья итерация.

Шаг 2.

Шаг 3.

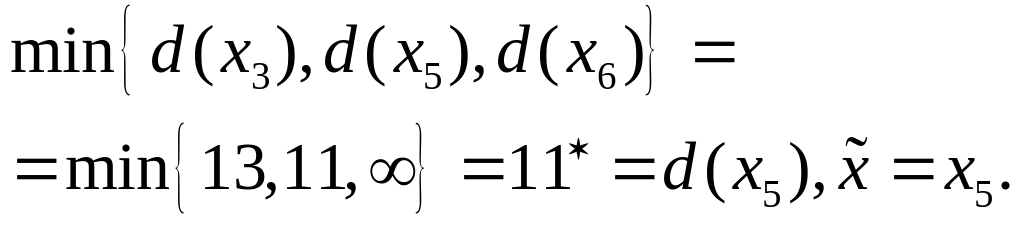
Шаг 4.

возвращение
на 2-ой шаг.

Четвёртая итерация.

Шаг 2.

Шаг 3.

Шаг 4.

возвращение
на 2-ой шаг.

Пятая итерация.

Шаг 2.

Шаг 3.

Шаг 4.

конец
1-го этапа.

Этап 2.

Первая итерация.

Шаг 5.
Составим множество вершин, непосредственно
предшествующих

с постоянными метками

Проверим для
этих двух вершин выполнение равенства
(3):

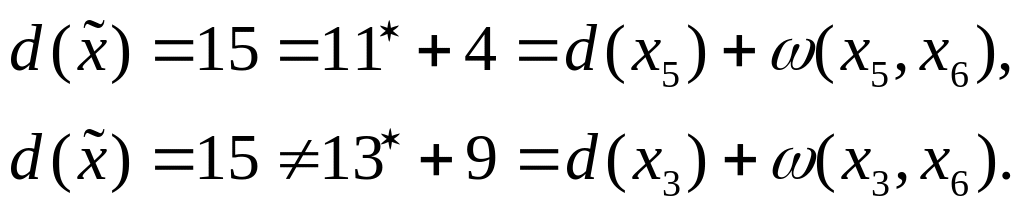
Включаем дугу
(х₅,х₆) в
кратчайший путь.

.

Шаг 6.

,
возвращение на 5-ый шаг.

Вторая
итерация.

Шаг5.

Включаем дугу (х₁,х₅)
в кратчайший путь.

Шаг 6.

,
завершение второго этапа.

Итак
кратчайший путь от вершины х₁
до вершины х₆
построен. Его длина (вес) равен 15, сам
путь образует следующая последовательность
дуг:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 августа 2021 года; проверки требуют 7 правок.

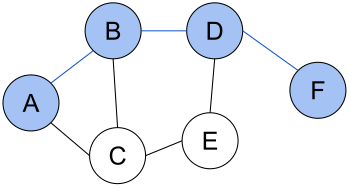
Кратчайший путь (A, B, D, F) между вершинами A и F в неориентированном графе без весов.

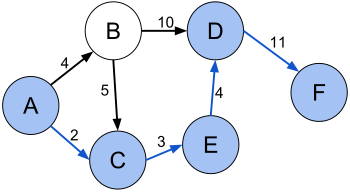
Кратчайший путь (A, C, E, D, F) между вершинами A и F во взвешенном ориентированном графе.

Зада́ча о кратча́йшем пути́ — задача поиска самого короткого пути (цепи) между двумя точками (вершинами) на графе, в которой минимизируется сумма весов рёбер, составляющих путь.

Задача о кратчайшем пути является одной из важнейших классических задач теории графов. Сегодня известно множество алгоритмов для её решения^[⇨].

У данной задачи существуют и другие названия: задача о минимальном пути или, в устаревшем варианте, задача о дилижансе.

Значимость данной задачи определяется её различными практическими применениями^[⇨]. Например, в GPS-навигаторах осуществляется поиск кратчайшего пути между точкой отправления и точкой назначения. В качестве вершин выступают перекрёстки, а дороги являются рёбрами, которые лежат между ними. Если сумма длин дорог между перекрёстками минимальна, тогда найденный путь самый короткий.

Определение[править | править код]

Задача поиска кратчайшего пути на графе может быть определена для неориентированного, ориентированного или смешанного графа. Далее будет рассмотрена постановка задачи в самом простом виде для неориентированного графа. Для смешанного и ориентированного графа дополнительно должны учитываться направления ребер.

Граф представляет собой совокупность непустого множества вершин и рёбер (наборов пар вершин). Две вершины на графе смежны, если они соединяются общим ребром. Путь в неориентированном графе представляет собой последовательность вершин $P=(v_{1},v_{2},ldots ,v_{n})in Vtimes Vtimes ldots times V$ , таких что $v_{i}$ смежна с $v_{{i+1}}$ для . Такой путь называется путём длиной из вершины $v_{1}$ в $v_{n}$ ( указывает на номер вершины пути и не имеет никакого отношения к нумерации вершин на графе).

Пусть $e_{{i,j}}$ — ребро соединяющее две вершины: $v_{i}$ и $v_{j}$ . Дана весовая функция , которая отображает ребра на их веса, значения которых выражаются действительными числами, и неориентированный граф . Тогда кратчайшим путём из вершины в вершину будет называться путь $P=(v_{1},v_{2},ldots ,v_{n})$ (где $v_{1}=v$ и $v_{n}=v'$ ), который имеет минимальное значение суммы $sum _{{i=1}}^{{n-1}}f(e_{{i,i+1}}).$ Если все ребра в графе имеют единичный вес, то задача сводится к определению наименьшего количества обходимых ребер.

Существуют различные постановки задачи о кратчайшем пути:

Задача о кратчайшем пути в заданный пункт назначения. Требуется найти кратчайший путь в заданную вершину назначения t, который начинается в каждой из вершин графа (кроме t). Поменяв направление каждого принадлежащего графу ребра, эту задачу можно свести к задаче о единой исходной вершине (в которой осуществляется поиск кратчайшего пути из заданной вершины во все остальные).
Задача о кратчайшем пути между заданной парой вершин. Требуется найти кратчайший путь из заданной вершины u в заданную вершину v.
Задача о кратчайшем пути между всеми парами вершин. Требуется найти кратчайший путь из каждой вершины u в каждую вершину v. Эту задачу тоже можно решить с помощью алгоритма, предназначенного для решения задачи об одной исходной вершине, однако обычно она решается быстрее.

В различных постановках задачи, роль длины ребра могут играть не только сами длины, но и время, стоимость, расходы, объём затрачиваемых ресурсов (материальных, финансовых, топливно-энергетических и т. п.) или другие характеристики, связанные с прохождением каждого ребра. Таким образом, задача находит практическое применение в большом количестве областей (информатика, экономика, география и др.).

Задача о кратчайшем пути с учётом дополнительных ограничений[править | править код]

Задача о кратчайшем пути очень часто встречается в ситуации, когда необходимо учитывать дополнительные ограничения. Наличие их может значительно повысить сложность задачи^[1]. Примеры таких задач:

Кратчайший путь, проходящий через заданное множество вершин. Можно рассматривать два ограничения: кратчайший путь должен проходить через выделенное множество вершин, и кратчайший путь должен содержать как можно меньше невыделенных вершин. Первое из них хорошо известна в теории исследования операций^[2].
Минимальное покрытие вершин ориентированного графа путями. Осуществляется поиск минимального по числу путей покрытия графа, а именно подмножества всех s-t путей, таких что, каждая вершина ориентированного графа принадлежит хотя бы одному такому пути^[3].
Задача о требуемых путях. Требуется найти минимальное по мощности множество s-t путей $P={p_{1},dots ,p_{m}}$ такое, что для любого $t_{i}in R$ найдется путь $p_{j}in P$ , накрывающий его. $R={t_{1},dots ,t_{k}}$ — множество некоторых путей в ориентированном графе G^[4].
Минимальное покрытие дуг ориентированного графа путями. Задача состоит в отыскании минимального по числу путей подмножества всех путей, такого, что каждая дуга принадлежит хотя бы одному такому пути. При этом возможно дополнительное требование о том, чтобы все пути исходили из одной вершины^[5].

Алгоритмы[править | править код]

В связи с тем, что существует множество различных постановок данной задачи, есть
наиболее популярные алгоритмы для решения задачи поиска кратчайшего пути на графе:

Алгоритм Дейкстры находит кратчайший путь от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса^[6].
Алгоритм Беллмана — Форда находит кратчайшие пути от одной вершины графа до всех остальных во взвешенном графе. Вес рёбер может быть отрицательным.
Алгоритм поиска A* находит маршрут с наименьшей стоимостью от одной вершины (начальной) к другой (целевой, конечной), используя алгоритм поиска по первому наилучшему совпадению на графе.
Алгоритм Флойда — Уоршелла находит кратчайшие пути между всеми вершинами взвешенного ориентированного графа^[6].
Алгоритм Джонсона находит кратчайшие пути между всеми парами вершин взвешенного ориентированного графа.
Алгоритм Ли (волновой алгоритм) основан на методе поиска в ширину. Находит путь между вершинами s и t графа (s не совпадает с t), содержащий минимальное количество промежуточных вершин (рёбер). Основное применение — трассировки электрических соединений на кристаллах микросхем и на печатных платах. Также используется для поиска кратчайшего расстояния на карте в стратегических играх.
Поиск кратчайшего пути на основе алгоритма Килдала^[7].

В работе (Черкасский и др., 1993)^[8] представлено ещё несколько алгоритмов для решения этой задачи.

Задача поиска кратчайшего пути из одной вершины во все остальные[править | править код]

В такой постановке задачи осуществляется поиск кратчайшего пути из вершины v во все остальные вершины на графе.

Невзвешенный ориентированный граф[править | править код]

Алгоритм	Сложность	Автор
Поиск в ширину	O(V+E)

Ориентированный граф с неотрицательными весами[править | править код]

Алгоритм	Сложность	Автор
–	O(V²EL)	Форд 1956
Алгоритм Беллмана — Форда	O(VE)	Беллман 1958^[9], Мур 1957^[10]
–	O(V² log V)	Данциг 1958, Данциг 1960, Minty (cf. Pollack&Wiebenson 1960), Whiting&Hillier 1960
Алгоритм Дейкстры со списком.	O(V²)	Leyzorek et al. 1957^[11], Дейкстра 1959^[12]
Алгоритм Дейкстры с модифицированной двоичной кучей	O((E + V) log V)	–
. . .	. . .	. . .
Алгоритм Дейкстры с использованием фибоначчиевой кучи	O(E + V log V)	Фридман&Тарьян 1984^[13], Фридман&Тарьян 1987^[14]
–	O(E log log L)	Джонсон 1982, Карлссон&Поблете 1983
Алгоритм Габова	O(E log_E/V L)	Габов 1983, Габов 1985
–	O(E + V√log L)	Ахуджа et al. 1990

Ориентированный граф с произвольными весами[править | править код]

Алгоритм	Сложность	Автор
Алгоритм Беллмана — Форда	O(VE)	Беллман^[9], Мур^[10]
Алгоритм Левита	O(VE)

Задача о кратчайшем пути между всеми парами вершин[править | править код]

Задача о кратчайшем пути между всеми парами вершин для невзвешенного ориентированного графа была поставлена Симбелом в 1953 году^[15], который обнаружил, что она может быть решена за линейное количество манипуляций (умножения) с матрицей. Сложность такого алгоритма O(V⁴).

Так же для решения данной задачи существуют другие более быстрые алгоритмы, такие как Алгоритм Флойда — Уоршелла со сложностью O(V³), и
Алгоритм Джонсона (является комбинацией алгоритмов Бэллмана-Форда и Дейкстры) со сложностью O(VE + V² log V).

Применение[править | править код]

Задача о поиске кратчайшего пути на графе может быть интерпретирована по-разному и применяться в различных областях. Далее приведены примеры различных применений задачи. Другие применения изучаются в дисциплине, которая занимается исследованием операций^[16].

Картографические сервисы[править | править код]

Алгоритмы нахождения кратчайшего пути на графе применяются для нахождения путей между физическими объектами на таких картографических сервисах, как карты Google или OpenStreetMap. В обучающем видео от Google можно узнать различные эффективные алгоритмы, которые применяются в данной сфере^[17].

Недетерминированная машина[править | править код]

Если представить недетерминированную абстрактную машину как граф, где вершины описывают состояния, а ребра определяют возможные переходы, тогда алгоритмы поиска кратчайшего пути могут быть применены для поиска оптимальной последовательности решений для достижения главной цели. Например, если вершинами являются состояния Кубика Рубика, а ребром представляет собой одно действие над кубиком, тогда алгоритм может быть применён для поиска решения с минимальным количеством ходов.

Сети дорог[править | править код]

Задача поиска кратчайшего пути на графе широко используется при определении наименьшего расстояния в сети дорог.

Сеть дорог можно представить в виде графа с положительными весами. Вершины являются дорожными развязками, а ребра дорогами, которые их соединяют. Веса рёбер могут соответствовать протяжённости данного участка, времени необходимому для его преодоления или стоимости путешествия по нему. Ориентированные ребра можно использовать для представления односторонних улиц. В таком графе можно ввести характеристику, которая указывает на то, что одни дороги важнее других для длительных путешествий (например автомагистрали). Она была формализована в понятии (идее) о магистралях^[18].

Для реализации подхода, где одни дороги важнее других, существует множество алгоритмов. Они решают задачу поиска кратчайшего пути намного быстрее, чем аналогичные на обычных графах.
Подобные алгоритмы состоят из двух этапов:

этап предобработки. Производится предварительная обработка графа без учёта начальной и конечной вершины (может длиться до нескольких дней, если работать с реальными данными). Обычно выполняется один раз и потом используются полученные данные.
этап запроса. Осуществляется запрос и поиск кратчайшего пути, при этом известны начальная и конечная вершина.

Самый быстрый алгоритм может решить данную задачу на дорогах Европы или Америки за доли микросекунды^[19].

Другие подходы (техники), которые применяются в данной сфере:

ALT
Arc Flags
Contraction hierarchies
Transit Node Routing
Reach based Pruning
Labeling

Постановка задачи линейного программирования[править | править код]

Пусть дан направленный граф (V, A), где V — множество вершин и A — множество рёбер, с начальной вершиной обхода s, конечной t и весами w_ij для каждого ребра (i, j) в A. Вес каждого ребра соответствует переменной программы x_ij.

Тогда задача ставится следующим образом: найти минимум функции $F=sum _{{ijin A}}w_{{ij}}x_{{ij}}$ , где $x_{{ij}}geq 0$ , при условии что для всех i и j выполняется следующее неравенство: $sum _{j}x_{{ij}}-sum _{j}x_{{ji}}={begin{cases}1,&{text{if }}i=s;\-1,&{text{if }}i=t;\0,&{text{ otherwise.}}end{cases}}$

См. также[править | править код]

IEEE 802.1aq
Транспортная сеть
Двунаправленный поиск

Примечания[править | править код]

↑ Применение теории графов в программировании, 1985.
↑ Применение теории графов в программировании, 1985, с. 138—139.
↑ Применение теории графов в программировании, 1985, с. 139—142.
↑ Применение теории графов в программировании, 1985, с. 144—145.
↑ Применение теории графов в программировании, 1985, с. 145—148.
↑ ¹ ² Дискретная математика. Комбинаторная оптимизация на графах, 2003.
↑ Применение теории графов в программировании, 1985, с. 130—131.
↑ Cherkassky, Goldberg, Radzik, 1996.
↑ ¹ ² Bellman Richard, 1958.
↑ ¹ ² Moore, 1957.
↑ M. Leyzorek, 1957.
↑ Dijkstra, 1959.
↑ Michael Fredman Lawrence, 1984.
↑ Fredman Michael, 1987.
↑ Shimbel, 1953.
↑ Developing algorithms and software for geometric path planning problems, 1996.
↑ Fast route planning.
↑ Highway Dimension, 2010.
↑ A Hub-Based Labeling Algorithm, 2011.
↑ Ladyzhensky Y., Popoff Y. Algorithm, 2006.

Литература[править | править код]

Евстигнеев В. А. Глава 3. Итеративные алгоритмы глобального анализа графов. Пути и покрытия // Применение теории графов в программировании / Под ред. А. П. Ершова. — Москва: Наука. Главная редакция физико-математической литературы, 1985. — С. 138—150. — 352 с.
Алексеев В.Е., Таланов В.А. Глава 3.4. Нахождения кратчайших путей в графе // Графы. Модели вычислений. Структуры данных. — Нижний Новгород: Издательство Нижегородского гос. университета, 2005. — С. 236—237. — 307 с. — ISBN 5–85747–810–8. Архивная копия от 13 декабря 2013 на Wayback Machine
Галкина В.А. Глава 4. Построение кратчайших путей в ориентированном графе // Дискретная математика. Комбинаторная оптимизация на графах. — Москва: Издательство “Гелиос АРВ”, 2003. — С. 75—94. — 232 с. — ISBN 5–85438–069–2.
Берж К. Глава 7. Задача о кратчайшем пути // Теория графов и её применения = Theorie des graphes et ses applications / Под ред. И. А. Вайнштейна. — Москва: Издательство иностранной литературы, 1962. — С. 75—81. — 320 с.
Ойстин Оре. Теория графов / Под ред. И. М. Овчинниковой. — Издательство наука, 1980. — 336 с. Архивная копия от 15 декабря 2013 на Wayback Machine
Виталий Осипов, Поиск кратчайших путей в дорожных сетях: от теории к реализации на YouTube.
Харари Ф. Глава 2. Графы // Теория графов / под ред. Г. П. Гаврилов — М.: Мир, 1973. — С. 27. — 301 с.
Cherkassky B. V., Goldberg A. V., Radzik T. Shortest paths algorithms: Theory and experimental evaluation (англ.) // Mathematical Programming — Springer Science+Business Media, 1996. — Vol. 73, Iss. 2. — P. 129–174. — ISSN 0025-5610; 1436-4646 — doi:10.1007/BF02592101
Ричард Беллман. On a routing problem // Quarterly of Applied Mathematics. — 1958. — Т. 16. — С. 87—90.
Dijkstra E. W. A note on two problems in connexion with graphs (англ.) // Numerische Mathematik / F. Brezzi — Springer Science+Business Media, 1959. — Vol. 1, Iss. 1. — P. 269—271. — ISSN 0029-599X; 0945-3245 — doi:10.1007/BF01386390
Moore E. F. The shortest path through a maze (англ.) // Proceedings of an International Symposium on the Theory of Switching (Cambridge, Massachusetts, 2–5 April 1957) — Harvard University Press, 1959. — Vol. 2. — P. 285—292. — 345 p. — (Annals of the Computation Laboratory of Harvard University; Vol. 30) — ISSN 0073-0750
M. Leyzorek, R. S. Gray, A. A. Gray, W. C. Ladew, S. R. Meaker, R. M. Petry, R. N. Seitz. Investigation of Model Techniques — First Annual Report — 6 June 1956 — 1 July 1957 — A Study of Model Techniques for Communication Systems (англ.). — Cleveland, Ohio: Case Institute of Technology, 1957.
Michael Fredman Lawrence, Роберт Андре Тарьян. Fibonacci heaps and their uses in improved network optimization algorithms (англ.) : journal. — Институт инженеров электротехники и электроники, 1984. — P. 338—346. — ISBN 0-8186-0591-X. — doi:10.1109/SFCS.1984.715934. Архивировано 11 октября 2012 года.
Michael Fredman Lawrence, Роберт Андре Тарьян. Fibonacci heaps and their uses in improved network optimization algorithms (англ.) // Journal of the Association for Computing Machinery : journal. — 1987. — Vol. 34, no. 3. — P. 596—615. — doi:10.1145/28869.28874.
Shimbel, Alfonso. Structural parameters of communication networks // Bulletin of Mathematical Biophysics. — 1953. — Т. 15, № 4. — С. 501—507. — doi:10.1007/BF02476438.
Sanders, Peter. Fast route planning. — Google Tech Talk, 2009. — 23 марта.. — «Шаблон:Inconsistent citations».
Chen, Danny Z. Developing algorithms and software for geometric path planning problems (англ.) // ACM Computing Surveys (англ.) (рус. : journal. — 1996. — December (vol. 28, no. 4es). — P. 18. — doi:10.1145/242224.242246.
Abraham, Ittai; Fiat, Amos; Goldberg, Andrew V.; Werneck, Renato F. Highway Dimension, Shortest Paths, and Provably Efficient Algorithms (англ.) // ACM-SIAM Symposium on Discrete Algorithms : journal. — 2010. — P. 782—793.
Abraham, Ittai; Delling, Daniel; Goldberg, Andrew V.; Werneck, Renato F. A Hub-Based Labeling Algorithm for Shortest Paths on Road Networks. Symposium on Experimental Algorithms] (англ.) : journal. — 2011. — P. 230—241.
Kroger, Martin. Shortest multiple disconnected path for the analysis of entanglements in two- and three-dimensional polymeric systems (англ.) // Computer Physics Communications (англ.) (рус. : journal. — 2005. — Vol. 168, no. 168. — P. 209—232. — doi:10.1016/j.cpc.2005.01.020.
Ladyzhensky Y., Popoff Y. Algorithm to define the shortest paths between all nodes in a graph after compressing of two nodes. Proceedings of Donetsk national technical university, Computing and automation. Vol.107. Donetsk (англ.) : journal. — 2006. — P. 68—75..^{[источник не указан 925 дней]}

Источник

Алгоритм Дейкстры. Разбор Задач

Время на прочтение
7 мин

Количество просмотров 35K

Поиск оптимального пути в графе. Такая задача встречается довольно часто и в повседневной жизни, и в мире технологий. Справиться с такими вызовами помогает подход, который должен быть в арсенале каждого программиста — алгоритм Дейкстры.

Если вы хотите найти ответить на вопросы, чем этот алгоритм лучше BFS (поиска в ширину), при каких условиях алгоритм применим, и какие теоретические и практические задачи можно с его помощью решать, читайте далее.

Введение

Алгоритм Дейкстры работает на ориентированных (с некоторыми дополнениями и на неориентированных) графах, и призван искать кратчайшие пути между заданной вершиной и всеми остальными вершинами в графе.

Как правило, граф обозначают как набор вершин и рёбер где число рёбер может быть задано , а вершин числом

Для каждого ребра в графе задан неотрицательный вес , а также вершина, из которой осуществляется поиск оптимальных путей.

Алгоритм Дейкстры может найти кратчайший путь между вершинами и в графе, только если существует хотя бы один путь между этими вершинами. Если это условие не выполняется, то алгоритм отработает корректно, вернув значение “бесконечность” для пары несвязанных вершин.

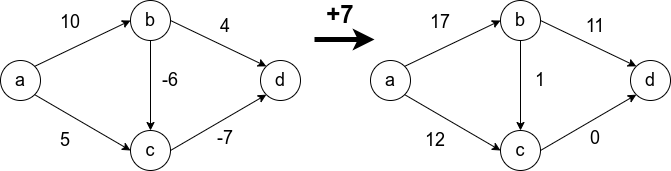
Условие неотрицательности весов рёбер крайне важно и от него нельзя просто избавиться. Не получится свести задачу к решаемой алгоритмом Дейкстры, прибавив наибольший по модулю вес ко всем рёбрам. Это может изменить оптимальный маршрут. На рисунке видно, что в первом случае оптимальный путь между и (сумма рёбер на пути наименьшая) изменяется при такой манипуляции. В оригинале путь проходит через , а после добавления семёрки ко всем рёбрам, оптимальный путь проходит через

Как ведёт себя алгоритм Дейкстры на исходном графе, мы разберём, когда выпишем алгоритм. Но для начала зададимся другим вопросом: “почему не применить поиск в ширину для нашего графа?”. Известно, что метод BFS находит оптимальный путь от произвольной вершины в ориентированном графе до любой другой вершины, но это справедливо только для рёбер с единичным весом.

Свести задачу к решаемой BFS можно, но если заменить все рёбра неединичной длины рёбрами длины , то граф очень разрастётся, и это приведёт к огромному числу действий при вычислении оптимального маршрута.

Чтобы этого избежать предлагается использовать алгоритм Дейкстры. Опишем его:

Инициализация:

Основный цикл алгоритма:

Пока все вершины не исследованы (или формально ), повторяем:

В итоге исполнения этого алгоритма, массив будет содержать все оптимальные пути, исходящие из .

Примеры работы

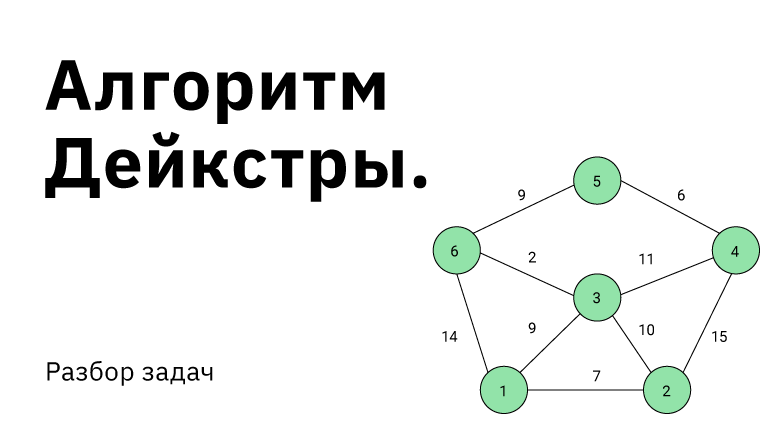
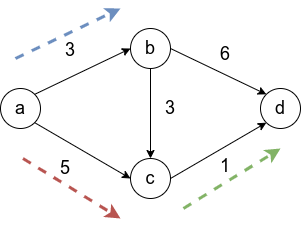
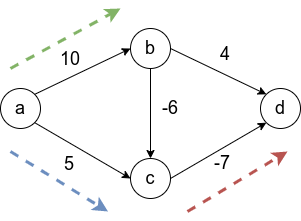
Рассмотрим граф выше, в нём будем искать пути от до всего остального.

Первый шаг алгоритма определит, что кратчайший путь до проходит по направлению синей стрелки и зафиксирует кратчайший путь. Второй шаг рассмотрит, все возможные варианты $inline A[v] + l_{vw}$ и окажется, что оптимальный вариант двигаться вдоль красной стрелки, поскольку меньше, чем и Добавляется длина кратчайшего пути до . И наконец, третьим шагом, когда три вершины уже лежат в , остается рассмотреть только два ребра и выбрать, лежащее вдоль зеленой стрелки.

Теперь рассмотрим граф с отрицательными весами, упомянутый выше. Напомню, алгоритм Дейкстры на таком графе может работать некорректно.

Первым шагом отбирается ребро вдоль синей стрелки, поскольку это ребро наименьшего веса из исходной вершины. Затем выбирается ребро Это зафиксирует навсегда неверный путь от к , в то время как оптимальный путь проходит через центр с отрицательным весом. Последним шагом, будет добавлена вершина .

Оценка сложности алгоритма

К этому моменту мы разобрали сам алгоритм, ограничения, накладываемые на его работу и ряд примеров его применения. Давайте упомянем какова вычислительная сложность этого алгоритма, поскольку это пригодится нам для решения задач, ради которых затевалась эта статья.
Базовый подход, основанный на циклах, предполагает проход по всем рёбрам каждого узла, что приводит к сложности .

Эффективная реализация предполагает использование кучи. Об этой структуре данных можно сказать коротко: она позволяет выполнять две операции за логарифмическое время. Первая операция — получение узла в дереве, с наименьшим ключом, и, вторая операция, вставка нового узла в дерево с новым ключом.

Что еще можно сказать о куче:

это сбалансированное бинарное дерево,
ключ текущего узла всегда меньше, либо равен ключей дочерних узлов.

Интересную задачу с использованием куч я разбирал ранее в этом посте.

Используя кучу в алгоритме Дейкстры, где в качестве ключей используются расстояния от вершины в неисследованной части графа (в алгоритме это ), до ближайшей вершины в уже покрытом (это множество вершин ), можно сократить вычислительную сложность до Доказательство справедливости этих оценок я оставляю за пределами этой статьи.

Далее перейдём к разбору задач!

Задача №1

Будем называть узким местом пути в графе ребро максимальной длины в этом пути. Путём с минимальным узким местом назовём такой путь между вершинами и , что не существует другого пути , чьё узкое место меньше по длине. Требуется построить алгоритм, который вычисляет путь с минимальным узким местом для двух данных вершин в графе. Асимптотическая сложность такого алгоритма должна быть

Решение

По условию задачи ребро с большим весом трактуется как узкое место. Вес в этом случае можно воспринимать как цену за проход по ребру. В результате решения задачи хотелось бы получить алгоритм, способный строить маршруты между узлами так, чтобы, если мы захотим провести любой другой путь, он будет содержать более тяжелые рёбра.

В случае классической задачи, поиска пути минимальной длины между двумя вершинами графа, мы поддерживаем в каждой посещенной алгоритмом вершине графа минимальную длину пути до этой вершины. Здесь стоит оговориться, что будем именовать множество посещенными вершинами, а V - X часть графа, для которой еще нужно найти величину пути или узкого места.

В отличии от классического алгоритма, решение этой задачи должно поддерживать величину актуального узкого места пути, приводящего в вершину v in X . А при добавлении новой вершины из V - X , мы должны смотреть не увеличивает ли ребро (v,u_1) величину узкого места пути, которое теперь приводит в u_1 .
Если ребро увеличивает узкое место, то лучше рассмотреть вершину u_2 , ребро до которой легче (v,u_1) . Поиск неувеличивающих узкое место ребёр нужно осуществлять не только среди соседей определенного узла , но и среди всех v in X , поскольку отдавая предпочтение вершине, путь в которую имеет наименьшее узкое место в данный момент, мы гарантируем, что мы не ухудшаем ситуацию для других вершин.

Последнее можно проиллюстрировать примером: если путь, оканчивающийся в вершине имеет узкое место величины , и есть вершина с ребром (p,q) веса , и с ребром (p,r) веса , то предпочтение отдаётся , алгоритм даст верный результат в обоих случая, если существует (q,r) веса или веса .

В результате разбора выше, предлагается руководствоваться следующей формулой при выборе очередной вершины из непосещенных и обновлении величин, которые мы поддерживаем.

$A(u) = min_{v in X}left(max left[A(v), wleft(v,uright)right]right), , u in V - X$

Стоит пояснить, что поиск по v in X осуществляется, только для существующих связей (v,u), а это вес ребра (v,u) .

Задача №2

Предлагается решить более практическую задачу. Пусть городов, между ними существуют пути, заданные массивом edges[i] = [city_a, city_b, distance_ab], а также дано целое число mileage.

Требуется найти такой город из данных, из которого можно добраться до наименьшего числа городов не превысив mileage.

Стоит отметить, что граф неориентированый, т.е. по пути между городами можно двигаться в обе стороны, а длина пути между городами a и c может быть получена как сумма длин путей a -> b и b -> c, если есть маршрут a -> b -> c

Решение

С решением данной проблемы нам поможет алгоритм Дейкстры и описанная выше реализация с помощью кучи. Поставщиком этой структуры данных станет библиотека heapq в Python.

Будем использовать алгоритм Дейкстры для того, чтобы подсчитать количество соседних городов, расстояние до которых меньше mileage, для каждого из городов. Соберем количества соседей в в одном месте и найдем минимум из них.

Поскольку наш граф неориентированный, то из любой его вершины можно добраться до произвольной вершины . Будем использовать алгоритм Дейкстры для того, чтобы для каждого из городов в графе построить кратчайшие пути до всех остальных городов, мы это уже умеем делать в теории. И чтобы, оптимизировать этот процесс, будем в его течении сразу отвергать пути, которые превышают mileage, а не делать постфактум, когда все пути получены.

Давайте опишем функцию решения:

def least_reachable_city(n, edges, mileage):
        """
        входные параметры:
            n --- количество городов,
            edges --- тройки (a, b, distance_ab),
            mileage --- максимально допустимое расстояние между городами 
            для соседства
        """
        # заполняем список смежности (adjacency list), в нашем случае это 
        # словарь, в котором ключи это города, а значения --- пары 
        # (<другой_город>, <расстояние_до_него>)

        graph = {}
        for u, v, w in edges:
            if graph.get(u, None) is None:
                graph[u] = [(v, w)]
            else:
                graph[u].append((v, w))
            if graph.get(v, None) is None:
                graph[v] = [(u, w)]
            else:
                graph[v].append((u, w))
        
        # локально объявим функцию, которая будет считать кратчайшие пути в 
        # графе от вершины, до всех вершин, удовлетворяющих условию
        def num_reachable_neighbors(city):
            # создаем кучу, из одного элемента с парой, задающей нулевую 
            # длину пути до самого исходного города
            heap = [(0, city)]
            # и массив, содержащий города и кратчайшие 
            # расстояния до них от исходного
            distances = {}
            # затем, пока куча не пуста, извлекаем ближайший 
            # от посещенных городов город
            while heap:
                currDist, neighb = heapq.heappop(heap)
                # если кратчайшее ребро ведет к городу, где мы уже знаем 
                # оптимальный маршрут, то завершаем итерацию
                if neighb in distances:
                    continue
                # в остальных случаях, и если сосед не является отправным 
                # городом, мы добавляем новую запись в массив кратчайших расстояний
                if neighb != city:    
                    distances[neighb] = currDist
                # обрабатываем всех смежных городов с соседом, добавляя их в кучу 
                # но только если: а) до них еще не известен кратчайший маршрут и б) путь до них через neighb не выходит за пределы mileage
                for node, d in graph[neighb]:
                    if node in distances:
                        continue
                    if currDist + d <= mileage:
                        heapq.heappush(heap, (currDist + d, node))
            # возвращаем количество городов, прошедших проверку
            return len(distances)
        
        # выполним поиск соседей для каждого из городов
        cities_neighbors = {num_reachable_neighbors(city): city for city in range(n)}
        # вернём номер города, у которого наименьшее число соседей
        # в пределах досигаемости
        return cities_neighbors[min(cities_neighbors)]

В функции выше, в комментариях, подробно описывается, как метод Дейкстры, реализованный на куче позволяет найти расстояния до всех городов, в пределах `mileage`. Основную сложность для понимания предстваляет цикл, работающий с кучей.

Заключение

Алгоритм Дейкстры это мощный инструмент в мире работы с графами, область применения его крайне широка. С его помощью можно оценить даже целесообразность добавления новой ветки метро, новой дороги или маршрута в компьютерной сети. Он прост в исполнении и интуитивно понятен, как другие жадные (greedy) алгоритмы. Вычислительная сложность решений задач с его помощью зачастую не выше . При некоторых условиях может достигать линейной сложности (существует алгоритм линейной сложности, решающий первую задачу, при условии, что граф неориентированный).

Стоит еще раз отметить, что алгоритм не работает, когда в графе существуют отрицательные веса. Для этого существует подход динамического программирования — алгоритм Беллмана – Форда, что может послужить темой другой статьи. Несмотря на это, алгоритм Дейкстры является представителем идеального баланса простоты и мощи, для решения прикладных задач.

Статья подготовлена в преддверии старта курса «Алгоритмы для разработчиков». Узнать о курсе подробнее, а также зарегистрироваться на бесплатный демоурок можно по ссылке.

Информация

[1] Условия задач взяты из книги «Algorithms Illuminated: Part 2: Graph Algorithms and Data Structures» от Tim Roughgarden,
[2] и с сайта leetcode.com.
[3] Решения авторские.

Источник

Проблема кратчайшего пути

Новая сеть https://www.guxs.net/

В этой статье будет проанализировано, как использовать алгоритм Дейкстры для решения проблемы кратчайшего пути.

Как показано ниже:

Как и на рисунке выше, каждую точку можно понимать как разветвление дороги, сегмент линии – это путь, а значение на отрезке – длина. Как найти минимальное значение от v0 до каждого разветвления на дороге, что является проблемой кратчайшего пути

Как использовать код для представления картинки выше?

Задача кратчайшего пути аналогична поиску по глубине и ширине, она основана на структуре данных графа, поэтому мы можем выбрать список смежности или примыкающую матрицу для представления приведенного выше графа. Класс пакета выглядит следующим образом:

public class Graph01 {

         // Используем список смежности для представления графа
    private LinkedList<Edge> [] graph ;
         // Сколько точек на картинке
    private int size;

    public Graph01(int size) {
        this.size = size;
        this.graph = new LinkedList[this.size];
        for (int i = 0; i < size; i++) {
            graph[i]=new LinkedList<>();
        }
    }

         // Как добавить очки
    public void addEdge(int s, int e, int w) {
        this.graph[s].add(new Edge(s, e, w));
    }

Это выглядит так:

Как изобразить грань между двумя точками?

Ребро имеет три атрибута описания, вершины с обеих сторон + вес

      // Класс обёртки края
    private class Edge {
                 // Значение начальной точки
        private int start;
                 // Конечная точка
        private int end;
                 // Веса
        private int weight;

        public Edge(int start, int end, int weight) {
            this.start = start;
            this.end = end;
            this.weight = weight;
        }
    }

Как представлять вершины

Используйте два атрибута для описания вершины, а именно dist и id. Например, если мы опишем v3, то его id = 3, dist – это расстояние до начальной точки v0, поэтому dist = 13

    // Класс пакета каждой точки на рисунке
    private class Vertex implements Comparable<Vertex> {
                 // Расстояние от начальной точки, указанной пользователем, до текущей точки
        private int dist;
                 // Идентификатор вершины (1 и 2 в v1 v2)
        private int id;

        public Vertex(int dist, int startId) {
            this.dist = dist;
            this.id = startId;
        }

        @Override
        public int compareTo(Vertex o) {
            if (o.dist > this.dist) return -1;
            else return 1;
        }
    }

Идея найти кратчайший путь

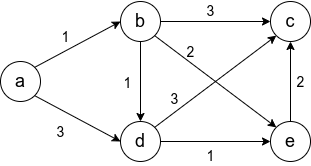
Посмотрите на этот график. Например, кратчайший путь, который мы ищем, это кратчайший путь от v0 до всех других вершин.Пройдите по этому графику в первом порядке

В поисках соседней точки v0 мы можем найти, что четыре точки v1, v2, v4 и v6 являются критическими точками v0, и затем мы соответственно обозначим четыре точки v1, v2, v4 и v6 следующим образом

  v1.dist = 13 // dist представляет расстояние от текущей точки до начальной точки
 v2.dist = 8
 v4.dist = 30
 v6.dist = 32

Но мы обнаружили, что прямое соединение не обязательно самое короткое, как показано ниже, хотя оно может достигать v4, ясно, что если вы будете следоватьv0 -> v2 -> v3 -> v4 Будет ближе,Это означает, что нам нужно постоянно обновлять значение dist от каждого узла до начальной точки

 v0.dist + v4.dist = 30
 v0.dist + v2.dist + v3.dist = 19

Итак, есть ли расстояние от точки до начальной точки v0, которое на 100% определено и не изменится? Да, это точка с наименьшим расстоянием среди всех ее критических точек.

Поэтому наш процесс кодирования выглядит следующим образом

Найти отправную точку
Добавьте отправную точку в очередь (потому что мы – обход в ширину)
Перебрать значения в очереди
1. Если текущая точка == конечная точка, перерыв
2. Возьмите точку с наименьшим расстоянием от очереди и запишите ее как текущую точку
3. Найти все прямые контактные точки текущей точки
4. Пройдите критические точки корневого узла одну за другой
  1. Как не был посещен, и текущий point.dist + длина текущего пути <dist следующей точки текущей точки (указывая, что был найден самый короткий путь, более короткий путь, чем исходный отмеченный путь), а затем обновите последнее значение первым
  2. Добавьте текущую точку во вспомогательный массив, который может восстановить длину пути
  3. Если следующая точка текущей точки не была посещена, отметьте ее как посещенную, а затем добавьте в очередь

По умолчанию все точки dist = Integer.MAXVALUE

Если вы посмотрите на это изображение и воспользуетесь ручкой, чтобы следовать приведенной выше логике, то обнаружите, что действительно можете найти кратчайший путь от v0 до различных других точек. Единственная часть, которую нелегко понять, – это место, где мы обведены черным.

Давайте объясним на примере, или на картинке выше:

Например, с самого начала:

На шаге 4, приведенном выше, мы можем перейти к непосредственной соседней точке v0 – v4, это первое посещение, поэтому мы можем продолжить обработку, а затем выполнить шаг 4.1, чтобы оценитьv0.dist + 30 < v4.dist Условие выполнено (по умолчанию dist = Integer.MAXVALUE для всех точек), поэтому мы обновляемv4.dist = v0.dist + 30 < v4.dist =30

После нескольких циклов циклов, предполагая, что это уже v3, мы продолжаем этап 4.1, чтобы судить.v3.dist + 6 < v4.dist Мы обнаружили, что он также был удовлетворен, потому что v4.dist = 30 был рассчитан в начале, поэтому мы дополнительно обновили это значение, чтобы сделатьv4.dist = v3.dist + 6 Итак, итерация ниже, мы можем получить кратчайший путь от начальной точки до всех точек

Алгоритм кратчайшего пути Дейкстры реализован следующим образом:

   public void dijkstra(int start, int end) {
        // отметим, был ли посещен
        boolean[] visited = new boolean[this.size];
                 // Обратный путь
        int [] resultArray = new int[this.size];
                 // Сохраняем все вершины в графе
        Vertex[] vertices = new Vertex[this.size];
        for (int i = 0; i < vertices.length; i++) {
            vertices[i]=new Vertex(Integer.MAX_VALUE,i);
        }

                 // Получить вершину и присвоить начальное значение 0
        Vertex startVertex = vertices[0];
        startVertex.dist = 0;
        visited[start] = true;
                 // Создаем очередь и ставим в очередь головной узел
        Queue<Vertex> queue = new PriorityQueue<>();
        queue.add(startVertex);

        while (!queue.isEmpty()) {
                         // Получить текущую точку, ближайшую к начальной точке dist
            Vertex minVertex = queue.poll();
                         // Если вершина была найдена, выход
            if (minVertex.id==end) break;

                         // Обход всех соседних точек текущей точки
            for (int i = 0; i < graph[minVertex.id].size(); i++) {
                                 // Получить их края по очереди
                Edge edge = graph[minVertex.id].get(i);
                                 // По информации о крае вынимаем критическую точку
                Vertex nextVertex = vertices[edge.end];

                                 // Если текущая точка + длина текущей стороны <длина от текущей точки до ее критической точки nextVertex, это означает, что найден обновленный путь точки этой прямой точки подключения, поэтому обновляются исходные данные прямой точки подключения
                if (minVertex.dist + edge.weight < nextVertex.dist) {
                                         // Обновляем исходное неточное значение пути
                    nextVertex.dist = minVertex.dist + edge.weight;

                    /**
                                           * Значение 0 0 0 2 0 0 0
                                           * Нижний индекс 0 1 2 3 4 5 6
                     *
                                           * Нижний индекс равен 3, а значение равно 2, что означает vertex2 перед vertex3 на рисунке.
                     */
                    resultArray[nextVertex.id]=minVertex.id;
                    if (!visited[nextVertex.id]){
                        queue.add(nextVertex);
                        visited[nextVertex.id]=true;
                    }
                }
            }
        }
        System.out.print(start);
        print( start,end ,resultArray);
    } 
   /**
           * Например:
           * Значение: 0 0 0 2 3 1 1
           * Подпись: 0 1 2 3 4 5 6
           * Как мы можем получить путь от 0 до 6? Вставьте метод в стек в следующем порядке, и вы можете получить путь, когда вы извлекаете стек
     * 
     *  | 0 0 |
     *  | 0 1 |
           * | 0 6 | Стек методов
     * ----------
     */
    private void print(int start, int end, int[] resultArray) {
        if (start==end) return;
        print(start,resultArray[end],resultArray);
        System.out.print("->"+end);
    }

Источник

Найти минимальный путь в нагруженном ориентированном графе из вершины в вершину по методу Форда-Беллмана.

Рассмотрим сначала общую задачу – нахождения минимального пути из вершины VНач в VКон.

Пусть D=(V,X) – нагруженный ориентированный граф, V={V1,…,Vn}, N>1. Введем величины , где I=1,…,N, K=0,1,2,…,N–1.

Для каждого фиксированного I и K величина равна длине минимального пути среди путей из VНач в Vi содержащих не более K дуг. Если путей нет, то .

Положим также .

Составляем матрицу длин дуг C(D)=[Cij] порядка N:

Утверждение. При I=2,…,N, K³0 выполняется равенство

. (3.1)

Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном ориентированном графе D из VНач в VКон.( VНач ≠ VКон)

записываем в виде матрицы, I– строка, K-столбец.

1) Составляем таблицу , I=1,…,N, K=0,…,N-1. Если , то пути из VНач в VКон нет. Конец алгоритма.

2) Если то это число выражает длину любого минимального пути из VНач в VКон. Найдем минимальное K1³1, при котором . По определению получим, что K1- минимальное число дуг в пути среди всех минимальных путей из VНач В VКон.

3) Затем определяем номера I2,…, такие, что

То есть, восстанавливаем по составленной таблице и матрице стоимости искомый минимальный путь из VНач в VКон.

Пример

Найдем минимальный путь из вершины V2 в V6 в ориентированном нагруженном графе D, изображенном на рис. 9. В рассматриваемом графе количество вершин N=7, следовательно, матрица длин дуг ориентированного графа D Будет иметь размерность 7×7.

Рис. 9.

Матрица длин дуг для рассматриваемого графа будет выглядеть следующим образом:

Согласно алгоритму, составляем таблицу стоимости минимальных путей из вершины V2 в вершину Vi не более, чем за K шагов, K=0,…N-1 (N=7, следовательно, K=0,…6). Как было определено выше, , и для всех остальных вершин Vi ≠ V2, то есть первый столбец таблицы состоит из элементов, равных , кроме элемента . Второй столбец таблицы повторяет вторую строку матрицы стоимости, поскольку представляет собой стоимость возможных путей из вершины V2 за один шаг. Далее по формуле (3.1) находим по столбцам все оставшиеся элементы таблицы. Например, чтобы найти элемент , складываем элементы столбца и первого столбца матрицы стоимости и выбираем минимальное из получившихся чисел:

В конечном итоге получаем следующую таблицу:

Теперь необходимо по построенной таблице и по матрице C(D) восстановить минимальный путь из вершины V2 в V6, который будет строиться с конца, то есть, начиная с вершины V6. Для этого выбираем минимальное из чисел, стоящих в строке, соответствующей V6 в таблице. Это число – 21 – длина минимального искомого пути. В первый раз такая длина была получена при количестве шагов, равном 4. В вершину V6 мы можем попасть за один шаг из вершин V1 и V7 (длина соответствующих дуг 8 и 5 соответственно – данные из матрицы C(D)). Выбираем минимальную по длине из этих дуг. Далее, в вершину V7 можно попасть из V4 и V5 (длина соответствующих дуг 7 и 3 соответственно). Продолжая аналогичным образом, найдем искомый путь за 4 шага минимальной длины из вершины V2 в V6: V2 V3 V5 V7 V6.

< Предыдущая		Следующая >

Источник

1. Нахождение кратчайших путей. Алгоритм Дейкстры

Определение[править | править код]

Задача о кратчайшем пути с учётом дополнительных ограничений[править | править код]

Алгоритмы[править | править код]

Задача поиска кратчайшего пути из одной вершины во все остальные[править | править код]

Невзвешенный ориентированный граф[править | править код]

Ориентированный граф с неотрицательными весами[править | править код]

Ориентированный граф с произвольными весами[править | править код]

Задача о кратчайшем пути между всеми парами вершин[править | править код]

Применение[править | править код]

Картографические сервисы[править | править код]

Недетерминированная машина[править | править код]

Сети дорог[править | править код]

Похожие задачи[править | править код]

Постановка задачи линейного программирования[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Алгоритм Дейкстры. Разбор Задач

Введение

Примеры работы

Оценка сложности алгоритма

Задача №1

Решение

Задача №2

Решение

Заключение

Информация

Проблема кратчайшего пути

Добавить комментарий Отменить ответ

1. Нахождение кратчайших путей. Алгоритм Дейкстры

Определение[править | править код]

Задача о кратчайшем пути с учётом дополнительных ограничений[править | править код]

Алгоритмы[править | править код]

Задача поиска кратчайшего пути из одной вершины во все остальные[править | править код]

Невзвешенный ориентированный граф[править | править код]

Ориентированный граф с неотрицательными весами[править | править код]

Ориентированный граф с произвольными весами[править | править код]

Задача о кратчайшем пути между всеми парами вершин[править | править код]

Применение[править | править код]

Картографические сервисы[править | править код]

Недетерминированная машина[править | править код]

Сети дорог[править | править код]

Похожие задачи[править | править код]

Постановка задачи линейного программирования[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Алгоритм Дейкстры. Разбор Задач

Введение

Примеры работы

Оценка сложности алгоритма

Задача №1

Решение

Задача №2

Решение

Заключение

Информация

Проблема кратчайшего пути

Вам также может понравиться

Как найти гипотенузу вписанного равнобедренного треугольника

Как в whatsapp найти группу по интересам

Как найти выключенный телефон по номеру теле2

Добавить комментарий Отменить ответ