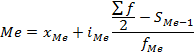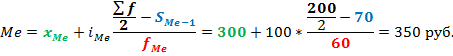Определение и свойства медианы треугольника
В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.
Определение медианы треугольника
Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.
Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).
Свойства медианы
Свойство 1 (основное)
Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.
В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:
Свойство 2
Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.
Свойство 3
Три медианы делят треугольник на 6 равновеликих треугольников.
Свойство 4
Наименьшая медиана соответствует большей стороне треугольника, и наоборот.
- AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
- AB – самая короткая сторона, следовательно, медиана CD – самая длинная.
Свойство 5
Допустим, известны все стороны треугольника (примем их за a, b и c).
Длину медианы ma, проведенную к стороне a, можно найти по формуле:
Примеры задач
Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.
Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S△ = 5 см 2 ⋅ 6 = 30 см 2 .
Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.
Решение
Воспользуемся формулой, приведенной в свойстве 5:
По сторонам треугольника найти его медиану
Рассмотрим задачу, в которой требуется по сторонам треугольника найти его медиану.
Даны стороны треугольника. Найти длину медианы, проведенной к наибольшей стороне.
Дано: ∆ ABC,
сторона AC — наибольшая,
1) На луче BO отложим отрезок OD, OD=BO.
2) Проведем отрезки AD и CD.
3) Рассмотрим четырехугольник ABCD.
AO=CO (так как BO — медиана треугольника ABC по условию);
BO=DO (по построению).
Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).
так как BO=1/2 BD (по построению),
Если ввести обозначение
формула для нахождения медианы треугольника по его сторонам примет вид:
Запоминать эту формулу не обязательно. При решении конкретной задачи следует привести все рассуждения.
Если медиана проведена не к наибольшей, а к наименьшей либо средней по величине стороне, решение задачи аналогично.
Соответственно, формулы для нахождения длины медианы в этих случаях:
Приём, который применили для решения задачи — метод удвоения медианы.
Свойства медианы треугольника. Итоговое повторение курса геометрии 7 – 9 класса
Свойства медианы треугольника
Итоговое повторение курса геометрии 7 – 9 класса
При изучении какой-либо темы школьного курса можно отобрать определенный минимум задач, овладев методами решения которых, учащиеся будут в состоянии решить любую задачу на уровне программных требований по изучаемой теме. Предлагаю рассмотреть задачи, которые позволят увидеть взаимосвязи отдельных тем школьного курса математики. Поэтому составленная система задач является эффективным средством повторения, обобщения и систематизации учебного материала в ходе подготовки учащихся к экзамену.
Для сдачи экзамена не лишними будут дополнительные сведения о некоторых элементах треугольника. Рассмотрим свойства медианы треугольника и задачи, при решении которых этими свойствами можно воспользоваться. В предложенных задачах реализуется принцип уровневой дифференциации. Все задачи условно поделены на уровни (уровень указан в скобках после каждого задания).
Вспомним некоторые свойства медианы треугольника
Свойство 1. Докажите, что медиана треугольника ABC, проведённая из вершины A, меньше полусуммы сторон AB и AC.
Отложим на продолжении медианы AM за точку M отрезок MK, равный AM. Тогда в четырёхугольнике ABKC диагонали пересекаются и точкой пересечения делятся пополам. Значит, ABKC — параллелограмм. Применяя неравенство треугольника к треугольнику ABK, получим, что
то, сложив почленно эти три неравенства, получим, что
2
AM + BN + CK 
> AB + BC + AC.
Отсюда следует, что AM + BN + CK > 
(AB + BC + AC).
Отложим на продолжении медианы AM за точку M отрезок MA1, равный AM. Тогда ABA1C — параллелограмм. Поэтому
BA1 = AC, 2AM = AA1 SDEF’ , то SAED+SBFD>SDEF , следовательно, указанным образом расположить точки невозможно.
так расположить точки нельзя.
Источник: Окружная олимпиада (Москва) , 2008 г, 11 класс
№32 Темы: Удвоение медианы. Ортоцентр и ортотреугольник Сложность:5 + Три точки, лежащие на одной прямой Подобные треугольники Классы: 9,10
В неравнобедренном треугольнике ABC точки H и M – точки пересечения высот и медиан соответственно. Через вершины A , B и C проведены прямые, перпендикулярные прямым AM , BM , CM соответственно. Докажите, что точка пересечения медиан треугольника, образованного проведенными прямыми, лежит на прямой MH .
Решение
Пусть A’B’C’ – треугольник, образованный
проведенными прямыми и G – точка пересечения его
медиан. Мы докажем, что M является серединой отрезка GH . Достроим треугольник BMC до параллелограмма BMCA1 . Отрезок MA1 делит сторону BC пополам, поэтому A1 лежит на прямой AM , причем AM = A1M (поскольку точка M делит медиану в отношении 2:1 ). Кроме того, BA1|| MC 
A’B’ и CA1|| MB A’C’ , поэтому BA1 и CA1 – высоты треугольника BA’C , значит A1 является ортоцентром треугольника BA’C , и
A’A1 BC . Стороны треугольника BA1M перпендикулярны
сторонам треугольника A’B’C’ соответственно, поэтому эти треугольники подобны, причем соответствующие прямые BC и
AG , содержащие медианы этих треугольников,
перпендикулярны. Значит, прямая A’G совпадает с прямой A’A1 . Пусть G’ – точка, симметричная точке H относительно M . Треугольники AHM и A1G’M симметричны относительно M , поэтому A1G’|| AH BC . Отсюда следует, что G’ лежит на прямой A’G . Аналогично, получаем, что G’ лежит на прямой B’G , то есть G’ совпадает с G .
Источник: Всероссийская олимпиада по математике, 2008 г, 9 класс
Отрабатываем умение: самостоятельно решать задачи.
Свойства медианы. Площадь треугольника
1. В треугольнике АВС медиана АМ перпендикулярна медиане BN. Найдите площадь треугольника АВС, если длина АМ равна 3, а длина BN равна 4.
2. Основание равнобедренного треугольника равно 2. Медианы, проведенные к боковым сторонам, взаимно перпендикулярны. Найдите площадь треугольника.
3. Две медианы равнобедренного треугольника взаимно перпендикулярны. Боковая сторона равна 
. Найдите площадь треугольника.
4. В треугольнике АВС медианы АD и ВE перпендикулярны, 
, 
. Чему равен квадрат третьей стороны?
5. Сторона треугольника равна 20, а медианы, проведенные к двум другим сторонам – 24 и 18. Найдите площадь треугольника.
6. Стороны треугольника равны 13, 14 и 15. Найти площади треугольников, на которые разбивается данный треугольник его медианами.
7. Площадь треугольника АВС равна 12. Из вершины тупого угла В проведена медиана BD, длина которой равна 3. Найдите длину стороны АС, если угол ABD – прямой.
8. Найдите площадь треугольника, если две его стороны равны 1 и 
, а медиана третьей стороны равна 2. (Указание – достроить до параллелограмма).
О т в е т: 
.
1. Одна сторона треугольника равна а, другая – b. Найдите третью сторону, если известно, что она равна медиане, проведенной к ней.
О т в е т: 
.
2. Основание равнобедренного треугольника 
, медиана боковой стороны 5. Найдите длины боковых сторон.
3. В равнобедренном треугольнике основание равно 
, а угол при основании равен 300. Найдите длину медианы, проведенной к боковой стороне.
4. Медианы треугольника равны 5, 
и 
. Докажите, что треугольник прямоугольный.
5. Числа 
, 
и 
выражают длины медиан некоторого треугольника. Докажите, что если выполняется равенство 
, то треугольник является прямоугольным.
Медиана, проведенная к гипотенузе
1. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна 3 см и делит прямой угол в отношении 2:1. Найдите меньший катет.
2. АА1, ВВ1, СС1 – медианы треугольника АВС. 
. Найдите 
.
3. Медианы треугольника АВС АА1, ВВ1 и СС1 пересекаются в точке О. .
см. 
см. Найдите ВО.
4. Гипотенуза прямоугольного треугольника в 4 раза больше проведенной к ней высоты. Найдите острые углы треугольника.
О т в е т: 150; 750.
5. В трапеции ABCD углы при основании AD равны 200 и 700, длина отрезка, соединяющего середины оснований, равна 3. Найдите длину отрезка, соединяющего середины диагоналей трапеции.
· , , Ленинградские математические кружки
· , Задачи по планиметрии, Издательство МЦНМО, 2001г
· интернет сайт http://zadachi. ***** Задачи по геометрии
· Всероссийская олимпиада по математике, 2008 год,
· Турнир им. Ломоносова, 2001 год
· Московская математическая регата, 2012/13 г, 8 класс
[spoiler title=”источники:”]
http://pandia.ru/text/79/216/60203.php
[/spoiler]
Центральную тенденцию данных можно рассматривать не только, как значение с нулевым суммарным отклонением (среднее арифметическое) или максимальную частоту (мода), но и как некоторую отметку (значение в совокупности), делящую ранжированные данные (отсортированные по возрастанию или убыванию) на две равные части. Половина исходных данных меньше этой отметки, а половина – больше. Это и есть медиана.
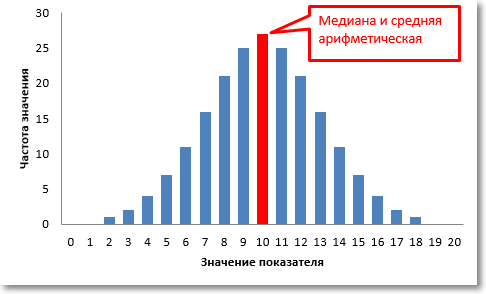
Итак, медиана в статистике – это уровень показателя, который делит набор данных на две равные половины. Значения в одной половине меньше, а в другой больше медианы. В качестве примера обратимся к набору нормально распределенных случайных чисел.
Очевидно, что при симметричном распределении середина, делящая совокупность пополам, будет находиться в самом центре – там же, где средняя арифметическая (и мода). Это, так сказать, идеальная ситуация, когда мода, медиана и средняя арифметическая совпадают и все их свойства приходятся на одну точку – максимальная частота, деление пополам, нулевая сумма отклонений – все в одном месте. Однако, жизнь не так симметрична, как нормальное распределение.
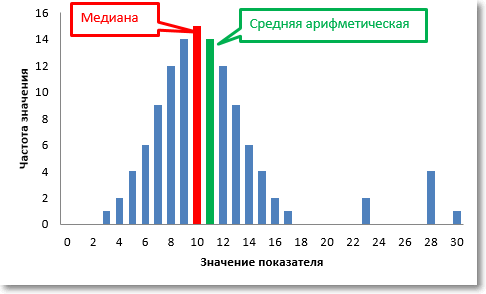
Допустим, мы имеем дело с техническими замерами отклонений от ожидаемой величины чего-нибудь (содержания элементов, расстояния, уровня, массы и т.д. и т.п.). Если все ОК, то отклонения, скорее всего, будут распределены по закону, близкому к нормальному, примерно, как на рисунке выше. Но если в процессе присутствует важный и неконтролируемый фактор, то могут появиться аномальные значения, которые в значительной мере повлияют на среднюю арифметическую, но при этом почти не затронут медиану.
Медиана выборки – это альтернатива средней арифметической, т.к. она устойчива к аномальным отклонениям (выбросам).
Математическим свойством медианы является то, что сумма абсолютных (по модулю) отклонений от медианного значения дает минимально возможное значение, если сравнивать с отклонениями от любой другой величины. Даже меньше, чем от средней арифметической, о как! Данный факт находит свое применение, например, при решении транспортных задач, когда нужно рассчитать место строительства объектов около дороги таким образом, чтобы суммарная длина рейсов до него из разных мест была минимальной (остановки, заправки, склады и т.д. и т.п.).
Формула медианы
Формула медианы в статистике для дискретных данных чем-то напоминает формулу моды. А именно тем, что формулы как таковой нет. Медианное значение выбирают из имеющихся данных и только, если это невозможно, проводят несложный расчет.
Первым делом данные ранжируют (сортируют по убыванию). Далее есть два варианта. Если количество значений нечетно, то медиана будет соответствовать центральному значению ряда, номер которого можно определить по формуле:
где
№Me – номер значения, соответствующего медиане,
N – количество значений в совокупности данных.
Тогда медиана обозначается, как
Это первый вариант, когда в данных есть одно центральное значение. Второй вариант наступает тогда, когда количество данных четно, то есть вместо одного есть два центральных значения. Выход прост: берется средняя арифметическая из двух центральных значений:
В интервальных данных выбрать конкретное значение не представляется возможным. Медиану рассчитывают по определенному правилу.
Для начала (после ранжирования данных) находят медианный интервал. Это такой интервал, через который проходит искомое медианное значение. Определяется с помощью накопленной доли ранжированных интервалов. Где накопленная доля впервые перевалила через 50% всех значений, там и медианный интервал.
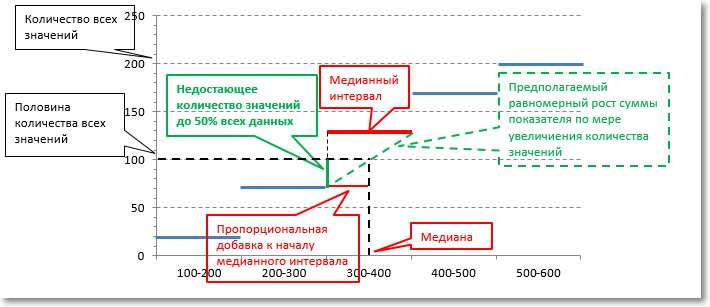
Не знаю, кто придумал формулу медианы, но исходили явно из того предположения, что распределение данных внутри медианного интервала равномерное (т.е. 30% ширины интервала – это 30% значений, 80% ширины – 80% значений и т.д.). Отсюда, зная количество значений от начала медианного интервала до 50% всех значений совокупности (разница между половиной количества всех значений и накопленной частотой предмедианного интервала), можно найти, какую долю они занимают во всем медианном интервале. Вот эта доля аккурат переносится на ширину медианного интервала, указывая на конкретное значение, именуемое впоследствии медианой.
Обратимся к наглядной схеме.
Немного громоздко получилось, но теперь, надеюсь, все наглядно и понятно. Чтобы при расчете каждый раз не рисовать такой график, можно воспользоваться готовой формулой. Формула медианы имеет следующий вид:
где xMe — нижняя граница медианного интервала;
iMe — ширина медианного интервала;
∑f/2 — количество всех значений, деленное на 2 (два);
S(Me-1)— суммарное количество наблюдений, которое было накоплено до начала медианного интервала, т.е. накопленная частота предмедианного интервала;
fMe — число наблюдений в медианном интервале.
Как нетрудно заметить, формула медианы состоит из двух слагаемых: 1 – значение начала медианного интервала и 2 – та самая часть, которая пропорциональна недостающей накопленной доли до 50%.
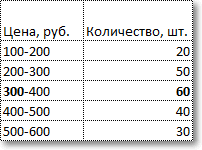
Для примера рассчитаем медиану по следующим данным.
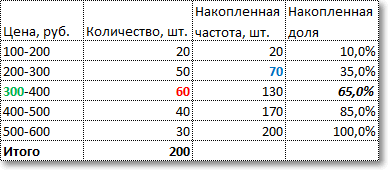
Требуется найти медианную цену, то есть ту цену, дешевле и дороже которой по половине количества товаров. Для начала произведем вспомогательные расчеты накопленной частоты, накопленной доли, общего количества товаров.
По последней колонке «Накопленная доля» определяем медианный интервал – 300-400 руб (накопленная доля впервые более 50%). Ширина интервала – 100 руб. Теперь остается подставить данные в приведенную выше формулу и рассчитать медиану.
То есть у одной половины товаров цена ниже, чем 350 руб., у другой половины – выше. Все просто. Средняя арифметическая, рассчитанная по этим же данным, равна 355 руб. Отличие не значительное, но оно есть.
Расчет медианы в Excel
Медиану для числовых данных легко найти, используя функцию Excel, которая так и называется — МЕДИАНА. Другое дело интервальные данные. Соответствующей функции в Excel нет. Поэтому нужно задействовать приведенную выше формулу. Что поделаешь? Но это не очень трагично, так как расчет медианы по интервальным данным – редкий случай. Можно и на калькуляторе разок посчитать.
Напоследок предлагаю задачку. Имеется набор данных. 15, 5, 20, 5, 10. Каково среднее значение? Четыре варианта:
а) 11;
б) 5;
в) 10;
г) 5, 10, 11.
Мода, медиана и среднее значение выборки – это разный способ определить центральную тенденцию в выборке.
Ниже видеоролик о том, как рассчитать медиану в Excel.
Поделиться в социальных сетях:
Изучаем статистику: средние значения
Один из разделов описательной статистики посвящен знакомству
с характеристиками числового набора: минимальное значение, максимальное
значение, размах, среднее арифметическое и медиана. Ученики должны научиться
определять их для набора чисел, заданного списком, таблицей или диаграммой
рассеивания.
Мы изучали этот материал в течение трех уроков. На первых
двух были введены новые понятия и решались задачи из учебного пособия (авт.
Ю.Н. Тюрин, А.А. Макаров, И.Р. Высоцкий, И.В. Ященко). Например. Найдите
наибольшее и наименьшее значение, размах, среднее значение и медиану набора
чисел: 12; 7; 25; 3; 19; 15. (Ответ: 25; 3; 22; 13,5; 13,5).
Однако естественно показать учащимся, зачем мы все это
изучаем. На третьем уроке мы решали задачи, в которых требуется выбрать
такое среднее, которое наилучшим образом отражает особенности данного набора
чисел в соответствии с их природой и требованиями задачи. В одних задачах не
сказано, какую характеристику надо искать, поэтому, чтобы ответить на вопрос
задачи, приходится примерять к поставленной задаче поочередно разные средние и
выяснять, какое подходит больше других. В этом случае ответом к задаче является
не число, а название подходящей характеристики. В других задачах присутствует
необходимость правильно интерпретировать полученные результаты, отнестись к ним
критически, попытаться найти здравое зерно даже там, где, на первый взгляд, «все
сделано неверно». И наконец, предложен и третий вид задач, в которых природа
данных накладывает определенные дополнительные требования на найденное значение
среднего: например, оно должно быть целым.
Тем самым мы не только продолжаем закреплять навык подсчета
среднего, но и демонстрируем возможности применения изученного в реальных
жизненных ситуациях. Ведь для учащихся важным фактором освоения нового является
осознание необходимости знания этого нового, то есть не только как
найти, но и зачем находить.
Данная статья состоит из двух частей. В первой дается описание наиболее
употребительных средних. Во второй части предлагается набор задач для решения в
классе и для самостоятельной работы учащихся.
Знакомимся со средними
Наибольшее и наименьшее значения
Слова «минимальный», «максимальный», «меньший», «больший»
интуитивно понятны учащимся, поэтому первые две характеристики: наибольшее
и наименьшее значения оставим без определения. Скажем, что в наборе,
упорядоченном по возрастанию, наименьшее число стоит на первом месте, а
наибольшее — на последнем.
В пособии имеются задания, в которых требуется найти
наибольшее или наименьшее значения среди чисел, указанных в таблице. К ним
добавим задания с другой формой представления данных — в виде диаграммы
рассеивания.
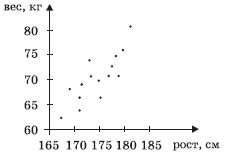
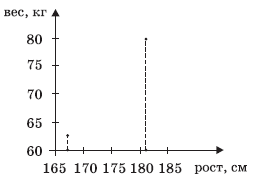
Задание. Имеется диаграмма 1 рассеивания, показывающая
взаимосвязь роста и веса 15 опрошенных юношей. Найти рост самого высокого и рост
самого низкого юноши (т.е. определить минимальное и максимальное значения набора
чисел, заданного диаграммой рассеивания).
Для этого будем использовать следующее: минимальный рост
соответствует абсциссе точки, расположенной левее других, а
максимальный — абсциссе крайней точки справа. Получим:
min ≈ 167 см, max ≈ 181 см.
Интересно, что остальные 13 точек участия в «обсуждении»
вообще не принимают. Их можно стереть — результат от этого не изменится (см.
диаграмму 2).
Диаграмма 1
Вторая особенность получаемого результата в том, что, в
отличие от работы с таблицей, данные, получаемые с помощью графиков и диаграмм,
являются не точными, а приближенными, то есть ответы могут отличаться.
Аналогично находим минимальное и максимальное значения веса,
как ординаты самой нижней и самой верхней точек.
Диаграмма 2
С каким же видом представления данных удобнее работать?
Преимущество таблицы заключается в точности получаемых
результатов, но работа с ней требует концентрации внимания на протяжении
длительного времени: нельзя пропустить искомое число, а оно может попасть в
любой исследуемый столбец. И если таблица содержит не 15 чисел, а 5000, то этот
аргумент становится решающим в пользу наглядного представления данных. Оно дает
менее точные результаты, зато обработка такой информации происходит за
считанные секунды. Даже если диаграмма будет содержать 5000 точек, нас будут
интересовать только две крайние, на остальные мы даже не посмотрим.
Размах
В отличие от предыдущих понятий, размах — это
незнакомая учащимся характеристика набора. Он показывает протяженность набора
вдоль числовой оси, меру его разброса.
Определение. Размах набора чисел (R) — это
разность между наибольшим и наименьшим числом набора.
Например, в предыдущем задании размах равен: R = 181 –
167 = 14 см.
Что показывает размах значений?
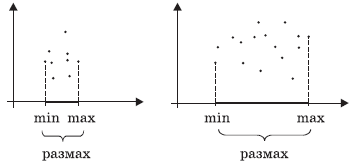
Сравним диаграммы 3 и 4:
|
|
Точки, изображенные на диаграмме 3, расположены ближе друг к
другу, соответственно, и максимальное и минимальное значение отличаются друг от
друга меньше, чем на диаграмме 4. Таким образом, размах показывает, сильно ли
отличаются числа набора друг от друга.
Маленький размах показывает, что исследуемая величина
принимала практически одинаковые значения. Большой размах показывает, что
некоторая величина принимает значительно отличающиеся друг от друга значения, то
есть нестабильность. Иногда большой размах свидетельствует о наличии
грубой ошибки измерений, о том, что какое-то из чисел попало в список случайно.
Если вычислить полусумму наименьшего и наибольшего значений
набора и обозначить ее с, а половину размаха обозначить 
то можно
утверждать, что все числа набора содержатся в промежутке 
На бытовом уровне
размах (а точнее, полуразмах) дает информацию о точности информации: расстояние
от дома до дачи (100 ± 5) км, цена на хлеб (14 ± 2) р. и т.д.
Среднее арифметическое
Определение. Средним арифметическим нескольких чисел (
) называется частное от деления суммы этих чисел на количество чисел.
Например, средним арифметическим чисел 4; 6; 11 является
число 
Зачастую среднее арифметическое называют просто «средним» в
силу его наибольшей популярности. Говорят о среднем балле аттестата,
среднегодовом потреблении населением фруктов. «Потребительская корзина» для
определенного слоя граждан рассчитывается исходя из средних показателей.
Рассмотрим следующий пример. На олимпиаде по математике
предлагалось решить пять задач по 4 балла за каждую. В протоколе указана сумма
баллов каждого из восьми участников этой олимпиады:
12; 14; 14; 16; 17; 18; 19; 200.
Для ускорения подсчета имеется автоматизированная система
обработки данных, которая находит среднее арифметическое любых введенных чисел.
Какой средний балл набрали участники олимпиады?
У данного набора среднее равно 38,75. Однако такую сумму
баллов никто из участников набрать не мог. К тому же семь чисел из данных восьми
намного меньше его. Все значения этого набора, кроме крайнего правого,
достаточно кучно попадают в интервал [12; 19], а 38,75 в него не попадает. Все
это говорит о том, что полученное среднее арифметическое не только не передает
особенностей данного набора чисел, но и вообще противоречит здравому смыслу.
Значит, либо в условие, либо в решение вкралась ошибка! Посмотрим еще раз на
данные числа. Теперь, получив явно бессмысленный результат, мы сможем более
критически отнестись к условию: первые семь чисел вполне реальны, а вот
последнее… Откуда оно взялось?! Видимо, оно случайно попало в этот список:
возможно, в результате описки. Однако обнаружение ошибки в условии не избавляет
нас от необходимости довести решение до конца. Можно, конечно, посоветовать
комиссии снова переписать результаты учащихся и ввести числа из нового,
«правильного» протокола. Но где гарантия, что в нем снова не будет опечатки?
Когда все результаты более или менее кучно располагаются на
числовой оси, кроме, быть может, нескольких ненадежных значений, анализировать
результаты можно! Достаточно высокую точность полученных значений будет
гарантировать применение других средних — в частности, урезанного среднего.
Для его нахождения сначала упорядочивают набор по возрастанию, а затем
отбрасывают слева и справа равное небольшое количество чисел. При этом «выбросы»
(или ошибки наблюдений) в дальнейших вычислениях не участвуют. У полученного
«урезанного» набора обычным образом находят среднее арифметическое. Оно и
является урезанным средним исходного набора.
Вернемся к задаче. Если отбросить по одному числу с каждой
стороны, то есть числа 12 и 200, то у оставшегося набора из шести чисел среднее
равно
Это и есть урезанное среднее. Оно неплохо передает реальное
среднее количество баллов, набранных юными математиками.
Некоторая аналогия с нахождением урезанного среднего
просматривается в правилах судейства во многих видах спорта. Например, в
соревнованиях по прыжкам с трамплина технику каждого прыжка оценивают 5 судей.
Чтобы получить объективные оценки, две из них — высшую и низшую — отбрасывают, а
для трех оставшихся находят сумму. Такой подход не дает возможности судьям
повышать баллы своим соотечественникам, а спортсменам затрудняет нечестный путь
к медалям.
Медиана
Медианой числового набора является число, которое
разделяет этот набор на две одинаковые по части.
Если набор упорядочен и в нем имеется нечетное количество
чисел (2n + 1), то медиана стоит посередине этого набора, на (n +
1)-м месте. Если упорядоченный набор состоит из четного количества чисел (2n),
то медианой является любое число, находящееся между двумя числами, которые стоят
в середине (под номерами n и n + 1). Обычно берется их полусумма.
В наборе 12; 14; 14; 16; 17; 18; 19; 200 медианой является
любое число из интервала (16; 17), например, 16,5. Напомним, что урезанное
среднее равнялось 16,3. Похоже!
Перейдем к решению задач.
Вычисляем средние
1. Про отличника. У отличника Коли были отметки по математике
«5», «5», «5», «5».
И вдруг в конце четверти он получил «2». Он знает, что
учитель математики выставляет четвертную отметку как среднее всех отметок,
имеющихся у ученика, и не признает пересдач. Какое среднее было бы
предпочтительнее для Коли, если он, естественно, надеется на пятерку в четверти?
Решение. 1. Попробуем начать с такого очень
распространенного способа выставления четвертных отметок, как нахождение
среднего арифметического:
Естественно, что любой учитель округлит этот результат в
меньшую сторону и выставит итоговую отметку «4». Значит, это среднее Колю не
устраивает.
Мы видим, что один неудачный ответ на балл снизил четвертную
отметку. Ведь до этого среднее арифметическое равнялось 5.
2. Помочь Колиной мечте сбыться может другое среднее, и не
одно! Например, если в качестве среднего учитель Коли возьмет медиану или
урезанное среднее, то в четверти Коле обеспечена пятерка:
— медиана набора 2, 5, 5, 5, 5 равна 5;
— урезанное среднее набора 5, 5, 5, равно
Ответ: медиана или урезанное среднее.
2. Про лодку. Рыбаки собираются порыбачить на озере. Но не
везде им обеспечен хороший улов. Чтобы найти рыбное место, они решили
воспользоваться лодкой с мотором. На лодке установлен мотор, который можно
регулировать по высоте, поднимая или глубже погружая его. Известно, что мотор
работает надежно и не перегревается во время работы, если опустить его как можно
ниже в глубь воды. Но тогда возникает опасность зацепить им за дно водоема.
Мотор устанавливается на желаемую высоту на берегу, в воде менять глубину
погружения нельзя. Какой информацией о глубине воды в озере надо располагать
рыбакам, чтобы не повредить мотор о дно?
Решение. Рыбаки должны узнать глубину озера вдоль
предполагаемого маршрута следования. Затем у полученного набора чисел надо найти
минимальное значение. Оно обеспечит им удачное прохождение и других,
более глубоких участков.
Ответ: минимальное значение.
3. Библиотека. Известно, что детская библиотека выдает в день
в среднем 180 книг. Сколько книг выдает библиотека в среднем за неделю? за
месяц? за год?
Решение. Под средним в данной задаче подразумевается
среднее арифметическое. Так как библиотека работает 6 дней в неделю, значит,
за неделю она выдает около 180
6
= 1080 книг. За 26 рабочих дней месяца она выдаст 18026
= 4700 книг. За 12 месяцев выдача составит 468012
= 56 000 книг.
Ответ: 1080 книг, около 4700 книг, около 56 000 книг.
Решая эту задачу, уместно обсудить вопрос точности полученных
результатов. Во-первых, из условия неясно, за какой период было получено
среднедневное значение. Если наблюдения велись лишь одну неделю, то к полученным
вычисленным значениям нужно относиться весьма скептически. Для получения более
точных результатов надо было проводить более длительное наблюдение, сопоставимое
по длительности с запрашиваемым периодом. А во-вторых, возможно, наблюдатели
«попали» на неделю «книжного бума», тогда результаты, распространенные на месяц
и тем более на год получатся явно завышенными. Возможна и обратная картина: нам
сообщили результаты, полученные в период летних каникул, значит, результаты
вычислений будут заниженными. Другими словами, к полученным числам нужно
относиться с большой осторожностью, если нет возможности уточнить, как было
проведено исследование, и за какой период было вычислено среднее значение 180
книг.
Этот пример показывает, что для получения достоверных
результатов исследований нужно соблюдать некоторые условия, следовать
определенным правилам, чтобы полученным выводам можно было доверять.
4. Метание молота. Спортивный клуб должен организовать
соревнования по метанию молота среди спортсменов с разной спортивной подготовкой
и разными достижениями. Для этого он должен пригласить необходимое количество
судей в сектор для метания. Судьи, с которыми сотрудничает клуб, точно отмечают
место падения молота, если находятся не далее четырех метров от него. Спортивный
клуб может запросить любую информацию о прошлых результатах приглашенных
спортсменов. Какой информацией должны располагать организаторы, чтобы пригласить
необходимое количество судей?
Решение. Надо запросить предыдущие результаты метания
молота всех участников и найти максимальный, минимальный результаты и размах.
Зная величину угла сектора для метания и максимальный результат, можно
вычислить длину дуги, вдоль которой через каждые 8 м надо расставить судей.
Количество таких рядов зависит от размаха результатов.
Если он окажется менее 8 м, то судьи могут стоять в один ряд. Если размах
окажется бóльшим, то чтобы успешно фиксировать как более далекие, так и близкие
результаты судей надо расставить в несколько рядов через каждые 8 м.
Ответ: максимальный результат, размах.
5. Отпуск на юге. Для успешной рекламы отдыха на Кипре
туристическая фирма запросила данные о погоде на острове за последние 10 лет.
Выяснилось, что за этот период было лишь 216 пасмурных или дождливых дней,
которые были равномерно распределены по запрашиваемым годам. Сколько дней в году
на острове Кипр светит солнце?
Решение. За 10 лет наблюдалось 3652 – 216 = 3436
солнечных дней. Значит, в среднем за один год — 343,6 дня. Поскольку в ответе
надо писать целое число дней, то можно округлить до целых, а можно и до
десятков: в рекламе круглые числа смотрятся лучше.
Ответ: около 340 дней.
Задачи для самостоятельного решения
1. а) Через речку хотят построить мост. Известно, что уровень
воды в реке меняется в течение года: весной при таянии снега повышается,
засушливым летом понижается. Какую характеристику уровня воды в реке надо
учитывать, чтобы построенный мост был над водой?
б) Периодически в средствах массовой информации нам сообщают
о стихийных бедствиях, в результате которых переполненные водой реки выходят из
своих берегов и даже затопляют улицы городов. Понимая возможность подобного
стихийного бедствия, не будет ли разумнее построить мост (а заодно и высокую
дамбу) как можно выше, насколько это будет технически возможно? Ведь гибель
людей несравнима ни с какими материальными затратами, позволяющими предупредить
беду.
2. За урок учительница вызывает в среднем 5 человек из класса
и каждому ставит отметку за устный ответ. Сколько отметок за устные ответы
выставит эта учительница за неделю, если она проводит в этом классе 5 уроков в
неделю? За четверть?
3. В забеге на 800 м принимали участие 19 спортсменов,
разделенных на группы, стартующие в разное время. Как судьи определили
победителя забега?
4. На зимние каникулы в одной из школ города Мурманска
учительница дала детям задание: следить за погодой и найти среднюю температуру.
Ежедневно в течение десяти дней в 15 часов Наташа записывала показания
термометра:
–13, –10, –15, 11, –9, –9, –11, –12, –10, –11.
А затем вычислила среднее арифметическое и получила –8,9.
а) Действительно ли в период наблюдений температура
колебалась вблизи этого числа?
б) Почему большинство значений (9 из 10) меньше найденного
среднего?
в) Как исправить ответ, если он неверный (заново повторить
наблюдение, естественно, нельзя)?
5. Имеются данные об успеваемости по химии 8 «А» и 8 «Б» : о
количестве учащихся, получивших ту или иную четвертную отметку. Данные занесены
в таблице:
|
Отметка
|
8 «А»
|
8 «Б»
|
|
5 |
6 чел. |
4 чел. |
|
4 |
12 чел. |
10 чел. |
|
3 |
6 чел. |
5 чел. |
Какой класс в среднем имеет лучшие результаты?
6. Лучший нападающий баскетбольной команды «Луч» за восемь
прошедших матчей принес своей команде 61 очко. Сколько в среднем очков добавлял
своей команде этот игрок за каждую игру?
Подводя итог сказанному, хочется отметить, что решение задач,
приведенных в этой статье, было встречено учениками с большим интересом. В их
глазах просматривалось и удивление: оказывается школьные знания имеют прямое
отношение к реальной жизни. Длинные формулировки задач не только не мешали
воспринимать задачу, а напротив, учащиеся успевали глубже погрузиться в
ситуацию, пропустить ее через себя. Сюжеты не были надуманными, они
согласовывались с имеющимся у детей жизненным опытом, поэтому даже слабо
подготовленные ученики на этих уроках проявляли необычную для них активность.
Решение некоторых задач проходило в форме жаркой, но доброжелательной дискуссии,
и доказать свою правоту могла только та сторона, которая аргументированно
отстаивала свою позицию, опираясь на строгие математические факты и здравый
смысл!
Решения и ответы
1. а) Максимальное значение уровня воды в реке.
б) Все зависит от массы обстоятельств: географического
положения реки, «поведения» реки в прошлом и др. Конечно, раз в 100–150 лет даже
на самой «мирной» реке может быть катастрофический паводок. Однако стоит ли
строить очень высокий мост через каждую речку, ожидая ужасного, но
маловероятного катаклизма?
2. Около 25 отметок; около 200 отметок.
3. Победитель затратил на преодоление дистанции минимальное
время.
4. а) Нет, в период наблюдений температура колебалась в
промежутке [–15; –9], которому найденное среднее не принадлежит;
б) потому что имеется число 11, которое существенно
отличается от всех остальных и поэтому меняет среднее в большую сторону;
в) найти урезанное среднее данного набора:
–9, –9, –10, –10, –11, –11, –12, –13, –15,
11. Оно приближенно равно 11,4.
5. 8 «А».
6. Около 8 очков.
Багишова О.
Почему для анализа лучше использовать медианные значения, а не средние
Интерпретируем статистику правильно.
Что такое среднее значение и почему оно не всегда корректно
Когда мы имеем дело со статистическими данными, их нужно как‑то структурировать. Сами по себе демографические и экономические показатели, такие как зарплата и продолжительность жизни, оценки, баллы и многое другое, представляют собой лишь беспорядочный массив чисел.
Чтобы привести их к порядку, можно использовать среднее арифметическое значение. Для этого надо сложить все числа и разделить на количество слагаемых:
(8+7+10+4+6+9)/6=7,3
И хотя среднее арифметическое легко посчитать, у него есть серьёзный недостаток: если один показатель сильно отличается от остальных, то он серьёзно искажает итоговый результат. Ситуацию хорошо описывает анекдот: «Чиновники едят мясо, а я — капусту. В среднем мы едим голубцы».
Среднее арифметическое может быть значительно больше или меньше большинства чисел. Так, в ряду «1, 2, 1, 1, 3, 8, 10, 1, 587» оно окажется равным 68,2. А если в общий расчёт попадёт девять человек со сбережениями в 100 тысяч рублей и один банкрот с полумиллионным долгом, средняя сумма накоплений составит 40 тысяч.
Проще говоря, среднее арифметическое может не отражать действительности.
Что такое медиана и чем она лучше
Чтобы застраховаться от подобных ошибок, вместо среднего значения можно применять медианное.
Медиана поможет найти именно тот показатель, который ближе всего к истинно среднему. На неё не влияют выбивающиеся из общей массы числа, поэтому она считается одним из самых надёжных и устойчивых показателей. Так, для упомянутого выше ряда «1, 2, 1, 1, 3, 8, 10, 1, 587» медиана будет равна 2. Если вместо 587 поставить 87, она всё равно будет равна 2, если 7 — тоже 2. Среднее арифметическое же в аналогичных случаях будет меняться: 12,7 и 3,8 соответственно.
С помощью медианы можно получить более точные данные и правильнее интерпретировать статистику. Например, при расчёте средней заработной платы, когда 19 сотрудников получают по 20 тысяч рублей, а директор — миллион. Среднее арифметическое в этом случае будет равным 69 тысячам рублей, а медиана — 20. Поэтому последнюю и предпочитают люди, работающие с цифрами: от бухгалтеров до учёных.
Медианное значение рассчитывается из числа или пары чисел, которые больше одной половины показателей и меньше другой. Чтобы найти медиану, надо упорядочить набор чисел и просто найти в нём середину. Вот так: «1, 1, 1, 1, 2, 3, 8, 10, 587».
Если в ряде чётное количество показателей, как например в «1, 1, 1, 1, 2, 3, 8, 10», надо взять два средних числа. Это 1 и 2. Их нужно сложить, а сумму разделить пополам:
(1+2)/2=1,5
Как посчитать медиану, когда данных много
В таком случае можно воспользоваться специальными инструментами.
Онлайн
Например, на сайте Calculator Soup. Достаточно скопировать данные в нужное окно и нажать на кнопку «Calculate». Помимо медианы, калькулятор сразу высчитает кучу других вещей: среднее арифметическое, минимальное и максимальное значение, количество показателей, общую сумму и так далее.
Excel
В редакторе таблиц есть функция «Медиана». Достаточно найти её в специальном окне и выделить массив данных, чтобы высчитать показатель. То же самое можно сделать в Google Docs.
Есть ли альтернативы медиане
Иногда может понадобиться найти не максимально усреднённый показатель, а наиболее частый. Например, когда нужно выяснить самый популярный размер в магазине одежды. В таком случае нужно использовать моду. Это значение, которое встречается чаще других. Так, в ряде «1, 2, 1, 1, 3, 8, 10, 1, 87», мода — это 1. Модой может быть сразу несколько чисел. Как и медиану, её можно посчитать с помощью онлайн‑калькулятора и Excel.
Помимо медианы, могут использоваться процентили, квантили и квартили. Они нужны для более сложных вычислений. Например, чтобы посчитать, сколько процентов людей в стране зарабатывают 50 тысяч рублей или меньше. Показатели разделяют данные на равные части: процентили — на 100, квантили — на 10, квартили — на четыре. Так, медиана — это 50‑й процентиль или второй квартиль.
Читайте также 🧐👨🏫📊
- 7 причин полюбить математику
- Почему мы верим догадкам и слухам больше, чем статистике
- 12 простых приёмов для ускоренной работы в Excel
- 10 увлекательных задач от советского математика
- Что такое золотое сечение и правда ли оно повсюду
Загрузить PDF
Загрузить PDF
Среднее значение, медиана и мода — значения, которые часто используются в статистике и математике. Эти значения найти довольно легко, но их легко и перепутать. Мы расскажем, что они из себя представляют и как их найти.
-
1
Сложите все числа, которые вам даны. Допустим, вам даны числа 2, 3 и 4. Сложим их: 2 + 3 + 4 = 9.
-
2
Сосчитайте количество чисел. У нас есть три цифры.
-
3
Разделите сумму чисел на их количество. Берем 9, делим на 3. 9/3 = 3. Среднее значение в данном случае равно 3. Помните, что не всегда получается целое число.
Реклама
-
1
Запишите все числа, которые вам даны, в порядке возрастания. Например, нам даны числа: 4, 2, 8, 1, 15. Запишите их от меньшего к большему, вот так: 1, 2, 4, 8, 15.
-
2
Найдите два средних числа. Мы расскажем, как это сделать, если у вас имеется четное количество чисел, и как это сделать, если количество чисел нечетное:
- Если у вас нечетное количество чисел, вычеркните левое крайнее число, затем правое крайнее число и так далее. Один оставшийся номер и будет искомой медианой. Если вам дан ряд чисел 4, 7, 8, 11, 21, тогда 8 — медиана, так как 8 стоит посередине.
- Если у вас четное количество чисел, вычеркните по одному числу с каждой стороны, пока у вас не останется два числа посередине. Сложите их и разделите на два. Это и есть значение медианы. Если вам дан ряд чисел 1, 2, 5, 3, 7, 10, то два средних числа — это 5 и 3. Сложим 5 и 3, получим 8, разделим на два, получим 4. Это и есть медиана.
Реклама
-
1
Запишите все числа в ряд. Например, вам даны числа 2, 4, 5, 5, 4 и 5. Запишите их в порядке возрастания.
-
2
Найдите число, которое чаще всего встречается. В данном случае это 5. Если два числа встречаются одинаково часто, то этот ряд двухвершинный или бимодальный, а если больше — то мультимодальный.
Реклама
Советы
- Вам будет легче найти моду и медиану, если вы запишете числа в порядке возрастания.
Реклама
Об этой статье
Эту страницу просматривали 355 010 раз.
