Как найти минимальную работу газа

Принято считать,
что если система совершает работу против
действия внешних сил, то эта работа
положительная.

Если внешние силы
совершают работу над системой, то работа
отрицательная.

Рассмотрим идеальный
газ, находящийся под поршнем в цилиндре
(рис. 11.6). Газ расширяется, и поршень
поднимается на бесконечно малую высоту
.
Силу,
действующую со стороны газа на поршень,
находим по формуле

,

где
– давление газа на поршень;– площадь поршня. Бесконечно малую
работу, совершаемую газом, можно найти
по формуле

,

где
– бесконечно малое изменение объёма
газа. Окончательно

(11.6)

Рис. 11.6

Элементарной
работой газа называется величина

.
(11.7)

Это выражение
остается справедливым для элементарной
работы произвольной физически однородной
и изотропной термодинамической системы
в равновесном процессе.

Работа
A₁₂
термодинамической системы в равновесном
процессе перехода из начального состояния
с объёмом V₁
в конечное состояние с объёмом V₂
(работа в конечном процессе) вычисляется
интегрированием.

При конечном
изменении объёма газа от
доработа

.
(11.8)

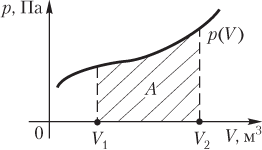
Изобразим процесс
перехода системы из начального состояния
1
в конечное состояние 2,
построив график зависимости P(V).
Элементарная работа
численно равна площади прямоугольника
с длинами сторон P
и dV.
Работа в конечном процессе, когда объём
изменяется от
до,
работа равна площади фигуры, ограниченной
отрезкомоси абсцисс, соответствующим этому
отрезку участком графика функцииP(V)
и проходящими через концы отрезка
параллельными оси ординат прямыми.

Рис. 11.7

Работа – это мера изменения внутренней энергии системы в процессе совершения работы. Работа является функцией процесса, но не является функцией состояния.

Работа идеального газа при изопроцессах

Вычислим
работу идеального газа при изопроцессах.

I.
Рассмотрим изобарический процесс
(рис. 11.8).

П

Рис.
11.8

ри изобарическом процессе.
Если в результате этого процесса объём
газа изменился отдо,
то работа газа

; (11.9)

Построим график
процесса в координатах
.
Работаграфически выражается площадью
заштрихованного прямоугольника.

II. Рассмотрим
изохорический процесс (рис. 11.9).
При изохорическом процессе
и изменение объёма газаdV = 0
равно нулю. Следовательно, согласно
формулам (11.6) и (11.9) работа
газа при изохорическом процессе равна
нулю.

III.
Рассмотрим
изотермический процесс.
При изотермическом процессе
и внутренняя энергия газа

. (11.10)

Изменение внутренней
энергии
,
т.к..

Если в результате
этого процесса объём газа изменился от
до,
то работа газа равна:.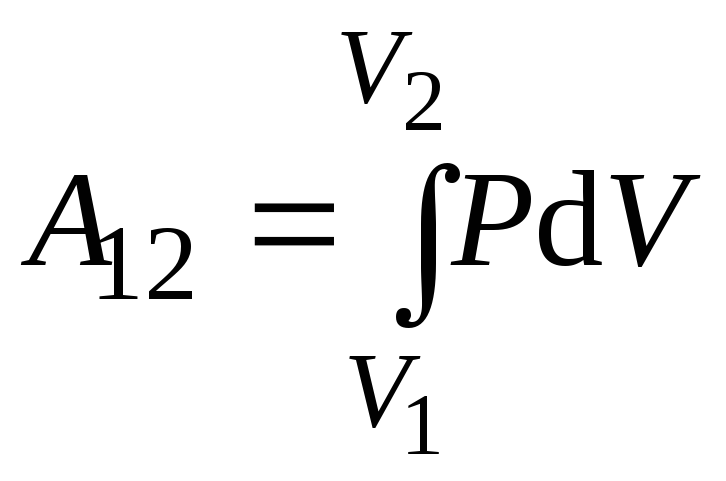

Но здесь
.
Найдём давлениеиз уравнения Менделеева – Клапейрона:

.

Тогда

,
и

.

Итак, при
изотермическом процессе:

. (11.11)

Строим график
процесса в координатах
.

Работа
графически выражается заштрихованной
площадью под изотермой.

11.3. Первое начало термодинамики

Рассмотрим газ в
теплоизолированном цилиндре
(теплоизолированную термодинамическую
систему), рис.
11.11. Цилиндр
разделен жесткой теплопроводящей
перегородкой на два отсека C
и
D.
Объём отсека С
поддерживается постоянным, над этой
частью газа не может быть совершена
работа. Объём отсека D
может меняться при помощи подвижного
поршня. За счет теплопроводящей
перегородки отсеки могут обмениваться
внутренней энергией.

Если в результате
совершения над системой C+D
внешними силами работы
,
система перешла из произвольного
состояния1
в произвольное состояние 2,
то при этом изменилась внутренняя
энергия системы. Тогда
.

Тогда,
изменение внутренней энергии газа в
отсекеС
произошло за счет теплообмена без
совершения работы и равно количеству
теплоты Q,
полученному газом через жёсткую
перегородку. Обозначим
изменение внутренней энергии газа в
отсекеD.
Тогда получим:
.
Это равенство является математическим
выражениемпервого
начала термодинамики.
Оно подразумевает, что полученное
термодинамической системой количество
теплоты Q
равно приращению её внутренней энергии
за вычетом работы над системой внешних
сил.

Если переход
системы из состояние 1
в состояние 2
является равновесным, то
=
–A,
где А
– работа системы против внешних сил.
В таком случае

. (11.12)

Это выражение
представляет собой интегральную форму
записи первого начала термодинамики.

Равенство
подразумевает, что полученное
термодинамической системой в равновесном
процессе количество теплоты Q
идет на приращение его внутренней
энергии
и совершение работы над внешними телами.

Для бесконечно
малого (элементарного) равновесного
процесса уравнение принимает вид:

. (11.13)

Это выражение
представляет собой дифференциальную
форму записи первого начала термодинамики.

Первое начало
термодинамики – это закон сохранения
и превращения энергии. I
начало термодинамики – частный случай
всеобщего закона сохранения энергии:
полная энергия замкнутой системы может
изменяться только качественно,
количественно оставаясь неизменной.

Таким образом,
первое начало термодинамики является
фундаментальным постулатом, утверждающим
собой закон сохранения энергии. Оно
устанавливает закон взаимопревращения
теплоты, энергии и работы. За всю историю
развития науки не обнаружено опытных
фактов, которые противоречили бы этому
постулату.

Дифференциальная
форма записи закона подчеркивает важные
свойства теплоты, энергии и работы.
Обратим на это внимание.

Внутренняя энергия
термодинамической системы (или тела) –
это сумма всех видов энергии (энергии
теплового движения атомов или молекул,
потенциальная энергия их взаимодействия
и т.п.), заключающихся в данной системе,
за исключением энергии, которой система
обладает в результате взаимодействия
с другими телами. Внутреннюю энергию
можно изменить двумя способами.

1.
Газ находится под поршнем. Вдвигая
поршень, совершаем работу. Газ
сжимается и нагревается, его внутренняя
энергия изменяется. Совершение работы
– первый способ изменения внутренней
энергии тела.

2. Но можно изменить
внутреннюю энергию тела и другим
способом, не совершая работы А,
а только подводя к телу тепло. Газ
находится под поршнем. Пусть поршень
закреплён. При подведении тепла к газу,
его внутренняя энергия меняется.

Подведение
некоторого количества теплоты – второй
способ изменения внутренней энергии
тела. Но тогда теплота и работа должны
быть эквивалентными формами передачи
энергии.

Работа – способ
передачи энергии. В процессе работы
происходит переход энергии из одного
вида энергии в другой.

Теплота – тоже
способ передачи энергии.

Внутренняя энергия
является функцией состояния системы
(или тела, если система состоит из одного
тела). Это означает, чтооднозначно определяется термодинамическим
состоянием тела, т.е. каждому состоянию
тела соответствует одно значение.

Если тело в состоянии
1
имеет энергию
,
а в состоянии2
– энергию
,
то изменение энергиине зависит от того, каким путём совершается
переход из одного состояния в другое.
Следовательно, бесконечно малое изменениевнутренней энергии является полным
дифференциалом (11.13).

Количества теплоты
и работы зависят от пути перехода системы
из начального в конечное состояние, они
не являются функциями состояния системы,
их бесконечно малые изменения
ине являются полными дифференциалами,
что подчёркивается в записи этих величин
в формуле (11.13).

В
СИ количество теплоты, энергия и работа
измеряются в джоулях (Дж).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

    Можно показать, что минимальная работа разделения газовой смеси равна работе изотермического сжатия компонентов смеси от давления, равного их парциальному давлению в смеси, до общего давления смеси. [c.547]

    На самый процесс разделения газовой смеси необходимо затратить определенное количество энергии. Минимальная работа разделения газовой смеси при температуре Т определяется уравнением [c.59]

    Минимальная работа разделения газовых смесей. Воздух и другие газовые смеси разделяют на составные части разными методами. Промышленное значение для разделения воздуха на кислород, азот, аргон, криптон, ксенон, неон имеет метод низкотемпературной ректификации, основанный на различии составов находящихся в равновесии жидких и паровых смесей. Если процесс смешения газов протекает без воздействия на него внешних сил, то обратный процесс (разделения газовой смеси на отдельные компоненты) сам совершаться не может и требует затраты энергии. При смешении газов происходит увеличение энтропии (необратимый процесс). [c.40]

    Имея в виду значение уравнению (4-4), получим минимальную работу разделения газовой смеси при температуре окружающей среды  [c.209]

    Вот почему минимальная работа разделения газовой смеси равна максимальной работе смешения компонентов данной газовой смеси, т. е. [c.116]

    Это уравнение показывает, что минимальная работа разделения газовой смеси равна сумме работ сжатия каждого газа от его парциального давления до давления смеси. [c.116]

    Минимальная работа разделения газовых смесей [c.45]

    МИНИМАЛЬНАЯ РАБОТА РАЗДЕЛЕНИЯ ГАЗОВЫХ СМЕСЕЙ [c.84]

    Минимальная работа разделения газовой смеси [c.11]

    ОСНОВНЫЕ СООТНОШЕНИЯ ТЕРМОДИНАМИКИ СМЕСЕЙ, РАСТВОРОВ И АДСОРБЦИИ Минимальная работа разделения газовых смесей [c.45]

    Минимальная работа разделения газовых смесей. Минимальная работа, которую необходимо затратить при обратимом разделении газов, определена общим соотношением (2.32). Для идеальных смесей и для многих реальных смесей теплота смешения ДЛсм = 0 и тогда минимальная работа разделения [c.48]

---

Бродянский В.М., Калинина Е.И.
Разделение газовых смесей

Глава вторая. Минимальная работа и КПД процесса разделения

Для оценки термодинамического совершенства любого процесса разделения необходимо провести сравнение его с идеальным. Идеальный процесс проходит при термодинамическом минимуме работы, который определяется ее затратой на обратимое проведение процесса разделения смеси (минимальная работа разделения).
Отношение минимальной работы разделения к реальной, затраченной в процессе, определяет эксергетический КПД процесса:
      η _e = l_мин / l_d   (2-1)

Величину l_d можно выразить через l_мин и сумму потерь в процессе Σ d:

      l_d=l_мин+ Σ d.

Всякое совершенствование процесса приводит к снижению Σ d, приближению l_d к l_мин и возрастанию η _e .

Значение l_d находится экспериментально или расчетным путем.

Минимальная работа разделения определяется из термодинамических положений с использованием идеальной модели процесса.

Для четкости изложения напомним определения некоторых терминов, связанных с процессами разделения.

Компонент смеси – входящее в смесь вещество определенного химического состава, содержание которого не зависит от наличия других веществ в смеси [6, 7].
Число n компонентов в смеси может быть n>2. Во многих случаях при n>3 смесь в первом приближении можно представить как бинарную, рассматривая две группы компонентов, близких по температурам кипения, как два компонента.

Фракция – смесь, полученная в процессе разделения и отличающаяся от исходной смеси повышенным содержанием одного или нескольких компонентов. В пределе фракция монет состоять из одного чистого компонента.

При разделении n-компонентной смеси можно получить n чистых компонентов, но неограниченное число фракций самого разнообразного состава.

Под процессом разделения мы будем понимать процесс получения из смеси компонентов или фракций, имеющих температуры и давления исходной смеси. Обычно температура смеси, как и продуктов разделения, принимается равной температуре окружающей среды T_см = T_i = T_ос = 293K.

Разделение может быть полным и неполным.
Полное разделение смеси – это процесс получения в чистом виде всех ее компонентов.
Неполное разделение смеси – процесс, в результате которого получается хотя бы одна фракция, не являющаяся чистым компонентом.

На практике разделение многокомпонентной смеси проводится в несколько стадий; на первой стадии получается несколько фракций. Часть из них является конечными продуктами; другая – поступает на дальнейшее разделение. Получение, например аргона из воздуха, в первой стадии сводится к получению аргонной фракции с повышенным содержанием аргона, из которой в следующей стадии вырабатывается сырой аргон, затем – аргон технический, и, в конечном итоге, – чистый аргон.

Минимальная работа разделения многокомпонентной смеси в общем виде

Для определения в общей виде минимальной работы разделения рассмотрим многокомпонентную смесь, имеющую объем V_см. Ее состояние характеризуется термодинамическими параметрами Р_см, Т_см, S_см, i_см, e_см. Примем также вначале, что смесь и ее компоненты – идеальные газы. Каждый из компонентов находится под своим парциальным давлением Р_i, при температуре Т_см в объеме V_см смеси.

Связь между параметрами смеси и компонентов до разделения можно по закону Дальтона записать следующим образом:

  (2-2)

  (2-3)

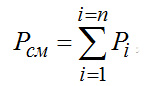
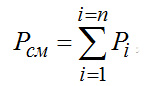
Парциальное давление каждого компонента равно общему давлению, умноженному на долю компонента N в смеси.

Чтобы получить чистые компоненты при Р_см и Т_см, необходимо изотермически повысить давление каждого из компонентов от Р_i до Р_см при одновременном уменьшении объема от V_i=V_см до парциального V_k = V_см*N_i. Определим для этих условий затрату работы и изменение параметров i, S, e в идеальной модели процесса разделения.

Такую модель можно представить в виде системы, состоящей из камеры с полупроницаемыми перегородками и компрессоров K₁, K₂, K_i, K_n для сжатия компонентов (рис.2-1).

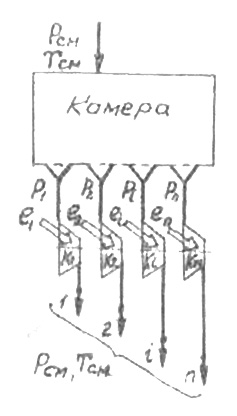
Рис. 2-1.

Смесь поступает в камеру, где давление равно Р_см и температура Т_см. Каждый компонент проходит через соответствующую полупроницаемую перегородку, которая пропускает только один компонент, и поступает в компрессор компонента с парциальным давлением P_i.

Таким образом, после камеры компоненты смеси разделены между собой и находятся под парциальными давлениями. Эта первая стадия процесса разделения проводится без затраты работы, т.к. параметры компонентов смеси остаются неизменными.

Во второй стадии проводится сжатие каждого из компонентов от P_i до P_см при Т=Т_см. При этом необходимо в каждом компрессоре затратить работу изотермического сжатия.

Для 1 кг идеального газа:

, кДж/кг;

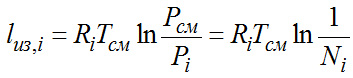
Для 1 моля:

, кДж/кмоль;

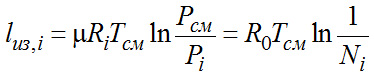
Для N_i долей газа в смеси L_i=N_i*l_из,i, кДж/кмоль смеси.

Общая затрата работы L_мин на n компонентов – минимальная работа разделения смеси – равна сумме работ изотермического сжатия всех ее компонентов:

  (2-4)

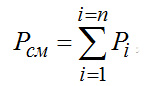
Таким образом, минимальная (или идеальная) работа полного разделении идеальной газовой снеси равна суммарной работе изотермического сжатия всех ее компонентов от парциального давления до давления смеси.

Рассмотренная модель процесса разделения применима для оценки любого способа разделения, т.к. затраты работы в обратимом процессе определяются только начальным н конечным состояниями и не зависят от пути процесса.

Следующая страница: Изменение термодинамических функций в процессе разделения

Теоретически минимальная работа

Cтраница 1

Теоретически минимальная работа ( АЬ0), необходимая для разделения смеси газов на несколько фракций заданного состава, как известно, связана с проведением вполне обратимых ( в термодинамическом смысле) процессов и зависит только от состава разделяемой смеси и составов получаемых фракций.
 [1]

Теоретически минимальная работа, необходимая для сжижения газа, может быть получена при условии, что отдельные процессы – понижение температуры газа и отнятие от него скрытой теплоты парообразования – будут проведены обратимо.
 [2]

С увеличением содержания кислорода в газообразном азоте теоретически минимальная работа разделения быстро уменьшается.
 [4]

При сравнении видно, что площадь, выражающая работу цикла Карно, больше площади, представляющей теоретически минимальную работу.
 [6]

Определить, какое количество холода необходимо для сжижения при атмосферном давлении 1 кг воздуха, вначале находящегося при температуре 290 К, и какую для этого необходимо затратить теоретически минимальную работу.
 [8]

Основным показателем, характеризующим экономичность любого метода сжижения газов, является расход энергии на сжижение 1 кг газа, а степень совершенства данного процесса может быть оценена путем сравнения фактического расхода энергии с теоретически минимальной работой, затрачиваемой на сжижение.
 [9]

Сам сжижаемый газ может служить хладоагентом для обратимого холодильного цикла. В этом случае для сжижения газа требуется теоретически минимальная работа, и цикл называется идеальным.
 [11]

Достижение низких температур связано с сжижением газов, и по существу техника глубокого охлаждения является техникой сжижения газов. Основным показателем, характеризующим экономичность любого метода сжижения газов, является расход энергии на сжижение 1 кгс газа, а степень совершенства данного процесса может быть определена путем сравнения фактического расхода энергии с теоретически минимальной работой, затрачиваемой на сжижение.
 [12]

Достижение низких температур связано с сжижением газов, и по существу техника глубокого охлаждения является техникой сжижения газов. Основным показателем, характеризующим экономичность любого метода сжижения газов, является расход энергии на сжижение 1 кг газа, а степень совершенства данного процесса может быть определена путем сравнения фактического расхода энергии с теоретически минимальной работой, затрачиваемой на сжижение.
 [14]

Достижение низких температур связано с сжижением газов, и по существу техника глубокого охлаждения является техникой сжижения газов. Основным показателем, характеризующим экономичность любого метода сжижения газов, является расход энергии на сжижение 1 кг газа, а степень совершенства данного процесса может быть определена путем сравнения фактического расхода энергии с теоретически минимальной работой, затрачиваемой на сжижение.
 [15]

Страницы:  

   1

Внутренняя энергия газа может изменяться в результате совершения газом работы и сообщения ему теплоты. Поэтому принято говорить о двух формах передачи энергии от одних тел к другим: о теплоте и работе.

Работа газа при произвольном процессе рассчитывается как площадь криволинейной трапеции под графиком p(V). На рис. 6.1 показана произвольная зависимость давления газа p от его объема V (объем газа в начальном состоянии V ₁; объем газа в конечном состоянии V ₂). Площадь заштрихованной фигуры совпадает с работой, совершенной газом.

Если зависимость p(V) представляет собой прямую линию, то работа численно равна площади прямолинейной трапеции.

В Международной системе единиц работа, совершаемая газом, измеряется в джоулях (1 Дж).

Работа газа при изобарном процессе (p = const) может быть вычислена по одной из формул:

A = p∆V, или A = νR∆T,

где p — давление газа; ΔV — изменение объема газа при переходе из начального в конечное состояние, ΔV = V ₂ − V ₁; V ₁ — объем газа в начальном состоянии; V ₂ — объем газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); ΔT — соответствующее изменение температуры газа, ΔT = T ₂ − T ₁; T ₁ — абсолютная температура начального состояния; T ₂ — абсолютная температура конечного состояния.

Работа газа при изохорном процессе (V = const) не совершается:

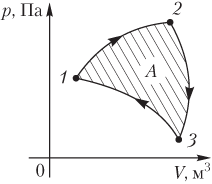
Работа газа при круговом (циклическом) процессе рассчитывается как площадь фигуры, ограниченной графиком функции p(V). На рис. 6.2 показан график произвольного кругового процесса; цифрами обозначены: 1 — исходное состояние идеального газа (оно совпадает с конечным); 2, 3 — промежуточные состояния газа.

Площадь заштрихованной фигуры совпадает с работой, совершенной газом при циклическом процессе.

Работа, совершаемая газом за цикл, может быть:

· положительной (прямой цикл);

· отрицательной (обратный цикл).

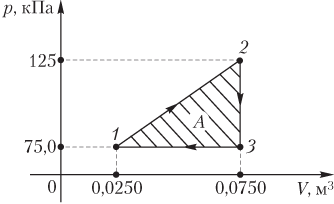
Пример 3. График циклического процесса, происходящего с некоторой массой идеального газа, в координатах p(V) имеет вид прямых, соединяющих точки (0,0250 м 3 ; 75,0 кПа), (0,0750 м 3 ; 125 кПа), (0,0750 м 3 ; 75,0 кПа). Определить абсолютную величину работы, совершаемой газом за цикл.

Решение. На рисунке изображен график циклического процесса в указанных термодинамических координатах p(V).

Величина искомой работы равна площади треугольника, ограниченного прямыми, соединяющими указанные точки:

A=12(125−75,0)⋅103⋅(0,0750−0,0250)=1,25⋅103 Дж=1,25 кДж.

Газ за цикл совершает работу 1,25 кДж.

Пример 4. Газ, состоящий из смеси 2,0 г водорода и 4,2 г гелия, при изобарном нагревании совершил работу 46 кДж. Во сколько раз увеличился объем газа, если его начальная температура была равна 300 К? Молярные массы водорода и гелия равны 2,0 и 4,0 г/моль соответственно.

Решение. Запишем формулу для расчета работы смеси газов при изобарном процессе:

где p — давление смеси газов (постоянная величина), p = const; V ₁ — объем смеси газов в начальном состоянии; V ₂ — объем смеси газов в конечном состоянии.

Давление смеси газов определяется законом Дальтона:

где p ₁ — парциальное давление водорода; p ₂ — парциальное давление гелия.

Давления указанных газов в смеси определяются следующими выражениями:

· парциальное давление водорода

где m ₁ — масса водорода; M ₁ — молярная масса водорода; T ₁ — температура смеси газов в начальном состоянии; V ₁ — объем смеси газов в начальном состоянии; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К);

· парциальное давление гелия

где m ₂ — масса гелия; M ₂ — молярная масса гелия.

Подстановка закона Дальтона и явного вида выражений для парциальных давлений водорода и гелия в формулу для работы, совершаемой смесью указанных газов, дает

Преобразование данного уравнения к виду

позволяет выразить искомое отношение объемов

Следовательно, при совершении указанной работы объем смеси увеличился в 10 раз.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9364 – | 7304 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Условие задачи:

(V_1=2) л, (V_2=3) л, (p_1=400) кПа. Найти работу газа, совершенную в процессе 1-2-3 (схема к задаче приведена справа).

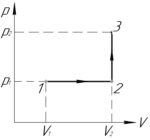
Задача №5.3.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

(V_1=2) л, (V_2=3) л, (p_1=400) кПа, (p_2=600) кПа, (A-?)

Решение задачи:

Работа газа (A), совершенная в процессе 1-2-3, равна сумме работ газа в процессах 1-2 и 2-3.

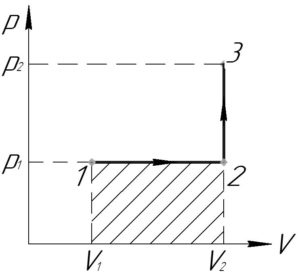
Процесс 1-2 — изобарный, поэтому работу газа (A_<1 — 2>) в этом процессе следует искать по такой формуле (численно работа равна площади фигуры под графиком процесса, на схеме к решению — заштриховано):

Процесс 2-3 — изохорный, работа газа (A_<2 — 3>) в этом процессе равна нулю, так как газ не изменяет своего объема (площадь фигуры под графиком этого процесса в координатах p-V также равна нулю).

В итоге формула (1) примет такой вид:

Переведём объемы газа (V_1) и (V_2) в систему СИ:

Ответ: 400 Дж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в кДж.)

На диаграмме p—V работе, совершаемой газом при переходе из начального состояния в конечное, соответствует площадь под линией, изображающей процесс перехода.

Для процесса 1—2—3 эта площадь показана на рисунке штриховкой. Таким образом, при переходе из состояния 1 в состояние 3 газ совершает работу

Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в кДж.)

На диаграмме p—V работе, совершаемой газом при переходе из начального состояния в конечное, соответствует площадь под линией, изображающей процесс перехода. Для процесса 1—2—3 эта площадь показана на рисунке штриховкой. Таким образом, при переходе из состояния 1 в состояние 3 газ совершает работу

Поясните,почему умножение идет 2х10^5 ,когда газ совершает работу от 1 до 2, вроде должно быть 1х10^5,а по ответу получается от 0 до 2.

На участке 1-2 вообще не совершается работа, так как объем газа на этом этапе не изменяется. Вся работа совершается на участке 2-3. Общее правило следующее, если процесс изображен на диаграмме , то работа равна площади под графиком со знаком плюс, если объем увеличивается, и со знаком минус, если уменьшается. Для тепловой машины, работающей по циклу, полезная работа равна площади ограниченной этим циклом, это укладывается в ранее озвученное правило. Когда мы идем по “верхней” части цикла, работа идет в +, потом возвращаемся по “нижней” в исходную точку, работа теперь идет в -, в результате остается только кусок внутри.

Алексей, вот Вы сказали, что “на участке 1-2 вообще не совершается работа, так как объем газа на этом этапе не изменяется.”

а на участке 2-3 ведь не меняется давление.Так почему работа там совершается? Разве не A=pV ?

Не, не так. Давайте разбираться.

Будем выводить формулу, по которой можно посчитать работу совершенную газом. Когда газ работает? Когда он что-то перемешает. Для этого должен как-то меняться его объем. Например, газ расширяется и толкает поршень вверх, а с ним и какой-то груз, вот Вам и работа. То есть без изменения объема нет работы.

Чтобы вывести формулу, рассмотрим модельную задачу. Рассмотрим цилиндрический сосуд с газом. Пусть сосуд закрыт подвижным поршнем площади . Давление газа равно . Определим, какую работу совершит газ, когда поршень сдвинется на малое расстояние . Так как это работа на малом перемещении, то назовем ее элементарной работой и обозначим через . Работа газа равна произведению силы, с которой он давит на поршень, на перемещение поршня (газ давит нормально, поэтому косинуса не возникает): . Но сила, с которой газ давит на поршень связана с давлением газа соотношением: . Если перемещение поршня мало, то можно считать, что давление газа не изменяется сильно и что оно остается постоянным. Тогда: . Но — это как раз изменение объема газа . Окончательно имеем: .

Получив эту формулу, можно забыть о том, как она выводилась (про сосуд и поршень), она оказывается верной для любого малого изменения объема.

Теперь, чтобы найти работу на конечном изменении объема нужно просуммировать работы по малым изменения, в математике это делается при помощи интеграла: Если внимательно приглядеться, то тут можно как раз увидеть площадь под линией процесса на диаграмме . Вот почему говорят, что для поиска работы надо искать площадь под графиком на этой диаграмме.

Для частных случаев формула приобретает вид:

1) при изобарном процессе давление выносится за знак интеграла и получаем:

2) при изохорном объем не изменяется, поэтому пределы интегрирования совпадают, интеграл равен нулю, работа равна нулю.

3) при изотермическом процессе, давление уже изменяется с объемом, поэтому надо добавить в рассмотрение уравнение Клапейрона-Менделеева: . Следовательно, . А значит работа при изотермическом процессе равна: