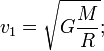Содержание
- Как найти минимальную скорость планеты
- Что такое скорость планеты
- Зачем нужно знать минимальную скорость планеты
- Как найти минимальную скорость планеты
- Выводы
- Как найти минимальную скорость планеты
- Первые шаги в поиске минимальной скорости планеты
- Расчет минимальной скорости планеты
- Пример расчета минимальной скорости планеты
- Итог
- Как найти минимальную скорость планеты
- Что такое минимальная скорость планеты?
- Формула для расчета минимальной скорости планеты
- Пример расчета минимальной скорости планеты
- Заключение
Как найти минимальную скорость планеты
Космические исследования стали для человечества настоящим вызовом. Наши ученые стали настоящими героями, которые каждый день открывают для нас новые грани Вселенной. Одной из важнейших задач в области космической науки является определение минимальной скорости планет. Об этом мы и поговорим в данной статье.
Что такое скорость планеты
Скорость планеты — это параметр, обозначающий, как быстро планета перемещается вокруг своей оси или вокруг звезды, вокруг которой она обращается. Величина скорости планеты измеряется в километрах в секунду или километрах в час. Она зависит от многих факторов, таких как масса планеты, расстояние до звезды, от которой планета обращается, и многих других.
Зачем нужно знать минимальную скорость планеты
Знание минимальной скорости планеты необходимо для того, чтобы понимать, какие планеты могут быть жизнеспособными. Если скорость планеты слишком мала, то она не сможет удерживать атмосферу вокруг себя, и в результате жизнь на этой планете будет невозможна. Если же скорость планеты слишком велика, то это может привести к различным катастрофам, таким как землетрясения, цунами и т.д. Таким образом, знание минимальной скорости планеты поможет ученым определить, на каких планетах может быть жизнь.
Как найти минимальную скорость планеты
Найти минимальную скорость планеты можно с помощью специальных моделей и математических вычислений. Одним из основных факторов, влияющих на скорость планеты, является масса планеты. Чем больше масса планеты, тем медленнее она будет двигаться. Также на скорость планеты влияет ее расстояние до звезды, вокруг которой она обращается. Чем меньше расстояние, тем быстрее она движется. В этом случае ученые используют закон всемирного тяготения.
Формула для определения скорости планеты выглядит так: V=2πR/T, где V — скорость планеты, R — радиус орбиты планеты, T — время одного оборота вокруг своей оси.
После определения элементов формулы происходит их дальнейший расчет. Существуют специальные программы, которые могут сделать это быстрее и точнее, чем вручную. Однако, чтобы понимать, как работают эти программы, необходимо обладать достаточными знаниями в области астрономии и математики.
Выводы
Таким образом, определение минимальной скорости планеты является очень важной задачей в области космической науки. Поиск ответа на этот вопрос поможет ученым понять, на каких планетах может быть жизнь, и какие риски связаны с быстрой или медленной скоростью планеты. Чтобы найти минимальную скорость планеты, нужно проводить математические расчеты и использовать специальные программы. Однако, для этого необходимо обладать достаточными знаниями в области астрономии и математики.
Как найти минимальную скорость планеты
Минимальная скорость планеты может быть важной информацией для астрономов и исследователей. Она позволяет предсказать траекторию движения планеты и понять ее поведение в космическом пространстве. Но как найти эту скорость?
Первые шаги в поиске минимальной скорости планеты
Для начала необходимо определить в какой системе координат проводится измерение. В большинстве случаев движение планеты вокруг звезды будет рассматриваться в гелиоцентрической системе координат. Это значит, что планета движется вокруг Солнца.
Однако можно произвести и расчеты в других системах координат. Например, в системе координат барицентрической, которая используется для рассмотрения движения планет между собой без учета влияния звезды. В этом случае, минимальная скорость планеты будет определяться исходя из ее расположения в момент наименьшего расстояния к другой планете.
Расчет минимальной скорости планеты
Для расчета минимальной скорости планеты необходимо знать ее орбитальные параметры: большую полуось орбиты, эксцентриситет и аргумент перицентра. Большая полуось орбиты – это расстояние от центра планеты до центра звезды в точке наибольшего удаления. Эксцентриситет – это мера отклонения формы орбиты от круговой. Аргумент перицентра – это угол между апоцентром орбиты и пересечением орбиты с плоскостью нулевого склонения.
Определив эти параметры, можно применить формулы, которые используются для расчета минимальной скорости. Одна из них:
v = sqrt(G * M * ((2 / r) — (1 / a)))
где v – минимальная скорость планеты, G – гравитационная постоянная (6,67 * 10^-11 м^3/(кг*с^2)), M – масса звезды (в килограммах), r – расстояние от звезды до планеты в момент наименьшего расстояния, a – большая полуось орбиты.
Другая формула для расчета минимальной скорости планеты:
v = sqrt(G * M * ((1 — e) / (1 + e)) * ((2 / (r * (1 + e))) — (1 / a)))
где e – эксцентриситет орбиты.
Пример расчета минимальной скорости планеты
Рассмотрим пример расчета минимальной скорости Земли. Большая полуось орбиты земли равна 149.6 миллионов километров, эксцентриситет орбиты – 0,0167. Масса Солнца составляет 1,9891 * 10^30 кг.
Используя первую формулу, получим:
v = sqrt(6,67*10^-11 * 1,9891*10^30 * ((2 / (149,6*10^9)) — (1 / (149,6*10^9 * 2))))
v = 29,78 км/с
Таким образом, минимальная скорость Земли в момент наименьшего расстояния от Солнца равна 29,78 км/с.
Итог
Нахождение минимальной скорости планеты является важным этапом в исследовании космического пространства и расчета траекторий. Для ее определения необходимо знать орбитальные параметры планеты и применить специальные формулы. Благодаря этой информации возможно предсказывать движение планет и проводить более точные исследования.
Как найти минимальную скорость планеты
При изучении нашей солнечной системы очень интересно узнать, какова минимальная скорость, необходимая планете, чтобы она не покинула орбиту вокруг своей звезды. Если планета движется медленнее, чем минимальная скорость, она будет падать к звезде и в конечном итоге уничтожится.
Что такое минимальная скорость планеты?
Минимальная скорость планеты — это такая скорость, при которой планета способна сохранять круговую орбиту вокруг своей звезды. Она зависит от массы звезды, скорости вращения звезды, массы планеты и ее расстояния от звезды.
Если масса звезды увеличивается, минимальная скорость планеты также увеличивается. Если скорость вращения звезды уменьшается, минимальная скорость планеты тоже уменьшается. Если масса планеты увеличивается, минимальная скорость планеты увеличивается, но не так сильно, как в случае с массой звезды. Наконец, если расстояние от звезды увеличивается, минимальная скорость планеты уменьшается. Это связано с уменьшением силы притяжения звезды, которая играет наиболее важную роль в сохранении орбиты планеты.
Формула для расчета минимальной скорости планеты
Формула для расчета минимальной скорости планеты:
v = sqrt(GM / r)
где:
- v — минимальная скорость планеты (м/с)
- G — гравитационная постоянная (6,674 * 10^-11 Н * м^2 / кг^2)
- M — масса звезды (кг)
- r — радиус орбиты планеты вокруг звезды (м)
Формула показывает, что минимальная скорость планеты пропорциональна квадратному корню из массы звезды и обратно пропорциональна квадратному корню радиуса орбиты. Это означает, что при увеличении радиуса орбиты скорость планеты может быть меньше, чтобы она могла сохранять орбиту вокруг звезды.
Пример расчета минимальной скорости планеты
Давайте рассмотрим пример расчета минимальной скорости планеты. Предположим, что у нас есть планета, вращающаяся вокруг звезды массой 2 * 10^30 кг и находящаяся на расстоянии 1 * 10^11 м от звезды. Какую минимальную скорость должна иметь планета для того, чтобы она могла сохранять орбиту?
Используя формулу:
v = sqrt(GM / r)
Мы можем рассчитать минимальную скорость:
v = sqrt((6.674 * 10^-11) * (2 * 10^30) / (1 * 10^11)) = 30 559 м/с
Таким образом, минимальная скорость планеты должна быть не менее 30 559 м/с, чтобы она могла сохранять орбиту вокруг звезды массой 2 * 10^30 кг.
Заключение
Минимальная скорость планеты — это важный параметр, определяющий ее способность сохранять орбиту вокруг своей звезды. Она зависит от многих факторов, таких как масса звезды, скорость вращения звезды, масса планеты и ее расстояние от звезды. Формула для ее расчета показывает, что минимальная скорость планеты пропорциональна квадратному корню из массы звезды и обратно пропорциональна квадратному корню радиуса орбиты. Пример расчета показал, что минимальная скорость планеты должна быть не менее 30 559 м/с для сохранения орбиты вокруг звезды массой 2 * 10^30 кг.
Если мы подбросим камень в воздух – он упадет на Землю. Если у самолета на высоте 10 километром отключаться двигатели – он тоже упадет на Землю. Но спутники и космические корабли, что мы запускаем в космос, не падают. Почему?
Все дело в том, с какой скоростью тот или иной объект удаляется от планеты. Хватит ли этому объекту энергии преодолеть притяжение планеты.
Телеграмм-канал Космос нас ждет – больше космоса и красоты. Подписывайтесь!
Первая космическая скорость
Это та самая минимальная скорость для выхода корабля или спутника на круговую орбиту, равную радиуса планеты, без учета вращения планеты и сопротивления ее атмосферы.
Если скорость будет превышать первую, но не достигнет второй космической скорости, то траектория тела из круговой начнет переходить в эллиптическую.
Впервые такую скорость смог достичь первый искусственный спутник Земли «Спутник-1» СССР 4 октября 1957 года.
Расчет
Вторая космическая скорость
Это минимальная скорость, которую следует придать телу для того, чтобы оно покинуло замкнутую орбиту и смогло улететь от небесного тела за пределы его гравитационного поля.
Иными словами, для Земли, это та скорость, с которой должны двигаться космические аппараты (КА) для полетов к другим объектам Солнечной системы: Луны, Марса и т.д.
Движение тела на второй космической скорости происходит по параболической траектории.
Впервые такую скорость развил Советский космический аппарат Луна-1 2 января 1959 года, чтобы преодолеть расстояние от Земли до Луны и изучить наш естественный спутник.
Расчет
Третья космическая скорость
Такую скорость необходимо придать телу, чтобы оно смогло покинуть Солнечную систему. Так как 99,8% массы Солнечной системы приходится на Солнце, то можно сказать, что КА надо преодолеть гравитационное притяжение Солнца.
Расчет
Для Солнечной системы это величина равна 16,650 км/с.
Самое выгодное расположение космодрома для подобного запуска – максимально близко к экватору, так как на экваторе самая большая скорость собственного вращения Земли вокруг своей оси и направление движения в сторону вращения Земли и в сторону орбитального движения Земли по орбите.
КА “Новые горизонты” покинул атмосферу Земли со скоростью близкой к третьей космической – 16,26 км /с. Относительно Солнца он имел скорость 45 км/с. Такой скорости недостаточно, чтобы покинуть Солнечную систему. Но благодаря гравитационному маневру у Юпитера, “Новые горизонты” добавил еще 4 км/с, что позволило ему покинуть Солнечную системы, предварительно показав нам карликовую планету Плутон.
Четвертая космическая скорость
Эта та скорость, которая позволит покинуть галактику в данной точке.
Четвертая космическая в основном не зависит от месторасположения Земли в Млечном пути. Она зависит от расположения и плотности звездного вещества в окрестностях Солнечной системы. А эти данные пока мало изучены.
Для нашей части галактики четвертая космическая скорость примерно равна 550 км/с.
Пятая космическая скорость
Эта скорость редко применима и является больше «фантазией», так как такую скорость необходимо развить для путешествия на другую планету в другую звездную систему, независимо от их взаимного расположения, с траекторией перпендикулярно плоскости эклиптики.
Для Земли эта скорость будет равна 43,6 км/с.
Почему спутники не падают на Землю
Этот вопрос поднимался в самом начале статьи. Теперь давайте на него ответим.
На спутник на орбите действует сила тяжести со стороны Земли. И под действием этой силы спутнику логичнее упасть.
Но, он летит вокруг Земли с первой космической скоростью – 7,9 км/с. Вспомните, чем больше скорость – тем сложнее затормозить. Вот и здесь, спутник и хотел бы упасть, но он не может затормозить и просто пролетает мимо Земли по инерции, тем самым продолжая бесконечное падение.
То есть, спутники падают, но промахиваются и не попадают в Землю.
Еще больше космоса и интересных фактов в телеграмм-канале.
Если Вам понравилась статья:
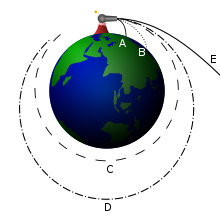
Анализ первой и второй космической скорости по Исааку Ньютону. Снаряды A и B падают на Землю. Снаряд C выходит на круговую орбиту, D — на эллиптическую. Снаряд E улетает в открытый космос.
Пе́рвая косми́ческая ско́рость (кругова́я ско́рость) — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты[1]. Первая космическая скорость для орбиты, расположенной вблизи поверхности Земли, составляет 7,91 км/с[2]. Впервые первая космическая скорость была достигнута космическим аппаратом СССР «Спутник-1» 4 октября 1957 года[3].
Вычисление и понимание[править | править код]
В инерциальной системе отсчёта на объект, движущийся по круговой орбите вокруг Земли, будет действовать только одна сила — сила тяготения Земли. При этом движение объекта не будет ни равномерным, ни равноускоренным. Происходит это потому, что скорость и ускорение (величины не скалярные, а векторные) в данном случае не удовлетворяют условиям равномерности/равноускоренности движения — то есть движения с постоянной (по величине и направлению) скоростью/ускорением. Действительно — вектор скорости будет постоянно направлен по касательной к поверхности Земли, а вектор ускорения — перпендикулярно ему к центру Земли, при этом по мере движения по орбите эти векторы постоянно будут менять своё направление. Поэтому в инерциальной системе отсчёта такое движение часто называют «движение по круговой орбите с постоянной по модулю скоростью».
Уравнение второго закона Ньютона для тела, принимаемого за материальную точку, движущегося по орбите вокруг планеты c радиальным распределением плотности, можно записать в виде[4]
где 




В общем случае при движении тела по окружности с постоянной по модулю скоростью 


Отсюда для первой космической скорости следует
Радиус орбиты складывается из радиуса планеты 

Подставляя численные значения для орбиты, расположенной вблизи поверхности Земли (h ≈ 0, M = 5,97·1024 кг, R0 = 6 371 000 м (радиус указывается в метрах), G=6.67·10^-11 м³·кг⁻¹·с⁻²), получаем
7900 м/с.
Период обращения спутника по круговой орбите равен:
При удалении спутника от центра Земли на расстояние 42 200 км период обращения становится равным 24 часа, то есть времени обращения Земли вокруг своей оси. Если запустить на круговую орбиту спутник на такой высоте в сторону вращения Земли в плоскости экватора, то он будет висеть над одним и тем же местом поверхности Земли на высоте 35 800 км (геостационарная орбита)[4].
С увеличением высоты орбиты первая космическая скорость уменьшается. Так, на высоте 100 км над поверхностью Земли она равна 7 844 м/с, а на высоте 300 км — 7 726 м/с[6].
Другое выражение первой космической скорости имеет вид: 


Если скорость тела направлена горизонтально и при этом больше первой космической скорости, но меньше второй космической, то орбита представляет собой эллипс[6].
См. также[править | править код]
- Космическая скорость
- Вторая космическая скорость
- Третья космическая скорость
- Четвёртая космическая скорость
Примечания[править | править код]
- ↑ Космические скорости // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 474—475. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ Кононович Э. В., Мороз В. И. Общий курс астрономии: учебное пособие / Под ред. В. В. Иванова. — 2-е изд., испр. — М.: Едиториал УРСС, 2004. — С. 91. — 544 с. — (Классический университетский учебник). — ISBN 5-354-00866-2.
- ↑ 1 2 Билимович Б. Ф. Законы механики в технике. — М., Просвещение, 1975. — Тираж 80000 экз. — с. 37-39
- ↑ 1 2 3 Ишлинский А. Ю. Классическая механика и силы инерции. — М.: Наука, 1987. — c. 47-48
- ↑ Савельев И. В. Курс общей физики. Т. 1. Механика. Молекулярная физика. — М.: Наука, 1987. — c. 178
- ↑ 1 2 Рябов Ю. А. Движение небесных тел. — 3-е изд., перераб. — М.: «Наука», 1977. — С. 146.
Ссылки[править | править код]
- Roger R. Bate; Donald D. Mueller; Jerry E. White. Fundamentals of astrodynamics. — New York: Dover Publications, 1971. — ISBN 978-0-486-60061-1.
Космическая скорость
[править]
Материал
из Википедии — свободной энциклопедии
Космическая
скорость (первая v1, вторая v2, третья v3 и четвёртая v4) —
это минимальная скорость, при которой
какое-либо тело в свободном движении с
поверхности небесного тела сможет:
-
v1 (круговая
скорость) — стать спутником небесного
тела (то
есть вращаться по круговой орбите
вокруг НТ на нулевой или пренебрежимо
малой высоте относительно поверхности); -
v2 (параболическая
скорость, скорость убегания) —
преодолеть гравитационное
притяжение небесного
тела и
уйти на бесконечность; -
v3 —
покинуть звёздную
систему,
преодолев притяжение звезды; -
v4 —
покинуть галактику.
Вторая
космическая скорость в раза
больше первой.
[Править]Первая и вторая космические скорости для различных объектов
|
Небесное |
Масса |
v1, |
v2, |
|
Луна |
0,0123 |
1,680 |
2,375 |
|
Меркурий |
0,055 |
3,05 |
4,3 |
|
Марс |
0,108 |
3,546 |
5,0 |
|
Венера |
0,82 |
7,356 |
10,22 |
|
Земля |
1 |
7,91 |
11,2 |
|
Уран |
14,5 |
15,6 |
22,0 |
|
Нептун |
17,5 |
24,0 |
|
|
Сатурн |
95,3 |
36,0 |
|
|
Юпитер |
318,3 |
61,0 |
|
|
Солнце |
333 |
437 |
617,7 |
|
Сириус |
325 |
10 |
|
|
Нейтронная |
666 |
200 |
|
|
Кварковая |
832 |
300 |
|
|
Чёрная |
832 |
не |
[править]
Первая космическая скорость
[править]
Материал
из Википедии — свободной энциклопедии
Анализ
первой и второй космической скорости
по Исааку Ньютону. Снаряды A и B падают
на Землю. Снаряд C выходит на круговую
орбиту, D — на эллиптическую. Снаряд
E улетает в открытый космос.
Пе́рвая
косми́ческая ско́рость (кругова́я
ско́рость) — скорость,
которую необходимо придать объекту,
который после этого не будет использовать
реактивное движение, чтобы вывести его
на круговую орбиту (пренебрегая
сопротивлением атмосферы и
вращением планеты).
Иными словами, первая космическая
скорость — это минимальная скорость,
при которой тело, движущееся горизонтально
над поверхностью планеты, не упадёт на
неё, а будет двигаться по круговой
орбите.
|
Содержание [убрать]
|
[Править]Вычисление
В инерциальной
системе отсчёта на
объект, движущийся по круговой орбите
вокруг Земли будет действовать только
одна сила — сила тяготения Земли.
При этом движение объекта не будет ни
равномерным, ни равноускоренным.
Происходит это потому, что скорость и
ускорение (величины не скалярные, а
векторные) в данном случае не удовлетворяют
условиям равномерности/равноускоренности
движения — то есть движения с
постоянной (по величине и направлению)
скоростью/ускорением. Действительно —
вектор скорости будет постоянно направлен
по касательной к поверхности Земли, а
вектор ускорения — перпендикулярно
ему к центру Земли, при этом по мере
движения по орбите эти векторы постоянно
будут менять свое направление. Поэтому
в инерциальной системе отсчета такое
движение часто называют «движение по
круговой орбите с постоянной по
модулю скоростью».
Часто
для удобства вычисления первой космической
скорости переходят к рассмотрению этого
движения в неинерциальной системе
отсчета — относительно Земли. В этом
случае объект на орбите будет находиться
в состоянии покоя, так как на него будут
действовать уже две силы: центробежная
сила и сила
тяготения.
Соответственно, для вычисления первой
космической скорости необходимо
рассмотреть равенство этих сил.
где m —
масса объекта, M —
масса планеты, G — гравитационная
постоянная (6,67259·10−11 м³·кг−1·с−2), —
первая космическая скорость, R —
радиус планеты. Подставляя численные
значения (для Земли M = 5,97·1024 кг, R = 6 371 км),
найдем
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Решебник по астрономии 11 класс на урок №8 (рабочая тетрадь) – Законы Кеплера
1. Сформулируйте законы Кеплера.
| Первый закон Кеплера | Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце |
| Второй закон Кеплера | Радиус-вектор планеты в равные промежутки времени описывают равновеликие площади |
| Третий закон Кеплера | Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит |
2. На рисунке 8.1 укажите точки афелия и перигелия.
3. Выведите формулы для вычисления перигелийного и афелийного расстояний по известным эксцентриситету и значению большой полуоси.
Перигелийное расстояние ПС = q; афелийное расстояние СА = Q. АП = 2a; ПО = ОА = a. Тогда: q = ОП — СО; e = СО/ОП; СО = e · a; Q = ОА + СО; q = a — ea = a(1 — e); Q = a + ea = a(1 + e).
4. Определите афелийное расстояние астероида Минск, если большая полуось его орбиты а = 2,88 а. е., а эксцентриситете = 0,24.
Решение.
5. Определите перигелийное расстояние астероида Икар, если большая полуось его орбиты а = 160 млн км, а эксцентриситет е = 0,83.
Решение.
6. Выполните задание.
Вариант 1.
1. На рисунке 8.1, а укажите точки орбиты, в которых:
а) скорость планеты максимальна;
б) потенциальная энергия максимальна;
в) кинетическая энергия минимальна.
2. Как изменяется скорость планеты при ее движении от афелия к перигелию? (Увеличится)
Вариант 2.
1. На рисунке 8.1, б укажите точки орбиты, в которых:
а) скорость планеты минимальна;
б) потенциальная энергия минимальна;
в) кинетическая энергия максимальна.
2. Как изменяется скорость Луны при ее движении от перигея к апогею? (Уменьшится)
7. Решите задачи.
Вариант 1.
1. Определите период обращения астероида Белоруссия, если большая полуось его орбиты а = 2,40 а. е.
2. Звездный период обращения Юпитера вокруг Солнца Т = 12 лет. Каково среднее расстояние от Юпитера до Солнца?
Вариант 2.
1. Период обращения малой планеты Шагал вокруг Солнца Т = 5,6 года. Определите большую полуось ее орбиты.
2. Большая полуось орбиты астероида Тихов а = 2,71 а. е. За какое время этот астероид обращается вокруг Солнца?