3.2.1. Как правильно понимать условия задачи?
Скорость тела увеличилась в n раз:
Скорость уменьшилась в n раз:
Скорость увеличилась на 2 м/с:
Во сколько раз увеличилась скорость?
Во сколько раз уменьшилась скорость?
Как изменилась скорость?
На сколько увеличилась скорость?
На сколько уменьшилась скорость?
Тело достигло наибольшей высоты:
Тело прошло половину расстояния:
Тело бросают с земли:
(последнее условие часто ускользает из вида — если у тела скорость равна нулю, например у ручки, лежащей на столе, оно может полететь само вверх?), начальная скорость направлена вверх.
Тело бросают вниз: начальная скорость направлена вниз.
Тело бросают вверх: начальная скорость направлена вверх.
В момент падения на землю:
Тело выпадает из аэростата (воздушного шара): начальная скорость равна скорости аэростата (воздушного шара) и направлена в ту же самую сторону.
3.2.2. Как по графику скорости определить ускорение?
Закон изменения скорости имеет вид:
Графиком этого уравнения является прямая линия. Так как — коэффициент перед t, то
является угловым коэффициентом прямой.
Для графика 1:
То, что график 1 «поднимается вверх», означает — проекция ускорения положительна, т. е. вектор направлен в положительном направлении оси Ox. Пересечение графика с осью — изменение направления движения на противоположное.
Для графика 2:
То, что график 2 «опускается вниз», означает — проекция ускорения отрицательна, т. е. вектор направлен в отрицательном направлении оси Ox. Пересечение графика с осью — изменение направления движения на противоположное.
Для определения и
выбираем такие точки на графике, в которых можно точно определить значения, как правило, это точки, находящиеся в вершинах клеток.
3.2.3. Как по графику скорости определить пройденный путь и перемещение?
Как сказано в пункте 3.1.6 путь можно как площадь под графиком зависимости скорости от ускорения. Простой случай показан в пункте 3.1.6. Рассмотрим более сложный вариант, когда график скорости пересекает ось времени.
Напомним, что путь может только увеличиваться, поэтому путь, который проехало тело в примере на рисунке 9 равен:
где
и
— площади фигур, закрашенных на рисунке.
Для определения перемещения нужно заметить, что в точках и
тело меняет направление движения. Проезжая путь
тело движется в положительном направлении оси Ox, так как график лежит над осью времени. Проезжая путь
тело движется в обратную сторону, в отрицательном направлении оси Ox так как график лежит под осью времени. Проезжая путь
, тело движется в положительном направлении оси Ox, так как график лежит над осью времени. Таким образом, перемещение равно:
Еще раз обратим внимание:
1) пересечение с осью времени означает поворот в обратную сторону;
2) площадь графика, лежащего под осью времени положительна и входит со знаком «+» в определение пройденного пути, но со знаком «−» в определении перемещения.
3.2.4. Как из графика зависимости ускорения от времени определить зависимость скорости от времени и координаты от времени?
Для того, чтобы определить требуемые зависимости необходимы начальные условия — значения скорости и координаты в момент времени Без начальных условий решить однозначно данную задачу невозможно, поэтому, как правило, в условии задачи они даны.
В данном примере постараемся привести все рассуждения в буквах, для того, чтобы частном примере (при подстановке цифр) не потерять суть действий.
Пусть в момент времени скорость тела равна нулю
и начальная координата
1) От 0 до
Начальные значения скорости и координаты определяем из начальных условий, а ускорение из графика:
следовательно, движение равноускоренное и закон изменения скорости имеет вид:
К концу данного промежутка времени () скорость (
) и координата (
) будут равны (вместо времени в формулы
и
нужно подставить
):
2) От до
Начальное значение скорости на этом промежутке должно быть равно конечному значению на предыдущем промежутке, начальное значение координаты равно конечному значению координаты на предыдущем промежутке, а ускорение определяем из графика:
следовательно, движение равноускоренное и закон изменения скорости имеет вид:
К концу данного промежутка времени () скорость (
) и координата (
) будут равны (вместо времени в формулы
и
нужно подставить
):
3) От до
Начальное значение скорости на этом промежутке должно быть равно конечному значению на предыдущем промежутке, начальное значение координаты равно конечному значению координаты на предыдущем промежутке, а ускорение определяем из графика:
следовательно, движение равноускоренное и закон изменения скорости имеет вид:
К концу данного промежутка времени () скорость (
) и координата (
) будут равны (вместо времени в формулы
и
нужно подставить
):
Для лучшего понимания построим полученные результаты на графике (см. рис.)
На графике скорости:
1) От 0 до прямая линия, «поднимающаяся вверх» (т. к.
);
2) От до
горизонтальная прямая линия (т. к.
);
3) От до
: прямая линия, «опускающаяся вниз» (т. к.
).
На графике координаты:
1) От 0 до : парабола, ветви которой направлены вверх (т. к.
);
2) От до
: прямая линия, поднимающаяся вверх (т. к.
);
3) От до
: парабола, ветви которой направлены вниз (т. к.
).
3.2.5. Как из графика закона движения записать аналитическую формулу закона движения?
Пусть дан график равнопеременного движения.
Закон равнопеременного движения имеет вид:
В этой формуле три неизвестные величины:
и
Для определения достаточно посмотреть на значение функции при
Для определения двух других неизвестных выбираем две точки на графике, значения которых мы можем точно определить — вершины клеток. Получим систему:
При этом считаем, что нам уже известно. Умножим 1-ое уравнение системы на
а 2-ое уравнение на
:
Вычтем из 1-го уравнения 2-ое, после чего получаем:
Полученное из данного выражения значение подставим в любое из уравнений системы (3.67) и решим полученное уравнение относительно
:
3.2.6. Как по известному закону движения определить закон изменения скорости?
Закон равнопеременного движения имеет вид:
Это его стандартный вид для данного типа движения и никак иначе он выглядеть не может, поэтому его стоит запомнить.
В данном законе коэффициент перед t — это значение начальной скорости, коэффициент пред — это ускорение, деленное пополам.
Например, пусть дан закон:
Тогда
И уравнение скорости имеет вид:
Таким образом, для решения подобных задач, необходимо точно помнить вид закона равнопеременного движения и смысл коэффициентов, входящих в это уравнение.
Однако можно пойти и иным путем. Вспомним формулу:
В нашем примере:
3.2.7. Как определить место и время встречи?
Пусть даны законы движения двух тел:
В момент встречи тела оказываются в одной координате, то есть и необходимо решить уравнение:
Перепишем его в виде:
Это квадратное уравнение, общее решение которого приводить не будем, в силу его громоздкости. Квадратное уравнение либо не имеет решений, что означает — тела не встретились; либо имеет одно решение — одна единственная встреча; либо имеет два решения — две встречи тел.
Полученные решения необходимо проверять на физическую реализуемость. Самое главное условие: и
то есть время встречи должно быть положительным.
3.2.8. Как определить путь за -ую секунду?
Пусть тело начинает движение из состояния покоя и за -ую секунду проходит путь Требуется найти, какой путь проходит тело за n-ую секунду.
Для решения этой задачи необходимо воспользоваться формулой (3.25):
Обозначим Тогда
Поделим уравнение на
и получим:
3.2.9. Как движется тело, брошенное вверх с высоты h?
Тело, брошено вверх с высоты h со скоростью
Уравнение координаты y в произвольный момент времени:
Уравнение проекции скорости в произвольный момент времени:
Время подъема до наивысшей точки полета определяется из условия
:
Для нахождения максимальной высоты H необходимо в необходимо подставить
:
Время всего полета определяется из условия
Получаем уравнение:
Это квадратное уравнение, которое имеет два решения, но в данной задаче тело может оказаться в координате только один раз. Поэтому среди полученных решений нужно одно «убрать». Главный критерий отсева — время полета не может быть отрицательным:
Скорость в момент падения:
3.2.10. Как движется тело, брошенное вниз с высоты h?
Тело, брошено вверх с высоты h со скоростью
Уравнение координаты y в произвольный момент времени:
Уравнение проекции скорости в произвольный момент времени:
Время всего полета определяется из уравнения:
Это квадратное уравнение, которое имеет два решения, но в данной задаче тело может оказаться в координате только один раз. Поэтому среди полученных решений нужно одно «убрать». Главный критерий отсева — время полета не может быть отрицательным:
Скорость в момент падения:
3.2.11. Как движется тело брошенное вверх с поверхности земли?
Тело брошено вверх с поверхности земли со скоростью
Уравнение координаты y в произвольный момент времени:
Уравнение проекции скорости в произвольный момент времени:
Время подъема до наивысшей точки полета определяется из условия
Для нахождения максимальной высоты H необходимо в (3.89) необходимо подставить
Время всего полета определяется из условия
Получаем уравнение:
Скорость в момент падения:
Заметьте, что что означает — время подъема равно времени падения на ту же высоту.
Также получили: то есть — с какой скоростью бросили, с такой же скоростью тело упало. Знак «−» в формуле
указывает, что скорость в момент падения направлена вниз, то есть против оси Oy.
3.2.12. Тело побывало на одной высоте дважды…
При бросании тела оно может дважды оказаться на одной высоте — первый раз при движении вверх, второй — при падении вниз.
1) Когда тело оказывается на высоте h?
Для тела, брошенного вверх с поверхности земли справедлив закон движения:
Когда тело окажется на высоте h его координата будет равна Получаем уравнение:
решение которого имеет вид:
2) Известны времена и
когда тело оказалось на высоте h. Когда тело окажется на максимальной высоте?
Время полета с высоты h назад до высоты h равно Как уже было показано, время подъема равно времени падения до той же высоты, поэтому время полета от высоты h до максимальной высоты равно:
Тогда время полета от начала движения до максимальной высоты:
3) Известны времена и
когда тело оказалось на высоте h. Чему равно время полета тела?
Все время полета равно:
4) Известны времена и
когда тело оказалось на высоте h. Чему равна максимальная высота подъема?
3.2.13. Как движется тело, брошенное горизонтально с высоты h?
Тело, брошено горизонтально с высоты h со скоростью
Проекции начальной скорости на оси:
Проекции ускорения:
Проекции скорости в произвольный момент времени t:
Модуль скорости в произвольный момент времени t:
Координаты тела в произвольный момент времени t:
Время полета определяется из условия
Для определения дальности полета необходимо в уравнение для координаты x вместо t подставить
Для определения скорости тела в момент падения необходимо в уравнение вместо t подставить
Угол, под которым падает тело на землю:
3.2.14. Как движется тело, брошенное под углом α к горизонту с высоты h?
Тело, брошено под углом α к горизонту с высоты h со скоростью
Проекции начальной скорости на оси:
Проекции ускорения:
Проекции скорости в произвольный момент времени t:
Модуль скорости в произвольный момент времени t:
Координаты тела в произвольный момент времени t:
Время полета до наивысшей точки определяется из условия
Скорость в наивысшей точке полета
Максимальная высота H определяется при подстановке в закон изменения координаты y времени
Все время полета находится из условия
получаем уравнение:
Это квадратное уравнение, которое имеет два решения, но в данной задаче тело может оказаться в координате только один раз. Поэтому среди полученных решений нужно одно «убрать». Главный критерий отсева — время полета не может быть отрицательным:
Если подставим в закон изменения координаты x время то получим дальность полета L:
Скорость в момент падения
Угол, который образует вектор скорости с горизонталью в произвольный момент времени:
Угол падения:
3.2.15. Как движется тело, брошенное под углом α к горизонту земли?
Тело, брошено под углом α к горизонту с поверхности земли со скоростью
Проекции начальной скорости на оси:
Проекции ускорения:
Проекции скорости в произвольный момент времени t:
Модуль скорости в произвольный момент времени t:
Координаты тела в произвольный момент времени t:
Время полета до наивысшей точки определяется из условия
Скорость в наивысшей точке полета
Максимальная высота H определяется при подстановке в закон изменения координаты y времени
Все время полета находится из условия
получаем уравнение:
Получаем
Снова получили, что то есть еще раз показали, что время подъема равно времени падения.
Если подставим в закон изменения координаты x время то получим дальность полета L:
Скорость в момент падения
Угол, который образует вектор скорости с горизонталью в произвольный момент времени:
Угол падения:
то есть
3.2.16. Что такое настильная и навесная траектории?
Решим следующую задачу: под каким углом нужно бросить тело с поверхности земли, чтобы тело упало на расстоянии L от точки броска?
Дальность полета определяется формулой:
Отсюда
Из физических соображений ясно, что угол α не может быть больше 90°, поэтому, из серии решений уравнения подходят два корня:
Траектория движения, для которой называется настильной траекторией. Траектория движения, для которой
называется навесной траекторией.
3.2.17. Как пользоваться треугольником скоростей?
Как было сказано в 3.6.1 треугольник скоростей в каждой задаче будет иметь свой вид. Рассмотрим на конкретном примере.
Тело бросили с вершины башни со скорость так, что дальность полета максимальна. К моменту падения на землю скорость тела равна
Сколько длился полет?
Построим треугольник скоростей (см. рис.). Проведем в ней высоту, которая, очевидно, равна Тогда площадь треугольника скоростей равна:
Здесь мы воспользовались формулой (3.121).
Найдем площадь этого же треугольника по другой формуле:
Так как это площади одного и того же треугольника, то приравняем формулы и
:
Откуда получаем
Как видно из формул для конечной скорости, полученных в предыдущих пунктах, конечная скорость не зависит от угла, под которым бросили тело, а зависит только значения начальной скорости и начальной высоты. Поэтому дальность полета по формуле зависит только от угла между начальной и конечной скоростью β. Тогда дальность полета L будет максимальной, если
примет максимально возможное значение, то есть
Таким образом, если дальность полета максимальна, то треугольник скоростей будет прямоугольным, следовательно, выполняется теорема Пифагора:
Откуда получаем
Свойством треугольника скоростей, который только что был доказан, можно пользоваться при решении других задач: треугольник скоростей является прямоугольным в задаче на максимальную дальность полета.
3.2.18. Как пользоваться треугольником перемещений?
Как было сказано в 3.6.2, треугольник перемещений в каждой задаче будет иметь свой вид. Рассмотрим на конкретном примере.
Тело бросают под углом β к поверхности горы, имеющей угол наклона α. С какой скоростью нужно бросить тело, чтобы оно упало ровно на расстоянии L от точки бросания?
Построим треугольник перемещений — это треугольник ABC (см. рис. 19). Проведем в нем высоту BD. Очевидно, что угол DBC равен α.
Выразим сторону BD из треугольника BCD:
Выразим сторону BD из треугольника ABD:
Приравняем и
:
Откуда находим время полета:
Выразим AD из треугольника ABD:
Выразим сторону DC из треугольника BCD:
Но Получаем
Подставим в это уравнение, полученное выражение для времени полета :
Окончательно получаем
3.2.19. Как решать задачи с помощью закона движения? (по горизонтали)
Как правило, в школе при решении задач на равнопеременное движение применяются формулы
Однако такой подход к решению трудно применить к решению многих задач. Рассмотрим конкретный пример.
Опоздавший пассажир подошёл к последнему вагону поезда в тот момент, когда поезд тронулся, начав движение с постоянным ускорением Единственная открытая дверь в одном из вагонов оказалась от пассажира на расстоянии
Какую наименьшую постоянную скорость он должен развить, чтобы успеть сесть в поезд?
Введем ось Ox, направленную вдоль движения человека и поезда. За нулевое положение примем начальное положение человека («2»). Тогда начальная координата открытой двери («1») L:
Дверь («1»), как и весь поезд, имеют начальную скорость равную нулю. Человек («2») начинает движение со скоростью
Дверь («1»), как и весь поезд, движется с ускорением a. Человек («2») движется с постоянной скоростью:
Закон движения и двери и человека имеет вид:
Подставим условия и
в уравнение для каждого из движущихся тел:
Мы составили уравнение движения для каждого из тел. Теперь воспользуемся уже известным алгоритмом для нахождения места и времени встречи двух тел — нам нужно приравнять и
:
Откуда получаем квадратное уравнение для определения времени встречи:
Это квадратное уравнение. Оба его решения имеют физический смысл — наименьший корень, это первая встреча человека и двери (человек с места может побежать быстро, а поезд не сразу наберет большую скорость, так что человек может обогнать дверь), второй корень — вторая встреча (когда уже поезд разогнался и догнал человека). Но наличие обоих корней означает — человек может бежать и медленнее. Скорость будет минимальна, когда уравнение будет иметь один единственный корень, то есть
Откуда находим минимальную скорость:
В таких задачах важно разобрать в условиях задачи: чему равны начальная координата, начальная скорость и ускорение. После этого составляем уравнение движения и думаем как дальше решать задачу.
3.2.20. Как решать задачи с помощью закона движения? (по вертикали)
Рассмотрим пример.
Свободно падающее тело прошло последние 10 м за 0,5 с. Найти время падения и высоту, с которой упало тело. Сопротивлением воздуха пренебречь.
Для свободного падения тела справедлив закон движения:
В нашем случае:
начальная координата:
начальная скорость:
Подставим условия в закон движения:
Подставляя в уравнение движения нужные значения времени, будем получать координаты тела в эти моменты.
В момент падения координата тела
За с до момента падения, то есть при
координата тела
Уравнения и
составляют систему уравнений, в которой неизвестны H и
Решая эту систему, получим:
Итак, зная вид закона движения (3.30), и используя условия задачи для нахождения и
получаем закон движения для данной конкретной задачи. После чего, подставляя нужные значения времени, получаем соответствующие значения координаты. И решаем задачу!
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Минимальная скорость при движении тела, брошенного под углом
Условие задачи:
Минимальная скорость при движении тела, брошенного под углом к горизонту, равна 5 м/с, а максимальная 10 м/с. Определить угол, под которым брошено тело.
Задача №1.6.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
Сделаем изображение к задаче, смотрите его справа.
Для объяснения решения я буду использовать следующий факт, что в любой момент времени скорость тела можно разложить на составляющие, тогда самую разлагаемую скорость можно найти по теореме Пифагора:
Теперь вспомним тот факт, что при движении тела, брошенного под углом к горизонту, горизонтальная составляющая скорости (v_x) не изменяется, поскольку движение вдоль (x) является равномерным (вдоль этой оси не действуют силы), а вертикальная составляющая скорости (v_y) меняется от максимального в момент бросания до нуля в наивысшей точке, и обратно. Причем в момент падения на землю обе составляющие (а значит и сама скорость) будут такими же, как при бросании (если, конечно же, принимать поверхность земли плоской, как у нас на рисунке).
Получается, что если скорость определяется приведенной выше формулой, то минимальное значение она примет в наивысшей точке, когда (v_y=0) м/с, а максимальное – в момент бросания и падения обратно на поверхность земли.
Взглянув на рисунок, можно увидеть, что угол между векторами, соответствующими этим скоростям, и есть угол бросания тела. Для этого прямоугольного треугольника косинус угла (alpha) определяется по следующей формуле.
Подставим известные данные и получим ответ:
[alpha = arccos frac<5><<10>> = 60^circ ]
Ответ: 60°.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.
[spoiler title=”источники:”]
http://easyfizika.ru/zadachi/kinematika/minimalnaya-skorost-pri-dvizhenii-tela-broshennogo-pod-uglom/
[/spoiler]
Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.
Скорость при прямолинейном равномерном движении
Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.
Векторный способ записи скорости при равномерном прямолинейном движении:![]()
s — вектор перемещения, ΔR— изменение радиус-вектора, t — время, а ∆t — его изменение.
Проекция скорости на ось ОХ:
![]()
sx — проекция перемещения на ось ОХ, ∆x — изменение координаты точки (ее абсциссы).
Знак модуля скорости зависит от направления вектора скорости и оси координат:
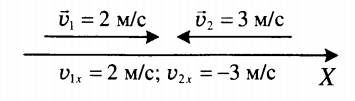
Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.
Дополнительные единицы измерения
- 1 км/ч (километр в час) = 1000 м/3600 с.
- 1 км/мин (километр в минуту) = 1000 м/60 с.
- 1 км/с (километр в секунду) = 1000 м/с.
- 1 м/мин (метр в минуту) = 1 м/60 с.
- 1 см/с (сантиметр в секунду) = 0,01 м/с.
Спидометр — прибор для измерения модули скорости тела.
График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:
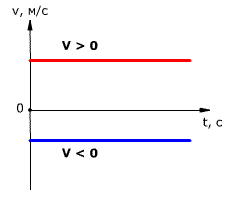
Определение направления движения по графику скорости
- Если график скорости лежит выше оси времени, тело движется в направлении оси ОХ.
- Если график скорости лежит ниже оси времени, тело движется против оси ОХ.
- Если график скорости совпадает с осью времени, тело покоится.
Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.
Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.
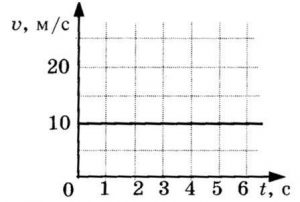
График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:
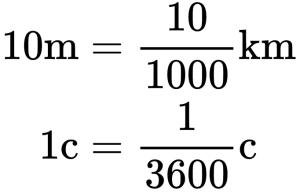
Теперь нужно разделить километры на часы:
![]()
Перемещение и координаты тела при равномерном прямолинейном движении
Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.
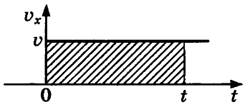
При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:
![]()
Вектор перемещения равен произведению вектора скорости на время движения:
![]()
Внимание!
При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.
Формула проекции перемещения:
![]()
График проекции перемещения
График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:
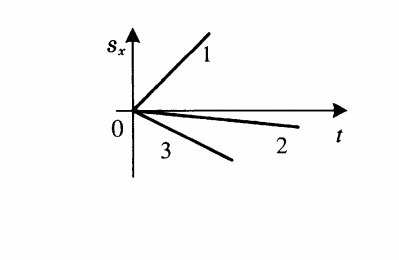
Определение направления движения по графику проекции перемещения
- Если луч лежит выше оси времени, тело движется в направлении оси ОХ.
- Если луч лежит ниже оси времени, тело движется против оси ОХ.
- Если луч совпадает с этой осью, тело покоится.
Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси sx.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси sx меньше.
График координаты
График координаты представляет собой график зависимости координаты от времени. Выглядит он так:
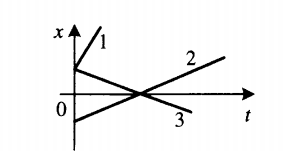
Так как график координаты представляет собой график линейной функции, уравнение координаты принимает вид:![]()
Определение направления движения тела по графику координаты
- Если с течением времени координата увеличивается (график идет снизу вверх), тело движется в направлении оси ОХ. На картинке выше этому соответствуют графики тел 1 и 2.
- Если с течением времени координата уменьшается (график идет сверху вниз), тело движется противоположно направлению оси ОХ. На картинке выше этому соответствует график тела 3.
- Если координата не изменяется, тело покоится.
Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.
Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.
Пример №2. График зависимости координаты тела от времени имеет вид:
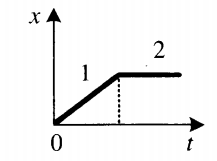
Изучите график и на его основании выберите два верных утверждения:
- На участке 1 скорость тела постоянна, а на участке 2 равна нулю.
- Проекция ускорения тела на участке 1 положительна, а на участке 2 — отрицательна.
- На участке 1 тело движется равномерно, а на участке 2 оно покоится.
- На участке 1 тело движется равноускорено, а на участке 2 оно движется равномерно.
- Проекция ускорения тела на участке 1 отрицательна, а на участке 2 — положительна.
На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?
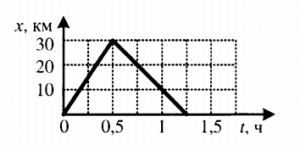
Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:
1,5 – 0,5 = 1 (час).
Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:
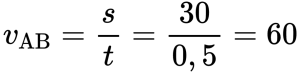
Скорость во время движения от В к А равна:
![]()
Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.
Задание EF17553
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v2 больше скорости первого тела v1 в n раз, где n равно…

Алгоритм решения
- Выбрать любой временной интервал.
- Выбрать для временного интервала начальные и конечные пути для каждого из графиков.
- Записать формулу скорости и вычислить ее для 1 и 2 тела.
- Найти n — отношение скорости второго тела к скорости первого тела
Решение
Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:
- Для графика 1: начальный путь s10 = 0 м. Конечный путь равен s1 = 80 м.
- Для графика 2: начальный путь s20 = 0 м. Конечный путь равен s2 = 120 м.
Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

Ответ: 1,5
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18768
На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении тела по оси Ox.
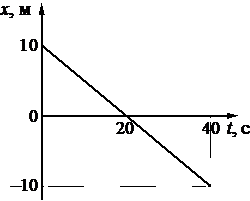
Какой из графиков соответствует зависимости от времени для проекции υx скорости этого тела на ось Ox?
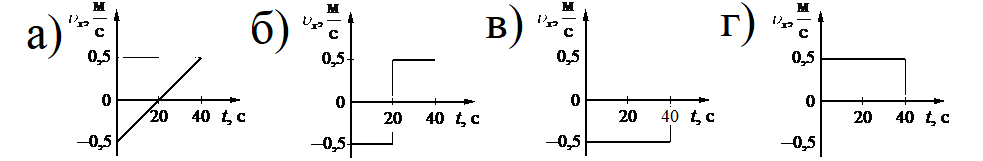
Алгоритм решения
- Записать уравнение координаты при равномерном прямолинейном движении.
- Выразить из уравнения проекцию скорости.
- Определить начальную и конечную координаты, а также время, в течение которого двигалось тело.
- Вычислить проекцию скорости.
- Выбрать соответствующий график.
Решение
Уравнение координаты при равномерном прямолинейном движении имеет вид:
![]()
Отсюда проекция скорости равна:
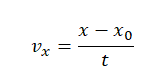
Начальная координата xo = 10 м, конечная x = –10 м. Общее время, в течение которого двигалось тело, равно 40 с.
Вычисляем проекцию скорости:
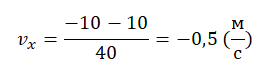
Этому значению соответствует график «в».
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18831
На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от t1=20 с до t2=50 с.

Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
Исходные данные:
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s = s1 + s2
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1 и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s1 и s2, а затем сложим их:

s1 + s2 = 100 + 100 = 200 (м)
Ответ: 200
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 13.5k
Одним из наиболее практичных применений дифференцирования является нахождение максимальных или минимальных значений функции реального мира, например, максимальной и минимальной скоростей движущегося объекта.
Вы можете думать о скорости как о более технической версии скорости .
Вот пример. Йо-йо движется прямо вверх и вниз. Его высота над землей как функция времени определяется функцией H ( t ) = t 3 – 6 t 2 + 5 t + 30, где t – в секундах, а H ( t ) – в дюймах. В момент времени t = 0 йо-йо находится на 30 дюймов над землей, а через 4 секунды он находится на высоте 18 дюймов, как показано на этом рисунке.

Высота йо-йо от 0 до 4 секунд.
Чтобы определить общее расстояние, которое проходит йо-йо, вам нужно сложить расстояния, пройденные на каждом участке пути йо-йо: верхняя нога, нижняя нога и вторая верхняя нога.
Во-первых, йо-йо поднимается с высоты 30 дюймов до 31, 1 дюйма (где находится первая точка поворота). Это расстояние около 1, 1 дюйма. Затем он снижается с 31, 1 до 16, 9 (высота второй точки разворота). Это расстояние 31, 1 минус 16, 9 или около 14, 2 дюймов. Наконец, йо-йо снова поднимается с 16, 9 дюйма до конечной высоты 18 дюймов. Это еще 1, 1 дюйма. Добавьте эти три расстояния, чтобы получить общее пройденное расстояние:

Примечание. Сравните этот ответ с общим смещением – 12, которое вы получите, вычитая конечную высоту йо-йо, 18 дюймов, из ее первоначальной высоты в 30 дюймов. Смещение отрицательно, потому что чистое движение вниз. И положительная величина смещения (а именно 12) меньше пройденного расстояния в 16, 4, потому что при смещении верхние ноги поездки йо-йо компенсируют часть расстояния вниз ногами. Проверьте математику:

Средняя скорость йо-йо определяется как общее пройденное расстояние, деленное на прошедшее время. Таким образом,

Допустим, вы определили, что максимальная скорость йо-йо составляет 5 дюймов в секунду, а ее минимальная скорость составляет –7 дюймов в секунду. Скорость –7 – это скорость 7, так что это максимальная скорость йо-йо. Его минимальная скорость равна нулю в двух точках разворота.
Хороший способ анализа максимальной и минимальной скорости состоит в рассмотрении функции скорости и ее графика. (Или, если вы испытываете жажду наказания, ознакомьтесь со следующим фетишем.) Скорость равна абсолютному значению скорости.
Скорость, V ( t ), является производной от положения (высота, в этой задаче). Таким образом:

Так, для проблемы йо-йо, функция скорости,

Посмотрите на график S ( t ) на следующем рисунке.

S ( t ) »/> Функция скорости йо-йо S ( t )
Глядя на этот график, легко увидеть, что максимальная скорость йо-йо происходит при t = 2

и что минимальная скорость равна нулю в двух x- точках пересечения.
Минимальная и максимальная скорость: для функции непрерывной скорости минимальная скорость равна нулю, когда максимальная и минимальная скорости имеют противоположные знаки или когда одна из них равна нулю. Когда максимальная и минимальная скорости являются как положительными, так и отрицательными, то минимальная скорость является меньшей из абсолютных значений максимальной и минимальной скоростей. Во всех случаях максимальная скорость больше абсолютных значений максимальной и минимальной скоростей. Это глоток или что?
Средняя скорость считается так: весь путь поделить на всё время движения. Формула одна и очень простая, но почему-то школьники часто путаются в задачах на среднюю скорость. Разберу три характерные задачи и основные ошибки. Возможно, статья будет полезна учителям и репетиторам, а также школьникам.
1. Половина пути
Первую половину пути поезд ехал со скоростью 60 км/ч, а вторую – 90 км/ч. С какой средней скоростью ехал поезд на всём пути?
Первым делом школьник захочет сложить эти две скорости и поделить пополам. Логично? Да. Но, к сожалению, неправильно.
Объясняю, почему. Поскольку первую половину пути поезд ехал с меньшей скоростью, то времени было затрачено больше, чем на вторую. А значит, вклад отдельных скоростей неравнозначен, и нельзя так просто делить пополам.
Тут школьник может впасть в панику. Что делать? Умножать? Делить? Непонятно. Воспользоваться напрямую формулой “расстояние поделить на время” не получится – ни расстояние, ни время нам неизвестно.
Для школьников, только начинающих изучать основы физики, бывает трудно оперировать с неизвестными величинами. Нам не дано ничего, кроме скоростей, как же быть? В качестве маленькой ступеньки к освоению неизвестности могу предложить следующий ход – сначала додумать неизвестные данные. Возьмём и сами решим, пусть поезд пройдет 180 километров, цифру возьмем так, чтобы легко делилась.
Тогда половина пути будет 90 километров. Поезд пройдет её за 1,5 часа. Вторую половину пути – за 1 час. Это легко посчитает любой школьник. Значит, общее время в пути будет 2,5 часа. Делим общее расстояние 180 километров на 2,5 часа, и получаем 72 км/ч.
Это просто и понятно, но учитель такую задачу не примет. Откуда мы взяли 180 километров, когда это неизвестно? Тем не менее, дав себе эти неизвестные данные, мы продумали алгоритм и довели задачу до ответа. Осталось формализовать это решение, так чтобы не использовать то, что не дано. Обозначим наши 180 километров за S, и опишем всё, что мы делали раньше, только вместо цифр используем буквы.
Получается, что зная ход решения “в цифрах”, мы переводим его в буквенные обозначения. И тут главное не остановиться на полдороги, не смущаться, что нам неизвестно расстояние. Ведь оно в конце сократилось, и средняя скорость оказалась независящей от расстояния (что вполне логично). И от школьника здесь требуются уже алгебраические умения – складывать дроби, переворачивать их.
Если подобная задача встретилась в тесте, где требуется только ответ, можно вообще не заморачиваться – так как средняя скорость в данной задаче не зависит от расстояния, можно посчитать при любом удобном расстоянии. По крайней мере, это лучше, чем сидеть и ломать голову, не зная, как подступиться к решению. Если же требуется оформление – тут числовое решение может помочь как переходный этап, чтобы понять, что именно делать с формулами, как их крутить-вертеть.
Школьникам часто бывает трудно переходить на новый уровень абстракции – от чисел к переменным, которые могут принимать разные числовые значения. В алгебре это тренируют, но там одна переменная икс, и иногда игреки встречаются. А в физике этих переменных пруд пруди, в каждой задаче они разные, и если ученик не освоил этот уровень, то физика кажется ему супер-трудной. Кроме того, в школе переход от чисел к переменным часто упускают, в программе отдельных навыков работы с формулами нет.
2. Средняя скорость по графику пути
Пусть нам дан график зависимости координаты от времени. Требуется определить среднюю скорость.
По графику видно, что движение состоит из четырех этапов:
- Тело стартует в нуле и через 2 секунды оказывается на координате 2 м.
- Тело останавливается, и в течение 4 секунд покоится в точке с координатой 2 м.
- Тело начинает движение, и через 2 секунды оказывается в точке 6 м.
- Тело движется в обратном направлении, и через 2 секунды оказывается в точке 5 м.
Проговорить, понять все эти этапы – важная часть решения. А дальше многие школьники начинают вычислять скорости движения на каждом этапе: На первом – 1 м/с, на втором – 0, на третьем – 2 м/с, на четвертом – 0,5 м/с. Вот это действие как раз лишнее. Для того, чтобы вычислить среднюю скорость, вовсе не обязательно знать скорости на каждом этапе!
Вспомним определение средней скорости – это весь путь, поделить на всё время. Поэтому просто по графику считаем весь путь – 6 метров “туда” и 1 метр “обратно”, в сумме 7 метров. Общее время движения – 10 секунд. Делим 7 метров на 10 секунд, получаем 0,7 м/с.
3. Средняя скорость по графику скорости
Бывает так, что нам дан график зависимости скорости от времени, и требуется определить среднюю скорость. Вот, к примеру, такой график.
Читаем график. Движение состоит из трёх этапов
- С начала движения до момента времени 2 с тело движется с постоянной скоростью 2 м/с
- От 2 до 6 с тело движется со скоростью 6 м/с
- В последние 4 секунды от 6 до 10 с тело замедляется, снижая свою скорость до нуля.
Попытки что-то сделать со значениями скорости самими по себе здесь обречены на провал. Опять надо найти весь путь и всё время движения. Путь по графику скорости определяется как площадь под графиком, причем если график идет ниже нуля, то соответствующие участки складываются.
Считаем площадь фигуры – два прямоугольника на первых двух этапах и треугольник на третьем. Первый этап – 4 м, второй этап – 24 м, третий этап – 12 м. Значит, весь путь будет 40 метров. Всё время 10 секунд, значит, средняя скорость 4 м/с.
Общие рекомендации для решения задач на среднюю скорость
1. Средняя скорость – это всегда весь путь делить на всё время. Данные об отдельных скоростях сами по себе не дадут полной информации о средней скорости. Используем только эту формулу.
2. Следует проанализировать конкретную ситуацию и понять, как можно применить формулу. Если кажется, что не хватает данных – не смущаться.
3. Данные по скоростям на отдельных этапах могут быть полезны для проверки готового ответа: средняя скорость должна лежать между минимальной и максимальной.
Спасибо, что прочитали до конца! Желаю школьникам хорошей учёбы, учителям – понятливых и любопытных учеников, родителям – чтобы дети радовали. Буду рада лайкам и новым подписчикам!
