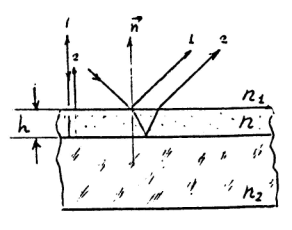
На поверхность линзы из
оптического стекла с показателем преломления n2 = 1,6 нанесена тонка пленка с показателем преломления n1 = 1,5. На линзу
нормально к поверхности падает пучок монохроматического света с длиной волны
0,60 мкм. Найти наименьшую толщина пленки, при нанесении которой отраженный
свет будет максимально ослаблен?
Решение.
Свет, проходя через
линзу, отражается от ее передней и задней поверхностей.
Чтобы избежать
отражения света, на поверхность линзы наносится пленка, толщина которой и
показатель преломления n выбираются таким
образом, чтобы в отраженном свете наблюдался интерференционный минимум. Причем n1 должен быть меньше n2 . Этот прием называется
просветлением оптики.
Условие максимального
ослабления света при интерференции имеет следующий вид.
D – оптическая разность хода лучей, отраженных от поверхности
линзы и пленки.
Так как оба
интерферирующих луча отражаются от оптически более плотной преграды с потерей
полуволны, то при нормальном падении лучей оптическая разность их хода равна D = 2dn.
Для наименьшей толщины
пленки m = 0. Поэтому 2dminn
= l/2. Отсюда dmin = l/4n = 0,60/(4•1,5) = 0,10 мкм.
Ответ: При минимальной
толщине пленки 0,10 мкм отраженный свет будет максимально ослаблен.
Источник: Пособие-репетитор для подготовки к централизованному тестированию. С.Н.Капельян, Л.А.Аксенович.
google.com/+ВикторЦекунов
Репетитор по математике, физике (Минск): Виктор Иванович.
Высшая математика и физика для студентов.
Профессиональный репетитор окажет помощь в решении задач, подготовит к экзаменам. Занятия в Серебрянке, индивидуально. (90 мин)
= 20 $.
Тел: +375(29) 127 61 86.
___________________________________________________________________________________
Оказываю
платные услуги: решение задач по физике. Оплата WebMoney.
Заказы направляйте сюда: Платные услуги
___________________________________________________________________________________
5.1. Фотометрия и геометрическая оптика.
5.2. Интерференция света.
5.3. Дифракция света.
5.4. Поляризация света.
5.5. Дисперсия и поглощение света.
5.6. Оптика движущихся источников.
5.7. Тепловое излучение. Квантовая природа света.
5.1. Фотометрия и геометрическая оптика.
5.1-1. На рабочем месте для переработки с/х продуктов необходимо создать
освещенность Е=150 лк. Определить силу света лампы, подвешенной на высоте 2 м.
Решение:
E = 150 лк
R = 2 м
I – ?
Закон освещённости:
E = Icosα/R² , (1)
где α – угол между падающими
лучами и нормалью к площадке.
Если лампа висит над рабочим местом, то α = 0 и cosα = 1. Из (1) найдём силу
света I
I = ER².
I = 150·2² = 600 кд.
Ответ: I = 600 кд.
5.1-2. Как
математически записать зависимость между E и cosα, если E₀
освящёность при α=0.
Решение:
α = 0
E₀
E = f(cosα) – ?
При
освещении бесконечно малой площадки точечным источником света закон
освещённости имеет вид
E = Icosα/r², (1)
где r –
расстояние от площадки до источника света; α –
угол падения лучей на площадку (угол между падающими лучами и нормалью к
площадке, восставленной в точке падения лучей);
I –
сила света источника.
При α = 0
из (1) имеем
E₀ = Icos0/r² или (т.к. cos0 = 1)
E₀ = I/r². (2)
Разделим (1) на (2)
E/E₀ = (Icosα/r²)/(I/r²)
или E/E₀ = cosα,
отсюда E = E₀cosα.
Ответ:
E = E₀cosα.
___________________________________________________________________________________ 5.2. Интерференция света.
5.2-1.
Определить толщину воздушной прослойки между линзой и стеклянной пластинкой
там, где в отражённом свете с длиной волны λ = 600 нм видно третье тёмное
кольцо Ньютона.
Решение:
λ = 600 нм
m = 3 (тёмное кольцо)
d − ?
В отражённом монохроматическом свете с длиной волны λ радиусы r тёмных колец
Ньютона равны
(1)
где m = 0,1,2, … − номер кольца, R – радиус кривизны выпуклой поверхности
линзы, d − толщина воздушной прослойки.
Из рис. для ∆АВС по теореме Пифагора имеем:
R² = (R – d)² + r² или R² = R² – 2Rd + d² + r², отсюда
– 2Rd + d² + r² = 0.
Ввиду малости d, пренебрегаем величиной d². Тогда из последнего равенства
получим
2Rd = r².
Подставляя сюда r² из (1), получим
2Rd = mRλ, отсюда
d = ½mλ.
d = ½·3·600 = 900 нм.
Ответ: d = ½mλ = 900 нм.
5.2-2.
Найти минимальную толщину плёнки с показателем преломления 1,33, при которой
свет с длиной волны 0,64 мкм испытывает максимальное отражение, а свет с длиной
волны 0,40 мкм не отражается совсем. Угол падения света равен 30°.
Решение:
n = 1,33
λ₁ = 0,64 мкм
λ₂ = 0,4 мкм
θ = 30° (угол падения света)
dmin − ?
Условие для интерференционных максимумов отражения света с длиной волны λ₁:
(1)
(m = 0,1,2, …)
Так как в (1) величины n, θ, λ₁ постоянны, то минимальная толщина d плёнки
будет при минимальном числе m.
Условие для интерференционных минимумов отражения света с длиной волны λ₂:
(2)
(k = (1,2, …)
Так как в (2) величины n, θ, λ₂ постоянны, то минимальная толщина d плёнки
будет при минимальном числе k.
В (1) и (2) левые части уравнений равны, поэтому равны их правые части:
Подставляя сюда λ₁ = 0,64 мкм и λ₂ = 0,4 мкм, получим
(2m + 1)·0,32 = k·0,4 или
5k – 8m = 4,
отсюда выражаем k
(3)
(m = 0,1,2, …), (k = (1,2, …).
Из (3) ясно, что минимальное число k будет при минимальном числе m. Задавая m = 0,1,2, …,
по (3) вычисляем k. Результаты занесём в таблицу.
Из таблицы видно, что при минимальном числе m = 2 получили минимальное натуральное
число k = 4.
Теперь из (2) при k = 4 (или из (1) при m = 2) получаем минимальную толщину
dmin плёнки:
___________________________________________________________________________________
5.3. Дифракция света.
5.3-1.
Лучи
света с длиной волны λ = 600 нм падают на дифракционную решетку под углом ϕ = 30⁰ к
нормали. За решеткой последний максимум виден под углом α.
Найти sinα, если
постоянная решетки равна d = 21 мкм.
Решение:
λ = 600·10⁻⁹ м
ϕ = 30⁰
k = max
d =
21·10⁻⁶ м
sinα − ?
При наклонном падении света на дифракционную решётку условие для главных
максимумов имеет вид:
d(sinα – sinϕ) = kλ, (1)
где ϕ –
угол падения света; α – угол дифракции; k = 0,
±1, ±2, … – порядок максимума.
Из (1) выражаем
sinα = kλ/d + sinϕ. (2)
Так как -1 ≤ sinα ≤ 1,
то по (2)
-1 ≤ kλ/d + sinϕ ≤ 1,
или -1 ≤ k·600·10⁻⁹/(21·10⁻⁶)
+ sin30⁰ ≤
1, или
-1 ≤ k/35 +
0,5 ≤ 1 (вычтем 0,5). Тогда
-1,5 ≤ k/35 ≤
0,5 (умножим на 35). Тогда
-52,5 ≤ k ≤
17,5, (k −
целые).
Отсюда последний максимум достигается при k = –
52. Тогда
из (2) находим
sinα = – 52·600·10⁻⁹/(21·10⁻⁶) + 0,5 = – 0,9857.
Ответ: sinα = – 0,9857.
5.3-2.
На дифракционную решетку с периодом 14 мкм падает нормально монохроматическая
световая волна. На экране, удалённом от решетки на 2 м, расстояние между
спектрами второго и третьего порядков 8,7 см. Какова длина волны падающего
света?
Решение:
d =
14·10⁻⁶ м
L = 2 м
k₂ = 2
k₃ = 3
x =
8,7·10⁻² м
λ − ?
Условия главных фраунгоферовых максимумов для дифракционной решётки при
нормальном падении света:
dsinθ = kλ, k = 1,
2, 3, … ;
Отсюда для порядков k₂ и k₃ имеем два уравнения
dsinθ₂ = k₂λ (*)
dsinθ₃ = k₃λ. (**)
Так как углы θ₂ и θ₃
малы, то sinθ₂ ≈ tgθ₂ = x₂/L и sinθ₃ ≈ tgθ₃ = x₃/L (см.
рис.). Тогда (*) и (**) примут вид
dx₂/L = k₂λ
dx₃/L = k₃λ,
отсюда
x₂ = k₂λL/d и x₃ = k₃λL/d.
Расстояние x между
спектрами второго и третьего порядков (см. рис.):
x = x₃ – x₂ или x = k₃λL/d – k₂λL/d,
отсюда находим длину волны λ света
λ = xd/( L(k₃ – k₂) ).
λ =
8,7·10⁻²·14·10⁻⁶/( 2· (3 – 2) ) = 6,09·10⁻⁷ м.
Ответ: λ = xd/( L(k₃ – k₂) ) = 6,09·10⁻⁷ м.
___________________________________________________________________________________ 5.4. Поляризация света.5.4-1. Чему
равна степень поляризации Р света, представляющего собой смесь естественного
света с плоскополяризованным, если отношение интенсивности поляризованного
света к интенсивности естественного равна 10?Решение:
η = Iпол/Iест = 10
P − ?
Степень поляризации P света:
P = (Imax – Imin)/(Imax + Imin), (1)
где Imax, Imin –
максимальная и минимальная интенсивности света, прошедшего через анализатор.
Известно, что естественный свет, пройдя через анализатор (поляризатор),
уменьшает свою интенсивность в два раза, т.е.
I₁ = Iест/2,
(2)
где I₁ –
интенсивность естественного света, прошедшего анализатор.
Имеем
Imax = Iпол + I₁ = Iпол + Iест/2;
Imin = I₁ = Iест/2.
Подставим Imax и Imin в (1)
P = (Iпол + Iест/2
– Iест/2)/(Iпол + Iест/2
+ Iест/2)
или
P = (Iпол)/(
Iпол + Iест) =
(Числитель и знаменатель разделим на Iест) = (Iпол/Iест)/(Iпол/Iест + 1).
P =
η/(η + 1).
P = 10/(10 + 1) = 0,909.
Ответ: P = η/(η + 1) = 0,909.
_______________________________________________________________________________________________
2018-07-01
Найти минимальную толщину пленки с показателем преломления 1,33, при которой свет с длиной волны 0,64 мкм испытывает максимальное отражение, а свет с длиной волны 0,40 мкм не отражается совсем. Угол падения света равен $30^{ circ}$.
Решение:
Учитывая
$2d sqrt{n^{2} – 1/4 } = left ( k + frac{1}{2} right ) cdot 0,64 мкм$ (яркая полоса)
$2d sqrt{n^{2} – 1/4 } = k^{ prime} cdot 0,40 мкм$ (темная полоса),
где $k, k^{ prime}$ – целые числа.
Таким образом, $64 left ( k + frac{1}{2} right ) = 40k^{ prime}$ или $4 (2k + l) = 5k^{ prime}$
Это означает, что для наименьших целочисленных решений
$k = 2, k^{ prime} = 4$
Следовательно, $d = frac{4 cdot 0,40}{2 sqrt{n^{2} – 1/4 } } = 0,65 мкм$.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,653 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,904 -
разное
16,900
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Примеры решения задач к теме
8.2. Интерференция света Основные формулы и методические указания
1.
Оптическая длина пути, проходимого
световым лучом в однородной среде с
показателем преломления n
(8.
2. 4)
где l
–
геометрическая длина пути светового
луча.
2.
Оптическая разность хода двух световых
лучей
(8.
2. 5)
3.
Условия возникновения максимума и
минимума интенсивности света от 2-х
когерентных источников соответственно
(8.
2. 6)
и
(8.
2. 7)
где l
– длина световой волны в вакууме,
–
порядок соответствующего максимума
или минимума интенсивности света.
4.
Положение на экране (от его центра)
последовательно расположенных максимумов
и минимумов интенсивности света
соответственно
(8.
2. 8)
и
(8.
2. 9)
где .
5.
Расстояние между интерференционными
полосами на экране, полученными от двух
когерентных источников света
(8.
2. 10)
где – расстояние от экрана до источников,
– расстояние между когерентными
источниками, причем
6.
Оптическая разность хода световых
лучей, отраженных от двух поверхностей
тонкой пластины или пленки, по обе
стороны которых одинаковые среды
(8.
2. 11)
где – толщина пластины или пленки,
– показатель их преломления,
– угол преломления,
– длина световой волны в вакууме.
7.
Условия образования максимумов и
минимумов интенсивности света в
отраженном свете от тонкой плоскопараллельной
пластины или пленки соответственно:
(8.
2. 12)
и
(8.
2. 13)
где – угол падения светового луча на пластину
или пленку.
8.
Радиусы темных и светлых колец Ньютона
в отражении света соответственно, при
условии, что между линзой и пластиной
вакуум (воздух)
(8.
2. 14)
(8.
2. 15)
Здесь
– радиус кривизны поверхности линзы,
соприкасающейся с параллельной пластиной,– длина световой волны в среде между
линзой и пластиной,– порядковый номер кольца (
соответствует центральному темному
пятну).
Задачи
на интерференцию света делятся в основном
на две группы: на интерференцию волн от
двух когерентных источников и на
интерференцию в тонких пластинах
(пленках). К задачам первой группы
относятся случаи интерференции,
получаемые с помощью щелей Юнга (опыт
Юнга), зеркала Ллойда, зеркал Френеля,
а также бипризмы Френеля. Для расчета
интерференционной картины в этом случае
используются формулы (8.2.7), (8.2.8) и (8.2.9),
предварительно определив (если это
необходимо) положение двух когерентных
источников. Вторую группу составляют
задачи на интерференцию как в
плоскопараллельных, так и в клинообразных
тонких слоях, а так же задачи на кольца
Ньютона. В этом случае соотношение
(8.2.10) позволяет вычислить оптическую
разность 2-х интерферирующих лучей,
отраженных от обеих поверхностей слоя.
По условиям (8.2.11) и (8.2.12) определяют
результат интерференции.
При
интерференции света, известной под
названием колец Ньютона, роль тонкой
пленки играет прослойка (обычно воздушная)
между пластиной и выпуклой поверхностью
прижатой к ней линзы. Формулы (8.2.13) и
(8.2.14) для радиусов колец выведены в
предположении, что эта прослойка окружена
одинаковыми средами, то есть пластинка
и линза должны иметь одинаковые показатели
преломления.
В
качестве примера решения задач по этой
теме, рассмотрим следующие задачи.
З а д а ч а 8. 2. 1
Свет от точечного монохроматического
источника
с длиной волны
м
падает на экран “Э” (рис. 8.2), в
котором имеются два маленьких отверстияи
(опыт Юнга), расположенных на расстоянии
3 м
от экрана. Расстояние междуи
м
().
Определить расстояние между максимумами
интенсивности света смежных
интерференционных полос (ширину светлой
или темной полосы) на экране.
|
Дано:
|
Решение
|
|
|
Искомое
расстояние между максимумами интенсивности
смежных интерференционных полос на
экране
определяется
как разность расстояний от центра
картины (т. 0) до двух соседних темных
полос с номерамии
,
то есть
Для
нахождения
и
воспользуемся
условием образования минимума
интенсивности света от 2-х когерентных
источников для чего из рис. 8.2 найдем
геометрическую разность хода 2-х лучей
где:
Вычитая
из первого второе, получим
или
Откуда
так как
Из
условия минимума
находим, что
(для
).
Следовательно,
ширина темных и светлых полос одинакова,
и равна
.
Подставляя
числовые значения, рассчитаем
м.
Ответ:
м.
З а д а ч а 8. 2. 2
Два когерентных источника, расстояние
между которыми
мм
удалены от экрана нам.
На длине экранасм
располагаетсяполос. Чему равна длина волны
монохроматического света, падающего
на экран.
|
Дано:
|
Решение
Так
Откуда |
|
|
|
Ответ:
м.
З а д а ч а 8. 2. 3
В опыте Юнга на пути одного из лучей
монохроматического света с длиной волны
м
поместили перпендикулярно лучу тонкую
стеклянную пластину с показателем
преломления.
При этом центральная светлая полоса
сместилась в положение, первоначально
занимаемое пятой светлой полосой. Какова
толщина стеклянной пластины?
|
Дано:
|
Решение
Внесенная
Так, |
|
|
.
Откуда
м.
Ответ:
м.
З а д а ч а 8. 2. 4
На мыльную пленку с
падает под углом 600
параллельный пучок белого света.
Определить наименьшую толщину пленки,
при которой в отраженном свете пленка
имеет желтую окраску (м).
|
Дано:
|
Решение
В интерференции |
|
|
Отсюда
толщина пленки равна
.
Минимальную
толщину пленки будем иметь при
.
м.
Ответ:
м.
З а д а ч а 8. 2. 5
Для уменьшения потерь света при отражении
от линзы фотоаппарата на поверхности
объектива (линзы) с показателем преломления
наносится тонкая прозрачная пленка с
.
При какой наименьшей ее толщине произойдет
максимальное ослабление отраженного
света, длина волны которого приходится
на среднюю часть видимого спектра см.
Считать, что лучи падают нормально к
поверхности объектива.
|
Дано:
|
Решение Свет, |
|
|
Рис.
8.3
величину
и тогда, с учетом того, что в задаче угол
падения равен нулю, полная разность
хода световых лучей составит,а
условие минимума интенсивности света
теперь будет таким
.
Откуда
Следовательно,
искомая минимальная толщина пленки
будет при условии
то есть
м.
Это
очень тонкая пленка, поэтому на практике
изготовляют пленку толщиной
,
естественно увеличиваяв нечетное число раз.
Ответ:
м.
З а д а ч а 8. 2. 6
На стеклянный клин с
нормально к его грани подает параллельный
пучок лучей монохроматического света
с длиной волным.
Числоинтерференционных полос приходящихся
насм
равно.
Определить уголклина.
|
Дано:
|
Решение Лучи |
|
|
Рис. 8.
4
Темные
полосы в отраженном свете видны на тех
участках клина, для которых полная
разность хода световых лучей кратна
нечетному числу половин длин волн, то
есть определяются тем же условием
минимума интенсивности света, что и для
плоскопараллельной пластины соответствующей
толщине клина
(1)
Здесь
учтено, что угол падения лучей равен
нулю.
Из
(1) следует, что
;
. (2)
Искомый
угол
при основании клина найдем из прямоугольного
треугольника, с учетом (2):
Так
как угол
<<1,
то,
и тогда
рад.
Для
того, чтобы выразить
в градусах, воспользуемся соотношением
между радианом и градусом, получим
.
Используя
соотношение между радианом и секундой:
рад
,
получим .
Ответ:
или
.
З а д а ч а 8. 2. 7
Найти радиус кривизны плосковыпуклой
линзы, лежащей на плоскопараллельной
стеклянной пластине, освещаемая нормально
падающим на неё монохроматическим
светом длиной волны
м.
Радиус восьмого темного кольца Ньютона
в отраженном свете равен 2 мм.
|
Дано:
|
Решение
Пучок Падающий |
|
|
о
Рис.
8.5
т стеклянной пластины (луч 2). Лучи
1, 2 когерентны. И в результате их положения
на выпуклой стороне линзы наблюдается
интерференция кольца. Темные кольца
видны в тех местах, где полная разность
хода этих лучейравна нечетному числу половин длин
волн, то есть
(1)
где – толщина
воздушной прослойки в том месте, где
видно интерференционное кольцо;
– длина
волны падающего света;
– номер темного кольца.
Величина
в (1) – добавочная разность хода,
возникающая при отражении луча 2 от
оптически более плотной среды (пластина).
После
упрощений, равенство (1) дает
. (2)
Из
прямоугольного треугольника ОАВ
(рис. 8.5) имеем
.
С
учетом того, что
,
получаем
. (3)
Из
(2) и (3) следует, что
,
откуда искомый радиус кривизны линзы
равен
м.
Ответ:
м.
Соседние файлы в папке Кононенко_Зеневич Методич. указания
- #
13.02.20164.13 Кб37._MU KZ (chast 3, page 23).doc
- #
13.02.20164.1 Кб31._MU KZ(chast 3, page 03_23).doc
- #
13.02.20164.1 Кб39._МУиКЗ по ФИЗИКЕ, часть1.doc
- #
- #
- #









 Рис. 8.
Рис. 8.