Обновлено: 23.05.2023
Система небесных координат используется в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение объектов на небесной сфере. Таким образом, система небесных координат является сферической системой координат, в которой третья координата — расстояние — часто неизвестна и не играет роли.
Системы небесных координат отличаются друг от друга выбором основной плоскости (см. Фундаментальная плоскость) и началом отсчёта. В зависимости от стоя́щей задачи, может быть более удобным использовать ту или иную систему. Наиболее часто используются горизонтальная и экваториальная системы координат. Реже — эклиптическая, галактическая и другие.
Высотой h светила называется дуга вертикального круга от математического горизонта до светила, или угол между плоскостью математического горизонта и направлением на светило. Высоты отсчитываются в пределах от 0° до +90° к зениту и от 0° до −90° к надиру.
Зенитным расстоянием z светила называется дуга вертикального круга от зенита до светила, или угол между отвесной линией и направлением на светило. Зенитные расстояния отсчитываются в пределах от 0° до 180° от зенита к надиру.
Азимутом A светила называется дуга математического горизонта от точки юга до вертикального круга светила, или угол между полуденной линией и линией пересечения плоскости математического горизонта с плоскостью вертикального круга светила. Азимуты отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от точки юга, в пределах от 0° до 360°. Иногда азимуты отсчитываются от 0° до +180° к западу и от 0° до −180° к востоку. (В геодезии и навигации азимуты отсчитываются от точки севера.)
Изменения координат при вращении небесной сферы
Высота h, зенитное расстояние z, азимут A и часовой угол t светил постоянно изменяются вследствие вращения небесной сферы, так как отсчитываются от точек, не связанных с этим вращением. Склонение δ, полярное расстояние p и прямое восхождение α светил при вращении небесной сферы не изменяются, но они могут меняться из-за движений светил, не связанных с суточным вращением.
В этой системе основной плоскостью является плоскость небесного экватора. Одной координатой при этом является склонение δ (реже — полярное расстояние p). Другой координатой — часовой угол t.
Склонением δ светила называется дуга круга склонения от небесного экватора до светила, или угол между плоскостью небесного экватора и направлением на светило. Склонения отсчитываются в пределах от 0° до +90° к северному полюсу мира и от 0° до −90° к южному полюсу мира.
Полярным расстоянием p светила называется дуга круга склонения от северного полюса мира до светила, или угол между осью мира и направлением на светило. Полярные расстояния отсчитываются в пределах от 0° до 180° от северного полюса мира к южному.
Часовым углом t светила называется дуга небесного экватора от верхней точки небесного экватора (то есть точки пересечения небесного экватора с верхней частью небесного меридиана) до круга склонения светила, или двугранный угол между плоскостями небесного меридиана и круга склонения светила. Часовые углы отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от верхней точки небесного экватора, в пределах от 0° до 360° (в градусной мере) или от 0 h до 24 h (в часовой мере). Иногда часовые углы отсчитываются от 0° до +180° (от 0 h до +12 h ) к западу и от 0° до −180° (от 0 h до −12 h ) к востоку.

В этой системе, как и в первой экваториальной, основной плоскостью является плоскость небесного экватора, а одной координатой — склонение δ (реже — полярное расстояние p). Другой координатой является прямое восхождение α.
Прямым восхождением (RA, α) светила называется дуга небесного экватора от точки весеннего равноденствия до круга склонения светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга склонения светила. Прямые восхождения отсчитываются в сторону, противоположную суточному вращению небесной сферы, в пределах от 0° до 360° (в градусной мере) или от 0 h до 24 h (в часовой мере).
RA — астрономический эквивалент земной долготы. И RA и долгота измеряют угол восток-запад вдоль экватора; обе меры берут отсчёт от нулевого пункта на экваторе. Для долготы, нулевой пункт — нулевой меридиан; для RA нулевой отметкой является место на небе, где Солнце пересекает небесный экватор, в направлении с юга на север (в весеннее равноденствие).
Склонение (δ) в астрономии — одна из двух координат экваториальной системы координат. Равняется угловому расстоянию на небесной сфере от плоскости небесного экватора до светила и обычно выражается в градусах, минутах и секундах дуги. Склонение положительно к северу от небесного экватора и отрицательно к югу.
- Объект на небесном экваторе имеет склонение 0°
- Склонение северного полюса небесной сферы равно +90°
- Склонение южного −90°
У склонения всегда указывается знак, даже если склонение положительно.
Склонение небесного объекта, проходящего через зенит, равно широте наблюдателя (если считать северную широту со знаком +, а южную отрицательной). В северном полушарии Земли для заданной широты φ небесные объекты со склонением δ > +90° − φ не заходят за горизонт, поэтому называются незаходящими. Если же склонение объекта δ [1]
В этой системе основной плоскостью является плоскость эклиптики. Одной координатой при этом является эклиптическая широта β, а другой — эклиптическая долгота λ.
Эклиптической широтой β светила называется дуга круга широты от эклиптики до светила, или угол между плоскостью эклиптики и направлением на светило. Эклиптические широты отсчитываются в пределах от 0° до +90° к северному полюсу эклиптики и от 0° до −90° к южному полюсу эклиптики.
Эклиптической долготой λ светила называется дуга эклиптики от точки весеннего равноденствия до круга широты светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга широты светила. Эклиптические долготы отсчитываются в сторону видимого годового движения Солнца по эклиптике, то есть с запада к востоку от точки весеннего равноденствия в пределах от 0° до 360°.
В этой системе основной плоскостью является плоскость нашей Галактики. Одной координатой при этом является галактическая широта b, а другой — галактическая долгота l.
Галактической широтой b светила называется дуга круга галактической широты от эклиптики до светила, или угол между плоскостью галактического экватора и направлением на светило.
Галактические широты отсчитываются в пределах от 0° до +90° к северному галактическому полюсу и от 0° до −90° к южному галактическому полюсу.
Галактической долготой l светила называется дуга галактического экватора от точки начала отсчёта C до круга галактической широты светила, или угол между направлением на точку начала отсчёта C и плоскостью круга галактической широты светила. Галактические долготы отсчитываются против часовой стрелки, если смотреть с северного галактического полюса, то есть к востоку от точки начала отсчёта C в пределах от 0° до 360°.
Точка начала отсчёта C находится вблизи направления на галактический центр, но не совпадает с ним, поскольку последний, вследствие небольшой приподнятости Солнечной системы над плоскостью галактического диска, лежит примерно на 1° к югу от галактического экватора. Точку начала отсчёта C выбирают таким образом, чтобы точка пересечения галактического и небесного экваторов с прямым восхождением 280° имела галактическую долготу 32,93192° (на эпоху 2000).
Координаты точки начала отсчёта C на эпоху 2000 в экваториальной системе координат составляют:
Наблюдения изменений небесных координат привели к величайшим открытиям в астрономии, которые имеют огромное значение для познания Вселенной. К ним относятся явления прецессии, нутации, аберрации, параллакса, собственных движений звёзд и другие. Небесные координаты позволяют решать задачу измерения времени, определять географические координаты различных мест земной поверхности. Широкое применение находят небесные координаты при составлении различных звёздных каталогов, при изучении истинных движений небесных тел — как естественных, так и искусственных — в небесной механике и астродинамике и при изучении пространственного распределения звёзд в проблемах звёздной астрономии.
Использование горизонтальной топоцентрической системы координат
Горизонтальная топоцентрическая система координат используется наблюдателем, находящимся в определённом месте на поверхности земного шара для определения положения какого-либо светила на небе.
Координаты небесных светил в данной системе координат могут быть получены с помощью угломерных инструментов и при наблюдениях в телескоп, смонтированный на азимутальной установке.
Большинство астрономических компьютерных программ способны выдавать положения светил в данной системе координат.
При наблюдениях следует учитывать поправку на рефракцию.
Использование первой экваториальной системы координат
Первая экваториальная система координат используется для определения точного времени и при наблюдениях в телескоп, смонтированный на экваториальной установке.
Использование второй экваториальной системы координат
Вторая экваториальная система координат является общепринятой в астрометрии.
В экваториальной гелиобарицентрической системе координат составляются современные звёздные карты и описываются положения светил в каталогах. При этом координаты светил приводятся к определённому положению небесного экватора и точки весеннего равноденствия, то есть к определённой эпохе (в астрономии применяются эпохи B1950 и J2000.0).
Экваториальная геоцентрическая система координат отличается от экваториальной гелиобарицентрической системы координат тем, что координаты звёзд скорректированы в ней из-за явления годичного параллакса, а положение небесного экватора и точки весеннего равноденствия приводятся к текущей дате.
Использование эклиптической системы координат
Эклиптическая геоцентрическая система координат используется в небесной механике для расчёта орбиты Луны, а также является основной или единственной в большинстве школ астрологии.
Эклиптическая гелиоцентрическая система координат используется для расчёта орбит планет и других тел Солнечной системы обращающихся вокруг Солнца.
Применение различных систем небесных координат
На практике, как правило, требуется пользоваться несколькими системами координат. Например для расчёта положения Луны на небе необходимо сначала рассчитать координаты Луны в эклиптической геоцентрической системе координат, пересчитать координаты в экваториальную геоцентрическую систему координат, затем перейти к горизонтальной топоцентрической системе координат.
Рассмотрим задачи на определение высоты звезд на небесной сфере. Небесной сферой мы называем представление о небе как о пустом глобусе с нашей планетой в центре и небесными объектами на его внутренней поверхности. Оно пришло к нам из древности и остается удобным. Когда мы смотрим на звезды, можно вообразить, что мы находимся внутри такого глобуса, внутри небесной сферы.

Зенитом называется точка, расположенная прямо над головой наблюдателя. Математическим горизонтом называется большой круг небесной сферы, все точки которого отстоят от зенита на 90 градусов (вершиной угла будет сам наблюдатель).

Как на земле можно найти любую точку по ее координатам (зная широту и долготу места), так и на небесную сферу нанесли воображаемую сетку. Небесный экватор — большой круг небесной сферы, плоскость которого перпендикулярна оси мира и совпадает с плоскостью земного экватора. Небесный экватор делит небесную сферу на два полушария: северное полушарие, с вершиной в северном полюсе мира, и южное полушарие, с вершиной в южном полюсе мира. Полюс мира — точка на небесной сфере, вокруг которой происходит видимое суточное движение звёзд из-за вращения Земли вокруг своей оси. Направление на северный полюс мира совпадает с направлением на географический север, а на Южный полюс мира — с направлением на географический юг. Северный полюс мира находится в созвездии Малой Медведицы и почти точно совпадает с Полярной звездой, южный — в созвездии Октант. Полюсы мира соединены на небесной сфере линиями (окружностями), называемыми небесными меридианами подобно воображаемым линиям меридианов на земле. Один из этих меридианов проходит через зенит. Горизонтальные воображаемые линии – окружности, параллельные экватору, называются параллелями так же, как и параллели на земле.
На земле широту отсчитывают от экватора. Экватор является нулевой широтой и точкой отсчета. На небе

Еще раз рассмотрим рисунок

Земной шар вращается вокруг солнца. Плоскость, в которой движется планета в своем годовом обходе вокруг светила, называется плоскостью эклиптики. На небесной сфере это плоскость, в которой движется солнце. Но планета вращается и вокруг своей оси, и эта ось наклонена к плоскости эклиптики под углом в 23 градуса. Именно по этой причине солнечные лучи падают на Землю под разными углами. Точка весеннего равноденствия – положение солнца, когда оно пересекает небесный экватор, переходя из южной половины небесной сферы в северную.
Теперь поговорим о том, что такое высота светила.
![]()
со знаком (+), если светило над горизонтом, и (-), если оно под горизонтом.

Кульминация— прохождение центра светила через небесный меридиан в процессе его суточного движения. Иначе — прохождение центром светила точки пересечения суточной параллели светила и небесного меридиана.
В течение суток все светила дважды пересекают небесный меридиан. Различают верхнюю и нижнюю кульминации светила. В верхней кульминации высота светила наибольшая, а в нижней — наименьшая. Для незаходящих светил обе кульминации происходят над горизонтом. Для восходящих и заходящих светил верхняя кульминация происходит над горизонтом, а нижняя под горизонтом. У невосходящих светил обе кульминации происходят под горизонтом и они недоступны наблюдениям.
На рисунке желтым показаны звезды в верхней кульминации, а красным – в нижней.

![]()
.

Теперь нарисуем расположение звезды в случае и в случае . Из рисунка видно, как определить высоту звезды в обоих случаях для верхней кульминации.

Для нижней кульминации светила

И еще один рисунок, поясняющий, что такое зенитное расстояние.

Теперь попробуем решать задачи. Необходимо просто применять элементарные геометрические знания и помнить: высота не может быть больше 90 градусов по модулю, но может быть отрицательной.
Задача 1. Определите высоту звезды Капеллы ( Возничего) в верхней кульминации на северном полярном круге (33′” width=”92″ height=”16″ />
). Склонение Капеллы 58′” width=”89″ height=”15″ />
.
![]()
укажите 4558.

В этой задаче , поэтому
![]()
![]()
, в бланк запишем 6925.
Задача 2. Определите высоту звезды Капеллы ( Возничего) в нижней кульминации на северном полярном круге (33′” width=”92″ height=”16″ />
). Склонение Капеллы 58′” width=”89″ height=”15″ />
.
![]()
укажите 4558.
Для нижней кульминации считаем по формуле:
![]()
![]()
, в бланк запишем 2231.
![]()
.
![]()
укажите 4558.
Рассмотрим рисунок для нижней кульминации. Если высота светила будет положительна, тогда звезда не зайдет. Следовательно, необходимо, чтобы




![]()
. В бланке ответ 4402.
Задача 4. Определите полуденную высоту Солнца в Петрозаводске (47′” width=”92″ height=”17″ />
) в день летнего солнцестояния. В ответе градусы и минуты запишите слитно без знаков, например, вместо 47′” width=”57″ height=”15″ />
укажите 6147.
![]()
(что меньше широты Петрозаводска), то
![]()
![]()
, в бланк запишем 5140.
![]()
) в день зимнего солнцестояния.
![]()
укажите 6147.
![]()
(что меньше широты Петрозаводска), то
![]()
![]()
, в бланк запишем 446.
![]()
. Определите полуденную высоту Солнца в этой местности в день зимнего солнцестояния.
![]()
укажите 7250.
В день летнего солнцестояния склонение Солнца равно 27″ width=”80″ height=”14″ />
, а в день зимнего сонцестояния – 27″ width=”93″ height=”14″ />
. Солнце на Юге, следовательно, .
![]()
, или
![]()
![]()

В день зимнего солнцестояния также , поэтому
![]()
![]()
, в бланке запишем 2556.
![]()
. Чему равна широта места наблюдения?
![]()
. Тогда
![]()
![]()
![]()
.
Если вы студент, значит перед вами стоит тысяча возможностей. Найдите в себе силы, чтобы использовать хотя бы одну из них.
Вопросы к экзамену
Для всех групп технического профиля
Учу детей тому, как надо учиться
Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.
Урок 02. Звезды и созвездия. Небесные координаты и звездные карты.
Наименование разделов и тем
Содержание учебного материала, лабораторные работы и практические занятия, самостоятельная работа обучающихся
Объем часов
Уровень освоения
Звезды и созвездия. Небесные координаты и звездные карты.
Звезды и созвездия. Видимая звездная величина. Небесная сфера. Особые точки небесной сферы. Небесные координаты. Звездные карты. Видимое движение звезд на различных географических широтах. Связь видимого расположения объектов на небе и географических координат наблюдателя. Кульминация светил.
Воспроизведение определений терминов и понятий (созвездие, высота и кульминация звезд). Объяснение наблюдаемых невооруженным глазом движения звезд на различных географических широтах.
Тема 2.1. Звезды и созвездия. Небесные координаты и звездные карты.
2.1.1. Звезды и созвездия. Видимая звездная величина
Невооруженным глазом видно на небе большое количество звезд. Их так много, что, кажется, не сосчитать, однако звезд, которые видны невооруженным глазом, около трех тысяч. В общем случае на небе можно насчитать до 2500-3000 звезд (в зависимости от вашего зрения) – а всего видимых звезд около 6000.
Вероятно, еще на заре цивилизации люди, стремясь как-то разобраться во множестве звезд и запомнить их расположение, мысленно объединяли их в определенные фигуры. Тысячи лет назад люди глядели на небо, считали звезды и мысленно соединяли их в разнообразные фигуры (созвездия), называя их именами персонажей древних мифов и легенд, животных и предметов.
У разных народов имелись свои мифы и легенды о созвездиях, свои названия, разное их количество. Деления были чисто условны, рисунки созвездия редко соответствовали названной фигуре, однако это существенно облегчало ориентирование по небу. Даже босоногие мальчики в древней Халдее или Шумерах знали небо лучше любого из нас.
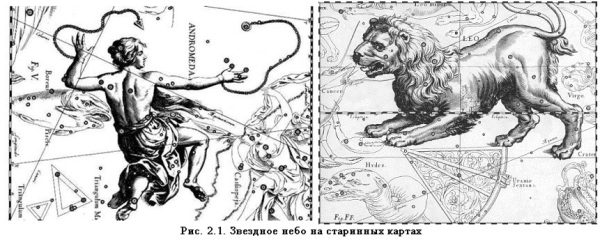
Созвездия – это определенные участки звездного неба, разделенные между собой строго установленными границами. Созвездия – область неба с характерной группой звезд и всеми звездами, находящимися внутри его границ. Соседство звезд, кажущиеся, в проекции на небесную сферу.
Старейшие по названиям считаются созвездия зодиакальные – пояс, вдоль которого происходит годичное движение Солнца, а также видимые пути Луны и планет. Так созвездия Телец – было известно > 4000 лет назад, так как в это время в этом созвездии находилась точка весеннего равноденствия.
У разных народов и в разное время был разный принцип деления звезд.
- 4 век до н.э. был список 809 звезд входящих в 122 созвездия.
- 18 век – Монголия – было 237 созвездий.
- 2 век – Птолемей (“Альмагеста”) – описано 48 созвездий.
- 15-16 век – период великих морских путешествий – описано 48 созвездий южного неба.
- В Русском звездном атласе Корнелия Рейссига, изданном в 1829г содержались 102 созвездия.
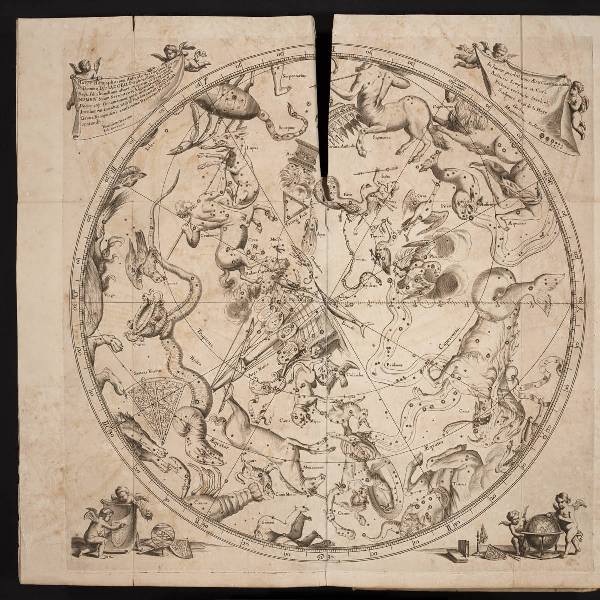
Созвездия Южного полушария автор Гевелий Ян, Уранография 1690 год

Атласы звёздного неба XVII века
Путаница с созвездиями прекращена в 1922г Международный астрономический союз разделил все небо на 88 созвездий, а границы окончательно установлены в 1928 году.
Среди всех 88 созвездий известное каждому Большая Медведица — одно из самых крупных.
Смотря на небо, нетрудно заметить, что звезды различны по яркости, или, как говорят астрономы, по блеску.
Видимые на небе невооруженным глазом звезды астрономы еще до нашей эры разделили на шесть величин. В 125г до НЭ Гиппарх (180-125, Греция) вводит деление звезд на небе по видимой яркости на звездные величины, обозначив самые яркие – первой звездной величины (1m), а еле видимые – 6m (т. е. разность в 5 звездных величин).
Звездная величина – видимая яркость (блеск) звезды. Звездная величина характеризует не размеры, а только блеск звезд. Чем слабее звезда, тем больше число, обозначающее ее звездную величину.
Когда ученые стали располагать приборами для измерения величины потока света, приходящего от звезд, оказалось, что от звезды первой величины света приходит в 2,5 раза больше, чем от звезды второй величины, от звезды второй величины в 2,5 раза больше, чем от звезды третьей величины, и т. д. Несколько звезд были отнесены к звездам нулевой величины, потому что от них света приходит в 2,5 раза больше, чем от звезд первой величины. А самая яркая звезда всего неба — Сириус (α Большого Пса) получила даже отрицательную звездную величину -1,5.
Было установлено, что поток энергии от звезды первой величины в 100 раз больше, чем от звезды шестой величины. К настоящему времени звездные величины определены для многих сотен тысяч звезд.
Звезды 1-й звездной величины – 1m, наиболее яркие назвали.
Звезды 2-й звездной величины – 2m, в 2,5 раза (точнее, 2,512) слабее по блеску звезд 1-й величины
Звезды 3-й звездной величины – 3m, в 2,5 раза (точнее, 2,512) слабее по блеску звезд 2-й величины
Звезды 4-й звездной величины – 4m, в 2,5 раза (точнее, 2,512) слабее по блеску звезд 3-й величины
Звезды 5-й звездной величины – 5m, в 2,5 раза (точнее, 2,512) слабее по блеску звезд 4-й величины
Звезды 6-й звездной величины – 6m, в 2,5 раза (точнее, 2,512) слабее по блеску звезд 5-й величины. Самые слабые по блеску из доступных невооруженному глазу Они слабее звезд 1-й звездной величины в 100 раз.
Всего на небе 22 звезды 1-й звездной величины, но блеск их не одинаков: одни из них несколько ярче 1-й величины, другие слабее. Так же обстоит дело со звездами 2-й, 3-й и последующих величин, поэтому для точного определения блеска той или иной пришлось ввести дробные числа. Измерения светового потока от звезд позволяют теперь определить их звездные величины с точностью до десятых и сотых долей.
Самая яркая звезда северного полушария неба Вега имеет блеск 0,14 звездной величины, а самая яркая звезда всего неба Сириус – минус 1,58 звездной величины, Солнце – минус 26,8.
Самые яркие звезды или наиболее интересные объекты из числа более слабых звезд получили собственные имена арабского и греческого происхождения (более 300 звезд имеют имена).
В 1603г Иоганн Байер (1572-1625, Германия) публикует каталог всех видимых звезд и впервые вводит их обозначение буквами греческого алфавита в порядке уменьшения блеска (наиболее яркие). Самые яркие – α, затем β, γ, δ, ε и т.д.
В каждом созвездии звезды обозначаются буквами греческого алфавита в порядке убывания их яркости. Наиболее яркая в этом созвездии звезда обозначается буквой α, вторая по яркости – β и т. д.
Звезды различаются не только по блеску, но и по цвету.
Они могут быть белыми, желтыми, красными. Чем краснее звезда, тем она холоднее. Солнце относится к желтым звездам.
С изобретением телескопа ученые получили возможность увидеть более слабые звезды, от которых приходит света гораздо меньше, чем от звезд шестой величины. Шкала звездных величин все дальше и дальше уходит в сторону их возрастания по мере того, как увеличиваются возможности телескопов. Так, например, хаббловский космический телескоп позволил получить изображение предельно слабых объектов – до тридцатой звездной величины.
Если Вы являетесь автором материалов или обладателем авторских прав, и Вы возражаете против его использования на моем интернет-ресурсе – пожалуйста, свяжитесь со мной. Информация будет удалена в максимально короткие сроки.
Спасибо тем авторам и правообладателям, которые согласны на размещение своих материалов на моем сайте! Вы вносите неоценимый вклад в обучение, воспитание и развитие подрастающего поколения.
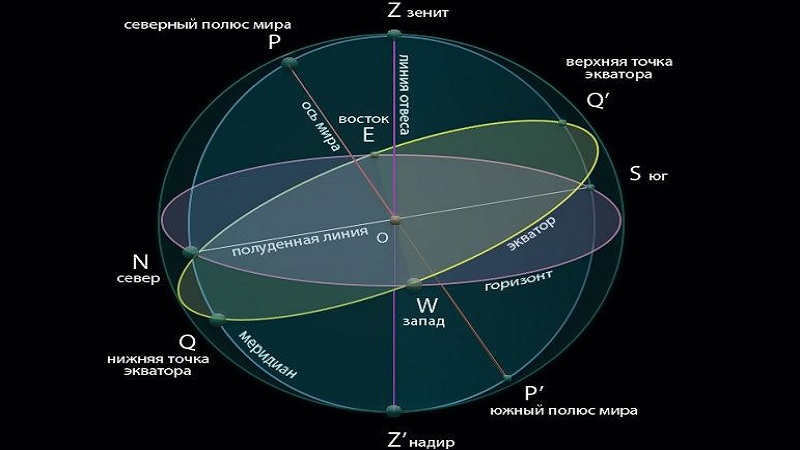
Для определения видимого положения небесных тел и изучения их движения в астрономии вводится понятие небесная сфера. Сфера имеет произвольные размеры и произвольный центр. В её центр в точке О помещён наблюдатель, а вращение сферы повторяет вращение небесного свода. Прямая ZOZ′ обозначает отвесную линию для наблюдателя, где бы он не находился. Верхняя точка над головой наблюдателя Z называется Зенит, а противоположная её точка Z′ – называется Надир. Большой круг SWNE перпендикулярен отвесной линии называется истинным горизонтом или математический горизонт. Математический горизонт делит сферу на две половины, видимую и невидимую для наблюдателя. Линия РР′ – называется ось мира, вокруг этой оси происходит вращение небесной сферы. Плоскость ЕQWQ′ перпендикулярна к оси мира называется небесный экватор. Он делит небесную сферу на два полушария – северное и южное. Большой круг небесной сферы PZQSP′Z′Q′N называется небесным меридианом. Небесный меридиан делит небесную сферу на Восточное и Западное полушарие. Линия NOS называется полуденной линией.
Положение основных элементов небесной сферы относительно друг друга зависит от географической широты места наблюдателя. Под углом к плоскости математического горизонта расположена ось мира РР′. Положения светил на небе определяется по отношению к основным плоскостям и связанным с ними линиями и точками небесной сферы и выражается количественно двумя величинами (центральными углами или дугами больших кругов) которые называются небесными координатами.
2 Горизонтальная система координат
Основной плоскостью горизонтальной системы координат является математический горизонт NWSE , а отчёт ведётся от Z зенита и от одной из точек математического горизонта. Одной координатной является зенитное расстояние z (Зенитное расстояние к югу zв = φ – δ; к северу zн = 180 – φ – δ) или высота светила над горизонтом h . Высотой h светила М называется высота вертикального круга mМ от математического горизонта до светила, или центральный угол mOM между плоскостью математического горизонта и направлением на светило М. Высоты отсчитываются от 0 до 90 к зениту и от 0 до -90 к надиру. Зенитным расстоянием светила называется дуга вертикального круга ZM от светила до зенита. z + h = 90 (1). Положение самого вертикального круга определяется дугой координатной – азимутом А. Азимутом А называется дуга математического горизонта Sm от точки юга S до вертикального круга, проходящего через светило. Азимуты отсчитывается в сторону вращения небесной сферы, т.е. к западу от точки юга, в пределах от 0 до 360. Система координат используется для непосредственных определений видимых положений светил с помощью угломерных инструментов.

3 Первая экваториальная система координат
Начало отсчёта – точка небесного экватора Q. Одной координатной является склонение. Склонением называется дуга mM часового круга PMmP′ от небесного экватора до светила. Отсчитываются от 0 до +90 к северному полюсу и от 0 до -90 к южному. p + = 90 . Положение часового круга определяется часовым углом t. Часовым углом светила М называется дуга небесного экватора Qm от верхней точки Q небесного экватора до часового круга PMmP′, проходящего через светило. Часовые углы отсчитываются в сторону суточного обращения небесной сферы, к западу от Q в пределах от 0 до360 или от 0 до 24 часов. Система координат используется в практической астрономии для определения точного времени и суточного вращения неба. Определяет Суточное движение Солнца, Луны и других светил.

4 Вторая экваториальная система координат
Одной координатной является склонение , другой прямое восхождение α. Прямое восхождение α светила М называется дуга небесного экватора ♈m от точки весеннего равноденствия ♈ до часового круга, проходящего через светило. Отсчитывается в сторону противоположную суточному вращению в пределах от 0 до до 360 или от 0 до 24 часов. Система используется для определения звёздных координат и составления каталогов. Определяет годичное движение Солнца и других светил.

5 Высота полюса мира над горизонтом, высота светила в меридиане
Высота полюса мира над горизонтом всегда равна астрономической широте места наблюдателя:
- Если склонение светила меньше географической широты, то оно кульминирует к югу от зенита на z= φ – δ или на высоте h= 90– φ + δ
- Если склонение светила равно географической широте, то оно кульминирует в зените и z= 0, а h= + 90
- Если склонение светила больше географической широты, то оно кульминирует к северу от зенита на z=с – φ или на высоте h= 90+ φ – с

6 Условия для восхода и заката светил
Для наблюдателя на полюсах будут только незаходящие светила.
Явление пересечения светилом небесного меридиана называется кульминацией светила.
Если светило пересекает верхнюю часть меридиана – наступает верхняя кульминация, если нижнюю – нижняя кульминация.
Для наблюдателя на полюсах будут только незаходящие светила.
Явление пересечения светилом небесного меридиана называется кульминацией светила.
Если светило пересекает верхнюю часть меридиана – наступает верхняя кульминация, если нижнюю – нижняя кульминация.
Читайте также:
- Периодичность технического обслуживания холодильного механического и весового оборудования кратко
- Основания прекращения брака кратко
- Уэльс географическое положение кратко
- Возрождение русских земель 14 15 века кратко
- Фейсбук плюсы и минусы кратко
Кульминация (астрономия) – момент прохождения светила через небесный меридиан в процессе его суточного движения. Иначе: моменты прохождения светилом точек пересечения суточной параллели светила и небесного меридиана.
Различают верхнюю и нижнюю кульминации. В момент верхней кульминации светило поднимается на максимальную высоту над горизонтом. В момент нижней кульминации светило опускается на минимальную высоту, в некоторых случаях может оказаться под горизонтом.
Также различают верхнюю кульминацию к северу и к югу от зенита. Если светило кульминирует к югу от зенита, то, в момент кульминации, его астрономический азимут равен 0°, а если светило кульминирует к северу от зенита, то его азимут в момент кульминации равен 180°.
Зная склонение светила δ и широту места наблюдения φ можно вычислить зенитные расстояния этого светила в моменты кульминаций:
zн = 180º – (φ + δ);
zв; ю. з = φ – δ;
zв; c.з = δ – φ.
Наборот, наблюдая какую-либо звезду в верхней и нижней кульминации можно определить её склонение и широту места наблюдения. Если верхняя кульминация звезды происходит к югу от зенита, то
δ = 90° – (zн+zв; ю. з) /2;
φ = 90° – (zн-zв; ю. з) /2;
а если к северу от зенита, то
δ = 90° – (zн-zв; ю. з) /2;
φ = 90° – (zн+zв; ю. з) /2.
Измерение высот звёзд и планет
В виду большого сходства между собой взятие высот звёзд и планет значительно затруднено по сравнению с Солнцем и Луной, кроме того взятие высот звёзд и планет производится, когда наблюдается линия видимого горизонта, то есть:
1) В период навигационных сумерек.
2) В период белых ночей в высоких широтах.
3) В период лунных ночей, но от лунной дорожки 25° вправо и влево.

На рисунке измерение высоты звезды находящейся у линии видимого горизонта и у вертикала светила.
Взятие высот звёзд и планет выполняют одним из следующим способом:
Первый способ:
Устанавливаем алидаду на отсчёт 0°00¢ и навести трубу на выбранную звезду или планету, затем наклоняя секстан и перемещая алидаду всё время удерживать изображение звезды в поле трубы и подводим ее к линии видимого горизонта, а затем измерить высоту выполняя покачивание секстана около вертикала светила. После точного соприкосновения звезды или планеты с линией видимого горизонта замечаем момент по часам с точностью до 1 секунды и снять отсчёт с лимба число градусов, а с отсчётного барабана – минуты с точностью до 0,2′.
Второй способ:
По формулам или при помощи звёздного глобуса рассчитать высоту звезды или планеты и установить на данный отсчёт алидаду. В результате этого изображение звезды будет у линии видимого горизонта.
Третий способ:
Установить алидаду на 0°00 и взять секстан за ручку левой рукой, в результате этого он окажется в перевёрнутом положении лимбом вверх. Наводим трубу на выбранную звезду. Перемещая алидаду подводим линию видимого горизонта к звезде. После этого берём секстан правой рукой нормально лимбом вниз и выполняем измерение высоты звезды или планеты обычным путем.
Автор капитан В.Н. Филимонов
Что такое кульминация звёзд
Как оказалось, не все знают, что такое кульминация звёзд. По определению, кульминация означает наиболее высокий момент чего-либо. Собственно говоря, в астрономии под этим подразумевают наивысший момент движения космического объекта.
Итак, кульминация звезды — это момент её прохождения сквозь небесный меридиан во время суточного движения светила.
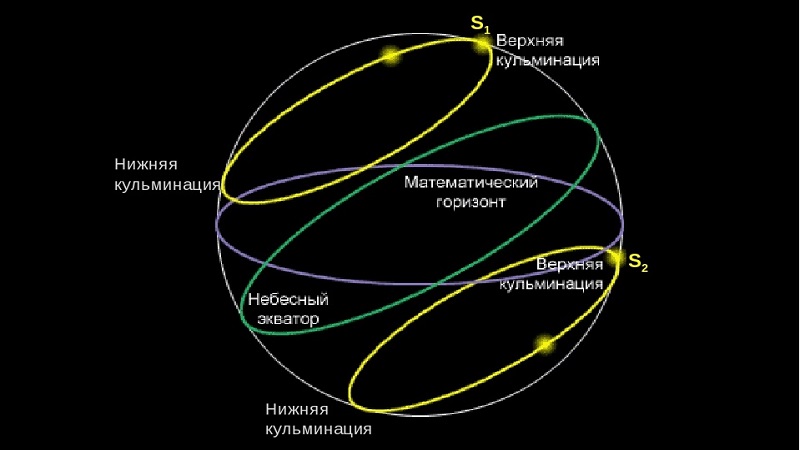
Стоит напомнить, что небесный меридиан является кругом сферы неба, который проходить сквозь зенит, полюс мира, а также южный полюс мира и надир.
Полюс мира представляет собой, можно сказать, отправную точку. Она лежит на небесной сфере, и как раз вокруг неё происходит видимое суточное движение звёзд. Причем перемещаются они по кругу параллельно экватору.
На Земле, как и в космосе — всегда есть на что посмотреть. Например сериалы Нетфликс, которые не оставят вас равнодушными.
Какая бывает кульминация звезд
Любое светило в течение суток пересекает меридиан неба в двух точках. Другими словами, вот этот момент и называется кульминацией.
Период между описываемым пересечением звёздных тел составляет половину суток, то есть 12 часов.
Так как кульминация звёзд происходит два раза за сутки, то она бывает двух видов:
- верхняя, когда высота светила достигает максимального значения;
- нижняя, наоборот, наступает в то время, когда высота звезды минимальна.
Как рассчитывается кульминация звёзд
Поскольку высота полюса мира над горизонтом равна географической широте местности, то определить значения момента пересечений звёздного тела и небесного меридиана не так уж сложно.
В действительности, верхняя и нижняя кульминация звезды рассчитывается по формуле:

где h — высота, ф — географическая широта и δ — склонение.
Получается, что если известно склонение и высота звезды в момент кульминации, то можно рассчитать географическую широту местности, откуда проводятся наблюдения.
Что интересно, незаходящая звезда для определённой географической широты наблюдается и в верхней, и в нижней кульминации. А вот если светило находится далеко от небесного экватора в сторону юга, то его пересечение с меридианом может быть незаметно.

Для понимания, как и когда происходит кульминация звёзд можно обратиться к нашему главному светилу. Правда, самый простой пример, это Солнце. Оно, как и другие звёзды, два раза в сутки пересекает небесный меридиан. И все мы хорошо знаем это время. Во-первых, верхняя солнечная кульминация-это полдень. Во-вторых, спустя половину суток (12 часов), наступает полночь или нижняя кульминация.
Как видно, люди долгое время наблюдали за движением небесных тел. Они выделили определённые особенности и научились применять их в своей жизни. В целом, само наблюдение за загадочными и светящимися звёздными точками, небесной сферой и космосом безумно увлекательное и красивое зрелище.
Оценка статьи:
![]() Загрузка…
Загрузка…
