Как найти минимальные многочлены матриц

Теорема Гамильтона-Кэли. Минимальный многочлен матрицы

Многочлен переменной называется аннулирующим для квадратной матрицы , если при подстановке в многочлен матрицы вместо переменной получаем нулевую матрицу, т.е. .

Напомним, что для любой квадратной матрицы многочлен называется характеристическим.

Теорема 7.7 Гамильтона–Кэли. Характеристический многочлен матрицы является аннулирующим для нее, т.е. .

В самом деле, обозначим через матрицу, присоединенную к характеристической матрице . Тогда из (7.7) следует

Правые части этих равенств можно рассматривать как многочлены с матричными коэффициентами (каждый коэффициент характеристического многочлена умножается на единичную матрицу). Из (7.27) следует, что λ-матрица делится на слева и справа без остатка, т.е. остаток равен нулевой матрице. По обобщенной теореме Безу остаток равен левому и правому значениям многочлена при подстановке матрицы вместо . Отсюда получаем , т.е. , что и требовалось доказать.

---

Пример 7.11. Показать, что характеристический многочлен матрицы является для нее аннулирующим.

Решение. Находим характеристический многочлен матрицы (см. пример 7.8)

Подставляя вместо переменной матрицу , получаем

что и требовалось показать.

---

Теорема Гамильтона-Кэли говорит о том, что для квадратной матрицы n-го порядка всегда найдется аннулирующий многочлен n-й степени (характеристический многочлен имеет n-ю степень). Возникает вопрос о существовании аннулирующего многочлена меньшей степени.

Минимальным многочленом матрицы называется ее аннулирующий многочлен наименьшей степени (со старшим коэффициентом, равным единице). Минимальный многочлен будем обозначать .

---

Свойства минимального многочлена матрицы

1. Любой аннулирующий многочлен матрицы делится на минимальный многочлен (без остатка). В частности, характеристический многочлен делится на минимальный многочлен.

Действительно, предположим противное, пусть аннулирующий многочлен делится на минимальный многочлен с остатком:

причем степень остатка меньше степени делителя . Тогда, подставляя вместо матрицу , получаем , так как и . Следовательно, — аннулирующий многочлен, степень которого меньше, чем степень минимального многочлена, что противоречит определению минимального многочлена. Таким образом, предположение оказалось ложным, т.е. любой аннулирующий многочлен делится на минимальный (без остатка). Поскольку по теореме Гамильтона-Кэли характеристический многочлен является аннулирующим, то он также делится на минимальный многочлен.

2. Для каждой квадратной матрицы минимальный многочлен единственный.

В самом деле, если бы существовали два минимальных многочлена, то они имели бы одну и ту же степень и делились бы друг на друга, т.е. отличались бы только постоянным множителем. Однако, старшие коэффициенты этих многочленов равны единице, поэтому такие многочлены совпадают.

3. Все собственные значения матрицы являются корнями минимального многочлена.

Действительно, из равенства следует, что λ-матрица делится (например, слева) на характеристическую матрицу , то есть , где — некоторая λ-матрица (левое частное). Найдем определитель левой и правой частей последнего равенства с учетом теоремы 2.2 и пункт З замечаний 2.2:

Подставляя в равенство (7.28) любой корень характеристического многочлена, получаем , т.е. , что и требовалось показать.

4. Если характеристический многочлен имеет вид (7.24), то минимальный многочлен этой матрицы можно представить в форме

где и т.д., причем .

Это утверждение следует из свойства 3.

5. Минимальный многочлен матрицы находится по формуле

где — наибольший общий делитель миноров (n-1)-го порядка характеристической матрицы .

Действительно, по свойству 1 характеристический многочлен делится на минимальный многочлен, т.е. , где — некоторый многочлен со старшим коэффициентом, равным единице. Умножив обе части равенства (см. свойство 3) на , получим в левой части характеристический многочлен, умноженный на единичную матрицу:

Сравним это равенство с (7.27):

При делении λ-матрицы слева на характеристическую матрицу частные (левые) должны совпадать в силу единственности деления. Поэтому

т.е. многочлен — делитель всех элементов присоединенной матрицы. Заметим, что степень многочлена должна быть максимальной, так как минимальный многочлен имеет наименьшую возможную степень, а сумма степеней этих двух многочленов в силу равенства фиксирована и равна . Поэтому многочлен — это наибольший общий делитель элементов присоединенной матрицы . Так как элементы присоединенной матрицы пропорциональны минорам (n-1)-го порядка характеристической матрицы, то .

Таким образом, , откуда следует формула (7.30).

6. Минимальный многочлен матрицы совпадает с последним инвариантным множителем характеристической матрицы .

В самом деле, наибольший общий делитель единственного минора n-го порядка характеристической матрицы отличается от определителя этой матрицы множителем , т.е. . Подставляя это выражение в (7.30), получаем

---

Способы нахождения минимального многочлена матрицы

Пусть — квадратная матрица n-го порядка. Требуется найти ее минимальный многочлен.

Первый способ.

1. Составить характеристическую матрицу .

2. Привести ее к нормальному диагональному виду .

Последний инвариантный множитель является минимальным многочленом матрицы (по свойству 6).

Второй способ.

1. Составить характеристическую матрицу .

2. Найти характеристический многочлен .

3. Найти наибольший общий делитель миноров (n-l)-ro порядка λ-матрицы .

4. По формуле (7.30) получить минимальный многочлен.

---

Пример 7.12. Найти минимальный многочлен матрицы , используя минимальный многочлен, найти степень с натуральным показателем .

Решение. Первый способ. 1. Составляем характеристическую матрицу

2. Приводим эту λ-матрицу к нормальному диагональному виду. Поменяем местами первую и третью строки. Выберем в качестве ведущего элемента единицу, оказавшуюся в левом верхнем углу матрицы. При помощи ведущего элемента делаем равными нулю остальные элементы первой строки и первого столбца:

Берем в качестве ведущего элемент и делаем равными нулю все остальные элементы второй строки и второго столбца. Затем умножаем вторую и третью строки на (-1), чтобы старшие коэффициенты диагональных элементов оказались равными единице. Получим нормальный диагональный вид:

Минимальный многочлен матрицы .

Второй способ. 1. Составляем характеристическую матрицу (7.32).

2. Находим характеристический многочлен (см. пример 7.11).

3. Находим миноры второго порядка характеристической матрицы . Ограничимся минорами, расположенными в первых двух строках:

Выражения для остальных миноров совпадают с найденными. Наибольший общий делитель многочленов равен , т.е. .

4. По формуле (7.30) получаем: .

Для проверки вычислим

Действительно, минимальный многочлен является аннулирующим, т.е. . Заметим, что для матрицы минимальный и характеристический многочлены отличаются только множителем .

Найдем теперь степень матрицы . Для этого рассмотрим многочлен . Разделим его на минимальный многочлен . Остаток от деления (многочлен степени не выше первой) представим в виде . Получим

где — частное, а — остаток. Найдем коэффициенты и , подставляя в равенство корни минимального многочлена:

– при имеем: ;

– при имеем: ;

Следовательно, . Поэтому . Теперь подставим вместо переменной матрицу

Результат совпадает с полученным в примере 7.10.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Минима́льный многочле́н ма́трицы — аннулирующий унитарный многочлен минимальной степени.

Свойства[править | править код]

• Минимальный многочлен делит характеристический многочлен матрицы.
• Любой аннулирующий многочлен делится на минимальный^[1].
• Минимальный многочлен единственен.
• Множество корней минимального многочлена совпадает с множеством корней характеристического многочлена матрицы.

Основная теорема[править | править код]

Теорема о минимальном многочлене Минимальный многочлен матрицы равен отношению характеристического многочлена матрицы к НОД элементов матрицы, присоединённой к матрице , где – единичная матрица

Примечания[править | править код]

Литература[править | править код]

• Гантмахер Ф. Р. Теория матриц. — 2-е изд.. — М.: Наука, 1966.
• Ланкастер П. Теория матриц. — М.: Наука, 1973.
• Прасолов В. В. Задачи и теоремы линейной алгебры. — М.: Наука, 1996. — 304 с. — ISBN 5-02-014727-3.

Это статья-заготовка по алгебре. Помогите Википедии, дополнив эту статью, как и любую другую.

Пусть дана
квадратная матрица
порядкас элементами из поля.
Если

произвольный
многочлен из кольца
,
то матрица

будет называться
значением
многочлена
при.

Нетрудно проверить,
что если

или
,
то
и, соответственно,.

Если многочлен

аннулируется матрицей
,
т. е.,
то матрицубудем называтьматричным
корнем многочлена
.

УТВЕРЖДЕНИЕ 1.
Всякая
матрица
служит корнем некоторого ненулевого
многочлена.

ДОКАЗАТЕЛЬСТВО.
Известно, что все квадратные матрицы
порядка
составляют над полеммерное
векторное пространство. Отсюда следует,
что система изматриц

линейно зависима
над полем
,
т. е. всуществуют такие элементы
,
не все равные нулю, что

.

Таким образом,
матрица

оказалась корнем ненулевого многочлена

,

степень которого
не превосходит
.
□

Матрица

является корнем и для некоторых таких
многочленов, старшие коэффициенты
которых равны единице
достаточно взять любой ненулевой
многочлен, аннулируемый матрицей
,
и разделить этот многочлен на его
старший коэффициент. Многочлен наименьшей
степени со старшим коэффициентом
,
аннулируемый, матрицей
,
называется минимальным
многочленом матрицы
.
Заметим, что минимальный многочлен
матрицы

определен однозначно, так как разность
двух таких многочленов имела бы меньшую
степень, чем каждый из них, но также
аннулировалась бы матрицей
.

УТВЕРЖДЕНИЕ 2.
Всякий
многочлен
,
аннулируемый матрицей,
делится нацело на минимальный многочленэтой матрицы.

ДОКАЗАТЕЛЬСТВО.
Разделим

на

с остатком

,

тогда

и из того, что
следует,
но степеньменьше степени,
что противоречит определению минимального
многочлена. □

Для доказательства
основной теоремы данного параграфа
потребуется вспомогательное утверждение.

ЛЕММА. Пусть

,
.
(1)

Если

(2)

то

(3)

ДОКАЗАТЕЛЬСТВО.
Достаточно доказать хотя бы первое из
двух утверждений леммы
второе доказывается аналогично.
Доказательство состоит в непосредственной
проверке справедливости равенства
(2), если многочленбудет заменен его записью (1), вместо

будет подставлено (3), а в качестве
будет взят многочлен

ТЕОРЕМА 1. Минимальный
многочлен матрицы
совпадает с последним инвариантным
множителемхарактеристической матрицы.

ДОКАЗАТЕЛЬСТВО.
Как следует из § 3.1

.
(4)

Значит, многочлены
ине будут нулевыми. Обозначим, далее,
черезматрицу, составленную из алгебраических
дополнений матрицы,
причём алгебраические дополнения
элементов каждой строки располагаются
в соответствующем столбце.

Тогда справедливо
равенство

.
(5)

С другой стороны,
так как элементами матрицы
служат взятые со знаками плюс или минус
минорыго
порядка матрицыи только они, а многочленесть общий наибольший делитель всех
этих миноров, то

,
(6)

причем наибольший
общий делитель элементов матрицы

равен
.

Из равенств (5),
(6) и (4) вытекает равенство

.

Это равенство
можно сократить на ненулевой множитель
.
Таким образом,

,

откуда

.
(7)

Это равенство
показывает, что остаток от деления
матрицыслева, на двучленравен нулю. Из леммы вытекает, что этот
остаток равен матрице.
Действительно, матрицаможет быть записана как матричныймногочлен,
коэффициенты которого являются
скалярными матрицами, т. е. перестановочные
с матрицей.
Таким образом
,
т. е. многочлен
действительно аннулируется матрицей.

Отсюда следует,
что многочлен
нацело делится на минимальныймногочлен матрицы,

.
(8)

Ясно, что старший
коэффициент многочлена
равен единице.

Так как
,
то по лемме остаток от левого деленияматрицына двучленравен нулю, т. е.

.
(9)

Равенства (8), (7) и
(9) приводят к равенству

.

Обе части этого
равенства можно сократить на общий
множитель
,
так как старший коэффициентэтого матричногомногочлена
является невырожденной матрицей. Таким
образом,

.

Мы помним, однако,
что наибольший общий делитель элементов
матрицы

равен
.
Поэтому многочлендолжен иметь нулевую степень, а так как
его старший коэффициент равен,
то.
Таким образом, ввиду (8),что и требовалось доказать. □

Так как, ввиду
(4), характеристический многочлен матрицы
нацело делится на многочлен,
то из доказанной сейчас теоремы вытекает
следующая

ТЕОРЕМА 2 (Гамильтона
Кэли).Всякая
матрица является корнем своего
характеристического многочлена.
□

ТЕОРЕМА 3. Если
матрицы
иподобны и если многочленаннулируется матрицей,
то он аннулируется и матрицей.

ДОКАЗАТЕЛЬСТВО.
Действительно, пусть
.

Если

,
то

.

Трансформируя
обе части этого равенства матрицей
,
получаем:

т.е.
.
□

СЛЕДСТВИЕ. Подобные
матрицы обладают одним и тем же
минимальным многочленом.
□

Пусть теперь
линейный оператор вмерном
линейном пространстве над полем.
Матрицы, задающие этот оператор в разных
базисах пространства, подобны между
собой. Общий минимальный многочлен
этих матриц называетсяминимальным
многочленом линейного оператора
.

Используя операции
над линейными операторами [2] можно
ввести понятие значения
многочлена

из кольца
при,
равном линейному оператору:
это

будет линейный
оператор

,

где
тождественный оператор.

Будем говорить,
что многочлен
аннулируется
линейным оператором
,
если
,
где
нулевой оператор.

Учитывая связь
между операциями над линейными
операторами и над матрицами можно
доказать следующее утверждение.

ТЕОРЕМА 4. Минимальный
многочлен линейного оператора
является тем однозначно определенным
многочленом наименьшей степени со
старшим коэффициентом,
который аннулируется оператором.
□

После этого
результаты, полученные выше, в частности
теорема Гамильтона
Кэли, могут быть переформулированы на
языке линейных операторов.

ЗАДАЧИ К ГЛАВЕ
III.

22. Привести
следующие
матрицы
к нормальной диагональной форме
посредством элементарных преобразований:

а)

б)

в)

г)

д)

е)

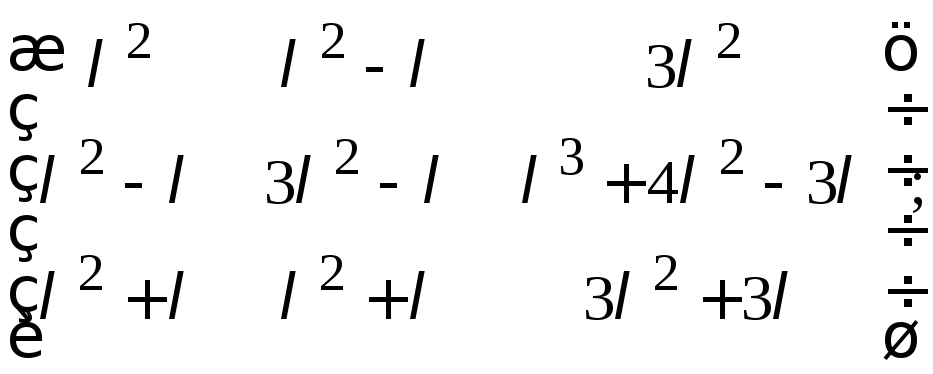
ж)

з)

и)

23. Привести
следующие
матрицы
к нормальной диагональной форме методом
нахождения делителей миноров:

а)

б)

в)

24. Привести
следующие
матрицы
к нормальной диагональной форме
используя комбинированный метод:

а)

б)

в)

г)

д)

е)

25. Выяснить,
эквивалентны ли между собой следующие
матрицы:

а)

б)

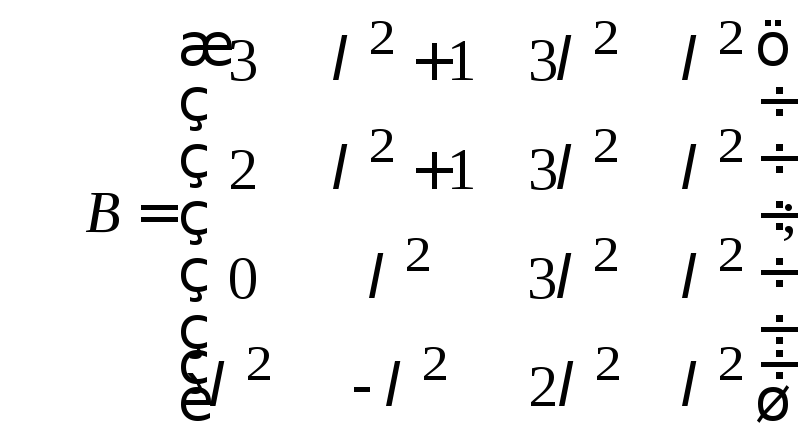
в)

26. Найти элементарные
делители следующих матриц:

а)

б)

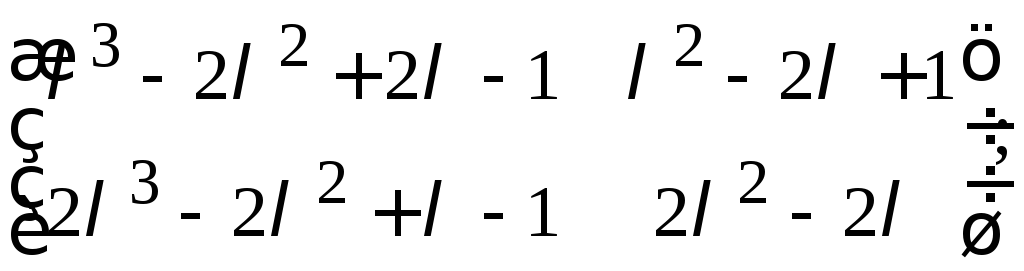
в)

27. Найти нормальную
диагональную форму квадратной
матрицы,
если известны её элементарные делители,
ранги порядок:

а)

б)

в)

28. Выяснить,
являются ли подобными между собой
следующие матрицы:

а)

б)

в)

г)

29.

а)

б)

в)

г)

д)

е)

ж)

з)

и)

к)

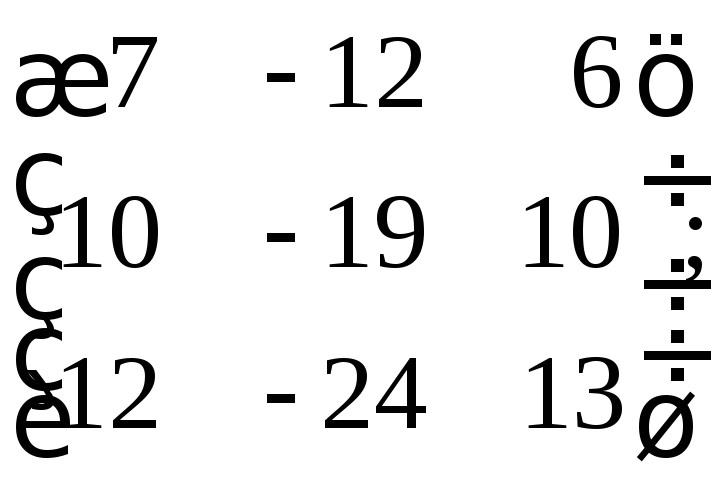
л)

м)

н)

о)

п)

30. Выяснить,
являются ли следующие матрицы подобными
некоторым диагональным матрицам в
полях рациональных, вещественных и
комплексных чисел:

а)

б)

в)

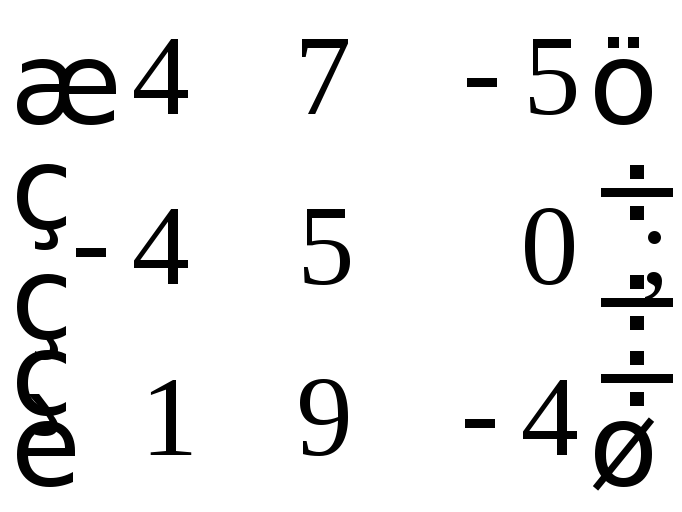
г)

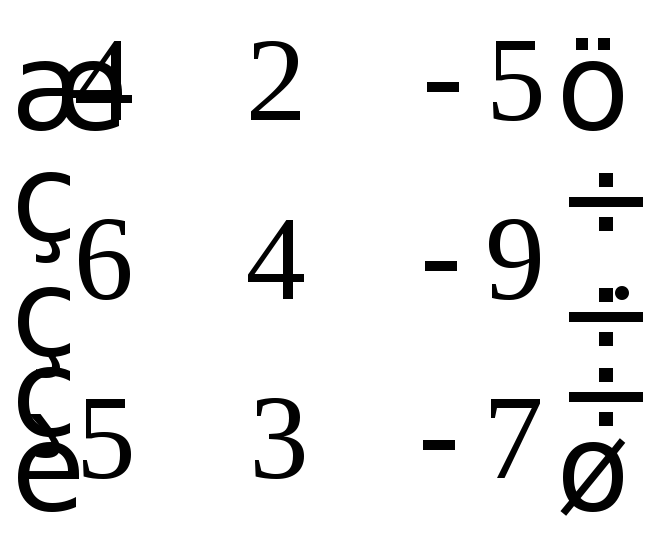
31. Найти минимальные
многочлены следующих матриц:

а)

б)

ОТВЕТЫ.

1.

а) да;

б) нет;

в) да;

г) да;

д)
нет.

2.

а) да;

б) нет;

в) да;

г) да;

д) нет;

е) нет;

ж) да.

3.

а) нет;

б) да;

в) да;

г) нет;

д) да;

е) нет;

ж) да.

4.

а)

;

б)

;

в)

.

5.

а)
;

б)
.

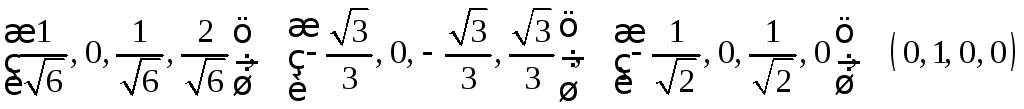6.

а)

;

б)

;

в)
.

7.

а) нет;

б)
да,

в)
да,

г) нет;

д)
да,

е)
да,

8.
.

9.

а) нет;

б) да;

в) да.

10.
Диагональная матрица является
ортогональной тогда и только тогда,
когда каждый диагональный элемент
равен
.

11.

а)

б)

в)

12.

а) нет;

б) да;

в) нет;

г) да.

13.

а)

б)
ни при каком

14.

а)

б)

в)

15.

а)

б)

в)

г)

д)

е)

ж)

з)

и)

к)

16.

а)

;

б)
;

в)
;

г)
;

д)
;

е)
.

17.

а)
;

б)
;

в)
;

г)
;

д)
.

18. Ответ определяется
неоднозначно.

а)

б)

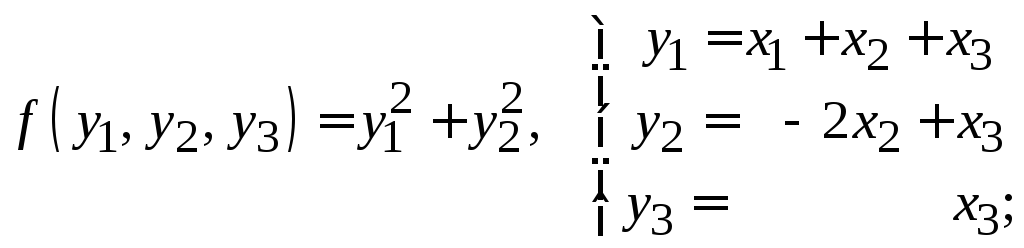
в)

г)

д)

е)

19. Ответ определяется
неоднозначно.

а)

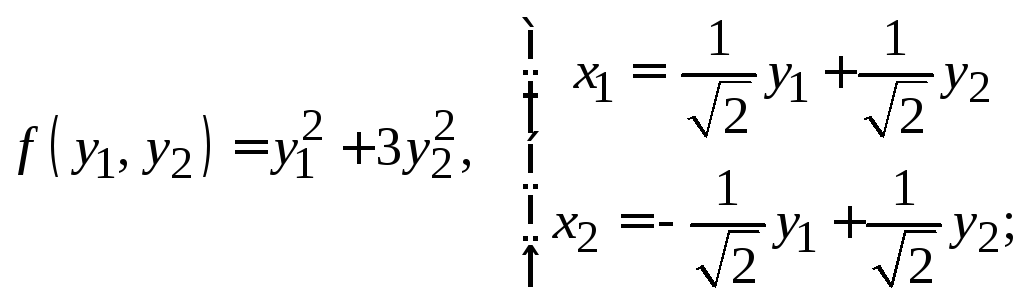
б)

в)

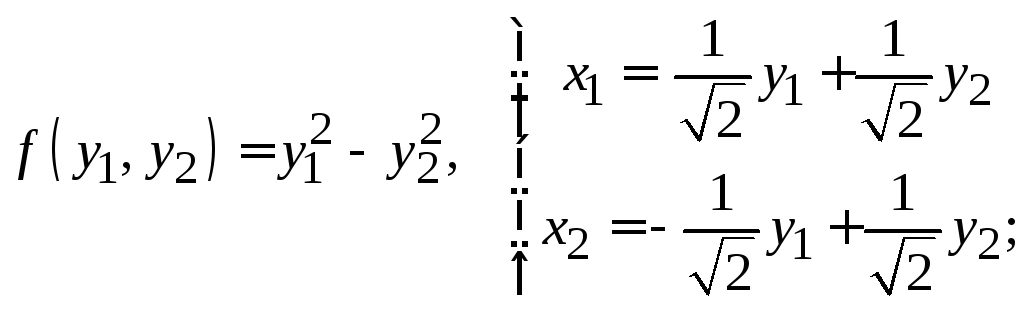
г)

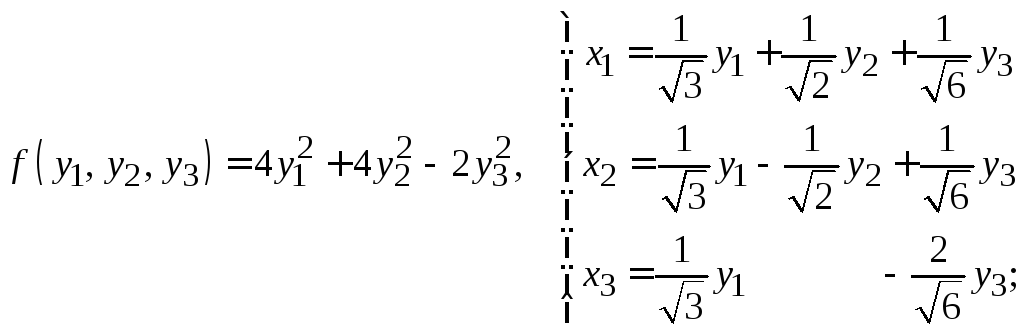
д)

е)

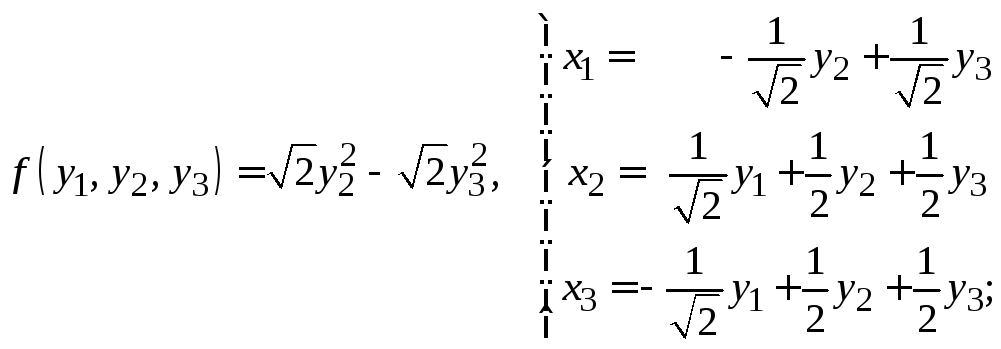
ж)

з)

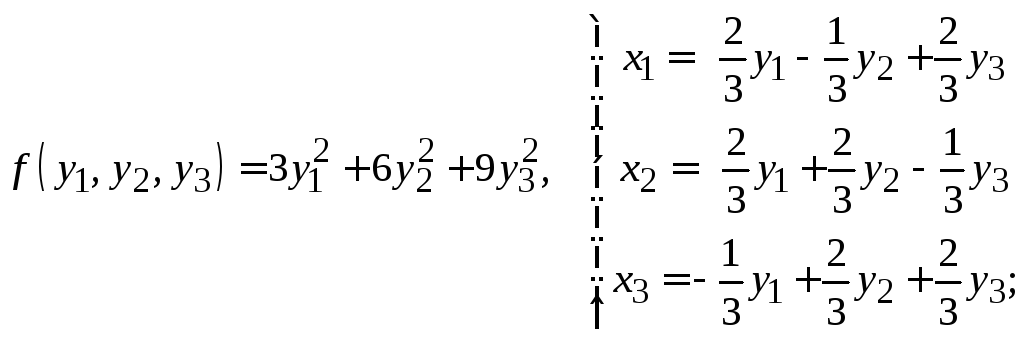
и)

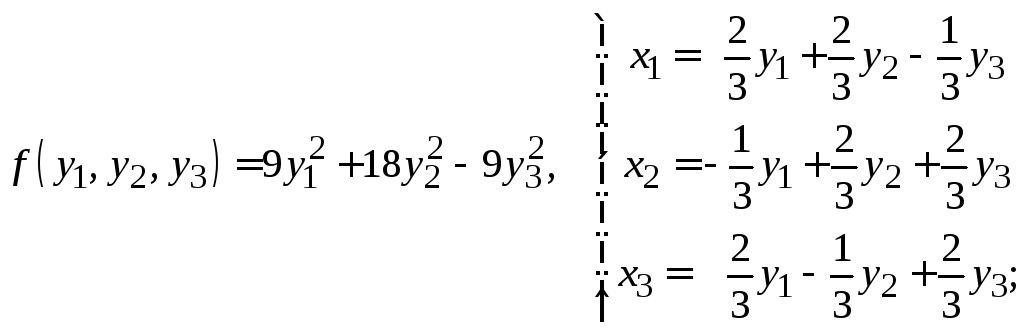
к)

л)

м)

20.

а) положительно
определённая;

б) не является
знакоопределённой;

в) не является
знакоопределённой;

г) положительно
определённая;

д) отрицательно
определённая;

е) не является
знакоопределённой.

21.

а)
для любого
;

б)
ни при каком значении
;

в)

;

г)

;

д)
ни при каком значении
;

е)

;

ж)

.

22.

а)

б)

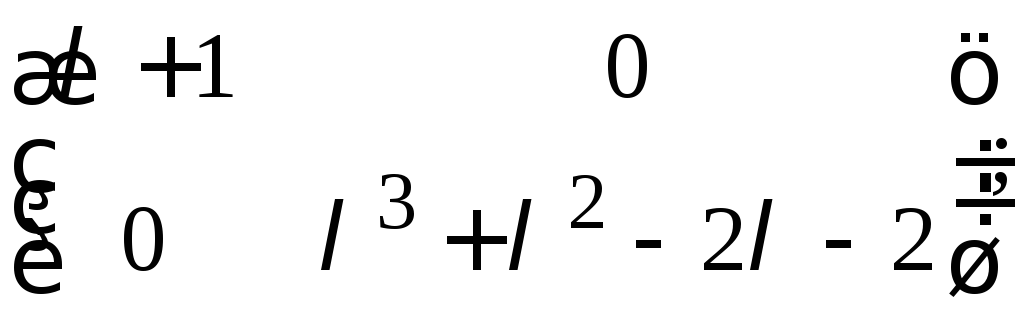
в)

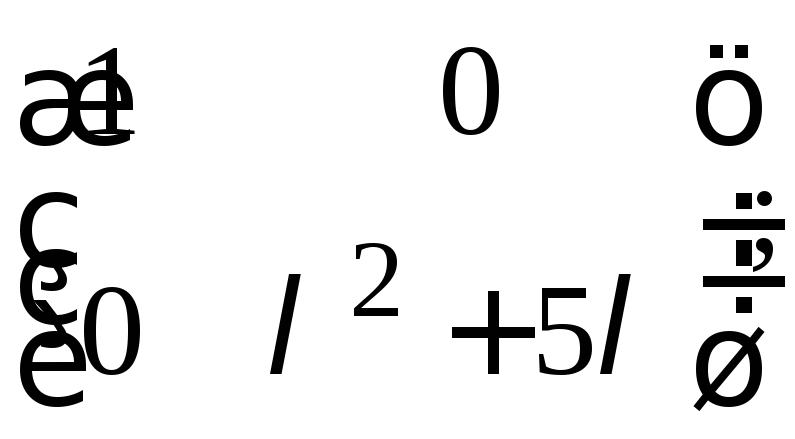
г)

д)

е)

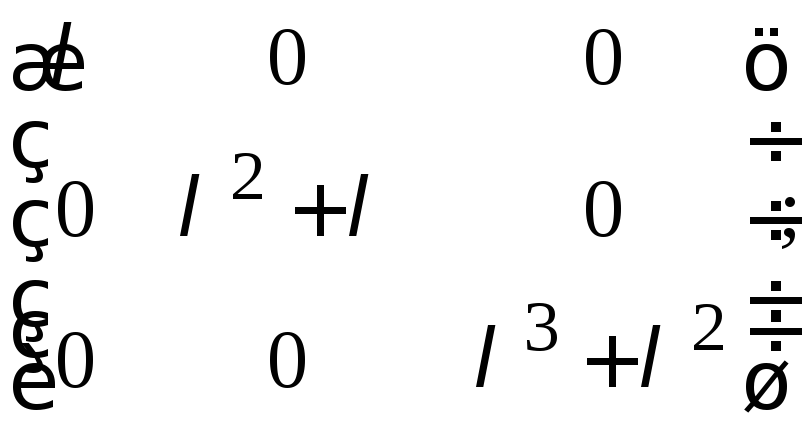
ж)

з)

и)

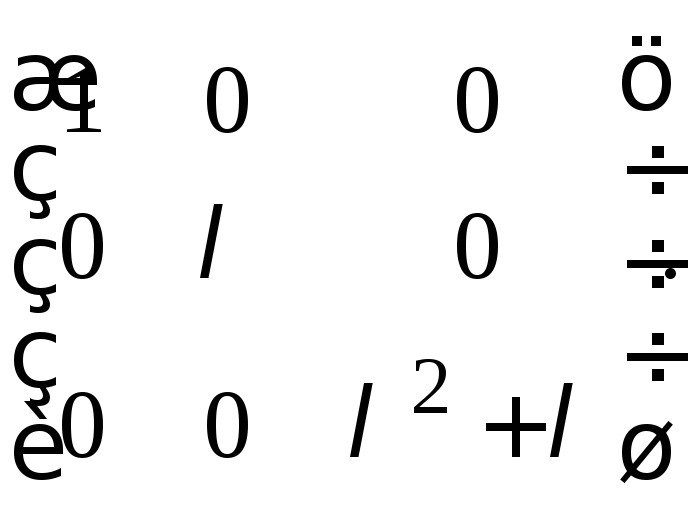
23.

а)

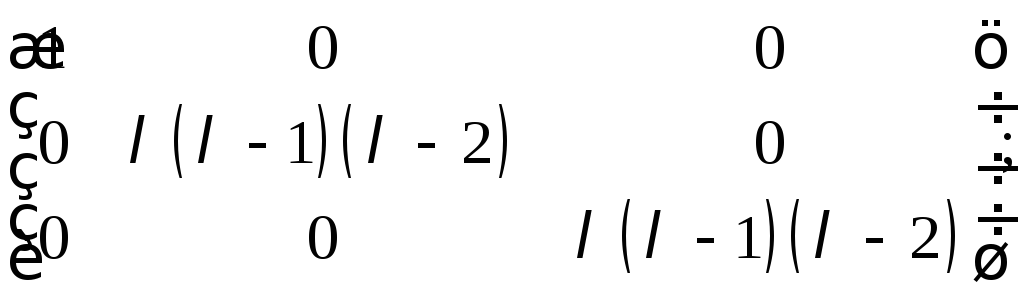
б)

в)

24.

а)

б)

в)
гдепорядок данной матрицы.

г)

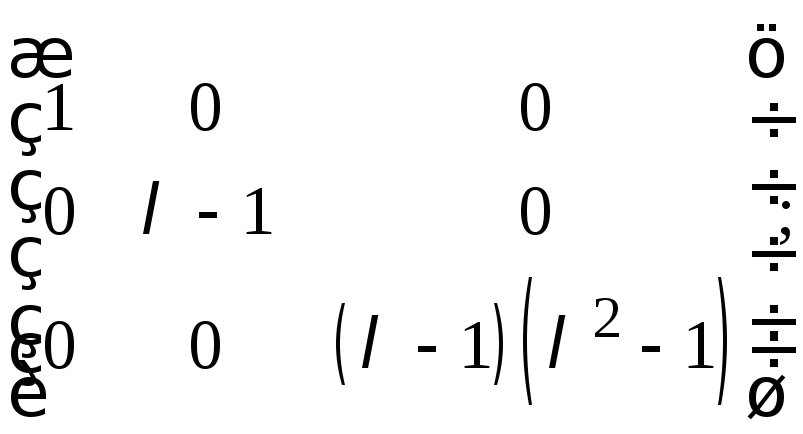
д)

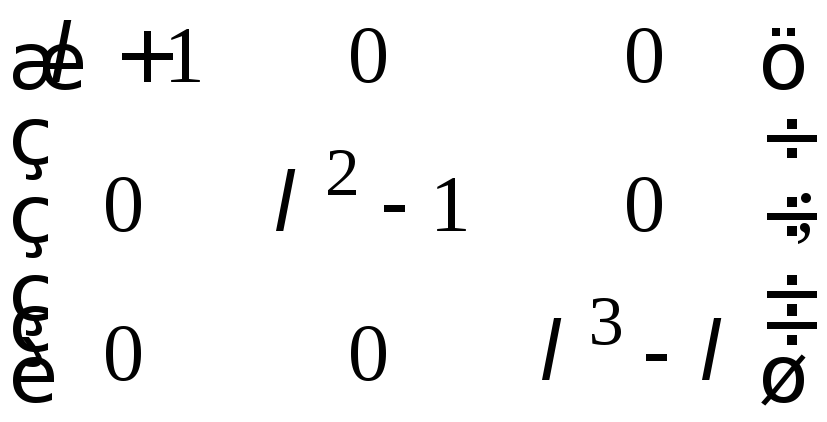
е)

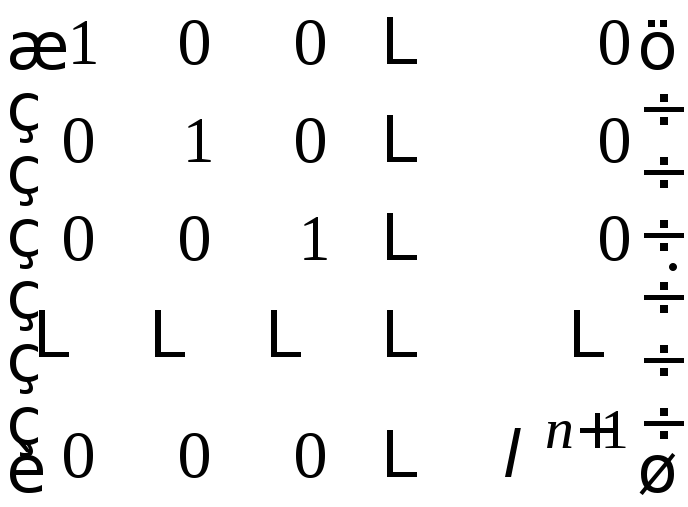
25.

а) эквивалентны;

б) не эквивалентны;

в) матрицы
иэквивалентны между собой и не эквивалентны
матрице.

26.

а)

б)

в) элементарных
делителей не существует.

27.

а)

б)

в)

28.

а) подобны;

б) подобны;

в) матрицы
иподобны между собой, но не подобны
матрице;

г) матрицы
иподобны между собой, но не подобны
матрице.

29.

а)

б)

в)

г)

д)

е)

ж)

з)

и)

к)

л)

м)

н)

о)

п)

30.

а) в поле рациональных
чисел подобна матрице

б)
в поле
вещественных чисел подобна матрице

в) в поле комплексных
чисел подобна матрице

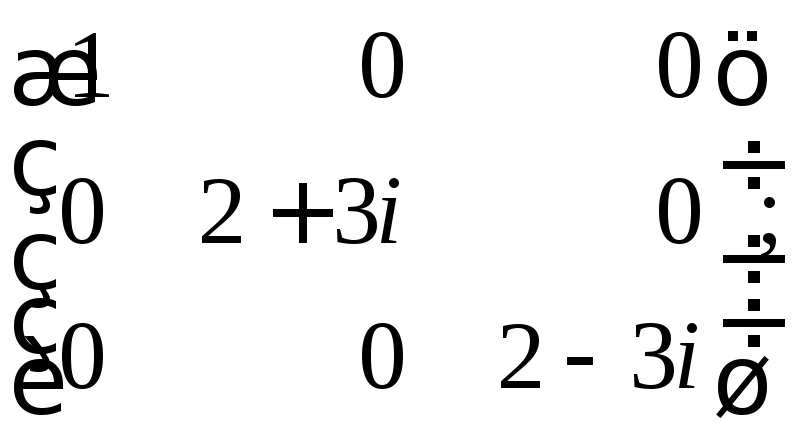
г) не подобна
диагональной матрице ни в каком поле.

31.

а)

б)

СПИСОК ЛИТЕРАТУРЫ.

1. Апатенок Р. Ф.,
   Маркина Л. М., Хейнман В. Б. Сборник задач
   по линейной алгебре и аналитической
   геометрии. 
   Минск: Высшая школа, 1990.

2. Ильин В. А., Позняк
   Э. Г. Линейная алгебра: Учеб.: Для
   ВУЗов. 
   М.: Физматлит, 2001.

3. Курош А. Г. Курс
   высшей алгебры. 
   М.: Наука, 1971.

4. Проскуряков И. В.
   Сборник задач по линейной алгебре. 
   М.: Наука, 1984.

5. Шипачёв В. С.
   Задачник по высшей математике: Учеб.
   пособие для ВУЗов. 
   М.: Высшая школа, 2002.

СОДЕРЖАНИЕ.

From Wikipedia, the free encyclopedia

In linear algebra, the minimal polynomial μ_A of an n × n matrix A over a field F is the monic polynomial P over F of least degree such that P(A) = 0. Any other polynomial Q with Q(A) = 0 is a (polynomial) multiple of μ_A.

The following three statements are equivalent:

1. λ is a root of μ_A,
2. λ is a root of the characteristic polynomial χ_A of A,
3. λ is an eigenvalue of matrix A.

The multiplicity of a root λ of μ_A is the largest power m such that ker((A − λI_n)^m) strictly contains ker((A − λI_n)^m−1). In other words, increasing the exponent up to m will give ever larger kernels, but further increasing the exponent beyond m will just give the same kernel. Formally, m is the nilpotent index of A–λI_n.

If the field F is not algebraically closed, then the minimal and characteristic polynomials need not factor according to their roots (in F) alone, in other words they may have irreducible polynomial factors of degree greater than 1. For irreducible polynomials P one has similar equivalences:

1. P divides μ_A,
2. P divides χ_A,
3. the kernel of P(A) has dimension at least 1.
4. the kernel of P(A) has dimension at least deg(P).

Like the characteristic polynomial, the minimal polynomial does not depend on the base field. In other words, considering the matrix as one with coefficients in a larger field does not change the minimal polynomial. The reason for this differs from the case with the characteristic polynomial (where it is immediate from the definition of determinants), namely by the fact that the minimal polynomial is determined by the relations of linear dependence between the powers of A: extending the base field will not introduce any new such relations (nor of course will it remove existing ones).

The minimal polynomial is often the same as the characteristic polynomial, but not always. For example, if A is a multiple aI_n of the identity matrix, then its minimal polynomial is X − a since the kernel of aI_n − A = 0 is already the entire space; on the other hand its characteristic polynomial is (X − a)ⁿ (the only eigenvalue is a, and the degree of the characteristic polynomial is always equal to the dimension of the space). The minimal polynomial always divides the characteristic polynomial, which is one way of formulating the Cayley–Hamilton theorem (for the case of matrices over a field).

Formal definition[edit]

Given an endomorphism T on a finite-dimensional vector space V over a field F, let I_T be the set defined as

where F[t ] is the space of all polynomials over the field F. I_T is a proper ideal of F[t ]. Since F is a field, F[t ] is a principal ideal domain, thus any ideal is generated by a single polynomial, which is unique up to units in F. A particular choice among the generators can be made, since precisely one of the generators is monic. The minimal polynomial is thus defined to be the monic polynomial which generates I_T. It is the monic polynomial of least degree in I_T.

Applications[edit]

An endomorphism φ of a finite-dimensional vector space over a field F is diagonalizable if and only if its minimal polynomial factors completely over F into distinct linear factors. The fact that there is only one factor X − λ for every eigenvalue λ means that the generalized eigenspace for λ is the same as the eigenspace for λ: every Jordan block has size 1. More generally, if φ satisfies a polynomial equation P(φ) = 0 where P factors into distinct linear factors over F, then it will be diagonalizable: its minimal polynomial is a divisor of P and therefore also factors into distinct linear factors. In particular one has:

• P = X^k − 1: finite order endomorphisms of complex vector spaces are diagonalizable. For the special case k = 2 of involutions, this is even true for endomorphisms of vector spaces over any field of characteristic other than 2, since X² − 1 = (X − 1)(X + 1) is a factorization into distinct factors over such a field. This is a part of representation theory of cyclic groups.
• P = X² − X = X(X − 1): endomorphisms satisfying φ² = φ are called projections, and are always diagonalizable (moreover their only eigenvalues are 0 and 1).
• By contrast if μ_φ = X^k with k ≥ 2 then φ (a nilpotent endomorphism) is not necessarily diagonalizable, since X^k has a repeated root 0.

These cases can also be proved directly, but the minimal polynomial gives a unified perspective and proof.

Computation[edit]

For a nonzero vector v in V define:

This definition satisfies the properties of a proper ideal. Let μ_T,v be the monic polynomial which generates it.

Properties[edit]

Example[edit]

Define T to be the endomorphism of R³ with matrix, on the canonical basis,

Taking the first canonical basis vector e₁ and its repeated images by T one obtains

of which the first three are easily seen to be linearly independent, and therefore span all of R³. The last one then necessarily is a linear combination of the first three, in fact

T³ ⋅ e₁ = −4T² ⋅ e₁ − T ⋅ e₁ + e₁,

so that:

μ_T, e1 = X³ + 4X² + X − I.

This is in fact also the minimal polynomial μ_T and the characteristic polynomial χ_T : indeed μ_T, e1 divides μ_T which divides χ_T, and since the first and last are of degree 3 and all are monic, they must all be the same. Another reason is that in general if any polynomial in T annihilates a vector v, then it also annihilates T ⋅v (just apply T to the equation that says that it annihilates v), and therefore by iteration it annihilates the entire space generated by the iterated images by T of v; in the current case we have seen that for v = e₁ that space is all of R³, so μ_T, e1(T ) = 0. Indeed one verifies for the full matrix that T³ + 4T² + T − I₃ is the zero matrix:

References[edit]

• Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, vol. 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556

Пусть – линейный оператор; – квадратная матрица порядка N ;

– произвольный базис в рассматриваемом пространстве V.

Степень матрицы А определяется обычным образом ; . Кроме того можно записать , где P и Q – целые неотрицательные числа.

Определение: Если – многочлен (целая рациональная функция) то многочленом от матрицы А называется квадратная матрица .

Определение: Многочленом от линейного оператора φ называется линейный оператор , где ; , кроме того (здесь Ix=X) и, очевидно, что .

Следствие:

Доказательство:

Следует из Определения произведения 2-х операторов. #

В силу изоморфизма (взаимооднозначного соответствия) линейных операторов φ и квадратных матриц А из следуют равенства и .

Определение: Говорят, что многочлен P(T) аннулирует линейный оператор φ (матрицу ), если .

Рассмотрим линейное пространство квадратных матриц порядка N, , пусть A0 – произвольная квадратная матрица порядка N, тогда матрицы будут л. н.з., если такие что . Это означает, что многочлен P(T) аннулирует матрицу A0.

Отсюда вытекает, что существует многочлен минимальной (min) степени, аннулирующий матрицу A0.

Определение: Минимальным многочленом матрицы А ( или линейного оператора φ) называется многочлен наименьшей степени со старшим коэффициентом равным 1, аннулирующий данную матрицу А (оператор φ).

Обозначение:  или соответственно.

Лемма: Пусть многочлен и квадратная матрица порядка N, связаны соотношением P(λ)E=(A– λE)C(λ), где , где – квадратные матрицы порядка N. Тогда P(A)=0.

Доказательство: Без доказательства.

Теорема: Всякий аннулирующий многочлен делится нацело на минимальный многочлен.

Доказательство:

Пусть P(T) – аннулирующий многочлен, тогда P(A)=0. Разделим P(T) на с остатком, т. е. , здесь Q(T) – частное, R(T) – остаток. Отметим, что (здесь deg – степень). Запишем: , т. е. R(T) – аннулирует матрицу А.

Отсюда вытекает, что , т. к. в противном случае () получили бы, что R(T) имеет степень меньшую, чем , чего не может быть, поэтому . #

Следствие: Минимальный многочлен единственен.

Доказательство:

Пусть и два минимальных многочлена. Они одинаковой степени, делятся нацело друг на друга и имеют коэффициенты при старшей степени равные единице. Поэтому очевидно, они совпадают. #

Отметим, что в любом базисе , при этом .

Теорема (Гамельтона-Келли): Всякий линейный оператор φ и его матрица аннулируется своим характеристическим многочленом .

Доказательство:

Рассмотрим матрицу (A–λE). Известно, что матрица обратная к данной имеет вид , где C(λ) – матрица из алгебраических дополнений (N-1)–го порядка относительно λ матрицы (A–λE).

Здесь , где .

Запишем: или . Умножая последнее равенство слева на получим: . Т. к. C(λ) – многочлен степени не выше (N-1) относительно λ, то взяв согласно Лемме получим, что . #

Следствия:

1) делится нацело на .

2) Т. к. корни минимального многочлена являются подмножеством корней характеристического многочлена (собственных значений оператора), то минимальный многочлен также разлагается на линейные множители.

< Предыдущая		Следующая >