Как найти минимальный член последовательности - Сайт, где вы сможете решить свои вопросы

Download Article

An arithmetic sequence is any list of numbers that differ, from one to the next, by a constant amount. For example, the list of even numbers, … is an arithmetic sequence, because the difference from one number in the list to the next is always 2.^[1] If you know you are working with an arithmetic sequence, you may be asked to find the very next term from a given list. You may also be asked to fill in a gap where a term is missing. Finally, you might want to know, for example, the 100th term, without actually writing out all 100 terms. A few simple steps can help you do any of these.

1

Find the common difference for the sequence. When you are presented with a list of numbers, you may be told that the list is an arithmetic sequence, or you may need to figure that out for yourself. The first step is the same in either case. Select the first two consecutive terms in the list. Subtract the first term from the second term. The result is the common difference of your sequence.^[2]
2

Check that the common difference is consistent. Finding the common difference for just the first two terms does not ensure that your list is an arithmetic sequence. You need to make sure that the difference is consistent for the whole list.^[3] Check the difference by subtracting two different consecutive terms in the list. If the result is consistent for one or two other pairs of terms, then you probably have an arithmetic sequence.

Advertisement
3

Add the common difference to the last given term. Finding the next term of an arithmetic sequence after you know the common difference is easy. Simply add the common difference to the last term of the list, and you will get the next number.^[4]

1

Verify that you are starting with an arithmetic sequence. In some cases, you may have a list of numbers with a missing term in the middle. Begin, as before, by checking that your list is an arithmetic sequence. Select any two consecutive terms and find the difference between them. Then check this against two other consecutive terms in the list. If the differences are the same, you can presume that you are working with an arithmetic sequence and proceed.
2

Add the common difference to the term before the space. This is similar to adding a term to the end of a sequence. Find the term that immediately precedes the space in your sequence. This is the “last” number that you know. Add your common difference to this term, to find the number that should fill in the space.^[5]
3

Subtract the common difference from the term following the space. To be sure that you have the correct answer, check from the other direction. An arithmetic sequence should be consistent going in either direction. If you move from left to right and add 4, then going in the opposite direction, from right to left, you would do the opposite and subtract 4.^[6]
4

Compare your results. The two results that you get, from adding up from the bottom or from subtracting down from the top should match. If they do, then you have found the value for the missing term. If they do not, then you need to check your work. You may not have a true arithmetic sequence.

1

Identify the first term of the sequence. Not every sequence begins with the numbers 0 or 1. Look at the list of numbers that you have and find the first term. This is your starting point, which can be designated using variables as a(1).
2

Define your common difference as d. Find the common difference for the sequence as before. In this working example, the common difference is , which is 5. Checking with other terms in the sequence provides the same result. We will note this common difference with the algebraic variable d.^[7]
3
Use the explicit formula. An explicit formula is an algebraic equation that you can use to find any term of an arithmetic sequence, without having to write out the full list. The explicit formula for an algebraic sequence is .^[8]
- The term a(n) can be read as “the nth term of a,” where n represents which number in the list you want to find and a(n) is the actual value of that number. For example, if you are asked to find the 100th item in an arithmetic sequence, then n will be 100. Note that n is 100, in this example, but a(n) will be the value of the 100th term, not the number 100 itself.
4

Fill in your information to solve the problem. Using the explicit formula for your sequence, fill in the information that you know to find the term that you need.^[9]

1

Rearrange the explicit formula to solve for other variables. Using the explicit formula^[10] and some basic algebra, you can find several pieces of information about an arithmetic sequence. In its original form, , the explicit formula is designed to solve for a_n and give you the nth term of a sequence. However, you can algebraically manipulate this formula and solve for any of the variables.
2
Find the first term of a sequence. You may know that the 50th term of an arithmetic sequence is 300, and you know that the terms have been increasing by 7 (the “common difference”), but you want to find out what the first term of the sequence was. Use the revised explicit formula that solves for a1 to find your answer.^[11]
- Use the equation , and fill in the information that you know. Since you know that the 50th term is 300, then n=50, n-1=49 and a(n)=300. You also are given that the common difference, d, is 7. Therefore, the formula becomes . This works out to . The sequence that you have began at 43, and counted up by 7. Therefore, it looks like 43,50,57,64,71,78…293,300.
3
Find the length of a sequence. Suppose you know all about the start and end of an arithmetic sequence, but you need to find out how long it is. Use the revised formula $n={frac {a(n)-a(1)}{d}}+1$ .^[12]
- Suppose you know that a given arithmetic sequence begins at 100 and increases by 13. You are also told that the final term is 2,856. To find the length of the sequence, use the terms a1=100, d=13, and a(n)=2856. Insert these terms into the formula to give $n={frac {2856-100}{13}}+1$ . If you work this out, you get $n={frac {2756}{13}}+1$ , which equals 212+1, which is 213. There are 213 terms in that sequence.
- This sample sequence would look like 100, 113, 126, 139… 2843, 2856.

Add New Question

Question

Given only the 10th and 15th term, how do I find the first three terms?

Subtract the 10th term from the 15th term and divide by 5: that gives you D, the difference between any two consecutive terms. Multiply D by 9, and subtract that amount from the 10th term; that gives you the first term.
Question

What is the formula for the sequence 8,16,32,64,___?

This is not an arithmetic sequence. Look up geometric sequences for whatever formula you’re interested in.
Question

How do I calculate the 5 terms of an arithmetic sequence if the first term is 8 and the last term is 100?

Subtract 8 from 100 = 92. Divide 92 by 4 (because with five terms there will be four intervals between the first and last term). That gives you 23, the size of each interval. So the sequence begins with 8 and has a common difference of 23.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

There are different kinds of sequences of numbers. Do not assume that a list of numbers is an arithmetic sequence. Always check at least two pairs of terms, or preferably three or four, to find the common difference between terms.

Video

Remember that d can be either positive or negative, depending if it is being added or subtracted.

Thanks for submitting a tip for review!

About This Article

Article SummaryX

To find a term in an arithmetic sequence, determine the common difference by subtracting the first number from the second number. Then, confirm that the difference is consistent between each number in the sequence by repeating the above equation with the second and third numbers, the third and fourth numbers, and so on. Once you’ve confirmed the common difference, all you have to do to find the missing number is add the common difference to preceding term in the sequence. If you want to learn how to find a term later on in a sequence of numbers, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 339,614 times.

Did this article help you?

Источник

Циклическим называется алгоритм, в
котором некоторая часть операция (тело
цикла последовательность команд)
выполняется многократно. Цикл не может
быть бесконечным, т.к. алгоритм должен
приводить к результату через конечное
число шагов. В цикл обязательно должен
входить блок проверки условия. В
зависимости от того, где располагается
это условие, циклы делятся на циклы типа
«пока» (условие располагается перед
телом цикла) и циклы типа «до» (условие
располагается после тела цикла.

Другой виз классификации циклов – это
циклы с параметром и циклы с выходом по
условию.

Лабораторная работа № 5. Циклы с параметром Теория

Цикл с параметром или цикл со счетчиком
используется для организации циклов,
в которых можно выделить параметр с
известным начальным значением, конечным
значением и определить закономерность,
по которому параметр изменяется при
каждой итерации цикла. Итерацией
цикла называется
каждое повторение исполнения тела
цикла Алгоритм работы оператора
цикла с параметром можно представить
следующей блок-схемой:

Для реализации этого алгоритма оператор
цикла с параметром имеет следующий вид:

for (парамер=нач.знач.;
условие_работы_цикла; изменение_параметра)

оператор_тела_цикла;

Если тело цикла состоит более чем из
одного оператора, эти операторы
заключаются в фигурные скобки. Как
видно из блок-схемы, в цикле for
проверка выполнения условия прекращения
работы цикла осуществляется перед
первой итерацией, и, таким образом,
возможен цикл for,
тело которого не выполняется ни разу.
В большинстве случаев параметр цикла
с каждой итерацией изменяется на одну
и ту же величину – шаг. В этом случае
блок схема может быть сокращена, и,
согласно ГОСТ принято еще одно
обозначения цикла с параметром:

Оператор соответствующий такой блок-схеме
имеет следующий вид:

for
(парам.=нач.знач.; парам.<=кон.знач.;
парам.=парам.+шаг)

Например:

for
(a=0; a<=3; a=a+0.1)

cout<<”sin(“<<a<<”)=”<<sin(a);

Если надо считать, сколько раз проработал
цикл, то шаг равен 1, и цикл можно назвать
не цикл с параметром, а цикл со счетчиком.
В этом случае в сокращенной блок-схеме
можно не указывать шаг.

Оператор соответствующий такой блок-схеме
имеет следующий вид:

for
(счетчик=нач.знач.; счетчик<=кон.знач.;
счетчик++)

Тип параметра можно описывать
непосредственно в цикле, но при этом
следует помнить, что за пределами цикла
этот параметр не определен.

Например:

for (int i=1; i<=10; i++)

Примеры

Вычислить 10 значений d:
d=a²-b²+ab-8,

c,
если a<-3

где b= c/3,
если -3a0

a+c+4, если
a>0

а изменяется с шагом 4, начальное значение
а равно -26 . Значение с – произвольное
число.

Исходные данные: Значение с –
вещественное число.

Результат: 10 значений d.

Тестовый пример: при с=3

i	a	d
1	-26	668
2	-22	476
3	-18	316
4	-14	188
5	-10	92
6	-6	28
7	-2	-7
8	2	-67
9	6	-63
10	10	-27

Дано натуральное n <10.
Получить n-значное
натуральное число.

Исходные данные: количество цифр n
– целый тип.

Результат: d – целый
тип.

Тестовый пример: проверяется только
количество цифр.

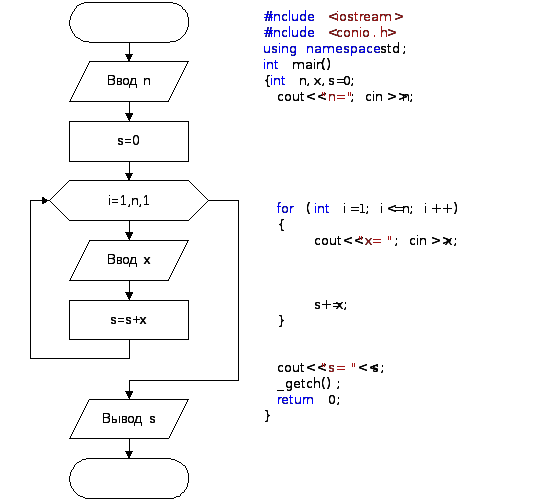
Вычислить сумму n
вещественных чисел.

Исходные данные: n –
количество введенных чисел – целый тип;
х – переменная, куда помещаются вводимые
числа – вещественный тип.

Результат: s – сумма
введенных чисел – вещественный тип.

При вычислении суммы выполняется
операция накопления данных в одной
переменной, в данном случае в переменной
s: s=s+x.
Эта операция должна выполняться n
раз. Для того чтобы в результате первой
операции накопления было получено
значение первого х, переменную S
предварительно надо очистить, т.е. s=0.

Тестовый пример: при n=7
и последовательности:1.2, 3, 5.6, 6.1, -4, -1,
4.2, s=17.1.

Во
многих языках программирования
отсутствует стандартная операция
возведения в степень. Необходимо написать
программу возведения в целую степень
вещественного числа.

Исходные данные: n –
степень, в которую возводится число –
целый тип. х – число, которое возводится
в степень n – вещественный
тип.

Результат: p –
вещественный тип.

Возвести в n-ю степень
число – значит перемножить это число
n раз

p=xxx…x

Операция перемножения х похожа на
операцию сложения, только знак «+»
заменяется на знак «*». Как и при сложении,
в результате первого действия умножения
надо получить само число х, т.е., и в этом
отличие от суммирования, первоначально
p должно быть равно 1.

Тестовый пример: При х=4 и n=5,
p=1024.

Ввести последовательность из n
целых чисел. Найти минимальный член
этой последовательности.

Исходные данные: n –
количество введенных чисел – целый тип;
а переменная, куда помещаются вводимые
числа – целый тип.

Результат: min – целый
тип.

Поиск минимального члена последовательности
чисел похож на процедуру определения
лучшего результат на соревновании
лыжников с раздельным стартом. Когда
первый лыжник прибегает на финиш, его
результат считается лучшим, т.е. в min
записывается этот результат. Затем,
когда прибегает очередной лыжник, его
результат сравнивается с лучшим (min),
и если этот результат меньше, то в
значение min записывается
этот результат. Следует обратить
внимание, что первоначальное значение
min не может равняться
нулю, так как в результате будет получен
этот ноль.

Поиск максимального элемента отличается
от поиска минимального только проверкой:
если новое значение больше текущего
максимального, в максимальное значение
записывается это новое значение.

Тестовый пример: при n=7,
последовательность: 8, 0, -1, 2, 10, 3, 5, min=-1.

Дана числовая последовательность
,
где n=1, … 15. Определить,
сколько отрицательных элементов в этой
последовательности.

Исходные данные: количество элементов
последовательности – 15.

Результат: количество отрицательных
элементов k – целый тип.

Для нахождения количества отрицательных
членов необходимо вычислить член
последовательности и сравнить его с 0,
если член меньше 0 увеличить k
на единицу. В начале задачи k
необходимо обнулить.

Тестовый пример: С помощью Excel
получаем k=6.

Рассмотренные алгоритмы относятся к
так называемым стандартным алгоритмам.
Отметим. что у всех этих алгоритмов
много общего. Рассмотрим следующую
таблицу:

этап	Сумма s	Произведение p	Количество k	Минимум min
До цикла	s=0	p=1	k=0	min=первый элемент
В цикле	1	Получение элемента последовательности	Получение элемента последовательности	Получение элемента последовательности	Получение элемента последовательности
2	Проверка, надо ли данный элемент суммировать (необязательно)	Проверка, надо ли данный элемент умножать (необязательно)	Проверка, удовлетворяет ли элемент условию	Проверка, элемент меньше Min?
3	s=s+элемент	p=p*элемент	k=k+1	min=элемент

Вычислить факториал k.
Факториалом называется произведение
k!=123…k.

Исходные данные: k –
целый тип.

Результат: fact
– тип long int.

Факториал числа очень быстро растет.
Поэтому результат должен иметь длинный
целый тип.

Тестовый пример: При k=5,
fact=120.

Даны натуральное число n,
символы s₁, …, s_n.
Известно, что среди s₁,
…, s_n
есть по крайней мере одна запятая. Найти
такое натуральное i, что
s_i – первая по порядку запятая;

Исходные данные: Количество элементов
n целое число, s
– вводимый символ.

Результат: k – номер
первой запятой.

Тестовый пример: при n=10
и последовательности ‘4hgj,e,6+,’
k=5.

Во многих задачах требуется выполнять
вычисления над элементами числовой
последовательности, в которой каждый
член a_n
является функцией натурального аргумента
n. В примере 6 приведен
вариант такой последовательности. Часто
по элементам числовой последовательности
требуется определить формулу для
вычисления n-го элемента.

Дана
числовая последовательность {a₁=2,
a₂=5, a₃=8,
…}. Члены последовательности с четными
номерами заменили на обратные им числа
(5 на -5). Найти сумму членов последовательности
с десятого по тридцать первый включительно.

Исходные данные: начальный член
последовательности 10, конечный член
последовательности – 31.

Результат: Сумма членов последовательности
s – целый тип.

Необходимо определить формулу для
вычисления члена последовательности
в зависимости от номера члена. С
увеличением номера на 1 член
последовательности изменяется на 3,
т.е. член зависит от 3*n.
При n=1 элемент равен 2.
Чтобы получить 2 необходимо из 3*n
вычесть 1. Таким образом a_n=3*n-1.

Чтобы определить четность номера
достаточно найти остаток от деления
номера на 2. Если остаток равен 0, то номер
четный.

Тестовый пример: с помощью Excel
получаем s=-33

Существуют
числовые последовательности, в которых
каждый новый член вычисляется через
предыдущие. Формула, в которой каждый
член последовательности вычисляется
через предыдущие, называется рекуррентной.
Рекуррентная формула, если она существует,
позволяет вычислить любой член
последовательности посредством
вычисления всех предыдущих членов.

Пусть a₀=1;
a_k=ka_k-1+1/k,
k=1,2,… . Дано натуральное число n.
Получить a_n.

Исходные данные: номер элемента n
– целый тип.

Результат: n-й элемент
последовательности а – вещественный
тип.

Тестовый пример: с помощью Excel
получаем при n=5, a_n
=278.12.

Рассмотрим пример более сложной
рекуррентной формулы

Дана числовая последовательность:
{a₁=0, a₂=4,
…, a_n=a_n_-1-3a_n_-2}.
Найти сумму отрицательных элементов
при n=25.

Исходные данные: количество элементов
n – целый тип, значение х
– a_n_-2целый тип,

y – a_n_-1 целый тип.

Результат: Сумма отрицательных
элементов S – целый тип.

Для вычисления нового значения a_n
необходимо знать 2 предыдущих значения.
Для получения нового значения a_n
надо знать a_n_-1
и a_n_-2
, которые необходимо сохранять в
дополнительных переменных.

Тестовый пример: с помощью Excel
получаем S= -1644128

Даны натуральное число n, символы s₁,
…, s_n. Выяснить, имеются ли в
последовательности s₁,
…, s_n такие члены
последовательности, что s_i и s_i+1
совпадает с буквой t.

Исходные данные: Количество элементов
n целое число, s
– вводимый символ.

Результат: k – количество
пар, равных t.

Для сравнения пар введенных символов
необходимо сохранять предыдущий
введенный символ в переменной а.

Тестовый пример:

при n=15 в последовательности
‘ertbyttbnvttvcd’ k=2.

Дано натуральное число n.
Определить, сколько у этого числа
делителей (1 и само число не учитывать).

Исходные данные: n –
целый тип.

Результат: количество делителей k-
целый тип.

Тестовый пример: при n=24,
k=6.

Даны натуральное число n,
символы. s₁, …, s_nПодсчитать наибольшее количество
идущих подряд запятых.

Исходные данные: натуральное число
n, вводимые символы s.

Результат: Максимальное количество
пробелов max целый тип.

Если введенный символ равен ‘,’ надо
увеличивать количество запятых идущих
подряд на 1 (k). Если символ
не запятая, надо проверить k,
если символ следует сразу же после
запятой (k>0) надо сравнить
k с максимальным количеством
запятых на данный момент. Если k>max,
надо изменить значения max.
После сравнения надо обнулить k
перед поиском количества в новой серии
запятых.

Тестовый пример:

при n=20, последовательность
’23,,wer,,,,,tyu,,,cv’,
max=5.

Задание 1 Написать программу и
отладить Пример 11 и 13

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Распишите, как найти наименьший член последовательности an = n ^ 2 + 16 / n

График убогий и по нему ничего не понять.

На этой странице сайта вы найдете ответы на вопрос Распишите, как найти наименьший член последовательности an = n ^ 2 + 16 / nГрафик убогий и по нему ничего не понять?,
относящийся к категории Математика. Сложность вопроса соответствует базовым
знаниям учеников 10 – 11 классов. Для получения дополнительной информации
найдите другие вопросы, относящимися к данной тематике, с помощью поисковой
системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и
задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям.
Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы
помогут найти нужную информацию.

Источник

Video

About This Article

Did this article help you?

Лабораторная работа № 5. Циклы с параметром Теория

Примеры

Вам также может понравиться

Как найти диктофон на самсунг галакси а51

Майнкрафт как найти бесплодные земли

Как быстро найти что то в ворде

Добавить комментарий Отменить ответ