Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 августа 2021 года; проверки требуют 7 правок.
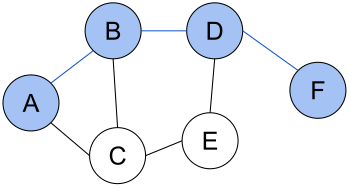
Кратчайший путь (A, B, D, F) между вершинами A и F в неориентированном графе без весов.
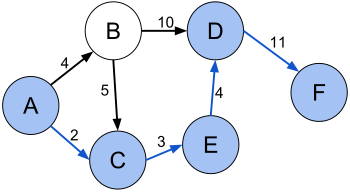
Кратчайший путь (A, C, E, D, F) между вершинами A и F во взвешенном ориентированном графе.
Зада́ча о кратча́йшем пути́ — задача поиска самого короткого пути (цепи) между двумя точками (вершинами) на графе, в которой минимизируется сумма весов рёбер, составляющих путь.
Задача о кратчайшем пути является одной из важнейших классических задач теории графов. Сегодня известно множество алгоритмов для её решения[⇨].
У данной задачи существуют и другие названия: задача о минимальном пути или, в устаревшем варианте, задача о дилижансе.
Значимость данной задачи определяется её различными практическими применениями[⇨]. Например, в GPS-навигаторах осуществляется поиск кратчайшего пути между точкой отправления и точкой назначения. В качестве вершин выступают перекрёстки, а дороги являются рёбрами, которые лежат между ними. Если сумма длин дорог между перекрёстками минимальна, тогда найденный путь самый короткий.
Определение[править | править код]
Задача поиска кратчайшего пути на графе может быть определена для неориентированного, ориентированного или смешанного графа. Далее будет рассмотрена постановка задачи в самом простом виде для неориентированного графа. Для смешанного и ориентированного графа дополнительно должны учитываться направления ребер.
Граф представляет собой совокупность непустого множества вершин и рёбер (наборов пар вершин). Две вершины на графе смежны, если они соединяются общим ребром. Путь в неориентированном графе представляет собой последовательность вершин 








Пусть 










Существуют различные постановки задачи о кратчайшем пути:
- Задача о кратчайшем пути в заданный пункт назначения. Требуется найти кратчайший путь в заданную вершину назначения t, который начинается в каждой из вершин графа (кроме t). Поменяв направление каждого принадлежащего графу ребра, эту задачу можно свести к задаче о единой исходной вершине (в которой осуществляется поиск кратчайшего пути из заданной вершины во все остальные).
- Задача о кратчайшем пути между заданной парой вершин. Требуется найти кратчайший путь из заданной вершины u в заданную вершину v.
- Задача о кратчайшем пути между всеми парами вершин. Требуется найти кратчайший путь из каждой вершины u в каждую вершину v. Эту задачу тоже можно решить с помощью алгоритма, предназначенного для решения задачи об одной исходной вершине, однако обычно она решается быстрее.
В различных постановках задачи, роль длины ребра могут играть не только сами длины, но и время, стоимость, расходы, объём затрачиваемых ресурсов (материальных, финансовых, топливно-энергетических и т. п.) или другие характеристики, связанные с прохождением каждого ребра. Таким образом, задача находит практическое применение в большом количестве областей (информатика, экономика, география и др.).
Задача о кратчайшем пути с учётом дополнительных ограничений[править | править код]
Задача о кратчайшем пути очень часто встречается в ситуации, когда необходимо учитывать дополнительные ограничения. Наличие их может значительно повысить сложность задачи[1]. Примеры таких задач:
- Кратчайший путь, проходящий через заданное множество вершин. Можно рассматривать два ограничения: кратчайший путь должен проходить через выделенное множество вершин, и кратчайший путь должен содержать как можно меньше невыделенных вершин. Первое из них хорошо известна в теории исследования операций[2].
- Минимальное покрытие вершин ориентированного графа путями. Осуществляется поиск минимального по числу путей покрытия графа, а именно подмножества всех s-t путей, таких что, каждая вершина ориентированного графа принадлежит хотя бы одному такому пути[3].
- Задача о требуемых путях. Требуется найти минимальное по мощности множество s-t путей
такое, что для любого
найдется путь
, накрывающий его.
— множество некоторых путей в ориентированном графе G[4].
- Минимальное покрытие дуг ориентированного графа путями. Задача состоит в отыскании минимального по числу путей подмножества всех путей, такого, что каждая дуга принадлежит хотя бы одному такому пути. При этом возможно дополнительное требование о том, чтобы все пути исходили из одной вершины[5].
Алгоритмы[править | править код]
В связи с тем, что существует множество различных постановок данной задачи, есть
наиболее популярные алгоритмы для решения задачи поиска кратчайшего пути на графе:
- Алгоритм Дейкстры находит кратчайший путь от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса[6].
- Алгоритм Беллмана — Форда находит кратчайшие пути от одной вершины графа до всех остальных во взвешенном графе. Вес рёбер может быть отрицательным.
- Алгоритм поиска A* находит маршрут с наименьшей стоимостью от одной вершины (начальной) к другой (целевой, конечной), используя алгоритм поиска по первому наилучшему совпадению на графе.
- Алгоритм Флойда — Уоршелла находит кратчайшие пути между всеми вершинами взвешенного ориентированного графа[6].
- Алгоритм Джонсона находит кратчайшие пути между всеми парами вершин взвешенного ориентированного графа.
- Алгоритм Ли (волновой алгоритм) основан на методе поиска в ширину. Находит путь между вершинами s и t графа (s не совпадает с t), содержащий минимальное количество промежуточных вершин (рёбер). Основное применение — трассировки электрических соединений на кристаллах микросхем и на печатных платах. Также используется для поиска кратчайшего расстояния на карте в стратегических играх.
- Поиск кратчайшего пути на основе алгоритма Килдала[7].
В работе (Черкасский и др., 1993)[8] представлено ещё несколько алгоритмов для решения этой задачи.
Задача поиска кратчайшего пути из одной вершины во все остальные[править | править код]
В такой постановке задачи осуществляется поиск кратчайшего пути из вершины v во все остальные вершины на графе.
Невзвешенный ориентированный граф[править | править код]
| Алгоритм | Сложность | Автор |
|---|---|---|
| Поиск в ширину | O(V+E) |
Ориентированный граф с неотрицательными весами[править | править код]
| Алгоритм | Сложность | Автор |
|---|---|---|
| – | O(V2EL) | Форд 1956 |
| Алгоритм Беллмана — Форда | O(VE) | Беллман 1958[9], Мур 1957[10] |
| – | O(V2 log V) | Данциг 1958, Данциг 1960, Minty (cf. Pollack&Wiebenson 1960), Whiting&Hillier 1960 |
| Алгоритм Дейкстры со списком. | O(V2) | Leyzorek et al. 1957[11], Дейкстра 1959[12] |
| Алгоритм Дейкстры с модифицированной двоичной кучей | O((E + V) log V) | – |
| . . . | . . . | . . . |
| Алгоритм Дейкстры с использованием фибоначчиевой кучи | O(E + V log V) | Фридман&Тарьян 1984[13], Фридман&Тарьян 1987[14] |
| – | O(E log log L) | Джонсон 1982, Карлссон&Поблете 1983 |
| Алгоритм Габова | O(E logE/V L) | Габов 1983, Габов 1985 |
| – | O(E + V√log L) | Ахуджа et al. 1990 |
Ориентированный граф с произвольными весами[править | править код]
| Алгоритм | Сложность | Автор |
|---|---|---|
| Алгоритм Беллмана — Форда | O(VE) | Беллман[9], Мур[10] |
| Алгоритм Левита | O(VE) |
Задача о кратчайшем пути между всеми парами вершин[править | править код]
Задача о кратчайшем пути между всеми парами вершин для невзвешенного ориентированного графа была поставлена Симбелом в 1953 году[15], который обнаружил, что она может быть решена за линейное количество манипуляций (умножения) с матрицей. Сложность такого алгоритма O(V4).
Так же для решения данной задачи существуют другие более быстрые алгоритмы, такие как Алгоритм Флойда — Уоршелла со сложностью O(V3), и
Алгоритм Джонсона (является комбинацией алгоритмов Бэллмана-Форда и Дейкстры) со сложностью O(VE + V2 log V).
Применение[править | править код]
Задача о поиске кратчайшего пути на графе может быть интерпретирована по-разному и применяться в различных областях. Далее приведены примеры различных применений задачи. Другие применения изучаются в дисциплине, которая занимается исследованием операций[16].
Картографические сервисы[править | править код]
Алгоритмы нахождения кратчайшего пути на графе применяются для нахождения путей между физическими объектами на таких картографических сервисах, как карты Google или OpenStreetMap. В обучающем видео от Google можно узнать различные эффективные алгоритмы, которые применяются в данной сфере[17].
Недетерминированная машина[править | править код]
Если представить недетерминированную абстрактную машину как граф, где вершины описывают состояния, а ребра определяют возможные переходы, тогда алгоритмы поиска кратчайшего пути могут быть применены для поиска оптимальной последовательности решений для достижения главной цели. Например, если вершинами являются состояния Кубика Рубика, а ребром представляет собой одно действие над кубиком, тогда алгоритм может быть применён для поиска решения с минимальным количеством ходов.
Сети дорог[править | править код]
Задача поиска кратчайшего пути на графе широко используется при определении наименьшего расстояния в сети дорог.
Сеть дорог можно представить в виде графа с положительными весами. Вершины являются дорожными развязками, а ребра дорогами, которые их соединяют. Веса рёбер могут соответствовать протяжённости данного участка, времени необходимому для его преодоления или стоимости путешествия по нему. Ориентированные ребра можно использовать для представления односторонних улиц. В таком графе можно ввести характеристику, которая указывает на то, что одни дороги важнее других для длительных путешествий (например автомагистрали). Она была формализована в понятии (идее) о магистралях[18].
Для реализации подхода, где одни дороги важнее других, существует множество алгоритмов. Они решают задачу поиска кратчайшего пути намного быстрее, чем аналогичные на обычных графах.
Подобные алгоритмы состоят из двух этапов:
- этап предобработки. Производится предварительная обработка графа без учёта начальной и конечной вершины (может длиться до нескольких дней, если работать с реальными данными). Обычно выполняется один раз и потом используются полученные данные.
- этап запроса. Осуществляется запрос и поиск кратчайшего пути, при этом известны начальная и конечная вершина.
Самый быстрый алгоритм может решить данную задачу на дорогах Европы или Америки за доли микросекунды[19].
Другие подходы (техники), которые применяются в данной сфере:
- ALT
- Arc Flags
- Contraction hierarchies
- Transit Node Routing
- Reach based Pruning
- Labeling
Похожие задачи[править | править код]
Существуют задачи, которые похожи на задачу поиска кратчайшего пути на графе.
- Поиск кратчайшего пути в вычислительной геометрии (см. евклидов кратчайший путь).
- Задача коммивояжёра. Требуется найти кратчайший маршрут, проходящий через указанные города (вершины) хотя бы по одному разу с последующим возвратом в исходный город. Данная задача относится к классу NP-трудных задач в отличие от задачи поиска кратчайшего пути, которая может быть решена за полиномиальное время в графах без циклов. Задача коммивояжёра решается неэффективно для больших наборов данных.
- Задача канадского путешественника и задача стохастического поиска кратчайшего пути являются обобщением рассматриваемой задачи, в которых обходимый граф заранее полностью неизвестен и изменяется во времени или следующий проход по графу вычисляется на основе вероятностей.
- Задача поиска кратчайшего пути, когда в графе происходят преобразования. Например, изменяется вес ребра или удаляется вершина[20].
Постановка задачи линейного программирования[править | править код]
Пусть дан направленный граф (V, A), где V — множество вершин и A — множество рёбер, с начальной вершиной обхода s, конечной t и весами wij для каждого ребра (i, j) в A. Вес каждого ребра соответствует переменной программы xij.
Тогда задача ставится следующим образом: найти минимум функции 


См. также[править | править код]
- IEEE 802.1aq
- Транспортная сеть
- Двунаправленный поиск
Примечания[править | править код]
- ↑ Применение теории графов в программировании, 1985.
- ↑ Применение теории графов в программировании, 1985, с. 138—139.
- ↑ Применение теории графов в программировании, 1985, с. 139—142.
- ↑ Применение теории графов в программировании, 1985, с. 144—145.
- ↑ Применение теории графов в программировании, 1985, с. 145—148.
- ↑ 1 2 Дискретная математика. Комбинаторная оптимизация на графах, 2003.
- ↑ Применение теории графов в программировании, 1985, с. 130—131.
- ↑ Cherkassky, Goldberg, Radzik, 1996.
- ↑ 1 2 Bellman Richard, 1958.
- ↑ 1 2 Moore, 1957.
- ↑ M. Leyzorek, 1957.
- ↑ Dijkstra, 1959.
- ↑ Michael Fredman Lawrence, 1984.
- ↑ Fredman Michael, 1987.
- ↑ Shimbel, 1953.
- ↑ Developing algorithms and software for geometric path planning problems, 1996.
- ↑ Fast route planning.
- ↑ Highway Dimension, 2010.
- ↑ A Hub-Based Labeling Algorithm, 2011.
- ↑ Ladyzhensky Y., Popoff Y. Algorithm, 2006.
Литература[править | править код]
- Евстигнеев В. А. Глава 3. Итеративные алгоритмы глобального анализа графов. Пути и покрытия // Применение теории графов в программировании / Под ред. А. П. Ершова. — Москва: Наука. Главная редакция физико-математической литературы, 1985. — С. 138—150. — 352 с.
- Алексеев В.Е., Таланов В.А. Глава 3.4. Нахождения кратчайших путей в графе // Графы. Модели вычислений. Структуры данных. — Нижний Новгород: Издательство Нижегородского гос. университета, 2005. — С. 236—237. — 307 с. — ISBN 5–85747–810–8. Архивная копия от 13 декабря 2013 на Wayback Machine
- Галкина В.А. Глава 4. Построение кратчайших путей в ориентированном графе // Дискретная математика. Комбинаторная оптимизация на графах. — Москва: Издательство “Гелиос АРВ”, 2003. — С. 75—94. — 232 с. — ISBN 5–85438–069–2.
- Берж К. Глава 7. Задача о кратчайшем пути // Теория графов и её применения = Theorie des graphes et ses applications / Под ред. И. А. Вайнштейна. — Москва: Издательство иностранной литературы, 1962. — С. 75—81. — 320 с.
- Ойстин Оре. Теория графов / Под ред. И. М. Овчинниковой. — Издательство наука, 1980. — 336 с. Архивная копия от 15 декабря 2013 на Wayback Machine
- Виталий Осипов, Поиск кратчайших путей в дорожных сетях: от теории к реализации на YouTube.
- Харари Ф. Глава 2. Графы // Теория графов / под ред. Г. П. Гаврилов — М.: Мир, 1973. — С. 27. — 301 с.
- Cherkassky B. V., Goldberg A. V., Radzik T. Shortest paths algorithms: Theory and experimental evaluation (англ.) // Mathematical Programming — Springer Science+Business Media, 1996. — Vol. 73, Iss. 2. — P. 129–174. — ISSN 0025-5610; 1436-4646 — doi:10.1007/BF02592101
- Ричард Беллман. On a routing problem // Quarterly of Applied Mathematics. — 1958. — Т. 16. — С. 87—90.
- Dijkstra E. W. A note on two problems in connexion with graphs (англ.) // Numerische Mathematik / F. Brezzi — Springer Science+Business Media, 1959. — Vol. 1, Iss. 1. — P. 269—271. — ISSN 0029-599X; 0945-3245 — doi:10.1007/BF01386390
- Moore E. F. The shortest path through a maze (англ.) // Proceedings of an International Symposium on the Theory of Switching (Cambridge, Massachusetts, 2–5 April 1957) — Harvard University Press, 1959. — Vol. 2. — P. 285—292. — 345 p. — (Annals of the Computation Laboratory of Harvard University; Vol. 30) — ISSN 0073-0750
- M. Leyzorek, R. S. Gray, A. A. Gray, W. C. Ladew, S. R. Meaker, R. M. Petry, R. N. Seitz. Investigation of Model Techniques — First Annual Report — 6 June 1956 — 1 July 1957 — A Study of Model Techniques for Communication Systems (англ.). — Cleveland, Ohio: Case Institute of Technology, 1957.
- Michael Fredman Lawrence, Роберт Андре Тарьян. Fibonacci heaps and their uses in improved network optimization algorithms (англ.) : journal. — Институт инженеров электротехники и электроники, 1984. — P. 338—346. — ISBN 0-8186-0591-X. — doi:10.1109/SFCS.1984.715934. Архивировано 11 октября 2012 года.
- Michael Fredman Lawrence, Роберт Андре Тарьян. Fibonacci heaps and their uses in improved network optimization algorithms (англ.) // Journal of the Association for Computing Machinery : journal. — 1987. — Vol. 34, no. 3. — P. 596—615. — doi:10.1145/28869.28874.
- Shimbel, Alfonso. Structural parameters of communication networks // Bulletin of Mathematical Biophysics. — 1953. — Т. 15, № 4. — С. 501—507. — doi:10.1007/BF02476438.
- Sanders, Peter. Fast route planning. — Google Tech Talk, 2009. — 23 марта.. — «Шаблон:Inconsistent citations».
- Chen, Danny Z. Developing algorithms and software for geometric path planning problems (англ.) // ACM Computing Surveys (англ.) (рус. : journal. — 1996. — December (vol. 28, no. 4es). — P. 18. — doi:10.1145/242224.242246.
- Abraham, Ittai; Fiat, Amos; Goldberg, Andrew V.; Werneck, Renato F. Highway Dimension, Shortest Paths, and Provably Efficient Algorithms (англ.) // ACM-SIAM Symposium on Discrete Algorithms : journal. — 2010. — P. 782—793.
- Abraham, Ittai; Delling, Daniel; Goldberg, Andrew V.; Werneck, Renato F. A Hub-Based Labeling Algorithm for Shortest Paths on Road Networks. Symposium on Experimental Algorithms] (англ.) : journal. — 2011. — P. 230—241.
- Kroger, Martin. Shortest multiple disconnected path for the analysis of entanglements in two- and three-dimensional polymeric systems (англ.) // Computer Physics Communications (англ.) (рус. : journal. — 2005. — Vol. 168, no. 168. — P. 209—232. — doi:10.1016/j.cpc.2005.01.020.
- Ladyzhensky Y., Popoff Y. Algorithm to define the shortest paths between all nodes in a graph after compressing of two nodes. Proceedings of Donetsk national technical university, Computing and automation. Vol.107. Donetsk (англ.) : journal. — 2006. — P. 68—75..[источник не указан 925 дней]
Алгоритм Дейкстры. Поиск оптимальных маршрутов на графе
Время на прочтение
3 мин
Количество просмотров 415K
Из многих алгоритмов поиска кратчайших маршрутов на графе, на Хабре я нашел только описание алгоритма Флойда-Уоршалла. Этот алгоритм находит кратчайшие пути между всеми вершинами графа и их длину. В этой статье я опишу принцип работы алгоритма Дейкстры, который находит оптимальные маршруты и их длину между одной конкретной вершиной (источником) и всеми остальными вершинами графа. Недостаток данного алгоритма в том, что он будет некорректно работать если граф имеет дуги отрицательного веса.
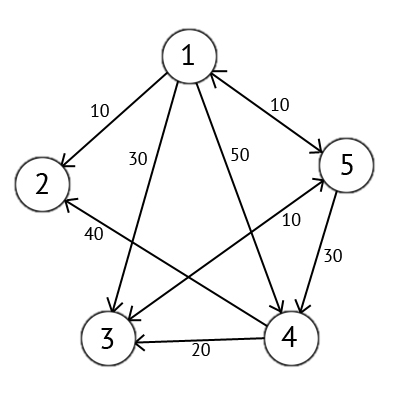
Для примера возьмем такой ориентированный граф G:
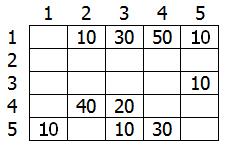
Этот граф мы можем представить в виде матрицы С:
Возьмем в качестве источника вершину 1. Это значит что мы будем искать кратчайшие маршруты из вершины 1 в вершины 2, 3, 4 и 5.
Данный алгоритм пошагово перебирает все вершины графа и назначает им метки, которые являются известным минимальным расстоянием от вершины источника до конкретной вершины. Рассмотрим этот алгоритм на примере.
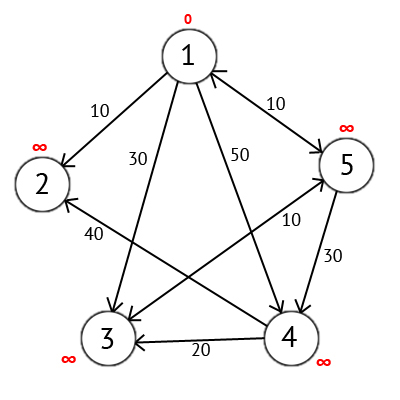
Присвоим 1-й вершине метку равную 0, потому как эта вершина — источник. Остальным вершинам присвоим метки равные бесконечности.
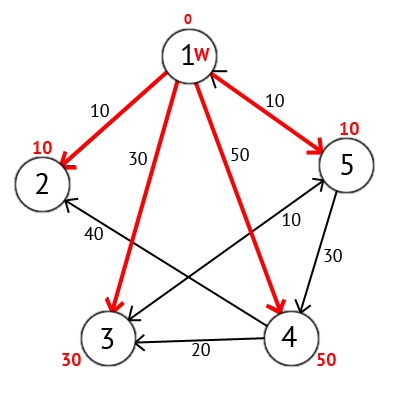
Далее выберем такую вершину W, которая имеет минимальную метку (сейчас это вершина 1) и рассмотрим все вершины в которые из вершины W есть путь, не содержащий вершин посредников. Каждой из рассмотренных вершин назначим метку равную сумме метки W и длинны пути из W в рассматриваемую вершину, но только в том случае, если полученная сумма будет меньше предыдущего значения метки. Если же сумма не будет меньше, то оставляем предыдущую метку без изменений.
После того как мы рассмотрели все вершины, в которые есть прямой путь из W, вершину W мы отмечаем как посещённую, и выбираем из ещё не посещенных такую, которая имеет минимальное значение метки, она и будет следующей вершиной W. В данном случае это вершина 2 или 5. Если есть несколько вершин с одинаковыми метками, то не имеет значения какую из них мы выберем как W.
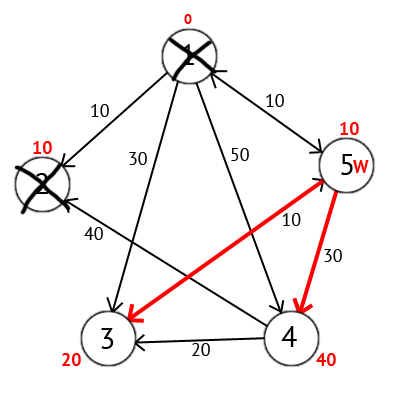
Мы выберем вершину 2. Но из нее нет ни одного исходящего пути, поэтому мы сразу отмечаем эту вершину как посещенную и переходим к следующей вершине с минимальной меткой. На этот раз только вершина 5 имеет минимальную метку. Рассмотрим все вершины в которые есть прямые пути из 5, но которые ещё не помечены как посещенные. Снова находим сумму метки вершины W и веса ребра из W в текущую вершину, и если эта сумма будет меньше предыдущей метки, то заменяем значение метки на полученную сумму.
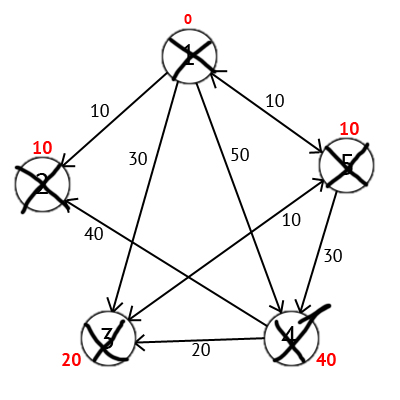
Исходя из картинки мы можем увидеть, что метки 3-ей и 4-ой вершин стали меньше, тоесть был найден более короткий маршрут в эти вершины из вершины источника. Далее отмечаем 5-ю вершину как посещенную и выбираем следующую вершину, которая имеет минимальную метку. Повторяем все перечисленные выше действия до тех пор, пока есть непосещенные вершины.
Выполнив все действия получим такой результат:
Также есть вектор Р, исходя из которого можно построить кратчайшие маршруты. По количеству элементов этот вектор равен количеству вершин в графе, Каждый элемент содержит последнюю промежуточную вершину на кратчайшем пути между вершиной-источником и конечной вершиной. В начале алгоритма все элементы вектора Р равны вершине источнику (в нашем случае Р = {1, 1, 1, 1, 1}). Далее на этапе пересчета значения метки для рассматриваемой вершины, в случае если метка рассматриваемой вершины меняется на меньшую, в массив Р мы записываем значение текущей вершины W. Например: у 3-ей вершины была метка со значением «30», при W=1. Далее при W=5, метка 3-ей вершины изменилась на «20», следовательно мы запишем значение в вектор Р — Р[3]=5. Также при W=5 изменилось значение метки у 4-й вершины (было «50», стало «40»), значит нужно присвоить 4-му элементу вектора Р значение W — P[4]=5. В результате получим вектор Р = {1, 1, 5, 5, 1}.
Зная что в каждом элементе вектора Р записана последняя промежуточная вершина на пути между источником и конечной вершиной, мы можем получить и сам кратчайший маршрут.
Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Задача
Дан ориентированный граф (G = (V, E)), а также вершина (s).
Найти длину кратчайшего пути от (s) до каждой из вершин графа. Длина пути — количество рёбер в нём.
BFS
BFS — breadth-first search, или же поиск в ширину.
Этот алгоритм позволяет решать следующую задачу.
Алгоритм работает следующим образом.
- Создадим массив (dist) расстояний. Изначально (dist[s] = 0) (поскольку расстояний от вершины до самой себя равно (0)) и (dist[v] = infty) для (v neq s).
- Создадим очередь (q). Изначально в (q) добавим вершину (s).
- Пока очередь (q) непуста, делаем следующее:
- Извлекаем вершину (v) из очереди.
- Рассматриваем все рёбра ((v, u) in E). Для каждого такого ребра пытаемся сделать релаксацию: если (dist[v] + 1 < dist[u]), то мы делаем присвоение (dist[u] = dist[v] + 1) и добавляем вершину (u) в очередь.
Визуализации:
-
https://visualgo.net/mn/dfsbfs
-
https://www.hackerearth.com/practice/algorithms/graphs/breadth-first-search/visualize/
Интуитивное понимание алгоритма
Можно представить, что мы поджигаем вершину (s). Каждый шаг алгоритма — это распространение огня на соседние вершины. Понятно, что огонь доберётся до вершины по кратчайшему пути.
Заметьте, что этот алгоритм очень похож на DFS — достаточно заменить очередь на стек и поиск в ширину станет поиском в глубину. Действительно, оба алгоритма при обработке вершины просто записывают всех непосещенных соседей, в которые из неё есть ребро, в структуру данных, и после этого выбирает следующую вершину для обработки в структуре данных. В DFS это стек (благодаря рекурсии), поэтому мы сначала записываем соседа, идем в обрабатываем его полностью, а потом начинаем обрабатывать следующего соседа. В BFS это очередь, поэтому мы кидаем сразу всех соседей, а потом начинаем обрабатывать вообще другую вершину – ту непосещенную, которую мы положили в очередь раньше всего.
Оба алгоритма позволяют обойти граф целиком – посетить каждую вершину ровно один раз. Поэтому они оба подходят для таких задач как: * поиск компонент связности * проверка графа на двудольность * построение остова
Реализация на C++
n — количество вершин в графе; adj — список смежности
vector<int> bfs(int s) {
// длина любого кратчайшего пути не превосходит n - 1,
// поэтому n - достаточное значение для "бесконечности";
// после работы алгоритма dist[v] = n, если v недостижима из s
vector<int> dist(n, n);
dist[s] = 0;
queue<int> q;
q.push(s);
while (!q.empty()) {
int v = q.front();
q.pop();
for (int u : adj[v]) {
if (dist[u] > dist[v] + 1) {
dist[u] = dist[v] + 1;
q.push(u);
}
}
}
return dist;
}Свойства кратчайших путей
Обозначение: (d(v)) — длина кратчайшего пути от (s) до (v).
Лемма 1. > Пусть ((u, v) in E), тогда (d(v) leq d(u) + 1).
Действительно, существует путь из (s) в (u) длины (d(u)), а также есть ребро ((u, v)), следовательно, существует путь из (s) в (v) длины (d(u) + 1). А значит кратчайший путь из (s) в (v) имеет длину не более (d(u) + 1),
Лемма 2. > Рассмотрим кратчайший путь от (s) до (v). Обозначим его как (u_1, u_2, dots u_k) ((u_1 = s) и (u_k = v), а также (k = d(v) + 1)).
> Тогда (forall (i < k): d(u_i) + 1 = d(u_{i + 1})).
Действительно, пусть для какого-то (i < k) это не так. Тогда, используя лемму 1, имеем: (d(u_i) + 1 > d(u_{i + 1})). Тогда мы можем заменить первые (i + 1) вершин пути на вершины из кратчайшего пути из (s) в (u_{i + 1}). Полученный путь стал короче, но мы рассматривали кратчайший путь — противоречие.
Корректность
Утверждение. > 1. Расстояния до тех вершин, которые были добавлены в очередь, посчитаны корректно. > 2. Вершины лежат в очереди в порядке неубывания расстояния, притом разность между кратчайшими расстояними до вершин в очереди не превосходит (1).
Докажем это по индукции по количеству итераций алгоритма (итерация — извлечение вершины из очереди и дальнейшая релаксация).
База очевидна.
Переход. Сначала докажем первую часть. Предположим, что (dist[v] + 1 < dist[u]), но (dist[v] + 1) — некорректное расстояние до вершины (u), то есть (dist[v] + 1 neq d(u)). Тогда по лемме 1: (d(u) < dist[v] + 1). Рассмотрим предпоследнюю вершину (w) на кратчайшем пути от (s) до (u). Тогда по лемме 2: (d(w) + 1 = d(u)). Следовательно, (d(w) + 1 < dist[v] + 1) и (d(w) < dist[v]). Но тогда по предположению индукции (w) была извлечена раньше (v), следовательно, при релаксации из неё в очередь должна была быть добавлена вершина (u) с уже корректным расстоянием. Противоречие.
Теперь докажем вторую часть. По предположению индукции в очереди лежали некоторые вершины (u_1, u_2, dots u_k), для которых выполнялось следующее: (dist[u_1] leq dist[u_2] leq dots leq dist[u_k]) и (dist[u_k] – dist[u_1] leq 1). Мы извлекли вершину (v = u_1) и могли добавить в конец очереди какие-то вершины с расстоянием (dist[v] + 1). Если (k = 1), то утверждение очевидно. В противном случае имеем (dist[u_k] – dist[u_1] leq 1 leftrightarrow dist[u_k] – dist[v] leq 1 leftrightarrow dist[u_k] leq dist[v] + 1), то есть упорядоченность сохранилась. Осталось показать, что ((dist[v] + 1) – dist[u_2] leq 1), но это равносильно (dist[v] leq dist[u_2]), что, как мы знаем, верно.
Время работы
Из доказанного следует, что каждая достижимая из (s) вершина будет добавлена в очередь ровно (1) раз, недостижимые вершины добавлены не будут. Каждое ребро, соединяющее достижимые вершины, будет рассмотрено ровно (2) раза. Таким образом, алгоритм работает за (O(V+ E)) времени, при условии, что граф хранится в виде списка смежности.
Неориентированные графы
Если дан неориентированный граф, его можно рассматривать как ориентированный граф с двумя обратными друг другу ориентированными рёбрами.
Восстановление пути
Пусть теперь заданы 2 вершины (s) и (t), и необходимо не только найти длину кратчайшего пути из (s) в (t), но и восстановить какой-нибудь из кратчайших путей между ними. Всё ещё можно воспользоваться алгоритмом BFS, но необходимо ещё и поддерживать массив предков (p), в котором для каждой вершины будет храниться предыдущая вершина на кратчайшем пути.
Поддерживать этот массив просто: при релаксации нужно просто запоминать, из какой вершины мы прорелаксировали в данную. Также будем считать, что (p[s] = -1): у стартовой вершины предок — некоторая несуществующая вершина.
Восстановление пути делается с конца. Мы знаем последнюю вершину пути — это (t). Далее, мы сводим задачу к меньшей, переходя к нахождению пути из (s) в (p[t]).
Реализация BFS с восстановлением пути
// теперь bfs принимает 2 вершины, между которыми ищется пути
// bfs возвращает кратчайший путь из s в t, или же пустой vector, если пути нет
vector<int> bfs(int s, int t) {
vector<int> dist(n, n);
vector<int> p(n, -1);
dist[s] = 0;
queue<int> q;
q.push(s);
while (!q.empty()) {
int v = q.front();
q.pop();
for (int u : adj[v]) {
if (dist[u] > dist[v] + 1) {
p[u] = v;
dist[u] = dist[v] + 1;
q.push(u);
}
}
}
// если пути не существует, возвращаем пустой vector
if (dist[t] == n) {
return {};
}
vector<int> path;
while (t != -1) {
path.push_back(t);
t = p[t];
}
// путь был рассмотрен в обратном порядке, поэтому его нужно перевернуть
reverse(path.begin(), path.end());
return path;
}Проверка принадлежности вершины кратчайшему пути
Дан ориентированный граф (G), найти все вершины, которые принадлежат хотя бы одному кратчайшему пути из (s) в (t).
Запустим из вершины (s) в графе (G) BFS — найдём расстояния (d_1). Построим транспонированный граф (G^T) — граф, в котором каждое ребро заменено на противоположное. Запустим из вершины (t) в графе (G^T) BFS — найдём расстояния (d_2).
Теперь очевидно, что (v) принадлежит хотя бы одному кратчайшему пути из (s) в (t) тогда и только тогда, когда (d_1(v) + d_2(v) = d_1(t)) — это значит, что есть путь из (s) в (v) длины (d_1(v)), а затем есть путь из (v) в (t) длины (d_2(v)), и их суммарная длина совпадает с длиной кратчайшего пути из (s) в (t).
Кратчайший цикл в ориентированном графе
Найти цикл минимальной длины в ориентированном графе.
Попытаемся из каждой вершины найти кратчайший цикл, проходящий через неё, с помощью BFS. Это делается аналогично обычному BFS: мы должны найти расстояний от вершины до самой себя, при этом не считая, что оно равно (0).
Итого, у нас (|V|) запусков BFS, и каждый запуск работает за (O(|V| + |E|)). Тогда общее время работы составляет (O(|V|^2 + |V| |E|)). Если инициализировать массив (dist) единожды, а после каждого запуска BFS возвращать исходные значения только для достижимых вершин, решение будет работать за (O(|V||E|)).
Задача
Дан взвешенный ориентированный граф (G = (V, E)), а также вершина (s). Длина ребра ((u, v)) равна (w(u, v)). Длины всех рёбер неотрицательные.
Найти длину кратчайшего пути от (s) до каждой из вершин графа. Длина пути — сумма длин рёбер в нём.
Алгоритм Дейкстры
Алгоритм Дейкстры решает приведённую выше задачу. Он работает следующим образом.
- Создать массив (dist) расстояний. Изначально (dist[s] = 0) и (dist[v] = infty) для (v neq s).
- Создать булёв массив (used), (used[v] = 0) для всех вершин (v) — в нём мы будем отмечать, совершалась ли релаксация из вершины.
- Пока существует вершина (v) такая, что (used[v] = 0) и (dist[v] neq infty), притом, если таких вершин несколько, то (v) — вершина с минимальным (dist[v]), делать следующее:
- Пометить, что мы совершали релаксацию из вершины (v), то есть присвоить (used[v] = 1).
- Рассматриваем все рёбра ((v, u) in E). Для каждого ребра пытаемся сделать релаксацию: если (dist[v] + w(v, u) < dist[u]), присвоить (dist[u] = dist[v] + w(v, u)).
Иными словами, алгоритм на каждом шаге находит вершину, до которой расстояние сейчас минимально и из которой ещё не была произведена релаксация, и делает её.
Посчитаем, за сколько работает алгоритм. Мы (V) раз ищем вершину минимальным (dist), поиск минимума у нас линейный за (O(V)), отсюда (O(V^2)). Обработка ребер у нас происходит суммарно за (O(E)), потому что на каждое ребро мы тратим (O(1)) действий. Так мы находим финальную асимптотику: (O(V^2 + E)).
Реализация на C++
Рёбра будем хранить как pair<int, int>, где первое число пары — куда оно ведёт; а второе — длина ребра.
// INF - infinity - бесконечность
const long long INF = (long long) 1e18 + 1;
vector<long long> dijkstra(int s) {
vector<long long> dist(n, INF);
dist[s] = 0;
vector<bool> used(n);
while (true) {
// находим вершину, из которой будем релаксировать
int v = -1;
for (int i = 0; i < n; i++) {
if (!used[i] && (v == -1 || dist[i] < dist[v])) {
v = i;
}
}
// если не нашли подходящую вершину, прекращаем работу алгоритма
if (v == -1) {
break;
}
for (auto &e : adj[v]) {
int u = e.first;
int len = e.second;
if (dist[u] > dist[v] + len) {
dist[u] = dist[v] + len;
}
}
}
return dist;
}Восстановление пути
Восстановление пути в алгоритме Дейкстры делается аналогично восстановлению пути в BFS (и любой динамике).
Дейкстра на сете
Искать вершину с минимальным (dist) можно гораздо быстрее, используя такую структуру данных как очередь с приоритетом. Нам нужно хранить пары ((dist, index)) и уметь делать такие операции: * Извлечь минимум (чтобы обработать новую вершину) * Удалить вершину по индексу (чтобы уменьшить (dist) до какого-то соседа) * Добавить новую вершину (чтобы уменьшить (dist) до какого-то соседа)
Для этого используют, например, кучу или сет. Удобно помимо сета хранить сам массив dist, который его дублирует, но хранит элементы по порядку. Тогда, чтобы заменить значение ((dist_1, u)) на ((dist_2, u)), нужно удалить из сета значение ((dist[u], u)), сделать (dist[u] = dist_2;) и добавить в сет ((dist[u], u)).
Данный алгоритм будет работать за (V O(log V)) извлечений минимума и (O(E log V)) операций уменьшения расстояния до вершины (может быть сделано после каждого ребра). Поэтому алгоритм работает за (O(E log V)).
Заметьте, что этот алгоритм не лучше и не хуже, чем без сета, который работает за (O(V^2 + E)). Ведь если (E = O(V^2)) (граф почти полный), то Дейкстра без сета работает быстрее, а если, наример, (E = O(V)), то Дейкстра на сете работает быстрее. Учитывайте это, когда выбираете алгоритм.
Рассмотрим пример нахождение кратчайшего пути. Дана сеть автомобильных дорог, соединяющих области города. Некоторые дороги односторонние. Найти кратчайшие пути от центра города до каждого города области.
Для решения указанной задачи можно использовать алгоритм Дейкстры — алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Работает только для графов без рёбер отрицательного веса.
Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.
Кружками обозначены вершины, линиями – пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначен их вес – длина пути. Рядом с каждой вершиной красным обозначена метка – длина кратчайшего пути в эту вершину из вершины 1.
Инициализация
Метка самой вершины 1 полагается равной 0, метки остальных вершин – недостижимо большое число (в идеале — бесконечность). Это отражает то, что расстояния от вершины 1 до других вершин пока неизвестны. Все вершины графа помечаются как непосещенные.
Первый шаг
Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6. Обходим соседей вершины по очереди.
Первый сосед вершины 1 – вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна сумме кратчайшего расстояния до вершины 1 (значению её метки) и длины ребра, идущего из 1-й во 2-ю, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2 (10000), поэтому новая метка 2-й вершины равна 7.
Аналогично находим длины пути для всех других соседей (вершины 3 и 6).
Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит. Вершина 1 отмечается как посещенная.
Второй шаг
Шаг 1 алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7.
Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4.
Вершина 1 уже посещена. Следующий сосед вершины 2 — вершина 3, так как имеет минимальную метку из вершин, отмеченных как не посещённые. Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9, а 9 < 17, поэтому метка не меняется.
Ещё один сосед вершины 2 — вершина 4. Если идти в неё через 2-ю, то длина такого пути будет равна 22 (7 + 15 = 22). Поскольку 22<10000, устанавливаем метку вершины 4 равной 22.
Все соседи вершины 2 просмотрены, помечаем её как посещенную.
Третий шаг
Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим следующие результаты.
Четвертый шаг
Пятый шаг
Шестой шаг
Таким образом, кратчайшим путем из вершины 1 в вершину 5 будет путь через вершины 1 — 3 — 6 — 5, поскольку таким путем мы набираем минимальный вес, равный 20.
Займемся выводом кратчайшего пути. Мы знаем длину пути для каждой вершины, и теперь будем рассматривать вершины с конца. Рассматриваем конечную вершину (в данном случае — вершина 5), и для всех вершин, с которой она связана, находим длину пути, вычитая вес соответствующего ребра из длины пути конечной вершины.
Так, вершина 5 имеет длину пути 20. Она связана с вершинами 6 и 4.
Для вершины 6 получим вес 20 — 9 = 11 (совпал).
Для вершины 4 получим вес 20 — 6 = 14 (не совпал).
Если в результате мы получим значение, которое совпадает с длиной пути рассматриваемой вершины (в данном случае — вершина 6), то именно из нее был осуществлен переход в конечную вершину. Отмечаем эту вершину на искомом пути.
Далее определяем ребро, через которое мы попали в вершину 6. И так пока не дойдем до начала.
Если в результате такого обхода у нас на каком-то шаге совпадут значения для нескольких вершин, то можно взять любую из них — несколько путей будут иметь одинаковую длину.
Реализация алгоритма Дейкстры
Для хранения весов графа используется квадратная матрица. В заголовках строк и столбцов находятся вершины графа. А веса дуг графа размещаются во внутренних ячейках таблицы. Граф не содержит петель, поэтому на главной диагонали матрицы содержатся нулевые значения.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 0 | 7 | 9 | 0 | 0 | 14 |
| 2 | 7 | 0 | 10 | 15 | 0 | 0 |
| 3 | 9 | 10 | 0 | 11 | 0 | 2 |
| 4 | 0 | 15 | 11 | 0 | 6 | 0 |
| 5 | 0 | 0 | 0 | 6 | 0 | 9 |
| 6 | 14 | 0 | 2 | 0 | 9 | 0 |
Реализация на C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#define SIZE 6
int main()
{
int a[SIZE][SIZE]; // матрица связей
int d[SIZE]; // минимальное расстояние
int v[SIZE]; // посещенные вершины
int temp, minindex, min;
int begin_index = 0;
system(“chcp 1251”);
system(“cls”);
// Инициализация матрицы связей
for (int i = 0; i<SIZE; i++)
{
a[i][i] = 0;
for (int j = i + 1; j<SIZE; j++) {
printf(“Введите расстояние %d – %d: “, i + 1, j + 1);
scanf(“%d”, &temp);
a[i][j] = temp;
a[j][i] = temp;
}
}
// Вывод матрицы связей
for (int i = 0; i<SIZE; i++)
{
for (int j = 0; j<SIZE; j++)
printf(“%5d “, a[i][j]);
printf(“n”);
}
//Инициализация вершин и расстояний
for (int i = 0; i<SIZE; i++)
{
d[i] = 10000;
v[i] = 1;
}
d[begin_index] = 0;
// Шаг алгоритма
do {
minindex = 10000;
min = 10000;
for (int i = 0; i<SIZE; i++)
{ // Если вершину ещё не обошли и вес меньше min
if ((v[i] == 1) && (d[i]<min))
{ // Переприсваиваем значения
min = d[i];
minindex = i;
}
}
// Добавляем найденный минимальный вес
// к текущему весу вершины
// и сравниваем с текущим минимальным весом вершины
if (minindex != 10000)
{
for (int i = 0; i<SIZE; i++)
{
if (a[minindex][i] > 0)
{
temp = min + a[minindex][i];
if (temp < d[i])
{
d[i] = temp;
}
}
}
v[minindex] = 0;
}
} while (minindex < 10000);
// Вывод кратчайших расстояний до вершин
printf(“nКратчайшие расстояния до вершин: n”);
for (int i = 0; i<SIZE; i++)
printf(“%5d “, d[i]);
// Восстановление пути
int ver[SIZE]; // массив посещенных вершин
int end = 4; // индекс конечной вершины = 5 – 1
ver[0] = end + 1; // начальный элемент – конечная вершина
int k = 1; // индекс предыдущей вершины
int weight = d[end]; // вес конечной вершины
while (end != begin_index) // пока не дошли до начальной вершины
{
for (int i = 0; i<SIZE; i++) // просматриваем все вершины
if (a[i][end] != 0) // если связь есть
{
int temp = weight – a[i][end]; // определяем вес пути из предыдущей вершины
if (temp == d[i]) // если вес совпал с рассчитанным
{ // значит из этой вершины и был переход
weight = temp; // сохраняем новый вес
end = i; // сохраняем предыдущую вершину
ver[k] = i + 1; // и записываем ее в массив
k++;
}
}
}
// Вывод пути (начальная вершина оказалась в конце массива из k элементов)
printf(“nВывод кратчайшего путиn”);
for (int i = k – 1; i >= 0; i–)
printf(“%3d “, ver[i]);
getchar(); getchar();
return 0;
}
Результат выполнения
Назад: Алгоритмизация
- 1. Как работает алгоритм Дейкстры
- 2. Пример алгоритма Дейкстры
- 3. Алгоритм Дейкстры. Псевдокод.
- 4. Код для алгоритма Дейкстры
Алгоритм Дейкстры
позволяет нам найти кратчайший путь между любыми двумя вершинами графа.
Он отличается от минимального остовного дерева тем, что кратчайшее расстояние между двумя вершинами может не включать все вершины графа.
Как работает алгоритм Дейкстры
Алгоритм Дейкстры работает на том основании, что любой подпуть B -> D кратчайшего пути A -> D между вершинами A и D также является кратчайшим путем между вершинами B и D.
Дейкстра использовал это свойство в противоположном направлении, т.е. мы переоцениваем расстояние каждой вершины от начальной вершины. Затем мы посещаем каждый узел и его соседей, чтобы найти кратчайший подпуть к этим соседям.
Алгоритм использует «жадный» подход в том смысле, что мы находим следующее лучшее решение, надеясь, что конечный результат является лучшим решением для всей задачи.
Пример алгоритма Дейкстры
Проще начать с примера, а затем подумать об алгоритме.
Алгоритм Дейкстры. Псевдокод.
Нам нужно сохранять расстояние пути каждой вершины. Мы можем сохранить его в массиве размера v, где v – количество вершин.
Нам также хотелось бы получить кратчайший путь, а не только знать его длину. Для этого мы сопоставляем каждую вершину с последней обновленной длиной пути.
Как только алгоритм закончен, мы можем вернуться от вершины назначения к исходной вершине, чтобы найти путь.
Очередь с минимальным приоритетом может использоваться для эффективного получения вершины с наименьшим расстоянием пути.
function dijkstra(G, S) for each vertex V in G distance[V] <- infinite previous[V] <- NULL If V != S, add V to Priority Queue Q distance[S] <- 0 while Q IS NOT EMPTY U <- Extract MIN from Q for each unvisited neighbour V of U tempDistance <- distance[U] + edge_weight(U, V) if tempDistance < distance[V] distance[V] <- tempDistance previous[V] <- U return distance[], previous[]Код для алгоритма Дейкстры
Реализация алгоритма Дейкстры в C ++ приведена ниже. Сложность кода может быть улучшена, но абстракции удобны для связи кода с алгоритмом.
#include <iostream> #include <vector> #define INT_MAX 10000000 using namespace std; void DijkstrasTest(); int main() { DijkstrasTest(); return 0; } class Node; class Edge; void Dijkstras(); vector<Node*>* AdjacentRemainingNodes(Node* node); Node* ExtractSmallest(vector<Node*>& nodes); int Distance(Node* node1, Node* node2); bool Contains(vector<Node*>& nodes, Node* node); void PrintShortestRouteTo(Node* destination); vector<Node*> nodes; vector<Edge*> edges; class Node { public: Node(char id) : id(id), previous(NULL), distanceFromStart(INT_MAX) { nodes.push_back(this); } public: char id; Node* previous; int distanceFromStart; }; class Edge { public: Edge(Node* node1, Node* node2, int distance) : node1(node1), node2(node2), distance(distance) { edges.push_back(this); } bool Connects(Node* node1, Node* node2) { return ( (node1 == this->node1 && node2 == this->node2) || (node1 == this->node2 && node2 == this->node1)); } public: Node* node1; Node* node2; int distance; }; /////////////////// void DijkstrasTest() { Node* a = new Node('a'); Node* b = new Node('b'); Node* c = new Node('c'); Node* d = new Node('d'); Node* e = new Node('e'); Node* f = new Node('f'); Node* g = new Node('g'); Edge* e1 = new Edge(a, c, 1); Edge* e2 = new Edge(a, d, 2); Edge* e3 = new Edge(b, c, 2); Edge* e4 = new Edge(c, d, 1); Edge* e5 = new Edge(b, f, 3); Edge* e6 = new Edge(c, e, 3); Edge* e7 = new Edge(e, f, 2); Edge* e8 = new Edge(d, g, 1); Edge* e9 = new Edge(g, f, 1); a->distanceFromStart = 0; // set start node Dijkstras(); PrintShortestRouteTo(f); } /////////////////// void Dijkstras() { while (nodes.size() > 0) { Node* smallest = ExtractSmallest(nodes); vector<Node*>* adjacentNodes = AdjacentRemainingNodes(smallest); const int size = adjacentNodes->size(); for (int i=0; i<size; ++i) { Node* adjacent = adjacentNodes->at(i); int distance = Distance(smallest, adjacent) + smallest->distanceFromStart; if (distance < adjacent->distanceFromStart) { adjacent->distanceFromStart = distance; adjacent->previous = smallest; } } delete adjacentNodes; } } // Find the node with the smallest distance, // remove it, and return it. Node* ExtractSmallest(vector<Node*>& nodes) { int size = nodes.size(); if (size == 0) return NULL; int smallestPosition = 0; Node* smallest = nodes.at(0); for (int i=1; i<size; ++i) { Node* current = nodes.at(i); if (current->distanceFromStart < smallest->distanceFromStart) { smallest = current; smallestPosition = i; } } nodes.erase(nodes.begin() + smallestPosition); return smallest; } // Return all nodes adjacent to 'node' which are still // in the 'nodes' collection. vector<Node*>* AdjacentRemainingNodes(Node* node) { vector<Node*>* adjacentNodes = new vector<Node*>(); const int size = edges.size(); for(int i=0; i<size; ++i) { Edge* edge = edges.at(i); Node* adjacent = NULL; if (edge->node1 == node) { adjacent = edge->node2; } else if (edge->node2 == node) { adjacent = edge->node1; } if (adjacent && Contains(nodes, adjacent)) { adjacentNodes->push_back(adjacent); } } return adjacentNodes; } // Return distance between two connected nodes int Distance(Node* node1, Node* node2) { const int size = edges.size(); for(int i=0; i<size; ++i) { Edge* edge = edges.at(i); if (edge->Connects(node1, node2)) { return edge->distance; } } return -1; // should never happen } // Does the 'nodes' vector contain 'node' bool Contains(vector<Node*>& nodes, Node* node) { const int size = nodes.size(); for(int i=0; i<size; ++i) { if (node == nodes.at(i)) { return true; } } return false; } /////////////////// void PrintShortestRouteTo(Node* destination) { Node* previous = destination; cout << "Distance from start: " << destination->distanceFromStart << endl; while (previous) { cout << previous->id << " "; previous = previous->previous; } cout << endl; } // these two not needed vector<Edge*>* AdjacentEdges(vector<Edge*>& Edges, Node* node); void RemoveEdge(vector<Edge*>& Edges, Edge* edge); vector<Edge*>* AdjacentEdges(vector<Edge*>& edges, Node* node) { vector<Edge*>* adjacentEdges = new vector<Edge*>(); const int size = edges.size(); for(int i=0; i<size; ++i) { Edge* edge = edges.at(i); if (edge->node1 == node) { cout << "adjacent: " << edge->node2->id << endl; adjacentEdges->push_back(edge); } else if (edge->node2 == node) { cout << "adjacent: " << edge->node1->id << endl; adjacentEdges->push_back(edge); } } return adjacentEdges; } void RemoveEdge(vector<Edge*>& edges, Edge* edge) { vector<Edge*>::iterator it; for (it=edges.begin(); it<edges.end(); ++it) { if (*it == edge) { edges.erase(it); return; } } }