
Пример решения задачи по расчету минимального момента сопротивления Wx сечения стальной балки, обеспечивающего её прочность.
Задача
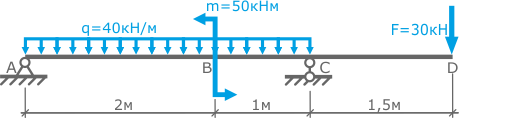
Для заданной стальной балки требуется определить минимальный момент сопротивления сечения Wx для последующего подбора двутавра и расчета размеров других сечений балки по условию прочности.
Допустимые напряжения [σ]=160МПа.
Другие примеры решений >
Помощь с решением задач >
Решение
Предыдущие пункты решения задачи:
- Определение опорных реакций
- Построение эпюр внутренних поперечных сил и изгибающих моментов.
Прежде чем приступать к расчету размеров сечений балки обеспечивающих ее прочность, определим минимально необходимую величину момента сопротивления сечения Wx.
Момент сопротивления сечений зависит от их формы, размеров и расположения.
Его минимально необходимая величина рассчитывается из условия прочности по нормальным напряжениям при изгибе:
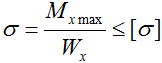
откуда получаем
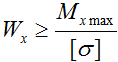
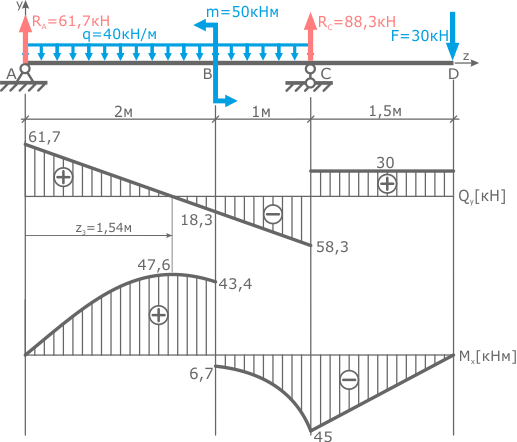
По построенной эпюре Mx видно, что максимальная величина изгибающего момента составляет 47,6 кНм, поэтому
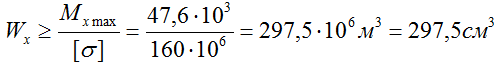
Таким образом, какую бы форму не имело сечение балки, для обеспечения ее прочности момент сопротивления сечения в данном случае должен иметь величину не менее 297,5 см3.
Теперь можно перейти к определению размеров поперечного сечения балки:
- Расчет диаметра круглого сечения >
- Расчет размеров прямоугольного сечения >
- Подбор номера двутавра >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
По Правилам Регистра[9] требуется
определить минимальное сопротивление
и минимальный момент сопротивления Ii
поперечного сечения корпуса судна
относительно нейтральной оси. Ii
определяется из двух позиций:
1. Исходя из нормальных напряжений от
общего изгиба, соответствующего опасным
напряжениям:
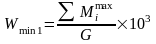
,
где
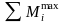
– максимальная алгебраическая сумма
моментов, кНм, согласно таблице 2.1.
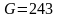
МПа;
Подставляя
получим:
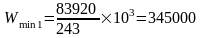
см3;
2. С другой стороны, минимальный момент
сопротивления определяется как стандарт
общей прочности исходя из многолетних
наблюдений:
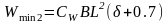
;
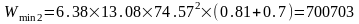
см3;
Размеры
всех непрерывных, продольных связей
корпуса, обеспечивающих момент
сопротивления должны быть неизменными
в пределах средней части судна.
Момент
инерции поперечного сечения корпуса
должен быть не менее:
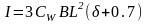
;
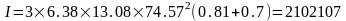
см4;
Для судов
ограниченного района плавания минимальный
момент инерции следует умножать на
редукционный коэффициент 0
, определяемый по формуле:
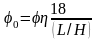
,
где φ = 1.25-0.25L⸱10-2
≤ 1
φ = 1
η = 0.72 – коэффициент
использования материала для стали ReH
= 355МПа;
L/H = 21 –
максимальное отношение длины к высоте
борта для судов R2-RSN;
Подставляя получим:
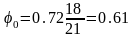
;
Тогда минимальный момент инерции будет
равен:
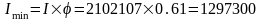
см4;
2.4 Определение фактических моментов сопротивления и моментов инерции поперечного сечения
Фактические моменты сопротивления
и моменты инерции в первом приближении
определяются по спроектированному
ранее чертежу мидель – шпангоута. Для
этого на схеме изображаем половину
сечения с указанием всех связей, которые
будут учитываться при общем изгибе
судна. Такое сечение называется
эквивалентным брусом. В это сечение
входят все листовые конструкции и все
непрерывные продольные связи.
Расчет ведем в табличной форме. За
ось сравнения принимаем ОП.
В таблице 2.3 приняты следующие сокращения:
F – площадь элемента, см;
z – отстояние от оси
сравнения(ОП), м;
Fz – статический момент
площади, см2◦м;
Fz2 – переносный
момент инерции, см2◦м2;
I – собственный момент
инерции связи, см2◦м2;
Отстояние нейтральной оси от оси
сравнения, м, определяем по формуле:
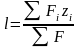
;
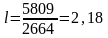
м;
Момент инерции полного поперечного
сечения корпуса относительно нейтральной
оси определяем по формуле:
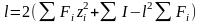
;
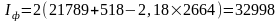
см2×м2;
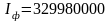
см4;

Таблица 2.5 – Определение
геометрических характеристик
эквивалентного бруса в первом приближении
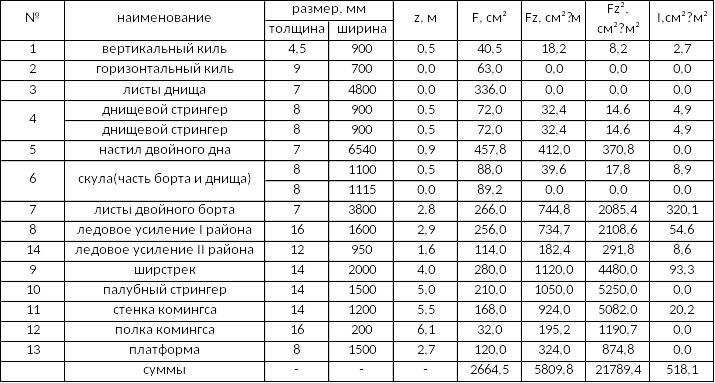
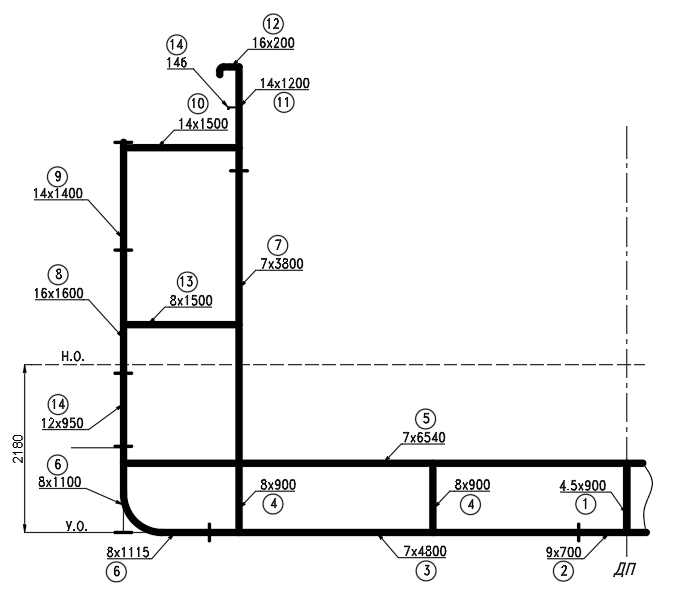
Рисунок 2.1 – Схема эквивалентного бруса
Фактические моменты сопротивления:
Днища:
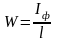
;

см3;
Палубы:
Для судов с надпалубными непрерывными
продольными связями (например, непрерывными
продольными комингсами) фактический
момент сопротивления палубы определяется
делением момента инерции сечения корпуса
относительно нейтральной оси на величину
zm
– вычисляемую по формуле:
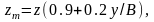
где z – расстояние от нейтральной оси
до верхней кромки непрерывной надпалубной
связи, учитываемой при определении Wп,
4 м;
у – горизонтальное отстояние от ДП
корпуса до верхней кромки непрерывной
надпалубной связи, 5 м;
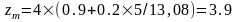
м;
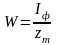
;

см3;
Сравним полученные значения с требуемыми:
Wдн ≥ Wmin;
1422995 См3 ˃ 700703 см3 – условие выполняется;
Wплб ≥ Wmin;
846112 См3 ˃ 700703 см3 – условие выполняется;
Общая прочность судна обеспечена.
Соседние файлы в предмете Основы кораблестроения
- #
28.08.2022158.49 Кб8Башарин В.С. 17кс1. Мидель-шпангоут.dwg
- #
28.08.20221.33 Mб13Башарин В.С. 17кс1. Общее расположение.dwg
- #
28.08.2022164.7 Кб8Башарин В.С. 17кс1. Теоретический чертёж.dwg
- #
- #
- #
- #
- #
- #
В предыдущей статье я рассказывал о моментах инерции, с которыми неразрывно связаны моменты сопротивления. Именно о них сейчас и пойдёт речь. Так что если читатель ещё не читал её — самое время!
А пока нам следует разобраться, что чему сопротивляется. И вообще, является ли организация своего протестного движения моментом сопротивления?
Что такое моменты сопротивления?
В статье про изгиб мы с вами разбирались в том, как найти максимальные напряжения в зоне чистого изгиба
Спойлер:

Где a — максимальное расстояние по интересующей нас оси.
Но чтобы упростить себе расчеты и допускать меньше ошибок, соотношение

Принято называть моментом сопротивления.
Тут может возникнуть вопрос: “Ну так а может не стоило вводить новую величину, а просто оперировать моментами инерции?”
На самом деле так действительно можно сделать, но столкнувшись с большим количеством расчетов читатель и сам наверняка начнет выписывать момент сопротивления. Упрощая алгоритм расчета, мы стремимся исключить возможные ошибки и ускорить сами расчеты. Ведь вместо трехэтажных дробей гораздо удобнее оперировать уже готовым значением.
То есть:
Осевой момент сопротивления – по сути отношение момента инерции к расстоянию до наиболее удаленной от этой оси точки:
По аналогии с полярным моментом инерции для расчетов круглых и близких к ним тел используется полярный момент сопротивления:
Момент сопротивления имеет размерность см3.
Как определить моменты сопротивления простых сечений?
1. Момент сопротивления прямоугольного сечения:
Где Ix:
2. Момент сопротивления квадратного сечения. Частный случай предыдущего пункта:
Где Ix:
3. Момент сопротивления сечения круга:
Где Ix:
4. Момент сопротивления сечения кольцо:
Расчет момента сопротивления сложного сечения
В качестве примера, определим момент инерции и момент сопротивления сечения, изображенного на рисунке ниже:d =20 см, a = 6 см.
1. Определим момент инерции сечения, как разность моментов инерции круга с диаметром d и квадрата со стороной a:
2. Определим момент сопротивления сечения:
3. А теперь давайте попробуем найти разность моментов сопротивления сечения. Будет ли она отличаться от ответа, полученного из двух предыдущих пунктов?
То есть момент сопротивления сечения определяется только через момент инерции! Напрямую складывая/вычитая моменты сопротивления вы получите неправильный ответ!
Подведем небольшой итог:
Момент сопротивления неразрывно связан с моментом инерции.
Моменты сопротивления упрощают расчет нормальных напряжений при изгибе (что особенно важно — максимальных нормальных напряжений), что делает прочностные расчёты при подборе сечения заметно легче и быстрее.
Информация о произведении
Автор: Марк Ершов
Редактор, факт-чекер: К.А.Овчинников
Условия использования: свободное некоммерческое использование при условии указания людей участвовавших в его создании и ссылку на первоисточник (статьи на действующем сайте интернет-журнала «Стройка Века»).
Для коммерческого использования — обращаться на почту:
buildxxvek@gmail.com
Список использованных источников
- Александров А.В. Сопротивление материалов: Учеб. для ВУЗов/ А.В. Александров, В.Д. Потапов, Б.П. Державин; под ред. А.В. Александрова – 3-е изд. испр. – М.: Высш. шк., 2003. – 560 с.: ил. ISBN 5-06-003732-0
- Дарков А.В., Шпиро Г.С. Сопротивление материалов – Учеб. для техн. вузов – 5-е изд. перераб. и дополн. – М.: Высш. шк., 1989 – 624 с. ил.
- Г.И. Беликов. Геометрические характеристики поперечных сечений стержней. Учебно-практическое пособие. — Волгоград: ВолгГАСУ, 2015. — 56 с. — ISBN 978-5-98276-752-3
4 799
При расчете стальных балок необходимо руководствоваться СП 16.13330 «Стальные конструкции».
В данном обзоре я рассмотрю расчет балок 1-го класса напряженно-деформированного состояния (напряжения по всей площади напряжения не превышают расчетного сопротивления стали). Расчёт подкрановых, бистальных, защемленных и многопролетных балок будет рассмотрен отдельно.
Элементы конструкции должны иметь запас прочности по 1-му и 2-му предельному состоянию.
По 1-му предельному состоянию проверяется прочность элементов. Нагрузки для расчета по 1-му предельному состоянию выше, чем по 2-му предельному состоянию т.к. используются коэффициенты запаса для нагрузок.
По 2-му предельному состоянию проверяются деформации конструкции.
Расчеты по 1-му предельному состоянию:
- Расчет на прочность при действии изгибающего момента
- Расчет на прочность при действии поперечной силы
- Расчет на прочность стенки балки при действии сосредоточенной силы
- Расчет на прочность в опорном сечении
- Расчет на общую устойчивость
- Расчет на устойчивость стенок и поясных листов балки
Расчеты по 2-му предельному состоянию:
- Расчет прогиба балки
1. Расчет на прочность при действии изгибающего момента
В первую очередь необходимо подобрать балку по изгибающему моменту.
Прочность стальной балки на изгиб проверяется по следующей формуле (п.8.2.1 СП 16.13330.2011 или 5.12 СНиП II-23-81*):
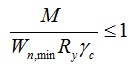
где M – максимальный момент, возникающий в балке (находится по эпюре моментов);
Wn,min – момент сопротивления сечения (находится по таблице или вычисляется для данного профиля), у сечения обычно 2-а момента сопротивления сечения, в расчетах используется Wx если нагрузка перпендикулярна оси х-х профиля или Wy если нагрузка перпендикулярна оси y-y;
Ry – расчетное сопротивление стали при изгибе (задается в соответствии с выбором стали);
γc – коэффициент условий работы (данный коэффициент можно найти в таблице 1 СП 16.13330.2011 Стальные конструкции либо таблице 6* СНиП II-23-81) для балок сплошного сечения коэффициент равен 0,9, при расчете по сечению, ослабленному отверстиями 1,1.
Из этой формулы можно вычислить минимально требуемый момент сопротивления сечения.
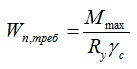
Вначале вычисляем максимальный момент от нагрузок. На этом этапе мы еще не знаем массу балки и ее можно не учитывать при предварительном расчете.
Далее выбираем марку стали. При выборе марки стали необходимо учитывать класс конструкции и климатические условия эксплуатации – если конструкция эксплуатируется в холодном климате в неотапливаемом здании, то марка стали не должна быть хрупкой. Прочность стали выбирается исходя из экономического расчета – несмотря на то, что с увеличением марки стали ее стоимость увеличивается, сечение балки из более прочной стали может быть меньше и соответственно будут меньше нагрузки. Для того, чтобы выбрать оптимальную марку стали необходимо сделать несколько расчетов и оценить их.
После того, как мы предварительно рассчитали минимальный момент сопротивления сечения (Wn) подбираем из сортамента профиль, имеющий W не много выше чем требуемый и имеющий наименьшую массу. Для балок оптимальным профилем является двутавр, швеллер. Возможно использование составного сечения из листов. При расчете важно правильно учесть положение профиля – Wx используется, если ось x-x перпендикулярна направлению приложения нагрузки. Соответственно профиль необходимо располагать так, чтобы момент сопротивления сечения был максимальным (от того как расположить профиль многое зависит).
После выбора сечения необходимо прибавить к изгибающему моменту момент, создаваемый массой балки и вновь проверить сечение.
Если балка расположена под углом, то расчет прочности при изгибе производят по следующей формуле:
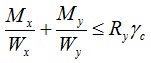
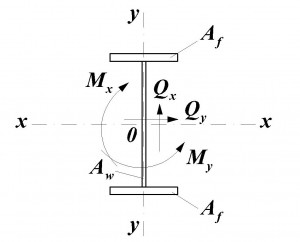
где требуется разложить силу на направляющие по оси х-х и у-у и отдельно вычислить максимальные моменты Mx и My вокруг оси х-х и у-у соответственно.
В СП 16.13330.2011 дополнительно требуют учитывать бимомент, формула выглядит следующим образом:
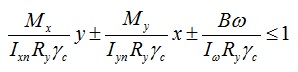
где
x и y — расстояния от главных осей до рассматриваемой точки;
Ixn,Iyn — моменты инерции сечения, находятся по таблице согласно ГОСТ-у на выбранный профиль;
B — бимомент;
Iω — секториальный момент инерции сечения, можно найти в приложении 3 руководства по подбору сечений стальных конструкций;
ω — секториальная площадь.
Здесь рассматриваются несколько точек, как правило 4 крайние точки профиля и для них проверяют условия, знаки подбирают согласно эпюрам напряжения. Подробно расчет профилей с учетом бимомента расписано в книге Д.В.Бычкова Строительная механика стержневых тонкостенных конструкций.
Для прогонов наклонной кровли из швеллера для упрощения расчета бимомент можно не учитывать т.к. он разгружает профиль на 10-15%, и это будет запасом прочности. В других случаях рекомендуется принимать конструктивные меры препятствующие возникновению закручивающего момента.
2. Расчет на прочность при действии поперечной силы
Далее необходимо проверить профиль на действие касательных (поперечных) сил по формуле:
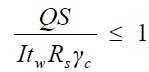
где Q – наибольшая поперечная сила (можно определить согласно эпюре Q), для балки наибольшее значение получается на опорах;
S – статический момент сдвигаемой части сечения (определяется по таблице для выбранного профиля);
I – момент инерции сечения (определяется по таблице для выбранного профиля);
tw – толщина стенки балки;
Rs — расчетное сопротивление стали сдвигу, равно 0,58 от Ry согласно Таблице 2 СП 16.13330.2011;
γc – коэффициент условий работы (данный коэффициент можно найти в таблице 1 СП Стальные конструкции) для балок сплошного сечения коэффициент равен 0,9, при расчете по сечению, ослабленному отверстиями 1,1.
Если профиль не удовлетворяет условию, то необходимо увеличить сечение.
3. Расчет на прочность стенки балки при действии сосредоточенной силы
Расчет на прочность стенки балки, не укрепленной ребрами жесткости, при действии сосредоточенной силы и в опорных сечениях определяют по формуле:
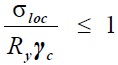
где
![]()
здесь F – расчетное значение нагрузки;
lef – условная длина распределения нагрузки;
tw – толщина стенки балки.
Условную длину распределения нагрузки можно определить по формуле
![]()
для следующих случаев:
для прокатной балки:
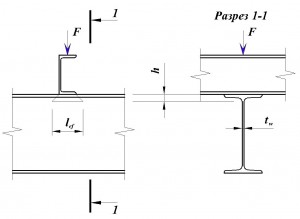
где b – ширина полки швеллера
h – сумма толщины верхней полки и радиуса закругления
для сварной балки:
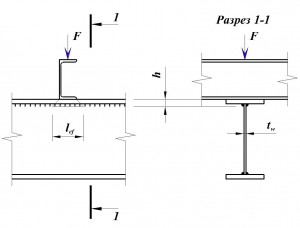
где h – сумма толщины верхней полки и катета сварного шва.
4. Расчет на прочность в опорном сечении
Расчет на прочность в опорном сечении балки (при Mx=0 и My=0) следует определять по формулам:
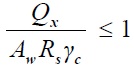
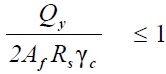
где Aw– площадь сечения стенки,
Af– площадь сечения полки,
Rs–расчетное сопротивление стали сдвигу.
При ослаблении стенки отверстиями для болтов левую часть формулы необходимо умножить на коэффициент α, который находиться по формуле:![]()
где s – шаг отверстий в одном ряду;
d – диаметр отверстия.
Расчет на прочность для защемленных и неразрезных балок мы рассмотрим отдельно.
5. Расчет на общую устойчивость
Далее необходимо проверить балку на устойчивость.
Данный расчет можно не выполнять:
а) при передаче нагрузки через сплошной жесткий настил (плиты железобетонные, плоский или профилированный металлический настил, волнистая сталь и т.п.), непрерывно опирающийся на сжатый пояс балки и надежно с ним связанный (с помощью сварки, болтов, самонарезающих винтов), при этом силы трения учитывать не стоит;
б) если условная гибкость сжатого пояса балки меньше предельных значений. Условная гибкость вычисляется по формуле:
![]()
Предельное значение гибкости пояса вычисляется по формулам:
при приложении нагрузке к верхнему поясу![]()
при приложении нагрузке к нижнему поясу
![]()
независимо от уровня приложения нагрузки при расчете участка балки между связями или при чистом изгибе
![]()
где b – ширина сжатого пояса;
t – толщина сжатого пояса;
h – расстояние (высота) между осями поясных листов.
Примечания
- Значения предельной гибкости определены при 1≤ h/b ≤6 и 15≤ b/t ≤35; для балок с отношением b/t<15 в формулах следует принимать b/t=15.
- Для балок с фрикционными поясными соединениями предельную гибкость следует умножать на 1,2
Проверка общей устойчивости при изгибе в плоскости стенки, совпадающей с плоскостью симметрии сечения, осуществляется по следующей формуле:
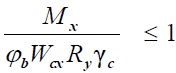
если изгиб происходит в 2-х плоскостях (и наличии секториальных напряжений), тогда проверку осуществляют по формуле:
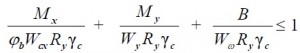
где φb – коэффициент устойчивости при изгибе, подробный расчет коэффициента устойчивости (φb) приведен в приложении Ж СП 16.13330.2011 Стальные конструкции;
Wcx – момент сопротивления сечения относительно оси x-x, вычисленного для сжатого пояса;
Wy – момент сопротивления сечения относительно оси y-y, совпадающий с плоскостью изгиба;
Wω – секторальный момент сопротивления сечения.
При расчете значения φbза расчетную длину балки lef следует принимать расстояние между точками закрепления сжатого пояса от поперечных смещений. При отсутствии связей lef=l (где l – пролет балки).
Если в процессе расчета выясняется, что общая устойчивость балки не обеспечивается, то следует уменьшить расчетную длину сжатого пояса, изменив систему связей.
6. Расчет устойчивости стенок и поясных листов балки
Устойчивость стенок балок 1-го класса следует считать обеспеченной если условная гибкость стенки, вычисленная по формуле:
![]()
где:
hef — расчетная высота стенки, принимаемая согласно требованиям 7.3.1 СП 16.13330.2011;
tw — толщина стенки балки;
Ry — расчетно сопротивление стали при изгибе;
E — модуль упругости стали равный 210 ГПа (210 000 МПа)
Условная гибкость стенки не должна превышать значений:
3,5 – при отсутствии местного напряжения в балках с двухсторонними поясными швами;
3,2 – при отсутствии местного напряжения в балках с односторонними поясными швами;
2,5 – при наличии местного напряжения в балках с двухсторонними поясными швами.
Если условная гибкость стенки выше требуемой, то стенки необходимо усилить ребрами жесткости и сделать проверку согласно п. 8.5.3 СП 16.13330.2011.
7. Расчет прогиба балки
Расчет на 2-е предельное состояние балки заключается в расчете максимального прогиба.
Высокие деформации могут привезти к нарушению герметичности, невозможности эксплуатации, плохому эстетическому восприятию конструкции, поэтому конструкция не должна сильно деформироваться. Предельные прогибы конструкций приведены в приложении Е СП 20.13330 Нагрузки и воздействия
К примеру, для балки покрытия, длиной 6 м, предельный прогиб составляет 1/200 длины пролета т.е. 30 мм.
Формула определения прогиба зависит от способа приложения нагрузки, например однопролетной шарнирно-закрепленной с равномерно-распределенной нагрузкой прогиб рассчитывается по формуле:
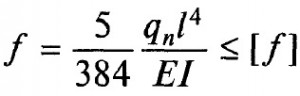
где q – равномерно-распределенная нагрузка, выраженная в кг/м (Н/м);
l – длина балки в метрах;
E – модуль упругости (для стали равен 200-210 ГПа);
I – момент инерции сечения.
Для других способов нагрузки балки формулы смотрите в справочниках по сопротивлению материалов.
Если расчетный прогиб больше допускаемого, то следует увеличить сечение балки.
____________________________________________________________
Как найти расчетный момент и поперечную силу читайте в статье Построение эпюр балки
Как правильно закрепить балку на колонне читайте в статье Опорные узлы балки
Как рассчитать балку в SCAD и подобрать сечение читайте в статье Расчет балки в SCAD
В этой статье начнем говорить об изгибе. Здесь я расскажу, что такое изгиб. Посмотрим, какие виды изгибов бывают. А также рассмотрим основные расчеты при этом виде деформации: расчеты на прочность и жесткость.
Что такое изгиб?
Изгиб – это вид деформации, при котором происходит искривление (изгиб) продольной оси стержня, а в поперечных сечениях стержня возникают изгибающие моменты, и почти всегда поперечные силы.
Поперечные силы и изгибающие моменты называют внутренними силовыми факторами (ВСФ).
Как определяют внутренние силовые факторы при изгибе?
Для определения поперечных сил и изгибающих моментов, используется метод сечений. Как обычно, стержни мысленно рассекаются на части:

Действие частей друг на друга заменяется внутренними силовыми факторами:

И рассматривая равновесие одной из частей, находятся поперечная сила и изгибающий момент в сечении:

Для стержней, работающих на изгиб, обязательно рассчитывают и строят эпюры внутренних силовых факторов. Как рассчитывать и строить эпюры поперечных сил и изгибающих моментов можно прочитать, перейдя по ссылке чуть ниже.
Виды изгибов
В зависимости от возникающих в поперечных сечениях ВСФ, принято выделять различные виды изгибов.
Поперечный (прямой) изгиб


Поперечный (прямой) изгиб – это вид деформации, при котором в поперечных сечениях стержня возникают два внутренних силовых фактора: поперечные силы и изгибающие моменты.
Чистый изгиб


При чистом же изгибе в сечениях возникают исключительно изгибающие моменты.
Другие виды изгибов
Чистый и поперечный изгиб — это наиболее простые виды изгибов, только их и будем рассматривать в этой статье. Однако, ты должен знать, что существуют и более сложные виды сопротивления: косой изгиб, изгиб с кручением, внецентренное растяжение (сжатие). Такие темы, как правило, изучаются во втором семестре.
Расчеты на прочность при изгибе
Теперь предлагаю поговорить о расчётах на прочность при поперечном изгибе. При этом виде деформации расчёты проводятся и по нормальным напряжениям и по касательным. Но так как зачастую касательные напряжения в несколько раз меньше нормальных, основным здесь является расчёт по нормальным напряжениям, а расчёт по касательным напряжениям — проверочный.
Условие прочности
Условие прочности по нормальным напряжениям такое же, как и при растяжении (сжатии):
Нормальные напряжения в сечениях при поперечном изгибе, определяются по следующей формуле:

где Mизг – изгибающий момент в сечении;
W – момент сопротивления сечения;
Моменты сопротивления сечений можно вычислить по данным формулам.
Расчет на жесткость при изгибе
В качестве примера возьмём балку, загруженную распределенной нагрузкой по всей длине. Для этой балки подберем двутавровое сечение (ГОСТ 8239-89) по сортаменту из условия прочности. Затем проверим жесткость такой балки, если допустимое перемещение равно [V] = 2 см.

Для такой балки наиболее опасным сечением будет сечение в заделке (точка A), для которого изгибающий момент будет равен:

А эпюра будет выглядеть следующим образом:

Более подробно о построении эпюры изгибающих моментов можно почитать, перейдя по указанной ссылке.
Теперь, зная значение максимального изгибающего момента, найдем минимально требуемый момент сопротивления, чтобы балка удовлетворяла условию прочности:

По сортаменту выбираем двутавр №36, у которого:

Более подробно, о прочностных расчетах при изгибе, можно узнать здесь.
Проверка балки на жесткость
Мы предварительно подобрали поперечное сечение балки, а теперь, нужно проверить, выполняется ли условие жесткости для такой балки, с таким сечением.

Нетрудно догадаться, что свободный торец балки (точка K) будет иметь наибольшее перемещение. Именно для этого сечения будем производить расчет на жесткость.

Для определения прогиба точки K можно воспользоваться шаблонной формулой, которая уже выведена конкретно для расчетной схемы, как у нас (консольной балки, загруженной по всей длине распределенной нагрузкой):

Подставим все численные значения и найдем прогиб точки K:

Таким образом, условие жесткости не выполняется:

Подбор нового сечения из условия жесткости
Подберем новое поперечное сечение! Для этого нужно найти минимально требуемый момент инерции из условия жесткости:



Выбираем следующий по списку сортамента двутавр №40, у которого:
Вычислим прогиб с учетом нового профиля:

Теперь жесткость балки обеспечена:
Таким образом, окончательно принимаем двутавр №40. Который одновременно удовлетворяет условиям прочности и жесткости.
