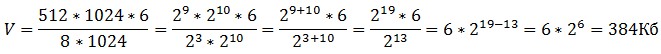Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 128×128 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
2
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 128×128 пикселей при условии, что в изображении могут использоваться 128 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
3
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 512×512 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
4
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 1024×1024 пикселей при условии, что в изображении могут использоваться 16 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
5
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 320×640 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Пройти тестирование по этим заданиям
Задание:
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 1024 на 512 пикселов при условии, что в изображении могут использоваться 64 различных цвета? В ответе запишите только целое число, единицу измерения писать не нужно.
Дано:
размер изображения 1024Х512 пикселей.
N = 64 цвета в палитре.
Решение:
1. Необходимо рассчитать информационный объем одного пикселя для этого используем формулу N=2I, где N – количество цветов в палитре, а I – количество информации на один цвет или пиксель.
64 = 26, отсюда I = 6 бит.
2. Что бы рассчитать минимальный объем изображения мы должны умножить размер изображения на количество информации на один цвет или пиксель – 1024 * 512 * 6 = 3145728 бит
3. В ответе нам необходимо указать в Килобайтах
3145728 бит / (8*1024)= 384 Килобайта
Решение без калькулятора
Ответ: 384
Урок посвящен разбору задания 7 ЕГЭ по информатике
Содержание:
- Объяснение заданий 7 ЕГЭ по информатике
- Кодирование текстовой информации
- Кодирование графической информации
- Кодирование звуковой информации
- Определение скорости передачи информации
- Решение заданий 7 ЕГЭ по информатике
- Тема: Кодирование изображений
- Тема: Кодирование звука
- Тема: Кодирование видео
- Тема: Скорость передачи данных
7-е задание: «Кодирование графической и звуковой информации, объем и передача информации»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 5 минут.
Проверяемые элементы содержания: Умение определять объём памяти, необходимый для хранения графической и звуковой информации
До ЕГЭ 2021 года — это было задание № 9 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
“Если вычисления получаются слишком громоздкими, значит, Вы неправильно решаете задачу. Удобно выделить во всех множителях степени двойки, тогда умножение сведётся к сложению
показателей степеней, а деление – к вычитанию”
ФГБНУ “Федеральный институт педагогических измерений”
Кодирование текстовой информации
I = n * i
где:
Кодирование графической информации
Рассмотрим некоторые понятия и формулы, необходимые для решения ЕГЭ по информатике данной темы.
- Пиксель – это наименьший элемент растрового изображения, который имеет определенный цвет.
- Разрешение – это количество пикселей на дюйм размера изображения.
- Глубина цвета — это количество битов, необходимое для кодирования цвета пикселя.
- Если глубина кодирования составляет i битов на пиксель, код каждого пикселя выбирается из 2i возможных вариантов, поэтому можно использовать не более 2i различных цветов.
- N — количество цветов
- i — глубина цвета
- В цветовой модели RGB (красный (R), зеленый (G), синий (B)): R (0..255) G (0..255) B (0..255) -> получаем 28 вариантов на каждый из трех цветов.
- R G B: 24 бита = 3 байта — режим True Color (истинный цвет)
- I — объем памяти, требуемый для хранения изображения
- M — ширина изображения в пикселях
- N — высота изображения в пикселях
- i — глубина кодирования цвета или разрешение
- где N – количество пикселей (M * N) и i – глубина кодирования цвета (разрядность кодирования)
- Следует также помнить формулы преобразования:
Формула для нахождения количества цветов в используемой палитре:
i = log2N
Найдем формулу объема памяти для хранения растрового изображения:
I = M * N * i
где:
Или можно формулу записать так:
I = N * i битов
* для указания объема выделенной памяти встречаются разные обозначения (V или I).
1 Мбайт = 220 байт = 223 бит,
1 Кбайт = 210 байт = 213 бит
Кодирование звуковой информации
Познакомимся с понятиями и формулами, необходимыми для решения заданий 7 ЕГЭ по информатике.
- Оцифровка или дискретизация – это преобразование аналогового сигнала в цифровой код.
- T – интервал дискретизации (измеряется в с)
- ƒ — частота дискретизации (измеряется в Гц, кГц)
- Частота дискретизации определяет количество отсчетов, т.е. отдельных значений сигнала, запоминаемых за 1 секунду. Измеряется в герцах, 1 Гц (один герц) – это один отсчет в секунду, а, например, 7 кГц – это 7000 отсчетов в секунду.
- Разрядность кодирования (глубина, разрешение) — это число битов, используемое для хранения одного отсчёта.
- Получим формулу объема звукового файла:
- I — объем
- β — глубина кодирования
- ƒ — частота дискретизации
- t — время
- S — количество каналов
Дискретизация, объяснение задания 7 ЕГЭ
* Изображение взято из презентации К. Полякова
Разрядность кодирования
* Изображение взято из презентации К. Полякова
Для хранения информации о звуке длительностью t секунд, закодированном с частотой дискретизации ƒ Гц и глубиной кодирования β бит требуется бит памяти:
I = β * ƒ * t * S
S для моно = 1, для стерео = 2, для квадро = 4
Пример: при ƒ=8 кГц, глубине кодирования 16 бит на отсчёт и длительности звука 128 с. потребуется:
✍ Решение:
I = 8000*16*128 = 16384000 бит
I = 8000*16*128/8 = 23 * 1000 * 24 * 27 / 23 = 214 / 23 =211 =
= 2048000 байт
Определение скорости передачи информации
- Канал связи всегда имеет ограниченную пропускную способность (скорость передачи информации), которая зависит от свойств аппаратуры и самой линии связи(кабеля)
- I — объем информации
- v — пропускная способность канала связи (измеряется в битах в секунду или подобных единицах)
- t — время передачи
Объем переданной информации I вычисляется по формуле:
I = V * t
* Вместо обозначения скорости V иногда используется q
* Вместо обозначения объема сообщения I иногда используется Q
Скорость передачи данных определяется по формуле:
V = I/t
и измеряется в бит/с
Егифка ©:
Решение заданий 7 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Тема: Кодирование изображений
7_1:
Какой минимальный объем памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 160 х 160 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Типовые задания для тренировки
✍ Решение:
- Используем формулу нахождения объема:
- Подсчитаем каждый сомножитель в формуле, стараясь привести числа к степеням двойки:
- M x N:
160 * 160 = 20 * 2³ * 20 * 2³ = 400 * 26 = = 25 * 24 * 26
256 = 28 т.е. 8 бит на пиксель (из формулы кол-во цветов = 2i)
I = 25 * 24 * 26 * 23 = 25 * 213 - всего бит на всё изображение
(25 * 213) / 213 = 25 Кбайт
Результат: 25
Детальный разбор задания 7 ЕГЭ по информатике предлагаем посмотреть в видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование изображений:
ЕГЭ по информатике задание 7.2:
Рисунок размером 128 на 256 пикселей занимает в памяти 24 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.
Типовые задания для тренировки
✍ Решение:
- По формуле объема файла изображения имеем:
- где M * N — общее количество пикселей. Найдем это значение, используя для удобства степени двойки:
128 * 256 = 27 * 28 = 215
i = I / (M*N)
23 * 3 * 210 * 23: i = (23 * 3 * 210 * 23) / 215 = = 3 * 216 / 215 = 6 бит
26 = 64 вариантов цветов в цветовой палитре
Результат: 64
Смотрите видеоразбор задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование изображений:
ЕГЭ по информатике задание 7.3:
После преобразования растрового 256-цветного графического файла в 4-цветный формат его размер уменьшился на 18 Кбайт. Каков был размер исходного файла в Кбайтах?
Типовые задания для тренировки
✍ Решение:
- По формуле объема файла изображения имеем:
- i можно найти, зная количество цветов в палитре:
где N — общее количество пикселей,
а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)
до преобразования: i = 8 (28 = 256) после преобразования: i = 2 (22 = 4)
I = x * 8 I - 18 = x * 2
x = I / 8
I - 18 = I / 4
4I - I = 72
3I = 72
I = 24
Результат: 24
Подробный разбор 7 задания ЕГЭ смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование изображений:
ЕГЭ по информатике задание 7.4:
Цветное изображение было оцифровано и сохранено в виде файла без использования сжатия данных. Размер полученного файла – 42 Мбайт. Затем то же изображение было оцифровано повторно с разрешением в 2 раза меньше и глубиной кодирования цвета увеличили в 4 раза больше по сравнению с первоначальными параметрами. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной оцифровке.
Типовые задания для тренировки
✍ Решение:
- По формуле объема файла изображения имеем:
- В такого рода задачах необходимо учесть, что уменьшение разрешения в 2 раза, подразумевает уменьшение в 2 раза пикселей отдельно по ширине и по высоте. Т.е. в целом N уменьшается в 4 раза!
- Составим систему уравнений на основе имеющихся сведений, в которой первое уравнение будет соответствовать данным до преобразования файла, а второе уравнение — после:
где N — общее количество пикселей или разрешение,
а i — глубина цвета (количество бит, выделенное на 1 пиксель)
42 = N * i I = N / 4 * 4i
i = 42 / N
[ I= frac {N}{4} * 4* frac {42}{N} ]
I = 42
Результат: 42
Тема: Кодирование изображений:
ЕГЭ по информатике задание 7.5:
Изображение было оцифровано и сохранено в виде растрового файла. Получившийся файл был передан в город А по каналу связи за 72 секунды. Затем то же изображение было оцифровано повторно с разрешением в 2 раза больше и глубиной кодирования цвета в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б, пропускная способность канала связи с городом Б в 3 раза выше, чем канала связи с городом А.
Сколько секунд длилась передача файла в город Б?
Типовые задания для тренировки
✍ Решение:
- По формуле скорости передачи файла имеем:
- По формуле объема файла изображения имеем:
- Для данной задачи, необходимо уточнить, что разрешение на самом деле имеет два сомножителя (пикселей по ширине * пикселей по высоте). Поэтому при увеличении разрешения в два раза, увеличатся оба числа, т.е. N увеличится в 4 раза вместо двух.
- Изменим формулу получения объема файла для города Б:
- Для города А и Б заменим значения объема в формуле для получения скорости:
- Подставим значение скорости из формулы для города А в формулу для города Б:
- Выразим t:
где I — объем файла, а t — время
где N — общее количество пикселей или разрешение,
а i — глубина цвета (количество бит, выделенное на 1 пиксель)
[ I= frac {2*N * i}{3} ]
Город А:
[ V= frac {N*i}{72} ]
Город Б:
[ 3*V= frac{frac {4*N*i}{3}}{t} ]
или:
[ t*3*V= frac {4*N*i}{3} ]
[ frac {t*3*N*i}{72}= frac {4*N*i}{3} ]
t = 4 * 72 / (3 * 3) = 32 секунды
Результат: 32
Другой способ решения смотрите в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование изображений:
ЕГЭ по информатике задание 7.6:
Камера делает фотоснимки размером 1024 х 768 пикселей. На хранение одного кадра отводится 900 Кбайт.
Найдите максимально возможное количество цветов в палитре изображения.
Типовые задания для терировки
✍ Решение:
- Количество цветов зависит от глубины кодирования цвета, которая измеряется в битах. Для хранения кадра, т.е. общего количества пикселей выделено 900 Кбайт. Переведем в биты:
900 Кбайт = 22 * 225 * 210 * 23 = 225 * 215
1024 * 768 = 210 * 3 * 28
[ frac {225 * 2^{15}}{3 * 2^{18}} = frac {75}{8} approx 9 ]
9 бит на 1 пиксель
29 = 512
Результат: 512
Смотрите подробное решение на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование изображений:
7_8: Демоверсия ЕГЭ 2018 информатика:
Автоматическая фотокамера производит растровые изображения размером 640×480 пикселей. При этом объём файла с изображением не может превышать 320 Кбайт, упаковка данных не производится.
Какое максимальное количество цветов можно использовать в палитре?
✍ Решение:
- По формуле объема файла изображения имеем:
- Посмотрим, что из формулы нам уже дано:
I = N * i
где N — общее количество пикселей или разрешение, а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)
I = 320 Кбайт, N = 640 * 420 = 307200 = 75 * 212 всего пикселей, i - ?
количество цветов = 2i
320 Кбайт = 320 * 210 * 23 бит = 320 * 213 бит
[ i = frac {I}{N} = frac {320 * 2^{13}}{75 * 2^{12}} approx 8,5 бит ]
2i = 28 = 256
Результат: 256
Подробное решение данного 7 (9) задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
7_21: : ЕГЭ по информатике задание 7.21:
Для хранения в информационной системе документы сканируются с разрешением 300 ppi. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 5 Мбайт. В целях экономии было решено перейти на разрешение 150 ppi и цветовую систему, содержащую 16 цветов. Средний размер документа, отсканированного с изменёнными параметрами, составляет 512 Кбайт.
Определите количество цветов в палитре до оптимизации.
Типовые задания для тренировки
✍ Решение:
- По формуле объема файла изображения имеем:
- Так как по заданию имеем разрешение, выраженное в пикселях на дюйм, то фактически это означает:
- Формула количества цветов:
- Посмотрим, что из формулы нам уже дано до экономного варианта и при экономном варианте:
I = N * i
где N — общее количество пикселей или разрешение, а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель).
I = значение ppi2 * N * i
количество цветов = 2i
Неэкономный вариант: I = 5 Мбайт = 5 * 223 бит, N - ?, i - ? 300 ppi Экономный вариант: I = 512 Кбайт = 29 * 213 бит = 222 бит, N - ?, i = 4 бит (24 = 16) 150 ppi
N = I / (i * 150*150 ppi) N = 222 / (4 * 22500)
I = N * 300*300 ppi * i 5 * 223 = (222 * 300 * 300 * i) / (22500 * 4);
i = (5 * 223 * 22500 * 4) / (222 * 300 * 300) = 9000 / 900 = 10 бит
210 = 1024
Результат: 1024
Тема: Кодирование звука
7_7:
На студии при четырехканальной (квадро) звукозаписи с 32-битным разрешением за 30 секунд был записан звуковой файл. Сжатие данных не производилось. Известно, что размер файла оказался 7500 Кбайт.
С какой частотой дискретизации (в кГц) велась запись? В качестве ответа укажите только число, единицы измерения указывать не нужно.
Типовые задания для тренировки
✍ Решение:
- По формуле объема звукового файла получим:
- Из задания имеем:
I = β * t * ƒ * S
I= 7500 Кбайт β= 32 бита t= 30 секунд S= 4 канала
[ ƒ = frac {I}{S*B*t} = frac {7500 * 2^{10} * 2^3 бит}{2^7 * 30}Гц = frac { 750 * 2^6}{1000}КГц = 2^4 = 16 ]
24 = 16 КГц
Результат: 16
Для более детального разбора предлагаем посмотреть видео решения данного 7 задания ЕГЭ по информатике:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование звука:
ЕГЭ по информатике задание 7_9:
Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза выше и частотой дискретизации в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд; пропускная способность канала связи с городом Б в 4 раза выше, чем канала связи с городом А.
Сколько секунд длилась передача файла в город A? В ответе запишите только целое число, единицу измерения писать не нужно.
Типовые задания для тренировки
✍ Решение:
- Для решения понадобится формула нахождения скорости передачи данных формулы:
- Вспомним также формулу объема звукового файла:
- Выпишем отдельно, все данные, касающиеся города Б (про А практически ничего не известно):
V = I/t
I = β * ƒ * t * s
где:
I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S — кол-во каналов (если не указывается, то моно)
город Б: β - в 2 раза выше ƒ - в 3 раза меньше t - 15 секунд, пропускная способность (скорость V) - в 4 раза выше
город А: βБ / 2 ƒБ * 3 IБ / 2 VБ / 4 tБ / 2, tБ * 3, tБ * 4 - ?
t = t/2
t = t * 3
t = t * 4
[ t_А = frac {15}{2} * 3 * 4 ]
90 секунд
Результат: 90
Подробное решение смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование звука:
ЕГЭ по информатике задание 7.10:
Музыкальный фрагмент был записан в формате стерео (двухканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 30 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось.
Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.
Типовые задания для тренировки
✍ Решение:
- Вспомним формулу объема звукового файла:
- Выпишем отдельно, все данные, касающиеся первого состояния файла, затем второго состояния — после преобразования:
I = β * ƒ * t * S
I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S -количество каналов
1 состояние: S = 2 канала I = 30 Мбайт
2 состояние: S = 1 канал β = в 2 раза выше ƒ = в 1,5 раза ниже I = ?
I = I / 2
I = I * 2
I = I / 1,5
I = 30 Мбайт / 2 * 2 / 1,5 = 20 Мбайт
Результат: 20
Смотрите видеоразбор данной задачи:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование звуковых файлов:
ЕГЭ по информатике задание 7_11:
Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 100 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 3 раза выше и частотой дискретизации в 4 раз меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд.
✍ Решение:
- Вспомним формулу объема звукового файла:
- Выпишем отдельно, все данные, касающиеся файла, переданного в город А, затем преобразованного файла, переданного в город Б:
I = β * ƒ * t * S
I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
А: t = 100 c.
Б: β = в 3 раза выше ƒ = в 4 раза ниже t = 15 c.
✎ 1 способ решения:
tA для преобразов. = 100 секунд * 3 / 4 = 75 секунд
75 / 15 = 5
Ответ: 5
✎ 2 способ решения:
А: tА = 100 c. VА = I / 100
Б: β = в 3 раза выше ƒ = в 4 раза ниже t = 15 c. IБ = (3 / 4) * I VБ = ((3 / 4) * I) / 15
[ frac {V_Б}{V_А} = frac {3/_4 * I}{15} * frac {100}{I} = frac {3/_4 * 100}{15} = frac {15}{3} = 5 ]
(((3/4) * I) / 15) * (100 / I)= (3/4 * 100) / 15 = 15/3 = 5
Результат: 5
Подробный видеоразбор задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование звука:
ЕГЭ по информатике задание 7_12:
Производится четырёхканальная (квадро) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Запись длится 2 минуты, её результаты записываются в файл, сжатие данных не производится.
Определите приблизительно размер полученного файла (в Мбайт). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 10.
✍ Решение:
- Вспомним формулу объема звукового файла:
- Для простоты расчетов пока не будем брать во внимание количество каналов. Рассмотрим, какие данные у нас есть, и какие из них необходимо перевести в другие единицы измерения:
I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S — количество каналов
β = 32 бита ƒ = 32кГц = 32000Гц t = 2 мин = 120 с
(32 * 32000 * 120) / 223 = =( 25 * 27 * 250 * 120) / 223 = = (250*120) / 211 = = 30000 / 211 = = (24 * 1875) / 211 = = 1875 / 128 ~ 14,6
14,6 * 4 = 58,5
Результат: 60
Смотрите подробное решение:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование звука:
7_19: Государственный выпускной экзамен ГВЭ 2018 (информатика ГВЭ ФИПИ, задание 7):
Производится двухканальная (стерео) цифровая звукозапись. Значение сигнала фиксируется 48 000 раз в секунду, для записи каждого значения используется 32 бит. Запись длится 5 минут, её результаты записываются в файл, сжатие данных не производится.
Какая из приведённых ниже величин наиболее близка к размеру полученного файла?
1) 14 Мбайт
2) 28 Мбайт
3) 55 Мбайт
4) 110 Мбайт
✍ Решение:
- По формуле объема звукового файла имеем:
I — объем β — глубина кодирования = 32 бита ƒ — частота дискретизации = 48000 Гц t — время = 5 мин = 300 с S — количество каналов = 2
I = 48000 * 32 * 300 * 2
48000 | 2 24000 | 2 12000 | 2 6000 | 2 = 375 * 27 3000 | 2 1500 | 2 750 | 2 375 | 2 - уже не делится 187,5
300 | 2 = 75 * 22 150 | 2 75 | 2 - уже не делится 37,5
I = 375 * 75 * 215
I = 375 * 75 * 215 / 223 = 28125 / 28
210 = 1024 1024 * 2 2048 * 2 4096 * 2 8192 * 2 16384 * 2 32768
210 * 25 = 215 = 32768 210 * 24 = 214 = 16384
215 / 28 = 27 = 128 214 / 28 = 26 = 64
Результат: 4
Подробное решение ГВЭ задания 7 2018 года смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование звука:
7_20:
Производится двухканальная (стерео) звукозапись с частотой дискретизации 4 кГц и 64-битным разрешением. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится.
Определите приблизительно размер получившегося файла (в Мбайтах). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 2.
✍ Решение:
- По формуле объема звукового файла имеем:
I — объем β — глубина кодирования = 32 бита ƒ — частота дискретизации = 48000 Гц t — время = 5 мин = 300 с S — количество каналов = 2
ƒ = 4 кГЦ = 4 * 1000 Гц ~ 22 * 210 B = 64 бит = 26 / 223 Мбайт t = 1 мин = 60 c = 15 * 22 c S = 2
I = 26 * 22 * 210 * 15 * 22 * 21 / 223 = 15/4 ~ 3,75
Результат: 4
Видеоразбор задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование видео
7_22:
Камера снимает видео без звука с частотой 120 кадров в секунду, при этом изображения используют палитру, содержащую 224 = 16 777 216 цветов. При записи файла на сервер полученное видео преобразуют так, что частота кадров уменьшается до 20, а изображения преобразуют в формат, использующий палитру из 256 цветов. Другие преобразования и иные методы сжатия не используются. 10 секунд преобразованного видео в среднем занимают 512 Кбайт.
Сколько Мбайт в среднем занимает 1 минута исходного видео?
Типовые задания для тренировки
✍ Решение:
- Посмотрим, как изменялись параметры файла до преобразования и после:
ДО: ƒ = 120, i = 24 бит ПОСЛЕ: ƒ = 20, i = 8 бит (28 = 256) t = 10 секунд I = 512 Кбайт = 29 Кбайт
за 10 секунд: I * 18 = 29 * 18 Кбайт = (29 * 18) . 210 Мбайт = 9 Мбайт
за 1 мин: 9 * 6 = 54 Мбайт
Результат: 54
Тема: Скорость передачи данных
ЕГЭ по информатике задание 7_13:
Скорость передачи данных через ADSL-соединение равна 128000 бит/с. Передача текстового файла через это соединение заняла 1 минуту.
Определите, сколько символов содержал переданный текст, если известно, что он был представлен в 16-битной кодировке Unicode.
Типовые задания для тренировки
✍ Решение:
- Вспомним формулу скорости передачи данных:
* Вместо Q можно использовать обозначение I (для объема файла)
V - скорость Q - объем t - время
V = 128000 бит/с = 210 * 125 бит/с t = 1 мин = 60 с = 22 * 15 с 1 символ кодируется 16-ю битами всего символов - ?
Q = 210 * 125 * 22 * 15 = = 212 * 1875 бит на все символы
кол-во символов = 212 * 1875 / 16 = 212 * 1875 / 24 =
= 28 * 1875 = 480000
Результат: 480000
Разбор 7 задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Скорость передачи информации:
ЕГЭ по информатике задание 7_14:
У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 217 бит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 216 бит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 8 Мбайт по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 1024 Кбайт этих данных.
Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей?
Типовые задания для тренировки
✍ Решение:
- Вспомним формулу скорости передачи данных:
* Вместо Q можно использовать обозначение I (для объема файла)
V - скорость Q - объем t - время
Вася: V = 217 бит/с Петя: V = 216 бит/с Общий объем Q = 8 Мбайт
Q = 8Мбайт = 8 * 223 бит = 23 * 223 = 226 бит
t1 = 1024 Кбайт / 217 = 210 * 213 бит / 217 = = 210 / 24 = 64 с
t2 = 226 / 216 = 210 = 1024 c
t = t1 + t2 = 64 + 1024 = 1088
Результат: 1088
Подробный разбор смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Скорость передачи информации:
ЕГЭ по информатике задание 7_15:
Сколько секунд потребуется модему, передающему сообщения со скоростью 32000 бит/с, чтобы передать 16-цветное растровое изображение размером 800 x 600 пикселей, при условии, что в каждом байте закодировано максимально возможное число пикселей?
Типовые задания для тренировки
✍ Решение:
- Вспомним формулу скорости передачи данных:
* Вместо Q можно использовать обозначение I (для объема файла)
V - скорость Q - объем t - время
N — общее количество пикселей или разрешение, i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)
Q = 4 * 480000
t = 4 * 480000 / 32000 = 60 секунд
Результат: 60
Тема: Скорость передачи информации:
ЕГЭ по информатике задание 7_16:
Каково время (в минутах) передачи полного объема данных по каналу связи, если известно, что передано 9000 Мбайт данных, причем треть времени передача шла со скоростью 60 Мбит в секунду, а остальное время – со скоростью 90 Мбит в секунду?
✍ Решение:
- Формула скорости передачи данных:
* Вместо Q можно использовать обозначение I (для объема файла)
V - скорость Q - объем t - время
1 Мбайт = 8 Мбит
Q = 9000 Мбайт * 8 = 72000 Мбит
(60 * 1/3t) + (90 * 2/3t) = 72000
вынесем t за скобки, получим уравнение:
t * (20 + 60) = 72000
выразим t:
t = 72000 / 80 = 900 с = 15 мин
Результат: 15
Решение задания можно посмотреть и на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Скорость передачи информации:
ЕГЭ по информатике задание 7.17:
Документ объемом 5 Мбайт можно передать с одного компьютера на другой двумя способами:
А) Сжать архиватором, передать архив по каналу связи, распаковать
Б) Передать по каналу связи без использования архиватора.
Какой способ быстрее и насколько, если
- средняя скорость передачи данных по каналу связи составляет 218 бит в секунду,
- объем сжатого архиватором документа равен 20% от исходного,
- время, требуемое на сжатие документа – 7 секунд, на распаковку – 1 секунда?
В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого.
Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.
Типовые задания для тренировки
✍ Решение:
-
Рассмотрим способ А:
- Сначала найдем объем документа, зная, что он составляет 20% от исходного:
Q (объем) = 5 Мбайт * 0.2 = 1 Мбайт = 1 * 223 бит
V - скорость Q - объем t - время
t = Q / V + 7 + 1 = 8 + 223 / 218 = 8 + 25 = 40 c
Рассмотрим способ Б:
t = Q / V = 5 * 223 / 218 = 5 * 25 = 5 * 32 = 160 c
160 с - 40 с = 120 с
Результат: А120
Решение также можно посмотреть в видеоуроке:
📹 YouTube здесьздесь
Тема: Скорость передачи информации:
ЕГЭ по информатике задание 7_18:
Документ объёмом 20 Мбайт можно передать с одного компьютера на другой двумя способами:
А) сжать архиватором-1, передать архив по каналу связи, распаковать;
Б) сжать архиватором-2, передать архив по каналу связи, распаковать;
Какой способ быстрее и насколько, если
- средняя скорость передачи данных по каналу связи составляет 220 бит в секунду,
- объём документа, сжатого архиватором-1, равен 20% от исходного,
- на сжатие документа архиватором-1 требуется 15 секунд, на распаковку — 2 секунды,
- объём документа, сжатого архиватором-2, равен 10% от исходного,
- на сжатие документа архиватором-2 требуется 20 секунд, на распаковку — 4 секунды?
В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого.
Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.
✍ Решение:
-
Рассмотрим способ А:
- Сначала найдем объем документа, зная, что он составляет 20% от исходного:
Q (объем) = 20 Мбайт * 0.2 = 4 Мбайт = 22 * 223 бит = 225 бит
V - скорость Q - объем t - время
tA = 225 / 220 + 17 с = 25 + 17 = 49 с
Рассмотрим способ Б:
Q (объем) = 20 Мбайт * 0.1 = 2 Мбайт = 21 * 223 бит = 224 бит
tБ = 224 / 220 + 24 с = 24 + 24 = 40 с
49 - 40 = 9 с
Результат: Б9
Тема: Скорость передачи информации:
Решение 7 ЕГЭ по информатике, задание 7_19:
Документ (без упаковки) можно передать по каналу связи с одного компьютера на другой за 1 минуту и 40 секунд. Если предварительно упаковать документ архиватором, передать упакованный документ, а потом распаковать на компьютере получателя, то общее время передачи (включая упаковку и распаковку) составит 30 секунд. При этом на упаковку и распаковку данных всего ушло 10 секунд. Размер исходного документа 45 Мбайт.
Чему равен размер упакованного документа (в Мбайт)?
✍ Решение:
- Выпишем исходные данные для двух состояний документа, используя неизвестное x для искомого параметра — объема:
неупакованный:
I1 = 45 Мбайт t1 = 100 секунд (60 секунд + 40 секунд = 100)
упакованный:
I2 = x Мбайт t2 = 20 секунд (30 секунд - 10 секунд = 20)
45 = 100 х = 20
х = (45 * 20) / 100 = 9 Мбайт
Результат: 9
-
1) 64 * 64 = 4096 пикселей в изображении
2) N = 2^i
256 = 2^i
i = 8 бит – глубина кодирования одного пикселя
3) 4096 * 8 бит = 32768 бит = 32768 бит / 8 = 4096 байт / 1024 = 4 килобайта
Ответ: 4 Кб нужен минимальный объем видеопамяти для хранения этого изображения
- Комментировать
- Жалоба
- Ссылка
Найди верный ответ на вопрос ✅ «Какой минимальный объем памяти потребуется для хранения растрового изображения размером 64*64 пикселя, если в изображении используется …» по предмету 📙 Информатика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Новые вопросы по информатике
Главная » Информатика » Какой минимальный объем памяти потребуется для хранения растрового изображения размером 64*64 пикселя, если в изображении используется палитра из 256 цветов.
Решение задач на кодирование графической информации.
-
Нахождение объема видеопамяти
В задачах такого типа используются понятия:
-
объем видеопамяти,
-
графический режим,
-
глубина цвета,
-
разрешающая способность экрана,
-
палитра.
Во всех подобных задачах требуется найти ту или иную величину.
Видеопамять – это специальная оперативная память, в которой формируется графическое изображение. Иными словами для получения на экране монитора картинки её надо где-то хранить. Для этого и существует видеопамять. Чаще всего ее величина от 512 Кб до 4 Мб для самых лучших ПК при реализации 16,7 млн. цветов.
Объем видеопамяти рассчитывается по формуле: V=I*X*Y, где I – глубина цвета отдельной точки, X, Y –размеры экрана по горизонтали и по вертикали (произведение х на у – разрешающая способность экрана).
Экран дисплея может работать в двух основных режимах: текстовом и графическом.
В графическом режиме экран разделяется на отдельные светящиеся точки, количество которых зависит от типа дисплея, например 640 по горизонтали и 480 по вертикали. Светящиеся точки на экране обычно называют пикселями, их цвет и яркость может меняться. Именно в графическом режиме появляются на экране компьютера все сложные графические изображения, создаваемыми специальными программами, которые управляют параметрами каждого пикселя экрана. Графические режимы характеризуются такими показателями как:
– разрешающая способность (количество точек, с помощью которых на экране воспроизводится изображение) – типичные в настоящее время уровни разрешения 800*600 точек или 1024*768 точек. Однако для мониторов с большой диагональю может использоваться разрешение 1152*864 точки.
– глубина цвета (количество бит, используемых для кодирования цвета точки), например, 8, 16, 24, 32 бита. Каждый цвет можно рассматривать как возможное состояние точки, Тогда количество цветов, отображаемых на экране монитора может быть вычислено по формуле K=2I , где K – количество цветов, I – глубина цвета или битовая глубина.
Кроме перечисленных выше знаний учащийся должен иметь представление о палитре:
– палитра (количество цветов, которые используются для воспроизведения изображения), например 4 цвета, 16 цветов, 256 цветов, 256 оттенков серого цвета, 216 цветов в режиме называемом High color или 224 , 232 цветов в режиме True color.
Учащийся должен знать также связи между единицами измерения информации, уметь переводить из мелких единиц в более крупные, Кбайты и Мбайты, пользоваться обычным калькулятором и Wise Calculator.
Уровень «3»
1. Определить требуемый объем видеопамяти для различных графических режимов экрана монитора, если известна глубина цвета на одну точку.
|
Режим экрана |
Глубина цвета (бит на точку) |
||||
|
4 |
8 |
16 |
24 |
32 |
|
|
640 на 480 |
|||||
|
800 на 600 |
|||||
|
1024 на 768 |
|||||
|
1280 на 1024 |
Решение:
-
Всего точек на экране (разрешающая способность): 640 * 480 = 307200
2. Необходимый объем видеопамяти V= 4 бит * 307200 = 1228800 бит = 153600 байт = 150 Кбайт.
3. Аналогично рассчитывается необходимый объем видеопамяти для других графических режимов. При расчетах учащийся пользуется калькулятором для экономии времени.
Ответ:
|
Режим экрана |
Глубина цвета (бит на точку) |
||||
|
4 |
8 |
16 |
24 |
32 |
|
|
640 на 480 |
150 Кб |
300 Кб |
600 Кб |
900 Кб |
1,2 Мб |
|
800 на 600 |
234 Кб |
469 Кб |
938 Кб |
1,4 Мб |
1,8 Мб |
|
1024 на 768 |
384 Кб |
768 Кб |
1,5 Мб |
2,25 Мб |
3 Мб |
|
1280 на 1024 |
640 Кб |
1,25 Мб |
2,5 Мб |
3,75 Мб |
5 Мб |
2. Черно-белое (без градаций серого) растровое графическое изображение имеет размер 10 ´10 точек. Какой объем памяти займет это изображение?
Решение:
-
Количество точек -100
-
Так как всего 2 цвета черный и белый. то глубина цвета равна 1 ( 21 =2)
-
Объем видеопамяти равен 100*1=100 бит
3. Для хранения растрового изображения размером 128 x 128 пикселей отвели 4 КБ памяти. Каково максимально возможное число цветов в палитре изображения.
Решение:
-
Определим количество точек изображения. 128*128=16384 точек или пикселей.
-
Объем памяти на изображение 4 Кб выразим в битах, так как V=I*X*Y вычисляется в битах. 4 Кб=4*1024=4 096 байт = 4096*8 бит =32768 бит
-
Найдем глубину цвета I =V/(X*Y)=32768:16384=2
-
N=2I , где N – число цветов в палитре. N=4
Ответ: 4
4. Сколько бит видеопамяти занимает информация об одном пикселе на ч/б экране (без полутонов)?([6],C. 143, пример 1)
Решение:
Если изображение Ч/Б без полутонов, то используется всего два цвета –черный и белый, т.е. К=2, 2i =2, I= 1 бит на пиксель.
Ответ: 1 пиксель
5. Какой объем видеопамяти необходим для хранения четырех страниц изображения, если битовая глубина равна 24, а разрешающая способность дисплея- 800 х 600 пикселей?
Решение:
-
Найдем объем видеопамяти для одной страницы: 800*600*24=11520000 бит =1440000 байт =1406,25 Кб ≈1, 37 Мб
-
1,37*4 =5,48 Мб ≈5.5 Мб для хранения 4 страниц.
Ответ: 5.5 Мб
Уровень «4»
6.Определить объем видеопамяти компьютера, который необходим для реализации графического режима монитора High Color с разрешающей способностью 1024 х 768 точек и палитрой цветов из 65536 цветов.
Методические рекомендации:
Если ученик помнит, что режим High Color – это 16 бит на точку, то объем памяти можно найти, определив число точек на экране и умножив на глубину цвета, т.е. 16. Иначе ученик может рассуждать так:
Решение:
1. По формуле K=2I , где K – количество цветов, I – глубина цвета определим глубину цвета. 2I =65536
Глубина цвета составляет: I = log265 536 = 16 бит (вычисляем с помощью программы Wise Calculator)
2.. Количество точек изображения равно: 1024´768 = 786 432
3. Требуемый объем видеопамяти равен: 16 бит ´ 786 432 = 12 582 912 бит = 1572864 байт = 1536 Кб =1,5 Мб (»1,2 Мбайта). Приучаем учеников, переводя в другие единицы, делить на 1024, а не на 1000.
Ответ: 1,5 Мб
7. В процессе преобразования растрового графического изображения количество цветов уменьшилось с 65536 до 16. Во сколько раз уменьшится объем занимаемой им памяти? (2.70, [3])
Решение:
Чтобы закодировать 65536 различных цветов для каждой точки, необходимо 16 бит. Чтобы закодировать 16 цветов, необходимо всего 4 бита. Следовательно, объем занимаемой памяти уменьшился в 16:4=4 раза.
Ответ: в 4 раза
8. Достаточно ли видеопамяти объемом 256 Кбайт для работы монитора в режиме 640 ´ 480 и палитрой из 16 цветов?
Решение:
-
Узнаем объем видеопамяти, которая потребуется для работы монитора в режиме 640х480 и палитрой в 16 цветов. V=I*X*Y=640*480*4 (24 =16, глубина цвета равна 4),
V= 1228800 бит = 153600 байт =150 Кб.
-
150
Ответ: достаточно
9. Укажите минимальный объем памяти (в килобайтах), достаточный для хранения любого растрового изображения размером 256 х 256 пикселей, если известно, что в изображении используется палитра из 216 цветов. Саму палитру хранить не нужно.
-
128
-
512
-
1024
-
2048
(ЕГЭ_2005, уровень А)
Решение:
Найдем минимальный объем памяти, необходимый для хранения одного пикселя. В изображении используется палитра из 216 цветов, следовательно, одному пикселю может быть сопоставлен любой из 216 возможных номеров цвета в палитре. Поэтому, минимальный объем памяти, для одного пикселя будет равен log2 216 =16 битам. Минимальный объем памяти, достаточный для хранения всего изображения будет равен 16*256*256 =24 * 28 * 28 =220 бит=220 : 23 =217 байт = 217 : 210 =27 Кбайт =128 Кбайт, что соответствует пункту под номером 1.
Ответ: 1
10. Используются графические режимы с глубинами цвета 8, 16. 24, 32 бита. Вычислить объем видеопамяти, необходимые для реализации данных глубин цвета при различных разрешающих способностях экрана.
Примечание: задача сводится в конечном итоге к решению задачи №1 (уровень «3», но ученику самому необходимо вспомнить стандартные режимы экрана.
11. Сколько секунд потребуется модему, передающему сообщения со скоростью 28800 бит/с, чтобы передать цветное растровое изображение размером 640 х 480 пикселей, при условии, что цвет каждого пикселя кодируется тремя байтами? (ЕГЭ_2005, уровень В)
Решение:
-
Определим объем изображения в битах:
3 байт = 3*8 = 24 бит,
V=I*X*Y=640*480*24 бит =7372800 бит
-
Найдем число секунд на передачу изображения: 7372800 : 28800=256 секунд
Ответ: 256.
12. Сколько секунд потребуется модему, передающему сообщения со скоростью 14400 бит/сек, чтобы передать цветное растровое изображение размером 800 х 600 пикселей, при условии, что в палитре 16 миллионов цветов? (ЕГЭ_2005, уровень В)
Решение:
Для кодирования 16 млн. цветов требуется 3 байта или 24 бита (Графический режим True Color). Общее количество пикселей в изображении 800 х 600 =480000. Так как на 1 пиксель приходится 3 байта, то на 480000 пикселей приходится 480000*3=1 440 000 байт или 11520000 бит. 11520000 : 14400 = 800 секунд.
Ответ: 800 секунд.
13. Современный монитор позволяет получать на экране 16777216 различных цветов. Сколько бит памяти занимает 1 пиксель?
Решение:
Один пиксель кодируется комбинацией двух знаков «0» и «1». Надо узнать длину кода пикселя.
2х =16777216, log2 16777216 =24 бит
Ответ: 24.
14. Каков минимальный объем памяти ( в байтах), достаточный для хранения черно-белого растрового изображения размером 32 х 32 пикселя, если известно, что в изображении используется не более 16 градаций серого цвета.
Решение:
-
Глубина цвета равна 4, т.к. 16 градаций цвета используется.
-
32*32*4=4096 бит памяти для хранения черно-белого изображения
-
4096 : 8 = 512 байт.
Ответ: 512 байт
Уровень «5»
15. Монитор работает с 16 цветной палитрой в режиме 640*400 пикселей. Для кодирования изображения требуется 1250 Кбайт. Сколько страниц видеопамяти оно занимает? (Задание 2,Тест I-6)
Решение:
1. Т.к. страница –раздел видеопамяти, вмещающий информацию об одном образе экрана одной «картинки» на экране, т.е. в видеопамяти могут размещаться одновременно несколько страниц, то, чтобы узнать число страниц надо поделить объем видеопамяти для всего изображения на объем памяти на 1 страницу. К-число страниц, К=Vизобр/V1 стр
Vизобр =1250 Кб по условию
-
Для этого вычислим объем видеопамяти для одной страницы изображения с 16 цветовой палитрой и разрешающей способностью 640*400.
V1 стр = 640*400*4 , где 4- глубина цвета (24 =16)
V1 стр = 1024000 бит = 128000 байт =125 Кб
3. К=1250 : 125 =10 страниц
Ответ: 10 страниц
16. Страница видеопамяти составляет 16000 байтов. Дисплей работает в режиме 320*400 пикселей. Сколько цветов в палитре?
Решение:
1. V=I*X*Y – объем одной страницы, V=16000 байт = 128000 бит по условию. Найдем глубину цвета I.
I=V/(X*Y).
I= 128000 / (320*400)=1.
2. Определим теперь, сколько цветов в палитре. K=2I , где K – количество цветов, I – глубина цвета. K=2
Ответ: 2 цвета.
17. Сканируется цветное изображение размером 10´10 см. Разрешающая способность сканера 600 dpi и глубина цвета 32 бита. Какой информационный объем будет иметь полученный графический файл. (2.44, [3], аналогично решается задача 2.81 [3])
Решение:
1. Разрешающая способность сканера 600 dpi (dot per inch — точек на дюйм) означает, что на отрезке длиной 1 дюйм сканер способен различить 600 точек. Переведем разрешающую способность сканера из точек на дюйм в точки на сантиметр:
600 dpi : 2,54 » 236 точек/см (1 дюйм = 2.54 см.)
2. Следовательно, размер изображения в точках составит 2360´2360 точек. (умножили на 10 см.)
3. Общее количество точек изображения равно:
2360´2360 = 5 569 600
4. Информационный объем файла равен:
32 бит ´ 5569600 = 178 227 200 бит » 21 Мбайт
Ответ: 21 Мбайт
18. Объем видеопамяти равен 256 Кб. Количество используемых цветов -16. Вычислите варианты разрешающей способности дисплея. При условии, что число страниц изображения может быть равно 1, 2 или 4.
Решение:
-
Если число страниц равно 1, то формулу V=I*X*Y можно выразить как
256 *1024*8 бит = X*Y*4 бит, (так как используется 16 цветов, то глубина цвета равна 4 бит.)
т.е. 512*1024 = X*Y; 524288 = X*Y.
Соотношение между высотой и шириной экрана для стандартных режимов не различаются между собой и равны 0,75. Значит, чтобы найти X и Y, надо решить систему уравнений:
Выразим Х=524288/ Y, подставим во второе уравнение, получим Y2 =524288*3/4=393216. Найдем Y≈630; X=524288/630≈830
Вариантом разрешающей способности может быть 630 х 830.
2. Если число страниц равно 2, то одна страница объемом 256:2=128 Кбайт, т.е
128*1024*8 бит = X*Y*4 бит, т.е. 256*1024 = X*Y; 262144 = X*Y.
Решаем систему уравнений:
Х=262144/ Y; Y2 =262144*3/4=196608; Y=440, Х=600
Вариантом разрешающей способности может быть 600 х 440.
4. Если число страниц равно 4, то 256:4 =64; 64*1024*2=X*Y; 131072=X*Y; решаем систему
X=131072/Y; Y2 =131072*3/4=98304; Y≈310, X≈420
Ответ: одна страница – 630 х 830
две страницы – 600 х 440
три страницы – 420 х 310
19. Часть страниц многотомной энциклопедии является цветными изображениями в шестнадцати цветовой палитре и в формате 320 ´ 640 точек. Страницы, содержащие текст, имеют формат — 32 строки по 64 символа в строке. Сколько страниц книги можно сохранить на жестком магнитном диске объемом 20 Мб, если каждая девятая страница энциклопедии — цветное изображение?
Решение:
-
Так как палитра 16 цветная, то глубина цвета равна 4 (2 4 =16)
-
4 ´ 320 ´ 640 = 819200 бит = 102400 байт =100 Кбайт – информации содержит каждая графическая страница.
-
32 ´ 64 = 2048 символов = 2048 байт = 2 Кбайт – содержит каждая текстовая страница.
-
Пусть Х — число страниц с графикой, тогда так как каждая 9 страница – графическая, следует, что страниц с текстом в 8 раз больше, т.е. 8Х — число страниц с текстом. Тогда все страницы с графикой будут иметь объем 110Х, а все страницы с текстом – объем 2* 8Х=16Х.
-
Известно, что диск составляет 20 Мб = 20480 Кб. Составим уравнение:
100Х + 16Х = 20480. Решив уравнение, получим Х ≈ 176, 5. Учитывая, что Х –целое число, берем число 176 –страниц с графикой.
-
176*8 =1408 страниц с текстом. 1408+176 = 1584 страниц энциклопедии.
Ответ: таким образом, на жестком магнитном диске объемом 20 Мб можно разместить 1584 страницы энциклопедии (176 графических и 1408 текстовых).
-
Определение разрешающей способности экрана и установка графического режима экрана.
Уровень «3»
20. Установить графический режим экрана монитора, исходя из объема установленной видеопамяти и параметров монитора.
Решение:
Установка графического режима экрана монитора
-
Ввести команду [Настройка-Панель управления – Экран] или щелкнуть по индикатору монитора на панели задач.
-
На появившейся диалоговой панели Свойства: экран выбрать вкладку Настройка.
-
С помощью раскрывающегося списка Цветовая палитра выбрать глубину цвета. С помощью ползунка Область экрана выбрать разрешение экрана
21. Определить марку монитора, разрешение экрана, глубину цвета собственного компьютера, объем видеопамяти. (Аналогично, см. задачу 1, а так же используя кнопку Дополнительно, выбрать вкладку Адаптер для определения объема видеопамяти.)
Уровень «4»
Методические рекомендации
Для решения задач этого уровня учащиеся также должны знать о ещё одной характеристике экрана, такой как Частота обновления экрана. Эта величина обозначает, сколько раз меняется за секунду изображение на экране. Чем чаще меняется изображение, тем меньше заметно мерцание и тем меньше устают глаза. При длительной работе за компьютером рекомендуется обеспечить частоту не менее 85 Гц. Кроме этого учащиеся должны уметь подбирать оптимальную разрешающую способность экрана, определять для конкретного объема видеопамяти оптимальный графический режим.
22. Установить различные графические режимы экрана монитора вашего компьютера:
а) режим с максимально возможной глубиной цвета;
б) режим с максимально возможной разрешающей способностью;
в) оптимальный режим.
Решение:
а) Выбрать контекстное меню Рабочего стола, Свойства, (можно вызвать меню и двойным щелчком на панели управления по значку экрана). В появившемся диалоговом окне Свойства: Экран выбрать вкладку Настойка или Параметры. Максимально возможную глубину цвета можно выбрать из списка Цветовая палитра (или Качество цветопередачи), где выбрать пункт Самое высокое 32 бита (True color24, или 32 бита) Эта операция может требовать перезагрузки компьютера.
б) Чтобы установить режим с максимально возможной разрешающей способностью надо на этой же вкладке Свойства:Экран переместить движок на панели Область экрана (Разрешение экрана) слева направо и выбрать например 1280 х 1024. В зависимости от видеокарты при изменении разрешения экрана может потребоваться перезагрузка компьютера. Но чаще всего выдается диалоговое окно, предупреждающее о том, что сейчас произойдет пробное изменение разрешения экрана. Для подтверждения щелкнуть на кнопке Ок.
При попытке изменить разрешение экрана выдается диалоговое окно с запросом о подтверждении изменений. Если не предпринимать никаких действий, то через 15 секунд восстанавливается прежнее разрешение. Это предусмотрено на случай сбоя изображения. Если экран выглядит нормально, следует щелкнуть на кнопке ДА и сохранить новое разрешение.
в) Для установки оптимального графического режима экрана надо исходить из объема видеопамяти, частоты обновления экрана и учитывать здоровье сберегающие факторы.
Для настройки частоты обновления экрана надо всё в той же вкладке Свойства:Экран щелкнуть по вкладке Дополнительно. В диалоговом окне свойств видеоадаптера выбрать вкладку Адаптер. Выбрать в списке Частота обновления и выбрать пункт Оптимальный –максимально возможная частота обновления экрана, доступная при текущем разрешении экрана для данной видеокарты и монитора.
Так чем меньше разрешение экрана, тем больше размеры значков на рабочем столе. Так оптимальным разрешением экрана может быть размеры экрана 800 х 600 точек при глубине цвета 32 бит и частотой обновления 85 Гц.
23. Объем страницы видеопамяти -125 Кбайт. Монитор работает с 16 цветной палитрой. Какова разрешающая способность экрана. (Задание 8,Тест I-6)
Решение:
-
Так как глубина цвета равна 4 (24 =16), то имеем V=4*X*Y
-
В формуле объема видеопамяти объем выражен в битах, а в условии задачи дан в Кбайтах, поэтому обе части равенства надо представить в байтах:
125*1024=(X*Y*4)/8 (делим справа на 8 – переводим в байты, умножаем слева на 1024 –переводим в байты)
3. Далее решаем уравнение: 4*X*Y = 125*1024 * 8
X*Y = 125*1024*2=250*1024=256000
4. Наиболее часто в паре разрешающей способности экрана встречается число 640, например 640*200, 640*400, 640*800. Попробуем разделить полученное число на 640
256000:640=400
Ответ: Разрешающая способность экрана равна 640*400
24. Какие графические режимы работы монитора может обеспечить видеопамять объемом в 1 МБ? (2.78 [3])
Решение:
Задача опирается на решение задачи №2.76 [3] (решение см. задачу №1 данного электронного пособия), а затем проводится анализ и делаем вывод. Видеопамять объемом 1 МБ может обеспечить следующие графические режимы:
-
640 х 480 (при глубине цвета 4, 8, 16, 24 бит)
-
800 х 600 (при глубине цвета 4, 8, 16 бит)
-
1024 х 768 (при глубине цвета 4, 8 бит)
-
1280 х 1024 (при глубине цвета 4 бита)
Ответ: 640 х 480 (4, 8, 16, 24 бит), 800 х 600 (4, 8, 16 бит), 1024 х 768 (4, 8 бит), 1280 х 1024 (4 бита)
Уровень «5»
25. Определить максимально возможную разрешающую способность экрана для монитора с диагональю 15″ и размером точки экрана 0,28 мм.
Решение:
1. Задача сводится к нахождению числа точек по ширине экрана. Выразим размер диагонали в сантиметрах. Учитывая ,что 1 дюйм=2,54 см., имеем: 2,54 см • 15 = 38,1 см.
2. Определим соотношение между высотой и шириной экрана для часто встречающегося режима экрана 1024х768 точек: 768 : 1024 = 0,75.
3. Определим ширину экрана. Пусть ширина экрана равна L, а высота h,
h:L =0,75, тогда h= 0,75L.
По теореме Пифагора имеем:
L2 + (0,75L)2 = 38,12
1,5625 L2 = 1451,61
L2 ≈ 929
L ≈ 30,5 см.
4. Количество точек по ширине экрана равно:
305 мм : 0,28 мм = 1089.
Следовательно, максимально возможным разрешением экрана монитора является 1024х768.
Ответ: 1024х768.
26. Определить соотношение между высотой и шириной экрана монитора для различных графических режимов. Различается ли это соотношение для различных режимов? а)640х480; б)800х600; в)1024х768; а)1152х864; а)1280х1024. Определить максимально возможную разрешающую способность экрана для монитора с диагональю 17″ и размером точки экрана 0,25 мм.
Решение:
1. Определим соотношение между высотой и шириной экрана для перечисленных режимов, они почти не различаются между собой:
|
640×480 |
800×600 |
1024×768 |
1152×864 |
1280×1024 |
|
0,75 |
0,75 |
0,75 |
0,75 |
0,8 |
2. Выразим размер диагонали в сантиметрах:
2,54 см • 17 = 43,18 см.
3. Определим ширину экрана. Пусть ширина экрана равна L, тогда высота равна 0,75L (для первых четырех случаев) и 0,8L для последнего случая.
По теореме Пифагора имеем:
|
L2 + (0,75L)2 = 43,182 |
L2 + (0,8L)2 = 43,182 |
4. Количество точек по ширине экрана равно:
|
345 мм : 0,25 мм = 1380 |
337 мм: 0,25 мм = 1348 |
Следовательно, максимально возможным разрешением экрана монитора является. 1280х1024
Ответ: 1280х1024
-
Кодировка цвета и изображения.
Методические рекомендации:
Учащиеся пользуются знаниями, полученными ранее Системы счисления, перевод чисел из одной системы в другую.
Используется и теоретический материал темы:
Цветное растровое изображение формируется в соответствие с цветовой моделью RGB, в которой тремя базовыми цветами являются Red (красный), Green (зеленый) и Blue (синий). Интенсивность каждого цвета задается 8-битным двоичным кодом, который часто для удобства выражают в шестнадцатеричной системе счисления. В этом случае используется следующий формат записи RRGGBB.
Уровень «3»
27. Запишите код красного цвета в двоичном, шестнадцатеричном и десятичном представлении.
Решение:
Красный цвет соответствует максимальному значению интенсивности красного цвета и минимальным значениям интенсивностей зеленого и синего базовых цветов, что соответствует следующим данным:
|
Коды/Цвета |
Красный |
Зеленый |
Синий |
|
двоичный |
11111111 |
00000000 |
00000000 |
|
шестнадцатеричный |
FF |
00 |
00 |
|
десятичный |
256 |
0 |
0 |
28. Сколько цветов будет использоваться, если для каждого цвета пикселя взято 2 уровня градации яркости? 64 уровня яркости каждого цвета?
Решение:
1. Всего для каждого пикселя используется набор из трех цветов (красный, зеленый, синий) со своими уровнями яркости (0-горит, 1-не горит). Значит, K=23 =8 цветов.
2.643 =262144
Ответ: 8; 262 144 цвета.
Уровень «4»
29. Заполните таблицу цветов при 24- битной глубине цвета в 16- ричном представлении.
Решение:
При глубине цвета в 24 бита на каждый из цветов выделяется по 8 бит, т.е для каждого из цветов возможны 256 уровней интенсивности (28 =256). Эти уровни заданы двоичными кодами (минимальная интенсивность -00000000, максимальная интенсивность -11111111). В двоичном представлении получается следующее формирование цветов:
|
Название цвета |
Интенсивность |
||
|
Красный |
Зеленый |
Синий |
|
|
Черный |
00000000 |
00000000 |
00000000 |
|
Красный |
11111111 |
00000000 |
00000000 |
|
Зеленый |
00000000 |
11111111 |
00000000 |
|
Синий |
00000000 |
00000000 |
11111111 |
|
Белый |
11111111 |
11111111 |
11111111 |
Переведя в 16-ричную систему счисления имеем:
|
Название цвета |
Интенсивность |
||
|
Красный |
Зеленый |
Синий |
|
|
Черный |
00 |
00 |
00 |
|
Красный |
FF |
00 |
00 |
|
Зеленый |
00 |
FF |
00 |
|
Синий |
00 |
00 |
FF |
|
Белый |
FF |
FF |
FF |
30. На «маленьком мониторе» с растровой сеткой размером 10 х 10 имеется черно-белое изображение буквы «К». Представить содержимое видеопамяти в виде битовой матрицы, в которой строки и столбцы соответствуют строкам и столбцам растровой сетки.
1
Х
2 3 4 5 6 7 8 9 10
|
|
|||||||||
10
Y
Решение:
Для кодирования изображения на таком экране требуется 100 бит (1 бит на пиксель) видеопамяти. Пусть «1» означает закрашенный пиксель, а «0» – не закрашенный. Матрица будет выглядеть следующим образом:
0000000000
0001000100
0001001000
0001010000
0001100000
0001010000
0001001000
0001000100
0000000000
0000000000
Эксперименты:
1. Поиск пикселей на мониторе.
Вооружиться увеличительным стеклом и попытаться увидеть триады красных, зеленых и синих (RGB –от англ. «Red – Green –Blue» точек на экране монитора.
Существуют разные технологии изготовления электронно-лучевых трубок. Если трубка выполнена по технологии «теневая маска», тогда можно увидеть настоящую мозаику из точек. В других случаях, когда вместо маски с отверстиями используется система нитей из люминофора трех основных цветов (апертурная решетка), картина будет совсем иной. Газета приводит очень наглядные фотографии трех типичных картин, которые могут увидеть «любопытные ученики».
Ребятам полезно было бы сообщить, что желательно различать понятия «точки экрана» и пиксели. Понятие «точки экрана» – физически реально существующие объекты. Пиксели- логические элементы изображения. Как это можно пояснить? Вспомним. Что существует несколько типичных конфигураций картинки на экране монитора: 640 х 480, 600 х 800 пикселей и другие. Но на одном и том же мониторе можно установить любую из них.. Это значит, что пиксели это не точки монитора. И каждый их них может быть образован несколькими соседними светящимися точками ( в пределе одной). По команде окрасить в синий цвет тот или иной пиксель, компьютер, учитывая установленный режим дисплея, закрасит одну или несколько соседних точек монитора. Плотность пикселей измеряется как количество пикселей на единицу длины. Наиболее распространены единицы, называемые кратко как (dots per inch- количество точек на дюйм, 1 дюйм = 2, 54 см). Единица dpi общепринята в области компьютерной графики и издательского дела. Обычно плотность пикселей для экранного изображения составляет 72 dpi или 96dpi.
2. Проведите эксперимент в графическом редакторе в случае, если для каждого цвета пикселя взято 2 уровня градации яркости? Какие цвета вы получите? Оформите в виде таблицы.
Решение:
|
Красный |
Зеленый |
Синий |
Цвет |
|
0 |
0 |
0 |
Черный |
|
0 |
1 |
0 |
Зеленый |
|
0 |
0 |
1 |
Синий |
|
1 |
1 |
1 |
Белый |
|
1 |
0 |
0 |
Красный |
|
0 |
1 |
1 |
Бирюзовый |
|
1 |
1 |
0 |
Желтый |
|
1 |
0 |
1 |
Малиновый |
Векторная графика:
-
Задачи на кодирование векторного изображения.
-
Получение векторного изображения с помощью векторных команд
Методические рекомендации:
При векторном подходе изображение рассматривается как описание графических примитивов, прямых, дуг, эллипсов, прямоугольников, окружностей, закрасок и пр. Описываются положение и форма этих примитивов в системе графических координат.
Т
|
Команда |
Действие |
|
Линия к X1, Y1 |
Нарисовать линию от текущей позиции в позицию (X1, Y1). |
|
Линия X1, Y1, X2,Y2 |
Нарисовать линию с координатами начала X1, Y1 и координатами конца X2, Y2. Текущая позиция не устанавливается. |
|
Окружность X,Y,R |
Нарисовать окружность; X,Y – координаты центра, а R – длина радиуса. |
|
Эллипс X1, Y1, X2,Y2 |
Нарисовать эллипс, ограниченный прямоугольником; (X1, Y1) –координаты левого верхнего, а (X2,Y2) – правого нижнего угла прямоугольника. |
|
Прямоугольник X1, Y1, X2,Y2 |
Нарисовать прямоугольник; (X1, Y1)- координаты левого верхнего угла, (X2,Y2) – координаты правого нижнего угла прямоугольника. |
|
Цвет рисования Цвет |
Установить текущий цвет рисования. |
|
Цвет закраски Цвет |
Установить текущий цвет закраски |
|
Закрасить X,Y, ЦВЕТ ГРАНИЦЫ |
Закрасить произвольную замкнутую фигуру; X, Y – координаты любой точки внутри замкнутой фигуры, ЦВЕТ ГРАНИЦЫ –цвет граничной линии. |
1. Задачи на кодирование векторного изображения.
Уровень «3»
-
Описать букву «К» последовательностью векторных команд.
1 2 3 4 5 6 7 8 9 10
X
|
|
|||||||||
10
Y