|
0 / 0 / 0 Регистрация: 02.06.2014 Сообщений: 11 |
|
|
1 |
|
Определение минимальной длины пути в дереве02.06.2014, 16:00. Показов 3754. Ответов 14
Добрый день. Очень нужна помощь! Необходимо решить задачу:
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
02.06.2014, 16:00 |
|
14 |
|
Модератор 35326 / 19427 / 4065 Регистрация: 12.02.2012 Сообщений: 32,457 Записей в блоге: 13 |
|
|
02.06.2014, 18:33 |
2 |
|
Поиск в ширину.
1 |
|
2833 / 1642 / 254 Регистрация: 03.12.2007 Сообщений: 4,222 |
|
|
02.06.2014, 23:05 |
3 |
|
Минимальной длины? А что, в дереве от корня до листа может быть несколько путей?
1 |
|
0 / 0 / 0 Регистрация: 02.06.2014 Сообщений: 11 |
|
|
03.06.2014, 11:20 [ТС] |
4 |
|
Catstail, А как с помощью поиска в ширину решить эту задачу? Somebody, в дереве несколько листов, они могут быть разной высоты, от корня до этих листов разные пути. Нужно найти минимальный из них
0 |
|
Модератор 35326 / 19427 / 4065 Регистрация: 12.02.2012 Сообщений: 32,457 Записей в блоге: 13 |
|
|
03.06.2014, 12:02 |
5 |
|
Rozumnaya, а Somebody-то прав… Если к одной вершине ведет несколько путей, значит в графе есть циклы. Но дерево – это граф без циклов.
0 |
|
0 / 0 / 0 Регистрация: 02.06.2014 Сообщений: 11 |
|
|
03.06.2014, 17:40 [ТС] |
6 |
|
К одной вершине ведет только один путь, просто листы могут быть на разной высоте.
0 |
|
Модератор 35326 / 19427 / 4065 Регистрация: 12.02.2012 Сообщений: 32,457 Записей в блоге: 13 |
|
|
03.06.2014, 17:47 |
7 |
|
Тогда нужно формулировать задачу по-другому: Найти в дереве лист минимальной высоты
0 |
|
0 / 0 / 0 Регистрация: 02.06.2014 Сообщений: 11 |
|
|
03.06.2014, 18:01 [ТС] |
8 |
|
я написала задание в том виде, в котором оно было нам дано. Но по сути нужно найти этот лист минимальной высоты, и результатом программы должна быть длина пути от корня до этого листа
0 |
|
Catstail Модератор 35326 / 19427 / 4065 Регистрация: 12.02.2012 Сообщений: 32,457 Записей в блоге: 13 |
||||
|
03.06.2014, 18:07 |
9 |
|||
|
Решение
Добавлено через 1 минуту
1 |
|
0 / 0 / 0 Регистрация: 02.06.2014 Сообщений: 11 |
|
|
03.06.2014, 18:10 [ТС] |
10 |
|
Спасибо большое! А программа результатом выдаст длину или этот самый лист?
0 |
|
Catstail Модератор 35326 / 19427 / 4065 Регистрация: 12.02.2012 Сообщений: 32,457 Записей в блоге: 13 |
||||
|
03.06.2014, 18:19 |
11 |
|||
|
РешениеПрограмма выдает лист. Но если чуть подправить, то выдаст (высоту, лист)
1 |
|
0 / 0 / 0 Регистрация: 02.06.2014 Сообщений: 11 |
|
|
12.06.2014, 17:37 [ТС] |
12 |
|
task tree = snd (foldl ( acc z -> if (fst z) < (fst acc) then z else acc) (head ls) (tail ls)) не могли бы вы объяснить, как работает эта строчка?
0 |
|
Mysterious Light 4163 / 2066 / 424 Регистрация: 19.07.2009 Сообщений: 3,125 Записей в блоге: 24 |
||||
|
12.06.2014, 18:06 |
13 |
|||
|
Давайте немного упростим аналогичную строку из последнего кода:
От Вами процитированного кода это отличается отсутствием ведущего snd. Суть в том, что здесь итеративно (см. описание foldl1) ищется такой элемент списка ls (объясните, что он выражает?), который обладает наименшей первой компоненты (что она выражает?).
2 |
|
Модератор 35326 / 19427 / 4065 Регистрация: 12.02.2012 Сообщений: 32,457 Записей в блоге: 13 |
|
|
12.06.2014, 19:40 |
14 |
|
Давайте немного упростим – на глаз стало длиннее…
0 |
|
Algiz 163 / 163 / 22 Регистрация: 23.02.2011 Сообщений: 347 |
||||
|
15.06.2014, 19:09 |
15 |
|||
|
Для любого количества потомков
1 |
Бинарное дерево поиска из 9 элементов
Бинарное дерево поиска (англ. binary search tree, BST) — структура данных для работы с упорядоченными множествами.
Бинарное дерево поиска обладает следующим свойством: если — узел бинарного дерева с ключом , то все узлы в левом поддереве должны иметь ключи, меньшие , а в правом поддереве большие .
Содержание
- 1 Операции в бинарном дереве поиска
- 1.1 Обход дерева поиска
- 1.2 Поиск элемента
- 1.3 Поиск минимума и максимума
- 1.4 Поиск следующего и предыдущего элемента
- 1.4.1 Реализация с использованием информации о родителе
- 1.4.2 Реализация без использования информации о родителе
- 1.5 Вставка
- 1.5.1 Реализация с использованием информации о родителе
- 1.5.2 Реализация без использования информации о родителе
- 1.6 Удаление
- 1.6.1 Нерекурсивная реализация
- 1.6.2 Рекурсивная реализация
- 2 Задачи о бинарном дереве поиска
- 2.1 Проверка того, что заданное дерево является деревом поиска
- 2.2 Задачи на поиск максимального BST в заданном двоичном дереве
- 2.3 Восстановление дерева по результату обхода preorderTraversal
- 3 См. также
- 4 Источники информации
Операции в бинарном дереве поиска
Для представления бинарного дерева поиска в памяти будем использовать следующую структуру:
struct Node: T key // ключ узла Node left // указатель на левого потомка Node right // указатель на правого потомка Node parent // указатель на предка
Обход дерева поиска
Есть три операции обхода узлов дерева, отличающиеся порядком обхода узлов:
- — обход узлов в отсортированном порядке,
- — обход узлов в порядке: вершина, левое поддерево, правое поддерево,
- — обход узлов в порядке: левое поддерево, правое поддерево, вершина.
func inorderTraversal(x : Node):
if x != null
inorderTraversal(x.left)
print x.key
inorderTraversal(x.right)
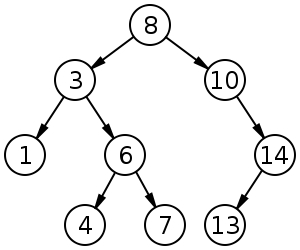
При выполнении данного обхода вершины будут выведены в следующем порядке: 1 3 4 6 7 8 10 13 14.
func preorderTraversal(x : Node)
if x != null
print x.key
preorderTraversal(x.left)
preorderTraversal(x.right)
При выполнении данного обхода вершины будут выведены в следующем порядке: 8 3 1 6 4 7 10 14 13.
func postorderTraversal(x : Node)
if x != null
postorderTraversal(x.left)
postorderTraversal(x.right)
print x.key
При выполнении данного обхода вершины будут выведены в следующем порядке: 1 4 7 6 3 13 14 10 8.
Данные алгоритмы выполняют обход за время , поскольку процедура вызывается ровно два раза для каждого узла дерева.
Поиск элемента
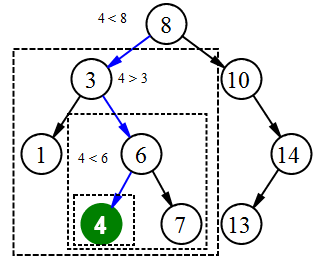
Поиск элемента 4
Для поиска элемента в бинарном дереве поиска можно воспользоваться следующей функцией, которая принимает в качестве параметров корень дерева и искомый ключ. Для каждого узла функция сравнивает значение его ключа с искомым ключом. Если ключи одинаковы, то функция возвращает текущий узел, в противном случае функция вызывается рекурсивно для левого или правого поддерева. Узлы, которые посещает функция образуют нисходящий путь от корня, так что время ее работы , где — высота дерева.
Node search(x : Node, k : T):
if x == null or k == x.key
return x
if k < x.key
return search(x.left, k)
else
return search(x.right, k)
Поиск минимума и максимума
Чтобы найти минимальный элемент в бинарном дереве поиска, необходимо просто следовать указателям от корня дерева, пока не встретится значение . Если у вершины есть левое поддерево, то по свойству бинарного дерева поиска в нем хранятся все элементы с меньшим ключом. Если его нет, значит эта вершина и есть минимальная. Аналогично ищется и максимальный элемент. Для этого нужно следовать правым указателям.
Node minimum(x : Node):
if x.left == null
return x
return minimum(x.left)
Node maximum(x : Node):
if x.right == null
return x
return maximum(x.right)
Данные функции принимают корень поддерева, и возвращают минимальный (максимальный) элемент в поддереве. Обе процедуры выполняются за время .
Поиск следующего и предыдущего элемента
Реализация с использованием информации о родителе
Если у узла есть правое поддерево, то следующий за ним элемент будет минимальным элементом в этом поддереве. Если у него нет правого поддерева, то нужно следовать вверх, пока не встретим узел, который является левым дочерним узлом своего родителя. Поиск предыдущего выполнятся аналогично. Если у узла есть левое поддерево, то предыдущий ему элемент будет максимальным элементом в этом поддереве. Если у него нет левого поддерева, то нужно следовать вверх, пока не встретим узел, который является правым дочерним узлом своего родителя.
Node next(x : Node):
if x.right != null
return minimum(x.right)
y = x.parent
while y != null and x == y.right
x = y
y = y.parent
return y
Node prev(x : Node):
if x.left != null
return maximum(x.left)
y = x.parent
while y != null and x == y.left
x = y
y = y.parent
return y
Обе операции выполняются за время .
Реализация без использования информации о родителе
Рассмотрим поиск следующего элемента для некоторого ключа . Поиск будем начинать с корня дерева, храня текущий узел и узел , последний посещенный узел, ключ которого больше .
Спускаемся вниз по дереву, как в алгоритме поиска узла. Рассмотрим ключ текущего узла . Если , значит следующий за узел находится в правом поддереве (в левом поддереве все ключи меньше ). Если же , то , поэтому может быть следующим для ключа , либо следующий узел содержится в левом поддереве . Перейдем к нужному поддереву и повторим те же самые действия.
Аналогично реализуется операция поиска предыдущего элемента.
Node next(x : T):
Node current = root, successor = null // root — корень дерева
while current != null
if current.key > x
successor = current
current = current.left
else
current = current.right
return successor
Вставка
Операция вставки работает аналогично поиску элемента, только при обнаружении у элемента отсутствия ребенка нужно подвесить на него вставляемый элемент.
Реализация с использованием информации о родителе
func insert(x : Node, z : Node): // x — корень поддерева, z — вставляемый элемент
while x != null
if z.key > x.key
if x.right != null
x = x.right
else
z.parent = x
x.right = z
break
else if z.key < x.key
if x.left != null
x = x.left
else
z.parent = x
x.left = z
break
Реализация без использования информации о родителе
Node insert(x : Node, z : T): // x — корень поддерева, z — вставляемый ключ if x == null return Node(z) // подвесим Node с key = z else if z < x.key x.left = insert(x.left, z) else if z > x.key x.right = insert(x.right, z) return x
Время работы алгоритма для обеих реализаций — .
Удаление
Нерекурсивная реализация
Для удаления узла из бинарного дерева поиска нужно рассмотреть три возможные ситуации. Если у узла нет дочерних узлов, то у его родителя нужно просто заменить указатель на . Если у узла есть только один дочерний узел, то нужно создать новую связь между родителем удаляемого узла и его дочерним узлом. Наконец, если у узла два дочерних узла, то нужно найти следующий за ним элемент (у этого элемента не будет левого потомка), его правого потомка подвесить на место найденного элемента, а удаляемый узел заменить найденным узлом. Таким образом, свойство бинарного дерева поиска не будет нарушено. Данная реализация удаления не увеличивает высоту дерева. Время работы алгоритма — .
| Случай | Иллюстрация |
|---|---|
| Удаление листа | 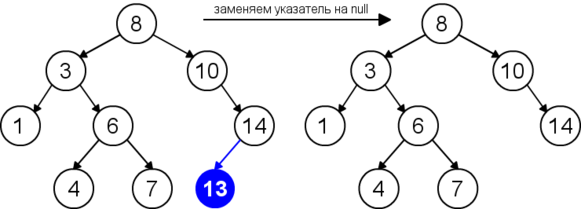
|
| Удаление узла с одним дочерним узлом | 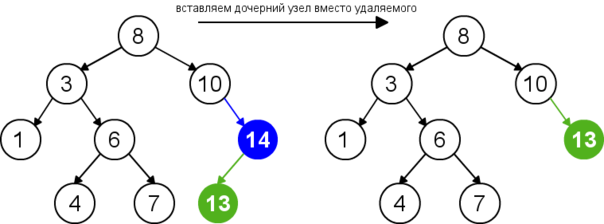
|
| Удаление узла с двумя дочерними узлами | 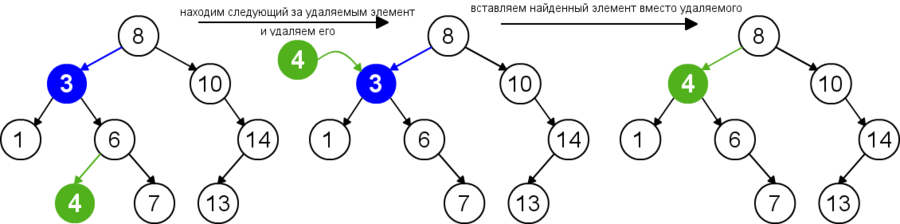
|
func delete(t : Node, v : Node): // — дерево, — удаляемый элемент p = v.parent // предок удаляемого элемента if v.left == null and v.right == null // первый случай: удаляемый элемент - лист if p.left == v p.left = null if p.right == v p.right = null else if v.left == null or v.right == null // второй случай: удаляемый элемент имеет одного потомка if v.left == null if p.left == v p.left = v.right else p.right = v.right v.right.parent = p else if p.left == v p.left = v.left else p.right = v.left v.left.parent = p else // третий случай: удаляемый элемент имеет двух потомков successor = next(v, t) v.key = successor.key if successor.parent.left == successor successor.parent.left = successor.right if successor.right != null successor.right.parent = successor.parent else successor.parent.right = successor.right if successor.right != null successor.right.parent = successor.parent
Рекурсивная реализация
При рекурсивном удалении узла из бинарного дерева нужно рассмотреть три случая: удаляемый элемент находится в левом поддереве текущего поддерева, удаляемый элемент находится в правом поддереве или удаляемый элемент находится в корне. В двух первых случаях нужно рекурсивно удалить элемент из нужного поддерева. Если удаляемый элемент находится в корне текущего поддерева и имеет два дочерних узла, то нужно заменить его минимальным элементом из правого поддерева и рекурсивно удалить этот минимальный элемент из правого поддерева. Иначе, если удаляемый элемент имеет один дочерний узел, нужно заменить его потомком. Время работы алгоритма — .
Рекурсивная функция, возвращающая дерево с удаленным элементом :
Node delete(root : Node, z : T): // корень поддерева, удаляемый ключ
if root == null
return root
if z < root.key
root.left = delete(root.left, z)
else if z > root.key
root.right = delete(root.right, z)
else if root.left != null and root.right != null
root.key = minimum(root.right).key
root.right = delete(root.right, root.key)
else
if root.left != null
root = root.left
else if root.right != null
root = root.right
else
root = null
return root
Задачи о бинарном дереве поиска
Проверка того, что заданное дерево является деревом поиска
| Задача: |
| Определить, является ли заданное двоичное дерево деревом поиска. |
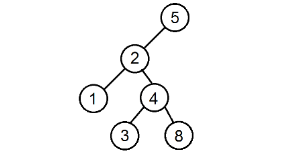
Пример дерева, для которого недостаточно проверки лишь его соседних вершин
Для того чтобы решить эту задачу, применим обход в глубину. Запустим от корня рекурсивную логическую функцию, которая выведет , если дерево является BST и в противном случае. Чтобы дерево не являлось BST, в нём должна быть хотя бы одна вершина, которая не попадает под определение дерева поиска. То есть достаточно найти всего одну такую вершину, чтобы выйти из рекурсии и вернуть значение . Если же, дойдя до листьев, функция не встретит на своём пути такие вершины, она вернёт значение .
Функция принимает на вход исследуемую вершину, а также два значения: и , которые до вызова функции равнялись и соответственно, где — очень большое число, т.е. ни один ключ дерева не превосходит его по модулю. Казалось бы, два последних параметра не нужны. Но без них программа может выдать неверный ответ, так как сравнения только вершины и её детей недостаточно. Необходимо также помнить, в каком поддереве для более старших предков мы находимся. Например, в этом дереве вершина с номером находится левее вершины, в которой лежит , чего не должно быть в дереве поиска, однако после проверки функция бы вернула .
bool isBinarySearchTree(root: Node): // Здесь root — корень заданного двоичного дерева. bool check(v : Node, min: T, max: T): // min и max — минимально и максимально допустимые значения в вершинах поддерева. if v == null return true if v.key <= min or max <= v.key return false return check(v.left, min, v.key) and check(v.right, v.key, max) return check(root, , )
Время работы алгоритма — , где — количество вершин в дереве.
Задачи на поиск максимального BST в заданном двоичном дереве
| Задача: |
| Найти в данном дереве такую вершину, что она будет корнем поддерева поиска с наибольшим количеством вершин. |
Если мы будем приведённым выше способом проверять каждую вершину, мы справимся с задачей за . Но её можно решить за , идя от корня и проверяя все вершины по одному разу, основываясь на следующих фактах:
- Значение в вершине больше максимума в её левом поддереве;
- Значение в вершине меньше минимума в её правом поддереве;
- Левое и правое поддерево являются деревьями поиска.
Введём и , которые будут хранить минимум в левом поддереве вершины и максимум в правом. Тогда мы должны будем проверить, являются ли эти поддеревья деревьями поиска и, если да, лежит ли ключ вершины между этими значениями и . Если вершина является листом, она автоматически становится деревом поиска, а её ключ — минимумом или максимумом для её родителя (в зависимости от расположения вершины). Функция записывает в количество вершин в дереве, если оно является деревом поиска или в противном случае. После выполнения функции ищем за линейное время вершину с наибольшим значением .
int count(root: Node): // root — корень заданного двоичного дерева.
int cnt(v: Node):
if v == null
v.kol = 0
return = 0
if cnt(v.left) != -1 and cnt(v.right) != -1
if v.left == null and v.right == null
v.min = v.key
v.max = v.key
v.kol = 1
return 1
if v.left == null
if v.right.max > v.key
v.min = v.key
v.kol = cnt(v.right) + 1
return v.kol
if v.right == null
if v.left.min < v.key
v.max = v.key
v.kol = cnt(v.left) + 1
return v.kol
if v.left.min < v.key and v.right.max > v.key
v.min = v.left.min
v.max = v.right.max
v.kol = v.left.kol + v.right.kol + 1
v.kol = cnt(v.left) + cnt(v.right) + 1
return v.kol
return -1
return cnt(root)
Алгоритм работает за , так как мы прошлись по дереву два раза за время, равное количеству вершин.
Восстановление дерева по результату обхода preorderTraversal
| Задача: |
| Восстановить дерево по последовательности, выведенной после выполнения процедуры . |
Восстановление дерева поиска по последовательности ключей
Как мы помним, процедура выводит значения в узлах поддерева следующим образом: сначала идёт до упора влево, затем на каком-то моменте делает шаг вправо и снова движется влево. Это продолжается до тех пор, пока не будут выведены все вершины. Полученная последовательность позволит нам однозначно определить расположение всех узлов поддерева. Первая вершина всегда будет в корне. Затем, пока не будут использованы все значения, будем последовательно подвешивать левых сыновей к последней добавленной вершине, пока не найдём номер, нарушающий убывающую последовательность, а для каждого такого номера будем искать вершину без правого потомка, хранящую наибольшее значение, не превосходящее того, которое хотим поставить, и подвешиваем к ней элемент с таким номером в качестве правого сына. Когда мы, желая найти такую вершину, встречаем какую-нибудь другую, уже имеющую правого сына, проходим по ветке вправо. Мы имеем на это право, так как если такая вершина стоит, то процедура обхода в ней уже побывала и поворачивала вправо, поэтому спускаться в другую сторону смысла не имеет. Вершину с максимальным ключом, с которой будем начинать поиск, будем запоминать. Она будет обновляться каждый раз, когда появится новый максимум.
Процедура восстановления дерева работает за .
Разберём алгоритм на примере последовательности .
Будем выделять красным цветом вершины, рассматриваемые на каждом шаге, чёрным жирным — их родителей, курсивом — убывающие подпоследовательности (в случаях, когда мы их рассматриваем) или претендентов на добавление к ним правого ребёнка (когда рассматривается вершина, нарушающая убывающую последовательность).
| Состояние
последовательности |
Действие | Пояснение |
|---|---|---|
| 8 2 1 4 3 5 | Делаем вершину корнем. | Первая вершина всегда будет корнем, так как вывод начинался с него. |
| 8 2 1 4 3 5 | Находим убывающую подпоследовательность. Каждую вершину подвешиваем к последней из взятых ранее в качестве левого сына. | Каждая последующая вершина становится левым сыном предыдущей, так как выводя ключи, мы двигались по дереву поиска влево, пока есть вершины. |
| 8 2 1 4 3 5 | ||
| 8 2 1 4 3 5 | Для вершины, нарушившей убывающую последовательность, ищем максимальное значение, меньшее его. В данном случае оно равно . Затем добавляем вершину. | На моменте вывода следующего номера процедура обратилась уже к какому-то из правых поддеревьев, так как влево идти уже некуда. Значит, нам необходимо найти узел, для которого данная вершина являлась бы правым сыном. Очевидно, что в её родителе не может лежать значение, которое больше её ключа. Но эту вершину нельзя подвесить и к меньшим, иначе нашёлся бы более старший предок, также хранящий какое-то значение, которое меньше, чем в исследуемой. Для этого предка вершина бы попала в левое поддерево. И тогда возникает противоречие с определением дерева поиска. Отсюда следует, что родитель определяется единственным образом — он хранит максимум среди ключей, не превосходящих значения в подвешиваемой вершине, что и требовалось доказать. |
| 8 2 1 4 3 5 | Находим убывающую подпоследовательность. Каждую вершину подвешиваем к последней из взятых ранее в качестве левого сына. | Зайдя в правое поддерево, процедура обхода снова до упора начала двигаться влево, поэтому действуем аналогичным образом. |
| 8 2 1 4 3 5 | Для этой вершины ищем максимальное значение, меньшее его. Затем добавляем вершину. | Здесь процедура снова обратилась к правому поддереву. Рассуждения аналогичны. Ключ родителя этой вершины равен . |
См. также
- Поисковые структуры данных
- Рандомизированное бинарное дерево поиска
- Красно-черное дерево
- АВЛ-дерево
Источники информации
- Википедия — Двоичное дерево поиска
- Wikipedia — Binary search tree
- Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4
От обхода в ширину к алгоритму Дейкстры
Время на прочтение
9 мин
Количество просмотров 77K
Вместо введения
Разбирал свои старые, так сказать, «заметки», и наткнулся на эту. У меня же еще нет инвайта на хабре, подумал я, и решил опубликовать. В этой статье я расскажу, как разобраться в алгоритме Дейкстры поиска кратчайших путей из данной вершины в графе. При чем я приду к нему естественным образом от алгоритма обхода графа в ширину.
В комментариях попросили рассказать подробнее о структуре данных, скрывающейся за priority_queue в STL C++. В конце статьи приводится краткий рассказ и ее реализация.
Обход графа в ширину
Первый алгоритм, который хотелось бы описать, и который однозначно нельзя пропустить — это обход графа в ширину. Что же это такое? Давайте немного отойдем от формального описания графов, и представим себе такую картину. Выложим на земле веревки, пропитанные чем-нибудь горючим, одинаковой длины так, чтобы ни одна из них не пересекалась, но некоторые из них касались концами друг с другом. А теперь подожжем один из концов. Как будет вести себя огонь? Он равномерно будет перекидываться по веревкам на соседние пересечения, пока не загорится все. Нетрудно обобщить эту картину и на трехмерное пространство. Именно так в жизни будет выглядеть обход графа в ширину. Теперь опишем более формально. Пусть мы начали обход в ширину из какой-то вершины V. В следующий момент времени мы будем просматривать соседей вершины V (соседом вершины V назовем вершины, имеющий общее ребро с V). И так до тех пор, пока все вершины в графе не будут просмотрены.
Реализация обхода в ширину
Пусть мы находимся в какой-то вершине в процессе обхода в ширину, тогда воспользуемся очередью, в которую будем добавлять всех соседей вершины, исключая те, в которых мы уже побывали.
void bfs(int u) {
used[u] = true;
queue<int> q;
q.push(u);
while (!q.empty()) {
int u = q.front();
q.pop();
for (int i = 0; i < (int) g[u].size(); i++) {
int v = g[u][i];
if (!used[v]) {
used[v] = true;
q.push(v);
}
}
}
}
В этой реализации g — это список смежных вершин, т.е. в g[u] лежит список смежных вершин с u(в качестве списка использован std::vector), used — это массив, который позволяет понять, в каких вершинах мы уже побывали. Здесь обход в ширину не делает ничего, кроме самого обхода в ширину. Казалось бы, зачем? Однако его можно легко модифицировать для того, чтобы искать то, что нам нужно. Например расстояние и путь от какой-либо вершины до всех остальных. Следует заметить, что ребра не имеют веса, т.е. граф не взвешенный. Приведем реализацию поиска расстояний и путей.
void bfs(int u) {
used[u] = true;
p[u] = u;
dist[u] = 0;
queue<int> q;
q.push(u);
while (!q.empty()) {
int u = q.front();
q.pop();
for (int i = 0; i < (int) g[u].size(); i++) {
int v = g[u][i];
if (!used[v]) {
used[v] = true;
p[v] = u;
dist[v] = dist[u] + 1;
q.push(v);
}
}
}
}
Здесь p — это массив предков, т.е. в p[v] лежит предок вершины v, dist[v] — это расстояние от вершины из которой мы начинали обход, до вершины v. Как восстановить путь? Это сделать довольно легко, просто пройдя по массиву предков нужной нам вершины. Например, рекурсивно:
void print_way(int u) {
if (p[u] != u) {
print_way(p[u]);
}
cout << u << ' ';
}
Кратчайшие пути
Все дальнейшие рассуждения будут верны только если веса ребер не отрицательны.
Теперь перейдем к взвешенным графам, т.е. ребра графа имеют вес. Например длина ребра. Или плата за проход по нему. Или время, которое требуется для прохода по нему. Задача — найти кратчайший путь из одной вершины, в какую-нибудь другую. В этой статье я буду отталкиваться от обхода в ширину, не помню, чтобы видел такой подход где-нибудь еще. Возможно я это пропустил. Итак, давайте посмотрим еще раз на реализацию обхода в ширину, а конкретно на условие добавления в очередь. В обходе в ширину мы добавляем в очередь только те вершины, в которых мы еще не были. Теперь же изменим это условие и будем добавлять те вершины, расстояние до которых можно уменьшить. Очевидно, что очередь опустеет тогда и только тогда, когда не останется ни одной вершины, до которой можно уменьшить расстояние. Процесс уменьшения пути из вершины V, назовем релаксацией вершины V.
Следует заметить, что изначально путь до всех вершин равен бесконечности(за бесконечность возьмем какую-нибудь достаточно большую величину, а именно: такую, что ни один путь не будет иметь длины, большей величины бесконечности). Этот алгоритм напрямую следует из обхода в ширину, и именно до него я дошел сам, когда решал первую в жизни задачу на кратчайшие пути в графе. Стоит упомянуть, что такой способ ищет кратчайший пути от вершины, из которой мы начали алгоритм, до всех остальных. Приведу реализацию:
const int INF = 1e+9;
vector< pair<int, int> > g[LIM]; // В g[u] лежит список пар: (длина пути между вершиной u и v, вершина v)
void shortcut(int u) {
fill(dist, dist + n, INF);
dist[u] = 0;
p[u] = u;
queue<int> q;
q.push(u);
while (!q.empty()) {
int u = q.front();
q.pop();
for (int i = 0; i < (int) g[u].size(); i++) {
int v = g[u][i].second, len = g[u][i].first;
if (dist[v] > dist[u] + len) {
p[v] = u;
dist[v] = dist[u] + len;
q.push(v);
}
}
}
}
Почему храним в списке смежности именно такие пары? Чуть позже станет понятно, когда мы усовершенствуем этот алгоритм, но, честно говоря, для данной реализации пары можно хранить и наоборот. Можно немного улучшить добавление в очередь. Для этого стоит завести массив bool, в котором будем помечать, находится ли сейчас вершина, которою нужно прорелаксировать, в очереди.
const int INF = 1e+9;
vector< pair<int, int> > g[LIM];
bool inque[LIM];
void shortcut(int u) {
fill(dist, dist + n, INF);
dist[u] = 0;
p[u] = u;
queue<int> q;
q.push(u);
inque[u] = true;
while (!q.empty()) {
int u = q.front();
q.pop();
inque[u] = false;
for (int i = 0; i < (int) g[u].size(); i++) {
int v = g[u][i].second, len = g[u][i].first;
if (dist[v] > dist[u] + len) {
p[v] = u;
dist[v] = dist[u] + len;
if (!inque[v]) {
q.push(v);
inque[v] = true;
}
}
}
}
}
Если присмотреться, то этот алгоритм очень похож на алгоритм Левита, но все-таки это не он, хотя в худшем случае работает за ту же асимптотику. Давайте грубо оценим это. В худшем случае нам придется проводить релаксацию каждый раз, когда мы проходим по какому-либо ребру. Итого O(n * m). Оценка довольно грубая, но на начальном этапе этого вполне хватит. Стоит так же заметить, что это именно худший случай, а на практике даже такая реализация работает довольно быстро. А теперь, самое интересное!… барабанная дробь… Улучшим наш алгоритм до алгоритма Дейксты!
Алгоритм Дейкстры
Первая оптимизация, которая приходит на ум. А давайте релаксировать те вершины, путь до которой сейчас минимальный? Собственно, именно эта идея и пришла мне в один прекрасный день в голову. Но, как оказалось, эта идея пришла первому далеко не мне. Первому она пришла замечательному ученому Эдсгеру Дейкстре. Более того, именно он доказал, что выбирая вершину для релаксации таким образом, мы проведем релаксацию не более, чем n раз! На интуитивном уровне понятно, что если до какой-то вершины путь сейчас минимальный, то еще меньше сделать его мы не сможем. Более формально можно прочитать здесь или на Википедии .
Теперь дело осталось за малым, понять как эффективно искать вершину с минимальным расстоянием до нее. Для этого воспользуемся очередью с приоритетами (куча, heap). В stl есть класс, который реализует ее и называется priority_queue. Приведу реализацию, которая, опять же, напрямую следует из предыдущего(описанного в этой статье) алгоритма.
void dijkstra(int u) {
fill(dist, dist + n, INF);
dist[u] = 0;
p[u] = u;
priority_queue< pair<int, int>, vector< pair<int, int> >, greater< pair<int, int> > > q;
q.push(make_pair(0, u));
while (!q.empty()) {
pair<int, int> u = q.top();
q.pop();
if (u.first > dist[u.second]) continue;
for (int i = 0; i < (int) g[u.second].size(); i++) {
int v = g[u.second][i].second, len = g[u.second][i].first;
if (dist[v] > dist[u.second] + len) {
p[v] = u.second;
dist[v] = dist[u.second] + len;
q.push(make_pair(dist[v], v));
}
}
}
}
Скорее всего не совсем понятно, что здесь происходит. Начнем с объявления очереди с приоритетами. Здесь первый аргумент шаблона — данные, которые хранятся в очереди, а конкретно пары вида (расстояние до вершины, номер вершины), второй аргумент шаблона — это контейнер, в котором будут храниться данные, третий аргумент, компаратор(находится, кстати, в заголовочном файле functional). Почему нам нужен какой-то другой компаратор? Потому что при стандартном объявлении priority_queue< pair<int, int> >, доставать получится только те вершины, расстояние до которых максимально, а нам-то нужно совсем наоборот. Асимптотика такого решения поставленной задачи O(n * log(n) + m * log(n)).
Действительно, всего у нас n релаксаций, а вершину с минимальной длиной пути до нее, мы ищем за log(n) (именно такая асимптотика у стандартной очереди с приоритетами stl). Так же следует заметить, что у нас может получится так, что мы добавили в очередь одну и ту же вершину, но с разными путями до нее. Например, мы провели релаксацию из вершины A, у которой в соседях вершина C, а потом провели релаксацию из вершины B, у которой так же в соседях вершина C, для ухода от проблем, связанных с этим, будем просто пропускать те вершины, которые мы достали из очереди, но расстояние из очереди до которых не актуально, т.е. больше, чем текущее кратчайшее. Для этого в реализации присутствует строчка if (u.first > dist[u.second]) continue;.
Вместо заключения
Оказалось, что на самом деле очень легко писать Дейкстру за O(n * log(n) + m * log(n))!
Дополнение
В комментариях попросили рассказать, как можно реализовать своими руками priority_queue.
Пусть перед нами стоит следующая задача (как в алгоритме Дейкстры).
Нужно поддерживать структуру данных, которая удовлетворяет следующим требованиям:
1) Добавление не более, чем за O(log(n)) времени.
2) Удаление минимального элемента не более, чем за O(log(n)) времени.
3) Поиск минимума за O(1) времени.
Оказывается, что этим требованиям удовлетворяет структура данных, которую в русско-язычной литературе обычно называют «куча», в англо-язычной «heap» или «priority queue».
Вообще говоря, куча — это дерево. Давайте рассмотрим свойства этого дерева подробнее. Пусть у нас уже построена куча, тогда определим ее следующим образом — для каждой вершины в куче верно, что элемент в этой вершине не больше, чем элементы в ее потомках. Тогда в корне дерева лежит минимальный элемент, что позволяет нам в дальнейшем искать минимум за O(1).
Теперь доопределим нашу кучу так, чтобы и остальные свойства выполнялись. Назовем уровнем вершины в дереве расстояние от корня до нее. Запретим добавлять новый уровень в куче, до тех пор пока не заполнен целиком предыдущий. Более формально: пусть текущая максимальная высота дерева H, тогда запрещено добавлять вершины на высоту H + 1, пока есть возможность добавить ее на высоту H. Действительно, при таких условиях высота кучи всегда не более, чем O(log(n)).
Осталось научиться добавлять и удалять элементы в кучу.
Реализовывать кучу будем на бинарном дереве, в котором будет не более одной вершины с количеством потомков меньшим двух. Дерево будем хранить в массиве, тогда потомки вершины на позиции pos, будут лежать на позициях 2 * pos и 2 * pos + 1, а родитель будет лежать на позиции pos / 2.
Добавлять элемент будем на первое возможное вакантное место на текущем максимальном уровне, затем выполнять операцию, которая называется «просеивание вверх». Это значит, что пока родитель добавленного элемента больше, чем сам элемент, то поменять позиции добавленного элемента и родителя, повторять рекурсивно до корня. Докажем, что при этом не нарушаются свойства кучи. Это просто, так как текущий элемент меньше, чем родитель, то он так же и меньше, чем все потомки родителя.
void push(const value_t& value) {
data.push_back(value);
sift_up(data.size() - 1);
}
void sift_up(size_t position) {
size_t parent_position = position / 2;
if (!cmp(data[position], data[parent_position])) {
swap(data[position], data[parent_position]);
sift_up(parent_position);
}
}
Удалять минимальный элемент будем следующим образом: сначала поменяем местами корень дерева с последним элементом на максимальном уровне, затем удалим вершину, в которой был этот элемент (теперь там будет минимум). Свойства кучи после этого нарушатся, а чтобы их восстановить нужно выполнить операцию, которая называется «просеивание вниз». Начинаем от корня рекурсивно: для текущего элемента находим из потомков минимальный, меняем местами с текущим элементом, рекурсивно запускаемся для вершины, с которой поменяли текущий элемент. Заметим, что после этой операции, свойства кучи выполняются.
void pop() {
swap(data[1], data.back());
data.pop_back();
sift_down(1);
}
void sift_down(size_t position) {
size_t cmp_position = position;
if (2 * position < data.size() && !cmp(data[2 * position], data[cmp_position])) {
cmp_position = 2 * position;
}
if (2 * position + 1 < data.size() && !cmp(data[2 * position + 1], data[cmp_position])) {
cmp_position = 2 * position + 1;
}
if (cmp_position != position) {
swap(data[cmp_position], data[position]);
sift_down(cmp_position);
}
}
Так как высота дерева O(log(n)), то добавление и удаление будет работать за O(log(n)).
Весь код
template<typename value_t, typename cmp_t>
class heap_t {
public:
heap_t() :
data(1) {
}
bool empty() const {
return data.size() == 1;
}
const value_t& top() const {
return data[1];
}
void push(const value_t& value) {
data.push_back(value);
sift_up(data.size() - 1);
}
void pop() {
swap(data[1], data.back());
data.pop_back();
sift_down(1);
}
private:
void sift_up(size_t position) {
size_t parent_position = position / 2;
if (!cmp(data[position], data[parent_position])) {
swap(data[position], data[parent_position]);
sift_up(parent_position);
}
}
void sift_down(size_t position) {
size_t cmp_position = position;
if (2 * position < data.size() && !cmp(data[2 * position], data[cmp_position])) {
cmp_position = 2 * position;
}
if (2 * position + 1 < data.size() && !cmp(data[2 * position + 1], data[cmp_position])) {
cmp_position = 2 * position + 1;
}
if (cmp_position != position) {
swap(data[cmp_position], data[position]);
sift_down(cmp_position);
}
}
cmp_t cmp;
vector<value_t> data;
};
This problem is pretty much equivalent to the minimum sum subsequence problem, and can be solved in a similar manner by dynamic programming.
We will calculate the following arrays by using DF searches:
dw1[i] = minimum sum achievable by only using node i and its descendants.
pw1[i] = predecessor of node i in the path found for dw1[i].
dw2[i] = second minimum sum achevable by only using node i and its descendants,
a path that is edge-disjoint relative to the path found for dw1[i].
If you can calculate these, take min(dw1[k], dw1[k] + dw2[k]) over all k. This is because your path will take one of these basic shapes:
k k
| or /
| /
|
All of which are covered by the sums we’re taking.
Calculating dw1
Run a DFS from the root node. In the DFS, keep track of the current node and its father. At each node, assume its children are d1, d2, ... dk. Then dw1[i] = min(min{dw1[d1] + cost[i, d1], dw1[d2] + cost[i, d2], ..., dw1[dk] + cost[i, dk]}, min{cost[i, dk]}). Set dw1[i] = 0 for leaf nodes. Don’t forget to update pw1[i] with the selected predecessor.
Calculating dw2
Run a DFS from the root node. Do the same thing you did for dw1, except when going from a node i to one of its children k, only update dw2[i] if pw1[i] != k. You call the function recursively for all children however. It would look something like this in pseudocode:
df(node, father)
dw2[node] = inf
for all children k of node
df(k, node)
if pw1[node] != k
dw2[node] = min(dw2[node], dw1[k] + cost[node, k], cost[node, k])
Теги: Двоичное дерево поиска. БДП. Итреативные алгоритмы работы с двоичным деревом поиска.
Двоичное дерево поиска. Итеративная реализация.
Двоичные деревья – это структуры данных, состоящие из узлов, которые хранят значение, а также ссылку на свою левую и правую ветвь. Каждая ветвь, в свою очередь, является деревом.
Узел, который находится в самой вершине дерева принято называть корнем (root), узлы, находящиеся в самом низу дерева и не имеющие потомков называют листьями (leaves).
Ветви узла называют потомками (descendants). По отношению к своим потомкам узел является родителем (parent) или предком (ancestor). Также, развивая аналогию, имеются сестринские узлы (siblings – родные братья или сёстры) – узлы с общим родителем. Аналогично, у узла могут быть дяди (uncle nodes) и дедушки и бабушки (grandparent nodes). Такие названия помогают понимать различные алгоритмы.
Двоичное дерево. На этом рисунке узел 10 корень, 7 и 12 его наследники. 6, 9, 11, 14 – листья. 7 и 12, также как и 6 и 9 являются сестринскими узлами, 10 – это дедушка узла 6, а 12 – дядя узла 6 и узла 9
Двоичные деревья одна из самых простых структур (по сравнению, например, с другими деревьями). Они обычно реализуют самый базовый и самый естественный способ классификации элементов – делят их по определённому признаку, размещая одну группу в левом поддереве, а другую группу в правом. В поддеревьях рекурсивно поддерживается такой же порядок, за счёт чего узлы дерева упорядочиваются.
Двоичное дерево поиска (далее ДДП) – это несбалансированное двоичное дерево, в котором элементы БОЛЬШЕ корневого размещаются справа, а элементы, которые МЕНЬШЕ размещаются слева.
Такое размещение – слева меньше, справа больше – не обязательно, можно располагать элементы, которые меньше, справа. Отношение БОЛЬШЕ и МЕНЬШЕ – это не обязательно естественная сортировка по величине, это некоторая бинарная операция, которая позволяет разбить элементы на две группы.
Для реализации бинарного дерева поиска будем использовать структуру Node, которая содержит значение, ссылку на правое и левое поддерево, а также ссылку на родителя. Ссылка на родительский узел, в принципе, не является обязательной, однако сильно упрощает и ускоряет все алгоритмы. Далее, ради тренировки, мы ещё рассмотрим реализацию без ссылки на родителя.
ЗАМЕЧАНИЕ: мы рассматриваем случай, когда в дереве все значения разные и не равны NULL. Деревья с повторяющимися узлами рассмотрим позднее.
Обычно в качестве типа данных мы используем void* и далее передаём функции сравнения через указатели. В этот раз будем использовать пользовательский тип и макросы.
typedef int T;
#define CMP_EQ(a, b) ((a) == (b))
#define CMP_LT(a, b) ((a) < (b))
#define CMP_GT(a, b) ((a) > (b))
typedef struct Node {
T data;
struct Node *left;
struct Node *right;
struct Node *parent;
} Node;
Сначала, как обычно, напишем функцию, которая создаёт новый узел. Она принимает в качестве аргументов значение и указатель на своего родителя. Корневой элемент не имеет родителя, значение указателя parent равно NULL.
Node* getFreeNode(T value, Node *parent) {
Node* tmp = (Node*) malloc(sizeof(Node));
tmp->left = tmp->right = NULL;
tmp->data = value;
tmp->parent = parent;
return tmp;
}
Разберёмся со вставкой. Возможны следующие ситуации
- 1) Дерево пустое. В этом случае новый узел становится корнем ДДП.
- 2) Новое значение меньше корневого. В этом случае значение должно быть вставлено слева. Если слева уже стоит элемент, то повторяем эту же операцию, только в качестве корневого узла рассматриваем левый узел. Если слева нет элемента, то добавляем новый узел.
- 3) Новое значение больше корневого. В этом случае новое значение должно быть вставлено справа. Если справа уже стоит элемент, то повторяем операцию, только в качестве корневого рассматриваем правый узел. Если справа узла нет, то вставляем новый узел.
Пусть нам необходимо поместить в ДДП следующие значения
10 7 9 12 6 14 11 3 4
Первое значение становится корнем.
Дерево с одним узлом. Равных NULL потомков не рисуем
Второе значение меньше десяти, так что оно помещается слева.
Если значение меньше, то помещаем его слева
Число 9 меньше 10, так что узел должен располагаться слева, но слева уже стоит значение. 9 больше 7, так что новый узел становится правым потомком семи.
Двоичное дерево поиска после добавления узлов 10, 7, 9
Число 12 помещается справа от 10.
6 меньше 10 и меньше 7…
Добавляем оставшиеся узлы 14, 3, 4, 11
Добавили последовательно 10, 7, 9, 12, 6, 14, 3, 11, 4
Функция, добавляющая узел в дерево
Два узла. Первый – вспомогательная переменная, чтобы уменьшить писанину, второй – тот узел, который будем вставлять.
Node *tmp = NULL; Node *ins = NULL;
Проверяем, если дерево пустое, то вставляем корень
if (*head == NULL) {
*head = getFreeNode(value, NULL);
return;
}
Проходим по дереву и ищем место для вставки
tmp = *head;
Пока не дошли до пустого узла
while (tmp) {
Если значение больше, чем значение текущего узла
if (CMP_GT(value, tmp->data)) {
Если при этом правый узел не пустой, то за корень теперь считаем правую ветвь и начинаем цикл сначала
if (tmp->right) {
tmp = tmp->right;
continue;
Если правой ветви нет, то вставляем узел справа
} else {
tmp->right = getFreeNode(value, tmp);
return;
}
Также обрабатываем левую ветвь
} else if (CMP_LT(value, tmp->data)) {
if (tmp->left) {
tmp = tmp->left;
continue;
} else {
tmp->left = getFreeNode(value, tmp);
return;
}
} else {
exit(2);
}
}
Весь код
void insert(Node **head, int value) {
Node *tmp = NULL;
Node *ins = NULL;
if (*head == NULL) {
*head = getFreeNode(value, NULL);
return;
}
tmp = *head;
while (tmp) {
if (CMP_GT(value, tmp->data)) {
if (tmp->right) {
tmp = tmp->right;
continue;
} else {
tmp->right = getFreeNode(value, tmp);
return;
}
} else if (CMP_LT(value, tmp->data)) {
if (tmp->left) {
tmp = tmp->left;
continue;
} else {
tmp->left = getFreeNode(value, tmp);
return;
}
} else {
exit(2);
}
}
}
Рассмотрим результат вставки узлов в дерево. Очевидно, что структура дерева будет зависеть от порядка вставки элементов. Иными словами, форма дерева зависит от порядка
вставки элементов.
Если элементы не упорядочены и их значения распределены равномерно, то дерево будет достаточно сбалансированным, то есть путь от вершины до всех листьев будет одинаковый.
В таком случае максимальное время доступа до листа равно log(n), где n – это число узлов, то есть равно высоте дерева.
Но это только в самом благоприятном случае. Если же элементы упорядочены, то дерево не будет сбалансировано и растянется в одну сторону, как список; тогда
время доступа до последнего узла будет порядка n. Это слабая сторона ДДП, из-за чего применение этой структуры ограничено.
Дерево, которое получили вставкой чередующихся возрастающей и убывающей последовательностей (слева) и полученное при вставке упорядоченной последовательности (справа)
Для решения этой проблемы можно производить балансировку дерева, или использовать структуры, которые автоматически проводят самобалансировку во время вставки и удаления.
Поиск в дереве
Известно, что слева от узла располагается элемент, который меньше чем текущий узел. Из чего следует, что если у узла нет левого наследника, то он является минимумом в дереве.
Таким образом, можно найти минимальный элемент дерева
Node* getMinNode(Node *root) {
while (root->left) {
root = root->left;
}
return root;
}
Аналогично, можно найти максимальный элемент
Node* getMaxNode(Node *root) {
while (root->right) {
root = root->right;
}
return root;
}
Опять же, если дерево хорошо сбалансировано, то поиск минимума и максимума будет иметь сложность порядка log(n), а в случае плохой балансировки стремится к n.
Поиск нужного узла по значению похож на алгоритм бинарного поиска в отсортированном массиве. Если значения больше узла, то продолжаем поиск в правом поддереве, если меньше, то продолжаем в левом. Если узлов уже нет, то элемент не содержится в дереве.
Node *getNodeByValue(Node *root, T value) {
while (root) {
if (CMP_GT(root->data, value)) {
root = root->left;
continue;
} else if (CMP_LT(root->data, value)) {
root = root->right;
continue;
} else {
return root;
}
}
return NULL;
}
Удаление узла
Существует три возможных ситуации.
- 1) У узла нет наследников (удаляем лист). Тогда он просто удаляется, а его родитель обнуляет указатель на него.
Просто исключаем его из дерева
- 2) У узла один наследник. В этом случае узел подменяется своим наследником.
- 3) У узла оба наследника. В этом случае узел не удаляем, а заменяем его значение на максимум левого поддерева. После этого удаляем максимум левого поддерева. (Напомню, что мы условились, что слева элементы меньше корневого).
У узла 7 два наследника. Находим максимум его левого поддерева (это 6)
Узел не удаляем, а копируем на его место значение максимума левого поддерева и удаляем этот узел
Копируем на его место единственного наследника
Максимум левого поддерева имеет не более одного наследника, так что он удаляется просто. Известно, что все значения слева от корня меньше корня. Соответственно, максимум левого поддерева будет, с одной стороны, больше всех элементов левого поддерева, с другой стороны меньше всех значений правого поддерева.
Наша функция будет принимать в качестве аргумента узел, который необходимо удалить.
if (target->left && target->right) {
//Оба наследника есть
} else if (target->left) {
//Есть только левый наследник
} else if (target->right) {
//Есть только правый наследник
} else {
//Нет наследников
}
free(target);
Если нет наследников, то нужно узнать, каким поддеревом относительно родителя является узел
if (target == target->parent->left) {
target->parent->left = NULL;
} else {
target->parent->right = NULL;
}
Если есть только правый или только левый наследник, подменяем наследником удаляемый узел. Перед этим нужно узнать, правым или левым наследником является удаляемый узел.
if (target == target->parent->left) {
target->parent->left = target->left;
} else {
target->parent->right = target->left;
}
или
if (target == target->parent->right) {
target->parent->right = target->right;
} else {
target->parent->left = target->right;
}
Если оба наследника, то сначала находим максимум левого поддерева
Node *localMax = findMaxNode(target->left);
Затем подменяем значение удаляемого узла на него
target->data = localMax->data;
После чего удаляем этот узел
removeNodeByPtr(localMax); return;
Здесь мы использовали рекурсию, хотя я обещал этого не делать. Вызов будет всего один, так как известно, что максимум не содержит обоих наследников и является правым наследником
своего родителя. Если хотите заменить вызов функции, то придётся скопировать оставшийся код.
Весь код
void removeNodeByPtr(Node *target) {
if (target->left && target->right) {
Node *localMax = findMaxNode(target->left);
target->data = localMax->data;
removeNodeByPtr(localMax);
return;
} else if (target->left) {
if (target == target->parent->left) {
target->parent->left = target->left;
} else {
target->parent->right = target->left;
}
} else if (target->right) {
if (target == target->parent->right) {
target->parent->right = target->right;
} else {
target->parent->left = target->right;
}
} else {
if (target == target->parent->left) {
target->parent->left = NULL;
} else {
target->parent->right = NULL;
}
}
free(target);
}
Упростим работу и сделаем обёртку вокруг функции, чтобы она удаляла узел по значению
void deleteValue(Node *root, T value) {
Node *target = getNodeByValue(root, value);
removeNodeByPtr(target);
}
Для проверки можно ввести функцию печати дерева. Так как мы ещё не научились обходить деревья, вывод осавляет желать лучшего.
void printTree(Node *root, const char *dir, int level) {
if (root) {
printf("lvl %d %s = %dn", level, dir, root->data);
printTree(root->left, "left", level+1);
printTree(root->right, "right", level+1);
}
}
Проверка
void main() {
Node *root = NULL;
insert(&root, 10);
insert(&root, 12);
insert(&root, 8);
insert(&root, 9);
insert(&root, 7);
insert(&root, 3);
insert(&root, 4);
printTree(root, "root", 0);
printf("max = %dn", findMaxNode(root)->data);
printf("min = %dn", findMinNode(root)->data);
deleteValue(root, 4);
printf("parent of 7 is %dn", getNodeByValue(root, 7)->parent->data);
printTree(root, "root", 0);
deleteValue(root, 8);
printTree(root, "root", 0);
printf("------------------n");
deleteValue(root, 10);
printTree(root, "root", 0);
getch();
}
Q&A
Всё ещё не понятно? – пиши вопросы на ящик
Кольцевой двусвязный список

 Сообщение было отмечено Rozumnaya как решение
Сообщение было отмечено Rozumnaya как решение