Как найти минимальный угол треугольника - Сайт, где вы сможете решить свои вопросы

Как найти меньший угол данного треугольника?

В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла = 39гр. Как найти меньший угол данного треугольника?

Пусть ABC – треугольник, и угол B – ппрямой.
Пусть BL – высота, проведенная из вершины прямого угла B,
BM – бисектриса, проведенная из угла B, при этом на стороне АС
точки находятся в таком порядке: A, L, M, C
Начертите такой треугольник, чтобы было понятнее.

Имеем – угол ABM = 45. угол MBC = 45 ( так как BM – биссектриса угла ABC)
Угол LBM = 39 гр (по условию)

Поэтому угол LBC = угол LBM + угол MBC = 39 гр + 45 гр = 84 гр
Но в прямоугольном треугольнике LBC сумма
угол LBC + угол BCL = 90 гр
Но угол LBC = 84 гр, следовательо угол BCL = 6 гр
Угол BCL – есть угол BCA нашего треугольника ABC

Угол LBA = угол MBA – угол LBM = 45 гр – 39 гр =6 гр
Но в прямоугольном треугольнике LBA сумма
угол LBA + угол BAL = 90 гр
Но угол LBA = 6 гр, следовательо угол BAL = 84 гр
Угол BAL – есть угол BAC нашего треугольника ABC

Итак, углы заданного треугольника ABC
угол BCA = 6 гр, угол BAC = 84 гр
Наименьший угол BCA = 6 гр.

Остроугольный, прямоугольный и тупоугольный треугольники.

Виды треугольников

Остроугольный треугольник — это треугольник,
в котором все углы острые.

Прямоугольный треугольник — это треугольник,
в котором один из углов прямой.

Тупоугольный треугольник — это треугольник,
в котором один из углов тупой.

Как определить вид треугольника

Для того, чтобы понять какой треугольник — остроугольный, прямоугольный или тупоугольный
нужно знать какая градусная мера у углов в треугольнике.

Если один из углов в треугольнике прямой, значит треугольник прямоугольный. Все углы острые в треугольнике — значит треугольник остроугольный. Если в треугольнике один из углов тупой, значит треугольник тупоугольный.

В произвольном треугольнике все углы острые, или два угла острые, а третий прямой или тупой. Если в треугольнике вам известно, что один углов тупой или прямой, значит сумма двух других углов не больше 90 градусов.

В прямоугольном треугольнике стороны напротив острых углов называются катетами, а сторона напротив прямого угла называется гипотенузой.

Градусные меры острого, тупого, прямого углов в треугольниках

Чтобы понять как называется угол и как называется треугольник с этими углами — надо знать его градусную меру:

Острый угол в любом из треугольников не больше 90 градусов.
Прямой угол в любом из треугольников равен 90 градусам.
Тупой угол в любом из треугольников больше 90 градусов, но меньше 180 градусов.

Свойства сторон и углов треугольника

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.

a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Сумма углов треугольника равна 180°

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Величина большего угла треугольника не может быть меньшей, чем 60°.

где α – больший угол треугольника.

Величина меньшего угла треугольника не может быть большей, чем 60°.

где β – меньший угол треугольника.

Фигура	Рисунок	Формулировка
Треугольник
Большая сторона треугольника		Против большей стороны треугольника лежит больший угол
Больший угол треугольника	Против большего угла треугольника лежит большая сторона
Меньшая сторона треугольника		Против меньшей стороны треугольника лежит меньший угол
Меньший угол треугольника	Против меньшего угла треугольника лежит меньшая сторона
Длины сторон треугольника
Углы треугольника
Внешний угол треугольника
Больший угол треугольника
Меньший угол треугольника
Теорема косинусов
Теорема синусов

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Сумма углов треугольника равна 180°

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Величина большего угла треугольника не может быть меньшей, чем 60°.

где α – больший угол треугольника.

Величина меньшего угла треугольника не может быть большей, чем 60°.

где β – меньший угол треугольника.

Треугольник

Большая сторона треугольника
	Против большей стороны треугольника лежит больший угол
Больший угол треугольника
	Против большего угла треугольника лежит большая сторона
Меньшая сторона треугольника
	Против меньшей стороны треугольника лежит меньший угол
Меньший угол треугольника
	Против меньшего угла треугольника лежит меньшая сторона
Длины сторон треугольника

Углы треугольника

Внешний угол треугольника

Больший угол треугольника

Меньший угол треугольника

Теорема косинусов

Теорема синусов

Треугольник

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Большая сторона треугольника

Свойство большей стороны треугольника:

Против большей стороны треугольника лежит больший угол

Больший угол треугольника

Свойство большего угла треугольника:

Против большего угла треугольника лежит большая сторона

Меньшая сторона треугольника

Свойство меньшей стороны треугольника:

Против меньшей стороны треугольника лежит меньший угол

Меньший угол треугольника

Свойство меньшего угла треугольника:

Против меньшего угла треугольника лежит меньшая сторона

Длины сторон треугольника

Углы треугольника

Свойство углов треугольника:

Сумма углов треугольника равна 180°

Внешний угол треугольника

Свойство внешнего угла треугольника:

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Больший угол треугольника

Свойство большего угла треугольника:

Величина большего угла треугольника не может быть меньшей, чем 60°.

где α – больший угол треугольника.

Меньший угол треугольника

Свойство меньшего угла треугольника:

Величина меньшего угла треугольника не может быть большей, чем 60°.

где β – меньший угол треугольника.

Теорема косинусов

Теорема синусов

Свойство меньшего угла треугольника:

[spoiler title=”источники:”]

http://colibrus.ru/ostrougolnyy-pryamougolnyy-i-tupougolnyy-treugolniki/

http://www.resolventa.ru/demo/obsh/diagege.htm

[/spoiler]

Источник

0 / 0 / 0

Регистрация: 09.11.2020

Сообщений: 20

Найти наименьший из углов треугольника

11.11.2020, 16:29. Показов 2030. Ответов 25

Здравствуйте, подскажите как сделать задачу. Совсем не могу разобраться
C++
На плоскости задан треугольник длинами своих сторон.
Найти наименьший из углов треугольника в градусах. Значения сторон вводить в диалоге, иметь возможность повторного обращения.

2439 / 1178 / 436

Регистрация: 08.11.2016

Сообщений: 3,261

11.11.2020, 16:44

1. запрашиваете ввод трех переменных – стороны треугольника
2. по введенным значениям вычисляете площадь по формуле Герона, только сперва вычисляете подкоренное выражение и анализируете это значение: если оно отрицательно – треугольник не существует, если равно нулю – треугольник вырожденный, наименьший угол равен 0 градусов, если значение положительно и больше нуля идем дальше.
3. Извлекаете квадратный корень и получаете площадь
4. далее из формулы площади S = a * h / 2 выражаете высоту через основание (любая из введенных сторон)
5. воспользовавшись одним из определений синуса угла: “в прямоугольном треугольнике синус угла равен отношению противолежащего катета к гипотенузе” – вычисляете углы через арксинус отношения высоты к стороне треугольника образующей гипотенузу прямоугольного треугольника с высотой h.
6. находите наименьший угол
7. выводите результат.

7427 / 5021 / 2891

Регистрация: 18.12.2017

Сообщений: 15,694

11.11.2020, 16:55

Сообщение от Annemesski

вычисляете площадь по формуле Герона

Annemesski, зачем ТС Герон если есть формула косинусов ?
$https://www.cyberforum.ru/cgi-bin/latex.cgi?cos(alpha)=frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$

2439 / 1178 / 436

Регистрация: 08.11.2016

Сообщений: 3,261

11.11.2020, 16:57

Сообщение от Yetty

зачем ТС Герон если есть формула косинусов ?

есть, но один пень проверять существование треугольника, это можно сделать по Герону, а его результат использовать для вычисления углов, формулы чуть проще чем теорема синусов или косинусов.

7427 / 5021 / 2891

Регистрация: 18.12.2017

Сообщений: 15,694

11.11.2020, 17:07

Сообщение от Annemesski

пень проверять существование треугольника, это можно сделать по Герону

во-первых это не требуется по задаче:

Сообщение от AnastasiaYakub

На плоскости задан треугольник

а если бы даже и требовалось, треугольник существует когда сумма двух его сторон больше третьей. вычислять площадь, в частности по теореме Герона конечно не нужно

Celly

158 / 148 / 25

Регистрация: 23.01.2011

Сообщений: 319

11.11.2020, 17:15

C++

#include <iostream>
#include <cmath>
 
bool IsValidTriangle(int a, int b, int c)
{
    if (!((a + b) > c))
        return false;
 
    if (!((b + c) > a))
        return false;
 
    if (!((a + c) > b))
        return false;
 
    return true;
}
 
/*
            beta
             /
            /  
           /    
         a/      b
         /        
        /          
  alpha/____________gamma
             c
 */
 
int main(int argc, const char * argv[])
{
    double a = 0.0, b = 0.0, c = 0.0;
    std::cout << "Input a = ";
    std::cin >> a;
    std::cout << "Input b = ";
    std::cin >> b;
    std::cout << "Input c = ";
    std::cin >> c;
 
    if (!IsValidTriangle(a, b, c))
    {
        std::cout << "Invalid triangle -- a = " << a << ", b = " << b << ", c = " << c << std::endl;
        return -1;
    }
 
    double alpha = 0.0, beta = 0.0, gamma = 0.0;
 
    alpha = std::acos((a * a + c * c - b * b)/(2 * a * c)) * 180 / M_PI;
    beta = std::acos((a * a + b * b - c * c)/(2 * a * b)) * 180 / M_PI;
    gamma = std::acos((b * b + c * c - a * a)/(2 * b * c)) * 180 / M_PI;
 
    std::cout << "alpha = " << alpha << std::endl;
    std::cout << "beta  = " << beta << std::endl;
    std::cout << "gamma = " << gamma << std::endl;
 
    return 0;
}

7427 / 5021 / 2891

Регистрация: 18.12.2017

Сообщений: 15,694

11.11.2020, 17:18

Celly, почему тип параметров функции int если стороны double ?

также требуется найти min:

Сообщение от AnastasiaYakub

Найти наименьший из углов треугольника в градусах.

2439 / 1178 / 436

Регистрация: 08.11.2016

Сообщений: 3,261

11.11.2020, 17:22

Yetty, в моем решении нужно

7427 / 5021 / 2891

Регистрация: 18.12.2017

Сообщений: 15,694

11.11.2020, 17:22

Сообщение от AnastasiaYakub

возможность повторного обращения

…

158 / 148 / 25

Регистрация: 23.01.2011

Сообщений: 319

11.11.2020, 17:24

Сообщение от Yetty

Celly, почему тип параметров функции int если стороны double ?

На автомате, когда функцию писал.

Сообщение от Yetty

также требуется найти min:

Для самостоятельной работы.

7427 / 5021 / 2891

Регистрация: 18.12.2017

Сообщений: 15,694

11.11.2020, 17:26

Сообщение от Annemesski

в моем решении нужно

Ваше решение, мягко говоря нерационально

Добавлено через 59 секунд

Сообщение от Celly

Для самостоятельной работы.

в таких случаях предупреждают, а не просто сбрасывают код. в целом конечно направление решения верное, только ТС конечно лучше оформить вычисления в виде функции

2439 / 1178 / 436

Регистрация: 08.11.2016

Сообщений: 3,261

11.11.2020, 17:31

Yetty, чем оно не рационально?

7427 / 5021 / 2891

Регистрация: 18.12.2017

Сообщений: 15,694

11.11.2020, 17:41

Сообщение от Annemesski

чем оно не рационально?

сравните предложенный Вами способ решение с кодом сообщения #6 и сделайте выводы сами

Добавлено через 4 минуты
угол определяется непосредственно – для его определения площадь треугольника находить не нужно

0 / 0 / 0

Регистрация: 09.11.2020

Сообщений: 20

11.11.2020, 17:42

[ТС]

Всем Спасибо! Задача уже решена, покопалась в формулах и все получилось) решение больше не требуется)

Annemesski

2439 / 1178 / 436

Регистрация: 08.11.2016

Сообщений: 3,261

11.11.2020, 17:58

сравниваем

C++

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
#include <algorithm>
 
int main()
{
    double a, b, c;
    std::cin >> a >> b >> c;
    double p = (a + b + c) / 2;
    double Ss = p *(p - a) * (p - b) * (p - c);
    if (p < 0)
        std::cout << "impossible" << std::endl;
    else if (p < 1e:8)
        std::cout << "minimum = 0" << std::endl;
    else
    {
        double h = 2 * sqrt(Ss) / a;
        double alpha = asin(h / b);
        double betta = asin(h / c);
        double gamma = M_PI - alpha - betta;
        std::cout << "minimum = " << 180 / M_PI * std::min(std::min(a, b), c) << std::endl;
    }
 
    return 0;
}

7427 / 5021 / 2891

Регистрация: 18.12.2017

Сообщений: 15,694

11.11.2020, 18:48

Сообщение от Annemesski

сравниваем

и ? Вы не можете сделать вывод или не можете подсчитать количество действий ? делаю это вместо Вас:
количество действий, то есть математических операций (для нахождения cos (или sin)):
3+6+1+2+1 = 13 (Ваш вариант)
5+2+1 = 8 (вариант сообщения #6)

кроме того наличие sqrt и трёх делений ещё больше замедляет работу

2439 / 1178 / 436

Регистрация: 08.11.2016

Сообщений: 3,261

11.11.2020, 18:55

Yetty, научитесь считать: количество действий в посте 6 – 8 * 2 + 2 = 18 (если последний угол считать как у меня, в оригинале там 24), у меня 16, а если если учитывать дороговизну корня, то учитывайте и то, что с вашей стороны 10 умножений и 2 деления у меня 4 умножения и 3 деления 12 против 7.

7427 / 5021 / 2891

Регистрация: 18.12.2017

Сообщений: 15,694

11.11.2020, 19:22

Annemesski, научитесь читать, что Вам пишут:

Сообщение от Yetty

для нахождения cos (или sin)

у Вас – 13 действий против 8 действий в другом варианте

2439 / 1178 / 436

Регистрация: 08.11.2016

Сообщений: 3,261

11.11.2020, 19:31

Yetty, в итоге это не даёт экономии, взялись считать, считайте решение полностью, у меня вычисление второго угла обходится дешевле, и пусть что вычисление первого дороже, суммарно по трем углам все равно дешевле. Ну да Гильберт Вам судья.

7427 / 5021 / 2891

Регистрация: 18.12.2017

Сообщений: 15,694

11.11.2020, 19:54

Сообщение от Annemesski

количество действий в посте 6 – 8 * 2 + 2 = 18 (если последний угол считать как у меня, в оригинале там 24), у меня 16

при правильной записи (с доп.переменными qa=a*a, qb=b*b, qc=c*c) действий будет меньше чем в Вашем варианте

про sqrt и деления уже говорил, повторяться смысла не вижу

IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604	11.11.2020, 19:54
20

Источник

$begingroup$

Sum of angles of a triangle is 180 degress. So while studying trigonometric ratios , I got surprised at cos0 and cos 180 values. Although cosine is ratio of adjecent and hypotenuse ,in case of cos0 with value 1 or cos180 with value 0, i doubt that how can it be called as triangle where one angle is 0 or 180 degree?

It would be just be just a straight line rather than called as triangle,isn’t it? Also I want to know what could be the minimum and maxmimum value of angle in the triangle ?

asked Jul 3, 2018 at 5:26

$endgroup$

$begingroup$

What you described at the first part is what we call degeneracy, some people accept degenerate triangle as triangle, but if you don’t we have no minimum (nor maximum) angle:

Give me a triangle with an angle $alpha$ I can create a triangle with an angle $alpha/2$ and a(different) triangle with angle $(alpha+180)/2$(degrees), the first triangle shows that $alpha$ is not minimal angle, and second shows that $alpha$ is not maximal angle.

answered Jul 3, 2018 at 5:44

ℋoloℋolo

9,7682 gold badges15 silver badges39 bronze badges

$endgroup$

$begingroup$

The usual “SOH CAH TOA” definition of trigonometry is only useful in non-degenerate right triangles (usually first discussed in Geometry in the U.S). And in this case, you are right. It’s hard to imagine a right triangle with $0^circ$ or $180^circ$, or even worse, negative angles or angles greater than $180^circ$. In order to approach these angles, you need new definition of trigonometry (although still related to “SOH CAH TOA”). You need “Unit Circle Approach”. Let $P(x,y)$ be a terminal point on a unit circle centered at origin where we moved a distance $vertthetavert$ along its arc, starting at the point $(1,0)$. We define:
$sintheta=y$, $costheta=x$, $tantheta=frac{y}{x}$.

If $theta$ is exactly $180^circ$, the point $P$ ends up at $(-1,0)$. According to this new definition, $cos 180^circ$ becomes $-1$

answered Jul 3, 2018 at 6:02

Harry HongHarry Hong

3551 gold badge2 silver badges9 bronze badges

$endgroup$

$begingroup$

In a sense, there are two different notions of trigonometric functions — although they do agree with each other on their common domain, so to speak.

One concept is that of trigonometric functions of an acute angle in a right triangle. This definition ONLY makes sense for angles $0^{circ}<theta<90^{circ}$, or $0<theta<frac{pi}{2}$ in radians. There’s no smallest or largest possible value of $theta$ here (for example, $theta$ can be an arbitrarily small positive number). But from this point of view, expressions like “$cos(0^{circ})$” or “$cos(180^{circ})$” certainly do NOT make any sense, because there are no such right triangles.

But then there’s a much more general concept of trigonometric functions as functions defined for all real numbers. Geometrically, one possible way to introduce them is via the unit circle. With this definition, statements such as “$cos(0^{circ})=1$” or “$cos(180^{circ})=-1$” make perfect sense. And by the way, note that for angles lying within the first quadrant this definition coincides with the right triangle definition.

So the answer depends on the context. There are certainly no triangles with angles of $0^{circ}$ or $180^{circ}$. Whether that invalidates trig functions of such angles or not… see above.

answered Jul 3, 2018 at 5:54

zipirovichzipirovich

14.5k1 gold badge24 silver badges34 bronze badges

$endgroup$

You must log in to answer this question.

Not the answer you’re looking for? Browse other questions tagged

.

Источник

Как найти угол, если известны стороны

Многоугольником называется фигура на плоскости, состоящая из трёх и более сторон, которые пересекаются в трёх и более точках. Многоугольник называется выпуклым, если каждый его угол меньше 180º. Обычно, в качестве многоугольников рассматривают именно выпуклые многоугольники. Для нахождения углов многоугольника нужно иметь минимально необходимый набор исходных данных. Пусть для многоугольника известны длины всех его сторон.

Инструкция

Многоугольник называется правильным, если его стороны равны между собой, а так же все углы равны между собой.
Если заранее известно, что многоугольник является правильным, то углы можно высчитать по формуле
?? = 180? * (n – 2)/n, где n – количество сторон многоугольника.
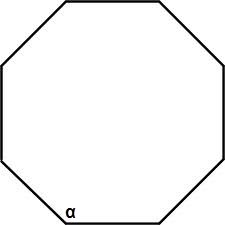
Например, в случае правильного восьмиугольника
?? = 180? * (8 – 2)/8 = 135?

Для неправильного треугольника с известными сторонами, углы можно рассчитать по теореме косинусов, например, для угла ?? в приведённом рисунке формула примет вид
cos?? = (b? + c? – a?) / 2 • b • c

Для нахождения углов неправильных многоугольников с количеством сторон больше 3 наличие длин сторон не является достаточным условием.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.

Угол треугольника через три стороны
Угол прямоугольного треугольника через две стороны
Угол треугольника через высоту и катет
Угол при основании равнобедренного треугольника через
биссектрису и боковую сторону
Угол при основании равнобедренного треугольника через
биссектрису и основание
Угол между боковыми сторонами равнобедренного треугольника
через биссектрису и боковую сторону
Острый угол прямоугольного треугольника через катет и
площадь
Острый угол между боковыми сторонами равнобедренного
треугольника через площадь и боковую сторону

Угол треугольника через три стороны

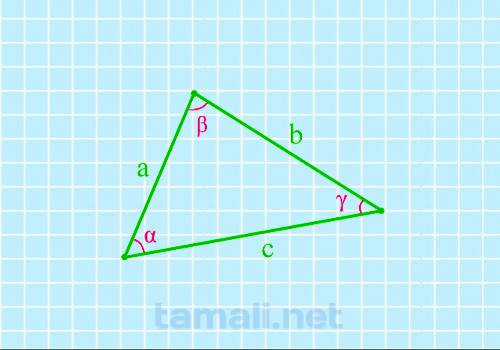
Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить

cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb

где a, b, c — стороны треугольника.

Цифр после
запятой:

Результат в:

Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.

Угол прямоугольного треугольника через две стороны

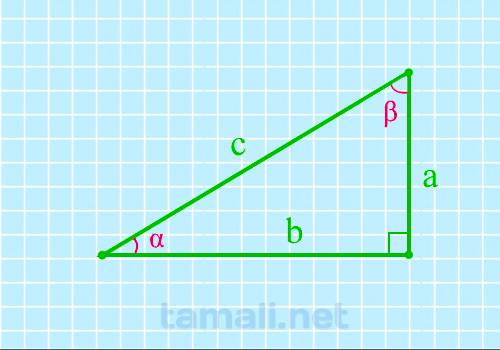
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.

sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a

где a, b — катеты, c — гипотенуза.

Цифр после запятой:

Результат в:

Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.

Острый угол прямоугольного треугольника через катет и площадь

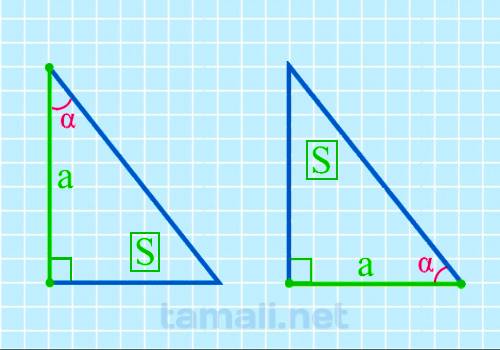
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:

tg(α) = a² / 2S

где a — катет, S — площадь прямоугольного треугольника.

Цифр после
запятой:

Результат в:

Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.

Угол треугольника через высоту и катет

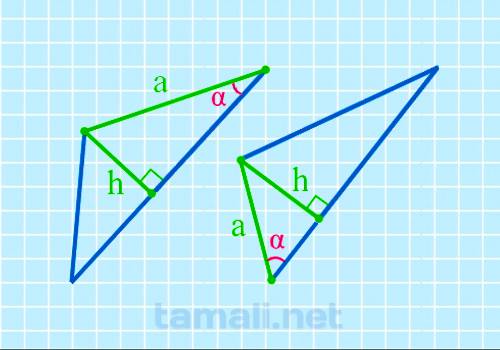
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.

sin α = h / a

где h — высота, a — катет.

Цифр после запятой:

Результат в:

Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°

Угол при основании равнобедренного треугольника через биссектрису и основание

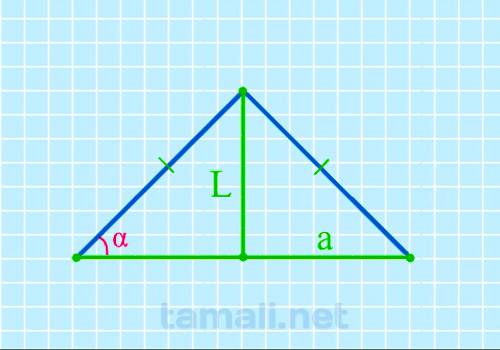
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:

tg α = L / (a/2)

где L — биссектриса, a — основание.

Цифр после
запятой:

Результат в:

Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º

Угол при основании равнобедренного треугольника через биссектрису и боковую сторону

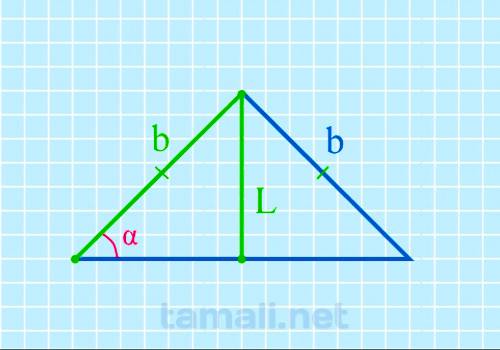
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:

sin α = L / b

где L — биссектриса, b — боковая сторона.

Цифр после
запятой:

Результат в:

Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.

Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону

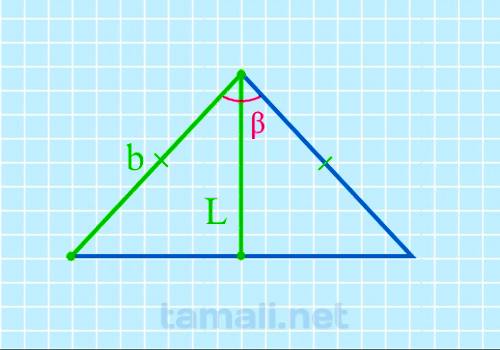
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).

2cos(β) = L / b

где L — биссектриса, b — боковая сторона.

Цифр после
запятой:

Результат в:

Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º

Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону

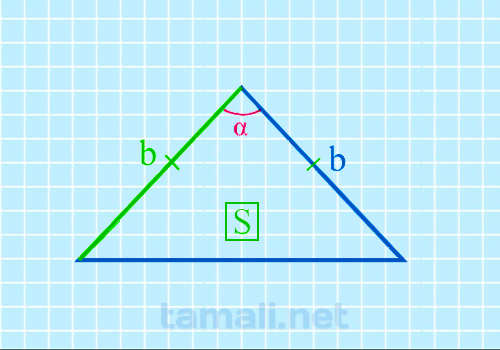
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:

sin(α) = 2S / b²

где b — боковая сторона равнобедренного треугольника, S — площадь.

Цифр после
запятой:

Результат в:

Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º

Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.

Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.

Источник

Как найти меньший угол данного треугольника?

Остроугольный, прямоугольный и тупоугольный треугольники.

Виды треугольников

Как определить вид треугольника

Градусные меры острого, тупого, прямого углов в треугольниках

Свойства сторон и углов треугольника

Найти наименьший из углов треугольника

You must log in to answer this question.

Not the answer you’re looking for? Browse other questions tagged .

Как найти угол, если известны стороны

Угол треугольника через три стороны

Угол прямоугольного треугольника через две стороны

Острый угол прямоугольного треугольника через катет и площадь

Угол треугольника через высоту и катет

Угол при основании равнобедренного треугольника через биссектрису и основание

Угол при основании равнобедренного треугольника через биссектрису и боковую сторону

Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону

Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую сторону

Вам также может понравиться

Как найти сборку в доте по названию

Как помочь дочке найти работу

Как найти название сигнализации по брелку

Добавить комментарий Отменить ответ

Not the answer you’re looking for? Browse other questions tagged

.

Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону