Как найти минимум действия - Сайт, где вы сможете решить свои вопросы

При́нцип наиме́ньшего де́йствия Га́мильтона, также просто принцип Гамильтона (точнее — при́нцип стациона́рности де́йствия) — способ получения уравнений движения физической системы при помощи поиска стационарного (часто — экстремального, обычно, в связи со сложившейся традицией определения знака действия, — наименьшего) значения специального функционала — действия. Назван в честь Уильяма Гамильтона, использовавшего этот принцип для построения так называемого гамильтонова формализма в классической механике.

Принцип стационарности действия — наиболее важный среди семейства экстремальных принципов. Не все физические системы имеют уравнения движения, которые можно получить из этого принципа, однако все фундаментальные взаимодействия ему подчиняются, в связи с чем этот принцип является одним из ключевых положений современной физики. Получаемые с его помощью уравнения движения имеют название уравнений Эйлера — Лагранжа.

Первую формулировку принципа дал П. Мопертюи (фр. P. Maupertuis) в 1744 году, сразу же указав на его универсальную природу и считая его приложимым к оптике и механике. Из данного принципа он вывел законы отражения и преломления света.

История[править | править код]

Ещё античные натурфилософы (например, Аристотель) предполагали, что «природа ничего не делает напрасно и во всех своих проявлениях избирает кратчайший или легчайший путь»^[1]. Однако конкретный смысл терминов «кратчайший» или «легчайший» при этом не уточнялся^[2]. Клавдий Птолемей показал, что при отражении луча света его общий путь является кратчайшим в том случае, когда угол отражения равен углу падения, что и наблюдается на практике. Однако он предостерёг, что в случае преломления света путь (ломаная линия) уже не будет кратчайшим.

Первым в истории науки вариационный принцип сформулировал Пьер Ферма в 1662 году, и он относился именно к преломлению света. Ферма показал, что критерием в данном случае является не путь, а время — луч преломляется под таким углом, чтобы суммарное время в пути было минимально^[3]. В современных обозначениях принцип Ферма можно записать как

${displaystyle T=int limits _{mathbf {A} }^{mathbf {B} }{frac {ds}{v}}=int limits _{mathbf {A} }^{mathbf {B} }{frac {n}{c}},ds={text{min}},}$

где — показатель преломления среды, — скорость света в вакууме.

Математическое исследование и развитие принципа Ферма провёл Христиан Гюйгенс^[4], после чего тему активно обсуждали крупнейшие учёные XVII века. Лейбниц в 1669 году ввёл в физику фундаментальное понятие действия: «Формальные действия движения пропорциональны… произведению количества материи, расстояний, на которые они передвигаются, и скорости».

Параллельно с анализом основ механики развивались методы решения вариационных задач. Исаак Ньютон в своих «Математических началах натуральной философии» (1687 год) поставил и решил первую вариационную задачу: найти такую форму тела вращения, движущегося в сопротивляющейся среде вдоль своей оси, для которой испытываемое сопротивление было бы наименьшим. Почти одновременно появились и другие вариационные проблемы: задача о брахистохроне (1696), форма цепной линии и др.

Решающие события произошли в 1744 году. Леонард Эйлер опубликовал первую общую работу по вариационному исчислению («Метод нахождения кривых, обладающих свойствами максимума либо минимума»), а Пьер Луи де Мопертюи в трактате «Согласование различных законов природы, которые до сих пор казались несовместимыми» дал первую формулировку принципа наименьшего действия: «путь, которого придерживается свет, является путём, для которого количество действия будет наименьшим». Он продемонстрировал выполнение этого закона как для отражения, так и для преломления света. В ответ на статью Мопертюи Эйлер опубликовал (в том же 1744 году) работу «Об определении движения брошенных тел в несопротивляющейся среде методом максимумов и минимумов», и в этом труде он придал принципу Мопертюи общемеханический характер: «Так как все явления природы следуют какому-нибудь закону максимума или минимума, то нет никакого сомнения, что и для кривых линий, которые описывают брошенные тела, когда на них действуют какие-нибудь силы, имеет место какое-то свойство максимума или минимума». Далее Эйлер сформулировал этот закон: траектория тела осуществляет минимум . Затем он применил его, выведя законы движения в однородном поле тяжести и в нескольких других случаях.

В 1746 году Мопертюи в новой работе согласился с мнением Эйлера и провозгласил самую общую версию своего принципа: «Когда в природе происходит некоторое изменение, количество действия, необходимое для этого изменения, является наименьшим возможным. Количество действия есть произведение массы тел на их скорость и на расстояние, которое они пробегают». В развернувшейся широкой дискуссии Эйлер поддержал приоритет Мопертюи и аргументировал всеобщий характер нового закона: «вся динамика и гидродинамика могут быть с удивительной лёгкостью раскрыты посредством одного только метода максимумов и минимумов».

Новый этап начался в 1760—1761 годах, когда Жозеф Луи Лагранж ввёл строгое понятие вариации функции, придал вариационному исчислению современный вид и распространил принцип наименьшего действия на произвольную механическую систему (то есть не только на свободные материальные точки). Тем самым было положено начало аналитической механике. Дальнейшее обобщение принципа осуществил Карл Густав Якоб Якоби в 1837 году — он рассмотрел проблему геометрически, как нахождение экстремалей вариационной задачи в конфигурационном пространстве с неевклидовой метрикой. В частности, Якоби указал, что при отсутствии внешних сил траектория системы представляет собой геодезическую линию в конфигурационном пространстве.

В 1834—1835 годах Уильям Роуэн Гамильтон опубликовал ещё более общий вариационный принцип, из которого следовали все более ранние как частные случаи:

${displaystyle delta {mathcal {S}}=delta int limits _{t_{1}}^{t_{2}}L{big (}mathbf {q} (t),mathbf {dot {q}} (t),t{big )},dt=0.}$

Здесь — лагранжиан динамической системы, — обобщённые координаты. Гамильтон положил этот принцип в основу своей «гамильтоновой механики» и дал решение вариационной задачи в виде «канонических уравнений».

Подход Гамильтона оказался универсальным и высокоэффективным в математических моделях физики, особенно для квантовой механики. Его эвристическая сила была подтверждена при создании общей теории относительности, когда Давид Гильберт применил гамильтонов принцип для вывода окончательных уравнений гравитационного поля (1915 год).

В классической механике[править | править код]

Принцип наименьшего действия служит фундаментальной и стандартной основой лагранжевой и гамильтоновой формулировок механики.

Вначале рассмотрим построение таким образом лагранжевой механики. На примере физической системы с одной^[5] степенью свободы, напомним, что действие — это функционал относительно (обобщённых) координат (в случае одной степени свободы — одной координаты q(t) ), то есть оно выражается через q(t) так, что каждому мыслимому варианту функции q(t) сопоставляется некоторое число — действие (в этом смысле можно сказать, что действие как функционал есть правило, позволяющее для любой заданной функции q(t) вычислить вполне определённое число — также называемое действием). Действие имеет вид

{displaystyle S[q]=int {mathcal {L}}{big (}q(t),{dot {q}}(t),t{big )},dt,}

где есть лагранжиан системы, зависящий от обобщённой координаты , её первой производной по времени , а также, возможно, и явным образом от времени . Если система имеет большее число степеней свободы , то лагранжиан зависит от большего числа обобщённых координат ${displaystyle q_{i}(t), i=1,2,dots ,n}$ и их первых производных по времени. Таким образом, действие является скалярным функционалом, зависящим от траектории тела.

То, что действие является скаляром, позволяет легко записать его в любых обобщённых координатах, главное только, чтобы положение (конфигурация) системы однозначно ими характеризовалось (например, вместо декартовых это могут быть полярные координаты, расстояния между точками системы, углы или их функции и т. д.).

Действие можно вычислить для совершенно произвольной траектории q(t) , какой бы «дикой» и «неестественной» она ни была. Однако в классической механике среди всего набора возможных траекторий существует одна единственная, по которой тело действительно пойдёт. Принцип стационарности действия как раз и даёт ответ на вопрос, как действительно будет двигаться тело:

Между двумя заданными точками тело движется так, чтобы действие было стационарным.

Это значит, что если задан лагранжиан системы, то мы с помощью вариационного исчисления можем установить, как именно будет двигаться тело, сначала получив уравнения движения — уравнения Эйлера — Лагранжа, а затем решив их. Это позволяет не только серьёзно обобщить формулировку механики, но и выбирать наиболее удобные координаты для каждой определённой задачи, не ограничиваясь декартовыми, что может быть очень полезно для получения наиболее простых и легко решаемых уравнений.

Аналогично гамильтонова механика получается из принципа наименьшего действия. Действие в этом случае наиболее естественно записать^[6] как

${displaystyle S[p,q]=int {Big (}sum _{i}p_{i},dq_{i}-{mathcal {H}}(q,p,t),dt{Big )}=int {Big (}sum _{i}p_{i}{dot {q}}_{i}-{mathcal {H}}(q,p,t){Big )},dt,}$

где ${displaystyle {mathcal {H}}(q,p,t)equiv {mathcal {H}}(q_{1},q_{2},dots ,q_{N},p_{1},p_{2},dots ,p_{N},t)}$ — функция Гамильтона данной системы; $qequiv q_{1},q_{2},dots ,q_{N}$ — (обобщённые) координаты,
$pequiv p_{1},p_{2},dots ,p_{N}$ — сопряжённые им (обобщённые) импульсы,
характеризующие вместе в каждый данный момент времени динамическое состояние системы и, являясь каждое функцией времени, характеризуя, таким образом, эволюцию (движение) системы. В этом случае для получения уравнений движения системы в форме канонических уравнений Гамильтона надо проварьировать записанное так действие независимо по всем $q_{i}$ и $p_{i}$ .

Необходимо заметить, что если из условий задачи принципиально можно найти закон движения, то это автоматически не означает, что можно построить функционал, принимающий стационарное значение при истинном движении. Примером может служить совместное движение электрических зарядов и монополей — магнитных зарядов — в электромагнитном поле. Их уравнения движения невозможно вывести из принципа стационарности действия. Аналогично некоторые гамильтоновы системы имеют уравнения движения, не выводимые из этого принципа^{[источник не указан 308 дней]}.

Примеры[править | править код]

Тривиальные примеры помогают оценивать использование принципа действия через уравнения Эйлера — Лагранжа. Свободная частица (масса m и скорость v) в евклидовом пространстве перемещается по прямой линии. Используя уравнения Эйлера — Лагранжа, это можно показать в полярных координатах следующим образом. В отсутствие потенциала функция Лагранжа просто равна кинетической энергии

${displaystyle {frac {1}{2}}mv^{2}={frac {1}{2}}m({dot {x}}^{2}+{dot {y}}^{2})}$

в ортогональной системе координат (x, y) .

В полярных координатах кинетическая энергия и, следовательно, функция Лагранжа становится

${displaystyle L={frac {1}{2}}m({dot {r}}^{2}+r^{2}{dot {varphi }}^{2}).}$

Радиальная и угловая компонента уравнений становятся, соответственно:

${displaystyle {frac {d}{dt}}left({frac {partial L}{partial {dot {r}}}}right)-{frac {partial L}{partial r}}=0quad Rightarrow quad {ddot {r}}-r{dot {varphi }}^{2}=0,}$

${displaystyle {frac {d}{dt}}left({frac {partial L}{partial {dot {varphi }}}}right)-{frac {partial L}{partial varphi }}=0quad Rightarrow quad {ddot {varphi }}+{frac {2}{r}}{dot {r}}{dot {varphi }}=0.}$

Решение этих двух уравнений:

с константами a, b, c, d, определяющимися начальными условиями. Таким образом, действительно, решение — это прямая линия, заданная в полярных координатах.

В механике сплошных сред и классической теории поля[править | править код]

Аналогично вводится понятие действия в механике сплошной среды и классической теории поля. В них действие включает в себя интеграл от лагранжевой плотности, зависящей от параметров среды (поля) в каждой точке пространства и их производных по пространственным координатам и времени. Получаемые варьированием действия уравнения движения становятся уравнениями в частных производных.

Принцип стационарности действия оказался одним из самых простых способов обеспечить релятивистскую инвариантность уравнений движения — для этого достаточно, чтобы лагранжева плотность была скаляром (инвариантом) при преобразованиях системы референции, например, преобразованиях Лоренца. Из-за этого роль принципа существенно возросла в релятивистской физике. В частности, теорема Нётер, определяющая сохраняющиеся величины при временно́й эволюции полевых систем, относится именно к лагранжевым системам.

Надо заметить, что применение принципа стационарности действия к теории калибровочных полей (например, к электродинамике) иногда сталкивается с некоторыми специфическими проблемами, впрочем, разрешимыми.

В квантовой механике[править | править код]

В квантовой механике, в соответствии с копенгагенской интерпретацией, не требуется знать, каким конкретно образом движется частица. Более того, в формулировке Фейнмана утверждается, что:

частица движется из начального состояния в конечное сразу по всем мыслимым траекториям (которых, очевидно, бесконечное число). Амплитуда вероятности перехода из одного заданного состояния в другое является суммой амплитуд по всем этим траекториям и записывается в виде функционального интеграла

${displaystyle psi =int [Dx],e^{iS[x]/hbar }.}$

Здесь — это условная запись бесконечнократного функционального интегрирования по всем траекториям x(t), а hbar — постоянная Планка. Подчеркнём, что в принципе действие в экспоненте появляется (или может появляться) само́, при изучении оператора эволюции в квантовой механике, однако для систем, имеющих точный классический (неквантовый) аналог, оно в точности равно обычному классическому действию.

Математический анализ этого выражения в классическом пределе — при достаточно больших S/hbar , то есть при очень быстрых осцилляциях мнимой экспоненты, показывает, что подавляющее большинство всевозможных траекторий в этом интеграле взаимосокращаются при этом в пределе (формально при ). Для почти любого пути найдется такой путь, на котором набег фазы будет в точности противоположным, и они в сумме дадут нулевой вклад. Не сокращаются лишь те траектории, для которых действие близко к экстремальному значению (для большинства систем — минимуму). Это — чисто математический факт из теории функций комплексного переменного; на нём, например, основан метод стационарной фазы.

В результате частица в полном согласии с законами квантовой механики движется одновременно по всем траекториям, но в обычных условиях в наблюдаемые значения дают вклад только траектории, близкие к стационарным (то есть классическим). Поскольку квантовая механика переходит в классическую в пределе больших энергий, то можно считать, что это — квантовомеханический вывод классического принципа стационарности действия.

Открытие формулировки квантования в терминах функциональных интегралов (часто также говорят: «интегралы по путям», «интегралы по траекториям» или «суммирование историй»), как и установление её связи с классическим пределом, принадлежит Ричарду Фейнману, творчески развившему идею Поля Дирака.

Уравнение Шрёдингера можно получить^[7] из принципа наименьшего действия, рассматривая как уравнение Эйлера

${displaystyle {frac {partial L}{partial psi }}-sum _{k=0}^{3}{frac {partial }{partial x_{k}}}{frac {partial L}{partial left({frac {partial psi }{partial x_{k}}}right)}}=0}$

вариационной задачи, в которой плотность лагранжиана имеет вид

${displaystyle L=ihbar psi ^{*}{frac {partial psi }{partial t}}-{frac {hbar ^{2}}{2m}}nabla psi ^{*}nabla psi -U(r,t)psi ^{*}psi -ihbar {frac {partial psi ^{*}}{partial t}}psi }$

В квантовой теории поля[править | править код]

В квантовой теории поля принцип стационарности действия также успешно применяется. В лагранжеву плотность здесь входят операторы соответствующих квантовых полей. Хотя правильнее тут в сущности (за исключением классического предела и отчасти квазиклассики) говорить не о принципе стационарности действия, а о фейнмановском интегрировании по траекториям в конфигурационном или фазовом пространстве этих полей — с использованием упомянутой только что лагранжевой плотности.

Дальнейшие обобщения[править | править код]

Более широко, под действием понимают функционал, задающий отображение из конфигурационного пространства на множество вещественных чисел и, в общем, он не обязан быть интегралом, потому что нелокальные действия в принципе возможны, по крайней мере, теоретически. Более того, конфигурационное пространство не обязательно является функциональным пространством, потому что может иметь некоммутативную геометрию.

См. также[править | править код]

Действие (физическая величина)

Примечания[править | править код]

↑ Эйлер Л. Диссертация о принципе наименьшего действия, с разбором возражений славнейшего проф. Кёнига, выдвинутых против этого принципа // Вариационные принципы механики. — М.: Физматгиз, 1959. — С. 96—108.
↑ Румянцев, 1988, с. 181.
↑ Ферма П. Синтез для рефракции // Вариационные принципы механики. — М.: Физматгиз, 1959. — С. 6—10.
↑ Гюйгенс X. Трактат о свете. — М.—Л.: Гостехиздат, 1935. — 172 с.
↑ Для системы со многими степенями свободы всё записывается аналогично, только вместо одной обобщённой координаты используется несколько (или даже — для бесконечномерных систем — бесконечное количество) обобщённых координат $q_{1},q_{2},dots$ . Пример системы с одной степенью свободы рассматривается вначале для простоты.
↑ На этот раз приведён не одномерный пример.
↑ Кушниренко, 1971, с. 38.

Литература[править | править код]

Бердичевский В. Л. Вариационные принципы механики сплошной среды. — М.: Наука, 1983. — 448 с.
Вариационные принципы механики. Сб. статей классиков науки / Под ред. Л. С. Полака. — М.: Физматгиз, 1959. — 932 с.
Веретенников В. Г., Синицын В. А. Метод переменного действия. 2-е изд. — М.: Физматлит, 2005. — 272 с. — ISBN 5-9221-0569-8.
Гантмахер Ф. Р. Лекции по аналитической механике. 2-е изд. — М.: Наука, 1966. — 300 с.
Добронравов В. В. Основы аналитической механики. — М.: Высшая школа, 1976. — 264 с.
Ландау Л. Д., Лифшиц Е. М. Механика. — Издание 4-е, исправленное. — М.: Наука, 1988. — 215 с. — («Теоретическая физика», том I). — ISBN 5-02-013850-9.
Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
Ланцош К. Вариационные принципы механики. — М.: Мир, 1965. — 408 с.
Лич Дж. У. Классическая механика. — М.: Иностр. литература, 1961. — 174 с.
Павленко Ю. Г. Лекции по теоретической механике. — М.: Физматлит, 2002. — 392 с. — ISBN 5-9221-0241-9.
Парс Л. А. Аналитическая динамика. — М.: Наука, 1971. — 636 с.
Полак Л. С. В. Р. Гамильтон и принцип стационарности действия. — М.: Изд-во АН СССР, 1936. — 272 с.
Румянцев В. В. Леонард Эйлер и вариационные принципы механики // Развитие идей Леонарда Эйлера и современная наука. — М.: Наука, 1988. — 518 с. — ISBN 5-02-000002-7. — С. 180—207.
Фейнман Р., Хибс А. Квантовая механика и интегралы по траекториям. Пер с англ. — М.: Мир, 1968. — 384 с.
Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Т. 6: Электродинамика. Пер. с англ. 3-е изд. — М.: Эдиториал УРСС, 2004. — 352 с. — ISBN 5-354-00704-6. — Глава 19: Принцип наименьшего действия.
Кушниренко А. Н. Введение в квантовую теорию поля. — М.: Высшая школа, 1971. — 304 с.

Источник

Принцип наименьшего действия в аналитической механике

Причина данной публикации — неоднозначная статья на тему принципа наименьшего действия (ПНД), опубликованная на ресурсе несколько дней назад. Неоднозначна она потому, что её автор в популярной форме пытается донести до читателя один из основополагающих принципов математического описания природы, и это частично ему удается. Если бы не одно но, притаившееся в конце публикации. Под спойлером приведена полная цитата данного отрывка

Не все так просто

На самом деле я немного обманул, сказав, что тела всегда двигаются так, чтобы минимизировать действие. Хотя в очень многих случаях это действительно так, можно придумать ситуации, в которых действие явно не минимально.

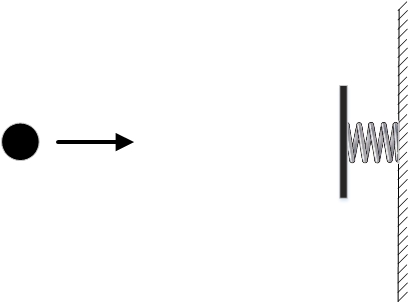
Например, возьмем шарик и поместим его в пустое пространство. На некотором отдалении от него поставим упругую стенку. Допустим, мы хотим, чтобы через некоторое время шарик оказался в том же самом месте. При таких заданных условиях шарик может двигаться двумя разными способами. Во-первых, он может просто оставаться на месте. Во-вторых, можно его толкнуть по направлению к стенке. Шарик долетит до стенки, отскочит от нее и вернется обратно. Понятно, что можно толкнуть его с такой скоростью, чтобы он вернулся в точно нужное время.

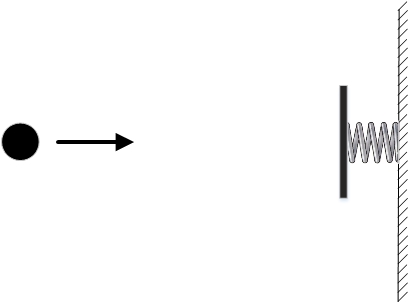
Оба варианта движения шарика возможны, но действие во втором случае получится больше, потому что все это время шарик будет двигаться с ненулевой кинетической энергией.

Как же спасти принцип наименьшего действия, чтобы он был справедлив и в таких ситуациях? Об этом мы поговорим в следующий раз.

Так в чем же, с моей точки зрения, проблема?

Проблема в том, что автор, приводя данный пример допустил ряд фундаментальных ошибок. Она усугубляется тем, что планируемая вторая часть, со слов автора, будет опираться на эти ошибки. Руководствуясь принципом наполнения ресурса достоверной информацией я вынужден выступить с разъяснением своей позиции по данному вопросу более развернуто, и формат комментариев для этого маловат.

Данная статья расскажет о том, как строится механика на базе ПНД, и постарается объяснить читателю, что проблема, которую ставит автор цитируемой публикации отсутствует.

1. Определение действия по Гамильтону. Принцип наименьшего действия

— функция Лагранжа, для некоторой механической системы, в которой (опуская аргументы в дальнейшем) T — кинетическая энергия системы; П — потенциальная её энергия; q(t) — вектор обобщенных координат этой системы, являющийся функцией времени. при этом полагают, что моменты времени t₁ и t₂ — фиксированы.

Почему функционал, а не функция? Потому, что функция, по определению есть правило, по которому одному числу из области определения (аргументу функции) ставится в соответствие другое число из области значений. Функционал отличается тем, что качестве его аргумента выступает не число, а целая функция. В данном случае это закон движения механической системы q(t), определенный по крайней мере на промежутке времени между t₁ и t₂.

Многолетние (и это мягко сказано!) труды ученых-механиков (включая умопомрачительного Леонарда Эйлера), позволили сформулировать

Принцип наименьшего действия:

Механическая система, для которой задана функция Лагранжа , движется таким образом, что закон её движения q(t) доставляет минимум функционалу

называемому действием по Гамильтону.

Уже из самого определения ПНД следует тот факт, что данный принцип приводит к уравнениям движения лишь для ограниченного класса механических систем. Для каких? А давайте разберемся.

2. Границы применимости принципа наименьшего действия. Некоторые определения для самых маленьких

Как следует из определения, опять таки, функции Лагранжа, ПНД позволяет получить уравнения движения для механических систем, силовое воздействие на которые определяется исключительно потенциальной энергией. Для того чтобы разобраться, о каких системах идет речь, дадим несколько определений, которые, для экономии объема статьи я помещаю под спойлер

Рассмотрим движущуюся по траектории AB точку, к которой приложена сила . Бесконечно малое перемещение точки по траектории определяется вектором , направленным по касательной к траектории.

Элементарной работой силы на перемещении называют скалярную величину, равную

Тогда, полная работа силы на перемещении точки по траектории AB есть криволинейный интеграл

Кинетической энергией точки T называют работу, которую должны совершить приложенные к точке массой m силы, для того чтобы из состояния покоя перевести точку в движение со скоростью

В соответствии со вторым законом Ньютона

Вычислим строго стоящее под знаком интеграла скалярное произведение, для чего продифференцируем по времени скалярное произведение вектора скорости самого на себя

С другой стороны,

Дифференцируя это равенство по времени, имеем

Сравнивая (1) и (2) приходим к выводу, что

Тогда, спокойно вычисляем работу, раскрывая криволинейный интеграл через определенный, взяв в качестве пределов модуль скорости точки в начале и в конце траектории

Пусть точка перемещается в пространстве по произвольной траектории AB. Вычислим, какую работу при этом совершит сила (3)

Так как проекции силы на оси координат зависят исключительно от этих самых координат, всегда можно найти функцию

Тогда, выражение для работы преобразуется к виду

где — значения функции U(x, y, z) в точках A и B соответственно. Таким образом работа рассматриваемой нами силы не зависит от траектории точки, а определяется только значениями функции U в начале и в конце траектории. Такая сила называется консервативной силой, а соответствующая ей функция U(x, y, z) — силовой функцией. Очевидно, что , а так же равенство нулю работы консервативной силы при движении по замкнутой траектории. Говорят так же, что функция U(x, y, z) задает в пространстве силовое поле.

Потенциальной энергией точки, в пространстве с заданным силовым полем, называют работу внешних сил, приложенных к ней, которую они совершают при перемещении точки в заданное координатами (x, y, z) положение в пространстве из некоторого произвольного положения, выбранного в качестве начала отсчета уровня потенциальной энергии.

— потенциальная энергия точки в положении A, а

— потенциальная энергия точки в положении B. Учитывая всё вышесказанное снова вычислим работу потенциальных сил на перемещении из точки A в точку B

Таким образом, работа консервативных сил равна изменению потенциальной энергии точки, взятому с обратным знаком

причем выбор уровня, на котором мы считаем потенциальную энергию равной нулю совершенно не влияет на результат. Отсюда можно сделать вывод, что уровень отсчета потенциальной энергии можно выбрать совершенно произвольно.

3. Понятие о вариациях обобщенных координат. Постановка вариационной задачи

где s — число степеней свободы данной системы.

Действительный, но неизвестный пока нам, закон движения данной системы определяется зависимость обобщенных координат (4) от времени. Рассмотрим одну из обобщенных координат , полагая аналогичные рассуждения и для всех остальных координат.

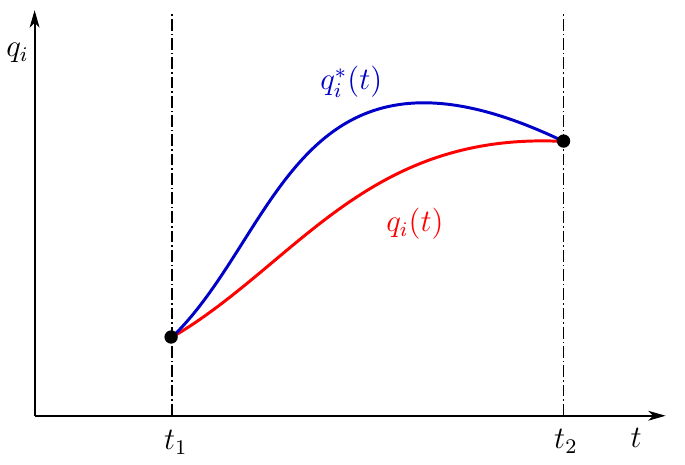
Рисунок 1. Действительное и окольное движение механической системы

На рисунке зависимость изображена красной кривой. Выберем два произвольных фиксированных момента времени t₁ и t₂, полагая t₂ > t₁. Положение системы договоримся называть начальным положением системы, а — конечным положением системы.

Однако, я ещё раз настаиваю на том, чтобы нижеследующий текст был прочтен внимательно! Несмотря на то, что мы задаемся начальным и конечным положением системы, ни первое положение, ни второе, нам заранее неизвестны! Равно как и неизвестен закон движения системы! Эти положения рассматриваются именно как начальное и конечное положение, безотносительно конкретных значений.

Далее мы полагаем, что из начального положения в конечное система может придти разными путями, то есть зависимость может быть любой кинематически возможной. Действительное движение системы будет существовать в единственном варианте (красная кривая), остальные кинематически возможные варианты будем называть окольными движениями (синяя кривая на рисунке). Разность между действительным и окольным движением

будем называть изохронными вариациями обобщенных координат

В данном контексте вариации (5) следует понимать как бесконечно малые функции, выражающие отклонение окольного движения от действительного. Малая «дельта» для обозначения выбрана не случайно и подчеркивает принципиальное отличие вариации от дифференциала функции. Дифференциал — главная линейная часть приращения функции, вызванного приращением аргумента. В случае с вариацией изменение значения функции при постоянном значении аргумента вызвано изменением вида самой функции! Мы не варьируем аргумент, в роли которого выступает время, поэтому вариация называется изохронной. Мы варьируем правило по которому каждому значению времени приводится в соответствие некоторое значение обобщенных координат!

По сути, мы варьируем закон движения, по которому система из начального состояния перемещается в конечное состояние. Начальное и конечное состояние определяются действительным законом движения, но я ещё раз подчеркиваю — их конкретные значения нам не известны и могут быть любыми кинематически возможными, мы лишь полагаем, что они существуют и система гарантированно перемещается из одного положения в другое! В начальном и конечном положении системы мы не варьируем закон движения, поэтому вариации обобщенных координат в начальном и конечном положении равны нулю

Исходя из принципа наименьшего действия, действительное движение системы должно быть таким, чтобы доставлять минимум функционалу действия. Варьирование координат вызывает изменение функционала действия. Необходимым условием достижения функционалом действия экстремального значения является равенство нулю его вариации

4. Решение вариационной задачи. Уравнения Лагранжа 2-го рода

Загоним всё под один интеграл, и так как для вариаций справедливы все операции над бесконечно малыми величинами, преобразуем этот крокодил к виду

Исходя из определения обобщенной скорости

Тогда выражение (8) преобразуется к виду

Второе слагаемое интегрируется по частям

Исходя из условия (7), имеем

тогда, получаем уравнение

При произвольных пределах интегрирования равенство нулю определенного интеграла обеспечивается равенством нулю подынтегральной функции

С учетом того, что вариации обобщенных координат независимы, (11) справедливо только в случае равенства нулю всех коэффициентов при вариациях, то есть

Никто не мешает нам умножить каждое из уравнений на (-1) и получить более привычную запись

Уравнения (12) и есть решение задачи. И вот на этом моменте ещё раз внимание — решение вариационной задачи по принципу наименьшего действия, это не функция, доставляющая минимум действию по Гамильтону, а система дифференциальных уравнений, решая которое таковую функцию можно найти. В данном случае это дифференциальное уравнение Лагранжа 2-го рода, записанное через функцию Лагранжа, то есть в формулировке для консервативных механических систем.

И всё, на этом принцип наименьшего действия заканчивается, а начинается теория обыкновенных дифференциальных уравнений, которая, в частности, гласит, что решением уравнения (12) является вектор-функция вида

где C₁. C_2s — произвольные константы интегрирования.

ПНД — фундаментальный принцип, позволяющий получить уравнения движения системы, для которой определена функция Лагранжа

Точка! В задачах аналитической механики вышеперечисленные выкладки больше не нужно проделывать, достаточно использовать их результат (12). Функция, удовлетворяющая уравнению (12) есть закон движения системы, удовлетворяющей ПНД.

5. Задача с шариком и стенкой

Теперь вернемся к той задаче, с которой всё началось — об одномерном движении шарика около абсолютно упругой стенки. Разумеется, для данной задачи можно получить дифференциальные уравнения движения. Так как это дифференциальные уравнения движения, то любое, я подчеркиваю это, любое их решение доставляет минимум функционалу действия, а значит ПНД выполняется! Общее решение уравнений движения шарика можно изобразить в виде так называемого фазового портрета рассматриваемой механической системы. Вот этот фазовый портрет

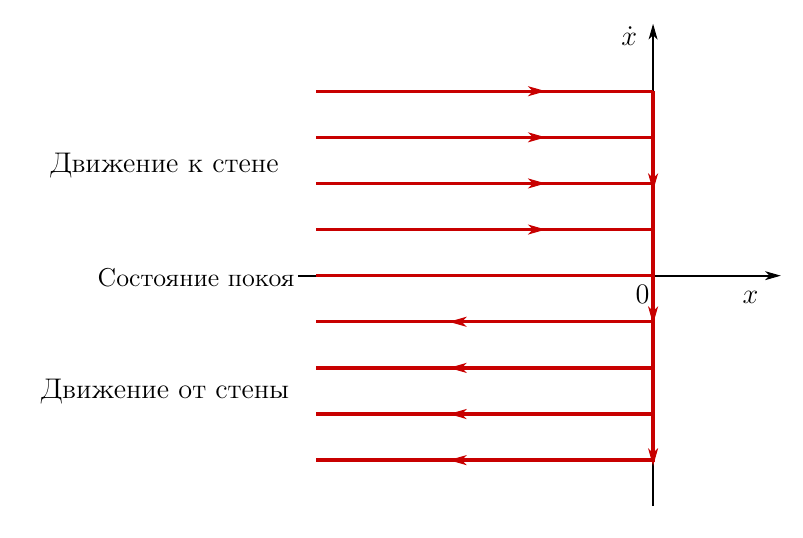
Рисунок 2. Фазовый портрет системы в задаче с шариком

По горизонтальной оси откладывается координата шарика, по вертикальной — проекция скорости на ось x. Может это покажется странным, но данный чертеж отражает все возможные фазовые траектории движения шарика, при любых начальных, или если вам так хочется, краевых условиях. На самом деле параллельных прямых на графике бесконечно много, на чертеже показаны некоторые из них и направление движения по фазовой траектории.

Это — общее решение уравнения движения шарика. Каждая из этих фазовых траекторий доставляет минимум функционалу действия, что непосредственно следует из выкладок, проделанных выше.

Что делает автор задачи? Он говорит: вот шарик покоится, и за промежуток времени от t_A до t_B действие равно нулю. Если шарик толкнуть к стенке, то за тот же промежуток времени действие будет больше, так как у шарика отличная от нуля и неизменная кинетическая энергия. Но почему шарик движется к стенке, ведь в покое действие будет меньше? Значит ПНД испытвает проблемы и не работает! Но мы обязательно решим это в следующей статье.

То что говорит автор — бред. Почему? Да потому, что он сравнивает действия на различных ветвях одной и той же действительной фазовой траектории! Между тем, при применении ПНД, сравнивается действие на действительной траектории и на множестве окольных траекторий. То есть происходит сравнение действия на реальной траектории с действием на тех траекториях, которых нет в природе, и никогда не будет!

Не понятно? Объясню ещё более доходчиво. Рассмотрим состояние покоя. Оно описывается ветвью фазового портрета, совпадающего с осью абсцисс. Координата не меняется с течением времени. Это действительное движение. А какое же движение будет окольным. Любое другое кинематически возможное. Например малые колебания шарика около рассматриваемого нами положения покоя. Задача допускает колебания шарика вдоль оси х? Допускает, значит такое движение кинематически возможно и может рассматриваться как одно их окольных

Почему же шарик таки покоится? Да потому, что действие в состоянии покоя, вычисленное на фиксированном промежутке времени от t_A до t_B, будет меньше действия, при малых колебаниях на том же промежутке времени. Значит колебаниям и любому другому «шевелению» шарика природа предпочитает покой. В полном соответствии с ПНД.

Допустим мы толкнули шарик в сторону стенки. Пусть мы толкнули его как хочет автор, со скоростью, подобранной из краевых условий, так чтобы в момент времени t_B шарик оказался в том же положении, откуда стартовал. Шарик, с постоянной скоростью долетит до стенки, упруго отскочит и вернется в начальное положение в момент времени t_B, опять таки с постоянной скоростью. Ок, это действительное движение. Какое движение будет одним из окольных? Например, если шарик будет двигаться к стенке и от стенки со скоростью, меняющейся со временем. Такое движение возможно кинематически? Возможно. Почему же модуль скорости шарика не меняется? Да потому, что действие на такой фазовой траектории будет иметь минимальное значение, в сравнении с любом другим вариантом, где скорость зависит от времени.

Вот и всё. Ничего такого волшебного тут не происходит. ПНД работает безо всяких проблем.

Выводы и пожелания

ПНД — фундаментальный закон природы. Из него, в частности, вытекают законы механики, например дифференциальные уравнения движения (12). ПНД говорит нам о том, что природа устроена так, что уравнение движения консервативной механической системы выглядит именно как выражение (12) и никак иначе. Большего от него и не требуется.

Не нужно придумывать проблем там где их нет.

НАИМЕ́НЬШЕГО ДЕ́ЙСТВИЯ ПРИ́НЦИП

В книжной версии

Том 21. Москва, 2012, стр. 698

Скопировать библиографическую ссылку:

НАИМЕ́НЬШЕГО ДЕ́ЙСТВИЯ ПРИ́НЦИП, интегральный вариационный принцип механики. Формулируется в разл. формах, отличающихся друг от друга классом сравниваемых кинематически возможных движений и выбором некоторого определённого интеграла, называемого действием , значения которого сравниваются для истинного и кинематически возможных движений.

[spoiler title=”источники:”]

http://bigenc.ru/physics/text/2245107

[/spoiler]

Источник

Принцип наименьшего действия в аналитической механике +29

Математика, Научно-популярное

Рекомендация: подборка платных и бесплатных курсов Python – https://katalog-kursov.ru/

Предыстория

Задача о движении шарика

Не все так просто

На самом деле я немного обманул, сказав, что тела всегда двигаются так, чтобы минимизировать действие. Хотя в очень многих случаях это действительно так, можно придумать ситуации, в которых действие явно не минимально.

Например, возьмем шарик и поместим его в пустое пространство. На некотором отдалении от него поставим упругую стенку. Допустим, мы хотим, чтобы через некоторое время шарик оказался в том же самом месте. При таких заданных условиях шарик может двигаться двумя разными способами. Во-первых, он может просто оставаться на месте. Во-вторых, можно его толкнуть по направлению к стенке. Шарик долетит до стенки, отскочит от нее и вернется обратно. Понятно, что можно толкнуть его с такой скоростью, чтобы он вернулся в точно нужное время.

Оба варианта движения шарика возможны, но действие во втором случае получится больше, потому что все это время шарик будет двигаться с ненулевой кинетической энергией.

Как же спасти принцип наименьшего действия, чтобы он был справедлив и в таких ситуациях? Об этом мы поговорим в следующий раз.

Так в чем же, с моей точки зрения, проблема?

1. Определение действия по Гамильтону. Принцип наименьшего действия

Действием по Гамильтону называют функционал

$S = intlimits_{t_1}^{t_2} , Lleft(mathbf q(t), dot{mathbf q}(t) right) , dt$

где

Принцип наименьшего действия:

Механическая система, для которой задана функция Лагранжа , движется таким образом, что закон её движения q(t) доставляет минимум функционалу

$S = intlimits_{t_1}^{t_2} , Lleft(mathbf q(t), dot{mathbf q}(t) right) , dt to min$

называемому действием по Гамильтону.

2. Границы применимости принципа наименьшего действия. Некоторые определения для самых маленьких

Работа силы на перемещении

Рассмотрим движущуюся по траектории AB точку, к которой приложена сила

$vec F$ . Бесконечно малое перемещение точки по траектории определяется вектором

, направленным по касательной к траектории.

Элементарной работой силы

$vec F$ на перемещении

называют скалярную величину, равную

Тогда, полная работа силы на перемещении точки по траектории AB есть криволинейный интеграл

$A = intlimits_{AB} , vec F cdot dvec s$

Кинетическая энергия точки

Кинетической энергией точки T называют работу, которую должны совершить приложенные к точке массой m силы, для того чтобы из состояния покоя перевести точку в движение со скоростью

Вычислим кинетическую энергию, согласно данному определению. Пусть точка начинает движение из состояния покоя под действием приложенных к ней сил. На отрезке траектории AB она приобретает скорость

$vec v$ . Вычислим работу, совершенную приложенными к точке силами, которые, по принципу независимости действия сил, заменим равнодействующей

$vec F$

$T = A = intlimits_{AB} , vec F cdot dvec s$

В соответствии со вторым законом Ньютона

$vec F = m , vec a = m , frac{dvec v}{dt}$

тогда

$T = intlimits_{AB} , vec F cdot dvec s = m , intlimits_{AB} frac{dvec v}{dt} , cdot dvec s = m intlimits_{AB} , vec v cdot dvec v$

$frac{d}{dt}(vec v cdot vec v) = frac{dvec v}{dt} cdot vec v + vec v cdot frac{dvec v}{dt} = 2 , vec v cdot frac{dvec v}{dt} quad (1)$

С другой стороны,

Дифференцируя это равенство по времени, имеем

$frac{d}{dt}(vec v cdot vec v) = frac{d}{dt}(v^2) = 2 , v , frac{dv}{dt} quad(2)$

Сравнивая (1) и (2) приходим к выводу, что

$T = m intlimits_{AB} vec v cdot dvec v = m intlimits_0^v v , dv = frac{m,v^2}{2}$

Консервативные силы и потенциальная энергия точки

Рассмотрим действующую на точку силу, причем такую, что величина и направление этой силы зависит исключительно от положения точки в пространстве

$A = intlimits_{AB} vec F cdot dvec s = intlimits_{AB} left(F_x , dx + F_y , dy + F_z , dzright)$

такую, что

$F_x = frac{partial U}{partial x},quad F_y = frac{partial U}{partial y},quad F_z = frac{partial U}{partial z}$

Тогда, выражение для работы преобразуется к виду

$A = intlimits_{AB} left(frac{partial U}{partial x} , dx + frac{partial U}{partial y} , dy + frac{partial U}{partial z} , dzright) = intlimits_{U_A}^{U_B} , dU=U_B - U_A$

где

— значения функции U(x, y, z) в точках A и B соответственно. Таким образом работа рассматриваемой нами силы не зависит от траектории точки, а определяется только значениями функции U в начале и в конце траектории. Такая сила называется консервативной силой, а соответствующая ей функция U(x, y, z) — силовой функцией. Очевидно, что

, а так же равенство нулю работы консервативной силы при движении по замкнутой траектории. Говорят так же, что функция U(x, y, z) задает в пространстве силовое поле.

Потенциальной энергией точки, в пространстве с заданным силовым полем, называют работу внешних сил, приложенных к ней, которую они совершают при перемещении точки в заданное координатами (x, y, z) положение в пространстве из некоторого произвольного положения, выбранного в качестве начала отсчета уровня потенциальной энергии.

Выберем на рассмотренной ранее траектории точки произвольную точку O, лежащую между точками A и B. Положим, что в точке О потенциальная энергия равна нулю. Тогда, согласно определению

— потенциальная энергия точки в положении A, а

$A_{AB} = A_{AO} + A_{OB} = U_O - U_A + U_B - U_O = (U_O - U_A) - (U_O - U_B) = Pi_A - Pi_B$

$A_{AB} = Pi_A - Pi_B = -(Pi_B - Pi_A) = -Delta Pi$

3. Понятие о вариациях обобщенных координат. Постановка вариационной задачи

Итак, рассмотрим теперь механическую систему, движущуюся под действием потенциальных сил, положение которой однозначно задается вектором обобщенных координат

где s — число степеней свободы данной системы.

, полагая аналогичные рассуждения и для всех остальных координат.

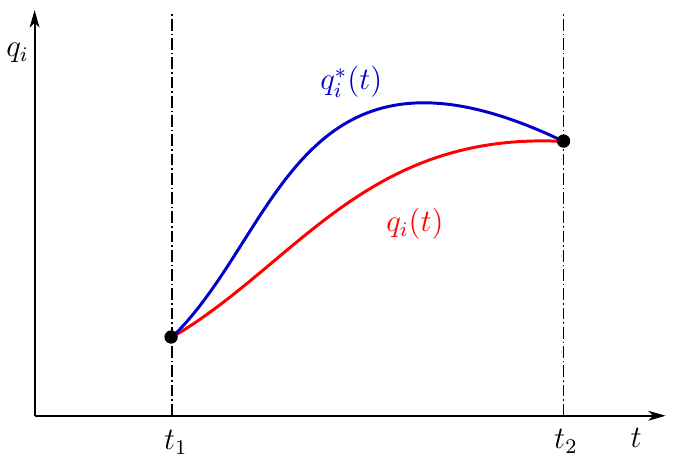
Рисунок 1. Действительное и окольное движение механической системы

На рисунке зависимость

изображена красной кривой. Выберем два произвольных фиксированных момента времени t₁ и t₂, полагая t₂ > t₁. Положение системы

договоримся называть начальным положением системы, а

— конечным положением системы.

Далее мы полагаем, что из начального положения в конечное система может придти разными путями, то есть зависимость

может быть любой кинематически возможной. Действительное движение системы будет существовать в единственном варианте (красная кривая), остальные кинематически возможные варианты будем называть окольными движениями

$mathbf q^{*} = mathbf q^{*}(t)$ (синяя кривая на рисунке). Разность между действительным и окольным движением

$delta q_i(t) = q^{*}_i(t) - q_i(t),quad forall i=overline{1,s}quad (5)$

будем называть изохронными вариациями обобщенных координат

$delta q_i(t_1) = delta q_i(t_2) = 0,quad forall i=overline{1,s}quad(6)$

$delta S = delta intlimits_{t_1}^{t2} , L(q_1,dots,q_s,,dot q_1,dots,dot q_s),dt = 0quad(7)$

4. Решение вариационной задачи. Уравнения Лагранжа 2-го рода

Решим поставленную нами вариационную задачу, для чего вычислим полную вариацию функционала действия и приравняем её к нулю

$begin{align} delta S = & intlimits_{t_1}^{t2} , L(q_1 + delta q_1,dots,q_s + delta q_s,,dot q_1 + deltadot q_1,dots,dot q_s + deltadot q_s),dt - \ &- intlimits_{t_1}^{t2} , L(q_1,dots,q_s,,dot q_1,dots,dot q_s),dt = 0 end{align}$

$intlimits_{t_1}^{t_2}left[ sumlimits_{i=1}^s frac{partial L}{partial q_i}delta q_i + sumlimits_{i=1}^s frac{partial L}{partial dot q_i}delta dot q_i right],dt = 0quad(8)$

Исходя из определения обобщенной скорости

$delta dot q_i = frac{d(delta q_i)}{dt}$

Тогда выражение (8) преобразуется к виду

$intlimits_{t_1}^{t_2}left[ sumlimits_{i=1}^s frac{partial L}{partial q_i}delta q_i , dt + sumlimits_{i=1}^s frac{partial L}{partial dot q_i}d(delta q_i) right] = 0$

Второе слагаемое интегрируется по частям

$sumlimits_{i=1}^s frac{partial L}{partial dot q_i}delta q_i|_{t_1}^{t_2} + intlimits_{t_1}^{t_2}left[ sumlimits_{i=1}^s frac{partial L}{partial q_i}delta q_i - sumlimits_{i=1}^s frac{d}{dt}left(frac{partial L}{partial dot q_i}right)delta q_i right],dt = 0quad(10)$

Исходя из условия (7), имеем

$sumlimits_{i=1}^s frac{partial L}{partial dot q_i}delta q_i|_{t_1}^{t_2} = 0$

тогда, получаем уравнение

$intlimits_{t_1}^{t_2}left[ sumlimits_{i=1}^s left( frac{partial L}{partial q_i} - frac{d}{dt}left(frac{partial L}{partial dot q_i}right) right) , delta q_i right],dt = 0$

$sumlimits_{i=1}^s left[ frac{partial L}{partial q_i} - frac{d}{dt}left(frac{partial L}{partial dot q_i}right) right] , delta q_i = 0quad(11)$

$frac{partial L}{partial q_i} - frac{d}{dt}left(frac{partial L}{partial dot q_i}right) =0, quad forall i = overline{1,s}$

Никто не мешает нам умножить каждое из уравнений на (-1) и получить более привычную запись

$frac{d}{dt}left(frac{partial L}{partial dot q_i}right) - frac{partial L}{partial q_i} =0, quad forall i = overline{1,s}quad(12)$

$mathbf q = mathbf q(t, C_1, C_2,dots,C_{2s})$

где C₁,…,C_2s — произвольные константы интегрирования.

Таким образом

ПНД — фундаментальный принцип, позволяющий получить уравнения движения системы, для которой определена функция Лагранжа

5. Задача с шариком и стенкой

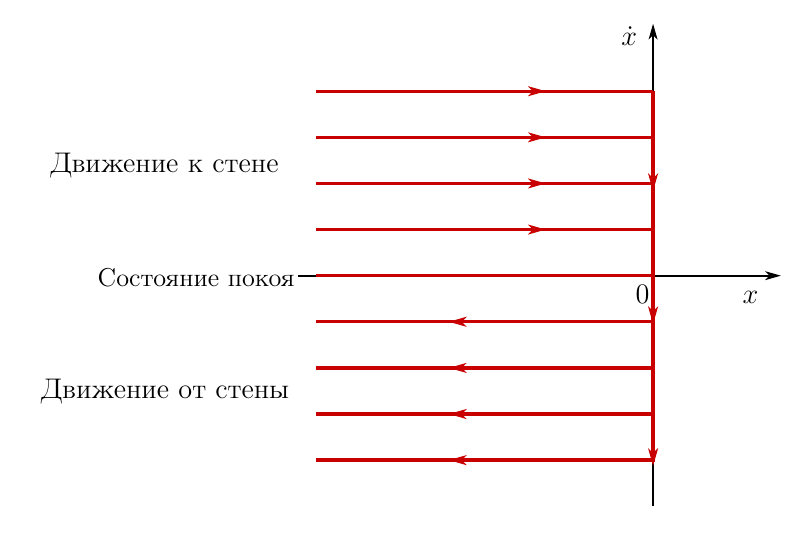
Рисунок 2. Фазовый портрет системы в задаче с шариком

Вот и всё. Ничего такого волшебного тут не происходит. ПНД работает безо всяких проблем.

Выводы и пожелания

Не нужно придумывать проблем там где их нет.

Источник

Главная >> Фейнмановские лекции по физике >> Том 6

Когда я учился в школе, наш учитель физики, по фамилии Бадер, однажды зазвал меня к себе после урока и сказал: «У тебя вид такой, как будто тебе все страшно надоело; послушай-ка об одной интересной вещи». И он рассказал мне нечто, что мне показалось поистине захватывающим. Даже сейчас, хотя с тех пор прошла уже уйма времени, это продолжает меня увлекать. И всякий раз, когда я вспоминаю о сказанном, я вновь принимаюсь за работу. И на этот раз, готовясь к лекции, я поймал себя на том, что вновь анализирую все то же самое. И, вместо того чтобы готовиться к лекции, я взялся за решение новой задачи. Предмет, о котором я говорю,— это принцип наименьшего действия.

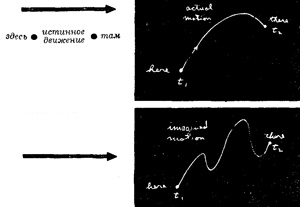
– Вот что сказал мне тогда мой учитель Бадер: «Пусть, к примеру, у тебя имеется частица в поле тяжести; эта частица, выйдя откуда-то, свободно движется куда-то в другую точку. Ты подбросил ее, скажем, кверху, а она взлетела, а потом упала.

От исходного места к конечному она прошла за какое-то время. Попробуй теперь какое-то другое движение. Пусть для того, чтобы перейти «отсюда сюда», она двигалась уже не так, как раньше, а вот так:

но все равно очутилась на нужном месте в тот же самый момент времени, что и раньше».

«И вот,— продолжал учитель,— если ты подсчитаешь кинетическую энергию в каждый момент времени на пути частицы, вычтешь из нее потенциальную энергию и проинтегрируешь разность по всему тому времени, когда происходило движение, то увидишь, что число, которое получится, будет больше, чем при истинном движении частицы.

Иными словами, законы Ньютона можно сформулировать не в виде F=ma, а вот как: средняя кинетическая энергия минус средняя потенциальная энергия достигает своего самого наименьшего значения на той траектории, по которой предмет двигается в действительности от одного места к другому.

Попробую пояснить тебе это чуть понятнее.
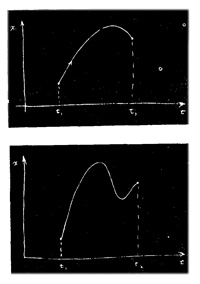
Если взять поле тяготения и обозначить траекторию частицы x(t), где х — высота над землей (обойдемся пока одним измерением; пусть траектория пролегает только вверх и вниз, а не в стороны), то кинетическая энергия будет y₂m(dx/dt)², a потенциальная энергия в произвольный момент времени будет равна mgx.

Теперь я для какого-то момента движения по траектории беру разность кинетической и потенциальной энергий и интегрирую по всему времени от начала до конца. Пусть в начальный момент времени t_x движение началось на какой-то высоте, а кончилось в момент t₂ на другой определенной высоте.

Тогда интеграл равен ∫^t2_t1[1/2m(dx/dt)² – mgx]dt

Истинное движение совершается по некоторой кривой (как функция времени она является параболой) и приводит к какому-то определенному значению интеграла. Но можно представить себе какое-то другое движение: сперва резкий подъем, а потом какие-то причудливые колебания.

Можно подсчитать разность потенциальной и кинетической энергий на таком пути… или на любом другом. И самое поразительное — что настоящий путь это тот, по которому этот интеграл наименьший.
Давай проверим это. Для начала разберем такой случай: у свободной частицы вовсе нет потенциальной энергии. Тогда правило говорит, что при переходе от одной точки к другой за заданное время интеграл от кинетической энергии должен оказаться наименьшим. А это значит, что частица обязана двигаться равномерно. (И это правильно, мы же с тобой знаем, что скорость в таком движении постоянна.) А почему равномерно? Разберемся в этом. Если бы было иначе, то временами скорость частицы превысила бы среднюю, а временами была бы ниже ее, а средняя скорость была бы одинаковой, потому что частице надо было бы дойти «отсюда сюда» за условленное время. Например, если тебе нужно попасть из дому в школу на своей машине за определенное время, то сделать это можно по-разному: ты можешь сперва гнать, как сумасшедший, а в конце притормозить, или ехать с одинаковой скоростью, или сначала можешь даже отправиться в обратную сторону, а уж потом повернуть к школе, и т. д. Во всех случаях средняя скорость, конечно, должна быть одной и той же — частное от деления расстояния от дома до школы на время. Но и при данной средней скорости ты иногда двигался слишком быстро, а иногда чересчур медленно. А средний квадрат чего-то, что отклоняется от среднего, как известно, всегда больше квадрата среднего; значит, интеграл от кинетической энергии при колебаниях скорости движения всегда будет больше, нежели при движении с постоянной скоростью. Ты видишь, что интеграл достигнет минимума, когда скорость будет постоянной (при отсутствии сил). Правильный путь таков.

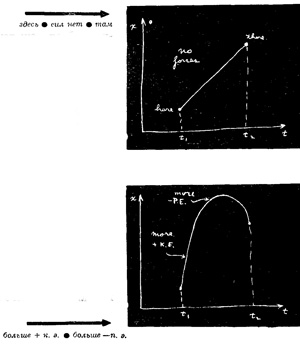Предмет же, подброшенный в поле тяжести вверх, сперва поднимается быстро, а потом все медленнее. Происходит это потому, что он обладает и потенциальной энергией, а наименьшего значения должна достигать разность между кинетической и потенциальной энергиями.. Раз потенциальная энергия возрастает по мере подъема, то меньшая разность получится, если как можно быстрее достичь тех высот, где потенциальная энергия велика. Тогда, вычтя из кинетической энергии этот высокий потенциал, мы добьемся уменьшения среднего. Так что выгоднее такой путь, который идет вверх и поставляет добрый отрицательный кусок за счет потенциальной энергии.

Вот и все, что сказал мне мой учитель, потому что он был очень хороший учитель и знал, когда пора остановиться. Сам я, увы, не таков. Мне трудно остановиться вовремя. И поэтому вместо того, чтобы просто разжечь в вас интерес своим рассказом, я хочу запугать вас, хочу, чтобы вам стало тошно от сложности жизни,— попробую доказать то, о чем я рассказал. Математическая задача, которую мы будем решать, очень трудна и своеобразна. Имеется некоторая величина S, называемая действием. Она равна кинетической энергии минус потенциальная, проинтегрированная по времени:

Но, с другой стороны, нельзя ни двигаться слишком быстро, ни подняться слишком высоко, потому что на это потребуется чересчур много кинетической энергии. Надо двигаться достаточно быстро, чтобы подняться и спуститься за определенное время, имеющееся в твоем распоряжении. Так что не следует стараться взлететь слишком высоко, а просто надо достичь какого-то разумного уровня. В итоге оказывается, что решение есть своего рода равновесие между желанием раздобыть как можно больше потенциальной энергии и желанием как можно сильней уменьшить количество кинетической энергии — это стремление добиться максимального уменьшения разности кинетической и потенциальной энергий».

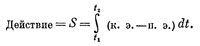
Не забудьте, что и п. э. и к. э.— обе функции времени. Для любого нового мыслимого пути это действие принимает свое определенное значение. Математическая задача состоит в том, чтобы определить, для какой кривой это число меньше, чем для других.

Вы скажете: «О, это просто обычный пример на максимум и минимум. Надо подсчитать действие, продифференцировать его и найти минимум».

Но погодите. Обычно у нас бывает функция какой-то переменной и нужно найти значение переменной, при котором функция становится наименьшей или наибольшей. Скажем, имеется стержень, нагретый посредине. По нему растекается тепло и в каждой точке стержня устанавливается своя температура. Нужно найти точку, где она выше всего. Но у нас речь идет совсем об ином — каждому пути в пространстве отвечает свое число, и предполагается найти тот путь, для которого это число минимально. Это совсем другая область математики. Это не обычное исчисление, а вариационное (так его называют).

В этой области математики имеется много своих задач. Скажем, окружность обычно определяют как геометрическое место точек, расстояния которых от данной точки одинаковы, но окружность можно определить и иначе: это та из кривых данной длины, которая ограничивает собою наибольшую площадь. Любая другая кривая такого же периметра ограничивает площадь меньшую, чем окружность. Так что если поставить задачу: найти кривую данного периметра, ограничивающую наибольшую площадь, то перед нами будет задача из вариационного исчисления, а не из того исчисления, к которому вы привыкли.

Итак, мы хотим взять интеграл по пути, пройденному телом. Сделаем это так. Все дело в том, чтобы вообразить себе, что существует истинный путь и что любая другая кривая, которую мы проведем,— не настоящий путь, так что если подсчитать для нее действие, то получится число, превышающее то, которое мы получим для действия, соответствующего настоящему пути.

Итак, задача: найти истинный путь. Где он пролегает? Один из способов конечно, мог бы состоять в том, чтобы подсчитать действие для миллионов и миллионов путей и потом посмотреть, при каком пути это действие наименьшее. Вот тот путь, при котором действие минимально, и будет настоящим.

Такой способ вполне возможен. Однако можно сделать проще. Если имеется величина, обладающая минимумом (из обычных функций, скажем, температура), то одно из свойств минимума состоит в том, что при удалении от него на расстояние первого порядка малости функция отклоняется от минимального своего значения только на величину второго порядка. А в любом другом месте кривой сдвиг на малое расстояние изменяет значение функции тоже на величину первого порядка малости. Но в минимуме легкие уходы в сторону в первом приближении не приводят к изменению функции.

Это-то свойство мы и собираемся использовать для расчета настоящего пути.

Если путь правильный, то кривая, чуть-чуть отличная от него, не приведет в первом приближении к изменению в величине действия. Все изменения, если это был действительно минимум, возникнут только во втором приближении.

Это легко доказать. Если при каком-то отклонении от кривой возникают изменения в первом порядке, то эти изменения в действии пропорциональны отклонению. Они, по всей вероятности, увеличат действие; иначе это не был бы минимум. Но раз изменения пропорциональны отклонению, то перемена знака отклонения уменьшит действие. Выходит, что при отклонении и одну сторону действие возрастает, а при отклонении в обратную сторону — убывает. Единственная возможность того, чтобы это действительно был минимум,— это чтобы в первом приближении никаких изменений не происходило и изменения были бы пропорциональны квадрату отклонения от настоящего пути.

Итак, мы пойдем по следующему пути: обозначим через x(t) (с чертой внизу) истинный путь — тот, который мы хотим найти. Возьмем некоторый пробный путь x(t), отличающийся от искомого на небольшую величину, которую мы обозначим η(t).

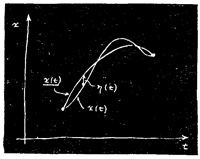Идея состоит в том, что если мы подсчитаем действие S на пути x(t), то разность между этим S и тем действием, которое мы вычислили для пути x(t) (для простоты оно будет обозначено S), или разность между S_ и S, должна быть в первом приближении по η нулем. Они могут отличаться во втором порядке, но в первом разность обязана быть нулем.

И это должно соблюдаться для любой η. Впрочем, не совсем для любой. Метод требует принимать во внимание только те пути, которые все начинаются и кончаются в одной и той же паре точек, т. е. всякий путь должен начинаться в определенной точке в момент t₁ и кончаться в другой определенной точке в момент t₂. Эти точки и моменты фиксируются. Так что наша функция г) (отклонение) должна быть равна нулю на обоих концах: η(t₁)=0 и η(t₂)=0. При этом условии наша математическая задача становится полностью определенной.

Если бы вы не знали дифференциального исчисления, вы могли бы проделать такую же вещь для отыскания минимума обычной функции f(x). Вы бы задумались над тем, чтб случится, если взять f(x) и прибавить к х малую величину h, и доказывали бы, что поправка к f(x) в первом порядке по h должна в минимуме быть равна нулю. Вы бы подставили x+h вместо х и разложили бы j(x+h) с точностью до первой степени h. . ., словом, повторили бы все то, что мы намерены сделать с η.

Если мы теперь внимательно взглянем на это, то увидим, что два первых написанных здесь члена отвечают тому действию S, которое я написал бы для искомого истинного пути х. Я хочу сосредоточить ваше внимание на изменении S, т. е. на разности между S и тем S_, которое получилось бы для истинного пути. Эту разность мы будем записывать как bS и назовем ее вариацией S. Отбрасывая «второй и высшие порядки», получаем для σS

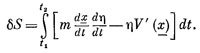
Теперь задача выглядит так. Вот передо мной некоторый интеграл. Я не знаю еще, каково это ж, но я твердо знаю, что, какую η я ни возьму, этот интеграл должен быть равен нулю. «Ну что ж,— подумаете вы,— единственная возможность для этого — это чтобы множитель при η был равен нулю». Но как быть с первым слагаемым, где есть dη/dt? Вы скажете: «Если η обращается в ничто, то и ее производная такое же ничто; значит, коэффициент при dv/dt должен тоже быть нулем». Ну это не совсем верно. Это не совсем верно потому, что между отклонением η и его производной имеется связь; они не полностью независимы, потому что η(t) должно быть нулем и при t₁ и при t₂.

При решении всех задач вариационного исчисления всегда пользуются одним и тем же общим принципом. Вы чуть сдвигаете то, что хотите варьировать (подобно тому, как это сделали мы, добавляя η), бросаете взгляд на члены первого порядка, затем расставляете все так, чтобы получился интеграл в таком виде: «сдвиг (η), умноженный на что получится», но чтобы в нем не было никаких производных от η (никаких dη/dt). Непременно нужно так все преобразовать, чтобы осталось «нечто», умноженное на η. Сейчас вы поймете, отчего это так важно. (Существуют формулы, которые подскажут вам, как в некоторых случаях можно это проделать без каких-либо выкладок; но они не так уж общи, чтобы стоило заучивать их; лучше всего проделывать выкладки так, как это делаем мы.)

Как же я могу переделать член dη/dt, чтобы в нем появилось η? Я могу добиться этого, интегрируя по частям. Оказывается, что в вариационном исчислении весь фокус в том и состоит, чтобы расписать вариацию S и затем проинтегрировать по частям так, чтобы производные от η исчезли. Во всех задачах, в которых появляются производные, проделывается такой же фокус.

Припомните общий принцип интегрирования по частям. Если у вас есть произвольная функция f, умноженная на dη/dt и проинтегрированная по t, то вы расписываете производную от η/t

В первый член должны быть подставлены пределы интегрирования t₁ и t₂. Тогда я получу под интегралом член от интегрирования по частям и последний член, оставшийся при преобразовании неизменным.
А теперь происходит то, что бывает всегда,— проинтегрированная часть исчезает. (А если не исчезает, то нужно переформулировать принцип, добавив условия, обеспечивающие такое исчезновение!) Мы уже говорили, что η на концах пути должна быть равна нулю. Ведь в чем состоит наш принцип? В том, что действие минимально при условии, что варьируемая кривая начинается и кончается в избранных точках. Это значит, что η(t₁)=0 и η(t₂)=0. Поэтому проинтегрированный член получается равным нулю. Мы собираем воедино остальные члены и пишем

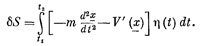
Вариация S теперь приобрела такой вид, какой мы хотели ей придать: что-то стоит в скобках (обозначим его F), и все это умножено на η(t) и проинтегрировано от t_t до t₂.
У нас вышло, что интеграл от какого-то выражения, умноженного на η(t), всегда равен нулю:

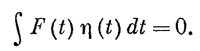
Стоит какая-то функция от t; умножаю ее на η(t) и интегрирую ее от начала до конца. И какова бы ни была η, я получаю нуль. Это означает, что функция F(t) равна нулю. В общем-то это очевидно, но я на всякий случай покажу вам один из способов доказательства.

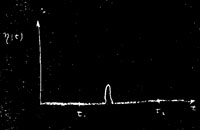Пусть в качестве η(t) я выберу нечто, что равно нулю всюду, при всех t, кроме одного, заранее выбранного значения t. Оно остается нулем, пока я не дойду до этого t, затем оно подскакивает на мгновение и сразу же осаживает назад. Если вы берете интеграл от этой т), умноженной на какую-то функцию F, то единственное место, в котором вы получите что-то ненулевое,— это там, где η(t) подскакивало; и у вас получится значение F в этом месте на интеграл по скачку. Сам но себе интеграл по скачку не равен нулю, но после умножения на F он должен дать нуль. Значит, функция в том месте, где был скачок, должна оказаться нулем. Но ведь скачок можно было сделать в любом месте; значит, F должна быть нулем всюду.

Мы видим, что если наш интеграл равен нулю при какой угодно η, то коэффициент при η должен обратиться в нуль. Интеграл действия достигает минимума на том пути, который будет удовлетворять такому сложному дифференциальному уравнению:

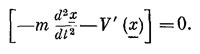
На самом деле оно не так уж сложно; вы его уже встречали прежде. Это просто F=ma. Первый член — это масса, умноженная на ускорение; второй — это производная от потенциальной энергии, т. е. сила.

Итак, мы показали (по крайней мере для консервативной системы), что принцип наименьшего действия приводит к правильному ответу; он утверждает, что путь, обладающий минимумом действия,— это путь, удовлетворяющий закону Ньютона.

Нужно сделать еще одно замечание. Я не доказал, что это минимум. Может быть, это максимум. На самом деле это и не обязательно должен быть минимум. Здесь все так же, как в «принципе кратчайшего времени», который мы обсуждали, изучая оптику. Там тоже мы сперва говорили о «кратчайшем» времени. Однако выяснилось, что бывают положения, в которых это время не обязательно «кратчайшее». Фундаментальный принцип заключается в том, чтобы для любых отклонений первого порядка от оптического пути изменения во времени были бы равны нулю; здесь та же самая история. Под «минимумом» мы на самом деле подразумеваем, что в первом порядке малости изменения величины S при отклонениях от пути должны быть равны нулю. И это не обязательно «минимум».

Теперь я хочу перейти к некоторым обобщениям. В первую очередь всю эту историю можно было бы проделать и в трех измерениях. Вместо простого х я тогда имел бы х, у и z как функции t, и действие выглядело бы посложнее. При трехмерном движении вы должны использовать полную кинетическую энергии): (т/2), умноженное на квадрат всей скорости. Иначе говоря

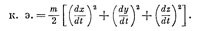
Кроме того, потенциальная энергия теперь является функцией х, у и z. А что можно сказать о пути? Путь есть некоторая кривая общего вида в пространстве; ее не так легко начертить, но идея остается прежней. А как обстоит дело с η? Что ж, и η имеет три компоненты. Путь можно сдвигать и по x, и по у, и по z, или во всех трех направлениях одновременно. Так что η теперь вектор. От этого сильных усложнений не получается. Раз нулю должны быть равны лишь вариации первого порядка, то можно провести расчет последовательно с тремя сдвигами. Сперва можно сдвинуть ц только в направлении х и сказать, что коэффициент должен обратиться в нуль. Получится одно уравнение. Потом мы сдвинем ц в направлении у и получим второе. Затем сдвинем в направлении z и получим третье. Можно все, если угодно, проделать в другом порядке. Как бы то ни было, возникает тройка уравнений. Но ведь закон Ньютона — это тоже три уравнения в трех измерениях, по одному для каждой компоненты. Вам предоставляется самим убедиться, что это все действует и в трех измерениях (работы здесь не так много). Между прочим, можно взять какую угодно систему координат, полярную, любую, и сразу получить законы Ньютона применительно к этой системе, рассматривая, что получится, когда произойдет сдвиг η вдоль радиуса или по углу, и т. д.

Метод может быть обобщен и на произвольное число частиц. Если, скажем, у вас есть две частицы и между ними действуют какие-то силы и имеется взаимная потенциальная энергия, то вы просто складываете их кинетические энергии и вычитаете из суммы потенциальную энергию взаимодействия. А что вы варьируете? Пути обеих частиц. Тогда для двух частиц, движущихся в трех измерениях, возникает шесть уравнений. Вы можете варьировать положение частицы 1 в направлении х, в направлении у и в направлении z, и то же самое проделать с частицей 2, так что существует шесть уравнений. И так и должно быть. Три уравнения определяют ускорение частицы 1 через силу, действующую на нее, а три других — ускорение частицы 2 из-за силы, действующей на нее. Следуйте всегда тем же правилам игры, и вы получите закон Ньютона для произвольного числа частиц.

Я сказал, что мы получим закон Ньютона. Это не совсем верно, потому что в закон Ньютона входят и неконсервативные силы, например трение. Ньютон утверждал, что та равно всякой F. Принцип же наименьшего действия справедлив только для консервативных систем, таких, где все силы могут быть получены из потенциальной функции. Но ведь вы знаете, что на микроскопическом уровне, т. е. на самом глубинном физическом уровне, неконсервативных сил не существует. Неконсервативные силы (такие, как трение) появляются только от того, что мы пренебрегаем микроскопическими сложными эффектами: просто слишком много частиц приходится анализировать. Фундаментальные же законы могут быть выражены в виде принципа наименьшего действия.

Позвольте перейти к дальнейшим обобщениям. Положим, нас интересует, что будет, когда частица движется релятивистски. Пока мы не получили правильного релятивистского уравнения движения; F=ma верно только в нерелятивистских движениях. Встает вопрос: существует ли в релятивистском случае соответствующий принцип наименьшего действия? Да, существует. Формула в релятивистском случае такова:

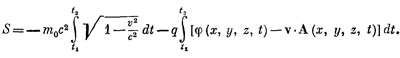
Первая часть интеграла действия — это произведение массы покоя т₀ на с² и на интеграл от функции скорости √(1- v²/c²). Затем вместо того, чтобы вычитать потенциальную энергию, мы имеем интегралы от скалярного потенциала φ и от векторного потенциала А, умноженного на v. Конечно, здесь приняты во внимание только электромагнитные силы. Все электрические и магнитные поля выражены в терминах φ и А. Такая функция действия дает полную теорию релятивистского движения отдельной частицы в электромагнитном поле.

Конечно, вы должны понимать, что всюду, где я написал v, прежде чем делать выкладки, следует подставить dx/dt вместо v_x и т. д. Кроме того, там, где я писал просто х, у, z, вы должны представить себе точки в момент t: x(t), y(t), z(t). Собственно, только после таких подстановок и замен v у вас получится формула для действия релятивистской частицы. Пусть самые умелые из вас попытаются доказать, что эта формула для действия действительно дает правильные уравнения движения теории относительности. Позвольте лишь посоветовать для начала отбросить А, т. е. обойтись пока без магнитных полей. Тогда вы должны будете получить компоненты уравнения движения dp/dt=—qVφ, где, как вы, вероятно, помните, p=mv√(1-v²/c²).

Включить в рассмотрение векторный потенциал А намного труднее. Вариации тогда становятся несравненно более сложными. Но в конце сила оказывается равной тому, чему следует: g(E+v × B). Но позабавьтесь с этим сами.

Мне хотелось бы подчеркнуть, что в общем случае (к примеру, в релятивистской формуле) под интегралом в действии уже не стоит разность кинетической и потенциальной энергий. Это годилось только в нерелятивистском приближении. Например, член m_oc²√(1-v²/c²) -это не то, что называют кинетической энергией. Вопрос о том, каким должно быть действие для произвольного частного случая, может быть решен после некоторого числа проб и ошибок. Это задача того же типа, что и определение, каковы должны быть уравнения движения. Вы просто должны поиграть с известными вам уравнениями и посмотреть, можно ли их написать в виде принципа наименьшего действия.

Еще одно замечание по поводу терминологии. Ту функцию, которую интегрируют по времени, чтобы получить действие S, называют лагранжианом Λ. Это функция, зависящая только от скоростей и положений частиц. Так что принцип наименьшего действия записывается также в виде

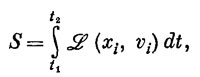
где под х_iи v_i подразумеваются все компоненты координат и скоростей. Если вы когда-нибудь услышите, что кто-то говорит о «лагранжиане», знайте, что речь идет о функции, применяемой для получения S. Для релятивистского движения в электромагнитном поле

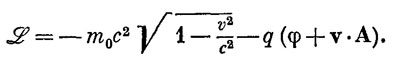
Кроме того, я должен отметить, что самые дотошные и педантичные люди не называют S действием. Его именуют «первой главной функцией Гамильтона». Но читать лекцию о «принципе наименьшей первой главной функции Гамильтона» было свыше моих сил. Я назвал это «действием». Да к тому же все больше и больше людей называют это «действием». Видите ли, исторически действием было названо нечто другое, не столь полезное для науки, но я думаю, что разумнее изменить определение. Теперь и вы начнете именовать новую функцию действием, а вскоре и все вообще станут называть ее этим простым именем.

Теперь я хочу сообщить вам по поводу нашей темы кое-что, похожее на те рассуждения, которые я вел по поводу принципа кратчайшего времени. Существует разница в самом существе закона, утверждающего, что некоторый интеграл, взятый от одной точки до другой, имеет минимум,— закона, который сообщает нам что-то обо всем пути сразу, и закона, который говорит, что когда вы двигаетесь, то, значит, есть сила, приводящая к ускорению. Второй подход докладывает вам о каждом вашем шаге, он прослеживает ваш путь пядь за пядью, а первый выдает сразу какое-то общее утверждение обо всем пройденном пути. Толкуя о свете, мы говорили о связи этих двух подходов. Теперь я хочу объяснить вам, отчего должны существовать дифференциальные законы, если имеется такой принцип — принцип наименьшего действия. Причина вот в чем: рассмотрим действительно пройденный в пространстве и времени путь. Как и прежде, обойдемся одним измерением, так что можно будет начертить график зависимости х от t. Вдоль истинного пути S достигает минимума. Положим, что у нас есть этот путь и что он проходит через некоторую точку а пространства и времени и через другую соседнюю точку b.

Теперь, если весь интеграл от t₁ до t₂ достиг минимума, необходимо, чтобы интеграл вдоль маленького участочка от а до b тоже был минимальным. Не может быть, чтобы часть от а до b хоть чуточку превосходила минимум. Иначе вы могли бы подвигать туда-сюда кривую на этом участочке и снизить немного значение всего интеграла.

Значит, любая часть пути тоже должна давать минимум. И это справедливо для каких-угодно маленьких долек пути. Поэтому тот принцип, что весь путь должен давать минимум, можно сформулировать, сказав, что бесконечно малая долька пути — это тоже такая кривая, на которой действие минимально. И если мы возьмем достаточно короткий отрезок пути — между очень близкими друг к другу точками а и b,— то уже неважно, как меняется потенциал от точки к точке вдали от этого места, потому что, проходя весь ваш коротенький отрезочек, вы почти не сходите с места. Единственное, что вам нужно учитывать,— это изменение первого порядка малости в потенциале. Ответ может зависеть только от производной потенциала, а не от потенциала в других местах. Так, утверждение о свойстве всего пути в целом становится утверждением о том, что происходит на коротком участке пути, т. е. дифференциальным утверждением. И эта дифференциальная формулировка включает производные от потенциала, т. е. силу в данной точке. Таково качественное объяснение связи между законом в целом и дифференциальным законом.

Когда мы говорили о свете, то обсуждали также вопрос: как все-таки частица находит правильный путь? С дифференциальной точки зрения это понять легко. В каждый момент частица испытывает ускорение и знает только то, что ей положено делать в это мгновение. Но все ваши инстинкты причин и следствий встают на дыбы, когда вы слышите, что частица «решает», какой ей выбрать путь, стремясь к минимуму действия. Уж не «обнюхивает» ли она соседние пути, прикидывая, к чему они приведут — к большему или к меньшему действию? Когда мы на пути света ставили экран так, чтобы фотоны не могли перепробовать все пути, мы выяснили, что они не могут решить, каким путем идти, и получили явление дифракции.

Но верно ли это и для механики? Правда ли, что частица не просто «идет верным путем», а пересматривает все другие мыслимые траектории? И что если, ставя преграды на ее пути, мы не дадим ей заглядывать вперед, то мы получим некий аналог явления дифракции? Самое чудесное во всем этом — то, что все действительно обстоит так. Именно это утверждают законы квантовой механики. Так что наш принцип наименьшего действия сформулирован не полностью. Он состоит не в том, что частица избирает путь наименьшего действия, а в том, что она «чует» все соседние пути и выбирает тот, вдоль которого действие минимально, и способ этого выбора сходен с тем, каким свет отбирает кратчайшее время. Вы помните, что способ, каким свет отбирает кратчайшее время, таков: если свет пойдет по пути, требующему другого времени, то придет он с другой фазой. А полная амплитуда в некоторой точке есть сумма вкладов амплитуд для всех путей, по которым свет может ее достичь. Все те пути, у которых фазы резко различаются, ничего после сложения не дают. Но если вам удалось найти всю последовательность путей, фазы которых почти одинаковы, то мелкие вклады сложатся, и в точке прибытия полная амплитуда получит заметное значение. Важнейшим путем становится тот, возле которого имеется множество близких путей, дающих ту же фазу.

В точности то же происходит и в квантовой механике. Законченная квантовая механика (нерелятивистская и пренебрегающая спином электрона) работает так: вероятность того, что частица, выйдя из точки 1 в момент t₁, достигнет точки 2 в момент t₂, равна квадрату амплитуды вероятности. Полная амплитуда может быть записана в виде суммы амплитуд для всех возможных путей — для любого пути прибытия. Для любого x(t), которое могло бы возникнуть для любой мыслимой воображаемой траектории, нужно подсчитать амплитуду. Затем их все нужно сложить. Что же мы примем за амплитуду вероятности некоторого пути? Наш интеграл действия говорит нам, какой обязана быть амплитуда отдельного пути. Амплитуда пропорциональна e^tS/h, где S — действие на этом пути. Это значит, что если мы представим фазу амплитуды в виде комплексного числа, то фазовый угол будет равен S/h. Действие S имеет размерность энергии на время, и у постоянной Планка размерность такая же. Это постоянная, которая определяет, когда нужна квантовая механика.

И вот как все это срабатывает. Пусть для всех путей действие S будет весьма большим по сравнению с числом h. Пусть какой-то путь привел к некоторой величине амплитуды. Фаза рядом проложенного пути окажется совершенно другой, потому что при огромном S даже незначительные изменения S резко меняют фазу (ведь h чрезвычайно мало). Значит, рядом лежащие пути при сложении обычно гасят свои вклады. И только в одной области это не так — в той, где и путь и его сосед— оба в первом приближении обладают одной и той же фазой (или, точнее, почти одним и тем же действием, меняющимся в пределах h). Только такие пути и принимаются в расчет. А в предельном случае, когда постоянная Планка h стремится к нулю, правильные квантовомеханические законы можно подытожить, сказав: «Забудьте обо всех этих амплитудах вероятностей. Частица и впрямь движется по особому пути — именно по тому, по которому S в первом приближении не меняется». Такова связь между принципом наименьшего действия и квантовой механикой. То обстоятельство, что таким способом можно сформулировать квантовую механику, было открыто в 1942 г. учеником того же самого учителя, мистера Бадера, о котором я вам рассказывал. [Первоначально квантовая механика была сформулирована при помощи дифференциального уравнения для амплитуды (Шредингер), а также при помощи некоторой матричной математики (Гейзенберг).]

Теперь я хочу потолковать о других принципах минимума в физике. Есть очень много интересных принципов такого рода. Я не буду их все перечислять, а назову еще только один. Позже, когда мы доберемся до одного физического явления, для которого существует превосходный принцип минимума, я расскажу вам о нем. А сейчас я хочу показать, что необязательно описывать электростатику при помощи дифференциального уравнения для поля; можно вместо этого потребовать, чтобы некоторый интеграл обладал максимумом или минимумом. Для начала возьмем случай, когда плотность зарядов известна ловсюду, а нужно найти потенциал φ в любой точке пространства. Вы уже знаете, что ответ должен быть такой:

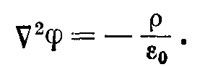
Другой способ утверждать то же самое заключается в следующем: надо вычислить интеграл U*

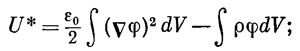
это объемный интеграл. Он берется по всему пространству. При правильном распределении потенциала φ(x, у, z) это выражение достигает минимума.

Мы можем показать, что оба эти утверждения относительно электростатики эквивалентны. Предположим, что мы выбрали произвольную функцию φ. Мы хотим показать, что когда в качестве φ мы возьмем правильное значение потенциала _φ плюс малое отклонение f, то в первом порядке малости изменение в U* будет равно нулю. Так что мы пишем

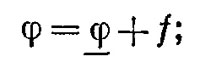
здесь φ — это то, что мы ищем; но мы проварьируем φ, чтобы увидеть, каким он должен быть для того, чтобы вариация U* оказалась первого порядка малости. В первом члене U* нам нужно написать

Это нужно проинтегрировать по х, у и по z. И здесь напрашивается тот же фокус: чтобы избавиться от df/dx, мы проинтегрируем по х по частям. Это приведет к добавочному дифференцированиюφ по х. Это та же основная идея, с помощью которой мы избавились от производных по t. Мы пользуемся равенством

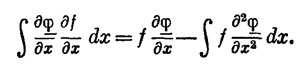
Проинтегрированный член равен нулю, так как мы считаем f равным нулю на бесконечности. (Это отвечает обращению η в нуль при t₁ и t₂. Так что наш принцип более точно формулируется следующим образом: U* для правильного φ меньше, чем для любого другого φ(х, у, z), обладающего теми же значениями на бесконечности.) Затем мы проделаем то же с у и с z. Наш интеграл ΔU* обратится в

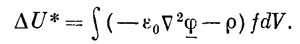
Чтобы эта вариация была равна нулю при любом произвольном f, коэффициент при f должен быть равен нулю. Значит,

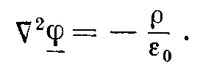
Мы вернулись к нашему старому уравнению. Значит, наше «минимальное» предложение верно. Его можно обобщить, если слегка изменить выкладки. Вернемся назад и проинтегрируем по частям, не расписывая все покомпонентно. Начнем с того, что напишем следующее равенство:

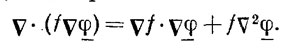
Продифференцировав левую часть, я могу показать, что она в точности равна правой. Это уравнение подходит для того, чтобы провести интегрирование по частям. В нашем интеграле ΔU* мы заменяем Vφ*Vf на fV²φ+V*(fVφ) и затем интегрируем это по объему. Член с дивергенцией после интегрирования по объему заменяется интегралом по поверхности:

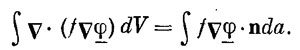
А поскольку мы интегрируем по всему пространству, то поверхность в этом интеграле лежит на бесконечности. Значит, f=0, и мы получаем прежний результат.

Только теперь мы начинаем понимать, как решать задачи, в которых мы не знаем, где расположены все заряды. Пусть мы имеем проводники, на которых как-то распределены заряды. Если потенциалы на всех проводниках зафиксированы, то наш принцип минимума все еще разрешается применять. Интегрирование в U* мы проведем только по области, лежащей снаружи всех проводников. Но раз мы не можем на проводниках менять (φ, то на их поверхности f=0, и поверхностный интеграл

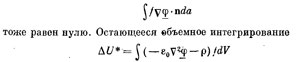
нужно проделывать только в промежутках между проводниками. И мы, конечно, снова получаем уравнение Пуассона

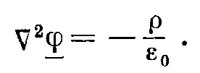
Мы, стало быть, показали, что наш первоначальный интеграл U* достигает минимума и тогда, когда он вычисляется в пространстве между проводниками, каждый из которых находится при фиксированном потенциале [это значит, что каждая пробная функция φ(ж, у, z) должна равняться заданному потенциалу проводника, когда (х, у, z) — точки поверхности проводника]. Существует интересный частный случай, когда заряды расположены только на проводниках. Тогда

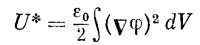
и наш принцип минимума говорит нам, что в случае, когда у каждого проводника есть свой заранее заданный потенциал, потенциалы в промежутках между ними пригоняются так, что интеграл U* оказывается как можно меньше. А что это за интеграл? Член Vφ — это электрическое поле. Значит, интеграл — это электростатическая энергия. Правильное поле и есть то единственное, которое из всех полей, получаемых как градиент потенциала, отличается наименьшей полной энергией.

Я хотел бы воспользоваться этим результатом, чтобы решить какую-нибудь частную задачу и показать вам, что все эти вещи имеют реальное практическое значение. Предположим, что я взял два проводника в форме цилиндрического конденсатора.

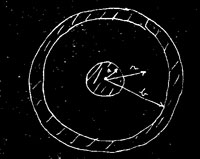У внутреннего проводника потенциал равен, скажем, V, а у внешнего — нулю. Пусть радиус внутреннего проводника будет равен а, а внешнего — b. Теперь мы можем предположить, что распределение потенциалов между ними — любое. Но если мы возьмем правильное значение φ и вычислим
(ε₀/2) ∫ (Vφ)² dV то должна получиться энергия системы 1/2CV².

Так что с помощью нашего принципа можно подсчитать и емкость С. Если же мы возьмем неправильное распределение потенциала и попытаемся этим методом прикинуть емкость конденсатора, то придем к чересчур большому значению емкости при фиксированном V. Любой предполагаемый потенциал φ, не точно совпадающий с истинным его значением, приведет и к неверной величине С, большей, чем нужно. Но если неверно выбранный потенциал ср является еще грубым приближением, то емкость С получится уже с хорошей точностью, потому что погрешность в С — величина второго порядка по сравнению с погрешностью в φ.

Предположим, что мне неизвестна емкость цилиндрического конденсатора. Тогда, чтобы узнать ее, я могу воспользоваться этим принципом. Я просто буду испытывать в качестве потенциала разные функции φ до тех пор, пока не добьюсь наинизшего значения С. Допустим, к примеру, что я выбрал потенциал, отвечающий постоянному полю. (Вы, конечно, знаете, что на самом деле поле здесь не постоянно; оно меняется как 1/r) Если поле постоянно, то это означает, что потенциал линейно зависит от расстояния. Чтобы напряжение на проводниках было каким нужно, функция φ должна иметь вид

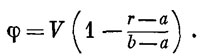
Эта функция равна V при r=а, нулю при r=b, а между ними имеется постоянный наклон, равный —V/(b—а). Значит, чтобы определить интеграл U*, надо только помножить квадрат этого градиента на ε_о/2 и проинтегрировать по всему объему. Проведем этот расчет для цилиндра единичной длины. Элемент объема при радиусе r равен 2πrdr. Проводя интегрирование, я нахожу, что моя первая проба дает такую емкость:

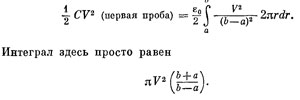
Так я получаю формулу для емкости, которая хотя и неправильна, но является каким-то приближением:

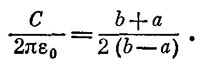
Конечно, она отличается от правильного ответа С=2πε₀/ln (b/а), но в общем-то она не так уж плоха. Давайте попробуем сравнить ее с правильным ответом для нескольких значений b/a. Вычисленные мною числа приведены в следующей таблице.

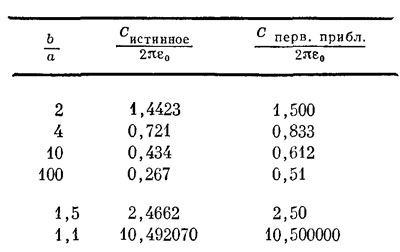
Даже когда b/а=2 (а это приводит уже к довольно большим отличиям между постоянным и линейным полем), я все еще получаю довольно сносное приближение. Ответ, конечно, как и ожидалось, чуть завышен. Но если тонкую проволочку поместить внутри большого цилиндра, то все выглядит уже гораздо хуже. Тогда поле изменяется очень сильно и замена его постоянным полем ни к чему хорошему не приводит. При b/а=100 мы завышаем ответ почти вдвое. Для малых b/а положение выглядит намного лучше. В противоположном пределе, когда промежуток между проводниками не очень широк (скажем, при b/а=1,1), постоянное поле оказывается весьма хорошим приближением, оно дает значение С с точностью до десятых процента.

А теперь я расскажу вам, как усовершенствовать этот расчет. (Ответ для цилиндра вам, разумеется, известен, но тот же способ годится и для некоторых других необычных форм конденсаторов, для которых правильный ответ вам может быть и не известен.) Следующим шагом будет подыскание лучшего приближения для неизвестного нам истинного потенциала φ. Скажем, можно испытать константу плюс экспоненту φ и т. д. Но как вы узнаете, что у вас получилось лучшее приближение, если вы не знаете истинного φ? Ответ: Подсчитайте С; чем оно ниже, тем к истине ближе. Давайте проверим эту идею. Пусть потенциал будет не линейным, а, скажем, квадратичным по r, а электрическое поле не постоянным, а линейным. Самая общая квадратичная форма, которая обращается в φ=О при r=b и в φ=F при r=а, такова:

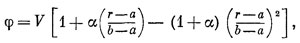
где α — постоянное число. Эта формула чуть сложнее прежней. В нее входит и квадратичный член, и линейный. Из нее очень легко получить поле. Оно равно просто

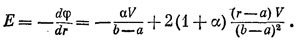
Теперь это нужно возвести в квадрат и проинтегрировать по объему. Но погодите минутку. Что же мне принять за α? За ф я могу принять параболу, но какую? Вот что я сделаю: подсчитаю емкость при произвольном α. Я получу

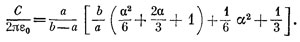
Это выглядит малость запутанно, но так уж выходит после интегрирования квадрата поля. Теперь я могу выбирать себе а. Я знаю, что истина лежит ниже, чем все, что я собираюсь вычислить. Что бы я ни поставил вместо а, ответ все равно получится слишком большим. Но если я продолжу свою игру с α и постараюсь добиться наинизшего возможного значения С, то это наинизшее значение будет ближе к правде, чем любое другое значение. Следовательно, мне теперь надо подобрать α так, чтобы значение С достигло своего минимума. Обращаясь к обычному дифференциальному исчислению, я убеждаюсь, что минимум С будет тогда, когда α =— 2b/(b+a). Подставляя это значение в формулу, я получаю для наименьшей емкости

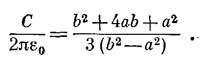
Я прикинул, что дает эта формула для С при различных значениях b/а. Эти числа я назвал С (квадратичные). Привожу таблицу, в которой сравниваются С (квадратичные) с С (истинными).

Например, когда отношение радиусов равно 2:1, я получаю 1,444. Это очень хорошее приближение к правильному ответу, 1,4423. Даже при больших Ыа приближение остается довольно хорошим — оно намного лучше первого приближения. Оно остается сносным (завышение только на 10%) даже при b/а=10 : 1.Большое расхождение наступает только при отношении 100 : 1. Я получаю С равным 0,346 вместо 0,267. С другой стороны, для отношения радиусов 1,5 совпадение превосходное, а при b/а=1,1 ответ получается 10,492065 вместо положенного 10,492070. Там, где следует ожидать хорошего ответа, он оказывается очень и очень хорошим.

Я привел все эти примеры, во-первых, чтобы продемонстрировать теоретическую ценность принципа минимального действия и вообще всяких принципов минимума, и, во-вторых, чтобы показать вам их практическую полезность, а вовсе не для того, чтобы подсчитать емкость, которую мы и так великолепно знаем. Для любой другой формы вы можете испробовать приближенное поле с несколькими неизвестными параметрами (наподобие α) и подогнать их под минимум. Вы получите превосходные численные результаты в задачах, которые другим способом не решаются.

Добавление. сделанное после лекции

СМОТРИТЕ ТАКЖЕ:

Социальные комментарии Cackle

Источник

Когда
я учился в школе, наш учитель физики, по фамилии Бадер, однажды зазвал меня к
себе после урока и сказал: «У тебя вид такой, как будто тебе все страшно
надоело; послушай-ка об одной интересной вещи». И он рассказал мне нечто, что
мне показалось поистине захватывающим. Даже сейчас, хотя с тех пор прошла уже
уйма времени, это продолжает меня увлекать. И всякий раз, когда я вспоминаю о
сказанном, я вновь принимаюсь за работу. И на этот раз, готовясь к лекции, я
поймал себя на том, что вновь анализирую все то же самое. И, вместо того чтобы
готовиться к лекции, я взялся за решение новой задачи. Предмет, о котором я
говорю, – это принцип наименьшего действия.

Вот
что сказал мне тогда мой учитель Бадер: «Пусть, к примеру, у тебя имеется
частица в поле тяжести; эта частица, выйдя откуда-то, свободно движется куда-то
в другую точку. Ты подбросил ее, скажем, кверху, а она взлетела, а потом упала.

От
исходного места к конечному она прошла за какое-то время. Попробуй теперь
какое-то другое движение. Пусть для того, чтобы перейти «отсюда сюда», она двигалась
уже не так, как раньше, а вот так:

но
все равно очутилась на нужном месте в тот же самый момент времени, что и
раньше».

«И
вот,- продолжал учитель,- если ты подсчитаешь кинетическую энергию в каждый
момент времени на пути частицы, вычтешь из нее потенциальную энергию и
проинтегрируешь разность по всему тому времени, когда происходило движение, то
увидишь, что число, которое получится, будет больше, чем при истинном движении
частицы.

Иными
словами, законы Ньютона можно сформулировать не в виде , а вот как: средняя
кинетическая энергия минус средняя потенциальная энергия достигает своего
самого наименьшего значения на той траектории, по которой предмет двигается в
действительности от одного места к другому.

Попробую
пояснить тебе это чуть понятнее.

Если
взять поле тяготения и обозначить траекторию частицы , где – высота над землей
(обойдемся пока одним измерением; пусть траектория пролегает только вверх и
вниз, а не в стороны), то кинетическая энергия будет , а потенциальная энергия в
произвольный момент времени будет равна .

Теперь
я для какого-то момента движения по траектории беру разность кинетической и
потенциальной энергий и интегрирую по всему времени от начала до конца. Пусть в
начальный момент времени движение началось на какой-то высоте,
а кончилось в момент на другой определенной высоте.

Тогда
интеграл равен

Истинное
движение совершается по некоторой кривой (как функция времени она является
параболой) и приводит к какому-то определенному значению интеграла. Но можно
представить себе какое-то другое движение: сперва резкий подъем, а потом
какие-то причудливые колебания.

Можно
подсчитать разность потенциальной и кинетической энергии на таком пути… или
на любом другом. И самое поразительное – что настоящий путь это тот, по
которому этот интеграл наименьший.

Давай
проверим это. Для начала разберем такой случай: у свободной частицы вовсе нет
потенциальной энергии. Тогда правило говорит, что при переходе от одной точки к
другой за заданное время интеграл от кинетической энергии должен оказаться
наименьшим. А это значит, что частица обязана двигаться равномерно. (И это
правильно, мы же с тобой знаем, что скорость в таком движении постоянна.) А
почему равномерно? Разберемся в этом. Если бы было иначе, то временами скорость
частицы превысила бы среднюю, а временами была бы ниже ее, а средняя скорость
была бы одинаковой, потому что частице надо было бы дойти «отсюда сюда» за
условленное время. Например, если тебе нужно попасть из дому в школу на своей
машине за определенное время, то сделать это можно по-разному: ты можешь сперва
гнать, как сумасшедший, а в конце притормозить, или ехать с одинаковой
скоростью, или сначала можешь даже отправиться в обратную сторону, а уж потом
повернуть к школе, и т. д. Во всех случаях средняя скорость, конечно, должна
быть одной и той же – частное от деления расстояния от дома до школы на время.
Но и при данной средней скорости ты иногда двигался слишком быстро, а иногда чересчур
медленно. А средний квадрат чего-то, что отклоняется от среднего, как известно,
всегда больше квадрата среднего; значит, интеграл от кинетической энергии при
колебаниях скорости движения всегда будет больше, нежели при движении с
постоянной скоростью. Ты видишь, что интеграл достигнет минимума, когда
скорость будет постоянной (при отсутствии сил). Правильный путь таков.

Предмет
же, подброшенный в поле тяжести вверх, сперва поднимается быстро, а потом все
медленнее. Происходит это потому, что он обладает и потенциальной энергией, а
наименьшего значения должна достигать разность между кинетической и
потенциальной энергиями. Раз потенциальная энергия возрастает по мере подъема,
то меньшая разность получится, если как можно быстрее достичь тех высот, где
потенциальная энергия велика. Тогда, вычтя из кинетической энергии этот высокий
потенциал, мы добьемся уменьшения среднего. Так что выгоднее такой путь, который идет вверх и поставляет добрый отрицательный кусок потенциальной
энергии.

Но,
с другой стороны, нельзя ни двигаться слишком быстро, ни подняться слишком
высоко, потому что на это потребуется чересчур много кинетической энергии. Надо
двигаться достаточно быстро, чтобы подняться и спуститься за определенное
время, имеющееся в твоем распоряжении. Так что не следует стараться взлететь
слишком высоко, а просто надо достичь какого-то разумного уровня. В итоге
оказывается, что решение есть своего рода равновесие между желанием раздобыть
как можно больше потенциальной энергии и желанием как можно сильней уменьшить
количество кинетической энергии – это стремление добиться максимального
уменьшения разности кинетической и потенциальной энергий».

Вот
и все, что сказал мне мой учитель, потому что он был очень хороший учитель и
знал, когда пора остановиться. Сам я, увы, не таков. Мне трудно остановиться
вовремя. И поэтому вместо того, чтобы просто разжечь в вас интерес своим
рассказом, я хочу запугать вас, хочу, чтобы вам стало тошно от сложности жизни,
– попробую доказать то, о чем я рассказал. Математическая задача, которую мы
будем решать, очень трудна и своеобразна. Имеется некоторая величина , называемая
действием. Она равна кинетической энергии минус потенциальная,
проинтегрированная по времени:

Не
забудьте, что и п. э. и к. э. – обе функции времени. Для любого нового
мыслимого пути это действие принимает свое определенное значение.
Математическая задача состоит в том, чтобы определить, для какой кривой это
число меньше, чем для других.

Вы
скажете: «О, это просто обычный пример на максимум и минимум. Надо подсчитать
действие, продифференцировать его и найти минимум».

Но
погодите. Обычно у нас бывает функция какой-то переменной и нужно найти
значение переменной, при котором функция становится наименьшей или наибольшей.
Скажем, имеется стержень, нагретый посредине. По нему растекается тепло и в
каждой точке стержня устанавливается своя температура. Нужно найти точку, где она
выше всего. Но у нас речь идет совсем об ином – каждому пути в пространстве
отвечает свое число, и предполагается найти тот путь, для которого это число
минимально. Это совсем другая область математики. Это не обычное исчисление, а
вариационное (так его называют).

В
этой области математики имеется много своих задач. Скажем, окружность обычно
определяют как геометрическое место точек, расстояния которых от данной точки
одинаковы, но окружность можно определить и иначе: это та из кривых данной
длины, которая ограничивает собою наибольшую площадь. Любая другая кривая
такого же периметра ограничивает площадь меньшую, чем окружность. Так что если
поставить задачу: найти кривую данного периметра, ограничивающую наибольшую
площадь, то перед нами будет задача из вариационного исчисления, а не из того
исчисления, к которому вы привыкли.

Итак,
мы хотим взять интеграл по пути, пройденному телом. Сделаем это так. Все дело в
том, чтобы вообразить себе, что существует истинный путь и что любая другая
кривая, которую мы проведем, – не настоящий путь, так что если подсчитать для
нее действие, то получится число, превышающее то, которое мы получим для
действия, соответствующего настоящему пути.

Итак,
задача: найти истинный путь. Где он пролегает? Один из способов конечно, мог бы
состоять в том, чтобы подсчитать действие для миллионов и миллионов путей и потом
посмотреть, при каком пути это действие наименьшее. Вот тот путь, при котором
действие минимально, и будет настоящим.

Такой
способ вполне возможен. Однако можно сделать проще. Если имеется величина,
обладающая минимумом (из обычных функций, скажем, температура), то одно из
свойств минимума состоит в том, что при удалении от него на расстояние первого
порядка малости функция отклоняется от минимального своего значения только на
величину второго порядка. А в любом другом месте кривой сдвиг на малое
расстояние изменяет значение функции тоже на величину первого порядка малости.
Но в минимуме легкие уходы в сторону в первом приближении не приводят к
изменению функции.

Это-то
свойство мы и собираемся использовать для расчета настоящего пути.

Если
путь правильный, то кривая, чуть-чуть отличная от него, не приведет в первом
приближении к изменению в величине действия. Все изменения, если это был
действительно минимум, возникнут только во втором приближении.

Это
легко доказать. Если при каком-то отклонении от кривой возникают изменения в
первом порядке, то эти изменения в действии пропорциональны отклонению. Они, по
всей вероятности, увеличат действие; иначе это не был бы минимум. Но раз
изменения пропорциональны отклонению, то перемена знака отклонения уменьшит
действие. Выходит, что при отклонении в одну сторону действие возрастает, а при
отклонении в обратную сторону – убывает. Единственная возможность того, чтобы
это действительно был минимум, – это чтобы в первом приближении никаких
изменений не происходило и изменения были бы пропорциональны квадрату
отклонения от настоящего пути.

Итак,
мы пойдем по следующему пути: обозначим через (с чертой внизу) истинный путь –
тот, который мы хотим найти. Возьмем некоторый пробный путь , отличающийся от искомого
на небольшую величину, которую мы обозначим .

Идея
состоит в том, что если мы подсчитаем действие на пути , то разность между этим и тем действием,
которое мы вычислили для пути (для простоты оно будет обозначено ), или разность
между и
, должна
быть в первом приближении по нулем. Они могут отличаться во
втором порядке, но в первом разность обязана быть нулем.

И
это должно соблюдаться для любой . Впрочем, не совсем для любой. Метод
требует принимать во внимание только те пути, которые все начинаются и
кончаются в одной и той же паре точек, т. е. всякий путь должен начинаться в
определенной точке в момент и кончаться в другой определенной
точке в момент .
Эти точки и моменты фиксируются. Так что наша функция (отклонение) должна быть
равна нулю на обоих концах: и . При этом условии наша
математическая задача становится полностью определенной.

Если
бы вы не знали дифференциального исчисления, вы могли бы проделать такую же
вещь для отыскания минимума обычной функции . Вы бы задумались над тем, что
случится, если взять и прибавить к малую величину , и доказывали бы,
что поправка к в
первом порядке по должна в минимуме быть равна нулю.
Вы бы подставили вместо и разложили бы с точностью до первой
степени ,
словом, повторили бы все то, что мы намерены сделать с .

Итак,
идея наша заключается в том, что мы подставляем в формулу для действия

где
через обозначена
потенциальная энергия. Производная – это, естественно, производная от плюс производная
от , так
что для действия я получаю такое выражение:

Теперь
это нужно расписать подетальней. Для квадратичного слагаемого я получу

Но
постойте-ка! Ведь мне не нужно заботиться о порядках выше первого. Я могу
убрать все слагаемые, в которых есть и высшие степени, и ссыпать их в
ящик под названием «второй и высшие порядки». Из этого выражения туда попадет
только одна вторая степень, но из чего-то другого могут войти и высшие. Итак,
часть, связанная с кинетической энергией, такова:

Дальше
нам нужен потенциал в точках . Я считаю малой и могу
разложить в
ряд Тэйлора. Приближенно это будет ; в следующем приближении (из-за
того, что здесь стоят обычные производные) поправка равна , умноженной на скорость
изменения по
отношению к и
т. д.:

Для
экономии места я обозначил через производную по . Слагаемое с и все, стоящие за
ним, попадают в категорию «второй и высшие порядки». И о них больше нечего
беспокоиться. Объединим все, что осталось:

Если
мы теперь внимательно взглянем на это, то увидим, что два первых написанных
здесь члена отвечают тому действию , которое я написал бы для искомого
истинного пути .
Я хочу сосредоточить ваше внимание на изменении , т. е. на разности между и тем , которое
получилось бы для истинного пути. Эту разность мы будем записывать как и назовем ее
вариацией .
Отбрасывая «второй и высшие порядки», получаем для

Теперь
задача выглядит так. Вот передо мной некоторый интеграл. Я не знаю еще, каково
это , но
я твердо знаю, что, какую я ни возьму, этот интеграл должен
быть равен нулю. «Ну что ж,- подумаете вы,- единственная возможность для этого –
это чтобы множитель при был равен нулю». Но как быть с
первым слагаемым, где есть ? Вы скажете: «Если обращается в
ничто, то и ее производная такое же ничто; значит, коэффициент при должен тоже быть
нулем». Ну это не совсем верно. Это не совсем верно потому, что между
отклонением и
его производной имеется связь; они не полностью независимы, потому что должно быть нулем
и при и
при .

При
решении всех задач вариационного исчисления всегда пользуются одним и тем же
общим принципом. Вы чуть сдвигаете то, что хотите варьировать (подобно тому,
как это сделали мы, добавляя ), бросаете взгляд на члены первого
порядка, затем расставляете все так, чтобы получился интеграл в таком виде:
«сдвиг ,
умноженный на что получится», но чтобы в нем не было никаких производных от (никаких ). Непременно
нужно так все преобразовать, чтобы осталось «нечто», умноженное на . Сейчас вы
поймете, отчего это так важно. (Существуют формулы, которые подскажут вам, как
в некоторых случаях можно это проделать без каких-либо выкладок; но они не так
уж общи, чтобы стоило заучивать их; лучше всего проделывать выкладки так, как
это делаем мы.)

Как
же я могу переделать член , чтобы в нем появилось ? Я могу добиться
этого, интегрируя по частям. Оказывается, что в вариационном исчислении весь
фокус в том и состоит, чтобы расписать вариацию и затем проинтегрировать по частям
так, чтобы производные от исчезли. Во всех задачах, в которых
появляются производные, проделывается такой же фокус.

Припомните
общий принцип интегрирования по частям. Если у вас есть произвольная функция , умноженная на и
проинтегрированная по , то вы расписываете производную от :

В
интересующем вас интеграле стоит как раз последнее слагаемое, так что

В
нашей формуле для за функцию принимается произведение на ; поэтому я
получаю для выражение

В
первый член должны быть подставлены пределы интегрирования и . Тогда я получу под
интегралом член от интегрирования по частям и последний член, оставшийся при
преобразовании неизменным.

А
теперь происходит то, что бывает всегда, – проинтегрированная часть исчезает.
(А если не исчезает, то нужно переформулировать принцип, добавив условия,
обеспечивающие такое исчезновение!) Мы уже говорили, что на концах пути должна быть
равна нулю. Ведь в чем состоит наш принцип? В том, что действие минимально при
условии, что варьируемая кривая начинается и кончается в избранных точках. Это
значит, что и
. Поэтому
проинтегрированный член получается равным нулю. Мы собираем воедино остальные
члены и пишем

Вариация
теперь
приобрела такой вид, какой мы хотели ей придать: что-то стоит в скобках
(обозначим его ),
и все это умножено на и проинтегрировано от до .

У
нас вышло, что интеграл от какого-то выражения, умноженного на , всегда равен
нулю:

Стоит
какая-то функция от ; умножаю ее на и интегрирую ее от начала
до конца. И какова бы ни была , я получаю нуль. Это означает, что
функция равна
нулю. В общем-то это очевидно, но я на всякий случай покажу вам один из
способов доказательства.

Пусть
в качестве я
выберу нечто, что равно нулю всюду, при всех , кроме одного, заранее выбранного
значения .
Оно остается нулем, пока я не дойду до этого , затем оно подскакивает на мгновение
и сразу же осаживает назад. Если вы берете интеграл от этой , умноженной
на какую-то функцию , то единственное место, в котором вы
получите что-то ненулевое, – это там, где подскакивало; и у вас получится
значение в
этом месте на интеграл по скачку. Сам по себе интеграл по скачку не равен нулю,
но после умножения на он должен дать нуль. Значит, функция
в том месте, где был скачок, должна оказаться нулем. Но ведь скачок можно было
сделать в любом месте; значит, должна быть нулем всюду.

Мы
видим, что если наш интеграл равен нулю при какой угодно , то коэффициент при должен обратиться
в нуль. Интеграл действия достигает минимума на том пути, который будет
удовлетворять такому сложному дифференциальному уравнению:

На
самом деле оно не так уж сложно; вы его уже встречали прежде. Это просто . Первый член –
это масса, умноженная на ускорение; второй – это производная от потенциальной
энергии, т. е. сила.

Итак,
мы показали (по крайней мере для консервативной системы), что принцип
наименьшего действия приводит к правильному ответу; он утверждает, что путь,
обладающий минимумом действия,- это путь, удовлетворяющий закону Ньютона.

Нужно
сделать еще одно замечание. Я не доказал, что это минимум. Может быть, это
максимум. На самом деле это и не обязательно должен быть минимум. Здесь все так
же, как в «принципе кратчайшего времени», который мы обсуждали, изучая оптику.
Там тоже мы сперва говорили о «кратчайшем» времени. Однако выяснилось, что
бывают положения, в которых это время не обязательно «кратчайшее».
Фундаментальный принцип заключается в том, чтобы для любых отклонений первого
порядка от оптического пути изменения во времени были бы равны нулю; здесь та
же самая история. Под «минимумом» мы на самом деле подразумеваем, что в первом
порядке малости изменения величины при отклонениях от пути должны быть
равны нулю. И это не обязательно «минимум».

Теперь
я хочу перейти к некоторым обобщениям. В первую очередь всю эту историю можно
было бы проделать и в трех измерениях. Вместо простого я тогда имел бы , и как функции , и действие
выглядело бы посложнее. При трехмерном движении вы должны использовать полную
кинетическую энергию: , умноженное на квадрат всей
скорости. Иначе говоря,

Кроме
того, потенциальная энергия теперь является функцией , и . А что можно сказать о
пути? Путь есть некоторая кривая общего вида в пространстве; ее не так легко
начертить, но идея остается прежней. А как обстоит дело с ? Что ж, и имеет три
компоненты. Путь можно сдвигать и по , и по , и по , или во всех трех направлениях
одновременно. Так что теперь вектор. От этого сильных
усложнений не получается. Раз нулю должны быть равны лишь вариации первого
порядка, то можно провести расчет последовательно с тремя сдвигами. Сперва
можно сдвинуть только
в направлении и
сказать, что коэффициент должен обратиться в нуль. Получится одно уравнение.
Потом мы сдвинем в направлении и получим второе. Затем
сдвинем в направлении и получим третье. Можно все, если
угодно, проделать в другом порядке. Как бы то ни было, возникает тройка
уравнений. Но ведь закон Ньютона – это тоже три уравнения в трех измерениях, по
одному для каждой компоненты. Вам предоставляется самим убедиться, что это все
действует и в трех измерениях (работы здесь не так много). Между прочим, можно
взять какую угодно систему координат, полярную, любую, и сразу получить законы
Ньютона применительно к этой системе, рассматривая, что получится, когда
произойдет сдвиг вдоль радиуса или по углу, и т. д.

Метод
может быть обобщен и на произвольное число частиц. Если, скажем, у вас есть две
частицы и между ними действуют какие-то силы и имеется взаимная потенциальная
энергия, то вы просто складываете их кинетические энергии и вычитаете из суммы
потенциальную энергию взаимодействия. А что вы варьируете? Пути обеих частиц.
Тогда для двух частиц, движущихся в трех измерениях, возникает шесть уравнений.
Вы можете варьировать положение частицы 1 в направлении , в направлении и в направлении , и то же самое
проделать с частицей 2, так что существует шесть уравнений. И так и должно
быть. Три уравнения определяют ускорение частицы 1 через силу, действующую на
нее, а три других – ускорение частицы 2 из-за силы, действующей на нее.
Следуйте всегда тем же правилам игры, и вы получите закон Ньютона для
произвольного числа частиц.

Я
сказал, что мы получим закон Ньютона. Это не совсем верно, потому что в закон
Ньютона входят и неконсервативные силы, например трение. Ньютон утверждал, что равно всякой . Принцип же
наименьшего действия справедлив только для консервативных систем, таких, где
все силы могут быть получены из потенциальной функции. Но ведь вы знаете, что
на микроскопическом уровне, т. е. на самом глубинном физическом уровне,
неконсервативных сил не существует. Неконсервативные силы (такие, как трение)
появляются только от того, что мы пренебрегаем микроскопическими сложными эффектами:
просто слишком много частиц приходится анализировать. Фундаментальные же законы
могут быть выражены в виде принципа наименьшего действия.

Позвольте
перейти к дальнейшим обобщениям. Положим, нас интересует, что будет, когда
частица движется релятивистски. Пока мы не получили правильного релятивистского
уравнения движения; верно только в нерелятивистских
движениях. Встает вопрос: существует ли в релятивистском случае соответствующий
принцип наименьшего действия? Да, существует. Формула в релятивистском случае
такова:

Первая
часть интеграла действия – это произведение массы покоя на и на интеграл от функции
скорости .
Затем вместо того, чтобы вычитать потенциальную энергию, мы имеем интегралы от
скалярного потенциала и от векторного потенциала , умноженного на . Конечно, здесь
приняты во внимание только электромагнитные силы. Все электрические и магнитные
поля выражены в терминах и . Такая функция действия дает полную
теорию релятивистского движения отдельной частицы в электромагнитном поле.

Конечно,
вы должны понимать, что всюду, где я написал , прежде чем делать выкладки, следует
подставить вместо
и т. д.
Кроме того, там, где я писал просто , , , вы должны представить себе точки в
момент : , , . Собственно,
только после таких подстановок и замен у вас получится формула для действия
релятивистской частицы. Пусть самые умелые из вас попытаются доказать, что эта
формула для действия действительно дает правильные уравнения движения теории
относительности. Позвольте лишь посоветовать для начала отбросить , т. е. обойтись
пока без магнитных полей. Тогда вы должны будете получить компоненты уравнения
движения ,
где, как вы, вероятно, помните, .

Включить
в рассмотрение векторный потенциал намного труднее. Вариации тогда
становятся несравненно более сложными. Но в конце сила оказывается равной тому,
чему следует: .
Но позабавьтесь с этим сами.

Мне
хотелось бы подчеркнуть, что в общем случае (к примеру, в релятивистской
формуле) под интегралом в действии уже не стоит разность кинетической и
потенциальной энергий. Это годилось только в нерелятивистском приближении.
Например, член –
это не то, что называют кинетической энергией. Вопрос о том, каким должно быть
действие для произвольного частного случая, может быть решен после некоторого
числа проб и ошибок. Это задача того же типа, что и определение, каковы должны
быть уравнения движения. Вы просто должны поиграть с известными вам уравнениями
и посмотреть, можно ли их написать в виде принципа наименьшего действия.

Еще
одно замечание по поводу терминологии. Ту функцию, которую интегрируют по
времени, чтобы получить действие , называют лагранжианом . Это функция,
зависящая только от скоростей и положений частиц. Так что принцип наименьшего
действия записывается также в виде

где
под и подразумеваются
все компоненты координат и скоростей. Если вы когда-нибудь услышите, что кто-то
говорит о «лагранжиане», знайте, что речь идет о функции, применяемой для
получения .
Для релятивистского движения в электромагнитном поле

Кроме
того, я должен отметить, что самые дотошные и педантичные люди не называют действием. Его
именуют «первой главной функцией Гамильтона». Но читать лекцию о «принципе
наименьшей первой главной функции Гамильтона» было свыше моих сил. Я назвал это
«действием». Да к тому же все больше и больше людей называют это «действием».
Видите ли, исторически действием было названо нечто другое, не столь полезное
для науки, но я думаю, что разумнее изменить определение. Теперь и вы начнете
именовать новую функцию действием, а вскоре и все вообще станут называть ее
этим простым именем.

Теперь
я хочу сообщить вам по поводу нашей темы кое-что, похожее на те рассуждения,
которые я вел по поводу принципа кратчайшего времени. Существует разница в
самом существе закона, утверждающего, что некоторый интеграл, взятый от одной
точки до другой, имеет минимум, – закона, который сообщает нам что-то обо всем
пути сразу, и закона, который говорит, что когда вы двигаетесь, то, значит,
есть сила, приводящая к ускорению. Второй подход докладывает вам о каждом вашем
шаге, он прослеживает ваш путь пядь за пядью, а первый выдает сразу какое-то
общее утверждение обо всем пройденном пути. Толкуя о свете, мы говорили о связи
этих двух подходов. Теперь я хочу объяснить вам, отчего должны существовать
дифференциальные законы, если имеется такой принцип – принцип наименьшего
действия. Причина вот в чем: рассмотрим действительно пройденный в пространстве
и времени путь. Как и прежде, обойдемся одним измерением, так что можно будет
начертить график зависимости от . Вдоль истинного пути достигает
минимума. Положим, что у нас есть этот путь и что он проходит через некоторую
точку пространства и времени и через другую
соседнюю точку .

Теперь,
если весь интеграл от до достиг минимума, необходимо,
чтобы интеграл вдоль маленького участочка от до тоже был минимальным. Не может быть,
чтобы часть от до
хоть
чуточку превосходила минимум. Иначе вы могли бы подвигать туда-сюда кривую на
этом участочке и снизить немного значение всего интеграла.

Значит,
любая часть пути тоже должна давать минимум. И это справедливо для каких-угодно
маленьких долек пути. Поэтому тот принцип, что весь путь должен давать минимум,
можно сформулировать, сказав, что бесконечно малая долька пути – это тоже такая
кривая, на которой действие минимально. И если мы возьмем достаточно короткий
отрезок пути – между очень близкими друг к другу точками и , – то уже неважно, как
меняется потенциал от точки к точке вдали от этого места, потому что, проходя
весь ваш коротенький отрезочек, вы почти не сходите с места. Единственное, что
вам нужно учитывать, – это изменение первого порядка малости в потенциале.
Ответ может зависеть только от производной потенциала, а не от потенциала в
других местах. Так, утверждение о свойстве всего пути в целом становится
утверждением о том, что происходит на коротком участке пути, т. е.
дифференциальным утверждением. И эта дифференциальная формулировка включает
производные от потенциала, т. е. силу в данной точке. Таково качественное
объяснение связи между законом в целом и дифференциальным законом.

Когда
мы говорили о свете, то обсуждали также вопрос: как все-таки частица находит
правильный путь? С дифференциальной точки зрения это понять легко. В каждый
момент частица испытывает ускорение и знает только то, что ей положено делать в
это мгновение. Но все ваши инстинкты причин и следствий встают на дыбы, когда
вы слышите, что частица «решает», какой ей выбрать путь, стремясь к минимуму
действия. Уж не «обнюхивает» ли она соседние пути, прикидывая, к чему они
приведут – к большему или к меньшему действию? Когда мы на пути света ставили
экран так, чтобы фотоны не могли перепробовать все пути, мы выяснили, что они
не могут решить, каким путем идти, и получили явление дифракции.

Но
верно ли это и для механики? Правда ли, что частица не просто «идет верным
путем», а пересматривает все другие мыслимые траектории? И что если, ставя
преграды на ее пути, мы не дадим ей заглядывать вперед, то мы получим некий
аналог явления дифракции? Самое чудесное во всем этом – то, что все
действительно обстоит так. Именно это утверждают законы квантовой механики. Так
что наш принцип наименьшего действия сформулирован не полностью. Он состоит не
в том, что частица избирает путь наименьшего действия, а в том, что она «чует»
все соседние пути и выбирает тот, вдоль которого действие минимально, и способ
этого выбора сходен с тем, каким свет отбирает кратчайшее время. Вы помните,
что способ, каким свет отбирает кратчайшее время, таков: если свет пойдет по
пути, требующему другого времени, то придет он с другой фазой. А полная
амплитуда в некоторой точке есть сумма вкладов амплитуд для всех путей, по
которым свет может ее достичь. Все те пути, у которых фазы резко различаются,
ничего после сложения не дают. Но если вам удалось найти всю последовательность
путей, фазы которых почти одинаковы, то мелкие вклады сложатся, и в точке
прибытия полная амплитуда получит заметное значение. Важнейшим путем становится
тот, возле которого имеется множество близких путей, дающих ту же фазу.

В
точности то же происходит и в квантовой механике. Законченная квантовая
механика (нерелятивистская и пренебрегающая спином электрона) работает так:
вероятность того, что частица, выйдя из точки 1 в момент , достигнет точки 2 в
момент ,
равна квадрату амплитуды вероятности. Полная амплитуда может быть записана в
виде суммы амплитуд для всех возможных путей – для любого пути прибытия. Для
любого ,
которое могло бы возникнуть для любой мыслимой воображаемой траектории, нужно
подсчитать амплитуду. Затем их все нужно сложить. Что же мы примем за амплитуду
вероятности некоторого пути? Наш интеграл действия говорит нам, какой обязана
быть амплитуда отдельного пути. Амплитуда пропорциональна , где – действие на этом пути.
Это значит, что если мы представим фазу амплитуды в виде комплексного числа, то
фазовый угол будет равен . Действие имеет размерность энергии
на время, и у постоянной Планка размерность такая же. Это постоянная, которая
определяет, когда нужна квантовая механика.

И
вот как все это срабатывает. Пусть для всех путей действие будет весьма большим по
сравнению с числом . Пусть какой-то путь привел к
некоторой величине амплитуды. Фаза рядом проложенного пути окажется совершенно
другой, потому что при огромном даже незначительные изменения резко меняют фазу
(ведь чрезвычайно
мало). Значит, рядом лежащие пути при сложении обычно гасят свои вклады. И
только в одной области это не так – в той, где и путь и его сосед – оба в
первом приближении обладают одной и той же фазой (или, точнее, почти одним и
тем же действием, меняющимся в пределах ). Только такие пути и принимаются в
расчет. А в предельном случае, когда постоянная Планка стремится к нулю,
правильные квантовомеханические законы можно подытожить, сказав: «Забудьте обо
всех этих амплитудах вероятностей. Частица и впрямь движется по особому пути –
именно по тому, по которому в первом приближении не меняется».
Такова связь между принципом наименьшего действия и квантовой механикой. То
обстоятельство, что таким способом можно сформулировать квантовую механику,
было открыто в 1942 г. учеником того же самого учителя, мистера Бадера, о
котором я вам рассказывал. [Первоначально квантовая механика была
сформулирована при помощи дифференциального уравнения для амплитуды
(Шредингер), а также при помощи некоторой матричной математики (Гейзенберг).]

Теперь
я хочу потолковать о других принципах минимума в физике. Есть очень много
интересных принципов такого рода. Я не буду их все перечислять, а назову еще
только один. Позже, когда мы доберемся до одного физического явления, для
которого существует превосходный принцип минимума, я расскажу вам о нем. А
сейчас я хочу показать, что необязательно описывать электростатику при помощи
дифференциального уравнения для поля; можно вместо этого потребовать, чтобы
некоторый интеграл обладал максимумом или минимумом. Для начала возьмем случай,
когда плотность зарядов известна повсюду, а нужно найти потенциал в любой точке
пространства. Вы уже знаете, что ответ должен быть такой:

Другой
способ утверждать то же самое заключается в следующем: надо вычислить интеграл

;

это
объемный интеграл. Он берется по всему пространству. При правильном
распределении потенциала это выражение достигает минимума.

Мы
можем показать, что оба эти утверждения относительно электростатики
эквивалентны. Предположим, что мы выбрали произвольную функцию . Мы хотим
показать, что когда в качестве мы возьмем правильное значение
потенциала плюс
малое отклонение , то в первом порядке малости
изменение в будет
равно нулю. Так что мы пишем

;

здесь
– это
то, что мы ищем; но мы проварьируем , чтобы увидеть, каким он должен быть
для того, чтобы вариация оказалась первого порядка малости. В
первом члене нам
нужно написать

Единственный
член первого порядка, который будет меняться, таков:

Во
втором члене подынтегральное
выражение примет вид

;

изменяющаяся
часть здесь равна . Оставляя только меняющиеся члены,
получим интеграл

Дальше,
руководствуясь нашим старым общим правилом, мы должны очистить интеграл от всех
производных по .
Посмотрим, что это за производные. Скалярное произведение равно

Это
нужно проинтегрировать по , и по . И здесь напрашивается тот же фокус:
чтобы избавиться от , мы проинтегрируем по по частям. Это
приведет к добавочному дифференцированию по . Это та же основная идея, с помощью
которой мы избавились от производных по . Мы пользуемся равенством

Проинтегрированный
член равен нулю, так как мы считаем равным нулю на бесконечности. (Это
отвечает обращению в нуль при и . Так что наш принцип более
точно формулируется следующим образом: для правильного меньше, чем для любого
другого ,
обладающего теми же значениями на бесконечности.) Затем мы проделаем то же с и с . Наш интеграл обратится в

Чтобы
эта вариация была равна нулю при любом произвольном , коэффициент при должен быть равен
нулю. Значит,

Мы
вернулись к нашему старому уравнению. Значит, наше «минимальное» предложение
верно. Его можно обобщить, если слегка изменить выкладки. Вернемся назад и
проинтегрируем по частям, но расписывая все покомпонентно. Начнем с того, что
напишем следующее равенство:

Продифференцировав
левую часть, я могу показать, что она в точности равна правой. Это уравнение подходит
для того, чтобы провести интегрирование по частям. В нашем интеграле мы заменяем на и затем
интегрируем это по объему. Член с дивергенцией после интегрирования по объему
заменяется интегралом по поверхности:

А
поскольку мы интегрируем по всему пространству, то поверхность в этом интеграле
лежит на бесконечности. Значит, , и мы получаем прежний результат.

Только
теперь мы начинаем понимать, как решать задачи, в которых мы не знаем, где
расположены все заряды. Пусть мы имеем проводники, на которых как-то
распределены заряды. Если потенциалы на всех проводниках зафиксированы, то наш
принцип минимума все еще разрешается применять. Интегрирование в мы проведем
только по области, лежащей снаружи всех проводников. Но раз мы не можем на
проводниках менять , то на их поверхности , и поверхностный
интеграл

тоже
равен нулю. Остающееся объемное интегрирование

нужно
проделывать только в промежутках между проводниками. И мы, конечно, снова
получаем уравнение Пуассона

Мы,
стало быть, показали, что наш первоначальный интеграл достигает минимума и
тогда, когда он вычисляется в пространстве между проводниками, каждый из
которых находится при фиксированном потенциале [это значит, что каждая пробная
функция должна
равняться заданному потенциалу проводника, когда – точки поверхности проводника].

Существует
интересный частный случай, когда заряды расположены только на проводниках.
Тогда

и
наш принцип минимума говорит нам, что в случае, когда у каждого проводника есть
свой заранее заданный потенциал, потенциалы в промежутках между ними
пригоняются так, что интеграл оказывается как можно меньше. А что
это за интеграл? Член – это электрическое поле. Значит,
интеграл – это электростатическая энергия. Правильное поло и есть то
единственное, которое из всех полей, получаемых как градиент потенциала,
отличается наименьшей полной энергией.

Я
хотел бы воспользоваться этим результатом, чтобы решить какую-нибудь частную
задачу и показать вам, что все эти вещи имеют реальное практическое значение.
Предположим, что я взял два проводника в форме цилиндрического конденсатора.

У
внутреннего проводника потенциал равен, скажем, , а у внешнего – нулю. Пусть радиус
внутреннего проводника будет равен , a внешнего – . Теперь мы можем предположить,
что распределение потенциалов между ними – любое. Но если мы возьмем правильное
значение и
вычислим ,
то должна получиться энергия системы . Так что с помощью нашего принципа можно
подсчитать и емкость . Если же мы возьмем неправильное
распределение потенциала и попытаемся этим методом прикинуть емкость
конденсатора, то придем к чересчур большому значению емкости при фиксированном . Любой
предполагаемый потенциал , не точно совпадающий с истинным его
значением, приведет и к неверной величине , большей, чем нужно. Но если неверно
выбранный потенциал является еще грубым приближением, то
емкость получится
уже с хорошей точностью, потому что погрешность в – величина второго порядка по
сравнению с погрешностью в .

Предположим,
что мне неизвестна емкость цилиндрического конденсатора. Тогда, чтобы узнать
ее, я могу воспользоваться этим принципом. Я просто буду испытывать в качестве
потенциала разные функции до тех пор, пока не добьюсь
наинизшего значения . Допустим, к примеру, что я выбрал
потенциал, отвечающий постоянному полю. (Вы, конечно, знаете, что на самом деле
поле здесь не постоянно; оно меняется как .) Если поле постоянно, то это
означает, что потенциал линейно зависит от расстояния. Чтобы напряжение на
проводниках было каким нужно, функция должна иметь вид

Эта
функция равна при
, нулю
при , а
между ними имеется постоянный наклон, равный . Значит, чтобы определить интеграл , надо только
помножить квадрат этого градиента на и проинтегрировать по всему объему.
Проведем этот расчет для цилиндра единичной длины. Элемент объема при радиусе равен . Проводя
интегрирование, я нахожу, что моя первая проба дает такую емкость:

Интеграл
здесь просто равен

Так
я получаю формулу для емкости, которая хотя и неправильна, но является каким-то
приближением:

Конечно,
она отличается от правильного ответа , но в общем-то она не так уж плоха.
Давайте попробуем сравнить ее с правильным ответом для нескольких значений . Вычисленные мною
числа приведены в следующей таблице.


2	1,4423	1,500
4	0,721	0,833
10	0,434	0,612
100	0,267	0,51
1,5	2,4662	2,50
1,1	10,492070	10,500000

Даже
когда (а
это приводит уже к довольно большим отличиям между постоянным и линейным
полем), я все еще получаю довольно сносное приближение. Ответ, конечно, как и
ожидалось, чуть завышен. Но если тонкую проволочку поместить внутри большого
цилиндра, то все выглядит уже гораздо хуже. Тогда поле изменяется очень сильно
и замена его постоянным полем ни к чему хорошему не приводит. При мы завышаем ответ
почти вдвое. Для малых положение выглядит намного лучше. В
противоположном пределе, когда промежуток между проводниками не очень широк
(скажем, при ),
постоянное поле оказывается весьма хорошим приближением, оно дает значение с точностью до десятых
процента.

А
теперь я расскажу вам, как усовершенствовать этот расчет. (Ответ для цилиндра
вам, разумеется, известен, но тот же способ годится и для некоторых других
необычных форм конденсаторов, для которых правильный ответ вам может быть и не
известен.) Следующим шагом будет подыскание лучшего приближения для
неизвестного нам истинного потенциала . Скажем, можно испытать константу
плюс экспоненту и
т. д. Но как вы узнаете, что у вас получилось лучшее приближение, если вы не
знаете истинного ? Ответ: Подсчитайте ; чем оно ниже,
тем к истине ближе. Давайте проверим эту идею. Пусть потенциал будет не
линейным, а, скажем, квадратичным по , а электрическое поле не постоянным,
а линейным. Самая общая квадратичная форма, которая обращается в при и в при , такова:

где
–
постоянное число. Эта формула чуть сложнее прежней. В нее входит и квадратичный
член, и линейный. Из нее очень легко получить поле. Оно равно просто

Теперь
это нужно возвести в квадрат и проинтегрировать по объему. Но погодите минутку.
Что же мне принять за ? За я могу принять параболу, но какую?
Вот что я сделаю: подсчитаю емкость при произвольном . Я получу

Это
выглядит малость запутанно, но так уж выходит после интегрирования квадрата
поля. Теперь я могу выбирать себе . Я знаю, что истина лежит ниже, чем
все, что я собираюсь вычислить. Что бы я ни поставил вместо , ответ все равно получится
слишком большим. Но если я продолжу свою игру с и постараюсь добиться наинизшего
возможного значения , то это наинизшее значение будет
ближе к правде, чем любое другое значение. Следовательно, мне теперь надо
подобрать так,
чтобы значение достигло
своего минимума. Обращаясь к обычному дифференциальному исчислению, я
убеждаюсь, что минимум будет тогда, когда . Подставляя это
значение в формулу, я получаю для наименьшей емкости

Я
прикинул, что дает эта формула для при различных значениях . Эти числа я
назвал (квадратичные).
Привожу таблицу, в которой сравниваются (квадратичные) с (истинными).


2	1,4423	1,444
4	0,721	0,733
10	0,434	0,475
100	0,267	0,346
1,5	2,4662	2,4667
1,1	10,492070	10,492065

Например,
когда отношение радиусов равно 2:1, я получаю 1,444. Это очень хорошее
приближение к правильному ответу, 1,4423. Даже при больших приближение остается
довольно хорошим – оно намного лучше первого приближения. Оно остается сносным
(завышение только на 10%) даже при . Большое расхождение наступает
только при отношении 100:1. Я получаю равным 0,346 вместо 0,267. С другой
стороны, для отношения радиусов 1,5 совпадение превосходное, а при ответ получается
10,492065 вместо положенного 10,492070. Там, где следует ожидать хорошего
ответа, он оказывается очень и очень хорошим.

Я
привел все эти примеры, во-первых, чтобы продемонстрировать теоретическую
ценность принципа минимального действия и вообще всяких принципов минимума, и,
во-вторых, чтобы показать вам их практическую полезность, а вовсе не для того,
чтобы подсчитать емкость, которую мы и так великолепно знаем. Для любой другой
формы вы можете испробовать приближенное поле с несколькими неизвестными
параметрами (наподобие ) и подогнать их под минимум. Вы
получите превосходные численные результаты в задачах, которые другим способом
не решаются.

Источник

История[править | править код]

В классической механике[править | править код]

Примеры[править | править код]

В механике сплошных сред и классической теории поля[править | править код]

В квантовой механике[править | править код]

В квантовой теории поля[править | править код]

Дальнейшие обобщения[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Принцип наименьшего действия в аналитической механике

Не все так просто

1. Определение действия по Гамильтону. Принцип наименьшего действия

2. Границы применимости принципа наименьшего действия. Некоторые определения для самых маленьких

3. Понятие о вариациях обобщенных координат. Постановка вариационной задачи

4. Решение вариационной задачи. Уравнения Лагранжа 2-го рода

5. Задача с шариком и стенкой

Выводы и пожелания

НАИМЕ́НЬШЕГО ДЕ́ЙСТВИЯ ПРИ́НЦИП

Принцип наименьшего действия в аналитической механике +29

Предыстория

Не все так просто

1. Определение действия по Гамильтону. Принцип наименьшего действия

2. Границы применимости принципа наименьшего действия. Некоторые определения для самых маленьких

3. Понятие о вариациях обобщенных координат. Постановка вариационной задачи

4. Решение вариационной задачи. Уравнения Лагранжа 2-го рода

5. Задача с шариком и стенкой

Выводы и пожелания

СМОТРИТЕ ТАКЖЕ:

Вам также может понравиться

Как найти на телефоне архив whatsapp

Ведьма в петербурге как найти

Как найти музыку название которой не знаешь

Добавить комментарий Отменить ответ