Как найти минимум функции 4 степени - Сайт, где вы сможете решить свои вопросы

Степенная функция. В данной статье мы рассмотрим вычисление максимума (минимума) указанной функции. В предыдущей статье мы с вами рассмотрели задачи на нахождение максимума (минимума) функции с числом «е». Здесь представлены примеры без числа «е». Некоторые примеры, в которых требуется найти наибольшее или наименьшее значение функции, вообще можно решить без нахождения производной.

В любом случае, советую вам ознакомится с этой статьёй, если вы ещё этого не сделали. Рассмотрим задачи:

Найдите точку максимума функции у = (х – 2)²(х – 4)+5

Для этого найдём производную, приравняем её к нулю, найдём корни полученного уравнения:

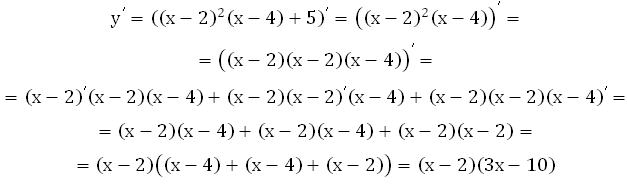
Обратите внимание, что мы сразу представили результат в виде произведения, рекомендую делать именно так. Зачем вам упрощать его до многочлена, а затем снова раскладывать его на множители? Для дальнейших действий проще сразу представить в виде произведения.

Находим нули производной:

Полученные точки разбивают числовую ость на интервалы.

Посмотрим, как ведёт себя график функции на этих интервалах. Возьмём значения из них, подставим их в производную и определим знак:

На интервале (–∞;2) функция возрастает, на интервале (2;10/3) функция убывает. Значит х = 2 это точка максимума.

Второй способ:

Перебираем значения х от – 5 до 5 подставляем в функцию и вычисляем. Затем по полученным значениям функции определяем точку максимума.

Почему берём интервал от – 5 до 5? Потому, что большинство ответов на ЕГЭ в подобных задачах лежат в этих пределах. Если будет необходимо, то берите интервал шире. Для наглядности можете построить график.

Решите предложенным способом самостоятельно, а затем посмотрите решение.

*Данный способ использовать осторожно, в будущем возможно изменение типов заданий входящих в ЕГЭ и такой подход может не сработать.

Ответ: 2

Найдите точку максимума функции у = (х – 3)²(х – 10) – 9

Это аналогичная задача.

Для этого найдём производную, приравняем её к нулю, найдём корни полученного уравнения:

Находим нули производной:

Полученные точки разбивают числовую ость на интервалы.

Посмотрим, как ведёт себя график функции на этих интервалах. Возьмём значения из интервалов, подставим их в производную и определим знак:

На интервале (–∞;3) функция возрастает, на интервале (3;23/3) функция убывает. Значит, х = 3 это точка максимума.

Вторым способом попробуйте решить сами.

Ответ: 3

Найдите наименьшее значение функции у = (х–3)²(х–6)–1 на отрезке [4;6].

Так как интервал дан (при чём он небольшой), то здесь рекомендую подставить целые значения из него (4, 5 и 6) в функцию:

Наименьшее значение функции на заданном отрезке равно – 5.

Ответ: – 5

Решите самостоятельно:

Посмотреть решение

Найдите наибольшее значение функции у=(х+6)²(х–1)–6 на отрезке [– 9;–2].

Данную задачу можно решать любым из двух способов. Интервал здесь маленьким не назовёшь, но и в то же время он невелик.

Решим её подстановкой всех значений из интервала.

Подставим – 9, – 8, – 7, – 6, – 5, – 4, – 3, –2.

Наибольшее значение функции равно – 6.

Ответ: – 6

Решите самостоятельно:

Посмотреть решение

Подведём итог. Как видите, задачи решаются по простому алгоритму. Важно для успешного решения знать таблицу производных, правила дифференцирования и производную сложной функции, свойства производной для исследования графиков функций.

Конечно, когда используем метод подстановки значений из интервала, то знать всё это, казалось бы, не обязательно, но такой подход помогает не всегда. Советую использовать его лишь как дополнительный инструмент.

Мы продолжим рассматривать задачи в этой рубрике, не пропустите!

Успехов вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.

(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.

(- 9): функция возрастает, а потом убывает – максимум.

(-7): минимум.

(3): максимум.

Все вышесказанное можно обобщить следующими выводами:

– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

Найдите производную функции (f'(x)).
Найдите корни уравнения (f'(x)=0).
Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
Определите знак производной в каждом промежутке (методом интервалов).
Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
– если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
– если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
– если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:

(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).

Ответ. (-2).

Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов

Скачать статью

Источник

Найти экстремумы функции

Данный калькулятор предназначен для нахождения экстремумов функции.
Следует различать понятия точек экстремума и экстремумов функции. Точки экстремума – точки максимума и минимума функции, это значения на оси Ox. Точка x₀ является точкой максимума функции y=f(x), если для всех x из ее окрестности выполняется неравенство f(x₀)≥f(x). Точка x₀ является точкой минимума функции y=f(x), если из ее окрестности для всех x выполняется неравенство f(x₀)≤f(x). Значения функции, которые соответствуют точкам экстремума, называются экстремумами функции, это значения на оси Oy.
Для того чтобы найти экстремумы функции можно использовать любой из трех условий экстремума, если функция удовлетворяет эти условиям.
Первым достаточным условием экстремума являются следующие утверждения: если в точке x₀ функция непрерывна, и в ней производная меняет знак с плюса на минус, то точка x₀ является точкой максимума, а если в данной точке производная меняет знак с минуса на плюс, то x₀ – точка минимума.

Вторым признаком экстремума является следующее утверждение: если производная второго порядка от x₀ больше нуля, то x₀ – точка минимума; если меньше нуля, то x₀ – точка максимума.
Третье достаточное условие экстремума функции заключается в следующем. Пусть функция y=f(x) имеет производные до n-ого порядка в окрестности точки x0 и производные до n+1-ого порядка в самой точке x₀; пусть f’(x₀)= f’’(x₀)= f’’’(x₀)=…=f⁽ⁿ⁾( x₀)=0 и f⁽ⁿ⁺¹⁾( x₀)≠0. Тогда, если n – нечетное, то x₀ – точка экстремума. Если f⁽ⁿ⁺¹⁾( x₀)>0, то x₀ – точка минимума, а, если f⁽ⁿ⁺¹⁾( x₀)<0, то x₀ – точка максимума.
Для того чтобы найти экстремумы функции, введите эту функцию в ячейку. Основные примеры ввода функций для данного калькулятора указаны ниже.

Для получения полного хода решения нажимаем в ответе Step-by-step.

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Источник

Экстремумы функции

С помощью данного сервиса можно найти наибольшее и наименьшее значение функции одной переменной f(x) с оформлением решения в Word. Если же задана функция f(x,y), следовательно, необходимо найти экстремум функции двух переменных. Также можно найти интервалы возрастания и убывания функции.

Решение онлайн
Видеоинструкция
Оформление Word
Также решают

Необходимое условие экстремума функции одной переменной

Уравнение f’₀(x^*) = 0 – это необходимое условие экстремума функции одной переменной, т.е. в точке x^* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x^с, в которых функция не возрастает и не убывает.

Достаточное условие экстремума функции одной переменной

Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x^* выполняется условие:

f’₀(x^*) = 0

f”₀(x^*) > 0

то точка x^* является точкой локального (глобального) минимума функции.

Если в точке x^* выполняется условие:

f’₀(x^*) = 0

f”₀(x^*) < 0

то точка x^* – локальный (глобальный) максимум.

Пример №1. Найти наибольшее и наименьшее значения функции:
на отрезке [1; 3].

Решение.

Критическая точка одна x₁ = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).

Вычисляем значения функции на концах отрезка и в критической точке.

f(1)=9, f(2)=⁵/₂, f(3)=3 ⁸/₈₁

Ответ: f_min=⁵/₂ при x=2; f_max=9 при x=1

Пример №2. С помощью производных высших порядков найти экстремум функции y=x-2sin(x).

Решение.

Находим производную функции: y’=1-2cos(x). Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=±^π/₃+2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x=^π/₃+2πk, k∈Z – точки минимума функции; , значит x=-^π/₃+2πk, k∈Z – точки максимума функции.

Пример №3. Исследовать на экстремум фцнкцию в окрестностях точки x=0.

Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0, то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).

Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x₀ или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.

Пример №4. Разбить число 49 на два слагаемых, произведение которых будет наибольшим.

Решение. Обозначим x – первое слагаемое. Тогда (49-x) – второе слагаемое.

Произведение будет максимальным: x·(49-x) → max

или

49x – x²

Наибольший объем цилиндра

Найти размеры цилиндра наибольшего объема, изготовленного из заготовки в форме шара радиуса R.

Решение:

Объем цилиндра равен: V = πr²H

где H = 2h,

Подставим эти значения в целевую функцию.

V → max

Найдем экстремум функции. Поскольку функция объема V(h) зависит только от одной переменной, то найдем производную с помощью сервиса Производная онлайн и приравняем ее к нулю.

dV/dh = 2πR² – 6πh²

dV/dh = 0

2πR² – 6πh² = 0 или R² = 3h²

Откуда

При высоте и радиусе основания размеры цилиндра будут наибольшими.

Источник

Найдём производную заданной функции:

Найдем нули производной:

Получим корни:

Отметим на числовой оси найденные корни, определим знаки производной функции на полученных интервалах и изобразим поведение функции:

Получили, что в точке x=4 производная меняет свой знак в отрицательного на положительный. Таким образом, точка х=4 это искомая точка минимума.

Ответ: 4

Задача

Найдём производную заданной функции:

Найдем нули производной:

Получим корни: х₁=–1 и х₂=1

Получили, что в точке x=1 производная меняет свой знак в отрицательного на положительный. Таким образом, точка х=1 это искомая точка минимума.

Ответ: 1

Задача

Найдём производную заданной функции:

Приравняем производную к нулю и решим уравнение:

Построим числовую ось, отметим на ней найденные нули производной. Далее определим знаки производной функции на полученных интервалах подставляя произвольные значения из каждого в выражение производной и схематично изобразим возрастание и убывание функции:

В точке х=1 производная меняет знак с отрицательного на положительный, значит это есть искомая точка минимума.

Ответ: 1

Задача

Найдём производную функции:

Найдем нули производной:

3х²+10х+7=0

Решая квадратное уравнение получим:

*Это точки возможного максимума (минимума) функции.

Построим числовую ось, отметим нули производной. Определим знаки производной, подставляя произвольное значение из каждого интервала в выражение производной функции и схематично изобразим возрастание и убывание на интервалах:

3∙(–3)² + 10∙(–3) + 7 = 4 > 0

3∙(–2)² + 10∙(–2) + 7 = –1 < 0

3∙0² – 10∙0 + 7 = 7 > 0