MathCAD
с помощью встроенных функций решается
только задача поиска локального
экстремума. Чтобы найти глобальный
максимум (или минимум), требуется либо
сначала вычислить все их локальные
значения и потом выбрать из них наибольший
(наименьший), либо предварительно
просканировать
с
некоторым шагом рассматриваемую область,
чтобы выделить из нее подобласть
наибольших (наименьших) значений функции
и осуществить поиск глобального
экстремума, уже находясь в его окрестности.
Второй вариант таит в себе опасность
уйти в окрестность другого локального
экстремума, но часто может быть
предпочтительнее при решении практических
задач.
Для
поиска локальных экстремумов имеются
две встроенные функции, которые могут
применяться как в пределах вычислительного
блока, так и автономно.
-
Minimize
(f, x1, … ,хn)
– вектор значений аргументов, при
которых функция f
достигает минимума; -
Maximize
(f, x1, … ,хn)
– вектор значений аргументов, при
которых функция f
достигает максимума; -
f(x1,
… ,хn)–
заданная целевая функция; -
x1,
… ,хn
– аргументы, по которым производится
минимизация(максимизация).
Всем
аргументам функции f
предварительно следует присвоить
некоторые значения, причем для тех
переменных, по которым производится
минимизация, они будут восприниматься
как начальные приближения.
Пример
7. Поиск локального экстремума в
окрестности заданной точки.
Найти
максимум функции
![]() в
в
окрестности точки (4;5).
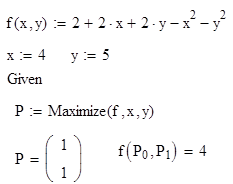
Ответ:
функция имеет максимум, равный 4, в
точке(1;1).
Пример
8. Поиск условного экстремума функции.
Найти
минимум функции
![]() при
при
условиях
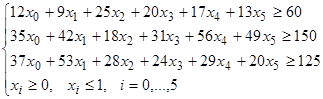 .
.
Решение.
-
Задаем
целевую функцию, матрицу системы
ограничений и вектор правой части этой
системы -
Задаем
начальное приближение решения.
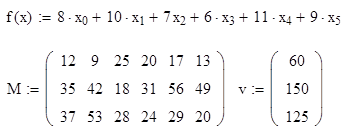
3.
С помощью вычислительного блока находим
минимальное значение функции и значение
вектора, на котором достигается это
значение.
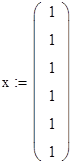
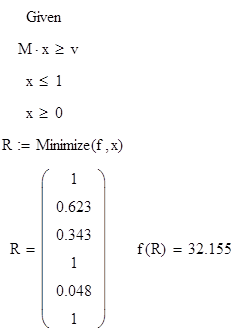
Ответ:
минимум функции равен 32.155 и достигается
в точке (1,0.623,0.343,1,0.048,1).
Контрольные
вопросы.
-
Что
значит отделить корень
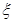 уравнения
уравнения
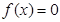 ?
? -
Какие
функции могут быть использованы для
решения нелинейных уравнений? -
Опишите
конструкцию вычислительного блока. -
В
чем состоит градиентный метод? -
В
чем различие между функциями Find
и Minner
для решения систем нелинейных уравнений? -
Где
необходимо расположить ограничительные
условия при решении задачи оптимизации? -
Как
ограничено число ограничительных
условий для решения задачи оптимизации?
Варианты заданий
Вариант
1
-
Решить
уравнение
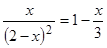 ,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
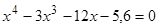 .
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
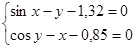
-
Найти
максимум функции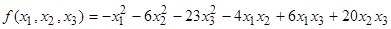 .
.
Вариант
2
-
Решить
уравнение
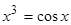 ,
,
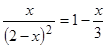 ,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
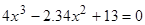 .
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
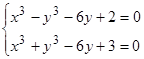 .
. -
Найти
максимум функции
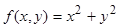 при
при
ограничении
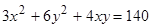 .
.
Вариант
3
-
Решить
уравнение
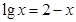 ,
,
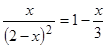 ,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
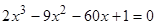 .
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
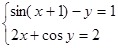 .
. -
Найти
максимум функции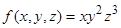 при
при
ограничении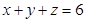 .
.
Вариант
4
-
Решить
уравнение
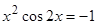 ,
,
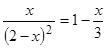 ,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
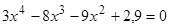 .
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
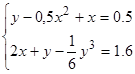 .
. -
Найти
максимум функции
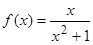 .
.
Вариант
5
-
Решить
уравнение
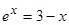 ,
,
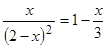 ,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
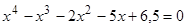 .
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
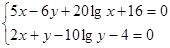 .
. -
Найти
минимальное и максимальное значения
функции
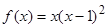 .
.
Вариант
6
-
Решить
уравнение
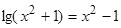 ,
,
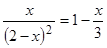 ,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
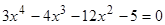 .
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
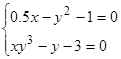 .
. -
Найти
максимум функции
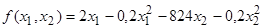 при
при
условиях
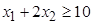 ,
,
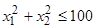 ,
,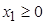
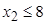 .
.
Вариант
7
-
Решить
уравнение
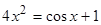 ,
,
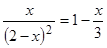 ,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
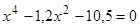 .
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
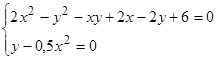 .
.
Выполнить
проверку. -
Найти
минимум функции
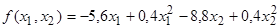 при
при
условиях
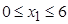 ,
,
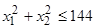 ,
,
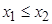 .
.
Вариант
8
-
Решить
уравнение
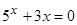 ,
,
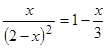 ,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
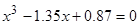 .
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
 .
.
Выполнить
проверку. -
Найти
минимум функции
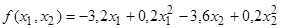 при
при
условиях
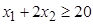 ,
,
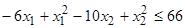 ,
,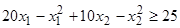 .
.
Вариант
9
-
Решить
уравнение
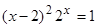 ,
,
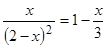 ,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
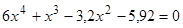 .
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
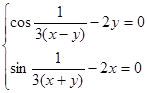 .
.
Выполнить
проверку -
Найти
минимум функции
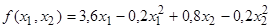 при
при
условиях
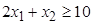 ,
,
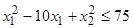 ,
,
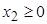 .
.
Вариант
10
-
Решить
уравнение, предварительно оделив корни
7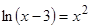 ,
,
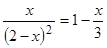 ,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
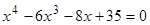 .
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
![]() .
.
Выполнить проверку.
-
Найти
минимум функции
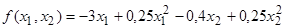 при
при
условиях
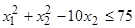 ,
,
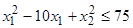 ,
,
 .
.
![]()
Тема
4:
Элементы программирования в пакете
инженерных расчетов MathCAD.
Цель
работы:
Изучение возможностей символьного
пакета MathCAD для программирования условных
и циклических выражений. Приобретение
навыков написания простейших
программ.
Используемые
программные средства:
Пакет MathCAD.
Теоретические
сведения.
Д ля
ля
повышения гибкости Mathcad в системе
предусмотрена возможность написания
небольших программ для решения тех
проблем, которые не могут быть реализованы
стандартными средствами. Обычно прибегать
к программированию приходится в тех
случаях, когда стандартные средства
либо не могут решить задачу, либо
неэффективны. Для написания программ
используется программная палитра,
которая вызывается кнопкой панели
управления. Как видно, всего имеется 10
операторов, из которых и строится
программа. Причём операторы должны
вводиться только из палитры, писать их
“вручную” не рекомендуется.
Практическая
часть
Для
примера приведём простую программу
возвращающую 1, если число чётное, и 0 в
противном случае.
![]() –
–
начинаем создание программы с кнопки
Add
Line.
Вертикальная линия играет роль операторных
скобок.
![]() –
–
оператор локального присваивания. В
программе нельзя использовать оператор
присваивания “:=”, вместо него
используется оператор локального
присваивания, отличие которого заключается
в том, что локальная переменная определена
только внутри своего блока и при выходе
из программы теряет своё значение.
Пример:
![]()
–![]()
условный
оператор создаёт конструкцию видa:![]()
где
первый операнд выполняется, если
справедливо условие являющееся вторым
операндом. Из всех программных операторов
оператор условия является, пожалуй,
наиболее важным. Его приходится
использовать практически во всех
создаваемых алгоритмах. Как уже показано,
условный оператор if
имеет два маркера. В правый маркер
вводится условие, в левый – операция,
которая должна быть проделана в случае,
если условие выполнится (если же оно не
выполнится, система просчитывает
программу, пропуская данный фрагмент).
В маркер оператора может быть внесено
несколько выражений условий или операций.
В случае задания комплекса условий
будьте предельно внимательны и всегда
помните, чем отличаются формы его
определения через программный блок и
с использованием логического умножения.
Неверное задание формы комплекса условий
– самая распространенная ошибка при
работе с данным оператором.
Пример:
Функция возвращает остаток от деления
на 2:
![]()
![]()
![]()
После
того, как функция определена, она может
использоваться наравне со встроенными
функциями.
С оператором if
возможны более сложные конструкции при
использовании ещё одного оператора
–![]()
реализующего альтернативу. Аналог
традиционной конструкции Если
… То … Иначе … .
Т.е. оператор предназначен для определения
тог![]() о
о
действия, которое должно быть выполнено,
если условие оператора if
окажется истинным. Одновременно может
быть использовано несколько условных
операторов if.
Оператор otherwise
в таком случае будет задействован, если
не выполняется условия всех операторов
if.
![]() –
–
оператор
цикла обеспечивает повторяющиеся
вычисления, если известно количество
шагов.
Первый операнд – переменная
цикла, это интервальная переменная и
её![]()
значения определены во втором операнде.
Третий операнд – тело цикла может
состоять из блока операторов и выполняется
пока не исчерпаются все значения
переменной цикла.
Пример:

Рассмотрим
программу упорядочения чисел по убыванию
в одномерном массиве. Пусть дан массив
чисел: Мы воспользуемся вложенными
циклами и в качестве тела цикла по i
используем ещё один цикл по j.
З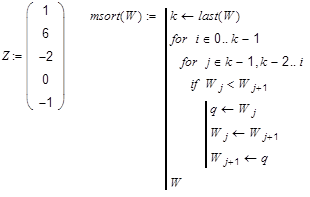 десь
десь
реализован простейший алгоритм
сортировки, так называемый “метод
пузырька”. На самом деле, большие
числа как бы всплывают наверх при каждом
шаге цикла по i, в то время как в цикле
по j на каждом шаге происходит сравнение
пары чисел и замена, если большее число
находится ниже, причём эта замена
осуществляется снизу.
О тметим,
тметим,
что в системе имеется стандартная
функция сортировки sort().
Примечание:
второй цикл мы организовали с отрицательным
шагом от конечного значения к начальному.
Можно использовать программные
возможности Mathcad просто для задания
функций более сложного вида.
![]() –
–
оператор
break
введён для повышения гибкости
программирования и позволяет закончить
цикл досрочно, не исчерпав всего списка.
Как правило, ввиду того, что цикл бывает
нужным остановить при выполнении
некоторого условия, данный оператор
почти всегда используется с условным
оператором if.
Р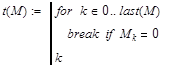 ассмотрим
ассмотрим
следующую задачу: нам необходимо найти
первое вхождение 0 в числовом массиве
и вернуть его индекс. Мы приводим
работающую программу, где введена
функция last(M)
которая возвращает последний индекс
массива. Возвращаемым значением программы
является последний выполняемый оператор
– k.
![]()
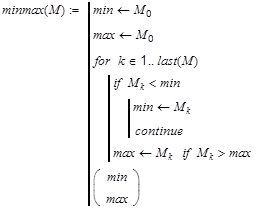 –
–
ещё один полезный оператор позволяющий
прервать выполнение текущей итерации
и перейти к следующей.
Рассмотрим
например задачу нахождения максимального
и минимального элемента
массива.
Действительно, если
![]() ,
,
то нет смысла проверять
![]() ,
,
а лучше перейти к следующему шагу цикла.
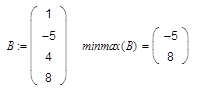
![]()
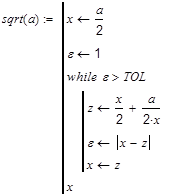
![]() –
–
оператор цикла с предусловием используется
в тех случаях, когда заранее неизвестно
количество шагов необходимых для решения
задачи. Условие проверяется перед
началом каждого шага цикла.
Реализуем,
например алгоритм вычисления квадратного
корня a
используя
итерационную формулу
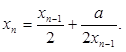
![]()
![]()
![]()
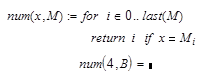 –
–
оператор
return
служит для прекращения работы программы
и возврата результата. Обычно данный
оператор используется при описании
действий алгоритма в случае ошибочной
ситуации.
Допустим нам необходимо
вычислить позицию первого вхождения
числа в массив.
Рассмотрим
в качестве ещё одного примера вопрос,
как программным способом построить
скалярное произведение.
В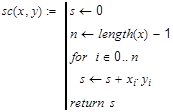 ычислим
ычислим
квадрат модуля вектора
Оператор
return
здесь может быть опущен.
В качестве
возвращаемого значения в программе
используется результат последней
операции. Обратите внимание, что в
программах мы не пользуемся оператором
присваивания :=, а вводим оператор
локального присваивания. Переменные,
определённые в программе, теряют значение
при выходе из неё.
![]()
![]()
![]() –
–
оператор
on
error
служит для обработки ошибочных ситуаций
типа “деления на нуль”. Данный
оператор по своему синтаксису полностью
соответствует условному оператору if.
В правый его маркер следует внести
величину или выражение, ошибка в
вычислении которого должнв быть
зарегистрирована. В левом маркере
следует прописать условие, которое
должно быть выполнено в случае ошибочной
ситуации.
Например, нам необходимо
описать функцию
![]() ,
,
чтобы не было особенности в 0.
![]() тогда:
тогда:
![]()
Примечание.
Оператор
on
error
может
использоваться в арифметических
выражениях.
Варианты
заданий
Вариант
1
-
Составить
программу которая будет менять местами
2 строки матрицы. -
Используя
оператор on error для предотвращения
появления ошибки “деление на нуль”,
вычислить функцию
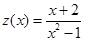 .
. -
Написать
программу, где функции, возвращающая
–1, 0 или 1 в зависимости от знака аргумента
(соответственно «-», 0, «+»).
Вариант
2
-
Составить
программу, которая будет выводить сумму
геометрической прогрессии, при заданных
значениях
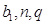 .
. -
Написать
программу по выводу матрицы размером
3х3, где на второстепенной диагонали
стояли бы 1. -
Вычислить
значение функции
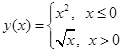 .
.
Вариант
3
-
Вычислить
сумму чисел 1+2+3+….+n. -
Для
x изменяющего от -2 до 2 вычислить значение
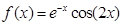 .
. -
Составить
программу по вычислению длины вектора.
Вариант
4
1.Создайте
программу pr(n)
для вычисления произведения
чисел
1*2*3*….*n.
2.Создайте
программу для вычисления и вывода двух
корней квадратного уравнения
![]() .
.
3.Используя
оператор on error для предотвращения
появления ошибки “деление на нуль”,
вычислить функцию
![]() .
.
Вариант
5
-
Создайте
программу для вычисления и вывода двух
корней квадратного уравнения
f(x)=ax2+bx+c. -
Дано
натуральное число n, действительное x.
Вычислить
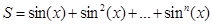 .
. -
Написать
программу по выводу на экран знака «+»
(«-»), если значение
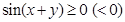 .
.
Вариант
6
-
Написать
программу, которая будет выводить
единичную матрицу. -
Вычислить
значение
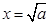 ,
,
используя итерационную процедуру
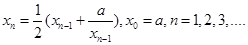 В
В
качестве приближенного значения корня
квадратного берется такое значение
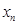 ,
,
которое удовлетворяет условию
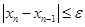 ,
,
где
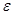 –
–
заданная точность вычисления. -
Вычислить
 ,
,
где
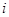 меняется
меняется
от 0 до 10.
Вариант
7
-
Составить
программу, которая будет выводить сумму
арифметической прогрессии при заданных
значениях
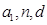 .
. -
Составим
программу для вычисления переменной
z по формуле
 .
. -
Написать
программу, которая выводит абсолютное
значение функции
 .
.
Вариант
8
-
Определить
функцию, которая равна 1, если аргумент
размещён между чётным и нечётным числом,
и 0 в противном случае. -
Вычислить
сумму бесконечной геометрической
прогрессии со знаменателем 0,4 и начальным
элементом -8. -
Написать
программу по выводу на экран матрицы,
каждый элемент которой будет вычисляться
по правилу:
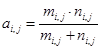 ,
,
где
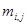 и
и
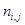 –
–
элементы матриц соответственно
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
На чтение 6 мин Просмотров 1.9к.
Содержание
- 1. Поиск экстремума функции
- 2. Экстремум функции одной переменной
- 3. Условный экстремум
- Александр Малыгин
- 2 Комментарии “ Оптимизация функций одной и нескольких переменных в PTC MathCAD ”
9. Нахождение экстремумов функций 
MathCAD позволяет находить экстремумы функций, которые имеют конечное количество экстремумов. Для нахождения экстремума используются функции Minimize и Maximize .
На рис.14 показан пример использования функции нахождения минимума. Нахождение максимума происходит аналогично, за исключением того, что функцию Minimize необходимо заменить на Maximize . В данном примере показан случай, когда максимум функции не может быть найден.
8.6.1. Экстремум функции одной переменной
Поиск экстремума функции включает в себя задачи нахождения локального и глобального экстремума. Последние называют еще задачами оптимизации. Рассмотрим конкретный пример функции f(x), показанной графиком на рис. 8.8 на интервале (-2,5). Она имеет глобальный максимум на левой границе интервала, глобальный минимум, локальный максимум, локальный минимум и локальный максимум на правой границе интервала (в порядке слева направо).
В Mathcad с помощью встроенных функций решается только задача поиска локального экстремума. Чтобы найти глобальный максимум (или минимум), требуется либо сначала вычислить все их локальные значения и потом выбрать из них наибольший (наименьший), либо предварительно просканиро-вать с некоторым шагом рассматриваемую область, чтобы выделить из нее подобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности. Последний путь таит в себе некоторую опасность уйти в зону другого локального экстремума, но часто может быть предпочтительнее из соображений экономии времени.

Рис. 8.8. График функции f(х)=х 4 +5х 3 -10х
Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно.
- Minimize (f, x1, . ,хм) — вектор значений аргументов, при которых функция f достигает минимума;
- Maximize (f, х1, . ,хм) — вектор значений аргументов, при которых функция f достигает максимума;
- f (x1, . , хм. ) — функция;
- x1, . , xм — аргументы, по которым производится минимизация (максимизация).
Всем аргументам функции f предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения. Примеры вычисления экстремума функции одной переменной (рис. 8.8) без дополнительных условий показаны в листингах 8.11- 8.12. Поскольку никаких дополнительных условий в них не вводится, поиск экстремумов выполняется для любых значений.
Листинг 8.11. Минимум функции одной переменной
Листинг 8.12. Максимум функции одной переменной
Как видно из листингов, существенное влияние на результат оказывает выбор начального приближения, в зависимости от чего в качестве ответа выдаются различные локальные экстремумы. В последнем случае численный метод вообще не справляется с задачей, поскольку начальное приближение х=-10 выбрано далеко от области локального максимума, и поиск решения уходит в сторону увеличения f (х).
1. Поиск экстремума функции
Задачи поиска экстремума функции означают нахождение ее максимума (наибольшего значения) или минимума (наименьшего значения) в некоторой области определения ее аргументов. Ограничения значений аргументов, задающих эту область, как и прочие дополнительные условия, должны быть определены в виде системы неравенств и (или) уравнений. В таком случае говорят о задаче на условный экстремум.
Для решения задач поиска максимума и минимума в Mathcad имеются встроенные функции Minerr, Minimize и Maximize. Все они используют те же градиентные численные методы, что и функция Find для решения уравнений.
2. Экстремум функции одной переменной
Поиск экстремума функции включает в себя задачи нахождения локального и глобального экстремума. Последние называют еще задачами оптимизации. Рассмотрим конкретный пример функции f(x), показанной графиком на рис.2 на интервале (-2,5). Она имеет глобальный максимум на левой границе интервала, глобальный минимум, локальный максимум, локальный минимум и локальный максимум на правой границе интервала (в порядке слева направо).
В Mathcad с помощью встроенных функций решается только задача поиска локального экстремума. Чтобы найти глобальный максимум (или минимум), требуется либо сначала вычислить все их локальные значения и потом выбрать из них наибольший (наименьший), либо предварительно просканировать с некоторым шагом рассматриваемую область, чтобы выделить из нее подобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности. Последний путь таит в себе некоторую опасность уйти в зону другого локального экстремума, но часто может быть предпочтительнее из соображений экономии времени.
 Рис. 1. График функции f(х)=х 4 +5х 3 -10х
Рис. 1. График функции f(х)=х 4 +5х 3 -10х
Построим график заданной функции (рис.1). По графику видны участки локальных экстремумов функции.
Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно.
· Minimize (f, x1, … ,хм) — вектор значений аргументов, при которых функция f достигает минимума;
· Maximize (f, х1, … ,хм) — вектор значений аргументов, при которых функция f достигает максимума;
Всем аргументам функции f предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения. Примеры вычисления экстремума функции одной переменной (рис.1) без дополнительных условий показаны в листинге на рис.2. Поскольку никаких дополнительных условий в них не вводится, поиск экстремумов выполняется для любых значений.


 Рис.2. Поиск локальных экстремумов функции одной переменной
Рис.2. Поиск локальных экстремумов функции одной переменной
Как видно из листинга, существенное влияние на результат оказывает выбор начального приближения, в зависимости от чего в качестве ответа выдаются локальные различные экстремумы. В последнем случае численный метод вообще не справляется с задачей, поскольку начальное приближение х=-10 выбрано далеко от области локального максимума, и поиск решения уходит в сторону увеличения f (х).
3. Условный экстремум
В задачах на условный экстремум функции минимизации и максимизации должны быть включены в вычислительный блок, т. е. им должно предшествовать ключевое слово Given. В промежутке между Given и функцией поиска экстремума с помощью булевых операторов записываются логические выражения (неравенства, уравнения), задающие ограничения на значения аргументов минимизируемой функции. На рис.3 показаны примеры поиска условного экстремума на различных интервалах, определенных неравенствами. Сравните результаты работы этого листинга с двумя предыдущими.



Рис. 3. Три примера поиска условного экстремума функции
Не забывайте о важности выбора правильного начального приближения и в случае задач на условный экстремум. Например, если вместо условия — 3 Скачать пример
Александр Малыгин
Объект обсуждения – программное обеспечение для выполнения автоматизированного конструкторского и технологического проектирования, разработки управляющих программ, вопросы, связанные с разработкой прикладных САПР.
2 Комментарии “ Оптимизация функций одной и нескольких переменных в PTC MathCAD ”
Спасибо, очень информативано! Скажите, а для 9 переменных такая же функция и такой же принцип используется?
Функция будет другая. Вы сами подбираете вид функции, остальное аналогично.
Mathcad: ищем экстремум функции двух переменных
Поиск экстремума функции двух переменных принципиально не отличается от случая одной переменной и выполняется стандартными функциями Minimize и Maximize. Проблема состоит в том, как правильно выбрать начальную точку (x,y), от которой будет выполняться поиск решения. Если у анализируемой функции несколько стационарных точек, может быть найден только “мусор”, точней, найдётся ближайшая к начальной стационарная точка, не являющаяся экстремумом, или не найдётся ничего:

экстремум функции 2 переменных не находится – неверные начальные точки
Поэтому более правильным путём представляется реализация анализа функции на экстремум, ведь Mathcad математики не отменял 🙂
Для заданной функции Z(x,y) = x3+2xy+y2 найдём первые и вторые частные производные, определим стационарные точки, в которых обращаются в ноль первые частные производные, затем выполним проверку достаточных условий локальных экстремумов:
D=Zxx*Zyy-Zxy2>0, Zxx>0– точка локального минимума,D>0, Zxx<0– точка локального максимума.
После этого выполним поиск экстремума от точки, близкой к найденной, с помощью стандартной функции MathCAD, которая годится, скорее, для уточнения решений, чем для анализа.

правильный поиск экстремума функции 2 переменных в Mathcad
![]() Скачать этот пример в архиве .zip с документом .xmcd для Mathcad 14/15 (58 Кб)
Скачать этот пример в архиве .zip с документом .xmcd для Mathcad 14/15 (58 Кб)
22.03.2017, 13:27 [16056 просмотров]
Пример решения задачи оптимизации в программе Mathcad
Пример
Дана нелинейная целевая функция
f(x,y)=x4–2y→min
Ограничения
4x+y–2=0
x2+y2≤50
Решение
Для поиска минимального или максимального значения функции в Mathcad имеются функции:
Minimize(f, x1, x2, …xn)
Maximize(f, x1, x2, …xn)
f — функция без аргументов для максимизации и минимизации значений;
x1, x2, …xn — скалярные переменные, найденные в системе уравнений.
Записываем решение в пакете Mathcad
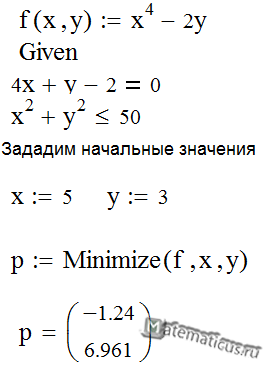
![]() 3024
3024
