Как найти минимум функции методом дихотомии

Как найти минимум функции методом дихотомии

1) Первые два
приближения возьмем на расстоянии от середины
выбранного отрезка :

;

.

Так как ,то нужно выполнить
следующее приближение.

Значения функции
в этих точках

;

Так как
,
то правый отрезокотбрасываем, т.е.
считаем, что минимум функции находится
на отрезке .

Итак, перед второй
итерацией считаем, что
.

2) Вторые два
приближения возьмем на расстоянии от середины отрезка
:

;

.

Так как ,то нужно выполнить
следующее приближение.

Значения функции
в этих точках

Так
как
,
то левый отрезокотбрасываем, т.е.
считаем, что минимум функции находится
на отрезке .

Итак, перед третьей
итерацией считаем, что
.

3) Третьи два
приближения возьмем на расстоянии от середины отрезка
:

;

.

Так как ,то нужно выполнить
следующее приближение.

Значения функции
в этих точках

Так
как
,
то левый отрезокотбрасываем, т.е.
считаем, что минимум функции находится
на отрезке .

Итак, перед четвертой
итерацией считаем, что
.

4) Четвертые два
приближения возьмем на расстоянии от середины отрезка
:

;

.

Так как ,то нужно выполнить
следующее приближение.

Значения функции
в этих точках

Так
как
,
то левый отрезокотбрасываем, т.е.
считаем, что минимум функции находится
на отрезке .

Итак, перед пятой
итерацией считаем, что
.

5) Пятые два
приближения возьмем на расстоянии от середины отрезка
:

;

.

Так как ,то нужно выполнить
следующее приближение.

Значения функции
в этих точках

Так
как
,
то правый отрезокотбрасываем, т.е.
считаем, что минимум функции находится
на отрезке .

Итак, перед шестой
итерацией считаем, что
.

6) Шестые два
приближения возьмем на расстоянии от середины отрезка
:

;

.

Так как ,то процесс
последовательных приближений можно
считать законченным и середину отрезка
т.е. точку
принять за решение.

Итак, ;число приближений.

Ниже приведены
расчеты нахождения минимума функции
методом дихотомии, выполненные с помощью
компьютерной программы.

5.2 Поиск минимума методом «золотого сечения»

1) Находим первые
два приближения по формулам:

,где
–
пропорция«золотого
сечения».

Для отрезка имеем

Так как и,то правый отрезокотбрасываем и
считаем, что ,ане меняется.

Так как ,то нужно выполнить
следующее приближение.

2) Теперь по правилу
«золотого сечения» делим отрезок ,причем точкауже находится
внутри этого отрезка, а точку ищем
как точку, симметричную точке относительно
середины отрезка ,
т.е. по формуле

Так как ,
а,то левый отрезокотбрасываем и
считаем, что ,ане меняется.

Так как ,то нужно выполнить
следующее приближение.

3) Теперь по правилу
«золотого сечения» делим отрезок ,причем точкауже находится
внутри этого отрезка, а точку ищем
как точку, симметричную точке относительно
середины отрезка ,
т.е. по формуле

Так как ,
а,то левый отрезокотбрасываем и
считаем, что ,ане меняется.

Так как ,то нужно выполнить
следующее приближение.

4) Теперь по правилу
«золотого сечения» делим отрезок ,причем точкауже находится
внутри этого отрезка, а точку ищем
как точку, симметричную точке относительно
середины отрезка ,
т.е. по формуле

Так как ,
и,то правый отрезокотбрасываем и
считаем, что ,ане меняется.

Так как ,то нужно выполнить
следующее приближение.

5) Теперь по правилу
«золотого сечения» делим отрезок ,причем точкауже находится
внутри этого отрезка, а точку ищем
как точку, симметричную точке относительно
середины отрезка ,
т.е. по формуле

Так как ,
и,то правый отрезокотбрасываем и
считаем, что ,ане меняется.

Так как ,то нужно выполнить
следующее приближение.

6) Теперь по правилу
«золотого сечения» делим отрезок ,причем точкауже находится
внутри этого отрезка, а точку ищем как точку,
симметричную точке относительно
середины отрезка ,
т.е. по формуле

Так как ,
а,то левый отрезокотбрасываем и
считаем, что ,ане меняется.

Так как ,то процесс
последовательных приближений можно
считать законченным и середину отрезка
т.е. точку
принять за решение.

Итак, ;число приближений.

Ниже приведены
расчеты нахождения минимума функции
методом «золотого сечения», выполненные
с помощью компьютерной программы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Аннотация: Данная лекция рассматривает задачи однопараметрической
оптимизации и приводит наиболее распространенные методы решения этих
задач, в частности, такие как метод дихотомии, метод Фибоначчи, метод
“золотого сечения”, метод Ньютона; также формулируются их
основные характеристики, определяется область применения и выясняются
преимущества и недостатки данных методов.

Однопараметрическая
оптимизация (поиск экстремумов функций одной
переменной) является самостоятельной и часто встречаемой задачей.
Кроме того, к ней сводится гораздо более сложная задача – поиск
экстремума функции многих переменных.

1. Метод дихотомии.

Рассмотрим простейший однопараметрический метод безусловной
оптимизации – метод дихотомии.
Этот метод является методом прямого
поиска. В нем при поиске экстремума
целевой функции используются только вычисленные значения целевой функции.

Дана функция F(x). Необходимо найти overline{x}, доставляющий минимум (или максимум) функции F(x) на интервале [a,b] с заданной точностью varepsilon, т.е. найти

overline{x} = arg min F(x), ; overline{x} in [a,b].

Запишем словесный алгоритм метода.

1) На каждом шаге процесса поиска делим отрезок [a,b]
пополам, x=(a+b)/2 – координата середины отрезка [a,b].

2) Вычисляем значение функции F(x) в окрестности 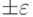pm varepsilon вычисленной точки x, т.е.

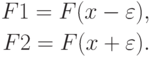
begin{align*} F1=F(x-varepsilon), \ F2=F(x+varepsilon). end{align*}

3) Сравниваем F1 и F2 и отбрасываем
одну из половинок отрезка [a,b]
(рис. 9.1).

При поиске минимума:

Если F1<F2, то отбрасываем отрезок [x,b], тогда b=x.
(рис. 9.1.а)

Иначе отбрасываем отрезок [a,x], тогда a=x. (рис. 9.1.б)

При поиске максимума:

Если F1<F2, то отбрасываем отрезок [a,x], тогда a=x.

Иначе отбрасываем отрезок [x,b],
тогда b=x.

4) Деление отрезка [a,b] продолжается,
пока его длина не станет меньше заданной точности varepsilon, т.е. |b-a| le varepsilon

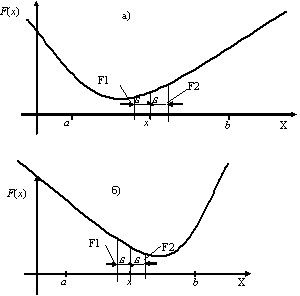
Поиск экстремума функции F(x) методом дихотомии

Рис.
9.1.
Поиск экстремума функции F(x) методом дихотомии

Схема алгоритма метода
дихотомии представлена на
рис 9.2.

На рис 9.2: c – константа,

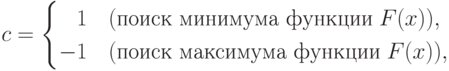
c= begin{cases} phantom{-} 1 & (text{поиск минимума функции} ; F(x)), \ -1 & (text{поиск максимума функции} ; F(x)), end{cases}

При выводе x – координата точки, в которой функция F(x) имеет минимум (или максимум), FM – значение функции F(x) в этой точке.

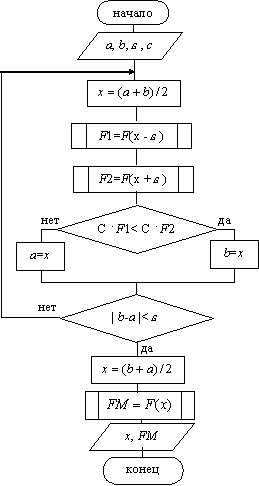
Схема алгоритма метода дихотомии

Рис.
9.2.
Схема алгоритма метода дихотомии

Источник

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

  • 1 Введение
  • 2 Метод половинного деления
    • 2.1 Метод половинного деления как метод поиска корней функции
      • 2.1.1 Изложение метода
      • 2.1.2 Реализация метода на С++ и числовой пример
    • 2.2 Метод половинного деления как метод оптимизации
  • 3 Метод хорд
    • 3.1 Изложение метода
  • 4 Комбинация метода хорд и метода половинного деления
  • 5 Список литературы
  • 6 См. также

Введение

Существует довольно очевидная теорема: “Если непрерывная функция на концах некоторого интервала имеет значения разных знаков, то внутри этого интервала у нее есть корень (как минимум, один, но м.б. и несколько)”. На базе этой теоремы построено численное нахождение приближенного значения корня функции. Обобщенно этот метод называется дихотомией, т.е. делением отрезка на две части. Обобщенный алгоритм выглядит так:

  1. Задать начальный интервал [X_{left}..X_{right}];
  2. Убедиться, что на концах функция имеет разный знак;
  3. Повторять
пока не будет достигнута нужная точность.

Варианты метода дихотомии различаются выбором точки деления. Рассмотрим варианты дихотомии: метод половинного деления и метод хорд.

Метод половинного деления

Метод половинного деления известен также как метод бисекции. В данном методе интервал делится ровно пополам.

Такой подход обеспечивает гарантированную сходимость метода независимо от сложности функции – и это весьма важное свойство. Недостатком метода является то же самое – метод никогда не сойдется быстрее, т.е. сходимость метода всегда равна сходимости в наихудшем случае.

Метод половинного деления:

  1. Один из простых способов поиска корней функции одного аргумента.
  2. Применяется для нахождения значений действительно-значной функции, определяемому по какому-либо критерию (это может быть сравнение на минимум, максимум или конкретное число).

Метод половинного деления как метод поиска корней функции

Изложение метода

Перед применением метода для поиска корней функции необходимо отделить корни одним из известных способов, например, графическим методом. Отделение корней необходимо в случае, если неизвестно на каком отрезке нужно искать корень.

Будем считать, что корень t функции f(x)=0 отделён на отрезке [a,b]. Задача заключается в том, чтобы найти и уточнить этот корень методом половинного деления. Другими словами, требуется найти приближённое значение корня с заданной точностью eps.

Пусть функция f непрерывна на отрезке [a,b],

f(a)cdot f(b)<0, ; eps=0,01 и tin[a,b] – единственный корень уравнения f(x)=0, ; ale tle b.

(Мы не рассматриваем случай, когда корней на отрезке [a,b] несколько, то есть более одного. В качестве eps можно взять и другое достаточно малое положительное число, например, 0,001.)

Поделим отрезок [a,b] пополам. Получим точку c= frac {a+b}{2}, ; a<c<b и два отрезка [a,c], ; [c,b].

Новый отрезок [a_1;b_1] делим пополам. Получаем середину этого отрезка c_1=frac {a_1+b_1}{2} и так далее.

Для того, чтобы найти приближённое значение корня с точностью до eps >0, необходимо остановить процесс половинного деления на таком шаге n, на котором |b_n-c_n|<eps и вычислить x=frac {a_n+b_n}{2}. Тогда можно взять tapprox x.

Реализация метода на С++ и числовой пример

Решим уравнение 4-e^x-2x^2=0 методом половинного деления. Графическим методом находим отрезок [0; ,1], которому принадлежит искомый корень. Так как f(0)cdot f(1)<0, то принимаем a=0, ; b=1.

Ниже приведен пример программы на Си++, которая решает поставленную задачу.

Программа 1. Корень уравнения 

#include <iostream>
#include <cmath>
using namespace std;
const double epsilon = 1e-2;
 
double f(double x)
{
    return 4- exp(x) - 2*x^2;
}
 
int main()
{
    double a, b, c;
    a = 0;
    b = 2;
    while (b - a > epsilon){
        c = (a + b) / 2;
        if(f(b) * f(c) < 0)
            a = c;
        else
            b = c;
    }
    cout << (a + b) / 2 << endl;
    return 0;
}

Искомый корень x approx 0.88281. Вычисления проводились с точностью 0.01.

Промежуточные вычисления представлены в таблице ниже.

n an bn cn bn-cn
1 0 1 0.5 0.5
2 0.5 1 0.75 0.25
3 0.75 1 0.875 0.125
4 0.875 1 0.9375 0.0625
5 0.875 0.9375 0.90625 0.03125
6 0.875 0.90625 0.890625 0.015625
7 0.875 0.890625 0.8828125 0.0078125

Метод половинного деления как метод оптимизации

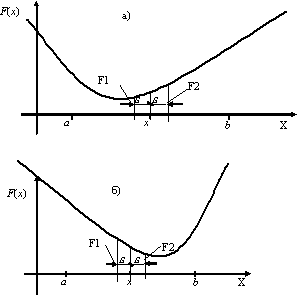
Рис. 1. Поиск экстремума функции методом половинного деления

Рис. 1. Поиск экстремума функции F(x) методом половинного деления

Рис. 2. Схема алгоритма метода половинного деления

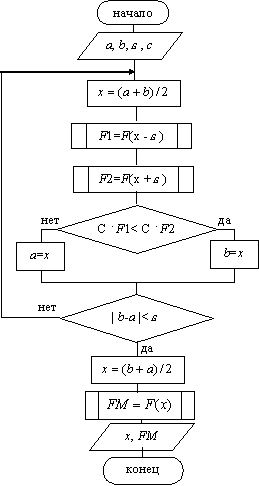
Рис. 2. Схема алгоритма метода половинного деления

Однопараметрическая оптимизация (поиск экстремумов функций одной переменной) является самостоятельной и часто встречаемой задачей. Кроме того, к ней сводится гораздо более сложная задача – поиск экстремума функции многих переменных.

Рассмотрим метод половинного деления как простейший однопараметрический метод безусловной оптимизации. Данный метод является методом прямого поиска. В нем при поиске экстремума целевой функции используются только вычисленные значения целевой функции.

Дана функция F(x). Необходимо найти overline{x}, доставляющий минимум (или максимум) функции F(x) на интервале [a,b] с заданной точностью varepsilon, т.е. найти

overline{x} = arg min F(x), ; overline{x} in [a,b].

Запишем словесный алгоритм метода.

  1. На каждом шаге процесса поиска делим отрезок [a,b] пополам, x=frac {a+b}{2} – координата середины отрезка [a,b].
  2. Вычисляем значение функции F(x) в окрестности pm varepsilon вычисленной точки x, т.е.
    F_1=F(x-varepsilon),; F_2=F(x+varepsilon).
  3. Сравниваем F_1 и F_2 и отбрасываем одну из половинок отрезка [a,b] (рис. 1).
    • При поиске минимума:
    • При поиске максимума:
  4. Деление отрезка [a,b] продолжается, пока его длина не станет меньше заданной точности varepsilon, т.е. |b-a| le varepsilon.

Схема алгоритма метода представлена на рис 2.

На рис 2:

c– константа,
c =begin{cases} quad 1 , quad (min ; F(x)), \-1, quad (max ; F(x)). end{cases}

При выводе x – координата точки, в которой функция F(x) имеет минимум (или максимум), F_M – значение функции F(x) в этой точке.

Метод хорд

Недостаток деления отрезка строго пополам проистекает от того, что он использует лишь знак функции, игноририруя отклонение (абсолютную величину). Но очевидно, что чем меньше (по абсолютной величине) значение функции, тем ближе мы находимся к корню. Метод хорд предлагает делить отрезок в точке, отстоящей от краев отрезка пропорционально абсолютному значению функции на краях. (Название “метод хорд” происходит от того, что точка деления является пересечением отрезка [(X_{left},; F(X_{left})), ; (X_{right},; F(X_{right}))] – хорды – с осью абцисс.)

Изложение метода

Метод основан на замене функции f(x) на каждом шаге поиска хордой, пересечение которой с осью X дает приближение корня.

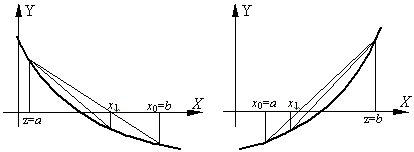
Рис. 3. Метод хорд

Рис. 3. Метод хорд

При этом в процессе поиска семейство хорд может строиться:

  1. при фиксированном левом конце хорд, т.е. z=a, тогда начальная точка x_0=b (рис. 3а);
  2. при фиксированном правом конце хорд, т.е. z=b, тогда начальная точка x_0=a (рис. 3б);

В результате итерационный процесс схождения к корню реализуется рекуррентной формулой:

  • для случая а):
x_{n+1}=x_n - frac{f(x_n)}{f(x_n)-f(a)} (x_n - a);
  • для случая б):
x_{n+1}=x_n - frac{f(x_n)}{f(x_n)-f(b)} (x_n - b);

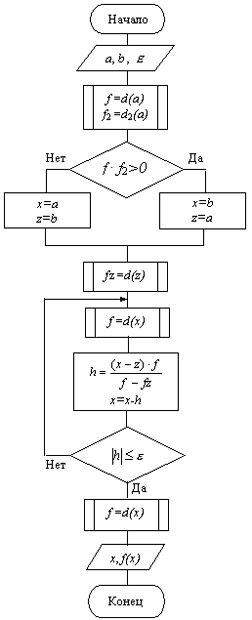
Рис. 4. Схема алгоритма уточнения корня методом хорд

Рис. 4. Схема алгоритма уточнения корня методом хорд

Процесс поиска продолжается до тех пор, пока не выполнится условие
|x_{n+1}-x_n| le varepsilon или | h| le varepsilon .

Метод обеспечивает быструю сходимость, если f(z)cdot f''(z) > 0, т.е. хорды фиксируются в том конце интервала [a,b], где знаки функции f(z) и ее кривизны f совпадают.

Схема алгоритма уточнения корня методом хорд представлена на рис. 4.

Комбинация метода хорд и метода половинного деления

Метод хорд можно применить в качестве “последнего штриха” после того, как метод половинного деления гарантирует требуемую точность – это не улучшит существенно гарантируемой точности, но, скорее всего, на несколько порядков повысит точность решения.

Если применять аналогичное уточнение к интервалу, полученному методом хорд, то эффект будет значительно слабее. Это ещё раз иллюстрирует тот факт, что метод хорд очень хорошо работает в условиях малого интервала (близости обеих границ интервала к корню), но неспособен сам создать себе эти условия (приблизить обе границы к корню).

На вопрос о том, стоит ли использовать попеременное применение метода половинного деления и метода хорд, ответ отрицателен. После того, как метод хорд приближает одну из границ почти вплотную к корню, методу половинного деления придётся долго работать, чтобы гарантировать заданную точность, т.к. метод хорд ее гарантировать не может.

Поэтому лучше использовать в качестве точки деления что-то среднее: если метод половинного деления предлагает использовать X_{halfdiv}, а метод хорд – X_{chord}, то возьмем X_{halfdiv}*K+X_{chord}*(1-K). Коэффициент K in [0..1].

Чему должен быть равен коэффициент K? Его следует не задавать, а вычислять по ходу работы: если при очередной операции интервал уменьшился более чем в два раза (это то, что гарантирует метод половинного деления), то значит, нужно больше доверять методу хорд (уменьшить K), и наоборот.

Может показаться, что при большом доверии к методу хорд этот комбинированный метод работает так же, как метод хорд. На самом деле, это не так: метод хорд передвигает по направлению к корню только одну границу, а комбинированный метод даже при высоком доверии к методу хорд передвигает и вторую границу, обеспечивая лучшие условия для работы метода хорд, а значит – для ещё большего доверия к нему.

Список литературы

  • http://dmitrykarpov.nm.ru/misc/dihotomy.htm
  • http://mathfunc.narod.ru/met_dih.html
  • http://www.intuit.ru/department/mathematics/mathprog/9/
  • http://www.intuit.ru/department/calculate/intromathmodel/4/3.html
  • http://calc-x.com/chm/dich.php
  • http://elib.ispu.ru/library/math/sem1/kiselev1/node84.html

См. также

  • Практикум ММП ВМК, 4й курс, осень 2008
Источник

Эта статья посвящена двум алгоритмам поиска — дихотомии и градиентному спуску (как ни странно, на хабре не писали ни про один из них).

Дихотомия

Дихотомия — поиск делением пополам.

Допустим есть отсортированный массив чисел:
a[10] = {0,15,23,37,42,51,69,74,81,99}

Нам надо узнать, каким по счёту в этом массиве находится число 74. Можно, конечно, пройтись по всем элементам массива по порядку и найти нужное число, но тогда, в худшем случае, это займёт O(n) операций. Для небольших значений n это не критично, но при больших значениях n или при большом количестве запросов поиска, это может сильно уменьшить время работы программы. В таком случае можно воспользоваться дихотомией: будем разбивать наш массив на две части и смотреть, в какой из них находится искомое число, далее делаем ту же операцию с найденной частью, и так до тех пор, пока найденная часть не будет состоять из одного элемента.

На примере с нашим массивом:

Разобьём его на две части:
{0,15,23,37,42} и {51,69,74,81,99}. Искомое число 74 находится во второй части. Разобьём её ещё на две:
{51,69,74} и {81,99}. Искомое число находится в первой части. Разобьём её:
{51,69} и {74}. Искомое число находится во второй части. Вторая часть состоит из одного элемента, значит это и есть искомое число.

Теперь реализация этого примера на C++:

int a[10] = {0,15,23,37,42,51,69,74,81,99};
int l = 0;
int r = 9;
while(l<r)
{
 int m = (l+r)/2;
 if(a[m]>=74)
   r = m;
 else
   l = m+1;
}
cout<<l;

Гардиентный спуск

Алгоритм предназначен для нахождения минимума/макчимума функции на заданном отрезке.

К примеру, нужно найти минимум функции y=x*x на интервале [-4,+4]:

image

В данном случае минимум функции y=0 при x=0.

Гардиентный спуск работает следующим образом:

1) Берётся какое-либо значение для шага, не привышающее размер интервала, на котором ищем.
2) Берётся любое значение x, такое, что x+шаг и x-шаг не выходили за пределы интервала.
3) Ищем значение функции для x.
4) Ищем значение функции для x+шаг. Если значении функции f(x+шаг) уменьшилось, по сравнению со значением f(x), то x=x+шаг.
5) Ищем значение функции для x-шаг. Если значении функции f(x-шаг) уменьшилось, по сравнению со значением f(x), то x=x-шаг.
6) Если и f(x+шаг), и f(x-шаг) больше f(x), то уменьшаем шаг в два раза.

Повторяем пункты 3-6 до тех пор, пока шаг>eps, где eps — точность поиска.

Вот как работает алгоритм:

Нашли х и шаг. f(х+шаг) оказалось меньше, чем f(x) и f(x-шаг). Теперь х=х+шаг.

image

Дальше опять повторяется предыдущая ситуация:

image

image

На следующем шаге и f(x+шаг) и f(x-шаг) больше f(x), значит уменьшаем шаг в два раза:

image

image

В конце-концов, мы находим ответ.

Вот реализация алгоритма на C++:

const double eps = 0.001;
double x,step;
x = -3;
step = 1;
while(step>eps)
{
 if(x*x>(x-step)*(x-step))
   x-=step;
 else
  if(x*x>(x+step)*(x+step))
    x+=step;
  else
    step/=2;
}
cout<<x;

Оба алгоритма часто приходится использовать в спортивном программировании, в разных типах задач: поиск максимума/минимума функции(дихотомия и градиентный спуск), поиск в массиве(дихотомия), приближённое решение уравнений(дихотомия и градиентный спуск), часто используются в геометрических задачах(например для поиска точек пересечения отрезка и окружности).

Источник

Домашнее задание №1#

В рамках первого домашнего задания от вас требуется:

  1. Установить python;

  2. Установить среду разработки на вкус;

  3. Реализовать один из численных методов описанных ниже.

Метод и функция, для которой его необходимо применить в обязательном порядке, определяются вариантом, которые перечисленны ниже.

Варианты#

Вариант №

Метод

(f(x))

1

Бисекции

(ln x – dfrac{1}{x})

2

Хорд

(e^x + x)

3

Ньютона

(dfrac{1}{x} – 2x)

4

Золотого сечения

(log (lvert x rvert+1))

5

Градиентного спуска

(tanh x + x^2)

6

Бисекции

(log x + 1)

7

Хорд

(arctan x – dfrac{1}{2})

8

Ньютона

(e^x – dfrac{1}{2})

9

Золотого сечения

(lvert x-1rvert + x^2)

10

Градиентного спуска

(x^2 + 2x – 3)

11

Бисекции

(tan 2x – 1 – x)

12

Хорд

(2e^{-x} – x)

13

Ньютона

(e^{-3x^2} – x)

14

Золотого сечения

(e^{lvert x-1rvert} – x^2)

15

Градиентного спуска

(cosh x + x)

16

Бисекции

(e^{-3x} + 1 – x)

17

Хорд

(e^{-x^2} – x)

18

Ньютона

(e^{-x^2} – x^2)

19

Золотого сечения

(e^{-x^2})

20

Градиентного спуска

(arctan x + x^2)

21

Бисекции

(3e^{-3x} – x)

22

Хорд

(e^{-x^3} – 1 – x^3)

23

Ньютона

(2e^{-3x} + 1 – x)

24

Золотого сечения

(sinh(lvert xrvert+1) – x^2)

25

Градиентного спуска

(-arctan e^{-x^2})

Численные методы поиска минимума или корня скалярной функции#

В рамках первого домашнего задания от вас потребуется реализовать численный метод поиска корня уравнения вида

(1)#[f(x) = 0,]

или численный метод поиска минимума скалярной функции (f):

(2)#[f(x) sim min_{x in X}.]

В обоих случаях (f) — скалярная функция одного аргумента, т.е. (fcolon mathbb{R} to mathbb{R}).

Это задание нацелено в первую очередь на освоение синтаксиса языка python, поэтому ниже приводится подробное описание алгоритмов работы каждого метода, а вам предлагается реализовать один из них средствами python. К вашему решению предъявляются следующие требования:

  1. Решение должно быть оформлено в виде скрипта python (файл с расширением “.py”, а не блокнот jupyter)!

  2. Ввод параметров должен осуществляться пользователем средствами стандартного потока ввода.

  3. Численный метод должен быть оформлен в виде отдельной процедуры (python функции).

  4. Введенные пользователем данные должны передаваться процедуре численного метода в качестве аргументов.

  5. Процедура численного метода должна возвращать найденный корень или минимум, если алгоритм сошелся, и значение None, если алгоритм не применим или разошелся.

  6. Реализованный метод должен печатать отладочную информацию в стандартный поток вывода.

  7. Реализованный метод поиска корня должен быть протестирован на каких-то простых примерах.

Tip

Ваш численный метод так или иначе должен будет вызывать функцию (f) и/или (f’) внутри себя на каждой итерации, чтобы двигаться в сторону корня или минимума.

Самый простой способ этого добиться — определить функцию (f(x)) (и/или (f'(x))) глобально и тогда на неё можно будет ссылаться внутри вашего метода. Хотя такое решение и будет приниматься преподавателем, оно не является идеальным: такая реализация ищет корень одной конкретной функции (f(x)), а для того, чтобы найти корень любой другой функции, придется модифицировать исходный код.

Более гибкое решение подразумевает передачу искомой функции (f(x)) (и/или (f'(x))) в качестве аргумента в метод поиска корня. В python функции можно передавать в качестве аргументов другим функциям точно также, как и любые другие переменные (иными словами функции в python — объекты первого класса).

Метод бисекции#

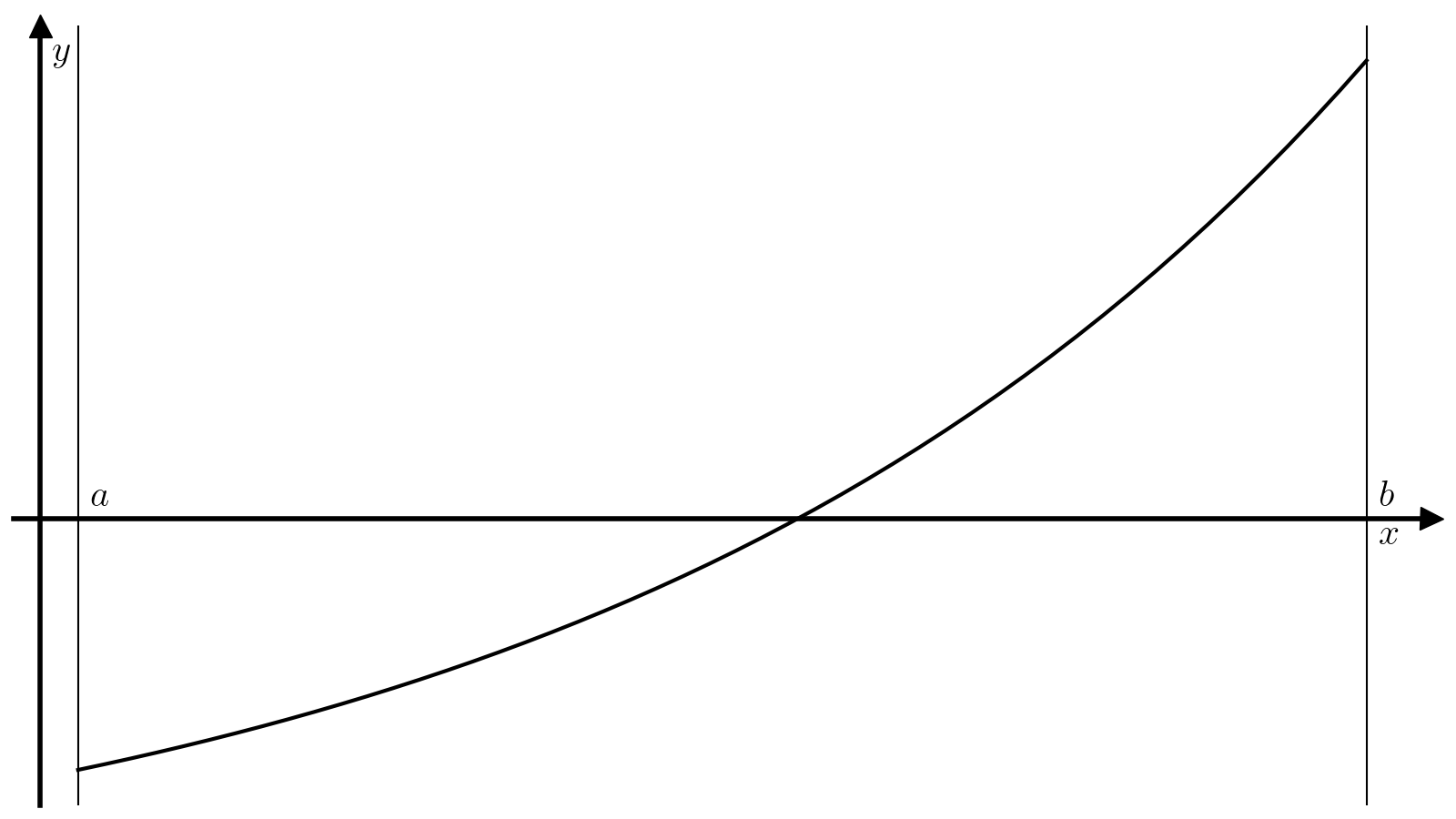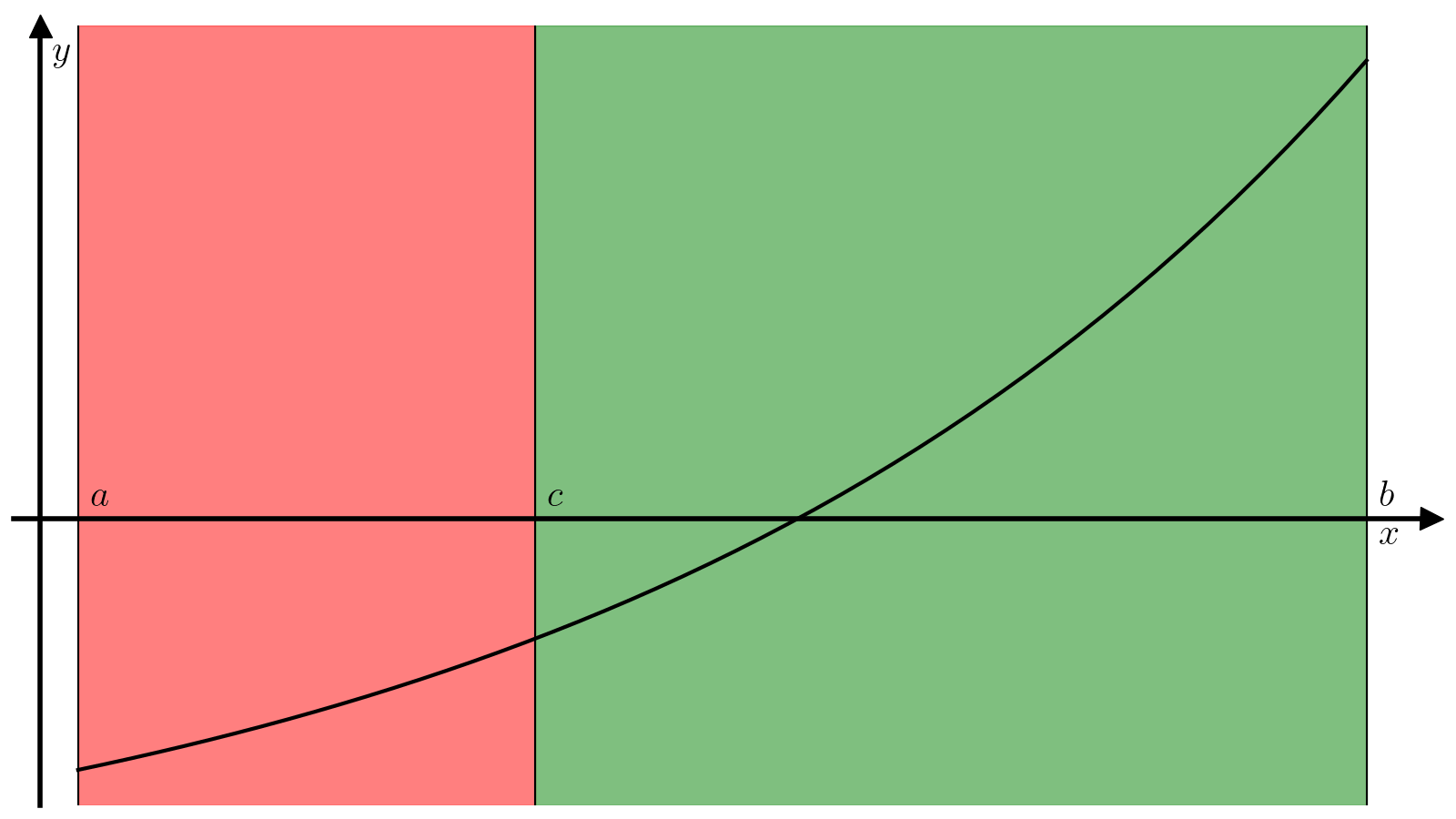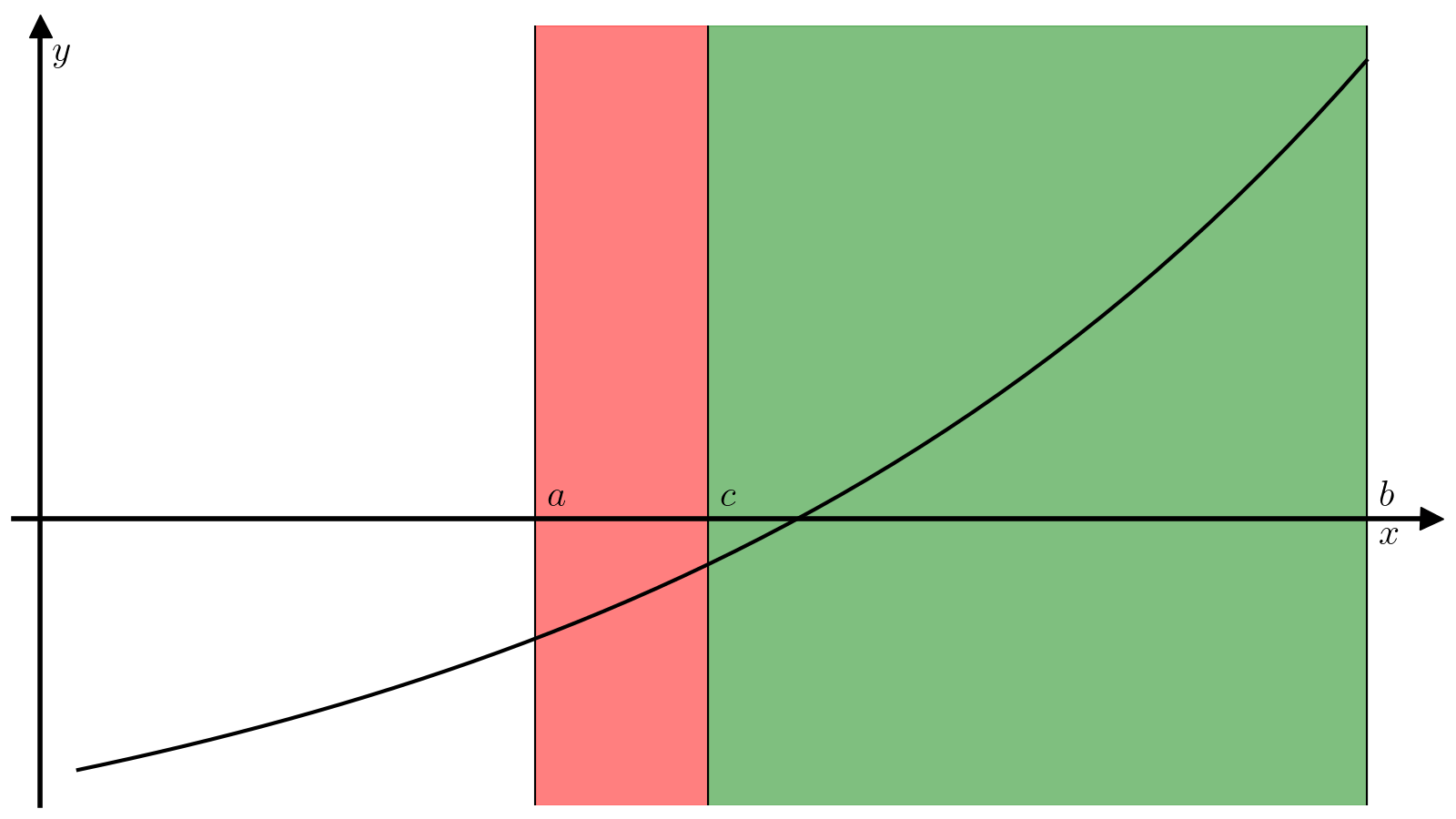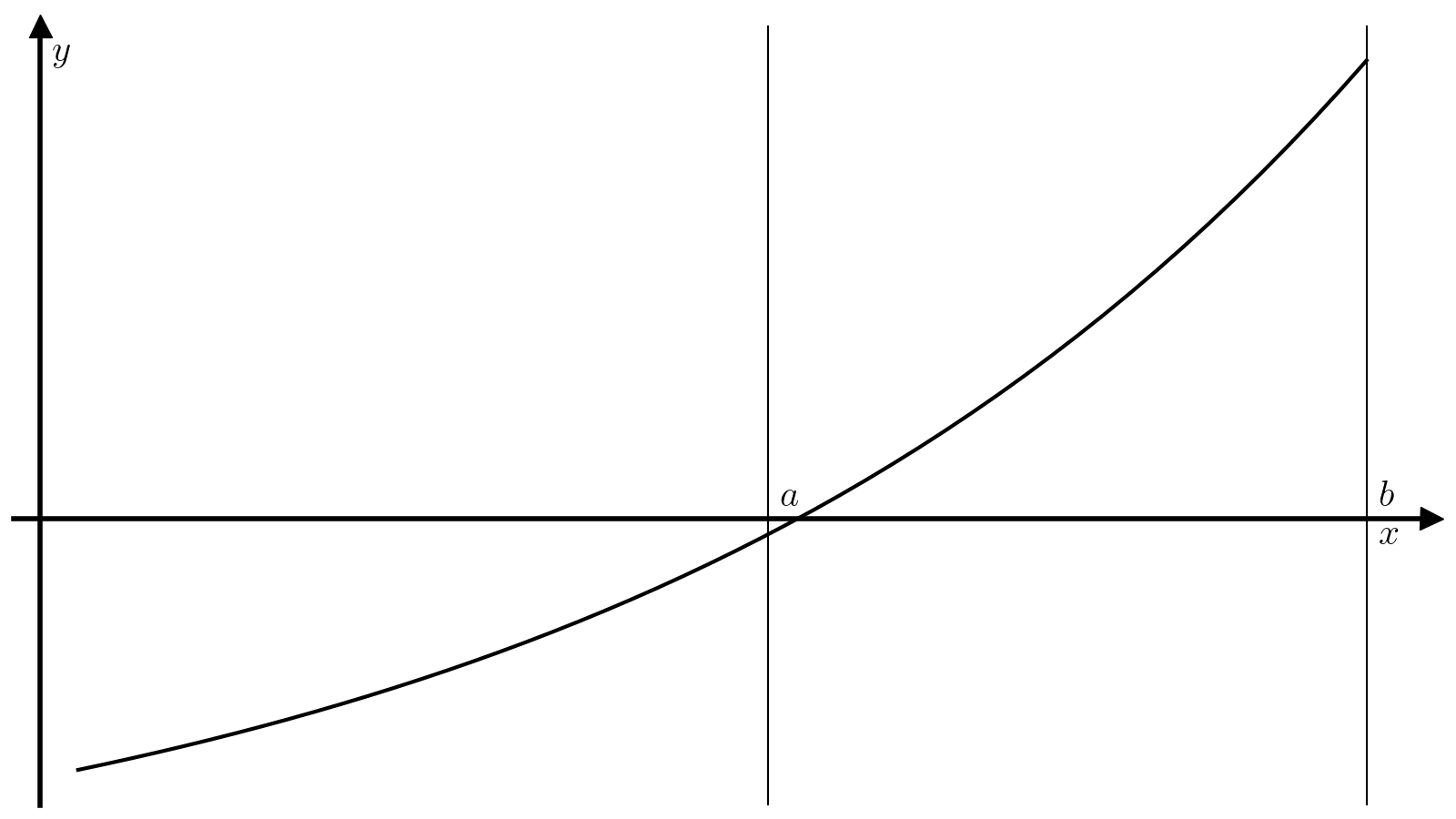
Метод бисекции — один из самых примитивных методов решения уравнений вида (1), который ищет корень непрерывной на некотором отрезке ([a, b]) функции. Для работы этого метода требуется, чтобы значение функции (f) на концах отрезка ([a, b]) были разного знака:

(3)#[f(a)f(b)<0. ]

Тогда из теоремы о промежуточном значении следует, что найдется минимум один корень функции (f) на отрезке ([a, b]), а метод бисекции позволяет найти этот корень с произвольной точностью.

Основная идея алгоритма поиска корня методом бисекции заключается в следующем. Поделим отрезок ([a, b]) пополам, т.е. найдем точку (c):

(4)#[c = dfrac{a + b}{2}.]

В зависимости от значения величины (f(c)), реализуется один из следующих вариантов.

  • (f(c) = 0), т.е. уравнение (1) решено и (c) — его корень;

  • (f(c) f(a) < 0), т.е. можно продолжить поиск корная на отрезке ([a, c]);

  • (f(c) f(a) > 0), а значит (f(c) f(b) < 0) и можно продолжить поиск корня на отрезке ([c, b]).

Итого, с помощью одного такого шага мы или найдем корень, или сузим вдвое длину отрезка, на котором ищется корень. Обычно такие шаги применяют многократно до тех пор, пока не будет достигнута необходимая точность (длина отрезка ([a, b])) и невязка (модуль значения функции (|f(c)|)), т.е. критерием сходимости метода является одновременное выполнение двух условий

[begin{split}
begin{cases}
|b – a| < delta, \
|f(c)| < varepsilon.
end{cases}
end{split}]

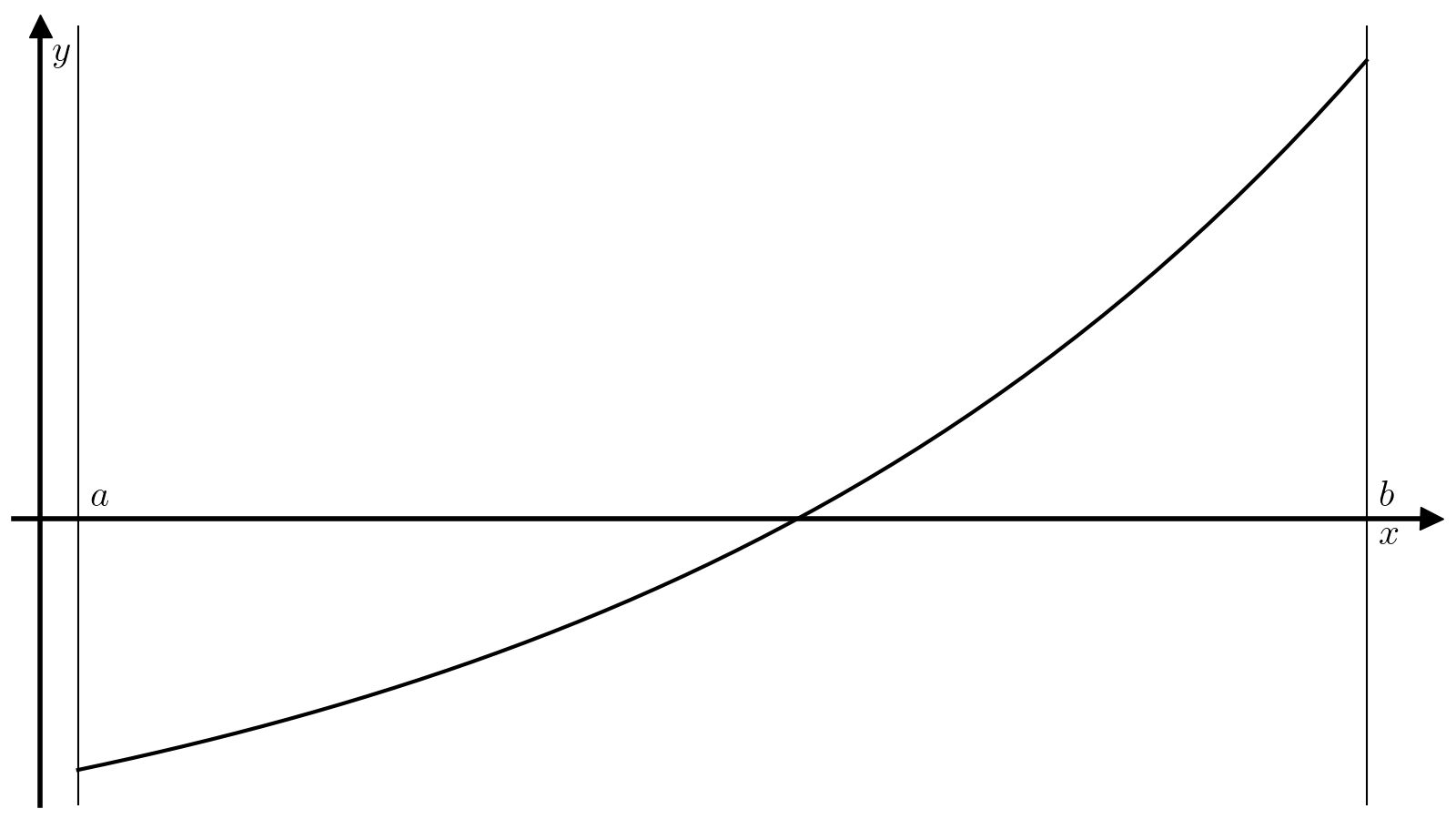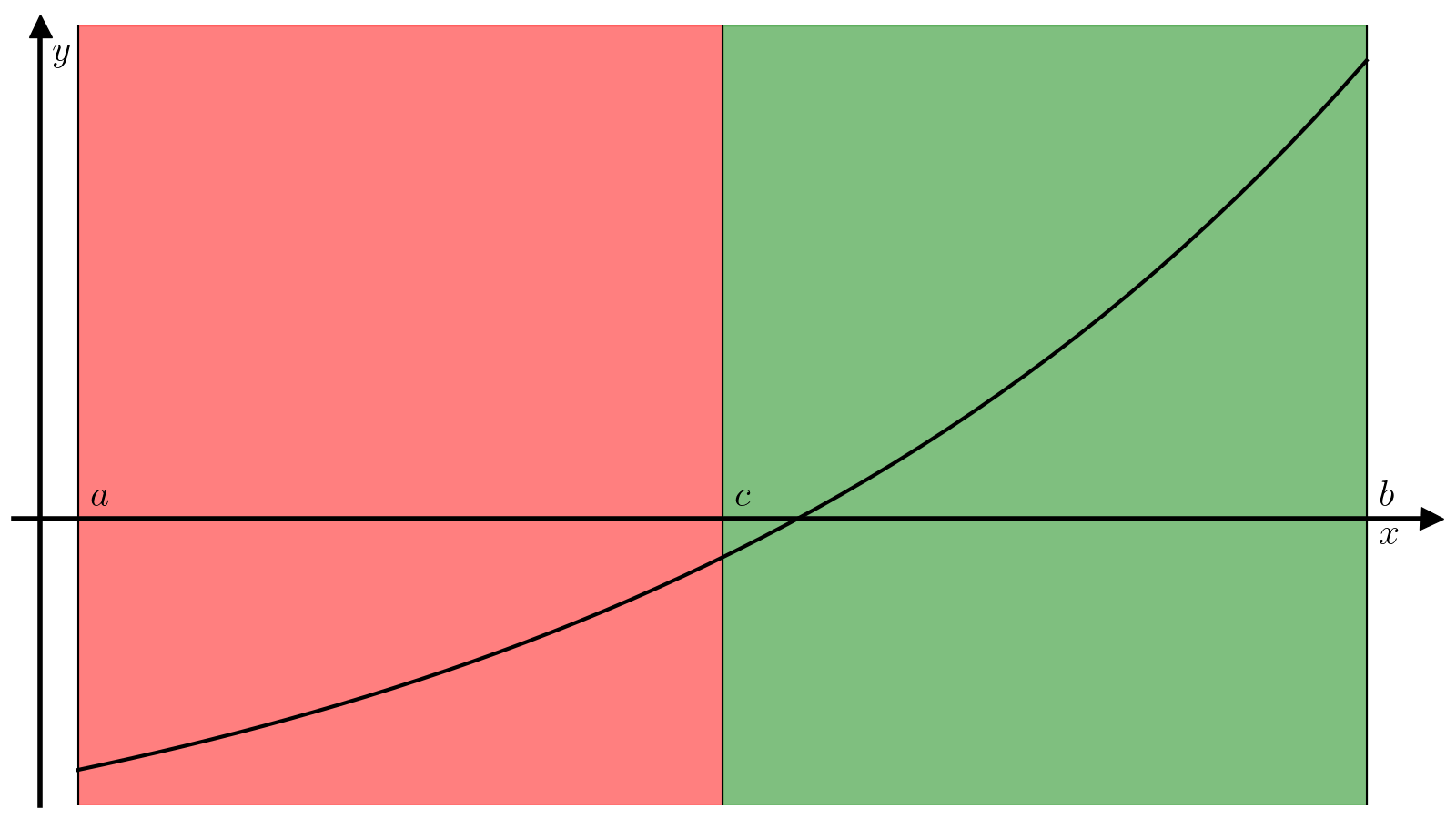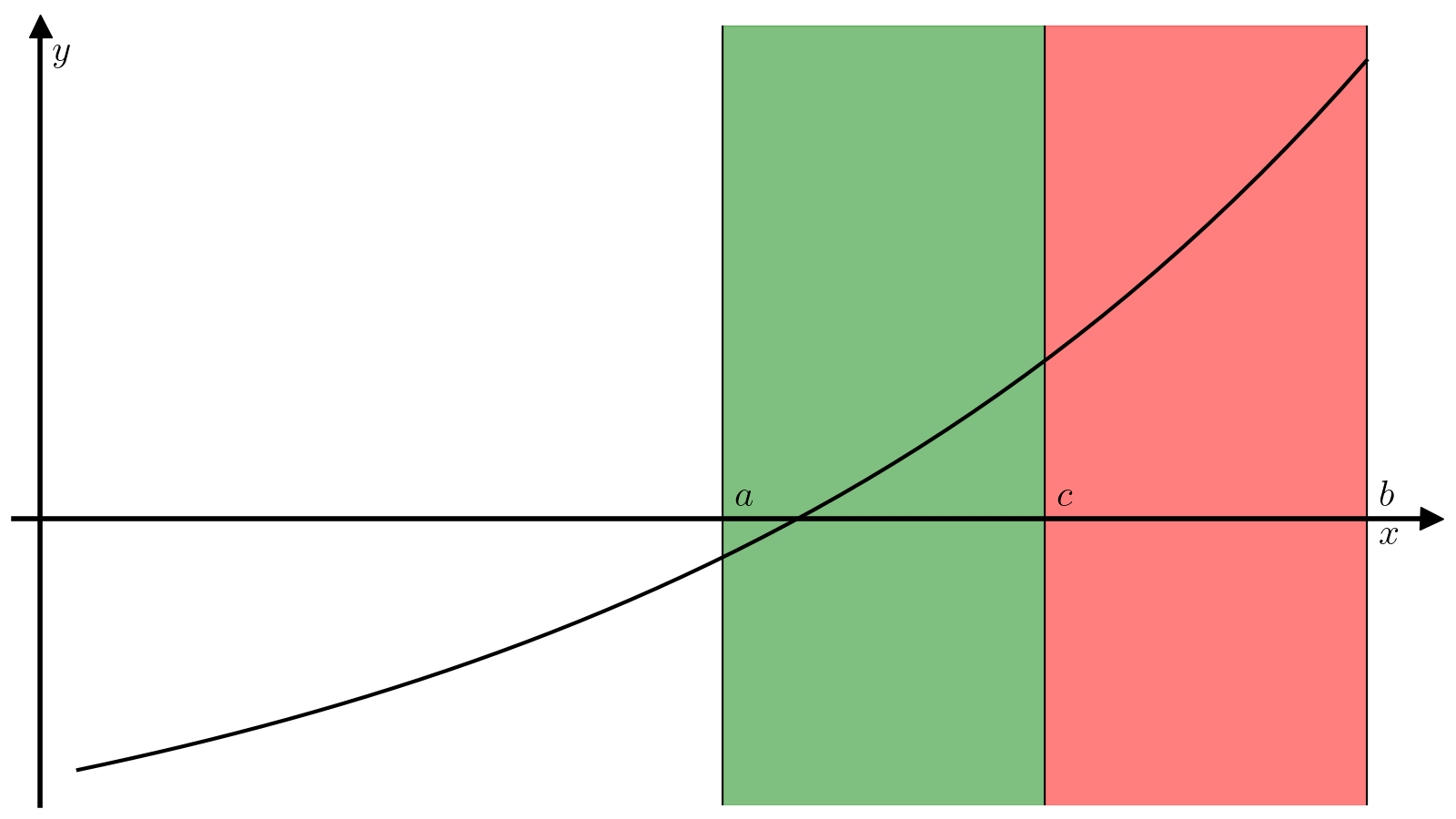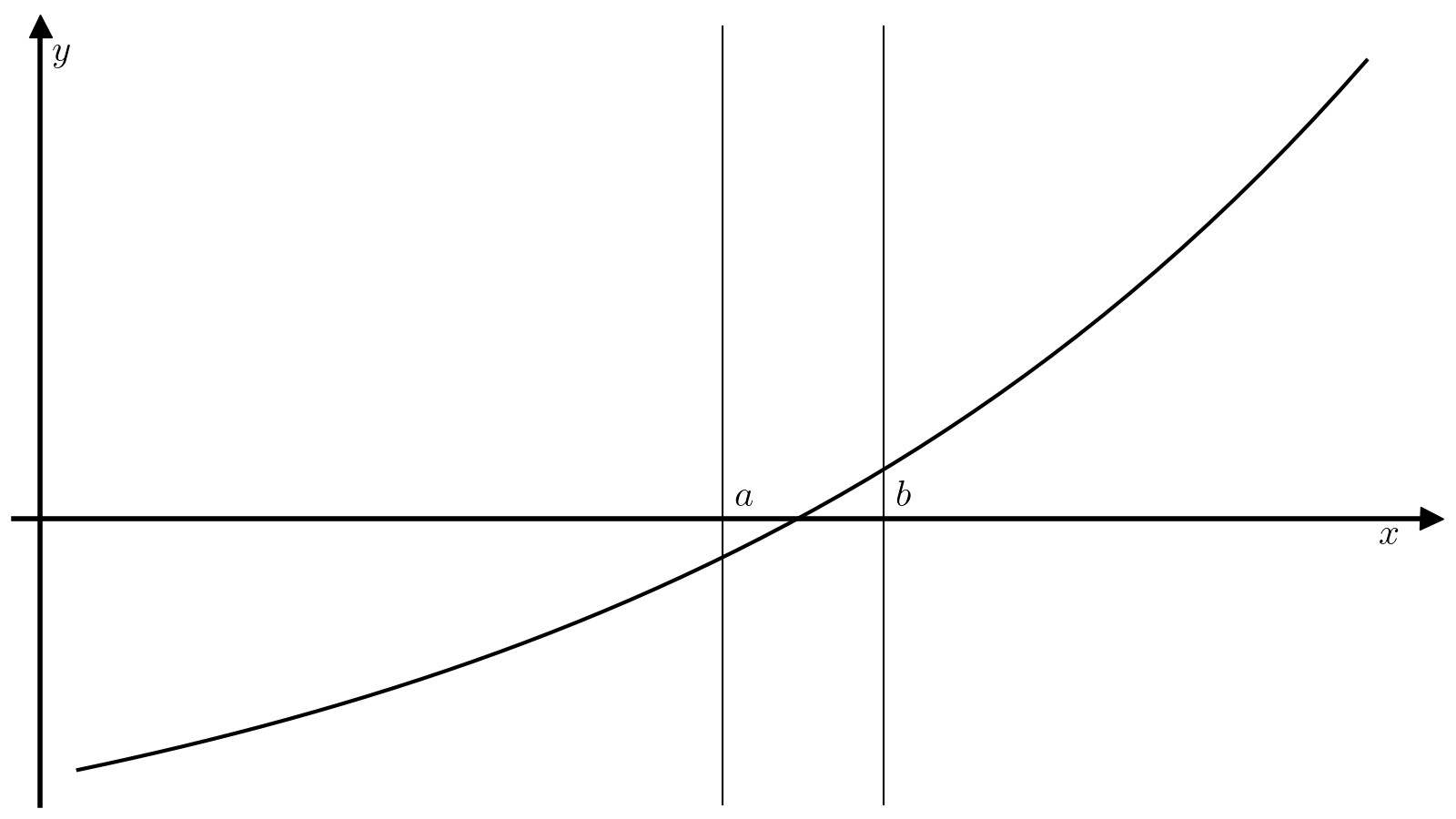
../../_images/bisection.gif

Пусть заданы требуемые точность delta и невязка epsilon. Тогда алгоритма поиска минимума корня функции f на отрезке [a, b] методом бисекции состоит из следующих шагов.

  1. Проверить выполнение условия (3). Если условие не выполняется, то решения на заданном интервале нет, либо оно не единственно. Работа алгоритма немедленно завершается. Если условие выполняется, то перейти к следующему шагу.

  2. Найти середину отрезка c по формуле (4).

  3. Проверить выполнение критериев остановки. Если |f(c)| < epsilon и |b-a|< delta, то принять, что c — искомый корень и работа алгоритма прекращается немедленно. Иначе перейти к следующему шагу.

  4. Проверить, на каком из двух отрезков [a, c] или [c, b] функция меняет знак. Если f(a) f(c) < 0, то b = c. Иначе, a = c. Вернуться к шагу №2.

Метод хорд#

Идея метода хорд очень похожа на идею метода бисекции. Корень тоже ищется на отрезке ([a, b]), на концах которого непрерывная функция (f) должна иметь разные знаки.

(5)#[f(a)f(b)<0. ]

На каждой итерации отрезок тоже делится на две части, но не пополам, а по следующей схеме. Через точки ((a, f(a))) и ((b, f(b))) проводится прямая

[
y = f(a) dfrac{x – b}{a – b} + f(b) dfrac{a – x}{a – b},
]

которую называют хордой или секущей. Эта прямая пересекает ось абсцисс в точке

(6)#[c = a – dfrac{f(b)(b-a)}{f(b) – f(a)} in (a, b),]

которая определяет деление отрезка ([a, b]) на два отрезка меньшей длинны: ([a, c]) и ([c, b]). Если точка (c) сама по себе не является корнем, то поиск продолжается на одном из двух этих отрезков. Обычно такие шаги применяют многократно до тех пор, пока не будет достигнута необходимая точность (длина отрезка ([a, b])) и невязка в средней точке (модуль значения функции (|f(c)|)), т.е. критерием сходимости метода является одновременное выполнение двух условий

[begin{split}
begin{cases}
|b – a| < delta, \
|f(c)| < varepsilon.
end{cases}
end{split}]

../../_images/secant.gif

Пусть заданы требуемые точность delta и невязка epsilon. Тогда алгоритма поиска минимума корня функции f на отрезке [a, b] методом хорд состоит из следующих шагов.

  1. Проверить выполнение условия (5). Если условие не выполняется, то решения на заданном интервале нет, либо оно не единственно. Работа алгоритма немедленно завершается. Если условие выполняется, то перейти к следующему шагу.

  2. Найти точку c по формуле (6).

  3. Проверить выполнение критериев остановки. Если |f(c)| < epsilon и |b-a|< delta, то принимается, что c — искомый корень и работа алгоритма прекращается немедленно. Иначе, перейти к следующему шагу.

  4. Выяснить, на каком из двух отрезков [a, c] или [c, b] функция меняет знак. Если f(a) f(c) < 0, то b = c. Иначе, a = c. Вернуться к шагу №2.

Метод Ньютона#

Метод касательных (он же метод Ньютона) накладывает дополнительные требования на функцию (f): кроме непрерывности самой функции (f) требуется и непрерывность производной (f’). Другое отличие заключается в виде начального приближения: предыдущие два методы требовали отрезок, а метод Ньютона всего одну точку.

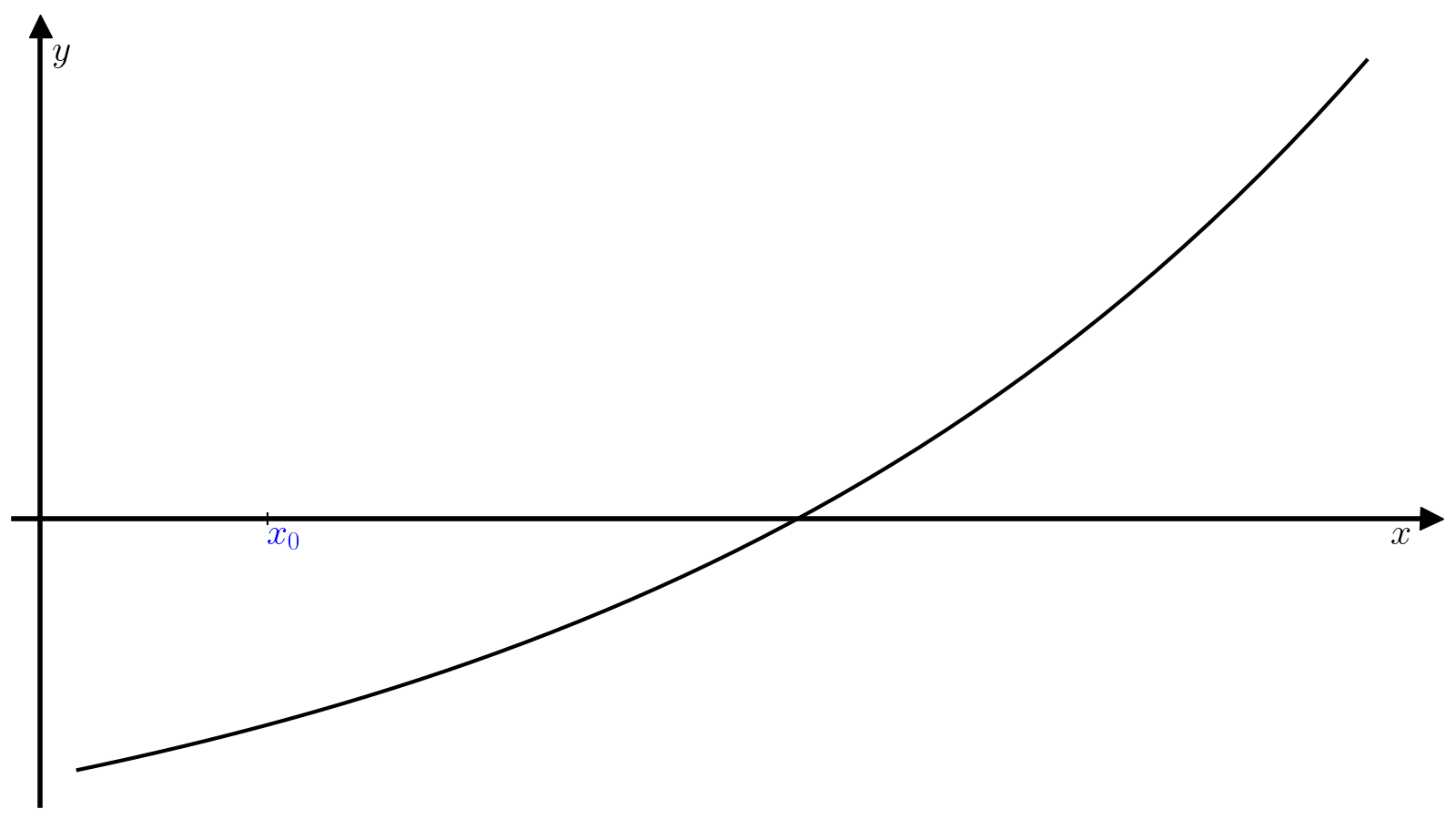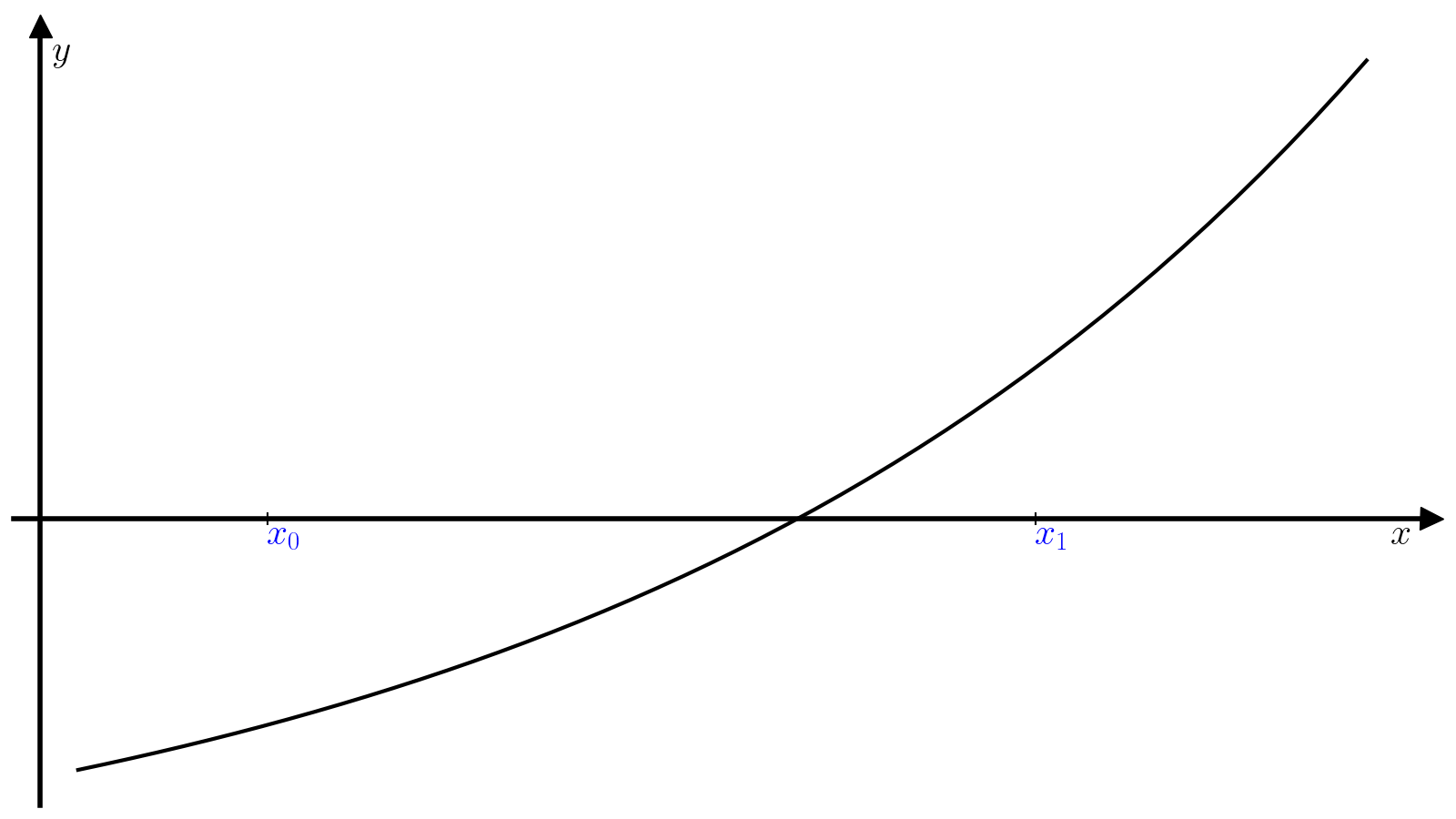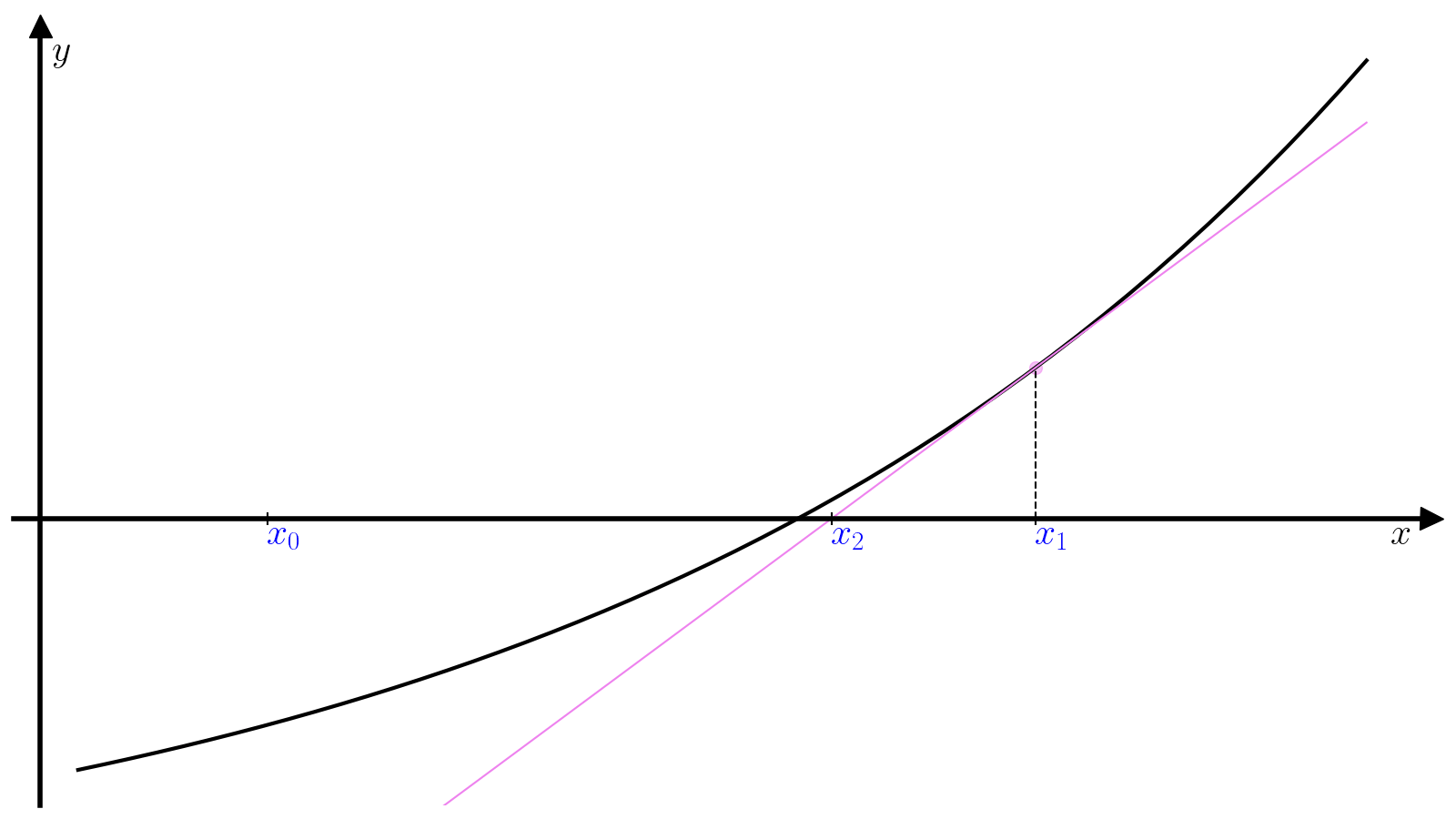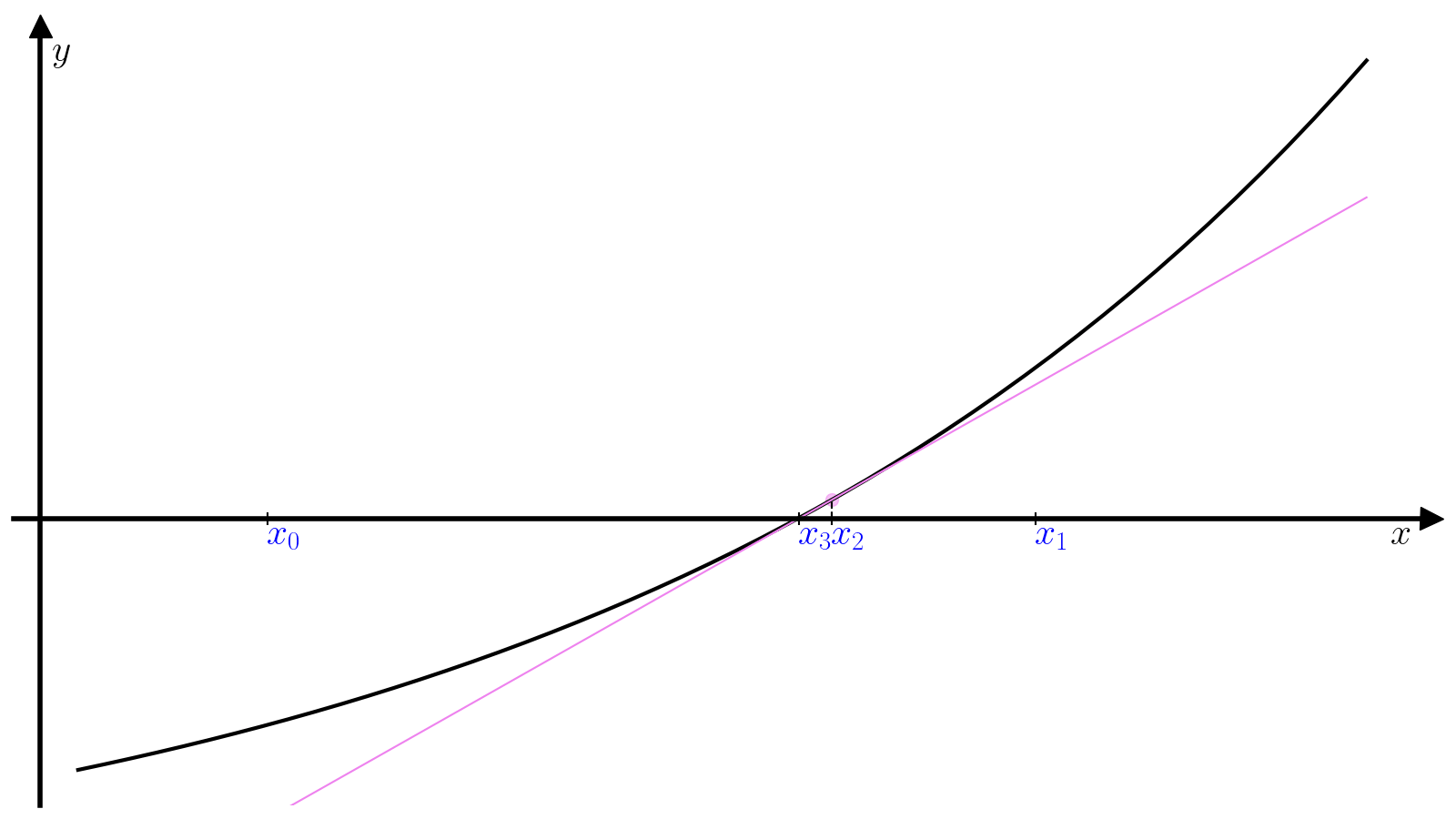
Пусть задано начальное приближение (x_0). Идея метода Ньютона заключается в том, чтобы аппроксимировать кривую (f(x)) касательной в окрестности точки (x_0) и найти следующее приближение (x_1) к корню функции (f(x)) как пересечение этой касательной с осью абсцисс. Касательная (hat{f}) к функции (f) в точке (x_0) определяется уравнением

[hat{f}(x) = f'(x_0)(x – x_0) + f(x_0),]

а координата (x_1) её точки пересечения с осью абсцисс выражением

[x_1 = x_0 – dfrac{f(x_0)}{f'(x_0)}.]

Далее (x_1) используется в качестве начального приближения на следующей итерации, чтобы найти (x_2) и так далее.

(7)#[x_{i+1} = x_{i} – dfrac{f(x_i)}{f'(x_i)}.]

Условием сходимости является достаточная близость нулевого приближения (x_0) к корню. Гарантировать требуемую точность на каждой конкретной итерации не представляется возможным, поэтому погрешность обычно оценивают как величину (|x_{i+1} – x_i|), т.е. критерием сходимости является выполнение условий

[begin{split}
begin{cases}
|x_{i + 1} – x_i| < delta, \
|f(x_{i+1})| < varepsilon.
end{cases}
end{split}]

Так как метод Ньютона может разойтись, если приближение далеко от корня, то кроме контроля невязки и точности требуется ограничивать максимальное количество итераций, чтобы исключить возможность попадания в бесконечный цикл.

../../_images/newton.gif

Пусть заданы требуемые точность delta, невязка epsilon, максимальное количество итераций max_iter и начальное приближение x0. Тогда алгоритма поиска корня функции f методом Ньютона состоит из следующих шагов.

  1. Инициализировать счетчик iter нулевым значением, а переменную x_previous значением x0.

  2. Вычислить следующее приближение x_next на основе предыдущего x_previous по формуле (7).

  3. Если |x_next - x_previous| < delta и f(x_next) < epsilon, то принять, что x1 — искомый корень и работа алгоритма прекращается немедленно. Иначе, перейти к шагу №4.

  4. Если iter == max_iter, то принять, что алгоритм Ньютона разошелся и работа алгоритма прекращается немедленно. Иначе, перейти к шагу №5.

  5. Присвоить переменной x_previous значение переменной x_next, увеличить счетчик iter на 1 и вернуться к шагу №2.

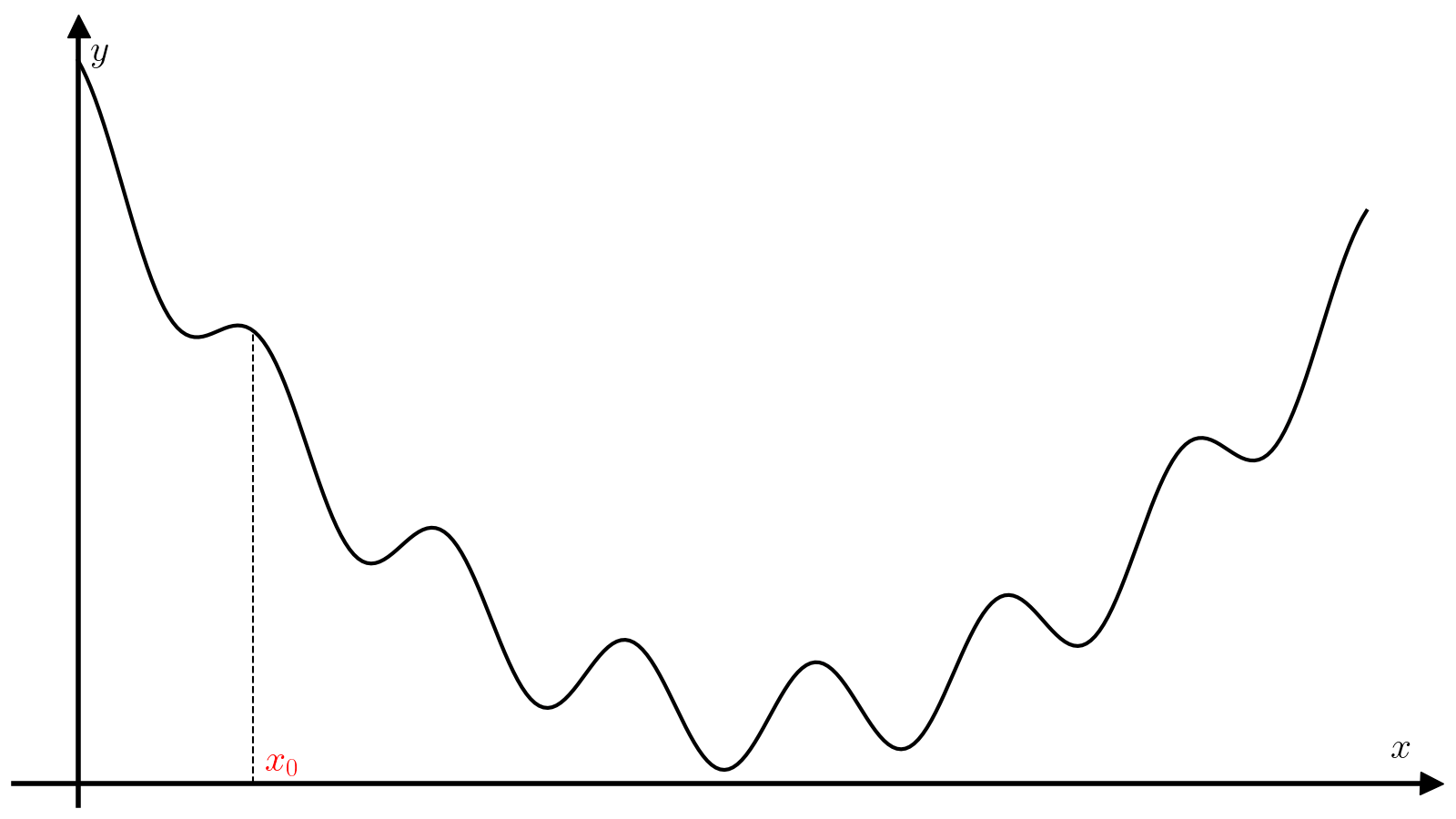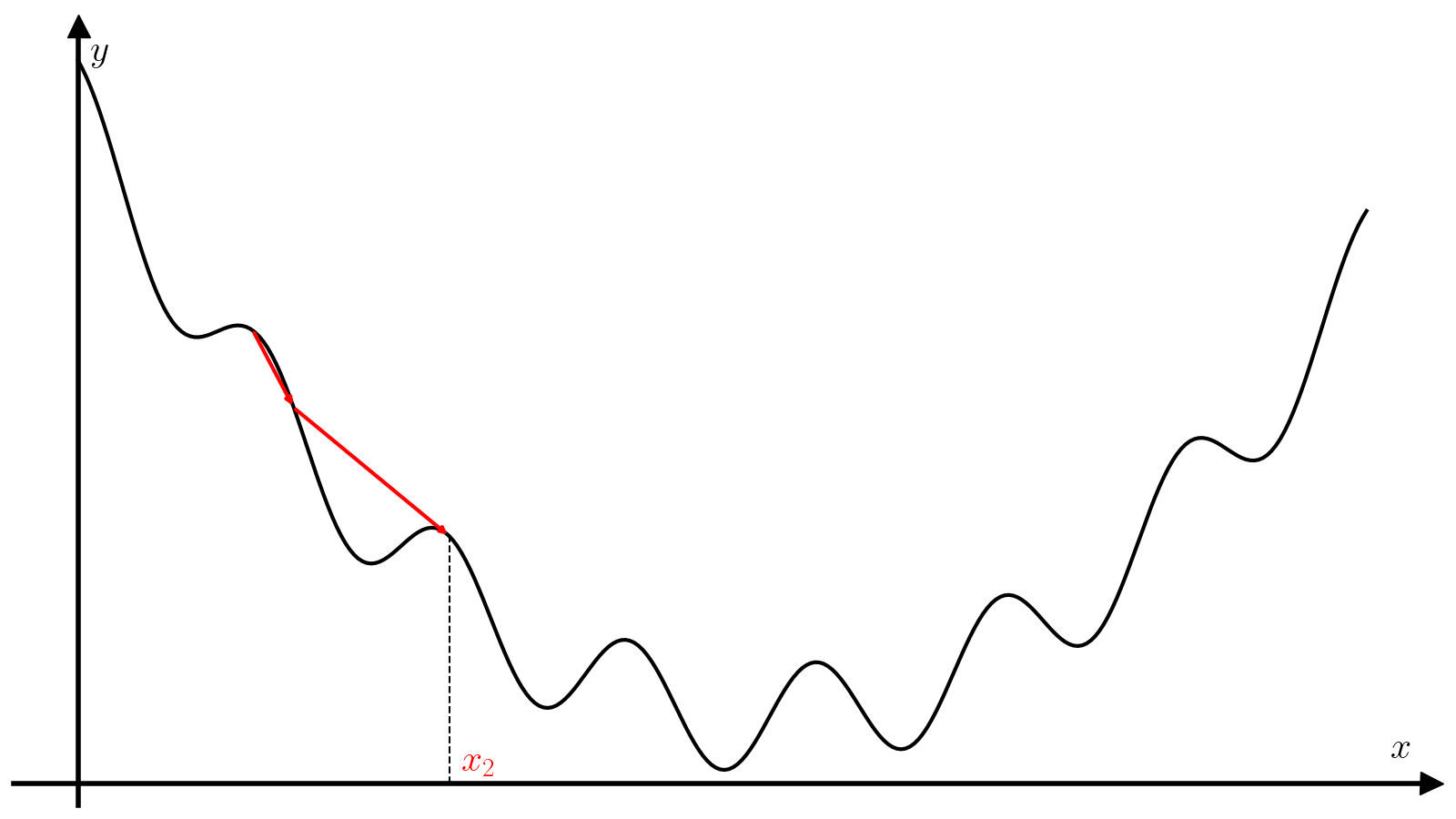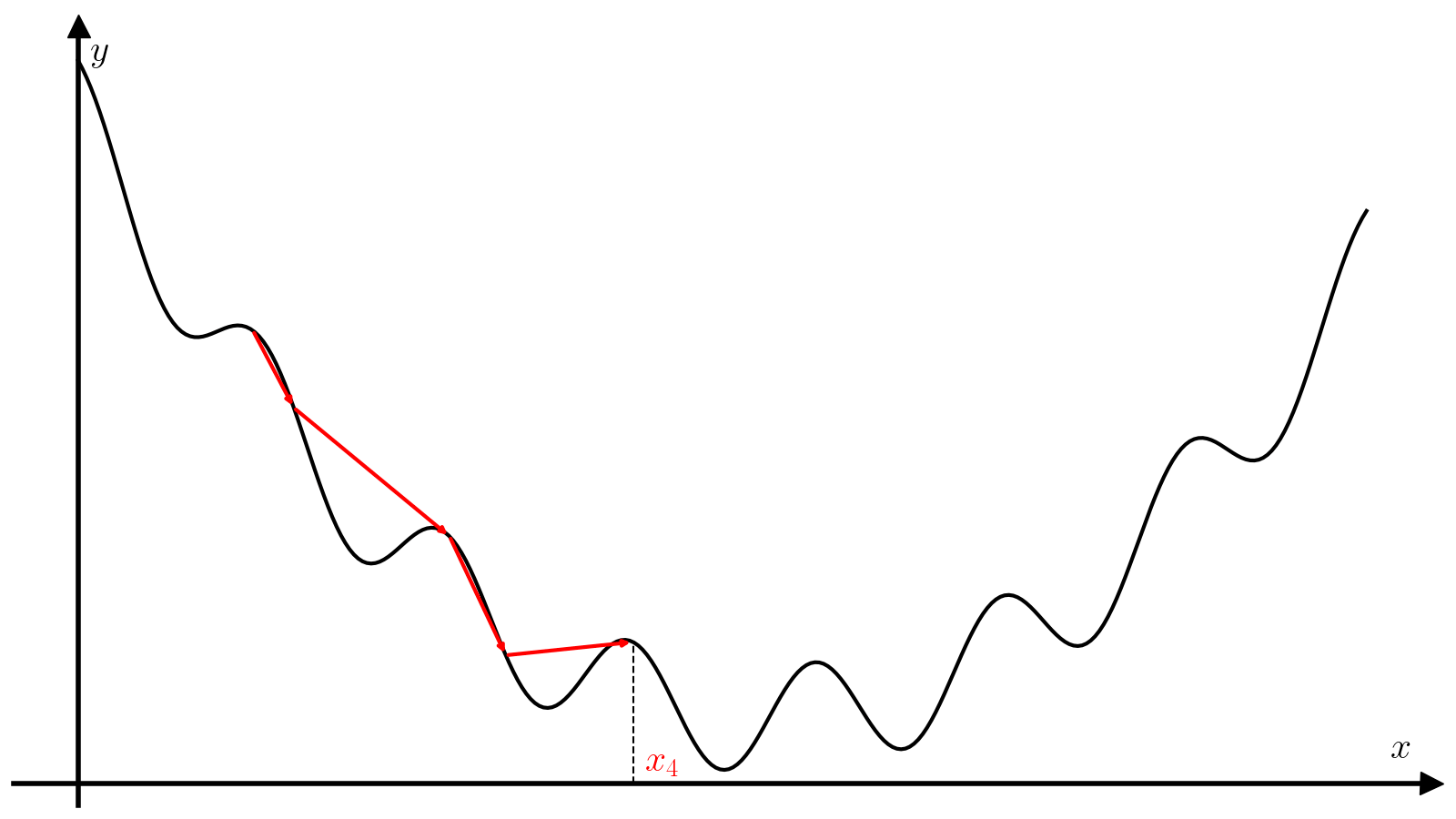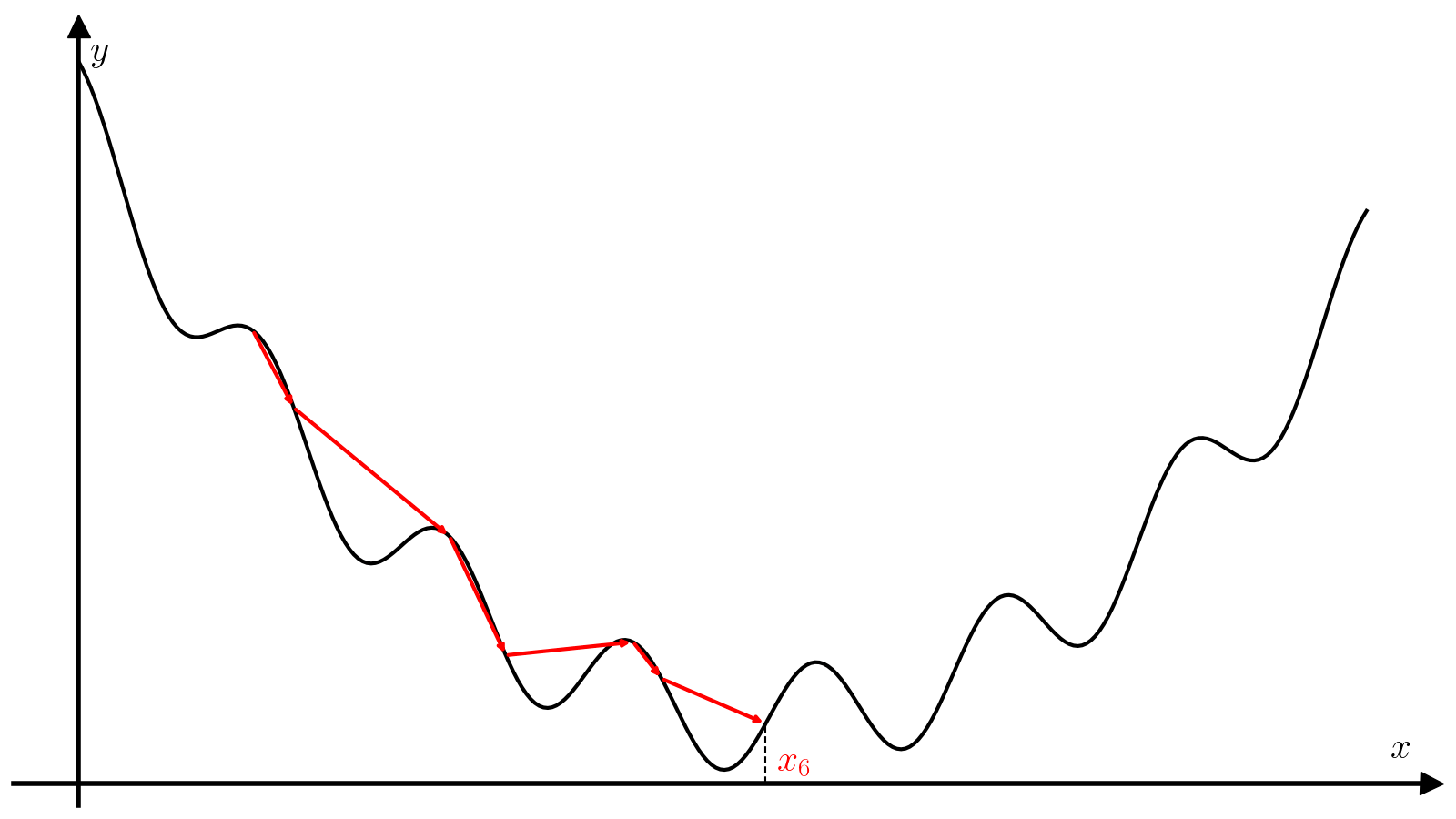
Метод дихотомии (метод золотого сечения)#

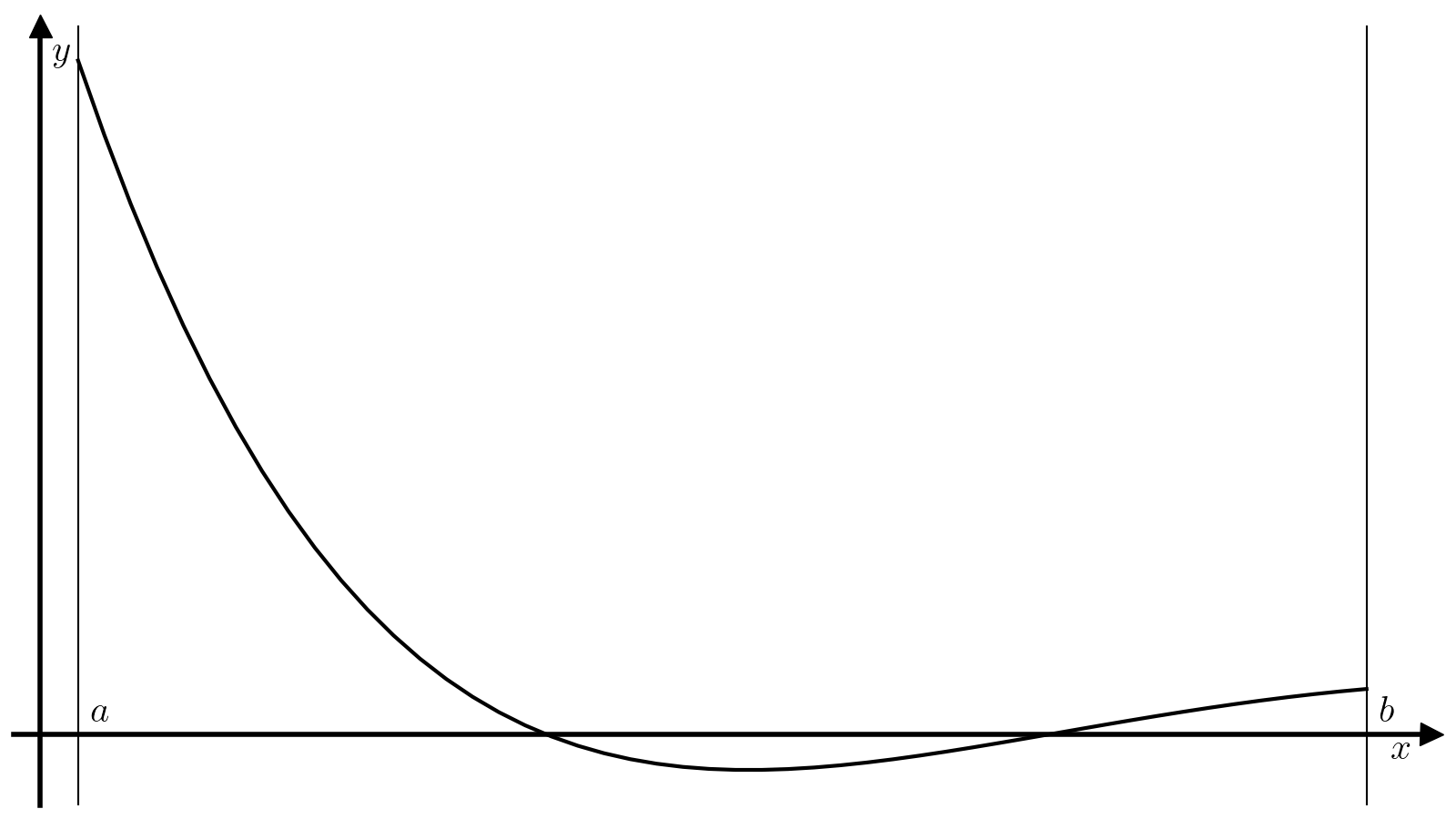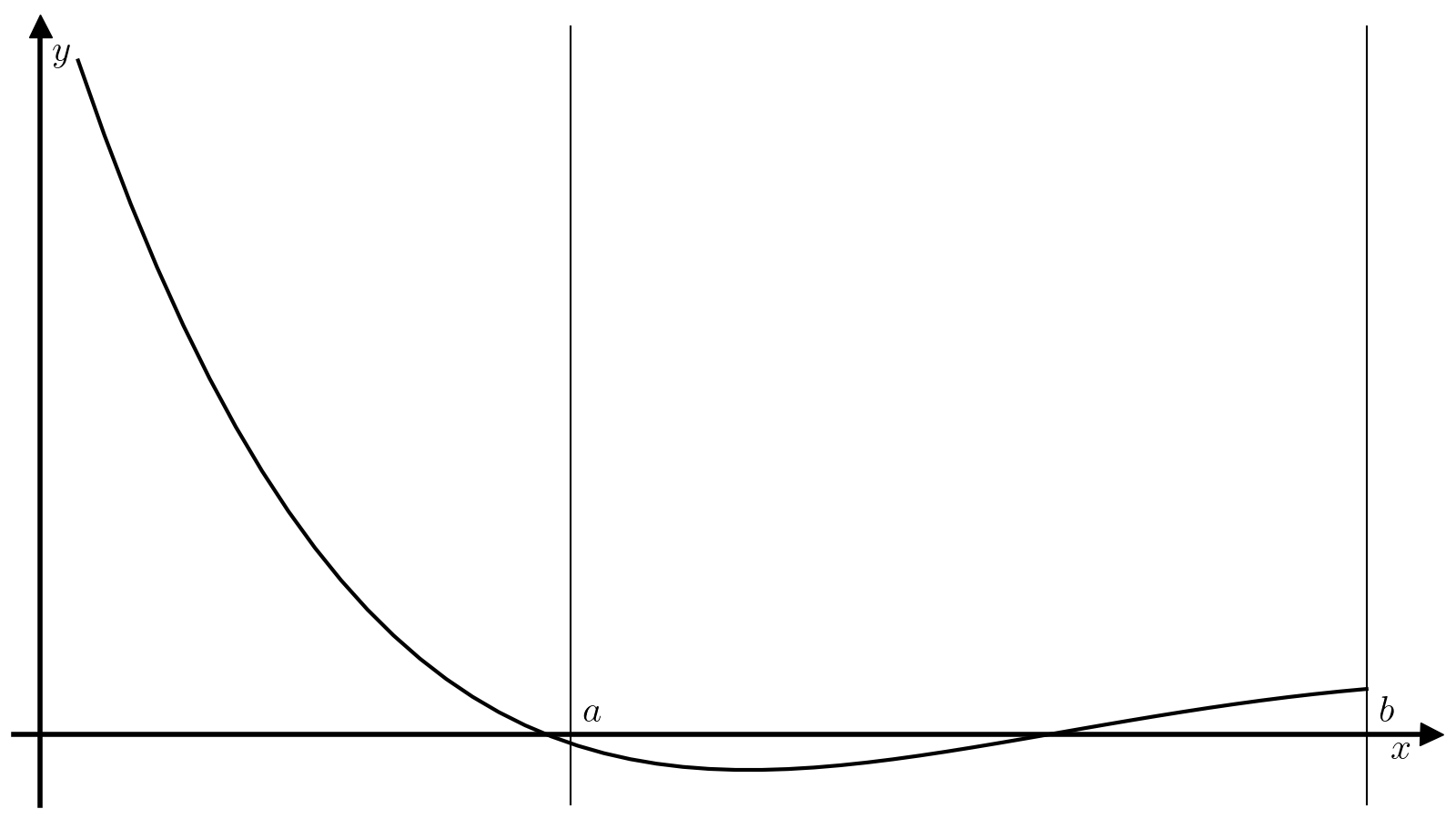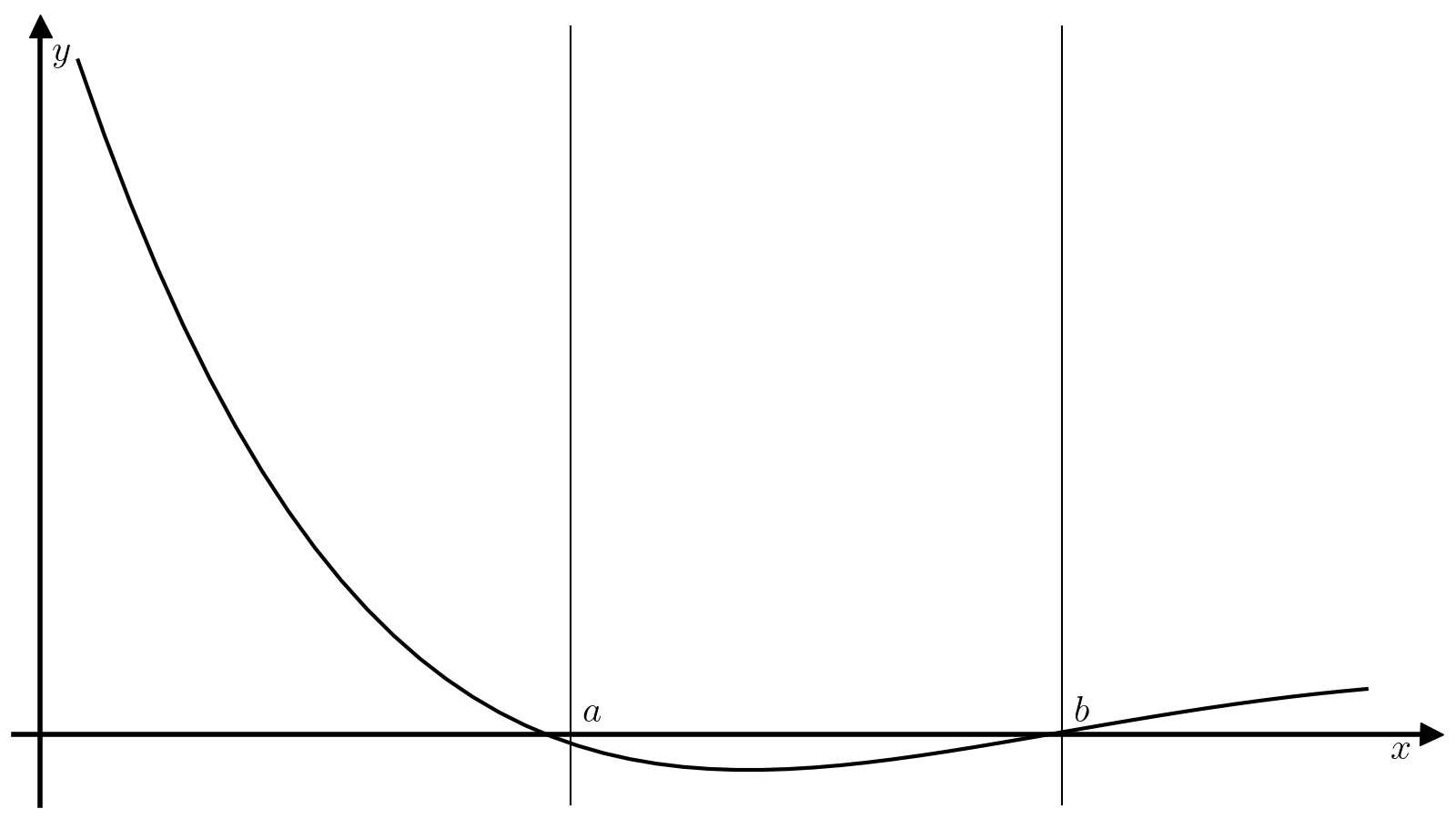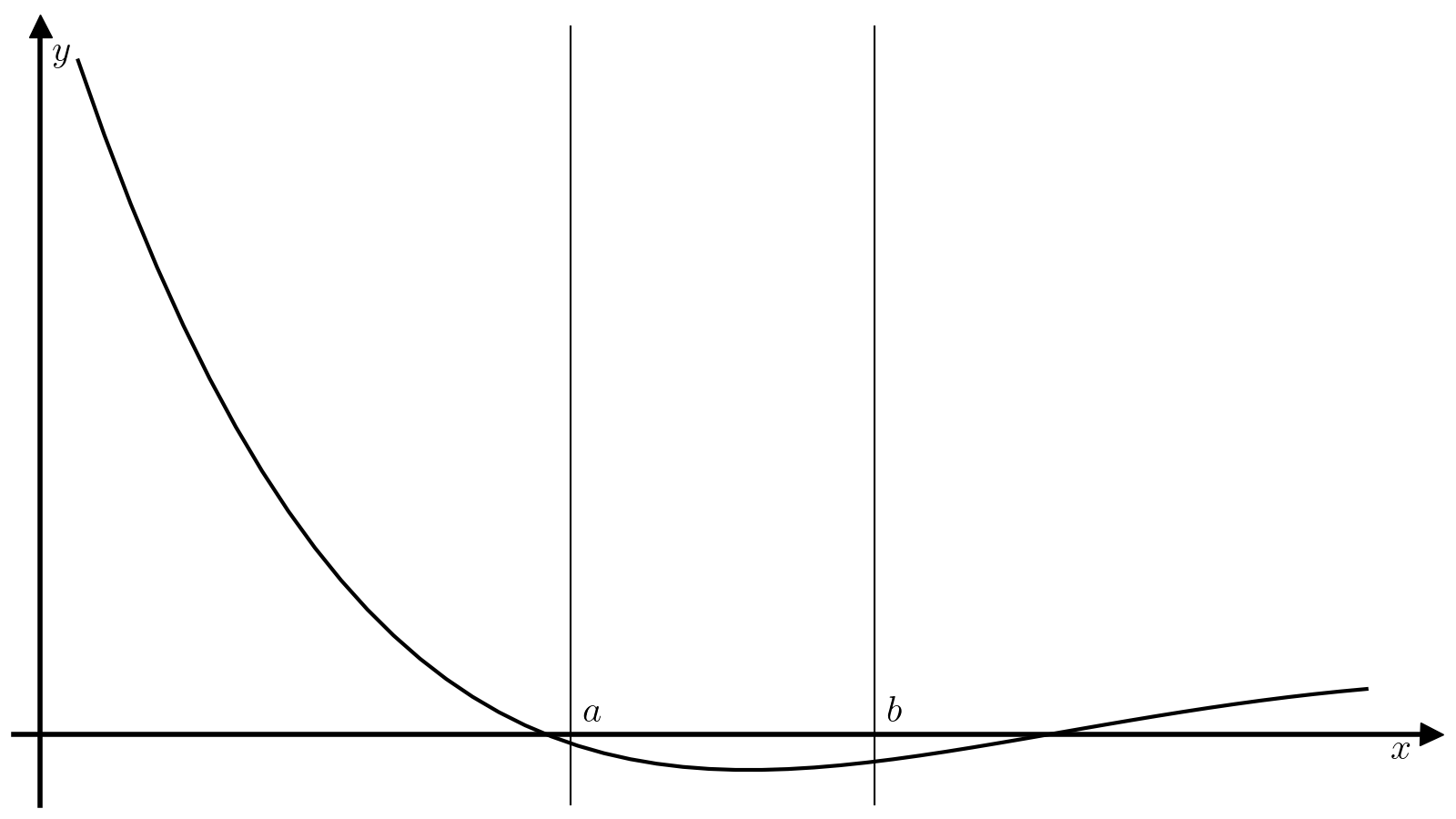
Метод дихотомии предназначен для поиска минимумов унимодальной функции. Непрерывная функция (fcolon mathbb{R} to mathbb{R}) называется унимодальной на отрезке ([a, b]), если (exists! c in [a, b]), такая, что:

  1. (c) — глобальный минимум функции (f), т.е. (f(c) = f_* = minlimits_{xin[a, b]} f(x));

  2. функция (f) монотонно убывает на отрезке ([a, c]);

  3. функция (f) монотонно растёт на отрезке ([c, b]);

Унимодальная функция имеет ровно один локальный минимум, который одновременно является и единственным глобальным. Идея метода дихотомии основывается на том, что если (f) унимодальна на отрезке ([a, b]), то разбив отрезок ([a, b]) двумя точками (x_1) и (x_2), (x_1 < x_2), можно легко уточнить положение минимума функции (f):

  • Если (f(x_1) > f(x_2)), то минимум достигается на отрезке ([x_1, b]). Действительно, на отрезке ([c, b]) функция (f) монотонно растет по определению, а значит (x_1) не может находиться внутри отрезка ([c, b]), так как (f(x_2) < f(x_1)) при том, что (x_2 > x_1). Единственная альтернатива — (x_1in[a, c]), т.е. минимум достигается на отрезке ([x_1, b]).

  • Если (f(x_1) < f(x_2)), то минимум достигается на отрезке ([a, x_2]).

Note

Корректное определение унимодальной функции подразумевает несколько более общее определение, в котором точка минимума (c) как бы превращается в отрезок ([c_1, c_2]), каждая точка которого является глобальным минимумом. Описанный здесь метод дихотомии сходится и для таких функций.

После сужения отрезка ([a, b]) до ([x_1, b]) или ([a, x_2]) можно повторить процедуру деления отрезка на три части произвольное количество раз до достижения необходимой точности. За точность принимается длинна отрезка ([a, b]) (величина (b – a)), т.е. критерием сходимости алгоритма считается выполнение условия

[
|b – a| < delta.
]

Метод золотого сечения — частный, который предписывает выбирать (x_1) и (x_2) по формулам

(8)#[begin{split}begin{cases}
x_1 = dfrac{a + b}{2} – (b – a)(dfrac{1}{Phi} – dfrac{1}{2}), \
x_2 = dfrac{a + b}{2} + (b – a)(dfrac{1}{Phi} – dfrac{1}{2}),
end{cases}end{split}]

где (Phi = dfrac{1 + sqrt{5}}{2}) — золотое сечение. Выбор (x_1) и (x_2) позволяет на каждой следующей итерации вычислять значение функции только в одной новой точке, а значит минимизирует необходимое для достижения требуемой точности количество вычислений значений функции (f(x)).

../../_images/dichotomy.gif

Пусть задана требуемая точность delta. Тогда алгоритма поиска минимума функции f на отрезке [a, b] методом золотого сечения состоит из следующих шагов.

  1. Найти x1 и x2 по формулам (8).

  2. Если f(x1) > f(x2), то a = x1. Иначе, b = x_2.

  3. Если b - a < delta, то требуемая точность достигнута и принимается, что c = (a + b) / 2 — положение глобального минимума и работа алгоритма завершается. Иначе, вернуться к шагу №1.

Note

Выбор (x_1) и (x_2) по формулам (8) позволяет сэкономить вычисления на втором и следующих итерация. Например, если на предыдущей итерации алгоритм попал в ветку, где (f(x_1) > f(x_2)), то на следующей итерации (a = x_1) и можно показать, что (x_1) на следующей итерации совпадает с (x_2) на предыдущей и можно переиспользовать вычисленные на предыдущей итерации значения (x_2) и (f(x_2)) как значения (x_1) и (f(x_1)) на следующей.

Метод градиентного спуска#

Метод градиентного спуска — один из самых распространенных методов минимизации функции. Для его работы требуется не только непрерывность самой функции (f), но ещё и непрерывность её первой производной (f’).

Известно, что в случае функции нескольких переменных (fcolon mathbb{R}^n to mathbb{R}), градиент (nabla f(x)) определяет направление наискорейшего роста в окрестности точки (x). И наоборот, в противоположном направлении функция (f) убывает быстрее всего. Метод градиентного спуска опирается на это свойство градиента: на каждой итерации алгоритма совершается шаг в направлении антиградиента ((-nabla f(x))), т.е. направлении наискорейшего спуска.

Градиент (nabla f) функции (fcolon mathbb{R} to mathbb{R}) совпадает с её производной и один шаг градиентного спуска в таком случае задается формулой

[
x_{i + 1} = x_i – alpha_i f'(x_i),
]

где (x_i) — текущее приближение, (x_{i+1}) — следующее приближение, а (alpha_i) — шаг градиентного спуска на (i)-й итерации.

Если (f) строго выпукла, то при наложении определенных требований на последовательность ({alpha_0, alpha_1, …, alpha_i, …}) можно доказать, что метод градиентного спуска сойдется к глобальному минимуму. Но даже при не выполнении этих условий метод градиентного спуска может сойтись, но тогда гарантировать сходимость не представляется возможным. В качестве контроля сходимости иногда используется величина градиента, так как в экстремальной точке дифференцируемой функции производная равна нулю. Иными словами, критерием остановки алгоритма градиентного спуска иногда выступает условие

[
|f'(x_i + 1)| < varepsilon.
]

Так как гарантировать достижение даже локального минимума в общем случае невозможно, то также требуется ограничивать максимальное количество итераций, чтобы исключить возможность попадания в бесконечный цикл.

Вам предлагается реализовать метод градиентного спуска с постоянным шагом (alpha).

(9)#[x_{i + 1} = x_i – alpha f'(x_i).]

Правильный подбор этого параметра критические влияет на сходимость алгоритма. Слишком маленький шаг потребует много итераций для сходимости и почти наверняка застрянет в первом встреченном локальном минимуме. Слишком большой шаг может разойтись, а может сравнительно быстро сойтись при удачном стечении обстоятельств и почти наверняка проскочит минимум, что хорошо, если минимум локальный, и плохо, если минимум глобальный.

../../_images/gradient.gif

Пусть задана величина epsilon, максимальное число итераций max_iter, шаг градиентного спуска alpha и начальное приближение x0. Тогда алгоритм поиска минимума функции f с производной f_prime на отрезке [a, b] методом золотого сечения состоит из следующих шагов.

  1. Инициализировать переменную iter нулем, а переменную x_previous величиной x_next;

  2. Найти следующее приближение x_next по формуле (9): x_next = x_previous - alpha * f_prime(x_previous);

  3. Если |f_prime(x_next)| < epsilon, то принять, что x_next — найденный минимум, алгоритма завершает свою работу. Иначе, перейти к шагу №4.

  4. Увеличить значение переменной iter на 1 и, если iter == max_iter, принять, что метод разошелся и алгоритм завершает работу. Иначе, вернуться к шагу №2.

Источник

Добавить комментарий