Как найти минимум функции методом ньютона - Сайт, где вы сможете решить свои вопросы

Для метода Ньютона
нужно задать начальное приближение из условия

,иначе процесс
сходимости не гарантирован.

Если ,
тои.

Следовательно, в
качестве начального приближения следует
выбрать точку .

1) Находим первое
приближение по формуле

;

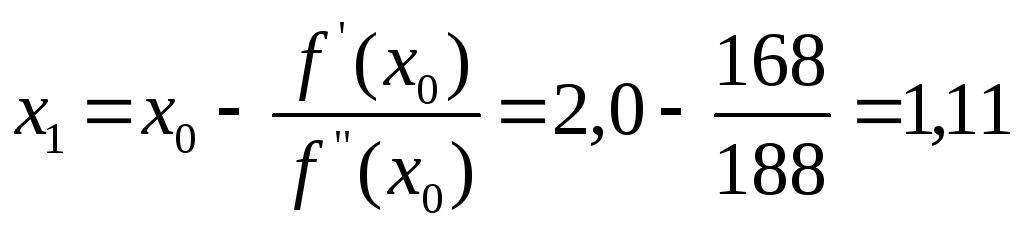
Так как
,
то требуется второе приближение.

2) Находим второе
приближение по формуле

Так как
,
то требуется третье приближение.

3) Находим третье
приближение по формуле

Так как
,
то процесс последовательных приближений
можно считать законченным и значение
принять за точку минимума.

Итак, ;число приближений.

Ниже приведены
расчеты нахождения минимума функции
методом Ньютона, выполненные с помощью
компьютерной программы.

Заметим, что в
случае выбора за начальное приближение
точки ,процесс все же
сойдется, но за большее число приближений.

Результаты всех
расчетов сведем в таблицу

№	Название метода поиска	Число приближений	Точка минимума
1	Метод дихотомии	12	(0,69; -22,04)
2	Метод «золотого сечения»	8	(0,68; -22,04)
3	Метод Ньютона	3	(0,69; -22,04)

Выводы: При поиске минимума функции на отрезке

самым быстрым
оказался метод Ньютона (4 приближения).

6 Лабораторная работа №6. Численное решение обыкновенных дифференциальных уравнений методами Эйлера, модифицированного метода Эйлера с пересчетом, Рунге-Кутты.

Задание.

Методами Эйлера,
модифицированным методом Эйлера с
пересчетом и методом Рунге-Кутты 4-го
порядка найти частное решение обыкновенного
дифференциального уравнения 1-го порядка
вида
,
с начальным условием ,на интервалес шагом.

Решение.

6.1
Найдем сначала точное решение
дифференциального уравнения .

Это уравнение
сводится к уравнению с разделяющимися
переменными с помощью подстановки .Тогдаи
уравнение примет вид Разделяя переменные,
получим

Частное решение
при начальном условии :

Итак, точное решение
имеет вид: .

Протабулируем
полученное решение на
интервалес шагоми результаты
расчетов сведем в таблицу 6.1

Таблица 6.1 Результаты
табулирования функции

6.2
Решение дифференциального уравнения
методом Эйлера.

Итерационная
формула метода Эйлера для дифференциального
уравнения имеет вид: .

У нас
;
;
;

.

Результаты расчетов
сведены в таблицу 6.2

Номер точки n
0	0,0	1,00	0,0+1,00=1,00
1	0,1	1,10	0,1+1,10=1,20
2	0,2	1,22	0,2+1,22=1,42
3	0,3	1,36	0,3+1,36=1,66
4	0,4	1,53	0,4+1,53=1,93
5	0,5	1,72

6.3
Решение дифференциального уравнения
модифицированным
методом Эйлера с пересчетом.

Итерационная
формула модифицированного метода Эйлера
с пересчетом для дифференциального
уравнения имеет вид:

,где

Результаты расчетов
сведены в таблицу 6.3

№ точки n
0	0,0	1,00	0,0+1,00=1,00
1	0,1	1,11	0,1+1,11=1,21
2	0,2	1,24	0,2+1,24=1,44
3	0,3	1,40	0,3+1,40=1,70
4	0,4	1,58	0,4+1,58=1,98
5	0,5	1,79

6.4
Решение дифференциального уравнения
методом Рунге-Кутты
4-го порядка.

где

Результаты расчетов
сведены в таблицу 6.4

Номер точки n
0	0,0	1,00	0+1=1
1	0,1	1,11	0,1+1,11=1,21
2	0,2	1,24	0,2+1,24=1,44
3	0,3	1,40	0,3+1,4=1,7
4	0,4	1,58	0,4+1,58=1,98
5	0,5	1,79

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

У этого термина существуют и другие значения, см. Метод (значения).

Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить ноль первой производной либо градиента в случае многомерного пространства.

Описание метода[править | править код]

Обоснование[править | править код]

Чтобы численно решить уравнение f(x)=0 методом простой итерации, его необходимо привести к эквивалентному уравнению: , где varphi — сжимающее отображение.

Для наилучшей сходимости метода в точке очередного приближения $x^{*}$ должно выполняться условие ${displaystyle varphi '(x^{*})=0}$ . Решение данного уравнения ищут в виде , тогда:

${displaystyle varphi '(x^{*})=1+alpha '(x^{*})f(x^{*})+alpha (x^{*})f'(x^{*})=0.}$

В предположении, что точка приближения «достаточно близка» к корню и что заданная функция непрерывна ${displaystyle (f(x^{*})approx f({tilde {x}})=0)}$ , окончательная формула для такова:

${displaystyle alpha (x)=-{frac {1}{f'(x)}}.}$

С учётом этого функция определяется:

${displaystyle varphi (x)=x-{frac {f(x)}{f'(x)}}.}$

При некоторых условиях эта функция в окрестности корня осуществляет сжимающее отображение.

В этом случае алгоритм нахождения численного решения уравнения f(x)=0 сводится к итерационной процедуре вычисления:

${displaystyle x_{n+1}=x_{n}-{frac {f(x_{n})}{f'(x_{n})}}.}$

По теореме Банаха последовательность приближений стремится к корню уравнения f(x)=0 .

Иллюстрация метода Ньютона (синим изображена функция , ноль которой необходимо найти, красным — касательная в точке очередного приближения $scriptstyle {x_{n}}$ ). Здесь мы можем увидеть, что последующее приближение $scriptstyle {x_{{n+1}}}$ лучше предыдущего $scriptstyle {x_{n}}$ .

Геометрическая интерпретация[править | править код]

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к графику исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.

Пусть 1) вещественнозначная функция непрерывно дифференцируема на интервале ;
2) существует искомая точка ${displaystyle x^{*}in (a,,b)}$ : ${displaystyle f(x^{*})=0}$ ;
3) существуют C > 0 и такие, что

для ${displaystyle xin (a,,x^{*}-delta ]cup [x^{*}+delta ,,b)}$
и
для ${displaystyle xin (x^{*}-delta ,,x^{*})cup (x^{*},,x^{*}+delta )}$ ;
4) точка ${displaystyle x_{n}in (a,,b)}$ такова, что ${displaystyle f(x_{n})neq 0}$ .
Тогда формула итеративного приближения $x_{n}$ к $x^{{*}}$
может быть выведена из геометрического смысла касательной следующим образом:

${displaystyle f'(x_{n})=mathrm {tg} ,alpha _{n}={frac {Delta y}{Delta x}}={frac {f(x_{n})-0}{x_{n}-x_{n+1}}}={frac {0-f(x_{n})}{x_{n+1}-x_{n}}},}$

где ${displaystyle alpha _{n}}$ — угол наклона касательной прямой
${displaystyle y(x)=f(x_{n})+(x-x_{n})cdot mathrm {tg} ,alpha _{n}}$
к графику
в точке ${displaystyle (x_{n};f(x_{n}))}$ .

Следовательно (в уравнении касательной прямой полагаем ${displaystyle y(x_{n+1})=0}$ ) искомое выражение для $x_{{n+1}}$ имеет вид :

${displaystyle x_{n+1}=x_{n}-{frac {f(x_{n})}{f'(x_{n})}}.}$

Если ${displaystyle x_{n+1}in (a,,b)}$ , то это значение можно использовать в качестве следующего приближения к
$x^{{*}}$ .

Если ${displaystyle x_{n+1}notin (a,,b)}$ , то имеет место «перелёт» (корень $x^{{*}}$ лежит рядом с границей ). В этом случае надо (воспользовавшись идеей метода половинного деления) заменять
$x_{{n+1}}$ на
${displaystyle {frac {x_{n}+x_{n+1}}{2}}}$
до тех пор, пока точка «не вернётся» в область поиска
.

Замечания. 1) Наличие непрерывной производной даёт возможность строить непрерывно меняющуюся касательную на всей области поиска решения .
2) Случаи граничного (в точке или в точке ) расположения искомого решения $x^{{*}}$ рассматриваются аналогичным образом.
3) С геометрической точки зрения равенство
${displaystyle f'(x_{n})=0}$
означает, что касательная прямая к графику

в точке
${displaystyle (x_{n};f(x_{n}))}$ –
параллельна оси

и при
${displaystyle f(x_{n})neq 0}$
не пересекается с ней в конечной части.
4) Чем больше константа C > 0 и чем меньше константа из пункта 3 условий,
тем для ${displaystyle x_{n}in (a,,x^{*}-delta ]cup [x^{*}+delta ,,b)}$
пересечение касательной к графику и оси ближе к точке ${displaystyle (x^{*};;0)}$ ,
то есть тем ближе значение $x_{{n+1}}$ к искомой ${displaystyle x^{*}in (a,,b)}$ .

Итерационный процесс начинается с некоторого начального приближения
${displaystyle x_{0}in (a,,b)}$ ,
причём между
${displaystyle x_{0}in (a,,b)}$
и искомой точкой
${displaystyle x^{*}in (a,,b)}$
не должно быть других нулей функции
,
то есть «чем ближе $x_{0}$
к искомому корню $x^{{*}}$ ,
тем лучше». Если предположения о нахождении $x^{{*}}$ отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях.

Для предварительно заданных ${displaystyle varepsilon _{x}>0}$ , ${displaystyle varepsilon _{f}>0}$
итерационный процесс завершается если
${displaystyle leftvert {frac {f(x_{n})}{f'(x_{n})}}rightvert approx vert x_{n+1}-x_{n}vert <varepsilon _{x}}$ и
${displaystyle vert f(x_{n+1})vert <varepsilon _{f}}$ .
В частности, для матрицы дисплея ${displaystyle varepsilon _{x}}$ и ${displaystyle varepsilon _{f}}$ могут быть рассчитаны,
исходя из масштаба отображения графика ,
то есть если $x_{n}$ и $x_{{n+1}}$ попадают в один вертикальный, а ${displaystyle f(x_{n})}$ и ${displaystyle f(x_{n+1})}$ в один горизонтальный ряд.

Алгоритм[править | править код]

Задается начальное приближение $x_{0}$ .
Пока не выполнено условие остановки, в качестве которого можно взять ${displaystyle |x_{n+1}-x_{n}|<varepsilon }$ или ${displaystyle |f(x_{n+1})|<varepsilon }$ (то есть погрешность в нужных пределах), вычисляют новое приближение: ${displaystyle x_{n+1}=x_{n}-{frac {f(x_{n})}{f'(x_{n})}}}$ .

Пример[править | править код]

Иллюстрация применения метода Ньютона к функции $f(x)=cos x-x^{3}$ с начальным приближением в точке $x_{0}=0{,}5$ .
График последовательных приближений.	График сходимости.
Согласно способу практического определения скорость сходимости может быть оценена как тангенс угла наклона графика сходимости, то есть в данном случае равна двум.

Рассмотрим задачу о нахождении положительных , для которых $cos x=x^{3}$ . Эта задача может быть представлена как задача нахождения нуля функции $f(x)=cos x-x^{3}$ . Имеем выражение для производной $f'(x)=-sin x-3x^{2}$ . Так как для всех и $x^{3}>1$ для x>1 , очевидно, что решение лежит между 0 и 1. Возьмём в качестве начального приближения значение $x_{0}=0{,}5$ , тогда:

${begin{matrix}x_{1}&=&x_{0}-{dfrac {f(x_{0})}{f'(x_{0})}}&=&1{,}112;141;637;097,\x_{2}&=&x_{1}-{dfrac {f(x_{1})}{f'(x_{1})}}&=&underline {0{,}}909;672;693;736,\x_{3}&=&x_{2}-{dfrac {f(x_{2})}{f'(x_{2})}}&=&underline {0{,}86}7;263;818;209,\x_{4}&=&x_{3}-{dfrac {f(x_{3})}{f'(x_{3})}}&=&underline {0{,}865;47}7;135;298,\x_{5}&=&x_{4}-{dfrac {f(x_{4})}{f'(x_{4})}}&=&underline {0{,}865;474;033;1}11,\x_{6}&=&x_{5}-{dfrac {f(x_{5})}{f'(x_{5})}}&=&underline {0{,}865;474;033;102}.end{matrix}}$

Подчёркиванием отмечены верные значащие цифры. Видно, что их количество от шага к шагу растёт (приблизительно удваиваясь с каждым шагом): от 1 к 2, от 2 к 5, от 5 к 10, иллюстрируя квадратичную скорость сходимости.

Условия применения[править | править код]

Иллюстрация расхождения метода Ньютона, применённого к функции $scriptstyle {f(x)=x^{3}-2x+2}$ с начальным приближением в точке $scriptstyle {x_{0}=0}$ .

Рассмотрим ряд примеров, указывающих на недостатки метода.

Контрпримеры[править | править код]

Если начальное приближение недостаточно близко к решению, то метод может не сойтись.

Пусть

${displaystyle f(x)=x^{3}-2x+2.}$

Тогда

$x_{{n+1}}=x_{{n}}-{frac {x_{n}^{3}-2x_{n}+2}{3x_{n}^{2}-2}}.$

Возьмём ноль в качестве начального приближения. Первая итерация даст в качестве приближения единицу. В свою очередь, вторая снова даст ноль. Метод зациклится и решение не будет найдено. В общем случае построение последовательности приближений может быть очень запутанным.

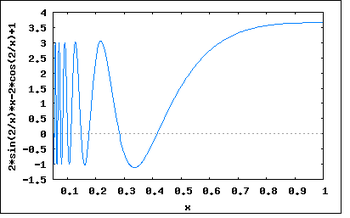
График производной функции $scriptstyle {f(x)=x+x^{2}sin(2/x)}$ при приближении к нулю справа.

Если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня.

Рассмотрим функцию:

${displaystyle f(x)={begin{cases}0,&x=0,\x+x^{2}sin left({dfrac {2}{x}}right),&xneq 0.end{cases}}}$

Тогда и всюду, кроме 0.

В окрестности корня производная меняет знак при приближении к нулю справа или слева. В то время, как ${displaystyle f(x)geqslant x-x^{2}>0}$ для .

Таким образом не ограничено вблизи корня, и метод будет расходиться, хотя функция всюду дифференцируема, её производная не равна нулю в корне, бесконечно дифференцируема везде, кроме как в корне, а её производная ограничена в окрестности корня.

Если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена.

Рассмотрим пример:

${displaystyle f(x)=x+x^{4/3}.}$

Тогда ${displaystyle f'(x)=1+(4/3)x^{1/3}}$ и ${displaystyle f''(x)=(4/9)x^{-2/3}}$ за исключением x=0 , где она не определена.

На очередном шаге имеем $x_{n}$ :

${displaystyle x_{n+1}=x_{n}-{frac {f(x_{n})}{f'(x_{n})}}={frac {(1/3)x_{n}^{4/3}}{(1+(4/3)x_{n}^{1/3})}}.}$

Скорость сходимости полученной последовательности составляет приблизительно 4/3. Это существенно меньше, нежели 2, необходимое для квадратичной сходимости, поэтому в данном случае можно говорить лишь о линейной сходимости, хотя функция всюду непрерывно дифференцируема, производная в корне не равна нулю, и бесконечно дифференцируема везде, кроме как в корне.

Если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.

Пусть

${displaystyle f(x)=x^{2}.}$

Тогда и следовательно . Таким образом сходимость метода не квадратичная, а линейная, хотя функция всюду бесконечно дифференцируема.

Ограничения[править | править код]

Пусть задано уравнение f(x)=0 , где и надо найти его решение.

Ниже приведена формулировка основной теоремы, которая позволяет дать чёткие условия применимости. Она носит имя советского математика и экономиста Леонида Витальевича Канторовича (1912—1986).

Теорема Канторовича.

Если существуют такие константы , что:

${displaystyle {frac {1}{|f'(x)|}}<A}$ на , то есть сут и не равна нулю;
${displaystyle left|{frac {f(x)}{f'(x)}}right|<B}$ на , то есть ограничена;
на , и ${displaystyle |f''(x)|leqslant Cleqslant {frac {1}{2AB}}}$ ;

Причём длина рассматриваемого отрезка ${displaystyle |a-b|<{frac {1}{AB}}left(1-{sqrt {1-2ABC}}right)}$ . Тогда справедливы следующие утверждения:

на существует корень $x^{*}$ уравнения ${displaystyle f(x)=0colon exists x^{*}in [a,;b]colon f(x^{*})=0}$ ;
если ${displaystyle x_{0}={frac {a+b}{2}}}$ , то итерационная последовательность сходится к этому корню: ${displaystyle left{x_{n+1}=x_{n}-{frac {f(x_{n})}{f'(x_{n})}}right}to x^{*}}$ ;
погрешность может быть оценена по формуле ${displaystyle |x^{*}-x_{n}|leqslant {frac {B}{2^{n-1}}}(2ABC)^{2^{n-1}}}$ .

Из последнего из утверждений теоремы в частности следует квадратичная сходимость метода:

${displaystyle |x^{*}-x_{n}|leqslant {frac {B}{2^{n-1}}}(2ABC)^{2^{n-1}}={frac {1}{2}}{frac {B}{2^{n-2}}}left((2ABC)^{2^{n-2}}right)^{2}=alpha |x^{*}-x_{n-1}|^{2}.}$

Тогда ограничения на исходную функцию f(x) будут выглядеть так:

функция должна быть ограничена;
функция должна быть гладкой, дважды дифференцируемой;
её первая производная равномерно отделена от нуля;
её вторая производная должна быть равномерно ограничена.

Историческая справка[править | править код]

Метод был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов» (лат. «De analysi per aequationes numero terminorum infinitas»), адресованной в 1669 году Барроу, и в работе «Метод флюксий и бесконечные ряды» (лат. «De metodis fluxionum et serierum infinitarum») или «Аналитическая геометрия» (лат. «Geometria analytica») в собраниях трудов Ньютона, которая была написана в 1671 году. В своих работах Ньютон вводит такие понятия, как разложение функции в ряд, бесконечно малые и флюксии (производные в нынешнем понимании). Указанные работы были изданы значительно позднее: первая вышла в свет в 1711 году благодаря Уильяму Джонсону, вторая была издана Джоном Кользоном в 1736 году уже после смерти создателя. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения $x_{n}$ , а последовательность полиномов и в результате получал приближённое решение .

Впервые метод был опубликован в трактате «Алгебра» Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе «Общий анализ уравнений» (лат. «Analysis aequationum universalis»). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений $x_{n}$ вместо более трудной для понимания последовательности полиномов, использованной Ньютоном. Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента.

В 1879 году Артур Кэли в работе «Проблема комплексных чисел Ньютона — Фурье» (англ. «The Newton-Fourier imaginary problem») был первым, кто отметил трудности в обобщении метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов.

Обобщения и модификации[править | править код]

Иллюстрация последовательных приближений метода одной касательной, применённого к функции $scriptstyle {f(x)=e^{x}-2}$ с начальным приближением в точке $scriptstyle {x_{0}=1{,}8}$ .

Метод секущих[править | править код]

Родственный метод секущих является «приближённым» методом Ньютона и позволяет не вычислять производную. Значение производной в итерационной формуле заменяется её оценкой по двум предыдущим точкам итераций:

${displaystyle f'(x_{n})approx {frac {f(x_{n})-f(x_{n-1})}{x_{n}-x_{n-1}}}}$ .

Таким образом, основная формула имеет вид

${displaystyle x_{n+1}=x_{n}-f(x_{n})cdot {frac {x_{n}-x_{n-1}}{f(x_{n})-f(x_{n-1})}}.}$

Этот метод схож с методом Ньютона, но имеет немного меньшую скорость сходимости. Порядок сходимости метода равен золотому сечению — 1,618…

Замечания. 1) Для начала итерационного процесса требуются два различных значения
$x_{0}$ и
$x_{1}$ .
2) В отличие от «настоящего метода Ньютона» (метода касательных), требующего хранить только ${displaystyle x_{n}}$
(и в ходе вычислений — временно ${displaystyle f(x_{n})}$ и ${displaystyle f'(x_{n})}$ ),
для метода секущих требуется сохранение
${displaystyle x_{n-1}}$ ,
${displaystyle x_{n}}$ ,
${displaystyle f(x_{n-1})}$ ,
${displaystyle f(x_{n})}$ .
3) Применяется, если вычисление f'(x) затруднено
(например, требует большого количества машинных ресурсов: времени и/или памяти).

Метод одной касательной[править | править код]

В целях уменьшения числа обращений к значениям производной функции применяют так называемый метод одной касательной.

Формула итераций этого метода имеет вид:

${displaystyle x_{n+1}=x_{n}-{frac {1}{f'(x_{0})}}f(x_{n}).}$

Суть метода заключается в том, чтобы вычислять производную лишь один раз, в точке начального приближения $x_{0}$ , а затем использовать это значение на каждой последующей итерации:

${displaystyle alpha (x)=alpha _{0}=-{dfrac {1}{f'(x_{0})}}.}$

При таком выборе $alpha _{0}$ в точке $x_{0}$ выполнено равенство:

${displaystyle varphi '(x_{0})=1+alpha _{0}f'(x_{0})=0,}$

и если отрезок, на котором предполагается наличие корня $x^{*}$ и выбрано начальное приближение $x_{0}$ , достаточно мал, а производная непрерывна, то значение ${displaystyle varphi '(x^{*})}$ будет не сильно отличаться от ${displaystyle varphi '(x_{0})=0}$ и, следовательно, график пройдёт почти горизонтально, пересекая прямую y=x , что в свою очередь обеспечит быструю сходимость последовательности точек приближений к корню.

Этот метод является частным случаем метода простой итерации. Он имеет линейный порядок сходимости.

Метод Ньютона-Фурье[править | править код]

Метод Ньютона-Фурье – это расширение метода Ньютона, выведенное Жозефом Фурье для получения оценок на абсолютную ошибку аппроксимации корня, в то же время обеспечивая квадратичную сходимость с обеих сторон.

Предположим, что f(x) дважды непрерывно дифференцируема на отрезке [a, b] и что f имеет корень на этом интервале. Дополнительно положим, что f′(x), f″(x) ≠ 0 на этом отрезке (например, это верно, если f(a) < 0, f(b) > 0, и f″(x) > 0 на этом отрезке). Это гарантирует наличие единственного корня на этом отрезке, обозначим его α. Эти рассуждения относятся к вогнутой вверх функции. Если она вогнута вниз, то заменим f(x) на −f(x), поскольку они имеют одни и те же корни.

Пусть x₀ = b будет правым концом отрезка, на котором мы ищем корень, а z₀ = a – левым концом того же отрезка. Если x_n найдено, определим

${displaystyle x_{n+1}=x_{n}-{frac {f(x_{n})}{f'(x_{n})}},}$

которое выражает обычный метод Ньютона, как описано выше. Затем определим

${displaystyle z_{n+1}=z_{n}-{frac {f(z_{n})}{f'(x_{n})}},}$

где знаменатель равен f′(x_n), а не f′(z_n). Итерации x_n будут строго убывающими к корню, а итерации z_n – строго возрастающими к корню. Также выполняется следующее соотношение:

${displaystyle lim _{nto infty }{frac {x_{n+1}-z_{n+1}}{(x_{n}-z_{n})^{2}}}={frac {f''(alpha )}{2f'(alpha )}}}$

таким образом, расстояние между x_n и z_n уменьшается квадратичным образом.

Многомерный случай[править | править код]

Обобщим полученный результат на многомерный случай.

Пусть необходимо найти решение системы:

${displaystyle left{{begin{array}{lcr}f_{1}(x_{1},;x_{2},;ldots ,;x_{n})&=&0,\ldots &&\f_{m}(x_{1},;x_{2},;ldots ,;x_{n})&=&0.end{array}}right.}$

Выбирая некоторое начальное значение ${displaystyle {vec {x}}^{[0]}}$ , последовательные приближения ${displaystyle {vec {x}}^{[j+1]}}$ находят путём решения систем уравнений:

${displaystyle f_{i}+sum _{k=1}^{n}{frac {partial f_{i}}{partial x_{k}}}(x_{k}^{[j+1]}-x_{k}^{[j]})=0,qquad i=1,;2,;ldots ,;m,}$

где ${displaystyle {vec {x}}^{[j]}=(x_{1}^{[j]},;x_{2}^{[j]},;ldots ,;x_{n}^{[j]}),quad j=0,;1,;2,;ldots }$ .

Применительно к задачам оптимизации[править | править код]

Пусть необходимо найти минимум функции многих переменных ${displaystyle f({vec {x}})colon mathbb {R} ^{n}to mathbb {R} }$ . Эта задача равносильна задаче нахождения нуля градиента . Применим изложенный выше метод Ньютона:

${displaystyle nabla f({vec {x}}^{[j]})+H({vec {x}}^{[j]})({vec {x}}^{[j+1]}-{vec {x}}^{[j]})=0,quad j=1,;2,;ldots ,;n,}$

где — гессиан функции .

В более удобном итеративном виде это выражение выглядит так:

${displaystyle {vec {x}}^{[j+1]}={vec {x}}^{[j]}-H^{-1}({vec {x}}^{[j]})nabla f({vec {x}}^{[j]}).}$

В случае квадратичной функции метод Ньютона находит экстремум за одну итерацию.

Нахождение матрицы Гессе связано с большими вычислительными затратами, и зачастую не представляется возможным. В таких случаях альтернативой могут служить квазиньютоновские методы, в которых приближение матрицы Гессе строится в процессе накопления информации о кривизне функции.

Метод Ньютона — Рафсона[править | править код]

Метод Ньютона — Рафсона является улучшением метода Ньютона нахождения экстремума, описанного выше. Основное отличие заключается в том, что на очередной итерации каким-либо из методов одномерной оптимизации выбирается оптимальный шаг:

${displaystyle {vec {x}}^{[j+1]}={vec {x}}^{[j]}-lambda _{j}H^{-1}({vec {x}}^{[j]})nabla f({vec {x}}^{[j]}),}$

где ${displaystyle lambda _{j}=arg min _{lambda }f({vec {x}}^{[j]}-lambda H^{-1}({vec {x}}^{[j]})nabla f({vec {x}}^{[j]})).}$
Для оптимизации вычислений применяют следующее улучшение: вместо того, чтобы на каждой итерации заново вычислять гессиан целевой функции, ограничиваются начальным приближением ${displaystyle H(f({vec {x}}^{[0]}))}$ и обновляют его лишь раз в шагов, либо не обновляют вовсе.

Применительно к задачам о наименьших квадратах[править | править код]

На практике часто встречаются задачи, в которых требуется произвести настройку свободных параметров объекта или подогнать математическую модель под реальные данные. В этих случаях появляются задачи о наименьших квадратах:

$F({vec {x}})=|{vec {f}}({vec {x}})|=sum _{{i=1}}^{m}f_{i}^{2}({vec {x}})=sum _{{i=1}}^{m}(varphi _{i}({vec {x}})-{mathcal {F}}_{i})^{2}to min .$

Эти задачи отличаются особым видом градиента и матрицы Гессе:

$nabla F({vec {x}})=2J^{T}({vec {x}}){vec {f}}({vec {x}}),$

$H({vec {x}})=2J^{T}({vec {x}})J({vec {x}})+2Q({vec {x}}),qquad Q({vec {x}})=sum _{{i=1}}^{m}f_{i}({vec {x}})H_{i}({vec {x}}),$

где — матрица Якоби вектор-функции , $H_{i}({vec {x}})$ — матрица Гессе для её компоненты $f_{i}({vec {x}})$ .

Тогда очередной шаг определяется из системы:

$left[J^{T}({vec {x}})J({vec {x}})+sum _{{i=1}}^{m}f_{i}({vec {x}})H_{i}({vec {x}})right]{vec {p}}=-J^{T}({vec {x}}){vec {f}}({vec {x}}).$

Метод Гаусса — Ньютона[править | править код]

Метод Гаусса — Ньютона строится на предположении о том, что слагаемое $J^{T}({vec {x}})J({vec {x}})$ доминирует над . Это требование не соблюдается, если минимальные невязки велики, то есть если норма сравнима с максимальным собственным значением матрицы $J^{T}({vec {x}})J({vec {x}})$ . В противном случае можно записать:

$J^{T}({vec {x}})J({vec {x}}){vec {p}}=-J^{T}({vec {x}}){vec {f}}({vec {x}}).$

Таким образом, когда норма близка к нулю, а матрица имеет полный столбцевой ранг, шаг мало отличается от ньютоновского (с учётом ), и метод может достигать квадратичной скорости сходимости, хотя вторые производные и не учитываются. Улучшением метода является алгоритм Левенберга — Марквардта, основанный на эвристических соображениях.

Обобщение на комплексную плоскость[править | править код]

Бассейны Ньютона для полинома пятой степени $scriptstyle {p(x)=x^{5}-1}$ . Разными цветами закрашены области притяжения для разных корней. Более тёмные области соответствуют большему числу итераций.

До сих пор в описании метода использовались функции, осуществляющие отображения в пределах множества вещественных значений. Однако метод может быть применён и для нахождения нуля функции комплексной переменной. При этом процедура остаётся неизменной:

${displaystyle z_{n+1}=z_{n}-{frac {f(z_{n})}{f'(z_{n})}}.}$

Особый интерес представляет выбор начального приближения $z_{0}$ . Ввиду того, что функция может иметь несколько нулей, в различных случаях метод может сходиться к различным значениям, и вполне естественно возникает желание выяснить, какие области обеспечат сходимость к тому или иному корню. Этот вопрос заинтересовал Артура Кэли ещё в 1879 году, однако разрешить его смогли лишь в 70-х годах двадцатого столетия с появлением вычислительной техники. Оказалось, что на пересечениях этих областей (их принято называть областями притяжения) образуются так называемые фракталы — бесконечные самоподобные геометрические фигуры.

Ввиду того, что Ньютон применял свой метод исключительно к полиномам, фракталы, образованные в результате такого применения, обрели название фракталов Ньютона или бассейнов Ньютона.

Реализация[править | править код]

Scala[править | править код]

object NewtonMethod {

  val accuracy = 1e-6

  @tailrec
  def method(x0: Double, f: Double => Double, dfdx: Double => Double, e: Double): Double = {
    val x1 = x0 - f(x0) / dfdx(x0)
    if (abs(x1 - x0) < e) x1
    else method(x1, f, dfdx, e)
  }

  def g(C: Double) = (x: Double) => x*x - C

  def dgdx(x: Double) = 2*x

  def sqrt(x: Double) = x match {
    case 0 => 0
    case x if (x < 0) => Double.NaN
    case x if (x > 0) => method(x/2, g(x), dgdx, accuracy) 
  }
}

Python[править | править код]

from math import sin, cos
from typing import Callable
import unittest


def newton(f: Callable[[float], float], f_prime: Callable[[float], float], x0: float, 
	eps: float=1e-7, kmax: int=1e3) -> float:
	"""
	solves f(x) = 0 by Newton's method with precision eps
	:param f: f
	:param f_prime: f'
	:param x0: starting point
	:param eps: precision wanted
	:return: root of f(x) = 0
	"""
	x, x_prev, i = x0, x0 + 2 * eps, 0
	
	while abs(x - x_prev) >= eps and i < kmax:
		x, x_prev, i = x - f(x) / f_prime(x), x, i + 1

	return x


class TestNewton(unittest.TestCase):
	def test_0(self):
		def f(x: float) -> float:
			return x**2 - 20 * sin(x)


		def f_prime(x: float) -> float:
			return 2 * x - 20 * cos(x)


		x0, x_star = 2, 2.7529466338187049383

		self.assertAlmostEqual(newton(f, f_prime, x0), x_star)


if __name__ == '__main__':
	unittest.main()

PHP[править | править код]

<?php
// PHP 5.4
function newtons_method(
	$a = -1, $b = 1, 
	$f = function($x) {
	
		return pow($x, 4) - 1;
	
	},
	$derivative_f = function($x) {

		return 4 * pow($x, 3);
	
	}, $eps = 1E-3) {

        $xa = $a;
        $xb = $b;

        $iteration = 0;

        while (abs($xb) > $eps) {

            $p1 = $f($xa);
            $q1 = $derivative_f($xa);
            $xa -= $p1 / $q1;
            $xb = $p1;
            ++$iteration;

        }

        return $xa;

}

Octave[править | править код]

function res = nt()
  eps = 1e-7;
  x0_1 = [-0.5,0.5];
  max_iter = 500;
  xopt = new(@resh, eps, max_iter);   
  xopt
endfunction
function a = new(f, eps, max_iter)
  x=-1;
  p0=1;
  i=0;
 while (abs(p0)>=eps)
    [p1,q1]=f(x);
    x=x-p1/q1;
   p0=p1;
   i=i+1;
 end
 i
 a=x;
endfunction
function[p,q]= resh(x)   % p= -5*x.^5+4*x.^4-12*x.^3+11*x.^2-2*x+1;
   p=-25*x.^4+16*x.^3-36*x.^2+22*x-2;
   q=-100*x.^3+48*x.^2-72*x+22;
endfunction

Delphi[править | править код]

// вычисляемая функция
function fx(x: Double): Double;
begin
  Result := x * x - 17;
end;

// производная функция от f(x)
function dfx(x: Double): Double;
begin
  Result := 2 * x;
end;

function solve(fx, dfx: TFunc<Double, Double>; x0: Double): Double;
const
  eps = 0.000001;
var
  x1: Double;
begin
  x1 := x0 - fx(x0) / dfx(x0); // первое приближение
  while (Abs(x1-x0) > eps) do begin // пока не достигнута точность 0.000001
    x0 := x1;
    x1 := x1 - fx(x1) / dfx(x1); // последующие приближения
  end;
  Result := x1;
end;

// Вызов
solve(fx, dfx,4));

C++[править | править код]

#include <stdio.h>
#include <math.h>

#define eps 0.000001
double fx(double x) { return x * x - 17;} // вычисляемая функция
double dfx(double x) { return 2 * x;} // производная функции

typedef double(*function)(double x); // задание типа function

double solve(function fx, function dfx, double x0) {
  double x1  = x0 - fx(x0) / dfx(x0); // первое приближение
  while (fabs(x1 - x0) > eps) { // пока не достигнута точность 0.000001
    x0 = x1;
    x1 = x0 - fx(x0) / dfx(x0); // последующие приближения
  }
  return x1;
}

int main () {
  printf("%fn", solve(fx, dfx, 4)); // вывод на экран
  return 0;
}

C[править | править код]

typedef double (*function)(double x);

double TangentsMethod(function f, function df, double xn, double eps) {
   double x1  = xn - f(xn)/df(xn);
   double x0 = xn;
   while(abs(x0-x1) > eps) {
      x0 = x1;
      x1 = x1 - f(x1)/df(x1);
   }
   return x1;
}

//Выбор начального приближения
xn = MyFunction(A)*My2Derivative(A) > 0 ? B : A;

double MyFunction(double x) { return (pow(x, 5) - x - 0.2); } //Ваша функция
double MyDerivative(double x) { return (5*pow(x, 4) - 1); } //Первая производная
double My2Derivative(double x) { return (20*pow(x, 3)); } //Вторая производная

//Пример вызова функции
double x = TangentsMethod(MyFunction, MyDerivative, xn, 0.1)

Haskell[править | править код]

import Data.List ( iterate' )

main :: IO ()
main = print $ solve ( x -> x * x - 17) ( * 2) 4

-- Функция solve универсальна для всех вещественных типов значения которых можно сравнивать.
solve = esolve 0.000001

esolve epsilon func deriv x0 = fst . head $ dropWhile pred pairs
  where
    pred (xn, xn1) = (abs $ xn - xn1) > epsilon -- Функция pred определяет достигнута ли необходимая точность.
    next xn = xn - func xn / deriv xn -- Функция next вычисляет новое приближение.
    iters   = iterate' next x0        -- Бесконечный список итераций.
    pairs   = zip iters (tail iters)  -- Бесконечный список пар итераций вида: [(x0, x1), (x1, x2) ..].

Литература[править | править код]

Акулич И. Л. Математическое программирование в примерах и задачах : Учеб. пособие для студентов эконом. спец. вузов. — М. : Высшая школа, 1986. — 319 с. : ил. — ББК 22.1 А44. — УДК 517.8^(G).
Амосов А. А., Дубинский Ю. А., Копченова Н. П. Вычислительные методы для инженеров : Учеб. пособие. — М. : Высшая школа, 1994. — 544 с. : ил. — ББК 32.97 А62. — УДК 683.1^(G). — ISBN 5-06-000625-5.
Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы. — 8-е изд. — М. : Лаборатория Базовых Знаний, 2000.
Вавилов С. И. Исаак Ньютон. — М. : Изд. АН СССР, 1945.
Волков Е. А. Численные методы. — М. : Физматлит, 2003.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М. : Мир, 1985.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М. : Наука, 1970. — С. 575—576.
Коршунов Ю. М., Коршунов Ю. М. Математические основы кибернетики. — Энергоатомиздат, 1972.
Максимов Ю. А.,Филлиповская Е. А. Алгоритмы решения задач нелинейного программирования. — М. : МИФИ, 1982.
Морозов А. Д. Введение в теорию фракталов. — МИФИ, 2002.

См. также[править | править код]

Метод простой итерации
Двоичный поиск
Метод дихотомии
Метод секущих
Метод Мюллера
Метод хорд
Метод бисекции
Фрактал
Численное решение уравнений
Целочисленный квадратный корень
Быстрый обратный квадратный корень

Ссылки[править | править код]

«Бассейны Ньютона» на сайте fractalworld.xaoc.ru
«Исаак Ньютон» на сайте www.scottish-wetlands.org
«Математические работы Канторовича» на сайте Института математики СО РАН
Hazewinkel, Michiel, ed. (2001), Newton method, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Weisstein, Eric W. Newton’s Method (англ.) на сайте Wolfram MathWorld.
Newton’s method, Citizendium.
Mathews, J., The Accelerated and Modified Newton Methods, Course notes.
Wu, X., Roots of Equations, Course notes.

Источник

В этом разделе мы сконцентрируемся сначала на методах, которые используют информацию о гессиане функции, а затем рассмотрим, как, сохраняя высокоуровневую идею метода Ньютона, обойтись без гессиана.

Метод Ньютона

Итак, наша задача – безусловная оптимизация гладкой функции

$$
f(x) to min_{x in mathbb{R}^d}.
$$

Как и при оптимизации методом градиентного спуска, мы будем искать направление уменьшения функционала. Но в этот раз мы будем использовать не линейное приближение, а квадратичное:

$$
f(x + Delta x) approx f(x) + langle nabla f(x), Delta x rangle + frac{1}{2}langle Delta x, B(x) Delta x rangle.
$$

Формула Тейлора говорит нам брать $B(x) = nabla^2 f(x)$. Приравняв к нулю градиент этой квадратичной аппроксимации, мы получаем направление спуска для метода Ньютона:

$$
Delta x = [B(x)]^{-1} nabla f(x).
$$

Обозначим $B_k = B(x_k), H_k = B_k^{-1}$. В таком случае мы можем записать итеративный алгоритм спуска:

$$
x_{k+1} = x_{k} – alpha_k cdot H_k nabla f(x_k).
$$

В литературе методом Ньютона называется такой метод при $alpha_k = 1$, при другом размере шаге $alpha_k in (0, 1)$ этот метод называют дэмпированным (damped) методом Ньютона.

Обсудим, в чем главная особенность метода Ньютона и в чем заключается выигрыш по сравнению с классическим градиентным спуском. Таких особенностей две.

Скорость сходимости метода Ньютона

Первая связана со скоростью его сходимости. А именно – в окрестности решения он сходится квадратично.

Теорема. Пусть функция $f$ имеет достаточно гладкий гессиан и сильно выпукла в точке оптимума $x^*$. Тогда $exists r > 0$, что для всякого $x_0 : Vert x_0 – x^*Vert leq r$ для метода Ньютона с $alpha_k = 1$ верно $Vert x_{k+1} – x^* Vert leq c Vert x_k – x^* Vert^2$ для константы $c$ зависящей только от $f$.

Набросок доказательства для интересующихся.

Немного поясним терминологию. Под достаточно гладким гессианом мы подразумеваем то, что он должен быть _липшицевым_ и дифференцируемым, из чего следует, что

$$
Vert nabla^2 f(x) – nabla^2 f(y) Vert leq L Vert x – y Vert,
$$

а также

$$
Vert left[nabla^3 f(x)right] (x – y, x – y, cdot) Vert leq L Vert x – yVert^2,
$$

где $left[nabla^3 f(x)right] (x – y, x – y, cdot)$ – результат подстановки $(x – y)$ в качестве двух первых аргументов в трилинейную форму $left[nabla^3 f(x)right]$. Под сильной выпуклостью мы подразумеваем здесь $mu$-сильную выпуклость, которую здесь строго определять излишне (подробнее см. в этой статье), но из которой следует, что гессиан отделён от нуля:

$$lambda_{min}(nabla^2 f(x)) geq mu$$

Разложим градиент по формуле Тейлора в точке $x_k$ с остаточным членом в форме Лагранжа:

$$
0 = nabla f(x^*) = nabla f(x_k) + nabla^2 f(x_k) (x^* – x_k) + frac{1}{2} nabla^3 f(xi_k) [x^* – x_k]^2.
$$

Умножим с обеих сторон на обратный гессиан и получаем:

$$
x_k – [nabla^2 f(x_k)]^{-1} nabla f(x_k) – x^* = frac{1}{2} [nabla^2 f(x_k)]^{-1}nabla^3 f(xi_k) [x^* – x_k]^2.
$$

Воспользуемся формулой шага $x_{k+1} = x_k – [nabla^2 f(x_k)]^{-1} nabla f(x_k)$, тогда в левой части равенства у нас $x_{k+1} – x^*$. Посчитаем норму и воспользуемся гладкостью:

$$
Vert x_{k+1} – x^* Vert leq frac{L}{2} Vert [nabla^2 f(x_k)]^{-1} Vert Vert x^* – x_k Vert^2.
$$

Теперь воспользуемся сильной выпуклостью в точке оптимума. Поскольку мы предполагаем, что точка старта достаточно близко к точке оптимума, то по гладкости можем считать, что в точке $x_k$ у нас есть хотя бы $mu/2$-сильная выпуклость. Тогда получаем:

$$
Vert x_{k+1} – x^* Vert leq frac{L}{4mu} Vert x_k – x^* Vert^2.
$$

$$tag*{$blacksquare$}$$

Метод Ньютона и плохо обусловленные задачи

Второе приятное свойство заключается в устойчивости метода Ньютона к плохой обусловленности задачи (в отличие от метода градиентного спуска). Разберёмся, что это значит. Когда мы говорим о плохой обусловленности задачи, мы имеем в виду, что гессиан в точке оптимума плохо обусловлен, то есть отношение максимального и минимального собственных чисел является большим числом. Геометрически это значит, что линии уровня функции вблизи оптимума похожи на очень вытянутые эллипсоиды; мы уже обсуждали, что в такой ситуации градиентный спуск может работать медленно. А как справится метод Ньютона? Оказывается, намного лучше. И связано это с его инвариантностью к линейным преобразованиям.

А именно, рассмотрим функцию $hat f(y) = f(Ay)$ для некоторой невырожденной матрицы $A$. Обозначим $x = Ay$. Посмотрим, как связаны градиент и гессиан новой функции с градиентом и гессианом старой. Воспользуемся производной сложной функции:

$$
nabla_y hat f = A^top_x nabla f,
$$

$$
nabla^2_y hat f = A^top nabla^2_x f A
$$

Рассмотрим теперь траекторию $x_0, x_1, ldots, x_K$ метода Ньютона, запущенного из точки $x_0$ для поиска минимума функции $f$, и траекторию $y_0, y_1, ldots,y_K$ метода Ньютона, запущенного для поиска минимума функции $hat f$. Если $x_0 = A y_0$, то для всех $k$ будет верно $x_k = A y_k$, то есть траектории получаются одна из другой при помощи этого линейного преобразования, другими словами, траектории исходной и новой функции подобны.

Для интересующихся доказательствами.

Докажем по индукции. Для $k=0$ это дано по условию. Теперь докажем шаг индукции:

$$
y_{k+1} = y_{k} – alpha_k [ nabla^2_{y_k} hat f]^{-1} nabla_{y_k} hat f =
$$

$$
y_k – alpha_k (A^{-1} [nabla^2_{A y_k} f] A^{-top}) (A^{top} nabla_{A y_k} f).
$$

По предположению индукции $x_k = A y_k$, тогда получаем:

$$
y_{k+1} = A^{-1} ( x_k – alpha [nabla^2 hat f(x_k)] nabla f(x_k) ) = A^{-1} x_{k+1} Rightarrow x_{k+1} = A y_{k+1}.
$$

$$tag*{$blacksquare$}$$

Вернёмся теперь к плохо обусловленной задаче минимизации функции $f$. Рассмотрим линейное преобразование $A = (nabla^2_{x^*} f)^{-1/2}$ и функцию $hat f(x) = f(Ax)$. Тогда для функции $hat f$ число обусловленности гессиана в точке оптимума равно в точность единице (проверьте это!), а траектории для этой новой, хорошо обусловленной функции, и старой, плохо обусловленной, подобны. В частности, метод Ньютона не будет, как градиентный спуск, долго метаться где-то на задворках вытянутой эллиптической «ямки» вокруг оптимума, а быстро ринется к центру.

Можно сказать, что метод Ньютона правильно улавливает кривизну линий уровня функции и это позволяет ему быстрее сходиться к оптимуму. Эту идею стоит запомнить, она появляется в некоторых вдохновлённых методами второго порядка модификациях SGD.

Также еще можно заметить, что свойства, которые мы требуем от функции в теореме о квадратичной сходимости, вообще говоря, не сохраняются при линейных преобразованиях: могут поменяться константы липшицевости и сильной выпуклости. Это простое замечание побудило исследователей ввести класс самосогласованных функций, более широкий и линейно инвариантный, для которого метод Ньютона также сходится. Подробнее об этом можно узнать в разделе 9.6 книги S. Boyd & L. Vandenberghe, Convex Optimization.

Слабости метода Ньютона

От хорошего переходим к плохому: к слабостям метода Ньютона. Во-первых, мы имеем квадратичную скорость сходимости только в окрестности оптимума. А если мы стартуем из произвольно удалённой точки, то нам, как и в случае градиентного спуска, требуется подбор шага $alpha_k$ при помощи линейного поиска (что нам вряд ли по карману). Если подбирать шаг не хочется, можно прибегнуть к интересному теоретическому методу получения гарантий на глобальную сходимость – добавлению кубической регуляризации.

Немного деталей для пытливых

В случае кубической регуляризации мы хотим обеспечить не просто аппроксимацию, но и оценку сверху:

$$
f(x + Delta x) leq f(x) + langle nabla f(x), Delta x rangle + frac{1}{2}langle Delta x, nabla^2 f(x) Delta x rangle + frac{M}{6} Vert Delta x Vert^3_2.
$$

По сути, мы задаем кубическую модель, которую мы можем уже оптимзировать по $Delta x$. Тогда мы получаем следующую итеративную процедуру проксимального вида:

$$
x_{k+1} = argmin_{y} biggl{ f(x_k) + langle nabla f(x_k), y – x_k rangle + frac{1}{2}langle y-x_k, nabla^2 f(x_k) (y – x_k) rangle + frac{M}{6} Vert y – x_k Vert^3_2
biggl}
$$

В таком случае можно использовать, например, постоянный размер шага и иметь гарантии на сходимость. Этот метод в последнее время стал пользоваться популярностью в теоретических исследованиях, в том числе в распределенной оптимизации.

Также можно задаться простым вопросом: а можем ли мы пользоваться подобным разложением с регуляризацией для большего числа членов разложения по формуле Тейлора? На самом деле да, только коэффициент $M$ нужно подбирать чуть более специфично. Такие методы называются тензорными методами.

Другая проблема кроется в формуле пересчета следующей итерации: вычисление и обращение гессиана. Конечно, вместо обращения гессиана можно честно решать систему линейных уравнений, но асимптотика остается прежней: $O(d^3)$, а от затрат памяти на хранение матрицы $O(d^2)$ вообще некуда деться. А это значит, что, например, решать линейную регрессию с ~10000 признаками методом Ньютона попросту невозможно.

Есть и третья, малозаметная проблема: дословно метод Ньютона не работает для невыпуклых задач, поскольку $nabla^2 f(x)$ не будет положительно опредленной и $Delta x$ перестанет быть направлением спуска. Для решения этой проблемы можно немного «подпортить» нашу аппроксимацию и рассмотреть матрицу вида $B_k = nabla^2 f(x_k) + Delta_k$, такую что $B_k$ станет положительно определенной, и уже её подставлять в нашу квадратичную модель. Идея подмены гессиана на что-то более подходящее – это главная идея квазиньютоновских методов, обсуждаемых далее.

Итак, общие выводы:

Метод Ньютона – теоретически оптимальный метод, который автоматически улавливает кривизну функции в окрестности оптимума.
Для размерности $d > 1000$ он уже не является эффективным, поскольку требует вычисления и хранения гессиана, а также решения системы линейных уравнений с его участием (что может быть в общем случае очень дорого).

Квазиньютоновские методы

Чтобы придумать, как бороться с проблемами метода Ньютона, нужно посмотреть на него с другой стороны, а для этого мы обратимся ненадолго к решению задачи нахождения нуля векторной функции.

Метод касательной

Итак, рассмотрим совершенно новую задачу. Пусть дана функция $g colon mathbb{R}^n to mathbb{R}^n$ и нужно найти её ноль, то есть такое $x^*$, что $g(x^*) = 0$. Связь с оптимизацией (_по крайней мере в выпуклом случае_) довольно проста: если взять $g(x) = nabla f(x)$, то корень уравнения $g(x) = 0$ и будет точкой оптимума.

Сначала рассмотрим одномерный случай $d=1$. Как найти ноль функции с помощью итеративной процедуры? Логично поступить следующим образом: проводим касательную $y = g'(x_n)(x – x_n) + g(x_n)$ к графику функции и находим точку $x_{n+1}$, в которой линейная аппроксимация обнуляется:

$$0 = g'(x_n)(x_{n+1} – x_n) + g(x_n),$$

откуда получаем формулу пересчета

$$
x_{n+1} = x_n – frac{g(x_n)}{g'(x_n)}.
$$

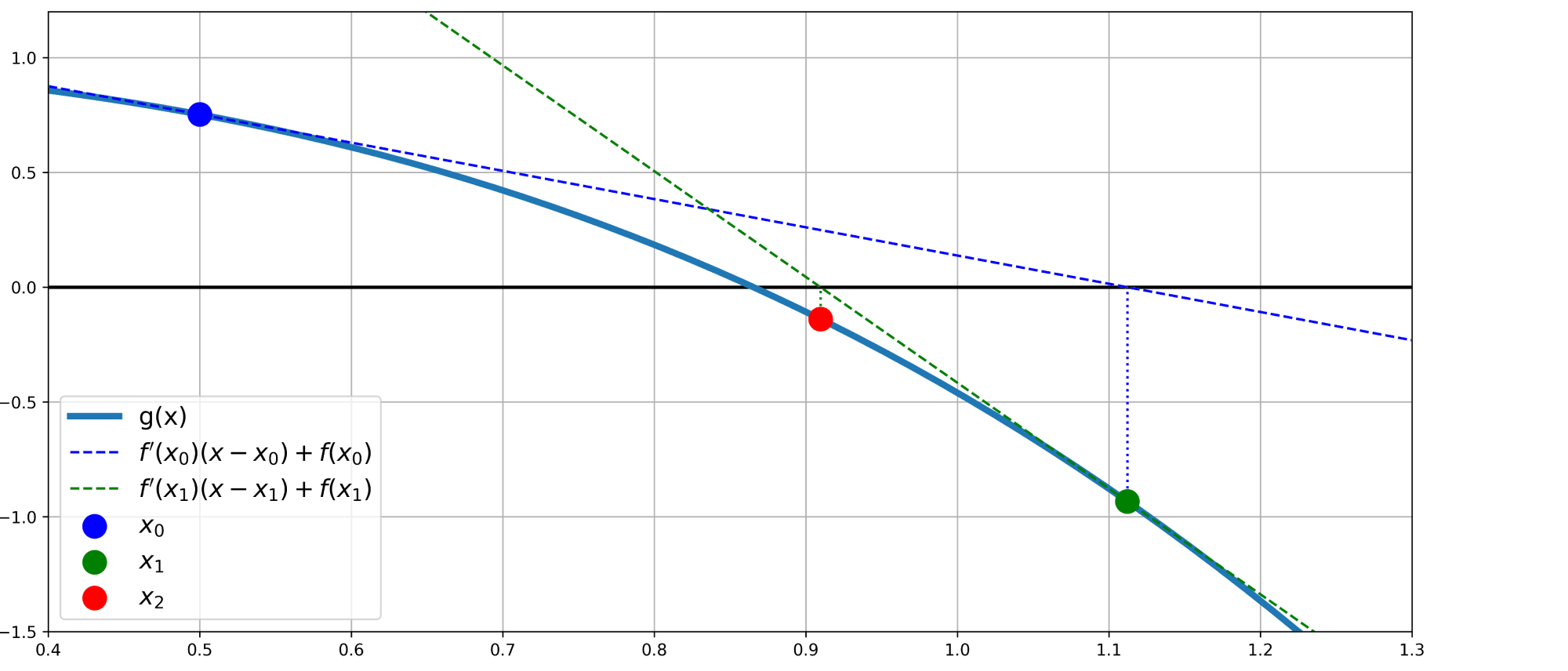
Известно, что этот метод обладает квадратичной скоростью сходимости в одномерном мире, что очень перекликается с методом Ньютона для оптимизации – и не просто так.

Если рассмотреть многомерный случай, то вычисление производной заменяется на вычисление якобиана векторнозначной функции $g$. В случае $g = nabla f$ наш якобиан становится гессианом и получаем в точности обычный метод Ньютона для оптимизации:

$$
x_{n+1} = x_n – left[nabla^2_{x_n} fright]^{-1} nabla_{x_n} f.
$$

Метод секущей и общая схема квазиньютоновских методов

Пусть мы хотим найти такую точку $x^*$, что $g(x^*) = 0$. В одномерном случае мы можем подменить вычисление $g'(x_n)$ вычислением её приближения $g(x_n) – g(x_{n-1}) / (x_n – x_{n-1})$. Откуда получаем формулу пересчета:

$$
x_{n+1} = x_{n} – frac{x_n – x_{n-1}}{g(x_n) – g(x_{n-1})} g(x_n)
$$

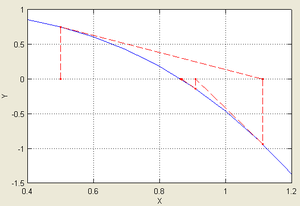
Графически, этот метод выглядит следующим образом:

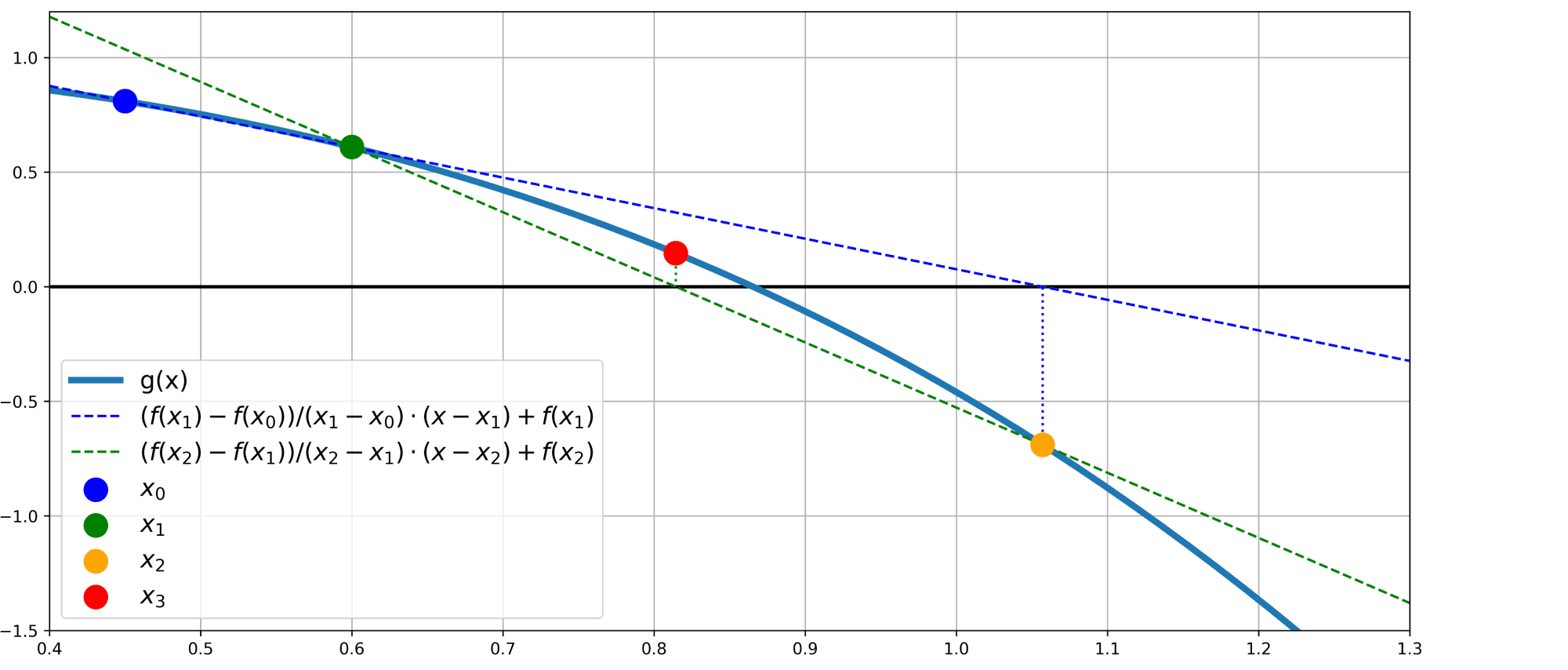
Скорость сходимости этого метода несколько ниже, чем у метода Ньютона (линейная, а не квадратичная), но зато мы теперь не должны вычислять производную! В текущем виде, используя просто подмену градиента на его конечно-разностную аппроксимацию, не очевидно, как обобщить этот метод на произвольную размерность. Но, если посмотреть на название метода и на картинку, как он работает, мы видим, что мы по сути проводим через два предыдущих приближения секущую, а затем выбираем ноль этой секущей в качестве следующей точки. В многомерном случае мы можем выписать соответствующее ей уравнение $y = B_k(x – x^k) + g(x^{k})$, где $B_k$ – матрица размера $d times d$, которая должна удовлетворять так называемому уравнению секущей (secant equation):

$$
B_k(x^k – x^{k-1}) = g(x^k) – g(x^{k-1}).
$$

Теперь, чтобы выбрать следующую точку, нужно найти ноль секущей, то есть

$$
B_k(x^{k+1} – x^{k}) + g(x^k) = 0 iff x^{k+1} = x^k – B_k^{-1} g(x^k).
$$

А теперь рассмотрим $g(x) = nabla f(x)$ и добавим в итеративную схему выше размер шага. Тогда мы получаем общую итеративную схему квазиньютоновских методов:

$$
x^{k+1} = x^k – alpha_k B_k^{-1} nabla f(x^k).
$$

При этом необходимо выбирать такие $B_k$, чтобы они

(а) были симметричными и положительно определенными и

(б) удовлетворяли уравнению секущей

$$B_k(x^{k} – x^{k-1}) = nabla f(x^k) – nabla f(x^{k-1})$$

Первое требование восходит к двум соображениям. Первое – $B_k$ должно приближать гессиан, а он в идеале в окрестности точки минимума как раз является симметричным и положительно определенным. Второе соображение проще: в противном случае $d_k = -B_k^{-1} nabla f(x^k)$ попросту не будет направлением спуска. Несмотря на эти два свойства, выбор по прежнему остается достаточно широким, откуда возникает большое разнообразие квазиньютоновских методов. Мы рассмотрим один классический и широко известный метод BFGS (Broyden, Fletcher, Goldfarb, Shanno).

BFGS

Сначала заметим, что в самом алгоритме в первую очередь используется обратная матрица к $B_k$, которую мы обозначим $H_k = B_k^{-1}$. Тогда выбирать $B_k$ – это тоже самое, что выбирать $H_k$. Введем еще два стандартных обозначения, чтобы можно было проще записывать все последующие формулы: $s_k = x_{k+1} – x_{k} = alpha_k d_{k}$ и $y_k = nabla f(x^{k+1}) – nabla f(x^k)$. В их терминах уравнение секущей для $H_k$ выглядит максимально просто: $H_{k} y_{k-1} = s_{k-1}$.

Теперь введем некоторое искусственное требование, которое гарантирует единственность $H_{k+1}$ – выберем ближайшую подходящую матрицу к $H_k$, удовлетворяющую описанным выше условиям:

$$
H_{k+1} = text{argmin}_Hleft{left.frac12Vert H – H_k Vertright| Н = H^top, H y_k = s_kright}
$$

Вообще говоря, при выборе разных норм $Vert cdot Vert$ мы будем получать разные квазиньютоновские алгоритмы. Рассмотрим один достаточно общий класс норм (аналог взвешенных $ell_2$ норм в матричном мире):

$$
Vert A Vert := Vert W^{1/2} A W^{1/2} Vert_F,
$$

где $Vert cdot Vert_F$ – это Фробениусова норма

$$Vert C Vert_F^2 = langle C, Crangle_F = text{tr}(C^top C) = sum_{i,j} C_{ij}^2,$$

а $W$ – некоторая симметричная и положительно определенная матрица весов, которую мы выберем таким образом, что она будет сама по себе удовлетворять уравнению секущей $Ws_k = y_k$.

Сразу уточним, что матрица весов в таком случае меняется на каждой итерации и, по сути, на каждой итерации мы имеем разные задачи оптимизации, само же предположение задает дополнительную похожесть на обратный гессиан, поскольку можно взять в качестве весов усредненый гессиан

$$W = bar G_k = [int_0^1 nabla^2 f(x_k + tau alpha_k p_k) dtau]$$

Решив описанную выше оптимизационную задачу, мы получаем матрицу $H_{k+1}$, не зависящую явным образом от матрицы весов:

Эта формула как раз является ключевой в алгоритме BFGS. Чтобы заметить одно крайне важное свойство этой формулы, раскроем скобки:

$$
H_{k+1} = H_k – rho_k (H_k y_k s_k^{top} + s_k y_k^top H_k) + rho_k^2 (s_k y_k^top H_k y_k s_k^top) + rho_k s_k s_k^top.
$$

Отсюда мы видим, что нам в этой формуле достаточно умножать матрицу на вектор и складывать матрицы, что можно делать за $O(d^2)$ операций! То есть мы победили один из самых страшных минусов метода Ньютона. Воспользовавшись тем, что $ y_k^top H_k y_k $ и $1/rho_k = y_k^top s_k = s_k^top y_k$ – числа, перепишем формулу в более computational friendly стиле:

$$
H_{k+1} = H_k + rho_k^2 (1/rho_k + y_k^top H_k y_k)(s_k s_k^top) – rho_k (H_k y_k s_k^{top} + s_k y_k^top H_k).
$$

Общие выводы:

Итерации BFGS вычислительно проще итераций метода Ньютона и не требуют вычисления гессиана;
По скорости сходимости BFGS уступает методу Ньютона, но все равно является достаточно быстрым;
По прежнему требуется $O(d^2)$ памяти, что по-прежнему вызывает проблемы при большой размерности ($10^4-10^5$).
Время выполнения итерации $O(d^2)$ гораздо лучше, чем $O(d^3)$ метода Ньютона, но всё ещё оставляет желать лучшего.

Казалось бы, избавиться от $O(d^2)$ нельзя принципиально, ведь нужно как-то взаимодействовать с матрицей $H_k$ размера $O(d^2)$, а она не факт что разреженная. Но и в этом случае можно добиться улучшения до линейной сложности (как у градиентных методов!).

L-BFGS

При взаимодействии с матрицами существует два основных способа хранить их дешевле, чем «по-честному». Первый способ – пользоваться разреженностью матрицы, а второй – низкоранговыми разложениями или чем-то близким. Поскольку сейчас мы не хотим добавлять предположений на задачу, которую мы решаем, то единственный выход – это пользоваться структурой $H_k$, возникающей в BFGS.

Если внимательно взглянуть на формулы обновления $ (1) $, то их можно переписать в следующем виде:

$$
H_{k+1} = V(s_k, y_k)^top H_k V(s_k, y_k) + U(s_k, y_k),
$$ $$
V(s_k, y_k) = I – rho_k y_k s_k^top, U(s_k,y_k) = rho_k s_k s_k^top
$$

Для того, чтобы перейти от $H_k$ к $H_{k+1}$, можно хранить не матрицу $H_{k}$, а набор пар из k пар $(s_i, y_i)_{i=1,ldots,k}$ и начальное приближение $H_0$ (например, $H_0 = gamma I$ для некоторого $gamma > 0$), чтобы «восстановить» $H_k$. Пользуясь такой структурой, мы можем хранить матрицу $H_{k+1}$ при помощи лишь $(k+1) cdot 2d + 1$ чисел, а не $d^2$. К сожалению, такая структура имеет довольно простую проблему: при $k > d/2$ затраты памяти становятся только выше.

Возникает простая идея – а давайте хранить только последние $m = text{const}$ обновлений! Таким образом, мы получаем алгоритм L-BFGS, который имеет уже линейные $O(md)$ затраты памяти и, что немаловажно, такие же линейные затраты $O(md)$ на итерацию, ведь умножение матриц $V$ и $U$ на вектор может осуществляться за линейное время.

Общие выводы:

L-BFGS обладает линеной сложностью итерации, линейными требованиями по дополнительной памяти и к тому же требует вычислять только градиенты!
Производительность сильно зависит от константы $m$, отвечающей за точность аппроксимации гессиана;
Как и все методы из этого раздела, требует точного, а не стохастического вычисления градиентов.

Практические аспекты

Из всех перечисленных в этом разделе методов важнее всего отметить L-BFGS как самый практичный. Он реализован в любой* библиотеке, которая имеет дело с оптимизацией чего-либо и может быть эффективным, если удаётся вычислить градиенты (и значения функций для линейного поиска размера шага). К сожалению, это получается не всегда: при больших размерах датасета вычисление честного градиента и значения для функционалов вида суммы

$$
L(X,Y) = sum_{i=1}^N L(x_i, y_i)
$$

не представляется возможным за разумное время. В таком случае мы вынуждены вернуться в мир стохастического градиентного спуска. Общая идея более тонкого учёта геометрии линий уровня функции потерь, в чём-то напоминающая происходящее в методе Ньютона, находит применение и в ряде вариаций SGD, но, конечно, порождает совершенно другие методы.

Что же касается самого метода Ньютона, его можно несколько оптимизировать, если смириться с тем, что всё вычисляется неточно. Во-первых, обратную матрицу к гессиану матрицу на самом деле не нужно ни хранить, ни даже вычислять. Давайте разберёмся, почему. Умножить $(nabla^2f)^{-1}$ на вектор $v$ – это то же самое, что решить систему с левой частью $nabla^2f$ и правой частью $v$, а для решения систем уравнений существуют эффективные итеративные методы, не меняющие левой части системы, а требующие лишь уметь умножать её на разные векторы. При этом умножать гессиан на вектор можно при помощи автоматического дифференцирования. Кроме того, можно на кажом шаге неточно решать систему, получая таким образом неточный метод Ньютона. Теория предписывает решать систему все точнее с ростом номера итерации, но на практике нередко используют фиксированное и небольшое число шагов итеративных методов решения систем линейных уравнений.

Источник

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

1 Постановка задачи одномерной оптимизации
2 Метод Ньютона
- 2.1 Ограничения
- 2.2 Проблема области сходимости
3 Метод парабол
4 Числовой пример
5 Литература
6 Смотри также

Постановка задачи одномерной оптимизации

Задача одномерной оптимизации определяется следующим образом:

Допустимое множество — множество ;
Целевую функцию — отображение ;
Критерий поиска (max или min).

Тогда решить задачу $f(x)to min_{xinmathrm{X}}$ означает одно из:

Показать, что .
Показать, что целевая функция не ограничена.
Найти $x^*inmathbb{X}:;f(x^*)=min_{xinmathbb{X}}f(vec{x})$ .
Если , то найти $inf_{xinmathbb{X}}f(x)$ .

Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек x_0 таких, что всюду в некоторой их окрестности для минимума и для максимума.

Если допустимое множество , то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.

Метод Ньютона

Это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727), под именем которого и обрёл свою известность. Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. В случае решения задач оптимизации предполагается, что функция f(x) дважды непрерывно дифференцируема. Отыскание минимума функции f(x) производится при помощи отыскания стационарной точки, т.е. точки x^* , удовлетворяющей уравнению f'(x)=0 , которое решается методом Ньютона.

Если x^k – точка, полученная на k-м шаге, то функция f'(x) аппроксимируется своим уравнением касательной:

а точка $x^{k+1}$ выбирается как пересечение этой прямой с осью , т.е.

$x^{k+1} = x^k - frac{f'(x^k)}{f''(x^k)}$ .

Неудобство этого метода состоит в необходимости вычисления в каждой точке первой и второй производных. Значит, он применим лишь тогда, когда функция f(x) имеет достаточно простую аналитическую форму, чтобы производные могли быть вычислены в явном виде вручную. Действительно, всякий раз, когда решается новая задача, необходимо выбрать две специфические подпрограммы (функции) вычисления производных f'(x) и f''(x) , что не позволяет построить общие алгоритмы, т.е. применимые к функции любого типа.

Когда начальная точка итераций x_0 достаточно близка к искомому минимуму, скорость сходимости метода Ньютона в общем случае квадратическая. Однако, глобальная сходимость метода Ньютона, вообще говоря, не гарантируется.

Хороший способ гарантировать глобальную сходимость этого метода состоит в комбинировании его с другим методом для быстрого получения хорошей аппроксимации искомого оптимума. Тогда несколько итераций метода Ньютона, с этой точкой в качестве исходной, достаточны для получения превосходной точности.

Ограничения

Пускай задано уравнение f(x)=0! , где и надо найти его решение.

Ниже приведена формулировка основной теоремы, которая позволяет дать чёткие условия применимости.
Теорема Канторовича.

Если существуют такие константы , что:

$frac{1}{|f'(x)|}<A!$ на , то есть существует и не равна нулю;
$left|frac{f(x)}{f'(x)}right|<B!$ на , то есть ограничена;
на , и $|f''(x)|leq C leq frac{1}{2AB}!$ ;

Причём длина рассматриваемого отрезка $|a-b|<frac{1}{AB}left(1- sqrt{1-2ABC}right)!$ . Тогда справедливы следующие утверждения:

на существует корень уравнения ;
если $x_0=frac{a+b}{2}!$ , то итерационная последовательность сходится к этому корню: $left{ x_{n+1}=x_n-frac{f(x_n)}{f'(x_n)}right}to x^*!$ ;
погрешность может быть оценена по формуле $|x^*-x_n|leqfrac{B}{2^{n-1}}(2ABC)^{2^{n-1}}!$ .

Из последнего из утверждений теоремы в частности следует квадратичная сходимость метода:

$|x^*-x_n|leqfrac{B}{2^{n-1}}(2ABC)^{2^{n-1}}=frac{1}{2}frac{B}{2^{n-2}}left((2ABC)^{2^{n-2}}right)^2=alpha |x^*-x_{n-1}|^2!$

Тогда ограничения на исходную функцию f(x)! будут выглядеть так:

функция должна быть ограничена;
функция должна быть гладкой, дважды дифференцируемой;
её первая производная равномерно отделена от нуля;
её вторая производная должна быть равномерно ограничена.

В случае решения задачи оптимизации под функцией понимаем ее производную.

Проблема области сходимости

Запишем итерационный процесс:

$x^{k+1} = x^k - frac{f'(x^k)}{f''(x^k)}$ .

Известно, что условием сходимости этого процесса будет неравенство

где $S(x) = x^k - frac{f'(x^k)}{f''(x^k)}$ , отсюда получем условие сходимости:

$|frac{f'(x)f'''(x)}{(f'(x))^2}| le q < 1$ .

В силу того что мы ищем корень уравнения , существует такая окрестность, где , но в общем случае эта область будет мала, то есть нужно подбирать начальное приближение достаточно близко расположенным к корню.

Теорма о сходимости метода Ньютона
Пусть – простой вещественный корень уравнения , а функция – дважды дифференцируема в некоторой окрестности , причем первая произодная нигде не обращается в нуль.

Тогда, следуя обозначениям

$0 < m_1 = inf_{xin U_r(x^*)}|f'(x)|, M_2 = sup_{xin U_r(x^*)}|f''(x)|$ ,

При выборе начального приближения из той же окрестности такого, что

$frac{M_2|x^0 - x^*|}{2m_1} = q < 1$ ,

итерационная последовательность

$x^{k+1} = x^k - frac{f(x^k)}{f'(x^k)}, k = 0,1, dots$

будет сходиться к , причем для погрешности на k-м шаге буддет справедлива оценка:

$|x^k - x^*| le q^{2^k - 1}|x^0 - x^*|$ .

Метод парабол

Относительно метода Ньютона этот метод обладает тем преимуществом, что он не требует вычисления производных функции f(x) . Однако, его сходимость может быть гарантирована лишь для достаточно регулярных функций (непрерывных и много раз дифференцируемых).

В этом методе вычисляется значение функции сразу в трех близлежащих точках x_0 - h , x_0 , x_0 + h , где h – малое число. Через эти три точки проводится интерполяционная парабола:

Минимум параболы достигается при , т.е. при $x^* = frac{-b}{2a}$ . Для трех точек получаем систему трех линейных уравнений для коэффициентов a, b, c. Находим a и b и тогда:

$x^{k+1} = x^k - 0.5hfrac{f(x^k + h) - f(x^k - h)}{f(x^k + h) - 2f(x^k) + f(x^k - h)}$ .

Числовой пример

Сравним работу методов Ньютона и парабол на примере много экстремальной функции при одинаковом начальном приближении:

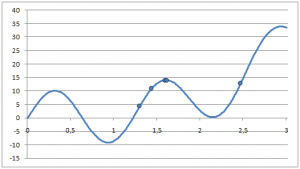
Поиск экстремума

(номер итерации)	полученное методом Ньютона	полученное методом парабол
0	1.3	1.3	53.89938129	53.89938129
1	2.472235424	2.472080749	67.28692280	67.27673489
2	1.449211232	1.452275085	34.85893188	34.25354559
3	1.626598277	1.624678936	-5.832725638	-5.389540219
4	1.601301575	1.601390533	0.095723918	0.074598093
5	1.60170464	1.601718525	1.59821E-05	-0.003280363
6	1.601704707	1.601718641	4.0945E-13	-0.00330785

Код функций на С++, с помощью которых были произведены все расчеты можно скачать тут.

Литература

А.А.Самарский, А.В.Гулин. Численные методы М.: Наука, 1989.
А.А.Самарский. Введение в численные методы М.: Наука, 1982.
Н.В.Соснин. Численные методы. Конспект лекций (сост. Д.В.Ховратович, Е.А.Попов).
М.М.Потапов. Методы оптимизаций. Конспект лекций (сост. М.Л.Буряков).
Е.А.Волков. Численные методы. — М.: Физматлит, 2003.

Смотри также

Практикум ММП ВМК, 4й курс, осень 2008

Источник

Здравствуйте, уважаемые читатели. Продолжаем разбираться в Matlab. И сегодня наша тема связанна с численной оптимизацией — нахождением локальных и глобальных экстремумов функций одной или нескольких переменных в среде Matlab.

Общие сведения

Итак, в этом блоке ничего про Matlab не будет, лишь информация о понятии оптимизации. Это понятие сводится к терминам минимума и максимума функции, или, если коротко — экстремумам.

Под минимумом понимают такое значение функции, которое в некоторой окрестности этой функции, принимает наименьшее значение из всех возможных значений в этой окрестности. Соответственно максимум — это наибольшее значение функции в какой-либо окрестности.

Если не понятно — вот простой пример с всеми известной параболой:

У этой функции есть один минимум, и он находится в точке x = 0. Эта точка называется точкой минимума, а само значение этой функции есть минимум (он тоже равен 0). Максимумов у этой функции нет, но если бы функцию перевернули вверх ногами, то он бы появился.

Часто встречаются сложные функции, у которых есть несколько и минимумов и максимумов. И в таком случае, разделяют понятия локального и глобального экстремума. Локальный — это тот экстремум, который определен в некоторой области, а глобальный — на всей области определения функции. На рисунке выше представлен глобальный минимум параболы.

И теперь, когда вы хоть как то познакомились с понятиями оптимизации и нахождения экстремумов функции, можем перейти к нахождению максимумов и минимумов в Matlab. Далее, как обычно мы будем разбирать примеры различной сложности. Часть примеров будет содержать в себе стандартные команды Matlab для нахождения минимума и максимума функции, а другая часть — это реализация метода с нуля.

Стандартные методы Matlab

Разберем 2 задачи нахождения минимума в Matlab:

1 пример. Вычислить минимум функции f(x)=-x^1/x, определив графически интервал его локализации. Вычисления провести с минимальным шагом по аргументу 1*10^-5

Для начала создадим скрипт, который отобразит эту функцию. Вот код для этого:

x = 0.00001:0.00001:10;
y = -x.^(x.^(-1));
plot (x,y);
hold on;
grid on;

Запускаем скрипт и получаем:
По графику функции делаем вывод, что имеется один минимум, и его координаты находятся в интервале 2.5 — 3, то есть мы сократим интервал поиска минимума.

Теперь создадим еще один скрипт, дадим ему название first.m и пропишем в него функцию:

function fun=first(x)
fun = -x.^(x.^(-1));
end

Таким образом в этом m-файле мы определили функцию. Теперь в командном окне мы пропишем следующий код:

>> [x,y] = fminbnd(@first,2.5,3)

И получаем такие значения:
x = 2.7183 — координата точки минимума
y = -1.4447 — значение минимума

В этой части кода мы использовали стандартный метод Matlab для нахождения минимума функции — fminbnd. мы передаем 3 параметра — саму функцию и интервалы для поиска минимума. Стоит отметить, что этот метод подходит только для функций, зависящих от одной переменной.

Итак, для этой задачи мы создали 2 скрипт-файла, которые вы можете скачать в конце статьи.

2 пример. Вычислить минимум функции двух переменных x⁴+y⁴-2x²+4xy-2y²+1 с точность 1*10-5.
Координаты начальной точки поиска [1.0,-1.0].

Для начала построим график функции от двух переменных — для этого создадим новый скрипт и пропишем там этот код:

[x y] = meshgrid(-2:0.1:2, -2:0.1:2);
z = x.^4 + y.^4 - 2*x.^2 + 4 * x.*y - 2*y.^2 + 1;
surf(x,y,z);

Функция surf позволяет строить трехмерные графики и отображать глубину значений функции для лучшего понимания. Запускаем скрипт — в итоге получился такой график:
Как видно из графика, имеется два участка, где присутствует локальный минимум (темно-синие участки), и наша задача найти координаты и значения двух этих точек. Воспользуемся стандартными инструментами Matlab и создадим новый скрипт с именем second.m, в котором и пропишем код:

function fun=second(x)
fun = x(1)^4 + x(2)^4 - 2*x(1)^2 + 4 * x(1)*x(2) - 2*x(2)^2 + 1;
end

После этого, в командной строке, как и для первой задачи, прописываем стандартную функцию Matlab:

>> [z,f,exitflag,output] = fminsearch(@second, [1.0,-1.0], optimset('TolX',1e-5))

Получаем такой вывод:

z = 1.4142   -1.4142
f = -7.0000
exitflag = 1
output = 
    iterations: 40
    funcCount: 74
    algorithm: 'Nelder-Mead simplex direct search'
    message: [1x196 char]

Для нахождение минимумов в Matlab на этот раз мы использовали функцию fminsearch. Эта функция реализует симплекс — метод Нелдера-Мида. В выводе мы получили несколько переменных: в z записались значения координат точек минимума, в f само значение этого минимума. А в переменных exitflag и output помещены условия прерывания процесса поиска и информация об оптимизации соответственно.

В итоге у нас опять получилось 2 m-файла.

Метод Ньютона Matlab

А теперь попробуем сами реализовать метод Ньютона для оптимизации функции.

3 пример. Методом Ньютона найти точку минимума x* и минимальное значение f* функции f(x)=(x-2)⁴-lnx на отрезке xє[2;3] c точностью 10^-7

Начнем с того, что создадим новый скрипт и назовем его Newton.m. Затем пропишем в нем код:

function [Xk, Yk] = Newton(f,diap)
    a = diap(1); % границы
    b = diap(2);
    df = char(diff(sym(f))); % символьно ищем первую 
    ddf = char(diff(sym(df))); % и вторую производные
    F = inline(f); % преобразуем в функции
    F1 = inline(df);
    F2 = inline(ddf);
    eps = 0.0000001; % задаем точность
    if F(a)*F2(a) > 0 % проверка с какой границы начинать искать
        Xk = b;
    else
        Xk = a;
    end
    while abs(F1(Xk)) > eps
        X0 = Xk; % X0 - значение предыдущего шага
        Xk =  X0 - (F1(X0)/(F2(X0))); % расчет нового значения
        Yk = F(Xk);
    end
end

Вполне понятная функция, которая работает с первой и второй производной символьной функции, которую получает в качестве параметра. Также в параметрах принимается диапазон. Эта функция возвращает координаты точки и значение экстремума.
Теперь нам осталось вызвать эту функцию в командном окне:

>> fun = '(x-2)^4 - log(x)';
>> diap = [2,3];
>> [Xk, Yk] = Newton(fun, diap);

В итоге получилось:
Xk = 2.4663
Yk = -0.8554

Не будем приводить график, но вы сами можете проверить, что значения найдены правильно. Важно сказать, что этот метод позволяет найти только локальный экстремум, и если на выбранном диапазоне есть несколько экстремумов, то метод может найти не тот, который нужен вам.

Также, очень важно задавать как можно узкий диапазон поиска, иначе метод может работать некорректно, особенно это проявляется с периодическими функциями по типу cos(x) и т.п.

Заключение

Ну что ж, в этой статье мы рассмотрели некоторые методы для нахождения экстремумов в Matlab. Мы использовали как стандартные методы, так и реализовали метод Ньютона в среде Matlab. Их исходники чуть ниже.
Скачать исходники

На этом сегодня все, оставляйте ваши комментарии и задавайте вопросы.

Источник

Выводы: При поиске минимума функции на отрезке

6 Лабораторная работа №6. Численное решение обыкновенных дифференциальных уравнений методами Эйлера, модифицированного метода Эйлера с пересчетом, Рунге-Кутты.

Описание метода[править | править код]

Обоснование[править | править код]

Геометрическая интерпретация[править | править код]

Алгоритм[править | править код]

Пример[править | править код]

Условия применения[править | править код]

Контрпримеры[править | править код]

Ограничения[править | править код]

Историческая справка[править | править код]

Обобщения и модификации[править | править код]

Метод секущих[править | править код]

Метод одной касательной[править | править код]

Метод Ньютона-Фурье[править | править код]

Многомерный случай[править | править код]

Применительно к задачам оптимизации[править | править код]

Метод Ньютона — Рафсона[править | править код]

Применительно к задачам о наименьших квадратах[править | править код]

Метод Гаусса — Ньютона[править | править код]

Обобщение на комплексную плоскость[править | править код]

Реализация[править | править код]

Scala[править | править код]

Python[править | править код]

PHP[править | править код]

Octave[править | править код]

Delphi[править | править код]

C++[править | править код]

C[править | править код]

Haskell[править | править код]

Литература[править | править код]

См. также[править | править код]

Ссылки[править | править код]

Метод Ньютона

Скорость сходимости метода Ньютона

Метод Ньютона и плохо обусловленные задачи

Слабости метода Ньютона

Квазиньютоновские методы

Метод касательной

Метод секущей и общая схема квазиньютоновских методов

BFGS

L-BFGS

Практические аспекты

Материал из MachineLearning.

Содержание

Постановка задачи одномерной оптимизации

Метод Ньютона

Ограничения

Проблема области сходимости

Метод парабол

Числовой пример

Литература

Смотри также

Общие сведения

Стандартные методы Matlab

Метод Ньютона Matlab

Заключение

Вам также может понравиться

Как найти способ привязать рентген лайтбокс

Как найти уровень прибыль

Йотацизм как исправить

Добавить комментарий Отменить ответ