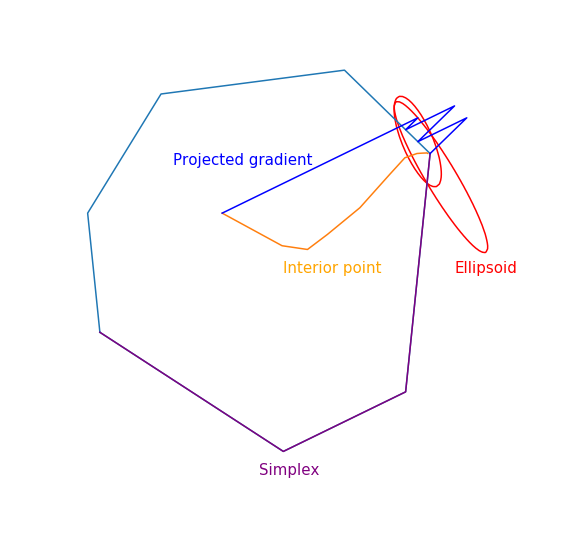
Обзор основных методов математической оптимизации для задач с ограничениями
Время на прочтение
7 мин
Количество просмотров 44K
Я долго готовился и собирал материал, надеюсь в этот раз получилось лучше. Эту статью посвящаю основным методам решения задач математической оптимизации с ограничениями, так что если вы слышали, что симплекс-метод — это какой-то очень важный метод, но до сих пор не знаете, что он делает, то возможно эта статья вам поможет.
P. S. Статья содержит математические формулы, добавленные макросами хабраредактора. Говорят, что они иногда не отображаются. Также есть много анимаций в формате gif.
Преамбула
Задача математической оптимизации — это задача вида «Найти в множестве
элемент
такой, что для всех
из
выполняется
», что в научной литературе скорее будет записано как-то так
Исторически так сложилось, что популярные методы такие как градиентный спуск или метод Ньютона работают только в линейных пространствах (причем желательно простых, например
). На практике же часто встречаются задачи, где нужно найти минимум не в линейном пространстве. Например нужно найти минимум некоторой функции на таких векторах
, для которых
, это может быть обусловлено тем, что
обозначают длины каких-либо объектов. Или же например, если
представляют координаты точки, которая должна быть на расстоянии не больше
от
, т. е.
. Для таких задач градиентный спуск или метод Ньютона уже напрямую не применить. Оказалось, что очень большой класс задач оптимизации удобно покрывается «ограничениям», подобными тем, что я описал выше. Иначе говоря, удобно представлять множество
в виде системы равенств и неравенств
Задачи минимизации над пространством вида
таким образом стали условно называть «задачами без ограничений» (unconstrained problem), а задачи над множествами, заданными наборами равенств и неравенств — «задачами с ограничениями» (constrained problem).
Технически, совершенно любое множество
можно представить в виде одного равенства или неравенство с помощью индикатор-функции, которая определяется как
однако такая функция не обладает разными полезными свойствами (выпуклость, дифференцируемость и т. п.). Тем не менее, часто можно представить
в виде нескольких равенств и неравенств, каждое из которых такими свойствами обладает. Основная теория подведена под случай
где
— выпуклые (но не обязательно дифференцируемые) функции,
— матрица. Для демонстрации работы методов я буду использовать два примера:
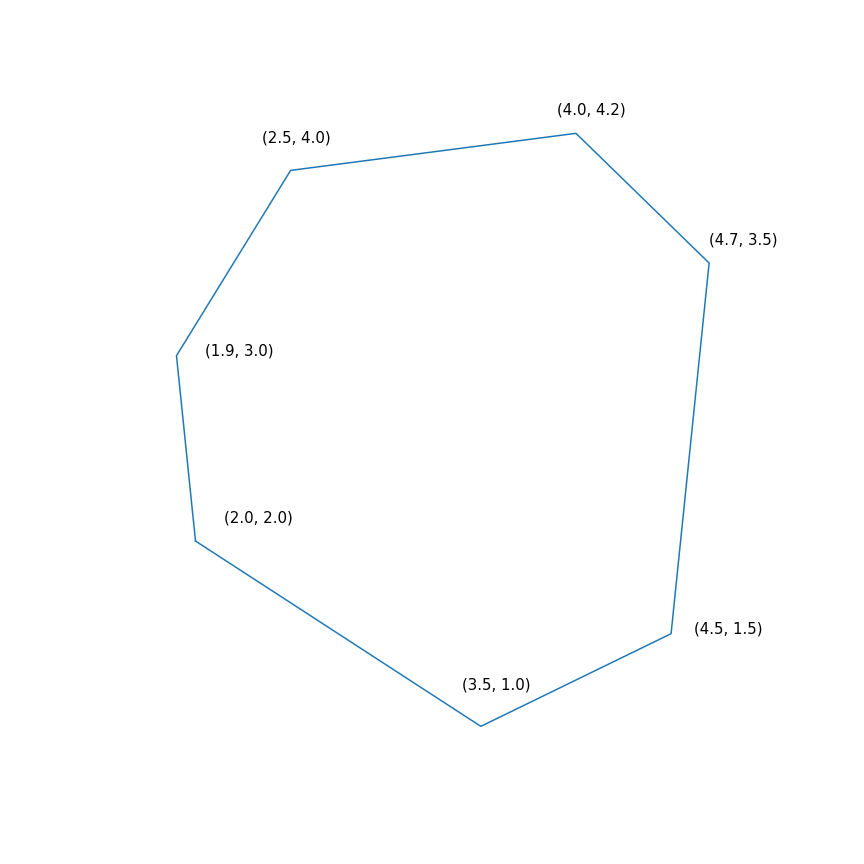
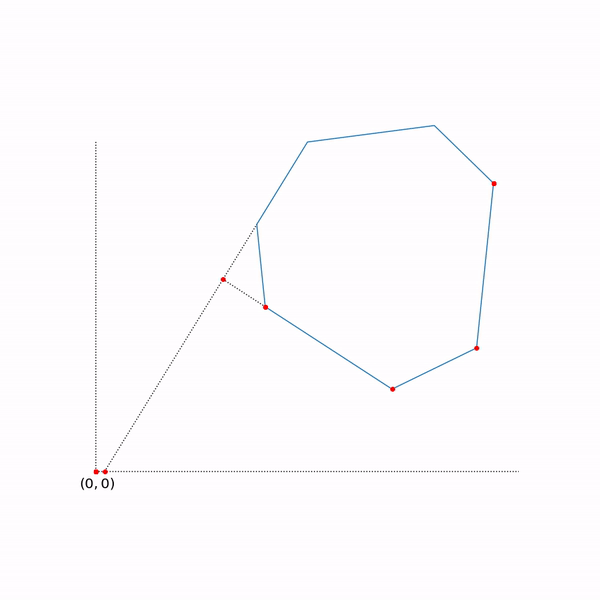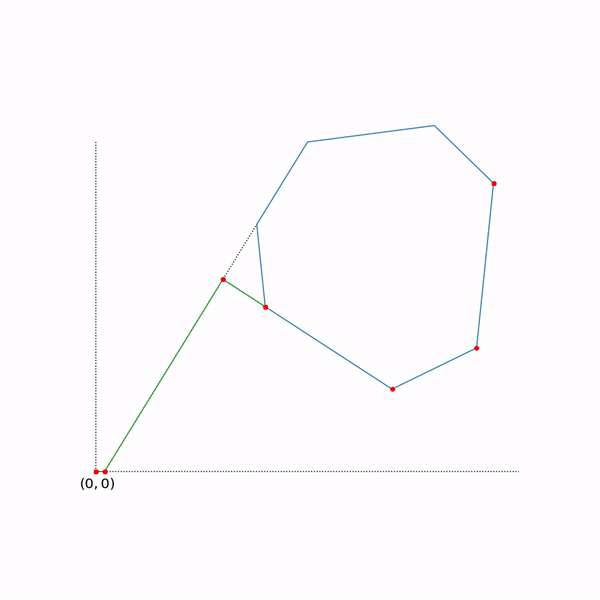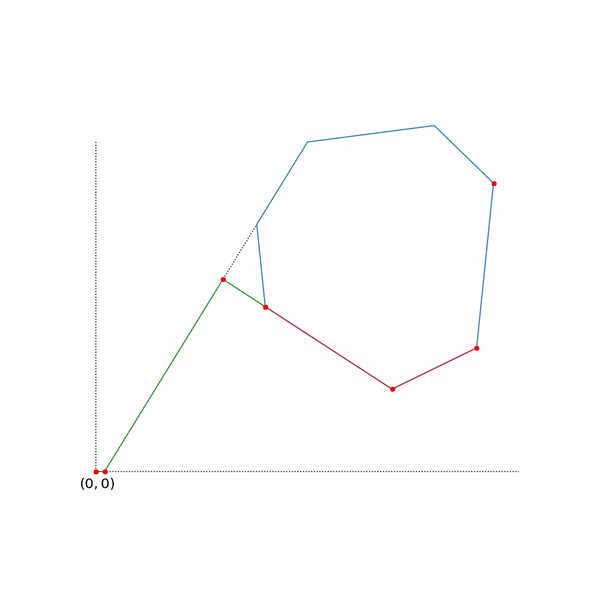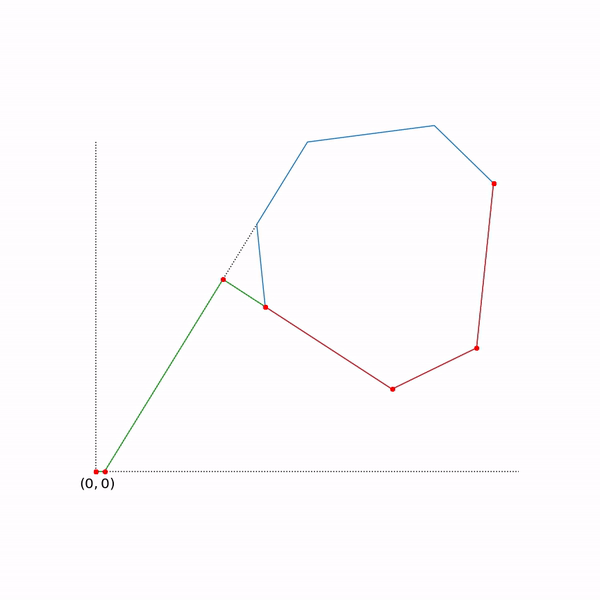
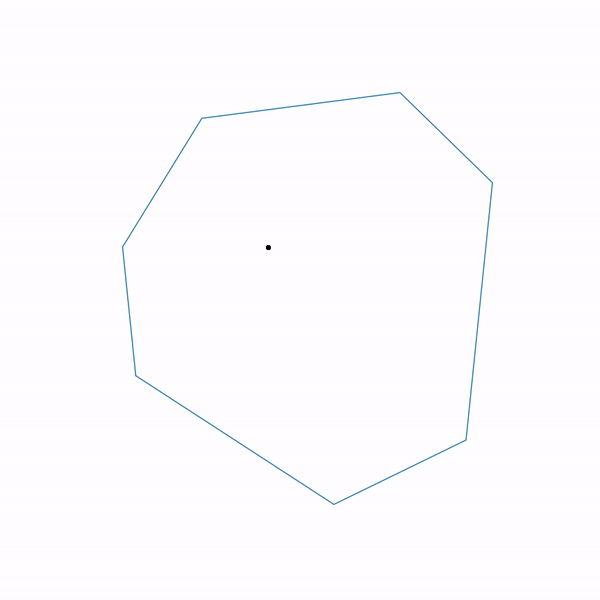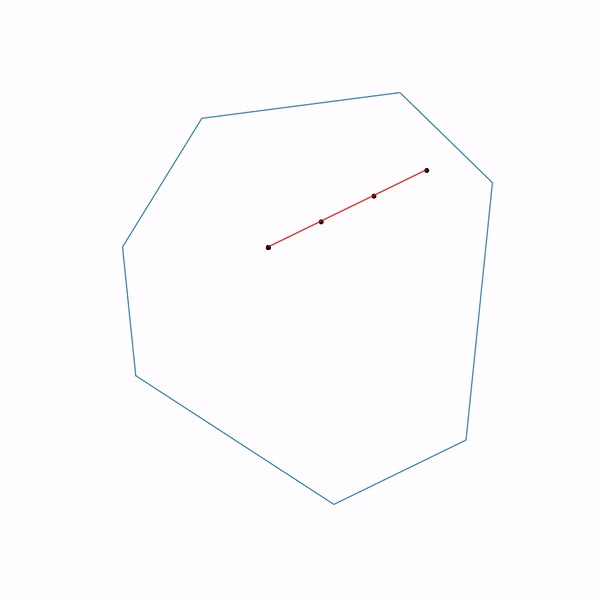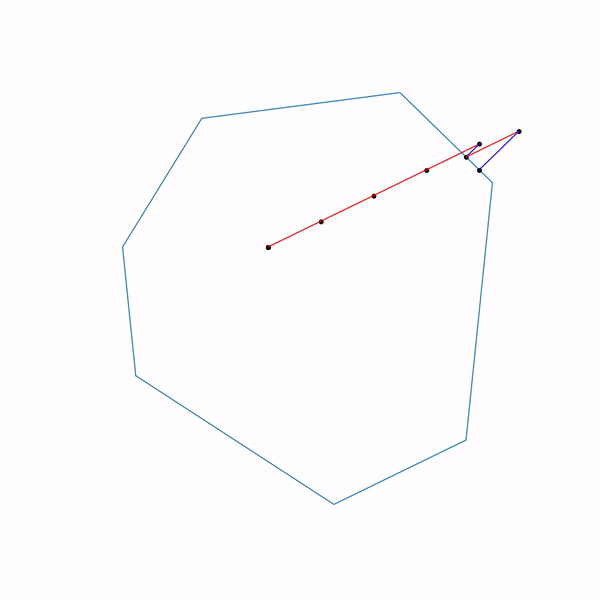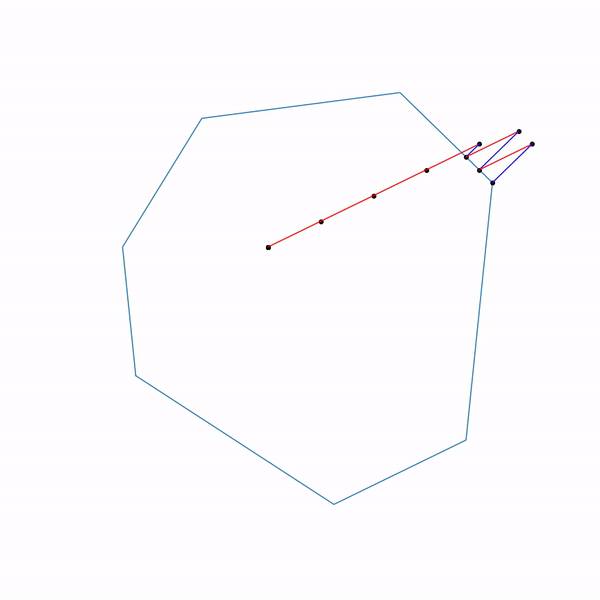
- Задача линейного программирования
По сути эта задача состоит в том, чтобы найти самую дальнюю точку многоугольника в направлении (2, 1), решение задачи — точка (4.7, 3.5) — самая «правая» в многоугольнике). А вот собственно и сам многоугольник
- Минимизация квадратичной функции с одним квадратичным ограничением
Симплекс-метод
Из всех методов, которые я покрываю этим обзором, симплекс-метод наверно является самым известным. Метод был разработан специально для линейного программирования и единственный из представленных достигает точного решения за конечное число шагов (при условии, что для вычислений используется точная арифметика, на практике это обычно не так, но в теории возможно). Идея симплекс-метода состоит из двух частей:
- Системы линейных неравенств и равенств задают многомерные выпуклые многогранники (политопы). В одномерном случае это точка, луч или отрезок, в двумерном — выпуклый многоугольник, в трехмерном — выпуклый многогранник. Минимизация линейной функции — это по сути нахождение самой «дальней» точки в определенном направлении. Думаю, интуиция должна подсказывать, что этой самой дальней точкой должна быть некая вершина, и это действительно так. В общем случае, для системы из
неравенств в
-мерном пространстве вершина — это точка, удовлетворяющая системе, для которой ровно
из этих неравенств обращаются в равенства (при условии, что среди неравенств нет эквивалентных). Таких точек всегда конечное число, хоть их и может быть очень много.
- Теперь у нас есть конечный набор точек, вообще говоря можно их просто взять и перебрать, то есть сделать что-то такое: для каждого подмножества из
неравенств решить систему линейных уравнений, составленных на выбранных неравенствах, проверить, что решение подходит в исходную систему неравенств и сравнить с другими такими точками. Это довольно простой неэффективный, но рабочий метод. Симплекс-метод вместо перебора двигается от вершины к вершине по ребрам таким образом, чтобы значений целевой функции улучшалось. Оказывается, если у вершины нет «соседей», в которых значений функции лучше, то она оптимальна.
Симплекс-метод является итеративным, то есть он последовательно по чуть-чуть улучшает решение. Для таких методов нужно с чего-то начинать, в общем случае это делается с помощью решения вспомогательной задачи
Если для решения этой задачи
такое, что
, то выполняется
, иначе исходная задача вообще задана на пустом множестве. Чтобы решить вспомогательную задачу, можно также использовать симплекс-метод, начальной же точкой можно взять
с произвольным
. Нахождение начальной точки можно условно назвать первой фазой метода, нахождение решение исходной задачи можно условно назвать второй фазой метода.
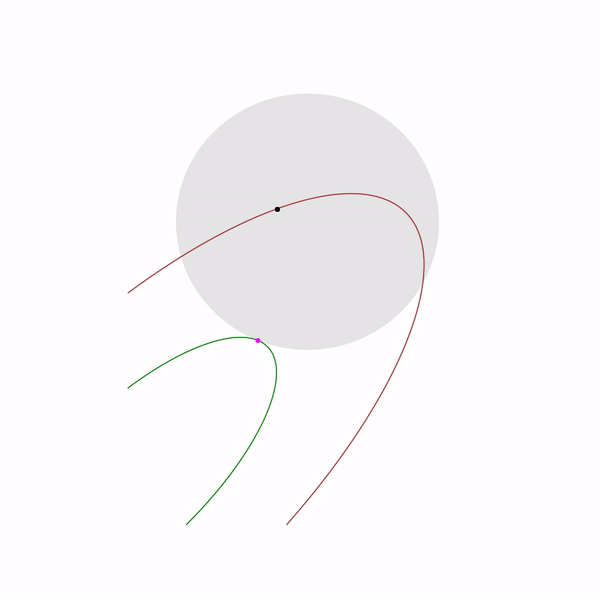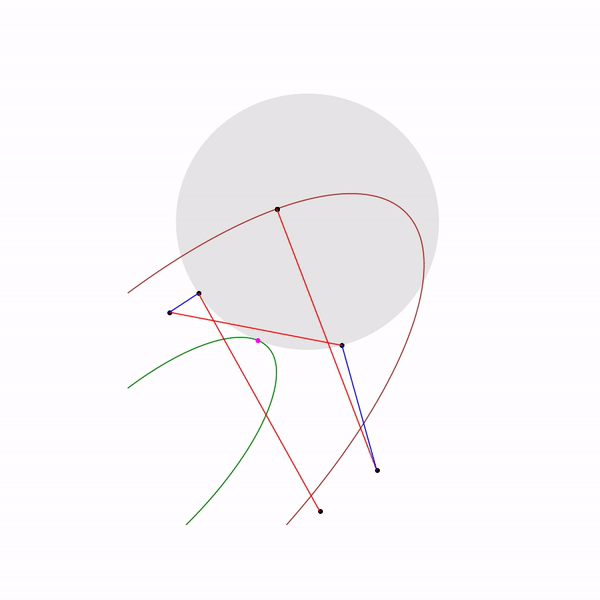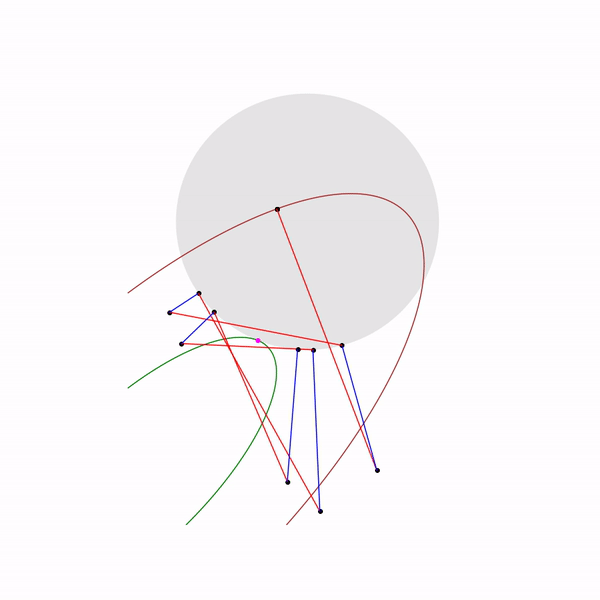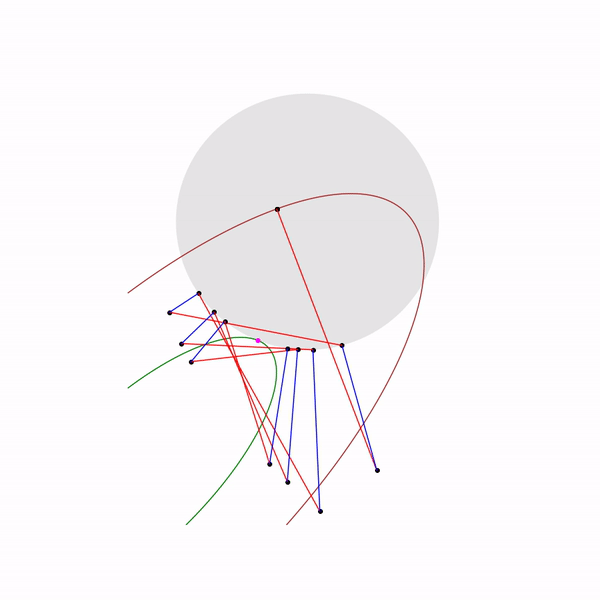
Траектория двухфазового симплекс-метода
Траектория была сгенерирована с помощью scipy.optimize.linprog.
Проективный градиентный спуск
Про градиентный спуск я недавно писал отдельную статью, в которой в том числе кратко описал и этот метод. Сейчас этот метод вполне себе живой, но изучается как часть более общего проксимального градиентного спуска. Сама идея метода совсем банальна: если мы применяем градиентный спуск к выпуклой функции
, то при правильном выборе параметров получаем глобальный минимум
. Если же после каждого шага градиентного спуска корректировать полученную точку, взяв вместо нее её проекцию на замкнутое выпуклое множество
, то в результате мы получим минимум функции
на
. Ну или более формально, проективный градиентный спуск — это алгоритм, который последовательно вычисляет
где
Последнее равенство определяет стандартный оператор проекции на множество, по сути это функция, которая по точке
вычисляет ближайшую к ней точку множества
. Роль расстояния здесь играет
, стоит отметить, что здесь можно использовать любую норму, тем не менее проекции с разными нормами могут отличаться!
На практике проективный градиентный спуск используется только в особых случаях. Основная его проблема состоит в том, что вычисление проекции может быть еще более сложной задачей, чем исходная, а её нужно вычислять много раз. Самый распространенный случай, для которого удобно применять проективный градиентный спуск — это «коробочные ограничения», которые имеют вид
В этом случае проекция вычисляется очень просто, по каждой координате получается
Применение проективного градиентного спуска для задач линейного программирования совершенно бессмысленно, тем не менее если это все-таки сделать, то выглядеть будет как-то так
Траектория проективного градиентного спуска для задачи линейного программирования
А вот как выглядит траектория проективного градиентного спуска для второй задачи, если
выбирать большой размер шага
и если
выбирать небольшой размер шага
Метод эллипсоидов
Этот метод примечателен тем, что является первым полиномиальным алгоритмом для задач линейного программирования, его можно считать многомерным обобщением метода бисекции. Я начну с более общего метода разделяющей гиперплоскости:
- На каждом шаге метода есть некоторое множество, которое содержит решение задачи.
- На каждом шаге строится гиперплоскость, после чего из множества удаляются все точки, лежащие по одну сторону выбранной гиперплоскости, и, возможно, к этому множеству добавятся какие-то новые точки
Для задач оптимизации построение «разделяющей гиперплоскости» основано на следующем неравенстве для выпуклых функций
Если зафиксировать
, то для выпуклой функции
полупространство
содержит только точки со значением не меньше, чем в точке
, а значит их можно отсечь, так как эти точки не лучше, чем та, что мы уже нашли. Для задач с ограничениями можно аналогичным образом избавиться от точек, которые гарантированно нарушают какое-то из ограничений.
Самый простой вариант метода разделяющей гиперплоскости — это просто отсекать полупространства без добавления каких-либо точек. В результате на каждом шаге у нас будет некий многогранник. Проблема этого метода в том, что количество граней многогранника скорее всего будет возрастать от шага к шагу. Более того, оно может расти экспоненциально.
Метод эллипсоидов собственно на каждом шаге хранит эллипсоид. Точнее, после проведения гиперплоскости строится эллипсоид минимального объема, который содержит одну из частей исходного. Этого получается добиться за счет добавления новых точек. Эллипсоид всегда можно задать положительно определенной матрицей и вектором (центром эллипсоида) следующим образом
Построение минимального по объему эллипсоида, содержащего пересечение полупространства и другого эллипсоида, можно осуществить с помощью в меру громоздких формул. К сожалению на практике этот метод оказался все еще на так хорош, как симплекс-метод или метод внутренней точки.
А вот собственно как он работает для
линейного программирования
и для
квадратичного программирования
Метод внутренней точки
Этот метод имеет долгую историю развития, одни из первых предпосылок появились примерно в то же время, когда был разработан симплекс-метод. Но в то время он был еще недостаточно эффективен, чтобы использоваться на практике. Позднее в 1984 был разработан вариант метода специально для линейного программирования, который был хорош как в теории, так и на практике. Более того, метод внутренней точки не ограничен только линейным программированием в отличие от симплекс-метода, и сейчас он является основным алгоритмом для задач выпуклой оптимизации с ограничениями.
Базовая идея метода — замена ограничений на штраф в виде так называемой барьерной функции. Функция
называется барьерной функцией для множества
, если
Здесь
— внутренность
,
— граница
. Вместо исходной задачи предлагается решать задачу
и
заданы только на внутренности
(по сути отсюда и название), свойство барьера гарантирует, что у
минимум по
существует. Более того, чем больше
, тем больше влияние
. При достаточно разумных условиях можно добиться того, что если устремить
к бесконечности, то минимум
будет сходиться к решению исходной задачи.
Если множество
задано в виде набора неравенств
, то стандартным выбором барьерной функции является логарифмический барьер
Точки минимума
функции
для разных
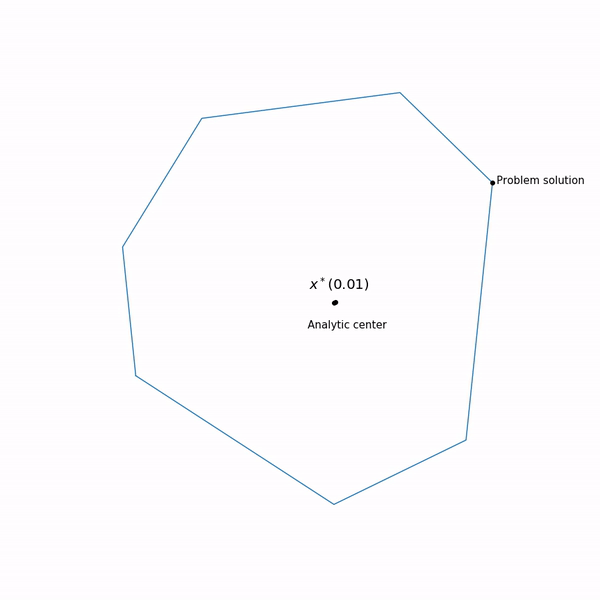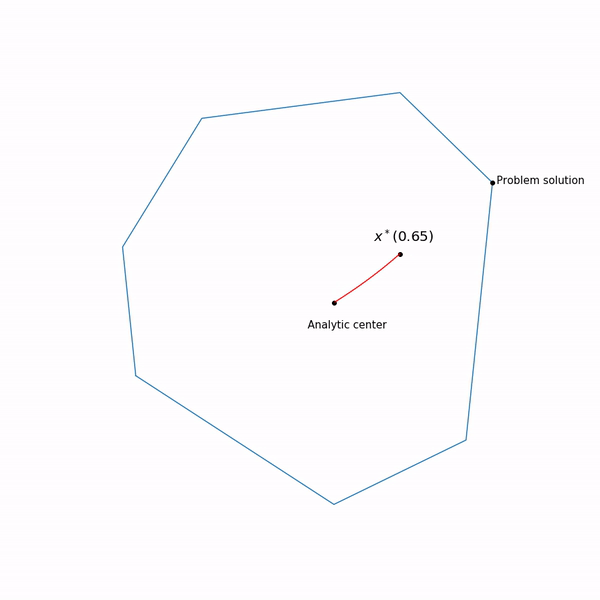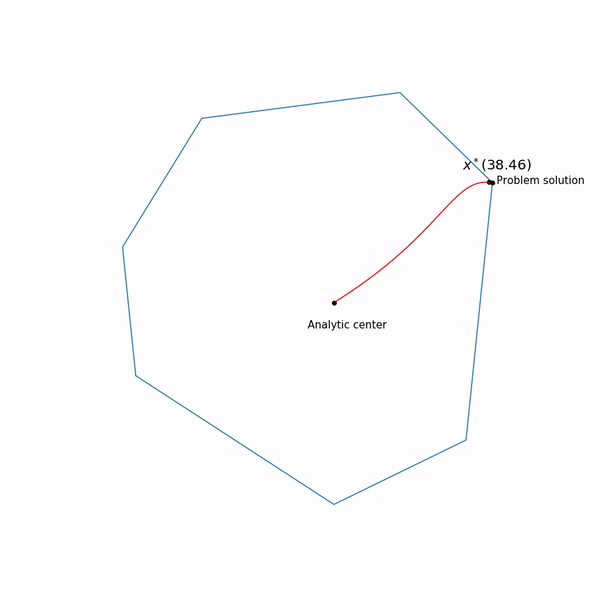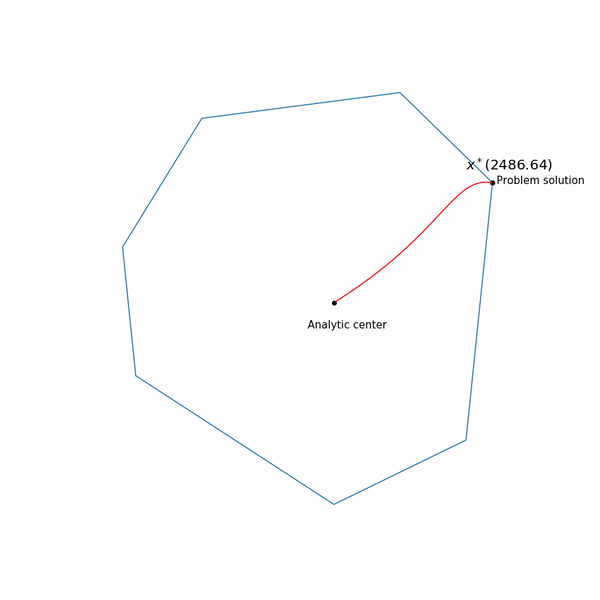
образует кривую, которую обычно называют центральный путь, метод внутренний точки как бы пытается следовать этому пути. Вот так он выглядит для
Примера с линейным программированием
Аналитический центр — это просто
Наконец сам метод внутренней точки имеет следующий вид
- Выбрать начальное приближение
,
- Выбрать новое приближение методом Ньютона
- Увеличить
Использование метода Ньютона здесь очень важно: дело в том, что при правильном выборе барьерной функции шаг метода Ньютона генерирует точку,
которая остается внутри нашего множества
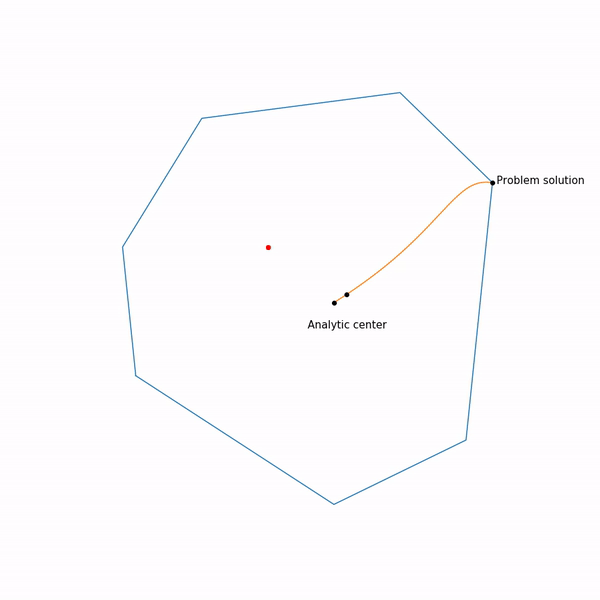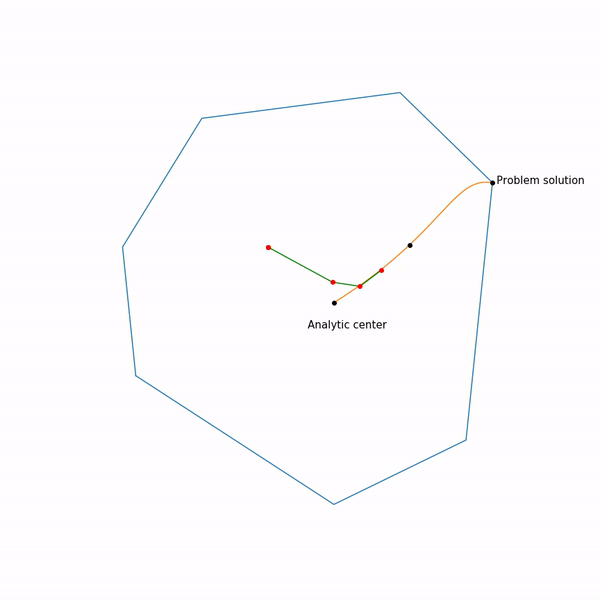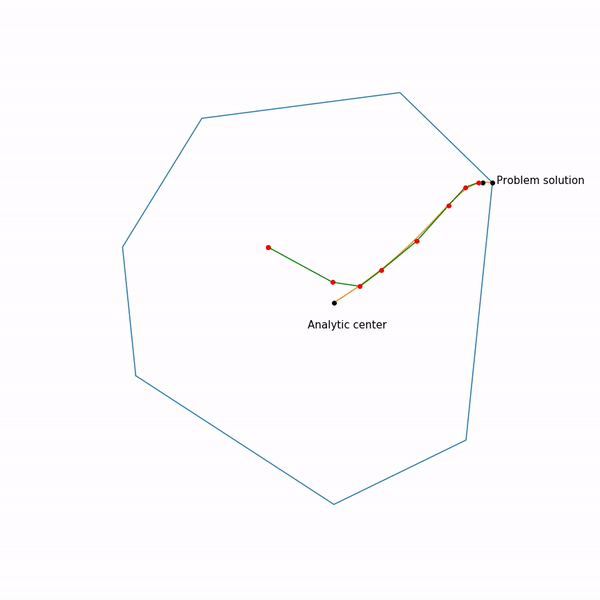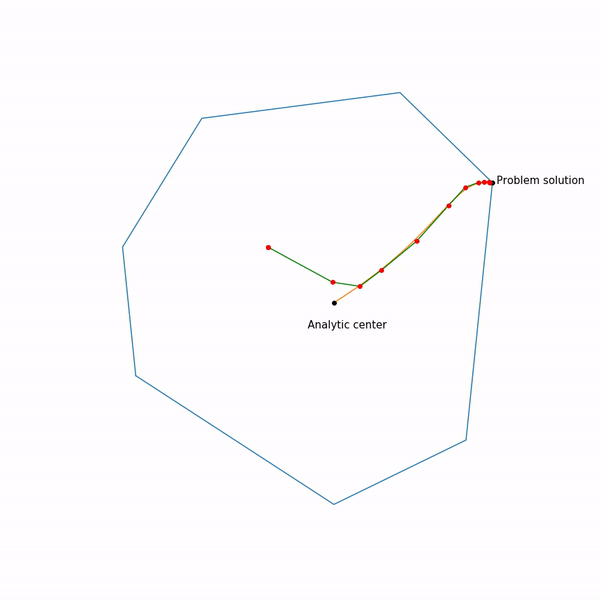
, поэкспериментировали, в таком виде не всегда выдает. Ну и наконец, так выглядит траектория метода внутренней точки
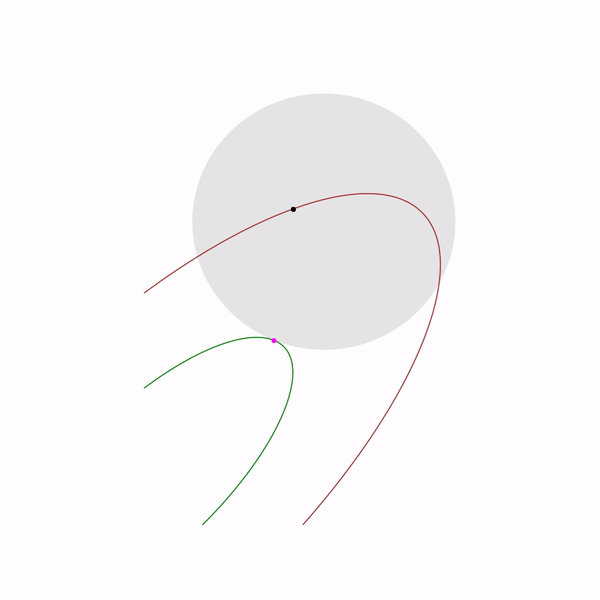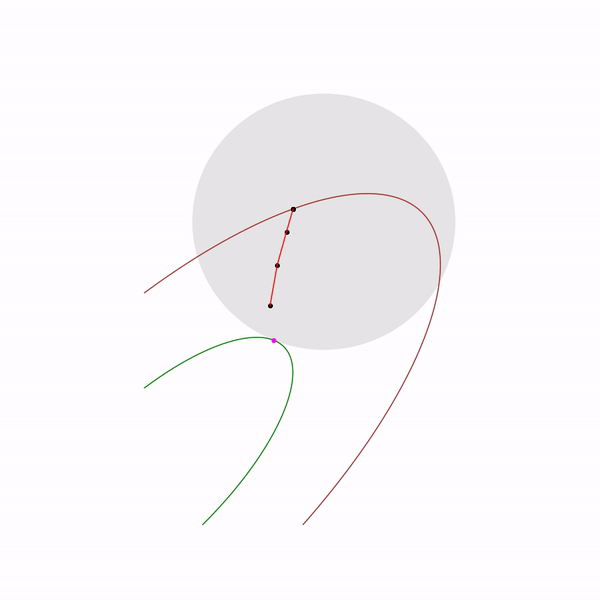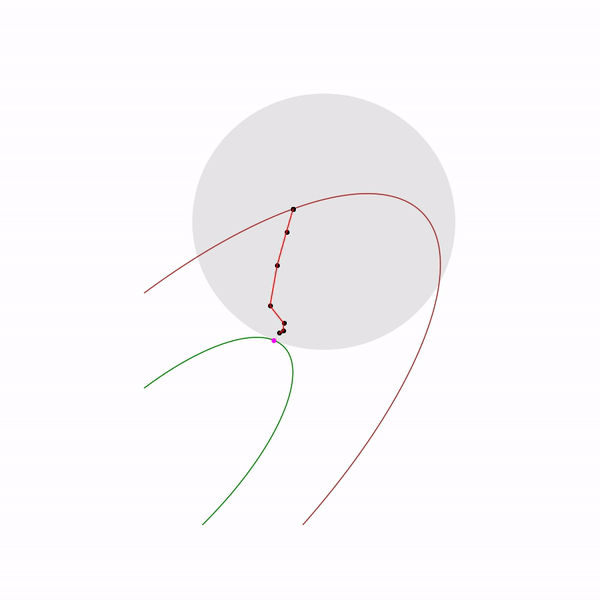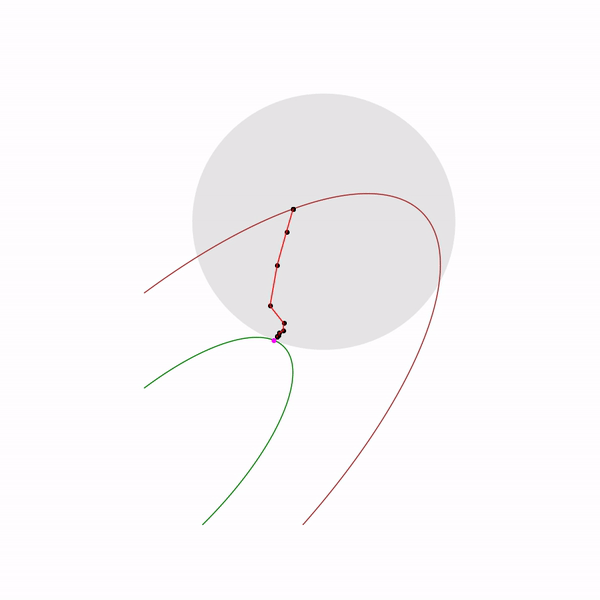
Задача линейного программирования
Прыгающая черная точка — это
, т.е. точка, к которой мы пытаемся приблизиться шагом метода Ньютона на текущем шаге.
Задача квадратичного программирования
5.h=−h/4. В точке x1 функция оказалась большей, чем в x0, следовательно, мы перешагнули точку минимума и организуем спуск в обратном направлении.
6.Если h >ε / 4 , тогда повторить с п.2, иначе перейти к п.7.
7.xm = x0, fm = f0 , конец.
Скорость сходимости данного метода существенно зависит от удачного выбора начального приближения x0 и шага h. Шаг h следует выбирать как половину оценки расстояния от x0 до предполагаемого минимума xm.
Метод квадратичной параболы
Для ускорения спуска к минимуму из некоторой точки x0 используют локальные свойства функции вблизи этой точки. Так, скорость и направление убывания можно определить по величине и знаку первой производной. Вторая производная характеризует направление выпуклости: если f”>0, то функция имеет выпуклость вниз, иначе – вверх. Вблизи локального безусловного минимума дважды дифференцируемая функция всегда выпукла вниз. Поэтому, если вблизи точки минимума функцию аппроксимировать квадратичной параболой, то она будет иметь минимум. Это свойство и используется в методе квадратичной параболы, суть которого в следующем.
Вблизи точки x0 выбираются три точки x1, x2, x3. Вычисляются значения y1, y2, y3. Через эти точки проводится квадратичная парабола
|
p(x − x )2 |
+ q(x − x ) + r = pz2 + qz + r, |
||||||||||||||||||||
|
3 |
3 |
||||||||||||||||||||
|
z = x − x3, |
z1 = x1 − x3, |
z2 = x2 − x3, |
r = y3, |
(2.1) |
|||||||||||||||||
|
( y − y |
3 |
)z |
2 |
−( y |
2 |
− y |
3 |
)z |
( y − y |
3 |
)z2 |
−( y |
2 |
− y |
3 |
)z2 |
|||||
|
p = |
1 |
1 |
, q = |
1 |
2 |
1 |
. |
||||||||||||||
|
z1z2 (z1 − z2 ) |
z1z2 (z2 − z1) |
||||||||||||||||||||
Если p>0, то парабола имеет минимум в точке zm = −q /(2 p).. Следова-
тельно, можно аппроксимировать положение минимума функции значением xm1 = x3 + zm и, если точность не достигнута, следующий спуск производить,
используя эту новую точку и две предыдущие. Получается последовательность xm1, xm2 , xm3, … , сходящаяся к точке xm.
Алгоритм метода можно записать следующим образом
Задается x0, h и ε.
1.Выбираем 3 точки: x1 = x0 − h, x2 = x0, x3 = x0 + h ,
|
2. |
Вычисляем y1 = f (x1), y2 = f (x2 ), y3 = f (x3) . |
|
3. |
Проверяем положительность знака второй производной: |
h2 f ′′ y1 − 2 y2 + y3 > 0 , если да, то переходим к п.4,
иначе начальное приближение x0 выбрано неудачно (в x0 имеется выпуклость вверх) и следует закончить вычисления с таким сообщением.
4.Вычисляем z1, z2, p, q, r, zm по вышеприведенным формулам (2.1).
5.Переименовываем точки, отбрасывая точку x1:
x1=x2, y1=y2, x2=x3, y2=y3, x3=x3+zm, y3=f(x3).
Начало: Математика для чайников. Глава 1. Что такое математическая абстракция.
Предыдущая глава: Математика для чайников. Глава 17. Численные методы
В прошлой главе мы говорили о численных методах. Тогда я вскользь упомянул, что эти методы можно применять в задачах математической оптимизации. А сегодня мы рассмотрим методы оптимизации более подробно. Для начала, давайте разберемся, а что вообще такое оптимизация? Часто некоторые деятели (всякие там «эффективные» менеджеры) занимаются имитацией бурной деятельности, а потом гордо говорят, что они что-то там «оптимизируют». Но если рассмотреть оптимизацию с точки зрения математики, то таких «деятелей» легко вывести на чистую воду. Потому что в математике есть строгое, четкое и однозначное определение оптимизации.
И так, оптимизация – это нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств. И это касается любой оптимизации. Так что если кто-то гордо говорит, что он занимается «оптимизацией», но его действия не подходят под это определение, он нагло врет.
Рассмотрим определение оптимизации на конкретном примере. Допустим, некий «эффективный менеджер» занимается оптимизацией производственных затрат. Что это значит? Это значит, что он минимизирует функцию затрат. Почему затраты – это функция? Потому что она зависит от различных факторов, которые можно выразить числами. Более того, производственные затраты можно вычислить: сложить затраты на покупку материалов, на зарплату рабочих, на электричество и другие затраты. Но, надо понимать, что зависимость является функцией только в том случае, если эта зависимость однозначная. То есть, если при одних и тех же параметрах: количество и ценах закупленных материалов, суммы косвенных затрат и так далее результат одинаков.
Но тут возникает очень интересный нюанс. Лучший способ минимизировать затраты – вообще остановить производство, всех уволить и закрыть предприятие. Тогда затраты будут нулевые, то есть, самые минимальные, что и требовалось по условиям задачи, что вряд ли устроит собственника. Как можно выйти из этой ситуации? Очень просто. Добавить в условия задачи ограничение: прибыль (или доход) не должна уменьшиться меньше, чем определенное значение. Хотя… можно вообще поставить задачу по-другому: максимизировать прибыль.
В вышеописанной задачи могут быть и другие ограничения, например, производственные мощности и емкость рынка сбыта: невозможно произвести и продать бесконечное количество продукции.
А теперь давайте подумаем, а как «эффективный менеджер» будет выполнять поставленную задачу по оптимизации. У него должны быть полномочия что-то менять, например, увеличить выпуск одного вида продукции и уменьшить выпуск другого. От его решения зависит оптимизируемая величина (целевая функция). А вот параметры, которые он волен менять и от которых зависит целевая функция называются параметры оптимизации.
А теперь разберем математическую формулировку задачи оптимизации. Как правило, она выглядит так:
Здесь f – целевая функция, x со стрелочкой – это вектор (набор из нескольких чисел). Иначе можно записать:
где n – количество параметров оптимизации. Здесь мы поставили цель минимизации целевой функции. Чаще всего именно такая цель и ставиться при оптимизации. Если надо функцию максимизировать, мы можем просто взять ее со знаком минус, иным словами:
Это то же самое, что:
Тоже касается и неравенств, чтобы заменить «меньше или равно» на «больше или равно» нам надо перед функцией в правой части поставить знак минус. Почему я обращаю на это внимание? Потому что зачастую разные алгоритмы оптимизации предполагают именно минимизацию, или именно условия «больше или равно». А реально может быть по-разному. Но, зная этот лайфхак, можно легко преобразовать формулы.
Теперь поговорим о том, как решают задачи оптимизации. Если у нас задача задана аналитически в виде формулы, и ограничения не заданы, то мы можем просто найти точки перегиба функции методом производной. Например:
Определим ее производную:
Если забыли, что такое производная, то можете заглянуть сюда:
· Математика для чайников. Глава 9. Основы матанализа | Александр Шуравин. | Яндекс Дзен (yandex.ru)
· Математика для чайников. Глава 11. Почему делить на нуль нельзя или кое-что о пределах. | Александр Шуравин. | Яндекс Дзен (yandex.ru)
· Математика для чайников. Глава 14. Производная | Александр Шуравин. | Яндекс Дзен (yandex.ru)
Идем дальше. Решаем уравнение:
Проверим, построив график функции:
Как видим, без условий все просто. А если добавить условия? Только не говорите что тоже просто, тут есть хитрый подвох. Нельзя, например, просто так взять и исключить из рассмотрения точки перегиба, которые не удовлетворяют условиям. Давайте проверим.
Пусть у нас задача оптимизации поставлена вот так:
Наша единственная точка перегиба вылетает. И… означает ли это, что задача не имеет решения? Вовсе нет. Просто в этом случае минимум будет в точке x=1. Действительно, слева от этой точки – запретная зона, а справа функция идет вверх. У нас только одна эта точка (x=1) и остается.
Но тут мы просто догадались. Правда, в математике нет такого метода решения, как «догадались». Как мы будем действовать в общем случае? В этом случае нужно свести задачу к задаче безусловной оптимизации. Например, можно использовать метод штрафных функций. Под штрафной функцией понимают некоторое слагаемое, которое прибавляется к целевой функции:
Важно, чтобы с этим слагаемым целевая функция имела те же самые экстремумы.
В общем, идея состоит в том, что мы ограничения заменяем штрафной функцией. В данном случае мы можем применить вот такую штрафную функцию:
Ее производная определена только на участке x>1 и равна нулю. Таким образом, нам надо рассмотреть точку x=1 и корни уравнения:
При x>1
Но при заданных условиях корней нет. У нас остается только точка x=1. Докажем, что
При x>1.
Пусть:
Тогда
Вычалим f(1):
Таким образом:
Что и требовалось доказать.
Итак, мы узнали, что такое оптимизация, как задачу оптимизации сформулировать строго математически и как вывести на чистую воду «эффективных» менеджеров, занимающихся имитацией бурной деятельности, прикрываясь громким словом «оптимизация». Еще мы разобрали конкретный пример решения задачи оптимизации.
Теперь поговорим об оптимизации в более широком смысле. В самом общем случае, под оптимизацией понимается нахождение наилучшего решения. Таким образом, оптимизационные задачи приходиться решать в самых разных областях человеческой деятельности. Но все они, так или иначе, сводятся к математике. Почему? Потому что для решения любой оптимизационной задачи необходимо построить математическую модель исследуемого объекта и провести вычислительный эксперимент. Иначе никак.
Основу вычислительного эксперимента при решении оптимизационной задачи составляет триада «модель-алгоритм-программа». Иными словами, оптимизационная задача решается, главным образом, на компьютере, именно поэтому материал данной статьи очень важен для будущих айтишников.
В общем случае задача оптимизации решается в три этапа. На первом этапе строиться математическая модель исследуемого объекта, которая отражает самые важные свойства объекта (в математической форме, естественно). Второй этап – разрабатывается алгоритм для обсчета этой модели на компьютере. Таким образом, модель должна быть представлена в такой форме, чтобы было удобно применять численные методы (см. Математика для чайников. Глава 17. Численные методы | Александр Шуравин. | Дзен (dzen.ru)). Ну и третий этап – на основании разработанных алгоритмов написать компьютерную программу, которая и произведет необходимые вычисления.
Существует даже целая научная дисциплина о том, как решать оптимизационные задачи. И называется эта дисциплина теория оптимизации. Ценность теории оптимизации состоит в том, что она универсальная по отношению к различным задачам, в частности:
– в математической экономике;
– в IT-науках: оптимальное управление, робототехника, машинное обучение;
– в технике: оптимальное планирование информационных и компьютерных сетей, оптимальная структура технических систем;
– в численном анализе: аппроксимация, регрессия, решение линейных и нелинейных систем управления и т. д.
Теория оптимизация, как вы поняли, изучает задачи оптимизации и как их решать. А с чего начать изучения задач оптимизации? Разумеется, с их классификации. Почему? Если мы знаем, к какому классу отнести наша задачу, то мы можем применить к ней тот метод решения, который применяется для задач данного класса.
Задачи оптимизации классифицируются по:
– типу параметров оптимизации (непрерывные, дискретные и целочисленные);
– по размерности (одномерные и многомерные, иногда отдельно выделают двумерные). Под мерностью понимают количество неизвестных, например, если неизвестное одно, чаще всего оно обозначается как x – то это одномерная задача, если неизвестных две (например, x и y), то двумерная, если это многомерная задача. В многомерной задаче неизвестные принято обозначать x1,x2,…xn;
– по наличию ограничений (безусловная оптимизация, где ограничений нет и условная, где они есть);
– по характеру значений задачи оптимизации подразделяются на детерминированные, где все значения строго определены и на стохастические, где есть случайные величины;
– по виду целевой функции и ограничений задачи оптимизации делятся на линейные и нелинейные.
И так, подытожим. Если нам надо что-то оптимизировать, мы строит математическую модель, формулируем задачу оптимизации, и решаем ее. Для того, чтобы решить, мы определяем, к какому классу задач относится эта задача и берет метод, предназначенный для решения именно этого класса задач. О самих методах я расскажу в будущих статьях, ибо впихнуть все это в одну статью нереально, так как там «много букв (и цифр, и формул)».