Можно сделать так:
from sympy import solveset, symbols, Interval, Min, Max
x = symbols('x')
lower_bound = -5
upper_bound = 5
f = x**2
zeros = solveset(f, x, domain=Interval(lower_bound, upper_bound))
assert zeros.is_FiniteSet # If there are infinite solutions the next line will hang.
res_min = Min(f.subs(x, lower_bound), f.subs(x, upper_bound), *[f.subs(x, i) for i in zeros])
res_max = Max(f.subs(x, lower_bound), f.subs(x, upper_bound), *[f.subs(x, i) for i in zeros])
Результат:
In [29]: res_min
Out[29]: 0
In [30]: res_max
Out[30]: 25
PS в следующей версии SymPy должны добавить функции sympy.calculus.util.minimum() и sympy.calculus.util.maximum():
from sympy.calculus.util import minimum, maximum
interv = Interval(-5, 5)
res_min = minimum(f, interv)
res_max = maximum(f, interv)
Источник (с) @smichr
Updated: How do I find the minimum of a function on a closed interval [0,3.5] in Python? So far I found the max and min but am unsure how to filter out the minimum from here.
import sympy as sp
x = sp.symbols('x')
f = (x**3 / 3) - (2 * x**2) + (3 * x) + 1
fprime = f.diff(x)
all_solutions = [(xx, f.subs(x, xx)) for xx in sp.solve(fprime, x)]
print (all_solutions)
JohanC
70.1k8 gold badges32 silver badges64 bronze badges
asked Aug 28, 2016 at 15:05
2
Since this PR you should be able to do the following:
from sympy.calculus.util import *
f = (x**3 / 3) - (2 * x**2) - 3 * x + 1
ivl = Interval(0,3)
print(minimum(f, x, ivl))
print(maximum(f, x, ivl))
print(stationary_points(f, x, ivl))
answered Oct 25, 2019 at 19:55
smichrsmichr
16.2k2 gold badges23 silver badges33 bronze badges
2
Perhaps something like this
from sympy import solveset, symbols, Interval, Min
x = symbols('x')
lower_bound = 0
upper_bound = 3.5
function = (x**3/3) - (2*x**2) - 3*x + 1
zeros = solveset(function, x, domain=Interval(lower_bound, upper_bound))
assert zeros.is_FiniteSet # If there are infinite solutions the next line will hang.
ans = Min(function.subs(x, lower_bound), function.subs(x, upper_bound), *[function.subs(x, i) for i in zeros])
answered Aug 30, 2016 at 19:22
asmeurerasmeurer
85.7k26 gold badges167 silver badges240 bronze badges
2
Here’s a possible solution using sympy:
import sympy as sp
x = sp.Symbol('x', real=True)
f = (x**3 / 3) - (2 * x**2) - 3 * x + 1
#f = 3 * x**4 - 4 * x**3 - 12 * x**2 + 3
fprime = f.diff(x)
all_solutions = [(xx, f.subs(x, xx)) for xx in sp.solve(fprime, x)]
interval = [0, 3.5]
interval_solutions = filter(
lambda x: x[0] >= interval[0] and x[0] <= interval[1], all_solutions)
print(all_solutions)
print(interval_solutions)
all_solutions is giving you all points where the first derivative is zero, interval_solutions is constraining those solutions to a closed interval. This should give you some good clues to find minimums and maximums 🙂
answered Aug 28, 2016 at 15:14
BPLBPL
10.4k8 gold badges57 silver badges115 bronze badges
4
The f.subs commands show two ways of displaying the value of the given function at x=3.5, the first as a rational approximation, the second as the exact fraction.
answered Aug 28, 2016 at 17:13
Bill BellBill Bell
20.9k5 gold badges42 silver badges58 bronze badges
Домашнее задание №1#
В рамках первого домашнего задания от вас требуется:
-
Установить
python; -
Установить среду разработки на вкус;
-
Реализовать один из численных методов описанных ниже.
Метод и функция, для которой его необходимо применить в обязательном порядке, определяются вариантом, которые перечисленны ниже.
Варианты#
|
Вариант № |
Метод |
(f(x)) |
|---|---|---|
|
1 |
Бисекции |
(ln x – dfrac{1}{x}) |
|
2 |
Хорд |
(e^x + x) |
|
3 |
Ньютона |
(dfrac{1}{x} – 2x) |
|
4 |
Золотого сечения |
(log (lvert x rvert+1)) |
|
5 |
Градиентного спуска |
(tanh x + x^2) |
|
6 |
Бисекции |
(log x + 1) |
|
7 |
Хорд |
(arctan x – dfrac{1}{2}) |
|
8 |
Ньютона |
(e^x – dfrac{1}{2}) |
|
9 |
Золотого сечения |
(lvert x-1rvert + x^2) |
|
10 |
Градиентного спуска |
(x^2 + 2x – 3) |
|
11 |
Бисекции |
(tan 2x – 1 – x) |
|
12 |
Хорд |
(2e^{-x} – x) |
|
13 |
Ньютона |
(e^{-3x^2} – x) |
|
14 |
Золотого сечения |
(e^{lvert x-1rvert} – x^2) |
|
15 |
Градиентного спуска |
(cosh x + x) |
|
16 |
Бисекции |
(e^{-3x} + 1 – x) |
|
17 |
Хорд |
(e^{-x^2} – x) |
|
18 |
Ньютона |
(e^{-x^2} – x^2) |
|
19 |
Золотого сечения |
(e^{-x^2}) |
|
20 |
Градиентного спуска |
(arctan x + x^2) |
|
21 |
Бисекции |
(3e^{-3x} – x) |
|
22 |
Хорд |
(e^{-x^3} – 1 – x^3) |
|
23 |
Ньютона |
(2e^{-3x} + 1 – x) |
|
24 |
Золотого сечения |
(sinh(lvert xrvert+1) – x^2) |
|
25 |
Градиентного спуска |
(-arctan e^{-x^2}) |
Численные методы поиска минимума или корня скалярной функции#
В рамках первого домашнего задания от вас потребуется реализовать численный метод поиска корня уравнения вида
(1)#[f(x) = 0,]
или численный метод поиска минимума скалярной функции (f):
(2)#[f(x) sim min_{x in X}.]
В обоих случаях (f) — скалярная функция одного аргумента, т.е. (fcolon mathbb{R} to mathbb{R}).
Это задание нацелено в первую очередь на освоение синтаксиса языка python, поэтому ниже приводится подробное описание алгоритмов работы каждого метода, а вам предлагается реализовать один из них средствами python. К вашему решению предъявляются следующие требования:
-
Решение должно быть оформлено в виде скрипта
python(файл с расширением “.py”, а не блокнотjupyter)! -
Ввод параметров должен осуществляться пользователем средствами стандартного потока ввода.
-
Численный метод должен быть оформлен в виде отдельной процедуры (
pythonфункции). -
Введенные пользователем данные должны передаваться процедуре численного метода в качестве аргументов.
-
Процедура численного метода должна возвращать найденный корень или минимум, если алгоритм сошелся, и значение
None, если алгоритм не применим или разошелся. -
Реализованный метод должен печатать отладочную информацию в стандартный поток вывода.
-
Реализованный метод поиска корня должен быть протестирован на каких-то простых примерах.
Tip
Ваш численный метод так или иначе должен будет вызывать функцию (f) и/или (f’) внутри себя на каждой итерации, чтобы двигаться в сторону корня или минимума.
Самый простой способ этого добиться — определить функцию (f(x)) (и/или (f'(x))) глобально и тогда на неё можно будет ссылаться внутри вашего метода. Хотя такое решение и будет приниматься преподавателем, оно не является идеальным: такая реализация ищет корень одной конкретной функции (f(x)), а для того, чтобы найти корень любой другой функции, придется модифицировать исходный код.
Более гибкое решение подразумевает передачу искомой функции (f(x)) (и/или (f'(x))) в качестве аргумента в метод поиска корня. В python функции можно передавать в качестве аргументов другим функциям точно также, как и любые другие переменные (иными словами функции в python — объекты первого класса).
Метод бисекции#
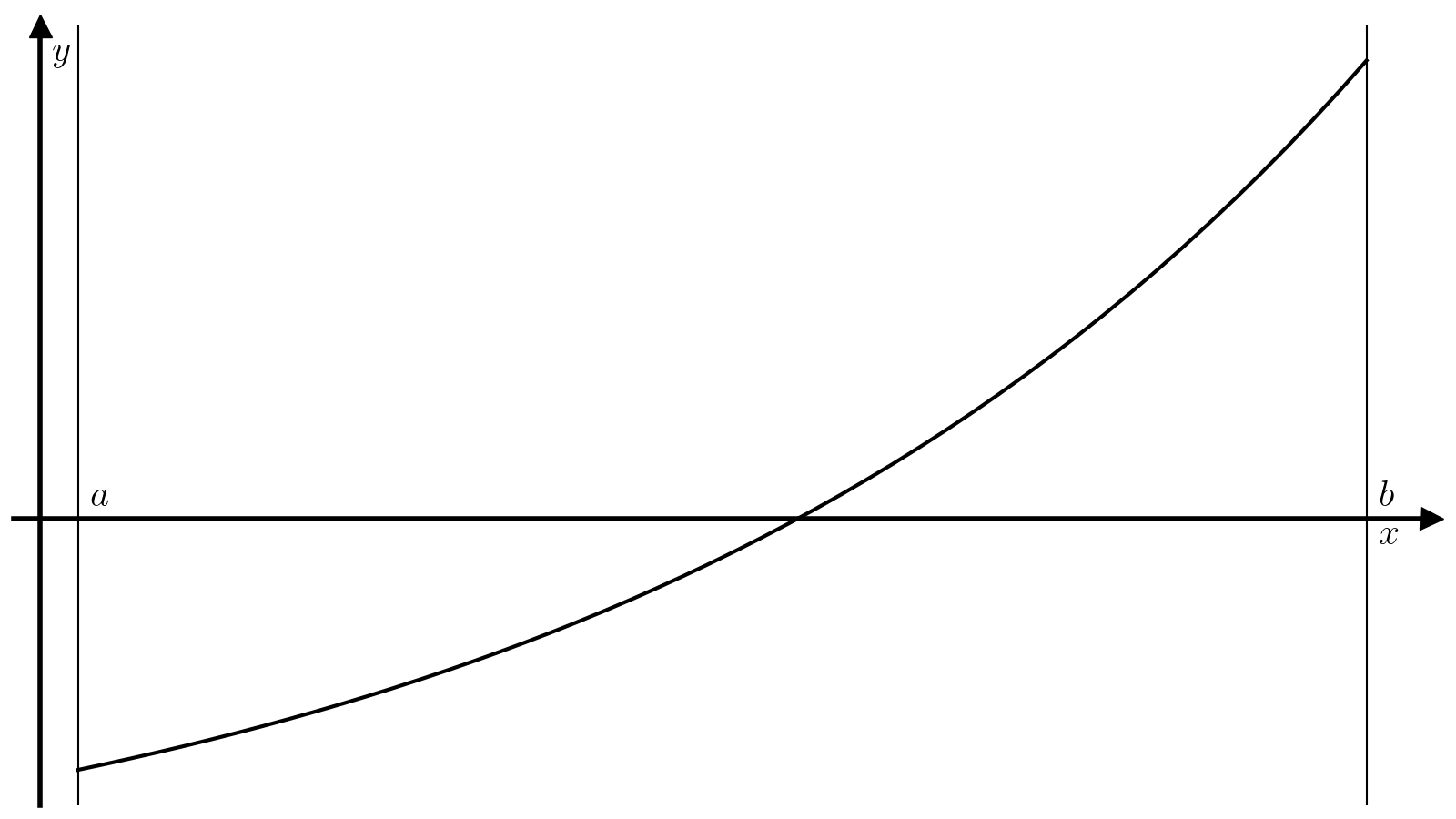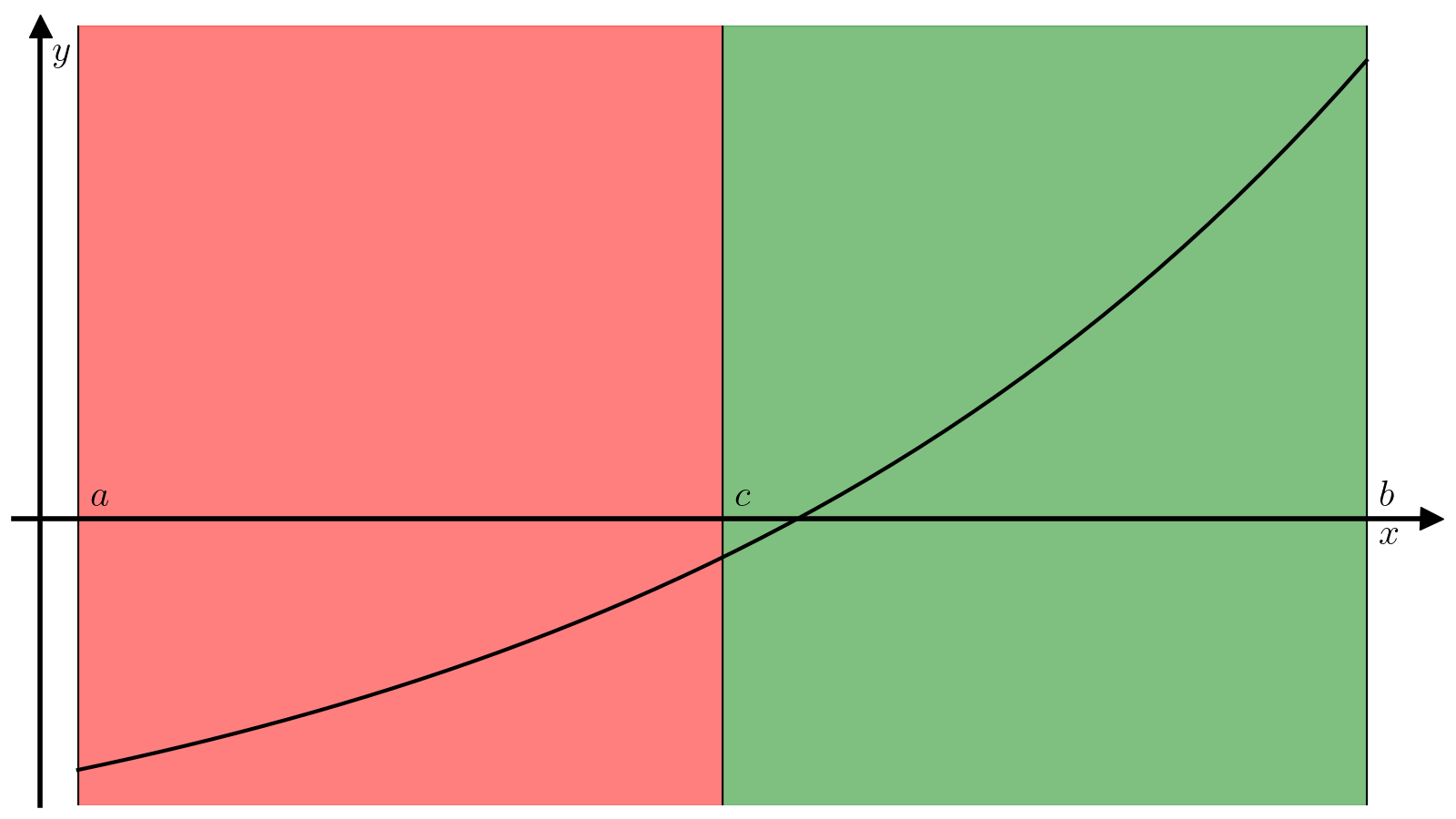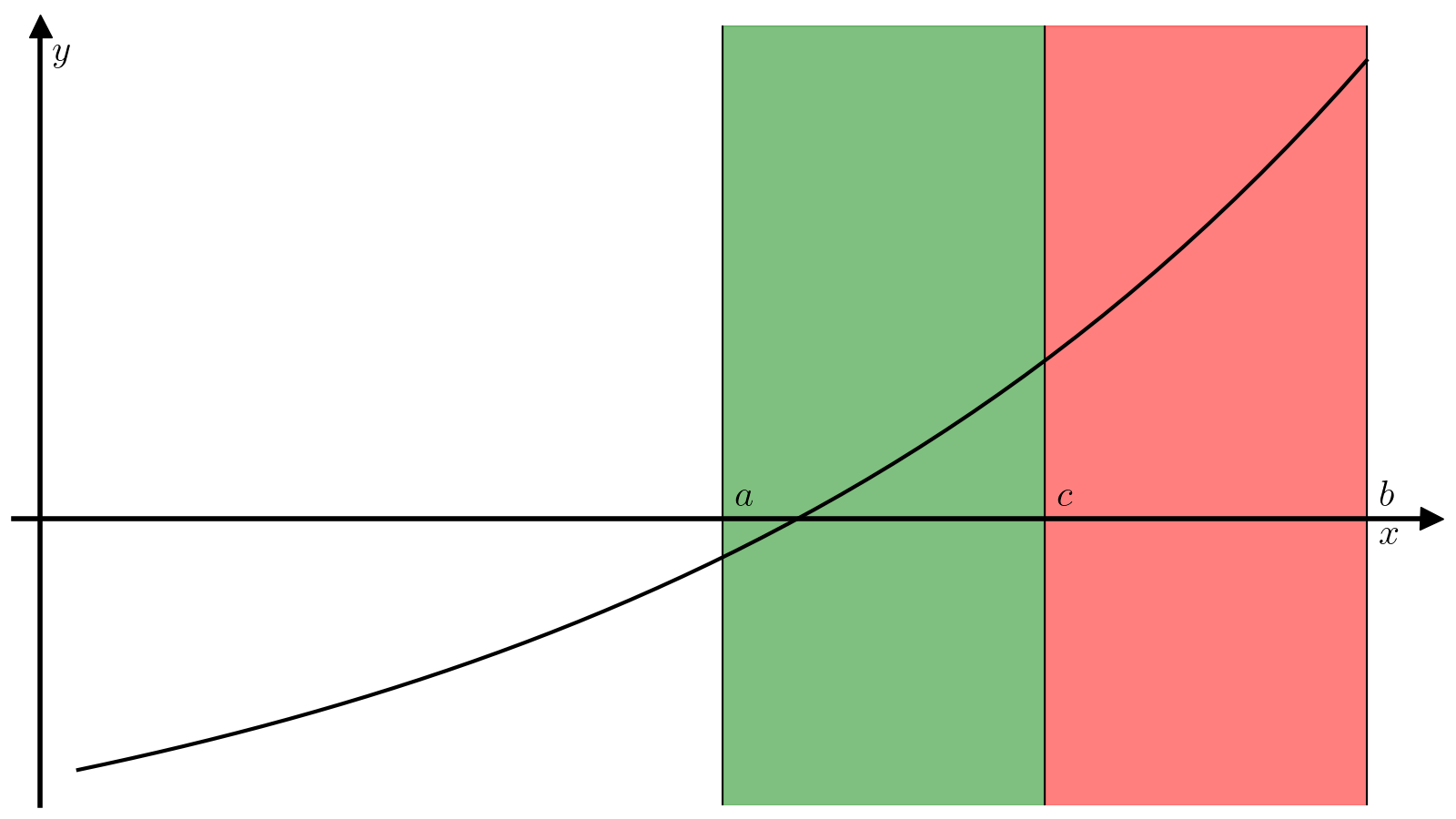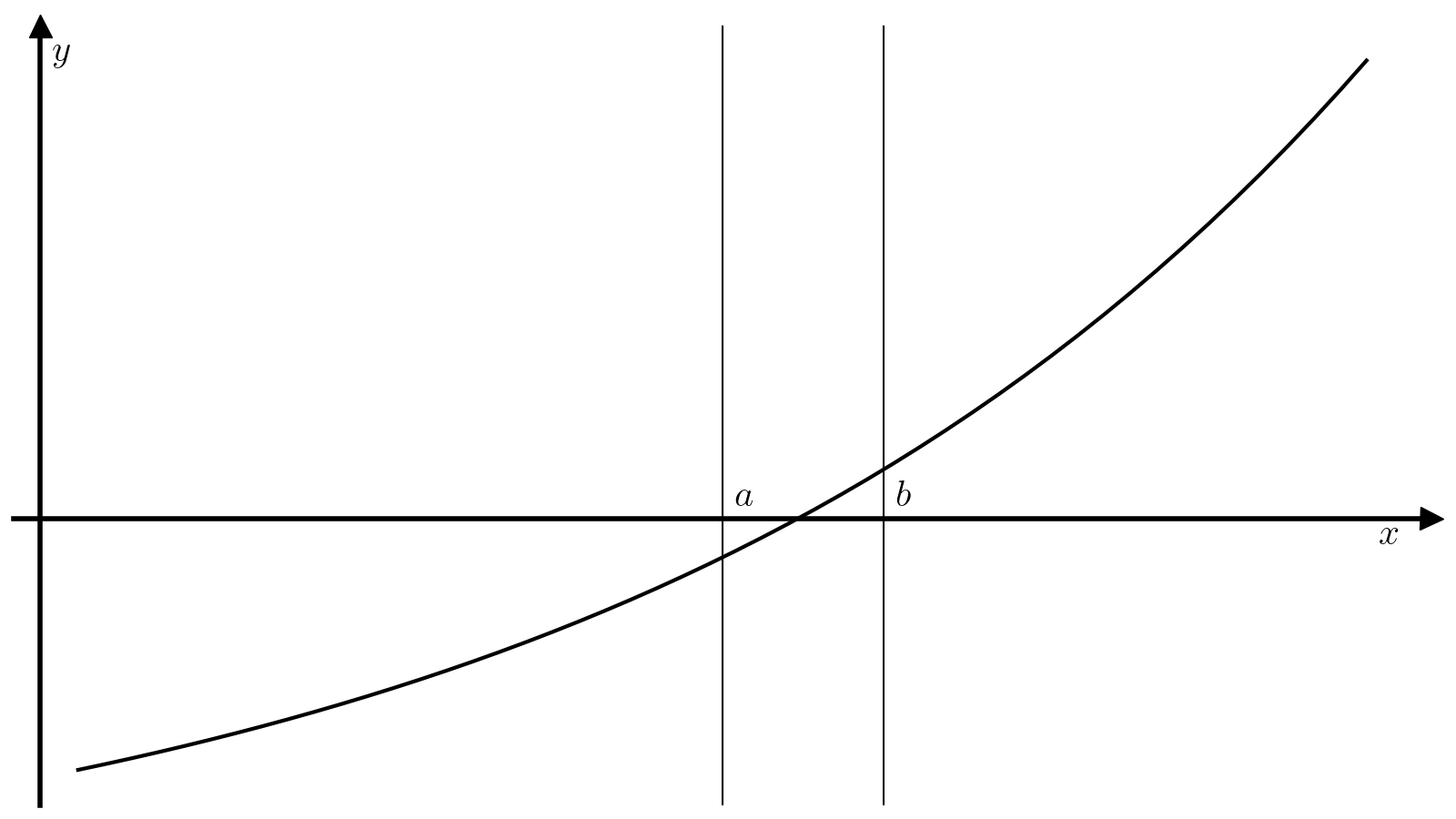
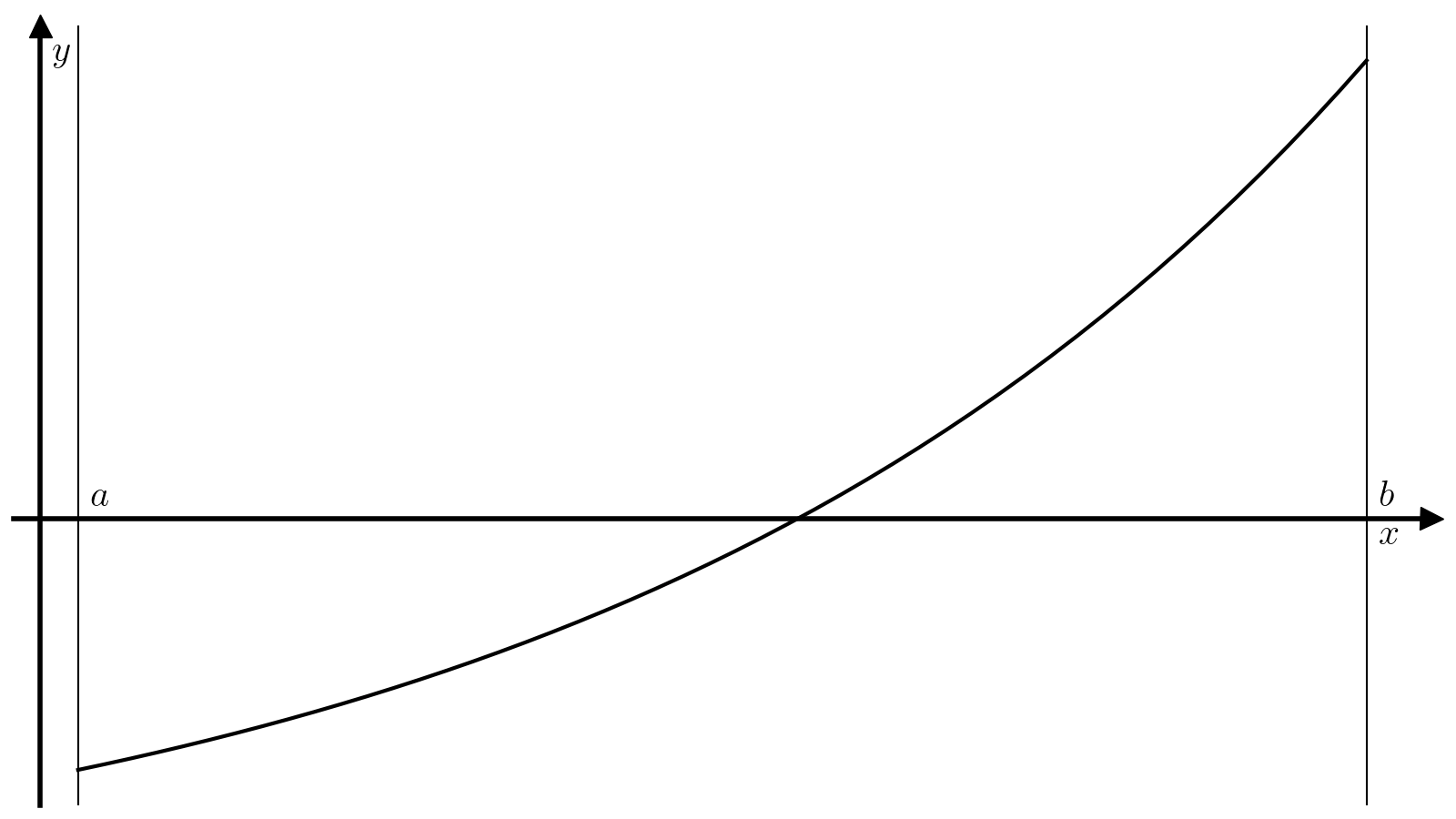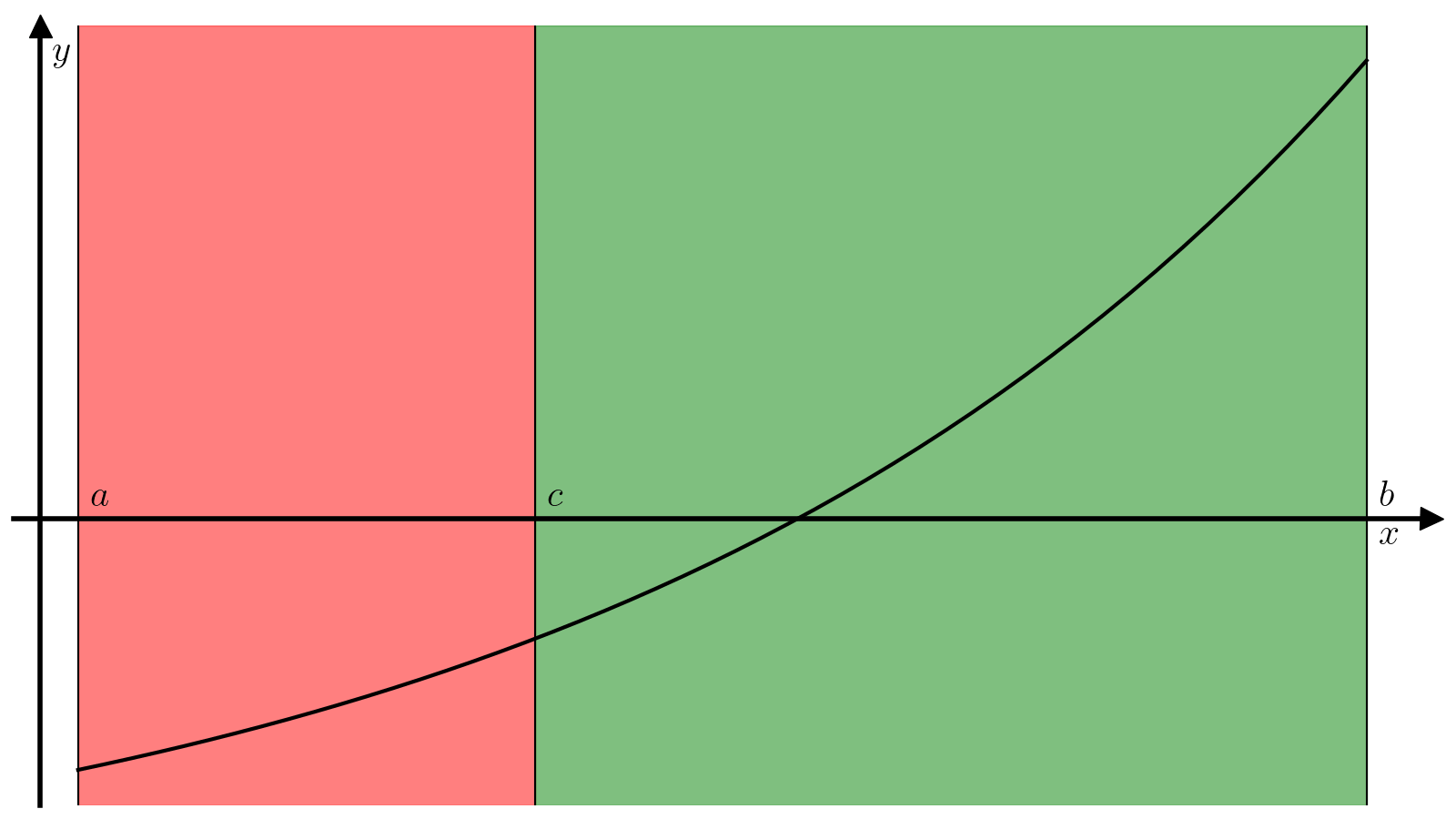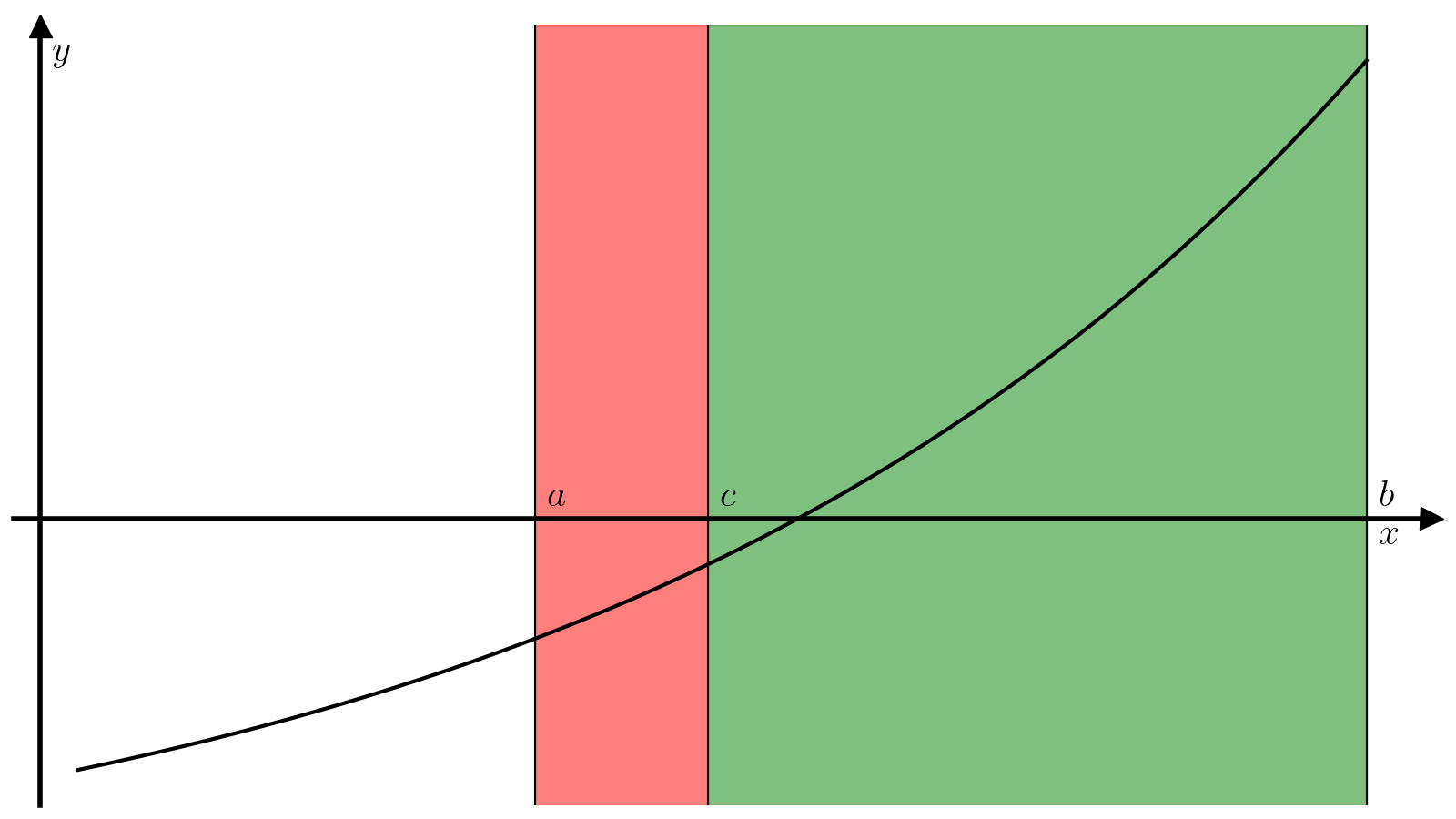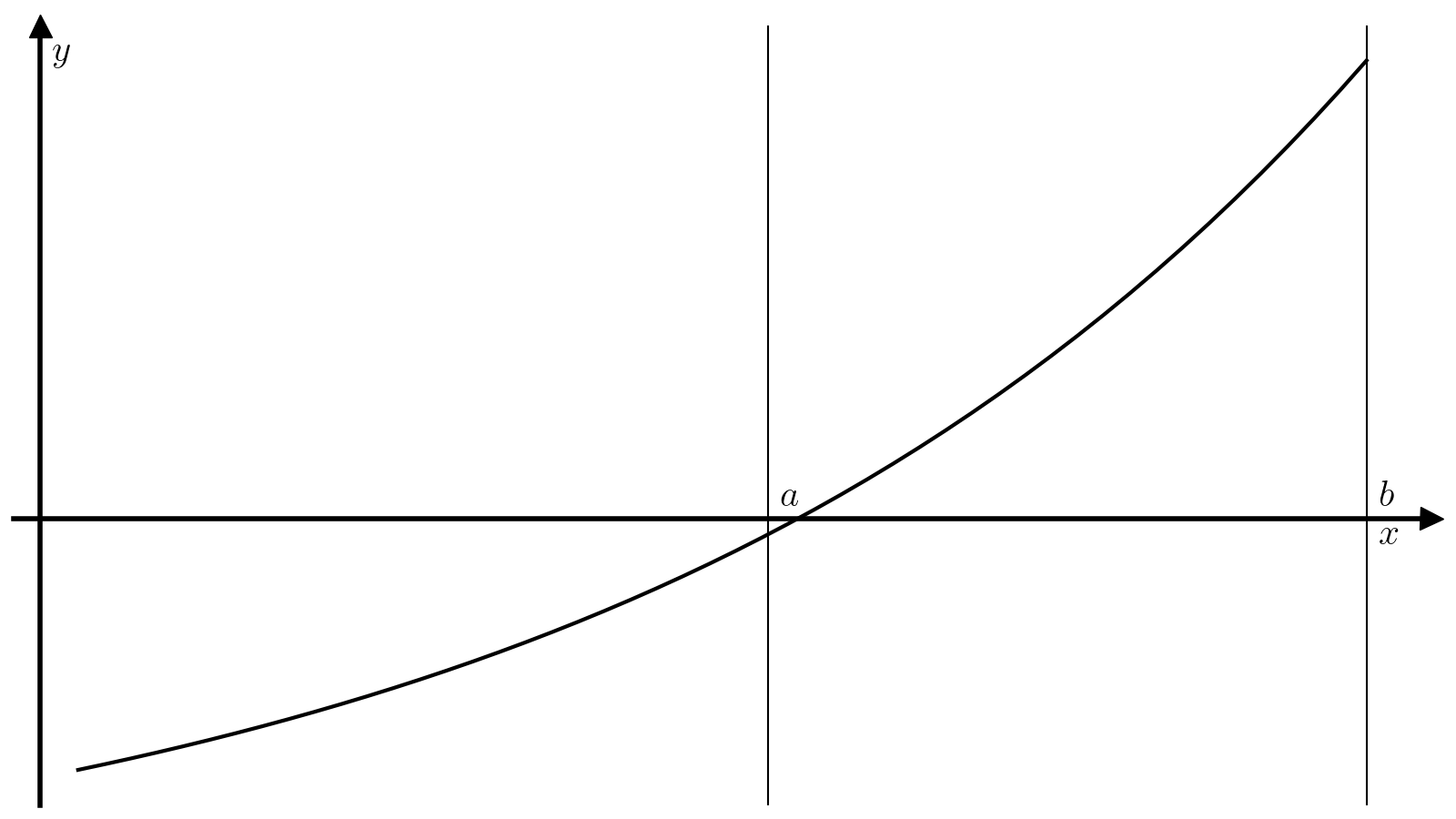
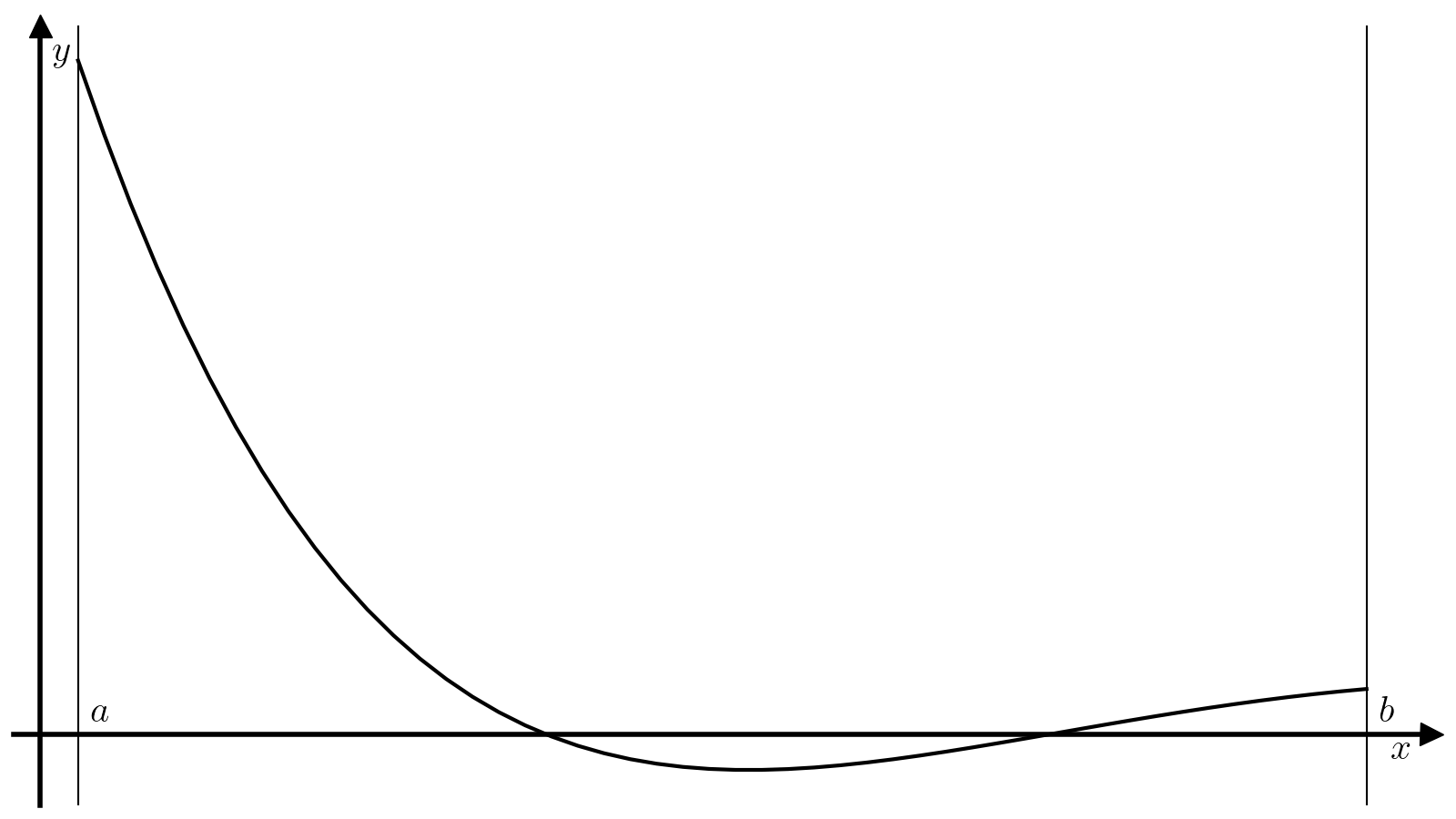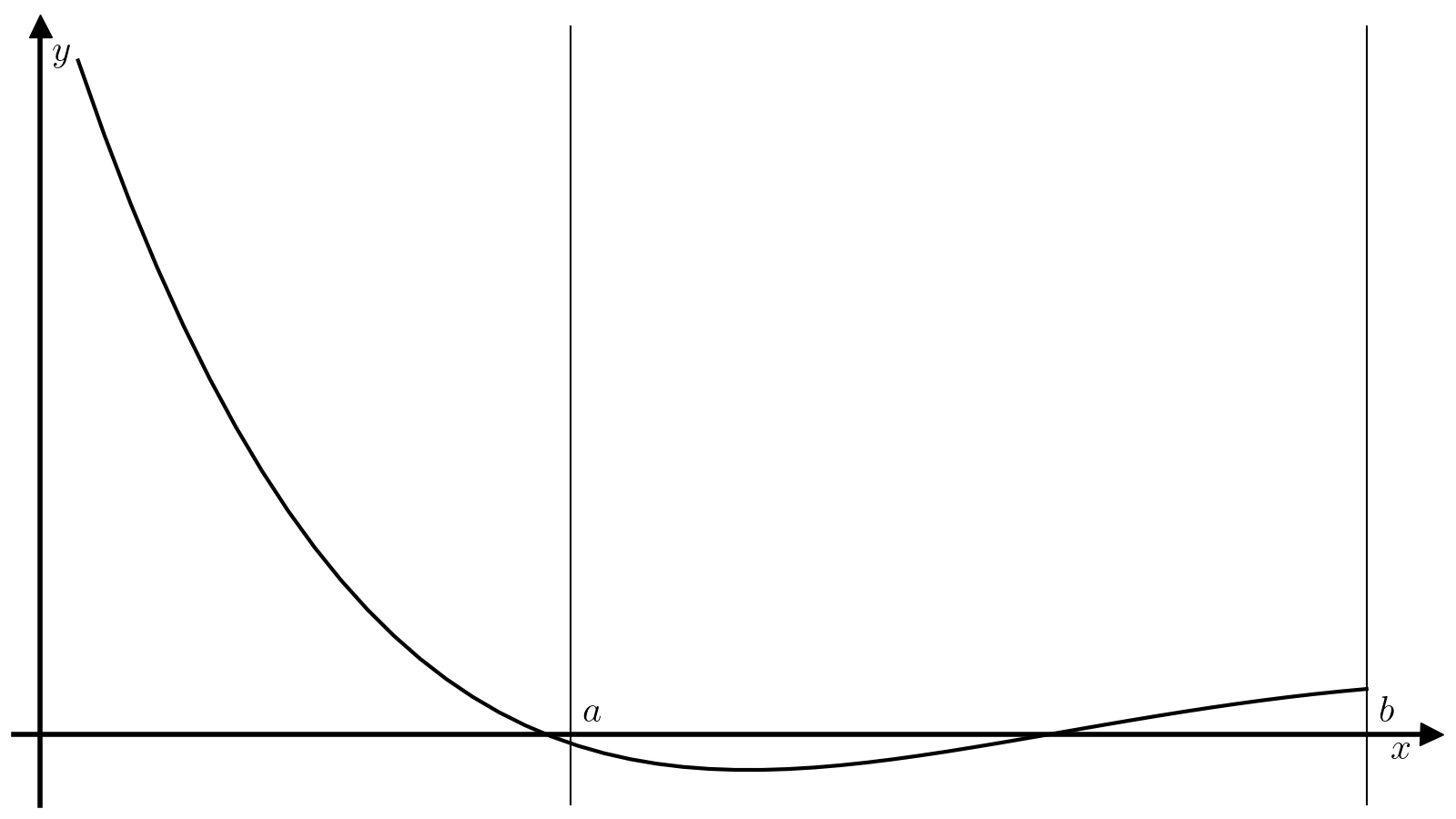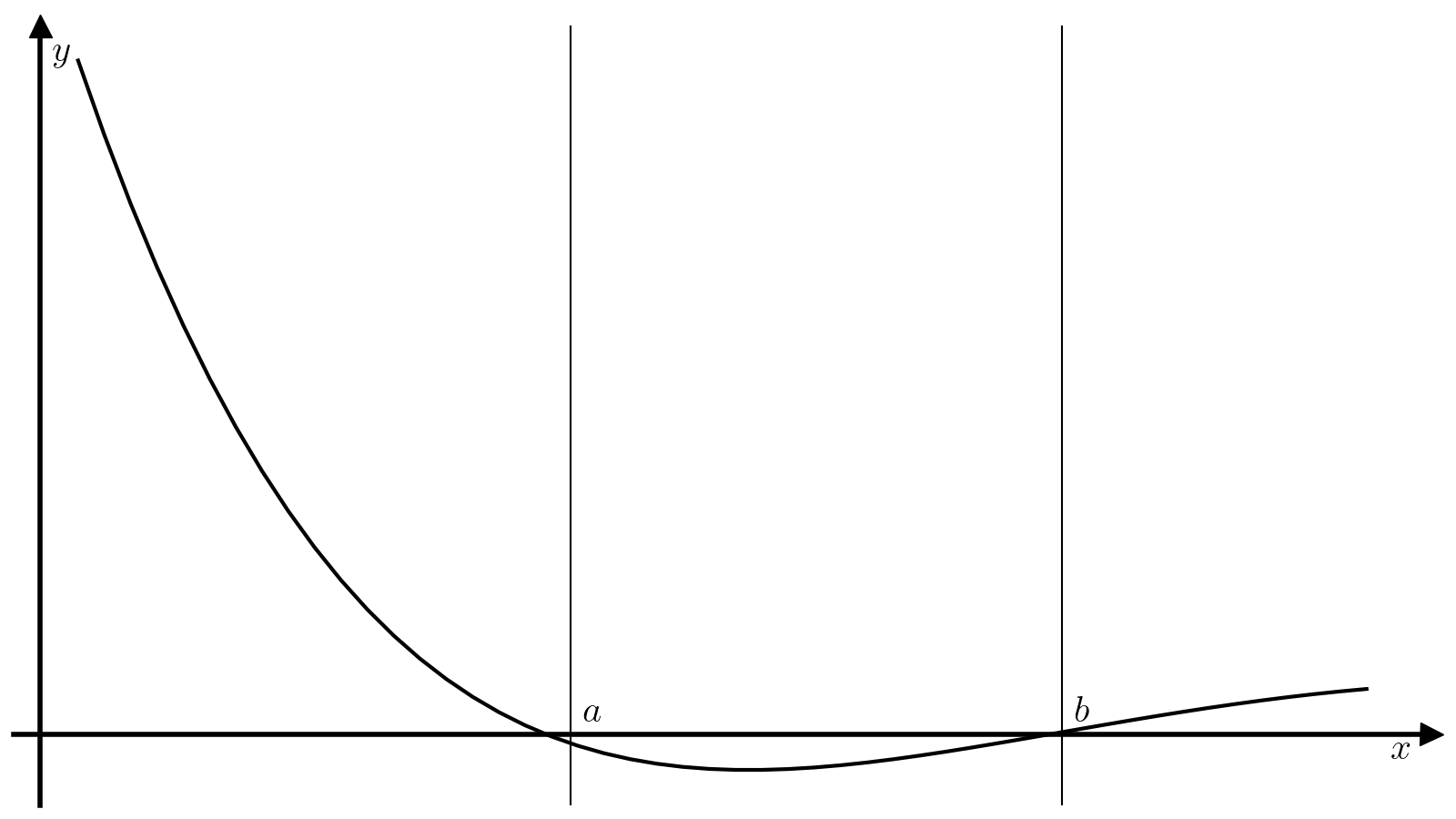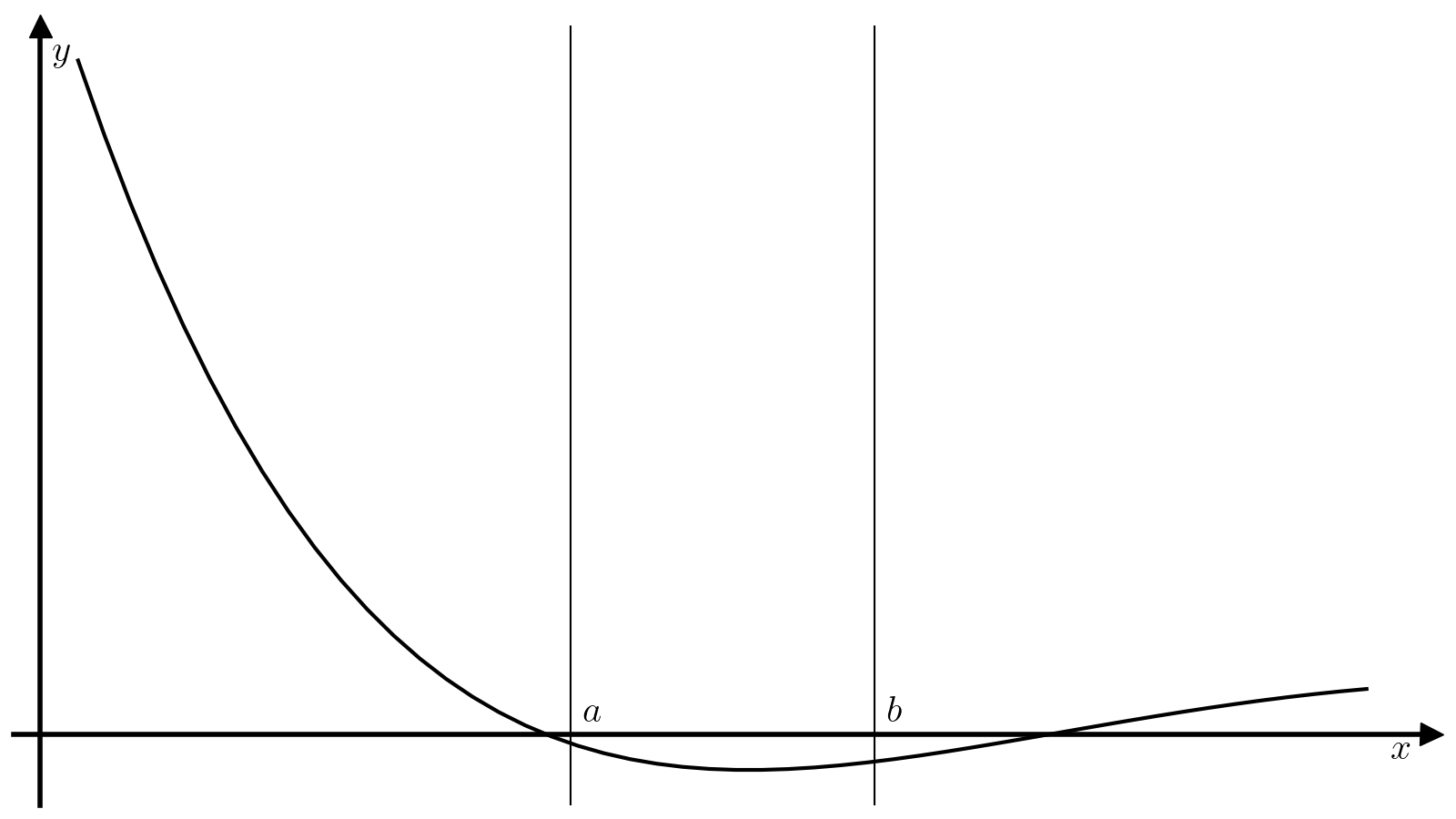
Метод бисекции — один из самых примитивных методов решения уравнений вида (1), который ищет корень непрерывной на некотором отрезке ([a, b]) функции. Для работы этого метода требуется, чтобы значение функции (f) на концах отрезка ([a, b]) были разного знака:
(3)#[f(a)f(b)<0. ]
Тогда из теоремы о промежуточном значении следует, что найдется минимум один корень функции (f) на отрезке ([a, b]), а метод бисекции позволяет найти этот корень с произвольной точностью.
Основная идея алгоритма поиска корня методом бисекции заключается в следующем. Поделим отрезок ([a, b]) пополам, т.е. найдем точку (c):
(4)#[c = dfrac{a + b}{2}.]
В зависимости от значения величины (f(c)), реализуется один из следующих вариантов.
-
(f(c) = 0), т.е. уравнение (1) решено и (c) — его корень;
-
(f(c) f(a) < 0), т.е. можно продолжить поиск корная на отрезке ([a, c]);
-
(f(c) f(a) > 0), а значит (f(c) f(b) < 0) и можно продолжить поиск корня на отрезке ([c, b]).
Итого, с помощью одного такого шага мы или найдем корень, или сузим вдвое длину отрезка, на котором ищется корень. Обычно такие шаги применяют многократно до тех пор, пока не будет достигнута необходимая точность (длина отрезка ([a, b])) и невязка (модуль значения функции (|f(c)|)), т.е. критерием сходимости метода является одновременное выполнение двух условий
[begin{split}
begin{cases}
|b – a| < delta, \
|f(c)| < varepsilon.
end{cases}
end{split}]
Пусть заданы требуемые точность delta и невязка epsilon. Тогда алгоритма поиска минимума корня функции f на отрезке [a, b] методом бисекции состоит из следующих шагов.
-
Проверить выполнение условия (3). Если условие не выполняется, то решения на заданном интервале нет, либо оно не единственно. Работа алгоритма немедленно завершается. Если условие выполняется, то перейти к следующему шагу.
-
Найти середину отрезка
cпо формуле (4). -
Проверить выполнение критериев остановки. Если
|f(c)| < epsilonи|b-a|< delta, то принять, чтоc— искомый корень и работа алгоритма прекращается немедленно. Иначе перейти к следующему шагу. -
Проверить, на каком из двух отрезков
[a, c]или[c, b]функция меняет знак. Еслиf(a) f(c) < 0, тоb = c. Иначе,a = c. Вернуться к шагу №2.
Метод хорд#
Идея метода хорд очень похожа на идею метода бисекции. Корень тоже ищется на отрезке ([a, b]), на концах которого непрерывная функция (f) должна иметь разные знаки.
(5)#[f(a)f(b)<0. ]
На каждой итерации отрезок тоже делится на две части, но не пополам, а по следующей схеме. Через точки ((a, f(a))) и ((b, f(b))) проводится прямая
[
y = f(a) dfrac{x – b}{a – b} + f(b) dfrac{a – x}{a – b},
]
которую называют хордой или секущей. Эта прямая пересекает ось абсцисс в точке
(6)#[c = a – dfrac{f(b)(b-a)}{f(b) – f(a)} in (a, b),]
которая определяет деление отрезка ([a, b]) на два отрезка меньшей длинны: ([a, c]) и ([c, b]). Если точка (c) сама по себе не является корнем, то поиск продолжается на одном из двух этих отрезков. Обычно такие шаги применяют многократно до тех пор, пока не будет достигнута необходимая точность (длина отрезка ([a, b])) и невязка в средней точке (модуль значения функции (|f(c)|)), т.е. критерием сходимости метода является одновременное выполнение двух условий
[begin{split}
begin{cases}
|b – a| < delta, \
|f(c)| < varepsilon.
end{cases}
end{split}]
Пусть заданы требуемые точность delta и невязка epsilon. Тогда алгоритма поиска минимума корня функции f на отрезке [a, b] методом хорд состоит из следующих шагов.
-
Проверить выполнение условия (5). Если условие не выполняется, то решения на заданном интервале нет, либо оно не единственно. Работа алгоритма немедленно завершается. Если условие выполняется, то перейти к следующему шагу.
-
Найти точку
cпо формуле (6). -
Проверить выполнение критериев остановки. Если
|f(c)| < epsilonи|b-a|< delta, то принимается, чтоc— искомый корень и работа алгоритма прекращается немедленно. Иначе, перейти к следующему шагу. -
Выяснить, на каком из двух отрезков
[a, c]или[c, b]функция меняет знак. Еслиf(a) f(c) < 0, тоb = c. Иначе,a = c. Вернуться к шагу №2.
Метод Ньютона#
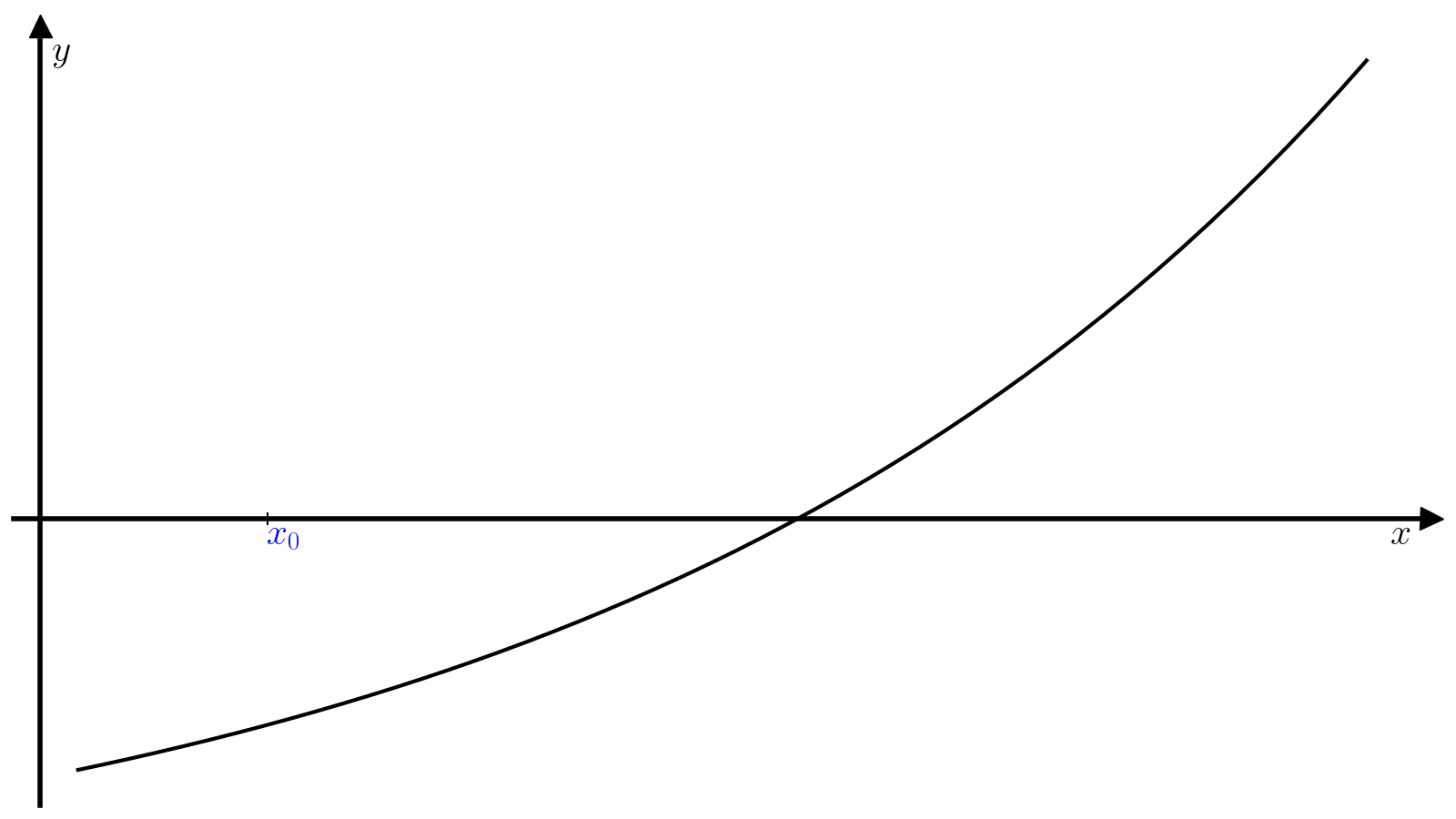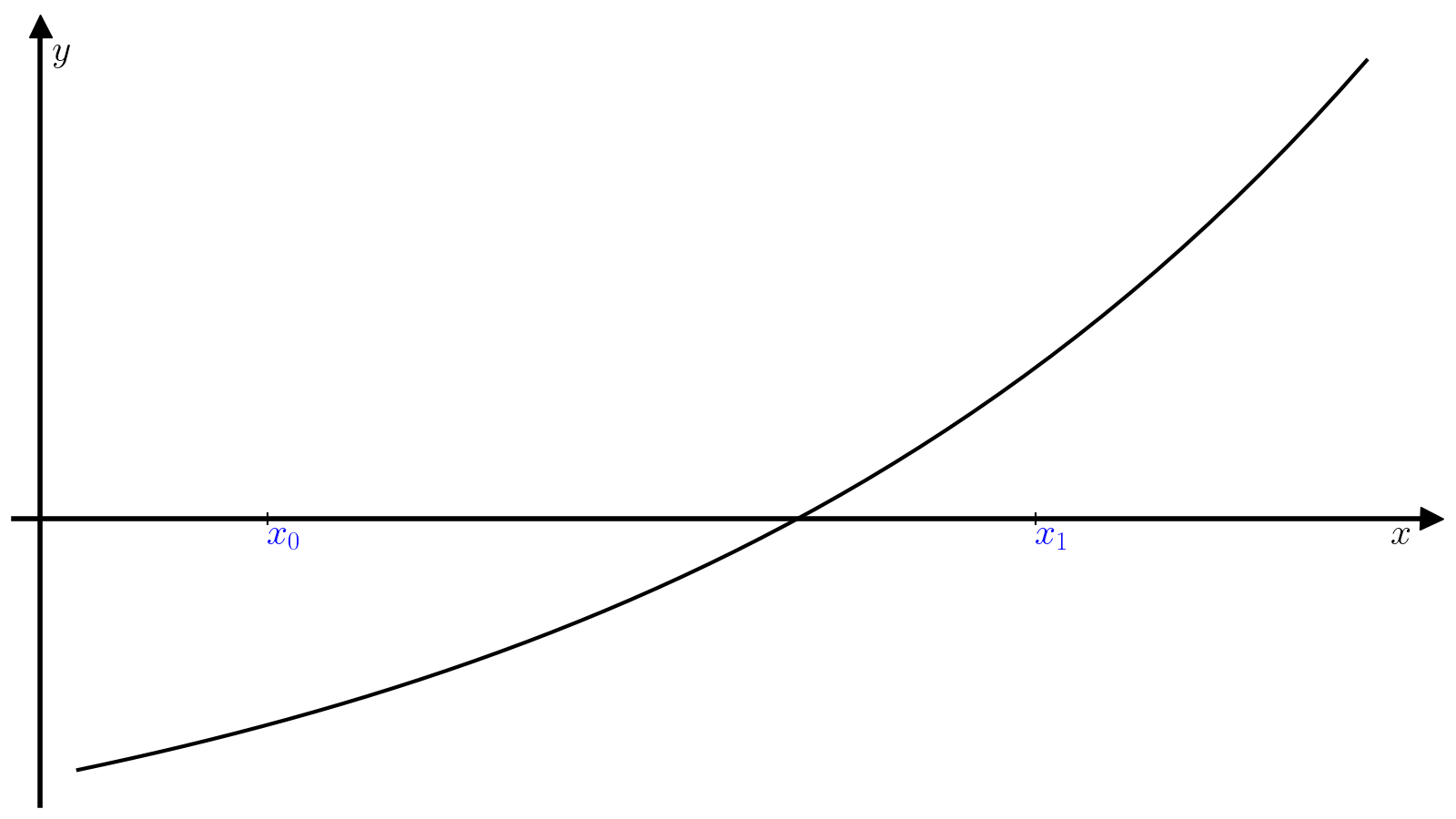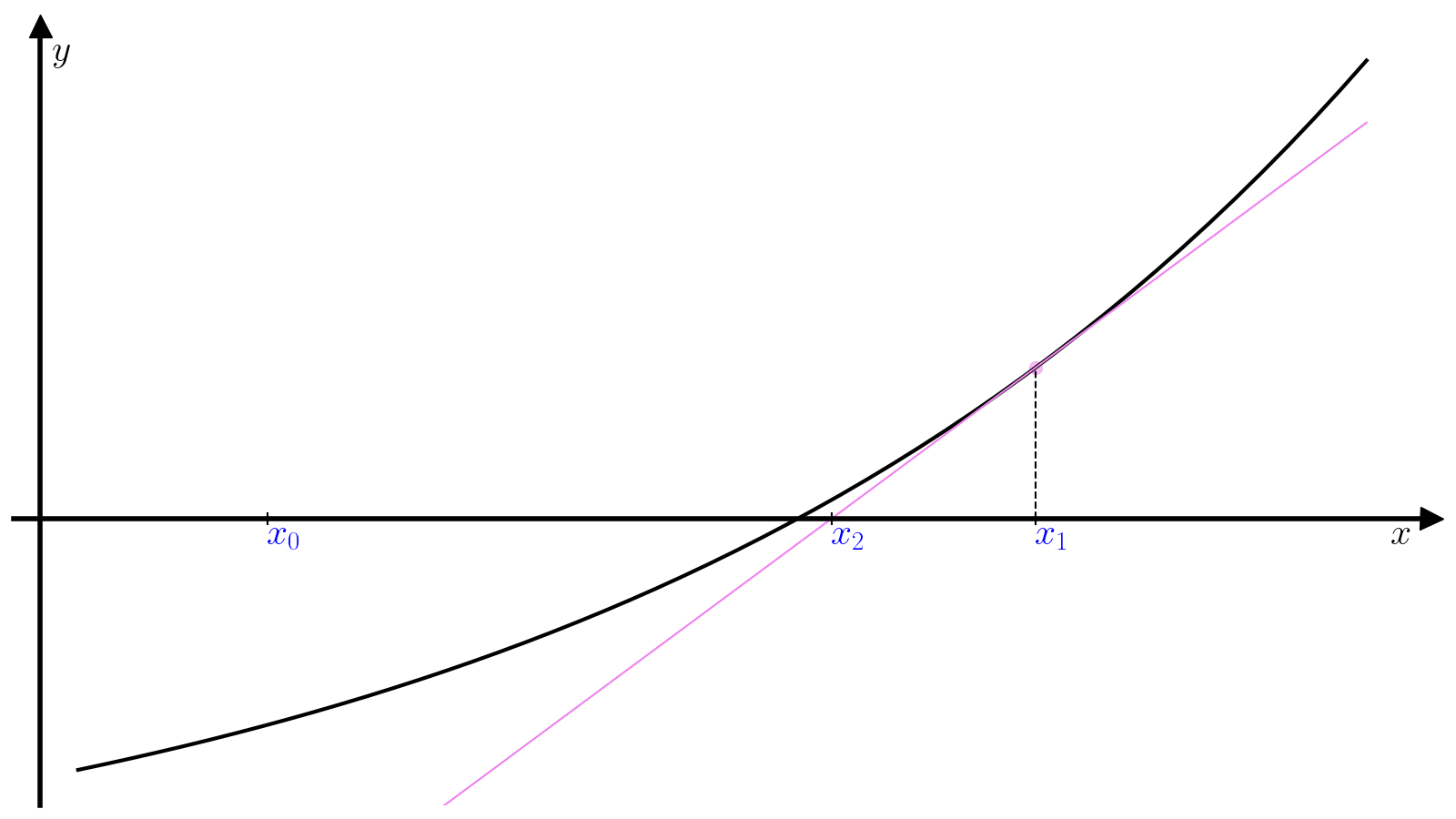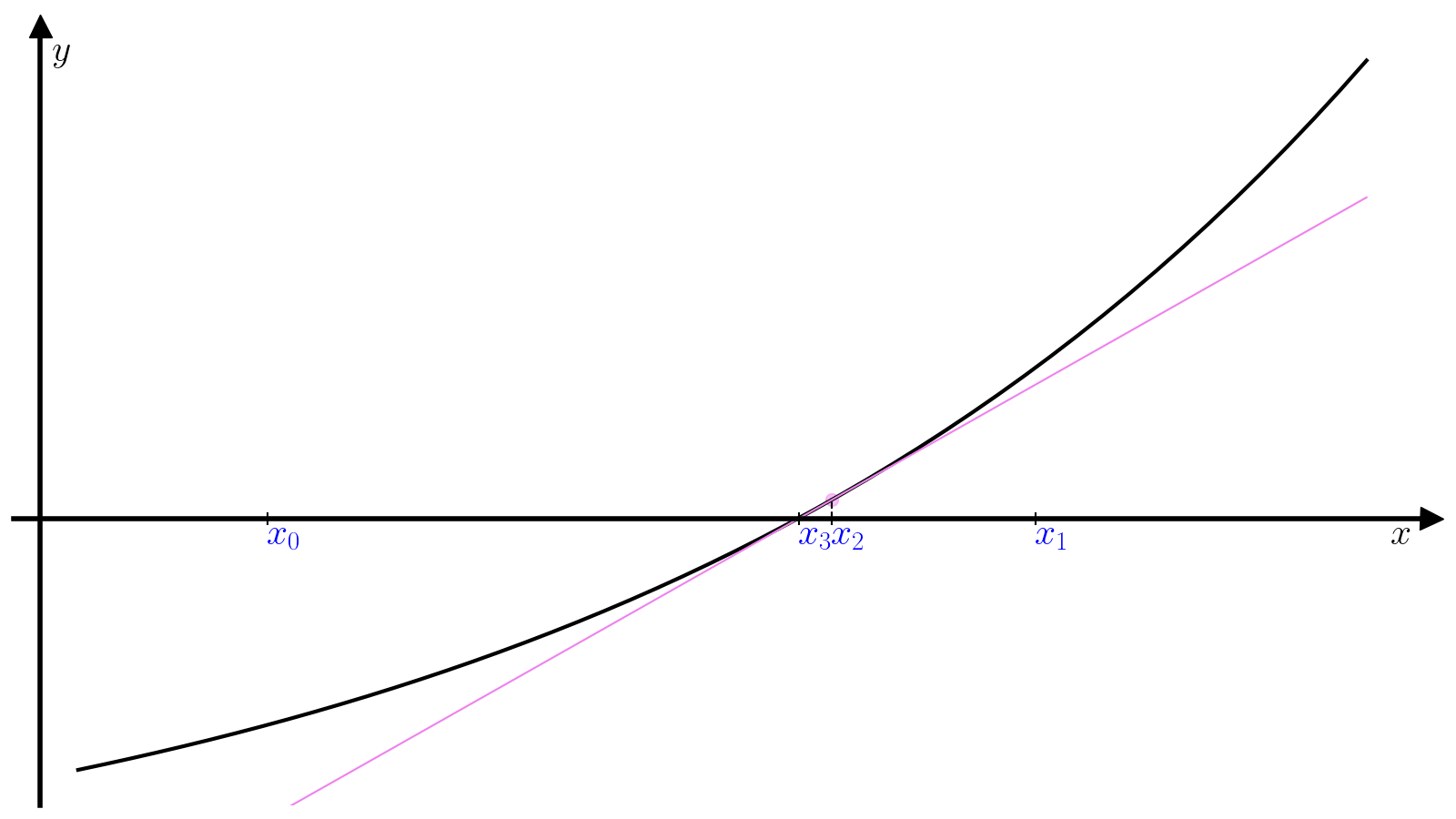
Метод касательных (он же метод Ньютона) накладывает дополнительные требования на функцию (f): кроме непрерывности самой функции (f) требуется и непрерывность производной (f’). Другое отличие заключается в виде начального приближения: предыдущие два методы требовали отрезок, а метод Ньютона всего одну точку.
Пусть задано начальное приближение (x_0). Идея метода Ньютона заключается в том, чтобы аппроксимировать кривую (f(x)) касательной в окрестности точки (x_0) и найти следующее приближение (x_1) к корню функции (f(x)) как пересечение этой касательной с осью абсцисс. Касательная (hat{f}) к функции (f) в точке (x_0) определяется уравнением
[hat{f}(x) = f'(x_0)(x – x_0) + f(x_0),]
а координата (x_1) её точки пересечения с осью абсцисс выражением
[x_1 = x_0 – dfrac{f(x_0)}{f'(x_0)}.]
Далее (x_1) используется в качестве начального приближения на следующей итерации, чтобы найти (x_2) и так далее.
(7)#[x_{i+1} = x_{i} – dfrac{f(x_i)}{f'(x_i)}.]
Условием сходимости является достаточная близость нулевого приближения (x_0) к корню. Гарантировать требуемую точность на каждой конкретной итерации не представляется возможным, поэтому погрешность обычно оценивают как величину (|x_{i+1} – x_i|), т.е. критерием сходимости является выполнение условий
[begin{split}
begin{cases}
|x_{i + 1} – x_i| < delta, \
|f(x_{i+1})| < varepsilon.
end{cases}
end{split}]
Так как метод Ньютона может разойтись, если приближение далеко от корня, то кроме контроля невязки и точности требуется ограничивать максимальное количество итераций, чтобы исключить возможность попадания в бесконечный цикл.
Пусть заданы требуемые точность delta, невязка epsilon, максимальное количество итераций max_iter и начальное приближение x0. Тогда алгоритма поиска корня функции f методом Ньютона состоит из следующих шагов.
-
Инициализировать счетчик
iterнулевым значением, а переменнуюx_previousзначениемx0. -
Вычислить следующее приближение
x_nextна основе предыдущегоx_previousпо формуле (7). -
Если
|x_next - x_previous| < deltaиf(x_next) < epsilon, то принять, чтоx1— искомый корень и работа алгоритма прекращается немедленно. Иначе, перейти к шагу №4. -
Если
iter == max_iter, то принять, что алгоритм Ньютона разошелся и работа алгоритма прекращается немедленно. Иначе, перейти к шагу №5. -
Присвоить переменной
x_previousзначение переменнойx_next, увеличить счетчикiterна 1 и вернуться к шагу №2.
Метод дихотомии (метод золотого сечения)#
Метод дихотомии предназначен для поиска минимумов унимодальной функции. Непрерывная функция (fcolon mathbb{R} to mathbb{R}) называется унимодальной на отрезке ([a, b]), если (exists! c in [a, b]), такая, что:
-
(c) — глобальный минимум функции (f), т.е. (f(c) = f_* = minlimits_{xin[a, b]} f(x));
-
функция (f) монотонно убывает на отрезке ([a, c]);
-
функция (f) монотонно растёт на отрезке ([c, b]);
Унимодальная функция имеет ровно один локальный минимум, который одновременно является и единственным глобальным. Идея метода дихотомии основывается на том, что если (f) унимодальна на отрезке ([a, b]), то разбив отрезок ([a, b]) двумя точками (x_1) и (x_2), (x_1 < x_2), можно легко уточнить положение минимума функции (f):
-
Если (f(x_1) > f(x_2)), то минимум достигается на отрезке ([x_1, b]). Действительно, на отрезке ([c, b]) функция (f) монотонно растет по определению, а значит (x_1) не может находиться внутри отрезка ([c, b]), так как (f(x_2) < f(x_1)) при том, что (x_2 > x_1). Единственная альтернатива — (x_1in[a, c]), т.е. минимум достигается на отрезке ([x_1, b]).
-
Если (f(x_1) < f(x_2)), то минимум достигается на отрезке ([a, x_2]).
Note
Корректное определение унимодальной функции подразумевает несколько более общее определение, в котором точка минимума (c) как бы превращается в отрезок ([c_1, c_2]), каждая точка которого является глобальным минимумом. Описанный здесь метод дихотомии сходится и для таких функций.
После сужения отрезка ([a, b]) до ([x_1, b]) или ([a, x_2]) можно повторить процедуру деления отрезка на три части произвольное количество раз до достижения необходимой точности. За точность принимается длинна отрезка ([a, b]) (величина (b – a)), т.е. критерием сходимости алгоритма считается выполнение условия
[
|b – a| < delta.
]
Метод золотого сечения — частный, который предписывает выбирать (x_1) и (x_2) по формулам
(8)#[begin{split}begin{cases}
x_1 = dfrac{a + b}{2} – (b – a)(dfrac{1}{Phi} – dfrac{1}{2}), \
x_2 = dfrac{a + b}{2} + (b – a)(dfrac{1}{Phi} – dfrac{1}{2}),
end{cases}end{split}]
где (Phi = dfrac{1 + sqrt{5}}{2}) — золотое сечение. Выбор (x_1) и (x_2) позволяет на каждой следующей итерации вычислять значение функции только в одной новой точке, а значит минимизирует необходимое для достижения требуемой точности количество вычислений значений функции (f(x)).
Пусть задана требуемая точность delta. Тогда алгоритма поиска минимума функции f на отрезке [a, b] методом золотого сечения состоит из следующих шагов.
-
Найти
x1иx2по формулам (8). -
Если
f(x1) > f(x2), тоa = x1. Иначе,b = x_2. -
Если
b - a < delta, то требуемая точность достигнута и принимается, чтоc = (a + b) / 2— положение глобального минимума и работа алгоритма завершается. Иначе, вернуться к шагу №1.
Note
Выбор (x_1) и (x_2) по формулам (8) позволяет сэкономить вычисления на втором и следующих итерация. Например, если на предыдущей итерации алгоритм попал в ветку, где (f(x_1) > f(x_2)), то на следующей итерации (a = x_1) и можно показать, что (x_1) на следующей итерации совпадает с (x_2) на предыдущей и можно переиспользовать вычисленные на предыдущей итерации значения (x_2) и (f(x_2)) как значения (x_1) и (f(x_1)) на следующей.
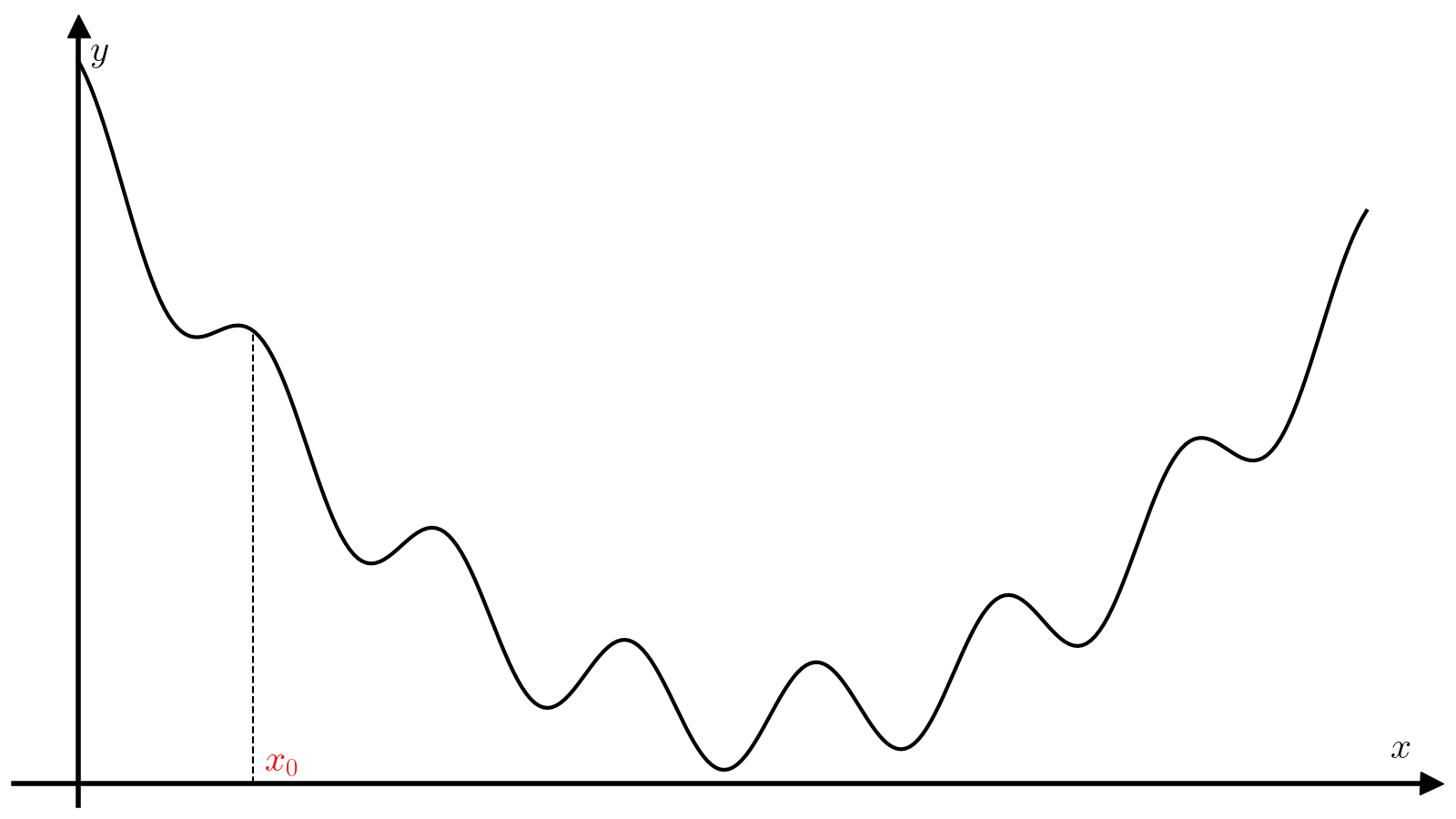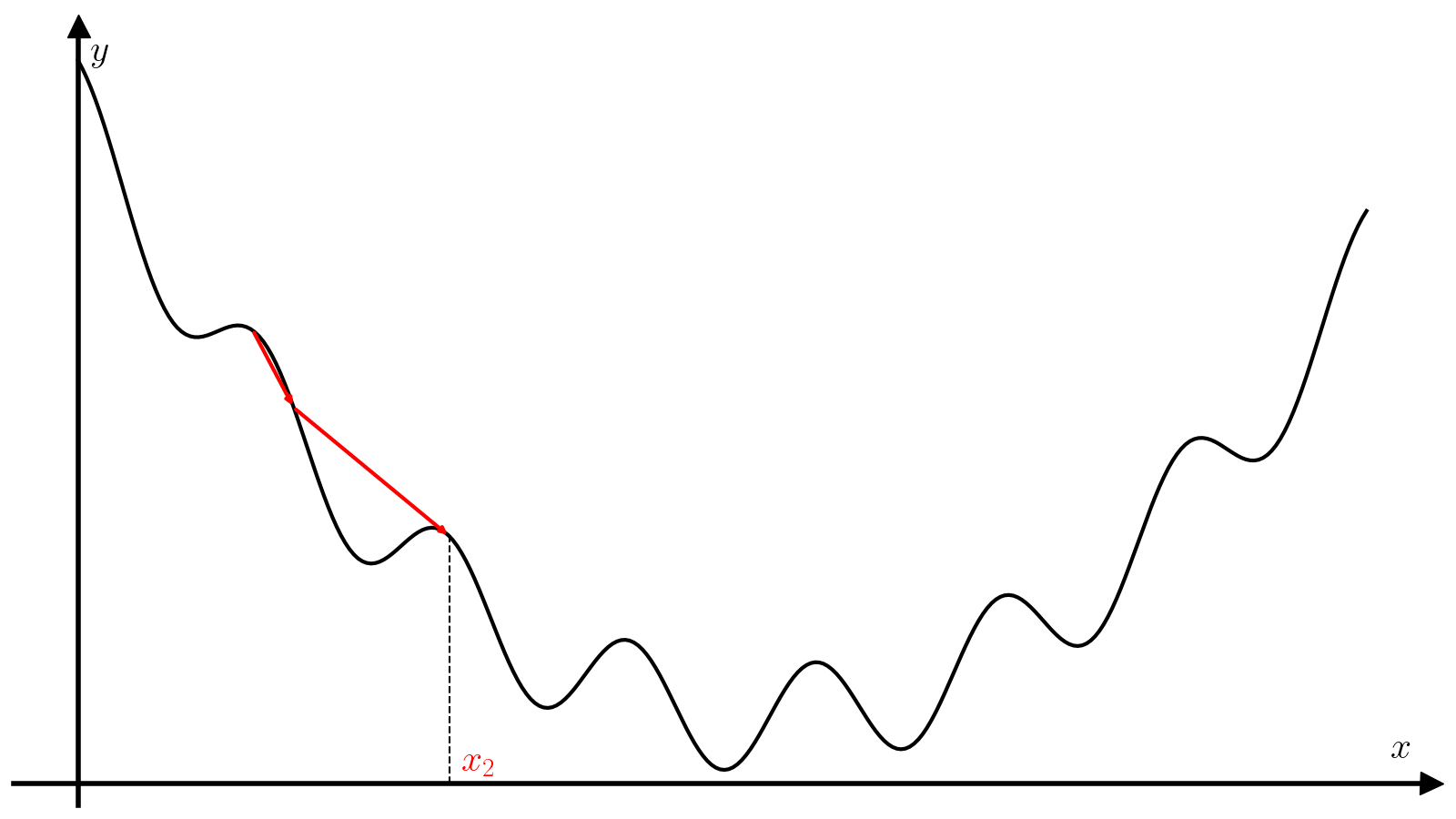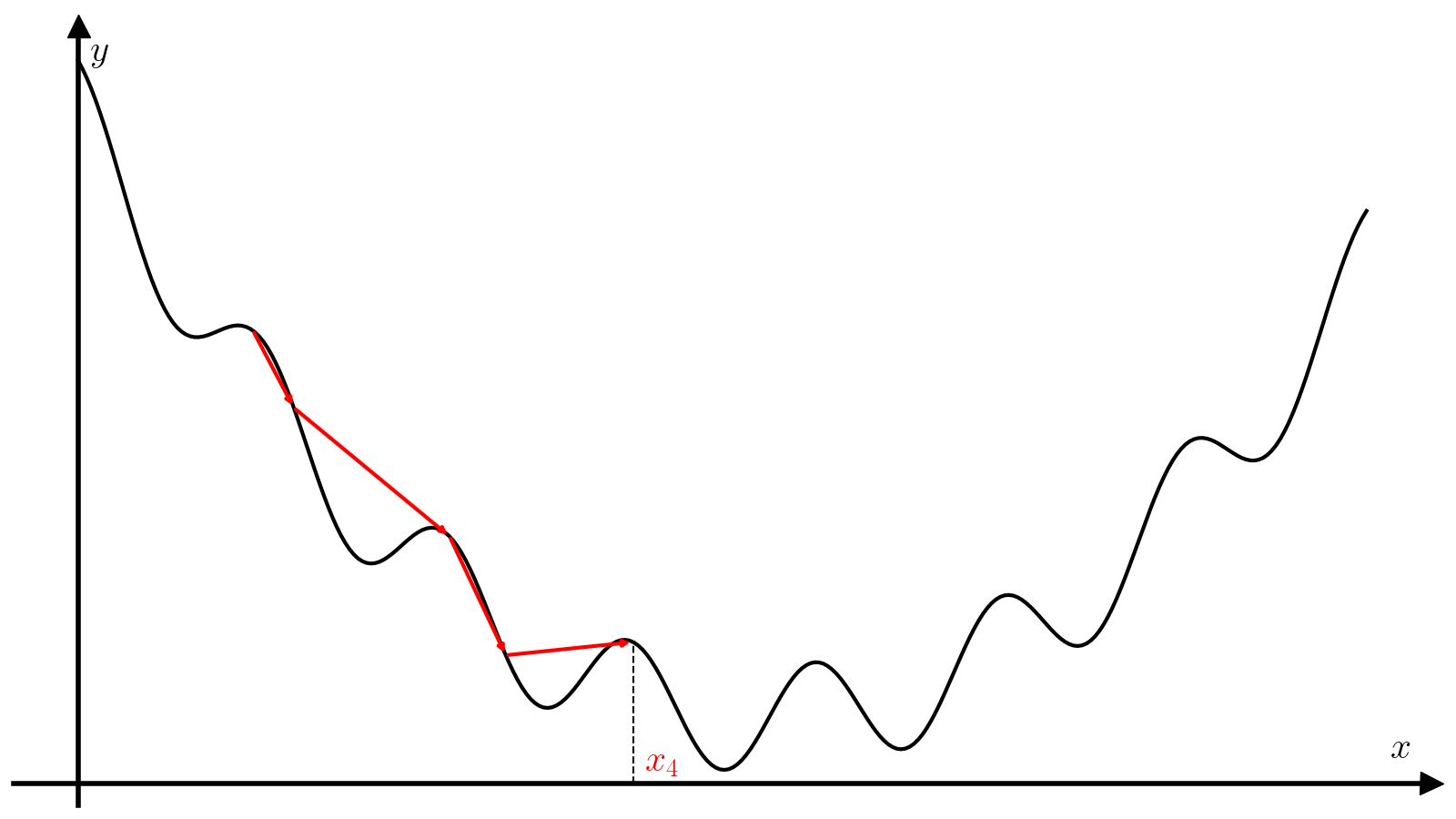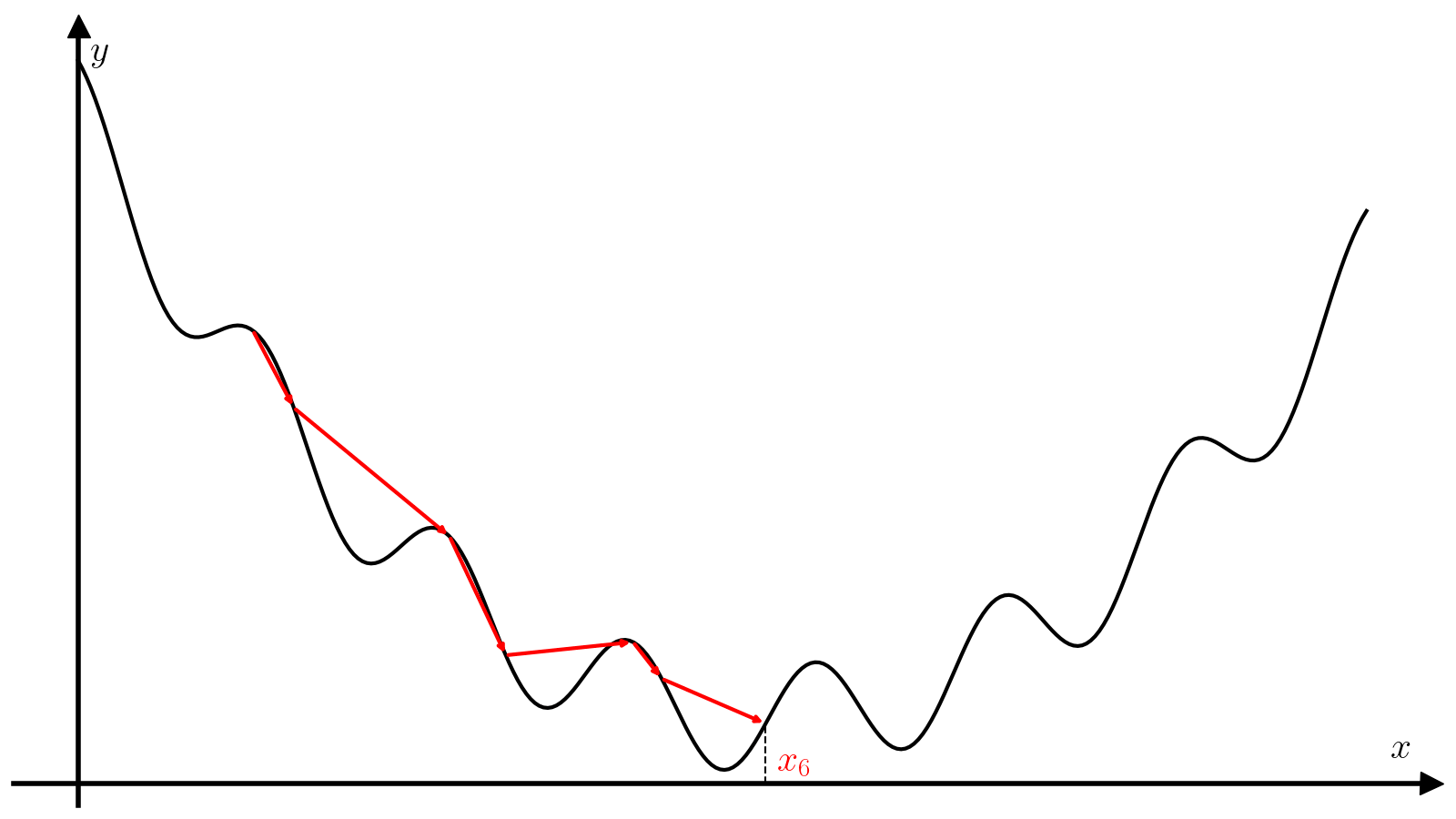
Метод градиентного спуска#
Метод градиентного спуска — один из самых распространенных методов минимизации функции. Для его работы требуется не только непрерывность самой функции (f), но ещё и непрерывность её первой производной (f’).
Известно, что в случае функции нескольких переменных (fcolon mathbb{R}^n to mathbb{R}), градиент (nabla f(x)) определяет направление наискорейшего роста в окрестности точки (x). И наоборот, в противоположном направлении функция (f) убывает быстрее всего. Метод градиентного спуска опирается на это свойство градиента: на каждой итерации алгоритма совершается шаг в направлении антиградиента ((-nabla f(x))), т.е. направлении наискорейшего спуска.
Градиент (nabla f) функции (fcolon mathbb{R} to mathbb{R}) совпадает с её производной и один шаг градиентного спуска в таком случае задается формулой
[
x_{i + 1} = x_i – alpha_i f'(x_i),
]
где (x_i) — текущее приближение, (x_{i+1}) — следующее приближение, а (alpha_i) — шаг градиентного спуска на (i)-й итерации.
Если (f) строго выпукла, то при наложении определенных требований на последовательность ({alpha_0, alpha_1, …, alpha_i, …}) можно доказать, что метод градиентного спуска сойдется к глобальному минимуму. Но даже при не выполнении этих условий метод градиентного спуска может сойтись, но тогда гарантировать сходимость не представляется возможным. В качестве контроля сходимости иногда используется величина градиента, так как в экстремальной точке дифференцируемой функции производная равна нулю. Иными словами, критерием остановки алгоритма градиентного спуска иногда выступает условие
[
|f'(x_i + 1)| < varepsilon.
]
Так как гарантировать достижение даже локального минимума в общем случае невозможно, то также требуется ограничивать максимальное количество итераций, чтобы исключить возможность попадания в бесконечный цикл.
Вам предлагается реализовать метод градиентного спуска с постоянным шагом (alpha).
(9)#[x_{i + 1} = x_i – alpha f'(x_i).]
Правильный подбор этого параметра критические влияет на сходимость алгоритма. Слишком маленький шаг потребует много итераций для сходимости и почти наверняка застрянет в первом встреченном локальном минимуме. Слишком большой шаг может разойтись, а может сравнительно быстро сойтись при удачном стечении обстоятельств и почти наверняка проскочит минимум, что хорошо, если минимум локальный, и плохо, если минимум глобальный.
Пусть задана величина epsilon, максимальное число итераций max_iter, шаг градиентного спуска alpha и начальное приближение x0. Тогда алгоритм поиска минимума функции f с производной f_prime на отрезке [a, b] методом золотого сечения состоит из следующих шагов.
-
Инициализировать переменную
iterнулем, а переменнуюx_previousвеличинойx_next; -
Найти следующее приближение
x_nextпо формуле (9):x_next = x_previous - alpha * f_prime(x_previous); -
Если
|f_prime(x_next)| < epsilon, то принять, чтоx_next— найденный минимум, алгоритма завершает свою работу. Иначе, перейти к шагу №4. -
Увеличить значение переменной
iterна 1 и, еслиiter == max_iter, принять, что метод разошелся и алгоритм завершает работу. Иначе, вернуться к шагу №2.
Обновлено: как найти минимум функции на закрытом интервале [0,3,5] в Python? До сих пор я нашел максимум и минимум, но не уверен, как отсчитать минимум отсюда.
import sympy as sp
x = sp.symbols('x')
f = (x**3 / 3) - (2 * x**2) + (3 * x) + 1
fprime = f.diff(x)
all_solutions = [(xx, f.subs(x, xx)) for xx in sp.solve(fprime, x)]
print (all_solutions)
2016-08-28 15:05
3
ответа
После этого PR вы должны уметь делать следующее:
from sympy.calculus.util import *
f = (x**3 / 3) - (2 * x**2) - 3 * x + 1
ivl = Interval(0,3)
print(minimum(f, ivl))
print(maximum(f, ivl))
print(stationary_points(f, ivl))
2019-10-25 22:55
Возможно как то так
from sympy import solveset, symbols, Interval, Min
x = symbols('x')
lower_bound = 0
upper_bound = 3.5
function = (x**3/3) - (2*x**2) - 3*x + 1
zeros = solveset(function, x, domain=Interval(lower_bound, upper_bound))
assert zeros.is_FiniteSet # If there are infinite solutions the next line will hang.
ans = Min(function.subs(x, lower_bound), function.subs(x, upper_bound), *[function.subs(x, i) for i in zeros])
2016-08-30 19:22
Вот возможное решение с использованием sympy:
import sympy as sp
x = sp.Symbol('x', real=True)
f = (x**3 / 3) - (2 * x**2) - 3 * x + 1
#f = 3 * x**4 - 4 * x**3 - 12 * x**2 + 3
fprime = f.diff(x)
all_solutions = [(xx, f.subs(x, xx)) for xx in sp.solve(fprime, x)]
interval = [0, 3.5]
interval_solutions = filter(
lambda x: x[0] >= interval[0] and x[0] <= interval[1], all_solutions)
print(all_solutions)
print(interval_solutions)
all_solutions дает вам все точки, где первая производная равна нулю, interval_solutions ограничивает эти решения для закрытого интервала. Это должно дать вам хорошие подсказки, чтобы найти минимумы и максимумы:-)
2016-08-28 15:14
Команды f.subs показывают два способа отображения значения данной функции при x=3.5, первый – в качестве рационального приближения, второй – в качестве точной дроби.
2016-08-28 17:13
In this Python tutorial, we will learn about the “Python Scipy Minimize“, where we will know how to find the minimum value of a given function and cover the following topics.
- Python Scipy Minimize
- Python Scipy Minimize Multiple Variables
- Python Scipy Minimize Bounds
- Python Scipy Minimize Constraints
- Python Scipy Minimize Scalar
- Python Scipy Minimize Powell
- Python Scipy Minimize Not Working
- Python Scipy Minimize Trust-Constr
The Python Scipy module scipy.optimize has a method minimize() that takes a scalar function of one or more variables being minimized.
The syntax is given below.
scipy.optimize.minimize(fun, x0, method=None, args=(), jac=None, hessp=None, hess=None, constraints=(), tol=None, bounds=None, callback=None, options=None)Where parameters are:
- fun(callable): To minimize is the objective function.
- x0(shape(n), ndarray): First intuition. an array of real objects, where n is the total number of independent variables, and the size of the array is (n,).
- method(str or callable): Solver type ought to be one of trust-Krylov, Nelder-Mead, CG, Powell, BFGS, L-BFGS-B, TNC, COBYLA,trust-exact, Newton-CG, SLSQP, dogleg, trust-ncg, trust-constr.
- args(tuple): Additional arguments supplied to the derivatives of the objective function.
- jac(bool, cs , 2 or 3 point): An approach to calculating the gradient vector. only for BFGS, CG, L-BFGS-B, Newton-CG, TNC, dogleg, SLSQP, trust-ncg, trust-exact,trust-krylov, and trust-constr If it’s a callable, it ought to be a function that gives back the gradient vector: “jac(x, *args) -> array_like, shape (n,)”. Where x is an array with the shape (n,), and args is a tuple of the fixed parameters. The objective function and gradient are considered to be returned by fun if jac is a Boolean and is True.
- hessp(callable): Hessian of the objective function multiplied by p, a random vector. Specifically for Newton-CG, trust-ncg, trust-krylov, and trust-constr. Hessp or hess must only be given once. Hessp will be disregarded if hess is supplied. The Hessian must be multiplied by any vector using hessp: “hessp(x, p, *args) -> ndarray shape (n,)”. Where args is a tuple containing the fixed parameters, p is an arbitrary vector of dimension (n), and x is an (n,) ndarray.
- hess: The Hessian matrix computation method. only for the Dogleg, Newton-CG, Trust-NCG, Trust-Exact, Trust-Krylov, and Trust-Constr algorithms. This should output the Hessian matrix if it is callable: “ess(x, *args) -> {LinearOperator, spmatrix, array}, (n, n)”. Where args is a tuple of the fixed parameters and x is an array of size (n, n). To choose a finite difference scheme for the numerical estimation of the hessian, the keywords “2-point,” “3-point,” and “cs” can also be used.
- constraints(dict,constraint): limits the definition. only in relation to SLSQP, COBYLA, and trust-constr. A single object or a set of objects that specify constraints for the optimization problem are referred to as “trust-constr” constraints. Available constraints are: NonLinear or Linear Constraints.
- tol(float): Tolerance for ending. When tol is supplied, the chosen minimization algorithm equalizes all pertinent solver-specific tolerances with tol. Use solver-specific settings for fine-grained control.
- bounds(bounds or sequence): For the L-BFGS-B, Nelder-Mead, TNC, Powell, SLSQP, and trust-constr techniques, bounds on the variables. The boundaries can be specified in one of two ways: Instance of the class Bounds and for each element in x, a list of (min, max) pairs is given. To specify no bound, use the word none.
- callback(): After each iteration, called. It is callable with the signature for “trust-constr.”
- options(dict): A list of possible solvers.
The method minimize() returns res(A OptimizeResult object is used to represent the optimization result. The solution array x, success, a Boolean indication indicating if the optimizer successfully terminated, and message, which explains the termination reason, are important features).
Let’s take an example by following the below step:
Let’s think about the Rosenbrock function minimization issue. Rosen uses this function and its corresponding derivatives.
Import the required method or libraries using the below python code.
from scipy import optimizeAn easy way to use the Nelder-Mead approach is using the below code.
data_x0 = [2.1, 0.5, 0.9, 1.7, 1.1]
result = optimize.minimize(optimize.rosen, data_x0, method='Nelder-Mead', tol=1e-5)
result.x
This is how to use the method minimize() Python Scipy to minimize the function with different methods.
Read: Python Scipy Chi-Square Test
Python Scipy Minimize Multiple Variables
Here in this section, we will create a method manually that will take several parameters or variables, to find the minimum value of the function using the method minimize() of module scipy.optimize. Follow the below steps to create a method.
Import the required libraries using the below python code.
from scipy import optimizeDefine the method using the below code.
def fun(paramt):
# print(paramt) # <-- As you can see, params is an array in NumPy.
x, y, z = paramt # <-- You might want to give the component variables names to make them easier to read.
return x**2 + y**3 + z**3Define the initial guess and pass the guess or function to a method minimize() using the below code.
first_guess = [0.5, 0.5, 0.5]
res = optimize.minimize(fun, first_guess)Check the result or values for the several variables that we defined in the function using the below code.
res.x
This is how to find the minimum value for multiple variables by creating a method in Python Scipy.
Read: Python Scipy Matrix + Examples
Python Scipy Minimize Bounds
The Python Scipy module scipy.optimize contains a method Bounds() that defined the bounds constraints on variables.
The constraints takes the form of a general inequality : lb <= x <= ub
The syntax is given below.
scipy.optimize.Bounds(lb, ub, keep_feasible=False)Where parameters are:
- ub, lb(array_data): Independent variable lower and upper boundaries. Each array needs to be the same size as x or it must be a scalar, in which case a bound will apply to all the variables equally. To fix a variable, equalize the parts of lb and ub. To remove boundaries from all or some variables, use np.inf along with the appropriate sign. Remember that you can mix constraints of different types, such as interval, one-sided, or equality, by adjusting the various lb and ub components as required.
- keep_feasible(boolean): Whether to continue making the constraint elements workable after iterations. This property was set for all components with a single value. False is the default. has no impact on equality restrictions.
Let’s take an example by following the below steps:
Import the required method and define the bound using the below python code.
from scipy.optimize import BoundsDefine the bounds using the below code.
Bounds(2,7)
This is how to define the bounds using the method Bounds() of Python Scipy.
Read: Scipy Linalg – Helpful Guide
Python Scipy Minimize Constraints
Here in this section, we will create constraints and pass the constraints to a method scipy.optimize.minimize() of Python Scipy.
Define the constraints using the below python code.
s[0] + s[1] = 1Creating a function that must equal zero would be an equality (type=’eq’) constraint using the below code.
def cont(s):
return s[0] + s[1] - 1Then, we create a dict of your constraint (or, if there are multiple, a list of dicts) using the below code.
constarnt = {'type':'eq', 'fun': cont}
const_real(t):
return np.sum(np.iscomplex(s))And be sure to mention both constraints using the below code.
constarnt = [{'type':'eq', 'fun': const},
{'type':'eq', 'fun': const_real}]Next, we input constraints into minimizing method as shown in the below code.
scipy.optimize.minimize(function, data_x0, constraints=constarnt)This is how to input the constraints into the method minimize().
Read: Scipy Stats Zscore + Examples
Python Scipy Minimize Scalar
The Python Scipy module scipy.optimize.minimize contains a method minimize_scalar() that takes the scalar function of one variable that needs to minimize. If your function is a one-variable scalar function, you can use the minimize_scalar() function to get the function’s minimum value and the value that minimizes it.
The syntax is given below.
scipy.optimize.minimize_scalar(fun, bounds=None, args=(), bracket=None, method='brent', options=None, tol=None)Where parameters are:
- fun(callable): Objective function. A scalar must be returned by a scalar function.
- bounds(sequence): Bounds are a required parameter for the method “bounded” and have to contain the two items that make up the optimization bounds.
- args(tuple): Additional inputs given to the objective function.
- bracket(sequence): For the methods “golden” and “brent,” the bracketing interval is defined by the bracket, which may have three items (a, b, and c) so that a b c, and fun(b) fun(a), fun(c), or two items (a and c), which are taken to be the starting interval for a downhill bracket search. It’s not always a given that the solution will meet the condition a == x = c.
- method: Solver type. ought to be one of Golden, Bounded, and Brent.
- options(dict): A list of possible solvers.
- tol(float): Tolerance for terminating. Use solver-specific settings for fine-grained control.
The method minimize() returns res(A OptimizeResult object is used to represent the optimization result).
Let’s understand with an example by following the below steps:
Import the required method or libraries using the below python code.
from scipy import optimizeCreate a function that we are going to minimize using the below code.
def fun(s):
return (s - 3) * s * (s + 3)**3Pass the above function to a method minimize_scalar() to find the minimum value using the below code.
result = optimize.minimize_scalar(fun)
result.x
This is how to apply the method minimize_scalar() on the function to find the minimum value.
Read: Scipy Signal – Helpful Tutorial
Python Scipy Minimize Powell
The Python Scipy method minimize() that we have learned above sub-section accepts the method Powell that uses a modified version of Powell’s technique to minimize a scalar function of one or more variables.
The syntax is given below.
scipy.optimize.minimize(fun, x0,method='Powell', bounds=None, 'xtol': 0.0002, 'ftol': 0.0002, 'maxiter': None, 'maxfev': None, 'disp': False, 'direc': None, 'return_all': False})Where parameters are:
- disp(boolean): To print convergence messages, set to True.
- xtol(float): Acceptable relative error in the xopt solution for convergence.
- ftol(float): Relative error is
fun(xopt)acceptable for convergence. - maxiter, maxfev(int): Maximum number of function evaluations and iterations permitted. If neither maxiter nor maxfev is set, the default value is N*1000, where N is the number of variables. The minimization process will end when the first value is reached if both maxiter and maxfev are set.
- direc(ndarray): Initial set of Powell technique direction vectors.
- return_all(boolean): If True is selected, the best solutions for each iteration will be returned in a list.
For the rest of the parameters, please visit the first section of this tutorial.
Read: Scipy Rotate Image + Examples
Python Scipy Minimize Not Working
If we find that method minimize() is not working, which means any provided input or parameters, etc, aren’t provided in the way that they should be. Sometimes we provide vectors in place of scalars to a method, or invalid parameters and functions.
This kind of mistake generates an error or tells that the minimize not working. To avoid the error, follow the proper documentation about the method minimize() how to use this method, and what kind of valid value or parameters it accepts. For demonstration purposes, there is an error on StackOverflow.
Python Scipy Minimize Trust-Constr
The method trust-exact is compatible with the Python Scipy function minimize (), which we learned about in the previous section. Using a trust-exact method with a function minimize() that is almost accurate to minimize the scalar function of one or more variables.
The syntax is given below.
scipy.optimize.minimize(fun, x0, args=(), method='trust-exact', jac=None, hess=None, tol=None, callback=None, options={})Where parameters are:
- intial_tr_radius(float): Initial radius of trust-region.
- max_tr_radius(float): Radius of the trust-region at its maximum value. Over this value, no additional steps will be suggested.
- eta(float): Acceptance criteria for proposed steps that are dependent on trust regions.
- gtol(float): Before a termination is successful, the gradient norm must be lower than the gtol.
For the rest of the parameters, please refer to the first section of this tutorial.
You may also like to read the following Python SciPy tutorial.
- Scipy Optimize – Helpful Guide
- Python Scipy Stats Skew
- Python Scipy Stats Mode with Examples
- Python Scipy Stats Multivariate_Normal
- Scipy Constants – Multiple Examples
- Scipy Sparse – Helpful Tutorial
- Scipy Rotate Image + Examples
So, in this tutorial, we have learned about “Python Scipy Minimize” and covered the following topics.
- Python Scipy Minimize
- Python Scipy Minimize Multiple Variables
- Python Scipy Minimize Bounds
- Python Scipy Minimize Constraints
- Python Scipy Minimize Scalar
- Python Scipy Minimize Powell
- Python Scipy Minimize Not Working
- Python Scipy Minimize Trust-Constr
Python is one of the most popular languages in the United States of America. I have been working with Python for a long time and I have expertise in working with various libraries on Tkinter, Pandas, NumPy, Turtle, Django, Matplotlib, Tensorflow, Scipy, Scikit-Learn, etc… I have experience in working with various clients in countries like United States, Canada, United Kingdom, Australia, New Zealand, etc. Check out my profile.