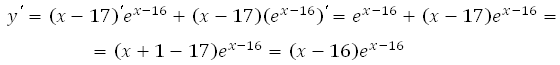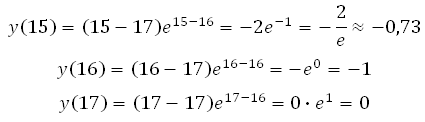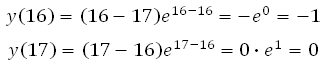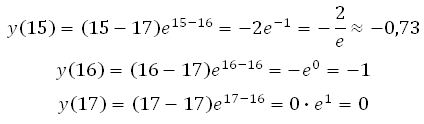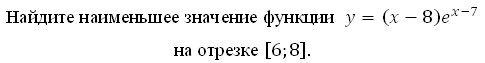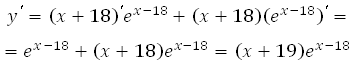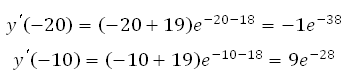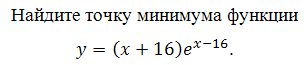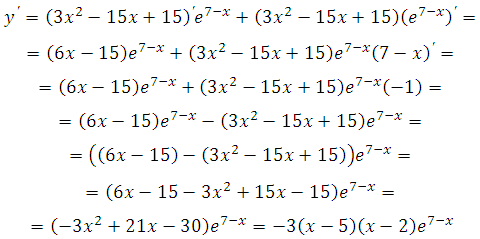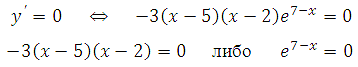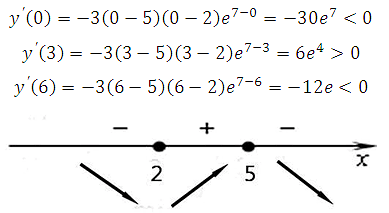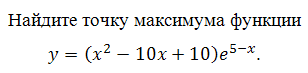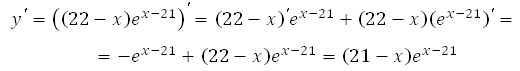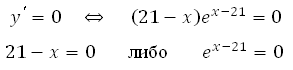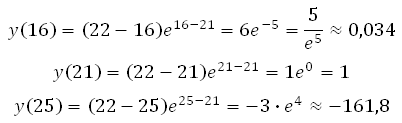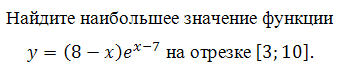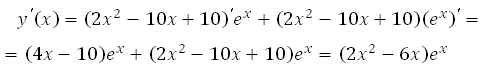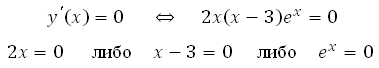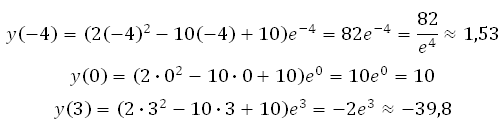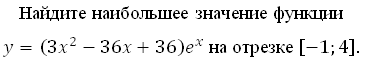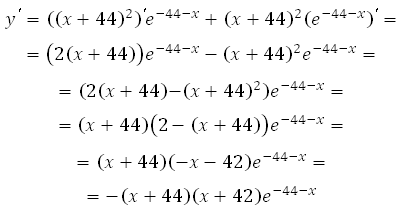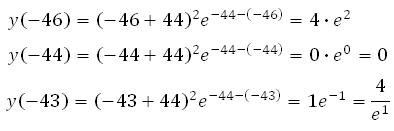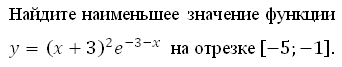Как найти минимум функции с экспонентой

  Функции с числом е. Друзья! На сайте «Математический тандем» проходит конкурс «Лучший комментатор декабря 2012 года», так что добро пожаловать, будут призы. В данной статье мы с вами рассмотрим задачи, входящие в сотав типовых заданий экзамена по математике, связанные с исследованием функций (где присутствует число е).

Рекомендую вам ещё раз внимательно прочитать статью «Исследование функций. Это нужно знать!» и освежить в памяти изложенную информацию. Не устану повторять, что для того чтобы решать задачи на нахождение наибольшего или наименьшего значения, задачи на нахождение экстремумов, важно понимать свойства производной для исследования функций, знать таблицу производных и правила дифференцирования.

После решения каждой задачи есть разъяснения другого подхода к решению (я обещал вам «хитрости» — они здесь). Рекомендую посмотреть, выглядит график показательной функции.

Рассмотрим задачи:

Найдите наименьшее значение функции у = (х–17)е^х–16 

на отрезке [15;17].

Мы знаем, что для того, чтобы найти наибольшее или наименьшее значение функции на отрезке, необходимо вычислить её значение на границах заданного интервала и в точках, где производная равна нулю. Действуем по алгоритму:

1. Найдём производную заданной функции:

2. Найдем нули производной на заданном отрезке, то есть приравниваем производную к нулю и вычислим корни уравнения:

*Выражение е^х-16 не равно нулю ни при каких х, так как известно, что показательная функция имеет положительные значения на всей области определения.

3. Определяем принадлежит ли найденная точка интервалу.

Точка х = 16  принадлежит интервалу  [15;17]. Значит значение функции будем вычислять в точках  15, 16 и 17:

*Учтите, что число е ≈ 2,71.  Это нецелое число и неконечная десятичная дробь, поэтому любое выражение с этим числом в подобных задачах на ЕГЭ не является верным ответом, но вы всё равно его проанализируйте. В данной задаче, если мы  –2 разделим на число 2,71  то результат будет лежать в пределах от –1 до 0 (можно посчитать столбиком для проверки).

4. Делаем вывод.

Таким образом, наименьшее значение функции равно  –1.

Ответ: –1

В этой статье  я обещал вам какие-то там «хитрости», которые можно использовать при решении. Если вы поняли теорию производной и знаете, как находить максимальные и минимальные значения, то тогда читайте дальше — представленный приём будет хорошим дополнительным «инструментом» и позволит решать подобные задания мгновенно.

Итак! Мы знаем, что ответом в задачах на ЕГЭ в части В должно быть целое число, либо конечная десятичная дробь.

Посмотрите на данную функцию. Сразу можно сказать, что  значение функции будет являться целым числом только при х = 16 или при х = 17,  и  ни при каких других значениях х. Поэтому достаточно вычислить:

и далее записать ответ.

Ещё один путь решения (без нахождения производной). Сразу подставляем в функцию все целые значения из интервала (их всего три 15, 16 и 17), вычисляем и выбираем наименьшее значение:

Решите самостоятельно:

Посмотреть решение 

Найдите точку минимума функции у = (х + 18)е^х-18   

1. Найдём производную заданной функции:

2. Найдем нули производной:

Получаем, что х = –19.  

*Выражение е^х-18 не равно нулю ни при каких х, так как известно, что показательная функция имеет положительные значения на всей области определения.

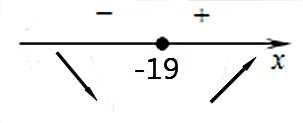
3. Определим знаки производной функции на интервалах (подставляем любые произвольные значения в производную) и изобразим на рисунке поведение функции:

В точке х = –19 функция меняет знак с отрицательного на положительный, значит это искомая точка минимума.

Ответ: –19 

Как решать быстрее данный тип задач?

Когда мы получили производную и приравняли её к нулю:

(х + 19)е^х–18 = 0

Далее получили, что х=–19. Данное решение и будет являться ответом задачи. 

*То есть, в при решении данного типа задач, можно обойтись без определения знаков производной на интервалах. Но будьте осторожны! В других заданиях на нахождение максимума (минимума), где получите несколько нулей производной, её знаки на интервалах нужно определять обязательно.

Решите самостоятельно:

Посмотреть решение 

Найдите точку максимума функции у = (3х² – 15х + 15)е^7–х

Найдём производную заданной функции:

Найдем нули производной:

Число е^7-х не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное. 

Решаем  – 3 (х–5)(х–2) = 0.  Получим х₁ = 5  и  х₂ = 2 .

Определим знаки производной функции (подставляя любые значения из интервалов в найденную производную) и изобразим на рисунке поведение функции:

В точке х = 5 функция меняет знак с положительного на отрицательный, значит это искомая точка максимума.

Ответ: 5

Решите самостоятельно:

Посмотреть решение 

Найдите наибольшее значение функции у = (22 – х)е^х–21  

на отрезке [16;25].

Найдём производную заданной функции:

Найдем нули производной:

Число е^х-21 не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное, значит х = 21.

Полученное значение принадлежит интервалу [16;25].

Вычислим значения данной в условии функции в точках 16, 21  и 25:

*То есть на границах интервала и в точке, где производная обращается в нуль.

Первый результат меньше единицы (это понятно и без вычислений).

Третий результат так же меньше единицы (отрицательное число).

Значит наибольшее значение функции на заданном  интервале равно 1.

*Помните, что ответы с числом е (по требованиеям ЕГЭ) не являются верными.

Ответ: 1

Если у вас всё-таки неразрешимые проблемы с нахождением производной, то подставляйте в исходную функцию все целые значения из интервала и выбирайте наибольшее полученное значение.

*Кроме того, по данной функции сразу видно, что её значение будет целым числом только при х = 21 или при х = 22.

Можете подставить только их в функцию, далее произвести вычисления и выбрать наибольшее значение.

Решите самостоятельно:

Посмотреть решение 

Найдите наибольшее значение функции у = (2х² – 10х + 10)е ^х

на отрезке [–4; 3].

Необходимо определить значения на границах интервала, и в точках, где производная обращается в нуль.

Найдём производную заданной функции:

Найдем нули производной:

Произведение множителей равно нулю, когда какой либо из этих множителей  равен нулю.

Число е^х не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное.

Значит  решением  являются корни: х₁=0  и  х₂=3

Обе точки принадлежат интервалу [–4;3], х=3 совпадает с границей интервала.

Вычисляем значения функции в точках: – 4, 0 и 3:  

Значит наибольшее значение функции равно 10.

Ответ: 10

*Как вы уже поняли, можно в заданную функцию можно подставить все целые значения х из интервала, и таким образом найти наибольшее значение функции. Но в данном случае придётся перебрать 8 чисел (–4;–3;–2;–1;0;1;2;3).

Решите самостоятельно:

Посмотреть решение 

Найдите наименьшее значение функции  у = (х + 44)²е^–44–х    

на отрезке  [– 46; –43] 

Найдём производную заданной функции:

Обратите внимание, что результат мы представили сразу в виде множителей, это будет удобно при вычислении нулей производной.

Найдем нули производной:

Решением являются корни:  х₁= – 44   и   х₂= – 42. 

Заданному интервалу [– 46;–43]  принадлежит только точка  х = – 44.

Вычисляем значения функции в точках – 46, – 44 и – 43, то есть на границах интервала и в точке, где производная равна нулю:

Наименьшее значение функции равно 0.

Ответ: 0

*Как это задание решить быстро?

Учитывая, что ответом должно быть целое число, видно что значение данной функции будет целым только при х= – 44 и х= 44.

указанному в условии интервалу принадлежит х= – 44, вычисляем:

Решите самостоятельно:

Посмотреть решение 

В данной рубрике продолжим рассматривать задачи, не пропустите!

На этом закончим. Всем удачи!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

28 апреля 2012

По определению, показательная функция — это выражение вида y = a^x, где a > 0. Но в задаче B15 встречаются только функции вида y = e^x. В крайнем случае, y = e^{kx + b}. Причина в том, что производные этих функций считаются очень легко:

(e^x)’ = e^x;
(e^{kx + b})’ = k · e^{kx + b}.

Как видите, если в показателе стоит просто переменная x, ничего не меняется. А если там будет линейное выражение вида kx + b, то спереди добавляется множитель k. Эта формула — частный случай производной сложной функции.

Задачи на вычисление наибольшего/наименьшего значения

Все задачи B15 с показательной функцией решаются по стандартной схеме — см. «Общая схема решения задач B15». Но если требуется найти наименьше/наибольшее значение функции, есть одна фишка:

Показатель должен быть равен нулю. Потому что e⁰ = 1 — нормальное число, его можно записать в ответ. В отличие от чисел e¹, e², которые вообще не представимы в виде десятичной дроби.

Данное замечание реально сокращает объем вычислений. Аналогичное правило есть у логарифмов — см. «Как считать логарифмы еще быстрее». И это вполне логично, поскольку логарифмы и показательные функции — родственные объекты.

А теперь разберем конкретные задачи.

Задача. Найдите наименьшее значение функции на отрезке [−1; 5]:

y = (x² − 5x + 5)e^{x − 3}

Сначала находим производную и раскладываем ее на множители:

y’ = ((x² − 5x + 5)e^{x − 3})’ = … = (x² − 3x)e^{x − 3} = x(x − 3)e^{x − 3}

Затем приравниваем полученное выражение к нулю и находим корни:

x(x − 3)e^{x − 3} = 0;
x₁ = 0; x₂ = 3.

Оба корня принадлежат отрезку [−1; 5]. Итого получаем четыре точки: два корня и два конца отрезка. Осталось вычислить значение функции в этих точках:

y(−1) = ((−1)² − 5 · (−1) + 5)e^{−1 − 3} = … = 11e⁻⁴;
y(0) = (0² − 5 · 0 + 5)e^{0 − 3} = … = 5e⁻³;
y(3) = (3² − 5 · 3 + 5)e^{3 − 3} = … = −1;
y(5) = (5² − 5 · 5 + 5)e^{5 − 3} = … = 5e².

Заметим, что из этих четырех чисел в бланк можно записать только y = −1. Кроме того, это единственное отрицательное число. Следовательно, это число и будет наименьшим.

Задача. Найдите наибольшее значение функции на отрезке [0; 6]:

y = (2x − 7)e^{8 − 2 · x}

Как и в прошлый раз, вычисляем производную функции и раскладываем ее на множители:

y’ = (y = (2x − 7)e^{8 − 2 · x})’ = … = (16 − 4x)e^{8 − 2 · x} = 4(4 − x)e^{8 − 2 · x}

Приравниваем производную к нулю и находим корни:

y’ = 0;
4(4 − x)e^{8 − 2 · x} = 0;
x = 4.

Корень x = 4 принадлежит отрезку [0; 6]. Мы ищем наибольшее значение, поэтому подставляем этот корень, а также концы отрезка в исходную функцию. Имеем:

y(0) = (2 · 0 − 7)e^{8 − 2 · 0} = … = −7e⁸;
y(4) = (2 · 4 − 7)e^{8 − 2 · 4} = … = 1;
y(6) = (2 · 6 − 7)e^{8 − 2 · 6} = … = 5e⁻⁴.

Итак, ответом может быть только число y = 1.

Задачи на вычисление точек максимума/минимума

В задачах на точки максимума/минимума нельзя применять приведенное выше правило, поэтому считаем все по стандартной схеме.

Задача. Найдите точку минимума функции:

y = (x − 12)e^{x − 11}

В первую очередь считаем производную:

y’ = (y = (x − 12)e^{x − 11})’ =
= (x − 12)’ · e^{x − 11} + (x − 12) · (e^{x − 11})’ =
= 1 · e^{x − 11} + (x − 12)e^{x − 11} =
= (1 + x − 12)e^{x − 11} =
= (x − 11)e^{x − 11}

Приравниваем производную к нулю:

y’ = 0;
(x − 11)e^{x − 11} = 0;
x − 11 = 0;
x = 11.

Множитель e^{x − 11} никогда не равен нулю, поэтому мы избавились от него. Осталось начертить координатную ось и расставить знаки производной:

Итак, в точке x = 11 знак производной меняется с минуса на плюс. Считаем всегда в направлении оси — слева направо. Значит, x = 11 — это точка минимума.

Задача. Найдите точку максимума функции:

y = (2x² − 34x + 34)e^{6 − x}

Снова считаем производную:

y’ = ((2x² − 34x + 34)e^{6 − x})’ =
= (2x² − 34x + 34)’ · e^{6 − x} + (2x² − 34x + 34) · (e^{6 − x})’ =
= (4x − 34)e^{6 − x} + (2x² − 34x + 34) · (−1) · e^{6 − x}

Напомню, что производная сложной показательной функции считается по формуле:

(e^{kx + b})’ = k · e^{kx + b};
(e^{6 − x})’ = (−1) · e^{6 − x}.

Производная получилась довольно навороченная. Разложим ее на множители, для этого вынесем e^{6 − x} за скобку. Имеем:

(4x − 34)e^{6 − x} + (2x² − 34x + 34) · (−1) · e^{6 − x} =
= e^{6 − x} · (4x − 34 − 2x² + 34x − 34) =
= e^{6 − x} · (−2x² + 38x − 68)

Приравниваем полученное выражение к нулю:

e^{6 − x} · (−2x² + 38x − 68) = 0;
−2x² + 38x − 68 = 0;
x² − 19x + 34 = 0;
…
x₁ = 17; x₂ = 2.

Множитель e^{6 − x} снова можно безболезненно убрать, поскольку он никогда не равен нулю. Осталось отметить полученные точки и знаки производной на координатной прямой:

Обратите внимание: на рисунке отмечены знаки производной функции: y = e^{6 − x} · (−2x² + 38x − 68) — а вовсе не многочлена x² − 19x + 34, как думают некоторые ученики. В скобках стоит квадратичная функция, ее график — парабола ветвями вниз, поскольку a = −2 < 0.

В точке x = 17 знак производной меняется с плюса на минус. Значит, это точка максимума, что и требовалось найти.

Смотрите также:

1. Задача B15: частный случай при работе с квадратичной функцией
2. Специфика работы с логарифмами в задаче B15
3. Тест к уроку «Что такое числовая дробь» (легкий)
4. Типичные задачи B12 с функциями
5. Однородные тригонометрические уравнения: общая схема решения
6. ЕГЭ 2022, задание 6. Касательная и уравнение с параметром

Сайты, меню, вход, новости

Этот раздел содержит задачи ЕГЭ по математике на темы, связанные с исследованием функций и их производных. В частности, речь идёт о поиске максимальных и минимальных значений функций, заданных аналитически, то есть формулой.

Таким образом,

• если в задании стоит требование определить точки экстремума в ответе следует писать найденные значения x,
• если нужно указать сами экстремумы, то нужно определить значения y в этих точках, подставив их в формулу функции y = f(x).

Что касается наибольших и наименьших значений функции на заданном отрезке, то для непрерывной функции они могут достигаться как внутри отрезка, так и на его концах. Графические иллюстрации к этой теме можно посмотреть здесь.
Если наибольшего (наименьшего) значения функция достигает во внутренней точке отрезка, то эта точка совпадает с точкой соответствующего экстремума. Для ответа на такой вопрос задания следует сравнить значения функции в точках экстремума с её значениями на концах отрезка. (На практике для решения этой задачи не обязательно определять вид экстремума, достаточно вычислить значения функции в критических точках и на концах отрезка и сравнить их между собой.)

1. Задачи на нахождение точек экстремума функции.
2. Задачи на нахождение экстремумов функции.
3. Задачи на определение наибольшего (наименьшего) значения функции на отрезке.

В 2022 году это задание имеет номер 11.

Задачи на нахождение точек экстремума функции.

Алгоритм нахождения точек экстремума.

1) Найти область определения функции.
2) Найти её производную f ‘(x).
3) Найти точки, в которых f ‘(x) не существует.
4) Найти точки в которых f ‘(x) = 0.
5) Отметить на числовой прямой область определения функции и все точки, выявленные в п.3 и п.4. Получатся промежутки области определения, на которых производная сохраняет постоянный знак.
6) Определить знак f ‘(x) для каждого промежутка. (Чаще всего это делается подстановкой «удобного» значения x из этого промежутка в полученную в п.2 формулу для производной.)
7) Определить по знакам производной участки возрастания и убывания функции и сделать выводы о наличии или отсутствии экстремума и его характере в каждой из критических точек.

Теперь проверьте свои силы. Сначала постарайтесь решить задачу самостоятельно, затем сравните ответ, потом можно раскрыть моё решение. Если ваше решение не совпадает с моим, оно не обязательно является неправильным.

Внимание:
Для усиления обучающего эффекта ответы и решения загружаются отдельно для каждой задачи последовательным нажатием кнопок на желтом фоне. (Когда задач много, кнопки могут появиться с задержкой. Если кнопок не видно совсем, проверьте, разрешен ли в вашем браузере JavaScript.)

Задачи на нахождение экстремумов функции.

1) Находим точки экстремумов функции и определяем их характер так же, как в задачах выше.
2) Определяем значения функции в точках максимума или минимума в соответствии с вопросом задачи.
3) Если точек максимума (минимума) на области определения функции несколько, то максимумы (минимумы) называются локальными, а самый большой (самый маленький) называется глобальным максимумом (минимумом) или наибольшим (наименьшим) значением функции. Ещё раз читаем вопрос задачи и выбираем нужный.

Задачи на определение наибольшего (наименьшего) значения функции на отрезке.

Непрерывная на отрезке функция достигает своего наименьшего и наибольшего значений либо во внутренних точках промежутка, либо на его концах. Поэтому для решения задач этого раздела достаточно определить значения функции в точках экстремума и сравнить их с её значениями на концах отрезка. Выявлять тип экстремума необязательно.

Если не будет соблюдено хотя бы одно из двух условий — функция окажется разрывной или в качестве промежутка будет задан интервал (полуинтервал), то потребуется полный анализ поведения функции и её производной, и не факт, что ответ будет существовать. На ЕГЭ задач с такими усложненными условиями пока не обнаружено, а те, кому просто интересно, могут пройти по ссылке и посмотреть здесь.

Вернуться и повторить другие задачи на производную.

1. Задачи на определение характеристик производной по графику функции.
2. Задачи на определение характеристик функции по графику её производной.
3. Задачи на геометрический смысл производной.
4. Задачи на физический смысл производной.

Вернуться  к списку заданий первой части профильного уровня ЕГЭ по математке.