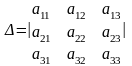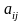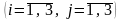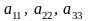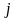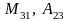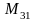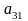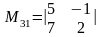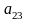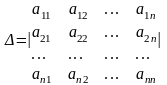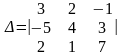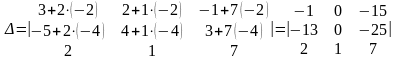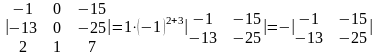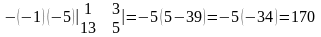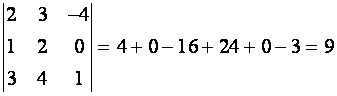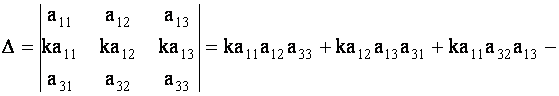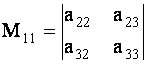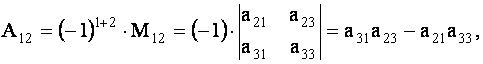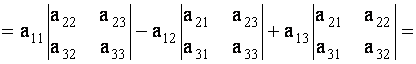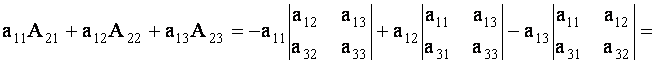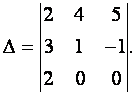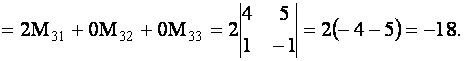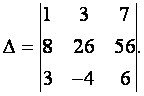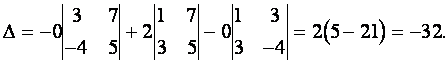Разложение определителя по строке (столбцу)
Пусть дана квадратная матрица 3-го порядка

Одной из характеристик матрицы является ее определитель – число, вычисленное по правилу

Коэффициент при Aij в этой формуле (соответствующий определитель 2-го порядка) называется Минором этого элемента (от слова “младший”).
Дадим строгое определение минора элемента матрицы.
Минором элемента матрицы называется определитель Mij, полученный из матрицы А путем вычеркивания из матрицы i-й строки и j-го столбца.
Например, определитель второго порядка
Является минором элемента A12 матрицы (1.4) (из матрицы А вычеркнута 1-я строка и 2-й столбец).
Теперь, используя понятие минора, правило вычисления Определителя матрицы 3-го порядка можно записать так:
det A= A11 × M11 – A12 × M12 + A13 × M13. (1.6)
Эта формула называется разложением определителя по первой строке, она позволяет свести вычисление определителя 3-го порядка к вычислению трех определителей 2-го порядка.
Назовем число Aij = (–1)I+J× Mij Алгебраическим дополнением элемента Aij. Очевидно, что

Знак, который приписывается минору соответствующего элемента определителя, можно записать в следующей таблице:
С помощью алгебраических дополнений формулу (1.6) можно записать так:

Итак, Определитель равен сумме произведений элементов первой строки на их алгебраические дополнения.
Можно доказать, что это правило справедливо для произвольной строки или столбца определителя. Результат вычисления определителя не зависит от того, по какой строке или столбцу записывается разложение типа (1.8). Справедлива общая теорема.
Определитель матрицы равен сумме произведений элементов произвольной строки (столбца) матрицы на их алгебраические дополнения.
Например, разлагая по второй строке, получим

Разложите этот определитель по первой строке и сравните ответ. Убедитесь, что результат будет таким же.
Заметим, что справедлива теорема: сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.
| < Предыдущая | Следующая > |
|---|
Мы уже знакомы с понятием определителя матрицы. Также мы рассмотрели правила вычисления детерминантов (определителей) первого и второго порядка. Познакомимся с различными вариантами нахождения определителей третьего порядка.
Вычисление определителей по правилу треугольника
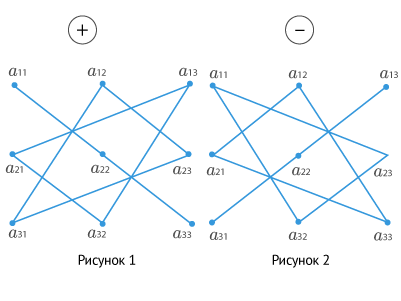
Схематически раскрытие определителя по этому правилу выглядит так:
Согласно рисункам №1 и №2 мы перемножаем элементы, соединенные прямыми. Произведения элементов будут иметь определенные знаки: для рисунка 1 — «+», для рисунка 2 — «-».
| Произведения, которые берутся со знаком «+» | Произведения, которые берутся со знаком «-» |
|---|---|
| a11⋅a22⋅a33a_{11} cdot a_{22} cdot a_{33} | a13⋅a22⋅a31a_{13}cdot a_{22}cdot a_{31} |
| a12⋅a23⋅a31a_{12} cdot a_{23} cdot a_{31} | a12⋅a33⋅a21a_{12}cdot a_{33}cdot a_{21} |
| a13⋅a32⋅a21a_{13} cdot a_{32} cdot a_{21} | a11⋅a23⋅a32a_{11}cdot a_{23}cdot a_{32} |
На рисунке 1 мы видим равнобедренные треугольники с основаниями, параллельными главной диагонали; на рисунке 2 — равнобедренные треугольники с основаниями, параллельными второй (побочной) диагонали. Поэтому данное правило имеет такое название.
Определитель может быть вычислен по формуле:
∣a11a12a13a21a22a23a31a32a33∣=begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}=
=a11⋅a22⋅a33+a12⋅a23⋅a31+a13⋅a32⋅a21−a13⋅a22⋅a31−a12⋅a33⋅a21−a11⋅a23⋅a32=a_{11}cdot a_{22}cdot a_{33}+a_{12}cdot a_{23}cdot a_{31}+a_{13}cdot a_{32}cdot a_{21}-a_{13}cdot a_{22}cdot a_{31}-a_{12}cdot a_{33}cdot a_{21}-a_{11}cdot a_{23}cdot a_{32}.
Примеры
Рассмотрим примеры нахождения определителя по правилу треугольника.
Найти определитель ∣925148637∣begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix} по правилу треугольника.
По правилу треугольника определитель третьего порядка равен:
∣925148637∣=9⋅4⋅7+2⋅8⋅6+5⋅3⋅1−5⋅4⋅6−2⋅7⋅1−9⋅8⋅3=begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix}=9cdot4cdot7+2cdot8cdot6+5cdot3cdot1-5cdot4cdot6-2cdot7cdot1-9cdot8cdot3=
=252+96+15−120−14−216=13=252+96+15-120-14-216=13.
Найти определитель ∣21−46−3510−1∣begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix} по правилу треугольника.
Искомый определитель третьего порядка равен:
∣21−46−3510−1∣=begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix}=
=2⋅(−3)⋅(−1)+1⋅5⋅1+(−4)⋅0⋅6−(−4)⋅(−3)⋅1−1⋅(−1)⋅6−2⋅5⋅0=6+5−12+6=5=2cdot(-3)cdot(-1)+1cdot5cdot1+(-4)cdot0cdot6-(-4)cdot(-3)cdot1-1cdot(-1)cdot6-2cdot5cdot0=6+5-12+6=5.
При вычислении определителей таким способом можно легко совершить ошибку из-за невнимательности. Чтобы избежать таких ошибок существует второй способ, называемый правилом Саррюса, или способом «параллельных полосок».
Вычисление определителей по правилу Саррюса
Правило Саррюса также именуют способом присоединения двух строк/столбцов или правилом параллельных полосок.
Основная идея этого правила состоит в приписывании первого и второго столбца справа от определителя.
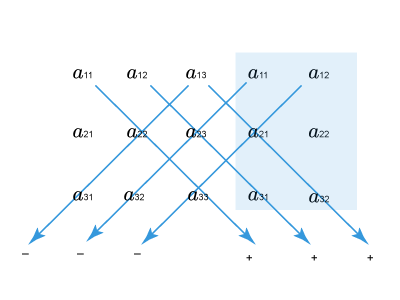
Вычисления будем производить по следующей схеме:
Перемножаем элементы, соединенные прямыми. Данные произведения берем со знаком «+», если диагональ, на которой они стоят, является главной или параллельной ей; со знаком «-», если она является второй (побочной) или параллельной ей.
| Произведения, которые берутся со знаком «+» | Произведения, которые берутся со знаком «-» |
|---|---|
| a11⋅a22⋅a33a_{11} cdot a_{22} cdot a_{33} | a13⋅a22⋅a31a_{13}cdot a_{22}cdot a_{31} |
| a12⋅a23⋅a31a_{12} cdot a_{23} cdot a_{31} | a11⋅a23⋅a32a_{11}cdot a_{23}cdot a_{32} |
| a13⋅a21⋅a32a_{13} cdot a_{21} cdot a_{32} | a12⋅a21⋅a33a_{12}cdot a_{21}cdot a_{33} |
В общем виде вычисление по правилу Саррюса можно записать следующим образом:
∣a11a12a13a21a22a23a31a32a33∣=∣a11a12a13a21a22a23a31a32a33∣a11a12a21a22a31a32=begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}=begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}begin{matrix}a_{11}&a_{12}\a_{21}&a_{22}\a_{31}&a_{32}end{matrix}=
=a11⋅a22⋅a33+a12⋅a23⋅a31+a13⋅a21⋅a32−a13⋅a22⋅a31−a11⋅a23⋅a32−a12⋅a21⋅a33=a_{11}cdot a_{22}cdot a_{33}+a_{12}cdot a_{23}cdot a_{31}+a_{13}cdot a_{21}cdot a_{32}-a_{13}cdot a_{22}cdot a_{31}-a_{11}cdot a_{23}cdot a_{32}-a_{12}cdot a_{21}cdot a_{33}.
Сравнивая эти два способа вычисления определителей, видим одинаковые множители, которые во втором случае немного переставлены местами.
Возможность допустить ошибку, вычисляя определитель по правилу Саррюса, намного меньше.
Примеры
Найти определитель ∣925148637∣begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix} по правилу Саррюса.
Приписываем два первых столбца справа от определителя и вычисляем его:
∣925148637∣921463=begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix}begin{matrix}9&2\1&4\6&3end{matrix}=
=9⋅4⋅7+2⋅8⋅6+5⋅1⋅3−5⋅4⋅6−9⋅8⋅3−2⋅1⋅7=252+96+15−120−216−14=13=9cdot4cdot7+2cdot8cdot6+5cdot1cdot3-5cdot4cdot6-9cdot8cdot3-2cdot1cdot7=252+96+15-120-216-14=13.
Найти определитель ∣21−46−3510−1∣begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix} по правилу Саррюса.
Приписываем два первых столбца справа от определителя и вычисляем его:
∣21−46−3510−1∣216−310=begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix}begin{matrix}2&1\6&-3\1&0end{matrix}=
=2⋅(−3)⋅(−1)+1⋅5⋅1+(−4)⋅6⋅0−(−4)⋅(−3)⋅1−2⋅5⋅0−1⋅6⋅(−1)=6+5−12+6=5=2cdot(-3)cdot(-1)+1cdot5cdot1+(-4)cdot6cdot0-(-4)cdot(-3)cdot1-2cdot5cdot0-1cdot6cdot(-1)=6+5-12+6=5.
Существует еще одна вариация правила Саррюса. Она состоит в приписывании первой и второй строки снизу от определителя. Вычисления производятся аналогично.
Минор и алгебраическое дополнение
Прежде чем перейти к рассмотрению еще одного способа вычисления определителей 3-го порядка разберем 2 понятия: минор, алгебраическое дополнение.
Минор
Минором MijM_{ij} к элементу aija_{ij} определителя n-го порядка называется определитель (n−1)(n-1)-го порядка, который получается из исходного определителя вычеркиванием ii-той строки и jj-того столбца.
Таким образом, минор — это определитель, который остается после вычеркивания определенной строки и определенного столбца. Например, M11M_{11} получается вычеркиванием 1-й строки и 1-го столбца, M23M_{23} — вычеркиванием 2-й строки и 3-го столбца.
Алгоритм нахождения миноров:
- вычеркиваем ii-ю строку;
- вычеркиваем jj-й столбец;
- записываем определитель, который получили в результате действий 1 и 2.
Примеры
Найти миноры матрицы F=(925148637)F=begin{pmatrix}9&2&5\1&4&8\6&3&7end{pmatrix}.
Те строки и столбцы, которые будем вычеркивать, обозначим зеленым цветом.
M11=∣925148637∣=∣4837∣=4⋅7−3⋅8=28−24=4M_{11}=begin{vmatrix}color{green}9&color{green}2&color{green}5\color{green}1&4&8\color{green}6&3&7end{vmatrix}=begin{vmatrix}4&8\3&7end{vmatrix}=4cdot7-3cdot8=28-24=4,
M12=∣925148637∣=∣1867∣=1⋅7−6⋅8=7−48=−41M_{12}=begin{vmatrix}color{green}9&color{green}2&color{green}5\1&color{green}4&8\6&color{green}3&7end{vmatrix}=begin{vmatrix}1&8\6&7end{vmatrix}=1cdot7-6cdot8=7-48=-41,
M13=∣925148637∣=∣1463∣=1⋅3−6⋅4=3−24=−21M_{13}=begin{vmatrix}color{green}9&color{green}2&color{green}5\1&4&color{green}8\6&3&color{green}7end{vmatrix}=begin{vmatrix}1&4\6&3end{vmatrix}=1cdot3-6cdot4=3-24=-21,
M21=∣925148637∣=∣2537∣=2⋅7−3⋅5=14−15=−1M_{21}=begin{vmatrix}color{green}9&2&5\color{green}1&color{green}4&color{green}8\color{green}6&3&7end{vmatrix}=begin{vmatrix}2&5\3&7end{vmatrix}=2cdot7-3cdot5=14-15=-1,
M22=∣925148637∣=∣9567∣=9⋅7−6⋅5=63−30=33M_{22}=begin{vmatrix}9&color{green}2&5\color{green}1&color{green}4&color{green}8\6&color{green}3&7end{vmatrix}=begin{vmatrix}9&5\6&7end{vmatrix}=9cdot7-6cdot5=63-30=33,
M23=∣925148637∣=∣9263∣=9⋅3−6⋅2=27−12=15M_{23}=begin{vmatrix}9&2&color{green}5\color{green}1&color{green}4&color{green}8\6&3&color{green}7end{vmatrix}=begin{vmatrix}9&2\6&3end{vmatrix}=9cdot3-6cdot2=27-12=15,
M31=∣925148637∣=∣2548∣=2⋅8−4⋅5=16−20=−4M_{31}=begin{vmatrix}color{green}9&2&5\color{green}1&4&8\color{green}6&color{green}3&color{green}7end{vmatrix}=begin{vmatrix}2&5\4&8end{vmatrix}=2cdot8-4cdot5=16-20=-4,
M32=∣925148637∣=∣9518∣=9⋅8−1⋅5=72−5=67M_{32}=begin{vmatrix}9&color{green}2&5\1&color{green}4&8\color{green}6&color{green}3&color{green}7end{vmatrix}=begin{vmatrix}9&5\1&8end{vmatrix}=9cdot8-1cdot5=72-5=67,
M33=∣925148637∣=∣9214∣=9⋅4−1⋅2=36−2=34M_{33}=begin{vmatrix}9&2&color{green}5\1&4&color{green}8\color{green}6&color{green}3&color{green}7end{vmatrix}=begin{vmatrix}9&2\1&4end{vmatrix}=9cdot4-1cdot2=36-2=34.
Найти миноры матрицы G=(21−46−3510−1)G=begin{pmatrix}2&1&-4\6&-3&5\1&0&-1end{pmatrix}.
Те строки и столбцы, которые будем вычеркивать, обозначим зеленым цветом.
M11=∣21−46−3510−1∣=∣−350−1∣=(−3)⋅(−1)−0⋅5=3−0=3M_{11}=begin{vmatrix}color{green}2&color{green}1&color{green}-4\color{green}6&-3&5\color{green}1&0&-1end{vmatrix}=begin{vmatrix}-3&5\0&-1end{vmatrix}=(-3)cdot(-1)-0cdot5=3-0=3,
M12=∣21−46−3510−1∣=∣651−1∣=6⋅(−1)−1⋅5=−6−5=−11M_{12}=begin{vmatrix}color{green}2&color{green}1&color{green}-4\6&color{green}-3&5\1&color{green}0&-1end{vmatrix}=begin{vmatrix}6&5\1&-1end{vmatrix}=6cdot(-1)-1cdot5=-6-5=-11,
M13=∣21−46−3510−1∣=∣6−310∣=6⋅0−1⋅(−3)=0+3=3M_{13}=begin{vmatrix}color{green}2&color{green}1&color{green}-4\6&-3&color{green}5\1&0&color{green}-1end{vmatrix}=begin{vmatrix}6&-3\1&0end{vmatrix}=6cdot0-1cdot(-3)=0+3=3,
M21=∣21−46−3510−1∣=∣1−40−1∣=1⋅(−1)−0⋅(−4)=−1−0=−1M_{21}=begin{vmatrix}color{green}2&1&-4\color{green}6&color{green}-3&color{green}5\color{green}1&0&-1end{vmatrix}=begin{vmatrix}1&-4\0&-1end{vmatrix}=1cdot(-1)-0cdot(-4)=-1-0=-1,
M22=∣21−46−3510−1∣=∣2−41−1∣=2⋅(−1)−1⋅(−4)=−2+4=2M_{22}=begin{vmatrix}2&color{green}1&-4\color{green}6&color{green}-3&color{green}5\1&color{green}0&-1end{vmatrix}=begin{vmatrix}2&-4\1&-1end{vmatrix}=2cdot(-1)-1cdot(-4)=-2+4=2,
M23=∣21−46−3510−1∣=∣2110∣=2⋅0−1⋅1=0−1=−1M_{23}=begin{vmatrix}2&1&color{green}-4\color{green}6&color{green}-3&color{green}5\1&0&color{green}-1end{vmatrix}=begin{vmatrix}2&1\1&0end{vmatrix}=2cdot0-1cdot1=0-1=-1,
M31=∣21−46−3510−1∣=∣1−4−35∣=1⋅5−(−3)⋅(−4)=5−12=−7M_{31}=begin{vmatrix}color{green}2&1&-4\color{green}6&-3&5\color{green}1&color{green}0&color{green}-1end{vmatrix}=begin{vmatrix}
1&-4\-3&5end{vmatrix}=1cdot5-(-3)cdot(-4)=5-12=-7,
M32=∣21−46−3510−1∣=∣2−465∣=2⋅5−6⋅(−4)=10+24=34M_{32}=begin{vmatrix}2&color{green}1&-4\6&color{green}-3&5\color{green}1&color{green}0&color{green}-1end{vmatrix}=begin{vmatrix}2&-4\6&5end{vmatrix}=2cdot5-6cdot(-4)=10+24=34,
M33=∣21−46−3510−1∣=∣216−3∣=2⋅(−3)−6⋅1=−6−6=−12M_{33}=begin{vmatrix}2&1&color{green}-4\6&-3&color{green}5\color{green}1&color{green}0&color{green}-1end{vmatrix}=begin{vmatrix}2&1\6&-3end{vmatrix}=2cdot(-3)-6cdot1=-6-6=-12.
Алгебраическое дополнение
Алгебраическим дополнением AijA_{ij} к элементу aija_{ij} определителя nn-го порядка называется число Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij},
где ii, jj — соответствующие строка и столбец,
MijM_{ij} — минор к элементу aija_{ij}.
Алгоритм нахождения алгебраических дополнений:
- найти сумму номеров строки (i)(i) и столбца (j)(j);
- найти минор MijM_{ij} по алгоритму нахождения миноров, который представлен выше;
- подставить значения, полученные на шагах 1 и 2, в формулу Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij}.
Примеры
Найти алгебраические дополнения матрицы F=(925148637)F=begin{pmatrix}9&2&5\1&4&8\6&3&7end{pmatrix}.
A11=(−1)1+1⋅M11=(−1)2⋅∣4837∣=4A_{11}=(-1)^{1+1}cdot M_{11}= (-1)^{2}cdotbegin{vmatrix}4&8\3&7end{vmatrix}=4,
A12=(−1)1+2⋅M12=(−1)3⋅∣1867∣=41A_{12}=(-1)^{1+2}cdot M_{12}= (-1)^{3}cdotbegin{vmatrix}1&8\6&7end{vmatrix}=41,
A13=(−1)1+3⋅M13=(−1)4⋅∣1463∣=−21A_{13}=(-1)^{1+3}cdot M_{13}= (-1)^{4}cdotbegin{vmatrix}1&4\6&3end{vmatrix}=-21,
A21=(−1)2+1⋅M21=(−1)3⋅∣2537∣=1A_{21}=(-1)^{2+1}cdot M_{21}= (-1)^{3}cdotbegin{vmatrix}2&5\3&7end{vmatrix}=1,
A22=(−1)2+2⋅M22=(−1)4⋅∣9567∣=33A_{22}=(-1)^{2+2}cdot M_{22}= (-1)^{4}cdotbegin{vmatrix}9&5\6&7end{vmatrix}=33,
A23=(−1)2+3⋅M23=(−1)5⋅∣9263∣=−15A_{23}=(-1)^{2+3}cdot M_{23}= (-1)^{5}cdotbegin{vmatrix}9&2\6&3end{vmatrix}=-15,
A31=(−1)3+1⋅M31=(−1)4⋅∣2548∣=−4A_{31}=(-1)^{3+1}cdot M_{31}=(-1)^{4}cdotbegin{vmatrix}2&5\4&8end{vmatrix}=-4,
A32=(−1)3+2⋅M32=(−1)5⋅∣9518∣=−67A_{32}=(-1)^{3+2}cdot M_{32}=(-1)^{5}cdotbegin{vmatrix}9&5\1&8end{vmatrix}=-67,
A33=(−1)3+3⋅M33=(−1)6⋅∣9214∣=34A_{33}=(-1)^{3+3}cdot M_{33}=(-1)^{6}cdotbegin{vmatrix}9&2\1&4end{vmatrix}=34.
Найти алгебраические дополнения матрицы G=(21−46−3510−1)G=begin{pmatrix}2&1&-4\6&-3&5\1&0&-1end{pmatrix}.
A11=(−1)1+1⋅M11=(−1)2⋅∣−350−1∣=3A_{11}=(-1)^{1+1}cdot M_{11}=(-1)^{2}cdotbegin{vmatrix}-3&5\0&-1end{vmatrix}=3,
A12=(−1)1+2⋅M12=(−1)3⋅∣651−1∣=11A_{12}=(-1)^{1+2}cdot M_{12}=(-1)^{3}cdotbegin{vmatrix}6&5\1&-1end{vmatrix}=11,
A13=(−1)1+3⋅M13=(−1)4⋅∣6−310∣=3A_{13}=(-1)^{1+3}cdot M_{13}=(-1)^{4}cdotbegin{vmatrix}6&-3\1&0end{vmatrix}=3,
A21=(−1)2+1⋅M21=(−1)3⋅∣1−40−1∣=1A_{21}=(-1)^{2+1}cdot M_{21}=(-1)^{3}cdotbegin{vmatrix}1&-4\0&-1end{vmatrix}=1,
A22=(−1)2+2⋅M22=(−1)4⋅∣2−41−1∣=2A_{22}=(-1)^{2+2}cdot M_{22}=(-1)^{4}cdotbegin{vmatrix}2&-4\1&-1end{vmatrix}=2,
A23=(−1)2+3⋅M23=(−1)5⋅∣2110∣=1A_{23}=(-1)^{2+3}cdot M_{23}=(-1)^{5}cdotbegin{vmatrix}2&1\1&0end{vmatrix}=1,
A31=(−1)3+1⋅M31=(−1)4⋅∣1−4−35∣=−7A_{31}=(-1)^{3+1}cdot M_{31}=(-1)^{4}cdotbegin{vmatrix}1&-4\-3&5end{vmatrix}=-7,
A32=(−1)3+2⋅M32=(−1)5⋅∣2−465∣=−34A_{32}=(-1)^{3+2}cdot M_{32}=(-1)^{5}cdotbegin{vmatrix}2&-4\6&5end{vmatrix}=-34,
A33=(−1)3+3⋅M33=(−1)6⋅∣216−3∣=−12A_{33}=(-1)^{3+3}cdot M_{33}=(-1)^{6}cdotbegin{vmatrix}2&1\6&-3end{vmatrix}=-12.
Зная, что такое миноры и алгебраические дополнения, рассмотрим вычисление определителя по строке и столбцу.
Вычисление определителя по строке или столбцу
Определитель матрицы равен сумме произведений элементов строки (столбца) на их алгебраические дополнения.
Алгоритм вычисления определителя по строке или столбцу:
- находим алгебраические дополнения элементов строки или столбца;
- находим произведения элементов на их алгебраические дополнения;
- находим сумму, полученных на шаге 2, произведений.
Примеры
Найти определитель ∣925148637∣begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix} по 2 столбцу.
∣925148637∣=2⋅A12+4⋅A22+3⋅begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix}=2cdot A_{12}+4cdot A_{22}+3cdot
A32=2(−1)3M12+4(−1)4M22+3(−1)5M32=2(−1)3∣1867∣+4(−1)4∣9567∣+3(−1)5∣9518∣=A_{32}=2(-1)^{3}M_{12}+4(-1)^{4}M_{22}+3(-1)^{5}M_{32}=2(-1)^{3}begin{vmatrix}1&8\6&7end{vmatrix}+4(-1)^{4}begin{vmatrix}9&5\6&7end{vmatrix}+3(-1)^{5}begin{vmatrix}9&5\1&8end{vmatrix}=
=−2⋅(−41)+4⋅33−3⋅67=82+132−201=13=-2cdot(-41)+4cdot33-3cdot67=82+132-201=13.
Найти определитель ∣21−46−3510−1∣begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix} по 3 строке.
∣21−46−3510−1∣=1⋅A31+0⋅A32−1⋅A33=1(−1)4M31+0(−1)5M32−1(−1)6M33=begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix}=1cdot A_{31}+0cdot A_{32}-1cdot A_{33}=1(-1)^{4}M_{31}+0(-1)^{5}M_{32}-1(-1)^{6}M_{33}=
=1(−1)4∣1−4−35∣+0(−1)5∣2−465∣−1(−1)6∣216−3∣=−7+0+12=5=1(-1)^{4}begin{vmatrix}1&-4\-3&5end{vmatrix}+0(-1)^{5}begin{vmatrix}2&-4\6&5end{vmatrix}-1(-1)^{6}begin{vmatrix}2&1\6&-3end{vmatrix}=-7+0+12=5.
Любой из рассмотренных способов можно применять при нахождении определителей третьего порядка. В следующий раз мы разберем вычисление определителей матриц высших порядков.
Оформите решение задачи на заказ онлайн, если возникают трудности с выполнением!
Тест по теме «Как вычислить определитель матрицы третьего порядка»
Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений.
В данной теме рассмотрим понятия алгебраического дополнения и минора. Изложение материала опирается на термины, пояснённые в теме “Матрицы. Виды матриц. Основные термины”. Также нам понадобятся некоторые формулы для вычисления определителей. Так как в данной теме немало терминов, относящихся к минорам и алгебраическим дополнениям, то я добавлю краткое содержание, чтобы ориентироваться в материале было проще.
Содержание темы:
- Минор $M_{ij}$ элемента $a_{ij}$.
- Алгебраическое дополнение $A_{ij}$ элемента $a_{ij}$.
- Минор k-го порядка матрицы $A_{mtimes n}$. Главный минор, базисный минор, окаймляющий минор.
- Минор k-го порядка матрицы $A_{ntimes n}$. Дополнительный минор. Алгебраическое дополнение к минору квадратной матрицы.
Минор $M_{ij}$ элемента $a_{ij}$
Пусть задана квадратная матрица $A_{ntimes n}$ (т.е. квадратная матрица n-го порядка).
Минором $M_{ij}$ элемента $a_{ij}$ матрицы $A_{ntimes n}$ именуют определитель матрицы, полученной из матрицы $A$ вычёркиванием i-й строки и j-го столбца (т.е. строки и столбца, на пересечении которых находится элемент $a_{ij}$).
Для примера рассмотрим квадратную матрицу четвёртого порядка:
$A=left( begin{array} {cccc}
1 & 0 & -3 & 9\
2 & -7 & 11 & 5 \
-9 & 4 & 25 & 84\
3 & 12 & -5 & 58 end{array} right)$. Найдём минор элемента $a_{32}$, т.е. найдём $M_{32}$. Сперва запишем минор $M_{32}$, а потом вычислим его значение. Для того, чтобы составить $M_{32}$, вычеркнем из матрицы $A$ третью строку и второй столбец (именно на пересечении третьей строки и второго столбца расположен элемент $a_{32}$). Мы получим новую матрицу, определитель которой и есть искомый минор $M_{32}$:
Этот минор несложно вычислить, используя формулу №2 из темы вычисления определителей второго и третьего порядков:
$$
M_{32}=left| begin{array} {ccc}
1 & -3 & 9\
2 & 11 & 5 \
3 & -5 & 58 end{array} right|=
1cdot 11cdot 58+(-3)cdot 5cdot 3+2cdot (-5)cdot 9-9cdot 11cdot 3-(-3)cdot 2cdot 58-5cdot (-5)cdot 1=579.
$$
Итак, минор элемента $a_{32}$ равен 579, т.е. $M_{32}=579$.
Часто вместо словосочетания “минор элемента матрицы” в литературе встречается “минор элемента определителя”. Суть остается неизменной: чтобы получить минор элемента $a_{ij}$ нужно вычеркнуть из исходного определителя i-ю строку и j-й столбец. Оставшиеся элементы записывают в новый определитель, который и является минором элемента $a_{ij}$. Например, найдём минор элемента $a_{12}$ определителя
$left| begin{array} {ccc}
-1 & 3 & 2\
9 & 0 & -5 \
4 & -3 & 7 end{array} right|$. Чтобы записать требуемый минор $M_{12}$ нам понадобится вычеркнуть из заданного определителя первую строку и второй столбец:
Чтобы найти значение данного минора используем формулу №1 из темы вычисления определителей второго и третьего порядков:
$$
M_{12}=left| begin{array} {cc}
9 & -5\
4 & 7 end{array} right|=9cdot 7-(-5)cdot 4=83.
$$
Итак, минор элемента $a_{12}$ равен 83, т.е. $M_{12}=83$.
Алгебраическое дополнение $A_{ij}$ элемента $a_{ij}$
Пусть задана квадратная матрица $A_{ntimes n}$ (т.е. квадратная матрица n-го порядка).
Алгебраическое дополнением $A_{ij}$ элемента $a_{ij}$ матрицы $A_{ntimes n}$ находится по следующей формуле:
$$
A_{ij}=(-1)^{i+j}cdot M_{ij},
$$
где $M_{ij}$ – минор элемента $a_{ij}$.
Найдем алгебраическое дополнение элемента $a_{32}$ матрицы $A=left( begin{array} {cccc}
1 & 0 & -3 & 9\
2 & -7 & 11 & 5 \
-9 & 4 & 25 & 84\
3 & 12 & -5 & 58 end{array} right)$, т.е. найдём $A_{32}$. Ранее мы уже находили минор $M_{32}=579$, поэтому используем полученный результат:
Обычно при нахождении алгебраических дополнений не вычисляют отдельно минор, а уж потом само дополнение. Запись минора опускают. Например, найдем $A_{12}$, если $A=left( begin{array} {ccc}
-5 & 10 & 2\
6 & 9 & -4 \
4 & -3 & 1 end{array} right)$. Согласно формуле $A_{12}=(-1)^{1+2}cdot M_{12}=-M_{12}$. Однако чтобы получить $M_{12}$ достаточно вычеркнуть первую строку и второй столбец матрицы $A$, так зачем же вводить лишнее обозначение для минора? Сразу запишем выражение для алгебраического дополнения $A_{12}$:
Минор k-го порядка матрицы $A_{mtimes n}$
Если в предыдущих двух пунктах мы говорили лишь о квадратных матрицах, то здесь поведём речь также и о прямоугольных матрицах, у которых количество строк вовсе не обязательно равняется количеству столбцов. Итак, пусть задана матрица $A_{mtimes n}$, т.е. матрица, содержащая m строк и n столбцов.
Минором k-го порядка матрицы $A_{mtimes n}$ называется определитель, элементы которого расположены на пересечении k строк и k столбцов матрицы $A$ (при этом предполагается, что $k≤ m$ и $k≤ n$).
Например, рассмотрим такую матрицу:
$$A=left( begin{array} {cccc}
-1 & 0 & -3 & 9\
2 & 7 & 14 & 6 \
15 & -27 & 18 & 31\
0 & 1 & 19 & 8\
0 & -12 & 20 & 14\
5 & 3 & -21 & 9\
23 & -10 & -5 & 58 end{array} right)
$$
Запишем для неё какой-либо минор третьего порядка. Чтобы записать минор третьего порядка нам потребуется выбрать какие-либо три строки и три столбца данной матрицы. Например, возьмём строки №2, №4, №6 и столбцы №1, №2, №4. На пересечении этих строк и столбцов будут располагаться элементы требуемого минора. На рисунке элементы минора показаны синим цветом:
$$
left( begin{array} {cccc}
-1 & 0 & -3 & 9 \
boldblue{2} & boldblue{7} & 14 & boldblue{6} \
15 & -27 & 18 & 31\
boldblue{0} & boldblue{1} & 19 & boldblue{8}\
0 & -12 & 20 & 14\
boldblue{5} & boldblue{3} & -21 & boldblue{9}\
23 & -10 & -5 & 58 end{array} right);;
M=left|begin{array} {ccc}
2 & 7 & 6 \
0 & 1 & 8 \
5 & 3 & 9 end{array} right|.
$$
Миноры первого порядка находятся на пересечении одной строки и одного столбца, т.е. миноры первого порядка равны элементам заданной матрицы.
Минор k-го порядка матрицы $A_{mtimes n}=(a_{ij})$ называется главным, если на главной диагонали данного минора находятся только главные диагональные элементы матрицы $A$.
Напомню, что главными диагональными элементами именуют те элементы матрицы, у которых индексы равны: $a_{11}$, $a_{22}$, $a_{33}$ и так далее. Например, для рассмотренной выше матрицы $A$ такими элементами будут $a_{11}=-1$, $a_{22}=7$, $a_{33}=18$, $a_{44}=8$. На рисунке они выделены зелёным цветом:
$$left( begin{array} {cccc}
boldgreen{-1} & 0 & -3 & 9\
2 & boldgreen{7} & 14 & 6 \
15 & -27 & boldgreen{18} & 31\
0 & 1 & 19 & boldgreen{8}\
0 & -12 & 20 & 14\
5 & 3 & -21 & 9\
23 & -10 & -5 & 58 end{array} right)
$$
Например, если в матрице $A$ мы вычеркнем строки и столбцы с номерами 1 и 3, то на их пересечении будут расположены элементы минора второго порядка, на главной диагонали которого будут находиться только диагональные элементы матрицы $A$ (элементы $a_{11}=-1$ и $a_{33}=18$ матрицы $A$). Следовательно, мы получим главный минор второго порядка:
$$
M=left|begin{array} {cc}
boldgreen{-1} & -3 \
15 & boldgreen{18} end{array} right|
$$
Естественно, что мы могли взять иные строки и столбцы, – например, с номерами 2 и 4, получив при этом иной главный минор второго порядка.
Пусть некий минор $M$ k-го порядка матрицы $A_{mtimes n}$ не равен нулю, т.е. $Mneq 0$. При этом все миноры, порядок которых выше k, равны нулю. Тогда минор $M$ называют базисным, а строки и столбцы, на которых расположены элементы базисного минора, именуют базисными строками и базисными столбцами.
Для примера рассмотрим такую матрицу:
$$A=left( begin{array} {ccc}
-1 & 0 & 3 & 0 & 0 \
2 & 0 & 4 & 1 & 0\
1 & 0 & -2 & -1 & 0\
0 & 0 & 0 & 0 & 0 end{array} right)
$$
Запишем минор этой матрицы, элементы которого расположены на пересечении строк №1, №2, №3 и столбцов с №1, №3, №4. Мы получим минор третьего порядка (его элементы выделены в матрице $A$ фиолетовым цветом):
$$
left( begin{array} {ccc}
boldpurple{-1} & 0 & boldpurple{3} & boldpurple{0} & 0 \
boldpurple{2} & 0 & boldpurple{4} & boldpurple{1} & 0\
boldpurple{1} & 0 & boldpurple{-2} & boldpurple{-1} & 0\
0 & 0 & 0 & 0 & 0 end{array} right);;
M=left|begin{array} {ccc}
-1 & 3 & 0 \
2 & 4 & 1 \
1 & -2 & -1 end{array} right|.
$$
Найдём значение этого минора, используя формулу №2 из темы вычисления определителей второго и третьего порядков:
$$
M=left| begin{array} {ccc}
-1 & 3 & 0\
2 & 4 & 1 \
1 & -2 & -1 end{array} right|=4+3+6-2=11.
$$
Итак, $M=11neq 0$. Теперь попробуем составить любой минор, порядок которого выше трёх. Чтобы составить минор четвёртого порядка, нам придётся использовать четвёртую строку, однако все элементы этой строки равны нулю. Следовательно, в любом миноре четвёртого порядка будет нулевая строка, а это означает, что все миноры четвёртого порядка равны нулю. Миноры пятого и более высоких порядков составить мы не можем, так как матрица $A$ имеет всего 4 строки.
Мы нашли минор третьего порядка, не равный нулю. При этом все миноры высших порядков равны нулю, следовательно, рассмотренный нами минор – базисный. Строки матрицы $A$, на которых расположены элементы этого минора (первая, вторая и третья), – базисные строки, а первый, третий и четвёртый столбцы матрицы $A$ – базисные столбцы.
Данный пример, конечно, тривиальный, так как его цель – наглядно показать суть базисного минора. Вообще, базисных миноров может быть несколько, и обычно процесс поиска такого минора куда сложнее и объёмнее.
Введём ещё одно понятие – окаймляющий минор.
Пусть некий минор k-го порядка $M$ матрицы $A_{mtimes n}$ расположен на пересечении k строк и k столбцов. Добавим к набору этих строк и столбцов ещё одну строку и столбец. Полученный минор (k+1)-го порядка именуют окаймляющим минором для минора $M$.
Для примера обратимся к такой матрице:
$$A=left( begin{array} {ccccc}
-1 & 2 & 0 & -2 & -14\
3 & -17 & -3 & 19 & 29\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 19 & -20 & -98\
6 & 12 & 20 & 21 & 54\
-7 & 10 & 14 & -36 & 79 end{array} right)
$$
Запишем минор второго порядка, элементы которого расположены на пересечении строк №2 и №5, а также столбцов №2 и №4. Эти элементы выделены в матрице красным цветом:
$$
left( begin{array} {ccccc}
-1 & 2 & 0 & -2 & -14\
3 & boldred{-17} & -3 & boldred{19} & 29\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 19 & -20 & -98\
6 & boldred{12} & 20 & boldred{21} & 54\
-7 & 10 & 14 & -36 & 79 end{array} right);;
M=left|begin{array} {ccc}
-17 & 19 \
12 & 21 end{array} right|.
$$
Добавим к набору строк, на которых лежат элементы минора $M$, ещё строку №1, а к набору столбцов – столбец №5. Получим новый минор $M’$ (уже третьего порядка), элементы которого расположены на пересечении строк №1, №2, №5 и столбцов №2, №4, №5. Элементы минора $M$ на рисунке выделены красным цветом, а элементы, которые мы добавляем к минору $M$ – синим:
$$
left( begin{array} {ccccc}
-1 & boldblue{2} & 0 & boldblue{-2} & boldblue{-14}\
3 & boldred{-17} & -3 & boldred{19} & boldblue{29}\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 19 & -20 & -98\
6 & boldred{12} & 20 & boldred{21} & boldblue{54}\
-7 & 10 & 14 & -36 & 79 end{array} right);;
M’=left|begin{array} {ccc}
2 & -2 & -14 \
-17 & 19 & 29 \
12 & 21 & 54 end{array} right|.
$$
Минор $M’$ является окаймляющим минором для минора $M$. Аналогично, добавляя к набору строк, на которых лежат элементы минора $M$, строку №4, а к набору столбцов – столбец №3, получим минор $M”$ (минор третьего порядка):
$$
left( begin{array} {ccccc}
-1 & 2 & 0 & -2 & -14\
3 & boldred{-17} & boldblue{-3} & boldred{19} & 29\
5 & -6 & 8 & -9 & 41\
-5 & boldblue{11} & boldblue{19} & boldblue{-20} & -98\
6 & boldred{12} & boldblue{20} & boldred{21} & 54\
-7 & 10 & 14 & -36 & 79 end{array} right);;
M”=left|begin{array} {ccc}
-17 & -3 & 19 \
11 & 19 & -20 \
12 & 20 & 21 end{array} right|.
$$
Минор $M”$ также является окаймляющим минором для минора $M$.
Минор k-го порядка матрицы $A_{ntimes n}$. Дополнительный минор. Алгебраическое дополнение к минору квадратной матрицы.
Вновь вернёмся к квадратным матрицам. Введём понятие дополнительного минора.
Пусть задан некий минор $M$ k-го порядка матрицы $A_{ntimes n}$. Определитель (n-k)-го порядка, элементы которого получены из матрицы $A$ после вычеркивания строк и столбцов, содержащих минор $M$, называется минором, дополнительным к минору $M$.
Для примера рассмотрим квадратную матрицу пятого порядка:
$$
A=left( begin{array}{ccccc}
-1 & 2 & 0 & -2 & -14\
3 & -17 & -3 & 19 & 29\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 16 & -20 & -98\
-7 & 10 & 14 & -36 & 79 end{array} right)
$$
Выберем в ней строки №1 и №3, а также столбцы №2 и №5. На пересечении оных строк и столбцов будут элементы минора $M$ второго порядка. Эти элементы выделены в матрице $A$ зелёным цветом:
$$
left(begin{array}{ccccc}
-1 & boldgreen{2} & 0 & -2 & boldgreen{-14}\
3 & -17 & -3 & 19 & 29\
5 & boldgreen{-6} & 8 & -9 & boldgreen{41}\
-5 & 11 & 16 & -20 & -98\
-7 & 10 & 14 & -36 & 79 end{array} right);;
M=left|begin{array}{cc}
2 & -14 \
-6 & 41 end{array} right|.
$$
Теперь уберём из матрицы $A$ строки №1 и №3 и столбцы №2 и №5, на пересечении которых находятся элементы минора $M$ (элементы убираемых строк и столбцов показаны красным цветом на рисунке ниже). Оставшиеся элементы образуют минор $M’$:
$$
left( begin{array}{ccccc}
boldred{-1} & boldred{2} & boldred{0} & boldred{-2} & boldred{-14}\
3 & boldred{-17} & -3 & 19 & boldred{29}\
boldred{5} & boldred{-6} & boldred{8} & boldred{-9} & boldred{41}\
-5 & boldred{11} & 16 & -20 & boldred{-98}\
-7 & boldred{10} & 14 & -36 & boldred{79} end{array} right);;
M’=left|begin{array} {ccc}
3 & -3 & 19 \
-5 & 16 & -20 \
-7 & 14 & -36 end{array}right|.
$$
Минор $M’$, порядок которого равен $5-2=3$, является минором, дополнительным к минору $M$.
Алгебраическим дополнением к минору $M$ квадратной матрицы $A_{ntimes n}$ называется выражение $(-1)^{alpha}cdot M’$, где $alpha$ – сумма номеров строк и столбцов матрицы $A$, на которых расположены элементы минора $M$, а $M’$ – минор, дополнительный к минору $M$.
Словосочетание “алгебраическое дополнение к минору $M$” часто заменяют словосочетанием “алгебраическое дополнение минора $M$”.
Для примера рассмотрим матрицу $A$, для которой мы находили минор второго порядка
$
M=left| begin{array} {ccc}
2 & -14 \
-6 & 41 end{array} right|
$ и дополнительный к нему минор третьего порядка:
$M’=left| begin{array} {ccc}
3 & -3 & 19\
-5 & 16 & -20 \
-7 & 14 & -36 end{array} right|$. Обозначим алгебраическое дополнение минора $M$ как $M^*$. Тогда согласно определению:
$$
M^*=(-1)^alphacdot M’.
$$
Параметр $alpha$ равен сумме номеров строк и столбцов, на которых находится минор $M$. Этот минор расположен на пересечении строк №1, №3 и столбцов №2, №5. Следовательно, $alpha=1+3+2+5=11$. Итак:
$$
M^*=(-1)^{11}cdot M’=-left| begin{array} {ccc}
3 & -3 & 19\
-5 & 16 & -20 \
-7 & 14 & -36 end{array} right|.
$$
В принципе, используя формулу №2 из темы вычисления определителей второго и третьего порядков, можно довести вычисления до конца, получив значение $M^*$:
$$
M^*=-left| begin{array} {ccc}
3 & -3 & 19\
-5 & 16 & -20 \
-7 & 14 & -36 end{array} right|=-30.
$$
Определитель третьего порядка
Определитель
третьего порядка:
,
– элементы определителя
.
Следует
запомнить, что элементы
образуют
главную диагональ определителя, элементы
составляют его побочную диагональ.
Вычисление определителя третьего порядка.
-
Вычисление
определителя третьего порядка по
правилу треугольников

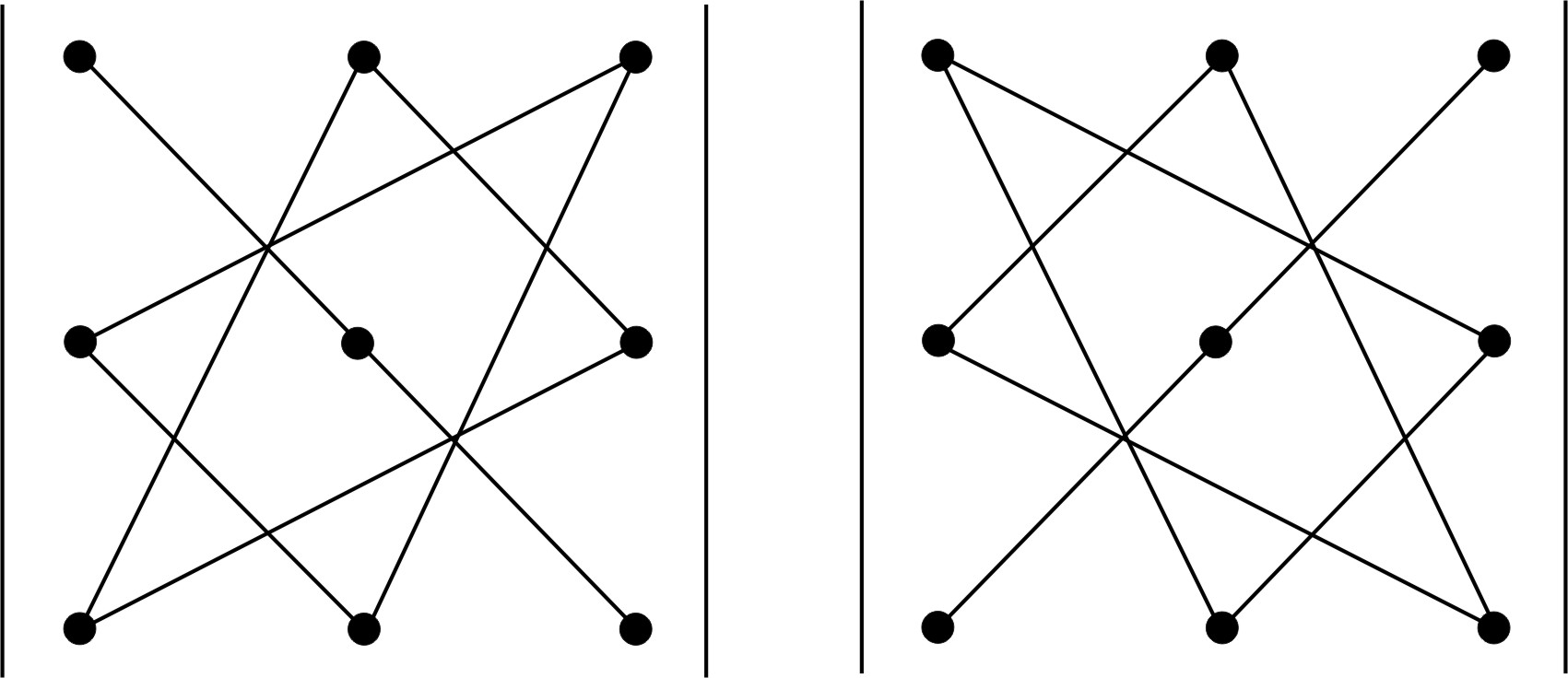
Рис.
1 Рис. 2
Данное правило
заключается в том, что первые три
слагаемые в правой части равенства
вычисляются так, как это показано на
Рис. 1, они представляют собой произведения
элементов, стоящих на главной диагонали
и вершинах двух треугольников, у которых
одна из сторон параллельна главной
диагонали. Остальные три слагаемых
правой части равенства вычисляются
аналогично (Рис. 2), только за основу
взята побочная диагональ. Причем эти
слагаемые берутся с обратным знаком.
Определение:
Минором данного элемента
определителя третьего порядка называется
определитель второго порядка, полученный
из данного определителя вычеркиванием
строки и столбца, на пересечении которых
стоит данный элемент.
– минор данного
элемента определителя третьего порядка.
Определение:
Алгебраическое дополнение
данного элемента – это минор, взятый
со знаком «плюс», если сумма
– четное число, и со знаком «минус», если
эта сумма нечетная.
– алгебраическое дополнение данного
элемента определителя третьего порядка.
.
Замечание.
Здесь
означает номер строки, а
– номер столбца, на пересечении которых
находится данный элемент.
Пример
2. Дана матрица
.
Найти
.
Решение
Минор
,
соответствующий элементу
,
есть определитель
.
Он получается, если вычеркнуть из данного
определителя третьего порядка третью
строку и первый столбец.

По
формуле (14) находим алгебраическое
дополнение для элемента
.
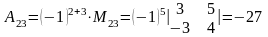
-
Разложение
определителя по элементам строки (или
столбца).
– разложение
определителя по элементам первой строки.

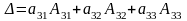
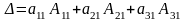
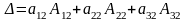
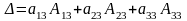
Определитель равен
сумме произведений элементов какой –
либо строки (или столбца) на их
алгебраические дополнения.
Замечание.
Все свойства
определителей второго порядка остаются
справедливыми для определителей третьего
и более высокого порядка.
Определители высших порядков
Определитель
n – го порядка.
.
– разложение
определителя n – го порядка по
элементам первой строки.
Замечание.
Для определителей
любых порядков остаются в силе определения
минора и алгебраического дополнения
данного элемента.
Пример
3. Вычислить определитель третьего
порядка
.
-
по
правилу треугольников -
используя
разложение по элементам строки (или
столбца) -
используя
разложение по элементам строки (или
столбца), с предварительным образованием
нулей.
Решение
-
Вычисляем
определитель по правилу треугольников,
используя формулу (2).

-
Разложим
определитель по элементам первой
строки, используя формулу (3)
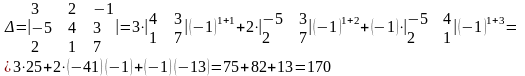
-
Используя
свойство (8), можно значительно упростить
вычисление определителя, получая нули
в некотором столбце или строке.
Умножая третью
строку на (- 4) и складывая ее со второй,
а умножая третью строку на (- 2) и складывая
ее с первой, получим
.
Вычислим этот определитель, разлагая
его по элементам второго столбца (т. к.
из трех элементов – два нуля):
.
Согласно свойству (3) , из первого столбца
выносим (-1), а из второго (-5), получаем
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пусть дана квадратная матрица третьего порядка
ОПРЕДЕЛЕНИЕ 1.8
Определителем третьего порядка, соответствующим данной квадратной матрице А, называется число
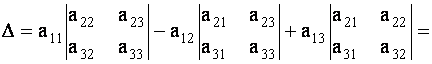 |
(1.7) |
Определитель третьего порядка обозначается символом
 |
(1.8) |
где числа называются его элементами.
Индексы у элемента
показывают номера строки и столбца, на пересечении которых записан этот элемент.
Например, элемент расположен на пересечении второй строки
и третьего столбца
.
Элементы образуют главную диагональ определителя, а элементы
побочную диагональ.
Определение имеет сложный по форме вид, поэтому для нахождения определителя третьего порядка предложены более простые правила. Так, согласно правилу треугольников необходимо:
- вычислить с собственными знаками произведения элементов , лежащих на главной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны этой диагонали ;
- найти произведения элементов, лежащих на побочной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали, и взять их с противоположными знаками ;
- найти общую сумму всех произведений.
ПРИМЕР 1.1.7
Все свойства определителей второго порядка справедливы и для определителей третьего порядка. Доказательства этих свойств основаны на вычислении определителя третьего порядка по формуле (1.7).
Например, покажем, что определитель, у которого элементы двух его строк пропорциональны, равен нулю. Действительно,
Аналогично проверяется справедливость и других свойств.
Пусть дан определитель (1.8) третьего порядка.
ОПРЕДЕЛЕНИЕ 1.9: Минором элемента
, где
определителя третьего порядка, называется определитель второго порядка, полученный из данного вычеркиванием
й строки и
го столбца. Так, например, минор
элемента
есть определитель
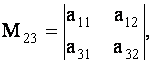
есть
С помощью миноров определитель (7) можно записать в виде
| (1.9) |
ОПРЕДЕЛЕНИЕ 1.10: Алгебраическим дополнением элемента
, где
, называется минор
этого элемента, взятый со знаком
. По определению 4.3 имеем
Например,
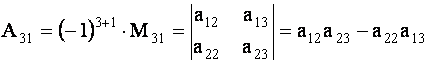
ТЕОРЕМА 1.1 Разложение определителя по элементам строки или столбца
Определитель третьего порядка равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения. Иными словами, имеют место шесть равенств:
| (1.11) |
Проверим, например, справедливость равенства
Согласно определениям минора и алгебраического дополнения получим
ТЕОРЕМА 1.2 Сумма произведений элементов какой- либо строки (столбца) определителя на алгебраические дополнения элементов любой другой его строки (столбца) равна нулю.
Для определенности выберем элементы первой строки и алгебраические дополнения
элементов второй строки определителя. Составим сумму произведений
и покажем, что эта сумма равна нулю.
Действительно,
Аналогично проверяется равенство нулю и всех других подобных сумм.
В заключение рассмотрим схему использования свойств определителя и теоремы разложения при вычислении определителя.
ПРИМЕР 1.1.8
Вычислить определитель
Решение. Разложим определитель по элементам третьей строки.
ПРИМЕР 1.1.9
Вычислить определитель
Решение. Прибавляя ко второй строке первую, умноженную на — 8,
получим 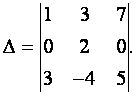
- Определители n-го порядка с примерами
- Курс математики
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее