sin(-a),cos(-a),tg(-a),ctg(-a). Минус в аргументе синуса, косинуса
И сразу два важных замечания.
Многие ученики думают, что если можно вынести минус из тригонометрической функции, то можно вынести и число, но это не так:
Квадрат меняет ситуацию. Всё дело в том, что (sin^2(-x)=(sin(-x) )^2=(-sin,x )^2=sin^2x), т.е. минус все равно выносится, но так как синуса два и они перемножаются, то в итоге получается плюс.
Примеры из ЕГЭ
Из рисунка видно, что и косинус, и синус положителен. Косинус из трех стандартных значений (frac<1><2>), (frac<sqrt<2>><2>), (frac<sqrt<3>><2>) принимает наименьшее т.е. (cos,frac<π><3>=frac<1><2>). Синус из трех стандартных значений будет равен среднему т.е. (sin,frac<π><4>=frac<sqrt<2>><2>). Получается:
Если вы не поняли почему (frac<π><3>) и (frac<π><4>) находятся на круге там, где мы из обозначили, то читайте статью « Как обозначать числа с пи на числовой окружности? ». А если не поняли, как мы нашли синус и косинус, то читайте статью « Как найти синус и косинус без тригонометрической таблицы ».
Пример (ЕГЭ). Найдите значение выражения (44sqrt<3>,tg,(-480^° )).
Решение. (44sqrt<3>,tg(-480^° )=-44sqrt<3>,tg(480^° )=-44sqrt<3>,tg(360^°+120^° )=-44sqrt<3>,tg(360^°+90^°+30^°)).
Находим (480^°) на окружности:
Соединяем точку, соответствующую (480^°) и центр окружности, и продляем до оси тангенсов:
Мы попадаем в самое маленькое (из стандартных) значение тангенса.
Значит, (tg(480^° )=-sqrt<3>).
В итоге имеем: (44sqrt <3>tg(-480^° )=-44sqrt<3>cdot(-sqrt<3>)=44cdot 3=132).
Ответ: (132).
Если вам не понятно, как мы нашли значение тангенса, то читайте статью « Как найти тангенс и котангенс без тригонометрической таблицы? ».
Доказательства формул с минусом в аргументе:
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
Отбор корней в тригонометрическом уравнение
В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
sqrt(2)cos^2x – cosx = 0
cosx(sqrt(2)cosx – 1) = 0
x1 = Pi/2 + Pin, n ∈ Z
sqrt(2)cosx – 1 = 0
x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
-7/2 меньше или равно 1/2 + n меньше или равно -2
-7/2 – 1/2 меньше или равно n меньше или равно -2 – 1/2
-4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8
Целых n в этом промежутке нет
-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8
Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
Обойдем раз против часовой стрелки
Обойдем 2 раза против часовой стрелки
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 – 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 – 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 – 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/
http://reshimvse.com/article.php?id=100
[/spoiler]
помогите пожалуйста найти минус пи на числовой окружности
Алина Логинова
Ученик
(96),
закрыт
3 года назад
Лучший ответ
Mister User
Оракул
(58273)
3 года назад
это там где 180 град
или -180 град
Остальные ответы
БЕШЕНЫЙ
Просветленный
(24274)
3 года назад
Спать пора уже а не минусы пи искать
Артём Хотин
Знаток
(405)
3 года назад
Если крайняя правая точка окружности – это ноль, то левая и есть минус пи.
Похожие вопросы
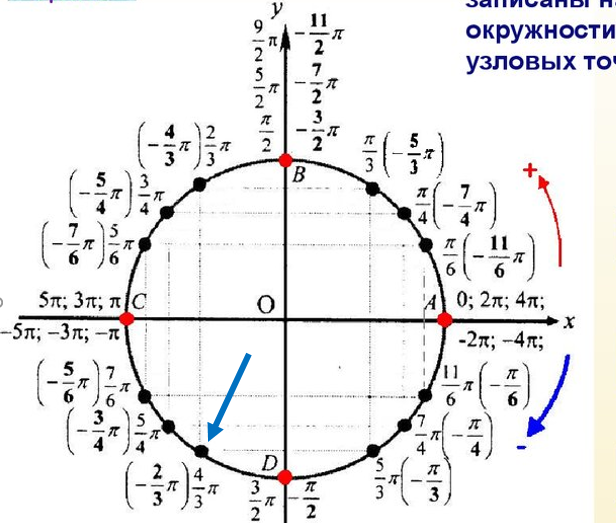
Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать! Если вы, конечно, собираетесь находить точки на числовой окружности.
Обозначаем числа (2π), (π), (frac{π}{2}), (-frac{π}{2}), (frac{3π}{2})
Как вы знаете из прошлой статьи, радиус числовой окружности равен (1). Значит, длина окружности равняется (2π) (вычислили по формуле (l=2πR)). С учетом этого отметим (2π) на числовой окружности. Чтобы отметить это число нужно пройти от (0) по числовой окружности расстояние равно (2π) в положительном направлении, а так как длина окружности (2π), то получается, что мы сделаем полный оборот. То есть, числу (2π) и (0) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки – это нормально для числовой окружности.

Теперь обозначим на числовой окружности число (π). (π) – это половина от (2π). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от (0) в положительном направлении половину окружности.

Отметим точку (frac{π}{2}). (frac{π}{2}) – это половина от (π), следовательно чтобы отметить это число, нужно от (0) пройти в положительном направлении расстояние равное половине (π), то есть четверть окружности.

Обозначим на окружности точки (-)(frac{π}{2}). Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.

Нанесем (-π). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.

Теперь рассмотрим пример посложнее. Отметим на окружности число (frac{3π}{2}). Для этого дробь (frac{3}{2}) переведем в смешанный вид (frac{3}{2})(=1)(frac{1}{2}), т.е. (frac{3π}{2})(=π+)(frac{π}{2}). Значит, нужно от (0) в положительную сторону пройти расстояние в пол окружности и еще в четверть.

Задание 1. Отметьте на числовой окружности точки (-2π),(-)(frac{3π}{2}).
Обозначаем числа (frac{π}{4}), (frac{π}{3}), (frac{π}{6})
Выше мы нашли значения в точках пересечения числовой окружности с осями (x) и (y). Теперь определим положение промежуточных точек. Для начала нанесем точки (frac{π}{4}), (frac{π}{3}) и (frac{π}{6}).
(frac{π}{4}) – это половина от (frac{π}{2}) (то есть, (frac{π}{4}) (=)(frac{π}{2})(:2)) , поэтому расстояние (frac{π}{4}) – это половина четверти окружности.

(frac{π}{4}) – это треть от (π) (иначе говоря,(frac{π}{3})(=π:3)), поэтому расстояние (frac{π}{3}) – это треть от полукруга.

(frac{π}{6}) – это половина (frac{π}{3}) (ведь (frac{π}{6})(=)(frac{π}{3})(:2)) поэтому расстояние (frac{π}{6}) – это половина от расстояния (frac{π}{3}).

Вот так они расположены друг относительно друга:

Замечание: Расположение точек со значением (0), (frac{π}{2}),(π), (frac{3π}{2}), (frac{π}{4}), (frac{π}{3}), (frac{π}{6}) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.
Разные расстояние на окружности наглядно:
Обозначаем числа (frac{7π}{6}), (-frac{4π}{3}), (frac{7π}{4})
Обозначим на окружности точку (frac{7π}{6}), для этого выполним следующие преобразования: (frac{7π}{6})(=)(frac{6π + π}{6})(=)(frac{6π}{6})(+)(frac{π}{6})(=π+)(frac{π}{6}). Отсюда видно, что от нуля в положительную сторону надо пройти расстояние (π), а потом еще (frac{π}{6}).

Отметим на окружности точку (-)(frac{4π}{3}). Преобразовываем: (-)(frac{4π}{3})(=-)(frac{3π}{3})(-)(frac{π}{3})(=-π-)(frac{π}{3}). Значит надо от (0) пройти в отрицательную сторону расстояние (π) и еще (frac{π}{3}).

Нанесем точку (frac{7π}{4}), для этого преобразуем (frac{7π}{4})(=)(frac{8π-π}{4})(=)(frac{8π}{4})(-)(frac{π}{4})(=2π-)(frac{π}{4}). Значит, чтобы поставить точку со значением (frac{7π}{4}), надо от точки со значением (2π) пройти в отрицательную сторону расстояние (frac{π}{4}).

Задание 2. Отметьте на числовой окружности точки (-)(frac{π}{6}),(-)(frac{π}{4}),(-)(frac{π}{3}),(frac{5π}{4}),(-)(frac{7π}{6}),(frac{11π}{6}), (frac{2π}{3}),(-)(frac{3π}{4}).
Обозначаем числа (10π), (-3π), (frac{7π}{2}) ,(frac{16π}{3}), (-frac{21π}{2}), (-frac{29π}{6})
Запишем (10π) в виде (5 cdot 2π). Вспоминаем, что (2π) – это расстояние равное длине окружности, поэтому чтобы отметить точку (10π), нужно от нуля пройти расстояние равное (5) окружностям. Нетрудно догадаться, что мы окажемся снова в точке (0), просто сделаем пять оборотов.

Из этого примера можно сделать вывод:
Числам с разницей в (2πn), где (n∈Z) (то есть (n) – любое целое число) соответствует одна и та же точка.
То есть, чтобы поставить число со значением больше (2π) (или меньше (-2π)), надо выделить из него целое четное количество (π) ((2π), (8π), (-10π)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».
Еще один вывод:
Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).
Теперь нанесем на окружность (-3π). (-3π=-π-2π), значит (-3π) и (–π) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в (-2π)).

Кстати, там же будут находиться все нечетные (π).
Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).
Сейчас обозначим число (frac{7π}{2}). Как обычно, преобразовываем: (frac{7π}{2})(=)(frac{6π}{2})(+)(frac{π}{2})(=3π+)(frac{π}{2})(=2π+π+)(frac{π}{2}). Два пи – отбрасываем, и получается что, для обозначения числа (frac{7π}{2}) нужно от нуля в положительную сторону пройти расстояние равное (π+)(frac{π}{2}) (т.е. половину окружности и еще четверть).

Отметим (frac{16π}{3}). Вновь преобразования: (frac{16π}{3})(=)(frac{15π + π}{3})(=)(frac{15π}{3})(+)(frac{π}{3})(=5π+)(frac{π}{3})(=4π+π+)(frac{π}{3}). Ясно, что от нуля надо пройти расстояние равное (π+)(frac{π}{3}) – и мы найдем место точки (frac{16π}{3}).

Нанесем на окружность число (-)(frac{21π}{2}).
(-)(frac{21π}{2})(= -)(frac{20π}{2})(-)(frac{π}{2})(=-10π-)(frac{π}{2}). Значит, место (-)(frac{21π}{2}) совпадает с местом числа (-)(frac{π}{2}).

Обозначим (-)(frac{29π}{6}).
(-)(frac{29π}{6})(=-)(frac{30π}{6})(+)(frac{π}{6})(=-5π+)(frac{π}{6})(=-4π-π+)(frac{π}{6}). Для обозначение (-)(frac{29π}{6}), на числовой окружности надо от точки со значением (–π) пройти в положительную сторону (frac{π}{6}).

Задание 3. Отметьте на числовой окружности точки (-8π),(-7π), (frac{11π}{4}),(-)(frac{7π}{3}),(frac{17π}{6}),(-)(frac{20π}{3}),(-)(frac{11π}{2}).
Скачать статью
какие координаты имеет точка минус пи на единичной окружности??
Разное
какие координаты имеет точка минус пи на единичной окружности??
Попроси больше объяснений
Следить
Отметить нарушение
Автор: Гость
Ответ(ы) на вопрос:
Гость:
координаты Вашей точки (-пи; 0) -Пи по оси абсцисс (ОХ) , и 0 по оси ординат (ОУ)
Пожаловаться
3
6
Risolvere per ?
cos(x)=1/2
7
Risolvere per x
sin(x)=-1/2
8
Преобразовать из градусов в радианы
225
9
Risolvere per ?
cos(x)=( квадратный корень из 2)/2
10
Risolvere per x
cos(x)=( квадратный корень из 3)/2
11
Risolvere per x
sin(x)=( квадратный корень из 3)/2
12
График
g(x)=3/4* корень пятой степени из x
13
Найти центр и радиус
x^2+y^2=9
14
Преобразовать из градусов в радианы
120 град. 2+n-72)=1/(n+9)
Мэтуэй | Популярные задачи
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | |||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.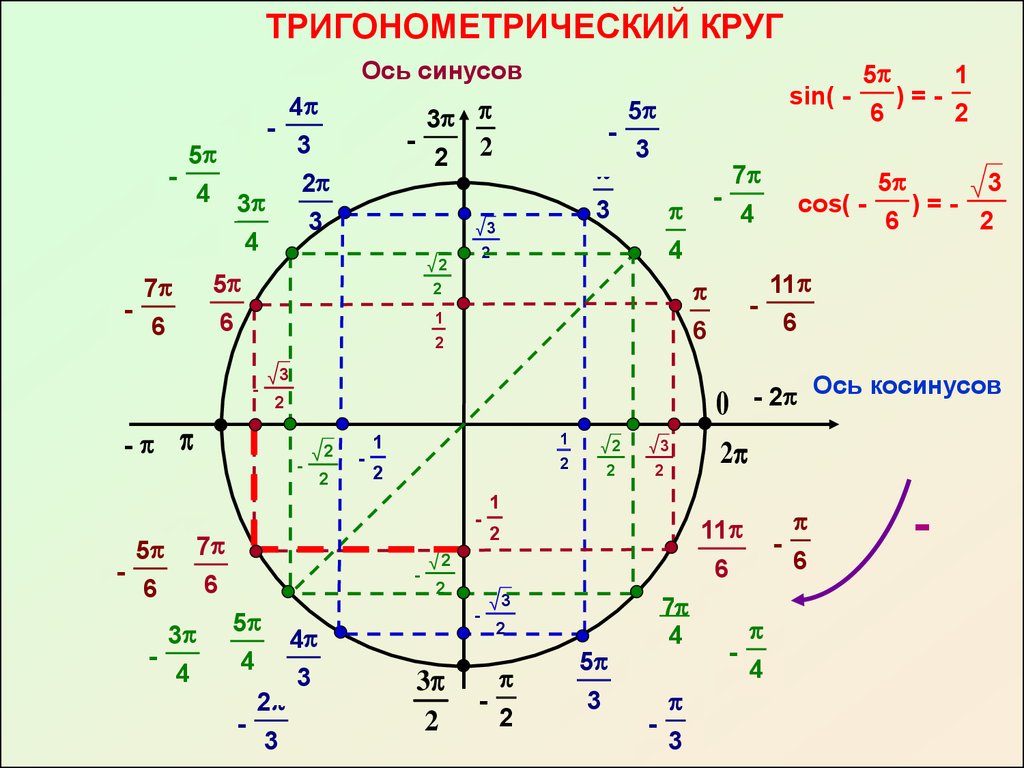 )/3 )/3 |
|
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
92
Давайте изучим единицу окружности/углов в стандартном положении/длине дуги 92=1text{.
 }) Единичный круг — самый важный график во всей тригонометрии, поскольку он является основой для определения всех тригонометрических функций.
}) Единичный круг — самый важный график во всей тригонометрии, поскольку он является основой для определения всех тригонометрических функций.
Рисунок 16.1.1. Единичный круг
Используя формулу длины окружности (C=2pi rtext{,}), мы можем легко определить, что длина окружности единичного круга равна (2 pi) (единица измерения). Итак, если мы начнем с любой точки по окружности и совершим один полный оборот по окружности, мы проедем расстояние (2pi) (единица измерения).
Как упоминалось выше, все тригонометрические функции определяются относительно этой окружности, и в этих определениях отправной точкой для вращения всегда является ((1,0)text{.}). Мы будем называть дуги вдоль единицы окружность, которая исходит из точки ((1,0)) как дуг в стандартной позиции . Когда мы удаляемся от этой точки в направлении против часовой стрелки, мы определяем размер результирующей дуги (части окружности) как положительное число. Когда мы движемся от точки ((1,0)) и движемся по часовой стрелке, мы определяем измерение дуги как отрицательное число. Для дуг, которые не исходят из точки ((1,0)text{,}), измерение всегда указывается как положительное число.
Для дуг, которые не исходят из точки ((1,0)text{,}), измерение всегда указывается как положительное число.
Рассмотрим дугу в стандартном положении, которая вращается на четверть оборота против часовой стрелки. Эта дуга показана на рисунке 16.1.2. Поскольку длина одного полного оборота равна (2pi) (единица), длина одной четверти оборота равна (frac{2pi}{4}), что упрощается до (frac{ pi}{2}text{.}) Поскольку изображенная дуга вращается против часовой стрелки, мы измеряем ее положительным значением.
Рисунок 16.1.2. Дуга (frac{pi}{2}) (единицы) в стандартном положении
Когда дуга находится в стандартном положении, угол от начала координат, стороны которого являются положительной осью (x) и линией от начала координат до конечной точки дуги, имеет измерение в радианах, численно эквивалентное измерению дуги . Мы называем такие углы углов в стандартном положении .
Рассмотрим угол в стандартном положении, который поворачивается на три восьмых оборота по часовой стрелке.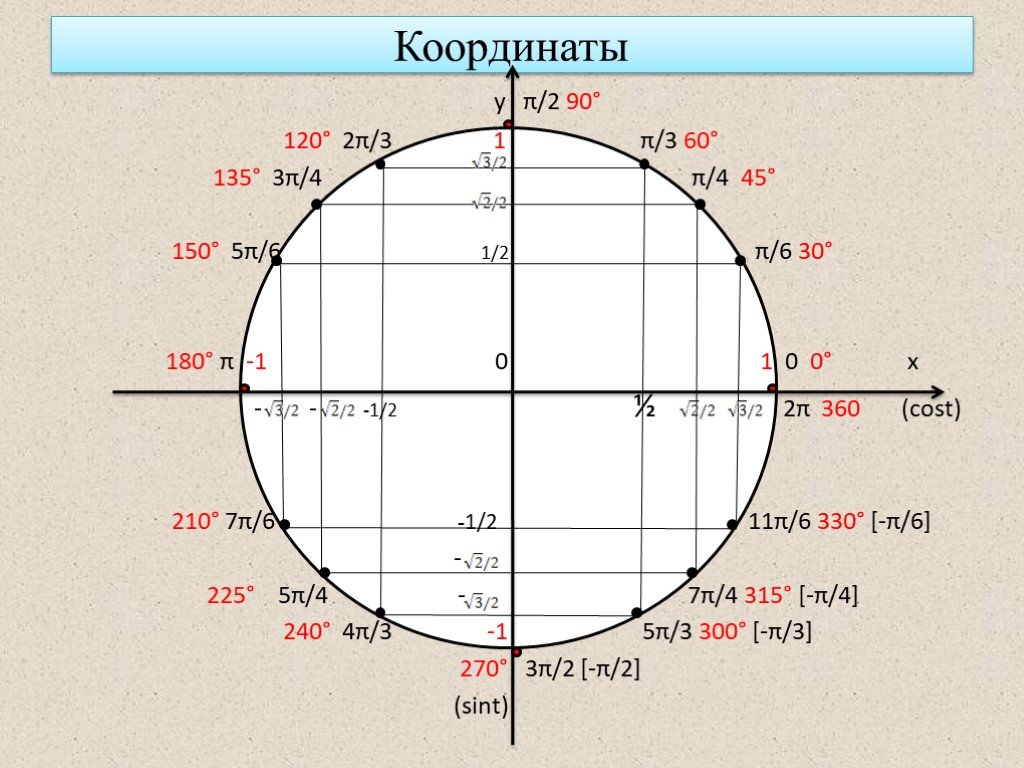 Этот угол показан на рисунке 16.1.3. В стандартном положении угол, который поворачивается на четверть оборота по часовой стрелке, заканчивается на отрицательной оси (y), а угол, который поворачивается на половину оборота по часовой стрелке, заканчивается на отрицательной оси (x). Поскольку (frac{3}{8}) находится на полпути между (frac{1}{2}) и (1text{,}), угол в стандартном положении, который поворачивает на три восьмых оборот по часовой стрелке должен заканчиваться на полпути в квадранте III.
Этот угол показан на рисунке 16.1.3. В стандартном положении угол, который поворачивается на четверть оборота по часовой стрелке, заканчивается на отрицательной оси (y), а угол, который поворачивается на половину оборота по часовой стрелке, заканчивается на отрицательной оси (x). Поскольку (frac{3}{8}) находится на полпути между (frac{1}{2}) и (1text{,}), угол в стандартном положении, который поворачивает на три восьмых оборот по часовой стрелке должен заканчиваться на полпути в квадранте III.
Рисунок 16.1.3. Угол (-frac{3pi}{4}), нарисованный в стандартном положении
Поскольку угол, показанный на рисунке 16.1.3, вращается по часовой стрелке, его измерение в радианах отрицательно. Поскольку вращение составляет три восьмых оборота, абсолютное значение его измерения в радианах равно (frac{3}{8}(2pi)), что упрощается до (frac{3pi}{4 }text{.}) Мы часто используем греческую букву (theta) (тета), когда обозначаем углы в стандартном положении, поэтому, используя эту ссылку, мы будем называть угол на рис. 16.1.3 как (theta =-frac{3pi}{4}) rad (читается как «радианы»). Мы будем называть аффилированную дугу вдоль единичной окружности как (t=-frac{3pi}{4}text {.})
16.1.3 как (theta =-frac{3pi}{4}) rad (читается как «радианы»). Мы будем называть аффилированную дугу вдоль единичной окружности как (t=-frac{3pi}{4}text {.})
Давайте проиллюстрируем (theta=frac{pi}{4}) рад. Поскольку измерение положительное, мы знаем, что вращение от положительной оси (x) происходит против часовой стрелки. Поскольку за один полный оборот приходится (2pi) рад, мы можем определить величину вращения в (frac{pi}{4}) рад, решив уравнение (frac{pi} {4}=2pi x), что дает нам (x=frac{1}{8}text{.}) Таким образом, конечная сторона угла попадает на полпути в квадрант I. Угол показан на рисунке 16.1.4.
Рисунок 16.1.4. Угол (frac{pi}{4}), нарисованный в стандартном положении
По причинам, которые станут очевидными, когда мы начнем вычислять тригонометрические функции, мы часто разбиваем единичный круг на 24 равные части. Это показано на рис. 16.1.5–рис. 16.1.12. В каждом из четырех квадрантов есть три угла интереса, которые заканчиваются в квадранте.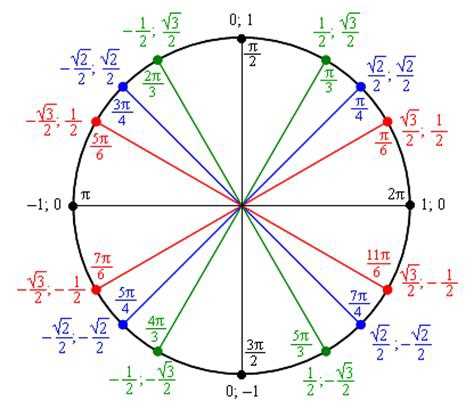 На рисунках слева каждая интересующая конечная сторона помечена своим наименьшим положительным измерением в радианах как доля (2pitext{.}). На рисунках справа дроби были уменьшены — это способ, которым ценности будут изложены в будущем.
На рисунках слева каждая интересующая конечная сторона помечена своим наименьшим положительным измерением в радианах как доля (2pitext{.}). На рисунках справа дроби были уменьшены — это способ, которым ценности будут изложены в будущем.
Рисунок 16.1.5. Ключевые углы, оканчивающиеся в квадранте IРисунок 16.1.6. Ключевые углы, которые заканчиваются в квадранте I
Рисунок 16.1.7. Ключевые углы, оканчивающиеся в квадранте II Рисунок 16.1.8. Ключевые углы, которые заканчиваются в квадранте II
Рисунок 16.1.9. Ключевые углы, заканчивающиеся в квадранте III Рисунок 16.1.10. Ключевые углы, которые заканчиваются в квадранте III
Рисунок 16.1.11. Ключевые углы, оканчивающиеся в квадранте IV Рисунок 16.1.12. Ключевые углы, которые заканчиваются в квадранте IV
На рис. 16.1.13 показаны точки, упомянутые выше, а также точки, в которых единичная окружность пересекает оси. На рис. 16.1.14 показан круг с ключевыми точками, помеченными отрицательными значениями (результат вращения по часовой стрелке). В следующем разделе мы добавим координаты каждой точки на график, и эта картинка станет основой для всей тригонометрии. Как вы, наверное, догадались, запоминание местоположения этих ключевых точек и их координат жизненно важно, если вы действительно хотите понять и освоить тригонометрию.
В следующем разделе мы добавим координаты каждой точки на график, и эта картинка станет основой для всей тригонометрии. Как вы, наверное, догадались, запоминание местоположения этих ключевых точек и их координат жизненно важно, если вы действительно хотите понять и освоить тригонометрию.
Рисунок 16.1.13. Ключевые углы/точки на единичной окружности
Рисунок 16.1.14. Ключевые углы/точки на единичной окружности
Как показано выше, при рисовании в стандартном положении несколько углов имеют одну и ту же конечную сторону. На самом деле нет ограничений на количество углов, заканчивающихся в любой заданной позиции. Углы, начерченные в стандартном положении и имеющие общую конечную сторону, называются котерминальными углами . Измерения котерминальных углов в радианах всегда отличаются на целое число, кратное (2pi), а углы, измерения которых в радианах отличаются на целое число, кратное (2pi), всегда котерминальны.
Пример 16.1.15.
Определите четыре угла, два положительных измерения и два отрицательных измерения, котерминальные углу (theta=frac{5pi}{7}text{.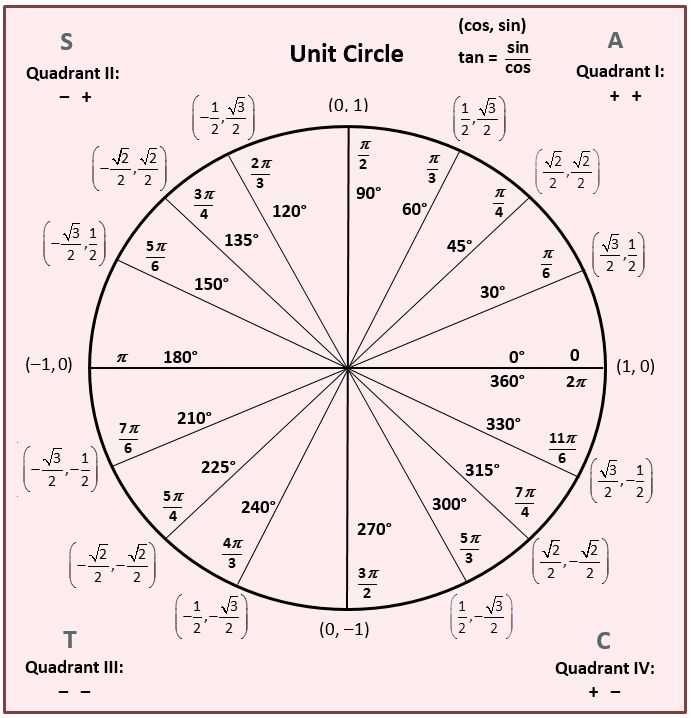 })
})
Решение
Нам нужно сложить и вычесть целые числа, кратные (2pi), к (frac{5pi}{7}), чтобы получить котерминальные углы к (thetatext{.} ) Это делается ниже.
begin{выравнивание*}
frac{5pi}{7}+2piamp=frac{5pi}{7}+frac{14pi}{7}\
amp=frac{19pi}{7}
end{выравнивание*}
begin{выравнивание*}
frac{5pi}{7}+2 cdot 2piamp=frac{5pi}{7}+4pi\
amp=frac{5pi}{7}+frac{28pi}{7}\
amp=frac{33pi}{7}
end{выравнивание*}
begin{выравнивание*}
frac{5pi}{7}-2piamp=frac{5pi}{7}-frac{14pi}{7}\
amp=-frac{9pi}{7}
end{выравнивание*}
begin{выравнивание*}
frac{5pi}{7}-2 cdot 2piamp=frac{5pi}{7}-4pi\
amp=frac{5pi}{7}-frac{28pi}{7}\
amp=-frac{23pi}{7}
end{align*}
В некоторых случаях предпочтительно измерять углы в градусах, а не в радианах. (На самом деле, некоторые студенты предпочли бы, чтобы это было сделано во всех контекстах. 🙂 Вы можете вспомнить, что в одном полном обороте есть (360^{circ}).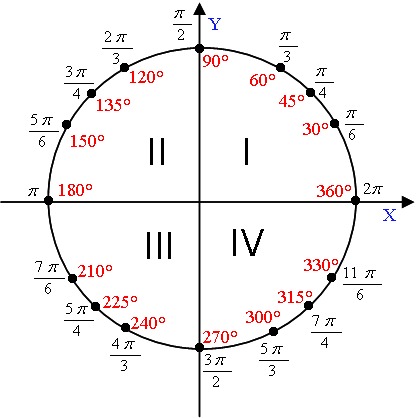 {circ}text{.}) 9{circ}text{.}) Первое, что нам нужно определить, это количество раз, когда 360 делится на 21 254. Это скажет нам, сколько полных оборотов сделано до окончательного частичного оборота.
{circ}text{.}) 9{circ}text{.}) Первое, что нам нужно определить, это количество раз, когда 360 делится на 21 254. Это скажет нам, сколько полных оборотов сделано до окончательного частичного оборота.
begin{уравнение*}
гидроразрыва {21 254} {60} приблизительно 59,039
end{equation*}
Это говорит нам о том, что угол составляет 59 полных оборотов плюс чуть больше. Поскольку вращение происходит против часовой стрелки, угол заканчивается в квадранте I.
Чтобы определить желаемый котерминальный угол, давайте вычтем 59{ круг}
конец{выравнивание*}
Длина дуги, s, проведенной по окружности с радиусом r и отрезанной под углом с вершиной в центре окружности с радианным измерением (theta), определяется уравнением ( s=rthetatext{.}) Это показано на рисунке 16.1.19. Когда мы решаем уравнение длины дуги для (thetatext{,}), мы получаем следующее уравнение, которое имеет поразительное значение в отношении радиана.
begin{уравнение*}
тета = гидроразрыва {s} {r}
end{уравнение*}
Рисунок 16.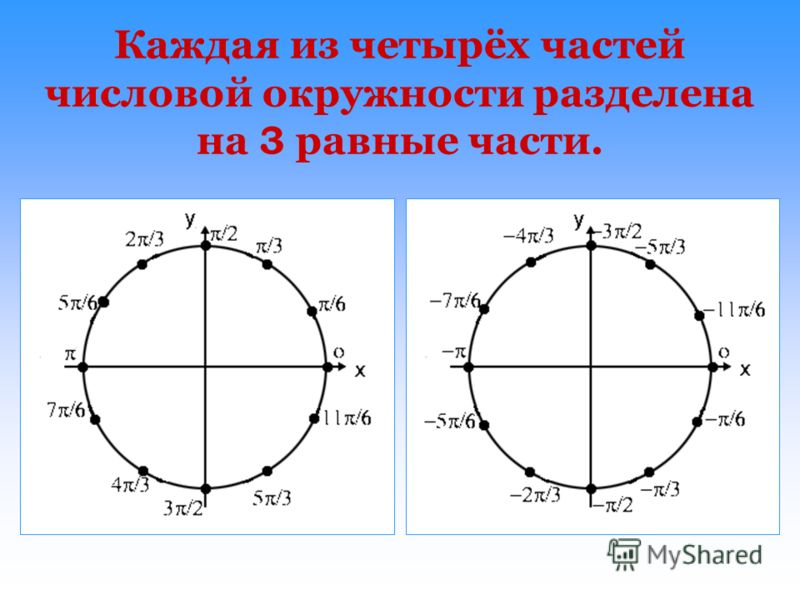 1.19. Длина дуги: (s=rtheta)
1.19. Длина дуги: (s=rtheta)
Предположим, вы начертили дугу длиной 7 см на окружности радиусом 21 см. Тогда измерение центрального угла выводится следующим образом.
begin{выравнивание*}
тетаамп=фрак{с} {r}\
amp=frac{7,text{см}}{21,text{см}}\
amp=frac{1}{3}
конец{выравнивание*}
Где блок? Единицы нет! Единицы cm делились на единицу и не оставляли ничего (по единицам) после себя.
Оказывается, единица измерения радиан — это что-то вроде бутафории. Когда мы говорим «три радиана», на самом деле мы имеем в виду «три». Так почему же мы вообще используем слово радиан? Чтобы контекстуал читателя к тому факту, что мы имеем в виду «три» как измерение угла или величины вращения. Поскольку радианы не являются реальным значением, мы обычно не пишем его — например, мы пишем (frac{pi}{2}) и контекстуально распознаем, что мы ссылаемся на «радианное измерение». При указании угловых измерений пропуск единицы измерения всегда указывает на то, что мы должны интерпретировать значение как измерение в радианах. По этой причине очень важно, чтобы вы включали символ градуса при указании измерения в градусах. 9{circ}) угол
По этой причине очень важно, чтобы вы включали символ градуса при указании измерения в градусах. 9{circ}) угол
Для каждого установленного значения (thetatext{,}) определите квадрант, в котором заканчивается угол, и определите угол с измерением между (0) и (2pi), котерминальный с (тетатекст{.})
5.
(theta=frac{226pi}{3})
Решение
Начнем с определения количества оборотов, оставшихся после совершения всех полных оборотов. Мы делаем это, разделив значение (theta) на (2pi) — количество радиан за один полный оборот.
begin{уравнение*}
гидроразрыва { гидроразрыва {226 пи} {3}} {2 пи} приблизительно 37,67
end{equation*}
Таким образом, угол составляет 37 полных оборотов плюс чуть меньше трех четвертей оборота. Поскольку вращение происходит против часовой стрелки ((theta) положительна), угол заканчивается в квадранте III.
begin{уравнение*}
frac{226pi}{3}-37 cdot 2pi=frac{4pi}{3}
end{equation*}
Это говорит нам о том, что угол измерения (frac{226pi}{3}) совпадает с углом измерения (frac{4pi}{3} текст{. })
})
6.
(тета=3,356)
Решение
Начнем с определения количества оборотов, оставшихся после совершения всех полных оборотов. Мы делаем это, разделив значение (theta) на (2pi) — количество радиан за один полный оборот.
begin{уравнение*}
frac{3,356}{2pi} приблизительно 534,12
end{equation*}
Таким образом, угол составляет 534 полных оборота плюс менее четверти оборота. Поскольку вращение происходит против часовой стрелки ((theta) положительна), угол заканчивается в квадранте I.
begin{уравнение*}
3,356-37 cdot 2pi примерно 0,779
end{equation*}
Это говорит нам о том, что угол измерения (3,356) угол (очень близок к тому, чтобы быть) сотерминальным с углом измерения (0,779text{.})
7.
(theta=-frac{1781pi}{2})
Решение
Начнем с определения количества оборотов, оставшихся после совершения всех полных оборотов. Мы делаем это, разделив значение (theta) на (2pi) — количество радиан за один полный оборот.
Мы делаем это, разделив значение (theta) на (2pi) — количество радиан за один полный оборот.
begin{уравнение*}
гидроразрыва { гидроразрыва {1781 пи} {2}} {2 пи} приблизительно 445,25
end{equation*}
Таким образом, угол составляет 445 полных оборотов плюс ровно четверть оборота. Поскольку вращение происходит по часовой стрелке ((theta) отрицательно), угол заканчивается на отрицательной оси (y) и совпадает с (frac{3pi}{2})
8.
(тета=-250)
Решение
Начнем с определения количества оборотов, оставшихся после совершения всех полных оборотов. Мы делаем это, разделив значение (theta) на (2pi) — количество радиан за один полный оборот.
begin{уравнение*}
frac{250}{2pi} приблизительно 39,79
end{equation*}
Таким образом, угол составляет 39 полных оборотов плюс немногим более трех четвертей оборота. Поскольку вращение происходит по часовой стрелке ((theta) отрицательно), угол заканчивается в квадранте I.