|
Nick_Volkov 0 / 0 / 0 Регистрация: 10.02.2017 Сообщений: 32 |
||||
|
1 |
||||
|
17.01.2018, 16:31. Показов 11325. Ответов 2 Метки нет (Все метки)
Как получить младший (старший) байт целого числа (2-байтового) Есть код в delphi
Как выполнить эти функции в C#? Возможно есть аналоги
0 |
|
aquaMakc 483 / 396 / 68 Регистрация: 14.02.2014 Сообщений: 1,930 |
||||
|
17.01.2018, 17:06 |
2 |
|||
|
Решение
3 |
|
0 / 0 / 0 Регистрация: 10.02.2017 Сообщений: 32 |
|
|
17.01.2018, 19:30 [ТС] |
3 |
|
Большое спасибо!
0 |
I know you can get the first byte by using
int x = number & ((1<<8)-1);
or
int x = number & 0xFF;
But I don’t know how to get the nth byte of an integer.
For example, 1234 is 00000000 00000000 00000100 11010010 as 32bit integer
How can I get all of those bytes? first one would be 210, second would be 4 and the last two would be 0.
![]()
Rob
5,1835 gold badges40 silver badges61 bronze badges
asked Oct 16, 2011 at 21:21
3
int x = (number >> (8*n)) & 0xff;
where n is 0 for the first byte, 1 for the second byte, etc.
answered Oct 16, 2011 at 21:24
Vaughn CatoVaughn Cato
63.2k5 gold badges82 silver badges128 bronze badges
3
For the (n+1)th byte in whatever order they appear in memory (which is also least- to most- significant on little-endian machines like x86):
int x = ((unsigned char *)(&number))[n];
For the (n+1)th byte from least to most significant on big-endian machines:
int x = ((unsigned char *)(&number))[sizeof(int) - 1 - n];
For the (n+1)th byte from least to most significant (any endian):
int x = ((unsigned int)number >> (n << 3)) & 0xff;
Of course, these all assume that n < sizeof(int), and that number is an int.
answered Oct 17, 2011 at 0:20
DmitriDmitri
9,1152 gold badges26 silver badges34 bronze badges
2
int nth = (number >> (n * 8)) & 0xFF;
Carry it into the lowest byte and take it in the “familiar” manner.
answered Oct 16, 2011 at 21:25
akappaakappa
10.2k3 gold badges39 silver badges55 bronze badges
If you are wanting a byte, wouldn’t the better solution be:
byte x = (byte)(number >> (8 * n));
This way, you are returning and dealing with a byte instead of an int, so we are using less memory, and we don’t have to do the binary and operation & 0xff just to mask the result down to a byte. I also saw that the person asking the question used an int in their example, but that doesn’t make it right.
I know this question was asked a long time ago, but I just ran into this problem, and I think that this is a better solution regardless.
answered Jun 13, 2019 at 22:43
1
//was trying to do inplace, would have been better if I had swapped higher and lower bytes somehow
uint32_t reverseBytes(uint32_t value) {
uint32_t temp;
size_t size=sizeof(uint32_t);
for(int i=0; i<size/2; i++){
//get byte i
temp = (value >> (8*i)) & 0xff;
//put higher in lower byte
value = ((value & (~(0xff << (8*i)))) | (value & ((0xff << (8*(size-i-1)))))>>(8*(size-2*i-1))) ;
//move lower byte which was stored in temp to higher byte
value=((value & (~(0xff << (8*(size-i-1)))))|(temp << (8*(size-i-1))));
}
return value;
}
answered Sep 24, 2022 at 12:51
FitoheFitohe
131 silver badge3 bronze badges
 Данный урок посвящён битовым операциям (операциям с битами, битовой математике, bitmath). Из него вы узнаете, как оперировать с битами – элементарными ячейками памяти микроконтроллера.
Данный урок посвящён битовым операциям (операциям с битами, битовой математике, bitmath). Из него вы узнаете, как оперировать с битами – элементарными ячейками памяти микроконтроллера.
Данная тема является одной из самых сложных для понимания в рамках данного курса уроков, так что давайте разберёмся, зачем вообще нужно уметь работать с битами:
- Гибкая и быстрая работа напрямую с регистрами микроконтроллера.
- Работа напрямую с внешними микросхемами (датчики и прочее), управление которыми состоит из записи и чтения регистров, данные в которых могут быть запакованы в байты самым причудливым образом.
- Более эффективное хранение данных: упаковка нескольких значений в одну переменную и распаковка обратно.
- Создание символов и другой информации для матричных дисплеев.
- Максимально быстрые вычисления.
- Разбор чужого кода.
Данный урок основан на оригинальном уроке по битовым операциям от Arduino, можете почитать его здесь – там всё описано чуть более подробно.
Двоичная система
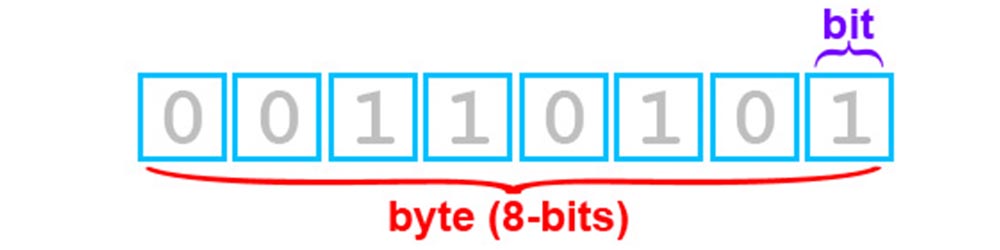
В цифровом мире, к которому относится также микроконтроллер, информация хранится, преобразуется и передается в цифровом виде, то есть в виде нулей и единиц. Соответственно элементарная ячейка памяти, которая может запомнить 0 или 1, называется бит (bit).
Минимальная ячейка памяти, которую мы можем изменить – 1 бит, а ячейка памяти, которая которая имеет адрес в памяти и мы можем к ней обратиться – байт, который состоит из 8-ми бит, каждый занимает своё место (примечание: в других архитектурах в байте может быть больше или меньше бит, в данном уроке речь идёт об AVR и 8-ми битном байте). 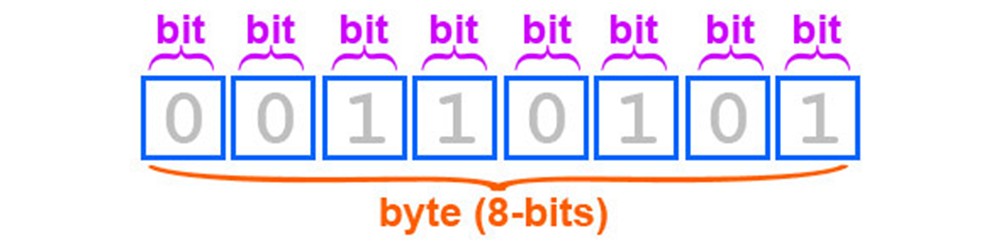 Вспомним двоичную систему счисления из школьного курса информатики:
Вспомним двоичную систему счисления из школьного курса информатики:
| Двоичная | Десятичная |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| … | … |
| 10000 | 16 |
Заметили последовательность?
Здесь также нужно увидеть важность степени двойки – на ней в битовых операциях завязано абсолютно всё. Давайте посмотрим на первые 8 степеней двойки в разных системах счисления:
| 2 в степени | DEC | BIN |
| 0 | 1 | 0b00000001 |
| 1 | 2 | 0b00000010 |
| 2 | 4 | 0b00000100 |
| 3 | 8 | 0b00001000 |
| 4 | 16 | 0b00010000 |
| 5 | 32 | 0b00100000 |
| 6 | 64 | 0b01000000 |
| 7 | 128 | 0b10000000 |
Таким образом, степень двойки явно “указывает” на номер бита в байте, считая справа налево (примечание: в других архитектурах может быть иначе). Напомню, что абсолютно неважно, в какой системе исчисления вы работаете – микроконтроллеру всё равно и он во всём видит единицы и нули. Если мы “включим” все биты в байте, то получится число 0b11111111 в двоичной системе или 255 в десятичной.
Если “сложить” полный байт в десятичном представлении каждого бита: 128+64+32+16+8+4+2+1 – получится 255. Нетрудно догадаться, что число 0b11000000 равно 128+64, то есть 192. Именно таким образом и получается весь диапазон от 0 до 255, который умещается в один байт. Если взять два байта – будет всё то же самое, просто ячеек будет 16, то же самое для 4 байт – 32 ячейки с единицами и нулями, каждая имеет свой номер согласно степени двойки.
Другие системы счисления
Данные в памяти микроконтроллера хранятся в двоичном представлении, но помимо него существуют и другие системы счисления, в которых мы можем работать. Переводить числа из одной системы счисления в другую не нужно: программе абсолютно всё равно, в каком формате вы скармливаете значение переменной, они автоматически будут интерпретированы в двоичный вид. Разные системы счисления введены в первую очередь для удобства программиста.
Теперь по сути: Arduino поддерживает четыре классических системы счисления: двоичную, восьмеричную, десятичную и шестнадцатеричную.
- Двоичная (Binary) имеет префикс 0b (ноль бэ) или B, то есть двоичное число 101 запишется как
0b101илиB101. - С десятичной (DEC) всё просто, пишем числа так, как они выглядят.
10это десять,25это двадцать пять и так далее. - Восьмеричная (Octal) может содержать числа от 0 до 7 и имеет префикс 0 (ноль), например
012. - 16-ричная (hexademical) система имеет 16 значений на один разряд, первые 10 как у десятичной, остальные – первые буквы латинского алфавита: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f. При записи имеет префикс 0x (ноль икс), число FF19 запишется как
0xFF19.
| Базис | Префикс | Пример | Особенности |
| 2 (двоичная) | B или 0b (ноль бэ) | B1101001 | цифры 0 и 1 |
| 8 (восьмеричная) | 0 (ноль) | 0175 | цифры 0 – 7 |
| 10 (десятичная) | нет | 100500 | цифры 0 – 9 |
| 16 (шестнадцатеричная) | 0x (ноль икс) | 0xFF21A | цифры 0-9, буквы A-F |
Основная фишка 16-ричной системы в том, что она позволяет записывать длинные десятичные числа короче, например один байт (255) запишется как 0xFF, два байта (65 535) как 0xFFFF, а жуткие три байта (16 777 215) как 0xFFFFFF.
Двоичная система обычно используется для наглядного представления данных и низкоуровневых конфигураций различного железа. Например конфиг кодируется одним байтом, каждый бит в нём отвечает за отдельную настройку (вкл/выкл), и передав один байт вида 0b10110100 можно сразу кучу всего настроить, к этому мы вернёмся в уроке работа с регистрами из раздела продвинутых уроков. В документации по этому поводу пишут в стиле “первый бит отвечает за это, второй за то” и так далее. Перейдём к изменению состояний битов.
Макросы для манипуляций с битами
В библиотеке Arduino.h есть несколько удобных макросов, которые позволяют включать и выключать биты в байте:
| Макрос | Действие |
bitRead(value, bit) |
Читает бит под номером bit в числе value |
bitSet(value, bit) |
Включает (ставит 1) бит под номером bit в числе value |
bitClear(value, bit) |
Выключает (ставит 0) бит под номером bit в числе value |
bitWrite(value, bit, bitvalue) |
Ставит бит под номером bit в состояние bitvalue (0 или 1) в числе value |
bit(bit) |
Возвращает 2 в степени bit |
| Другие встроенные макросы | |
_BV(bit) |
Возвращает 2 в степени bit |
bit_is_set(value, bit) |
Проверка на включенность (1) бита bit в числе value |
bit_is_clear(value, bit) |
Проверка на выключенность (0) бита bit в числе value |
Простой пример:
// тут myByte == 0 byte myByte = 0; // тут myByte станет 128 или 0b10000000 bitSet(myByte, 7); // тут myByte станет 192 или 0b11000000 bitWrite(myByte, 6, 1);
Этого уже достаточно для полноценной работы с регистрами. Так как это именно макросы, работают они максимально быстро и ничуть не хуже написанных вручную элементарных битовых операций. Чуть ниже мы разберём содержимое этих макросов и увидим, как они работают, а пока познакомимся с элементарными логическими операциями.
Примечание: число value из таблицы выше может иметь любой целочисленный тип, 1 байт (byte), 2 байта (int), 4 байта (long)
Битовые операции
Битовое И
И (AND), оно же “логическое умножение”, выполняется оператором & или and и возвращает следующее:
0 & 0 == 0 0 & 1 == 0 1 & 0 == 0 1 & 1 == 1
Основное применение операции И – битовая маска. Позволяет “взять” из байта только указанные биты:
myByte = 0b11001100; myBits = myByte & 0b10000111; // myBits теперь равен 0b10000100
То есть при помощи & мы взяли из байта 0b11001100 только биты 10000111, а именно – 0b11001100, и получили 0b10000100 Также можно использовать составной оператор &=
myByte = 0b11001100; myByte &= 0b10000000; // берём старший бит // myByte теперь 10000000
Битовое ИЛИ
ИЛИ (OR), оно же “логическое сложение”, выполняется оператором | или or и возвращает следующее:
0 | 0 == 0 0 | 1 == 1 1 | 0 == 1 1 | 1 == 1
Основное применение операции ИЛИ – установка бита в байте:
myByte = 0b11001100; myBits = myByte | 0b00000001; // ставим бит №0 // myBits теперь равен 0b11001101 myBits = myBits | bit(1); // ставим бит №1 // myBits теперь равен 0b11001111
Также можно использовать составной оператор |=
myByte = 0b11001100; myByte |= 16; // 16 - 2 в 4, включаем бит №4 // myByte теперь 0b11011100
Вы уже поняли, что указывать на нужные биты можно любым удобным способом: в бинарном виде (0b00000001 – нулевой бит), в десятичном виде (16 – четвёртый бит) или при помощи макросов bit() или _BV() (bit(7) даёт 128 или 0b10000000, _BV(7) делает то же самое)
Битовое НЕ
Битовая операция НЕ (NOT) выполняется оператором ~и просто инвертирует бит:
~0 == 1 ~1 == 0
Также она может инвертировать байт:
myByte = 0b11001100; myByte = ~myByte; // инвертируем // myByte теперь 00110011
Битовое исключающее ИЛИ
Битовая операция исключающее ИЛИ (XOR) выполняется оператором ^ или xor и делает следующее:
0 ^ 0 == 0 0 ^ 1 == 1 1 ^ 0 == 1 1 ^ 1 == 0
Данная операция обычно используется для инвертирования состояния отдельного бита:
myByte = 0b11001100; myByte ^= 0b10000000; // инвертируем 7-ой бит // myByte теперь 01001100
То есть мы взяли бит №7 в байте 0b11001100 и перевернули его в 0, получилось 0b01001100, остальные биты не трогали.
Битовый сдвиг
Битовый сдвиг – очень мощный оператор, позволяет буквально “двигать” биты в байте вправо и влево при помощи операторов >> и <<, и соответственно составных >>= и <<=. Если биты выходят за границы блока (8 бит, 16 бит или 32 бита) – они теряются.
myByte = 0b00011100; myByte = myByte << 3; // двигаем на 3 влево // myByte теперь 0b11100000 myByte >>= 5; // myByte теперь 0b00000111 myByte >>= 2; // myByte теперь 0b00000001 // остальные биты потеряны!
Битовый сдвиг делает не что иное, как умножает или делит байт на 2 в степени. Да, это операция деления, выполняющаяся за один такт процессора! К этому мы ещё вернёмся ниже. Посмотрите на работу оператора сдвига и сравните её с макросами bit() и _BV():
1 << 0 == 1 1 << 1 == 2 1 << 2 == 4 1 << 3 == 8 ... 1 << 8 == 256 1 << 9 == 512 1 << 10 == 1024
Возведение двойки в степень! Важный момент: при сдвиге дальше, чем на 15, нужно преобразовывать тип данных, например в ul: 1 << 17 даст результат 0, потому что сдвиг выполняется в ячейке int (как при умножении, помните?). Но если мы напишем 1ul << 17 – результат будет верный.
Применение на практике
Включаем-выключаем
Вспомним пример из пункта про битовое ИЛИ, про установку нужного бита. Вот эти варианты кода делают одно и то же:
myByte = 0b11000011; // ставим бит №3 разными способами // по сути - одно и то же myByte |= (1 << 3); myByte |= bit(3); myByte |= _BV(3); bitSet(myByte, 3); // myByte равен 0b11001011
Как насчёт установки нескольких бит сразу?
myByte = 0b11000011; // ставим бит №3 и 4 разными способами // по сути - одно и то же myByte |= (1 << 3) | (1 << 4); myByte |= bit(3) | bit(4); myByte |= _BV(3) | _BV(4); // myByte равен 0b11011011
Или прицельного выключения бит? Тут чуть по-другому, используя &= и ~
myByte = 0b11000011; // выключаем бит №1 разными способами // по сути - одно и то же myByte &= ~(1 << 1); myByte &= ~_BV(1); bitClear(myByte, 1); // myByte равен 0b11000001
Выключить несколько бит сразу? Пожалуйста!
myByte = 0b11000011; // выключаем биты №0 и 1 разными способами myByte &= ~( (1 << 0) | (1 << 1) ); myByte &= ~( _BV(0) | _BV(1) ); // myByte равен 0b11000000
Именно такие конструкции встречаются в коде высокого уровня и библиотеках, именно так производится работа с регистрами микроконтроллера. Вернёмся к устройству Ардуиновских макросов:
#define bitRead(value, bit) (((value) >> (bit)) & 0x01) #define bitSet(value, bit) ((value) |= (1UL << (bit))) #define bitClear(value, bit) ((value) &= ~(1UL << (bit))) #define bitWrite(value, bit, bitvalue) (bitvalue ? bitSet(value, bit) : bitClear(value, bit)) #define bit(b) (1UL << (b))
Я думаю, комментарии излишни: макросы состоят из тех же элементарных битовых операций и сдвигов!
Склейка и разбивание данных
Самая часто встречающаяся конструкция – склеивание двух байтов в один 2-х байтный тип данных. Для этого к младшему байту через ИЛИ прибавляется старший, сдвинутый на 8 влево:
int val = byte1 | (byte2 << 8);
Как это работает “на пальцах”: пусть byte1 равен 0b11111111, a byte2 – 0b00111100. Первым действием при помощи сдвига превращаем второй байт в 0b00111100 00000000, а вторым – соединяем его с первым байтом. Результат 0b0011110011111111.
Точно так же можно разбить переменную на отдельные байты. Младший байт получится автоматически (старший байт просто отсечётся при записи):
byte1 = val;
А вот старший нужно “задвинуть” на своё место:
byte2 = val >> 8;
Таким же образом можно склеить три байта, например три раздельных канала цвета (r, g, b) в один 24-бит цвет:
uint32_t color = ((uint32_t)r << 16) | (g << 8) | b;
Обратите внимание, красный канал r принудительно преобразуем к uint32_t, так как по умолчанию операция сдвига производится в 2-х байтной ячейке памяти, и без преобразования к 4 байтам данные будут потеряны!
Примечание: данный способ манипуляции с битами-байтами не самый оптимальный! См. урок по оптимизации кода, главу “Заменить сдвиг указателем”.
Быстрые вычисления
Как я уже говорил, битовые операции – самые быстрые. Если требуется максимальная скорость вычислений – их можно оптимизировать и подогнать под “степени двойки”, но иногда компилятор делает это сам, подробнее смотри в уроке про оптимизацию кода. Рассмотрим базовые операции:
- Деление на
2^n– сдвиг вправо наn. Например,val / 8можно записать какval >> 3. Компилятор не оптимизирует деление самостоятельно, что позволяет ускорить данную операцию приблизительно в 15 раз при ручной оптимизации. - Умножение на
2^n– сдвиг влево наn. Например,val * 8можно записать какval << 3. Компилятор оптимизирует умножение самостоятельно, поэтому в ручной оптимизации нет смысла. Но можно встретить в чужих исходниках. - Остаток от деления на
2^n– битовая маска наnмладших битов. Операции остатка от деленияval % (2^n)можно вычислить через битовую маску:val & (2^n - 1). Например,val % 8можно записать какval & 7, аval % 32можно записать какval & 31. Компилятор оптимизирует такие операции самостоятельно, поэтому в ручной оптимизации нет смысла. Но можно встретить в чужих исходниках.
Примечание: рассмотренные выше операции работают только с целочисленными типами данных!
Экономия памяти
При помощи битовых операций можно экономить немного памяти, пакуя данные в блоки. Например, переменная типа boolean занимает в памяти 8 бит, хотя принимает только 0 и 1. В один байт можно запаковать 8 логических переменных, например вот так:
Пакуем биты в байт, макро
// храним флаги как 1 бит
// макросы
#define B_TRUE(bp,bb) (bp) |= (bb)
#define B_FALSE(bp,bb) (bp) &= ~(bb)
#define B_READ(bp,bb) bool((bp) & (bb))
// вот так храним наши флаги, значения обязательно как степени двойки!
#define B_FLAG_1 1
#define B_FLAG_2 2
#define B_LED_STATE 4
#define B_BUTTON_STATE 8
#define B_BUTTON_FLAG 16
#define B_SUCCESS 32
#define B_END_FLAG 64
#define B_START_FLAG 128
// этот байт будет хранить 8 бит
byte boolPack1 = 0;
void setup() {
// суть такая: макрос функциями мы ставим/читаем бит в байте boolPack1
// записать true во флаг B_BUTTON_STATE
B_TRUE(boolPack1, B_BUTTON_STATE);
// записать false во флаг B_FLAG_1
B_FALSE(boolPack1, B_FLAG_1);
// прочитать флаг B_SUCCESS (для примера читаем в булин переменную)
boolean successFlag = B_READ(boolPack1, B_SUCCESS);
// либо используем в условии
if (B_READ(boolPack1, B_SUCCESS)) {
// выполнить при выполнении условия
}
}
void loop() { }
Вариант с Ардуино-функциями
// пример упаковки битовых флагов в байт
// при помощи ардуино-функций
byte myFlags = 0; // все флаги в false
// можно задефайнить названия
// цифры по порядку 0-7
#define FLAG1 0
#define FLAG2 1
#define FLAG3 2
#define FLAG4 3
#define FLAG5 4
#define FLAG6 5
#define FLAG7 6
#define FLAG8 7
void setup() {
// установить FLAG5 в true
bitSet(myFlags, FLAG5);
// установить FLAG1 в true
bitSet(myFlags, FLAG1);
// установить FLAG1 в false
bitClear(myFlags, FLAG1);
// считать FLAG5
bitRead(myFlags, FLAG5);
// условие с флагом 7
if (bitRead(myFlags, FLAG7)) {
// если FLAG7 == true
}
}
void loop() {}
Очень удобно храним целую пачку флагов (NEW!)
// вариант упаковки флагов в массив. ЛУЧШЕ И УДОБНЕЕ ПРЕДЫДУЩИХ ПРИМЕРОВ!
#define NUM_FLAGS 30 // количество флагов
byte flags[NUM_FLAGS / 8 + 1]; // массив сжатых флагов
// ============== МАКРОСЫ ДЛЯ РАБОТЫ С ПАЧКОЙ ФЛАГОВ ==============
// поднять флаг (пачка, номер)
#define setFlag(flag, num) bitSet(flag[(num) >> 3], (num) & 0b111)
// опустить флаг (пачка, номер)
#define clearFlag(flag, num) bitClear(flag[(num) >> 3], (num) & 0b111)
// записать флаг (пачка, номер, значение)
#define writeFlag(flag, num, state) ((state) ? setFlag(flag, num) : clearFlag(flag, num))
// прочитать флаг (пачка, номер)
#define readFlag(flag, num) bitRead(flag[(num) >> 3], (num) & 0b111)
// опустить все флаги (пачка)
#define clearAllFlags(flag) memset(flag, 0, sizeof(flag))
// поднять все флаги (пачка)
#define setAllFlags(flag) memset(flag, 255, sizeof(flag))
// ============== МАКРОСЫ ДЛЯ РАБОТЫ С ПАЧКОЙ ФЛАГОВ ==============
void setup() {
Serial.begin(9600);
clearAllFlags(flags);
writeFlag(flags, 0, 1);
writeFlag(flags, 10, 1);
writeFlag(flags, 12, 1);
writeFlag(flags, 15, 1);
writeFlag(flags, 15, 0);
writeFlag(flags, 29, 1);
// выводим все
for (byte i = 0; i < NUM_FLAGS; i++)
Serial.print(readFlag(flags, i));
}
void loop() {
}
Хороший трюк, может пригодиться! Я сделал удобную библиотеку для хранения битовых флагов, документация и примеры есть здесь.
Пример сжатия 1
Таким же способом можно паковать любые другие данные других размеров для удобного хранения или сжатия. Как пример – моя библиотека microLED, в которой используется следующий алгоритм: изначально необходимо хранить в памяти три цвета для каждого светодиода, каждый цвет имеет глубину 8 бит, т.е. в общей сложности тратится 3 байта на один светодиод RRRRRRRR GGGGGGGG BBBBBBBB. Для экономии места и удобства хранения можно сжать эти три байта в два (тип данных int), потеряв несколько оттенков результирующего цвета. Например вот так: RRRRRGGG GGGBBBBB. Сожмём и упакуем: есть три переменные каждого цвета, r, g, b:
int rgb = ((r & 0b11111000) << 8) | ((g & 0b11111100) << 3) | ((b & 0b11111000) >> 3);
Таким образом мы отбросили у красного и синего младшие (правые) биты, в этом и заключается сжатие. Чем больше битов отброшено – тем менее точно получится “разжать” число. Например сжимали число 0b10101010 (170 в десятичной) на три бита, при сжатии получили 0b10101000, т.е. потеряли три младших бита, и в десятичной уже получится 168. Для упаковки используется битовый сдвиг и маска, таким образом мы берём первые пять битов красного, шесть зелёного и пять синего, и задвигаем на нужные места в результирующей 16-битной переменной. Всё, цвет сжат и его можно хранить. Для распаковки используется обратная операция: выбираем при помощи маски нужные биты и сдвигаем их обратно в байт:
byte r = (data & 0b1111100000000000) >> 8; byte g = (data & 0b0000011111100000) >> 3; byte b = (data & 0b0000000000011111) << 3;
Таким образом можно сжимать, разжимать и просто хранить маленькие данные в стандартных типах данных.
Пример сжатия 2
Давайте ещё пример: нужно максимально компактно хранить несколько чисел в диапазоне от 0 до 3, то есть в бинарном представлении это 0b00, 0b01, 0b10 и 0b11. Видим, что в один байт можно запихнуть 4 таких числа (максимальное занимает два бита). Запихиваем:
// числа для примера byte val_0 = 2; // 0b10 byte val_1 = 0; // 0b00 byte val_2 = 1; // 0b01 byte val_3 = 3; // 0b11 byte val_pack = ((val_0 & 0b11) << 6) | ((val_1 & 0b11) << 4) | ((val_2 & 0b11) << 2) | (val_3 & 0b11); // получили 0b10000111
Как и в примере со светодиодами, мы просто брали нужные биты ( в этом случае младшие два, 0b11) и сдвигали их на нужное расстояние. Для распаковки делаем в обратном порядке:
byte unpack_1 = (val_pack & 0b11000000) >> 6; byte unpack_2 = (val_pack & 0b00110000) >> 4; byte unpack_3 = (val_pack & 0b00001100) >> 2; byte unpack_4 = (val_pack & 0b00000011) >> 0;
И получим обратно наши байты. Также маску можно заменить на более удобную для работы запись, задвинув 0b11 на нужное расстояние:
byte unpack_1 = (val_pack & 0b11 << 6) >> 6; byte unpack_2 = (val_pack & 0b11 << 4) >> 4; byte unpack_3 = (val_pack & 0b11 << 2) >> 2; byte unpack_4 = (val_pack & 0b11 << 0) >> 0;
Теперь, проследив закономерность, можно сделать для себя функцию или макрос чтения пакета:
#define UNPACK(x, y) ( ((x) & 0b11 << ((y) * 2)) >> ((y) * 2) )
Где x это пакет, а y – порядковый номер запакованного значения. Выведем посмотрим:
Serial.println(UNPACK(val_pack, 3)); Serial.println(UNPACK(val_pack, 2)); Serial.println(UNPACK(val_pack, 1)); Serial.println(UNPACK(val_pack, 0));
“Трюки” с битами
На битовых операциях можно сделать очень много всего интересного, и работать оно будет очень быстро и занимать мало места. Огромный список битовых трюков и хаков можно посмотреть в этой статье, их там очень много и все с примерами. Есть ещё один небольшой сборник самых простых и полезных хаков вот здесь (английский). Его я перевёл, смотрите ниже под спойлером. Другой вариант перевода (могут быть не все трюки) можно посмотреть здесь.
Целые числа
Перемотка бита
Перематывает один бит слева направо, то есть формирует последовательность 0b10000000, 0b01000000, 0b00100000, 0b00010000, 0b00001000, 0b00000100, 0b00000010, 0b00000001, 0b10000000, или 128, 64, 32, 16, 8, 4, 2, 1, 128
Вызывать циклично: x = ((x >> 1) | (x << 7));
Установка nго бита
x | (1<<n);
Выключение nго бита
x & ~(1<<n);
Инверсия nго бита
x ^ (1<<n);
Округление до ближайшей степени двойки
unsigned int v; // работает только с 32 битными числами v--; v |= v >> 1; v |= v >> 2; v |= v >> 4; v |= v >> 8; v |= v >> 16; v++;
Получение максимального целого
int maxInt = ~(1 << 31); int maxInt = (1 << 31) - 1; int maxInt = (1 << -1) - 1; int maxInt = -1u >> 1;
Получение минимального целого
int minInt = 1 << 31; int minInt = 1 << -1;
Умножение на 2
n << 1;
Деление на 2
n >> 1;
Умножение на mую степень двойки
n << m;
Деление на mую степень двойки
n >> m;
Остаток от деления
n & 0b1; // на 2 n & 0b11; // на 4 n & 0b111; // на 8 // ...
Проверка равенства
(a ^ b) == 0; // a == b !(a ^ b) // использовать внутри if()
Проверка на чётность (кратность 2)
(n & 1) == 1;
Обмен значениями
a = a ^ b ^ (b = a);
Проверка на одинаковый знак
(x ^ y) >= 0;
Смена знака
i = ~i + 1; // or i = (i ^ -1) + 1; // i = -i
Вернёт 2n
1 << n;
Является ли число степенью 2
n > 0 && !(n & (n - 1));
Остаток от деления на 2n на m
m & ((1 << n) - 1);
Среднее арифметическое
(x + y) >> 1; ((x ^ y) >> 1) + (x & y);
Получить mый бит из n (от младшего к старшему)
(n >> (m-1)) & 1;
Получить mый бит из n (от старшего к младшему)
n & ~(1 << (m-1));
Проверить включен ли nый бит
x & (1<<n)
Выделение самого правого включенного бита
x & (-x);
Выделение самого правого выключенного бита
~x & (x+1);
Выделение правого включенного бита
x | (x+1);
Выделение правого выключенного бита
x & (x-1);
Получение отрицательного значения
~n + 1; (n ^ -1) + 1;
if (x == a) x = b; if (x == b) x = a;
x = a ^ b ^ x;
Поменять смежные биты
((n & 10101010) >> 1) | ((n & 01010101) << 1);
Быстрый обратный квадратный корень
float Q_rsqrt( float number ) {
union {
float f;
uint32_t i;
} conv = {number};
conv.i = 0x5f3759df - ( conv.i >> 1 );
conv.f *= 1.5 - number * 0.5 * conv.f * conv.f;
return conv.f;
}
Быстрый квадратный корень (2 байта)
uint16_t root2(uint16_t x) {
uint16_t m, y, b;
m = 0x4000;
y = 0;
while (m != 0) {
b = y | m;
y >>= 1;
if (x >= b) {
x -= b;
y |= m;
}
m >>= 2;
}
return y;
}
Быстрый квадратный корень (4 байта)
uint32_t root4(uint32_t x) {
uint32_t m, y, b;
m = 0x4000ul << 16;
y = 0;
while (m != 0) {
b = y | m;
y >>= 1ul;
if (x >= b) {
x -= b;
y |= m;
}
m >>= 2ul;
}
return y;
}
float числа
Разбить float в массив бит (unsigned uint32_t)
typedef union {float flt; uint32_t bits} lens_t;
uint32_t f2i(float x) {
return ((lens_t) {.flt = x}).bits;
}
Вернуть массив бит обратно в float
float i2f(uint32_t x) {
return ((lens_t) {.bits = x}).flt;
}
Быстрый обратный квадратный корень
return i2f(0x5f3759df - f2i(x) / 2);
Быстрый nый корень из целого числа
float root(float x, int n) {
#DEFINE MAN_MASK 0x7fffff
#DEFINE EXP_MASK 0x7f800000
#DEFINE EXP_BIAS 0x3f800000
uint32_t bits = f2i(x);
uint32_t man = bits & MAN_MASK;
uint32_t exp = (bits & EXP_MASK) - EXP_BIAS;
return i2f((man + man / n) | ((EXP_BIAS + exp / n) & EXP_MASK));
}
Быстрая степень
return i2f((1 - exp) * (0x3f800000 - 0x5c416) + f2i(x) * exp);
Быстрый натуральный логарифм
#DEFINE EPSILON 1.1920928955078125e-07 #DEFINE LOG2 0.6931471805599453 return (f2i(x) - (0x3f800000 - 0x66774)) * EPSILON * LOG2;
Быстрая экспонента
return i2f(0x3f800000 + (uint32_t)(x * (0x800000 + 0x38aa22)));
Строки
Конвертировать в нижний регистр
(x | ' ');
('a' | ' ') => 'a'; // пример
('A' | ' ') => 'a'; // пример
Конвертировать в верхний регистр
(x & '_');
('a' & '_') => 'A'; // пример
('A' & '_') => 'A'; // пример
Инвертировать регистр
(x ^ ' ');
('a' ^ ' ') => 'A'; // пример
('A' ^ ' ') => 'a'; // пример
Позиция буквы в алфавите (англ)
(x & "x1F");
('a' & "x1F") => 1; // пример
('B' & "x1F") => 2; // пример
Позиция большой буквы в алфавите (англ)
(x & '?') или (x ^ '@');
('C' & '?') => 3; // пример
('Z' ^ '@') => 26; // пример
Позиция строчной буквы в алфавите (англ)
(x ^ '`');
('d' ^ '`') => 4; // пример
('x' ^ '`') => 24; // пример
Цвет
Быстрая конвертация цвета R5G5B5 в R8G8B8
R8 = (R5 << 3) | (R5 >> 2); G8 = (R5 << 3) | (R5 >> 2); B8 = (R5 << 3) | (R5 >> 2);
Приоритет операций
Чтобы не плодить скобки, нужно знать приоритет операций. В C++ он такой:
Приоритет операций
::++--()[].->++--+-!~(type)*&sizeofnew, new[]delete, delete[].*->**/%+-<<>><<=>>===!=&^|&&||?:=+=-=*=/=%=<<=>>=&=^=|=
Полезные страницы
- Набор GyverKIT – большой стартовый набор Arduino моей разработки, продаётся в России
- Каталог ссылок на дешёвые Ардуины, датчики, модули и прочие железки с AliExpress у проверенных продавцов
- Подборка библиотек для Arduino, самых интересных и полезных, официальных и не очень
- Полная документация по языку Ардуино, все встроенные функции и макросы, все доступные типы данных
- Сборник полезных алгоритмов для написания скетчей: структура кода, таймеры, фильтры, парсинг данных
- Видео уроки по программированию Arduino с канала “Заметки Ардуинщика” – одни из самых подробных в рунете
- Поддержать автора за работу над уроками
- Обратная связь – сообщить об ошибке в уроке или предложить дополнение по тексту ([email protected])

Данные в ассемблере.
Данные в ассемблере — понятие широкое. Программу в целом можно воспринимать как одну большую совокупность данных, однако мы уже знаем и помним, что она состоит из данных и кода — набора команд, необходимых для обработки данных.
Данные в ассемблере в узком понимании (буква, строка, символ, текстовый файл, звуковой файл, видеофайл, документ Word и т.п), а также сам код представляют собой определённую строго регламентированную последовательность чисел. Эта последовательность формируется при преобразовании программного текста в исполняемый файл, то есть написанный программистом код транслируется в машинный язык цифр.
Машина манипулирует минимальным блоком памяти размером в 1 байт. Байт состоит из 8 бит и может содержать 256 значений (2 в степени 8). Байтовый мир машин транслируется отладчиками, дизассемблерами и HEX-редакторами в 16-тиричном виде для более удобного восприятия человеком.
Для дальнейшего изучения вопроса нам понадобиться редактор HIEW. Он есть среди прочего необходимого в архиве DOS-1.rar, который необходимо скачать.
Байты, слова, двойные слова …
Фактически все программы — от простых до самых сложным представляют собой набор команд процессора, манипулирующих с данными.
Команды процессора представляют собой цифровые значения, имеющие свою структуру.
Открываем с помощью Hiew нашу программу PRG.COM (выбор файлов — F9). При помощи F4 выбираем режим отображения информации HEX (как вы уже знаете, шестнадцатиричный режим):
|
00000000: B4 09 BA 08–01 CD 21 C3–48 65 6C 6C–6F 20 57 6F + ¦ =!+Hello Wo 00000010: 72 6C 64 21–0D 0A 24 – – rld! $ |
Мы видим набор байт: B4 09 BA 08 01 CD 21 и т.д. Байты разделены дефисами на группы — по четыре в каждой.
Группы байт имеют названия:
- Группа из 2 байт называется Word («Слово»).
- Группа из 4 байт называется Double Word («Двойное слово»).
- Группа из 8 байт называется Quatro Bytes («Восемь байт»).
- Группа из 10 байт называется Tetro Bytes («Десять байт»).
В ассемблере имеются специальные директивы для резервирования памяти:
- DB — Define Bite.
- DW — Define Word.
- DD — Define Double Word.
- DQ — Define Quatro Bites
- DT — Define Tetro Bites.
Код и данные — это упорядоченная последовательность чисел.
Одну из этих директив мы использовали в нашем коде для резервирования памяти и заполнения её текстом:
|
message db “Hello World!”,0Dh,0Ah,‘$’ ; строка для вывода |
Переходим в режим декодирования (F4->Decode):
|
00000000: B409 mov ah,009 ;” “ 00000002: BA0801 mov dx,00108 ;” “ 00000005: CD21 int 021 00000007: C3 retn 00000008: 48 dec ax 00000009: 65 gs: 0000000A: 6C insb 0000000B: 6C insb 0000000C: 6F outsw 0000000D: 20576F and [bx][0006F],dl 00000010: 726C jb 00000007E 00000012: 64210D and fs:[di],cx 00000015: 0A24 or ah,[si] |
Для машины и код и данные — это строго упорядоченная последовательность цифр. Мы видим, что дизассемблер попытался перевести в код и нашу строку «Hello World!»,0Dh,0Ah,’$’, но мы можем различить её по набору байт от 48h до 24h.
Ассемблерный код также представлен в виде цифр. Шестнадцатеричное число B409 декодируется в инструкцию mov ah,009. При этом, очевидно, что B4 — это «mov ah», а 09 — это число «09» (ещё один ноль добавлен HIEW перед числом, чтобы показать его принадлежность именно к числовому значению и мы его не будем учитывать).
Во второй строке кода обратите внимание на последовательность байт: BA 08 01, которая декодируется в инструкцию:
|
00000002: BA0801 mov dx,00108 |
Понятно, что BA — это «mov dx», а 0801 — это число «0108 » (первый ноль добавил HIEW). Однако отображена оно в коде побайтно наоборот — зеркально.
Младший байт — меньший адрес.
Продолжаем изучать данные в ассемблере и переходим к очень важному моменту, который необходимо запомнить: Младший байт числа в памяти компьютера имеет меньший адрес, поэтому читается «попарно и задом на перёд». В дизассемблированном коде (как часть ассемблерной команды, либо в как часть стека) число будет выглядеть «обычно».
Ещё раз:
команда ассемблера обозначает: «поместить в регистр dx шестнадцатеричное число 108 (0108h). Число 108 побайтно выглядит как слово 01 08. 08 — это младший байт, 01 — старший. Слово 01 08 расположено в памяти по адресам 00000003: и 00000004:, значит 08 должно находится по младшему адресу — 00000003:, а 01 — по старшему — 00000004, как оно и есть.
Итак, 16-ти битное число 1234h в памяти будет храниться как последовательность байт 34 12. Windows программирование оперирует с 32 и 64 битными числами: 32 битное число 12345678h будет храниться как последовательность байт 78 56 34 12, а 64 битное число 123456789ABCDEF0h будет храниться как
последовательность байт F0 DE BC 9A 78 56 34 12.
Мой канал Old Programmer весь здесь: Программирование. Тематическое оглавление моего Zen-канала (Old Programmer). А здесь все о программировании на ассемблере.
Это вторая статья о числах в ассемблере. Первая здесь. Материал был взят из моей книги “Ассемблер и дизассемблирование” и частично переработан.
Параграф 1.7.
Представление чисел в компьютере
Беззнаковые целые числа в компьютере
Принцип представления беззнаковых целых чисел в компьютере достаточно прост:
- число должно быть переведено в двоичную систему счисления;
- должен быть определен объем памяти для этого числа.
Как мы уже говорили, это удобно делать, когда число представлено в шестнадцатеричной системе счисления, и тогда станет ясно, сколько ячеек памяти необходимо для хранения этого числа. Принято выделять: одинарные ячейки памяти (байты), двойные ячейки (слова), четвертные ячейки (четыре байта), наконец есть 8-байтовые. В языке ассемблера GAS (именно его я рассматриваю на своем канале) имеются специальные директивы для резервирования памяти для числовых констант и переменных:
- .byte – размещает каждое выражение как 1 байт
- .short – 2 байта
- .long – 4 байта
- .quad – 8 байт
Если речь идет о переменной, а чаще так и бывает, необходимо определить диапазон, в котором будет меняться значение переменной и, исходя из этого, резервировать для нее память. Поскольку современные процессоры Intel ориентированы на операции с 64-битными числами то, оптимальнее, все же ориентироваться на переменные такой же размерности.
Рассмотрим программу на языке C (700.c).
В данном программе задано четыре переменных: однобайтовая e, двухбайтовая c, четырехбайтовая t, восьмибайтовая a. С помощью этой программы, к выведем область памяти, где хранятся эти переменные. Вот дамп памяти, который выдает программа (рисунок 1).
Внимательно посмотрев на данную цепочку байтов, вы без труда обнаружите все наши переменные. Что важного можно почерпнуть из данной последовательности?
- Мы видим, что младшие байты чисел (переменных) в слове занимают в памяти младшие адреса. В свою очередь младшие слова в удвоенном слове — младший адрес. И, наконец, если рассматривать 64-битную переменную, то в ней младшее удвоенное слово должно занимать младший адрес. Это очень важный момент именно для анализа двоичного кода. В дальнейшем по одному виду области памяти вы сможете во многих случаях сразу идентифицировать переменные.
- Как видно на все переменные затрачивается объем памяти, кратный четырехбайтовой величине. После каждой инициализированной переменной компилятор вставляет директиву выравнивания по 32-битной границе (Align 4). Впрочем, все совсем не так просто, и при другом порядке следования переменных выравнивание может быть иным.
И так. 16-битное число 0xА890 в памяти будет храниться как последовательность байтов 90 A8, 32-битное число 0x67896512 как последовательность 12 65 89 67. И, наконец, 64-битное число 0xF5C68990D1327650 — как 50 76 32 D1 90 89 C6 F5.
Числа со знаком в компьютере
Поскольку в памяти нет ничего, кроме двоичных разрядов, то вполне логично было бы выделить для знака числа отдельный бит. Например, имея одну ячейку, мы могли бы получить диапазон чисел от –127 до 127 (11111111 – 01111111). Подход был бы не так уж и плох. Вот только пришлось бы вводить отдельно сложение для знаковых и беззнаковых чисел. Существует и другой, альтернативный способ введения знаковых чисел. Алгоритм построения заключается в том, что мы объявляем некоторое число заведомо положительным и далее ищем для него противоположное по знаку исходя из очевидно тождества: a + (– a) = 0.
На множестве однобайтовых чисел за единицу естественно взять двоичное число 00000001. Решая уравнение 00000001 + x = 00000000, мы приходим к неожиданному, на первый взгляд, результату x = 11111111, другими словами за -1 мы должны принять число 11111111 (255 в десятичном эквиваленте и FF в шестнадцатеричном). Попробуем развить нашу теорию. Очевидно, что -1 – (1) = -2, т. е. по логике вещей, за -2 мы должны принять число 11111110. Но с другой стороны число 00000010 вроде бы должно представлять +2. Посмотрите 11111110 + 00000010 = 00000000, т. е. выполняется очевидное тождество +2 + (-2) = 0. Итак, мы на верном пути и процесс можно продолжить (см. Рисунок 2).
Внимательно посмотрите на таблицу (рисунок 2). Что же у нас получилось? Знаковые числа оказываются в промежутке -128 до 127.
Таким образом, однобайтовое число можно интерпретировать и как число со знаком, и как беззнаковое число. Тогда, например, 11111111 в первом случае будет считаться -1, а во втором случае 255. Все зависит от нашей интерпретации. Еще интереснее операции сложения и вычитания. Эти операции будут выполняться по одной и той же схеме и для знаковых и для беззнаковых чисел. По этой причине и для операции сложения и для операции вычитания у процессора имеется всего по одной команде: add и sub. Разумеется, при выполнении действия может возникнуть переполнение или перенос в несуществующий разряд, но это отдельный разговор, и решить проблему можно, зарезервировав еще одну ячейку памяти. Все наши рассуждения легко переносятся на двух- четырех- и восьмибайтовые числа. Так максимальное двухбайтовое беззнаковое число будет 65 535, а знаковые числа окажутся в промежутке от –32 768 до 32 767. Еще один интересный момент касается старшего бита. Как мы видим, по нему можно определить знак. Но в данной схеме бит совсем не изолирован и участвует в формировании значения числа вместе с остальными битами.
Уметь хорошо ориентироваться в знаковых и беззнаковых числах очень важно для программиста на языке ассемблера. Встретив, скажем, команду
cmp rax, 0xFFFFFFFFFFFFFFFE
следует иметь в виду, что в действительности это, возможно, команда
cmp rax, -2
Рассмотрим последовательность переменных:
signed char e=-2;
short int c=-3;
int b=-4;
__int64_t a=-5;
Как видим, это все знаковые переменные с отрицательным значением. При выводе фрагмента памяти, содержащего данные переменные, получим следующую последовательность байтов:
fe00 00 00 fd ff 00 00 fc ff ff ff 00 00 00 00 fb ff ff ff ff ff ff ff
Итак, значение однобайтовой переменной -2 в памяти компьютера представлено байтом 0xFE, значение двухбайтовой переменной -3, представлено последовательностью 0xFFFD, значение четырехбайтовой переменной -4 — последовательностью 0xFFFFFFFC, и, наконец, отрицательное восьмибайтовая переменная со значением -5 представлена байтами 0xFFFFFFFFFFFFFFFB. Напоминаю, что при представлении восьмибайтового числа младшие четыре байта должны находиться по адресу, меньшему, чем старшие.
Вещественные числа
Для того чтобы использовать вещественные числа в командах процессора Intel(командах арифметического сопроцессора), они должны быть представлены в памяти компьютера в нормализованном виде. В общем случае нормализованный вид числа выглядит так:
Здесь ZN – знак числа, M – мантисса числа, обычно удовлетворяет условию M < 1, N – основание системы счисления, q показатель, в общем случае может быть и положительным и отрицательным числом. Числа, представленные таким образом, называют еще числами с плавающей точкой (или числами с плавающей запятой).
Рассмотрим конкретный пример. Попытаемся представить в нормализованном виде число 5,75. Переведем вначале это число в двоичную систему счисления. В данном случае это делается достаточно легко. Действительно, 5 — это 101, а 0,75 – это (1/2) + (1/4). Другими словами 5,75 = 0b101,11. Пишем далее 0b101.11 = 1.00111 * (2^3). Таким образом, мы имеем следующие компоненты нормализованного числа:
Заметим, что первая цифра мантиссы в таком представлении всегда равна 1, а, следовательно, ее можно и вообще не хранить, и в формате Intel так и поступают. Кроме этого нужно иметь в виду, что показатель q в действительности (для процессора Intel) хранится в памяти в виде суммы с некоторым числом, так чтобы всегда быть положительным. Процессор Intelможет работать с тремя типами вещественных чисел:
- короткое вещественное число. Всего для хранения отводиться 32 бита. Биты 0-22 резервируются для мантиссы. Биты 23-30 предназначены для хранения показателя q, сложенного с числом 127. Последний 31-й бит, предназначен для хранения знака числа (1 – знак отрицательный, 0 – положительный);
- длинное вещественное число. Для хранения такого числа отводится 64 бита. Биты 0-51 нужны для хранения мантиссы. Биты 52-62 предназначены для хранения числа q, сложенного с числом 1024. Последний 63-й бит определяет знак числа (1 – знак отрицательный, 0 – положительный);
- расширенное вещественное число. Для хранения числа отводится 80 битов. Биты 0-63 – мантисса числа. Биты 64-78 — показатель q, сложенный с числом 16383. 79-й, последний бит отводится для знака числа (1 – знак отрицательный, 0 – положительный).
Очевидно, пришла пора разобрать конкретный пример представления в памяти вещественного числа. Итак, пусть в программе на языке Си имеем объявление переменной:
float a=-80.5
Тип float – это короткое вещественное число, т. е. в памяти оно, согласно выше записанному, будет занимать 32 бита. Попытаемся теперь нашим обычным способом заглянуть в память. Вот они, четыре байта, которые и призваны представлять наше число:
00 00 a1 c2
Чтобы легче было разбираться, представим последовательность из четырех байтов в двоичном виде:
00000000 00000000 10100001 11000010
Или более понятным способом, начиная со старшего байта для выделения мантиссы, показателя и знака:
11000010 10100001 00000000 00000000
Выделим мантиссу. На нее отводиться 23 бита. Имеем, таким образом, двоичное число 0100001. Учтите, что биты мантиссы, отсчитываются, начиная со старшего (в данном случае 22-го) бита, а оставшиеся нули естественно отбрасываются, поскольку вся мантисса располагается справа от запятой. Правда, это еще не совсем мантисса. Как ранее было сказано, единица перед запятой в представлении отбрасывается. Так что мы должны восстановить ее. Поэтому мантиссой будет число 0b1,0100001. Знак всего числа, как мы видим, определяется единицей, следовательно, задает отрицательное число. А вот показатель нам следует получить из двоичного числа 0b10000101. В десятичном представлении это число 133. Вычитая число 127 (для короткого вещественного числа), получим 6. Следовательно, для того чтобы получить из мантиссы истинное дробное число, нужно сместить в ней точку на шесть разрядов вправо. Окончательно получаем 0b1010000,1. В шестнадцатеричной системе счисления это просто 0x50,8, а в десятичной получаем как раз 80,5.
В качестве тренировки я бы вам предложил следующую цепочку байтов:
00 80 fb 42
Попытайтесь доказать, что это есть ничто иное, как представление числа 125,75.
Из сказанного в данном разделе можно сделать вывод, что при использовании в программе вещественных чисел они могут стать приближенными еще до того, как с ними были произведены какие-либо действия. Это вызвано тем, что для записи чисел в память их нормализуют.
–> Глава 1. Параграф 1.8. <–Глава 1. Параграф 1.6.
Ассемблер вам в радость! Пока! Подписываемся на мой канал Old Programmer.
Я вижу, что вы забыли поставить ЛАЙК, не так ли?

 Сообщение было отмечено Nick_Volkov как решение
Сообщение было отмечено Nick_Volkov как решение
