Решения задач на метод максимального правдоподобия
Для оценивания неизвестных параметров статистических распределений наравне с методом моментов используют метод максимального (наибольшего) правдоподобия.
Суть метода: составить по специальной формуле функцию правдоподобия $L$, и найти оценку параметра $theta$ из условия максимизации функции правдоподобия (ФП) на определенной выборке ${x_i}$. Иногда ФП заменяют на логарифмическую функцию правдоподобия $l=ln L$ (ЛФП), что облегчает расчеты (вычисление производных).
Оценки, полученные данным методом, будут состоятельными, асимптотически эффективными и асимптотически нормальными. Несмещенность оценок надо проверять (это метод не гарантирует).
Примеры нахождения оценок по методу наибольшего правдоподобия вы найдете ниже. Удачи!
Понравилось? Добавьте в закладки
Примеры решений
Пример 1. Найти методом наибольшего правдоподобия оценку параметра p биномиального распределения, если в $n_1$ независимых испытаниях событие A появилось $m_1$ раз и в $n_2$ независимых испытаниях событие A появилось $m_2$ раз.
Пример 2. Используя метод наибольшего правдоподобия, оценить параметры $a$ и $sigma^2$ нормального распределения, если в результате $n$ независимых испытаний случайная величина $xi$ приняла значения $xi_1, xi_2,…,xi_n$.
Пример 3. Случайная величина $X$ (число появлений события $A$ в $m$ независимых испытаниях) подчинена закону распределения Пуассона с неизвестным параметром $lambda$. Найти методом наибольшего правдоподобия по выборке $x_1, x_2,…,x_n$ точечную оценку неизвестного параметра $lambda$ распределения Пуассона.
Пример 4. Случайная величина – время безотказной работы изделия имеет показательное распределение. В таблице приведены данные по времени работы в часах для 1000 изделий. Найти методом максимального правдоподобия точечную оценку неизвестного параметра $lambda$.
Пример 5. Найти методом наибольшего правдоподобия по выборке $x_1, x_2,…,x_n$ точечную оценку параметра $p$ геометрического распределения:
$$P(X=x_i)=(1-p)^{x_i-1} cdot p,$$
где $x_i$ – число испытаний, произведенных до появления события, $p$ – вероятность появления события в одном испытании.
Пример 6. Методом максимального правдоподобия найти точечную оценку параметра $lambda$ по данной выборке
Х 1-3 3-5 5-7 7-9 9-11 11-13 13-15 15-17 17-19
n 5 6 7 15 22 27 30 34 35
при условии, что соответствующая непрерывная случайная величина имеет плотность распределения $f(x)=lambda exp(lambda(x-20)), x le 20$.
Пример 7. Методом максимального правдоподобия найдите оценку параметра $theta$, если плотность имеет вид
$$
f(x)=frac{2x^3}{sqrt{2pi}} exp (-(x^4-theta)^2/2)
$$
и по наблюдениям 1.4 1.5 3.2 1.4 2.5 3.4 3.1 2.4 3.8 2.6
Выполним для вас задачи оценивания по ММП
Теория по ММП
Хотите немного больше знать о теоретических основах метода наибольшего правдоподобия для чайников? Тогда используйте ссылки ниже для изучения.
- Метод максимального правдоподобия
Вводятся свойства оценок параметров распределения (несмещенность, состоятельность, эффективность), доказывются теоремы. Далее рассматривается сам ММП, приводится сводная таблица оценок для разных типов распределений. - Методы нахождения оценок: метод максимального
правдоподобия
Лекция по ММП с теоретическими основами и примерами решений. - Видеоролик МФТИ о ММП
Короткий (буквально 4 минуты) ролик о сути метода. - Список учебников по математической статистике со ссылками
- Решенные контрольные по математической статистике
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 января 2021 года; проверки требуют 4 правки.
Ме́тод максима́льного правдоподо́бия или метод наибольшего правдоподобия (ММП, ML, MLE — англ. maximum likelihood estimation) в математической статистике — это метод оценивания неизвестного параметра путём максимизации функции правдоподобия[1]. Основан на предположении о том, что вся информация о статистической выборке содержится в функции правдоподобия.
Метод максимального правдоподобия был проанализирован, рекомендован и значительно популяризирован Р. Фишером между 1912 и 1922 годами (хотя ранее он был использован Гауссом, Лапласом и другими).
Оценка максимального правдоподобия является популярным статистическим методом, который используется для создания статистической модели на основе данных и обеспечения оценки параметров модели.
Метод максимального правдоподобия соответствует многим известным методам оценки в области статистики. Например, вы интересуетесь таким антропометрическим параметром, как рост жителей России. Предположим, у вас имеются данные о росте некоторого количества людей, а не всего населения. Кроме того, предполагается, что рост является нормально распределённой величиной с неизвестной дисперсией и средним значением. Среднее значение и дисперсия роста в выборке являются максимально правдоподобными к среднему значению и дисперсии всего населения.
Для фиксированного набора данных и базовой вероятностной модели, используя метод максимального правдоподобия, мы получим значения параметров модели, которые делают данные «более близкими» к реальным. Оценка максимального правдоподобия даёт уникальный и простой способ определить решения в случае нормального распределения.
Метод оценки максимального правдоподобия применяется для широкого круга статистических моделей, в том числе:
-
- линейные модели и обобщённые линейные модели;
- факторный анализ;
- моделирование структурных уравнений;
- многие ситуации, в рамках проверки гипотезы и доверительного интервала формирования;
- дискретные модели выбора.
Сущность метода[править | править код]
Пусть есть выборка 




называется оце́нкой максима́льного правдоподо́бия параметра 
Часто вместо функции правдоподобия 




,
Если функция правдоподобия дифференцируема, то необходимое условие экстремума — равенство нулю её градиента:
Достаточное условие экстремума может быть сформулировано как отрицательная определённость гессиана — матрицы вторых производных:
Важное значение для оценки свойств оценок метода максимального правдоподобия играет так называемая информационная матрица, равная по определению:
В оптимальной точке информационная матрица совпадает с математическим ожиданием гессиана, взятым со знаком минус:
Свойства[править | править код]
- Оценки максимального правдоподобия, вообще говоря, могут быть смещёнными (см. примеры), но являются состоятельными, асимптотически эффективными и асимптотически нормальными оценками. Асимптотическая нормальность означает, что
где 
Асимптотическая эффективность означает, что асимптотическая ковариационная матрица 
- где
— функция правдоподобия выборки
объёма
Примеры[править | править код]
Последнее равенство может быть переписано в виде:
где 

.
Такая оценка будет смещенной: 

.
Чтобы найти её максимум, приравняем к нулю частные производные:
откуда
— выборочное среднее, а
— выборочная дисперсия.
Применение метода[2][править | править код]
Обработка эксперимента[править | править код]
Предположим, что мы измеряем некоторую величину 



того, что величина 

![{displaystyle W(a)={frac {1}{sqrt {2pi sigma _{1}^{2}}}}exp left[-{frac {(x_{1}-a)^{2}}{2sigma _{1}^{2}}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d68b88e590ea137276642fa9f4d42c26ec1bffd)
Теперь предположим, что мы провели несколько таких измерений и получили 


![{displaystyle W(a)=prod _{i=1}^{n}{{frac {1}{sqrt {2pi sigma _{i}^{2}}}}exp left[-{frac {(x_{i}-a)^{2}}{2sigma _{i}^{2}}}right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd470d163e5a152107dc815da720b04e4c0a1a54)
Эта функция называется функцией правдоподобия. Наиболее вероятное значение измеряемой величины 

Продифференцируем логарифмическую функцию правдоподобия по 

Приравняем 



Крамер сформулировал следующую теорему:
Теорема: Не существует другого метода обработки результатов эксперимента, который дал бы лучшее приближение к истине, чем метод максимального правдоподобия.
Ошибки измерений[править | править код]
Предположим, что мы провели серию измерений и получили серию значений 
![W(a)={frac {1}{{sqrt {2pi sigma _{{a^{*}}}^{2}}}}}exp left[-{frac {(a^{*}-a)^{2}}{2sigma _{{a^{*}}}^{2}}}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3688162fd9df56c60d6d9aa54e03a0e02bcebde0)
Запишем логарифмическую функцию правдоподобия:
Возьмем первую производную:

Если 



Это называется первой магической формулой[2].
Условный метод максимального правдоподобия[править | править код]
Условный метод максимального правдоподобия (Conditional ML) используется в регрессионных моделях. Суть метода заключается в том, что используется не полное совместное распределение всех переменных (зависимой и регрессоров), а только условное распределение зависимой переменной по факторам, то есть фактически распределение случайных ошибок регрессионной модели. Полная функция правдоподобия есть произведение «условной функции правдоподобия» и плотности распределения факторов. Условный ММП эквивалентен полному варианту ММП в том случае, когда распределение факторов никак не зависит от оцениваемых параметров. Это условие часто нарушается в моделях временных рядов, например в авторегрессионной модели. В данном случае, регрессорами являются прошлые значения зависимой переменной, а значит их значения также подчиняются той же AR-модели, то есть распределение регрессоров зависит от оцениваемых параметров. В таких случаях результаты применения условного и полного метода максимального правдоподобия будут различаться.
См. также[править | править код]
- Правдоподобие принятой последовательности
- Метод моментов
- Обобщенный метод моментов
- Метод наименьших квадратов
- Метод инструментальных переменных
- EM-алгоритм
Примечания[править | править код]
- ↑ Фишер — 1912 г. Математический энциклопедический словарь, М.: Советская энциклопедия, 1988.
- ↑ 1 2 А.П. Онучин. Экспериментальные методы ядерной физики. — Новосибирск: Новосибирский государственный технический университет, 2010. — С. 297—303. — 336 с. — ISBN 978-5-7782-1232-9.
Литература[править | править код]
- Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. Начальный курс. — М.: Дело, 2007. — 504 с. — ISBN 978-5-7749-0473-0.
- Остапенко Р. И. Основы структурного моделирования в психологии и педагогике: учебно-методическое пособие для студентов психолого-педагогического факультета. — Воронеж.: ВГПУ, 2012. — 116 с. — ISBN 978-5-88519-886-8.
- Никулин М. С. Отношения правдоподобия критерий // Математическая энциклопедия / Виноградов И. М. (гл. ред.). — М.: Советская энциклопедия, 1984. — Т. 4. — С. 151. — 1216 с.
Практическое руководство по методу максимального правдоподобия
Время на прочтение
4 мин
Количество просмотров 13K
Как принять решение о покупке на основе 5-звездочных оценок от покупателей

Вам наверняка доводилось когда-либо в своей жизни принимать решение о покупке, основываясь на отзывах о товарах. Как социальным существам нам свойственно покупать вещи, которые рекомендуют другие покупатели.
Недавно, в поисках новых наушников, я просмотрел все товары, которые имеют оценку 5 звезд. Меня поразило, насколько сложно принять решение о покупке, основываясь только на отзывах покупателей. Мне пришло в голову взглянуть на отзывы товаров с точки зрения статистики.
В этой статье я объясняю метод оценки максимального правдоподобия на примере сравнения двух товаров, используя гипотетические оценки, полученные на основе мнений людей о товарах.

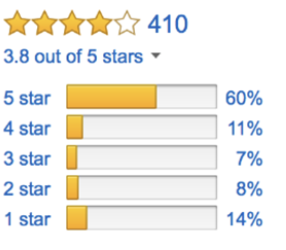
Если быть конкретным, то я смотрю на то, сколько раз товар получил оценку, отражающую степень удовлетворения людей этим товаром (от 1 до 5 звезд).
Оценка максимального правдоподобия — это метод, который определяет значения параметров модели. Значения параметров подбираются таким образом, чтобы они максимизировали вероятность того, что процесс написания отзыва о товаре, описанный моделью, дал оценку, которая будет более близка к реальной.
Давайте построим модель и оценим параметры таким образом, чтобы они максимизировали вероятность получения значений, наблюдаемых в реальных отзывах. Чтобы освежить в памяти вероятностные обозначения, упомянутые в этой статье, почитайте мою предыдущую статью по теме.
Мы хотим оценить θi — вероятность того, что люди оценят товар числом звезд равным i. Поскольку каждый новый рейтинг (оценка) имеет значение от 1 до 5, эта вероятность соответствует категориальному распределению Cat(θ).
![]()
Для каждого конкретного товара мы наблюдаем вектор рейтингов R= [r1,r2,r3,r4,r5]. Каждая оценка r_i — это общее количество i-звездных отзывов, полученных этим товаром.
Получение каждого i-звездного отзыва происходит с вероятностью θi. Поскольку каждый отзыв r независим от других, мы можем моделировать вероятность с помощью категориального распределения:
![]()
Вероятность наблюдения вектора событий R из N независимых отзывов задается полиномиальным распределением параметризованным θ:
![]()
Вычислить его логарифмическое правдоподобие можно следующим образом:
![]()
Что позволяет нам определить оценку максимального правдоподобия (Maximum Likelihood Estimator) θ для каждого из двух товаров. Для этого мы ищем θ, которая максимизирует правдоподобие L.
Обычно это делается путем дифференцирования функции правдоподобия по θ с использованием так называемых множителей Лагранжа.
![]()
Полагая, что все производные равны 0, мы получаем наиболее естественную оценку:
![]()
Следовательно, оценки максимального правдоподобия приведены ниже:
# количества звезд по отзывам
R_A = [10,6,10,27,109]
R_B = [57,33,29,45,246]
# оценки максимального правдоподобия
theta_A = R_A / np.sum(R_A)
theta_B = R_B / np.sum(R_B)
print("MLE for Product A: ", np.round(theta_A,3))
print("MLE for Product B: ", np.round(theta_B,3))
На основе этой оценки максимального правдоподобия θ для обеих моделей мы можем вычислить максимальное правдоподобие (Maximum Likelihood).
import math
import numpy as np
def f(n):
return math.factorial(n)
def mle(R, theta):
return (f(np.sum(R)) / (np.prod([f(r) for r in R]))) *
np.prod([theta[i]**R[i] for i in range(len(R))])
# максимальное правдоподобие
ml_A = mle(R_A,theta_A)
ml_B = mle(R_B,theta_B)
print("ML for Product A {:.7f}".format(ml_A))
print("ML for Product B {:.7f}".format(ml_B))
ml_products.py
Дает ли максимальное правдоподобие уверенность в том, что один из товаров предпочтительнее в глазах покупателей? Ответ не однозначен.
Здесь в игру вступает информационный критерий Акаике (Akaike Information Criterion), который дает нам некоторую доказательную базу. Оценка по информационному критерию Акаике награждает модели, которые достигают высокого показателя критерия адекватности (с низким максимальным правдоподобием), и штрафует модели, если они становятся чрезмерно сложными (большое количество параметров k).

Предпочтительной является модель с минимальным значением информационного критерия Акаике и максимальным правдоподобием, как показано ниже.
# информационный критерий Акаике
aic_A = 2*5 - 2*math.log(ml_A)
aic_B = 2*5 - 2*math.log(ml_B)
print("AIC for Product A: {:.2f}".format(aic_A))
print("AIC for Product B: {:.2f}".format(aic_B))
Таким образом, у нас есть некоторые свидетельства того, что люди, ответившие на опрос, предпочитают продукт B продукту A.
Мы только что рассмотрели, как использовать метод оценки максимального правдоподобия в простом контексте обзоров товаров.
Одним из недостатков метода оценки максимального правдоподобия является невозможность включить наши предпосылочные убеждения о тех параметрах, которые мы оцениваем. Например, у большинства отзывов в основном либо 5 звезд, либо 1 звезда, и очень мало средних значений.
Как я говорил в предыдущей статье, мы можем рассматривать байесовский анализ данных как расширение оценки максимального правдоподобия, что может лучше подойти в практических ситуациях. Больше информации об оценке максимального правдоподобия можно найти в этой замечательной статье.
Материал подготовлен в рамках курса «Математика для Data Science». Если вам интересно узнать подробнее о формате обучения и программе, познакомиться с преподавателем курса — приглашаем на день открытых дверей онлайн. Регистрация здесь.
Татьяна Васильевна Болотова
Эксперт по предмету «Экономика»
Задать вопрос автору статьи
Определение 1
Метод максимального правдоподобия – это рациональный способ построения оценки какого-либо неизвестного параметра, суть которого состоит в том, что за «наиболее правдоподобное» значение параметра принимается значение $Ө$, сводящее к максимуму вероятность получения при $n$ опытах следующую выборку $X = (x_1, …, x_n)$.
Методы нахождения оценок
В общем смысле точечная оценка неизвестного параметра $Ө$ – это любая статистика. В практической же деятельности чаще всего рассматриваются самые «качественные» оценки, при которых вероятность принятия ими значения максимально близкого к неизвестному значению $Ө$ при реализации случайной выборки будет наибольшей. Данные оценки делят на несмещенные, состоятельные и эффективные. При этом возникает вопрос о методах получения качественной оценки для произвольного параметра $Ө$ исследуемой случайной величины $X$. Наиболее распространены следующие методы нахождения оценок:
- Метод подстановки;
- Метод моментов;
- Метод наибольшего правдоподобия.
Метод подстановки – это наиболее простой метод отыскания точечных оценок. Он заключается в том, что оценкой неизвестного параметра $Ө$ является соответствующая выбранная числовая характеристика:
Рисунок 1. Формула. Автор24 — интернет-биржа студенческих работ
К примеру, по методу постановки оценка математического ожидания – это выборочное среднее, а оценка дисперсии – это выборочная дисперсия.
Все полученные по методу подстановки оценки являются состоятельными, но не гарантирована их эффективность и несмещенность. Пример смещенной оценки – выборочная дисперсия.
Рассмотрим далее метод моментов. Предположим, что $x_1, …, x_n$ – это выборка наблюдений некоторой случайной величины$X$, которая имеет распределение $Fx (x, Ө)$ содержащее вектор неизвестных параметров $Ө =( Ө_1, …, Ө_k)$. Допустим, что для данного распределения можно рассчитать начальные моменты
«Метод максимального правдоподобия с примерами» 👇
Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ
и центральные
Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ
некоторых порядков $r$.
Такие моменты называются функциями соответствующих неизвестных параметров $Ө_1, …, Ө_k$. Однако, для выборки можно рассчитать выборочные начальные моменты
Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ
Рисунок 5. Формула. Автор24 — интернет-биржа студенческих работ
Метод моментов заключается в том, что необходимо найти такой вектор параметров $Ө$, при котором будут равны теоретические и выборочные моменты, т.е. в решении системы уравнений:
Рисунок 6. Формула. Автор24 — интернет-биржа студенческих работ
Число уравнений в данной системе будет равняться количеству неизвестных параметров $k$. Чтобы получить оценки с помощью метода моментов, может быть выбран любой момент произвольного порядка, но, как правило, в практике используются только моменты низших порядков.
Как и при методе подстановок, все оценки, найденные по методу моментов, характеризуются как состоятельные, но не гарантируется их эффективность и несмещенность.
Точечные оценки, найденные при помощи метода моментов, носят название ММ-оценки.
Метод наибольшего правдоподобия рассмотрим в следующем пункте.
Сущность метода максимального правдоподобия
Определение 2
Под методом максимального правдоподобия в математической статистике понимается метод оценки неизвестного параметра посредством максимизации функции правдоподобия. Основой данного метода является предположение о том, что все данные о статистической выборке содержатся в функции правдоподобия. Описываемый метод был проанализирован Р. Фишером в начале 20-го века, который в дальнейшем его рекомендовал и популяризировал.
Оценка наибольшего правдоподобия – это достаточно популярный статистический метод, используемый с целью построения статистической модели на основе информации и обеспечения оценки всех параметров модели.
Метод наибольшего правдоподобия соответствует многим популярным методам статистической оценки. К примеру, вы рассматриваете такой антропометрический параметр, как рост жителей данной страны. Допустим, что вы располагаете данными о росте определенного количества людей, но не всего населения. Помимо этого, допускается, что рост – это нормально распределенная величина со средним значением и неизвестной дисперсией. Дисперсия роста и среднее значение в выборке будут являться максимально правдоподобными к дисперсии и среднему значению всего населения.
Используя фиксированный набор данных и базовой модели вероятностей в расчетах с помощью метода правдоподобия, будут получены такие значения параметров, которые будут делать данные «наиболее приближенные» к реальным. Метод максимального правдоподобия является уникальным и простым способом определения решения при нормальном распределении.
Метод наибольшего правдоподобия используются во многих статистических моделях:
- В линейных и обобщенных линейных моделях;
- В факторном анализе;
- При моделировании структурных уравнений;
- Во многих ситуациях, предполагающих проверку гипотезу и доверительный интервал формирования;
- В дискретных моделях выбора и т.д.
Метод наибольшего правдоподобия заключается в том, что оценкой вектора неизвестных параметров
Рисунок 7. Формула. Автор24 — интернет-биржа студенческих работ
выступает вектор
Рисунок 8. Формула. Автор24 — интернет-биржа студенческих работ
который доставляет максимум функции правдоподобия:
Рисунок 9. Формула. Автор24 — интернет-биржа студенческих работ
Иными словами, сущность метода наибольшего правдоподобия заключается в нахождении такого вектора параметров, при котором была бы наиболее вероятной реализация $x_1, … ,x_n$ случайной выборки $X_1,…, X_n$.
Точечные оценки, получаемые при методе наибольшего правдоподобия, носят название МП-оценки.
Пример использования метода максимального правдоподобия
Пусть необходимо найти при помощи метода максимально правдоподобия оценку заданного параметра p биноминального распределения
Рисунок 10. Формула. Автор24 — интернет-биржа студенческих работ
если в $n_1$ независимых испытания некоторое событие $A$ появлялось $m_1$ раз, а в $n_2 – m_2$ раз.
Для того, чтобы решить данную задачу, необходимо составить функцию правдоподобия:
Рисунок 11. Формула. Автор24 — интернет-биржа студенческих работ
Затем следует отыскать логарифмическую функцию:
Рисунок 12. Формула. Автор24 — интернет-биржа студенческих работ
На следующем этапе определяется первая производная p:
Рисунок 13. Формула. Автор24 — интернет-биржа студенческих работ
Найденную производную необходимо приравнять к нулю, тем самым записав уравнение правдоподобия.
Рисунок 14. Формула. Автор24 — интернет-биржа студенческих работ
После относительного решения полученного уравнения находим значение критической точки:
Рисунок 15. Формула. Автор24 — интернет-биржа студенческих работ
В данной точке вторая производная будет отрицательной, а, следовательно, данная точка является максимумом. Таким образом найденная точка принимается в качестве оценки по методу максимального правдоподобия неизвестной вероятности p биноминального распределения.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
В статистике наиболее часто применяемые
методы нахождения точечных оценок
параметров распределения являются:
– метод моментов (коротко (ММ);
– метод максимального правдоподобия
(коротко – ММП);
– метод наименьших квадратов (коротко
МНК).
2.1. Метод моментов (мм)
Суть метода моментов для нахождения
точечных оценок неизвестных параметров
заданного распределения состоит в том,
что приравнивается теоретические
моменты распределения соответствующим
эмпирическим моментам, найденные по
выборке.
Например, если распределение зависит
от одного параметра
![]() (задан вид плотности распределения
(задан вид плотности распределения![]() ),
),
то для нахождения его оценки нужно
решить относительно![]() одно уравнение:
одно уравнение:![]()
где
![]() –
–
есть функция от![]() .
.
Если распределение зависит от двух
параметров
![]() ,
,
(например, вид плотности распределения![]() ),
),
то надо решить систему уравнений:

относительно параметров
![]() .
.
И, наконец, если надо оценить
![]() параметров
параметров![]() , то надо решить одну из систем вида:
, то надо решить одну из систем вида:
(26)
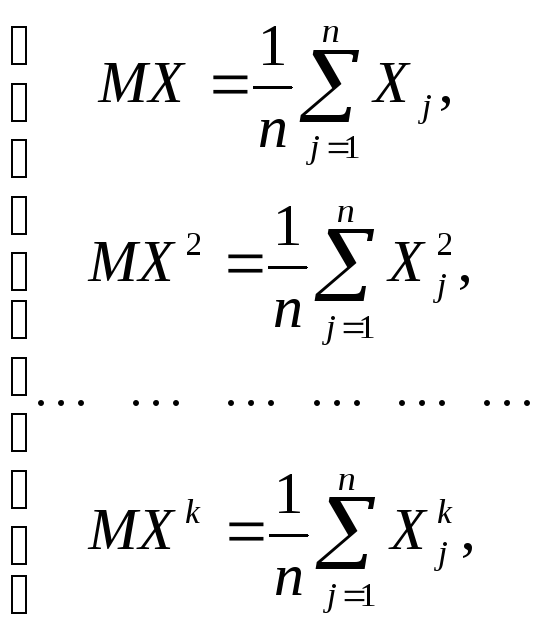 или
или
В этих системах мы видим, что присутствуют
моменты до
![]() го
го
порядков случайного события![]() и его центрированного,
и его центрированного,![]() .
.
Метод моментов является наиболее простым
методом оценки параметров, и он был
предложен в 1894г. Пирсоном. Оценки,
получаемые методом моментов, обычно
являются состоятельными, однако их
эффективность часто меньше единицы.
Пример 10. Найдём оценки параметров
нормального распределения с.в.![]() применяя,
применяя,
метода моментов.
Решение. Пусть дана выборка![]() найти точечные оценки параметров
найти точечные оценки параметров![]() и
и![]() .
.
По методу моментов приравниваем их,
соответственно, к выборочному среднему
и выборочной дисперсии:![]() начальный
начальный
момент первого порядка,![]() центральный
центральный
момент второго порядка и получаем

Таким образом, искомые оценки параметров
нормального распределения будут:
![]() и
и
![]()
2.2. Метод максимального правдоподобия (ммп)
Пусть
![]() выборка,
выборка,
полученная в результате проведения![]() независимых
независимых
наблюдений за с.в.![]() И пусть вид закона распределения
И пусть вид закона распределения
случайной величины![]() ,
,
например, вид функции плотности![]() известен, но неизвестен параметр
известен, но неизвестен параметр![]() ,
,
которым определяется этот закон.
Требуется по заданной выборке оценить
параметр![]()
Метод максимального правдоподобия
(ММП), предложен Р.Фишером в основе
которого, лежит понятие так называемой
функции «правдоподобия» .
Функцией правдоподобия, построенная
по выборке ![]() называется функция, зависящая от
называется функция, зависящая от
аргумента![]() и заданная в следующем виде:
и заданная в следующем виде:
(27)
![]()
Функция правдоподобияобладает
свойством «вполне мультипликативности»
по аргументам![]() ,
,
равномерна относительно параметру![]() ,
,
где![]() –
–
плотность распределения с.в.![]() в случаях, когда с.в.
в случаях, когда с.в.![]() являетсянепрерывной. Если же с.в.
являетсянепрерывной. Если же с.в.![]() являетсядискретной, то функция правдоподобия
являетсядискретной, то функция правдоподобия
определяется равенством
(28)
![]()
где
![]() .
.
Замечание.На основании этих
определений следует, чточем больше
значение функции![]() тем вероятнее (правдоподобнее) появление
тем вероятнее (правдоподобнее) появление
чисел![]() в результате данного проводимого опыта
в результате данного проводимого опыта
(эксперимента) при фиксированном![]() .
.
За точечную оценку параметра
![]() ,
,
согласно ММП, берут такое его значение![]() при
при
котором функция правдоподобия достигает
максимального своего значения.
Такая оценка, называемая оценкой
максимальной правдоподобия, является
решением уравнения
(29)
![]() .
.
Из курса математического анализа
известно, что функции
![]() и
и![]() достигают
достигают
своего максимума при одном и том же
значении![]() (самостоятельно убедитесь в этом), то
(самостоятельно убедитесь в этом), то
вместо отыскания максимального значения
функции
![]() ищут
ищут
(что проще, где в правых частях равенств
(27) и (28) каждое произведение превращается
сумму слагаемых) максимум функции
![]()
Таким образом, для нахождения оценки
максимального правдоподобия необходимо:
1. решить уравнение правдоподобия
(30)
![]()
2. следует отобрать то решение, которое
обращает функцию
![]() в
в
максимум, при этом удобно использовать
вторую производную: если
(31)
![]()
то точкой максимума будет
![]() .
.
В случаях, когда подлежат
оценке несколько параметров ![]() распределения, то оценки
распределения, то оценки![]() определяются
определяются
решением системы уравнений правдоподобия;

Пример 11. Найдём
оценку параметра
![]() в распределения Пуассона методом
в распределения Пуассона методом
математического правдоподобия.
Решение. В
данном примере
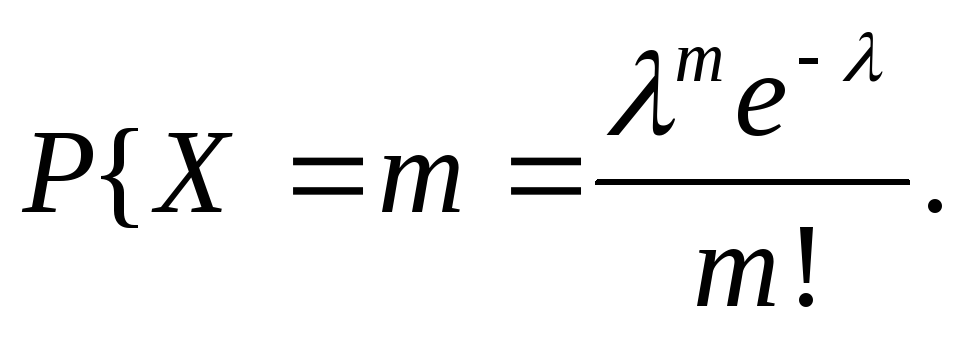
Поэтому
![]() .
.
Составляем функцию
правдоподобия для дискретной случайной
величины![]() :
:
по формуле (28) имеем
![]() .
.
Отсюда, после логарифмирования обе
части равенства получим
![]() .
.
Обе части равенства
продифференцируем по параметру
![]() ,
,
получим
![]()
Таким образом, уравнение правдоподобия
имеет вид:
(32)
 .
.
Следовательно,
(33)
![]() .
.
А так как из (32) следует, что
(34)
![]()
то найденная оценка
![]() является
является
оценкой максимального правдоподобия.
Итак,![]() .
.
Соседние файлы в папке Теория вероятностей от исмоилова
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
06.02.20162.36 Mб71~WRL0002.tmp



![I(theta )=E[g(theta )g(theta )^{T}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a56c920aaa8d5fe15496adeb6732a0079fcdc65b)



![f({mathbf {x}}mid theta )={begin{cases}{frac {1}{theta ^{n}}},&{mathbf {x}}in [0,theta ]^{n}subset {mathbb {R}}^{n}\0,&{mathbf {x}}not in [0,theta ]^{n}end{cases}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dd308dc7ec9548818ca9594269f7fceb7f95e97)

![left{{begin{matrix}displaystyle {frac {partial }{partial mu }}L({mathbf {x}}mid mu ,sigma ^{2})=0\[10pt]displaystyle {frac {partial }{partial sigma ^{2}}}L({mathbf {x}}mid mu ,sigma ^{2})=0\end{matrix}}right.Rightarrow left{{begin{matrix}displaystyle {frac {sum limits _{{i=1}}^{n}X_{i}-nmu }{sigma ^{2}}}=0\[10pt]displaystyle -{frac {n}{2sigma ^{2}}}+{frac {sum limits _{{i=1}}^{n}(X_{i}-mu )^{2}}{2left(sigma ^{2}right)^{2}}}=0\end{matrix}}right.,](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8218b0a9cf6582e8d729061d4e1fae7a3225257)















