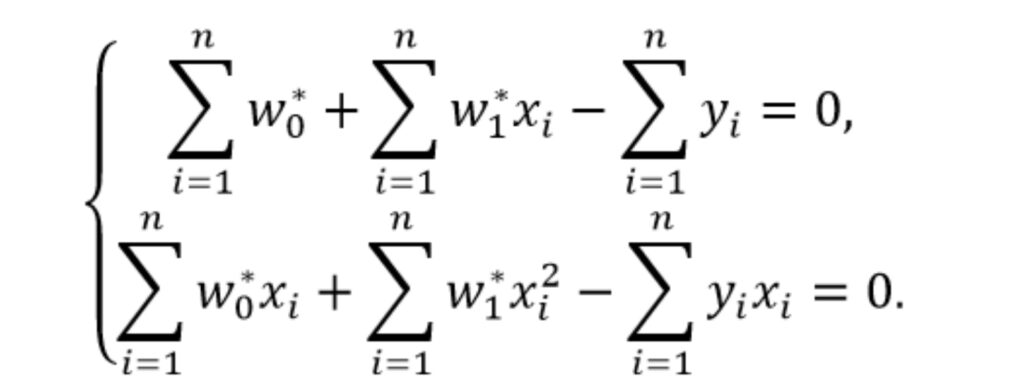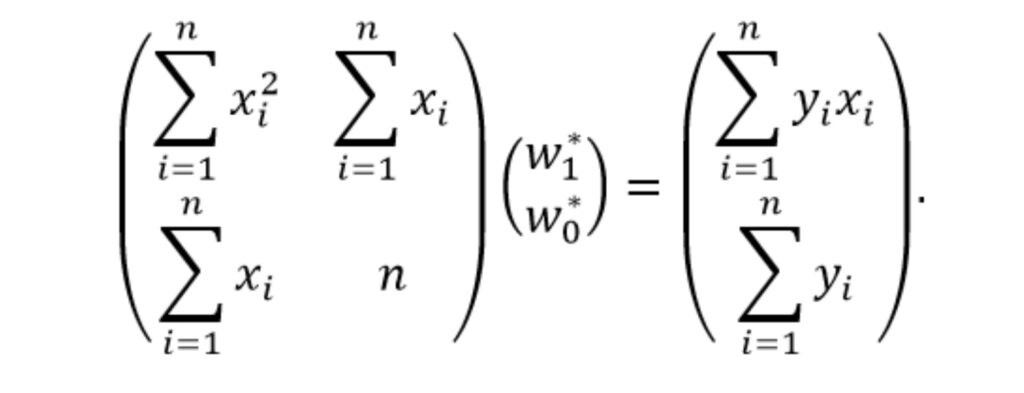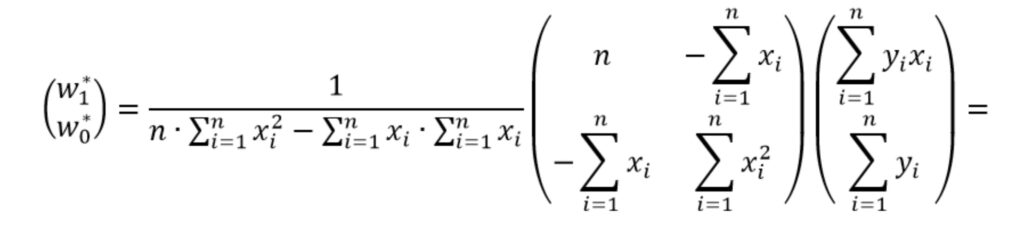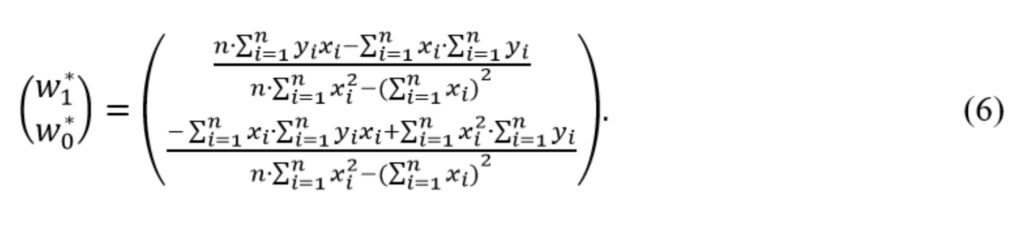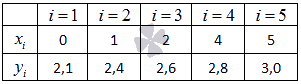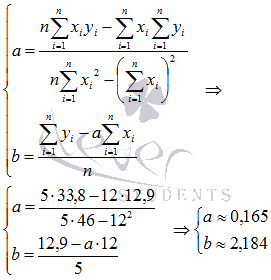Как найти мнк оценку - Сайт, где вы сможете решить свои вопросы

Запрос «МНК» перенаправляется сюда; см. также другие значения.

Пример кривой, проведённой через точки, имеющие нормально распределённое отклонение от истинного значения.

Метод наименьших квадратов (МНК) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от экспериментальных входных данных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.

История[править | править код]

До начала XIX в. учёные не имели определённых правил для решения системы уравнений, в которой число неизвестных меньше, чем число уравнений; до этого времени употреблялись частные приёмы, зависевшие от вида уравнений и от остроумия вычислителей, и потому разные вычислители, исходя из тех же данных наблюдений, приходили к различным выводам. Гауссу (1795) принадлежит первое применение метода, а Лежандр (1805) независимо открыл и опубликовал его под современным названием (фр. Méthode des moindres quarrés)^[1]. Лаплас связал метод с теорией вероятностей, а американский математик Эдрейн^ru_en (1808) рассмотрел его теоретико-вероятностные приложения^[2]. Метод распространён и усовершенствован дальнейшими изысканиями Энке, Бесселя, Ганзена и других.

Работы А. А. Маркова в начале XX века позволили включить метод наименьших квадратов в теорию оценивания математической статистики, в которой он является важной и естественной частью. Усилиями Ю. Неймана, Ф. Дэвида, А. Эйткена, С. Рао было получено множество немаловажных результатов в этой области^[3].

Суть метода наименьших квадратов[править | править код]

Пусть $y_{i}$ , набор скалярных экспериментальных данных, $x_{i}$ , набор векторных экспериментальных данных и предполагается, что зависит от .

Вводится некоторая (в простейшем случае линейная) скалярная функция , которая определяется вектором неизвестных параметров beta .

Ставится задача найти вектор beta такой, чтобы совокупность погрешностей ${displaystyle r_{i}=y_{i}-f(x_{i},{boldsymbol {beta }})}$ была в некотором смысле минимальной.

Согласно методу наименьших квадратов решением этой задачи является вектор beta , который минимизирует функцию

${displaystyle S({boldsymbol {beta }})=sum _{i=1}^{n}(y_{i}-f(x_{i},{boldsymbol {beta }}))^{2}.}$

В простейшем случае , и тогда результатом МНК будет среднее арифметическое входных данных.

Преимущество МНК перед минимизацией других видов ошибок состоит в том, что если дифференцируема по , то тоже дифференцируема. Приравнивание частных производных к нулю сводит задачу к решению системы уравнений, причём если зависит от линейно, то и система уравнений будет линейной.

Пример — система линейных уравнений[править | править код]

В частности, метод наименьших квадратов может использоваться для «решения» системы линейных уравнений

где прямоугольная матрица размера (то есть число строк матрицы A больше количества искомых переменных).

Такая система уравнений в общем случае не имеет решения. Поэтому эту систему можно «решить» только в смысле выбора такого вектора , чтобы минимизировать «расстояние» между векторами и . Для этого можно применить критерий минимизации суммы квадратов разностей левой и правой частей уравнений системы, то есть ${displaystyle (Ax-b)^{T}(Ax-b)rightarrow min _{x}}$ . Нетрудно показать, что решение этой задачи минимизации приводит к решению следующей системы уравнений

$A^{T}Ax=A^{T}bRightarrow x=(A^{T}A)^{{-1}}A^{T}b$

Используя оператор псевдоинверсии, решение можно переписать так:

$x=A^{+}b$

где A^+ — псевдообратная матрица для .

Эту задачу также можно «решить», используя так называемый взвешенный МНК (см. ниже), когда разные уравнения системы получают разный вес из теоретических соображений.

Строгое обоснование и установление границ содержательной применимости метода даны А. А. Марковым и А. Н. Колмогоровым.

МНК в регрессионном анализе (аппроксимация данных)[править | править код]

Пусть имеется значений некоторой переменной (это могут быть результаты наблюдений, экспериментов и т. д.) и соответствующих переменных . Задача заключается в том, чтобы взаимосвязь между и аппроксимировать некоторой функцией f(x,b) , известной с точностью до некоторых неизвестных параметров , то есть фактически найти наилучшие значения параметров , максимально приближающие значения f(x,b) к фактическим значениям . Фактически это сводится к случаю «решения» переопределенной системы уравнений относительно :

$f(x_{t},b)=y_{t},t=1,ldots ,n$ .

В регрессионном анализе и в частности в эконометрике используются вероятностные модели зависимости между переменными

$y_{t}=f(x_{t},b)+varepsilon _{t}$ ,

где $varepsilon _{t}$ — так называемые случайные ошибки модели.

Соответственно, отклонения наблюдаемых значений от модельных f(x,b) предполагается уже в самой модели. Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры , при которых сумма квадратов отклонений (ошибок, для регрессионных моделей их часто называют остатками регрессии) $e_{t}$ будет минимальной:

${hat b}_{{OLS}}=arg min _{{b}}RSS(b)$

где RSS — англ. Residual Sum of Squares^[4] определяется как:

$RSS(b)=e^{T}e=sum _{{t=1}}^{n}e_{t}^{2}=sum _{{t=1}}^{n}(y_{t}-f(x_{t},b))^{2}$

В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS — англ. Non-Linear Least Squares). Во многих случаях можно получить аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции RSS(b) , продифференцировав её по неизвестным параметрам , приравняв производные к нулю и решив полученную систему уравнений:

$sum _{{t=1}}^{n}(y_{t}-f(x_{t},b)){frac {partial f(x_{t},b)}{partial b}}=0$

МНК в случае линейной регрессии[править | править код]

Пусть регрессионная зависимость является линейной:

$y_{t}=sum _{{j=1}}^{k}b_{j}x_{{tj}}+varepsilon =x_{t}^{T}b+varepsilon _{t}$

Пусть y — вектор-столбец наблюдений объясняемой переменной, а — это -матрица наблюдений факторов (строки матрицы — векторы значений факторов в данном наблюдении, по столбцам — вектор значений данного фактора во всех наблюдениях). Матричное представление линейной модели имеет вид:

Тогда вектор оценок объясняемой переменной и вектор остатков регрессии будут равны

соответственно сумма квадратов остатков регрессии будет равна

$RSS=e^{T}e=(y-Xb)^{T}(y-Xb)$

Дифференцируя эту функцию по вектору параметров и приравняв производные к нулю, получим систему уравнений (в матричной форме):

$(X^{T}X)b=X^{T}y$

В расшифрованной матричной форме эта система уравнений выглядит следующим образом:

${begin{pmatrix}sum x_{{t1}}^{2}&sum x_{{t1}}x_{{t2}}&sum x_{{t1}}x_{{t3}}&ldots &sum x_{{t1}}x_{{tk}}\sum x_{{t2}}x_{{t1}}&sum x_{{t2}}^{2}&sum x_{{t2}}x_{{t3}}&ldots &sum x_{{t2}}x_{{tk}}\sum x_{{t3}}x_{{t1}}&sum x_{{t3}}x_{{t2}}&sum x_{{t3}}^{2}&ldots &sum x_{{t3}}x_{{tk}}\vdots &vdots &vdots &ddots &vdots \sum x_{{tk}}x_{{t1}}&sum x_{{tk}}x_{{t2}}&sum x_{{tk}}x_{{t3}}&ldots &sum x_{{tk}}^{2}\end{pmatrix}}{begin{pmatrix}b_{1}\b_{2}\b_{3}\vdots \b_{k}\end{pmatrix}}={begin{pmatrix}sum x_{{t1}}y_{{t}}\sum x_{{t2}}y_{{t}}\sum x_{{t3}}y_{{t}}\vdots \sum x_{{tk}}y_{{t}}\end{pmatrix}},$
где все суммы берутся по всем допустимым значениям .

Если в модель включена константа (как обычно), то $x_{{t1}}=1$ при всех , поэтому в левом верхнем углу матрицы системы уравнений находится количество наблюдений , а в остальных элементах первой строки и первого столбца — просто суммы значений переменных: $sum x_{{tj}}$ и первый элемент правой части системы — $sum y_{{t}}$ .

Решение этой системы уравнений и дает общую формулу МНК-оценок для линейной модели:

${hat {b}}_{{OLS}}=(X^{T}X)^{{-1}}X^{T}y=left({frac {1}{n}}X^{T}Xright)^{{-1}}{frac {1}{n}}X^{T}y=V_{x}^{{-1}}C_{{xy}}$

Для аналитических целей оказывается полезным последнее представление этой формулы (в системе уравнений при делении на n вместо сумм фигурируют средние арифметические). Если в регрессионной модели данные центрированы, то в этом представлении первая матрица имеет смысл выборочной ковариационной матрицы факторов, а вторая — вектор ковариаций факторов с зависимой переменной. Если кроме того данные ещё и нормированы на СКО (то есть в конечном итоге стандартизированы), то первая матрица имеет смысл выборочной корреляционной матрицы факторов, второй вектор — вектора выборочных корреляций факторов с зависимой переменной.

Немаловажное свойство МНК-оценок для моделей с константой — линия построенной регрессии проходит через центр тяжести выборочных данных, то есть выполняется равенство:

${bar {y}}={hat {b_{1}}}+sum _{{j=2}}^{{k}}{hat {b}}_{j}{bar {x}}_{j}$

В частности, в крайнем случае, когда единственным регрессором является константа, получаем, что МНК-оценка единственного параметра (собственно константы) равна среднему значению объясняемой переменной. То есть среднее арифметическое, известное своими хорошими свойствами из законов больших чисел, также является МНК-оценкой — удовлетворяет критерию минимума суммы квадратов отклонений от неё.

Простейшие частные случаи[править | править код]

В случае парной линейной регрессии $y_{t}=a+bx_{t}+varepsilon _{t}$ , когда оценивается линейная зависимость одной переменной от другой, формулы расчёта упрощаются (можно обойтись без матричной алгебры). Система уравнений имеет вид:

${displaystyle {begin{pmatrix}n&sum _{t=1}^{n}x_{t}\sum _{t=1}^{n}x_{t}&sum _{t=1}^{n}x_{t}^{2}\end{pmatrix}}{begin{pmatrix}a\b\end{pmatrix}}={begin{pmatrix}sum _{t=1}^{n}y_{t}\sum _{t=1}^{n}x_{t}y_{t}\end{pmatrix}}}$

Отсюда несложно найти оценки коэффициентов:

${displaystyle {begin{cases}{hat {b}}={frac {nsum _{t=1}^{n}x_{t}y_{t}-left(sum _{t=1}^{n}x_{t}right)left(sum _{t=1}^{n}y_{t}right)}{nsum _{t=1}^{n}x_{t}^{2}-left(sum _{t=1}^{n}x_{t}right)^{2}}},\{hat {a}}={frac {sum _{t=1}^{n}y_{t}-{hat {b}}sum _{t=1}^{n}x_{t}}{n}}.end{cases}}}$

Несмотря на то, что в общем случае модели с константой предпочтительней, в некоторых случаях из теоретических соображений известно, что константа должна быть равна нулю. Например, в физике зависимость между напряжением и силой тока имеет вид ; замеряя напряжение и силу тока, необходимо оценить сопротивление. В таком случае речь идёт о модели y=bx . В этом случае вместо системы уравнений имеем единственное уравнение

$left(sum x_{t}^{2}right)b=sum x_{t}y_{t}$ .

Следовательно, формула оценки единственного коэффициента имеет вид

${displaystyle {hat {b}}={frac {sum _{t=1}^{n}x_{t}y_{t}}{sum _{t=1}^{n}x_{t}^{2}}}}$ .

Случай полиномиальной модели[править | править код]

Если данные аппроксимируются полиномиальной функцией регрессии одной переменной ${displaystyle f(x)=b_{0}+sum limits _{i=1}^{k}b_{i}x^{i}}$ , то, воспринимая степени x^i как независимые факторы для каждого можно оценить параметры модели исходя из общей формулы оценки параметров линейной модели. Для этого в общей формуле достаточно учесть, что при такой интерпретации ${displaystyle x_{ti}x_{tj}=x_{t}^{i}x_{t}^{j}=x_{t}^{i+j}}$ и ${displaystyle x_{tj}y_{t}=x_{t}^{j}y_{t}}$ . Следовательно, матричные уравнения в данном случае примут вид:

${displaystyle {begin{pmatrix}n&sum limits _{n}x_{t}&ldots &sum limits _{n}x_{t}^{k}\sum limits _{n}x_{t}&sum limits _{n}x_{t}^{2}&ldots &sum limits _{n}x_{t}^{k+1}\vdots &vdots &ddots &vdots \sum limits _{n}x_{t}^{k}&sum limits _{n}x_{t}^{k+1}&ldots &sum limits _{n}x_{t}^{2k}end{pmatrix}}{begin{bmatrix}b_{0}\b_{1}\vdots \b_{k}end{bmatrix}}={begin{bmatrix}sum limits _{n}y_{t}\sum limits _{n}x_{t}y_{t}\vdots \sum limits _{n}x_{t}^{k}y_{t}end{bmatrix}}.}$

Статистические свойства МНК-оценок[править | править код]

В первую очередь отметим, что для линейных моделей МНК-оценки являются линейными оценками, как это следует из вышеприведённой формулы. Для несмещённости МНК-оценок необходимо и достаточно выполнения важнейшего условия регрессионного анализа: условное по факторам математическое ожидание случайной ошибки должно быть равно нулю. Данное условие, в частности, выполнено, если

математическое ожидание случайных ошибок равно нулю и
факторы и случайные ошибки — независимые случайные величины.

Первое условие для моделей с константой можно считать выполненным всегда, так как константа берёт на себя ненулевое математическое ожидание ошибок (поэтому модели с константой в общем случае предпочтительнее).

Второе условие — условие экзогенности факторов — принципиальное. Если это свойство не выполнено, то можно считать, что практически любые оценки будут крайне неудовлетворительными: они не будут даже состоятельными (то есть даже очень большой объём данных не позволяет в этом случае получить качественные оценки). В классическом случае делается более сильное предположение о детерминированности факторов, в отличие от случайной ошибки, что автоматически означает выполнение условия экзогенности. В общем случае для состоятельности оценок достаточно выполнения условия экзогенности вместе со сходимостью матрицы $V_{x}$ к некоторой невырожденной матрице при увеличении объёма выборки до бесконечности.

Для того, чтобы кроме состоятельности и несмещённости, оценки (обычного) МНК были ещё и эффективными (наилучшими в классе линейных несмещённых оценок), необходимо выполнение дополнительных свойств случайной ошибки:

Постоянная (одинаковая) дисперсия случайных ошибок во всех наблюдениях (отсутствие гетероскедастичности): $V(varepsilon _{t})=sigma ^{2}=const$ .

Отсутствие корреляции (автокорреляции) случайных ошибок в разных наблюдениях между собой $cov(varepsilon _{i},varepsilon _{j})=0quad forall 1leq i<jleq n$ .

Данные предположения можно сформулировать для ковариационной матрицы вектора случайных ошибок $V(varepsilon )=sigma ^{2}I$ .

Линейная модель, удовлетворяющая таким условиям, называется классической. МНК-оценки для классической линейной регрессии являются несмещёнными, состоятельными и наиболее эффективными оценками в классе всех линейных несмещённых оценок (в англоязычной литературе иногда употребляют аббревиатуру BLUE (Best Linear Unbiased Estimator) — наилучшая линейная несмещённая оценка; в отечественной литературе чаще приводится теорема Гаусса — Маркова). Как нетрудно показать, ковариационная матрица вектора оценок коэффициентов будет равна:

$V({hat {b}}_{{OLS}})=sigma ^{2}(X^{T}X)^{{-1}}$ .

Эффективность означает, что эта ковариационная матрица является «минимальной» (любая линейная комбинация оценок коэффициентов, и в частности сами оценки коэффициентов имеют минимальную дисперсию), то есть в классе линейных несмещённых оценок оценки МНК-наилучшие. Диагональные элементы этой матрицы — дисперсии оценок коэффициентов — важные параметры качества полученных оценок. Однако рассчитать ковариационную матрицу невозможно, поскольку дисперсия случайных ошибок неизвестна. Можно доказать, что несмещённой и состоятельной (для классической линейной модели) оценкой дисперсии случайных ошибок является величина:

$s^{2}=RSS/(n-k)$ .

Подставив данное значение в формулу для ковариационной матрицы, получим оценку ковариационной матрицы. Полученные оценки также являются несмещёнными и состоятельными. Важно также то, что оценка дисперсии ошибок (а значит и дисперсий коэффициентов) и оценки параметров модели являются независимыми случайными величинами, что позволяет получить тестовые статистики для проверки гипотез о коэффициентах модели.

Необходимо отметить, что если классические предположения не выполнены, МНК-оценки параметров не являются наиболее эффективными оценками (оставаясь несмещёнными и состоятельными). Однако ещё более ухудшается оценка ковариационной матрицы: она становится смещённой и несостоятельной. Это означает, что статистические выводы о качестве построенной модели в таком случае могут быть крайне недостоверными. Одним из вариантов решения этой проблемы является применение специальных оценок ковариационной матрицы, которые являются состоятельными при нарушениях классических предположений (стандартные ошибки в форме Уайта и стандартные ошибки в форме Ньюи-Уеста). Другой подход заключается в применении так называемого обобщённого МНК.

Обобщённый МНК[править | править код]

Метод наименьших квадратов допускает широкое обобщение. Вместо минимизации суммы квадратов остатков можно минимизировать некоторую положительно определённую квадратичную форму от вектора остатков $e^{T}We$ , где — некоторая симметрическая положительно определённая весовая матрица. Обычный МНК является частным случаем данного подхода, когда весовая матрица пропорциональна единичной матрице. Как известно, для симметрических матриц (или операторов) существует разложение $W=P^{T}P$ . Следовательно, указанный функционал можно представить следующим образом: $e^{T}P^{T}Pe=(Pe)^{T}Pe=e_{*}^{T}e_{*}$ , то есть этот функционал можно представить как сумму квадратов некоторых преобразованных «остатков».
Таким образом, можно выделить класс методов наименьших квадратов — LS-методы (Least Squares).

Доказано (теорема Айткена), что для обобщённой линейной регрессионной модели (в которой на ковариационную матрицу случайных ошибок не налагается никаких ограничений) наиболее эффективными (в классе линейных несмещённых оценок) являются оценки т. н. обобщённого МНК (ОМНК, GLS — Generalized Least Squares) — LS-метода с весовой матрицей, равной обратной ковариационной матрице случайных ошибок: $W=V_{{varepsilon }}^{{-1}}$ .

Можно показать, что формула ОМНК-оценок параметров линейной модели имеет вид

${hat {b}}_{{GLS}}=(X^{T}V^{{-1}}X)^{{-1}}X^{T}V^{{-1}}y$ .

Ковариационная матрица этих оценок соответственно будет равна

$V({hat {b}}_{{GLS}})=(X^{T}V^{{-1}}X)^{{-1}}$ .

Фактически сущность ОМНК заключается в определённом (линейном) преобразовании (P) исходных данных и применении обычного МНК к преобразованным данным. Цель этого преобразования — для преобразованных данных случайные ошибки уже удовлетворяют классическим предположениям.

Взвешенный МНК[править | править код]

В случае диагональной весовой матрицы (а значит и ковариационной матрицы случайных ошибок) имеем так называемый взвешенный МНК. В данном случае минимизируется взвешенная сумма квадратов остатков модели, то есть каждое наблюдение получает «вес», обратно пропорциональный дисперсии случайной ошибки в данном наблюдении: $e^{T}We=sum _{{t=1}}^{n}{frac {e_{t}^{2}}{sigma _{t}^{2}}}$ . Фактически данные преобразуются взвешиванием наблюдений (делением на величину, пропорциональную предполагаемому стандартному отклонению случайных ошибок), а к взвешенным данным применяется обычный МНК.

См. также[править | править код]

Обобщенный метод наименьших квадратов
Двухшаговый метод наименьших квадратов
Рекурсивный МНК
Алгоритм Гаусса — Ньютона

Примечания[править | править код]

↑ Legendre, On Least Squares. Translated from the French by Professor Henry A. Ruger and Professor Helen M. Walker, Teachers College, Columbia University, New York City. Архивная копия от 7 января 2011 на Wayback Machine (англ.)
↑ Александрова, 2008, с. 102.
↑ Линник, 1962, с. 21.
↑ Магнус, Катышев, Пересецкий, 2007, Обозначение RSS не унифицировано. RSS может быть сокращением от regression sum of squares, а ESS — error sum of squares, то есть, RSS и ESS будут иметь обратный смысл. с. 52. Издания 2004 года..

Литература[править | править код]

Линник Ю. В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. — 2-е изд. — М., 1962. (математическая теория)
Айвазян С. А. Прикладная статистика. Основы эконометрики. Том 2. — М.: Юнити-Дана, 2001. — 432 с. — ISBN 5-238-00305-6.
Доугерти К. Введение в эконометрику: Пер. с англ. — М.: ИНФРА-М, 1999. — 402 с. — ISBN 8-86225-458-7.
Кремер Н. Ш., Путко Б. А. Эконометрика. — М.: Юнити-Дана, 2003—2004. — 311 с. — ISBN 8-86225-458-7.
Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. Начальный курс. — М.: Дело, 2007. — 504 с. — ISBN 978-5-7749-0473-0.
Эконометрика. Учебник / Под ред. Елисеевой И. И. — 2-е изд. — М.: Финансы и статистика, 2006. — 576 с. — ISBN 5-279-02786-3.
Александрова Н. В. История математических терминов, понятий, обозначений: словарь-справочник. — 3-е изд.. — М.: ЛКИ, 2008. — 248 с. — ISBN 978-5-382-00839-4.
Витковский В. В. Наименьшие квадраты // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Митин И. В., Русаков В. С. Анализ и обработка экспериментальных данных. — 5-е издание. — 24 с.

Ссылки[править | править код]

Метод наименьших квадратов онлайн для зависимости y = a + bx с вычислением погрешностей коэффициентов и оцениванием автокорреляции.

Источник

Метод наименьших квадратов: формулы, код и применение

Время на прочтение
12 мин

Количество просмотров 30K

Традиционно в машинном обучении, при анализе данных, перед разработчиком ставится проблема построения объясняющей эти данные модели, которая должна сделать жизнь проще и понятней тому, кто этой моделью начинает пользоваться. Обычно это модель некоторого объекта/процесса, данные о котором собираются при регистрации ряда его параметров. Полученные данные, после выполнения различных подготовительных процедур, представляются в виде таблицы с числовыми данными (где строка – объект, а столбец – параметр), которые необходимо обработать, подставив их в те или иные формулы и посчитать по ним, используя какой-нибудь язык программирования.

Одним из часто встречающихся на практике методе, используемый в самых различных его модификациях, является метод наименьших квадратов (МНК). Этот метод был опубликован в современном виде более двухсот лет назад, именно поэтому особенное удивление вызывает то, что этот хрестоматийным метод не описан максимально подробно на самых популярных ресурсах, просвещённых анализу данных. Поэтому разработчик в попытках самостоятельно разобраться с МНК обращается к чтению самых различных бумажных и электронных изданий. После чего желание разобраться быстро улетучивается по причине того, что авторы этих ресурсов особо не «заморачиваются» над объяснениями выполняемых ими преобразований и допущений.

Обычно объяснение метода представляется в виде:

перегруженного математическими абстракциями «классического описания»;
«готовой процедурки», в которой выполняется программная реализация неких конечных выражений, полученных при каких-то начальных условиях.

Первый вид объяснения вызывает полное отторжение у новичка в виду отсутствия должного уровня математической подготовки и представляется непонятным нагромождением формул. А второй вид представляется неким черным ящиком, из которого чудесным образом извлекаются правильные значения. Из чего делается вывод, что все эти «математические изыскания» лишние, а нужно лишь найти на просторах интернета правильную процедуру и «прикрутить» её в проект, где она начинает выдавать значения «похожие на правильные». Подобный ситуативный путь решения проблемы разработчиком приводит к тому, что корректно проверить, модифицировать найденный код не представляется возможным и, соответственно, верифицировать получаемый результат тоже.

Триада

Данные проблемы возникают из-за того, что при описании МНК не описывается путь перехода от математического описания метода к его программной реализации. Данная проблема была давно преодолена одним из отцов-основателей математического моделирования в нашей стране академиком Самарским А.А., который предложил универсальную методологию вычислительного эксперимента в виде триады «модель-алгоритм-программа».

Из предложенной схемы становится видно, что путь от модели объекта к программе лежит через её алгоритмическое описание. Таким образом, в представленной парадигме для детального объяснения МНК нужно:

описать математическую модель объекта/процесса, анализируемые параметры которой формализуются в виде некой функциональной зависимости;
синтезировать алгоритм оценки искомых параметров модели на основе МНК;
выполнить программную реализацию полученного алгоритма.

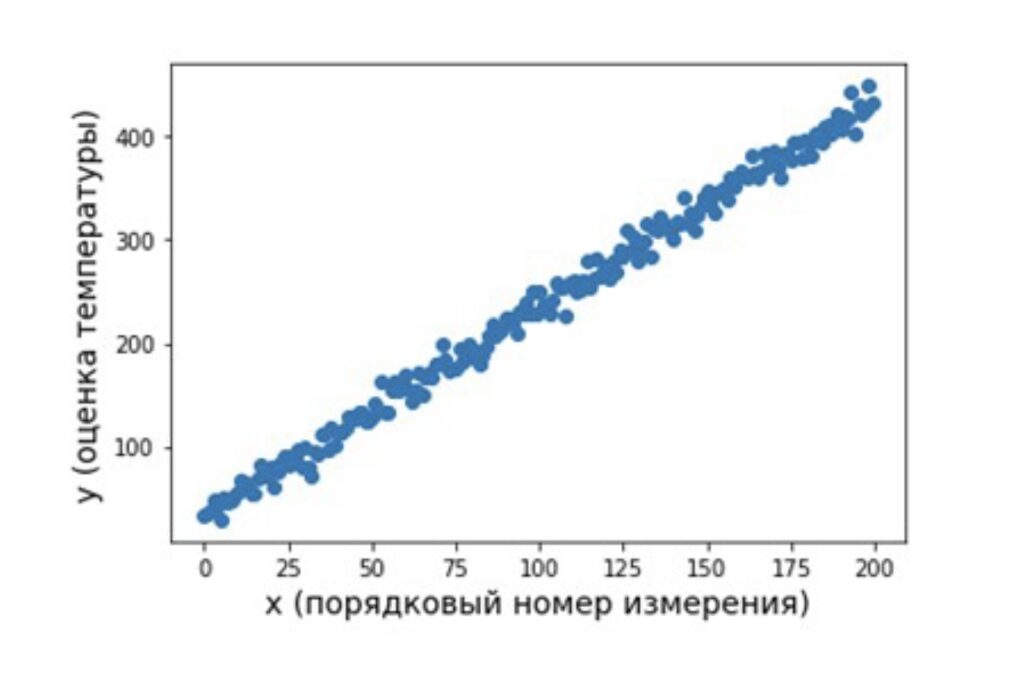
Попробуем абстракции последних абзацев пояснить на примере. Пусть в качестве моделируемого объекта будем рассматривать процесс измерения термометром температуры печи, которая линейно зависит от времени и флуктуирует в области истинного значения по нормальному закону. Необходимо по выполненным измерениям определить зависимость, по которой изменяется температура в печи. При этом ошибка найденной зависимости должна быть минимальной.

В качестве анализируемых данных будем рассматривать n значений температуры, измеренной в градусах, получаемые с использованием термометра и зависящие от времени. Эти данные представим в виде таблицы, где строки – это объекты, первый столбец – набор параметров (j=1), второй столбец – набор измеренных ответов:

т.е. случайная величина, распределённая по закону Гаусса с фиксированным значением среднеквадратического отклонения (СКО), нулевым математическим ожиданием (МО) и с автокорреляционной функцией в виде дельта-функции.

Ниже приведен код, генерирующий набор данных на python. Для реализации приведенного в статье кода потребуется импортировать несколько библиотек.

import random
import matplotlib.pyplot as plt
import numpy as np

def datasets_make_regression(coef, data_size, noise_sigma, random_state):
    x = np.arange(0, data_size, 1.)
    mu = 0.0
    random.seed(random_state)
    noise = np.empty((data_size, 1))
    y = np.empty((data_size, 1))

    for i in range(data_size):
        noise[i] = random.gauss(mu, noise_sigma)
        y[i] = coef[0] + coef[1]*x[i] + noise[i]

    return x, y

coef_true = [34.2, 2.] # весовые коэффициенты
data_size = 200 # размер генерируемого набора данных
noise_sigma = 10 # СКО шума в данных
random_state = 42
x_scale, y_estimate = datasets_make_regression(coef_true, data_size, noise_sigma, random_state)

plt.plot(x_scale, y_estimate, 'o') 
plt.xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('y (оценка температуры)', fontsize=14)

Сгенерированный набор данных будет иметь вид

Рисунок 1 – Зависимость температуры от времени

Математическая модель

Далее математическая модель будет описана три раза. Последовательно уровень абстракции при описании модели будет понижаться и конкретизироваться. Эти описания приведены для того, чтобы в дальнейшем материал, приведенный в статье, можно было соотнести с классическими изданиями.

Первое описание математической модели. Самое общее.

Поскольку мы рассматриваем процесс, который связывает набор наблюдаемых параметров и измеренных ответов с минимальной ошибкой этой связи, то математическую модель этого процесса в общем виде можно представить

Второе описание математической модели. Общее описание линейной модели.

Поскольку по условию задачи мы рассматриваем линейную зависимость, на которую влияет шум, имеющий нормальное распределение с нулевым средним значением, то используем линейную относительно параметров модель, а метрикой выберем расчёт СКО ошибки

Третье описание математической модели. Модель конкретизирована под условия примера.

Поскольку по условию задачи мы рассматриваем линейную зависимость одного параметра (поскольку j=1, то далее эту зависимость при описании опустим), на оценку которого влияет шум, имеющий нормальное распределение, то используем линейную модель с двумя коэффициентами

Обсуждение моделей

Было рассмотрено три модели, описывающих процесс изменения температуры в печи. Первая модель описана в наиболее общем виде, а третья приведена в виде, наиболее соответствующем начальным условиям задачи. В третьей модели учтен линейный закон изменения температуры (используется линейная модель) и нормальный закон распределения шума в измерениях (используется квадратичная функция ошибки).

Хочется отметить, что параметры математической модели процесса изменения температуры, описанной в выражении (2), в принципе, могут находиться не только методом наименьших квадратов, поскольку метрика с квадратичной функцией ошибки в явном виде не прописана. Такая общая форма записи приведена, поскольку не представляется возможным в кратком виде привести все возможные модификации МНК, у которого минимизация для различных условий может выполняться также различно.

В выражениях (3) и (4) линейные модели отличаются только количеством учитываемых параметров, причем третья модель – это редуцированная вторая модель, у которой только два коэффициента (один свободный и один весовой коэффициенты).

Далее с использованием выражения (4) и МНК, синтезируем алгоритмы, оценивающие параметры модели.

Алгоритмы и реализующие их программы

Далее будут выведены три алгоритма, результат работы которых позволит определить зависимость изменения температуры печи от времени. Последовательно сложность конечных выражений, используемых в алгоритмах, будет понижаться. Эти алгоритмы приведены для того, чтобы полученные выражения, можно было соотнести с классическими изданиями.

Начнем с применения правила дифференцирования функции представленной в виде суммы

применим правило дифференцирования сложной функции

применим правило дифференцирования функции представленной в виде суммы

применим правило дифференцирования функции представленной в виде суммы

Приравняем полученные производные к нулю и решим полученную систему уравнений

Раскроем скобки

Вынесем постоянные множители за скобки

Вынесем слагаемые с множителем «y» в правую часть уравнений

Поставим слагаемые с множителем «x» в левой части в порядке убывания степеней

Для решения полученной системы алгебраических уравнения представим её в матричной форме

Выразим вектор w* с искомыми весами выполнив умножение обеих частей равенства на обратную матрицу y

Полученное выражение (5) является решением системы уравнений и его можно уже использовать в качестве первого алгоритма оценки параметров модели. Ниже приведен код реализующий этот алгоритм.

def coefficient_reg_inv(x, y):
    size = len(x)
    # формируем и заполняем матрицу размерностью 2x2
    A = np.empty((2, 2))
    A[[0], [0]] = sum((x[i])**2 for i in range(0,size))
    A[[0], [1]] = sum(x)
    A[[1], [0]] = sum(x)
    A[[1], [1]] = size
    # находим обратную матрицу 
    A = np.linalg.inv(A)
    # формируем и заполняем матрицу размерностью 2x1
    C = np.empty((2, 1))
    C[0] = sum((x[i]*y[i]) for i in range(0,size))
    C[1] = sum((y[i]) for i in range(0,size))
    
    # умножаем матрицу на вектор
    ww = np.dot(A, C)
    return ww[1], ww[0]

[w0_1, w1_1] = coefficient_reg_analit(x_scale, y_estimate)
print(w0_1, w1_1)

Результат работы алгоритма:
[33.93193341] [2.01436546]

Выражение (5) можно упростить, выполнив аналитический расчет обратной матрицы.

Найти обратную матрицу можно с использованием, например, алгебраических дополнений. Для пояснения поиска обратной матрицы введем новую переменную A. Пусть

Перепишем выражение (5) в виде

Упростим выражение раскрыв скобки, чтобы получить более компактную форму записи

Теперь решение системы уравнений имеет вид

Полученное выражение (6) можно использовать в качестве второго алгоритма оценки параметров модели. Ниже приведен код, реализующий этот алгоритм.

def coefficient_reg_inv_analit(x, y):
    size = len(x)
    # выполним расчет числителя первого элемента вектора
    numerator_w1 = size*sum(x[i]*y[i] for i in range(0,size)) - sum(x)*sum(y)
    # выполним расчет знаменателя (одинаковый для обоих элементов вектора)
    denominator = size*sum((x[i])**2 for i in range(0,size)) - (sum(x))**2
    # выполним расчет числителя второго элемента вектора
    numerator_w0 = -sum(x)*sum(x[i]*y[i] for i in range(0,size)) + sum((x[i])**2 for i in range(0,size))*sum(y)
    
    # расчет искомых коэффициентов
    w1 = numerator_w1/denominator
    w0 = numerator_w0/denominator
    return w0, w1

[w0_2, w1_2] = coefficient_reg_inv_analit(x_scale, y_estimate)
print(w0_2, w1_2)

Результат работы алгоритма:
[33.93193341] [2.01436546]

Видно, что полученный результат совпадает с результатом, полученным с использованием выражения (5).

Выполним дальнейшее упрощение полученного выражения (6), чтобы получить более компактную форму записи.

раскроем скобки:

Ведем новые переменные используя термины математической статистики:

С учётом введённых переменных искомый вектор w* примет вид

Таким образом итоговое выражение представим в виде:

Полученное выражение (7) можно использовать в качестве третьего алгоритмаоценки параметров модели. Ниже приведен код, реализующий этот алгоритм.

def coefficient_reg_stat(x, y):
    size = len(x)
    avg_x = sum(x)/len(x) # оценка МО величины x
    avg_y = sum(y)/len(y) # оценка МО величины y
    # оценка МО величины x*y
    avg_xy = sum(x[i]*y[i] for i in range(0,size))/size
    # оценка СКО величины x 
    std_x = (sum((x[i] - avg_x)**2 for i in range(0,size))/size)**0.5
    # оценка СКО величины y
    std_y = (sum((y[i] - avg_y)**2 for i in range(0,size))/size)**0.5
    # оценка коэффициента корреляции величин x и y
    corr_xy = (avg_xy - avg_x*avg_y)/(std_x*std_y)
    
    # расчет искомых коэффициентов
    w1 = corr_xy*std_y/std_x
    w0 = avg_y - avg_x*w1
    return w0, w1

[w0_3, w1_3] = coefficient_reg_stat(x_scale, y_estimate)
print(w0_3, w1_3)

Результат работы алгоритма:
[33.93193341] [2.01436546]

Сравним полученные значения с результатом работы процедуры библиотеки sklearn.

from sklearn.linear_model import LinearRegression
# преобразование размерности массива x_scale для корректной работы model.fit
x_scale = x_scale.reshape((-1,1)) 
model = LinearRegression()
model.fit(x_scale, y_estimate)
print(model.intercept_, model.coef_)

Результат работы алгоритма:
[33.93193341] [2.01436546]

Видно, что полученный результат полностью совпадает с результатами, полученными ранее.

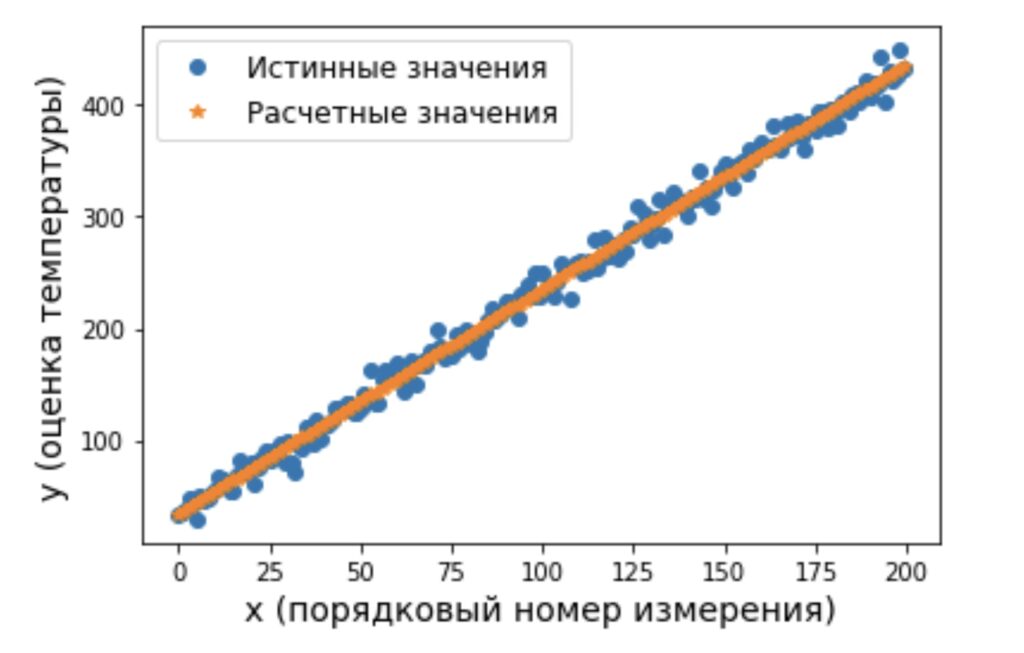
Итак, визуализируем полученный результат, построив прямую с использованием рассчитанных коэффициентов и сопоставим их с исходными данными (рисунок 2).

def predict(w0, w1, x_scale):
    y_pred = [w0 + val*w1 for val in x_scale]
    return y_pred

y_predict = predict(w0_1, w1_1, x_scale)

plt.plot(x_scale, y_estimate, 'o', label = 'Истинные значения')
plt.plot(x_scale, y_predict, '*', label = 'Расчетные значения')
plt.legend(loc = 'best', fontsize=12) 
plt.xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('y (оценка температуры)', fontsize=14)

Рисунок 2 – Зависимость температуры от времени

Обсуждение алгоритмов

Таким образом удалось выполнить оценку параметров модели, которая описывает процесс изменения температуры в печи с минимальной ошибкой. Выведенные выражения (5) – (7) и запрограммированные по ним три алгоритма, реализующие МНК при обработке одного набора измеренных температур, хотя и отличаются видом конечных выражений, дают одинаковые оценки. Последовательный вывод выражений, выполненный в статье, показывает, что эти выражения по сути «делают» одно и тоже, однако, позволяют давать различные интерпретации. При этом хочется отметить, что в алгоритмах (6) – (7) удалось уйти от процедуры обращения матрицы, которая при обработке реальных данных может выполняться нестабильно.

Ещё один пример. Анализируем остатки.

количество выбросов в выборке равно 10;
длительность импульса равна 1-му измерению;
амплитуда импульса равна 256;
позиция первого импульса соответствует 10-му измерению;
период следования импульсов – каждые 20 измерений.

ni = 10 # количество выбросов
ind_impuls = np.arange(ni, data_size, 20) # индексы выбросов
y_estimate_imp = y_estimate.copy() # выборка с выбросами
for i in range(0, ni):
    y_estimate_imp[ind_impuls[i]] += 256

[w0_imp, w1_imp] = coefficient_reg_stat(x_scale, y_estimate_imp)
y_pred_imp = predict(w0_imp, w1_imp, x_scale)
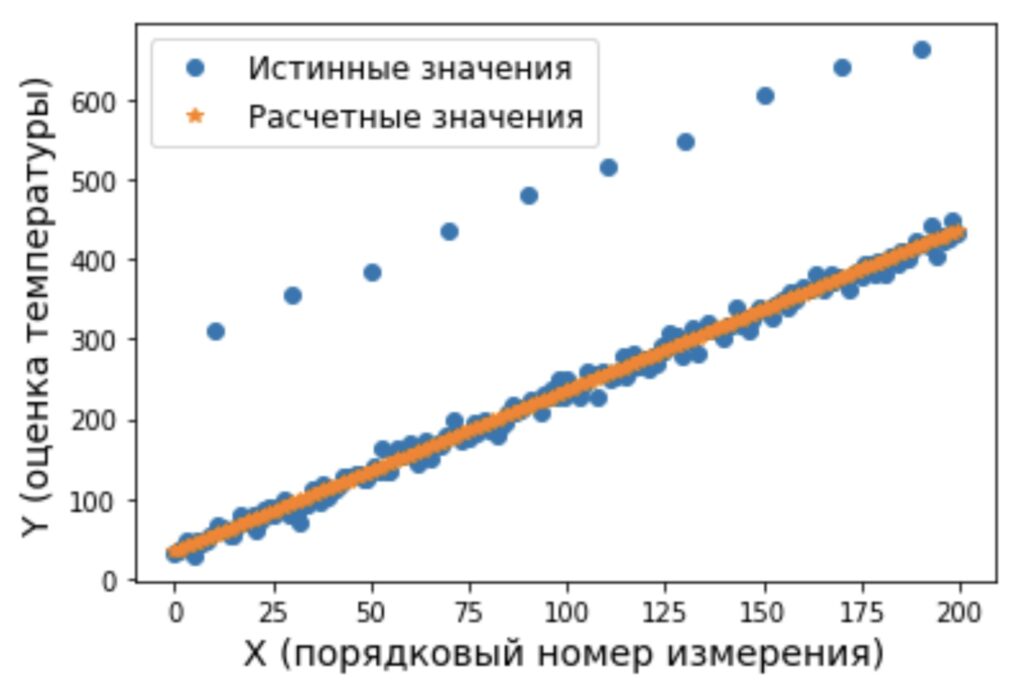
plt.plot(x_scale, y_estimate_imp, 'o', label = 'Истинные значения')
plt.plot(x_scale, y_pred_imp, '*', label = 'Расчетные значения')
plt.legend(loc = 'best', fontsize=12) 
plt.xlabel('x (порядковый номер измерения)', fontsize=14)
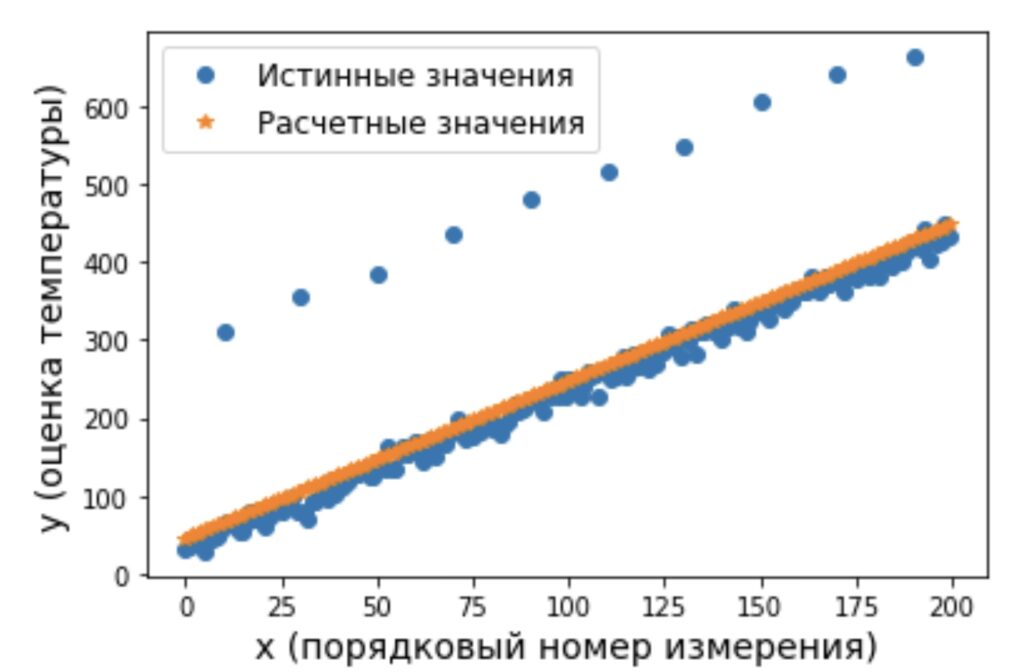
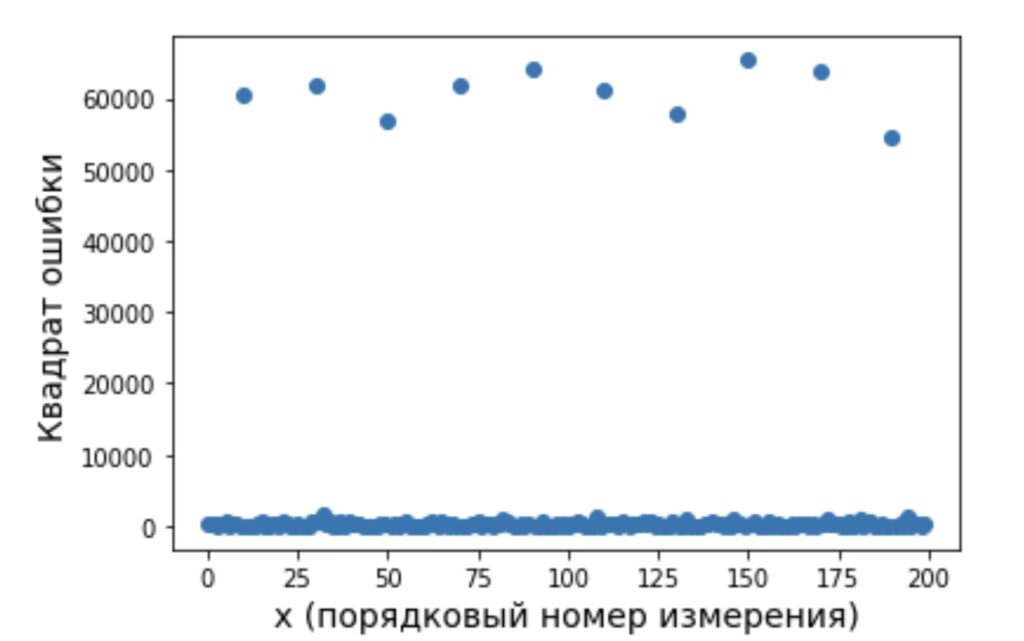
plt.ylabel('y (оценка температуры)', fontsize=14)

Рисунок 3 – Зависимость температуры от времени

На рисунке 3 видно, что появление выбросов сместило, рассчитанную по выражению (7) прямую в вверх. Модифицируем алгоритм оценки параметров модели за счет новой метрики, а именно оценки квадратов разности между измеренными и модельными данными, которая выполняется по выражению

Ниже приведен код, который выполняет этот расчет (8) и визуализирует полученный результат (рисунок 4).

SqErr = (y_pred_imp - y_estimate_imp)**2

plt.plot(x_scale, SqErr, 'o') 
plt.xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('Квадрат ошибки', fontsize=14)

Рисунок 4 – Оценка квадратов разности между измеренными и модельными данными

Для устранения влияния помехи на оценки параметров модели, получаемых с использованием алгоритмов, дополнительно введем процедуру цензурирования (отбрасывания) данных, которые имеют большое значение квадрата ошибки (8). С новыми начальными условиями алгоритм оценки параметров модели теперь дополняется следующей последовательностью действий

def censor_data(SqErr, nCensor):
    # индексы отсортированного во возрастанию массива с квадратами ошибок
    I = np.argsort(SqErr[:,0])
    ind_imp = I[-nCensor:]
    ind_imp = ind_imp[::-1] # разворот индексов массива
    w0 = np.empty((nCensor, 1))
    w1 = np.empty((nCensor, 1))

    for i in range(0,nCensor):
        # цензурирование данных
        x_scale_cens = np.delete(x_scale, ind_imp[0:i], 0)
        y_estimate_imp_cens = np.delete(y_estimate_imp, ind_imp[0:i], 0)
        # расчёт параметров модельной прямой
        w0[i], w1[i] = coefficient_reg_stat(x_scale_cens, y_estimate_imp_cens)
        y_pred2_cens = predict(w0[i], w1[i], x_scale_cens) 
    return w0, w1 

nCensor = 20 # количество отбрасываемых выбросов
[w0_с, w1_с] = censor_data(SqErr, nCensor)

plt.plot(coef_true[0], coef_true[1], 'o', label = 'Истинные значения')
plt.plot(w0_с, w1_с, '-*', label = 'Расчетные значения')
plt.legend(loc = 'best', fontsize=12)
plt.xlim((30, 50))
plt.ylim((1.85, 2.15))
plt.xlabel('w0', fontsize=18)
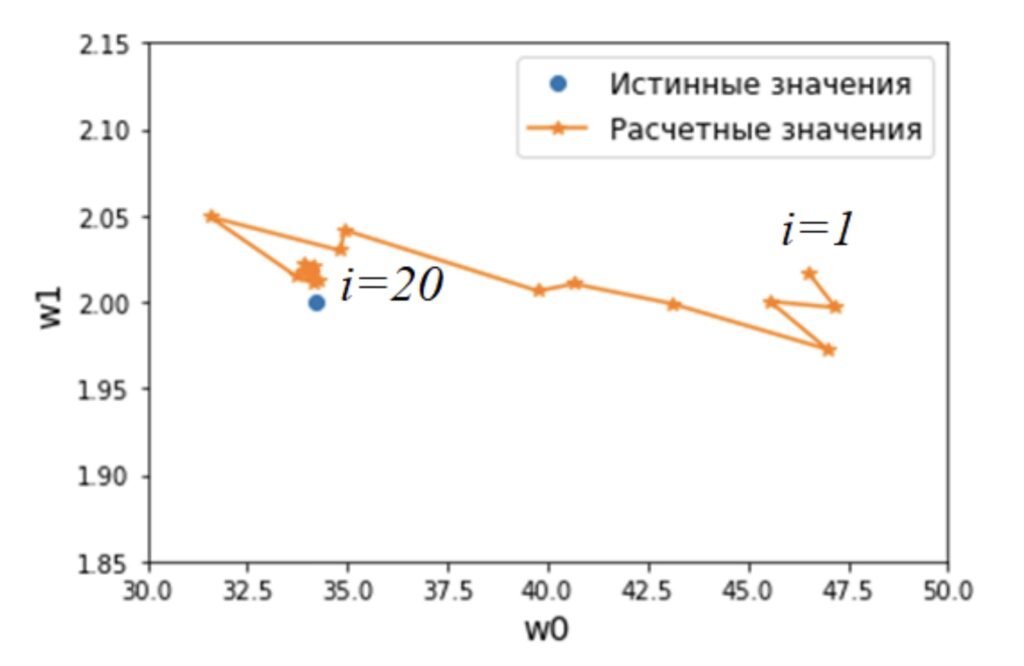
plt.ylabel('w1', fontsize=18)

По итогам работы алгоритма построим полученные оценки параметров модели (рисунок 5) по мере цензурирования данных.

Рисунок 5 – Оценки параметров модели по мере цензурирования данных

В результате работы рассматриваемого алгоритма видно (рисунок 5), что по мере цензурирования помеховых данных параметры модели приближаются к истинным (точка с оценкой параметров возле i=1 получена после удаления первой точки, точка с оценкой параметров возле i=20 получена после удаления двадцатой точки).

Ниже приведен код, который рассчитывает и строит на графике прямую (рисунок 6) с использованием параметров модели, полученной на последнем шаге алгоритма c цензурированием. На этом рисунке видно, что использование дополнительной процедуры цензурирования данных на основе анализа остаточной суммы квадратов, позволяет улучшить согласование оцениваемых параметров с истинными.

y_pred_censor = predict(w0_с[nCensor-1], w1_с[nCensor-1], x_scale)

plt.plot(x_scale, y_estimate_imp, 'o', label = 'Истинные значения')
plt.plot(x_scale, y_pred_censor, '*', label = 'Расчетные значения')
plt.legend(loc = 'best', fontsize=12)
plt.xlabel('X (порядковый номер измерения)', fontsize=14)
plt.ylabel('Y (оценка температуры)', fontsize=14)

Рисунок 6 – Зависимость температуры от времени

Обсуждение алгоритма

Был рассмотрен алгоритм оценки параметров модели, которая описывает процесс изменения температуры в печи при наличии помех в измерениях. Показано, как зная логику построения алгоритма его можно модифицировать под изменившиеся условия и получить необходимый результат (оценку параметров модели).

Безусловно, что приведенный в статье алгоритм оценки параметров модели с использованием процедуры цензурирования импульсных помеховых сигналов (в том виде, в котором он приведен в статье) не является оптимальным и универсальным. Он приведен здесь для иллюстрации возможностей модификации алгоритма, реализующего классический МНК. А также для демонстрации ещё одной важной метрики при использовании МНК – оценка квадратов разности между измеренными и модельными данными (8), которая является источником множества различных модификаций метода.

Заключение

В статье делается попытка «расколдовать» классический МНК, а также продемонстрировать удобство методологической интерпретации решения задачи в виде триады «модель-алгоритм-программа», которая позволяет осуществить бесшовный переход от модельной постановки задачи и задания начальных условий до её программной реализации. Ставилась задача в максимально доступной для читателя форме продемонстрировать последовательность математической мысли при решении задачи с применением МНК. Показать, как начальные условия влияют на полученные конечные выражения. Автор надеется, что статья будет полезной для всех тех, кто при решении различных задач анализа данных попытается применить или модифицировать классические методы и для этого попробует также с «карандашом в руках» выполнить вывод конечных выражений. Этот подход позволит разработчику применять на практике понятные для него алгоритмы, а не код, который работает «по неведомым» правилам.

Источник

Начнем статью сразу с примера. У нас есть некие экспериментальные данные о значениях двух переменных – x и y. Занесем их в таблицу.

	i=1	i=2	i=3	i=4	i=5
xi	0	1	2	4	5
yi	2,1	2,4	2,6	2,8	3,0

После выравнивания получим функцию следующего вида: g(x)=x+13+1.

Мы можем аппроксимировать эти данные с помощью линейной зависимости y=ax+b, вычислив соответствующие параметры. Для этого нам нужно будет применить так называемый метод наименьших квадратов. Также потребуется сделать чертеж, чтобы проверить, какая линия будет лучше выравнивать экспериментальные данные.

В чем именно заключается МНК (метод наименьших квадратов)

Главное, что нам нужно сделать, – это найти такие коэффициенты линейной зависимости, при которых значение функции двух переменных F(a, b)=∑i=1n(yi-(axi+b))2 будет наименьшим. Иначе говоря, при определенных значениях a и b сумма квадратов отклонений представленных данных от получившейся прямой будет иметь минимальное значение. В этом и состоит смысл метода наименьших квадратов. Все, что нам надо сделать для решения примера – это найти экстремум функции двух переменных.

Как вывести формулы для вычисления коэффициентов

Для того чтобы вывести формулы для вычисления коэффициентов, нужно составить и решить систему уравнений с двумя переменными. Для этого мы вычисляем частные производные выражения F(a, b)=∑i=1n(yi-(axi+b))2 по a и b и приравниваем их к 0.

δF(a, b)δa=0δF(a, b)δb=0⇔-2∑i=1n(yi-(axi+b))xi=0-2∑i=1n(yi-(axi+b))=0⇔a∑i=1nxi2+b∑i=1nxi=∑i=1nxiyia∑i=1nxi+∑i=1nb=∑i=1nyi⇔a∑i=1nxi2+b∑i=1nxi=∑i=1nxiyia∑i=1nxi+nb=∑i=1nyi

Для решения системы уравнений можно использовать любые методы, например, подстановку или метод Крамера. В результате у нас должны получиться формулы, с помощью которых вычисляются коэффициенты по методу наименьших квадратов.

n∑i=1nxiyi-∑i=1nxi∑i=1nyin∑i=1n-∑i=1nxi2b=∑i=1nyi-a∑i=1nxin

Мы вычислили значения переменных, при который функция
F(a, b)=∑i=1n(yi-(axi+b))2 примет минимальное значение. В третьем пункте мы докажем, почему оно является именно таким.

Это и есть применение метода наименьших квадратов на практике. Его формула, которая применяется для поиска параметра a, включает в себя ∑i=1nxi, ∑i=1nyi, ∑i=1nxiyi, ∑i=1nxi2, а также параметр
n – им обозначено количество экспериментальных данных. Советуем вам вычислять каждую сумму отдельно. Значение коэффициента b вычисляется сразу после a.

Обратимся вновь к исходному примеру.

Пример 1

Здесь у нас n равен пяти. Чтобы было удобнее вычислять нужные суммы, входящие в формулы коэффициентов, заполним таблицу.

	i=1	i=2	i=3	i=4	i=5	∑i=15
xi	0	1	2	4	5	12
yi	2,1	2,4	2,6	2,8	3	12,9
xiyi	0	2,4	5,2	11,2	15	33,8
xi2	0	1	4	16	25	46

Решение

Четвертая строка включает в себя данные, полученные при умножении значений из второй строки на значения третьей для каждого отдельного i. Пятая строка содержит данные из второй, возведенные в квадрат. В последнем столбце приводятся суммы значений отдельных строчек.

Воспользуемся методом наименьших квадратов, чтобы вычислить нужные нам коэффициенты a и b. Для этого подставим нужные значения из последнего столбца и подсчитаем суммы:

n∑i=1nxiyi-∑i=1nxi∑i=1nyin∑i=1n-∑i=1nxi2b=∑i=1nyi-a∑i=1nxin⇒a=5·33,8-12·12,95·46-122b=12,9-a·125⇒a≈0,165b≈2,184

У нас получилось, что нужная аппроксимирующая прямая будет выглядеть как y=0,165x+2,184. Теперь нам надо определить, какая линия будет лучше аппроксимировать данные – g(x)=x+13+1 или 0,165x+2,184. Произведем оценку с помощью метода наименьших квадратов.

Чтобы вычислить погрешность, нам надо найти суммы квадратов отклонений данных от прямых σ1=∑i=1n(yi-(axi+bi))2 и σ2=∑i=1n(yi-g(xi))2, минимальное значение будет соответствовать более подходящей линии.

σ1=∑i=1n(yi-(axi+bi))2==∑i=15(yi-(0,165xi+2,184))2≈0,019σ2=∑i=1n(yi-g(xi))2==∑i=15(yi-(xi+13+1))2≈0,096

Ответ: поскольку σ1<σ2, то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y=0,165x+2,184.

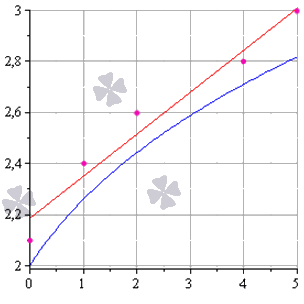
Как изобразить МНК на графике функций

Метод наименьших квадратов наглядно показан на графической иллюстрации. С помощью красной линии отмечена прямая g(x)=x+13+1, синей – y=0,165x+2,184. Исходные данные обозначены розовыми точками.

Поясним, для чего именно нужны приближения подобного вида.

Они могут быть использованы в задачах, требующих сглаживания данных, а также в тех, где данные надо интерполировать или экстраполировать. Например, в задаче, разобранной выше, можно было бы найти значение наблюдаемой величины y при x=3 или при x=6. Таким примерам мы посвятили отдельную статью.

Доказательство метода МНК

Чтобы функция приняла минимальное значение при вычисленных a и b, нужно, чтобы в данной точке матрица квадратичной формы дифференциала функции вида F(a, b)=∑i=1n(yi-(axi+b))2 была положительно определенной. Покажем, как это должно выглядеть.

Пример 2

У нас есть дифференциал второго порядка следующего вида:

d2F(a; b)=δ2F(a; b)δa2d2a+2δ2F(a; b)δaδbdadb+δ2F(a; b)δb2d2b

Решение

δ2F(a; b)δa2=δδF(a; b)δaδa==δ-2∑i=1n(yi-(axi+b))xiδa=2∑i=1n(xi)2δ2F(a; b)δaδb=δδF(a; b)δaδb==δ-2∑i=1n(yi-(axi+b))xiδb=2∑i=1nxiδ2F(a; b)δb2=δδF(a; b)δbδb=δ-2∑i=1n(yi-(axi+b))δb=2∑i=1n(1)=2n

Иначе говоря, можно записать так: d2F(a; b)=2∑i=1n(xi)2d2a+2·2∑xii=1ndadb+(2n)d2b.

Мы получили матрицу квадратичной формы вида M=2∑i=1n(xi)22∑i=1nxi2∑i=1nxi2n.

В этом случае значения отдельных элементов не будут меняться в зависимости от a и b. Является ли эта матрица положительно определенной? Чтобы ответить на этот вопрос, проверим, являются ли ее угловые миноры положительными.

Вычисляем угловой минор первого порядка: 2∑i=1n(xi)2>0. Поскольку точки xi не совпадают, то неравенство является строгим. Будем иметь это в виду при дальнейших расчетах.

Вычисляем угловой минор второго порядка:

det(M)=2∑i=1n(xi)22∑i=1nxi2∑i=1nxi2n=4n∑i=1n(xi)2-∑i=1nxi2

После этого переходим к доказательству неравенства n∑i=1n(xi)2-∑i=1nxi2>0 с помощью математической индукции.

Проверим, будет ли данное неравенство справедливым при произвольном n. Возьмем 2 и подсчитаем:

2∑i=12(xi)2-∑i=12xi2=2×12+x22-x1+x22==x12-2x1x2+x22=x1+x22>0

У нас получилось верное равенство (если значения x1 и x2 не будут совпадать).

Сделаем предположение, что данное неравенство будет верным для n, т.е. n∑i=1n(xi)2-∑i=1nxi2>0 – справедливо.
Теперь докажем справедливость при n+1, т.е. что (n+1)∑i=1n+1(xi)2-∑i=1n+1xi2>0, если верно n∑i=1n(xi)2-∑i=1nxi2>0.

Вычисляем:

(n+1)∑i=1n+1(xi)2-∑i=1n+1xi2==(n+1)∑i=1n(xi)2+xn+12-∑i=1nxi+xn+12==n∑i=1n(xi)2+n·xn+12+∑i=1n(xi)2+xn+12–∑i=1nxi2+2xn+1∑i=1nxi+xn+12==∑i=1n(xi)2-∑i=1nxi2+n·xn+12-xn+1∑i=1nxi+∑i=1n(xi)2==∑i=1n(xi)2-∑i=1nxi2+xn+12-2xn+1×1+x12++xn+12-2xn+1×2+x22+…+xn+12-2xn+1×1+xn2==n∑i=1n(xi)2-∑i=1nxi2++(xn+1-x1)2+(xn+1-x2)2+…+(xn-1-xn)2>0

Выражение, заключенное в фигурные скобки, будет больше 0 (исходя из того, что мы предполагали в пункте 2), и остальные слагаемые будут больше 0, поскольку все они являются квадратами чисел. Мы доказали неравенство.

Ответ: найденные a и b будут соответствовать наименьшему значению функции F(a, b)=∑i=1n(yi-(axi+b))2, значит, они являются искомыми параметрами метода наименьших квадратов (МНК).

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Метод наименьших квадратов (мнк).

Пример.

Экспериментальные
данные о значениях переменных х
и у
приведены
в таблице.

В
результате их выравнивания получена
функция

Используя
метод
наименьших квадратов ,
аппроксимировать эти данные линейной
зависимостью y=ax+b
(найти параметры а
и b).
Выяснить, какая из двух линий лучше (в
смысле метода наименьших квадратов)
выравнивает экспериментальные данные.
Сделать чертеж.

Суть метода наименьших квадратов (мнк).

Задача
заключается в нахождении коэффициентов
линейной зависимости, при которых
функция двух переменных а
и b
принимает
наименьшее значение. То есть, при данныха
и b
сумма квадратов отклонений экспериментальных
данных от найденной прямой будет
наименьшей. В этом вся суть метода
наименьших квадратов.

Таким
образом, решение примера сводится к
нахождению экстремума функции двух
переменных.

Вывод формул для нахождения коэффициентов.

Составляется
и решается система из двух уравнений с
двумя неизвестными. Находим частные
производные функции
по
переменныма
и b,
приравниваем эти производные к нулю.

Решаем
полученную систему уравнений любым
методом (например методом
подстановки
или методом
Крамера)
и получаем формулы для нахождения
коэффициентов по методу наименьших
квадратов (МНК).

При
данных а и
b функция
принимает
наименьшее значение. Доказательство
этого факта приведенониже
по тексту в конце страницы .

Вот
и весь метод наименьших квадратов.
Формула для нахождения параметра a
содержит суммы
,,,и
параметрn
– количество экспериментальных данных.
Значения этих сумм рекомендуем вычислять
отдельно. Коэффициент b
находится после вычисления a.

Пришло
время вспомнить про исходый пример.

Решение.

В
нашем примере n=5
. Заполняем
таблицу для удобства вычисления сумм,
которые входят в формулы искомых
коэффициентов.

Значения
в четвертой строке таблицы получены
умножением значений 2-ой строки на
значения 3-ей строки для каждого номера
i .

Значения
в пятой строке таблицы получены
возведением в квадрат значений 2-ой
строки для каждого номера i
.

Значения
последнего столбца таблицы – это суммы
значений по строкам.

Используем
формулы метода наименьших квадратов
для нахождения коэффициентов а
и b.
Подставляем в них соответствующие
значения из последнего столбца таблицы:

Следовательно,
y = 0.165x+2.184
– искомая аппроксимирующая прямая.

Осталось
выяснить какая из линий y
= 0.165x+2.184 или
лучше
аппроксимирует исходные данные, то есть
произвести оценку методом наименьших
квадратов.

Оценка погрешности метода наименьших квадратов.

Для
этого требуется вычислить суммы квадратов
отклонений исходных данных от этих
линий
и,
меньшее значение соответствует линии,
которая лучше в смысле метода наименьших
квадратов аппроксимирует исходные
данные.

Так
как
,
то прямаяy
= 0.165x+2.184
лучше приближает исходные данные.

Графическая иллюстрация метода наименьших квадратов (мнк).

На
графиках все прекрасно видно. Красная
линия – это найденная прямая y
= 0.165x+2.184,
синяя линия – это
,
розовые точки – это исходные данные.

На
практике при моделировании различных
процессов – в частности, экономических,
физических, технических, социальных –
широко используются те или иные способы
вычисления приближенных значений
функций по известным их значениям в
некоторых фиксированных точках.

Такого
рода задачи приближения функций часто
возникают:

при построении
приближенных формул для вычисления
значений характерных величин исследуемого
процесса по табличным данным, полученным
в результате эксперимента;
при численном
интегрировании, дифференцировании,
решении дифференциальных уравнений и
т. д.;
при необходимости
вычисления значений функций в
промежуточных точках рассматриваемого
интервала;
при определении
значений характерных величин процесса
за пределами рассматриваемого интервала,
в частности при прогнозировании.

Если
для моделирования некоторого процесса,
заданного таблицей, построить функцию,
приближенно описывающую данный процесс
на основе метода наименьших квадратов,
она будет называться аппроксимирующей
функцией (регрессией), а сама задача
построения аппроксимирующих функций
– задачей аппроксимации.

В
данной статье рассмотрены возможности
пакета MS Excel для решения такого рода
задач, кроме того, приведены методы и
приемы построения (создания) регрессий
для таблично заданных функций (что
является основой регрессионного
анализа).

В
Excel для построения регрессий имеются
две возможности.

Добавление
выбранных регрессий (линий тренда –
trendlines) в диаграмму, построенную на
основе таблицы данных для исследуемой
характеристики процесса (доступно лишь
при наличии построенной диаграммы);
Использование
встроенных статистических функций
рабочего листа Excel, позволяющих получать
регрессии (линии тренда) непосредственно
на основе таблицы исходных данных.

Добавление
линий тренда в диаграмму

Для
таблицы данных, описывающих некоторый
процесс и представленных диаграммой,
в Excel имеется эффективный инструмент
регрессионного анализа, позволяющий:

строить на основе
метода наименьших квадратов и добавлять
в диаграмму пять типов регрессий,
которые с той или иной степенью точности
моделируют исследуемый процесс;
добавлять к
диаграмме уравнение построенной
регрессии;
определять степень
соответствия выбранной регрессии
отображаемым на диаграмме данным.

На
основе данных диаграммы Excel позволяет
получать линейный, полиномиальный,
логарифмический, степенной, экспоненциальный
типы регрессий, которые задаются
уравнением:

y
= y(x)

где
x – независимая переменная, которая часто
принимает значения последовательности
натурального ряда чисел (1; 2; 3; …) и
производит, например, отсчет времени
протекания исследуемого процесса
(характеристики).

1.
Линейная регрессия хороша при моделировании
характеристик, значения которых
увеличиваются или убывают с постоянной
скоростью. Это наиболее простая в
построении модель исследуемого процесса.
Она строится в соответствии с уравнением:

y
= mx + b

где
m – тангенс угла наклона линейной регрессии
к оси абсцисс; b – координата точки
пересечения линейной регрессии с осью
ординат.

2.
Полиномиальная линия тренда полезна
для описания характеристик, имеющих
несколько ярко выраженных экстремумов
(максимумов и минимумов). Выбор степени
полинома определяется количеством
экстремумов исследуемой характеристики.
Так, полином второй степени может хорошо
описать процесс, имеющий только один
максимум или минимум; полином третьей
степени – не более двух экстремумов;
полином четвертой степени – не более
трех экстремумов и т. д.

В
этом случае линия тренда строится в
соответствии с уравнением:

y
= c0 + c1x + c2x2 + c3x3 + c4x4 + c5x5 + c6x6

где
коэффициенты c0, c1, c2,… c6 – константы,
значения которых определяются в ходе
построения.

3.
Логарифмическая линия тренда с успехом
применяется при моделировании
характеристик, значения которых вначале
быстро меняются, а затем постепенно
стабилизируются.

Строится
в соответствии с уравнением:

y
= c ln(x) + b

где
коэффициенты b, с – константы.

4.
Степенная линия тренда дает хорошие
результаты, если значения исследуемой
зависимости характеризуются постоянным
изменением скорости роста. Примером
такой зависимости может служить график
равноускоренного движения автомобиля.
Если среди данных встречаются нулевые
или отрицательные значения, использовать
степенную линию тренда нельзя.

Строится
в соответствии с уравнением:

y
= c xb

где
коэффициенты b, с – константы.

5.
Экспоненциальную линию тренда следует
использовать в том случае, если скорость
изменения данных непрерывно возрастает.
Для данных, содержащих нулевые или
отрицательные значения, этот вид
приближения также неприменим.

Строится
в соответствии с уравнением:

y
= c ebx

где
коэффициенты b, с – константы.

При
подборе линии тренда Excel автоматически
рассчитывает значение величины R2,
которая характеризует достоверность
аппроксимации: чем ближе значение R2 к
единице, тем надежнее линия тренда
аппроксимирует исследуемый процесс.
При необходимости значение R2 всегда
можно отобразить на диаграмме.

Определяется
по формуле:

Для
добавления линии тренда к ряду данных
следует:

активизировать
построенную на основе ряда данных
диаграмму, т. е. щелкнуть в пределах
области диаграммы. В главном меню
появится пункт Диаграмма;
после щелчка на
этом пункте на экране появится меню, в
котором следует выбрать команду Добавить
линию тренда.

Эти
же действия легко реализуются, если
навести указатель мыши на график,
соответствующий одному из рядов данных,
и щелкнуть правой кнопкой мыши; в
появившемся контекстном меню выбрать
команду Добавить линию тренда. На экране
появится диалоговое окно Линия тренда
с раскрытой вкладкой Тип (рис. 1).

После
этого необходимо:

Выбрать
на вкладке Тип необходимый тип линии
тренда (по умолчанию выбирается тип
Линейный). Для типа Полиномиальная в
поле Степень следует задать степень
выбранного полинома.

1.
В поле Построен на ряде перечислены все
ряды данных рассматриваемой диаграммы.
Для добавления линии тренда к конкретному
ряду данных следует в поле Построен на
ряде выбрать его имя.

При
необходимости, перейдя на вкладку
Параметры (рис. 2), можно для линии тренда
задать следующие параметры:

изменить название
линии тренда в поле Название
аппроксимирующей (сглаженной) кривой.
задать количество
периодов (вперед или назад) для прогноза
в поле Прогноз;
вывести в область
диаграммы уравнение линии тренда, для
чего следует включить флажок показать
уравнение на диаграмме;
вывести в область
диаграммы значение достоверности
аппроксимации R2, для чего следует
включить флажок поместить на диаграмму
величину достоверности аппроксимации
(R^2);
задать точку
пересечения линии тренда с осью Y, для
чего следует включить флажок пересечение
кривой с осью Y в точке;
щелкнуть на кнопке
OK, чтобы закрыть диалоговое окно.

Для
того, чтобы начать редактирование уже
построенной линии тренда, существует
три способа:

воспользоваться
командой Выделенная линия тренда из
меню Формат, предварительно выбрав
линию тренда;
выбрать команду
Формат линии тренда из контекстного
меню, которое вызывается щелчком правой
кнопки мыши по линии тренда;
двойным щелчком
по линии тренда.

На
экране появится диалоговое окно Формат
линии тренда (рис. 3), содержащее три
вкладки: Вид, Тип, Параметры, причем
содержимое последних двух полностью
совпадает с аналогичными вкладками
диалогового окна Линия тренда (рис.1-2).
На вкладке Вид, можно задать тип линии,
ее цвет и толщину.

Для
удаления уже построенной линии тренда
следует выбрать удаляемую линию тренда
и нажать клавишу Delete.

Достоинствами
рассмотренного инструмента регрессионного
анализа являются:

относительная
легкость построения на диаграммах
линии тренда без создания для нее
таблицы данных;
достаточно широкий
перечень типов предложенных линий
трендов, причем в этот перечень входят
наиболее часто используемые типы
регрессии;
возможность
прогнозирования поведения исследуемого
процесса на произвольное (в пределах
здравого смысла) количество шагов
вперед, а также назад;
возможность
получения уравнения линии тренда в
аналитическом виде;
возможность, при
необходимости, получения оценки
достоверности проведенной аппроксимации.

К
недостаткам можно отнести следующие
моменты:

построение линии
тренда осуществляется лишь при наличии
диаграммы, построенной на ряде данных;
процесс формирования
рядов данных для исследуемой характеристики
на основе полученных для нее уравнений
линий тренда несколько загроможден:
искомые уравнения регрессий обновляются
при каждом изменении значений исходного
ряда данных, но только в пределах области
диаграммы, в то время как ряд данных,
сформированный на основе старого
уравнения линии тренда, остается без
изменения;
в отчетах сводных
диаграмм при изменении представления
диаграммы или связанного отчета сводной
таблицы имеющиеся линии тренда не
сохраняются, то есть до проведения
линий тренда или другого форматирования
отчета сводных диаграмм следует
убедиться, что макет отчета удовлетворяет
необходимым требованиям.

Линиями
тренда можно дополнить ряды данных,
представленные на диаграммах типа
график, гистограмма, плоские ненормированные
диаграммы с областями, линейчатые,
точечные, пузырьковые и биржевые.

Нельзя
дополнить линиями тренда ряды данных
на объемных, нормированных, лепестковых,
круговых и кольцевых диаграммах.

Использование
встроенных функций Excel

В
Excel имеется также инструмент регрессионного
анализа для построения линий тренда
вне области диаграммы. Для этой цели
можно использовать ряд статистических
функций рабочего листа, однако все они
позволяют строить лишь линейные или
экспоненциальные регрессии.

В
Excel имеется несколько функций для
построения линейной регрессии, в
частности:

ТЕНДЕНЦИЯ;
ЛИНЕЙН;
НАКЛОН и ОТРЕЗОК.

А
также несколько функций для построения
экспоненциальной линии тренда, в
частности:

РОСТ;
ЛГРФПРИБЛ.

Следует
отметить, что приемы построения регрессий
с помощью функций ТЕНДЕНЦИЯ и РОСТ
практически совпадают. То же самое можно
сказать и о паре функций ЛИНЕЙН и
ЛГРФПРИБЛ. Для четырех этих функций при
создании таблицы значений используются
такие возможности Excel, как формулы
массивов, что несколько загромождает
процесс построения регрессий. Заметим
также, что построение линейной регрессии,
на наш взгляд, легче всего осуществить
с помощью функций НАКЛОН и ОТРЕЗОК, где
первая из них определяет угловой
коэффициент линейной регрессии, а вторая
– отрезок, отсекаемый регрессией на оси
ординат.

Достоинствами
инструмента встроенных функций для
регрессионного анализа являются:

достаточно простой
однотипный процесс формирования рядов
данных исследуемой характеристики для
всех встроенных статистических функций,
задающих линии тренда;
стандартная
методика построения линий тренда на
основе сформированных рядов данных;
возможность
прогнозирования поведения исследуемого
процесса на необходимое количество
шагов вперед или назад.

А
к недостаткам относится то, что в Excel
нет встроенных функций для создания
других (кроме линейного и экспоненциального)
типов линий тренда. Это обстоятельство
часто не позволяет подобрать достаточно
точную модель исследуемого процесса,
а также получить близкие к реальности
прогнозы. Кроме того, при использовании
функций ТЕНДЕНЦИЯ и РОСТ не известны
уравнения линий тренда.

Следует
отметить, что авторы не ставили целью
статьи изложение курса регрессионного
анализа с той или иной степенью полноты.
Основная ее задача – на конкретных
примерах показать возможности пакета
Excel при решении задач аппроксимации;
продемонстрировать, какими эффективными
инструментами для построения регрессий
и прогнозирования обладает Excel;
проиллюстрировать, как относительно
легко такие задачи могут быть решены
даже пользователем, не владеющим
глубокими знаниями регрессионного
анализа.

Примеры решения
конкретных задач

Рассмотрим
решение конкретных задач с помощью
перечисленных инструментов пакета
Excel.

Задача
1

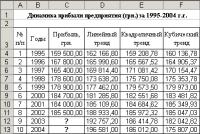
С
таблицей данных о прибыли автотранспортного
предприятия за 1995-2002 гг. необходимо
выполнить следующие действия.

Построить диаграмму.
В диаграмму
добавить линейную и полиномиальную
(квадратичную и кубическую) линии
тренда.
Вывести уравнения
полученных линий тренда, а также величины
достоверности аппроксимации R2 для
каждой из них.
Используя уравнения
линий тренда, получить табличные данные
по прибыли предприятия для каждой линии
тренда за 1995-2004 г.г.
Составить прогноз
по прибыли предприятия на 2003 и 2004 гг.

Решение
задачи

В диапазон ячеек
A4:C11 рабочего листа Excel вводим рабочую
таблицу, представленную на рис. 4.
Выделив диапазон
ячеек В4:С11, строим диаграмму.
Активизируем
построенную диаграмму и по описанной
выше методике после выбора типа линии
тренда в диалоговом окне Линия тренда
(см. рис. 1) поочередно добавляем в
диаграмму линейную, квадратичную и
кубическую линии тренда. В этом же
диалоговом окне открываем вкладку
Параметры (см. рис. 2), в поле Название
аппроксимирующей (сглаженной) кривой
вводим наименование добавляемого
тренда, а в поле Прогноз вперед на:
периодов задаем значение 2, так как
планируется сделать прогноз по прибыли
на два года вперед. Для вывода в области
диаграммы уравнения регрессии и значения
достоверности аппроксимации R2 включаем
флажки показывать уравнение на экране
и поместить на диаграмму величину
достоверности аппроксимации (R^2). Для
лучшего визуального восприятия изменяем
тип, цвет и толщину построенных линий
тренда, для чего воспользуемся вкладкой
Вид диалогового окна Формат линии
тренда (см. рис. 3). Полученная диаграмма
с добавленными линиями тренда представлена
на рис. 5.
Для получения
табличных данных по прибыли предприятия
для каждой линии тренда за 1995-2004 гг.
воспользуемся уравнениями линий тренда,
представленными на рис. 5. Для этого в
ячейки диапазона D3:F3 вводим текстовую
информацию о типе выбранной линии
тренда: Линейный тренд, Квадратичный
тренд, Кубический тренд. Далее вводим
в ячейку D4 формулу линейной регрессии
и, используя маркер заполнения, копируем
эту формулу c относительными ссылками
в диапазон ячеек D5:D13. Следует отметить,
что каждой ячейке с формулой линейной
регрессии из диапазона ячеек D4:D13 в
качестве аргумента стоит соответствующая
ячейка из диапазона A4:A13. Аналогично
для квадратичной регрессии заполняется
диапазон ячеек E4:E13, а для кубической
регрессии – диапазон ячеек F4:F13. Таким
образом, составлен прогноз по прибыли
предприятия на 2003 и 2004 гг. с помощью
трех трендов. Полученная таблица
значений представлена на рис. 6.

Задача
2

С
таблицей данных о прибыли автотранспортного
предприятия за 1995-2002 гг., приведенной в
задаче 1, необходимо выполнить следующие
действия.

Построить диаграмму.
В диаграмму
добавить логарифмическую, степенную
и экспоненциальную линии тренда.
Вывести уравнения
полученных линий тренда, а также величины
достоверности аппроксимации R2 для
каждой из них.
Используя уравнения
линий тренда, получить табличные данные
о прибыли предприятия для каждой линии
тренда за 1995-2002 гг.
Составить прогноз
о прибыли предприятия на 2003 и 2004 гг.,
используя эти линии тренда.

Решение
задачи

Следуя
методике, приведенной при решении задачи
1, получаем диаграмму с добавленными в
нее логарифмической, степенной и
экспоненциальной линиями тренда (рис.
7). Далее, используя полученные уравнения
линий тренда, заполняем таблицу значений
по прибыли предприятия, включая
прогнозируемые значения на 2003 и 2004 гг.
(рис. 8).

На
рис. 5 и рис. видно, что модели с
логарифмическим трендом, соответствует
наименьшее значение достоверности
аппроксимации

R2
= 0,8659

Наибольшие
же значения R2 соответствуют моделям с
полиномиальным трендом: квадратичным
(R2 = 0,9263) и кубическим (R2 = 0,933).

Задача
3

Получить ряды
данных для линейной и экспоненциальной
линии тренда с использованием функций
ТЕНДЕНЦИЯ и РОСТ.
Используя функции
ТЕНДЕНЦИЯ и РОСТ, составить прогноз о
прибыли предприятия на 2003 и 2004 гг.
Для исходных
данных и полученных рядов данных
построить диаграмму.

Решение
задачи

Воспользуемся
рабочей таблицей задачи 1 (см. рис. 4).
Начнем с функции ТЕНДЕНЦИЯ:

выделяем диапазон
ячеек D4:D11, который следует заполнить
значениями функции ТЕНДЕНЦИЯ,
соответствующими известным данным о
прибыли предприятия;
вызываем команду
Функция из меню Вставка. В появившемся
диалоговом окне Мастер функций выделяем
функцию ТЕНДЕНЦИЯ из категории
Статистические, после чего щелкаем по
кнопке ОК. Эту же операцию можно
осуществить нажатием кнопки (Вставка
функции) стандартной панели инструментов.
В появившемся
диалоговом окне Аргументы функции
вводим в поле Известные_значения_y
диапазон ячеек C4:C11; в поле Известные_значения_х
– диапазон ячеек B4:B11;
чтобы вводимая
формула стала формулой массива,
используем комбинацию клавиш + + .

Введенная
нами формула в строке формул будет иметь
вид: ={ТЕНДЕНЦИЯ(C4:C11;B4:B11)}.

В
результате диапазон ячеек D4:D11 заполняется
соответствующими значениями функции
ТЕНДЕНЦИЯ (рис. 9).

Для
составления прогноза о прибыли предприятия
на 2003 и 2004 гг. необходимо:

выделить диапазон
ячеек D12:D13, куда будут заноситься
значения, прогнозируемые функцией
ТЕНДЕНЦИЯ.
вызвать функцию
ТЕНДЕНЦИЯ и в появившемся диалоговом
окне Аргументы функции ввести в поле
Известные_значения_y – диапазон ячеек
C4:C11; в поле Известные_значения_х –
диапазон ячеек B4:B11; а в поле Новые_значения_х
– диапазон ячеек B12:B13.
превратить эту
формулу в формулу массива, используя
комбинацию клавиш Ctrl + Shift + Enter.
Введенная формула
будет иметь вид: ={ТЕНДЕНЦИЯ(C4:C11;B4:B11;B12:B13
)}, а диапазон ячеек D12:D13 заполнится
прогнозируемыми значениями функции
ТЕНДЕНЦИЯ (см. рис. 9).

Аналогично
заполняется ряд данных с помощью функции
РОСТ, которая используется при анализе
нелинейных зависимостей и работает
точно так же, как ее линейный аналог
ТЕНДЕНЦИЯ.

На
рис.10 представлена таблица в режиме
показа формул.

Для
исходных данных и полученных рядов
данных построена диаграмма, изображенная
на рис. 11.

Задача
4

С
таблицей данных о поступлении в
диспетчерскую службу автотранспортного
предприятия заявок на услуги за период
с 1 по 11 число текущего месяца необходимо
выполнить следующие действия.

Получить ряды
данных для линейной регрессии: используя
функции НАКЛОН и ОТРЕЗОК; используя
функцию ЛИНЕЙН.
Получить ряд
данных для экспоненциальной регрессии
с использованием функции ЛГРФПРИБЛ.
Используя
вышеназванные функции, составить
прогноз о поступлении заявок в
диспетчерскую службу на период с 12 по
14 число текущего месяца.
Для исходных и
полученных рядов данных построить
диаграмму.

Решение
задачи

Отметим,
что, в отличие от функций ТЕНДЕНЦИЯ и
РОСТ, ни одна из перечисленных выше
функций (НАКЛОН, ОТРЕЗОК, ЛИНЕЙН, ЛГРФПРИБ)
не является регрессией. Эти функции
играют лишь вспомогательную роль,
определяя необходимые параметры
регрессии.

Для
линейной и экспоненциальной регрессий,
построенных с помощью функций НАКЛОН,
ОТРЕЗОК, ЛИНЕЙН, ЛГРФПРИБ, внешний вид
их уравнений всегда известен, в отличие
от линейной и экспоненциальной регрессий,
соответствующих функциям ТЕНДЕНЦИЯ и
РОСТ.

1.
Построим линейную регрессию, имеющую
уравнение:

y
= mx+b

с
помощью функций НАКЛОН и ОТРЕЗОК, причем
угловой коэффициент регрессии m
определяется функцией НАКЛОН, а свободный
член b – функцией ОТРЕЗОК.

Для
этого осуществляем следующие действия:

заносим исходную
таблицу в диапазон ячеек A4:B14;
значение параметра
m будет определяться в ячейке С19. Выбираем
из категории Статистические функцию
Наклон; заносим диапазон ячеек B4:B14 в
поле известные_значения_y и диапазон
ячеек А4:А14 в поле известные_значения_х.
В ячейку С19 будет введена формула:
=НАКЛОН(B4:B14;A4:A14);
по аналогичной
методике определяется значение параметра
b в ячейке D19. И ее содержимое будет иметь
вид: =ОТРЕЗОК(B4:B14;A4:A14). Таким образом,
необходимые для построения линейной
регрессии значения параметров m и b
будут сохраняться соответственно в
ячейках C19, D19;
далее заносим в
ячейку С4 формулу линейной регрессии
в виде: =$C*A4+$D. В этой формуле ячейки С19
и D19 записаны с абсолютными ссылками
(адрес ячейки не должен меняться при
возможном копировании). Знак абсолютной
ссылки $ можно набить либо с клавиатуры,
либо с помощью клавиши F4, предварительно
установив курсор на адресе ячейки.
Воспользовавшись маркером заполнения,
копируем эту формулу в диапазон ячеек
С4:С17. Получаем искомый ряд данных (рис.
12). В связи с тем, что количество заявок
– целое число, следует установить на
вкладке Число окна Формат ячеек числовой
формат с числом десятичных знаков 0.

2.
Теперь построим линейную регрессию,
заданную уравнением:

y
= mx+b

с
помощью функции ЛИНЕЙН.

Для
этого:

вводим в диапазон
ячеек C20:D20 функцию ЛИНЕЙН как формулу
массива: ={ЛИНЕЙН(B4:B14;A4:A14)}. В результате
получаем в ячейке C20 значение параметра
m, а в ячейке D20 – значение параметра b;
вводим в ячейку
D4 формулу: =$C*A4+$D;
копируем эту
формулу с помощью маркера заполнения
в диапазон ячеек D4:D17 и получаем искомый
ряд данных.

3.
Строим экспоненциальную регрессию,
имеющую уравнение:

y
= bmx

с
помощью функции ЛГРФПРИБЛ оно выполняется
аналогично:

в диапазон ячеек
C21:D21 вводим функцию ЛГРФПРИБЛ как
формулу массива: ={ ЛГРФПРИБЛ
(B4:B14;A4:A14)}. При этом в ячейке C21 будет
определено значение параметра m, а в
ячейке D21 – значение параметра b;
в ячейку E4 вводится
формула: =$D*$C^A4;
с помощью маркера
заполнения эта формула копируется в
диапазон ячеек E4:E17, где и расположится
ряд данных для экспоненциальной
регрессии (см. рис. 12).

На
рис. 13 приведена таблица, где видны
используемые нами функции с необходимыми
диапазонами ячеек, а также формулы.

Величина R² называется
коэффициентом
детерминации.

Задачей построения
регрессионной зависимости является
нахождение вектора коэффициентов m
модели (1) при котором коэффициент R
принимает максимальное значение.

Для оценки значимости
R применяется F-критерий Фишера, вычисляемый
по формуле

где n
– размер выборки (количество экспериментов);

k – число коэффициентов
модели.

Если F превышает
некоторое критическое значение для
данных n
и k
и принятой доверительной вероятности,
то величина R считается существенной.
Таблицы критических значений F приводятся
в справочниках по математической
статистике.

Таким образом,
значимость R определяется не только его
величиной, но и соотношением между
количеством экспериментов и количеством
коэффициентов (параметров) модели.
Действительно, корреляционное отношение
для n=2 для простой линейной модели равно
1 (через 2 точки на плоскости можно всегда
провести единственную прямую). Однако
если экспериментальные данные являются
случайными величинами, доверять такому
значению R следует с большой осторожностью.
Обычно для получения значимого R и
достоверной регрессии стремятся к тому,
чтобы количество экспериментов
существенно превышало количество
коэффициентов модели (n>k).

Для построения
линейной регрессионной модели необходимо:

1) подготовить
список из n строк и m столбцов, содержащий
экспериментальные данные (столбец,
содержащий выходную величину Y
должен быть
либо первым, либо последним в списке);
для примера возьмем данные предыдущего
задания, добавив столбец с названием
“№ периода”, пронумеруем номера
периодов от 1 до 12. (это будут значения
Х)

2) обратиться к
меню Данные/Анализ
данных/Регрессия

Если пункт “Анализ
данных” в
меню “Сервис” отсутствует,
то следует обратиться к пункту
“Надстройки” того
же меню и установить флажок “Пакет
анализа”.

3) в диалоговом
окне “Регрессия” задать:

·
входной интервал Y;

·
входной интервал X;

·
выходной интервал – верхняя левая ячейка
интервала, в который будут помещаться
результаты вычислений (рекомендуется
разместить на новом рабочем листе);

4) нажать “Ok”
и проанализировать результаты.

Источник

Цель любого физического эксперимента — проверить, выполняется ли некоторая
теоретическая закономерность (модель), а также получить или уточнить
её параметры. Поскольку набор экспериментальных данных неизбежно ограничен,
а каждое отдельное измерение имеет погрешность, можно говорить лишь
об оценке этих параметров. В большинстве случаев измеряется не одна
величина, а некоторая функциональная зависимость величин друг от друга.
В таком случае возникает необходимость построить оценку параметров этой зависимости.

Пример. Рассмотрим процедуру измерения сопротивления некоторого резистора.
Простейшая теоретическая модель для резистора — закон Ома U=R⁢I,
где сопротивление R — единственный параметр модели. Часто при измерениях
возможно возникновение систематической ошибки — смещение нуля напряжения или тока.
Тогда для получения более корректной оценки сопротивления стоит использовать
модель с двумя параметрами: U=R⁢I+U0.

Для построения оценки нужны следующие компоненты

•

данные — результаты измерений {xi,yi}
и их погрешности {σi}
(экспериментальная погрешность является неотъемлемой
частью набора данных!);
•

модель y=f⁢(x|θ1,θ2,…) —
параметрическое описание исследуемой зависимости
(θ — набор параметров модели, например,
коэффициенты {k,b} прямой f⁢(x)=k⁢x+b);
•

процедура построения оценки параметров по
измеренным данным («оценщик»):

Рассмотрим самые распространенные способы построения оценки.

3.1 Метод минимума хи-квадрат

Обозначим отклонения результатов некоторой серии измерений от теоретической
модели y=f⁢(x|θ) как

Δ⁢yi=yi-f⁢(xi|θ),i=1⁢…⁢n,

где θ — некоторый параметр (или набор параметров),
для которого требуется построить наилучшую оценку. Нормируем Δ⁢yi
на стандартные отклонения σi и построим сумму

которую принято называть суммой хи-квадрат.

Метод минимума хи-квадрат (метод Пирсона) заключается в подборе такого
θ, при котором сумма квадратов отклонений от теоретической
модели, нормированных на ошибки измерений, достигает минимума:

Замечание. Подразумевается, что погрешность измерений σi указана только для
вертикальной оси y. Поэтому, при использовании метода следует выбирать оcи
таким образом, чтобы относительная ошибка по оси абсцисс была значительно меньше,
чем по оси ординат.

Данный метод вполне соответствует нашему интуитивному представлению
о том, как теоретическая зависимость должна проходить через экспериментальные
точки. Ясно, что чем ближе данные к модельной кривой, тем
меньше будет сумма χ2. При этом, чем больше погрешность точки, тем
в большей степени дозволено результатам измерений отклоняться от модели.
Метода минимума χ2 является частным случаем
более общего метода максимума правдоподобия (см. ниже),
реализующийся при нормальном (гауссовом) распределении ошибок.

Можно показать (см. [5]), что оценка по методу хи-квадрат является состоятельной,
несмещенной и, если данные распределены нормально,
имеет максимальную эффективность (см. приложение 5.2).

Замечание. Простые аналитические выражения для оценки методом хи-квадрат существуют
(см. п. 3.6.1, 3.6.4) только в случае линейной
зависимости f⁢(x)=k⁢x+b (впрочем, нелинейную зависимость часто можно
заменой переменных свести к линейной). В общем случае задача поиска
минимума χ2⁢(θ) решается численно, а соответствующая процедура
реализована в большинстве специализированных программных пакетов
по обработке данных.

3.2 Метод максимального правдоподобия.

Рассмотрим кратко один
из наиболее общих методов оценки параметров зависимостей —
метод максимума правдоподобия.

Сделаем два ключевых предположения:

•

зависимость между измеряемыми величинами действительно может
быть описана функцией y=f⁢(x|θ) при некотором θ;
•

все отклонения Δ⁢yi результатов измерений от теоретической модели
являются независимыми и имеют случайный (не систематический!) характер.

Пусть P⁢(Δ⁢yi) — вероятность обнаружить отклонение Δ⁢yi
при фиксированных {xi}, погрешностях {σi} и параметрах модели θ.
Построим функцию, равную вероятности обнаружить
весь набор отклонений {Δ⁢y1,…,Δ⁢yn}. Ввиду независимости
измерений она равна произведению вероятностей:

Функцию L называют функцией правдоподобия.

Метод максимума правдоподобия заключается в поиске такого θ,
при котором наблюдаемое отклонение от модели будет иметь
наибольшую вероятность, то есть

Замечание. Поскольку с суммой работать удобнее, чем с произведениями, чаще
используют не саму функцию L, а её логарифм:

ln⁡L=∑iln⁡P⁢(Δ⁢yi).

Пусть теперь ошибки измерений имеют нормальное распределение
(напомним, что согласно центральной предельной теореме нормальное распределение
применимо, если отклонения возникают из-за большого
числа независимых факторов, что на практике реализуется довольно часто).
Согласно (2.5), вероятность обнаружить в i-м измерении
отклонение Δ⁢yi пропорциональна величине

где σi — стандартная ошибка измерения величины yi. Тогда
логарифм функции правдоподобия (3.2) будет равен (с точностью до константы)

ln⁡L=-∑iΔ⁢yi22⁢σi2=-12⁢χ2.

Таким образом, максимум правдоподобия действительно будет соответствовать
минимуму χ2.

3.3 Метод наименьших квадратов (МНК).

Рассмотрим случай, когда все погрешности измерений одинаковы,
σi=const. Тогда множитель 1/σ2 в сумме χ2
выносится за скобки, и оценка параметра сводится к нахождению минимума суммы
квадратов отклонений:

S⁢(θ)=∑i=1n(yi-f⁢(xi|θ))2→min.

(3.3)

Оценка по методу наименьших квадратов (МНК) удобна в том случае,
когда не известны погрешности отдельных измерений. Однако тот факт, что
метод МНК игнорирует информацию о погрешностях, является и его основным
недостатком. В частности, это не позволяет определить точность оценки
(например, погрешности коэффициентов прямой σk и
σb) без привлечения дополнительных предположений
(см. п. 3.6.2 и 3.6.3).

3.4 Проверка качества аппроксимации

Значение суммы χ2 позволяет оценить, насколько хорошо данные описываются
предлагаемой моделью y=f⁢(x|θ).

Предположим, что распределение ошибок при измерениях нормальное.
Тогда можно ожидать, что большая часть отклонений данных от модели будет
порядка одной среднеквадратичной ошибки: Δ⁢yi∼σi.
Следовательно, сумма хи-квадрат (3.1) окажется по порядку
величины равна числу входящих в неё слагаемых: χ2∼n.

Замечание. Точнее, если функция f⁢(x|θ1,…,θp)
содержит p подгоночных параметров
(например, p=2 для линейной зависимости f⁢(x)=k⁢x+b),
то при заданных θ лишь n-p слагаемых в сумме хи-квадрат будут независимы.
Иными словами, когда параметры θ определены
из условия минимума хи-квадрат, сумму χ2 можно рассматривать как функцию
n-p переменных. Величину n-p называют числом степеней свободы задачи.

В теории вероятностей доказывается (см. [4] или [5]),
что ожидаемое среднее значение (математическое ожидание) суммы χ2
в точности равно числу степеней свободы:

Таким образом, при хорошем соответствии модели и данных,
величина χ2/(n-p) должна в среднем быть равна единице.
Значения существенно большие (2 и выше) свидетельствуют либо о
плохом соответствии теории и результатов измерений,
либо о заниженных погрешностях.
Значения меньше 0,5 как правило свидетельствуют о завышенных погрешностях.

Замечание. Чтобы дать строгий количественный критерий, с какой долей вероятности
гипотезу y=f⁢(x) можно считать подтверждённой или опровергнутой,
нужно знать вероятностный закон, которому подчиняется функция χ2.
Если ошибки измерений распределены нормально, величина хи-квадрат подчинятся
одноимённому распределению (с n-p степенями свободы).
В элементарных функциях распределение хи-квадрат не выражается,
но может быть легко найдено численно: функция встроена во все основные
статистические пакеты, либо может быть вычислена по таблицам.

3.5 Оценка погрешности параметров

Важным свойством метода хи-квадрат является «встроенная» возможность
нахождения погрешности вычисленных параметров σθ.

Пусть функция L⁢(θ) имеет максимум при θ=θ^, то есть
θ^ — решение задачи о максимуме правдоподобия. Согласно центральной предельной теореме мы ожидаем, что функция правдоподобия будем близка к нормальному распределению: L⁢(θ)∝exp⁡(-(θ-θ^)22⁢σθ2),
где σθ — искомая погрешность параметра. Тогда в окрестности θ^ функция χ2⁢(θ)=-2⁢ln⁡(L⁢(θ)) имеет вид параболы:

Легко убедиться, что:

Иными словами, при отклонении параметра θ на одну ошибку σθ от значения
θ^,
минимизирующего χ2, функция χ2⁢(θ) изменится на единицу. Таким образом для нахождения интервальной оценки для искомого параметра достаточно графическим или численным образом решить уравнение

Вероятностное содержание этого интервала будет равно 68% (его еще называют 1–σ интервалом).
Отклонение χ2 на 2 будет соответствовать уже 95% доверительному интервалу.

Замечание.
Приведенное решение просто использовать только в случае одного параметра. Впрочем, все приведенные рассуждения верны и в много-параметрическом случае. Просто решением уравнения 3.4 будет не отрезок, а некоторая многомерная фигура (эллипс в двумерном случае и гипер-эллипс при больших размерностях пространства параметров). Вероятностное содержание области, ограниченной такой фигурой будет уже не равно 68%, но может быть вычислено по соответствующим таблицам. Подробнее о многомерном случае в разделе 5.5.

3.6 Методы построения наилучшей прямой

Применим перечисленные выше методы к задаче о построении наилучшей прямой
y=k⁢x+b по экспериментальным точкам {xi,yi}.
Линейность функции позволяет записать решение в относительно
простом аналитическом виде.

Обозначим расстояние от i-й экспериментальной точки до искомой прямой,
измеренное по вертикали, как

и найдём такие параметры {k,b}, чтобы «совокупное» отклонение
результатов от линейной зависимости было в некотором смысле минимально.

3.6.1 Метод наименьших квадратов

Пусть сумма квадратов расстояний от точек до прямой минимальна:

S⁢(k,b)=∑i=1n(yi-(k⁢xi+b))2→min.

(3.5)

Данный метод построения наилучшей прямой называют методом наименьших
квадратов (МНК).

Рассмотрим сперва более простой частный случай, когда искомая прямая
заведомо проходит через «ноль», то есть b=0 и y=k⁢x.
Необходимое условие минимума функции S⁢(k), как известно,
есть равенство нулю её производной. Дифференцируя сумму (3.5)
по k, считая все величины {xi,yi} константами,
найдём

d⁢Sd⁢k=-∑i=1n2⁢xi⁢(yi-k⁢xi)=0.

Решая относительно k, находим

Поделив числитель и знаменатель на n, этот результат можно записать
более компактно:

Напомним, что угловые скобки означают усреднение по всем экспериментальным точкам:

В общем случае при b≠0 функция S⁢(k,b) должна иметь
минимум как по k, так и по b. Поэтому имеем систему из двух
уравнений ∂⁡S/∂⁡k=0, ∂⁡S/∂⁡b=0,
решая которую, можно получить (получите самостоятельно):

k=⟨x⁢y⟩-⟨x⟩⁢⟨y⟩⟨x2⟩-⟨x⟩2,b=⟨y⟩-k⁢⟨x⟩.

(3.7)

Эти соотношения и есть решение задачи о построении наилучшей прямой
методом наименьших квадратов.

Замечание. Совсем кратко формулу (3.7) можно записать, если ввести обозначение

Dx⁢y≡⟨x⁢y⟩-⟨x⟩⁢⟨y⟩=⟨x-⟨x⟩⟩⋅⟨y-⟨y⟩⟩.

(3.8)

В математической статистике величину Dx⁢y называют ковариацией.
При x≡y имеем дисперсию
Dx⁢x=⟨(x-⟨x⟩)2⟩.
Тогда

k=Dx⁢yDx⁢x,b=⟨y⟩-k⁢⟨x⟩.

(3.9)

3.6.2 Погрешность МНК в линейной модели

Погрешности σk и σb коэффициентов, вычисленных
по формуле (3.7) (или (3.6)), можно оценить в
следующих предположениях.
Пусть погрешность измерений величины x пренебрежимо мала: σx≈0,
а погрешности по y одинаковы для всех экспериментальных точек
σy=const, независимы и имеют случайный характер
(систематическая погрешность отсутствует).

Пользуясь в этих предположениях формулами для погрешностей косвенных
измерений (см. раздел (2.6)) можно получить следующие
соотношения:

σk=1n-2⁢(Dy⁢yDx⁢x-k2),

(3.10)

где использованы введённые выше сокращённые обозначения (3.8).
Коэффициент n-2 отражает число независимых <<степеней
свободы>>: n экспериментальных точек за вычетом двух
условий связи (3.7).

В частном случае y=k⁢x:

σk=1n-1⁢(⟨y2⟩⟨x2⟩-k2).

(3.12)

3.6.3 Недостатки и условия применимости МНК

Формулы (3.7) (или (3.6)) позволяют провести
прямую по любому набору экспериментальных данных, а полученные
выше соотношения — вычислить
соответствующую среднеквадратичную ошибку для её коэффициентов. Однако
далеко не всегда результат будет иметь физический смысл. Перечислим
ограничения применимости данного метода.

В первую очередь метод наименьших квадратов — статистический,
и поэтому он предполагает использование достаточно большого количества
экспериментальных точек (желательно n>10).

Поскольку метод предполагает наличие погрешностей только по y,
оси следует выбирать так, чтобы погрешность σx откладываемой
по оси абсцисс величины была минимальна.

Кроме того, метод предполагает, что все погрешности в опыте —
случайны. Соответственно, формулы (3.10)–(3.12)
применимы только для оценки случайной составляющей ошибки k
или b. Если в опыте предполагаются достаточно большие систематические
ошибки, они должны быть оценены отдельно. Отметим, что для
оценки систематических ошибок не существует строгих математических
методов, поэтому в таком случае проще и разумнее всего воспользоваться
графическим методом.

Одна из основных проблем, связанных с определением погрешностей методом
наименьших квадратов заключается в том, что он дает разумные погрешности даже в
том случае, когда данные вообще не соответствуют модели.
Если погрешности измерений известны, предпочтительно использовать
метод минимума χ2.

Наконец, стоит предостеречь от использования любых аналитических
методов «вслепую», без построения графиков. В частности, МНК не способен
выявить такие «аномалии», как отклонения от линейной зависимости,
немонотонность, случайные всплески и т.п. Все эти случаи требуют особого
рассмотрения и могут быть легко обнаружены визуально при построении графика.

3.6.4 Метод хи-квадрат построения прямой

Пусть справедливы те же предположения, что и для метода наименьших квадратов,
но погрешности σi экспериментальных точек различны. Метод
минимума хи-квадрат сводится к минимизации суммы квадратов отклонений,
где каждое слагаемое взято с весом wi=1/σi2:

χ2⁢(k,b)=∑i=1nwi⁢(yi-(k⁢xi+b))2→min.

Этот метод также называют взвешенным методом наименьших квадратов.

Определим взвешенное среднее от
некоторого набора значений {xi} как

где W=∑iwi — нормировочная константа.

Повторяя процедуру, использованную при выводе (3.7), нетрудно
получить (получите) совершенно аналогичные формулы для искомых коэффициентов:

k=⟨x⁢y⟩′-⟨x⟩′⁢⟨y⟩′⟨x2⟩′-⟨x⟩′⁣2,b=⟨y⟩′-k⁢⟨x⟩′,

(3.13)

с тем отличием от (3.7), что под угловыми скобками
⟨…⟩′
теперь надо понимать усреднение с весами wi=1/σi2.

Записанные формулы позволяют вычислить коэффициенты прямой,
если известны погрешности σyi. Значения σyi
могут быть получены либо из некоторой теории, либо измерены непосредственно
(многократным повторением измерений при каждом xi), либо оценены из
каких-то дополнительных соображений (например, как инструментальная погрешность).

Источник

История[править | править код]

Суть метода наименьших квадратов[править | править код]

Пример — система линейных уравнений[править | править код]

МНК в регрессионном анализе (аппроксимация данных)[править | править код]

МНК в случае линейной регрессии[править | править код]

Простейшие частные случаи[править | править код]

Случай полиномиальной модели[править | править код]

Статистические свойства МНК-оценок[править | править код]

Обобщённый МНК[править | править код]

Взвешенный МНК[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Метод наименьших квадратов: формулы, код и применение

Триада

Математическая модель

Первое описание математической модели. Самое общее.

Второе описание математической модели. Общее описание линейной модели.

Третье описание математической модели. Модель конкретизирована под условия примера.

Обсуждение моделей

Алгоритмы и реализующие их программы

Обсуждение алгоритмов

Ещё один пример. Анализируем остатки.

Обсуждение алгоритма

Заключение

В чем именно заключается МНК (метод наименьших квадратов)

Как вывести формулы для вычисления коэффициентов

Как изобразить МНК на графике функций

Доказательство метода МНК

Метод наименьших квадратов (мнк).

Суть метода наименьших квадратов (мнк).

Вывод формул для нахождения коэффициентов.

Оценка погрешности метода наименьших квадратов.

Графическая иллюстрация метода наименьших квадратов (мнк).

3.1 Метод минимума хи-квадрат

3.2 Метод максимального правдоподобия.

3.3 Метод наименьших квадратов (МНК).

3.4 Проверка качества аппроксимации

3.5 Оценка погрешности параметров

3.6 Методы построения наилучшей прямой

3.6.1 Метод наименьших квадратов

3.6.2 Погрешность МНК в линейной модели

3.6.3 Недостатки и условия применимости МНК

3.6.4 Метод хи-квадрат построения прямой

Вам также может понравиться

Как найти величину ускорения автомобиля

Как исправить ошибку yandex

Как решить найти значение выражения по математике

Добавить комментарий Отменить ответ