Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций. Частный случай разложения в ряд Тейлора в нулевой точке называется рядом Маклорена.
Ряд Тейлора был известен задолго до публикаций Брука Тейлора[1] — его использовали ещё в XIV веке в Индии[2], а также в XVII веке Грегори и Ньютон.
Ряды Тейлора применяются при аппроксимации функции многочленами.
В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Обобщением понятия ряда Тейлора в функциональном анализе является ряд Фантапье.
Определение[править | править код]
1. Многочленом Тейлора функции 



,
используемая в приближённых вычислениях, как обобщение следствия теоремы Лагранжа о среднем значении дифференцируемой функции:
- при
верно
.
При записи суммы использованы обозначение 


2. Рядом Тейлора в точке 



с общим членом
, зависящим от параметра
.
Другими словами, рядом Тейлора функции 


.[3]
Как указано ниже в примерах, наличия бесконечной дифференцируемости функции 


3. Рядом Тейлора в точке 


удовлетворяющей в некоторой окрестности 

называется степенной ряд
.
В отличие от вещественного случая, из условий следует, что найдётся такое значение радиуса 


4. В случае 
называется рядом Маклорена.
Аналитическая функция[править | править код]
1. Функция 








то есть 


Функция называется аналитической на промежутке (на множестве), если она является аналитической в каждой точке этого промежутка (множества).
2. Степенной ряд 


Если в 



Таким образом, для аналитической в точке 




Следствие. Функция 




3. Вопрос: будет ли для произвольной бесконечно дифференцируемой в точке 






Ответ: нет.
Существуют бесконечно дифференцируемые функции вещественной переменной, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности

Примеры. Функции вещественной переменной 

являются бесконечно дифференцируемыми в точке 
Следовательно, ряды Тейлора всех этих функций с параметром 
Однако, для любого 


в которых функции отличны от 
Таким образом, эти функции не являются в точке 
Доказательство
Доказательство проведём для функции 
Функция 
для всех 
Для 

Функция 



дополненная пределами слева
и справа 

Найдём производную функции 

По определению:

Поскольку для 

то
докажем, что для произвольного 

Применение правила Лопиталя непосредственно к частям
не приводит к результату.
Выполним замену переменной: 

Пусть 
Применяя правило Лопиталя 




.
Таким образом,
.
Найдём (для 
производных функции 
И так далее. Во всех случаях, очевидно,
получается произведение
на сумму целых отрицательных степеней

Конечная сумма
бесконечно малых является бесконечно малой.
Таким образом,

Вычисляя последовательно по определению (как выше) производные 

обнаруживаем, что все производные в
точке 
Область сходимости ряда Тейлора[править | править код]
Ряд Тейлора, являясь степенным рядом, имеет в качестве области сходимости круг (с центром в точке 
и интервал (с центром в точке 
1. Например, функция 





2. Радиус сходимости ряда Тейлора можно определить, например, по формуле Даламбера:
.
3. Рассмотрим для примера экспоненциальную функцию 



4. От параметра — точки разложения 
Например, разложим в общем случае (для произвольного 


Можно доказать с помощью формулы суммы геометрической прогрессии, что данный ряд, как функция аргумента 


Действительно,
.
Область сходимости ряда может быть задана неравенством 





Формула Тейлора[править | править код]
Предположим, что функция 









Достаточно легко доказать, что такой многочлен имеет вид 








Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
Различные формы остаточного члена[править | править код]
В форме Лагранжа:
В форме Коши:
В интегральной форме:
Ослабим предположения:
- В асимптотической форме (форме Пеано, локальной форме):
Критерий аналитичности функции[править | править код]
Основной источник: [5]
Предположим, что некоторую функцию 



Во-первых, необходимым условием аналитичности функции является сходимость ряда Тейлора в некоторой непрерывной области. Действительно, если ряд Тейлора сходится всего в одной точке, то это точка 

Во-вторых, по формуле Тейлора в ряд Тейлора с остаточным членом может быть разложена любая (а не только аналитическая) функция, бесконечно дифференцируемая в окрестности, содержащей точку 





Очевидно, что функция 






В качестве примера рассмотрим экспоненциальную функцию 



Остаточный член разложения этой функции в форме Лагранжа имеет вид 



Здесь используется, что на фиксированном промежутке экспонента ограничена некоторым числом 
Причем, как видно, предел остаточного члена равен нулю для любых 

Ряды Маклорена некоторых функций[править | править код]
- Гиперболические функции[6][10]:
- Обратные гиперболические функции[6][11]:
Формула Тейлора для функции двух переменных[править | править код]
Пусть функция 


Введём дифференциальный оператор
.
Тогда разложение (формула Тейлора) функции 



где 
Следует иметь в виду, что операторы 
в 



Аналогичным образом формула строится для функций любого числа переменных, меняется только число слагаемых в операторе 
В случае функции одной переменной 
Формула Тейлора многих переменных[править | править код]
Для получения формулы Тейлора функции 



Тогда разложение (формула Тейлора) функции по степеням 

где 

Для функции 


В другой форме ряд Тейлора можно записать таким образом:

Пример разложения в ряд Маклорена функции трёх переменных[править | править код]
Найдём выражение для разложения в ряд Тейлора функции трёх переменных 




Разложение в ряд Тейлора запишется в виде
Учитывая, что
получим
Например, при 
Примечания[править | править код]
- ↑ Taylor, Brook, Methodus Incrementorum Directa et Inversa [Direct and Reverse Methods of Incrementation] (London, 1715), pages 21-23 (Proposition VII, Theorem 3, Corollary 2). Translated into English in D. J. Struik, A Source Book in Mathematics 1200—1800 (Cambridge, Massachusetts: Harvard University Press, 1969), pages 329—332.
- ↑ Gupta R. C. The Madhava-Gregory series, Math. Education 7 (1973), B67-B70.
- ↑ Запорожец Г. И. «Руководство к решению задач по математическому анализу» — С. 371
- ↑ Н.С. Пискунов. Дифференциальное и интегральное исчисления. — Мифрил, 1996. — С. Том 1, глава 4, параграф 6.
- ↑ Н.С. Пискунов. Дифференциальное и интегральное исчисления для втузов. — тринадцатое. — МОСКВА “НАУКА”, 1985. — С. Том 2, глава 16, параграф 16.
- ↑ 1 2 3 4 5 6 Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. — 4-е изд. — М.: Наука, 1963.
- ↑ Цукер Р. Тригонометрические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 37—43. — 832 с. — 50 000 экз.
- ↑ Цукер Р. Обратные тригонометрические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 44—47. — 832 с. — 50 000 экз.
- ↑ При значении x, близком к 1, эта расчётная формула сходится медленно, т.е. даёт большую погрешность при приближении функции суммой первых нескольких членов ряда. Поэтому можно воспользоваться формулой
где
- ↑ Цукер Р. Гиперболические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 48—49. — 832 с. — 50 000 экз.
- ↑ Цукер Р. Обратные гиперболические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 50—53. — 832 с. — 50 000 экз.
Литература[править | править код]
- Ильин В. А., Садовничий В. А., Сендов Б. Х. Математический анализ, ч. 1, изд. 3, ред. А. Н. Тихонов. М.: Проспект, 2004.
- Камынин Л. И. Математический анализ. Т. 1, 2. — 2001.
- Киселёв В. Ю., Пяртли А. С., Калугина Т. Ф. Высшая математика. Первый семестр, Интерактивный компьютерный учебник.
- Маркушевич А. И. Теория аналитических функций. В 2 т. — Изд. 2-е. — М.: Наука, 1967. — Т. 1: Начала теории. — 486 с.
- Нарасимхан Р. Анализ на действительных и комплексных многообразиях. — пер. с англ. Е. М. Чирки. — М.: Мир, 1971. — 232 с.
- Петрова С. С., Романовска Д. А. К истории открытия ряда Тэйлора. // Историко-математические исследования. — М.: Наука, 1980. — № 25. — С. 10—24.
- Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов. В 2 т. — Изд. 13-е. — М.: Наука, Главная редакция физико-математической литературы, 1985. — Т. 1. — 432 с.
- Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов. В 2 т. — Изд. 13-е. — М.: Наука, Главная редакция физико-математической литературы, 1985. — Т. 2. — 560 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. В 3 т. — Изд. 8-е. — М.: ФИЗМАТЛИТ, 2003. — Т. I. — 680 с. — ISBN ISBN 5-9221-0156-0.
Разложение в ряд Тейлора
Если функция f(x) имеет на некотором интервале, содержащем точку а, производные всех порядков, то к ней может быть применена формула Тейлора:
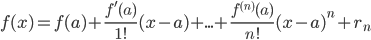 ,
,
где rn – так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа:
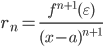 , где число x заключено между х и а.
, где число x заключено между х и а.
- Решение онлайн
- Видеоинструкция
Если для некоторого значения х rn→0 при n→∞, то в пределе формула Тейлора превращается для этого значения в сходящийся ряд Тейлора:
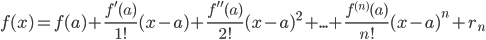
Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х, если:
- она имеет производные всех порядков;
- построенный ряд сходится в этой точке.
При а=0 получаем ряд, называемый рядом Маклорена:
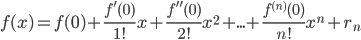
Разложение простейших (элементарных) функций в ряд Маклорена:
Пример №1. Разложить в степенной ряд функцию f(x)=2x.
Решение. Найдем значения функции и ее производных при х=0
f(x) = 2x, f(0) = 20=1;
f'(x) = 2xln2, f'(0) = 20 ln2= ln2;
f”(x) = 2x ln22, f”(0) = 20 ln22= ln22;
…
f(n)(x) = 2x lnn2, f(n)(0) = 20 lnn2= lnn2.
Подставляя полученные значения производных в формулу ряда Тейлора, получим:

Радиус сходимости этого ряда равен бесконечности, поэтому данное разложение справедливо для -∞<x<+∞.
Пример №2. Написать ряд Тейлора по степеням (х+4) для функции f(x)=ex.
Решение. Находим производные функции ex и их значения в точке х=-4.
f(x) = еx, f(-4) = е-4;
f'(x) = еx, f'(-4) = е-4;
f”(x) = еx, f”(-4) = е-4;
…
f(n)(x) = еx, f(n)( -4) = е-4.
Следовательно, искомый ряд Тейлора функции имеет вид:

Данное разложение также справедливо для -∞<x<+∞.
Пример №3. Разложить функцию f(x)=lnx в ряд по степеням (х-1),
( т.е. в ряд Тейлора в окрестности точки х=1).
Решение. Находим производные данной функции.
f(x)=lnx,  ,
,  ,
,  ,
, 

f(1)=ln1=0, f'(1)=1, f”(1)=-1, f”'(1)=1*2,…, f(n)=(-1)n-1(n-1)!
Подставляя эти значения в формулу, получим искомый ряд Тейлора:

С помощью признака Даламбера можно убедиться, что ряд сходится при ½х-1½<1. Действительно,

Ряд сходится, если ½х-1½<1, т.е. при 0<x<2. При х=2 получаем знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. При х=0 функция не определена. Таким образом, областью сходимости ряда Тейлора является полуоткрытый промежуток (0;2].
Пример №4. Разложить в степенной ряд функцию  .
.
Решение. В разложении (1) заменяем х на -х2, получаем:
 , -∞<x<∞
, -∞<x<∞
Пример №5. Разложить в ряд Маклорена функцию  .
.
Решение. Имеем 
Пользуясь формулой (4), можем записать:

подставляя вместо х в формулу –х, получим:

Отсюда находим: ln(1+x)-ln(1-x) =  –
– 
Раскрывая скобки, переставляя члены ряда и делая приведение подобных слагаемых, получим
 . Этот ряд сходится в интервале (-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.
. Этот ряд сходится в интервале (-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.
Замечание.
Формулами (1)-(5) можно пользоваться и для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням (х-а). Для этого над заданной функцией необходимо произвести такие тождественные преобразования, чтобы получить одну из функций (1)-(5), в которой вместо х стоит k(х-а)m, где k – постоянное число, m – целое положительное число. Часто при этом удобно сделать замену переменной t=х-а и раскладывать полученную функцию относительно t в ряд Маклорена.
Этот метод основан на теореме о единственности разложения функции в степенной ряд. Сущность этой теоремы состоит в том, что в окрестности одной и той же точки не может быть получено два различных степенных ряда, которые бы сходились к одной и той же функции, каким бы способом ее разложение ни производилось.
Пример №5а. Разложить в ряд Маклорена функцию  , указать область сходимости.
, указать область сходимости.
Решение. Сначала найдем 1-x-6x2=(1-3x)(1+2x), далее разложим дробь с помощью сервиса.
 на элементарные:
на элементарные: 
Дробь 3/(1-3x) можно рассматривать как сумму бесконечно убывающей геометрической прогрессии знаменателем 3x, если |3x| < 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд

с областью сходимости |x| < 1/3.
Пример №6. Разложить функцию  в ряд Тейлора в окрестности точки х=3.
в ряд Тейлора в окрестности точки х=3.
Решение. Эту задачу можно решить, как и раньше, с помощью определения ряда Тейлора, для чего нужно найти производные функции и их значения при х=3. Однако проще будет воспользоваться имеющимся разложением (5):
 =
= 
Полученный ряд сходится при  или –3<x-3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.
или –3<x-3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.
Пример №7. Написать ряд Тейлора по степеням (х-1) функции ln(x+2).
Решение.


Ряд сходится при  , или -2 < x < 5.
, или -2 < x < 5.
Пример №8. Разложить функцию f(x)=sin(πx/4) в ряд Тейлора в окрестности точки x=2.
Решение. Сделаем замену t=х-2:

Воспользовавшись разложением (3), в котором на место х подставим π/4t, получим:

Полученный ряд сходится к заданной функции при -∞<π/4t<+∞, т.е. при (-∞<x<+∞).
Таким образом,
 , (-∞<x<+∞)
, (-∞<x<+∞)
Приближенные вычисления с помощью степенных рядов
Степенные ряды широко используются в приближенных вычислениях. С их помощью с заданной точностью можно вычислять значения корней, тригонометрических функций, логарифмов чисел, определенных интегралов. Ряды применяются также при интегрировании дифференциальных уравнений.
Рассмотрим разложение функции в степенной ряд:

Для того, чтобы вычислить приближенное значение функции в заданной точке х, принадлежащей области сходимости указанного ряда, в ее разложении оставляют первые n членов (n – конечное число), а остальные слагаемые отбрасывают:

Для оценки погрешности полученного приближенного значения необходимо оценить отброшенный остаток rn(x). Для этого применяют следующие приемы:
- если полученный ряд является знакочередующимся, то используется следующее свойство: для знакочередующегося ряда, удовлетворяющего условиям Лейбница, остаток ряда по абсолютной величине не превосходит первого отброшенного члена.
- если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией.
- в общем случае для оценки остатка ряда Тейлора можно воспользоваться формулой Лагранжа: a<c<x (или x<c<a).
Пример №1. Вычислить ln(3) с точностью до 0,01.
Решение. Воспользуемся разложением  , где x=1/2 (см. пример 5 в предыдущей теме):
, где x=1/2 (см. пример 5 в предыдущей теме):

Проверим, можем ли мы отбросить остаток после первых трех членов разложения, для этого оценим его с помощью суммы бесконечно убывающей геометрической прогрессии:

Таким образом, мы можем отбросить этот остаток и получаем 
Пример №2. Вычислить  с точностью до 0,0001.
с точностью до 0,0001.
Решение. Воспользуемся биномиальным рядом. Так как 53 является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=53+5.



так как уже четвертый член полученного знакочередующегося ряда, удовлетворяющего признаку Лейбница, меньше требуемой точности:
 , поэтому его и следующие за ним члены можно отбросить.
, поэтому его и следующие за ним члены можно отбросить.
Многие практически нужные определенные или несобственные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, ибо ее применение связано с нахождением первообразной, часто не имеющей выражения в элементарных функциях. Бывает также, что нахождение первообразной возможно, но излишне трудоемко. Однако если подынтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью.
Пример №3. Вычислить интеграл ∫014sin(x)x с точностью до 10-5.
Решение. Соответствующий неопределенный интеграл  не может быть выражен в элементарных функциях, т.е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.
не может быть выражен в элементарных функциях, т.е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.
Разделив почленно ряд для sinx на x , получим:

Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем:


Так как полученный ряд удовлетворяет условиям Лейбница и  достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью.
достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью.
Таким образом, находим

Пример №4. Вычислить интеграл ∫014ex2 с точностью до 0,001.
Решение.

![]()
Проверим, можем ли мы отбросить остаток после второго члена полученного ряда.
 ≈0.0001<0.001
≈0.0001<0.001
Следовательно,  .
.
Формула Тейлора
5 разделов
от теории до практики
12 примеров
Примеры решения задач
видео
Примеры решения задач
-
Формула Тейлора с остаточным членом в форме Лагранжа.
Начать изучение
-
Формула Тейлора с остаточным членом в форме Пеано.
Начать изучение
-
Разложение основных элементарных функций по формуле Тейлора.
Начать изучение
-
Показательная функция.
Начать изучение
-
Гиперболические функции.
Начать изучение
-
Тригонометрические функции.
Начать изучение
-
Степенная функция.
Начать изучение
-
Логарифмическая функция.
Начать изучение
-
Примеры разложения функций по формулам Тейлора и Маклорена.
Начать изучение
-
Вычисление пределов с помощью формулы Тейлора.
Начать изучение
Формула Тейлора с остаточным членом в форме Лагранжа.
Лемма 1.
Если функция f(x) имеет в точке x_{0} производную n-го порядка, то существует многочлен P_{n}(x) степени не выше n такой, что tag{1} P_n(x_0)=f(x_{0}), P_{n}^{(k)}(x_{0})=f^{(k)}(x_{0}), k=overline{1,n}.
Этот многочлен представляется в виде tag{2}P_n(x)=f(x_{0})+frac{f'(x_{0})}{1!}(x-x_0)+frac{f″(x)}{2!}(x-x_0)^2+ldots+frac{f^{(n)}(x_0)}{n!}(x-x_0)^n.
Доказательство.
circ Пусть varphi(x)=(x-x_0)^m, где minmathbb{N}. Тогда varphi(x_0)=0,
tag{3}varphi^{(k)}(x_{0})=left{begin{array}{ll} 0, & если kneq m,\ k!, & если k=m.end{array}right. Из (3) следует, что многочлен P_n(x), заданный формулой (2), удовлетворяет условиям (1). Этот многочлен называют многочленом Тейлора n-го порядка для функции f(x) в точке x_{0}. bullet
Лемма 2.
Пусть функции f(x) и psi(x) определены в delta-окрестности точки x_0 и удовлетворяют следующим условиям:
- для каждого xin U_{delta}(x_0) существуют varphi^{(n+1)}(x) и psi^{(n+1)};
- tag{4}begin{array}{cc}varphi(x_0)=varphi'(x_0)=ldots=varphi^{(n)}(x_0)=0,\ psi(x_0)=psi'(x_0)=ldots=psi^{(n)}(x_0)=0;end{array}
- psi(x)neq 0, psi^{(k)}(x)neq 0 для xindot{U}_{delta}(x_{0}) и для k=overline{1,n+1}.
Тогда для каждого xindot{U}_{delta}(x_{0}) существует точка xi, принадлежащая интервалу с концами x_0 и x такая, что tag{5}frac{varphi(x)}{psi(x)}=frac{varphi^{(n+1)}(xi)}{psi^{(n+1)}(xi)}.
Доказательство.
circ Пусть, например, xin(x_0,x_0+delta). Тогда, применяя к функциям varphi и psi на отрезке [x_0,x] теорему Коши и учитывая, что varphi(x_0)=psi(x_0)=0 в силу условий (4), получаем tag{6}frac{varphi(x)}{psi(x)}=frac{varphi(x)-varphi(x_0)}{psi(x)-psi(x_0)}=frac{varphi'(xi_1)}{psi'(xi_1)}quad x_0 < xi_1 < x.
Аналогично, применяя к функциям varphi’ и psi’ на отрезке [x_{0},xi_{1}] теорему Коши, находим tag{7}frac{varphi'(xi_1)}{psi'(xi_1)}=frac{varphi'(xi_1)-varphi'(x_0)}{psi'(xi_1)-psi'(x_0)}=frac{varphi″(xi_2)}{psi'(xi_2)}quad x_0 < xi_1 < xi_2.
Из равенств (6) и (7) следует, что
frac{varphi(x)}{psi(x)}=frac{varphi'(xi_1)}{psi'(xi_1)}=frac{varphi″(xi_2)}{psi″(xi_2)},quad x_0 < xi_2 < xi_1 < x < x_0+delta.
Применяя теорему Коши последовательно к функциям varphi″ и psi″, varphi^{(3)} и psi^{(3)},ldots,varphi^{(n)} и psi^{(n)} на соответствующих отрезках, получаем
frac{varphi(x)}{psi(x)}=frac{varphi'(xi_1)}{psi'(xi_1)}=ldots=frac{varphi^{(n)}(xi_n)}{psi^{(n)}(xi_n)}=frac{varphi^{(n+1)}(xi)}{psi^{(n+1)}(xi)},
где x_0 < xi < xi_{n} < ldots < xi_{1} < x < x_0+delta.
Равенство (5) доказано для случая, когда xin(x_0,x_0+delta). Аналогично рассматривается случай, когда xin(x_0-delta,x_0). bullet
Теорема 1.
Пусть существует delta >0 такое, что функция f(x) имеет в delta-окрестности точки x_0 производные до (n+1)-го порядка включительно.
Тогда для любого xindot{U}_delta(x_0) найдется точка xi, принадлежащая интервалу Delta с концами x_{0} и x, такая, что
tag{8}f(x)=f(x_0)+frac{f'(x_{0})}{1!}(x-x_0)+ldots+frac{f^{(n)}(x_{0})}{n!}(x-x_0)^n+frac{f^{(n+1)}(xi)}{(n+1)!}(x-x_{0})^{n+1}.
Доказательство.
circ Пусть xindot{U}_delta(x_0), P_n(x)=displaystylesum_{k=0}^{n}frac{f^{(k)}(x_{0})}{k!}(x-x_0)^k — многочлен Тейлора для функции f(x). Обозначим
tag{9}r_{n}(x)=f(x)-P_n(x).
Так как многочлен P_{n}(x) удовлетворяет в силу леммы 1 условиям (1), то из равенства (9) следует, что
tag{10}r_n(x_0)=r_n'(x_0)=ldots=r_{n}^{(n)}(x_{0})=0.
Рассмотрим функции varphi(x)=r_n(x), psi(x)=(x-x_0)^{n+1}. Эти функции удовлетворяют условиям леммы 2, и поэтому для них выполняется равенство (5), то есть
tag{11}frac{varphi(x)}{psi(x)}=frac{r_n(x)}{(x-x_0)^{n+1}}=frac{r_n^{(n+1)}(xi)}{(n+1)!}=frac{f^{(n+1)}(xi)}{(n+1)!},quadxiinDelta,
так как P_n^{(n+1)}(x)equiv 0, psi^{(n+1)}(x)=(n+1)! Из равенств (11) и (9) следует формула (8). bullet
Замечание 1.
Функцию r_n(x)=displaystyle frac{f^{(n+1)}(xi)}{(n+1)!}(x-x_0)^{n+1} называют остаточным членом формулы Тейлора в форме Лагранжа. Формула (8) справедлива и при x=x_{0}.
Следствие.
Если функции varphi и psi дифференцируемы n раз при xgeq x_{0} и удовлетворяют условиям varphi^{(k)}(x_{0})=psi^{(k)}(x_{0}), k=overline{0,n-1}, varphi^{(n)}(x)>psi^{(n)}(x) при x > x_0, то varphi(x) > psi(x) при x > x_{0}.
circ Для n=1 утверждение доказано ранее (следствие 4 из теоремы Лагранжа). Обозначим f(x)=varphi(x)-psi(x). Тогда f^{(k)}(x_{0})=0 при k=overline{0,n-1}0, и по формуле (8) получаем f(x)=frac{1}{n!}(x-x_{0})^{n}f^{(n)}(xi).
Если x> x_{0}, то xi > x_0, f^{(n)}(xi)=varphi^{(n)}(xi)-psi^{(n)}(xi) > 0, и поэтому f(x) > 0, то есть varphi(x) > psi(x) при x > x_{0}. bullet
Пример 1.
Доказать, что:
- |sin t-t|leqdisplaystylefrac{t^2}{2} для tinmathbb{R};
- tag{12}x-frac{x^{3}}{3!} < sin x < x-frac{x^{3}}{3!}+frac{x^5}{5!} при x > 0.
Решение.
- triangle Применяя формулу (8) при n=2 и x_0=0 к функции f(t)=sin t, получаем sin t=t-displaystylefrac{sin{xi}}{2!}t^2, откуда следует, что |displaystyle sin t-t|leqfrac{t^{2}}{2},;tinmathbb{R}.
- Если f(x)=sin x, то f(0)=f^{(2)}(0)=f^{(4)}(0)=0, f'(0)=1, f^{(3)}(0)=-1, f^{(n)}(x)=(sin x)^{(n)}=displaystylesinleft(x+nfrac{pi}{2}right). Применяя формулу (8) при n=5, x_0=0, получаем sin x=x-frac{x^{3}}{3!}+frac{x^{5}}{5!}sin(xi+5frac{pi}{2}),откуда следует правое неравенство (12), так как, очевидно, left|displaystylefrac{x^{5}}{5!}sinleft(xi+5frac{pi}{2}right)right|leqdisplaystylefrac{x^{5}}{5!} при x >0. Используя формулу (8) для f(x)=sin x при n=3, x_0=0, докажем левое неравенство (12). blacktriangle
Формула Тейлора с остаточным членом в форме Пеано.
Теорема 2.
Если существует f^{(n)}(x_0), то tag{13}f(x)=sum_{k=0}^{n}frac{f^{(k)}(x_{0})}{k!}(x-x_{0})^{k}+o((x-x_{0})^{n}),qquad xrightarrow x_{0}.
Доказательство.
Из существования f^{(n)}(x_0) следует, что функция f(x) определена и имеет производные до (n-1)-го порядка включительно в delta-окрестности точки x_0. Обозначим varphi(x)=r_n(x), psi(x)=(x-x_0)^n, где функция r_n(x) определяется формулой (9). Функции varphi(x) и psi(x) удовлетворяют условиям леммы 2, если заменить номер n+1 на номер n-1 (см. равенства (10)). Используя лемму 2 и учитывая, что r_n^{(n-1)}(x_0)=0, получаем tag{14}frac{r_n(x)}{(x-x_0)^n}=frac{r_n^{(n-1)}(xi)-r_n^{n-1}(x_0)}{n!(xi-x_{0})}, где xi=xi(x) и tag{15}x_0 < xi < x < x_0+delta quad или quad x_0-delta < x < xi < x_0.
Пусть xrightarrow x_0, тогда из неравенств (15) следует, что xirightarrow
x_0, и в силу существования f^{(n)}(x_0) существует displaystylelim_{xrightarrow x_{0}}frac{r_n^{(n-1)}(x)-r_n^{(n-1)}(x_0)}{x-x_0}=displaystyle lim_{xrightarrow x_{0}}frac{r_n^{(n-1)}(xi)-r_n^{(n-1)}(x_0)}{xi-x_0}=r_n^{(n)}(x_0)=0, так как выполняются равенства (10). Таким образом, правая часть формулы (14) имеет при xrightarrow x_0 предел, равный нулю, а поэтому существует предел левой части этой формулы, также равный нулю. Это означает, что r_n(x)=o((x-x_0)^n), xrightarrow x_0, или f(x)-P_n(x)=o((x-x_0)^n), откуда следует равенство (13). bullet
Замечание 2.
Формулу (13) часто называют формулой Тейлора с остаточным членом в форме Пеано или
локальной формулой Тейлора.
Разложить функцию f(x) по формуле Тейлора в окрестности точки x_0 до o((x-x_0)^n) — значит представить ее в виде (13).
Теорема 3.
Если существует f^{(n)}(x_0) и если при xrightarrow x_0 tag{16}f(x)=a_0+a_1(x-x_0)+ldots+a_n(x-x_0)^n+o((x-x_0)^n), то tag{17}a_{k}=frac{f^{(k)}(x_0)}{k!},;k=overline{0,n}.
Доказательство.
circ По теореме 2 справедлива формула (13), и так как по условию выполняется равенство (16), то
tag{18}a_0+a_1(x-x_0)+ldots+a_n(x-x_0)^n+o((x-x_0)^n)=\=f(x_{0})+f'(x_{0})(x-x_0)+ldots+f^{(n)}(x_{0})frac{(x-x_{0})^{n}}{n!}+o((x-x_0)^n).
Переходя к пределу при xrightarrow x_{0} в равенстве (18), получаем a_{0}=f(x_{0}). Отбросив в левой и правой частях этого равенства одинаковые слагаемые a_{0} и f(x_{0}) и разделив обе части полученного равенства на x-x_0, имеем a_1+a_2(x-x_0)+ldots+a_n(x-x_0)^{n-1}+o((x-x_0)^{n-1})=\=f'(x_0)+frac{f″(x_{0})}{2!}(x-x_0)+ldots+frac{f^{(n)}(x_{0})}{n!}(x-x_0)^{n-1}+o((x-x_0)^{n-1}).
Переходя в этом равенстве к пределу при xrightarrow x_0, находим f'(x_{0})=a_{1}. Продолжая эти рассуждения, получаем равенства (17).bullet
Замечание 3.
Теорема 3 означает, что представление в виде (16) функции, имеющей в точке x_{0} производную n-го порядка, единственно: коэффициенты разложения (16) выражаются по формулам (17).
Пример 2.
Разложить функцию displaystyle frac{1}{1-x} по формуле Тейлора в окрестности точки x_{0}=0 до o(x^{n}).
Решение.
triangle Воспользуемся равенством (1+x+ldots+x^{n})(1-x)=1-x^{n+1}, откуда displaystyle frac{1}{1-x}=1+x+ldots+x^n+r_n(x), где r_n(x)=displaystylefrac{x^{n+1}}{1-x}=o(x^{n}) при xrightarrow 0. Таким образом,
tag{19}frac{1}{1-x}=1+x+ldots+x^n+o(x^n).
Так как функция displaystyle frac{1}{1-x} бесконечно дифференцируема при xneq 1 (имеет производные любого порядка), то по теореме 3 формула (19) дает искомое разложение. blacktriangle
Разложение основных элементарных функций по формуле Тейлора.
Если x_{0}=0 и существует f^{(n)}(0), то равенство (13) принимает вид
tag{20}f(x)=sum_{k=0}^{n}frac{f^{(k)}}{k!}x^k+o(x^n), xrightarrow 0.
Формулу (20) называют формулой Маклорена.
Замечание 4.
Пусть, функция f(x) бесконечно дифференцируема на интервале (-l,l). Если эта функция является четной, то ее производная — нечетная функция, и, наоборот, производная нечетной функции — четная функция (мы уже разбирали этот пример). Отсюда следует, что для нечетной функции f выполняются условия f^{(2k)}(0)=0, kinmathbb{N}, а для четной функции f — условия f^{(2k-1)}(0)=0, kinmathbb{N}, так как любая непрерывная нечетная функция принимает при x=0 значение нуль.
Поэтому формулу (20) для бесконечно дифференцируемой четной функции можно записать в виде tag{21}f(x)=sum_{k=0}^{n}frac{f^{(2k)}(0)}{(2k)!}x^{2k}+o(x^{2n+2}),quad xrightarrow 0, а для нечетной функции — в виде tag{22}f(x)=sum_{k=0}^{n}frac{f^{(2k+1)}(0)}{(2k+1)!}x^{2k+1}+o(x^{2n+2}),quad xrightarrow 0.
В формуле (21) остаточный член записан в виде o(x^{(2n+1)}), а не в виде o(x^{2n}), так как для четной функции f выполняется условие f^{(2n+1)}(0)=0, и поэтому член многочлена Тейлора, который следует за слагаемым displaystylefrac{f^{(2n)}(0)}{(2n)!}x^{2n} равен нулю. Аналогично рассматривается вопрос о записи остаточного члена формулы (22).
Показательная функция.
Если f(x)=e^x, то f(0)=1 и f^{(n)}(0)=1 при любом n. Поэтому формула (20) для функции e^{x} записывается в виде
tag{23}e^{x}=1+x+frac{x^{2}}{2!}+frac{x^{3}}{3!}+ldots+frac{x^{n}}{n!}+o(x^{n}), xrightarrow 0, или e^{x}=sum_{k=0}^{n}frac{x^{k}}{k!}+o(x^{n}), xrightarrow 0.
Гиперболические функции.
Так как f(x)=sh x — нечетная функция, f^{(2k+1)}(x)=ch x, f^{(2k+1)}(0)=1 при k=0,1,2,ldots, то по формуле (22) получаем
tag{24}sh x=x+frac{x^{3}}{3!}+frac{x^5}{5!}+ldots+frac{x^{2n+1}}{(2n+1)!}+o(x^{2n+2}), xrightarrow 0, или sh x=sum_{k=0}^{n}frac{x^{2k+1}}{(2k+1)!}+o(x^{2n+2}), xrightarrow 0.
Аналогично по формуле (21) находим tag{25}ch x=1+frac{x^{2}}{2!}+frac{x^{4}}{4!}+ldots+frac{x^{2n}}{(2n)!}+o(x^{2n+1}), xrightarrow 0,
или ch x=sum_{k=0}^{n}frac{x^{2k}}{(2k)!}+o(x^{2n+1}), xrightarrow 0.
Замечание 5.
Так как sh x=displaystyle frac{e^{x}-e^{-x}}{2}, ch x=displaystyle frac{e^{x}+e^{-x}}{2}, то формулы (24) и (25) можно получить, используя равенство (23) и равенство e^{-x}=displaystylesum_{k=0}^{n}frac{(-1)^{k}x^{k}}{k!}+o(x^{n}), xrightarrow 0.
Тригонометрические функции.
Функция f(x)=sin x является нечетной, f^{(2n+1)}(x)=sin left(x+displaystyle frac{pi}{2}(2n+1)right), откуда f^{(2n+1)}(0)=sinleft(frac{pi}{2}+pi nright)=cospi n= (-1)^n.
Поэтому по формуле (22) находим tag{26} sin x=x-frac{x^{3}}{3!}+frac{x^{5}}{5!}+ldots+(-1)^nfrac{x^{2n+1}}{(2n+1)!}+o(x^{2n+2}), xrightarrow 0,
или
sin x=sum_{k=0}^{n}(-1)^{k}frac{x^{2k+1}}{(2k+1)!}+o(x^{2n+2}),;xrightarrow 0.
Аналогично, f(x)=cos x — четная функция, f^{(2n)}(0)=displaystylecosleft(frac{pi}{2}2nright)=(-1)^{n}, и по формуле (21) получаем tag{27}cos x=1-frac{x^{2}}{2!}+frac{x^{4}}{4!}+ldots+(-1)^nfrac{x^{2n}}{(2n)!}+o(x^{2n+1}),;xrightarrow 0, или cos x=sum_{k=0}^{n}(-1)^{k}frac{x^{2k}}{(2k)!}+o(x^{2n+1}), xrightarrow 0.
Степенная функция.
Пусть f(x)=(1+x)^{alpha}, где alphainmathbb{R}. Тогда f^{(k)}(x)=alpha(alpha-1)ldots(alpha-(k-1))(1+x)^{alpha-k}, откуда получаем f^{(k)}(0)=alpha(alpha-1)ldots(alpha-(k-1)). Обозначим tag{28} C_{alpha}^0=1, C_{alpha}^k=frac{alpha(alpha-1)ldots(alpha-(k-1))}{k!}, kinmathbb{N}
Тогда по формуле (20) получим tag{29}(1+x)^{alpha}=sum_{k=0}^{n}C_{alpha}^{k}x^k+o(x^n), xrightarrow 0.
Отметим важные частные случаи формулы (29).
tag{30}frac{1}{1-x}=1+x+x^2+ldots+x^n+o(x^n), xrightarrow 0,
или frac{1}{1-x}=sum_{k=0}^{n}x^k+o(x^n), xrightarrow 0.
Напомним, что формула (30) была получена другим способом (пример 2).
tag{31}frac{1}{1+x}=1-x+x^{2}+ldots+(-1)^{n}x^n+o(x^n), xrightarrow 0,
или frac{1}{1+x}=sum_{k=0}^{n}(-1)^{k}x^k+o(x^n), xrightarrow 0.
Логарифмическая функция.
Если f(x)=ln (1+x), то f(0)=0,
f^{(k)}(x)=frac{(-1)^{k-1}(k-1)!}{(1+x)^{k}}, f^{(k)}(0)=(-1)^{k-1}(k-1)!,
и по формуле (20) находим tag{32}ln (1+x)=x-frac{x^{2}}{2}+frac{x^{3}}{3}+ldots+frac{(-1)^{n-1}}{n}x^{n}+o(x^{n}), xrightarrow 0,
или ln(1+x)=sum_{k=1}^nfrac{(-1)^{k-1}x^{k}}{k}+o(x^n), xrightarrow 0.
Заменяя в формуле (32) x на -x получаем tag{33}ln (1-x)=-x-frac{x^{2}}{2}-frac{x^{3}}{3}-ldots-frac{x^{n}}{n}+o(x^n), xrightarrow 0,
или ln (1-x)=-sum_{k=1}^nfrac{x^{k}}{k}+o(x^n), xrightarrow 0.
Примеры разложения функций по формулам Тейлора и Маклорена.
Пример 3.
Разложить по формуле Тейлора в окрестности точки x_0=0 до o(x^n) функцию f(x), если:
- f(x)=displaystyle frac{1}{sqrt{1+x}};
- f(x)=displaystyle frac{1}{3x+2};
- f(x)=displaystyle lnfrac{x-5}{x-4};
- f(x)=(x+3)e^{-2x}.
Решение.
- triangle Применяя формулу (29) при alpha=-displaystylefrac{1}{2}, получаем frac{1}{sqrt{1+x}}=sum_{k=0}^{n}C_{-1/2}^{k}x^k+o(x^n), xrightarrow 0,
где C_{-1/2}^{k}=frac{displaystyleleft(-frac{1}{2}right)left(-frac{1}{2}-1right)ldotsleft(-frac{1}{2}-(k-1)right)}{k!}=frac{(-1)^{k}1cdot 3ldots(2k-1)}{2^{k}k!}.Обозначим (2k-1)!!=1cdot 3ldots(2k-1), тогда tag{34}frac{1}{sqrt{1+x}}=1+sum_{k=1}^{n}frac{(-1)^{k}(2k-1)!!}{2^{k}k!}x^k+o(x^n), xrightarrow 0.
Из формулы (34) при n=3 находим tag{35}frac{1}{sqrt{1+x}}=1-frac{1}{2}x+frac{3}{8}x^2-frac{5}{16}x^3+o(x^3), xrightarrow 0. - Так как displaystylefrac{1}{3x+2}=frac{1}{2left(1+displaystylefrac{3}{2}xright)}, то, применяя формулу (31), получаем frac{1}{3x+2}=sum_{k=0}^{n}(-1)^{k}frac{3^{k}}{2^{k+1}}x^{k}+o(x^{n}), xrightarrow 0.
- Используя равенство displaystyleoperatorname{ln}frac{x-5}{x-4}=displaystyleoperatorname{ln}frac{5}{4}+operatorname{ln}frac{1-displaystylefrac{x}{5}}{1-displaystylefrac{x}{4}} и формулу (33), находим ln frac{x-5}{x-4}=lnfrac{5}{4}+sum_{k=1}^{n}frac{x^{k}}{k}left(frac{1}{4^{k}}-frac{1}{5^{k}}right)+o(x^{n}),;xrightarrow 0.
- Так как f(x)=xe^{-2x}+3e^{-2x}, то, применяя формулу (23), получаем f(x)=xleft(displaystylesum_{k=0}^{n-1}frac{(-1)^{k}2^{k}}{k!}x^{k}+o(x^{n-1})right)+3sum_{k=0}^{n}frac{(-1)^{k}2^{k}}{k!}x^{k}+o(x^{n}), x rightarrow 0,
или
f(x)=3+sum_{k=1}^{n}frac{(-1)^{k-1}2^{k-1}}{(k-1)!}x^k+sum_{k=1}^{n}frac{3(-1)^{k}2^{k}}{k!}x^k+o(x^n), xrightarrow 0,
то есть
f(x)=3+sum_{k=1}^{n}frac{(-1)^{k-1}2^{k-1}}{k!}(k-6)x^{k}+o(x^{n}), xrightarrow 0.quadblacktriangle
Пример 4.
Разложить по формуле Маклорена до o(x^{2n+1}) функцию f(x)=cos^{4}x.
Решение.
triangle Используя равенство cos^{2}x=displaystyle frac{1+cos 2x}{2}, получаем cos^{4}x=frac{1}{4}left(1+2cos{2x}+displaystyle frac{1+cos 4x}{2}right)=frac{3}{8}+frac{1}{2}cos{2x}+ displaystylefrac{1}{8}cos4x, откуда по формуле (27) находим
cos^{4}x=1+sum_{k=1}^{n}frac{(-1)^{k}2^{2k-1}}{(2k)!}(1+2^{2k-2})x^{2k}+o(x^{2n+1}), xrightarrow 0. blacktriangle
Замечание 6.
Если существует f^{(n+1)})(0) и известно разложение функции f'(x)=sum_{k=0}^{n}b_kx^k+o(x^n),
где b_k=displaystylefrac{f^{(k+1)(0)}}{k!}, то f(x)=f(0)+sum_{k=1}^{n+1}frac{f^{(k)}(0)}{k!}x^k+o(x^{n+1})=f(0)+sum_{k=0}^{n}frac{f^{(k+1)}(0)}{(k+1)k!}x^{k+1}+o(x^{n+1}), xrightarrow 0, то есть f(x)=f(0)+sum_{k=0}^{n}frac{b_{k}}{k+1}x^{k+1}+o(x^{n+1}), xrightarrow 0.
Пример 5.
Разложить по формуле Маклорена до o(x^{2n+1}) функции:
- operatorname{arctg}x;
- operatorname{arcsin}x;
- ln (1+sqrt{1+x^2}).
Решение.
- triangle Так как (operatorname{arctg}x)’=frac{1}{1+x^2}, то, используя формулу (31) и замечание 6, получаем frac{1}{1+x^{2}}=sum_{k=0}^{n}(-1)^k{x^{2k}}+o(x^{2n+1}), xrightarrow 0,
откуда
tag{36}operatorname{arctg}x=sum_{k=0}^{n}(-1)^{k}frac{x^{2k+1}}{2k+1}+o(x^{2n+2}), xrightarrow 0.
Из формулы (36) при n=2 находим
tag{37}operatorname{arctg}x=x-frac{x^3}{3}+frac{x^5}{5}+o(x^6).;xrightarrow 0. - Используя замечание 6, равенство (34) и формулу (operatorname{arcsin}x)’=displaystyle frac{1}{sqrt{1-x^{2}}}, получаем frac{1}{sqrt{1-x^{2}}}=1+sum_{k=1}^{n}displaystylefrac{(2k-1)!!}{2^{k}k!}x^{2k}+o(x^{2n+1}), xrightarrow 0,
откуда tag{38}operatorname{arcsin}x=x+sum_{k=1}^{n}displaystylefrac{(2k-1)!!}{2^{k}k!(2k+1)}x^{2k+1}+o(x^{2n+2}), xrightarrow 0.
Из формулы (38) при n=2 находим
tag{39}operatorname{arcsin}x=x+frac{1}{6}x^{3}+frac{3}{40}x^5+o(x^6), xrightarrow 0. - Так как (ln (1+sqrt{1+x^2}))’=frac{1}{sqrt{1+x^{2}}}, то, используя замечание 6 и разложение (34), получаем frac{1}{sqrt{1+x^{2}}}=1+sum_{k=1}^{n}frac{(-1)^{k}(2k-1)!!}{2^{k}k!}x^{2k}+o(x^{2n+1}), xrightarrow 0,
откуда tag{40}ln (1+sqrt{1+x^2})=x+sum_{k=1}^{n}frac{(-1)^{k}(2k-1)!!}{2^{k}k!(2k+1)}x^{2k+1}+o(x^{2n+2}), xrightarrow 0.Из формулы (40) при n=2 находим
tag{41}ln (1+sqrt{1+x^2})=x-frac{x^{3}}{6}+frac{3}{40}x^5+o(x^6), xrightarrow 0. blacktriangle
Пример 6.
Разложить по формуле Маклорена до o(x^6) функции:
- operatorname{tg}x;
- operatorname{th}x.
Решение.
- triangle Функция operatorname{tg}x является нечетной, и поэтому operatorname{tg}x=a_1x+a_3x^3+a_5x^5+o(x^6), xrightarrow 0, где a_1=1, так как operatorname{tg}xsim x при xrightarrow 0. Используя равенство sin x=cos xoperatorname{tg}x и разложения (26), (27), получаем
x-frac{x^3}{3!}+frac{x^5}{5!}+o(x^6)=(x+a_3x^3+a_5x^5+o(x^6))left(1-displaystylefrac{x^{2}}{2!}+frac{x^{4}}{4!}+o(x^5)right).
Приравнивая коэффициенты при x^3 и x^5, находим -displaystylefrac{1}{6}=-frac{1}{2}+a_{3}, displaystylefrac{1}{5!}=frac{1}{4!}-frac{a_{3}}{2!}+a_{5}, откуда a_3=displaystylefrac{1}{3}, a_{5}=displaystyle frac{2}{15}, и поэтому tag{42}operatorname{tg}x=x+displaystyle frac{x^{3}}{3}+displaystyle frac{2}{15}x^5+o(x^6), xrightarrow 0. - Так как operatorname{th}x — нечетная функция, то operatorname{th}x=a_1x+a_3x^3+a_5x^5+o(x^6), где a_{1}=1 (operatorname{th}xsim x при xrightarrow x). Применяя формулу sh x=ch xth x и используя разложения (24), (25), получаем x+frac{x^{3}}{3!}+frac{x^5}{5!}+o(x^{6})=(x+a_{3}x^{3}+a_{5}x^{5}+o(x^{6}))left(1+frac{x^{2}}{2!}+frac{x^{4}}{4!}+o(x^{5})right),
откуда, сравнивая коэффициенты при x^3 и x^5, находим a_{3}=-displaystyle frac{1}{3},;a_{5}=displaystyle frac{2}{15}. Следовательно,
tag{43}operatorname{th}x=x-frac{x^{3}}{3}+frac{2}{15}x^{5}+o(x^{6}). blacktriangle
Замечание 7.
Прием, использованный для нахождения разложений (42) и (43), называют методом неопределенных коэффициентов.
Замечание 8.
Разложение функции f(x) по формуле Тейлора (16) заменой x-x_{0}=t обычно сводится к разложению функции g(t)=f(x_0+t) по формуле Маклорена (20).
Пример 7.
Разложить по формуле Тейлора в окрестности точки x_0=-2 до o((x+2)^{n}) функцию f(x)=displaystyle frac{1}{x^{2}+5x}.
Решение.
triangle Так как f(x)=displaystylefrac{1}{5}left(frac{1}{x}-frac{1}{x+5}right), то, полагая x=t-2, получаем f(x)=g(t)=displaystylefrac{1}{5}left(frac{1}{t-2}-frac{1}{t+3}right)=frac{1}{5}left(-frac{1}{2left(1-frac{t}{2}right)}-frac{1}{3left(1+frac{t}{3}right)}right).
Применяя формулы (30) и (31), находим
g(t)=sum_{k=0}^{n}left(frac{(-1)^{k+1}}{5cdot 3^{k+1}}-frac{1}{5cdot 2^{k+1}}right)t^{k}+o(t^{n}), trightarrow 0, откуда f(x)=sum_{k=0}^{n}left(frac{(-1)^{k+1}}{5cdot 3^{k+1}}-frac{1}{5cdot 2^{k+1}}right)(x+2)^{k}+o((x+2)^n), xrightarrow-2.quadblacktriangle
Вычисление пределов с помощью формулы Тейлора.
Рассмотрим предел при xrightarrow 0 отношения displaystyle frac{f(x)}{g(x)}, где katex]f(0)=g(0)=0[/katex], то есть предел типа frac{0}{0}.
Будем предполагать, что f(0)=f'(0)=ldots=f^{(n-1)}(0)=0, f^{(n)}(0)neq 0.
Тогда разложение функции f по формуле Маклорена (20) имеет вид tag{44}f(x)=ax^n+o(x^n), xrightarrow 0, где aneq 0.
Аналогично, предполагая, что
g(0)=g'(0)=ldots=g^{(m-1)}(0)=0, g^{(m)}(0)neq 0.
по формуле (20) находим
tag{45}g(x)=bx^m+o(x^m), xrightarrow 0, где bneq 0.
Из равенств (44) и (45) следует, что
frac{f(x)}{g(x)}=frac{ax^n+o(x^n)}{bx^m+o(x^m)}, xrightarrow 0.
Если m=n, то displaystylelim_{xrightarrow 0}frac{f(x)}{g(x)}=displaystylefrac{a}{b}. В случае, когда n > m, получаем displaystylelim_{xrightarrow 0}frac{f(x)}{g(x)}=0; если же n < m, то displaystylelim_{xrightarrow 0}frac{f(x)}{g(x)}=infty.
Пример 8.
Найти displaystyle lim_{xrightarrow 0}frac{operatorname{tg}x-displaystylefrac{x}{1+x^2}}{sin x-sh x}.
Решение.
triangle Используя формулы (24), (26), (31) и (42),
получаем operatorname{tg}x-frac{x}{1+x^{2}}=x+frac{x^{3}}{3}-x(1-x^2)+o(x^3)=frac{4}{3}x^3+o(x^3),
sin x-operatorname{sh}x=x-frac{x^{3}}{6}-left(x+frac{x^{3}}{6}right)+o(x^{3})=-frac{x^{3}}{3}+o(x^{3}).
Следовательно, искомый предел равен -4. blacktriangle
Пример 9.
Найти displaystyle lim_{xrightarrow 0}frac{e(1+x)^{-1/x}-1}{x}.
Решение.
triangle Воспользуемся равенством (1+x)^{-1}/{x}=e^{-(1/x)operatorname{ln}(1+x)}. По формуле (32) получаем -displaystyle frac{1}{x}operatorname{ln}(1+x)=-1+displaystyle frac{x}{2}+o(x). Используя формулу (23), находим e(1+x)^{-1/x}-1=ecdot e^{-1+x/2+o(x)}-1=е^{x/2+o(x)}-1=frac{x}{2}+o(x).
Поэтому искомый предел равен displaystyle frac{1}{2}. blacktriangle
Пример 10.
Найти
lim_{xrightarrow 0}frac{ln(x+sqrt{1+x^{2}})+displaystylefrac{1}{sqrt{1+2x}}-ch(sqrt{3}x)}{th x-xcos x}.
Решение.
triangle Пусть f(x) и g(x) — соответственно числитель и знаменатель дроби. Тогда, используя формулы (43) и (27), получаем
g(x)=x-frac{x^{3}}{3}+o(x^4)-xleft(1-frac{x^{2}}{2}+o(x^3)right)=frac{x^{3}}{6}+o(x^4).
Поэтому числитель f(x) следует разложить до o(x^3). Применяя формулы (41), (35) и (25), находим
f(x)=x-frac{x^{3}}{6}+o(x^3)+left(1-x+frac{3}{2}x^2-frac{5}{2}x^3+o(x^3)right)-\-left(1+frac{3}{2}x^2+o(x^3)right)=-frac{16}{6}x^3+o(x^3).
Следовательно, искомый предел равен -16. blacktriangle
Локальная формула Тейлора часто используется при вычислении предела при xrightarrow x_0 функции (1+f(x))^{g(x)}, где f(x)rightarrow 0 и g(x)rightarrow infty при xrightarrow x_0. Если x_0=0 и разложение функции f по формуле Маклорена имеет вид (44), а функция g(x) представляется при xrightarrow 0 в виде g(x)=frac{1}{bx^n+o(x^n)},;где;bneq 0, ninmathbb{N},
то, используя формулу 16 (см.здесь), получаем
tag{46}lim_{xrightarrow 0}(1+f(x))^{g(x)}=lim_{xrightarrow 0}left(1+ax^n+o(x^n)right)^{1/(bx^n+o(x^n))}=e^{a/b}.
Пример 11.
Найти displaystyle lim_{xrightarrow 0}(e^{operatorname{tg}x}+operatorname{ln}(1-x))^{1/(arcsin{operatorname{sh}x}-x)}.
Решение.
triangle Используя формулы (39) и (24), получаем
arcsinoperatorname{sh}x-x=arcsinleft(x+frac{x^{3}}{6}+o(x^{4})right)-x=\=x+frac{x^{3}}{6}+frac{x^{3}}{6}+o(x^3)-x=frac{x^{3}}{3}+o(x^3).
Аналогично, разложив функции e^x,;operatorname{tg}x,operatorname{ln}(1-x) по формуле Маклорена до o(x^3), находим
e^{operatorname{tg}x}+operatorname{ln}(1-x)=e^{x+x^{3}/3+o(x^4)}-x-frac{x^{2}}{2}-frac{x^{3}}{3}+o(x^3)=\=1+x+frac{x^{3}}{3}+frac{x^{2}}{2}+frac{x^{3}}{6}+o(x^{3})-x-frac{x^{2}}{2}-frac{x^{3}}{3}+o(x^{3})=1+frac{x^{3}}{6}+o(x^3).
По формуле (46) находим, что искомый предел равен e^{1/2}. blacktriangle
При вычислении предела с помощью формулы Тейлора в конечной точке x_0neq 0 можем положить t=x-x_0 и свести задачу к вычислению предела при t=0.
Неопределенности видов displaystylefrac{infty}{infty}, 0cdotinfty, infty-infty обычно приводят к пределу типа displaystyle frac{0}{0}.
Пример 12.
Найти displaystyle lim_{xrightarrow +infty}x(sqrt{x^2+2x}-2sqrt{x^2+x}+x).
Решение.
triangle Обозначим f(x)=x(sqrt{x^{2}+2x}-2sqrt{x^{2}+x}+x), тогда f(x)=x^2left(displaystylesqrt{1+frac{2}{x}}-2sqrt{1+frac{1}{x}}+1right). Полагая displaystyle frac{1}{x}=t, получаем f(x)=g(t)=displaystylefrac{1}{t^{2}}(sqrt{1+2t}-2sqrt{1+t}+1). Используя формулу (29) при alpha=displaystyle frac{1}{2}, n=2, получаем
sqrt{1+t}=1+frac{1}{2}t-frac{1}{8}t^2+o(t^2),quad trightarrow 0.
Следовательно,
g(t)=frac{1}{t^{2}}left(1+t-frac{1}{2}t^{2}-2left(1+frac{1}{2}t-frac{1}{8}t^{2}right)+o(t^{2})+1right)=\=frac{1}{t^{2}}left(-frac{1}{4}t^{2}+o(t^{2})right),;trightarrow 0,
откуда находим, что искомый предел равен -displaystyle frac{1}{4}. blacktriangle
Let us solve #y”+y=0# by Power Series Method.
Let #y=sum_{n=0}^inftyc_nx^n#, where #c_n# is to be determined.
By taking derivatives,
#y’=sum_{n=1}^inftync_nx^{n-1} Rightarrow y”=sum_{n=2}^inftyn(n-1)c_nx^{n-2}#
We can rewrite #y”+y=0# as
#sum_{n=2}^inftyn(n-1)c_nx^{n-2}+sum_{n=0}^inftyc_nx^n=0#
by shifting the indices of the first summation by 2,
#Rightarrow sum_{n=0}^infty(n+2)(n+1)c_{n+2}x^n+sum_{n=0}^inftyc_nx^n=0#
by combining the summations,
#Rightarrow sum_{n=0}^infty[(n+2)(n+1)c_{n+2}+c_n]x^n=0#,
#Rightarrow (n+2)(n+1)c_{n+2}+c_n=0#
#Rightarrow c_{n+2}=-{c_n}/{(n+2)(n+1)}#
Let us look at even coefficients.
#c_2={-c_0}/{2cdot1}=-c_0/{2!}#
#c_4={-c_2}/{4cdot3}={-1}/{4cdot3}cdot{-c_0}/{2!}=c_0/{4!}#
#c_6={-c_4}/{6cdot5}={-1}/{6cdot5}cdot c_0/{4!}=-{c_0}/{6!}#
.
.
.
#c_{2n}=(-1)^n{c_0}/{(2n)!}#
Let us look at odd coefficients.
#c_3={-c_1}/{3cdot2}=-{c_1}/{3!}#
#c_5={-c_3}/{5cdot4}={-1}/{5cdot4}cdot{-c_1}/{3!}={c_1}/{5!}#
#c_7={-c_5}/{7cdot6}={-1}/{7cdot6}cdot{c_1}/{5!}=-{c_1}/{7!}#
.
.
.
#c_{2n+1}=(-1)^n{c_1}/{(2n+1)!}#
Hence, the solution can be written as:
#y=sum_{n=0}^inftyc_nx^n#
by splitting into even terms and odd terms,
#=sum_{n=0}^inftyc_{2n}x^{2n}+sum_{n=0}^inftyc_{2n+1}x^{2n+1}#
by pluggin in the formulas for #c_{2n}# and #c_{2n+1}# we found above,
#=c_0sum_{n=0}^infty(-1)^n{x^{2n}}/{(2n)!}+c_1 sum_{n=0}^infty(-1)^n{x^{2n+1}}/{(2n+1)!}#
by recognizing the power series,
#=c_0 cosx+c_1 sinx#
I hope that this was helpful.
Степенные ряды в форме рядов Тейлора и Маклорена
Степенные ряды и, в частности, ряды Тейлора являются одним из видов функциональных рядов.
Степенной ряд в общем виде записывается как:
a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n+…=∑k=0∞ak(x−x0)ka_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n+ldots=sumlimits_{k=0}^{infty} a_k(x-x_0)^k
где a0,a1,…,an,…a_0, a_1, ldots, a_n, ldots – постоянные, коэффициенты ряда,
x0x_0 – центр интервала сходимости ряда ∣x−x0∣<R|x-x_0|<R,
RR – радиус сходимости, когда для частичных сумм Sn(x)S_n(x) существует предел, сумма ряда S(x)S(x):
Sn(x)=a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n,limn→∞Sn(x)=S(x)S_n(x)= a_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n, quad limlimits_{n to infty } S_n (x) = S (x)
Возьмем функцию действительной переменной f(x)f(x), которая является бесконечно дифференцируемой в точке x0x_0. Такую функцию можно разложить в степенной ряд следующего вида:
f(x)=f(x0)+f′(x0)1!(x−x0)+f′′(x0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=∑k=0∞f(k)(x0)k!(x−x0)kf(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +dfrac{f{”}(x_0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
Этот ряд по степеням двучлена (x−x0)(x-x_0) называют рядом Тейлора.
В случае x0=0x_0=0 полученный степенной ряд:
f(x)=f(0)+f′(0)1!x+f′′(0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=∑k=0∞f(k)(x0)k!(x−x0)kf(x)=f(0)+dfrac{f{‘}( 0)}{1!} x +dfrac{f{”}(0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
называют рядом Маклорена.
Ряд Тейлора можно записать в другом виде. Полагая:
x−x0=t,f(x)=f(x0+t)=g(t)x-x_0=t, quad f(x)=f(x_0+t)=g(t)
ряд Тейлора
f(x)=f(x0+t)=f(0)+f′(x0)1!t+f′′(x0)2!t2+…+f(n)(x0)n!tn+…=∑k=0∞f(k)(x0)k!tkf(x)=f(x_0+t)=f(0)+dfrac{f{‘}(x_ 0)}{1!} t +dfrac{f{”}(x_0)}{2!}t^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}t^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}t^k
сводится к ряду Маклорена:
g(t)=g(0)+g′(0)1!t+…+g(n)(0)n!tn+…=∑k=0∞g(k)(0)k!tkg(t)=g(0)+dfrac{g{‘}( 0)}{1!}t +ldots+dfrac{g^{(n)}(0)}{n!}t^n +ldots =sumlimits_{k=0}^{infty} dfrac{g^{(k)}(0)}{k!}t^k
Как и в случае произвольного степенного ряда, ряды Тейлора и Маклорена имеют интервал сходимости.
Пример
Разложим в ряд Тейлора функцию:
f(x)=1xf(x)=dfrac{1}{x}
в окрестности точки x0=1x_0=1.
С помощью замены:
x−x0=x−1=tx-x_0=x-1=t
функция сводится к виду:
f(x)=f(t+1)=11+tf(x)=f(t+1)=dfrac {1}{1+t}
Полученное выражение при ∣t∣<1|t|<1 является суммой бесконечно убывающей геометрической прогрессии знаменателем (−t)(-t), и ряд записывается в виде:
11+t=1−t+t2−t3+…+(−1)ntn+…=∑k=0∞(−1)ktkdfrac {1}{1+t}=1-t+t^2-t^3+ldots+(-1)^{n}t^{n}+ldots =sumlimits_{k=0}^{infty} (-1)^{k}t^{k}
Возвращаясь к переменной xx, получаем разложение по степеням двучлена (x−1)(x-1):
1x=1−(x−1)+(x−1)2−(x−1)3+…+(−1)n(x−1)n+…=∑k=0∞(−1)k(x−1)k,∣x−1∣<1dfrac {1}{x}=1-(x-1)+ (x-1)^2-(x-1)^3+ldots+(-1)^{n}(x-1)^{n}+ldots =sumlimits_{k=0}^{infty} (-1)^{k}(x-1)^{k}, quad |x-1|<1
Формула Тейлора
Следствием разложения функции в степенной ряд является соответствующая формула Тейлора. Если функция f(x)f(x) имеет в точке x0x_0 производные до nn –го порядка включительно, то функцию f(x)f(x) можно представить с помощью формулы Тейлора:
f(x)=f(x0)+f′(x0)1!(x−x0)+…+f(n)(x0)n!(x−x0)n+Rn(x)f(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +R_n (x)
или
f(x)=∑k=0nf(k)(x0)k!(x−x0)k+Rn(x)f(x)= sumlimits_{k=0}^{n} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k +R_n (x),
где функция Rn(x)R_n (x) называется остаточным членом.
Формы остаточного члена
Существует несколько форм для остаточного члена. В частности, если f(x)f(x) дифференцируема (n+1)(n+1) раз в окрестности x0x_0, то Rn(x)R_n (x) может быть представлена в форме Лагранжа:
Rn(x)=f(n+1)(ξ)(n+1)!xn+1,x<ξ<x0R_n (x)=dfrac {f^{(n+1)}(xi)}{(n+1)!} x^{n+1}, quad x<xi<x_0 или x<ξ<x0x<xi<x_0.
Если функция f(x)f(x) дифференцируема (n−1)(n-1) раз в окрестности x0=0x_0=0, то Rn(x)R_n(x) может быть представлена в форме Пеано:
Rn(x)=o((x−x0)n)R_n(x)=o((x-x_0)^n).
Учитывая, что ряд Тейлора можно свести к ряду Маклорена, запишем формулу Тейлора для основных элементарных функций в окрестности x0=0x_0=0 и укажем соответствующие интервалы сходимости.
Показательная функция:
ex=1+x1!+x22!+x33!+…+xnn!+o(xn),∣x∣<∞e^x=1+dfrac{x}{1!} +dfrac{x^2}{2!} +dfrac{x^3}{3!}+ldots+dfrac{x^n}{n!}+o(x^n),quad |x|<infty
Тригонометрические функции:
sinx=x1!−x33!+x55!−x77!+…+(−1)n+1x2n−1(2n−1)!+o(x2n),∣x∣<∞sin x=dfrac{x}{1!} -dfrac{x^3}{3!} +dfrac{x^5}{5!} -dfrac{x^7}{7!} +ldots+dfrac{(-1)^{n+1}x^{2n-1}}{(2n-1)!}+ o(x^{2n}),quad |x|<infty
cosx=1−x22!+x44!−x66!+…+(−1)n+1x2n(2n)!+o(x2n+1),∣x∣<∞cos x=1 -dfrac{x^2}{2!} +dfrac{x^4}{4!} -dfrac{x^6}{6!} +ldots+dfrac{(-1)^{n+1}x^{2n}}{(2n)!}+ o(x^{2n+1}),quad |x|<infty
arctgx=x−x33+x55−x77+…+(−1)nx2n+12n+1+o(x2n+2),∣x∣≤1arctg x=x-dfrac{x^3}{3} +dfrac{x^5}{5} -dfrac{x^7}{7} +ldots+dfrac{(-1)^{n}x^{2n+1}}{2n+1}+ o(x^{2n+2}),quad |x|le{1}
Логарифмическая функция:
ln(1+x)=x1!−x22!+x33!−…+(−1)n+1xnn!+o(xn),x∈(−1;1]ln (1+x)=dfrac{x}{1!} -dfrac{x^2}{2!} +dfrac{x^3}{3!} -ldots+dfrac{(-1)^{n+1}x^{n}}{n!}+ o(x^n),quad xin (-1;1]
Степенная функция:
(1+x)α=1+α1!x+α(α−1)2!x2+α(α−1)(α−2)3!x3+…+α(α−1)…(α−n+1)n!xn+o(xn)(1+x)^alpha=1+dfrac{alpha }{1!}x+dfrac{alpha (alpha -1)}{2!}x^2 +dfrac{alpha (alpha -1)( alpha -2)}{3!} x^3 +ldots+dfrac{alpha (alpha -1) ldots ( alpha-n+1)} {n!} {x^n}+ o(x^n)
Пример 1
Разложим, используя формулу Тейлора, функцию
f(x)=(x+1)ln(x2+2x+2)f(x)=(x+1)ln (x^2+2x+2)
в окрестности точки x0=−1x_0=-1 с точностью до o((x+1)7)o((x+1)^7).
Выполнив замену переменной
x−x0=x+1=tx-x_0=x+1=t
получаем:
g(t)=tln(1+t2)g(t)=tln(1+t^2)
Используя разложение логарифмической функции, получаем:
g(t)=t(t21!−(t2)22!+(t2)33!+o((t2)3))=t3−t52+t76+o(t7)g(t)=t left( dfrac{t^2}{1!}-dfrac{(t^2)^2}{2!}+dfrac{(t^2)^3}{3!}+o((t^2)^3) right)=t^3-dfrac{t^5}{2}+dfrac{t^7}{6}+o(t^7)
Выполняем далее обратную замену переменной:
f(x)=(x+1)3−(x+1)52+(x+1)76+o((x+1)7)f(x)= (x+1)^3-dfrac{(x+1)^5}{2}+dfrac{(x+1)^7}{6}+o((x+1)^7)
Пример 2
Разложим, используя формулу Тейлора, функцию
f(x)=(x2−4x)cos(2x−4)f(x)=(x^2-4x)cos{(2x-4)}
в окрестности точки x0=2x_0=2 с точностью до o((x−5)5)o((x-5)^5).
Выполнив замену переменной:
x−x0=x−2=t,x=t+2x-x_0=x-2=t, quad x=t+2
получаем:
g(t)=(t2−4)cos2tg(t)=(t^2-4)cos{2t}
Используя разложение тригонометрической функции, получаем:
g(t)=(t2−4)(1−(2t)22!−(2t)44!+o(t5))=(t2−4)(1−2t2+2t43+o(t5))g(t) =(t^2-4) left( 1-dfrac{(2t)^2}{2!}-dfrac{(2t)^4}{4!}+o(t^5) right) =(t^2-4) left( 1-2t^2+dfrac{2t^4}{3}+o(t^5) right)
Раскрываем скобки, ограничиваясь слагаемыми со степенью t не выше пяти:
g(t)=(t2−2t4)−(4−8t2+8t43+o(t5))=−4+9t2−143t4+o(t5)g(t) =(t^2-2t^4)- left( 4-8t^2+dfrac{8t^4}{3}+o(t^5) right) =-4+9t^2-dfrac{14}{3} t^4+o(t^5)
Выполняя обратную замену переменной, получаем:
f(x)=−4+9(x−2)2−143(x−2)4+o((x−2)5)f(x)=-4+9(x-2)^2-dfrac{14}{3}(x-2)^4+o((x-2)^5)
Применение формулы Тейлора при x, стремящемся к бесконечности
При необходимости представить функцию с помощью формулы Тейлора при x→∞x to infty с точностью до o(1xn)oleft( dfrac {1} {x^n}right), последовательно:
- выполняем замену переменной t=1xt=dfrac{1}{x};
- полученную функцию g(t)g(t) представляем с помощью формулы Тейлора с необходимой точностью;
- с помощью обратной замены переменных находим искомое выражение для f(x)f(x).
Пример
Разложим, используя формулу Тейлора, функцию
f(x)=2x−x2−1f(x)=2x-sqrt{x^2-1}
с точностью до o(1×3)oleft( dfrac {1} {x^3}right) при x→+∞x to +infty.
Выполнив замену переменной
t=1x,x=1tt=dfrac{1}{x}, quad x=dfrac{1}{t}
получаем:
g(t)=2t−1t2−1=2−(1−t2)1/2tg(t)=dfrac {2}{t}-sqrt {dfrac{1}{t^2}-1}=dfrac{2-(1-t^2)^{1/2}}{t}
Учитывая требуемую точность o(t3)o(t^3), используем разложение степенной функции в ряд Тейлора с точностью до o(t4)o(t^4):
g(t)=2−(1−t22−t48)+o(t4)t=1t+t2−t38+o(t3)g(t)=dfrac {2-left( 1-dfrac{t^2}{2}-dfrac{t^4}{8}right)+o(t^4)}{t}=dfrac{1}{t}+dfrac{t}{2}-dfrac{t^3}{8}+o(t^3)
Выполняя обратную замену переменной, находим:
f(x)=x+12x−18×3+o(1×3),x→+∞f(x)=x+dfrac{1}{2x}- dfrac {1}{8x^3}+ oleft( dfrac {1} {x^3}right), quad x to +infty
Применение формула Тейлора при вычислении пределов
С помощью разложения функции с использованием формулы Тейлора при вычислении пределов можно избавиться от неопределённостями различного вида. Проиллюстрируем использование формулы Тейлора на примере вычисления предела функции с неопределенностью вида (00)left( dfrac {0} {0}right).
Пример 1
Вычислим, используя формулу Тейлора, предел:
limx→1ex−ecos(x−1)sin(x−1)limlimits_{x to 1 } dfrac {e^{x}-e cos{(x-1)}}{sin {(x-1)}}
Заменим ex{e^{x}} и тригонометрические функции их разложениями в степенные ряды в окрестности x0=1x_0=1, находим:
limx→1ex−ecos(x−1)sin(x−1)=limx→1(e+e(x−1)+e(x−1)22!+e(x−1)33!+…)−e(1−(x−1)22!+…)(x−1)−(x−1)33!+…=elimx→1(x−1)+(x−1)2+(x−1)36+…(x−1)−(x−1)36+…=elimx→11+(x−1)+(x−1)26+…1−(x−1)26+…=elimlimits_{x to 1 } dfrac {e^{x}-e cos{(x-1)}}{sin {(x-1)}}=limlimits_{x to 1} dfrac {left(e+e(x-1)+dfrac{e(x-1)^2}{2!}+dfrac{e(x-1)^3}{3!} +ldots right)-eleft( 1-dfrac{(x-1)^2}{2!}+ ldots right)} {(x-1)-dfrac{(x-1)^3}{3!}+ ldots}= elimlimits_{x to 1 } dfrac {(x-1)+(x-1)^2+ dfrac{(x-1)^3}{6}+ldots} {(x-1)- dfrac{(x-1)^3}{6}+ldots} =e limlimits_{x to 1 } dfrac {1+(x-1) +dfrac{(x-1)^2}{6}+ldots} {1- dfrac{(x-1)^2}{6}+ldots} =e






![{displaystyle R_{n}(x)={(x-a)^{n+1} over (n+1)!}f^{(n+1)}[a+theta (x-a)]qquad p=n+1;qquad 0<theta <1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a9581ea19ed64de9723d6f3725f0470e9a0f23c)
![{displaystyle R_{n}(x)={(x-a)^{n+1}(1-theta )^{n} over n!}f^{(n+1)}[a+theta (x-a)]qquad p=1;qquad 0<theta <1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/616cdc3cb043af06990a174a073b35ea0e3fbee1)

![{displaystyle R_{n}(x)=o[(x-a)^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7eca3be3644e41dedb8f25e26357ddb9a08386d)


![R_n(x,y)=dfrac {mathrm{T}^{(n+1)} f(xi,zeta)} {(n+1)!}, xi in [x_0,x], zeta in [y_0,y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/144e134c30b8d4c579305c2bbaf6591647deb6c9)











