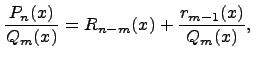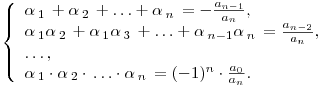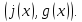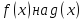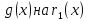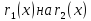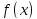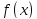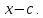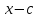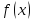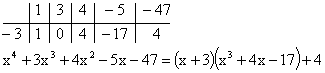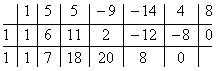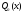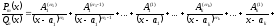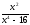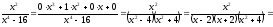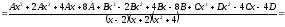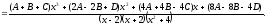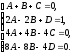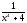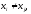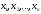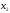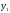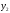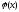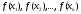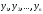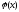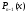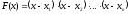Содержание:
Многочлен – это сумма одночленов, причем сам одночлен – это частный случай многочлена.
История многочелена:
Живший в 1050-1122 гг Омар Хаям известен в мире как мастер рубай. Однако имя Омара Хаяма также упоминается наряду с именами гениальных математиков. Именно Омар Хаям впервые представил общую формулу корней уравнения кубического многочлена
Многочлены от одной переменной и действия над ними
Определение многочленов от одной переменной и их тождественное равенство
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например, от переменной
По определению одночлена числа и буквы (в нашем случае одна буква — 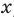
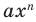
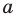
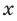
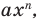
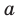
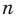
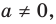
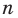
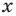
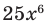
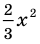
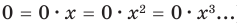
По определению многочлен от одной переменной 
многочленом от одной переменной 
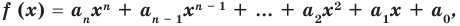
где коэффициенты 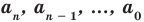
Если 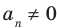
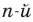
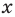
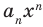
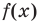
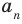
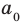
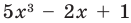
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена 
где 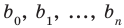
Теорема 1. Одночлены 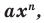
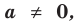
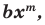
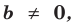
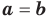
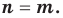
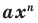
Поскольку равенство одночленов
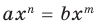
выполняется при всех значениях 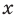
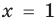
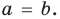
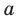
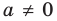
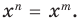
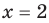
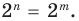
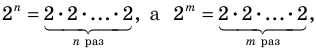
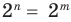
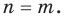
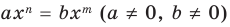
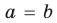
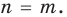
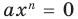
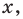
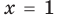
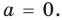
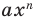
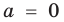
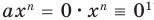
Далее любой одночлен вида 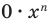
Теорема 2. Если многочлен 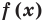
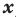
Для доказательства используем метод математической индукции. Пусть
При 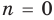
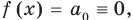
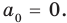
Предположим, что при 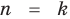
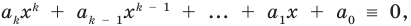
Докажем, что данное утверждение выполняется и при 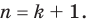
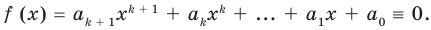
Поскольку равенство (3) выполняется при всех значениях 
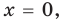

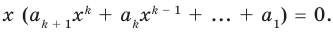
Равенство (4) должно выполняться при всех значениях 
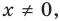
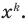
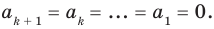
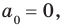
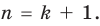
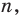
Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают 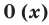
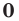
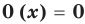
Теорема 3. Если два многочлена 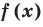
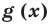
Пусть многочлен 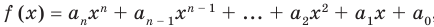
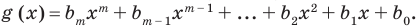
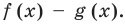
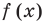
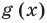
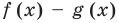
Но 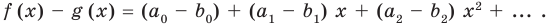
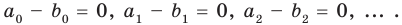
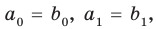
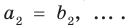
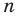
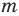
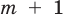
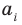
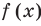
имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.
Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.
Пример:
Докажите, что выражение
является полным квадратом.
Решение:
► Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида 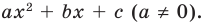
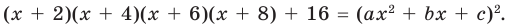
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях 
Из первого равенства получаем 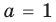
При 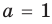
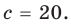
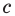
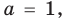
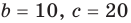
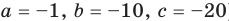
Действия над многочленами. Деление многочлена на многочлен с остатком
Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.
Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.
При сложении многочленов одной степени получаем многочлен этой же степени, хотя иногда можно получить многочлен меньшей степени. Например, 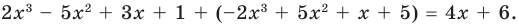
Например, 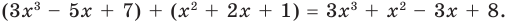
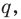
Определение: Многочлен 
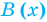
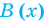

Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком. Говорят, что
многочлен 








Например, поскольку 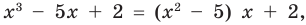
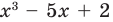
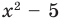
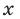
Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом.
Пример №1
Разделим многочлен 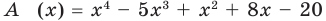
Решение:
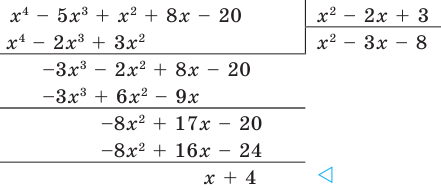
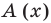
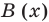
Если обозначить результат выполнения первого шага алгоритма через 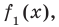
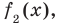
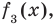
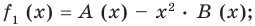
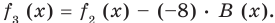
Сложим почленно равенства (1), (2), (3) и получим
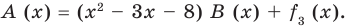
Учитывая, что степень многочлена 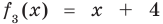
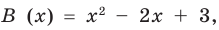
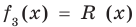
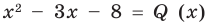
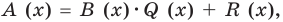
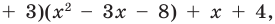
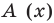
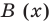
Очевидно, что приведенное обоснование можно провести для любой пары многочленов 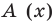
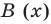
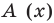
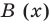
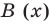
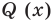
Отметим, что в случае, когда степень делимого 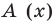
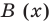
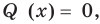
Теорема Безу. Корни многочлена. Формулы Виета
Рассмотрим деление многочлена 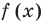
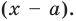
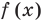
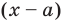
Это равенство выполняется тождественно, то есть при любом значении 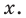
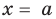
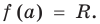
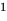
Теорема 1 (теорема Безу). Остаток от деления многочлена 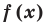
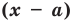
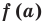
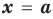
Пример №2
Докажите, что 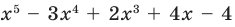
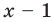
Решение:
► Подставив в 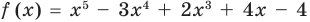
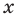
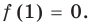
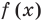

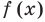

Определение: Число 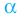
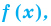
Если многочлен 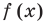

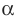
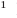
Действительно, если 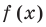
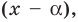

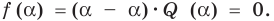
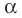
Справедливо и обратное утверждение. Оно является следствием теоремы Безу.
Теорема 2. Если число 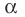
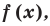
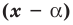
По теореме Безу остаток от деления 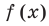

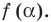
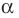
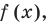
Обобщением теоремы 2 является следующее утверждение.
Теорема 3. Если многочлен 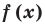
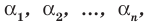
Для доказательства используем метод математической индукции.
При 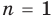
Допустим, что утверждение справедливо при 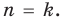
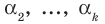
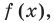
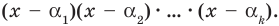
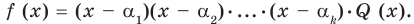
Докажем, что утверждение теоремы справедливо и при 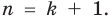
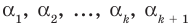
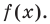
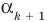
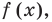
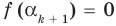
По условию все корни 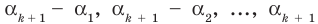
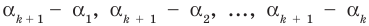
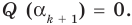
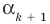
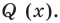
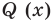
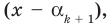
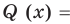
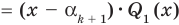
Это означает, что 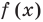
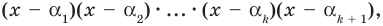
Таким образом, теорема справедлива для любого натурального
Следствие. Многочлен степени 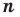
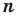
Допустим, что многочлен 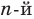
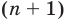
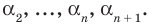
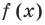
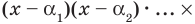
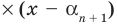
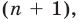
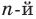
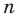
Пусть теперь многочлен 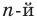
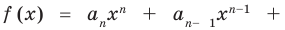
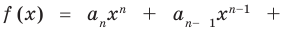
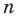
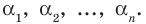
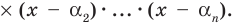
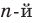
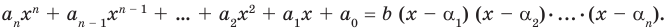
Если раскрыть скобки в правой части равенства (2) и приравнять коэффициенты при старших степенях, то получим, что 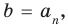
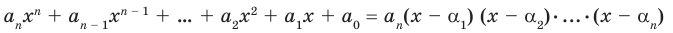
Сравнивая коэффициенты при одинаковых степенях 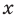
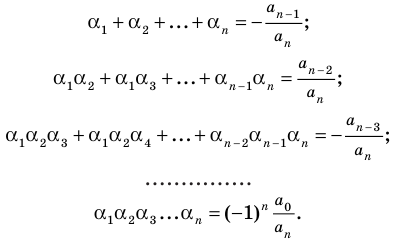
Например, при 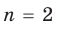
а при
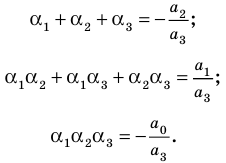
Выполнение таких равенств является необходимым и достаточным
условием того, чтобы числа 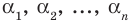
Формулы (3) и (4) справедливы не только для случая, когда все корни многочлена 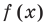
Если многочлен 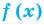
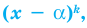
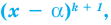


Например, если произведение 
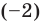
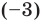
При использовании формул Виета в случае кратных корней необходимо каждый корень записать такое количество раз, которое равно его кратности.
Пример №3
Проверьте справедливость формул Виета для многочлена
Решение:
►
Поэтому 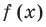
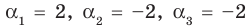
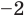
Проверим справедливость формулы (5). В нашем случае: 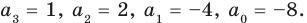
Как видим, все равенства выполняются, поэтому формулы Виета справедливы для данного многочлена.
Пример №4
Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения
Решение:
► Обозначим корни уравнения 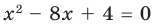
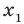
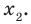
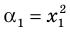
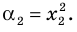
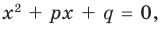
По формулам Виета имеем 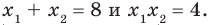
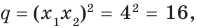
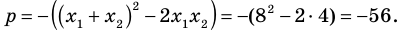
Схема Горнера
Делить многочлен 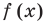
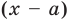
специальной схемы, которую называют схемой Горнера.
Пусть многочлен 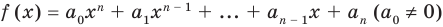
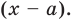
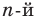
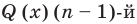
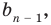
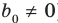
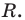
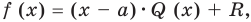
Левая и правая части полученного равенства тождественно равны, поэтому, перемножив многочлены, стоящие в правой части, можем приравнять коэффициенты при соответствующих степенях
Найдем из этих равенств коэффициенты 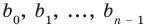
Как видим, первый коэффициент неполного частного равен первому коэффициенту делимого. Остальные коэффициенты неполного частного и остаток находятся одинаково: для того чтобы найти коэффициент 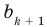
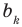
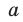
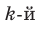
Пример №5
Разделите по схеме Горнера многочлен 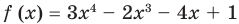
Решение:
► Запишем сначала все коэффициенты многочлена 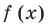
Таким образом,
Пример №6
Проверьте, является ли 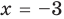
Решение:
► По теореме Безу остаток от деления многочлена 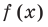
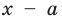
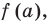
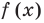
Поскольку 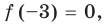
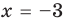
Нахождение рациональных корней многочлена с целыми коэффициентами
Теорема 4. Если многочлен с целыми коэффициентами 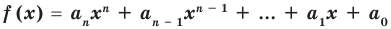
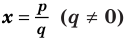
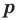
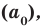
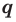
Если 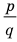
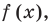
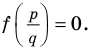
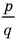
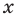
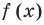
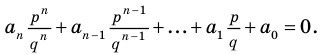
Умножим обе части равенства (1) на 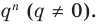
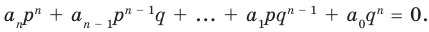
В равенстве (2) все слагаемые, кроме последнего, делятся на 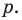
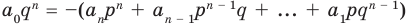
Но когда мы записываем рациональное число в виде 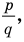
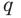
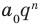
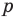
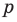
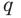
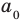
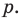
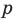
Аналогично все слагаемые равенства (2), кроме первого, делятся на 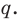
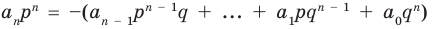
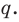
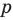
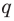
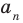
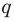
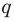
Отметим два следствия из этой теоремы. Если взять 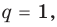
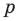
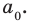
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене 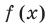
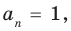
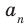
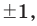
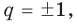
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Пример №7
Найдите рациональные корни многочлена
Решение:
► Пусть несократимая дробь 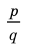
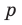
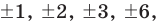
Таким образом, рациональные корни многочлена необходимо искать среди чисел 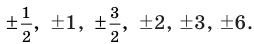
При 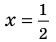
Кроме того, по схеме Горнера можно записать, что
Многочлен 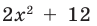
Пример №8
Разложите многочлен 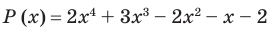
Решение:
► Ищем целые корни многочлена среди делителей свободного члена:
Подходит 1. Делим 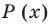

Тогда
Ищем целые корни кубического многочлена 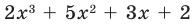
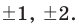
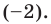
Имеем
Квадратный трехчлен 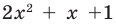
Ответ:
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен 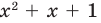
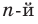
Например, многочлен четвертой степени раскладывается на произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Пример №9
Разложите на множители многочлен
Решение:
► Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен на произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
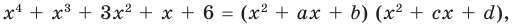
где 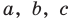
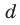
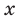
Получаем систему
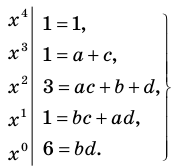
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что 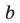
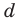
Коэффициенты 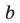
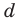
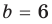
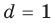
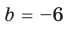
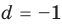
Для каждой пары значений 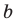
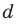
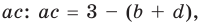
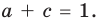
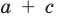
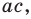
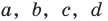
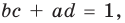
Как видим, системе (4) удовлетворяет набор целых чисел 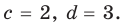
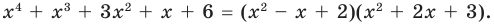
Поскольку квадратные трехчлены 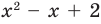
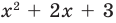
Деление многочлена на многочлен
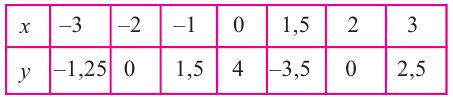
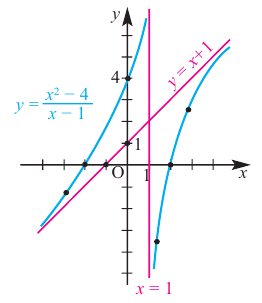
Задача. Объём подарочных коробок, размеры которых даны в сантиметрах, можно смоделировать функцией 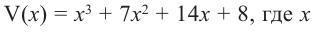
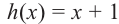
Исследование. Изучите, как правило деления многозначных чисел столбиком можно применить при делении многочлена.
a) Для каждого из двух случаев укажите, какие числа и какие многочлены соответствуют понятиям делимое, делитель и частное.
b) Как был найден первый член при делении многочлена? Каковы сходные и отличительные черты данного деления и деления многозначных чисел?
c) Как вы убедились,что каждое из двух делений выполнено правильно?
Выражение вида 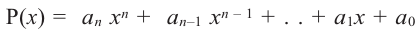
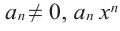
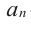
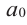
Деление целого числа па целое число можно проверить равенством
Аналогичное правило справедливо и при делении многочлена на многочлен. Если многочлен 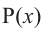
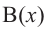
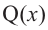
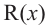
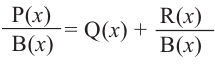
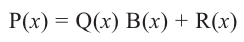
Здесь, степень многочлена 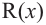
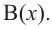
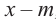
В этом случае:
Пример №10
а) Разделите многочлен 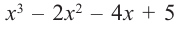
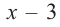
Ответ запишите в виде
b) Определите множество допустимых значений переменной.
c) Выполните проверку.
Решение:
b) При этом 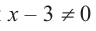
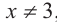
c) Должно выполняться тождество
Пример №11
Разделите 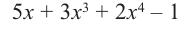
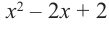
Решение:
запишем делимое в порядке убывания степеней. Введем в запись отсутствующие члены с коэффициентом равным 0.
Пример №12
1) Исследуйте деление столбиком многочлена 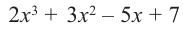
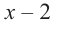
2) На каждом шаге деления делимое делится на старший член делителя, на 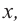
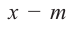
При делении многочлена на двучлен вида 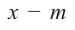
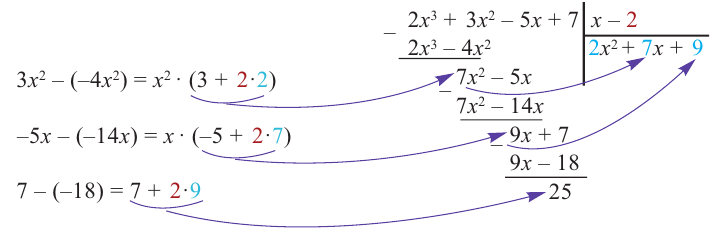
Пример №13
Разделите многочлен 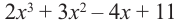
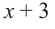
Решение:
коэффициенты делимого записываются в порядке убывания степеней (отсутствующий член записывается с коэффициентом равным нулю). Если двучлен имеет вид 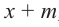
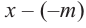
Запишем двучлен 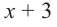
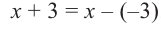
Таким образом, для делимого 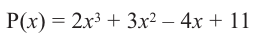
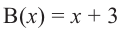
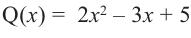
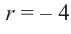
Деление можно записать в виде: 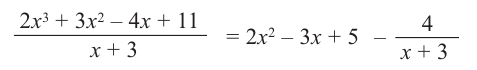
Теорема об остатке
Теорема об остатке (Теорема Безу)
Остаток от деления многочлена 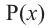
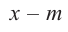
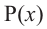
Доказательство: В равенстве 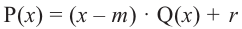
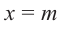
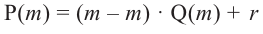
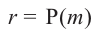
Пример №14
Найдите остаток от деления многочлена 
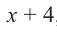
Решение: запишем делитель в виде 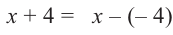
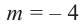
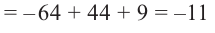
Проверим решение.
Теорема о разложении многочлена на множители
Значения переменной 
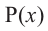
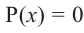
Теорема. Если число 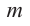
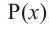
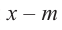
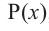
Действительно, если 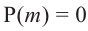
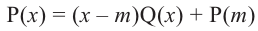
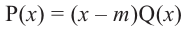
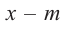
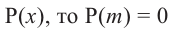
Пример №15
При помощи теоремы о разложении многочлена на множители определите, являются ли двучлены 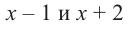
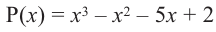
Решение: вычислим значение многочлена 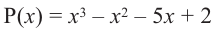
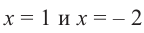
Значит, 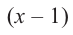
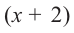
Пример №16
Зная, что 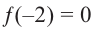
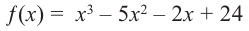
Решение: так как 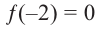
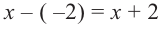
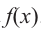
Учитывая, что 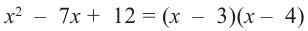
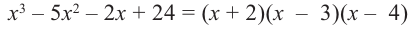
Отсюда получаем, что 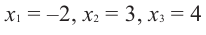
Примечание: Если многочлен задан в виде 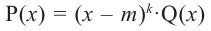
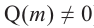
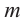
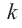
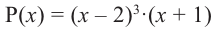
Нахождение рациональных корней
Теорема о рациональных корнях
Если для многочлена 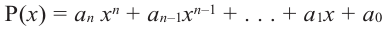
Доказательство. Пусть несократимая дробь 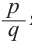
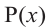
Умножим обе части равенства на
Так как в последнем равенстве каждый член, кроме члена 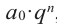
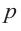
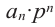
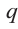
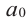
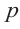
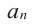
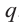
Пример №17
Найдите рациональные корни многочлена 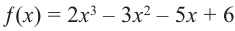
Решение: свободный член 6, старший коэффициент 2.
Для 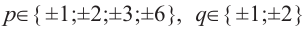
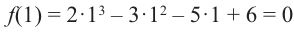
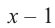
Так как, 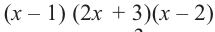
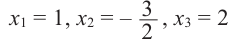
Следствие 1. Если старший коэффициент 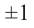
Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.
Пример №18
Найдите корни многочлена
Решение: по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.
Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.
Так как 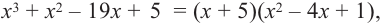
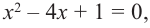
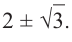
Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения 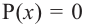
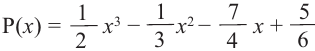
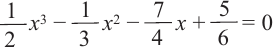
уравнение
Для нахождения рациональных корней выполните следующие действия.
1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.
2. Из этих чисел выбирается число 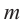
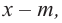
3. Для данного многочлена при помощи синтетического деления на двучлен 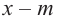
4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.
5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена 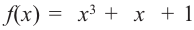
Проверим: 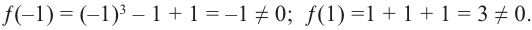
Основная теорема алгебры
Покажем на примере, что многочлен 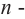
Пример №19
Найдите все корни многочлена
Решение: рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:
Значит, 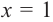
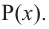
В выражении 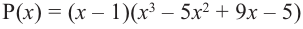
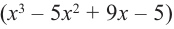
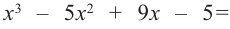
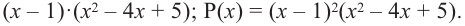
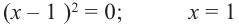
Корни:
Во всех рассмотренных нами примерах уравнение 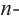
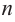
Теорема. Любой многочлен ненулевой степени имеет хотя бы один корень на множестве комплексных чисел.
Если 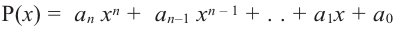
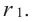
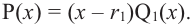
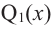
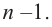
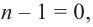
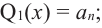
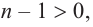
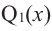
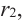
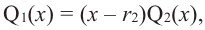
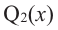
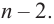
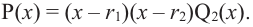
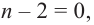
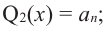
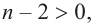
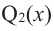
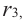
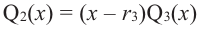
Продолжая процесс 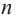
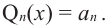
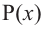
здесь числа 
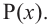
Следствие. Многочлен 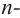
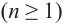
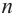
Отметим, что если комплексное число 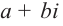
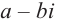
Любой многочлен с действительными коэффициентами можно представить в виде произведения двучленов вида 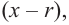
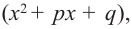
Отсюда можно сделать вывод, что многочлен нечетной степени с действительными коэффициентами всегда имеет действительные корни.
Пример №20
Запишите в виде произведения множителей многочлен наименьшей степени, если коэффициент при старшем члене равен 2, а корни равны 3 и
Решение: так как число 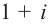
- Заказать решение задач по высшей математике
Пример №21
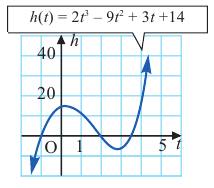
При движении скоростной карусели в Лунапарке изменение высоты (в метрах) кабины от нулевого уровня за первые 5 секунд можно смоделировать функцией 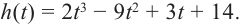
Решение: во всех случаях, кроме значений 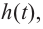
1. Проверим, является ли число 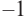
2. Число 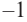
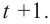
Учитывая, что 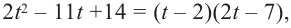
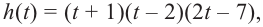
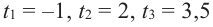
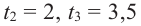
Функция-многочлен
График функции-многочлен
В стандартном виде функция – многочлен записывается как 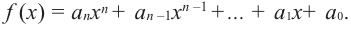
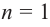
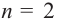
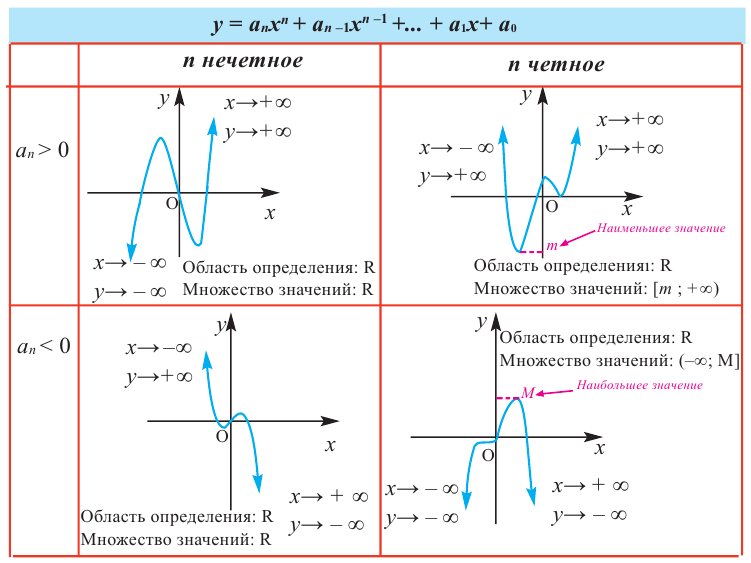
При возрастании значений аргумента по абсолютному значению многочлен ведет себя как функция старшего члена 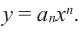
Пример №22
Определите характер поведения функции – многочлен в зависимости от степени и коэффициента при старшем члене при возрастании аргумента по абсолютному значению.
a) 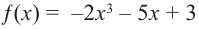
Решение: а) степень многочлена 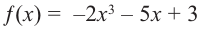
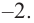
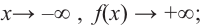
b) степень многочлена 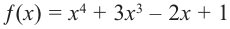
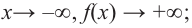
Пример №23
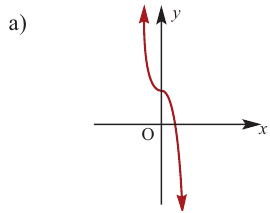
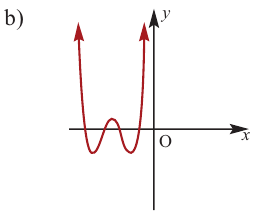
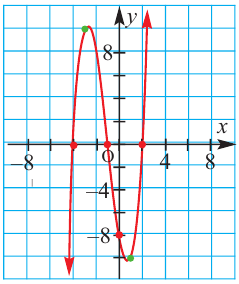
По графику определите как ведет себя функция – многочлен при неограниченном возрастании аргументов но абсолютному значению, четность или нечетность степени многочлена, знак коэффициента старшего члена.
Решение:
при
при
Многочлен нечетной степени
Решение:
при
при
Многочлен четной степени
Отметим, что если 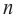
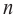
Алгоритм построения эскиза графика функции – многочлен.
1. Находятся точки пересечения графика с осями координат (если они есть). Эти точки отмечаются на координатной плоскости.
2. Вычисляются значения функции в некоторых точках между действительными нулями. Соответствующие точки отмечаются на координатной плоскости.
3. Определяется поведение графика при больших значениях аргумента по абсолютному значению.
4. На основе полученных данных строят схематически график.
Пример №24
Постройте график функции
Решение:
1. Применим теорему о рациональных корнях. Разложим многочлен на множители и найдем нули функции.
По теореме возможные рациональные нули надо искать среди чисел, которые являются делителями числа
Проверим 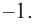
Значит, двучлен 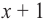
Зная, что 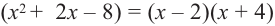
Отсюда находим нули 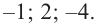
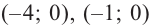
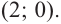
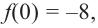
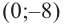
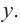
2. Найдем еще несколько значений функции в точках, не требующих сложных вычислений. Например, в точках 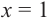
Отметим точки
3. Определим, как меняется график при уменьшении или увеличении значений 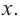
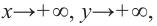
4. Соединим отмеченные точки и получим схематический график функции
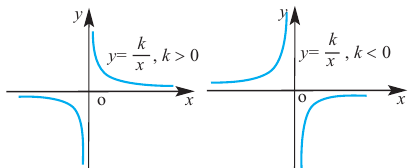
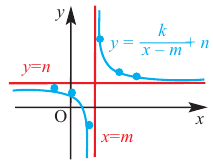
Рациональная функция
Рациональной функцией называется функция, которою можно представить в виде отношения двух многочленов:
Самым простым примером рациональной функции является функция
График функции 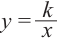
При стремлении значений 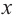
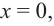
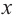
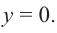
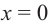
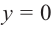
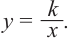
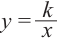
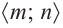
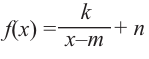
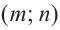
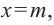
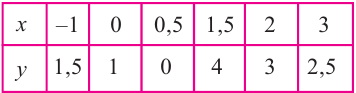
Пример №25
Постройте график функции
Решение: точки пересечения с осью 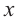
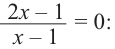
При 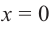
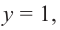
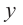
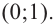
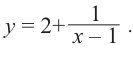
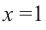
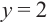
Отметим на координатной плоскости точки, соответствующие парам значений из таблицы и, учитывая горизонтальную и вертикальную асимптоту, изобразим ветви гиперболы, которые пересекают координатные оси в точках 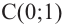
В общем случае, для построения графика рациональной функции надо найти точки пересечения с осями координат (если они есть) и ее асимптоты. Если выражение, которое задает рациональную функцию, имеет вид дроби, знаменатель которой обращается в нуль в точке 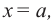
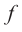
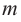
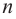
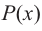
Для 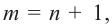
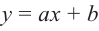
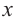
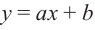
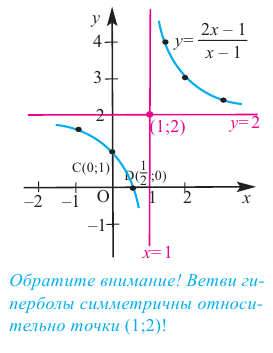
Пример №26
Найдите асимптоты и схематично изобразите график функции
Решение: Точки пересечения с осью 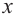
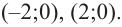
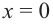
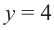
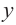
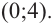
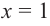
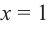
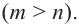
Для больших, но модулю, значений 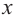
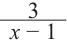
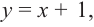
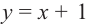
Отметим точки, координаты которых соответствуют парам из таблицы. Учитывая вертикальную и наклонную асимптоту, схематично изобразим график функции.
Многочлены в линейной алгебре
Многочленом от переменной х степени n называется выражение вида:
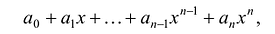
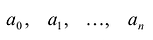
Если коэффициент 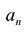
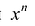
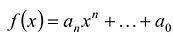
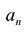
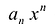
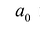
Два многочлена называются равными, если они имеют одинаковую степень и коэффициенты при одинаковых степенях равны.
Суммой многочленов 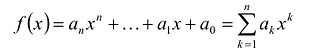
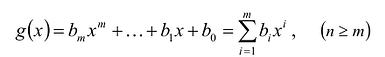
Произведением многочленов 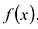
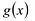
Легко проверить, что сложение и умножение многочленов ассоциативно, коммутативно и связаны между собой законом дистрибутивности.
Многочлен 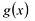
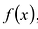
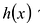
Теорема о делении с остатком
Для любых многочленов 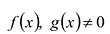
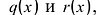
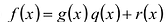
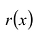
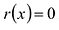
Многочлены g(x) и r(x) называются соответственно частным и остатком. Если g(x) делит 
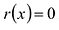
Число с называется корнем многочлена 

Теорема Безу
Число с является корнем многочлена 

Пусть с – корень многочлена 


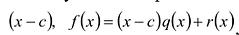
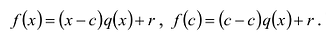

Обратно, пусть (х-с) делит 
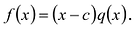
Следствие. Остаток от деления многочлена 
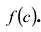
Многочлены первой степени называются линейными многочленами. Теорема Безу показывает, что разыскание корней многочлена 
Многочлен 
Пусть 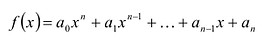
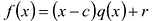
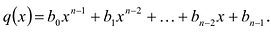
Число с-называется корнем кратности к многочлена 
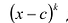

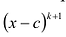

Чтобы поверить, будет ли число с корнем многочлена 

Число различных корней многочлена не превосходит его степени.
Большое значение имеет следующая основная теорема.
Основная теорема. Всякий многочлен с числовыми коэффициентами ненулевой степени имеет хотя бы один корень (может быть комплексный).
Следствие. Всякий многочлен степени 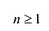
где 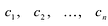

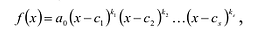
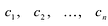

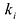
Если многочлен 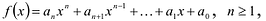
Значит, у многочлена с действительными коэффициентами комплексные корни входят парами.
Следствие. Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.
Пусть 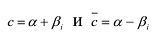


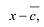
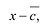

Утверждение 2. Многочлен с действительными коэффициентами степени 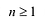
При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.
Рациональной дробью называется дробь где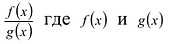
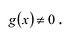

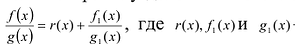
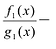
Лемма 1, Если 
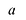
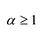
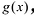
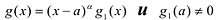
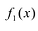
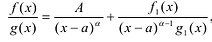
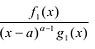
При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.
Лемма 2. Если 
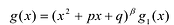
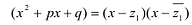
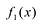
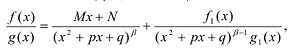
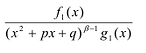
Рациональные дроби вида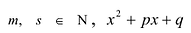
Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.
При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов.
Он состоит в следующем:
При этом если степень многочлена 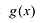
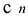
Число неизвестных 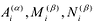
Таким образом, получается система n уравнений с n неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.
- Квадратичные формы – определение и понятие
- Системы линейных уравнений с примерами
- Линейное программирование
- Дифференциальное исчисление функций одной переменной
- Кривые второго порядка
- Евклидово пространство
- Матрица – виды, операции и действия с примерами
- Линейный оператор – свойства и определение
10. Многочлены от одной переменной и действия над ними.
10.1. ОПРЕДЕЛЕНИЕ МНОГОЧЛЕНОВ ОТ ОДНОЙ ПЕРЕМЕННОЙ И ИХ ТОЖДЕСТВЕННОЕ РАВЕНСТВО
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например от переменной х.
По определению одночлена числа и буквы (в нашем случае одна буква — х) в нем связаны только двумя действиями — умножением и возведением в натуральную степень. Если в этом одночлене произведение всех чисел записать перед буквой, а произведение всех степеней буквы записать как целую неотрицательную степень этой буквы (то есть записать одночлен в стандартном виде), то получим выражение вида ахn, где а — некоторое число. Поэтому одночлен от одной переменной х — это выражение вида ахп, где а — некоторое число, п — целое неотрицательное число. Если а 0, то показатель степени п переменной х называется степенью одночлена. Например, 25х6 —одночлен шестой степени, — х2/3— одночлен второй степени. Если одночлен является числом, не равным нулю, то его степень считается равной нулю. Для одночлена, заданного числом 0, понятие степени не определяется (поскольку 0 = 0 • х = 0 • х2 = 0 • х3…).
По определению многочлен от одной переменной х — это сумма одночленов от одной переменной х (в которой приведены подобные слагаемые, то есть все одночлены-слагаемые имеют различную степень). Поэтому
Определение 1. Многочленом от одной переменной х называется выражение вида
f (х) = аnхn + аn-1 хn-1 + … + а2х2+а1х +а0, (1)
где коэффициенты аn, аn-1, …., а0 – некоторые числа.
Если аn 0, то этот многочлен называют многочленом п-й степени от переменной х. При этом член аnхп называют старшим членом многочлена f (х), число аn — коэффициентом при старшем члене, а член а0 — свободным членом. Например, 5х3 – 2х + 1 — многочлен третьей степени, у которого свободный член равен 1, а коэффициент при старшем члене равен 5.
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена f (х) записывают так:
f (x) = b0xn + b1xn – 1 + … + b n – 1x + b n, где b0, b1, …, bn — некоторые числа.
Т е о р е м а 1. Одночлены ахn, где а ≠ 0, и bxm, где b ≠ 0, тождественно равны тогда и только тогда, когда а = b и п = т.д.
Одночлен ахn тождественно равен нулю тогда и только тогда, когда а = 0.
Поскольку равенство одночленов
aхn = bхn (2)
выполняется при всех значениях х (по условию эти одночлены тождественно равны), то, подставляя в это равенство х = 1, получаем, что a = b. Сокращая обе части равенства (2) на a (где a ≠ 0 по условию), получаем xn =xm . При х = 2 из этого равенства имеем: 2n = 2m. Поскольку 2n = 2• 2•… • 2 (n раз),
а 2m = 2 • 2 •… • 2 (m раз), то равенство 2n = 2m возможно только тогда, когда n = m.
Таким образом, из тождественного равенства axn = bxm (a 0, b 0) получаем, что a = b и n = m.
Если известно, что axn = 0 для всех х, то при х = 1 получаем a = 0. Поэтому одночлен axп тождественно равен нулю при a = 0 (тогда axn = 0 • xn = 0).
Далее любой одночлен вида 0 • хn будем заменять на 0.
Т е о р ем а 2. Если многочлен f (x) тождественно равен нулю (то
есть принимает нулевые значения при всех значениях х), то все
его коэффициенты равны нулю.
Для доказательства используем метод математической индукции.
Пусть f (x) = anхn + an-1хn-1 + … + a1х + a0 = 0 (тождественно).
При n = 0 имеем f (х) = a0 = 0, поэтому a0 = 0. То есть в этом случае утверждение теоремы выполняется.
Предположим, что при n = k это утверждение также выполняется: если многочлен akхk + ak-1хk-1 + … + a1х + a0 тождественно равен 0, то
ak = ak – 1 = … = a1 = a0 = 0.
Докажем, что данное утверждение выполняется и при n = k + 1. Пусть
f (x) = ak+1xk + akхk + … + a1х + a0 = 0. (3)
Поскольку равенство (3) выполняется при всех значениях х, то, подставляя в это равенство х = 0, получаем, что a0 = 0. Тогда равенство (3) обращается в следующее равенство: ak+1xk+1+ akxk + … + a1x = 0. Вынесем х в левой части этого равенства за скобки и получим
х (ak+1 + xk + akxk-1 + … + a1) = 0. (4)
Равенство (4) должно выполняться при всех значениях х. Для того чтобы оно выполнялось при х 0, должно выполняться тождество ak+1xk + akxk-1 + … + a1 = 0.
В левой части этого тождества стоит многочлен со степенями переменной от х0 до xk .Тогда по предположению индукции все его коэффициенты равны нулю: ak + 1 = ak = …= a1 = 0. Но мы также доказали, что a0 = 0,
поэтому наше утверждение выполняется и при n = k + 1. Таким образом, утверждение теоремы справедливо для любого целого неотрицательного n, то есть для всех многочленов.
Определение 2. Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают 0 (х) или просто 0 (поскольку 0 (х) = 0).
Теорема 3. Если два многочлена f (x) и g (x) тождественно равны,
то они совпадают (то есть их степени одинаковы и коэффициенты при одинаковых степенях равны).
Пусть многочлен f (х) = аnхn + аn-1хn – 1 + … + а2х2 + а1х + а0, а многочлен g (x) = bmxm + bm – 1xm – 1 + … + b2x2 + b1x + b0. Рассмотрим многочлен f (x) – g (x). Поскольку многочлены f (x) и g (x) по условию тождественно равны, то многочлен f (x) – g (x) тождественно равен 0. Таким образом, все его коэффициенты равны нулю.
Но f (x) – g (x) =(a0 – b0) + (a1 – b1) x +(а2 – b2) х2+ … .
Тогда a0 – b0 = 0, a1 – b1 = 0, а2 – b2 = 0, … . Отсюда a0 = b0, a1 = b1s а2 = b2, … . Как видим, если допустить, что у какого-то из двух данных многочленов степень выше, чем у второго многочлена (например, n больше m), то коэффициенты разности будут равны нулю. Поэтому начиная с (m + 1)-го номера все коэффициенты at также будут равны нулю. То есть действительно многочлены f (x) и g (x) имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.
Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.
Пример. Докажите, что выражение (х + 2)(х + 4)(х + 6)(х + 8) + 16 является полным квадратом.
Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида ах2 + bх + с (а ≠ 0).
Получаем тождество:
(х + 2)(х + 4)(х + 6)(х + 8) + 16 = (ах2 + bх + с)2. (5)
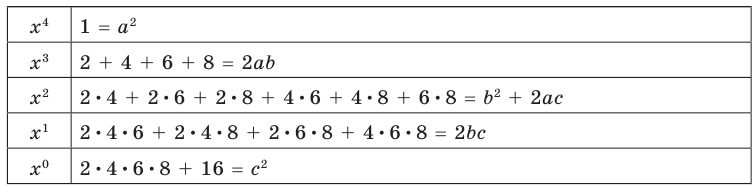
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях х, получаем систему равенств. Этот этап решения удобно оформлять в следующем виде:
|
x4 |
1 = a2 |
|
x3 |
2 + 4 + 6 + 8 = 2ab |
|
x2 |
2-4 + 2-6 + 2-8 + 4-6 + 4-8 + 6-8 = b2 + 2ac |
|
x1 |
2-4-6 + 2-4-8 + 2-6-8 + 4-6-8 = 2bc |
|
x0 |
2 – 4 – 6 – 8 + 16 = c2 |
Из первого равенства получаем а = 1 или а = -1.
При а = 1 из второго равенства имеем b = 10, а из третьего — с = 20. Как видим, при этих значениях а, b и с последние два равенства также выполняются. Следовательно, тождество (5) выполняется при а = 1, b = 10, с = 20 (аналогично можно также получить а = -1, b = -10, с = -20).
Таким образом, (х + 2)(х+ 4)(х+ 6)(х+8) + 16=(х2 +10х + 20)2.
Упражнения
1. Зная, что многочлены f (x) и g (x) тождественно равны, найдите значение
коэффициентов а, b, с, d:
1)f (x) = 2x2 – (3 – а) x + b, g (x) = cx3 + 2dx2 + x + 5;
2)f (x) = (а + 1) x3 + 2, g (x) = 3x3 + bx2 + (c – 1) x + d.
2. Найдите такие числа a.b.c чтобы данное равенство a(x2-1)+b(x-2)+c(x+2)=2 выполнялось при любых значениях x.
3. Докажите тождество:
1)(x – 1)(х +1)(х2 – х + 1)(х2 + х +1) =х6 – 1;
2)1+х4=(1+х +х2)(1-х +х2).
4. Докажите, что данное выражение является полным квадратом:
1)(х – 1)(х – 2)(х – 3)(х – 4) + 1;
2)(х + а)(х + 2а)(х + 3а)(х + 4а) + а4.
5. Найдите такие а и b, чтобы при любых значениях х выполнялось равенство: 3х4 + 4х3 + 8х2 + 3х + 2 = (3х2 + ах + 1)(х2 + х + b).
6. Запишите алгебраическую дробь 2/15х2+x-2 как сумму двух алгебраических дробей вида a/3x-1 и b/5x+2
10.2. ДЕЛЕНИЕ МНОГОЧЛЕНА НА МНОГОЧЛЕН С ОСТАТКОМ
Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.
Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.
При сложении многочленов одной степени можно получить многочлен этой же степени или многочлен меньшей степени.
Например, 2х3 – 5х2 + 3х + 1 + (-2х3 + 5х2 + х + 5) = 4х + 6.
При сложении многочленов разных степеней всегда получаем многочлен, степень которого равна большей из степеней слагаемых.
Например, (3х3 – 5х + 7) + (х2 + 2х + 1) = 3х3 + х2 – 3х + 8.
Деление многочлена на многочлен определяется аналогично делению целых чисел. Напомним, что число а делится на число b (b≠ 0), если существует такое число q, что а = b • q.
Определение 3. Многочлен А (х) делится на многочлен В (х) (где В (х) —не нулевой многочлен), если существует такой многочлен Q (x), что
А (х) = В (х) • Q (x).
Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком
Разделить с остатком многочлен А (х) на многочлен В (х) (где В (х) — не нулевой многочлен) — это означает найти такую пару многочленов Q (x) и R (x), что А (х) = В (х) • Q (x) + R (x), причем степень остатка R (x) меньше степени делителя В (х) (в этом случае многочлен Q (х) называют неполным частным.)
Например, поскольку х3 – 5х + 2 = (х2 – 5) х + 2, то при делении многочлена х3 – 5х + 2 на многочлен х2 – 5 получаем неполное частное х и остаток 2.
Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом:
Алгоритм. При делении многочленов от одной переменной переменные в делимом и в делителе размещают по убыванию степеней и делят старший член делимого на старший член делителя. Потом полученный результат умножают на делитель, и это произведение вычитают из делимого. С полученной разностью выполняют аналогичную операцию: делят ее старший член на старший член делителя и полученный результат снова умножают на делитель и т. д. Этот процесс продолжают до тех пор, пока не получится в остатке 0 (если один многочлен делится на другой) или пока в остатке не получится многочлен, степень которого меньше степени делителя.
Пример. Разделим многочлен А (х) = х4 – 5х3 + х2 + 8х – 20 на многочлен B(x)= х2 – 2х+3
Докажем, что полученный результат действительно является результатом деления А (х) на В (х) с остатком.
Если обозначить результат выполнения первого шага алгоритма через f1 (x), второго шага — через f2 (x), третьего — через f3 (x), то операцию деления, выполненную выше, можно записать в виде системы равенств:
f1(x) = А (х) – х2 • В (х); (1)
f2 (x) = A (x) – (-3х) • В (х); (2)
f3 (x) = f2(x) – (-8) • В (х). (3)
Сложим почленно равенства (1), (2), (3) и получим
А (х) = (х2 – 3х – 8) • В (х) + f3 (x). (4)
Учитывая, что степень многочлена f3 (x) = х + 4 меньше степени делителя
В (х) = х2 – 2х + 3, обозначим f3 (x) = R (x) (остаток), а х2 – 3х – 8 = Q (x) (неполное частное). Тогда из равенства (4) имеем: А (х) = В (х) – Q (x) + R (x), то есть х4 – 5х3 + х2 + 8х – 20 = (х2 – 2х + 3)(х2 – 3х – 8) + х + 4, а это и означает, что мы разделили А (х) на В (х) с остатком.
Очевидно, что приведенное обоснование можно провести для любой пары многочленов А (х) и В (х) в случае их деления столбиком. Поэтому описанный выше алгоритм позволяет для любых делимого А (х) и делителя В (х) (где В (х) — не нулевой многочлен) найти неполное частное Q (x) и остаток R (x).
То есть, имеет место следующая теорема.
Теорема 4. Для любой пары многочленов А (х) и В (х) (где В (х) — не нулевой многочлен) существует и притом единственная пара многочленов
Q(x) и R(x), такая, что А(х)=В(х)*Q(x) + R(x), причем сте-
пень R (x) меньше степени В (х) (или R (x) — нулевой многочлен).
Отметим, что в случае, когда степень делимого А (х) меньше степени делителя В (х), считают, что неполное частное Q (x) = 0, а остаток R (x) = А (х).
Упражнения
1.Выполните деление многочлена на многочлен:
1)3х3 – 5х2 + 2х – 8 на х – 2; 2) х10 + 1 на х2 + 1;
3)х5 + 3х3 + 8х – 6 на х2 + 2х + 3.
2. Выполните деление многочлена на многочлен с остатком:
1)4х4 – 2х3 + х2 – х + 1 на x2 + x + 2;
2)х5 + х4 + х3 + х2 + 1 на х2 – х – 2.
3.При каких значениях а и b многочлен А (х) делится без остатка на многочлен В(х)?
1)А (х) = х3 + ах + b, В (х) = х2 + 5х + 7;
2)А (х) = 2х3 – 5х2 + ах + b, В (х) = х2 – 4;
3)А (х) = х4 – х3 + х2 – ах + b, В (х) = х2 – х + 2.
4.Найдите неполное частное и остаток при делении многочлена А(х) на многочлен В(х) методом неопределенных коэффициентов:
1)А (х) = х3 + 6х2 + 11х + 6, В (х) = х2 – 1;
2)А (х) = х3 – 19х – 30, В (х) = х2 + 1.
10.3. ТЕОРЕМА БЕЗУ. КОРНИ МНОГОЧЛЕНА. ФОРМУЛЫ ВИЕТА
Рассмотрим деление многочлена f (x) на двучлен (х – а). Поскольку степень делителя равна 1, то степень остатка, который мы получим, должна быть меньше 1, то есть в этом случае остатком будет некоторое число R. Таким образом, если разделить многочлен f (x) на двучлен (х – а), то получим
f (x) = (х – а)*Q (x) + R.
Это равенство выполняется тождественно, то есть при любом значении х. При х = а имеем f (а) = R. Полученный результат называют теоремой Безу.
Те о р е м а 1 (теорема Безу). Остаток от деления многочлена f (х) на двучлен (х – а) равен f (а) (то есть значению многочлена при х = а).
Задача 1. Докажите, что х5 – 3х4 + 2х3 + 4х – 4 делится на х – 1 без остатка.
- Подставив в f (х) = х5 – 3х4 + 2х3 + 4х – 4 вместо х значение 1, получаем: f (1) = 0. Таким образом, остаток от деления f (х) на (х – 1) равен 0, то есть f (x) делится на (х – 1) без остатка.
О п р е д е л е н и е. Число α называют корнем многочлена f (x), если f (α) = 0.
Если многочлен f (х) делится на (х – α), то α — корень этого многочлена.
- Действительно, если f (х) делится на (х – α), то f (х) = (х – α)*Q (x) и поэтому f (α) = (α – α)*Q (α) = 0. Таким образом, α — корень многочлена f (х).
Справедливо и обратное утверждение. Оно является следствием теоремы Безу.
Т е о р е м а 2. Если число α является корнем многочлена f (x), то этот многочлен делится на двучлен (х – α) без остатка.
- По теореме Безу остаток от деления f (x) на (х – α) равен f (α). Но по условию α — корень f (x), таким образом, f (α) = 0.
Обобщением теоремы 2 является следующее утверждение.
Те о р е м а 3. Если многочлен f (x) имеет попарно разные корни α1, α2, …, αn, то он делится без остатка на произведение
(х – α1)(x – α2)*…*(х – αn).
- Для доказательства используем метод математической индукции.
При n= 1 утверждение доказано в теореме 2. Допустим, что утверждение справедливо при n = k. То есть если α1, α2, …, αk — попарно разные корни многочлена f (x), то он делится на произведение (х – α1)(х – α2)*…*(х – αk). Тогда
f (x) = (х – α1)(х – α2)*…*(х – αk)*Q (x). (1)
Докажем, что утверждение теоремы справедливо и при n = k + 1. Пусть α1, α2, …, αk, αk + 1 — попарно разные корни многочлена f (x). Поскольку αk + 1 — корень f (x), то f (αk + 1) = 0.
Принимая во внимание равенство (1), которое выполняется согласно предположению индукции, получаем:
f (αk + 1) = (αk + 1 – α1)(αk + 1 – α2)*…*(αk + 1 – αk)*Q (αk + 1) = 0.
По условию все корни α1, α2, …, αk, αk + 1 разные, поэтому ни одно из чисел αk + 1 – α1, αk + 1 – α2, …, αk + 1 – αk не равно нулю. Тогда Q (αk + 1) = 0. Таким образом, αk + 1 — корень многочлена Q (x). Тогда по теореме 2 Q (x) делится на (х – αk + 1), то есть Q (x) = (х – αk + 1)*Q1 (x) и из равенства (1) имеем
f (x) = (х – α1)(х – α2)*…*(х – αk)(х – αk + 1)* Q1(x).
Это означает, что f (х) делится на произведение
(х – α1)(х – α2)*…*(х – αk)(х – αk + 1),
то есть теорема доказана и при n = k + 1.
Таким образом, теорема справедлива для любого натурального n.
С л е д с т в и е. Многочлен степени n имеет не больше n разных корней.
- Допустим, что многочлен n-й степени имеет (n + 1) разных корней: α1, α2, …, αn, αn+ 1. Тогда f (x) делится на произведение (х – α1)(х – α2)*… *(х – αn + 1) — многочлен степени (n+ 1), но это невозможно. Поэтому многочлен n-й степени не может иметь больше, чем n корней.
Пусть теперь многочлен n-й степени f (x) = аnхn + аn– 1 хn–1 + … + а2х2 + а1х + а0 (an ≠ 0) имеет n разных корней α1, α2, …, αn. Тогда этот многочлен делится без остатка на произведение (х – α1)(х – α2)*…*(х – αn). Это произведение является многочленом той же n-й степени. Таким образом, в результате деления можно получить только многочлен нулевой степени, то есть число. Таким образом,
аnхn + аn – 1 хn – 1 + … + а2х2 + а1х + а0 = b (х – α1)(х – α2)*…*(х – αn). (2)
Если раскрыть скобки в правой части равенства (2) и приравнять коэффициенты при старших степенях, то получим, что b = аn, то есть
аnхn + аn – 1 хn – 1 + … + а2х2 + а1х + а0 = аn (х – α1)(х – α2)*…*(х – αn) (3)
Сравнивая коэффициенты при одинаковых степенях х в левой и правой частях тождества (3), получаем соотношения между коэффициентами уравнения и его корнями, которые называют формулами Виета:
|
a1+a2+…+an= – an-1/an; |
a1a2+a1a3+…+an-1an= an-2/an; |
(4) |
|
a1a2a3+a1a2a4+…+an-2an-1an= – an-3/an; |
||
|
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
||
|
a1a2a3…an= (-1)n * a0/an. |
Например, при n = 2 имеем:
a1+a2= – a1/a2, a1a2 = a0/a2
а при n = 3:
| a1+a2+a3= – a2/a3; |
a1a2+ a1a3+ a2a3 = a1/a3; |
(5) |
|
a1a2a3 = – a0/a3. |
Выполнение таких равенств является необходимым и достаточным условием того, чтобы числа α1, α2, …, αn были корнями многочлена f (x) = аnхn + аn – 1 хn – 1 + … + а2х2 + а1х + а0 (an ≠ 0). Формулы (3) и (4) справедливы не только для случая, когда все корни многочлена f (x) разные. Введем понятие кратного корня многочлена.
Если многочлен f (x) делится без остатка на (х – α)k, но не делится без остатка на (х – α)k + 1, то говорят, что число α является корнем кратности k многочлена f (x).
Например, если произведение (х + 2)3(х – 1)2(х + 3) записать в виде многочлена, то для этого многочлена число (–2) является корнем кратности 3, число 1 — корнем кратности 2, а число (–3) — корнем кратности 1.
При использовании формул Виета в случае кратных корней необходимо каждый корень записать такое количество раз, которое равно его кратности.
Задача 2. Проверьте справедливость формул Виета для многочлена
f (x) = х3 + 2х2 – 4х – 8.
- f(x) = х3 + 2х2 – 4х – 8 = х2 (х + 2) – 4 (х + 2) = (х + 2)(х2 – 4) = (х – 2)(х + 2)2 .
Поэтому f (х) имеет корни: α1 = 2, α2 = –2, α3 = –2 (поскольку (–2) — корень кратности 2). Проверим справедливость формулы (5).
В нашем случае: а3 = 1, а2 = 2, а1= –4, а0 = –8. Тогда
2+(-2)+(-2)=-2/1; 2*(-2)+2*(-2)+(-2)*(-2)=-4/1; 2*(-2)*(-2)=-(-8)/1
Как видим, все равенства выполняются, поэтому формулы Виета справедливы для данного многочлена.
Задача 3. Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения х2 – 8х + 4 = 0.
- Обозначим корни уравнения х2 – 8х + 4 = 0 через х1 и х2. Тогда корнями искомого уравнения должны быть числа a1=x12 и a2=x22 . Поэтому искомое уравнение имеет вид х2 + рх + q = 0,
где p=-(a1+a2)=-(x12+x22)=-((x1+x2)2-2x1x2), q=a1a2=x12x22=(x1x2)2
По формулам Виета имеем х1 + х2 = 8 и х1х2 = 4. Отсюда находим, что
q = (х1х2)2 = 42 = 16, а p = −((x1+x2)2-2x1x2) = -(82-2*4)=-56.
Таким образом, искомое уравнение имеет вид х2 – 56х + 16 = 0.
Упражнения
- Найдите остаток от деления многочлена х5 – 4х4 + 2х3 – 5х + 1 на х + 2.
- Найдите коэффициент а, зная, что остаток от деления многочлена х3 – ах2 + 5х – 3 на х – 1 равен 6.
- Многочлен f (х) при делении на х – 1 дает остаток 4, а при делении на х – 3 дает остаток 6. Найдите остаток от деления многочлена f (х) на х2 – 4х + 3.
- При каких значениях а и b многочлен х4 + 2х3 + ах2 – bх + 2 делится без остатка на х + 2, а при делении на х – 1 имеет остаток, который равен 3?
- Остаток от деления многочлена f (x) на 3х2 – 5х + 2 равен 7х + 1. Найдите остаток от деления этого многочлена на двучлены х – 1 и 3х – 2.
- Запишите формулы Виета при n = 4.
- Составьте кубический многочлен, который имеет корни 5, –2, 1 и коэффициент при старшем члене –2. Решите задачу двумя способами.
- При каких значениях а сумма квадратов корней трехчлена х2 – (а + 2) х + 3а равна 12?
- Какую кратность имеет корень 2 для многочлена
f (х) = х5 – 5х4 + 7х3 – 2х2 + 4х – 8?
- Составьте кубический многочлен, который имеет корень 3 кратности 2 и корень (–1), а коэффициент при старшем члене 2.
- Найдите такие а и b, чтобы число 3 было корнем кратности не меньше чем 2 для многочлена f (х) = х3 – 5х2 + ах + b.
- Составьте квадратное уравнение, корни которого противоположны корням уравнения х2 – 5х + 1 = 0.
- Составьте квадратное уравнение, корни которого обратны корням уравнения 2х2 – 5х + 1 = 0.
- Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения х2 + 6х + 3 = 0.
10.4. СХЕМА ГОРНЕРА
Делить многочлен f (x) на двучлен (х – а) иногда удобно с помощью специальной схемы, которую называют схемой Горнера.
- Пусть многочлен f (x) = а0хn + а1хn– 1 + … + аn – 1 х + аn (a0 ≠ 0) необходимо разделить на двучлен (х – а). В результате деления многочлена n-й степени на многочлен первой степени получим некоторый многочлен Q (x) (n – 1)-й степени (то есть Q (x) = b0x n – 1 + b1x n – 2 + … + bn – 2 x + b n – 1, где b0 ≠ 0) и остаток R. Тогда f (x) = (х – а)*Q (x) + R, то есть а0хn + а1хn – 1 + … + аn – 1 х + аn = = (х – а)*(b0xn – 1 + b1xn – 2 + … + bn – 2 x + bn – 1) + R. Левая и правая части полученного равенства тождественно равны, поэтому, перемножив многочлены, стоящие в правой части, можем приравнять коэффициенты при соответствующих степенях х:
Xn
а0 = b0
Xn-1
а1 = b1 – аb0
Xn-2
а2 = b2 – аb1
. . . . . .
. . . . . . . . . . . .
X1
аn – 1 = bn – 1 – аbn – 2
X0
аn = R – аbn – 1
Найдем из этих равенств коэффициенты b0, b1, …, bn – 1 и остаток R: b0 = а0, b1 = ab0 + a1, b2 = ab1 + a2, …, bn – 1 = abn – 2 + an – 1, R = abn – 1 + an.
Как видим, первый коэффициент неполного частного равен первому коэффициенту делимого. Остальные коэффициенты неполного частного и остаток находятся одинаково: для того чтобы найти коэффициент bk + 1 неполного частного, достаточно предыдущий найденный коэффициент bk умножить на а и добавить k-й коэффициент делимого. Эту процедуру целесобразно оформлять в виде специальной схемы-таблицы, которую называют схемой Горнера.
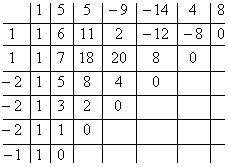
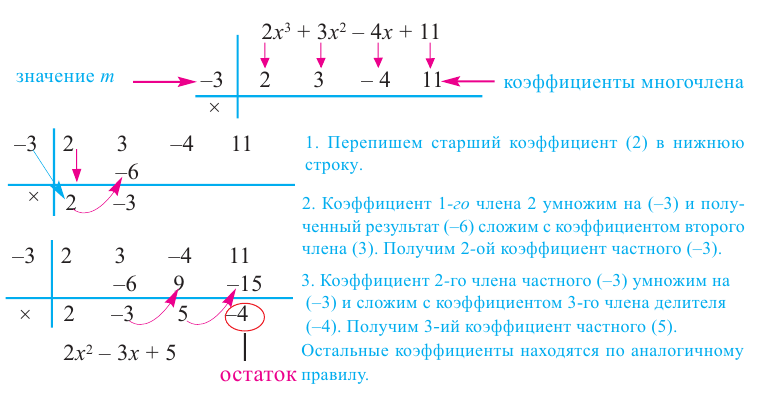
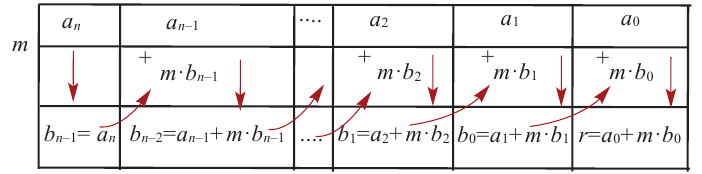
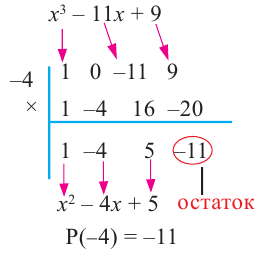
Пример 1. Разделите по схеме Горнера многочлен f (х) = 3х4 – 2х3 – 4х + 1 на двучлен х – 2.
Запишем сначала все коэффициенты многочлена f (х) (если в данном многочлене пропущена степень 2, то соответствующий коэффициент считаем равным 0), а потом найдем коэффициенты неполного частного и остаток по указанной схеме:
Таким образом, 3х4 – 2х3 – 4х +1 = (х – 2)(3х3 + 4х2 + 8х + 12) + 25.
Пример 2. Проверьте, является ли х = –3 корнем многочлена f (х) = 2х4 + 6х3 + 4х2 – 2х – 42.
- По теореме Безу остаток от деления многочлена f (х) на х – а равен f (а), поэтому найдем с помощью схемы Горнера остаток от деления f (х) на х – (–3) = х + 3
Поскольку f (–3) = 0, то х = –3 — корень многочлена f (х).
Упражнения
- Используя схему Горнера, найдите неполное частное и остаток от деления многочлена А (х) на двучлен В (х):
1) А (х) = х3 + 3х2 + 3х + 1; В (х) = х + 1;
2) А (х) = 5х3 – 26х2 + 25х – 4; В (х) = х – 5;
3) А (х) = х4 – 15х2 + 10х + 24; В (х) = х + 3.
- Используя схему Горнера, проверьте, делится ли многочлен f (x) на двучлен q (x):
1) f (х) = 4х3 – х2 – 27х – 18; q (x) = x + 2;
2) f (х) = х4 – 8х3 + 15х2 + 4х – 20; q (x) = x – 2.
- Разделите многочлен А (х) на двучлен В (х):
1) А (х) = 2х3 – 19х2 + 32х + 21; В (х) = х – 7;
2) А (х) = 4х3 – 24х2 + 21х – 5; В (х) = 2х – 1.
10.5. НАХОЖДЕНИЕ РАЦИОНАЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ.
Теорема 4. Если многочлен с целыми коэффициентами f (x) = anxn + an-1xn-1 + … + a1x+a0 имеет рациональный корень x=p/q (q ≠ 0, дробь p/q несократимая), то р является делителем свободного члена (a0), а q — делителем коэффициента при старшем члене аn.
Если p/q является корнем многочлена f (х), то f(p/q) = 0. Подставляем p/q вместо х в f(x) и из последнего равенства имеем
|
an * pn/qn + an-1 * pn-1/qn-1 + … + a1 * p/q + a0 = 0. |
(1) |
Умножим обе части равенства (1) на (q ≠ 0). Получаем
|
аnрn + an-1pn-1q + … + a1pqn-1 + a0qn = 0. |
(2) |
В равенстве (2) все слагаемые, кроме последнего, делятся на р. Поэтому
a0qn = -(аnрn + an-1pn-1q + … + a1pqn-1) делится на р.
Но когда мы записываем рациональное число в виде p/q, то эта дробь считается несократимой, то есть р и q не имеют общих делителей. Произведение a0qn может делиться на р (если р и q — взаимно простые числа) только тогда, когда a0 делится на р. Таким образом, р — делитель свободного члена a0.
Аналогично все слагаемые равенства (2), кроме первого, делятся на q. Тогда
anpn = -(an-1pn-1q + … + a1pq-1 + a0qn) делится на q. Поскольку р и q — взаимно простые числа, то an делится на q, следовательно, q — делитель коэффициента при старшем члене.
Отметим два следствия из этой теоремы. Если взять q = 1, то корнем многочлена будет целое число р — делитель a0. Таким образом, имеет место:
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене f (х) коэффициент аn = 1, то делителями аn могут быть только числа ±1, то есть q =±1, и имеет место:
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Задача 1 Найдите рациональные корни многочлена 2х3 – х2 + 12х – 6.
Пусть несократимая дробь p/q является корнем многочлена. Тогда р необходимо искать среди делителей свободного члена, то есть среди чисел ±1, ±2, ±3, ±6, а q — среди делителей старшего коэффициента: ±1, ±2.
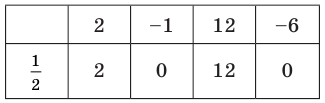
Таким образом, рациональные корни многочлена необходимо искать среди чисел ±1/2, ±1, +±3/2, ±2, ±3, ±6. Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера. При x = 1/2 имеем следующую таблицу.
Кроме того, по схеме Горнера можно записать, что
2х3 – х2 + 12х – 6 = (x – 1/2) (2x2 + 12).
Многочлен 2х2 + 12 не имеет действительных корней (а тем более рациональных), поэтому заданный многочлен имеет единственный рациональный корень x =1/2.
Задача 2 Разложите многочлен Р (х) = 2х4 + 3х3 – 2х2 – х – 2 на множители.
Ищем целые корни многочлена среди делителей свободного члена: ±1, ±2. Подходит 1. Делим Р (х) на х – 1 с помощью схемы Горнера.
Тогда Р (х) = (х – 1)(2х3 + 5х2 + 3х + 2). Ищем целые корни кубического многочлена 2х3 + 5х2 + 3х + 2 среди делителей его свободного члена: ±1, ±2. Подходит (–2). Делим на х + 2
Имеем Р (х) = (х – 1)(х + 2)(2х2 + х +1).
Квадратный трехчлен 2х2 + х +1 не имеет действительных корней и на линейные множители не раскладывается.
Ответ: Р (х) = (х – 1)(х + 2)(2х2 + х +1).
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен х2 + х + 1 не имеет действительных корней). Таким образом, многочлен n-й степени не всегда можно разложить на линейные множители. В курсах высшей алгебры доказывается, что многочлен нечетной степени всегда можно разложить на линейные и квадратные множители, а многочлен четной степени представить в виде произведения квадратных трехчленов.
Например, многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Задача 3 Разложите на множители многочлен х4 + х3 + 3х2 + х + 6.
Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен в произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
|
х4 + х3 + 3х2 + х + 6 = (х2 + ах + b)(х2 + сх + d), |
(3) |
где а, b, с и d — неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях х у них равны. Раскроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:
х4 + х3 + 3х2 + х + 6 = x4 + cx3 + dx2 +
+ ax3 + acx2 + adx +
+ bx2 + bcx + bd.
Получаем систему
 |
(4) |
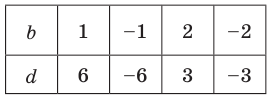
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что b и d могут быть только делителями числа 6. Все возможные варианты запишем в таблицу.
Коэффициенты b и d в равенстве (3) равноправны, поэтому мы не рассматриваем случаи b = 6 и d = 1 или b = –6 и d = –1 и т. д.
Для каждой пары значений b и d из третьего равенства системы (4) найдем ас = 3 – (b + d), а из второго равенства имеем а + с = 1.
Зная а + с и ас, по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения а, b, с, d подставим в четвертое равенство системы (4) bс + ad = 1, чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:
Как видим, системе (4) удовлетворяет набор целых чисел а = –1, b = 2, с = 2, d = 3. Тогда равенство (3) имеет вид
|
x4 + х3 + 3х2 + х + 6 = (х2 – х + 2)(х2 + 2х + 3). |
(5) |
Поскольку квадратные трехчлены х2 – х + 2 и х2 + 2х + 3 не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.
Упражнения
- Найдите целые корни многочлена:
1) х3 – 5х + 4;
2) 2x3 + x2 – 13x + 6;
3) 5х3 + 18х2 – 10х – 8;
4) 4х4 – 11х2 + 9х – 2.
- Найдите рациональные корни уравнения:
1) х3 – 3х2 + 2 = 0;
2) 2х3 – 5х2 – х + 1 = 0;
3) 3х4 + 5х3 – х2 – 5х – 2 = 0;
4) 3х4 – 8х3 – 2х2 + 7х – 2 = 0.
- Разложите многочлен на множители:
1) 2х3 – х2 – 5х – 2;
2) х3 + 9х2 + 23х +15;
3) х4 – 2х3 + 2х – 1;
4) х4 – 2х3 – 24х2 + 50х – 25.
- Найдите действительные корни уравнения:
1) х3 + х2 – 4х + 2 = 0;
2) х3 – 7х – 6 = 0;
3) 2х4 – 5х3 + 5х2 – 2 = 0;
4) 2х3 – 5х2 + 1 = 0.
5*. Разложите многочлен на множители методом неопределенных коэффициентов:
1) х4 + х3 – 5х2 + 13х – 6;
2) х4 – 4х3 – 20х2 + 13х – 2.
6*. Разложите многочлен на множители, заранее записав его с помощью метода неопределенных коэффициентов в виде (х2 + bх + с)2 – (mх + n)2: :
1) х4+ 4х – 1;
2) х4 – 4х3 – 1;
3) х4 + 4а3х – а4.
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ К РАЗДЕЛУ 1
- Область определения функции y = f (x) ¾ отрезок [– 2; 1]. Найдите область определения функции:
- Постройте график функции:
- Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют заданному условию:
4 (МТУСИ). Решите уравнение:
5 (МЭСИ). Решите систему уравнений:
- Решите неравенство:
- Докажите неравенство:
8 (СТАНКИН). Найдите все значения параметра а, при которых уравнение имеет точно три корня.
9 (МГАТХТ). Найдите все значения параметра а, при которых система уравнений не имеет решений.
10 (МГУ, ИСАиА). Найдите все значения параметра а, при которых система уравнений имеет единственное решение.
11 (МИСиС). При каких значениях параметра а неравенство
выполняется для всех отрицательных значений х?
12 (МГУ, мех.-мат. ф-т). При каких значениях параметра а уравнение
имеет точно три различных корня?
- При каких значениях параметра а уравнение
имеет три действительных корня, которые образуют геометрическую прогрессию?
Решите задачи (14–25) на составление уравнений или неравенств и их систем.
14 (МГТУ). Рабочий должен был по плану изготовить за несколько дней 72 детали. Так как каждый день он изготавливал на 2 детали меньше плана, то закончил работу через 3 дня после срока. Сколько деталей в день должен был изготовлять рабочий по плану?
15 (МГУ, хим. ф-т). Три одинаковых комбайна, работая вместе, убрали первое поле, а затем два из них убрали второе поле (другой площади). Вся работа заняла 12 часов. Если бы три комбайна выполнили половину всей работы, а затем оставшуюся часть сделал один из них, то работа заняла бы 20 часов. За какое время два комбайна могут убрать первое поле?
16 (РЭА). Производительность первого станка на 25 % больше производительности второго станка. Второй станок сделал деталей на 4 % больше, чем первый. На сколько процентов время, затраченное вторым станком на выполнение своей работы, больше времени первого станка?
17 (ГФА). Первая из труб наполняет бассейн водой в два раза быстрее, чем другая. Если половину бассейна наполнить только из первой трубы, а оставшуюся часть — только из второй, то для наполнения бассейна потребуется 6 час. За сколько часов можно наполнить бассейн только из первой трубы?
18 (МГУПБ). Два велосипедиста выезжают одновременно навстречу друг другу из пунктов А и В, расстояние между которыми 30 км, и встречаются через час. Не останавливаясь, они продолжают путь с той же скоростью, и первый прибывает в пункт В на 1,5 часа раньше, чем второй в пункт А. Определить скорость первого велосипедиста.
19 (МГУПБ). В течение 7 ч 20 мин судно прошло вверх по реке 35 км и вернулось обратно. Скорость течения равна 4 км в час. С какой скоростью судно шло по течению?
20 (ПГУ). Смешали 30 %-ный раствор соляной кислоты с 10 %-ным и получили 600 г 15 %-го раствора. Сколько граммов каждого раствора было взято?
21 (ВШЭ). Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40 % олова, а второй — 26 % меди. Процентное содержание цинка в первом и во втором сплавах одинаково. Сплавив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30 % цинка. Определить, сколько килограммов олова содержится в новом сплаве.
22 (МАИ). Найти такое двузначное число, в котором число его единиц на два больше числа десятков, а произведение искомого числа на сумму его цифр равно 144.
23 (ЛТА). Около дома посажены березы и липы, причем общее их количество более 14. Если количество лип увеличить вдвое, а количество берез увеличить на 18, то берез станет больше. Если увеличить вдвое количество берез, не изменяя количества лип, то лип все равно будет больше. Сколько берез и сколько лип было посажено?
24 (МГУ, эк. ф-т, ВШЭ). Группу людей пытались построить в колонну по 8 человек в ряд, но один ряд оказался неполным. Когда ту же группу людей перестроили по 7 человек в ряд, то все ряды оказались полными, а число рядов оказалось на 2 больше. Если бы тех же людей построили по 5 человек в ряд, то рядов было бы еще на 7 больше, причем один ряд был бы неполным. Сколько людей было в группе?
25 (МГУ, эк. ф-т). В магазине продаются гвоздики и розы. Гвоздика стоит 1 руб. 50 коп., роза — 2 руб. На покупку гвоздик и роз можно затратить не более 30 руб. 50 коп. При этом число гвоздик не должно отличаться от числа роз более чем на 6. Необходимо купить максимально возможное суммарное количество цветов, при этом гвоздик нужно купить как можно меньше. Сколько гвоздик и сколько роз будет куплено при указанных условиях?
После того, как мы разобрались с понятием тождеств, можно переходить к изучению тождественно равных выражений. Цель данной статьи – объяснить, что это такое, и показать на примерах, какие выражения будут тождественно равными другим.
Тождественно равные выражения: определение
Понятие тождественно равных выражений обычно изучается вместе с самим понятием тождества в рамках школьного курса алгебры. Приведем основное определение, взятое из одного учебника:
Тождественно равными друг другу будут такие выражения, значения которых будут одинаковы при любых возможных значениях переменных, входящих в их состав.
Также тождественно равными считаются такие числовые выражения, которым будут отвечать одни и те же значения.
Это достаточно широкое определение, которое будет верным для всех целых выражений, смысл которых при изменении значений переменных не меняется. Однако позже возникает необходимость уточнения данного определения, поскольку помимо целых существуют и другие виды выражений, которые не будут иметь смысла при определенных переменных. Отсюда возникает понятие допустимости и недопустимости тех или иных значений переменных, а также необходимость определять область допустимых значений. Сформулируем уточненное определение.
Тождественно равные выражения – это те выражения, значения которых равны друг другу при любых допустимых значениях переменных, входящих в их состав. Числовые выражения будут тождественно равными друг другу при условии одинаковых значений.
Фраза «при любых допустимых значениях переменных» указывает на все те значения переменных, при которых оба выражения будут иметь смысл. Это положение мы объясним позже, когда будем приводить примеры тождественно равных выражений.
Можно указать еще и такое определение:
Тождественно равными выражениями называются выражения, расположенные в одном тождестве с левой и правой стороны.
Примеры выражений, тождественно равных друг другу
Используя определения, данные выше, рассмотрим несколько примеров таких выражений.
Для начала возьмем числовые выражения.
Так, 2+4 и 4+2 будут тождественно равными друг другу, поскольку их результаты будут равны (6 и 6).
Точно так же тождественно равны выражения 3 и 30:10, (22)3 и 26(для вычисления значения последнего выражений нужно знать свойства степени).
А вот выражения 4-2 и 9-1 равными не будут, поскольку их значения разные.
Перейдем к примерам буквенных выражений. Тождественно равными будут a+b и b+a, причем от значений переменных это не зависит (равенство выражений в данном случае определяется переместительным свойством сложения).
Например, если a будет равно 4, а b – 5, то результаты все равно будут одинаковы.
Еще один пример тождественно равных выражений с буквами – 0·x·y·z и 0. Какими бы ни были значения переменных в этом случае, будучи умноженными на 0, они дадут 0. Неравные выражения – 6·x и 8·x, поскольку они не будут равны при любом x.
В том случае, если области допустимых значений переменных будут совпадать, например, в выражениях a+6 и 6+a или a·b·0 и 0, или x4 и x, и значения самих выражений будут равны при любых переменных, то такие выражения считаются тождественно равными. Так, a+8=8+a при любом значении a, и a·b·0=0 тоже, поскольку умножение на 0 любого числа дает в итоге 0. Выражения x4 и x будут тождественно равными при любых x из промежутка [0, +∞).
Но область допустимого значения в одном выражении может отличаться от области другого.
Например, возьмем два выражения: x−1 и x-1·xx. Для первого из них областью допустимых значений x будет все множество действительных чисел, а для второго – множество всех действующих чисел, за исключением нуля, ведь тогда мы получим 0 в знаменателе, а такое деление не определено. У этих двух выражений есть общая область значений, образованная пересечением двух отдельных областей. Можно сделать вывод, что оба выражения x-1·xx и x−1 будут иметь смысл при любых действительных значениях переменных, за исключением 0.
Основное свойство дроби также позволяет нам заключить, что x-1·xx и x−1 будут равными при любом x, которое не является 0. Значит, на общей области допустимых значений эти выражения будут тождественно равны друг другу, а при любом действительном x говорить о тождественном равенстве нельзя.
Если мы заменяем одно выражение на другое, которое является тождественно равным ему, то этот процесс называется тождественным преобразованием. Это понятие очень важно, и подробно о нем мы поговорим в отдельном материале.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
доказать тождество:
2t−(17−(t−7))=3(t−8)
.
Решение:
выпишем отдельно левую часть равенства и преобразуем, т. е. попытаемся доказать, что она равна правой части.
При раскрытии скобок (обеих) знаки поменяем, т. к. перед скобками стоит знак минус.
2t−(17−(t−7))=2t−17+(t−7)==2t¯−17+t¯−7=3t−24=3(t−8).
.
Получили, что левая часть исходного равенства равна правой.
Значит, исходное равенство — тождество.
Лекция
№6
Многочлены
от одной переменной
Выражение
вида ,
где —
некоторые числа и ,
называется многочленом
степени от
.
Два
многочлена называются тождественно
равными,
если их числовые значения совпадают
при всех значениях .
Многочлены и
тождественно
равны тогда и только тогда, когда они
совпадают, т.е. коэффициенты при одинаковых
степенях этих
многочленов одинаковы.
Операции
над многочленами:
-
Сумма
и разность многочленов:.
Суммой
и разностью многочленов и
называется
следующий многочлен:
Степень
полученного многочлена не
превосходит максимальной степени
многочленов и
.
-
Умножение
на одночлен:.
Умножим
одночлен на
многочлен :
т.е.
каждый член многочлена умножается на
одночлен. Здесь применяем правило работы
со степенями.
-
Умножение
многочленов:.
Умножим
многочлен на
:
В
итоге свели операцию умножения многочленов
к умножению одночлена на многочлен.
Заметим, что при умножении многочленов
степени и
получается
многочлен степени .
При умножении многочленов необходимо
каждый член одного многочлена умножить
на каждый член другого многочлена.
-
Деление
многочленов:.
Разделим
многочлен на
,
то есть представим выражение 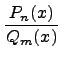
следующем виде:
где –
частное от деления, –
делимое, –
делитель, –
остаток.
При
делении многочлена на
многочлен ,
где ,
нужно найти многочлены и
такие,
чтобы выполнялось равенство
Теорема
Безу
Теорема
Безу. Остаток
от деления многочлена на
двучлен равен
значению этого многочлена при .
Следствие
1:
.
Таким
образом, число является
корнем многочлена тогда
и только тогда, когда многочлен делится
на двучлен без
остатка.
Если
многочлен делится
без остатка на ,
но не делится без остатка на ,
то число называется корнем
кратности для
многочлена .
Следствие
1. Многочлен степени
имеет
не более корней.
Следствие
2. Если
многочлен степени
имеет
корней
(среди которых могут быть равные), то он
представим в виде:
Теорема
Виета
Теорема
Виета. Если
многочлен степени
имеет
различных
корней ,
то имеют место следующие соотношения:
Замечание. Формулы
Виета сохраняют силу и при наличии
кратных корней, но в этом случае надо
каждый корень учитывается столько раз,
какова его кратность.
Наибольший
общий делитель многочленов (НОД).
Наибольшим
общим делителем отличным от нуля
многочленов
называется такой многочлен
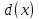
который является их общим делителем и,
вместе с тем, сам делится на любой другой
общий делитель этих многочленов.
Обозначается НОД многочленов
символом
Для
нахождения НОД многочленов применяется
алгоритм Евклида, который состоит в
следующем. Пусть даны многочлены
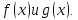
и получаем некоторый остаток

Делим затем
и получаем остаток
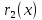
делим
и так далее. В этой цепочке мы должны
дойти до такого места, на котором деление
совершится нацело и поэтому процесс
остановится. Тот
остаток
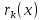
на который нацело делится предыдущий
остаток

и будет НОД многочленов
Корни
многочленов.
Если
то есть многочлен
обращается в нуль при подстановке в
него числа
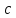
неизвестного, то

корнем многочлена
(или уравнения

Если
мы будем делить многочлен
на произвольный многочлен первой
степени, то остаток будет либо некоторым
многочленом нулевой степени либо нулём,
то есть во всяком случае некоторым
числом
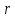
Следующая теорема
позволит найти остаток не прибегая к
самому делению многочлена, в случае,
когда производится деление на многочлен
вида
Остаток
от деления многочлена f(x)
на линейный многочлен
равен значению
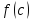
при
Действительно,
пусть
Беря
значения обеих частей этого равенства
при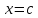
мы получаем:
что
доказывает теорему.
Следствие:
Число
с тогда и только тогда будет корнем
многочлена
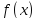
если
делится на
Кратные
корни.
Если
в разложении многочлена -степени
,
некоторые
множители окажутся одинаковыми, то
,
то -называется
корнем кратности ,
-кратности
и
т.д.
Теорема
. Если а является корнем
многочлена кратности
,
то для производной это
число является корнем кратности .
Доказательство. Пусть
,
где не
обращается в 0 при .
,
т.е. является
корнем кратности.
Следствие. Число а является
корнем кратности для
,…,
корнем кратности 1 для .
Условия
равенства двух многочленов
Определение.
Многочлены называются тождественно
равными, если при всех значениях
переменной их значения совпадают.
Теорема
1. У равных многочленов равны коэффициенты
при соответствующих степенях переменной.
Доказательство:
1.Если
коэффициенты при соответствующих
степенях переменной равны, то многочлены
равны.
При
любом значении х=с, значения многочленов
равны. А(с) – В(с) = 0
2.
Если многочлены равны, то и коэффициенты
при соответствующих значениях х равны.
А(х)
= В(х)А(х)
– В(х) = 0 при любом значении х=с.
Вычтем
значения многочленов в столбик:
Но
сумма может быть равна 0 при любом с
только если значения всех выражений в
скобках равно 0, значит ;
;
;
…
Границы
корней многочленов
Для
многочлена
1)
верхняя граница модулей корней –
число где
2)
верхняя граница положительных корней
– число где
B –
наибольшее число из модулей отрицательных
коэффициентов; k –
номер первого из отрицательных
коэффициентов;
3)
нижняя граница положительных корней –
число где
–
верхняя граница положительных корней
многочлена
4)
верхняя граница отрицательных корней
– число – где
–
верхняя граница положительных корней
многочлена
5)
нижняя граница отрицательных корней –
число – где
–
верхняя граница положительных корней
многочлена
Схема
Горнера
Схема
Горнера – один из простейших способов
деления многочлена на
бином x-a. Конечно, делением применение
схемы Горнера не исчерпывается, но для
начала рассмотрим именно это. Применение
алгоритма поясним на примерах.
Разделим на
.
Составим таблицу из двух строк: в первой
строке запишем коэффициенты многочлена по
убыванию степеней переменной. Заметьте,
что данный многочлен не содержит х, т.е.
коэффициент перед х равен 0. Так как мы
делим на ,
во второй строке запишем единицу:
Начнем
заполнять пустые ячейки во второй
строке. В первую пустую ячейку запишем
5, просто перенеся ее из соответствующей
ячейки первой строки:
Следующую
ячейку заполним по такому принципу:
Аналогично
заполним и четвертую: :
Для
пятой ячейки получим :
И,
наконец, для последней, шестой ячейки,
имеем :
Задача
решена, осталось только записать ответ:
Как
видите, числа, расположенные во второй
строке (между первым и последним), есть
коэффициенты многочлена, полученного
после деления на
.
Последнее число во второй строке означает
остаток от деления или, что то же самое,
значение многочлена при
.
Следовательно, если в нашем случае
остаток равен нулю, то многочлены делятся
нацело.
Полученный
результат говорит также и о том, что 1
является корнем многочлена .
Приведем
еще один пример. Разделим многочлен на
.
Сразу оговорим, что выражение нужно
представить в форме .
В схеме Горнера будет участвовать именно
-3.
Если
наша цель – найти все корни многочлена,
то схему Горнера можно применять
несколько раз подряд, – до тех пор, пока
мы не исчерпаем все корни. Например,
отыщем все корни многочлена .
Целые корни нужно искать среди делителей
свободного члена, т.е. среди делителей
8. Т.е., целыми корнями могут быть числа
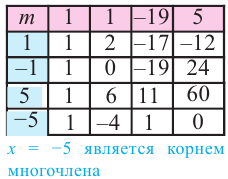
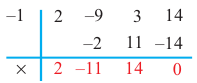
-8, -4, -2, -1, 1, 2, 4, 8. Проверим, к примеру, 1:
Итак,
в остатке имеем 0, т.е. единица действительно
является корнем данного многочлена.
Попробуем проверить единицу еще несколько
раз. Новую таблицу для этого создавать
не будем, а продолжим использование
предыдущей:
Вновь
в остатке ноль. Продолжим таблицу до
тех пор, пока не исчерпаем все возможные
значения корней:
Итог: .
Конечно,
данный метод подбора малоэффективен в
общем случае, когда корни не являются
целыми числами, но для целых корней
метод довольно-таки неплох.
Рациональные
дроби
Рассмотрим

где
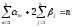
– многочлен n
– степени от x,
– константа.
Теорема
(о разложении правильной рациональной
дроби)
Если
и
– многочлены степени m
и n
соответственно, причем m<n
и коэффициенты этих многочленов
действительные числа, а
представляется в виде (1), то

Все
коэффициенты разложения (2) являются
действительными числами и определяются
однозначно.
Пример
1.
Представить
рациональную дробь
в виде простейших дробей над полем
вещественных чисел.
Решение.
Два
многочлена равны тогда и только тогда,
когда равны коэффициенты при одинаковых
степенях x.
Решая
систему получим:
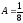
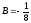
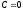
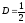
Имеем
разложение
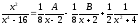
Пример
для самостоятельного решения.
Представить
рациональную дробь
в виде суммы простейших дробей над полем
комплексных чисел.
Указание.
Приравниваем
знаменатель к нулю


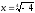
Извлекая корень, получим 4 корня
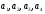
Представим

Данная дробь будет иметь вид
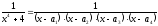
К
последней дроби применяем теорему о
разложении правильной рациональной
дроби.
Разложение
правильной рациональной дроби на
простейшие, знаменатель которой разложен
на попарно простые линейные множители.
Пусть
дана правильная дробь

при
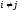
i,j=1,2,…,n.
В
этом случае справедлива формула Лагранжа:
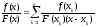
где

Интерполирование
Постановка
задачи.
Пусть
в точках
таких, что

Известны значения функции
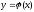
то есть на отрезке [a,b]
задана табличная (сеточная) функция
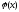
Таблица
1
|
x |
|
|
… |
|
|
y |
|
|
… |
|
Функция
f(x)
называется интерполирующей или
интерполяционной для
на отрезке [a,b],
если ее значения
в заданных точках

называемых узлами
интерполяции,
совпадают с заданными значениями функции

то есть с
соответственно.
Будем
считать, что интерполяционная функция
f(x)
есть многочлен степени n-1,
тогда задача интерполяции формулируется
так: для функции
заданной таблицей 1 найти многочлен
такой, чтобы выполнялась совокупность
условий интерполяции
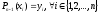
найти
многочлен
это значит, учитывая его каноническую
форму

найти
его n
коэффициентов
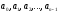
Обозначим через
и рассмотрим рациональную дробь

Она правильная, так как степень многочлена
в числителе меньше степени многочлена
стоящего в знаменателе. Мы можем применить
формулу Лагранжа для разложения дроби
на простейшие. Получим интерполяционную
формулу Лагранжа:
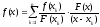
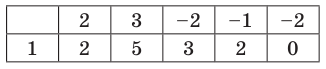
Пример.
Найти
многочлен наименьшей степени по данной
таблице его значений:
|
x |
-1 |
0 |
1 |
2 |
3 |
|
y |
6 |
5 |
0 |
3 |
2 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
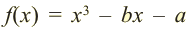
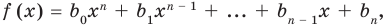
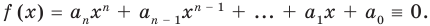
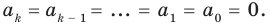
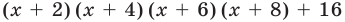
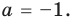
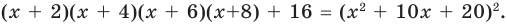
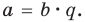
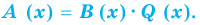
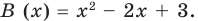
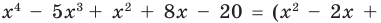
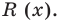
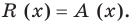
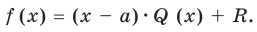
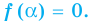
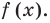
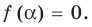
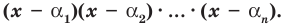
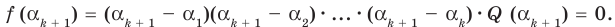

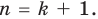
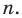
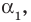
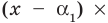
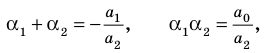
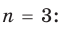
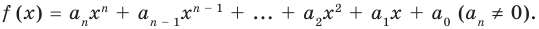
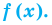
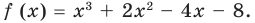
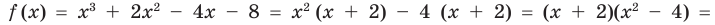
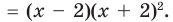
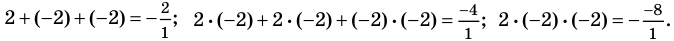
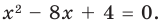
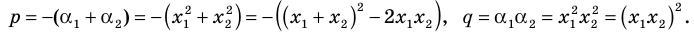
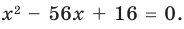
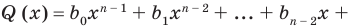
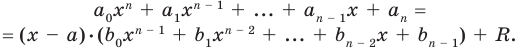
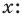


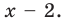

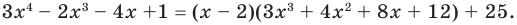
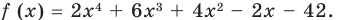
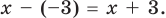

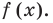
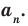
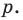
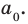
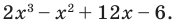
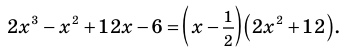
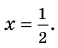
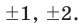
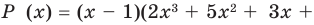
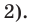
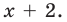

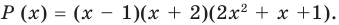
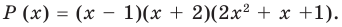
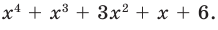
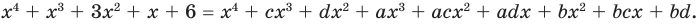

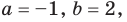
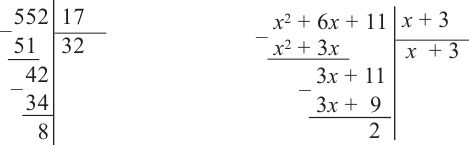
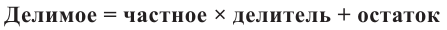
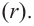
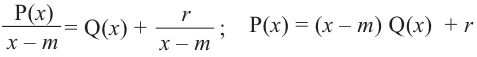
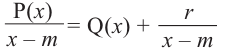
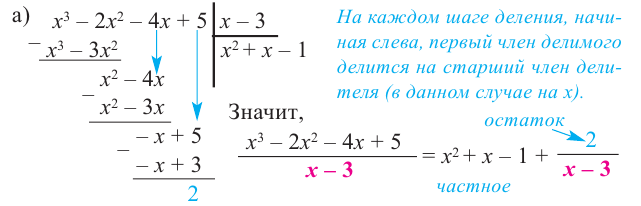
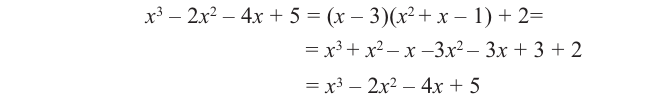
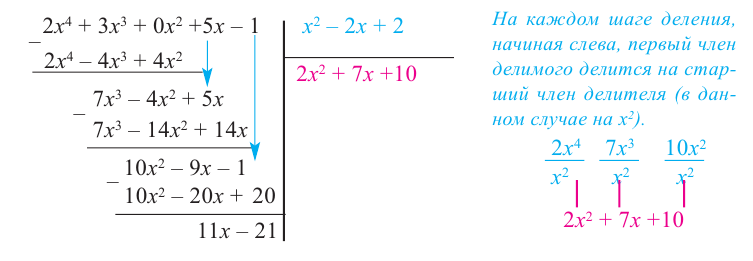
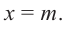
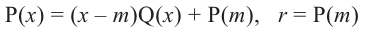
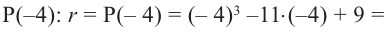
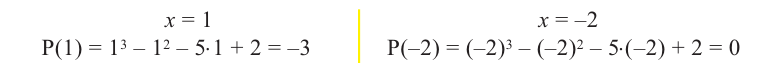
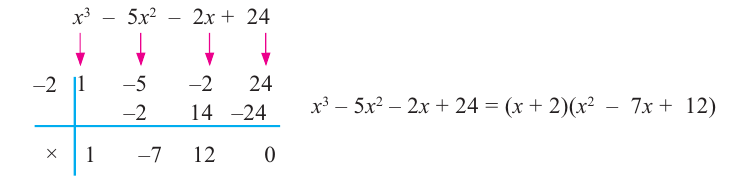
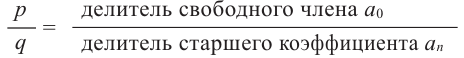
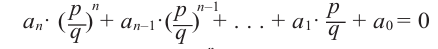
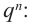
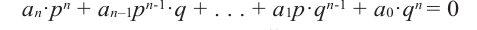
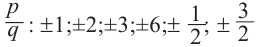
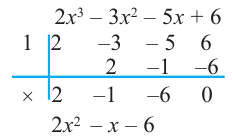
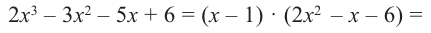
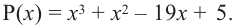
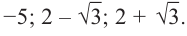
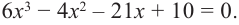
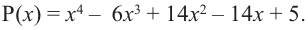
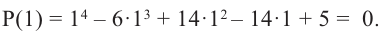
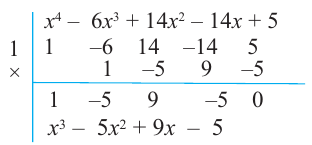
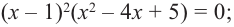
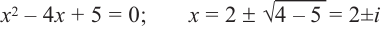
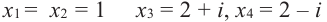
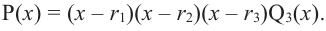
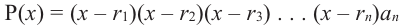
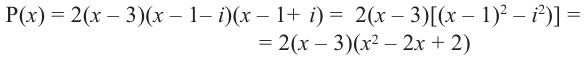
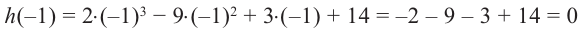
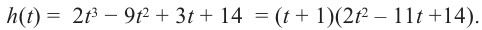
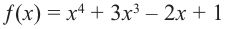
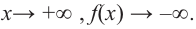
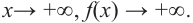
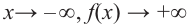
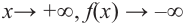
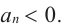
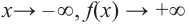
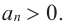
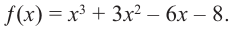
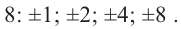
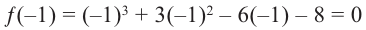
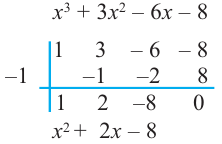
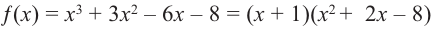
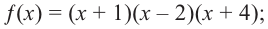
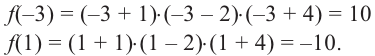
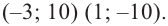
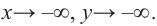
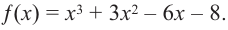
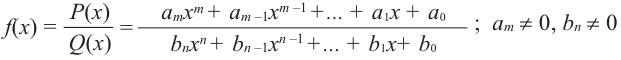
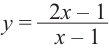
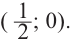
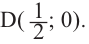
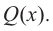
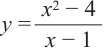
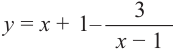
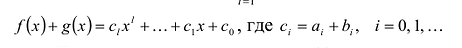
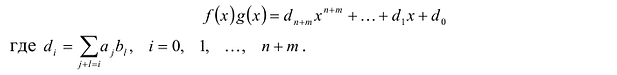
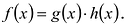
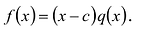
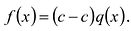
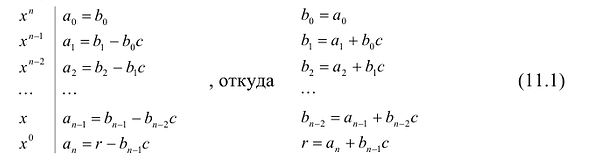

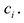
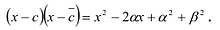
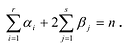
.jpg)















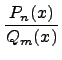 .
.