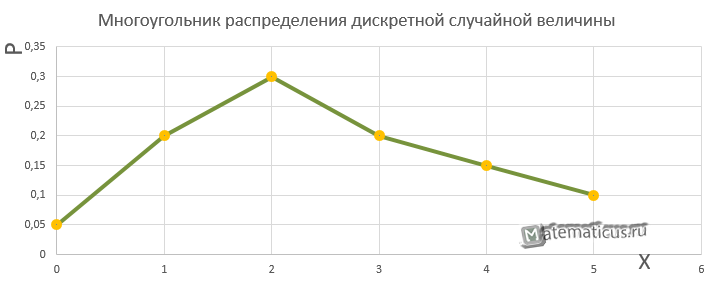
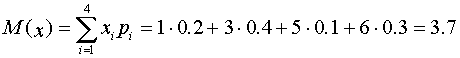Закон распределения дискретной случайной величины
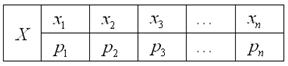
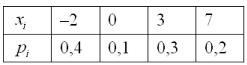
В задачах 12.1-12.10 требуется найти: а) математическое ожидание; б) дисперсию; в) среднее квадратическое отклонение дискретной случайной величины X по заданному закону её распределения, заданному таблично (в первой строке таблицы указаны возможные значения, во второй строке – вероятности возможных значений).
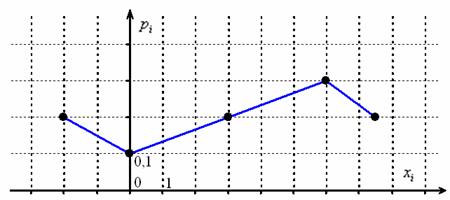
Закон распределения дискретной случайной величины можно изобразить графически. С этой целью на прямоугольной системе координат строят точки M1(x1; p1), M2(x2; p2), …, Mn(xn; pn), где xi – возможные значения случайной величины, а pi – соответствующие вероятности, и соединяют их последовательно отрезками прямых. Полученную фигуру называют многоугольником распределения. Построим многоугольник распределения дискретной случайной величины X, заданной следующим законом распределения:
| X | 1 | 3 | 5 | 6 |
| p | 0,2 | 0,4 | 0,1 | 0,3 |
Математическое ожидание:
Дисперсия: 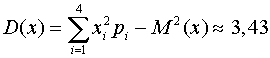
Среднее квадратическое отклонение: .
Перейти к онлайн решению своей задачи
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
2.2.6. Многоугольник распределения
Итак, пусть дискретная случайная величина задана своим законом распределения:
Многоугольником распределения вероятностей данной величины называют ломаную, звенья которой соединяют соседние точки . Иногда вместо «многоугольника»
используют термин полигон, но этот вариант больше в ходу в математической статистике.
Всё очень просто:
Задача 91
Построить многоугольник распределения вероятностей случайной величины
Решение: чертим прямоугольную систему координат, в которой по оси абсцисс отсчитываются – значения случайной величины, а по оси ординат
– их вероятности. Отмечаем на чертеже
точки , в данном случае их
пять, и соединяем «соседей» отрезками:
При выполнении чертежа от руки по возможности придерживайтесь следующего масштаба:
горизонтальная ось: 1 ед. = 2 тетрадные клетки (1 см);
вертикальная ось: 0,1 = 2 тетрадные клетки.
Если значения достаточно велики, то ось абсцисс можно «разорвать» (не чертить
её кусочек после единицы), и справа продолжить нумерацию, например, с 20.
Теперь обратите внимание на следующую важную вещь: помимо того, что дискретную случайную величину можно изобразить с
помощью многоугольника – её ведь можно ещё и ЗАДАТЬ этим способом. До сих пор мы делали это с помощью таблички, но никто же не мешает
использовать и чертёж!
Задача 92
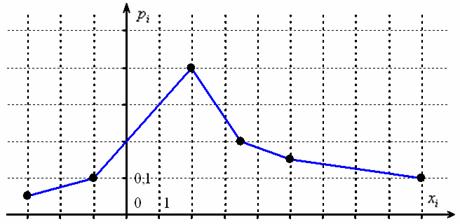
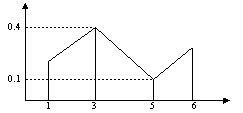
Дискретная случайная величина задана своим многоугольником
Записать закон распределения данной случайной величины, выполнить проверку.
Это задание для самостоятельного решения. И тут мы, кстати, видим изъян графического способа: по чертежу не всегда понятны точные
значения случайной величины и их вероятности.
На практике задачи с многоугольником встречаются довольно часто, но гораздо бОльшее распространение получила:


| Оглавление |
Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин

Многоугольник распределения
Итак, пусть дискретная случайная величина X задана своим законом распределения:
Многоугольником распределения вероятностей данной величины называют
ломаную, звенья которой соединяют соседние точки (xi ; pi ) . Иногда вместо
«многоугольника» используют термин полигон, но этот вариант больше в ходу в математической статистике.
Всё очень просто:
Задача 91
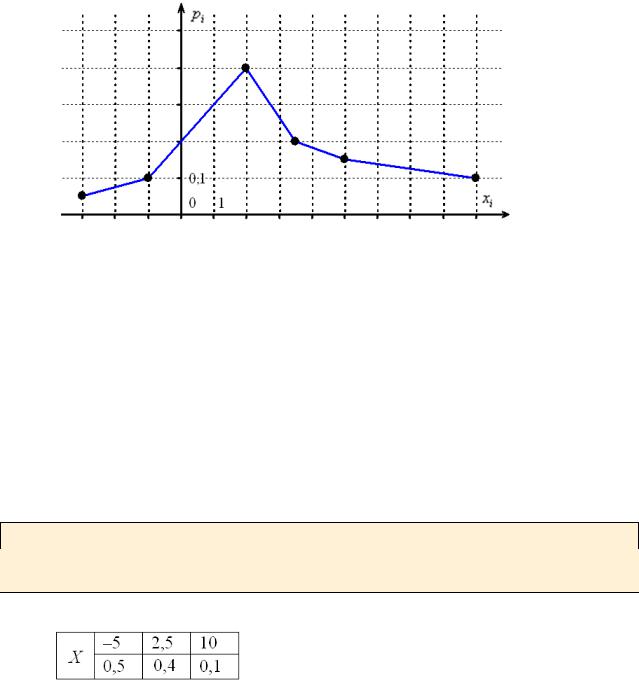
Построить многоугольник распределения вероятностей случайной величины X
Решение: чертим прямоугольную систему координат, в которой по оси абсцисс отсчитываются xi – значения случайной величины, а по оси ординат pi – их вероятности.
Отмечаем на чертеже точки (xi ; pi ) , в данном случае их пять, и соединяем «соседей» отрезками:
При выполнении чертежа от руки по возможности придерживайтесь следующего масштаба:
горизонтальная ось: 1 ед. = 2 тетрадные клетки (1 см); вертикальная ось: 0,1 = 2 тетрадные клетки.
Если значения xi достаточно велики, то ось абсцисс можно «разорвать» (не чертить её кусочек после единицы), и справа продолжить нумерацию, например, с 20.
Теперь обратите внимание на следующую важную вещь: помимо того, что дискретную случайную величину можно изобразить с помощью многоугольника – её ведь можно ещё и ЗАДАТЬ этим способом. До сих пор мы делали это с помощью таблички, но никто же не мешает использовать и чертёж!
|
Внимание! Это демо-версия книги, полную и свежую версию курса можно найти здесь: http://mathprofi.com/knigi_i_kursy/ |
105 |
Задача 92
Дискретная случайная величина X задана своим многоугольником
Записать закон распределения данной случайной величины, выполнить проверку.
Это задание для самостоятельного решения. И тут мы, кстати, видим изъян графического способа: по чертежу не всегда понятны точные значения случайной величины и их вероятности.
На практике задачи с многоугольником встречаются довольно часто, но гораздо бОльшее распространение получила:
Функция распределения случайной величины Стандартное обозначение: F (x)
Идля дискретной, и для непрерывной случайной величины она определяется одинаково:
…, где P( X x) – вероятность того, что случайная величина X примет значение,
МЕНЬШЕЕ, чем переменная x , которая «пробегает» все действительные значения от
«минус» до «плюс» бесконечности.
Построим функцию распределения для нашей подопытной игры:
Начинаем разбираться. Чему, например, равно значение F ( 20) ? Это вероятность того, что выигрыш будет меньше, чем –20. И это невозможное событие:
F ( 20) P( X 20) 0 . Совершенно понятно, что F (x) 0 и для всех «икс» из интервала ( ; 5) , а также для x 5 . Почему? По определению функции распределения:
F ( 5) P( X 5) 0 – вы согласны? Функция F (x) возвращает вероятность того, что в точке x 5 выигрыш будет СТРОГО МЕНЬШЕ «минус» пяти.
Таким образом: F (x) 0 , если x 5 .
|
Внимание! Это демо-версия книги, полную и свежую версию курса можно найти здесь: http://mathprofi.com/knigi_i_kursy/ |
106 |

На интервале 5 x 2,5 функция F (x) P( X x) 0,5 , поскольку левее любой точки этого интервала есть только одно значение x1 5 случайной величины, которое появляется с вероятностью 0,5. Кроме того, сюда же следует отнести точку x 2,5 , так как:
F (2,5) P( X 2,5) 0,5 – очень хорошо осознайте этот момент!
Таким образом, если 5 x 2,5 , то F (x) 0,5
Далее рассматриваем промежуток 2,5 x 10 . СТРОГО ЛЕВЕЕ любой точки этого промежутка находятся два выигрыша x1 5, x2 2,5, поэтому:
F (x) P( X x) 0,5 0,4 0,9
И, наконец, если x 10 , то F (x) P( X x) 0,5 0,4 0,1 1 , ибо все значения x1 5, x2 2,5, x3 10 случайной величины X лежат СТРОГО левее любой точки интервала x (10; )
Заметим, кстати, важную особенность: коль скоро функция F (x) характеризует вероятность, то она может принимать значения лишь из промежутка 0 F (x) 1 – и никакие другие!
Итак, функция распределения вероятностей ДСВ является кусочной и, как многие знают, в таких случаях принято использовать фигурные скобки:
|
0, |
если |
x 5 |
|
если |
5 x 2,5 |
|
|
0,5, |
||
|
F (x) |
||
|
0,9, |
если |
2,5 x 10 |
|
1, |
если |
x 10 |
График данной функции имеет разрывный «ступенчатый» вид:
Причём, функция F (x) или её график однозначно определяют сам закон распределения: в точке x1 5 высота «ступеньки» (разрыв) составляет p1 0,5 (следим
|
по графику), в точке x2 2,5 «скачок» разрыва равен |
p2 0,4 |
и, наконец, в точке x3 10 |
|
он равен в точности p3 0,1. |
|
Внимание! Это демо-версия книги, полную и свежую версию курса можно найти здесь: http://mathprofi.com/knigi_i_kursy/ |
107 |
Таким образом, функция распределения вероятностей – это ещё один способ ЗАДАТЬ случайную величину. И этот способ особо важен для непрерывной случайной величины – по той причине, что её невозможно описать таблицей (ввиду бесконечного и несчётного количества принимаемых значений). Однако, всему своё время, и НСВ – тоже.
Освоим технические моменты решения типовой задачи:
Задача 93
Построить функцию распределения случайной величины X
Найти вероятности того, что случайная величина примет значение из следующих промежутков:
|
P( 1 X 5), |
P(4 X 10), |
P( X 2), |
|||||
|
P(3 X 7), |
P(X 7), |
P |
X M (X ) |
(X ) …, пожалуй, достаточно. |
|||
|
Решение: На практике удобно использовать формальный алгоритм построения |
|||||||
|
функции распределения: |
|||||||
|
Сначала берём первое значение x1 2 и составляем нестрогое неравенство |
|||||||
|
x 2 . На этом промежутке F (x) 0 . |
|||||||
|
На промежутке 2 x 0 (между x1 и x2 ): |
|||||||
|
На промежутке 0 x 3 (между x2 |
и x3 ): |
||||||
|
На промежутке 3 x 7 (между x3 |
и x4 ): |
И, наконец, если x строго больше самого последнего значения x4 7 , то:
Легко заметить, что с увеличением «икс» идёт накопление (суммирование) вероятностей, и поэтому функцию F (x) иногда называют интегральной функцией
распределения. В практических задачах проведённые выше действия обычно выполняют устно, а результат сразу записывают под единую скобку:
|
Внимание! Это демо-версия книги, полную и свежую версию курса можно найти здесь: http://mathprofi.com/knigi_i_kursy/ |
108 |
Закон распределения дискретной случайной величины можно представить в графическом виде с помощью декартова системой координат, то есть если по оси OY отложить вероятности этих значений pi, a по оси OX значения случайной величины xi и соединив точки между собой получим многоугольником распределения.
Многоугольник распределения является одной из форм закона распределения случайной величины.
Пример
Закон распределения случайной дискретной величины X задан в виде таблицы.
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| p | 0.05 | 0.2 | 0.3 | 0.2 | 0.15 | 0.1 |
Требуется построить многоугольник распределения дискретной случайной величины.
Решение
Для построения многоугольник распределения дискретной СВ воспользуемся прямоугольной (декартовой) системой координат и на графике отметим точки в соответствии с таблицей выше:
(0; 0,05), (1; 0,2), (2; 0,3), (3; 0,2), (4; 0,15) и (5; 0,1)
Соединив точки между собой, построим многоугольника распределения дискретной случайной величины
7221
Случайной называют величину, которая в результате испытания примет одно и только одно
возможное значение, наперед не известное и зависящее от случайных причин,
которые заранее не могут быть учтены.
Случайные
величины обозначаются прописными буквами
, а их возможные значения – соответствующими строчными буквами
. Например, если случайная величина
имеет три возможных
значения, то они будут обозначены так:
.
Дискретной называют случайную
величину, которая принимает отдельные, изолированные возможные значения с
определенными вероятностями. Число возможных значений дискретной случайной
величины может быть конечным или бесконечным.
Законом распределения дискретной
случайной величины называют соответствие между возможными значениями и их
вероятностями; его можно задать таблично, аналитически (в виде формулы) и
графически.
При табличном задании закона
распределения дискретной случайной величины первая строка таблицы содержит
возможные значения, а вторая – их вероятности:
|
|
|
|
… |
|
|
|
|
|
… |
|
Приняв во внимание, что в одном
испытании случайная величина принимает одно и только одно возможное значение,
заключаем, что события
образуют полную
группу; следовательно, сумма вероятностей этих событий, то есть сумма
вероятностей второй строки таблицы, равна единице:
Если множество возможных значений
бесконечно
(счетно), то ряд
сходится и его
сумма равна единице.
Для наглядности закон распределения
дискретной случайной величины можно изобразить и графически. Для этого в
прямоугольной системе координат строят точки
, а затем соединяют их отрезками прямых. Полученную
фигуру называют многоугольником распределения.
Смежные темы решебника:
- Непрерывная случайная величина
- Функция распределения вероятностей
- Математическое ожидание
- Дисперсия и среднее квадратическое отклонение
Задача 1
В партии
из 25 кожаных курток 5 имеют скрытый дефект. Покупают 3 куртки. Найти закон
распределения числа дефектных курток среди купленных. Построить многоугольник
распределения.
Задача 2
Устройство
состоит из пяти независимых элементов. Вероятность безотказной работы каждого
элемента в одном опыте равна p=0,7. Для случайной
величины X элементов, безотказно работавших в одном опыте,
построить закон распределения, их графики, найти ее числовые характеристики.
Задача 3
С
вероятностью попадания при явном выстреле p=0.88 охотник стреляет по
дичи до первого попадания, но успевает сделать не более n=6
выстрелов.
ДСВ X – число
промахов:
а) Найти
закон распределения X.
б)
Построить многоугольник распределения.
в) Найти
вероятность событий: X<2, X<3,
1<X<3.
Задача 4
Составьте
закон распределения дискретной случайной величины ξ, вычислите ее
математическое ожидание, медиану, дисперсию, среднее квадратическое отклонение,
коэффициенты асимметрии и эксцесса, все моменты, а также начертите ее
многоугольник распределения и график функции распределения. Сделайте выводы по
результатам расчетов.
Производятся
последовательные испытания 5 приборов, причем испытания прекращаются сразу
после того, как проверяемый прибор окажется надежным. Вероятность выдержать
испытание для каждого прибора равна 0,8.
ξ – число испытаний, после которых закончится проверка.
Задача 5
В первой урне
6 шаров – 3 белых и 3 черных. Во второй 5 шаров –3 белых и 2 черных. Из первой
урны наудачу переложили во вторую 2 шара, после чего, из второй в первую
переложили 1 шар. Найти закон распределения случайной величины Х – числа белых
шаров в первой урне, после всех перекладываний шаров. Какова вероятность того,
что число белых шаров не больше, чем первоначально. Построить многоугольник
распределения.
Задача 6
В коробке
N=9 карандашей, из которых M=6 красных. Из этой коробки
наудачу извлекается n=5 карандашей.
а) Найти
закон распределения случайной величины X равной числу красных
карандашей в выборке.
б)
Построить многоугольник распределения.
в) Найти
вероятность события: 0<X<4.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 7
Производятся
последовательные испытания 5 приборов, причем испытания прекращаются сразу
после того, как проверяемый прибор оказался надежным. Вероятность выдержать
испытание для каждого прибора равна 0,8. X – число испытаний, после
которых закончится проверка. Составьте закон распределения случайной величины X,
вычислите ее математическое ожидание, дисперсию, среднее квадратическое
отклонение, а также начертите ее многоугольник распределения и график функции
распределения.
Задача 8
Проведено
n=5 независимых опытов. Вероятность взрыва в каждом опыте равна p=2/7.
Составить закон распределения числа взрывов, вычислить математическое ожидание,
дисперсию, среднеквадратическое отклонение и построить многоугольник
распределения.
Задача 9
Найти закон
распределения указанной дискретной СВ X и ее функции. распределения
F(x). Вычислить математическое ожидание М(Х), дисперсию D(X) и
среднее квадратичное отклонение σ(Х). Построить график
функции распределения F(x).
Вероятность отказа прибора за время испытания
на надежность равна 0,2; СВ Х – число приборов, отказавших в работе, среди 5
испытываемых.
Задача 10
В интернет-магазине
приобретается смартфон. Курьер приносит на дом покупателю 5 одинаковых
смартфонов, среди которых три (заранее неизвестно какие) бракованные.
Покупатель проверяет один за другим, пока не найдет хороший прибор, но делает
не более трех попыток.
Составить
закон распределения случайной величины – числа произведенных попыток.
Найти ее
математическое ожидание, дисперсию, среднее квадратическое отклонение.
Построить
функцию распределения.
Задача 11
В команде
9 спортсменов, из них 4 – первого разряда и 5 – второго. Наудачу отобраны 3
спортсмена. Найти ряд распределения дискретной случайной величины Х – числа
спортсменов второго разряда среди отобранных.
Задача 12
К контролеру с конвейера поступили 4 детали.
Вероятность брака для каждой детали равна 0,1. Детали проверяют одну за другой,
пока не наберут 2 доброкачественные.
Найти закон распределения вероятностей для числа проверенных деталей.
Задача 13
Двое рабочих,
выпускающих однотипную продукцию, допускают производство изделий второго сорта
с вероятностями соответственно равными 0,4 и 0,3. У каждого рабочего взято по 2
изделия. Для случайной величины Х –
числа изделий второго сорта среди отобранных для проверки четырех найти закон
распределения, математическое ожидание и дисперсию.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
На викторине
задаются 3 вопроса. Вероятность правильно ответить на первый – p, на
второй – r, на третий – s. После неправильного
ответа игрок выбывает из игры. Найти распределение числа правильных ответов.
Вычислить математическое ожидание. Решить задачу, если:
а) p=0.7; r=0.6; s=0.3;
б)
p=0.8; r=0.4; s=0.1.
Задача 15
На
некоторой остановке автобус останавливается только по требованию. Вероятность
остановки равна 0,2. За смену автобус проходит мимо этой остановки 5 раз.
Составить закон распределения числа остановки за смену, найти математическое
ожидание и дисперсию этой случайной величины.
Задача 16
Вероятность
того, что при составлении бухгалтерского баланса допущена ошибка, равна 0,3.
Аудитору на заключение представлено 3 баланса предприятия. Составить закон
распределения числа положительных заключений на проверяемые балансы.
Задача 17
Два товароведа
проверяют партию изделий. Производительность их труда соотносится как 5:4.
Вероятность определения брака первым товароведом составляет 85%, вторым – 90%.
Из проверенных изделий отбирают четыре. Найти а) математическое ожидание и б)
дисперсию числа годных изделий среди отобранных.
Задача 18
Два
станка выпускают детали с вероятностями брака 0,01 и 0,05 соответственно. В
выборке одна деталь выпущена первым станком и две – вторым. Найти распределение числа бракованных деталей
в выборке.
Задача 19
Монета
подбрасывается до тех пор, пока герб не выпадет 2 раза, но при этом делается не
более 4 бросаний. Найти распределение числа подбрасываний.
Задача 20
Вероятность
сдачи данного экзамена для каждого из n=5 студентов равна p=0.6.
Случайная величина X (СВ X) – число студентов, сдавших экзамен. Найти закон
распределения указанной дискретной СВ X и ее функцию распределения F(x).
Вычислить математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x). Построить график функции распределения F(x).