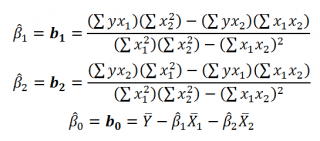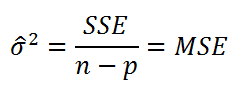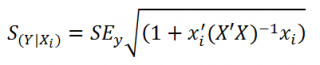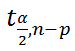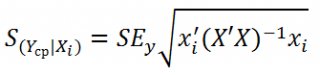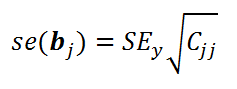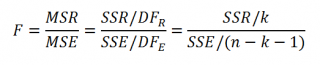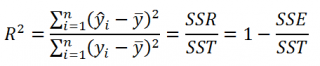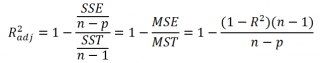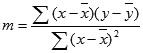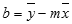Множественная линейная регрессия — это метод, который мы можем использовать для понимания взаимосвязи между двумя или более независимыми переменными и переменной отклика .
В этом руководстве объясняется, как выполнить множественную линейную регрессию в Excel.
Примечание. Если у вас есть только одна независимая переменная, вам следует вместо этого выполнить простую линейную регрессию .
Пример: множественная линейная регрессия в Excel
Предположим, мы хотим знать, влияет ли количество часов, потраченных на учебу, и количество сданных подготовительных экзаменов на балл, который студент получает на определенном вступительном экзамене в колледж.
Чтобы исследовать эту взаимосвязь, мы можем выполнить множественную линейную регрессию, используя часы обучения и подготовительные экзамены, взятые в качестве объясняющих переменных, и экзаменационный балл в качестве переменной ответа.
Выполните следующие шаги в Excel, чтобы провести множественную линейную регрессию.
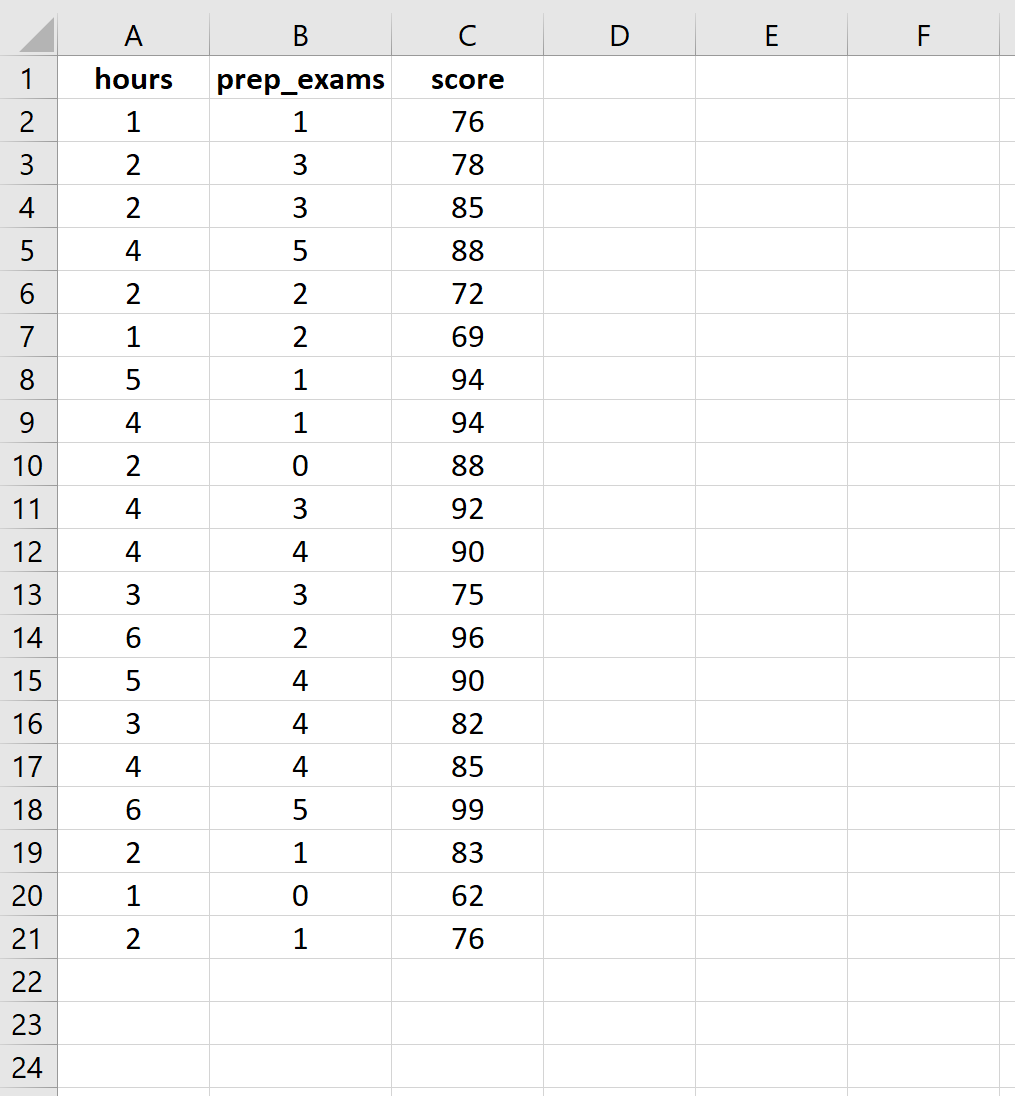
Шаг 1: Введите данные.
Введите следующие данные для количества часов обучения, сданных подготовительных экзаменов и результатов экзаменов, полученных для 20 студентов:
Шаг 2: Выполните множественную линейную регрессию.
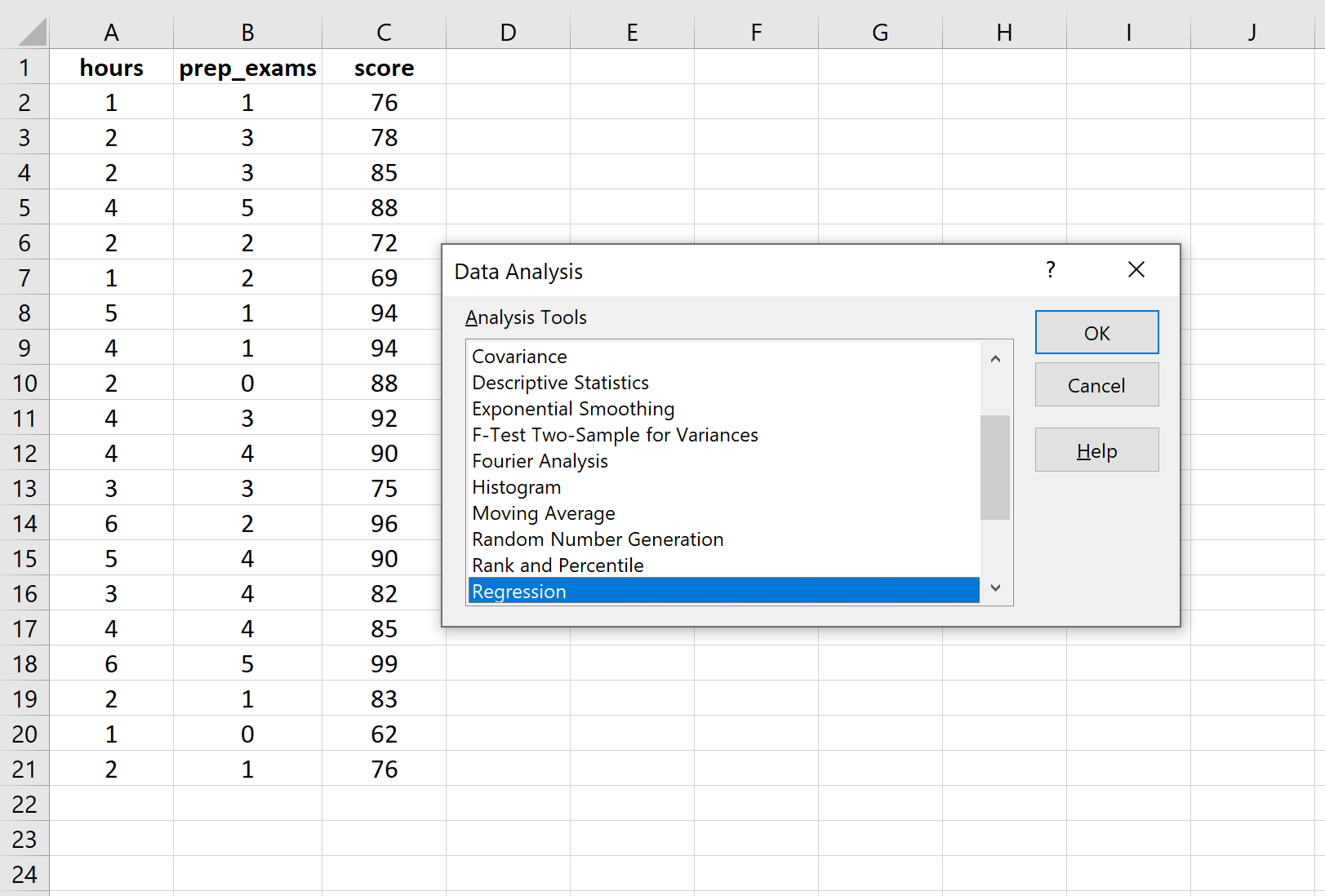
В верхней ленте Excel перейдите на вкладку « Данные » и нажмите « Анализ данных».Если вы не видите эту опцию, вам необходимо сначала установить бесплатный пакет инструментов анализа .
Как только вы нажмете « Анализ данных», появится новое окно. Выберите «Регрессия» и нажмите «ОК».
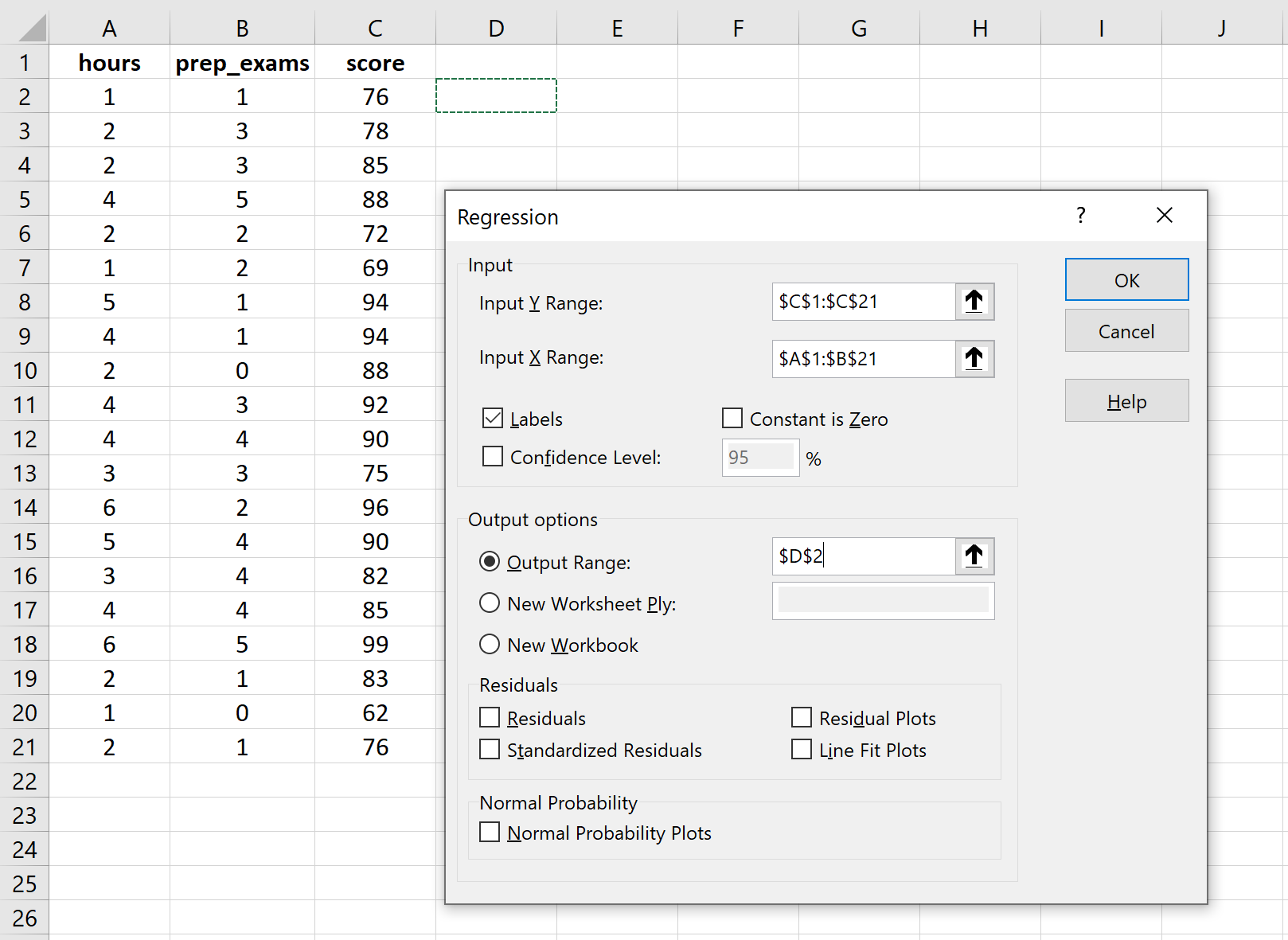
Для Input Y Range заполните массив значений для переменной ответа. Для Input X Range заполните массив значений для двух независимых переменных. Установите флажок рядом с Метки , чтобы Excel знал, что мы включили имена переменных во входные диапазоны. В поле Выходной диапазон выберите ячейку, в которой должны отображаться выходные данные регрессии. Затем нажмите ОК .
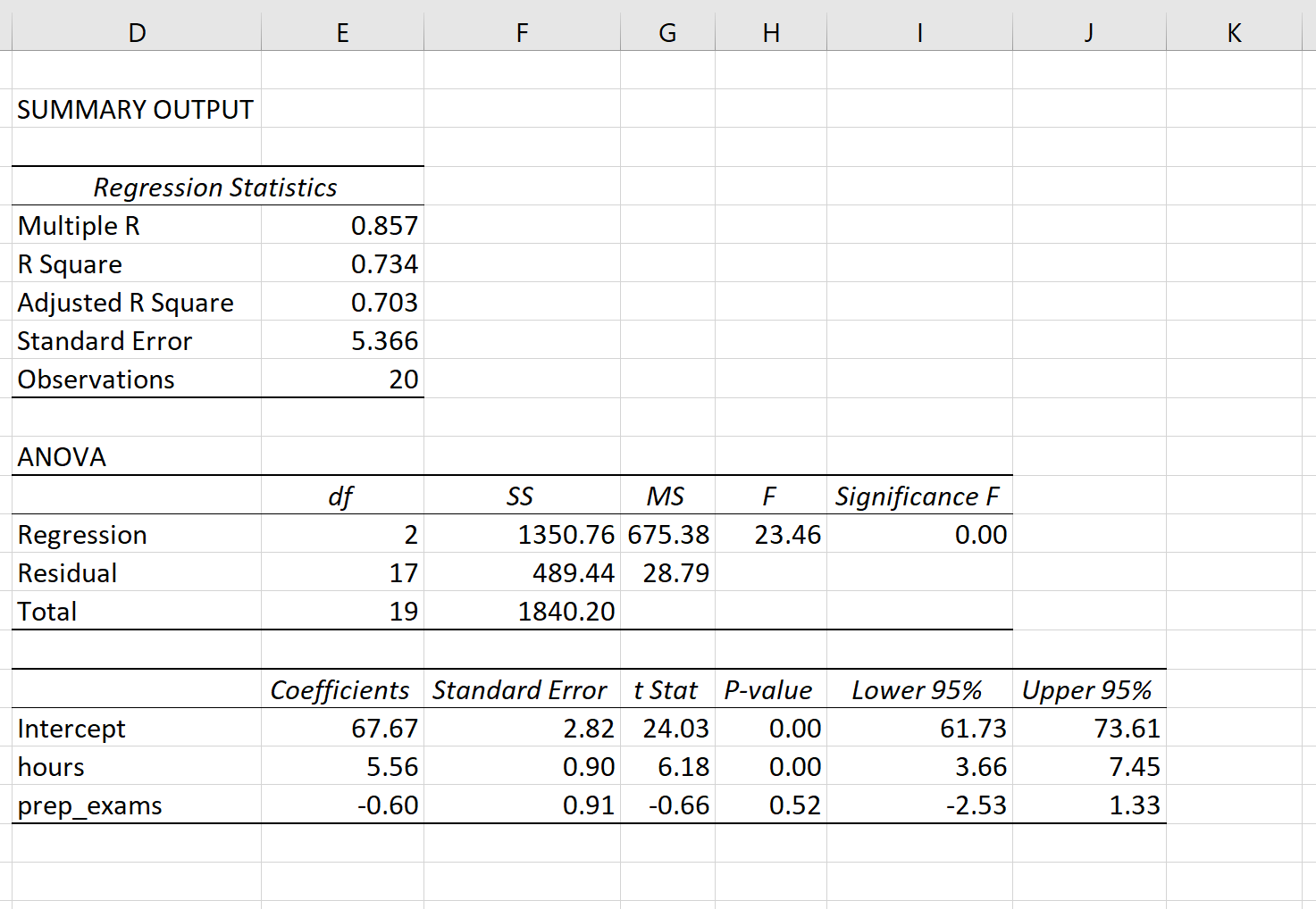
Автоматически появится следующий вывод:
Шаг 3: Интерпретируйте вывод.
Вот как интерпретировать наиболее релевантные числа в выводе:
R-квадрат: 0,734.Это известно как коэффициент детерминации. Это доля дисперсии переменной отклика, которая может быть объяснена объясняющими переменными. В этом примере 73,4% вариаций в экзаменационных баллах можно объяснить количеством часов обучения и количеством сданных подготовительных экзаменов.
Стандартная ошибка: 5,366.Это среднее расстояние, на которое наблюдаемые значения отходят от линии регрессии. В этом примере наблюдаемые значения отклоняются от линии регрессии в среднем на 5,366 единицы.
Ф: 23,46.Это общая F-статистика для регрессионной модели, рассчитанная как MS регрессии / остаточная MS.
Значение F: 0,0000.Это p-значение, связанное с общей статистикой F. Он говорит нам, является ли регрессионная модель в целом статистически значимой. Другими словами, он говорит нам, имеют ли объединенные две объясняющие переменные статистически значимую связь с переменной отклика. В этом случае p-значение меньше 0,05, что указывает на то, что независимые переменные количество часов обучения и сданных подготовительных экзаменов вместе имеют статистически значимую связь с экзаменационным баллом .
P-значения. Отдельные p-значения говорят нам, является ли каждая независимая переменная статистически значимой. Мы можем видеть, что изученные часы статистически значимы (p = 0,00), в то время как пройденные подготовительные экзамены (p = 0,52) не являются статистически значимыми при α = 0,05. Поскольку сданные подготовительные экзамены не являются статистически значимыми, мы можем принять решение удалить их из модели.
Коэффициенты: коэффициенты для каждой независимой переменной говорят нам о среднем ожидаемом изменении переменной отклика при условии, что другая независимая переменная остается постоянной. Например, ожидается, что за каждый дополнительный час, потраченный на учебу, средний экзаменационный балл увеличится на 5,56 при условии, что количество сданных подготовительных экзаменов останется неизменным.
Вот еще один способ подумать об этом: если учащийся А и учащийся Б сдают одинаковое количество подготовительных экзаменов, но учащийся А учится на один час больше, то ожидается, что учащийся А получит результат на 5,56 балла выше, чем учащийся Б.
Мы интерпретируем коэффициент для перехвата как означающий, что ожидаемая оценка экзамена для студента, который учится ноль часов и сдает нулевые подготовительные экзамены, составляет 67,67 .
Расчетное уравнение регрессии: мы можем использовать коэффициенты из выходных данных модели, чтобы создать следующее расчетное уравнение регрессии:
экзаменационный балл = 67,67 + 5,56*(часы) – 0,60*(подготовительные экзамены)
Мы можем использовать это оценочное уравнение регрессии, чтобы рассчитать ожидаемый балл экзамена для учащегося на основе количества часов, которые он изучает, и количества подготовительных экзаменов, которые он сдает. Например, студент, который занимается три часа и сдает один подготовительный экзамен, должен получить 83,75 балла:
экзаменационный балл = 67,67 + 5,56*(3) – 0,60*(1) = 83,75
Имейте в виду, что, поскольку пройденные подготовительные экзамены не были статистически значимыми (p = 0,52), мы можем решить удалить их, поскольку они не улучшают общую модель. В этом случае мы могли бы выполнить простую линейную регрессию, используя только часы изучения в качестве независимой переменной.
С результатами этого простого линейного регрессионного анализа можно ознакомиться здесь .
Дополнительные ресурсы
После выполнения множественной линейной регрессии есть несколько предположений, которые вы можете проверить, в том числе:
1. Тестирование на мультиколлинеарность с помощью VIF .
2. Тестирование на гетеродескедастичность с помощью теста Бреуша-Пагана .
3. Проверка нормальности с использованием графика QQ .
Рассмотрим использование
MS
EXCEL
для прогнозирования переменной
Y
на основании нескольких переменных Х, т.е. множественную регрессию.
Перед прочтением этой статьи рекомендуется освежить в памяти
простую линейную регрессию
– прогнозирование на основе значений только одного фактора.
Disclaimer
: Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей
Множественного регрессионного анализа.
Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения
Регрессии
– плохая идея.
Статья про
Множественный регрессионный анализ
получилась большая, поэтому ниже для удобства приведены ее разделы:
- Оценка неизвестных параметров
- Диаграмма рассеяния
-
Вычисление прогнозных значений Y
(отдельное наблюдение и среднее значение) и построение доверительных интервалов
- Стандартные ошибки и доверительные интервалы для коэффициентов регрессии
- Проверка гипотез
- Генерация данных для множественной регрессии с помощью заданного тренда
- Коэффициент детерминации
Прогнозирование единственной переменной Y на основании значений 2-х или более переменных Х называется
множественной регрессией
.
Множественная линейная регрессионная модель
(Multiple Linear Regression Model)
имеет вид Y=β
0
+β
1
*X
1
+β
2
*X
2
+…+β
k
*X
k
+ε. В этом случае переменная Y зависит от k поясняющих переменных Х, т.е.
регрессоров
. ε –
случайная ошибка
. Модель является линейной относительно неизвестных параметров β.
Оценка неизвестных параметров
В этой статье рассмотрим модель с 2-мя регрессорами. Сначала введем необходимые обозначения и понятия множественной регрессии.
Для описания зависимости Y от 2-х переменных
линейная модель
имеет вид:
Y=β
0
+β
1
*X
1
+β
2
*X
2
+ε.
Параметры этой модели β
i
нам неизвестны, но их можно оценить, используя случайную выборку (измеренные значения переменной Y от заданных Х). Оценки параметров модели (β
0
, β
1
, β
2
) обычно вычисляются
методом наименьших квадратов (МНК)
, который минимизирует сумму квадратов ошибок прогнозирования (критерий минимизации в англоязычной литературе обозначают как SSE – Sum of Squared Errors).
Соответствующие оценки параметров будем обозначать как
b
0
,
b
1
и
b
2
.
Ошибка ε имеет случайную природу и имеет свою функцию распределения со
средним значением
=0 и
дисперсией σ
2
.
Оценки
b
1
и
b
2
называются
коэффициентами регрессии
, они определяют влияние соответствующей переменной X, когда все остальные независимые переменные остаются
неизменными
.
Сдвиг (intercept)
или
постоянный
член
b
0
, определяет прогнозируемое значение Y, когда все поясняющие переменные Х равны 0 (часто
сдвиг
не имеет физического смысла в рамках модели и обусловлен лишь математическими вычислениями
МНК
).
Вычислив оценки, полученные методом
МНК,
позволяют прогнозировать значения переменной Y:
Y=
b
0
+
b
1
*X
1
+
b
2
*X
2
Примечание
: Для случая 2-х регрессоров, все спрогнозированные значения переменной Y будут лежать в плоскости (в
плоскости регрессии
).
В качестве примера рассмотрим технологический процесс изготовления нити:
Инженер, на основе имеющегося опыта, предположил, что
прочность нити
Y зависит от
концентрации исходного раствора
(Х
1
) и
температуры реакции
(Х
2
), и соответствует модели линейной регрессии. Для нахождения комбинации переменных Х, при которых Y принимает максимальное значение, необходимо определить коэффициенты регрессии, сделав выборку.
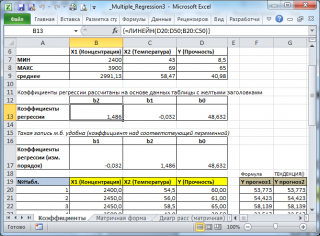
В MS EXCEL
коэффициенты множественной регрессии
удобнее всего вычислить с помощью функции
ЛИНЕЙН()
. Это сделано в
файле примера на листе Коэффициенты
. Чтобы вычислить оценки:
-
выделите 3 ячейки в одной строке (т.к. мы рассматриваем случай 2-х регрессоров, то будут вычислены 2
коэффициента регрессии
+
величина сдвига
= 3 значения, для вывода которых понадобится 3 ячейки). Пусть это будет диапазон
С8:Е8
; -
в
Строке формул
введите =
ЛИНЕЙН(D20:D50;B20:C50)
. Предполагается, что в столбце
В
содержатся прогнозируемые значения Y (в нашей модели это Прочность нити), в столбцах
С
и
D
содержатся значения контролируемых параметров Х (Х1 – Концентрация в столбце С и Х2 – Температура в столбце D). -
нажмите
CTRL
+
SHIFT
+
ENTER
(т.к. этоформула массива
).
В левой ячейке будет рассчитано значение
коэффициента регрессии
b
2
для переменной Х2, в средней ячейке – значение
коэффициента регрессии
b
1
для переменной Х1, в правой –
сдвиг
. Обратите внимание, что порядок вывода
коэффициентов
регрессии
обратный по отношению к расположению столбцов с данными соответствующих переменных Х (вычисленный коэффициент
b
2
располагается
левее
по отношению к
b
1
, тогда как значения переменной Х2 располагаются
правее
значений переменной Х1). Это может привести к путанице, поэтому лучше разместить коэффициенты над соответствующими столбцами с данными, как это сделано в строке 17
файла примера
.
Примечание
: В принципе без функции
ЛИНЕЙН()
можно обойтись, записав альтернативные формулы. Для этого в
файле примера на листе Коэффициенты
в столбцах
I
:
K
вычислены отклонения значений переменных Х
1i
, Х
2i
, Y
i
от их средних значений
, т.е.:
Далее коэффициенты регрессии рассчитываются по следующим формулам (эти формулы справедливы только при прогнозировании по 2-м независимым переменным Х):
При прогнозировании по 3-м и более независимым переменным Х формулы для вычисления
коэффициентов регрессии
значительно усложняются, поэтому следует использовать матричный подход.
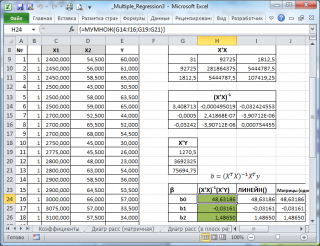
В
файле примера на листе Матричная форма
выполнены расчеты
коэффициентов регрессии
с помощью матричного подхода.
Расчет можно произвести как пошагово, так и одной
формулой массива
:
=МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП(B9:D33);(B9:D33)));МУМНОЖ(ТРАНСП(B9:D33);(E9:E33)))
Коэффициенты регрессии
(вектор
b
)
в этом случае вычисляются по формуле
b
=(X
T
X)
-1
(X
T
Y) или в другом виде записи
b
=(X
’
X)
-1
(X
’
Y)
Под Х подразумевается матрица, состоящая из столбцов значений переменной Х с дополнительным столбцом единиц, а под Y – вектор-столбец значений Y.
Символ
Т
или ‘ – это
транспонирование матрицы
, а обозначение
-1
говорит о
вычислении обратной матрицы
.
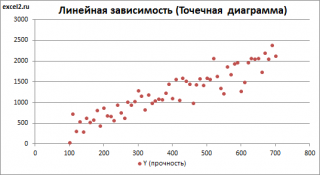
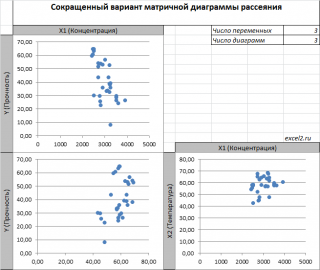
Диаграмма рассеяния
В случае
простой линейной регрессии
(один регрессор, т.е. одна переменная Х) для визуализации связи между прогнозируемым значением Y и переменной Х строят
диаграмму рассеяния
(двумерную).
В случае
множественной
линейной регрессии
двумерную диаграмму рассеяния можно построить только для анализа влияния каждого отдельного регрессора на Y (при этом остальные Х не меняются), т.е. так называемую Матричную диаграмму рассеивания (См.
файл примера лист Диагр расс (матричная)
).
К сожалению, такую диаграмму трудно интерпретировать.
Более того, матричная диаграмма может вводить в заблуждение (см.
Introduction
to
linear
regression
analysis
/
D
.
C
.
Montgomery
,
E
.
A
.
Peck
,
G
.
G
.
Vining
, раздел 3.2.5
), демонстрируя наличие или отсутствие линейной взаимосвязи между отдельным регрессором X
i
и Y.
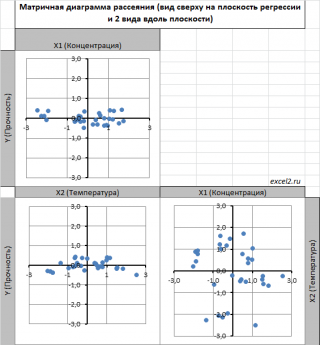
Для случая с 2-мя регрессорами можно предложить альтернативный вид матричной
диаграммы рассеяния
. В стандартной диаграмме рассеяния строятся проекции на координатные плоскости Х1;Х2, Y;X1 и Y;X2. Однако, если взглянуть на точки относительно
плоскости регрессии
, то картину, на мой взгляд, будет проще интерпретировать.
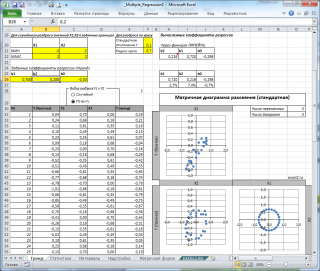
Сравним две матричные диаграммы рассеяния (см.
файл примера на листе «Диагр расс (в плоск регрессии)»
, построенные для одних и тех же наблюдений. Первая – стандартная,
вторая представляет собой вид сверху на плоскость регрессии и 2 вида вдоль плоскости.
На второй диаграмме становится очевидно, что разброс точек относительно плоскости регрессии совсем не большой и поэтому, скорее всего, построенная модель является полезной, а выбранные 2 переменные Х позволяют прогнозировать Y (конечно, для подтверждения этой гипотезы нужно
провести процедуру F-теста
).
Несколько слов о построении альтернативной матричной диаграммы рассеяния:
-
Перед построением необходимо нормировать значения наблюдений (для каждой переменной вычесть
среднее
и разделить на
стандартное отклонение
). В этом случае практически все точки на диаграммах будут находится в диапазоне +/-3 (по аналогии со
стандартным нормальным распределением
, 99% значений которого лежат в пределах +/-3 сигма). В этом случае, на диаграмме можно фиксировать мин/макс значений осей, чтобы EXCEL автоматически не модифицировал масштаб осей при изменении данных (это не всегда удобно);
-
Теперь координаты точек необходимо рассчитать в системе отсчета относительно плоскости регрессии (в которой плоскость Оху’ совпадает с плоскостью регрессии). Для этого необходимо найти
матрицу вращения
, например, через вращение приводящее к совмещению нормали к плоскости регрессии и вектора оси Z (0;0;1);
-
Новые координаты позволяют построить альтернативную матричную диаграмму. Кроме того, для удобства можно вращать систему координат вокруг новой оси Z, чтобы нагляднее представить себе распределение точек относительно плоскости регрессии (для этого использована Полоса прокрутки в ячейках
Q
31:
S
31
).
Вычисление прогнозных значений Y (отдельное наблюдение и среднее значение) и построение доверительных интервалов
После того, как нами были найдены тем или иным способом коэффициенты регрессии можно приступать к вычислению прогнозных значений Y на основе заданных значений переменных Х.
Уравнение прогнозирования или уравнение регрессии в случае 2-х независимых переменных (регрессоров) записывается в виде:
Y=
b
0
+
b
1
*
Х
1
+
b
2
*
Х
2
Примечание:
В MS EXCEL
прогнозное значение Y для заданных Х
1
и Х
2
можно также предсказать с помощью функции
ТЕНДЕНЦИЯ()
. При этом 2-й аргумент будет ссылкой на столбцы, содержащие все значения переменных Х
1
и Х
2
, а 3-й аргумент функции должен быть ссылкой на диапазон ячеек, содержащий 2 значения Х (Х
1i
и Х
2i
) для выбранного наблюдения i (см.
файл примера, лист Коэффициенты, столбец G
). Функция
ПРЕДСКАЗ()
, использованная нами в простой регрессии, не работает в случае
множественной регрессии
.
Найдя прогнозное значение Y, мы, таким образом, вычислим его точечную оценку. Понятно, что фактическое значение Y, полученное при наблюдении, будет, скорее всего, отличаться от этой оценки. Чтобы ответить на вопрос о том, на сколько хорошо мы можем предсказывать новые значения Y, нам потребуется построить
доверительный интервал
этой оценки, т.е. диапазон в котором с определенной заданной вероятностью, скажем 95%, мы ожидаем новое значение Y.
Доверительные интервалы
построим при фиксированном Х для:
- нового наблюдения Y;
- среднего значения Y (интервал будет уже, чем для отдельного нового наблюдения)
Как и в случае
простой линейной регрессии
, для построения
доверительных интервалов
нам потребуется сначала вычислить
стандартную ошибку модели
(standard error of the model)
, которая приблизительно показывает насколько велика ошибка предсказания значений переменной Y на основании значений переменных Х.
Для вычисления
стандартной ошибки
оценивают
дисперсию
ошибки ε, т.е. сигма^2
(ее часто обозначают как
MS
Е либо
MSres
)
. Затем, вычислив из полученной оценки квадратный корень, получим
Стандартную ошибку регрессии (часто обозначают как
SEy
или
sey
).
где SSE – сумма квадратов значений ошибок модели ei=yi – ŷi (
Sum of Squared Errors
). MSE означает Mean Square of Errors (среднее квадратов ошибок, точнее остатков).
Величина n-p – это количество
степеней свободы
(
df
–
degrees
of
freedom
), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y, р – количество оцениваемых параметров модели). В случае
простой множественной регрессии
с 2-мя регрессорами
число степеней свободы
равно n-3, т.к. при построении
плоскости регрессии
было оценено 3 параметра модели
b
(т.е. на это было «потрачено» 3
степени свободы
).
В MS EXCEL
стандартную ошибку
SEy можно вычислить формулы (см.
файл примера, лист Статистика
):
=
ИНДЕКС(ЛИНЕЙН($E$13:$E$43;$C$13:$D$43;;ИСТИНА);3;2)
Стандартная ошибка
нового наблюдения Y при заданных значениях Х (вектор Хi) вычисляется по формуле:
x
i
– вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.
Соответствующий доверительный интервал вычисляется по формуле:
где α (альфа) –
уровень значимости
(обычно принимают равным 0,05=5%)
р – количество оцениваемых параметров модели (в нашем случае = 3)
n-p – число степеней свободы
–
квантиль
распределения Стьюдента
(задает количество
стандартных ошибок
, в +/- диапазоне которых вероятность обнаружить новое наблюдение равно 1-альфа). Т.е. если
квантиль
равен 2, то диапазон шириной +/- 2
стандартных ошибок
относительно прогнозного значения Y будет с вероятностью 95% содержать новое наблюдение Y (для каждого заданного Хi). В MS EXCEL вычисления квантиля производят по формуле =
СТЬЮДЕНТ.ОБР.2Х(0,05;n-p)
, подробнее см.
в статье про распределение Стьюдента
.
– прогнозное значение Yi вычисляемое по формуле Yi=
b
0+
b
1*
Х1i+
b
2*
Х2i (точечная оценка).
Стандартная ошибка
среднего значения Y при заданных значениях Х (вектор Хi) будет меньше, чем стандартная ошибка отдельного наблюдения. Вычисления производятся по формуле:
x
i
– вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.
Соответствующий
доверительный интервал
вычисляется по формуле:
Прогнозное значение Yi (точечная оценка) используется тоже, что и для отдельного наблюдения.
Стандартные ошибки и доверительные интервалы для коэффициентов регрессии
В разделе
Оценка неизвестных параметров
мы получили точечные оценки
коэффициентов регрессии
. Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со
средним значением
и
дисперсией
. Но, чтобы перейти от
точечных оценок
к
интервальным
, необходимо вычислить соответствующие
стандартные ошибки
(т.е.
стандартные отклонения
)
коэффициентов регрессии
.
Стандартная ошибка коэффициента регрессии
b
j
(обозначается
se
(
b
j
)
) вычисляется на основании
стандартной ошибки
по следующей формуле:
где C
jj
является диагональным элементом матрицы (X
’
X)
-1
. Для коэффициента сдвига
b
0
индекс j=1 (верхний левый элемент), для
b
1
индекс j=2,
b
2
индекс j=3 (нижний правый элемент).
SEy –
стандартная ошибка регрессии
(см.
выше
).
В MS EXCEL
стандартные ошибки коэффициентов регрессии
можно вычислить с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН($E$13:$E$43;$C$13:$D$43;;ИСТИНА);2;j)
Примечание
: Подробнее о функции
ЛИНЕЙН()
см. статью
Функция MS EXCEL ЛИНЕЙН()
.
Применяя матричный подход
стандартные ошибки
можно вычислить и через обычные формулы (точнее через
формулу массива
, см.
файл примера лист Статистика
):
=
КОРЕНЬ(СУММКВРАЗН(E13:E43;F13:F43) /(n-p)) *КОРЕНЬ (ИНДЕКС (МОБР (МУМНОЖ(ТРАНСП(B13:D43);(B13:D43)));j;j))
При построении
двухстороннего доверительного интервала
для
коэффициента регрессии
его границы определяются следующим образом:
b
j
+/- t*Se(
b
j
)
где t – это
t-значение
, которое можно вычислить с помощью формулы =
СТЬЮДЕНТ.ОБР.2Х(0,05;n-p)
для
уровня значимости
0,05.
В результате получим, что найденный
доверительный интервал
с вероятностью 95% (1-0,05) накроет истинное значение
коэффициента регрессии
b
j
.
Здесь мы считаем, что
коэффициент регрессии
b
j
имеет
распределение Стьюдента
с n-p
степенями свободы
(n – количество наблюдений, т.е. пар Х и Y).
Проверка гипотез
Когда мы строим модель, мы предполагаем, что между Y и переменными X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X, возможен, когда все
коэффициенты регрессии
β
равны 0.
Чтобы убедиться, что вычисленная нами оценка
коэффициентов регрессии
не обусловлена лишь случайностью (они не случайно отличны от 0), используют
проверку гипотез
. В качестве
нулевой гипотезы
Н
0
принимают, что линейной связи нет, т.е. ВСЕ β=0. В качестве альтернативной гипотезы
Н
1
принимают, что ХОТЯ БЫ ОДИН коэффициент β <>0.
Процедура проверки значимости множественной регрессии, приведенная ниже, является обобщением
дисперсионного анализа
, использованного нами в случае
простой линейной регрессии (F-тест)
.
Если нулевая гипотеза справедлива, то
тестовая
F
-статистика
имеет
F-распределение
со степенями свободы
k
и
n
–
k
-1
, т.е. F
k, n-k-1
:
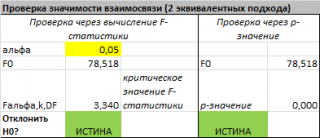
Проверку значимости регрессии можно также осуществить через вычисление
p
-значения
. В этом случае вычисляют вероятность того, что случайная величина F примет значение F
0
(это и есть
p-значение
), затем сравнивают p-значение с заданным
уровнем значимости α (альфа)
. Если
p-значение
больше уровня значимости
,
то нулевую гипотезу нет оснований отклонить, и регрессия незначима.
В MS EXCEL значение F
0
можно вычислить на основании значений выборки по вышеуказанной формуле или с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(E13:E43; C13:D43;;ИСТИНА);4;1)
В MS EXCEL для проверки гипотезы через
p
-значение
используйте формулу =F.РАСП.ПХ(F
0
;k;n-k-1)<
альфа
Если формула вернет ИСТИНА, то регрессия значима. Если формула вернет ЛОЖЬ, то у нас нет оснований отклонить нулевую гипотезу, т.е. «скорее всего» все коэффициенты регрессии равны 0 (см.
файл примера лист Статистика
, где показано эквивалентность обоих подходов проверки значимости регрессии).
В MS EXCEL критическое значение для заданного
уровня значимости
F
1-альфа, k, n-k-1
можно вычислить по формуле =
F.ОБР(1- альфа;k;n-k-1)
или =
F.ОБР.ПХ(альфа;k; n-k-1)
. Другими словами требуется вычислить
верхний альфа-
квантиль
F
-распределения
с соответствующими
степенями свободы
.
Таким образом, при значении статистики F
0
> F
1-альфа, k, n-k-1
мы имеем основание для отклонения нулевой гипотезы.
В программах статистики результаты процедуры
F
-теста
выводят с помощью стандартной таблицы
дисперсионного анализа
. В
файле примера такая таблица приведена на листе Надстройка
, которая построена на основе результатов, возвращаемых инструментом
Регрессия надстройки Пакета анализа MS EXCEL
.
Генерация данных для множественной регрессии с помощью заданного тренда
Иногда, бывает удобно сгенерировать значения наблюдений, имея заданный тренд.
Для решения этой задачи нам потребуется:
- задать значения регрессоров в нужном диапазоне (значения переменных Х);
-
задать коэффициенты регрессии (
b
); -
задать тренд (вычислить значения Y=
b
0
+
b
1
*
Х
1
+
b
2
*
Х
2
); - задать величину разброса Y вокруг тренда (варианты: случайный разброс в заданных границах или заданная фигура, например, круг)
Все вычисления выполнены в
файле примера, лист Тренд
для случая 2-х регрессоров. Там же построены
диаграммы рассеяния
.
Коэффициент детерминации
Коэффициент детерминации
R
2
показывает насколько полезна построенная нами
линейная регрессионная модель
.
По определению
коэффициент детерминации
R
2
равен:
R
2
=
Изменчивость объясненная моделью (
SSR
) / Общая изменчивость (
SST
).
Этот показатель можно вычислить с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(E13:E43;C13:D43;;ИСТИНА);3)
При добавлении в модель новой объясняющей переменной Х,
коэффициент детерминации
будет всегда расти. Поэтому, рост
коэффициента детерминации
не может служить основанием для вывода о том, что новая модель (с дополнительным регрессором) лучше прежней.
Более подходящей статистикой, которая лишена указанного недостатка, является
нормированный
коэффициент детерминации
(Adjusted R-squared):
где p – число независимых
регрессоров
(вычисления см.
файл примера лист Статистика
).
Видео занятия
Строим корреляционную матрицу. Для этого используем надстройку «Анализ данных»
Выбираем в диалоговом окне «Анализа данных» – корреляция.
Далее заполняем диалоговое окно:
Получим корреляционную матрицу:
Наблюдается тесная связь между переменной Y и Х1, Y и X2, так как попарные коэффициенты корреляции составляют 0,8602 и 0,7479 соответственно. Это выше 0,7 – связь достаточно тесная.
Межу объясняющими переменными Х1 и Х2 коэффициент составляет 0,6311. Он ниже других, но имеет значение больше 0,6. Значит между объясняющими переменными, может быть корреляционная связь (явление мультиколлинеарности). Для обнаружения мультиколлинеарности есть ряд критериев, например VIF-критерий.
Парные коэффициенты корреляции можно ещё найти с помощью статистической функции КОРРЕЛ.
Заполняем диалоговое окно статистической функции КОРРЕЛ.
Получаем тоже значение, что и корреляционной матрице для Y и X1: 0,860227
Аналогично по отдельности можем найти и другие парные коэффициенты корреляции.
Строим множественную регрессию. Для этого в надстройке «Анализ данных» выбираем регрессия. Заполняем диалоговое окно.
Выбираем уровень надёжности 98%. Для коэффициентов регрессии будет найден доверительный интервал с уровнем с доверительной вероятностью 98%. Так же выбираем остатки, график остатков. Эти данные необходимы нам для дальнейшего анализа во второй части.
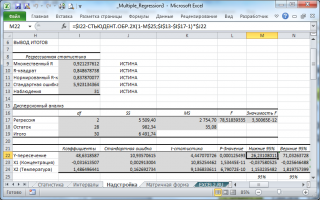
Получим.
Проведём анализ полученных данных.
Здесь выводятся: множественный коэффициент корреляции, коэффициент детерминации (R-квадрат), скорректированный коэффициент детерминации (нормированный R-квадрат), стандартная ошибка регрессии (S).
R-квадрат = RSS/TSS
Стандартная ошибка = (ESS/(n-m-1))^0.5
ESS (error sum of squares) – остаточная сумма квадратов.
Построенное уравнение регрессии объясняет изменение результативного показателя Y на 80,99%. Остальные 10,01% приходятся на случайные факторы и факторы не включённые в модель.
Здесь даны столбцы: со степенями свободы (df); суммой квадратов (SS), суммой квадратов, делённых на степень свободы (MS=SS/df). Так же дано значение F-критерия Фишера и вероятность принятия нулевой гипотезы о равенстве коэффициента детерминации нулю (Значимость F).
TSS (total sum of squares) – общая сумма квадратов отклонений зависимой переменной от средней или вся дисперсия зависимой переменной;
RSS (regression sum of squares) – сумма квадратов, обусловленная регрессией или объясненная часть всей дисперсии;
ESS (error sum of squares) – остаточная сумма квадратов, характеризующая влияние неучтенных факторов или необъясненная дисперсия.
F= (ESS/m)/(RSS/(n-m-1)), n=32 m=2
Значимость F= 3,51562998617576E-11 <<<<0.01. Не можем принять нулевую гипотезу, принимаем альтернативную. Коэффициент детерминации отличен от нуля. Уравнение значимо в целом.
Так же можно сравнить наблюдаемое значение F-критерия с критическим. Берём уровень значимости 0,01, число степеней свободы 2 и 29. И с помощью статистической функции F.ОБР.ПХ находим критическое значение распределения Фишера
F.ОБР.ПХ(0,01;2;29) = 5,420445
Наблюдаемое значение оказалось выше критического (61,766> 5,420445), отвергаем нулевую гипотезу – уравнение значимо в целом.
В данной таблице выводятся столбцы: коэффициентов регрессии; стандартных ошибок коэффициентов регрессии; t-статистик; вероятности принятия нулевой гипотезы для коэффициентов (Р-значение); доверительные интервалы для коэффициентов регрессии (95% интервал считается по умолчанию, 98% – мы задали сами в диалоговом окне регрессия).
Запишем полученное уравнение множественной регрессии.
Если P-значение < 0.05, то коэффициент регрессии можем принять значимым при 5% уровне.
Т. е. отвергаем нулевую гипотезу при 5% уровне значимости. Т. е. все коэффициенты полученного уравнения статистически значимы при 5% уровне, т. к. для них всех р-значение меньше 0,05.
Так же можем определить значимость коэффициентов, сравнивая наблюдаемые значения t-статистик с критическими. Находим критическое значения с помощью статистической функции СТЬЮДЕНТ.ОБР.2Х.
СТЬЮДЕНТ.ОБР.2Х(0,05;29)= 2,04523
Наблюдаемые значения t-статистик из таблицы, выше критического значения при 5% уровне значимости, отвергаем нулевую гипотезу. Коэффициенты регрессии являются статистически значимыми.
Так же можем получить расчёт для множественной регрессии, используя статистическую функцию Excel – ЛИНЕЙН.
Для неё берётся число столбцов, равное количеству объясняющих переменных плюс один (в нашем случае три), а количество строк всегда пять.
Выделяем диапазон: E37:G41. Ставим знак равно и находим функцию ЛИНЕЙН в статистических функциях.
Заполняем диалоговое окно:
Нажимаем клавиши
Получаем результат:
t-статистики определим делением коэффициента регрессии на стандартную ошибку.
Получим следующую таблицу.
Кроме t-статистики в этой таблице считает функция ЛИНЕЙН. t-статистики мы подсчитали сами дополнительно.
Принципиальное отличие функции ЛИНЕЙН от регрессии в пакете «Анализ данных» заключается в том, что при изменении самих данных, все значения в таблице ЛИНЕЙН пересчитываются автоматически сразу. А при работе с пакетом «анализа данных» надо запускать процесс ещё раз, т. е. вызывать диалоговое окно, заполнять его и нажимать «ок».
В следующей части мы рассмотрим тестирование полученной модели на наличие автокорреляции остатков и на наличие гетероскедастичности.
Материал подготовлен сайтом: https://pro-smysl.ru/
Онлайн помощь в решении задач, консультации, создание обучающих роликов.
Подписывайтесь на наши каналы:
https://vk.com/sm_smysl
https://www.youtube.com/@SMYS_L
Download Article
Easily create a multiple regression model in your Excel spreadsheet
Download Article
Trying to create a multiple regression model in Excel? It’s pretty easy to do using the built-in data analysis tools. Multiple regression is a great way to examine how multiple independent variables explain the variation in a dependent variable. This wikiHow guide will show you how to run a multiple regression in Microsoft Excel on Windows or Mac.
Things You Should Know
- You’ll need to enable the Analysis ToolPak, a built-in add-in for Excel, before running a regression analysis.
- Make sure your data is arranged in adjacent columns with the first row being the headers.
- Click “Data Analysis” in the “Data” tab and select “Regression” to set up the analysis.
Steps
-
1
Enable the data analysis add-in (if needed). Whether you’re studying statistics or doing regression professionally, Excel is a great tool for running the analysis. Excel has a built-in data analysis add-in called “Analysis ToolPak.” You can check to see if it’s active by clicking the Data tab. If you don’t see the Data Analysis option, you will need to enable it:[1]
- Windows:
- Open the File tab (or press Alt+F) and select Options (Windows).
- Click Add-Ins on the left side of the window.
- Select Excel Add-ins next to “manage” and click Go.
- In the new window, check the box next to “Analysis ToolPak”, then click OK. This will enable the built-in data analysis add-in.
- Mac:
- Click Tools and then Excel Add-ins.
- Check the box next to Analysis ToolPak and click OK.
- Note that you may need to click Browse to find the Analysis ToolPak.
- If the Data Analysis tool doesn’t appear in the Data tab, close and reopen Excel.
- Windows:
-
2
Enter your data or open your data file. Data must be arranged in immediately adjacent columns and labels should be in the first row of each column. This is a typical format for databases.
Advertisement
-
3
Click theData tab and click Data Analysis. This option is in the “Analysis” section near the far right of Data tab options.
- Another powerful tool is Excel’s Solver function, an optimization model feature.
-
4
Click Regression and then OK. This will open a new window for inputting the parameters of the regression model.
-
5
Input the dependent (Y) data range. To do so:
- Click the “Input Y Range” field.
- Highlight the column containing your dependent variable values.
- Click the Labels checkbox if your data has a header row.
-
6
Input the independent (X) data range. To do so:
- Click the “Input X Range” field.
- Highlight the column or columns containing your dependent variable values. This can include multiple columns if you have more than one independent variable.
- Note: The independent variable data columns must be adjacent to one another for the input to work.
-
7
Adjust the regression options (if needed). You can change the following parts of the analysis in the Regression window:
- The default confidence level is 95%. If you want to change this value, click the box next to Confidence Level and modify the adjacent value.
- Under “Output options,” select where you want the regression results to output.
- Select the desired options in the “Residuals” category. Graphical residual outputs are created by the Residual Plots and Line Fit Plots options.
-
8
Click OK and the analysis will be created. You’ll see the following information:
- Regression Statistics includes the correlation values, standard error, and number of observations.
- ANOVA is a table displaying the degrees of freedom, sum squares, mean squares, F value, and F significance. You can use this table to assess the statistical significance of the model.
- The confidence interval table shows the regression coefficient, standard error, significance, and confidence interval for each regression parameter (the intercept and the independent variable slopes).
Advertisement
Add New Question
-
Question
what is output range
Kyle Smith is a wikiHow Technology Writer, learning and sharing information about the latest technology. He has presented his research at multiple engineering conferences and is the writer and editor of hundreds of online electronics repair guides. Kyle received a BS in Industrial Engineering from Cal Poly, San Luis Obispo.
wikiHow Technology Writer
Expert Answer
The output range in the regression window is where the results of the analysis will appear. This can be in an existing sheet, a new sheet, or an entirely new workbook file.
-
Question
getting #NUM error p- values. What does it mean?
Kyle Smith is a wikiHow Technology Writer, learning and sharing information about the latest technology. He has presented his research at multiple engineering conferences and is the writer and editor of hundreds of online electronics repair guides. Kyle received a BS in Industrial Engineering from Cal Poly, San Luis Obispo.
wikiHow Technology Writer
Expert Answer
This could indicate that you don’t have enough observations to compute the significance of the model or its parameters. Try adding additional observations if this is the case.
-
Question
What is the formula of multiple regression used by Excel in the background?
Kyle Smith is a wikiHow Technology Writer, learning and sharing information about the latest technology. He has presented his research at multiple engineering conferences and is the writer and editor of hundreds of online electronics repair guides. Kyle received a BS in Industrial Engineering from Cal Poly, San Luis Obispo.
wikiHow Technology Writer
Expert Answer
Excel is using the linear regression formula y = m1x1 + m2x2 + … + b. It calculates the values using the least squares method.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
About This Article
Thanks to all authors for creating a page that has been read 810,943 times.
Is this article up to date?
В этой статье описаны синтаксис формулы и использование функции LINEST в Microsoft Excel. Ссылки на дополнительные сведения о диаграммах и выполнении регрессионного анализа можно найти в разделе См. также.
Описание
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Функцию ЛИНЕЙН также можно объединять с другими функциями для вычисления других видов моделей, являющихся линейными по неизвестным параметрам, включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Инструкции приведены в данной статье после примеров.
Уравнение для прямой линии имеет следующий вид:
y = mx + b
или
y = m1x1 + m2x2 +… + b
если существует несколько диапазонов значений x, где зависимые значения y — функции независимых значений x. Значения m — коэффициенты, соответствующие каждому значению x, а b — постоянная. Обратите внимание, что y, x и m могут быть векторами. Функция ЛИНЕЙН возвращает массив {mn;mn-1;…;m1;b}. Функция ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.
Синтаксис
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Аргументы функции ЛИНЕЙН описаны ниже.
Синтаксис
-
Известные_значения_y. Обязательный аргумент. Множество значений y, которые уже известны для соотношения y = mx + b.
-
Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.
-
Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.
-
-
Известные_значения_x. Необязательный аргумент. Множество значений x, которые уже известны для соотношения y = mx + b.
-
Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то массивы известные_значения_y и известные_значения_x могут иметь любую форму — при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).
-
Если массив известные_значения_x опущен, то предполагается, что это массив {1;2;3;…}, имеющий такой же размер, что и массив известные_значения_y.
-
-
Конст. Необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
-
Если аргумент конст имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.
-
Если аргумент конст имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.
-
-
Статистика. Необязательный аргумент. Логическое значение, которое указывает, требуется ли вернуть дополнительную регрессионную статистику.
-
Если статистика имеет true, то LINEST возвращает дополнительную регрессию; в результате возвращается массив {mn;mn-1,…,m1;b;sen,sen-1,…,se1;seb;r2;sey; F,df;ssreg,ssresid}.
-
Если аргумент статистика имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.
Дополнительная регрессионная статистика.
-
|
Величина |
Описание |
|---|---|
|
se1,se2,…,sen |
Стандартные значения ошибок для коэффициентов m1,m2,…,mn. |
|
seb |
Стандартное значение ошибки для постоянной b (seb = #Н/Д, если аргумент конст имеет значение ЛОЖЬ). |
|
r2 |
Коэффициент определения. Сравнивает предполагаемые и фактические значения y и диапазоны значений от 0 до 1. Если значение 1, то в выборке будет отличная корреляция— разница между предполагаемым значением y и фактическим значением y не существует. С другой стороны, если коэффициент определения — 0, уравнение регрессии не помогает предсказать значение y. Сведения о том, каквычисляется 2, см. в разделе “Замечания” далее в этой теме. |
|
sey |
Стандартная ошибка для оценки y. |
|
F |
F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными. |
|
df |
Степени свободы. Степени свободы используются для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН. Дополнительные сведения о вычислении величины df см. ниже в разделе “Замечания”. Далее в примере 4 показано использование величин F и df. |
|
ssreg |
Регрессионная сумма квадратов. |
|
ssresid |
Остаточная сумма квадратов. Дополнительные сведения о расчете величин ssreg и ssresid см. в подразделе “Замечания” в конце данного раздела. |
На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика.

Замечания
-
Любую прямую можно описать ее наклоном и пересечением с осью y:
Наклон (m):
Чтобы найти наклон линии, обычно записанной как m, возьмите две точки на строке (x1;y1) и (x2;y2); наклон равен (y2 – y1)/(x2 – x1).Y-перехват (b):
Y-пересечение строки, обычно записанное как b, — это значение y в точке, в которой линия пересекает ось y.Уравнение прямой имеет вид y = mx + b. Если известны значения m и b, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение. Можно также воспользоваться функцией ТЕНДЕНЦИЯ.
-
Если имеется только одна независимая переменная x, можно получить наклон и y-пересечение непосредственно, воспользовавшись следующими формулами:
Наклон:
=ИНДЕКС( LINEST(known_y,known_x’s);1)Y-перехват:
=ИНДЕКС( LINEST(known_y,known_x),2) -
Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель ЛИНЕЙН. Функция ЛИНЕЙН использует для определения наилучшей аппроксимации данных метод наименьших квадратов. Когда имеется только одна независимая переменная x, значения m и b вычисляются по следующим формулам:
где x и y — выборочные средние значения, например x = СРЗНАЧ(известные_значения_x), а y = СРЗНАЧ(известные_значения_y).
-
Функции ЛИННЕСТРОЙ и ЛОГЪЕСТ могут вычислять наилучшие прямые или экспоненциальное кривой, которые подходят для ваших данных. Однако необходимо решить, какой из двух результатов лучше всего подходит для ваших данных. Вы можетевычислить known_y(known_x) для прямой линии или РОСТ(known_y, known_x в) для экспоненциальной кривой. Эти функции без аргумента new_x возвращают массив значений y, спрогнозируемых вдоль этой линии или кривой в фактических точках данных. Затем можно сравнить спрогнозируемые значения с фактическими значениями. Для наглядного сравнения можно отобразить оба этих диаграммы.
-
Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов (ssresid). Затем Microsoft Excel подсчитывает общую сумму квадратов (sstotal). Если конст = ИСТИНА или значение этого аргумента не указано, общая сумма квадратов будет равна сумме квадратов разностей действительных значений y и средних значений y. При конст = ЛОЖЬ общая сумма квадратов будет равна сумме квадратов действительных значений y (без вычитания среднего значения y из частного значения y). После этого регрессионную сумму квадратов можно вычислить следующим образом: ssreg = sstotal – ssresid. Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента определения r2— индикатор того, насколько хорошо уравнение, выданное в результате регрессионного анализа, объясняет связь между переменными. Значение r2 равно ssreg/sstotal.
-
В некоторых случаях один или несколько столбцов X (предполагается, что значения Y и X — в столбцах) могут не иметь дополнительного прогнозируемого значения при наличии других столбцов X. Другими словами, удаление одного или более столбцов X может привести к одинаковой точности предсказания значений Y. В этом случае эти избыточные столбцы X следует не использовать в модели регрессии. Этот вариант называется “коллинеарность”, так как любой избыточный X-столбец может быть выражен как сумма многих не избыточных X-столбцов. Функция ЛИНЕЙН проверяет коллинеарность и удаляет все избыточные X-столбцы из модели регрессии при их идентификации. Удалены столбцы X распознаются в результатах LINEST как имеющие коэффициенты 0 в дополнение к значениям 0 se. Если один или несколько столбцов будут удалены как избыточные, это влияет на df, поскольку df зависит от числа X столбцов, фактически используемых для прогнозирования. Подробные сведения о вычислении df см. в примере 4. Если значение df изменилось из-за удаления избыточных X-столбцов, это также влияет на значения Sey и F. Коллинеарность должна быть относительно редкой на практике. Однако чаще всего возникают ситуации, когда некоторые столбцы X содержат только значения 0 и 1 в качестве индикаторов того, является ли тема в эксперименте участником определенной группы или не является ее участником. Если конст = ИСТИНА или опущен, функция LYST фактически вставляет дополнительный столбец X из всех 1 значений для моделирования перехвата. Если у вас есть столбец с значением 1 для каждой темы, если мальчик, или 0, а также столбец с 1 для каждой темы, если она является женщиной, или 0, последний столбец является избыточным, так как записи в нем могут быть получены из вычитания записи в столбце “самец” из записи в дополнительном столбце всех 1 значений, добавленных функцией LINEST.
-
Вычисление значения df для случаев, когда столбцы X удаляются из модели вследствие коллинеарности происходит следующим образом: если существует k столбцов известных_значений_x и значение конст = ИСТИНА или не указано, то df = n – k – 1. Если конст = ЛОЖЬ, то df = n – k. В обоих случаях удаление столбцов X вследствие коллинеарности увеличивает значение df на 1.
-
При вводе константы массива (например, в качестве аргумента известные_значения_x) следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть другими в зависимости от региональных параметров.
-
Следует отметить, что значения y, предсказанные с помощью уравнения регрессии, возможно, не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.
-
Основной алгоритм, используемый в функции ЛИНЕЙН, отличается от основного алгоритма функций НАКЛОН и ОТРЕЗОК. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то:
-
Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм функции ЛИНЕЙН используется для возвращения подходящих значений для коллинеарных данных, и в данном случае может быть найден по меньшей мере один ответ.
-
Наклон и ОТОКП возвращают #DIV/0! ошибка “#ЗНАЧ!”. Алгоритм функций НАКЛОН и ОТОКП предназначен для поиска только одного ответа, и в этом случае может быть несколько ответов.
-
-
Помимо вычисления статистики для других типов регрессии с помощью функции ЛГРФПРИБЛ, для вычисления диапазонов некоторых других типов регрессий можно использовать функцию ЛИНЕЙН, вводя функции переменных x и y как ряды переменных х и у для ЛИНЕЙН. Например, следующая формула:
=ЛИНЕЙН(значения_y, значения_x^СТОЛБЕЦ($A:$C))
работает при наличии одного столбца значений Y и одного столбца значений Х для вычисления аппроксимации куба (многочлен 3-й степени) следующей формы:
y = m1*x + m2*x^2 + m3*x^3 + b
Формула может быть изменена для расчетов других типов регрессии, но в отдельных случаях требуется корректировка выходных значений и других статистических данных.
-
Значение F-теста, возвращаемое функцией ЛИНЕЙН, отличается от значения, возвращаемого функцией ФТЕСТ. Функция ЛИНЕЙН возвращает F-статистику, в то время как ФТЕСТ возвращает вероятность.
Примеры
Пример 1. Наклон и Y-пересечение
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Известные значения y |
Известные значения x |
|---|---|
|
1 |
0 |
|
9 |
4 |
|
5 |
2 |
|
7 |
3 |
|
Результат (наклон) |
Результат (y-пересечение) |
|
2 |
1 |
|
Формула (формула массива в ячейках A7:B7) |
|
|
=ЛИНЕЙН(A2:A5;B2:B5;;ЛОЖЬ) |
Пример 2. Простая линейная регрессия
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Месяц |
Продажи |
|---|---|
|
1 |
3 100 ₽ |
|
2 |
4 500 ₽ |
|
3 |
4 400 ₽ |
|
4 |
5 400 ₽ |
|
5 |
7 500 ₽ |
|
6 |
8 100 ₽ |
|
Формула |
Результат |
|
=СУММ(ЛИНЕЙН(B1:B6; A2:A7)*{9;1}) |
11 000 ₽ |
|
Вычисляет предполагаемый объем продаж в девятом месяце на основе данных о продажах за период с первого по шестой месяцы. |
Пример 3. Множественная линейная регрессия
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Общая площадь (x1) |
Количество офисов (x2) |
Количество входов (x3) |
Время эксплуатации (x4) |
Оценочная цена (y) |
|---|---|---|---|---|
|
2310 |
2 |
2 |
20 |
142 000 ₽ |
|
2333 |
2 |
2 |
12 |
144 000 ₽ |
|
2356 |
3 |
1,5 |
33 |
151 000 ₽ |
|
2379 |
3 |
2 |
43 |
150 000 ₽ |
|
2402 |
2 |
3 |
53 |
139 000 ₽ |
|
2425 |
4 |
2 |
23 |
169 000 ₽ |
|
2448 |
2 |
1,5 |
99 |
126 000 ₽ |
|
2471 |
2 |
2 |
34 |
142 900 ₽ |
|
2494 |
3 |
3 |
23 |
163 000 ₽ |
|
2517 |
4 |
4 |
55 |
169 000 ₽ |
|
2540 |
2 |
3 |
22 |
149 000 ₽ |
|
-234,2371645 |
||||
|
13,26801148 |
||||
|
0,996747993 |
||||
|
459,7536742 |
||||
|
1732393319 |
||||
|
Формула (формула динамического массива, введенная в A19) |
||||
|
=ЛИНЕЙН(E2:E12; A2:D12; ИСТИНА; ИСТИНА) |
Пример 4. Использование статистики F и r2
В предыдущем примере коэффициент определения (r2)составляет 0,99675 (см. ячейку A17 в результатах для ЛИТН), что указывает на крепкая связь между независимыми переменными и ценой продажи. F-статистику можно использовать для определения случайности этих результатов с таким высоким значением r2.
Предположим, что на самом деле взаимосвязи между переменными не существует, просто статистический анализ вывел сильную взаимозависимость по взятой равномерной выборке 11 зданий. Величина “Альфа” используется для обозначения вероятности ошибочного вывода о существовании сильная взаимозависимости.
Значения F и df в результатах функции LINEST можно использовать для оценки вероятности возникновения более высокого F-значения. F можно сравнивать с критическими значениями в опубликованных F-таблицах или с помощью функции FРАСП в Excel для вычисления вероятности случайного возникновения большего F-значения. Соответствующее F-распределение имеет v1 и v2 степени свободы. Если n — количество точек данных и конст = ИСТИНА или опущен, то v1 = n – df – 1 и v2 = df. (Если конст = ЛОЖЬ, то v1 = n – df и v2 = df.) Функция FIST с синтаксисом FDIST(F;v1;v2) возвращает вероятность возникновения более высокого F-значения, случайного. В этом примере df = 6 (ячейка B18) и F = 459,753674 (ячейка A18).
Предположим, что альфа имеет значение 0,05, v1 = 11 – 6 – 1 = 4, а v2 = 6, критический уровень F составляет 4,53. Поскольку F = 459,753674 значительно больше 4,53, вероятность того, что F-значение этого высокой случайности превышает 4,53, крайне маловероятно. (Если значение “Альфа” = 0,05, гипотеза о том, что между known_y и known_x нет связи, отклоняется при превышении F критического уровня (4,53).) Функцию FDIST в Excel можно использовать для получения вероятности случайного возникновения F-значения. Например, FIST(459,753674, 4, 6) = 1,37E-7, очень небольшая вероятность. Можно сделать вывод о том, что формула регрессии полезна для предсказания оценочного значения офисных зданий в этой области, найдя критический уровень F в таблице или с помощью функции FDIST. Помните, что крайне важно использовать правильные значения 1 и 2, вычисленные в предыдущем абзаце.
Пример 5. Вычисление t-статистики
Другой тест позволяет определить, подходит ли каждый коэффициент наклона для оценки стоимости здания под офис в примере 3. Например, чтобы проверить, имеет ли срок эксплуатации здания статистическую значимость, разделим -234,24 (коэффициент наклона для срока эксплуатации здания) на 13,268 (оценка стандартной ошибки для коэффициента времени эксплуатации из ячейки A15). Ниже приводится наблюдаемое t-значение:
t = m4 ÷ se4 = –234,24 ÷ 13,268 = –17,7
Если абсолютное значение t достаточно велико, можно сделать вывод, что коэффициент наклона можно использовать для оценки стоимости здания под офис в примере 3. В таблице ниже приведены абсолютные значения четырех наблюдаемых t-значений.
Если обратиться к справочнику по математической статистике, то окажется, что t-критическое двустороннее с 6 степенями свободы равно 2,447 при Альфа = 0,05. Критическое значение также можно также найти с помощью функции Microsoft Excel СТЬЮДРАСПОБР. СТЬЮДРАСПОБР(0,05; 6) = 2,447. Поскольку абсолютная величина t, равная 17,7, больше, чем 2,447, срок эксплуатации — это важная переменная для оценки стоимости здания под офис. Аналогичным образом можно протестировать все другие переменные на статистическую значимость. Ниже приводятся наблюдаемые t-значения для каждой из независимых переменных.
|
Переменная |
t-наблюдаемое значение |
|---|---|
|
Общая площадь |
5,1 |
|
Количество офисов |
31,3 |
|
Количество входов |
4,8 |
|
Возраст |
17,7 |
Абсолютная величина всех этих значений больше, чем 2,447. Следовательно, все переменные, использованные в уравнении регрессии, полезны для предсказания оценочной стоимости здания под офис в данном районе.