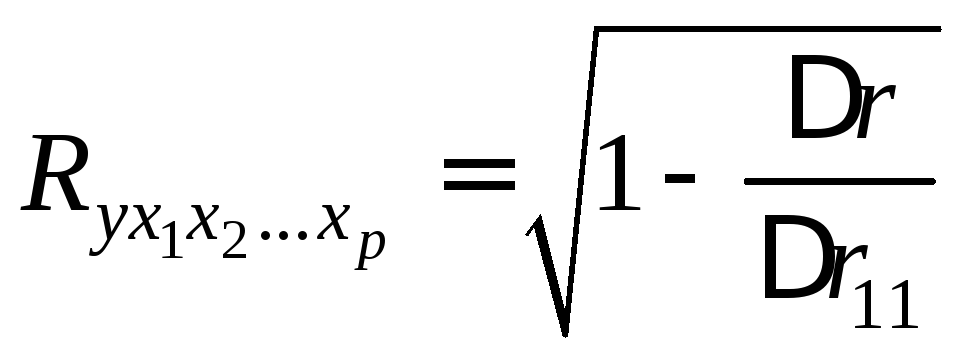Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 марта 2019 года; проверки требует 1 правка.
Множественный коэффициент корреляции – Характеризует тесноту линейной корреляционной связи между одной случайной величиной и некоторым множеством случайных величин. Более точно, если (ξ1,ξ2,…,ξk) – случайный вектор из Rk, тогда коэффициент множественной корреляции 
между ξ1 и ξ2,…,ξk численно равен коэффициенту парной линейной корреляции между величиной ξ1 и её наилучшей линейной аппроксимацией 
по переменным ξ2…,ξk, которая представляет собой линейную регрессию ξ1 на ξ2,…,ξk.
Свойства[править | править код]
Множественный коэффициент корреляции обладает тем свойством, что при условии
когда 
– это регрессия ξ1 на ξ2,…,ξk,
среди всех линейных комбинаций переменных ξ2,…,ξk переменная ξ1 будет иметь максимальный коэффициент корреляции с ξ1*, совпадающий с . В этом смысле множественный коэффициент корреляции является частным случаем канонического коэффициента корреляции. При k = 2 множественный коэффициент корреляции по абсолютной величине совпадает с коэффициентом парной линейной корреляции ρ12 между ξ1 и ξ2.
Вычисление[править | править код]
Множественный коэффициент корреляции вычисляется с помощью корреляционной матрицы 
по формуле
,
где 
– это определитель корреляционной матрицы, а 
– это алгебраическое дополнение элемента ρ11 = 1; здесь 
. Если 
, тогда с вероятностью 1 значения ξ1 совпадают с линейной комбинацией ξ2,…,ξk, следовательно, совместное распределение ξ1,ξ2,…,ξk лежит на гиперплоскости в пространстве Rk. С другой стороны, при 
все парные коэффициенты корреляции ρ12 = ρ13 = … = ρ1k = 0 равны нулю, следовательно, значения ξ1 не коррелируют с величинами ξ2,…,ξk. Верно и обратное утверждение.
Множественный коэффициент корреляции можно также вычислить по формуле
,
где 
– это дисперсия ξ1, а 
– дисперсия ξ1 относительно регрессии.
Выборочный множественный коэффициент корреляции[править | править код]
Выборочным аналогом множественного коэффициента корреляции служит величина 
, где 
и 
– это оценки для 
и , полученные по выборке объема n. Для проверки нуль-гипотезы об отсутствии взаимосвязи используется распределение статистики 
. При условии, что выборка взята из многомерного нормального распределения, величина 
будет обладать бета-распределением с параметрами 
, если . Для случая 
тип распределения известен, но практически не используется ввиду его громоздкости.
См. также[править | править код]
- Коэффициент детерминации
Литература[править | править код]
- Крамер Г. Математические методы статистики, пер. с англ., 2 изд., М., 1975;
- Кендалл М., Стьюард А., Статистические выводы и связи, пер. с англ., М., 1973.
Видео занятия
Строим корреляционную матрицу. Для этого используем надстройку «Анализ данных»
Выбираем в диалоговом окне «Анализа данных» – корреляция.
Далее заполняем диалоговое окно:
Получим корреляционную матрицу:
Наблюдается тесная связь между переменной Y и Х1, Y и X2, так как попарные коэффициенты корреляции составляют 0,8602 и 0,7479 соответственно. Это выше 0,7 – связь достаточно тесная.
Межу объясняющими переменными Х1 и Х2 коэффициент составляет 0,6311. Он ниже других, но имеет значение больше 0,6. Значит между объясняющими переменными, может быть корреляционная связь (явление мультиколлинеарности). Для обнаружения мультиколлинеарности есть ряд критериев, например VIF-критерий.
Парные коэффициенты корреляции можно ещё найти с помощью статистической функции КОРРЕЛ.
Заполняем диалоговое окно статистической функции КОРРЕЛ.
Получаем тоже значение, что и корреляционной матрице для Y и X1: 0,860227
Аналогично по отдельности можем найти и другие парные коэффициенты корреляции.
Строим множественную регрессию. Для этого в надстройке «Анализ данных» выбираем регрессия. Заполняем диалоговое окно.
Выбираем уровень надёжности 98%. Для коэффициентов регрессии будет найден доверительный интервал с уровнем с доверительной вероятностью 98%. Так же выбираем остатки, график остатков. Эти данные необходимы нам для дальнейшего анализа во второй части.
Получим.
Проведём анализ полученных данных.
Здесь выводятся: множественный коэффициент корреляции, коэффициент детерминации (R-квадрат), скорректированный коэффициент детерминации (нормированный R-квадрат), стандартная ошибка регрессии (S).
R-квадрат = RSS/TSS
Стандартная ошибка = (ESS/(n-m-1))^0.5
ESS (error sum of squares) – остаточная сумма квадратов.
Построенное уравнение регрессии объясняет изменение результативного показателя Y на 80,99%. Остальные 10,01% приходятся на случайные факторы и факторы не включённые в модель.
Здесь даны столбцы: со степенями свободы (df); суммой квадратов (SS), суммой квадратов, делённых на степень свободы (MS=SS/df). Так же дано значение F-критерия Фишера и вероятность принятия нулевой гипотезы о равенстве коэффициента детерминации нулю (Значимость F).
TSS (total sum of squares) – общая сумма квадратов отклонений зависимой переменной от средней или вся дисперсия зависимой переменной;
RSS (regression sum of squares) – сумма квадратов, обусловленная регрессией или объясненная часть всей дисперсии;
ESS (error sum of squares) – остаточная сумма квадратов, характеризующая влияние неучтенных факторов или необъясненная дисперсия.
F= (ESS/m)/(RSS/(n-m-1)), n=32 m=2
Значимость F= 3,51562998617576E-11 <<<<0.01. Не можем принять нулевую гипотезу, принимаем альтернативную. Коэффициент детерминации отличен от нуля. Уравнение значимо в целом.
Так же можно сравнить наблюдаемое значение F-критерия с критическим. Берём уровень значимости 0,01, число степеней свободы 2 и 29. И с помощью статистической функции F.ОБР.ПХ находим критическое значение распределения Фишера
F.ОБР.ПХ(0,01;2;29) = 5,420445
Наблюдаемое значение оказалось выше критического (61,766> 5,420445), отвергаем нулевую гипотезу – уравнение значимо в целом.
В данной таблице выводятся столбцы: коэффициентов регрессии; стандартных ошибок коэффициентов регрессии; t-статистик; вероятности принятия нулевой гипотезы для коэффициентов (Р-значение); доверительные интервалы для коэффициентов регрессии (95% интервал считается по умолчанию, 98% – мы задали сами в диалоговом окне регрессия).
Запишем полученное уравнение множественной регрессии.
Если P-значение < 0.05, то коэффициент регрессии можем принять значимым при 5% уровне.
Т. е. отвергаем нулевую гипотезу при 5% уровне значимости. Т. е. все коэффициенты полученного уравнения статистически значимы при 5% уровне, т. к. для них всех р-значение меньше 0,05.
Так же можем определить значимость коэффициентов, сравнивая наблюдаемые значения t-статистик с критическими. Находим критическое значения с помощью статистической функции СТЬЮДЕНТ.ОБР.2Х.
СТЬЮДЕНТ.ОБР.2Х(0,05;29)= 2,04523
Наблюдаемые значения t-статистик из таблицы, выше критического значения при 5% уровне значимости, отвергаем нулевую гипотезу. Коэффициенты регрессии являются статистически значимыми.
Так же можем получить расчёт для множественной регрессии, используя статистическую функцию Excel – ЛИНЕЙН.
Для неё берётся число столбцов, равное количеству объясняющих переменных плюс один (в нашем случае три), а количество строк всегда пять.
Выделяем диапазон: E37:G41. Ставим знак равно и находим функцию ЛИНЕЙН в статистических функциях.
Заполняем диалоговое окно:
Нажимаем клавиши
Получаем результат:
t-статистики определим делением коэффициента регрессии на стандартную ошибку.
Получим следующую таблицу.
Кроме t-статистики в этой таблице считает функция ЛИНЕЙН. t-статистики мы подсчитали сами дополнительно.
Принципиальное отличие функции ЛИНЕЙН от регрессии в пакете «Анализ данных» заключается в том, что при изменении самих данных, все значения в таблице ЛИНЕЙН пересчитываются автоматически сразу. А при работе с пакетом «анализа данных» надо запускать процесс ещё раз, т. е. вызывать диалоговое окно, заполнять его и нажимать «ок».
В следующей части мы рассмотрим тестирование полученной модели на наличие автокорреляции остатков и на наличие гетероскедастичности.
Материал подготовлен сайтом: https://pro-smysl.ru/
Онлайн помощь в решении задач, консультации, создание обучающих роликов.
Подписывайтесь на наши каналы:
https://vk.com/sm_smysl
https://www.youtube.com/@SMYS_L
Теория
Множественный коэффициент корреляции
При наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков вычисляется множественный коэффициент корреляции. Т.е. он используется для измерения тесноты связи при множественной корреляционной зависимости.
Множественный коэффициент корреляции в случае зависимости результативного признака от двух факторов вычисляется по формуле:
(15)
где – парные коэффициенты корреляции между признаками.
Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: .
Условие включения факторных признаков в регрессионную модель – наличие тесной связи между результативным и факторными признаками и как можно менее существенная связь между факторными признаками.
Значимость коэффициента множественной детерминации, а соответственно и адекватность всей модели и правильность выбора формы связи можно проверить с помощью критерия Фишера:
(16)
где R2 – коэффициент множественной детерминации (R2 );
k – число факторных признаков, включенных в уравнение регрессии.
Связь считается существенной, если Fрасч > Fтабл – табличного значения F–критерия для заданного уровня значимости α и числе степеней свободы ν1 = k, ν2 = n – k – 1.
Пример.
Известны следующие данные о выручке (у), спросе по номиналу (х1) и объем продаж (х2) корпоративных ценных бумаг. Рассчитать коэффициент множественной корреляции.
Таблица 3
Основные характеристики корпоративных ценных бумаг
|
№ |
Выручка Y, млрд.руб. |
Спрос по номиналу Х1, млрд.руб. |
Объем продаж по номиналу Х2, млрд.руб. |
|
1 |
3 |
6,8 |
3,5 |
|
2 |
5,4 |
11,2 |
6,7 |
|
3 |
5,9 |
9,1 |
6,8 |
|
4 |
4,8 |
6,9 |
5,9 |
|
5 |
3,3 |
6,4 |
3,8 |
|
6 |
3,4 |
6,9 |
4,3 |
|
7 |
5,3 |
12,2 |
6,9 |
|
Итого |
31,1 |
59,5 |
37,9 |
Множественный коэффициент корреляции составит:
Практическая
значимость уравнения множественной
регрессии оценивается с помощью
показателя множественной корреляции
и его квадрата – коэффициента детерминации.
Показатель
множественной корреляции характеризует
тесноту связи рассматриваемого набора
факторов с исследуемым признаком, или,
иначе, оценивает тесноту совместного
влияния факторов на результат.
Независимо от
формы связи показатель множественной
корреляции может быть найден как индекс
множественной корреляции:
где 
– общая дисперсия результативного
признака;
–остаточная
дисперсия для уравнения
.
Методика построения
индекса множественной корреляции
аналогична построению индекса корреляции
для парной зависимости. Границы его
изменения те же: от 0 до 1. Чем ближе его
значение к 1, тем теснее связь результативного
признака со всем набором исследуемых
факторов. Величина индекса множественной
корреляции должна быть больше или равна
максимальному парному индексу корреляции:
.
При правильном
включении факторов в регрессионный
анализ величина индекса множественной
корреляции будет существенно отличаться
от индекса корреляции парной зависимости.
Если же дополнительно включенные в
уравнение множественной регрессии
факторы третьестепенны, то индекс
множественной корреляции может
практически совпадать с индексом парной
корреляции (различия в третьем, четвертом
знаках). Отсюда ясно, что, сравнивая
индексы множественной и парной корреляции,
можно сделать вывод о целесообразности
включения в уравнение регрессии того
или иного фактора. Так, если
рассматривается как функция
и
и получен индекс множественной корреляции
,
а индексы парной корреляции при этом
были
и
,
то совершенно ясно, что уравнение парной
регрессии
охватывало 67,2 % колеблемости результативного
признака под влиянием фактора
,
а дополнительное включение в анализ
фактора
увеличило долю объясненной вариации
до 72,3,%, т. е. уменьшилась доля остаточной
вариации на 5,1 проц. пункта (с 32,8 до
27,7%).
Расчет индекса
множественной корреляции предполагает
определение уравнения множественной
регрессии и на его основе остаточной
дисперсии:
.
Можно пользоваться
следующей формулой индекса множественной
корреляции:
При линейной
зависимости признаков формула индекса
корреляции может быть представлена
следующим выражением:
,
где 
– стандартизованные коэффициенты
регрессии;
– парные коэффициенты корреляции
результата с каждым фактором.
Или, по-другому:
Формула индекса
множественной корреляции для линейной
регрессии получила название линейного
коэффициента множественной корреляции,
или, что то же самое, совокупного
коэффициента корреляции.
Возможно также
при линейной зависимости определение
совокупного коэффициента корреляции
через матрицу парных коэффициентов
корреляции:
где 
– определитель матрицы парных
коэффициентов корреляции;
–определитель
матрицы межфакторной корреляции.
Для уравнения
определитель матрицы коэффициентов
парной корреляции примет вид:
Определитель более
низкого порядка
остается, когда вычеркиваются из матрицы
коэффициентов парной корреляции первый
столбец и первая строка, что и соответствует
матрице коэффициентов парной корреляции
между факторами:
Как видим, величина
множественного коэффициента корреляции
зависит не только от корреляции результата
с каждым из факторов, но и от межфакторной
корреляции. Рассмотренная формула
позволяет определять совокупный
коэффициент корреляции, не обращаясь
при этом к уравнению множественной
регрессии, а используя лишь парные
коэффициенты корреляции.
При трех переменных
для двухфакторного уравнения регрессии
данная формула совокупного коэффициента
корреляции легко приводится к следующему
виду:
Индекс множественной
корреляции равен совокупному коэффициенту
корреляции не только при линейной
зависимости рассматриваемых признаков.
Тождественность этих показателей, как
и в парной регрессии, имеет место и для
криволинейной зависимости, нелинейной
по переменным.
В рассмотренных
показателях множественной корреляции
(индекс и коэффициент) используется
остаточная дисперсия, которая имеет
систематическую ошибку в сторону
преуменьшения. Эта ошибка тем более
значительна, чем больше параметров
определяется в уравнении регрессии при
заданном объеме наблюдений
.
Если число параметров при
равно
и приближается к объему наблюдений, то
остаточная дисперсия будет близка к
нулю, и коэффициент (индекс) корреляции
приблизится к единице даже при слабой
связи факторов с результатом. Для того
чтобы не допустить возможного преувеличения
тесноты связи, используетсяскорректированный
индекс (коэффициент) множественной
корреляции.
Скорректированный
индекс множественной корреляции содержит
поправку на число степеней свободы, а
именно остаточная сумма квадратов
делится на число степеней свободы
остаточной вариации
,
а общая сумма квадратов отклонений
– на число степеней свободы в целом по
совокупности
.
Формула
скорректированного индекса множественной
детерминации имеет вид:
где 
– число параметров при переменных
;
–число наблюдений.
Поскольку
,
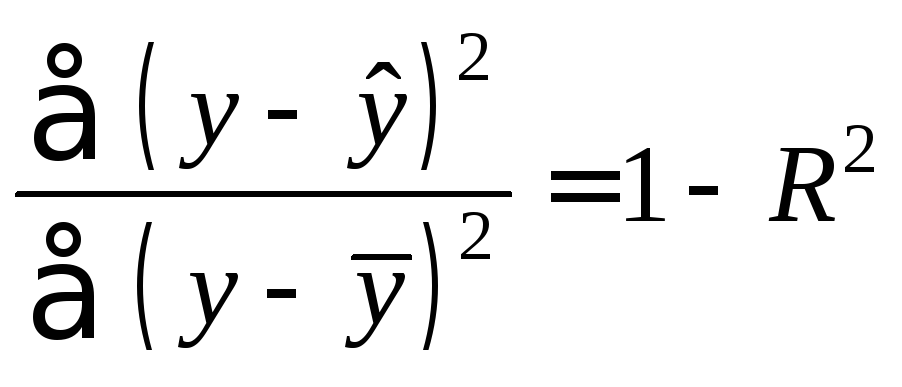
то величину скорректированного индекса
детерминации можно представить в виде
Чем больше величина
,
тем сильнее различия
и
.
Для линейной
зависимости признаков скорректированный
коэффициент множественной корреляции
определяется по той же формуле, что и
индекс множественной корреляции, т.е.
как корень квадратный из
.
Отличие состоит лишь в том, что в линейной
зависимости под
подразумевается число факторов,
включенных в регрессионную модель, а в
криволинейной зависимости
– число параметров при
и их преобразованиях (
,
и др.), которое может быть больше числа
факторов как экономических переменных.
Пример.
Предположим, что при
для линейного уравнения регрессии с
четырьмя факторами
,
а с учетом корректировки на число
степеней свободы
Чем больше объем
совокупности, по которой исчислена
регрессия, тем меньше различаются
показатели
и
.
Так, уже при
при том же значении
и т величина
составит 0,673.
В статистических
пакетах прикладных программ в процедуре
множественной регрессии обычно приводится
скорректированный коэффициент (индекс)
множественной корреляции (детерминации).
Величина коэффициента множественной
детерминации используется для оценки
качества регрессионной модели. Низкое
значение коэффициента (индекса)
множественной корреляции означает, что
в регрессионную модель не включены
существенные факторы – с одной стороны,
а с другой стороны – рассматриваемая
форма связи не отражает реальные
соотношения между переменными, включенными
в модель. Требуются дальнейшие исследования
по улучшению качества модели и увеличению
ее практической значимости.
Соседние файлы в папке 17-09-2014_11-49-43
- #
- #
- #
- #
- #
- #
- #
- #
Задача
По 20
предприятиям региона изучается зависимость выработки продукции на одного
работника
(тыс.руб.) от ввода в действие новых основных
фондов
(% от стоимости фондов на
конец года) и от удельного веса рабочих высокой квалификации в общей
численности рабочих
(смотри таблицу своего варианта).
Требуется:
Построить линейную модель множественной регрессии. Записать стандартизированное
уравнение множественной регрессии. На основе стандартизированных коэффициентов
регрессии и средних коэффициентов эластичности ранжировать факторы по степени
их влияния на результат.
Найти
коэффициенты парной, частной и множественной корреляции. Проанализировать их.
Найти
скорректированный коэффициент множественной детерминации. Сравнить его с
нескорректированным (общим) коэффициентов детерминации.
С
помощью
–критерия Фишера оценить статистическую
надежность уравнения регрессии и коэффициента детерминации
С
помощью частных
–критериев Фишера оценить целесообразность
включения в уравнение множественной регрессии фактора
после
и фактора
после
.
Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.
Решение
Для
удобства проведения расчетов поместим результаты промежуточных расчетов в
таблицу:
Найдем
средние квадратические отклонения признаков:
Расчет
парных коэффициентов корреляции и параметров линейного уравнения множественной
регрессии
1) Для
нахождения параметров линейного уравнения множественной регрессии:
необходимо
решить следующую систему линейных уравнений относительно неизвестных параметров
:
Решать систему уравнений
методом Крамера,
методом обратной матрицы или
методом Гаусса достаточно трудоемко, поэтому
воспользуемся готовыми формулами:
Рассчитаем
сначала парные коэффициенты корреляции:
Находим:
Таким
образом, получили следующее уравнение множественной регрессии:
Коэффициенты
стандартизированного уравнения регрессии
Коэффициенты
и
стандартизированного уравнения регрессии
находятся по формулам:
То есть
уравнение будет выглядеть следующим образом:
Так как
стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно
сказать, что ввод в действие новых основных фондов оказывает большее влияние на
выработку продукции, чем удельный вес рабочих высокой квалификации.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Коэффициенты
эластичности
Сравнивать
влияние факторов на результат можно также при помощи средних коэффициентов
эластичности:
Вычисляем:
Т.е.
увеличение только основных фондов (от своего среднего значения) или только
удельного веса рабочих высокой квалификации на 1% увеличивает в среднем
выработку продукции на 0,635% или 0,142% соответственно. Таким образом,
подтверждается большее влияние на результат
фактора
, чем фактора
.
Частные
и парные коэффициенты корреляции
2) Коэффициенты парной корреляции мы уже нашли:
Они
указывают на весьма сильную связь каждого фактора с результатом, а также
высокую межфакторную зависимость (факторы
и
явно коллинеарны, так как
). При такой сильной
межфакторной зависимости рекомендуется один из факторов исключить из
рассмотрения.
Частные
коэффициенты корреляции характеризуют тесноту связи между результатом и
соответствующим факторов при элиминировании (устранении влияния) других
факторов, включенных в уравнение регрессии.
При двух
факторах частные коэффициенты корреляции рассчитываются следующим образом:
Если
сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за
высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные
оценки тесноты связи. Именно по этой причине рекомендуется при наличии сильной
коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у
которого теснота парной зависимости меньше, чем теснота межфакторной связи.
Коэффициенты
множественной корреляции и детерминации
Коэффициент
множественной корреляции определить по формуле:
Коэффициент
множественной корреляции показывает на весьма сильную связь всего набора
факторов с результатом.
3)
Нескорректированный коэффициент множественной детерминации
оценивает долю вариации результата за счет
представленных в уравнении факторов в общей вариации результата. Здесь эта доля
составляет 98,4% и указывает на высокую степень обусловленности вариации
результата вариацией факторов, иными словами – на весьма тесную связь факторов
с результатом.
Скорректированный
коэффициент множественной корреляции:
определяет
тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает
такую оценку тесноты связи, которая не зависит от числа факторов и поэтому
может сравниваться по разным моделям с разным числом факторов. Оба коэффициента
указывают на высокую (более 98%) детерминированность результата
в модели факторами
и
.
Надежность
уравнения регрессии. Критерий Фишера
4) Оценку
надежности уравнения регрессии в целом и показателя тесноты связи
дает
–критерий Фишера:
В нашем
случае фактическое значение
–критерия Фишера:
Получили,
что
(при
)
(по таблице F-распределения Фишера-Снедекора, при уровне значимости α=0,05 и числе степеней свободы k1=2 и k2=20-2=18), то есть вероятность
случайно получить такое значение
– критерия не превышает допустимый уровень
значимости 5%. Следовательно, полученное значение не случайно, оно
сформировалось под влиянием существенных факторов, то есть подтверждается
статистическая значимость всего уравнения и показателя тесноты связи
.
5) С
помощью частных
–критериев Фишера оценим целесообразность
включения в уравнение множественной регрессии фактора
после
и фактора
после
при помощи формул:
Найдем
и
.
Получили,
что
. Следовательно, включение
в модель фактора
после того, как в модель включен фактор
статистически нецелесообразно: прирост
факторной дисперсии за счет дополнительного признака
оказывается незначительным, несущественным;
фактор
включать в уравнение после фактора
не следует.
Если
поменять первоначальный порядок включения факторов в модель и рассмотреть
вариант включения
после
, то результат расчета
частного
–критерия для
будет иным.
, то есть вероятность его
случайного формирования меньше принятого стандарта
. Следовательно, значение
частного
–критерия для дополнительно включенного
фактора
не случайно, является статистически значимым,
надежным, достоверным: прирост факторной дисперсии за счет дополнительного
фактора
является существенным.
Фактор
должен присутствовать в уравнении, в том числе
в варианте, когда он дополнительно включается после фактора
.
6) Общий
вывод состоит в том, что множественная модель с факторами
и
с
содержит неинформативный фактор
. Если исключить фактор
, то можно ограничится
уравнением парной регрессии:
