Загрузить PDF
Загрузить PDF
Множество значений (область значений) функции — все значения, которые принимает функция в ее области определения. Другими словами, это те значения у, которые вы получаете при подстановке всех возможных значений х. Все возможные значения х и называются областью определения функции. Выполните следующие действия для нахождения множества значений функции.
-

1
Запишите функцию. Например: f(x) = 3x2 + 6x -2. Подставив x в уравнение, мы сможем найти значение y. Эта квадратичная функция, и ее график — парабола.
-

2
Найдите вершину параболы. Если вам дана линейная функция или любая другая с переменной в нечетной степени, например, f(x) = 6x3+2x + 7, пропустите этот шаг. Но если вам дана квадратичная функция или любая другая с переменной х в четной степени, нужно найти вершину графика этой функции. Для этого используйте формулу х=-b/2a. В функции 3x2 + 6x -2 a = 3, b = 6, c = -2. Вычисляем: х = -6/(2*3)= -1.
- Теперь подставьте х= -1 в функцию, чтобы найти у. f(-1) = 3*(-1)2 + 6*(-1) -2 = 3 – 6 -2 = -5.
- Координаты вершины параболы (-1,-5). Нанесите ее на координатную плоскость. Точка лежит в третьем квадранте координатной плоскости.
-

3
Найдите еще несколько точек на графике. Для этого подставьте в функцию несколько других значений х. Так как член x2 положительный, то парабола будет направлена вверх. Для подстраховки подставим в функцию несколько значений x, чтобы узнать, какие значения y они дают.
- f(-2) = 3(-2)2 + 6(-2) -2 = -2. первая точка на параболе (-2, -2)
- f(0) = 3(0)2 + 6(0) -2 = -2. Вторая точка на параболе (0,-2)
- f(1) = 3(1)2 + 6(1) -2 = 7. Третья точка на параболе (1, 7).
-

4
Найдите множество значений функции на графике. Найдите наименьшее значение у на графике. Эта вершина параболы, где у=-5. Так как парабола лежит выше вершины, то множество значений функции y ≥ -5.
Реклама
-

1
Найдите минимум функции. Вычислите наименьшее значение у. Допустим, минимум функции у=-3. Это значение может становиться все меньше и меньше, вплоть до бесконечности, так что минимум функции не имеет заданной минимальной точки.
-

2
Найдите максимум функции. Допустим, максимум функции у= 10. Как и в случае с минимумом, максимум функции не имеет заданной максимальной точки.
-

3
Запишите множество значений. Таким образом, множество значений функции лежит в диапазоне от -3 до +10. Запишите множество значений функции как: -3 ≤ f(x) ≤ 10
- Но, допустим, минимум функции у=-3, а ее максимум — бесконечность (график функции уходит бесконечно вверх). Тогда множество значений функции: f(x) ≥ -3.
- С другой стороны, если максимум функции у=10, а минимум — бесконечность (график функции уходит бесконечно вниз), то множество значений функции: f(x) ≤ 10.
Реклама
-

1
Запишите множество координат. Из множества координат можно определить его область значения и область определения. Допустим, дано множество координат: {(2, -3), (4, 6), (3, -1), (6, 6), (2, 3)}.[1]
-

2
Перечислите значения у. Чтобы найти область значений множества, просто запишите все значения у: {-3, 6, -1, 6, 3}.[2]
-

3
Удалите все повторяющиеся значения у. В нашем примере удалите “6”: {-3, -1, 6, 3}.[3]
-

4
Запишите область значений в порядке возрастания. Областью значений множества координат {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} будет {-3, -1, 3, 6}.[4]
-

5
Убедитесь, что множество координат дано для функции. Чтобы это было так, каждому одному значению х должно соответствовать одно значение у. Например, множество координат {(2, 3) (2, 4) (6, 9)} дано не для функции, потому что одному значению х=2 соответствуют два разных значения у: у=3 и у=4.[5]
Реклама
-

1
Прочитайте задачу. «Ольга продает билеты в театр по 500 рублей за билет. Общая вырученная сумма за проданные билеты является функцией от количества проданных билетов. Какова область значений этой функции?»
-

2
Запишите задачу как функцию. В этом случае М — общая вырученная сумма за проданные билеты, а t — количество проданных билетов. Так как один билет стоит 500 рублей, надо умножить количество проданных билетов на 500, чтобы найти вырученную сумму. Таким образом, функция может быть записана в виде M(t) = 500t.
- Например, если она продаст 2 билета, нужно умножить 2 на 500 — в итоге получим 1000 рублей, вырученных за проданные билеты.
-

3
Найдите область определения. Для нахождения области значений вы должны сначала найти область определения. Это все возможные значения t. В нашем примере Ольга может продать 0 или больше билетов, — она не может продать отрицательное число билетов. Поскольку мы не знаем количество мест в театре, можно предположить, что теоретически она может продать бесконечное число билетов. И она может продавать только целые билеты (она не может продать, например, 1/2 билета). Таким образом, область определения функции t = любое неотрицательное целое число.
-

4
Найдите область значений. Это возможное количество денег, которые Ольга выручит от продажи билетов. Если вы знаете, что область определения функции — любое неотрицательное целое число, а функция имеет вид: М(t) = 5t, то вы можете найти вырученную сумму, подставив в функцию любое неотрицательное целое число (вместо t). Например, если она продаст 5 билетов, то М(5) = 5*500 = 2500 рублей. Если она продаст 100 билетов, то М(100) = 500 х 100 = 50000 рублей. Таким образом, область значений функции — любые неотрицательные целые числа, кратные пятистам.
- Это означает, что любое неотрицательное целое число, которое делится на 500, является значением у (вырученная сумма) нашей функции.
Реклама
Советы
- В более сложных случаях лучше сначала чертить график, используя область определения, и только потом находить область значений.
- Посмотрите, можете ли вы найти обратную функцию. Область определения обратной функции равна области значений исходной функции.
- Проверьте, повторяется ли функция. Любая функция, которая повторяется вдоль оси x, будет иметь ту же область значений для всей функции. Например, область значений для f(x) = sin(x) будет составлять от -1 до 1.
Реклама
Об этой статье
Эту страницу просматривали 454 618 раз.
Была ли эта статья полезной?
Множество значений функции
Онлайн калькулятор поможет найти множество значений (область значений) функции — все значения, которые принимает функция в ее области определения. Другими словами, это те значения у, которые получаются при подстановке всех возможных значений х.
Теперь рассмотрим следующий вопрос: Как найти множество значений функции? Решение этой задачи с помощью онлайн калькулятора не составит труда, просто введите нужную функцию и получите ответ.
Синтаксис
основных функций:
xa: x^a
|x|: abs(x)
√x: Sqrt[x]
n√x: x^(1/n)
ax: a^x
logax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]
sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]
arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]
areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция “И” ∧: &&
дизъюнкция “ИЛИ” ∨: ||
отрицание “НЕ” ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

subjects:mathematics:множество_значений_функции
Содержание
Математика ( Справочник )
-
-
Множество значений функции
-
Нахождение множества значений функции
Обозначения
-
D(f) — те значения, которые может принимать аргумент, т.е. область определения функции.
-
E(f) — те значения, которые может принимать функция, т.е. множество значений функции.
Способы нахождения областей значений функций.
-
последовательное нахождение значений сложных аргументов функции;
-
метод оценок/границ;
-
использование свойств непрерывности и монотонности функции;
-
использование производной;
-
использование наибольшего и наименьшего значений функции;
-
графический метод;
-
метод введения параметра;
-
метод обратной функции.
Рассмотрим некоторые из них.
Используя производную
Общий подход к нахождению множества значений непрерывной функции f(x) заключается в нахождении наибольшего и наименьшего значения функции f(x) в области ее определения (или в доказательстве того, что одно из них или оба не существуют).
В случае, если нужно найти множества значений функции на отрезке:
-
найти производную данной функции f ‘(x);
-
найти критические точки функции f(x) и выбрать те из них, которые принадлежат данному отрезку;
-
вычислить значения функции на концах отрезка и в выбранных критических точках;
-
среди найденных значений выбрать наименьшее и наибольшее значения;
-
Множество значений функции заключить между этими значениями.
Если областью определения функции является интервал, то используется та же схема, но вместо значений на концах используются пределы функции при стремлении аргумента к концам интервала. Значения пределов из не входят в множество значений.
Метод границ/оценок
Для нахождения множества значений функции сначала находят множество значений аргумента, а затем отыскивают соответствующие наименьше и наибольшее значения функции функции. Используя неравенства – определяют границы.
Суть состоит в оценке непрерывной функции снизу и сверху и в доказательстве достижения функцией нижней и верхней границы оценок. При этом совпадение множества значений функции с промежутком от нижней границы оценки до верхней обуславливается непрерывностью функции и отсутствием у неё других значений.
Свойства непрерывной функции
Другой вариант заключается в преобразовании функции в непрерывную монотонную, тогда используя свойства неравенств оценивают множество значений вновь полученной функции.
Последовательное нахождение значений сложных аргументов функции
Основан на последовательном отыскании множества значений промежуточных функций, из которых составлена функция
Области значений основных элементарных функций
| Функция | Множество значений |
|---|---|
| $y = kx+ b$ | E(y) = (-∞;+∞) |
| $y = x^{2n}$ | E(y) = [0;+∞) |
| $y = x^{2n +1}$ | E(y) = (-∞;+∞) |
| $y = k/x$ | E(y) = (-∞;0)u(0;+∞) |
| $y = x^{frac{1}{2n}}$ | E(y) = [0;+∞) |
| $y = x^{frac{1}{2n+1}}$ | E(y) = (-∞;+∞) |
| $y = a^{x}$ | E(y) = (0;+∞) |
| $y = log_{a}{x}$ | E(y) = (-∞;+∞) |
| $y = sin{x}$ | E(y) = [-1;1] |
| $y = cos{x}$ | E(y) = [-1;1] |
| $y = {rm tg}, x$ | E(y) = (-∞;+∞) |
| $y = {rm ctg}, x$ | E(y) = (-∞;+∞) |
| $y = arcsin{x}$ | E(y) = [-π/2; π/2] |
| $y = arccos{x}$ | E(y) = [0; π] |
| $y = {rm arctg}, x$ | E(y) = (-π/2; π/2) |
| $y = {rm arcctg}, x$ | E(y) = (0; π) |
Примеры
Найдите множество значений функции:
Используя производную
НЕ используя производную
Найдите наибольшее и наименьшее значения функции:
$f(x)=sin^{2}{x}+cos{x}-frac{1}{2}$
Используя метод границ/оценок
$y=5-4sin{x}$
$y=cos{7x}+5cos{x}$
$f(x)=1+2sin^{2}{x}$
$$
\ -1leqsin{x}leq 1
\ 0leqsin^{2}{x}leq 1
\ 0leq2sin^{2}{x}leq 2
\ 1leq1+2sin^{2}{x}leq 3
$$
Ответ: E(f) = [1; 3].
$f(x)=3-2^{3+{rm tg}^{2}, x}$
$$
\ -infty < {rm tg}, x < +infty
\ 0 leq {rm tg}^{2}, x < +infty
\ 3 leq 3+{rm tg}^{2}, x < +infty
\ 2^{3} leq 2^{3+{rm tg}^{2}, x} < +infty
\ -infty < -2^{3+{rm tg}^{2}, x} leq -8
\ -infty < 3-2^{3+{rm tg}^{2}, x} leq -5
$$
Ответ: E(f) = (–∞; -5].
$f(x)=2+sqrt{16-lg^{2}{x}}$
$$
\ -infty < lg{x} < +infty
\ 0 leq lg^{2}{x} < +infty
\ -infty < -lg^{2}{x} leq 0
\ -infty < 16-lg^{2}{x} leq 16
\ 0 leq sqrt{16-lg^{2}{x}} leq 4
\ 2 leq 2+sqrt{16-lg^{2}{x}} leq 6
$$
Ответ: E(f) = [2; 6].
$f(x)=sqrt{2-x}+sqrt{2+x}$
$y=sin{x}+cos{x}$
Используя непрерывную функцию
Иные
Использованная литература
Статьи:
-
Область значения функций в задачах ЕГЭ, Минюк Ирина Борисовна
-
Советы по нахождению множества значений функции, Беляева И., Федорова С.
-
Нахождение множества значений функции
-
Как решать задачи по математике на вступительных экзаменах, И.И.Мельников, И.Н.Сергеев
Рекомендуем
· Последние изменения: 2018/09/19 21:14 —
¶
Как найти множество значений функции
4 методика:Поиск множества значений функции по формулеПоиск множества значений функции на графикеПоиск области значений множества координатПоиск области значений в задачах
Множество значений (область значений) функции – все значения, которые принимает функция в ее области определения. Другими словами, это те значения у, которые вы получаете при подстановке всех возможных значений х. Все возможные значения х и называются областью определения функции. Выполните следующие действия для нахождения множества значений функции.
Шаги
Метод 1 из 4: Поиск множества значений функции по формуле
-

1
Запишите функцию. Например: f(x) = 3×2 + 6x -2. Эта квадратичная функция, и ее график – парабола.[1] -

2
Найдите вершину параболы. Если вам дана линейная функция или любая другая с переменной в нечетной степени, например, f(x) = 6×3+2x + 7, пропустите этот шаг. Но если вам дана квадратичная функция или любая другая с переменной х в четной степени, вы должны найти вершину графика этой функции. Для этого используйте формулу х=-b/2a.В функции 3×2 + 6x -2 a = 3, b = 6, c = -2. Вычисляем: х = -6/(2*3)= -1.[2]- Теперь подставьте х= -1 в функцию, чтобы найти у. f(-1) = 3*(-1)2 + 6*(-1) -2 = 3 – 6 -2 = -5.
- Координаты вершины параболы (-1,-5). Нанесите ее на координатную плоскость. Точка лежит в третьем квадранте координатной плоскости.
-

3
Найдите еще несколько точек на графике. Для этого подставьте в функцию несколько других значений х. Так как член x2 положительный, то парабола будет направлена вверх.[3]- f(-2) = 3(-2)2 + 6(-2) -2 = -2. первая точка на параболе (-2, -2)
- f(0) = 3(0)2 + 6(0) -2 = -2. Вторая точка на параболе (0,-2)
- f(1) = 3(1)2 + 6(1) -2 = 7. Третья точка на параболе (1, 7).
-

4
Найдите множество значений функции на графике. Найдите наименьшее значение у на графике. Эта вершина параболы, где у=-5. Так как парабола лежит выше вершины, то множество значений функции y ≥ -5.[4]
Метод 2 из 4: Поиск множества значений функции на графике
-

1
Найдите минимум функции. Вычислите наименьшее значение у. Допустим, минимум функции у=-3. -

2
Найдите максимум функции. Допустим, максимум функции у= 10. -

3
Запишите множество значений. Таким образом, множество значений функции лежит в диапазоне от -3 до +10. Запишите множество значений функции как: -3 ≤ f(x) ≤ 10- Но, допустим, минимум функции у=-3, а ее максимум – бесконечность (график функции уходит бесконечно вверх). Тогда множество значений функции: f(x) ≥ -3.
- С другой стороны, если максимум функции у=10, а минимум – бесконечность (график функции уходит бесконечно вниз), то множество значений функции: f(x) ≤ 10.
Метод 3 из 4: Поиск области значений множества координат
-

1
Запишите множество координат. Из множества координат можно определить его область значения и область определения. Допустим, дано множество координат: {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}.[5] -

2
Перечислите значения у. Чтобы найти область значений множества, просто запишите все значения у: {-3, 6, -1, 6, 3}.[6] -

3
Удалите все повторяющиеся значения у. В нашем примере удалите ” 6″: {-3, -1, 6, 3}.[7] -

4
Запишите область значений в порядке возрастания. Областью значений множества координат {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} будет {-3, -1, 3, 6}.[8] -
5
Убедитесь, что множество координат дано для функции. Чтобы это было так, каждому одному значению х должно соответствовать одно значение у. Например, множество координат {(2, 3) (2, 4) (6, 9)} дано не для функции, потому что одному значению х=2 соответствуют два разных значения у: у=3 и у=4.[9]
Метод 4 из 4: Поиск области значений в задачах
-

1
Прочитайте задачу. “Ольга продает билеты в театр по 500 рублей за билет. Общая вырученная сумма за проданные билеты является функцией от количества проданных билетов. Какова область значений этой функции? -

2
Запишите задачу как функцию. В этом случае М – общая вырученная сумма за проданные билеты, а t – количество проданных билетов. Так как один билет стоит 500 рублей, надо умножить количество проданных билетов на 500, чтобы найти вырученную сумму. Таким образом, функция может быть записана в виде M(t) = 500t.- Например, если она продаст 2 билета, вы должны умножить 2 на 500 и получить 1000 рублей, вырученных за проданные билеты.
-

3
Найдите область определения. Для нахождения области значений вы должны сначала найти область определения. Это все возможные значения t. В нашем примере Ольга может продать 0 или больше билетов, – она не может продать отрицательное число билетов. Поскольку мы не знаем количество мест в театре, можно предположить, что теоретически она может продать бесконечное число билетов. И она может продавать только целые билеты (она не может продать, например, 1/2 билета). Таким образом, область определения функции t = любое неотрицательное целое число. -

4
Найдите область значений. Это возможное количество денег, которые Ольга выручит от продажи билетов. Если вы знаете, что область определения функции – любое неотрицательное целое число, а функция имеет вид: М(t) = 5t, то вы можете найти вырученную сумму, подставив в функцию любое неотрицательное целое число (вместо t). Например, если она продаст 5 билетов, то М(5) = 5*500 = 2500 рублей. Если она продаст 100 билетов, то М(100) = 500 х 100 = 50000 рублей. Таким образом, область значений функции – любые неотрицательные целые числа, кратные пятистам.- Это означает, что любое неотрицательное целое число, которое делится на 500, является значением у (вырученная сумма) нашей функции.
Советы
- Посмотрите, можете ли вы найти обратную функцию. Область определения обратной функции равен области значений исходной функции.
«Элементарное введение
в математический анализ»
«Элементарное
введение в математический анализ»
Хоть деление математического знания на алгебру, геометрию и математический анализ и является очень условным, все-таки существует некоторый признак,
по которому математический анализ выделяется
из остальной математики.
Начать можно с вопроса: что же здесь анализируется?
Если совсем коротко, то ответ будет такой: функции. Только не все подряд, а определенного вида.
Поэтому прежде, чем делать дальнейшее уточнение, поговорим о том, что такое функция.
В самом общем виде функция — это правило,
по которому элементам одного множества ставятся в соответствие элементы любого другого множества.
Иногда эти множества называют, соответственно, областью определения и областью значений функции.
А иногда — когда слово «функция» заменяют более общим понятием «морфизм» — источником (source) и назначением (target) морфизма.
Здесь есть одно важное требование,
которое отличает функцию от любых других возможных правил сопоставления элементов двух множеств:
Чтобы правило сопоставления элементов
являлось функцией, каждому элементу первого множества должен быть сопоставлен ровно один элемент второго множества.
Это не означает, что различным элементам первого множества должны обязательно быть сопоставлены различные элементы из второго множества.
Поэтому, например, вот такое незатейливое правило функцией будет:
но и потому, что элементу а из множества А вообще не поставлен в соответствие
ни один элемент из множества В.
Заметим, что в последнем случае изображенное правило не будет функцией не только потому, что элементу b множества А поставлены в соответствие сразу два элемента из множества В,
Или по-другому:
функция — это чрезвычайно удобный способ упаковки знания
Смысл данного требования — в желании иметь определенность.
Вообще математическую функцию удобно понимать как модель некоторого контролируемого, или предсказуемого процесса — в частности, процесса репрезентации данных.
Рассмотрим в связи с только что сказанным еще один пример:
В данном случае правило f
сопоставляет каждому из трех человек их любимый завтрак.
То есть, «пробегая» по всем людям компании,
мы точно знаем их предпочтения, хоть они могут у некоторых людей и совпадать.
Формально это записывают так:
ее еще называют независимой переменной, или аргументом
Это значит, что если мы подставим на место переменной x
конкретный элемент из списка, мы всегда сможем узнать значение функции f на этом элементе
В данном случае, например,
В предыдущем примере такая определенность отсутствовала:
f (b) одновременно равнялось и нулю, и единице
Поэтому функцию еще иногда называют функциональной зависимостью — если элементы первого множества мы можем изменять произвольно,
то изменение значений уже строго зависит от того, как было задано правило f
Кстати сказать, множеству значений — неслучайно
в определении оно было нами названо «любым другим множеством» — никто не запрещает совпадать с первым:
g = понравившийся человек
вроде бы тоже сопоставляет каждому из членов группы их предпочтения — только в данном случае ими оказываются уже не продукты,
а члены той же группы.
Определить, какие из следующих диаграм задают функцию:
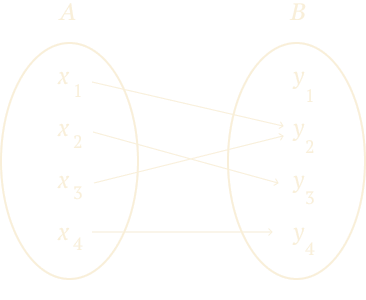
• табличный
• графический
• словесный
• аналитический (с помощью формулы)
II. Способы задания функции
Кроме рассмотренных нами выше диаграмм, существуют и другие способы задания функции:
Приведем примеры для каждого:
1. Табличный
На рисунке отображена
посещаемость сайта Яндекс
в 2009м году.
По горизонтали указаны месяцы,
по вертикали — количество человек, посетивших сайт в данном месяце.
Для наглядности точки на рисунке соединены линией.
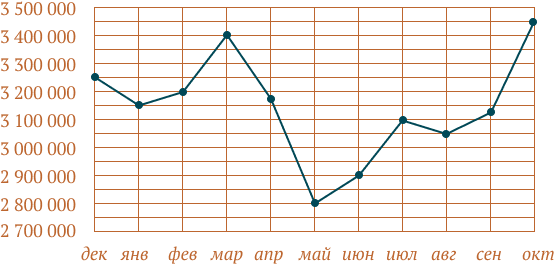
Заметьте, что изначально функция задана на множестве, состоящем всего из 11 отдельных элементов — в данном случае это месяцы года
И непрерывная линия, соединяющая соседние точки на графике — это уже не исходная функция, а так называемая интерполяция:
приближение, позволяющее предсказать промежуточные значения. Это делает графическое представление данных чрезвычайно наглядным
и удобным.
Однако, таблицы и отчасти графики хороши лишь для задания функций на конечных множествах.
Математики же, в основном, работают с множествами числовыми, которые, как правило, не являются конечными. В таких случаях правило сопоставления приходится определять либо словесно, либо с помощью формулы.
Рассмотрим в качестве примера такое правило, задающее функцию на множестве всех целых чисел: каждому числу функция f сопоставляет его остаток от деления на три.
Несмотря на то, что целых чисел бесконечно
много, по этому правилу мы в состоянии вычислить значение функции для любого целого числа:
Строго говоря, на формулу тоже можно смотреть как
на высказывание в некотором формализованном языке,
поэтому аналитический способ задания функции —
это продолжение словесного, доведенное математиками до совершенства.
4. Аналитический способ задания функции:
При аналитическом способе задания функции график уже имеет вспомогательный характер,
хотя непрерывная линия тут не является приближением — значения у функции есть
во всех точках кривой.
что, переходя от примера к примеру,
мы незаметно подошли к рассмотрению функций числовых, а в последнем примере функция была задана на множестве так называемых действительных чисел (в данном случае — неотрицательных).
Сейчас же пора сказать самое главное:
Это множество (обозначаемое буквой ℝ) — довольно сложный для понимания объект, и к его устройству
мы будем обращаться еще не раз.
Математический анализ как раз и занят преимущественно исследованием
поведения функций, областью определения и областью значений которых являются или вообще все действительные числа, или какие-то их подмножества.
с учетом принятых в математике обозначений мы можем сказать, что предметом изучения математического анализа являются функции вида
Разумеется, в большинстве своем все они заданы формулами, поскольку только формулы и можно анализировать математически — именно поэтому способ задания функции с помощью формулы был назван нами аналитическим.
Функцию, заданную формулой, можно раскладывать в ряд, интегрировать, брать производную
и совершать все те действия, которые, собственно,
и изучаются в полном курсе математического анализа. Если вспомнить, что функцию мы, в числе прочего, назвали удобным способом упаковки знания, то математический анализ — это множество техник по его распаковке.
С частью этих действий мы познакомим вас и на страницах нашего журнала.
А начнем мы наше более глубокое знакомство с техниками математического анализа с изучения числовых последовательностей.
Это вообще — то тоже в каком-то смысле функции — функции, заданные на множестве натуральных чисел, или, как их еще иногда называют — функции натурального аргумента
Последовательность — это занумерованное (возможно, бесконечное) множество элементов, в котором имеет значение порядок их следования
Этим последовательность отличается от обычного множества.
Еще одно отличие состоит в том, что элементы последовательности могут повторяться. Конечную последовательность иногда еще называют
«строкой» или «словом».
1010 и 0101 или АБЫРВАЛГ и ГЛАВРЫБА — это четыре разные последовательности, которым соответствуют два множества: {0, 1} и {А, Б, В, Г, Л, Р, Ы}.
Последовательность — это функция, областью определения которой является либо
(в случае бесконечной последовательности) множество всех натуральных чисел, либо
(в случае конечной последовательности длины n) — множество, состоящее из первых n натуральных чисел.
Для целей математического анализа особенно важны числовые последовательности, элементами которых являются вещественные, или действительные числа.
Пока для простоты любое действительное число мы будем представлять себе в виде бесконечной десятичной дроби.
При этом целому числу будет соответствовать дробь, у которой после запятой идут одни нули, рациональному числу (или обыкновенной дроби) будет соответствовать либо конечная десятичная, либо бесконечная периодическая,
а иррациональным числам,
то есть корням всех степеней, а также числам типа π и e – бесконечные непериодические десятичные дроби.
Тот факт, что всякая обыкновенная дробь либо представляется в виде конечной десятичной дроби, либо обязательно даст период, чрезвычайно важен.
Его доказательство мы подробно разбираем здесь
(начиная с десятой минуты):
Не менее важным фактом является
и то, что квадратный корень из целого положительного числа
(если он не является целым числом) не может быть представлен в виде
обыкновенной дроби, и поэтому необходимо будет иметь вид бесконечной непериодической десятичной дроби. Доказательство этого факта будет рассмотрено позже
И здесь возникает, пожалуй, самый главный вопрос в этой теме:
Как мы видим, все такие дроби сами
(с точностью до знака или места запятой)
есть не что иное, как бесконечные последовательности натуральных чисел:
Если последовательность — это функция,
а функция — это правило, сопоставляющее элементам одного множества элементы другого множества, то мы должны озаботиться и способами задания последовательностей,
в особенности — бесконечных.
Итак, бесконечная последовательность
считается заданной, если известно правило,
по которому для любого натурального n
можно найти значение n-го члена этой последовательности.
Как можно задать эти последовательности?
Во всех наших примерах, кроме последнего, видны
те или иные закономерности, поэтому их легко описать.
Обратимся снова
к нашим примерам.
Иначе говоря, последовательность задана,
если задан ее общий член.
Начнем с самого первого примера.
В принципе мы вправе выбрать любую форму записи — например, такую:
Но общепринятый способ обозначения немного иной:
То есть, члены последовательности обозначают
какой-либо буквой с нижним индексом, соответствующим номеру этого члена в данной последовательности.
Вторая последовательность
в этом смысле не сильно отличается от первой:
В принципе, их обе можно было бы задать
и графически, как определенные на конечном подмножестве натуральных чисел:
Первая последовательность
Вторая последовательность
Четвертая последовательность — вообще постоянная:
Третья последовательность
задается простейшей формулой:
для любого натурального
Бесконечную периодическую последовательность 0, 142857142857…..
можно задать словесно, сказав, например, что первый член последовательности равен нулю,
а, начиная со второго, каждый n-й член последовательности равен n-му остатку от деления 10 на 7 в алгоритме, переводящем обыкновенную дробь
последняя последовательность цифр представляет собой, как, возможно, кто-то уже догадался, начало десятичной формы записи числа π.
И здесь возникают серьезные сложности,
поскольку в последовательности этих цифр
не существует никакой очевидной закономерности, которую мы могли бы использовать при формулировании правила ее задания…
Давайте ненадолго оставим эту задачу и попробуем справиться с задачей попроще:
Поскольку √2 — число иррациональное,
то оно представимо лишь в виде бесконечной непериодической десятичной дроби, а, значит, последовательность цифр, входящих в такую
запись, тоже не имеет закономерностей.
задать последовательность цифр, входящих в десятичную запись √2 = 1,414213562373…
Здесь нам может помочь определение арифметического квадратного корня из числа a.
Так как же в таком случае быть?
Напоминаем, что арифметическим квадратным корнем из числа a ≥ 0 называется такое число b ≥ 0, квадрат которого равен a.
Поэтому мы можем последовательно приближаться к числу 2 с меньшей и большей стороны, подбирая его оценки с недостатком и с избытком сначала с точностью до целых, потом до десятых, затем до сотых и так далее «до бесконечности»…
В результате мы получим такую систему неравенств:
И таким образом
мы нашу
последовательность все же построим,
сопоставляя каждому номеру n последнюю цифру в соответствующей оценке √2 с недостатком (или, как говорят в таких случаях — слева, или снизу).
Обратите внимание, что если мы изобразим
нашу процедуру графически, то это будет выглядеть так, как если бы мы на числовой прямой отметили некоторую систему отрезков бесконечно уменьшающейся длины, оказывающихся вложенными друг в друга:
для понимания свойство множества действительных чисел заключается в том, что только в нем такая система вложенных отрезков будет иметь единственную общую точку!
В нашем примере такой единственной точкой и будет число, в точности равное квадратному корню из двух.
Это свойство называется принципом вложенных отрезков Кантора, и этот принцип эквивалентен
аксиоме полноты множества действительных чисел.
И вот основное
и, пожалуй,
самое загадочное
и сложное
мы аксиоматически полагаем, что действительные числа заполняют всю числовую прямую без каких-либо сколь-угодно малых пробелов!
Это означает, что у нас нет другого способа убедиться в том, что между ними и точками на прямой есть взаимно-однозначное соответствие — мы просто соглашаемся считать, что действительные числа устроены именно так!
Я прошу всех вдуматься в то, что здесь сейчас происходит:
Это соглашение позволяет нам, в частности, рассматривать последовательности и другого вида — а именно: ведь мы могли бы каждому номеру n ставить в соответствие не цифру, входящую в десятичную запись оценки √2 слева, а саму эту оценку, т. е. некоторую конечную десятичную дробь — то же самое мы можем проделать и с оценкой сверху.
В результате мы получим последовательность приближений √2 конечными десятичными дробями слева и справа (снизу и сверху). Соответствующие последовательности будут выглядеть следующим образом:
Последовательность a
и ограниченной сверху, последовательность b
и ограниченной снизу
И, согласно принципу вложенных отрезков, обе эти последовательности ограничены одним и тем же, единственным числом, равным √2. Но мы можем сказать и больше — мы можем сказать, что эти последовательности к этому числу сходятся, или, что тоже самое, что √2 — это их предел
Число А называется пределом последевательности x
если для любого положительного числа ε найдется такой номер k,
начиная с которого все члены последовательности будут отличаться от А менее, чем на ε.
Графически это можно изобразить так:
называется монотонно возрастающей
Как видно из рисунка, это означает, что на сколь-угодно малое расстояние
ε от А мы бы не отступили, начиная с какого-то номера k, все члены последовательности x⠀, x⠀⠀ , x⠀⠀ ⠀и т. д. будут иметь значения, лежащие в промежутке A ± ε.
Или, что то же самое — последовательность x⠀ устроена таким образом, что вне этого промежутка всегда окажется лишь конечное число ее элементов.
Заметим, что аксиома полноты или непрерывности не выполняется для множества таких чисел — система вложенных отрезков из нашего примера не будет иметь
в множестве рациональных чисел общей точки!
Все сказанное означает, что большая
часть действительных чисел определяется
в терминах пределов, то есть как последовательность тех или иных приближений рациональными числами,
или числами вида
без этой аксиомы было бы невозможно строгое построение математического анализа, было бы невозможно доказать существование значений
у степенной, показательной, логарифмической и всех тригонометрических
функций на естественных для них областях определения, и т.п.
нашего повествования неформально определили предмет математического анализа как изучение функций вида f :
Возможно,
теперь читателем стало более понятным, почему мы смогли себе это позволить.
И числовые последовательности во многом интересуют математиков именно с этой точки зрения — как последовательности приближений иррациональных чисел рациональными.
вернемся к отложенной нами на время проблеме того, как можно задать последовательность,
в которой n-му члену соответствует цифра, стоящая на n-м месте в десятичной записи
числа π
Для этого сначала вспомним, что вообще обозначает эта величина?
Наверное, многие помнят, что это отношение длины окружности к ее диаметру, и что оно постоянно для любой окружности
Вообще говоря, постоянство такого отношения — сам по себе далеко не тривиальный геометрический факт, который будет разобран нами в соответствующем разделе журнала.
Сейчас же мы хотим лишь обратить внимание читателей на то, что число, выражающее это отношение, как и квадратный корень из двух, тоже может быть определено лишь как последовательность приближений — например, как последовательность значений периметров вписанных в окружность единичного диаметра правильных n-угольников при бесконечно растущем числе n их углов.
Вписанные многоугольники можно заменить
на описанные — тогда их периметры будут образовывать не возрастающую, а убывающую последовательность, приближающуюся к числу π сверху. Или можно попытаться вычислить значения
и для той, и для другой, как сделал в свое время
Архимед, дойдя до n = 96, и получив свои знаменитые оценки:

то она, как мы и отмечали ранее, невероятно трудна — считается, что вычислить n-ю цифру в записи числа π столь же сложно, как и вычислить его приближение
с точностью до этой цифры.
Хотя известен как называемый spigot алгоритм, позволяющий довольно легко вычислить n-ю цифру числа — правда, в шестнадцатеричной системе счисления. (Spigot — англ. кран, клапан, контролирующий напор жидкости. Имеется в виду,
что алгоритм выдает цифры дозированно, как регулируемый вентиль.)
В любом случае такого рода задачи выходят далеко за рамки Введения.
Что же касается исходно поставленной задачи,
IV. Алгоритм приближения квадратного корня. Вавилонский метод
А закончить наше элементарное введение
в математический анализ хотелось бы рассмотрением алгоритма приближения квадратного корня, дошедшего до нас благодаря вавилонским глиняным клинописным табличкам, большая часть из которых датируется приблизительно 18 – 16 вв. д. н. э.!
Он так и называется — Вавилонский метод.
Предположим, что у нас есть какое-то положительное число А, квадратный корень из которого не является целым числом.
Основная идея метода состоит в наблюдении, что если a — приближенное значение √A с избытком, то b =
будет приближением с недостатком
(т. е. b < a), и наоборот,
но в любом случае a =
будет являться, во-первых, лучшим приближением,
чем a или b, и, во-вторых, всегда будет приближением
с избытком.

Это следует из так называемого неравенства между средним арифметическим и средним геометрическим:
Причем, равенство достигается только при x = y.
Это означает, что
Или A < a⠀< a.
То есть, мы имеем монотонно убывающую ограниченную
последовательность приближений:
A <…a⠀⠀⠀< a⠀ <….< a⠀< a⠀< a, где
Это означает, что
Или A < a⠀< a.
То есть, мы имеем монотонно убывающую ограниченную
последовательность приближений:
A <…a⠀⠀⠀< a⠀ <….< a⠀< a⠀< a, где
Такое задание последовательности, когда каждый последующий ее член определяется через предыдущие, называется рекурсивным.
И, значит, Вавилонский метод, действительно успешен, поскольку генерирует последовательность приближений, сходящуюся к √A.
Но мы теперь легко можем его найти
Как можно было бы увидеть соизмеримость
или несоизмеримость геометрически?
Давайте нарисуем прямоугольник шириной √2
и высотой 1. И попробуем «замостить» его квадратами со стороной, равной меньшей стороне нашего прямоугольника, т. е. 1.
Мы видим, что такой квадрат умещается
в прямоугольнике целиком всего один раз,
оставляя полоску размером 1 на √2 — 1.
Для большей наглядности исходный прямоугольник можно удлинить на еще один квадрат со стороной 1,
чтобы сразу увидеть один и тот же алгоритм:
в прямоугольник укладывается два квадрата, оставляя меньший прямоугольник с точно таким
же соотношением сторон.
V. √2 и геометрический смысл алгоритма Евклида.
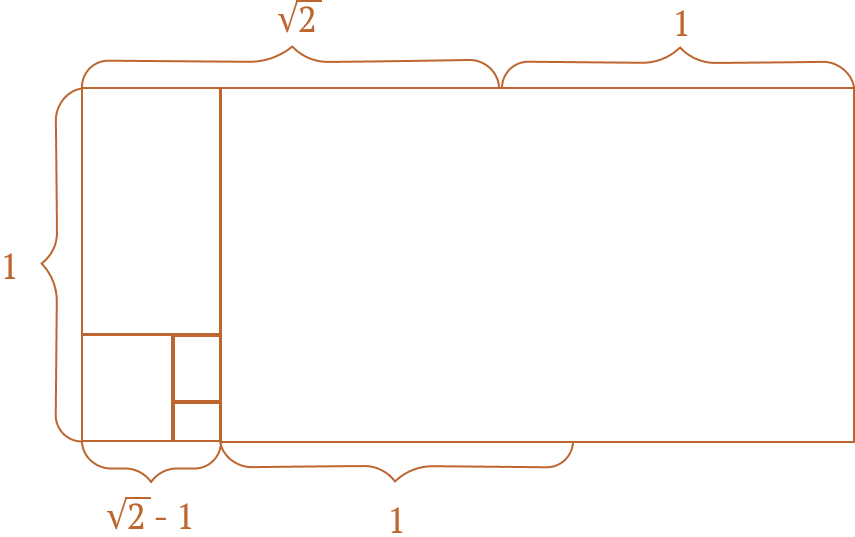
Мы утверждаем, что этот процесс никогда
не остановится, поскольку всякий раз мы будем получать подобные прямоугольники, и таким
образом ни в одном из них меньшая сторона
не уложится в большей целое число раз.
Этот факт можно заметить и чисто алгебраически. Действительно:
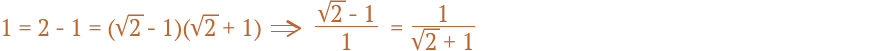
Из последнего равенства следует и еще одно доказательство несоизмеримости √2 с единицей,
что тождественно его иррациональности:
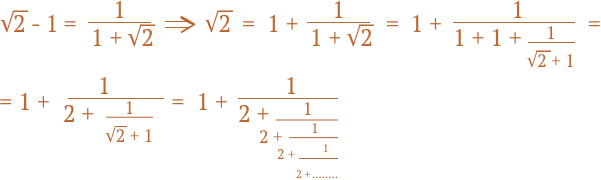

корень из двух оказался представлен в виде выражения, включающее его самого. А это значит, что вместо корня можно подставить все выражение, и процесс зациклится — т. е. данная цепная дробь никогда
не оборвется.
В то время как прямым следствием того же алгоритма Евклида (можно даже сказать — другой его формой) является представимость любого рационального числа
в виде конечной цепной дроби
То есть, мы видим, что, начиная со второго шага, имеет место так называемая бесконечная рекурсия —
Геометрически это означает, что какие бы два целых числа мы не взяли, то ситуации абсолютного самоподобия, √2 и 1, мы не получим
Алгоритм Евклида вообще-то является алгоритмом нахождения наибольшего общего делителя двух целых чисел а и b.
Вообще говоря, вопрос о соизмеримости
и несоизмеримости величин не такой уж и очевидный.
Или, говоря иначе, серия уменьшающихся прямоугольников должна оборваться, поскольку меньшая сторона рано или поздно уложится в большей целое число раз. Т. е. целые числа соизмеримы.
Греков он, например, в свое время абсолютно потряс.
Ну и действительно, интуитивно кажется чем-то очевидным, что если мой шаг имеет длину a, а ваш —длину b, то, сделав вдоль некоторой прямой по m и n шагов, соответственно, мы рано или поздно встретимся. Или нет?
Ну так вот, соизмеримыми будут такие
величины a и b, что найдется величина c, которая
«уложится» как в a, так и в b целое число раз, т. е. такая,
что a = mc и b = nc m, n⠀⠀N
Возвращаясь
к примеру с шагами,
это будет означать, что n шагов
длины а в точности совпадут с m шагов длины b.
В самом деле, если a = mc и b = nc, то na = mb = mnc.
На плоскости это будет соответствовать
примерно вот такой картинке:
Если принять за единицу длины длину одной клеточки,
то требуемая величина c здесь очевидным образом существует — в данном случае она равна 2.
Другими словами, деля большую сторону прямоугольника на меньшую с остатком, мы
на четвертом шаге геометрической версии алгоритма Евклида получили прямоугольник, меньшая сторона которого уложилась в большей целое число раз.
Длина этой стороны и есть наибольший общий делитель длин a и b. В случае, когда a и b целые числа, то такое деление заканчивается всегда — меньшая сторона длины
1 уложится целое число раз в большей стороне любой целочисленной длины.
Закончится оно и в случае, если a и b числа рациональные.
Но вот уже диагональ квадрата со стороной 1 оказывается несоизмеримой с единицей — так что грекам было, чему удивиться, согласитесь…
Журнал развивается и регулярно пополняется новыми материалами.





Подписывайтесь и знакомьтесь с ними первыми!

