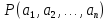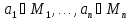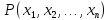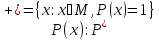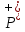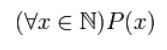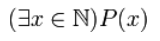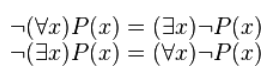Логика предикатов
Предикаты вслед за высказываниями являются следующим важным предметом, исследуемым математической логикой. Понятие предиката обобщает понятие высказывания, а теория предикатов представляет собой более тонкий инструмент, по сравнению с теорией высказываний, для изучения закономерностей процессов умозаключения и логического следования, составляющих предмет математической логики. В настоящей главе рассматриваются основы теории предикатов.
Понятие предиката
В высказывании все четко: это — конкретное утверждение о конкретных объектах — истинное или ложное. Предикат — предложение, похожее на высказывание, но все же им не являющееся: о нем нельзя судить, истинно оно или ложно. Дадим точное определение.
Определение 18.1. Определенным на множествах n-местным предикатом называется предложение, содержащее
переменных
, превращающееся в высказывание при подстановке вместо этих переменных любых конкретных элементов из множеств
соответственно.
Для n-местного предиката будем использовать обозначение . Переменные
называют предметными, а элементы множеств
, которые эти переменные пробегают, — конкретными предметами. Всякий n-местный предикат
, определенный на множествах
, представляет собой функцию п аргументов, заданную на указанных множествах и принимающую значения в множестве всех высказываний. Поэтому предикат называют также функцией-высказыванием.
Рассмотрим пример. Предложение “Река впадает в озеро Байкал” является одноместным предикатом, определенным над множеством всех названий рек. Подставив вместо предметной переменной
название “Баргузин”, получим высказывание “Река Баргузин впадает в озеро Байкал”. Это высказывание истинно. Подставив вместо предметной переменной
название “Днепр”, получим ложное высказывание “Река Днепр впадает в озеро Байкал”.
Другой пример. Предложение (выражение) “” является двухместным предикатом, заданным над множествами
. Множества, на которых задан двухместный предикат, совпадают (говорят, что “двухместный предикат задан на множестве
“). Пара действительных чисел 2, 2 превращает данный предикат в истинное высказывание: “
“, а пара чисел 2, 3 — в ложное: “
“.
Отметим еще один подход к понятию предиката. Как отмечалось, предикат , определенный на множествах
, превращается в конкретное высказывание
, если вместо предметных переменных
подставить в него конкретные предметы (элементы
) из множеств
соответственно. Это высказывание может быть либо истинным, либо ложным, т. е. его логическое значение равно 1 или 0. Следовательно, данный предикат определяет функцию
аргументов, заданную на множествах
принимающую значение в двухэлементном множестве
. Иногда эту функцию и называют предикатом.
Классификация предикатов
Определение 18.2. Предикат , заданный на множествах
, называется:
а) тождественно истинным, если при любой подстановке вместо переменных любых конкретных предметов
из множеств
соответственно он превращается в истинное высказывание
;
б) тождественно ложным, если при любой подстановке вместо переменных любых конкретных предметов из множеств
соответственно он превращается в ложное высказывание;
в) выполнимым (опровержимым), если существует по меньшей мере один набор конкретных предметов из множеств
соответственно, при подстановке которых вместо соответствующих предметных переменных в предикат
последний превратится в истинное (ложное) высказывание
.
Приведем примеры предикатов.
Одноместный предикат “Город расположен на берегу реки Волги”, определенный на множестве названий городов, является выполнимым, потому что существуют города, названия которых превращают данный предикат в истинное высказывание, или, иначе, удовлетворяют этому предикату (например, Ульяновск, Саратов и т. д.). Но данный предикат не будет тождественно истинным, потому что существуют города, названия которых превращают его в ложное высказывание, или, иначе, не удовлетворяют этому предикату (например, Прага, Якутск и т.д.). Этот же предикат являет собой пример опровержимого, но не тождественно ложного предиката (продумайте!).
В другом примере одноместный предикат ““, определенный на множестве действительных чисел, тождественно истинный. Наконец, двухместный предикат “
“, заданный также на множестве действительных чисел, является тождественно ложным предикатом, потому что любая пара действительных чисел превращает его в ложное высказывание (не удовлетворяет ему).
Отметим некоторые достаточно очевидные закономерности взаимосвязей между предикатами различных типов (рекомендуется осмыслить их):
1) каждый тождественно истинный предикат является выполнимым, но обратное неверно;
2) каждый тождественно ложный предикат является опровержимым, но обратное неверно;
3) каждый не тождественно истинный предикат будет опровержимым, но, вообще говоря, не будет тождественно ложным;
4) каждый не тождественно ложный предикат будет выполнимым, но, вообще говоря, не будет тождественно истинным.
Множество истинности предиката
Определение 18.3. Множеством истинности предиката , заданного на множествах
, называется совокупность всех упорядоченных n-систем
, в которых
, таких, что данный предикат обращается в истинное высказывание
при подстановке
. Это множество будем обозначать
. Таким образом,
Множество истинности “-местного предиката
представляет собой n-арное отношение между элементами множеств
. Если предикат
— одноместный, заданный над множеством
, то его множество истинности
является подмножеством множества
.
Например, множеством истинности двухместного предиката “Точка принадлежит прямой
“, заданного на множестве
всех точек плоскости и на множестве
всех прямых этой плоскости, является бинарное отношение принадлежности (инцидентности) между точками и прямыми плоскости. Другой пример. Множество истинности двухместного предиката
, заданного на множестве
, есть множество всех таких пар действительных чисел, которые являются координатами точек плоскости, образующими окружность с центром в начале координат и радиуса 3. Наконец, если
“
” — одноместный предикат над
, то
, или
.
В терминах множества истинности легко выразить понятия, связанные с классификацией предикатов (определение 18.2). В самом деле, n-местный предикат , заданный на множествах
, будет:
а) тождественно истинным тогда и только тогда, когда ;
б) тождественно ложным тогда и только тогда, когда ;
в) выполнимым тогда и только тогда, когда ;
г) опровержимым тогда и только тогда, когда .
На языке множеств истинности еще более отчетливо проясняются закономерности взаимосвязей между предикатами различных типов, отмеченные в конце предыдущего пункта. Проанализируйте их еще раз.
Равносильность и следование предикатов
Определение 18.4. Два n-местных предиката и
, заданных над одними и теми же множествами
, называются равносильными, если набор предметов (элементов)
превращает первый предикат в истинное высказывание
в том и только в том случае, когда этот набор предметов превращает второй предикат в истинное высказывание
.
Другими словами (на языке множеств истинности), предикаты и
равносильны тогда и только тогда, когда их множества истинности совпадают.
.
Утверждение о равносильности двух предикатов и
символически будем записывать так:
. Отношение равносильности предикатов является отношением эквивалентности, так что совокупность всех n-местных предикатов, определенных на множествах
, распадается на непересекающиеся классы равносильных предикатов (все они определяют одну и ту же функцию, заданную на множествах
и принимающую значения в двухэлементном множестве
). Переход от предиката
к равносильному ему предикату
называется равносильным преобразованием первого. Это понятие очень важно для школьной математики, потому что изучаемые в ней уравнения и неравенства представляют собой частные виды предикатов. Решение уравнения и неравенства есть поиск их множеств истинности. При таком поиске мы проделываем над уравнением и неравенством различные преобразования, и здесь важно, чтобы эти преобразования были равносильными, т. е. чтобы найденное множество оказалось бы множеством истинности именно исходного уравнения или неравенства. Аналогична ситуация при решении систем уравнений или неравенств.
Рассмотрим простой пример. Пусть требуется решить уравнение (найти множество истинности предиката): . Преобразуем его равносильным образом:
Ответ: — множество всех решений данного уравнения (множество истинности данного предиката).
Отметим следующее немаловажное обстоятельство: может быть так, что два предиката равносильны, если их рассматривать над одним множеством, и неравносильны, если их рассматривать над другим (в частности, объемлющим первое) множеством. Такова, например, ситуация с предикатами: и
.
Определение 18.5. Предикат , заданный над множествами
, называется следствием предиката
, заданного над теми же множествами, если он превращается в истинное высказывание на всех тех наборах значений предметных переменных из соответствующих множеств, на которых в истинное высказывание превращается предикат
.
Другими словами (в терминах множеств истинности), можно сказать, что предикат является следствием предиката
тогда и только тогда, когда
.
Утверждение о том, что предикат является следствием предиката
, будем символически записывать так:
.
Например, одноместный предикат, определенный на множестве натуральных чисел, “ делится на 3″ является следствием одноместного предиката, определенного на том же множестве, “
делится на 6″. Из двух предикатов, упомянутых перед последним определением, первый будет следствием второго, если считать, что оба предиката заданы на множестве
целых чисел.
Язык множеств истинности позволяет установить взаимосвязь между понятиями равносильности и следования предикатов: два предиката, определенные на одних и тех же множествах, равносильны тогда и только тогда, когда каждый из них является следствием другого. Кроме того, этот же язык дает возможность без труда установить следующие простые теоремы.
Теорема 18.6. Каждые два тождественно истинных (тождественно ложных) предиката, заданных на одних и тех же множествах, равносильны. Обратно, всякий предикат, равносильный тождественно истинному (тождественно ложному) предикату, сам является тождественно истинным (тождественно ложным) предикатом.
Теорема 18.7. Каждый тождественно истинный n-местный предикат является следствием любого другого n-местного предиката, определенного на тех же множествах. Каждый n-местный предикат является следствием любого тождественно ложного n-местного предиката, определенного на тех же множествах.
Теорема 18.8. Пусть и
— два n-местных предиката, определенные на одних и тех же множествах, такие, что
есть следствие
. Тогда:
а) если тождественно истинный (выполнимый), то и
тождественно истинный (выполнимый);
б) если тождественно ложный (опровержимый), то и
тождественно ложный (опровержимый).
Доказательство теоремы 18.8:
а) Поскольку , поэтому
. Если теперь
тождественно истинный предикат, то
(где
— множества, на которых определены n-местные предикаты
и
).
Но . Поэтому
, а, значит, предикат
— тождественно истинный предикат. Если же
— выполнимый предикат, то
. Но
. Тогда
и
— выполнимый предикат.
б) Пусть — тождественно ложный предикат. Тогда
. Но
, поэтому
. Следовательно, предикат
— тождественно ложный. Наконец, пусть
— опровержимый предикат. Тогда
. Поскольку, кроме того,
и
, то
.
Следовательно, предикат — опровержимый.
Отыщите самостоятельно в настоящем и предыдущем пунктах данной лекции утверждения, обосновывающие остальные сформулированные теоремы.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Министерство
образования и науки Российской Федерации
Дальневосточный
федеральный университет
Школа
естественных наук
И. А. Курочкина
Логика предикатов
Учебное
пособие
Владивосток
Издательский
дом Дальневосточного федерального
университета
2013
УДК
510.6
ББК
22.12
К
93
Курочкина,
И. А.
К93
Логика
предикатов:
учебное пособие / И. А. Курочкина. –
Владивосток : Издательский дом
Дальневосточного федерального
университета, 2013. – 44 с.
Пособие
является третьей частью курса лекций
по математической логике и теории
алгоритмов. Включает изложение
теоретического материала по логике
предикатов, примеры решений задач,
упражнения и варианты контрольных
работ.
Для
студентов, обучающихся по образовательным
программам бакалавриата и магистратуры
«Прикладная информатика».
УДК
510.6
ББК
22.12
©
Курочкина И.А., 2013
§ 1. Основные понятия
Определение.
n‑местным
предикатом, определенном на множествах
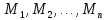
переменных
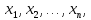
подстановке вместо этих переменных
любых конкретных элементов из множеств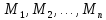
Для
n-местного
предиката будем использовать обозначение
Переменные

Элементы
множеств
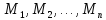
которые эти элементы пробегают –конкретные
предметы:
Итак,
предикат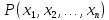
определенный на множествах
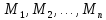
превращается в конкретное высказывание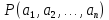
если вместо предметных переменных
подставить
в него конкретные предметы: элементы
из
множеств
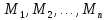
Это
высказывание может быть либо истинным,
либо ложным, то есть его логическое
значение равно 1 или 0.
Следовательно,
данный предикат определяет функцию
n-аргументов,
заданную на множествах
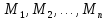
принимающий значение в двухэлементном
множестве {0,1}. Эту функцию и называютпредикатом.
§ 2. Классификация предикатов
Определение.
Предикат
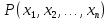
заданный на множествах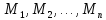
-
Тождественно-истинным,
если при любой подстановке вместо
переменных
любых
конкретных предметов
из
множествсоответственно он превращается в
истинное высказывание;
-
Тождественно-ложным,
если при любой подстановке вместо
переменных
,
любых конкретных предметовиз множеств
соответственно он превращается в ложное
высказывание; -
Выполнимым
(опровержимым),
если существует по крайней мере один
набор конкретных предметов
из множеств
соответственно,
при подстановке которого вместо
соответствующих предметных переменных
в предикат
он превращается в истинное (ложное)
высказывание.
Примеры:
-
Одноместный
предикат «Город x расположен на берегу
реки Волги».
Определен
на множестве названий городов, является
выполнимым.
-
Одноместный
предикат «»
определен на множестве R,
тождественно истинный. -
Двухместный
предикат «»
задан на множествеR,
тождественно ложный.
Утверждения:
-
Любой
тождественно-истинный предикат является
выполнимым, обратное неверно. -
Любой
тождественно-ложный является опровержимым,
обратное неверно. -
Любой
не тождественно-истинный предикат
будет опровержимым. -
Любой
не тождественно-ложный предикат будет
выполнимым.
§ 3. Множество истинности предиката
Определение.
Множеством
истинности
предиката
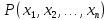
заданного на множествах
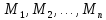
совокупность всех упорядоченныхn-систем
(n-арок)

в которых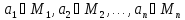
таких, что данный предикат обращается
в истинное высказывание
при подстановке
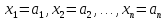
Это множество будем обозначатьP+.
Таким
образом, P+
= {<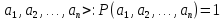
Множество
истинности n-местного предиката
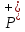
отношение между элементами множеств
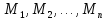
Пусть
P(x) –
одноместный предикат, M –
область определения предиката P(x).
множество истинности предиката
То
есть
является подмножеством множества M:
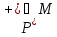
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Предикаты. Операции над предикатами
При изучении высказываний мы отмечали, что утверждение с переменными не является высказыванием. Можно, например, рассмотреть предложение %%P(x) : x^2 + 1 > 2%% с переменной %%x in mathbb R%%. Это предлождение не является высказыванием, так как нельзя сказать истинно оно или ложно. Однако, если заменить переменную %%x%% на какое-либо значение, например, %%x = 1%%, получаем высказывание %%2 > 2%%, которое является ложным. Заменив переменную %%x%% на значение %%x = 2%%, получим истинное высказывание %%5 > 2%%. Итак есть выражение %%P(x)%% не являющиееся высказыванием, но превращающееся в него при замене переменной %%x%% на ее произвольное значение из соответствующего множества.
Определение
Одноместным предикатом, определенным на множестве %%D%%, называется предложение с переменной, которое превращается в высказывание при замене этой переменной на ее значение из множества %%D%%. Одноместный предикат будем называть унарным или предикатом от одной переменной.
Примеры
Следующие предложения являются одноместными предикатами:
- %%P(x): x^ 2 + 1 > 2%%, где %%D%% — множество действительных чисел.
- %%Q(x):%% Длина отрезка равна %%1%%, где %%D%% — множество всех отрезков прямой.
Следующие предложения не являются одноместными предикатами:
- %%1 > 2%%.
- Прямая %%x%% параллельна прямой %%y%%.
%%n%%-местный предикат
%%n%%-местым предикатом с областью определения %%D = D_1 times D_2 times ldots times D_n%% называется предикат %%P(x_1, x_2, ldots, x_n)%% от %%n%% переменных, который превращается в высказывание при замене переменных %%x_1, x_2, ldots, x_n%% на их значения из множеств %%D_1, D_2, ldots, D_n%% соответственно.
Тогда предложение прямая %%x%% параллельна прямой %%y%% является двуместным предикатом %%P(x, y)%%, где %%X, Y%% — множество всех прямых.
Область определения предиката
Рассмотрим %%n%%-местный предикат %%P(x_1, x_2, ldots, x_n)%%. В этом случае переменные берутся из множеств %%D_1, D_2, ldots, D_n%% соответственно. Можно рассмотреть множество %%D = D_1 times D_2 times ldots times D_n%% — декартово произведение множеств %%D_1, D_2, ldots, D_n%%, элементами которого являются всевозможные упорядоченные %%n%%-ки %%(d_1, d_2, ldots, d_n)%% элементов исходных множеств.
Множество %%D%% называется областью определения предиката.
Область истинности
Областью истинности предиката %%P(x_1, x_2, ldots, x_n)%% называется множество всех %%n%%-ок %%(d_1, d_2, ldots, d_n) in D%% таких, что при замене %%x_1%% на %%d_1%%, %%x_2%% на %%d_2%%, …, %%x_n%% на %%d_n%% получается истинное высказывание.
Пример
На множестве %%D = { 1, 2, 3, 4, 5, 6, 7, 8, 9}%% рассмотрим одноместный предикат %%P(x): x%% — простое число. Найти область истинности предиката %%P(x)%%.
Обозначим область истинности буквой %%A%%. Тогда %%A%% состоит из таких элементов, при которых выполняется предикат %%P(x)%%. Поэтому %%A = {2, 3, 5, 7}%%.
Операции над предикатами
Аналогично операциям для высказываний вводятся операции для предикатов.
Пусть %%P(x)%% и %%Q(x)%% — одноместные предикаты, определенные на множестве %%D%%.
Отрицанием предиката %%P(x)%% называется новый предикат, обозначаемый %%overline{P(x)}%% и являющийся ложным для тех и только тех %%x%%, для которых предикат %%P(x)%% истинный.
Конъюнкцией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) land Q(x)%% и являющийся истинным для тех и только тех %%x%%, для которых предикаты %%P(x)%% и %%Q(x)%% истинны.
Дизъюнкцией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) lor Q(x)%% и являющийся ложным для тех и только тех %%x%%, для которых предикаты %%P(x)%% и %%Q(x)%% ложны.
Импликацией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) rightarrow Q(x)%% и являющийся ложным для тех и только тех %%x%%, для которых предикаты %%P(x)%% истинный, а %%Q(x)%% ложный.
Эквиваленцией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) leftrightarrow Q(x)%% и являющийся истинным для тех и только тех %%x%%, для которых предикаты %%P(x)%% и %%Q(x)%% имеют одинаковые значения.
Применяя операции над предикатами, мы получаем составные предикаты, которые будем называть формулами алгебры предикатов.
Предикаты %%P(x)%% и %%Q(x)%% эквивалентные , если для любого значения переменной %%x%% их значения истинности совпадают. Обозначают $$P(x) equiv Q(x).$$
Законы алгебры предикатов
Для предикатов справедливы все законы, аналогичные законам алгебры логики высказываний1.
В случае тождественно истинных и тождественно ложных предикатов имеем следующие определения.
Предикат %%P(x_1, x_2, ldots, x_n)%% называется тождественно истинным если при любой замене переменных %%x_1, x_2, ldots, x_n%% на их значения предикат превращается в истинное высказывание.
Предикат %%P(x_1, x_2, ldots, x_n)%% называется тождественно ложным если при любой замене переменных %%x_1, x_2, ldots, x_n%% на их значения предикат превращается в ложное высказывание.
Высказывание является частным случаем предиката, когда в предикате нет переменных. То есть высказывание является предикатом %%0%% порядка (от %%0%% переменных).
1. Законы алгебры логики высказываний.
Татьяна Шкляр
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Понятие предиката
Определение 1
Предикат – утверждение, которое содержит переменные, принимающие значение $1$ или $0$ (истинно или ложно) в зависимости от значений переменных.
Пример 1
Например, выражение $x=x^5$ является предикатом, т.к. оно является истинным при $x=0$ или $x=1$ и ложным при всех остальных значениях $x$.
Определение 2
Множество, на котором предикат принимает только истинные значения, называется множеством истинности предиката $I_p$.
Замечание 1
Предикатом в программировании является функция, которая принимает один или более аргументов и возвращает значения булева типа.
Предикат называется тождественно-истинным, если на любом наборе аргументов он принимает истинное значение:
$P (x_1, dots, x_n)=1$
Предикат называется тождественно-ложным, если на любом наборе аргументов он принимает ложное значение:
$P (x_1, dots, x_0)=0$
Предикат называется выполнимым, если хотя бы на одном наборе аргументов он принимает истинное значение.
Т.к. предикаты могут принимать только два значения (истинно/ложно или $0/1$), то к ним можно применять все операции алгебры логики: отрицание, конъюнкция, дизъюнкция и т.д.
Примеры предикатов
Пусть предикат $R(x, y)$: $«x = y»$ обозначает отношение равенства, где $x$ и $y$ принадлежат множеству целых чисел. В этом случае предикат R будет принимать истинное значение для всех равных $x$ и $y$.
Другой пример предиката — РАБОТАЕТ($x, y, z$) для отношения «$x$ работает в городе y в компании $z$».
Еще один пример предиката — НРАВИТСЯ($x, y$) для «x нравится y» для $x$ и $y$, которые принадлежат $M$ — множеству всех людей.
Таким образом, предикатом является все то, что утверждается или отрицается о субъекте суждения.
«Предикаты и кванторы» 👇
Операции над предикатами
Рассмотрим применение операций алгебры логики к предикатам.
Логические операции:
Определение 3
Конъюнкция двух предикатов $A(x)$ и $B(x)$ — предикат , который принимает истинное значение при тех и только тех значениях $x$ из $T$, при которых каждый из предикатов принимает истинное значение, а ложное значение — во всех остальных случаях. Множество истинности $T$ предиката — пересечение множеств истинности предикатов $A(x)$ и $B(x)$. Например: предикат $A(x)$: «$x$ — чётное число», предикат $B(x)$: «$x$ делится на $5$». Таким образом, предикатом будет выражение «$x$ — чётное число и делится на $5$» или «$x$ делится на $10$».
Определение 4
Дизъюнкция двух предикатов $A(x)$ и $B(x)$ — предикат , который принимает ложное значение при тех и только тех значениях $x$ из $T$, при которых каждый из предикатов принимает ложное значение и принимает истинное значение во всех остальных случаях. Множество истинности предиката — объединение областей истинности предикатов $A(x)$ и $B(x)$.
Определение 5
Отрицание предиката $A(x)$ — предикат, который принимает истинное значение при всех значениях $x$ из $T$, при которых предикат $A(x)$ принимает ложное значение и наоборот. Множество истинности предиката $A(x)$ — дополнение $T’$ к множеству $T$ в множестве $x$.
Определение 6
Импликация предикатов $A(x)$ и $B(x)$ — предикат , который является ложным при тех и только тех значениях $x$ из $T$, при которых $A(x)$ — истинно, а $B(x)$ — ложно, и принимает истинное значение во всех остальных случаях. Читается: «Если $A(x)$, то $B(x)$».
Пример 2
Пусть $A(x)$: «Натуральное число $x$ делится на $3$»;
$B(x)$: «Натуральное число $x$ делится на $4$».
Составим предикат: «Если натуральное число $x$ делится на $3$, то оно делится и на $4$».
Множество истинности предиката — объединение множества истинности предиката $B(x)$ и дополнения к множеству истинности предиката $A(x)$.
Над предикатами помимо логических операций можно выполнять квантовые операции: применение квантора всеобщности, квантора существования и т.д.
Кванторы
Определение 7
Кванторы — логические операторы, применение которых к предикатам превращает их в ложные или истинные высказывания.
Определение 8
Квантор — логические операции, которые ограничивают область истинности предиката и создают высказывание.
Чаще всего используют кванторы:
-
квантор всеобщности (обозначается символом $forall x$) — выражение «для всех $x$» («для любого $x$»);
-
квантор существования (обозначается символом $exists x$) — выражение «существует $x$ такое, что… »;
-
квантор единственности и существования (обозначается $exists !x$) — выражение «существует точно одно такое $x$, что… ».
В математической логике существует понятие связывание или квантификация, которые обозначают приписывание квантора к формуле.
Примеры применения кванторов
Пусть — предикат «$x$ кратно $7$».
С помощью квантора всеобщности можно записать следующие ложные высказывания:
-
любое натуральное число делится на $7$;
-
каждое натуральное число делится на $7$;
-
все натуральные числа делятся на $7$;
который будет иметь вид:
Рисунок 1.
Для записи истинных высказываний используем квантор существования:
-
существуют натуральные числа, которые делятся на $7$;
-
найдётся натуральное число, которое делится на $7$;
-
хотя бы одно натуральное число делится на $7$.
Запись будет иметь вид:
Рисунок 2.
Пусть на множестве $x$ простых чисел задан предикат : «Простое число является нечетным». Поставив перед предикатом слово «любое», получим ложное высказывание: «Любое простое число является нечетным» (например, $2$ является простым четным числом).
Поставим перед предикатом слово «существует» и получим истинное высказывание: «Существует простое число , которое является нечетным» (например, $x=3$ ).
Таким образом, предикат можно превратить в высказывание, если поставить перед предикатом квантор.
Операции над кванторами
Для построения отрицания высказываний, которые содержат кванторы, применяется правило отрицания кванторов:
Рисунок 3.
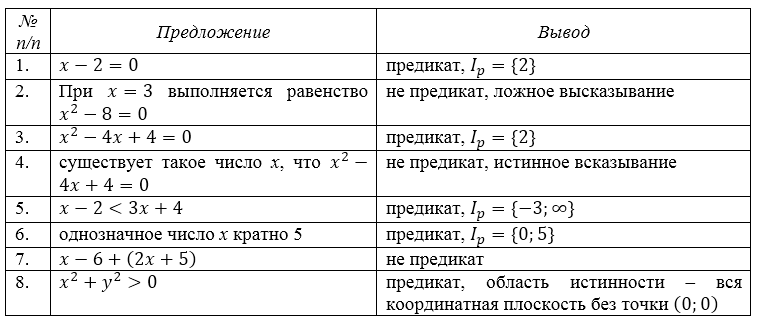
Рассмотрим предложения и выделим среди них предикаты, указав область истинности каждого из них:
Рисунок 4.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Определение. Предикатом называется повествовательное предложение, содержащее предметные переменные, определённые на соответствующих мно- жествах; при замене переменных конкретными значениями (элементами) этих множеств предложение обращается в высказывание, т. е. принимает значение «истинно» или «ложно».
Определение. Предикатом называется функция P : M n → B , где B = { 0,1 } , M – любое множество, 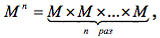
Множество M называется предметной областью предиката P ,
x1 , x2 ,…, xn – предметные переменные,
P – предикатный символ,
n – местность предиката,
декартово произведение M × M × … × M область определения предиката P .
Обозначение: P (x1 , x2 ,…, xn– n – местный предикат, заданный на множестве M .
Определение. Областью истинности предиката P называется подмножество Ip ⊆ Mn его предметной области, на элементах которого значения предиката равны 1.
Область истинности предиката, выраженного предикатной формулой, определяется областями истинности составляющих и применяемыми в формуле операциями: IPvQ = IP ∪ IQ, IP ∧ Q = IP ∩ IQ , IP→Q = IP ∪ IQ, I P = IP .
Задача 3.1. Найти область истинности предиката
P ( X, Y ) = (( X + Y ) – нечётно ) ∨ (( X – Y ) делятся на 3) , где X = {1;3;6;7}, Y = {2;4;5}.
Решение.
Составим таблицы истинности для предикатов P1 ( X, Y ) = (( X + Y) – нечётно), P2( X, Y ) = (( X – Y ) – делятся на 3) , P = P1 ∨ P2.
IP = I P1∨P2 = IP1 ∪ IP2 = {(1,2), (1,4), (3,2), (3,4), (6,5), (7,2), (7,4)} ∪ {(1,4), (7,4)} = {(1,2), (1,4), (3,2), (3,4), (6,4), (7,2), (7,4)}.
Ответ: IP = {(1,2), (1,4), (3,2), (3,4), (6,4), (7,2), (7,4)}.
Задача 3.2. Найти область истинности предиката
P ( X ) = (( число 3 не делитель x ) → ( x ≤ 6 ))
на множестве однозначных натуральных чисел.
Решение.
Определим области истинности предикатов P1 = {число 3 не не делитель x},
P2 = {x ≤ 6}, P = P1→ P2 .
IP1 = {1,2,4,5,7,8}, IP2 = {1,2,3,4,5,6}, IP = IP1→P2 = IP1 = {1,2,3,4,5,6,9}.
Ответ: I P = {1,2,3,4,5,6,9}.
Задачи для самостоятельного решения
Найти область истинности предиката
- P ( X, Y ) = ((( X – Y ) – нечетно ) ∧ ( min ( X, Y) – четно )), где X = {2;5;6;8};
- P ( X ,Y ) = (( X + Y )) – делится на 3) → (( X + Y ) > 5), где X = {2;5;6;8}, Y = {3;6;9};
- P ( X, Y ) = ((( X – Y ) – нечётно ) ∧ ( |Y-X| ≤ 1 )), где X = {5;8;9}, Y = {4;7;8;10};
- P ( X, Y ) = (( X – Y ) – чётно ) ∨ (( X + Y ) – делится на 3), где X = {5;8;9}, Y = {4;7;8;10};
- P ( X ) = (( число 3 делитель x ) ∨ ( x ≤ 6 )), заданного на множестве однозначных натуральных чисел;
- P ( X ) = ((( число 3 делитель x ) ∧ ( x > 6 )), заданного на множестве однозначных натуральных чисел;
- P ( X ) = (( x ≥ 3 ) ∧ ( x ≤ 10 )), заданного на множестве всех действительных чисел;
- P ( X ) = (( x2 ≤ 4 ) ∧ ( x -1 ≥ 1 )), заданного на множестве всех действительных чисел;
- P ( X ) = (( x ≤ 0 ) ∧ ( x2 – 2x ≤ 0 )), заданного на множестве всех действительных чисел;
- P ( X ) = (( x3 – 6x2 +11x – 6 = 0 ) ∧ ( x2 – 4x + 3 = 0 )),заданного на множестве всех действительных чисел.
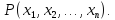
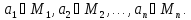
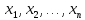
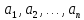
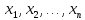
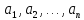 из
из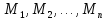 соответственно он превращается в
соответственно он превращается в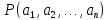 ;
;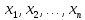 ,
,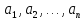 из множеств
из множеств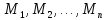 соответственно он превращается в ложное
соответственно он превращается в ложное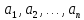 из множеств
из множеств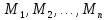
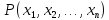 он превращается в истинное (ложное)
он превращается в истинное (ложное)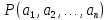 .
.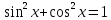 »
»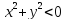 »
»